Логические задачи, задачи на логику. С ответами.

	Размер	Толщина	Фон
			White Cyan LGreen GYellw DpSkBl Coral DPink1 DPink2 SkBlue Orange OlivD1 OlivD2 LBlue PGreen Yellow Gold Blue Green Wheat Chocol Salmon Red HPink DPink Pink VioRed Magent Violet Plum Purple OrRed Bisque Bisqu2 LemC1 LemC2 Corns2 Honey2 Turqu1 Turqu2 SGrn1 SGrn2 Orchi1 Orang1 Gray golrod

«> Страница №4.

Начало   << Назад   Вперед >>   Конец
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] 

---

Как вы думаете, если полста разделить на половину, то сколько в итоге получится?

Ответ

Получится не 25, как многие могут подумать, а 100. Так как если 50 разделить на 1/2, то это равносильно умножению на 2.

---

Если три десятка умножить на четыре десятка, то сколько получится?

Ответ

Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200.

---

Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами).

Ответ

Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата. Поэтому их если и делают, то только прикрепив к люку шарнирами. У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка.

---

Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?

Ответ

Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1.

---

Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?

Ответ

Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.

---

Трехлитровый сосуд полностью заполнен тремя литрами воды. Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды. При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.

Ответ

Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев. Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).

---

Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?

Ответ

Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.

---

Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?

Ответ

Этим свойством обладает только шар.

---

Попробуйте сообразить, какой из выводов, указанных ниже, верный :

А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.

Ответ

Правильный вариант Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные.

---

Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.

Ответ

Книга стоит 2 доллара. Решение : полкниги стоит доллар, значит вся книга стоит 2 доллара.

---

Поделитесь с друзьями:

Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?

Ответ

Сейчас восемь часов.

---

Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок. Но в Японии на такие кроссовки накладываются очень большие пошлины. Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? (Никакой коррупционной и преступной составляющей здесь нет).

Ответ

Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями. То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака. В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе. В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.

---

5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?

Ответ

15 рыбаков съедят 15 карпов тоже за 5 дней.

Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов.

---

В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г. Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?

Ответ

Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке. Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2,25кг. В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок. И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.

---

Два колхозника решили узнать, у кого больше овец. Первый из них сказал : «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя».

Второй ему говорит : «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было).

Ответ

У первого колхозника 7 овец, у второго только 5. Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше. Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5.

---

В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?

Ответ

Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек. Если из первой половины добавить школьника в другую, то получится разница в 2 человека. Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения.

---

Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?

Ответ

Получится равенство : 888 + 88 + 8 + 8 + 8 = 1000.

---

На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые. Как определить эту монету за 2 взвешивания на чашечных весах?

Ответ

Варианты взвешиваний : 1) ложем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью. Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных. 2) ложем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета.

---

Как так могло оказаться, что половина числа 12 стало равно 7 ?

Ответ

Нужно написать число 12 римскими цифрами : IIX , далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7.

---

На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?

Ответ

Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.

---

Страница №4.

Начало   << Назад   Вперед >>   Конец
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] 

Поделитесь с друзьями:

Математические загадки на логику с ответами.

Самые сложные задачи в мире

Содержание

1. Польза занятий логикой и математикой
2. Уроки-игры
3. Математические задачи на логику для дошкольников
4. Математические задачи на логику: 1-2 класс
5. Математические задачи на логику: 3-4 класс
6. Занимательные математические задачи для учащихся 5-х классов с ответами
7. Математические головоломки
8. Визуальная тренировка для мозга
9. Загадки
10. Логические задачки
11. ПРАВИЛЬНЫЕ ОТВЕТЫ:
12. Самая сложная задача в мире

Польза занятий логикой и математикой

Элементарные математические представления помогают сформировать в детском саду. Базовые математические способности развивают в школе.

А чтобы ребёнок научился рассуждать логически, мыслить нестандартно — обычных арифметических и геометрических задач недостаточно.

Уже в дошкольном возрасте желательно выработать привычку ежедневно выполнять задания и упражнения на развитие логического мышления.

Благодаря регулярным тренировкам:

• ребёнок учится рассуждать, анализировать и делать правильные выводы;
• развивает сообразительность, память, внимание и интеллект;
• успехи повышают самооценку, интерес к обучению в школе, вдохновляют на победы в математических олимпиадах и конкурсах.

Уроки-игры

В школьных учебниках занимательного материала недостаточно. Однако опытный педагог умеет сделать привычные задания по математике интересными. В 1 классе это особенно важно, так как дети лучше откликаются на игровую форму обучения. Им скучно решать примеры, но все меняется, если учитель принесет на урок мяч и будет спрашивать верный ответ у поймавшего его.

Повысить активность детей позволяет игровой сюжет, присутствующий на занятии. Вариантов может быть множество. Например, за каждое выполненное задание ребятишки получают кусочек паззла, и в конце урока из них собирается картинка. Или класс отправляется спасать героя, попавшего в беду. На пути они встречают различных злодеев и побеждают их, решая задачки и примеры. Очень нравятся детям соревнования, когда класс делится на команды и каждая набирает жетоны за работу. Победителей можно наградить бумажными медалями. Таким образом, не всегда нужно искать занимательный материал. Иногда достаточно изменить форму его подачи.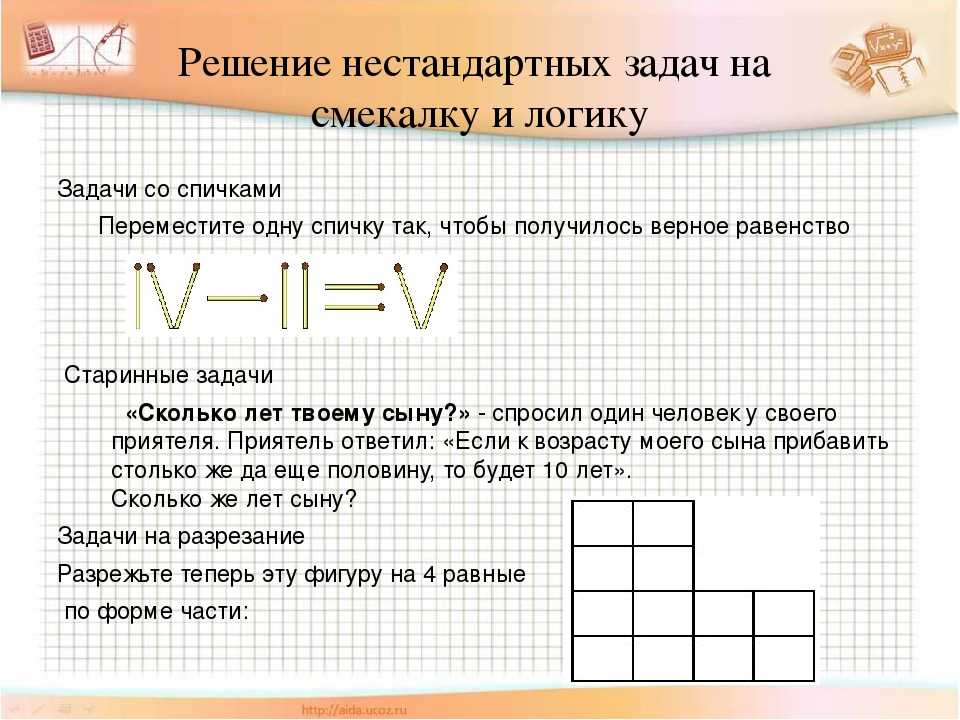

Математические задачи на логику для дошкольников

Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей. Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет.

1. На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
2. Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.
3. Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.
4. Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
5. Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
6. На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.
7. Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
8. У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.
9. Какие камни есть в море? Ответ: мокрые.Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.
10. Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
11. В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
12. Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
13. Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.
14. Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
15. Что все дети на земле делают одновременно? Ответ: взрослеют.

Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.

Математические задачи на логику: 1-2 класс

Но вот дети пошли в школу, буквально за первые месяцы учебы они начинают хорошо считать, ориентироваться в пространстве и времени. Задачки для дошкольников уже кажутся им простыми и неинтересными. Поэтому для таких деток мы приготовили несколько вариантов упражнений тренировки логики и смекалки, ориентируясь на их новые способности и возможности.

1. Первоклассника попросили назвать самое большое число. Что он ответил?
   Ответ: 31. Первоклассники каждый день записывают число месяца в тетрадь, самое большое число в месяце – 31.
2. На доске написаны два числа 4 и 5. Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая.
3. По узкой дороге может проехать только одна машина. С одной стороны дороги находится гора. Одна машина едет с горы, другая – под гору. Как им разминуться? Ответ: обе машины едут в одном направлении и разминаться им не придется.
4. Сколько раз из числа 10 можно отнять число 2? Ответ: один, т.к. уже после первого вычитания двойки останется число 8, а не 10.
5. На столе стоят 6 стаканов: в первые три налили воду, вторые три – пустые. Нужно расставить стаканы так, чтобы чередовались пустые и полные стаканы, но при этом можно взять в руки только один стакан. Как поступить, чтобы выполнить условие? Ответ: Взять второй стакан и перелить из него воду в пятый стакан. Второй стакан поставить на прежнее место.
6. За 10 часов 10 человек могут выкопать траншею длиной в 10 метров. Сколько нужно человек, чтобы они выкопали траншею диной в 100 метров за 100 часов? Ответ: 10 человек. На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров.
7. Школьники участвуют в соревнованиях по бегу. Ваня занимает третью позицию, Антон занимает вторую позицию. Саша обгоняет Антона. Какую позицию занимает Саша? Ответ: вторую, т.к. впереди Антона тоже кто-то бежит и этот кто-то пока первый.
8. Учитель положил на пол карандаш и попросил учеников перешагнуть через него, но никто не смог этого сделать. Почему? Ответ: карандаш лежит у стены и шагать детям некуда.
9. Таня и Алиса пошли в магазин и нашли 2 рубля. Сколько бы денег они нашли, если бы с ними пошла еще и Марина? Ответ: 2 рубля, т. к. размер находки никак не зависит от количества ее нашедших.
10. Из пункта А в пункт Б вышла кошка, а из пункта Б в пункт А вышла мышка. Когда они встретятся, кто из них будет ближе к пункту А, а кто к пункту Б? Ответ: они обе будут на одинаковом расстоянии от пункта А, и на одинаковом расстоянии от пункта Б.
11. На столе стояли 3 чашки с чаем. Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись.
12. Марина шла из дома в школу и встретила трех мужиков. У каждого за спиной был мешок. У первого мужика в мешке был один кот, у второго в мешке был один кот и один пес. У третьего в мешке было 2 пса. Сколько всего котов направлялось в школу? Ответ: один, сама Марина. Мужики с мешками шли в обратную от школы сторону.
13. В классе стоял стол с четырехугольной крышкой. Ученики отпилили один угол, что стало со столом, сколько углов осталось на крышке? Ответ: 5. Если отпилить один угол, то получим на его месте 2 новых, поэтому всего 5 углов.Примечание: на самом деле количество углов может зависеть и от того, как размышляет ребенок. Если он «пилит» стол по углам диагонали, т.е. распиливает его пополам, то вполне возможно, что у стола будет 3 угла. Если же один распил приходится на угол, а второй на сторону крышки, то может остаться и 4 угла. Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол.
14. На тарелке лежат 3 банана. Их нужно разделить между тремя девочками, чтобы на тарелке остался один банан. Ответ: одной девочке нужно отдать банан вместе с тарелкой.
15. Какое слово зашифровано: ООО? Ответ: ТРИО, т.е. ТРИ О.

Родители тоже могут составлять свои задачи для детей, ориентируясь на предложенные варианты. Чем чаще ребенок будет заниматься упражнениями на логику, тем быстрее будет работать его мозг, тем выше будет успеваемость в школе.

Математические задачи на логику: 3-4 класс

Дальнейшее обучение в школе имеет свои особенности: дети научились складывать двузначные числа, совершать с ними различные математические операции, в том числе умножение, деление. Логические математические задачи для школьников 3-4 класса должны охватывать уже полученные знания и совершенствовать их качество.

1. В кошельке лежит 15 копеек двумя монетами. Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком.
2. Шла Маша в Волгоград, а навстречу ей 10 ребят. У каждого в руках по лукошку, в каждом лукошке по кошке, а у каждой кошки по котенку. Сколько всего ребят шло в Волгоград? Ответ: одна Маша. Все остальные, сколько бы их не перечисляли, шли навстречу девочке, а значит в противоположную сторону от Волгограда.
3. Дедушка пилит бревна. Распил бревна пополам он делаем ан одну минуту. Сколько ему понадобится времени, чтобы распилить бревно на 10 частей? Ответ: 9 минут, т.к.чтобы распилить бревно на 10 частей, нужно сделать 9 распилов.
4. Мальчик пришел в амбар. В каждом углу амбара стояло по 3 мешка. На каждом мешке сидело по кошке, у каждой кошки было по котенку. Сколько всего ног было в амбаре? Ответ: две, только мальчика. Примечание: Как бы долго дети не перемножали между собой числа-«ноги» кошек и котят, стоит помнить, что у кошек – лапы, а ноги – только у мальчика.
5. Родители купили своим двум дочкам Маше и Лизе по коробке конфет. В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется.
6. Из ГОРОНО в школу пришли проверяющие. Они выбрали класс для проверки, но не все дети были готовы отвечать урок. Тем не менее, на каждый вопрос учителя весь класс поднимал руку, и тот, кого учитель вызывал к доске, отвечал блестяще. Как получилось, что учитель угадывал, кого вызвать отвечать? Ответ: решением этой задачи есть небольшая хитрость. Перед уроком школьники и учитель договорились, что те, кто наверняка знают ответ на поставленный вопрос, будут поднимать правую руку. А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался.
7. Что у коровы находится спереди, а у быка сзади? Ответ: буква «К». Корова, быК.
8. Когда маме исполнилось 31 год, дочери было 8. Сейчас мама старше дочери ровно в 2 раза. Сколько их обеим лет? Ответ: дочке 23, маме 46. Когда дочь родилась, маме было 31-8 = 23 года. Чтобы быть старше дочки в два раза, маме должно быть 23*2 = 46 лет. За это время дочь доросла до 23 лет.
9. Две одноклассницы Наташа и Лена живут в одном подъезде: Лена на втором этаже, а Наташа на четвертом. Наташа поднимается по ступенькам на четвертый этаж и проходит 60 ступенек. Сколько ступенек проходит Лена, которая поднимается на второй этаж? Ответ: 20. Чтобы подняться с первого этажа на четвертый, нужно пройти три пролета. 60_3=20 ступенек в одном пролете. А Лена поднимается с первого на второй этаж и проходит при этом только один пролет, все те же 20 ступенек.
10. Может ли страус называть себя птицей? Ответ: нет, не может. Страусы не умеют разговаривать.
11. Какая физическая величина не имеет ни высоты, ни глубины, ни ширины, ни длины, но ее можно измерить? Ответ: время, температура.
12. Задание на логику из серии «Юный Шерлок». На вызов о самоубийстве были вызваны представители уголовного розыска. В кабинете жертвы они обнаружили диктофон и включили его. На диктофоне была записана следующая фраза: «В моей смерти прошу никого не винить, жизнь не имеет смысла…» далее раздался выстрел. Как следователи поняли, что убийство сфабриковано? Ответ: убитый не мог перемотать запись на начало, это сделал кто-то другой.
13. Что не может поместиться даже в самую большую кастрюлю? Ответ: ее крышка.
14. В кастрюле налита вода до самого верха. Как отмерять жидкость, не используя никаких мерительных приспособлений, чтобы в кастрюле осталась только половина жидкости. Ответ: нужно наклонить кастрюлю и выливать воду до тех пор, пока не покажется с боковой части дно. Это и будет половина кастрюли.
15. Когда цифра «2» означает «10»? Ответ: на циферблате цифра «2» соответствует «10 минутам».

С каждым годом задания на развитие логики и смекалки должны становится все сложнее, иметь подвохи, хитрости, чтобы ребенок учился размышлять, уделять внимание деталям. А регулярные и систематические занятия обязательно принесут свои плоды.

Занимательные математические задачи для учащихся 5-х классов с ответами

Из гнезда вылетели три ласточки. Какова вероятность того, что через 15 секунд они будут находиться в одной плоскости? (Ответ: 100%, так как три точки всегда образуют одну плоскость)

На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты? (Ответ: 2 рубля и 1 рубль. Одна то не 1 рубль, а вот другая — 1 рубль)

С какой скоростью должна бежать собака, чтобы не слышать звона сковородки, привязанной к ее хвосту? (Ответ: Если выдумаете, что ей нужно бежать со сверхзвуковой скоростью, то вы ошибаетесь — собаке достаточно стоять на месте)

Один оборот вокруг Земли спутник делает за 1 ч 40 мин, а другой — за 100 минут. Как это может быть? (Ответ: 1 ч 40 мин = 100 мин)

Крыша одного дома несимметрична: один скат ее составляет с горизонталью угол 60 градусов, другой — угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упадет яйцо — в сторону более пологого или крутого ската? (Ответ: Петухи не кладут яйца)

В 12-этажном доме есть лифт. На первом этаже живут всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других? (Ответ: Независимо от распределения жильцов по этажам, кнопка «1»)

В двух кошельках лежат две монеты, причем в одном кошельке монет вдвое больше, чем в другом. Как такое может быть? (Ответ: Один кошелек лежит внутри другого)

Сын отца профессора разговаривает с отцом сына профессора, причем сам профессор в разговоре не участвует. Может ли такое быть? (Ответ: Да, может, если профессор — женщина)

Два сына и два отца съели 3 яйца. Сколько яиц съел каждый? (По одному яйцу каждый)

На складе было 5 цистерн с горючим, по 6 т в каждой. Из двух цистерн горючее выдали. Сколько цистерн осталось? (5)

Вообрази, что ты капитан футбольной команды. В районе 8 футбольных команд по 11 человек в каждой. Игроки вашей команды на 2 года моложе своего капитана, а игроки других — только на 1 год. Сколько лет капитану вашей команды? (Столько, сколько лет отвечающему)

Пара лошадей пробежала 20 км. Сколько километров пробежала каждая лошадь? (20 км)

Когда сороке исполнится 4 года, что с ней произойдет? (Будет жить пятый год)

Если в 11 часов ночи идет дождь, то возможно ли через 48 часов солнечная погода? (Нет, так как будет ночь)

Чтобы сварить 1 кг. мяса требуется один час. Сколько времени потребуется для варки ½ кг мяса? (1 час)

У Марины было целое яблоко, две половинки и 4 четвертинки. Сколько было у нее яблок? (3)

На грядке сидели 6 воробьев, к ним прилетели еще 5. Кот подкрался и схватил одного воробья. Сколько воробьев осталось на грядке? (Один, которого схватил кот. Остальные улетели)

Мальчик написал на бумажке число 86 и говорит своему товарищу: «Не производя никакой записи, увеличь это число на 12 и покажи мне ответ». Недолго думая, товарищ показал ответ. А вы это сделать сумеете? (Перевернуть бумажку «вверх ногами»)

В клетке находились 4 кролика. Четверо ребят купили по одному из этих кроликов и один кролик остался в клетке. Как это могло получиться? (Одного кролика купили вместе с клеткой)

Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток? (Три утки, одна за другой)

У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть? (Этот человек родился 29 февраля, т. е. день рождения у него бывает один раз в четыре года)

Что это такое: две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три, бросили их в четыре, чтобы четыре оставили одну? (Повар сидел на стуле, имеющем три ножки, пришла собака и утащила куриную ногу. Повар бросил стул в собаку, чтобы она оставила куриную ногу)

Часы бьют каждый час и отбивают столько ударов, сколько показывает часовая стрелка. Сколько ударов отобьют часы в течение 12 часов? (Количество ударов равняется 1+2+3+…+12…= 78. Сумма членов, равноотстоящих от концов (1+12,2+11,3+10,…) равны между собой — 13. Таких пар равноотстоящих от концов чисел имеется 6. Значит, 1+2+3+…+12=6 13=78)

Летели скворцы и встретились им деревья. Когда сели они по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось незанятым. Сколько было скворцов и сколько деревьев? (Предположим, что после того как скворцы сели на деревья по два, с каждого дерева взлетело по одному скворцу. Один из взлетевших скворцов может сесть на незанятое дерево, тогда на каждом дереве будет сидеть по одному скворцу. По условию, если на каждое дерево сядет по одному скворцу, то один скворец останется в воздухе. Значит, взлетело 2 скворца. Тогда общее число скворцов равно 4, а число деревьев З).

Математические головоломки

Вопрос 1. Какое число зашифровано?

Вопрос 2. Как поместить шары с цифрами, чтобы получить число 30?

Вопрос 3. Какая цифра получится в конце?

Замените знак вопроса числом, соответствующим приведенным ниже уравнениям. Найдите закономерность.

Визуальная тренировка для мозга

Вопрос 4. Разделите изображение на четыре части, которые сочетали бы всех видов насекомых:

Вопрос 5. Какой вид сверху на башню: А, В, С или D?

Вопрос 6. Каким образом представляются кубики для человека, который стоит в оранжевой точке и смотрит на фигуру в указанном направлении?

Вопрос 7. Быстро решите, какой фрукт необходимо добавить?

Вопрос 8. Смотрите внимательно и угадайте, кто вор?

Загадки

Вопрос 9. Примите жизненно важное решение. В комнате без света есть три двери: за первой спряталась ядовитая змея, за второй – лев, который не ел пару дней, в третьей вас ждет экзекуция на электрическом столе. Какую дверь безопаснее всего открыть?

Вопрос 10. Разминка на логику и память. В названии какого города спрятались имена ста девушек и одного парня?

Вопрос 11. Логическая загадка: у отца Фрэнка 5 сыновей. Имена его четырех сыновей — Фефе, Фифи, Фофо, Фуфу. Соответственно, как зовут его пятого сына?

Вопрос 12. Знаменитая загадка: по пути в Сент-Айвз я увидел мужчину с 7 женами. У каждой жены было 7 мешков. В каждом мешке было по 7 кошек. У каждого кота было 7 котят. Котенок, кошки, мешки, жены – сколько их направляются в Сент-Айвс?

Логические задачки

Вопрос 13. Как отмерить 4 литра воды, если есть 5-литровая и 3-х литровая емкости?

Вопрос 14. Как сделать цифру «4», но не сломать ни одну палочку.

Вопрос 15. В каком чайнике больше чая?

ПРАВИЛЬНЫЕ ОТВЕТЫ:

1-й Правильный ответ: 9.

2-й Правильный ответ:
Этот вопрос не может быть решен математически. Потому что сумма трех нечетных чисел не может быть четное число.

Но здесь важно ваше внимание. Если вы поместите шары с цифрами 11 и 13, то получите 24. Затем, если вы поместите шар с цифрой 9, но перевернете, то получите 24 + 6 = 30.

3-й Правильный ответ:
Если мы знаем, что каждое полученное число является степенью числа 4, получаем:
41 = 4
42 = 16
43 = 64
44 = 256

4-й Правильный ответ:

5-й Правильный ответ:

Если вы посмотрите на башню сверху, верхний слой будет оранжевым. Таким образом, ответ определенно не C.

Второй фиолетовый слой не будет виден сверху, потому что он такого же размера, как и верхний слой.

И третий слой также не будет виден, потому что он меньше, чем два верхних слоя.

Четвертый слой будет следующим, который будет виден сверху вокруг фиолетового слоя.

Последний будет самым крупным, и он оранжевый. В соответствии с этим, ответ будет A.

6-й Правильный ответ:

Пойдем шаг за шагом. Очевидно, что внизу 4 блока.

Над крайним правым блоком есть еще один. Таким образом, ответ определенно не C.

Самый высокий блок состоит из трех блоков в высоту.

Итак, ответ D.

7-й Правильный ответ:

Банан, Груша, Перец

8-й Правильные ответы:

9-й Правильные ответы:

С электрическим стулом. Палач скорее всего пойдет проверить, почему света нет, а вы сможете убежать.

10-й Правильный ответ:

Севастополь – Сева и 100 Поль.

11-й Правильный ответ:

Если у отца Фрэнка 5 сыновей, а имена 4 сыновей такие же, как указано выше, то Фрэнк уже 5-й сын.

12-й Правильный ответ:

Только я.

13-й Правильный ответ:

Налейте полную емкость в 5 литр;

Перелейте из нее в 3-х литровую емкость – получаем остаток 2 литра;

Выливаем 3 литра – остается только 2 литра воды;

Переливаем ее в 3-х литровую емкость;

Снова заполняем 5-ти литровую емкость

Переливаем в 3-х литровую емкость недостающий 1 литр воды и получаем остаток в 4 литра!

14-й Правильный ответ:

15-й Правильный ответ:

В первом. Нужно смотреть на положение носика.

Самая сложная задача в мире

Самой сложной задачей в мире официально признали задание из итальянской газеты, опубликованное в 1992 году. Составил ее философ по имени Джордж Булос. Условия задачи следующие:

Имеются три божества. Одно из них ‒ покровитель правды (А), другое ‒ покровитель лжи (В), третье ‒ покровитель случайностей (С). И первый всегда отвечает исключительно правду, второй лжет, а вот третий может лгать или не лгать в произвольной последовательности. Богов нужно распознать, задав им в общей сложности 3 вопроса. Отвечать они могут лишь «нет» или «да», причем на своем собственном языке (Da и Ja), так что придется еще догадаться, которое из слов означает «да», а которое ‒ «нет». Не разрешается задавать нескольким божествам один и тот же вопрос. Зато одному можно сразу задать два или даже три вопроса, тогда остальные останутся вовсе без вопросов. Иногда ответ на какой-либо вопрос влияет на то, кому и какой следующий вопрос задать. Бог случайностей отвечает, словно в его голове подбрасывается воображаемая монетка, причем аверс ‒ правда, а реверс ‒ ложь. Запрещено задавать парадоксальные вопросы, на которые можно дать ответ как нет, так и да, или нельзя дать ответ вовсе.

Самая сложная логическая задача имеет следующее решение:

Первым же вопросом необходимо отыскать того, кто НЕ является божеством случайностей. Вариантов таких вопросов много, но главное условие ‒ наличие в вопросе некоторых логических связей. Например: «Если ты — божество правды, а В ‒ божество случайностей, то Da ‒ это означает да?» Можно упростить решение, применяя условные фразы, которые противоречат фактам. Суть в том, что на любой из возможных вопросов (Q), заданный божеству правды или божеству лжи («Если я задам некий вопрос Q, ответ будет звучать как Ja?»), ответят Ja в том случае, если ответ должен быть да, и Da ‒ если ответ должен быть нет. Чтобы это доказать, автор предложил целых восемь вариантов вопросов. В конце, после того, как выяснили, кто божество правды, а кто лжи, оставшийся бог будет опознан методом исключения.

Источники

• https://logiclike.com/math-logic
• https://FB.ru/article/390638/interesnyie-zadaniya-po-matematike-igryi-i-zadaniya-s-otvetami-dlya-shkolnikov
• https://ChildAge.ru/obuchenie-i-obrazovanie/nachalnaya-shkola/samostoyatelnaya-rabota/matematicheskie-zadachi-na-smekalku-s-otvetami.html
• https://ped-kopilka.ru/uchiteljam-predmetnikam/matematika/zanimatelnye-zadachi-po-matematike-s-otvetami-5-klas.html
• https://joy-pup.com/puzzle/15-novyh-zadach-na-logiku/
• https://megatopof.ru/prochee/slozhnye-zadachi.html

 

 

Средняя школа – Проект изобретательности

Проект изобретательности – это общегородская специализированная учебная программа в школах Балтимора. Учащиеся проходят углубленные курсы математики и естественных наук в течение учебного дня вместо стандартной учебной программы и имеют возможности для постоянного обогащения и поддержки. Программа проводится в четырех государственных школах Балтимора (Гамильтон, Джеймс МакГенри, Маунт-Ройал и Роланд Парк). Принятые учащиеся переводятся на уровень изобретательности в одну из этих четырех средних школ на три года (6-8 классы). Учащиеся становятся членами этих новых промежуточных школ и участвуют в стандартных или курсовых работах с отличием (английский язык, обществознание и классы), предлагаемых в школе. Изобретательность хорошо подходит учащимся с хорошей академической успеваемостью и способностью быстро схватывать новый материал и концепции.

Посредством нашего процесса подачи заявок допущенные учащиеся средних школ распределяются по одной из четырех общегородских программ средних школ в следующих принимающих школах:

• • • Начальная/промежуточная школа Гамильтона
    • Начальная/промежуточная школа Джеймса МакГенри
    • Начальная/промежуточная школа Mount Royal
    • Начальная/промежуточная школа Roland Park

Наша цель

«Моему ребенку нравится математическая программа. Он так взволнован тем, что узнает так много нового и движется быстрее, чем в начальной школе».
— Находчивый родитель Учащийся 6-го класса

Наша программа для средних школ имеет долгую историю развития любознательности учащихся; способность решать проблемы; упорство; абстрактное, качественное, количественное и критическое мышление; и коммуникативные навыки, необходимые для успеха в карьере STEM или смежных областях. Мы хотим вдохновить наших учеников идти по сложной образовательной траектории в старших классах, продолжая изучение высшей математики и естественных наук в старших классах.

Преимущества

• Углубленный курс для разнообразной группы высоко мотивированных студентов.
• От международно признанной сингапурской математики в 6-м классе до проверенного с отличием курса алгебры средней школы I в 8-м классе.
• Экспериментальные и строгие научные и инженерные курсы.
• Возможность продемонстрировать независимые научные проекты и принять участие в математических конкурсах.
• Высокие стандарты успеваемости учащихся, способствующие академическому росту.
• Учителя, стремящиеся развивать позитивные и инклюзивные классы.

Преподаватели изобретательности

Преподаватели изобретательности обычно имеют ученые степени в своих специализированных областях. Они уделяют особое внимание формированию академических и личных привычек для достижения успеха на протяжении всей жизни. Наши преподаватели развивают любознательность, креативность, критическое мышление, умение решать проблемы, настойчивость, уверенное общение, уверенность в своих силах и лидерские качества.

Наш математический подход

Изобретательность начинается в 6-м классе сингапурской математики, всемирно признанной и проверенной учебной программы. Учащиеся переходят к предварительной алгебре в 7-м классе и с отличием по алгебре средней школы I в 8-м классе. Учебная программа переходит от конкретного к изобразительному, а затем к абстрактному пониманию, которое способствует мастерству и любви к математике.

Учебная программа по естественным наукам и технике

Учебная программа Ingenuity уделяет большое внимание процессу научных исследований и исследованию научных исследований. Учащиеся работают со своими учителями в начале года, тщательно разрабатывая научные проекты и соревнуясь в школьных научных ярмарках и общегородской научной ярмарке штата Морган.

Принципы проектирования основаны на долгосрочных проектах, которые способствуют решению реальных проблем и сотрудничеству.

• Основной момент учебной программы: учащиеся 7-го класса работают в группах над разработкой решений для снижения загрязнения азотом в Чесапикском заливе. Фонд Чесапикского залива был ценным партнером в наших классах.

Летние и послешкольные программы

Ingenuity предлагает летние программы по математике, чтобы обеспечить запоминание понятий. В течение учебного года учителя Ingenuity предлагают дополнительные занятия с тренерами, чтобы подготовить учащихся к успеху, и предлагают учащимся подготовиться к региональным математическим олимпиадам и научным ярмаркам.

Все учащиеся начинают свой путь изобретательности с двухнедельной летней академии, где студенты изучают сингапурский подход и налаживают отношения со своими сверстниками и учителями.

Результаты учащихся

В ноябре 2014 года Консорциум исследований в области образования в Балтиморе (BERC) опубликовал Предварительное исследование результатов учащихся в области изобретательности в 2008 и 2013 годах. тем не менее в Poly получили постоянные академические преимущества от своего предыдущего опыта Ingenuity. BERC сравнил учащихся Ingenuity с подходящей группой сравнения. BERC пришел к следующим выводам:

• Выпускники средней школы Ingenuity получили в среднем 3,5 кредита по математике по сравнению с 2,5 баллами среди учащихся сравнения. За углубленные научные баллы студенты Ingenuity получили 3,9 балла по сравнению с 2,7 балла среди их сверстников.
• Учащиеся Ingenuity получили значительно больше баллов Advanced Placement в старшей школе (9,3 против 5,8).
• Учащиеся Ingenuity достигли значительно более высокого среднего балла по окончании средней школы, чем сопоставимые учащиеся, со средним средним баллом 3,0 по сравнению с 2,5 в группе сравнения.
• Студенты Ingenuity получили значительно более высокие баллы на тестах PSAT и SAT по всем предметным областям.

Ключевые статистические данные

Согласно ежегодным оценкам программ, рост числа учащихся превышает средний национальный показатель по математике и естественным наукам.

• 100% учащихся 8-го класса с уровнем изобретательности принимаются в отборные средние школы в Балтиморе
• 99% учащихся 8-го класса поступают в среднюю школу с зачетом средней школы по алгебре I
• 50% учащихся Ingenuity входят в 10% лучших в стране в конце учебного года.

Стандарты

Философия проекта Ingenuity состоит в том, чтобы взращивать, развивать и поощрять участников Ingenuity. В соответствии с этой философией студенты должны соответствовать следующим требованиям на протяжении всей программы:

• Отличная посещаемость без пропусков без уважительной причины. Это включает в себя летние программы для изобретательности.
• Вести себя уважительно по отношению к однокурсникам и преподавателям Ingenuity и уважать важность работы. Студенты, не соответствующие стандартам посещаемости и поведения, будут исключены из программы.
• Поддерживайте средний балл 80 или выше по всем курсовым работам. Если в какое-либо время в течение года учащийся Ingenuity не проявляет последовательных усилий для соблюдения стандартов, учащегося и его/ее родителей попросят встретиться со школой и персоналом Ingenuity, чтобы оценить трудности учащегося и определить необходимые шаги для улучшения. в академической успеваемости. Учащиеся, которые постоянно не в состоянии выполнять требования Проекта, не будут повторно участвовать в программе на следующий год. Если учащиеся отказываются от занятий или их просят уйти из-за того, что они не соответствуют стандартам, они будут переведены в обычные классы.

Hamilton Middle School

6101 Old Harford Road, Baltimore, MD 21214, United States

410-396-6375

Locations / Schools

---

---

---

---

---

---

Sitemap

Online Curricula and Solutions | Imagine Learning

Добро пожаловать Winsor Learning — признанный лидер в области науки о чтении. ⯈ Прочтите пресс-релиз.

представьте себе

будущее

обучение

Подробнее

Свяжитесь с нами

Перспективные решения для образования

Представьте себе мир, в котором классы не знают границ — мир, который расширяет возможности преподавателей, привлекает учащихся K–12 и объединяет семьи. Imagine Learning предлагает образовательные решения, призванные расширить возможности преподавателей и повысить успеваемость учащихся.

► Ознакомьтесь с решениями

Продукты, разработанные для расширения возможностей преподавателей

Недавно объединенный портфель продуктов предоставляет услуги, которые творчески меняют возможности для всех преподавателей и учащихся K–12. Используйте информацию из данных в режиме реального времени, чтобы удовлетворить индивидуальные потребности каждого учащегося в обучении и обеспечить их успех не только сегодня, но и на всю жизнь в будущем.

► Ознакомьтесь с продуктами

Усовершенствуйте обучение с помощью новейших идей

Решение проблемы нехватки учителей

Найдите поддержку и креативные решения для решения проблемы нехватки учителей и вакансий. Imagine Learning может помочь в различных классах и предметах.

► Узнать больше

Преподавание информатики и программирования

Предоставьте учащимся 3–8 классов возможность изучать информатику в увлекательной, увлекательной и доступной форме с помощью Imagine Robotify.

► Узнать больше

Поощряйте совместную работу в классе

Ознакомьтесь со свежими идеями и советами от новых лидеров в области образования, чтобы поддержать благополучие преподавателей, стимулировать участие и сделать обучение совместным опытом, которого так жаждут учащиеся.

► Изучить

Портфолио Imagine Learning

Учебные программы

Если учащемуся нужна более строгая курсовая работа для ускорения индивидуального обучения или возможность восстановить кредиты, комплект учебных материалов Imagine Learning может помочь им достичь своих личных академических целей.

Узнать больше

Предлагайте учащимся увлекательные, подходящие для их возраста учебные занятия, чтобы они могли практиковаться и осваивать навыки для достижения успеха. Наш дополнительный пакет поддерживает вашу цель целенаправленного и индивидуального обучения для каждого учащегося.

Узнать больше

Основная учебная программа

В Imagine Learning Classroom учителя создают учебную среду, ориентированную на учащихся, и учащиеся берут на себя ответственность за свое обучение, выражают свое мнение по поводу содержания и делятся своим мнением в заданиях. Наша учебная программа, основанная на цифровых технологиях, помогает развивать необходимые навыки, необходимые для обучения учащихся на протяжении всей жизни.

Узнать больше

Услуги виртуальной школы

Имея доступ к крупнейшему стандартизированному каталогу курсов, вы можете предложить своим ученикам богатый и полезный опыт, преподаваемый вашими преподавателями или нашими высококвалифицированными, сертифицированными преподавателями. виртуальных инструкторов. Получите руководство, поддержку и цифровую учебную программу, необходимые для создания успешной виртуальной программы.

Подробнее

Истории прорывов в обучении

Опыт программирования с Imagine Robotify не требуется

Послушайте рассказы реальных преподавателей, не имеющих опыта программирования, которые используют Imagine Robotify на основе браузера для обучения учащихся программированию в средней школе Зейтц в Ривервью, штат Мичиган.