Вычитание обыкновенных дробей из натуральных чисел | Презентация к уроку по математике (5 класс):
Урок математики в 5 классе
Разработан по новым образовательным стандартам ФГОС ООО учителем математики МБОУ СОШ №5 г. Донской, Тульской области Будниковой Е.Н.
Тема урока:
«Вычитание обыкновенных дробей из натуральных чисел».
Тип урока: открытие нового знания.
Цели урока: Планируемые результаты.
Предметные:
Способствовать построению алгоритма выполнять вычитание обыкновенной дроби из натурального числа, научить выполнять вычитание обыкновенной дроби из натурального числа, применять новое правило при решении задач.
Метапредметные:
Формирование познавательных УУД:
- 2.Познавательные умения: самостоятельно выделять и формулировать цель, структурировать знания, уметь ставить и формулировать проблему и находить способы её устранения, создавать алгоритм действия.
- Формирование регулятивных УУД
3.
Ставить учебную задачу; осуществлять самоконтроль и самооценку учебных действий; выполнять по образцу алгоритм вычитания обыкновенных дробей из натуральных чисел; самостоятельно создавать алгоритм деятельности при решении проблем творческого и поискового характера; контролировать выполнение каждого действия (шага) алгоритма; грамотно применять математические понятия и термины, логично излагать свои мысли, комментировать ответ; аргументировать свою точку зрения; осуществлять взаимоконтроль при работе в парах.
Формирование коммуникативных УУД
4.Воспитывать культуру поведения при обсуждении любых вопросов, работе в парах, взаимной проверке; проводить контроль, коррекцию, оценка действий партнера.
Формирование личностных УУД
5. Проявлять интерес к изучению темы; желание решать проблему, используя приобретенные знания; осознание собственных достижений при освоении учебной темы.
Оборудование для урока: учебник для общеобразовательных учреждений « Математика.
5 класс». Авторы Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др. издательство « Просвещение», 2013, компьютер, проектор, экран, раздаточный материал.
Ресурсы:презентация.
Формы работы с учащимися: фронтальная, парная, индивидуальная.
План урока.
- Сообщение учащихся «Из истории возникновения дробей».
- Актуализация знаний учащихся. Повторение.
- Изучение нового материала.
- Решение задач.
- Игра «Кто быстрее?»
- Проверочная работа «Проверь себя!»
Ход урока.
1. Сообщение учащихся «Из истории возникновения дробей». ( Слайды 4-7).
С самых древних времён у людей появилась потребность в измерении длин, площадей, углов и
других величин. Для получения более точных результатов меры стали делить на части, что привело к появлению дробей. Первыми в практике людей появились самые простые дроби ( , , и т.д.). Лишь значительно позже греки, а затем индусы стали использовать в вычислениях и другие дроби.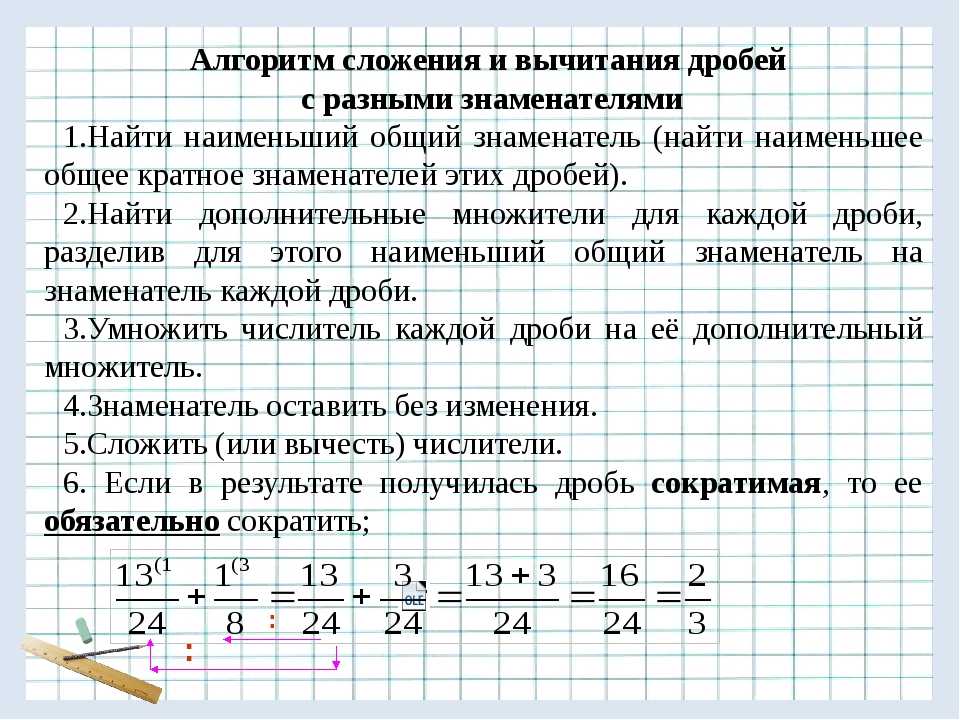
Запись дробей с помощью числителя и знаменателя появилась в Древней Греции, только греки знаменатель записывали сверху, а числитель – снизу. В привычном для нас виде дроби впервые стали записываться в Древней Индии около 1500 лет назад, но при этом индусы обходились без черты между числителем и знаменателем. А черта дроби стала употребляться только с 16 века.
Понятие «дробь» произошло от глаголов «раздроблять», «разбивать», «ломать». А в первых русских учебниках математики дроби так и назывались – «ломаные числа».
В древности и в Средние века учение о дробях считалось хотя и самым трудным, но и самым важным разделом арифметики.
Римский оратор Цицерон, живший в I веке до нашей эры, сказал: «Без знания дробей никто не может признаться знающим арифметику!»
2.Актуализация знаний учащихся ( повторение). ( Слайд 8).
1)Сформулируйте правило вычитания дробей с равными знаменателями.
2)Представьте 1в виде дробей со знаменателями 2; 3; 10.
3.Изучение нового материала. ( Слайды 9, 10).
1)Предложить учащимся самостоятельно ( на основе имеющихся у них знаний правила вычитания дробей с равными знаменателями и умения представлять натуральные числа в виде обыкновенных дробей с заданным знаменателем) выполнить действие 1- .
Учащиеся предлагают следующее решение:
1- =-=.
Затем, формулируется правило: «Чтобы из 1 вычесть дробь, надо 1 записать в виде дроби с данным знаменателем и выполнить вычитание дробей с равными знаменателями».
2) Предложить учащимся самостоятельно (на основе предыдущего примера) выполнить действие 4 — .
Учитель начинает побуждающий диалог. « Вы можете выполнить это действие? А в чём затруднение? А как можно преодолеть это затруднение ,используя имеющиеся у вас знания о вычитании дробей с одинаковыми знаменателями?»
Учащиеся предлагают следующее решение:
4 — = 3 — = 3
4 = 3 + 1 = 3 + = 3
Затем, формулируется правило: «Чтобы из натурального числа вычесть дробь надо его записать в виде смешанной дроби, дробная часть которого имеет данный знаменатель и выполнить вычитание дробей».
4. Закрепление нового материала. Решение задач.
№ 1(Слайд 11).
Вычислите.
А) 1 — = ? Б) 1 — =?
№ 2
Вычислите.
А) 3 — =? Б) 5 — =?
(Устно). Найдите неизвестное число. (Слайд 12).
Первое слагаемое | Второе слагаемое | Сумма |
1 | ||
1 | ||
1 | ||
1 | ||
Первое слагаемое | Второе слагаемое | Сумма |
2 | ||
4 | ||
5 | ||
6 |
Задача 1.
(Слайд 13).
Найдите длину отрезка ВD,
1) если АD = м, АВ = 1 м.
2) если AD = м, АВ = 4 м.
№ 3. Сравните значения выражений :
1 — и 1 —
1 способ:
и
Приводим к общему знаменателю
>
2 способ:
1 — > 1 —
Правило: из двух дробей с одинаковым числителем больше та, знаменатель которой меньше.
Индивидуально некоторым учащимся предлагается выполнить следующее задание.
( Слайд 15). Задача. Какая из двух дробей больше
Как проще сравнить эти дроби?
Решение. ( Слайд 16)
= 1- = 1 —
>
Задача 2.(Слайд 17).
Пончик может съесть торт за 20 минут, а Сиропчик съедает его за 30 минут. Какая часть торта останется через 1 минуту, если они будут есть его вместе?
Для решения задачи 1 учащийся приглашается к доске.
«Подумай!» (устно).
( Слайд 18).
Найдите длину отрезка CD, если АD = дм, ВC = дм, АВ = 1 дм.
«Для смекалистых». (Слайд 19).
Вычисли: 1 — ; 2 — ; 3 — ; 4 — ;…
Какие числа будут получаться, если продолжить эту цепочку разностей?
Чему равна разность, стоящая на 100-м месте?
5.(Слайд 20) Игра » Кто быстрее?» Идёт работа по парам, свои ответы учащиеся пишут на листочках и отдают учителю. Учитель складывает листы с ответами в том порядке, как их приносили учащиеся. Первые три пары, давшие правильные ответы, получают отметку «5».
Сумма всех чисел в квадрате равна 10. Какое число надо поставить в пустую клетку?
5 | |
? | |
1 | |
? | 2 |
? | |
2 | 1 |
Слайд 21.
( ответы)
6.Проверочная работа «Проверь себя!»( Слайд 22).
1 вариант 2 вариант
Вычисли.
- 1 — ; 1) 1 — ;
- 6 — ; 2) 8 — .
Слайд 23. (ответы) Учащиеся обмениваются тетрадями, идёт взаимопроверка решений по слайду 23.
Ответы:
1 вариант 2 вариант
- 1)
- 5 2) 7
7.Подведение итогов урока. Рефлексия.
Предлагается учащимся ответить на вопросы:
Что нового узнали на уроке?
Какие правила сформулировали?
Какие знания были использованы при решении задач?
Рефлексия проводится при помощи 3-х смайликов ( недовольство, равнодушие, радость).
Ваше отношение к уроку. Ваше отношение к вашей работе. Какое задание понравилось больше всего? Почему?
8.Домашнее задание.
П.9.
3, № 814 ,818 (б), 1 (по желанию).
№1.
Сравните значения выражений:
1 — и 1 — .
Сложение и вычитание обыкновенных и десятичных дробей. смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+
7 месяцев назад
Математика от Баканчиковой294 подписчика
Математика 5 класс. Продолжая тему «Десятичные дроби», сегодня мы расскажем Вам о том, как обращать обыкновенную дробь в десятичную. А начнём мы с объяснения для чего обращают обыкновенную дробь в десятичную. Оказывается это нужно для того, чтобы выполнить сложение или вычитание обыкновенной дроби и десятичной, т.к. не существует правил сложения и вычитания таких дробей. Мы дадим Вам и на конкретных примерах пошагово разберём правило обращения обыкновенной дроби в десятичную дробь. Затем поспорим с авторами современных учебников математики 5 класса о том, что при делении одного натурального числа на другое натуральное число получается обыкновенная дробь.
А для обращения обыкновенной дроби в десятичную, числитель необходимо представить сначала в виде десятичной дроби, а затем уже десятичную дробь разделить на знаменатель, потому что при делении десятичной дроби на натуральное число получается десятичная дробь. В заключении мы обратим Ваше внимание на примеры обыкновенных дробей, которые необходимо запомнить и обращать их в десятичные дроби устно. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:41 Для чего обращают обыкновенную дробь в десятичную?
01:56 Правило обращения обыкновенной дроби в десятичную дробь.
04:32 В чем я не согласна с авторами современных учебников математики 5 класса.
07:10 Эти обыкновенные дроби ты должен обращать в десятичные устно!
Если Вы впервые на нашем канале и у Вас остались вопросы или Вы хотите освежить в памяти некоторые действия над числами или арифметическими выражениями, то рекомендуем Вам посмотреть следующие видео:
Обыкновенные дроби. Как получаются.
Видео-урок: Вычитание рациональных чисел
Стенограмма видео
В этом видео мы научимся
вычитание рациональных чисел, включая дроби и десятичные дроби.
Прежде чем мы рассмотрим вычитание
рациональные числа, давайте вспомним, что такое рациональные числа.
Формальное определение рационального числа говорит, что рациональные числа — это числа, которые можно записать в виде 𝑝 над 𝑞, где 𝑝 и 𝑞 — целые числа, а 𝑞 не равно нулю. Рациональные числа можно составить деление двух целых чисел 𝑝 на 𝑞. Другой способ думать об этом — их можно записать в виде дроби от двух целых чисел. Значение не должно быть в этом форма должна быть рациональной. Например, 0,5 в настоящее время не записывается в виде 𝑝 над 𝑞, но мы знаем, что пять десятых равны одна половина. А поскольку 0,5 можно записать в форма один над двумя, это рационально.
Все целые числа, множество
целые числа и их противоположности являются рациональными числами. Подмножество целых чисел, которые
рациональны, все целые числа.
И подмножество целых чисел
натуральные числа, иногда называемые счетными числами. Натуральные числа – это множество
числа, начинающиеся с единицы и продолжающиеся вверх на единицу. Целые числа включают значение
нуль. Целые числа включают отрицательные
ценности. И рациональные значения могут быть десятичными
если их можно записать в виде дробей. Например, мы знаем, что 0,3
повторение равно одной трети. Таким образом, 0,3 повторения
рациональный.
Смешанные числа рациональны, поэтому
являются неправильными дробями. Но в этом видео мы хотим поговорить
о вычитании рациональных чисел, что напоминает мне то, что моя бабушка любила
сказать. Яблоки и апельсины! Позволь мне объяснить. Это просто выражение, когда
две группы или предметы практически невозможно сравнивать. И когда мы вычитаем рациональное
числа, мы не хотим пытаться вычитать значения, которые не записаны в одном и том же
форма.
Например, если мы хотим сказать
два с половиной минус 0,3 повторяя, мы начинаем со смешанного числа и пытаемся
вычитание повторяющегося десятичного числа. А это яблоки и апельсины.
Однако, если бы мы написали 0,3 повторяющихся как дробь, а мы переписали два с половиной как неправильную дробь, они то найти в той же форме, и мы могли бы вычесть. Итак, ключ к вычитанию рациональных числа сначала убедитесь, что вы помещаете свои значения в один и тот же формат. Мы должны вычесть яблоки из яблоки или апельсины из апельсинов. Итак, давайте рассмотрим несколько примеров.
Оценка две пятых минус четыре пятых, что дает число в его простейшей форме.
Когда мы смотрим на это выражение
две пятых минус четыре пятых, оба наших значения являются дробями. И у них есть общее
знаменатель. Так как обе дроби находятся в
одинаковой формы и имеют общий знаменатель, чтобы вычесть, мы просто вычитаем их
числители и знаменатель остаются прежними.
В нашем первом примере мы вычитание двух дробей. В нашем следующем примере мы будем думать о том, как мы будем вычитать смешанное число из смешанного числа.
Вычислить девять и три двенадцатых минус две и восемь двенадцатых. Дайте свой ответ в виде смешанного число.
Мы пытаемся вычесть смешанный
число из смешанного числа. И для этого существуют
несколько вещей, о которых мы должны подумать. Прежде всего, для дроби
части нашего смешанного числа, имеют ли они общий знаменатель? В этом случае они делают; у обоих есть
знаменатель 12. После этого мы могли преобразовать оба
из этих смешанных чисел в неправильные дроби.
Мы могли бы попытаться вычесть восемь двенадцатых из трех двенадцатых, но мы столкнулись с проблемой, потому что восемь двенадцатых больше трех двенадцатых. Итак, нам нужно переписать как минимум девять и три двенадцатых. Один из способов сделать это — взять один от нашей целой цифры девять и сделать эту восьмерку. И когда мы это сделаем, мы можем добавить 12 к нашему числителю. Это потому, что мы взяли один от всего нашего числа, равного двенадцати двенадцатым. И двенадцать двенадцатых плюс три двенадцатые равны пятнадцати двенадцатым. Восемь и пятнадцать двенадцатых равны до девяти и трех двенадцатых. просто по другому написано формат.
Тогда мы можем сказать восемь и пятнадцать
двенадцатые минус две и восемь двенадцатых.
В этом случае мы можем вычесть
целые числа и части смешанного числа. Чтобы вычесть восемь двенадцатых из
пятнадцать двенадцатых, мы говорим, что 15 минус восемь равно семи. И знаменатель остается прежним,
12. А теперь работаем в целом
количество штук. Восемь минус два равно шесть. А это значит девять и три
двенадцатые минус две и восемь двенадцатых будут равняться шести и семи двенадцатым. Это уже в виде
смешанный номер. И семь двенадцатых не может быть
уменьшаем дальше, делая шесть и семь двенадцатых нашим окончательным ответом.
В нашем следующем примере мы снова есть два смешанных числа, но на этот раз мы не начинаем с общего знаменатели.
Вычислите семь и одну четвертую минус четыре и пять восьмых. Дайте свой ответ в виде смешанного число.
Когда мы смотрим на выражение
семь и одна четвертая минус четыре и пять восьмых, оба числа смешанные.
Однако дробная доля
смешанные числа не имеют общего знаменателя. И мы знаем, для работы с
эти значения, нам нужно, чтобы они были в том же формате. Поскольку мы имеем дело с
знаменатели четыре и восемь, и мы знаем, что четыре — это множитель восемь, четыре раза
два равно восьми, а это значит, что мы можем переписать одну четвертую как две восьмых. Как только мы это сделаем, у нас будет семь и
две восьмых минус четыре и пять восьмых.
Тем не менее, мы еще не совсем
готовы вычитать, потому что мы пытаемся отнять пять восьмых от двух восьмых. А это значит, что для нашего первого
смешанное число семь и две восьмых, нам нужно заимствовать из целого числа
часть. Если отнять одно целое от
семь, мы оставляем шесть. И вся эта ценность, которую мы взяли
далеко равно дроби восемь восьмых. Если мы добавим две восьмых плюс
восемь восьмых, мы получаем десять восьмых.
Смешанное число шесть и
десять восьмых — это то же значение, что и семь и одна четвертая, записанные другим
формат.
Теперь мы готовы вычесть шесть и десять восьмых минус четыре и пять восьмых. Чтобы вычесть дробную часть, так как у нас есть общие знаменатели, мы скажем 10 минус пять. То есть мы вычитаем значения числителя. И знаменатель не меняется. Десять восьмых минус пять восьмых равняется пяти восьмым. И тогда мы вычитаем все количество порций. Шесть минус четыре равно двум, что дает нам результат две и пять восьмых. Пять восьмых нельзя упростить дальше. Два и пять восьмых — это смешанный число и наш окончательный ответ.
До сих пор мы только вычисляли
значения, которые уже заданы в том же формате. В нашем следующем примере нам нужно
найти отличие десятичной дроби от дроби.
Найдите разницу между минус 0,85 и две пятых, что дает ваш ответ в виде дроби в его простейшем виде. форма.
Разница между отрицательными 0,85 и две пятых можно записать как минус 0,85 минус две пятых. Но как только мы дойдем до этого момента, мы иметь проблему. И это то, что наши два значения даны в разных форматах, а значит, у нас есть выбор. Мы можем преобразовать две пятых в decimal, чтобы мы вычитали десятичную дробь из десятичной. Или мы можем конвертировать минус 0,85 в дробь, чтобы мы вычитали дробь из дроби. Оба метода будут работать, но мы было предложено дать ответ в виде дроби в ее простейшей форме. А значит, наверное, стоит это вычитание дроби из дроби.
А значит надо подумать
о том, как мы запишем минус 0,85 в виде дроби. Так как пять в отрицательном 0,85
в сотом месте мы говорим, что это минус восемьдесят пять сотых.
И как дробь, которая является отрицательной
85 на 100. Но прежде чем двигаться дальше, мы могли бы
хотим посмотреть, сможем ли мы упростить восемьдесят пять сотых. И 85, и 100 делятся на
пять. Минус 85 разделить на пять равно
минус 17, а 100 разделить на пять равно 20, что означает, что мы пытаемся сказать
минус 17 на 20 минус две пятых.
Однако теперь мы видим, что не
имеют общие знаменатели в наших двух дробях. Но мы знаем, что пять раз четыре
равно 20. А это значит, что мы можем умножить
две пятых на четыре больше четырех. Дважды четыре восемь и пять
умножить на четыре равно 20. Теперь у нас есть отрицательные семнадцать
двадцатые минус восемь двадцатых. Поскольку у нас есть общие знаменатели,
мы можем сделать вычитание, вычитая числители, что будет минус 17 минус
восемь. Знаменатель не меняется.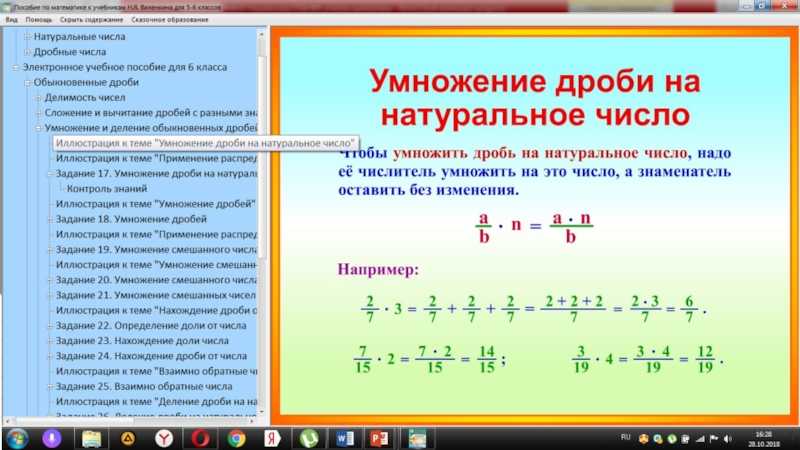
Остается 20. Отрицательное 17 минус восемь будет
равно отрицательному значению 17 плюс восемь. Это минус 25.
Итак, у нас есть минус 25 больше 20. Обе эти величины делятся к пяти. Минус 25 разделить на пять равно минус пять. 20 разделить на пять равно четырем. А это значит минус 0,85 минус две пятых равны отрицательным пяти четвертям.
Теперь мы готовы рассмотреть еще один пример.
Оценка семь четвертей минус отрицательная половина, давая ответ в его простейшей форме.
У нас есть выражение семь больше
четыре минус минус один больше двух. Мы признаем, что оба эти
значения являются дробями. Однако у них нет одинаковых
знаменатель. И мы знаем, чтобы добавить или
вычитание дробей, нам нужно сначала найти общий знаменатель. Мы ищем наименее распространенный
кратное от двух до четырех, иногда называемое LCM.
Если мы подумаем о кратных двум,
у нас есть два, четыре и шесть. Но четыре уже кратно
два. И это означает наименее распространенный
кратное двум и четырем будет четыре.
Мы не будем вносить никаких изменений в семь четвертых, но мы перепишем отрицательную половину как дробь с знаменатель четырех. Дважды два четыре. И отрицательный один умножить на два минус два. Это означает, что наше новое выражение будет быть семь четвертей минус отрицательные две четверти. Мы также помним, что когда мы вычитая отрицательное значение, мы можем переписать это как сложение. Итак, семь четвертей минус минус две четверти равны семи четвертям плюс две четверти.
Если у нас есть дроби с
общий знаменатель, мы складываем их вместе, складывая их числители. Семь плюс два будет девять. И знаменатель не
изменять. Семь четвертей плюс две четверти
равна девяти четвертям.
Мы хотим дать этот ответ в
простейшая форма. А это значит, что мы хотим проверить и
посмотрите, есть ли какие-либо общие делители в числителе и знаменателе. Девять и четыре не разделяют
общие факторы, кроме одного. И это делает дробь
девять четвертей в простейшей форме.
В нашем последнем вопросе мы поместим все эти навыки вместе, когда мы вычитаем значения в трех разных форматах.
Оценка пять двенадцатых минус минус одна треть минус 0,75.
В этом выражении имеем
дроби с необычными знаменателями и у нас есть десятичное значение. Чтобы сделать это вычитание,
нам понадобятся все три из этих значений в одном и том же формате. А это значит, что нам нужно
перепишите каждое из этих значений в виде дробей с общими знаменателями. Прежде чем мы займемся общим
знаменатели, давайте начнем с нашего десятичного значения и запишем его в виде дроби.
0,75 имеет пятёрку в сотых место, значит, в виде дроби 0,75 можно записать как 75 на 100. Но и 75, и 100 делятся на 25. 75 разделить на 25 равно трем, и 100 разделить на 25 равно четырем. Семьдесят пять сотых равны три четверти. Возможно также, что это значение, которое вы уже знаете. Это обычная десятичная дробь и обычная доля. Семьдесят пять сотых равны три четверти.
Тогда наше новое выражение
пять двенадцатых минус одна треть минус три четверти. И нам нужен общий знаменатель
из 12, 3 и 4. Чтобы найти этот общий знаменатель, мы
нужно наименьшее общее кратное. Если мы перечислим числа, кратные трем,
у нас есть три, шесть, девять, 12, 15. То же самое делаем для четырех,
где у нас есть четыре, восемь, 12 и 16. В этот момент мы признаем, что 12
кратно и трем, и четырем.
А значит 12 будет минимум
общее кратное между этими тремя значениями.
Затем мы хотим переписать все эти дроби со знаменателем 12. Пять двенадцатых остаются прежними. В этот момент мы также можем сказать, что вычитание минус одной трети — это то же самое, что и сложение. Если мы хотим записать одну треть как дробь со знаменателем 12, нам нужно умножить ее на четыре на четыре. А затем, чтобы переписать дробь три четверти со знаменателем 12, мы умножаем числитель и знаменателя на три, что означает, что наше новое выражение будет пять двенадцатых плюс четыре двенадцатые минус девять двенадцатых.
Когда у нас будут общие знаменатели,
мы можем складывать и вычитать, просто добавляя и вычитая числители. И знаменатель не будет
изменять. Итак, у нас есть пять плюс четыре минус
девять на 12. Пять плюс четыре равно девять, а девять
минус девять равно нулю.
Ноль двенадцатых равняется нулю. А это значит пять двенадцатых минус
минус одна треть минус 0,75 равно нулю.
Прежде чем мы закончим, давайте быстро пересмотрите ключевые моменты. При вычитании рациональных чисел в виде дробей, в том числе смешанных чисел, запишите все значения с общим знаменателем используя наименьшее общее кратное. При вычитании рациональных чисел как десятичные дроби и дроби, запишите все значения в виде десятичных дробей или, альтернативно, запишите все числа в виде дробей с общим знаменателем.
Что такое натуральные числа? Определение, свойства и примеры
Определение натуральных чисел
Натуральные числа — это все положительные целые числа от 1 до бесконечности. Их также называют счетными числами, так как они используются для подсчета предметов. Натуральные числа не включают 0 или отрицательные числа.
Числа нужны нам в повседневной жизни, будь то для подсчета предметов, определения времени или нумерации домов.
Числа, которые помогают нам в подсчете и представлении величин, называются натуральными числами. К ним относятся 1, 2, 3, 4, 5, 6 и так далее до бесконечности.
Здесь мы видим, что 1 — наименьшее натуральное число и каждое последующее натуральное число ровно на единицу больше предыдущего. Таким образом, числа, стоящие между этими числами, не являются натуральными числами, такими как дроби, десятичные дроби и т. д. с одним. Система разряда для числительных 1 (один) и 10 (десять) была впервые разработана вавилонянами.
Связанные рабочие листы
Типы натуральных чисел
- Нечетные натуральные числа
Нечетные натуральные числа — это положительные числа, которые не делятся на 2.
Например: 29, 677, 89901 и т. д.
- Четные натуральные числа
Четные натуральные числа — это положительные числа, которые делятся на 2.
Например: 28, 456, 6022 и т. д.
Свойства натуральных чисел
Вот некоторые важные свойства натуральных чисел.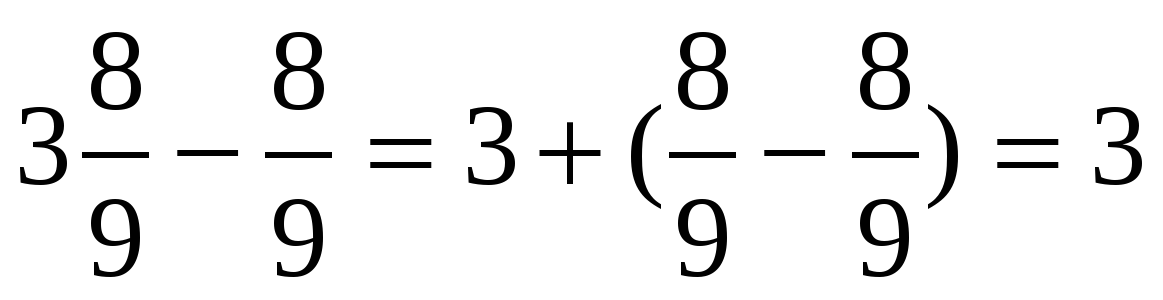
- Свойство закрытия
- Коммутативное свойство
- Ассоциативное свойство
- Распределительная собственность
- Свойство замыкания сложения и умножения
При сложении или умножении двух натуральных чисел результатом всегда будет натуральное число.
- Примеры замыкания свойства сложения: 2 + 2 = 4, 3 + 4 = 7, 5 + 5 = 10
В каждом случае результатом сложения натуральных чисел является натуральное число.
- Примеры свойства замыкания умножения: 2 × 2 = 4, 3 × 2 = 6, 5 × 5 = 25
В каждом случае результатом умножения натуральных чисел является натуральное число.
Однако в случае деления и вычитания это свойство не выполняется. Вычитание или деление двух натуральных чисел не всегда дает натуральное число.
- Примеры вычитания: 4 – 6 = –2, 5 – 3 = 2, 6 – 9 = –3
Во втором случае получилось натуральное число, а в первом и третьем нет.
- Примеры деления: 10 ÷ 3 = 3,33, 9 ÷ 3 = 3, 15 ÷ 4 = 3,75
Первый и третий случаи не привели к натуральным числам.
- Ассоциативное свойство сложения и умножения
Сумма или произведение натуральных чисел остается неизменным даже при изменении группировки чисел. Однако это не относится к делению и вычитанию.
- Примеры ассоциативного свойства сложения: 2 + (5 + 6) = 13 и (2 + 5) + 6 = 13
- Примеры ассоциативного свойства умножения: 2 × (3 × 4) = 24 и (2 × 3) × 4 = 24
Давайте теперь посмотрим на природу вычитания и деления с учетом этого свойства.
- Примеры вычитания: 4 – (10 – 2) = –4 и (4 – 10) – 2 = –8
- Примеры деления: 5 ÷ (6 ÷ 3) = 2,5 и (5 ÷ 6) ÷ 3 = 0,27
- Коммутативное свойство сложения и умножения
Если мы изменим порядок натуральных чисел при умножении и сложении, результат не изменится.
Например,
- 6 + 5 = 11 и 5 + 6 = 11
- 2 × 4 = 8 и 4 × 2 = 8
Свойство коммутативности не распространяется на вычитание и деление натуральных чисел.
Примеры вычитания и деления:
- 5 – 3 = 2 и 3 – 5 = –2
- 6 ÷ 3 = 2 и 3 ÷ 6 = 0,5
- Распределительная собственность
В соответствии с распределительным свойством умножения над сложением, если мы умножим сумму двух слагаемых на число или умножим каждое слагаемое по отдельности, а затем сложим их, результат будет таким же.
Пример: 2 × (5 + 3) = (2 x 5) + (2 x 3) = 16
Это свойство также верно в случае умножения вместо вычитания.
Пример: 2 x (5 – 3) = (2 x 5) – (2 x 3) = 4
Интересные факты
- Не существует самого большого натурального числа.
- Просто прибавив 1 к текущему натуральному числу, вы получите еще одно натуральное число.
- Натуральные числа продолжаются вечно.
Решенные примеры
Давайте лучше поймем концепцию на этих примерах.
- Выберите натуральные числа из следующего списка:
10, 6/2, 4.
66, 22, 1564, –6
Отв. Натуральными числами являются 10, 22 и 1564. Отрицательные числа, десятичные числа и дроби не считаются натуральными числами.
- Перечислите первые десять натуральных чисел.
Ответ. Ответ: 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10, так как натуральные числа начинаются с 1.
- В чем разница между любыми двумя последовательными натуральными числами?
Ответ. Разница между любыми двумя последовательными натуральными числами всегда равна 1.
Практические задачи
1
Между какими двумя натуральными числами лежит дробь 18/3?
10 и 12
5 и 7
7 и 9
12 и 14
Правильный ответ: 5 и 7
Потому что, разделив 18 на 3, мы получим число 6, которое лежит между 5 и 7
2
Если m и m два натуральных числа, то:
m + n = n + m
m – n = n – m
m / n = n / m
Ничего из перечисленного
Правильный ответ: m + n = n + m
Поскольку свойство коммутативности гласит, что если мы изменим порядок натуральных чисел во время умножения и сложения, результат не изменится.
Это свойство не распространяется на вычитание и деление.
3
Какое свойство натуральных чисел верно для 2 + (5 + 6) = 13 и (2 + 5) + 6 = 13?
ассоциативное свойство умножения
ассоциативное свойство вычитания
ассоциативное свойство сложения
замыкание сложения
Правильный ответ: ассоциативное свойство сложения
Ассоциативность сложения имеет место для данной задачи. Свойство утверждает, что сумма натуральных чисел остается неизменной, даже если их группировка варьируется.
4
Какой из следующих примеров правильно устанавливает коммутативное свойство?
6 + 5 = 11 и 5 + 6 = 11
2 + (5 + 6) = 13 и (2 + 5) + 6 = 13
2 × (5 + 3) = (2 x 5) + (2 x 3) = 16
4 – 6 = –2
Правильный ответ: 6 + 5 = 11 и 5 + 6 = 11
Поскольку свойство коммутативности гласит, что изменение порядка натуральных чисел при умножении и сложении приведет к не изменить результат.