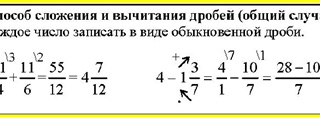
правила, примеры, решения, вычитание из целого числа смешанной дроби
В данной статье рассмотрим правила, согласно которым выполняется действие вычитания смешанных чисел. Разберем конкретные примеры и некоторые нюансы при их решении. Изучим вычитание обыкновенной дроби и натурального числа из смешанного числа, а также — вычитание смешанного числа из дроби и натурального числа. Рассматривать вычитание мы будем при условии вычитания из большего числа меньшее.
Вычитание смешанных чисел
Пусть в качестве исходных данных даны два смешанных числа: abc и def , необходимо выполнить вычитание данных смешанных чисел.
Нам известно, что любое смешанное число возможно представить, как сумму его целой и дробной части, тогда получим:
abc-def=a+bc-d+ef
Свойства действий сложения и вычитания дают возможность выполнить вычисление полученного выражения различными способами. Опираясь на значения дробных частей смешанных чисел
abc и def , необходимо придерживаться следующих схем вычисления:
- если дробная часть уменьшаемого больше, чем дробная часть вычитаемого:
bc>ef, то вычитание оптимально будет произвести так:
abc-def=(a-d)+bc-ef
Пример 1Произвести вычитание смешанных чисел: 356-249 .
Решение
Сравним дробные части смешанных чисел, т.е. 56 и 49 . Чтобы определить, какая из дробей больше, приведем их к общему наименьшем знаменателю или наименьшему общему кратному: НОК (6, 9) = 18. При этом дополнительным множителем для дроби 56 станет 18 : 6 = 3; а для дроби 49 – 18 : 9 = 2, поэтому : 56=5·36·3=1518 и 49=4·29·2=818 .
Оценим полученный результат: 1518>818, что означает 56>49. Т.е. дробная часть уменьшаемого больше дробной части вычитаемого, и тогда действие вычитания производится путем раздельного вычитания целых и дробных частей заданных смешанных чисел:
3-2=156-49=1518-818=15-818=718
Т.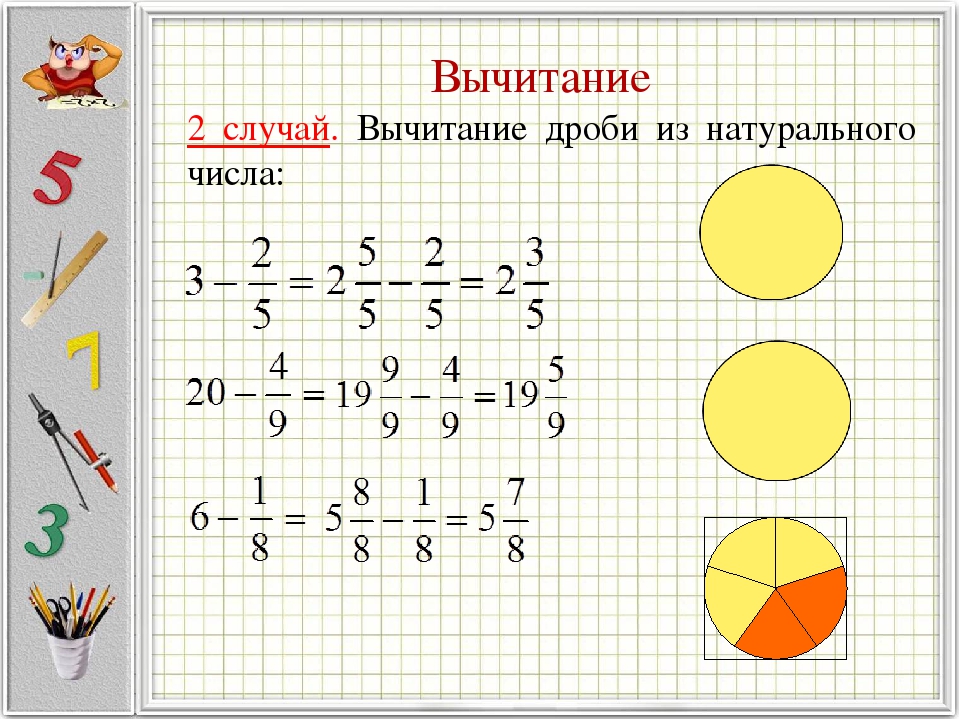
Ответ: 356-249=1718
- если дробные части заданных смешанных чисел равны: bc=ef , а, соответственно разность их равна нулю, то результатом вычитания таких смешанных чисел будет разность их целых частей:
abc-def=(a-d)+bc-ef=a-d+0=a-d
Пример 2Произвести вычитание смешанных чисел 15710 и 2710 .
Решение
Мы видим, что дробные части заданных чисел равны, т.е. их разность есть нуль. Таким образом, действие вычитания заданных чисел сводится к нахождению разности их целых частей: 15710-2710=15+710-2+710=15-2+710-710=15-2+0=13
Ответ: 15710-2710=13
- если дробная часть уменьшаемого меньше дробной части вычитаемого: bc<ef , то действие вычитания оптимально произвести так:
abc-def=a-d-ef+bc
Пример 3Произвести вычитание смешанных чисел: 2625-81415 .
Решение
Проведем сравнение дробных частей заданных чисел, определив для начала наименьший общий знаменатель: НОК (5, 15) = 15, тогда 25=2·35·3=615 .
Следовательно: 615<1415, т.е. дробная часть уменьшаемого меньше дробной части вычитаемого. Таким образом, находить разность заданных смешанных чисел будем так: 2625-81415=26615-81415=26+615-8+1415==26-8-1415+615=18-1415+615
Для начала вычтем дробь из натурального числа (в скобках): 18-1415=(17+1)-1415=17+1+1415=17+11+1415==17+1515-1415=17+115
Тогда 18-1415+615=17+115+615=17+115+615==17+715=17715
Ответ: 2625-81415=17715 .
Вычитание обыкновенной дроби из смешанного числа
Схема вычитания правильной дроби из смешанного числа такая же, как при действии вычитания смешанных чисел.
Пример 4Найти разницу: 356-415
Решение:
Приведем дробные части заданных чисел к единому наименьшему общему кратному: НОК (6, 15) = 30, тогда 65=5·56·5=2530 и 415=4·215·2=830 .
Таким образом, 56>415 .
В итоге вычитание возможно произвести так: 356-415=3+56-415=3+56-415=3+2530-830=3+1730=31730
Ответ: 356-415=31730
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 5Произвести действие вычитания: 127-37
Решение
Дробные части исходных чисел имеют одинаковый знаменатель, что дает возможность их легко сравнить. Понятно, что 27 меньше, чем 37.
Понятно, что 27 меньше, чем 37.
Тогда находить разницу будем так:
127-37=1+27-37=1-37+27=11-37+27==77-37+27=47+27=67
Ответ: 127-37=67.
Добавим еще одну, в общем очевидную деталь вычислений: если дробная часть смешанного числа равна вычитаемой дроби, то итогом вычисления будет число, равное целой части уменьшаемого смешанного числа. К примеру:
16311-311=16+311-311=16+311-311=16+0=16
Чтобы вычесть неправильную дробь из смешанного числа, необходимо выделить целую часть из неправильной дроби, а затем производить вычисление.
Вычислить значение разности: 7512-199 .
Решение: вычитаемая дробь является неправильной, выделим из нее целую часть и получим: 199=219
Приведем к общему знаменателю дробные части заданных чисел и согласно указанным выше схемам произведем вычитание смешанных чисел:
7512-219=7+512-2+19=7-2+512-19==5+1536-436=5+1136=51136
Ответ: 7512-199=51136 .
Вычитание натурального числа из смешанного
Определение 1Для совершения действия вычитания натурального числа из смешанного, необходимо вычесть заданное натуральное число из целой части смешанного числа, а дробную часть оставить без изменений: abc-n=a-n+bc
Пример 7Необходимо вычесть из смешанного числа 1511528 натуральное число 44.
Решение: 1511528-44=151+1528-44=151-44+1528=107+1528=1071528
Ответ: 1511528-44=1071528
Вычитание смешанного числа из обыкновенной дроби
Очевидно, что любое заданное смешанное число будет больше единицы. Уменьшаемая дробь должна быть больше вычитаемого, тогда эта дробь – неправильная. Необходимо выделить целую часть из неправильной дроби, и далее выполнение действия вычитания смешанного числа из обыкновенной дроби сведется к вычитанию смешанных чисел.
Пример 8Необходимо выполнить вычитание: 749-612
Решение
В первую очередь выделим целую часть неправильной уменьшаемой дроби: 749=829 , тогда заданный пример примет вид: 749-612=829-612
Найдем наименьший общий знаменатель: НОК (9, 2) = 18.
Получим: 29=2·29·2=418 и 12=1·92·9=918.
Тогда:
829-612=8418-6918=8+418-6+918=8-6-918+418==2-918+418=1+1-918+418=1+1-918+418==1+1-918+418=1+918+418=1+918+418==1+9+418=1+1318=11318
Ответ: 749-612=11318
Вычитание смешанного числа из натурального
Чтобы произвести действие вычитания смешанного числа из натурального, сначала от натурального числа отнимаем целую часть смешанного, после чего из полученного результата вычитаем дробную часть:
n-abc=n-a+bc=n-a-bc
Пример 9Необходимо вычесть из натурального числа 18 смешанное число.
Решение
18-535=18-5+35=18-5-35=13-35=12+1-35==12+1-35=12+11-35=12+55-35=12+5-35==12+25=1225
Ответ: 18-535=1225
Урок 73. вычитание смешанных дробей — Математика — 5 класс
Математика
5 класс
Урок № 73
Вычитание смешанных дробей
Перечень рассматриваемых вопросов:
– вычитание целого числа из смешанной дроби;
– вычитание дробного числа из смешанной дроби;
– вычитание смешанных дробей с общим знаменателем;
– вычитание смешанных дробей с разными знаменателями;
– вычитание смешанных дробей, когда дробная часть уменьшаемого меньше дробной части вычитаемого.
Тезаурус
Общий знаменатель – это число, которое без остатка делится на все указанные числа, для которых необходимо найти общий знаменатель.
Порядок убывания – расположение элементов от большего к меньшему.
Порядок возрастания – расположение элементов от меньшего к большему.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Вы уже знакомы с операцией сложения смешанных дробей, сводящейся к отдельному сложению целых и дробных частей. Вычитание смешанных дробей производится по тому же принципу: целая часть вычитается из целой части, дробная вычитается из дробной. Результаты этих разностей складываются.
В приведённом выражении вычитаем целые и дробные части. Разность целых чисел равна 3, разность дробных чисел равна тём седьмым. Складываем три и три седьмых, получается смешанная дробь: три целых три седьмых. Проверим правильность наших вычислений сложением. К полученной разности – три целых три седьмых – прибавим вычитаемое: две целых одну седьмую.
Результат сложения – пять целых четыре седьмых – равен уменьшаемому в первом выражении, значит, наши вычисления верные.
Если целые или дробные части уменьшаемого и вычитаемого равны, то вычитание выполняется таким же способом: отдельно вычитаем целые и дробные части.
Заменим смешанную дробь пять целых две пятых на равное ей число – четыре целых семь пятых. Теперь дробная часть уменьшаемого больше дробной части вычитаемого. Выполняем вычитание отдельно целых и дробных частей, полученные разности записываем смешанной дробью:
Наименьший общий знаменатель для пяти и трёх – это пятнадцать. Приведем дробные части к общему знаменателю. Дробная часть уменьшаемого получилась меньше дробной части вычитаемого. Преобразуем уменьшаемое. Смешанную дробь пять целых три пятнадцатых заменим равным ей числом – четыре целых восемнадцать пятнадцатых. Выполняем отдельно вычитание целых и дробных частей.
• приведём дроби к общему знаменателю 36;
• выполним сложение отдельно целых и дробных частей;
• дробная часть полученной смешанной дроби – неправильная дробь, выделим из неё целую часть и сложим с целой частью смешанной дроби.
Мы рассмотрели различные случаи вычитания смешанных дробей. Во всех этих случаях мы действовали по одному правилу: отдельно вычитали целые и дробные части, а затем складывали полученные результаты.
Тренировочные задания
Вычитание обыкновенных дробей объяснение и примеры Арифметик…
Привет, мой друг, тебе интересно узнать все про вычитание обыкновенных дробей объяснение , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое вычитание обыкновенных дробей объяснение , настоятельно рекомендую прочитать все из категории Арифметика
При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Пример.
вычитания дробей» / >Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так:
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Пример.
Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную дробь 7/7 и вычитают по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем ее в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.
Пример.
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
При подобных расчетах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого (что вычитаем).
Пример.
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно привести к общему знаменателю дробные части, а затем выполнить вычитание целой части из целой, а дробной из дробной.
Пример.
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример.
Так как у дробных частей разные знаменатели, то как и во втором случае, вначале приведем обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
3Поэтому, вспомнив вычитание правильной дроби из целого числа, займем единицу из целой части и представим эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.
Сложим полученную неправильную дробь 18/18 и дробную часть уменьшаемого и получим:
Все рассмотренные случаи можно описать с помощью правилвычитания смешанных чисел.
- Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
- Если дробная часть уменьшаемого меньше дробной части вычитаемого, то занимаем у целой части уменьшаемого единицу . Об этом говорит сайт https://intellect.icu . Эту единицу превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю.
- Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
- Вычитаем из целой части целую, а из дробной — дробную.

- Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про вычитание обыкновенных дробей объяснение Надеюсь, что теперь ты понял что такое вычитание обыкновенных дробей объяснение и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Дроби — как объяснить ребенку действия с дробями
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнееЧитайте также:
| Табличка на двери |
Как вычитать из целого дробь. Вычитание правильной дроби из целого числа. Как привести несколько дробей к одному и тому же знаменателю
Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.
Примеры вычитания дробей, знаменатели которых одинаковы
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
- 2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18. - Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.
- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.

- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
- Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 — 3/15.
Находим кратное чисел 18 и 15:
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и имеющих различные знаменатели.
Вычитание и имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Число, записанное в формате обычной дроби, содержит информацию о том, на сколько частей следует поделить целое (знаменатель) и сколько таких частей (числитель) составляет представляемое дробью значение. Целое число тоже дозволено трансформировать в дробный формат, дабы упростить математические операции с участием целых и дробных величин, скажем операцию вычитания.
Инструкция
1. Переведите целое число – «сокращаемое» – в формат неправильной дроби. Для этого в числитель поставьте само число, а в качестве знаменателя используйте единицу. После этого приведите полученное соотношение к тому же знаменателю, тот, что применяется в иной дроби – в «вычитаемом». Сделайте это умножением на знаменатель вычитаемого величин по обе стороны от дробной черты сокращаемого. Скажем, если из 15 надобно вычесть 4/5, то 15 нужно преобразовать так: 15 = 15/1 = (15*5)/(1*5) = 75/5.
2. Отнимите от числителя полученной в итоге первого шага неправильной обычной дроби числитель вычитаемой дроби. Полученное значение будет стоять над дробной чертой результирующего соотношения, а под черту разместите знаменатель вычитаемой дроби. Скажем, для примера, приведенного в предыдущем шаге, всю операцию дозволено записать так: 15 – 4/5 = 75/5 – 4/5 = (75-4)/5 = 71/5.
Скажем, для примера, приведенного в предыдущем шаге, всю операцию дозволено записать так: 15 – 4/5 = 75/5 – 4/5 = (75-4)/5 = 71/5.
3. Если числитель высчитанного значения огромнее знаменателя (неправильная дробь), класснее представить ее в виде смешанной дроби. Для этого поделите большее число на меньшее – полученная величина без остатка и будет целой частью. В числитель дробной части поставьте остаток от деления, а знаменатель оставьте без изменений. Позже такого реформирования итог описанного выше примера должен принять такой вид: 15 – 4/5 = 71/5 = 14 1/5.
4. Приведенный выше алгорифм приводит к итогу в формате обычной дроби, но зачастую бывает нужно получить в результате десятичную дробь. Дозволено произвести описанные в первых 2-х шагах операции, а после этого поделить числитель полученной дроби на ее знаменатель – полученное значение и будет десятичной дробью. Скажем: 15 – 4/5 = 71/5 = 14,2.
5. Альтернативный метод – первым же шагом перевести вычитаемую дробь в десятичный формат, то есть поделить ее числитель на знаменатель. Позже этого останется отнять вычитаемое от сокращаемого любым комфортным методом (в столбик, на калькуляторе, в уме). Тогда описанный выше пример дозволено записать так: 15 – 4/5 = 15 – 0,8 = 14,2.
Дробь – это специальная форма записи разумного числа. Она может быть представлена, как в десятичном, так и в обычном виде. Реформированием дробей занимаются детишки с пятого класса, эта операция имеет громадное прикладное значение, которое сгодится им как в математике, так и в иных областях умений.
Вам понадобится
- Учебник по математике за 5-ый класс
Инструкция
1. Одним из реформирований дробей является перевод их из смешанной в неправильную. Напомним, что смешанная дробь состоит из целого числа и верной дроби. Выходит, для того дабы исполнить это реформирование необходимо:1) Умножить знаменатель дроби на целую часть.2) К полученному числу прибавить числитель. 2)=23(65/100)=23(13/20)2) 40,1=40(1/10)
2)=23(65/100)=23(13/20)2) 40,1=40(1/10)
5. Для того дабы из обычного числа сделать дробь, представьте это число в виде частного 2-х чисел. Делимое, при этом, будет являться числителем, а делитель знаменателем.Пример:8=16/2=8/1=24/3
Обратите внимание!
Наблюдательно отсчитывайте число знаков позже запятой.
Полезный совет
Припомните правила округления.
Дробь является одним из элементов формул, для ввода которых в текстовом процессоре Word существует инструмент Microsoft Equation. С поддержкой него дозволено вводить всякие трудные математические либо физические формулы, уравнения и другие элементы, включающие в себя особые символы.
Инструкция
1. Дабы запустить инструмент Microsoft Equation нужно пройти по адресу: «Вставка» -> «Объект», в открывшемся диалоговом окне, на первой вкладке из списка необходимо предпочесть Microsoft Equation и нажать «Ок» либо два раза кликнуть на выбранном пункте. Позже запуска редактора формул, перед вами откроется панель инструментов и в тексте отобразится поле для ввода формулы: прямоугольник в пунктирной рамке. Панель инструментов поделена на сегменты, в всей из них находится комплект знаков действий либо выражений. При нажатии на одну из сегментов, развернется список находящихся в ней инструментов. Из открывшегося списка нужно предпочесть необходимый символ и кликнуть на нем. Позже выбора, указанный символ появится в выделенном прямоугольнике в документе.
2. Сегмент, в которой располагаются элементы для написания дробей, находится во 2-й строке панели инструментов. При наведении на нее курсора мыши, вы увидите всплывающую подсказку «Образцы дробей и радикалов». Кликните секцию один раз и разверните список. В вывалившемся меню есть образцы для дробей с горизонтальной и косой чертой. Среди появившихся вариантов вы можете предпочесть тот, тот, что подходит для вашей задачи. Кликните на необходимом варианте. Позже нажатия, в поле для ввода, которое открылось в документе, появится символ дроби и места для ввода числителя и знаменателя, обрамленные пунктирной линией. Курсор по умолчанию механически устанавливается в поле для ввода числителя. Введите числитель. Помимо цифр дозволено так же вводить математические символы, буквы либо знаки действий. Их дозволено вводить как с клавиатуры, так и из соответствующих сегментов панели инструментов Microsoft Equation. Позже вода числителя, нажатием клавиши TAB, перейдите к знаменателю. Перейти дозволено и кликнув мышью в поле для ввода знаменателя. Как только формула написана, кликните указателем мыши в любом месте документа, панель инструментов закроется, ввод дроби будет закончен. Дабы отредактировать дробь, двукратно нажмите на ней левой кнопкой мыши.
Курсор по умолчанию механически устанавливается в поле для ввода числителя. Введите числитель. Помимо цифр дозволено так же вводить математические символы, буквы либо знаки действий. Их дозволено вводить как с клавиатуры, так и из соответствующих сегментов панели инструментов Microsoft Equation. Позже вода числителя, нажатием клавиши TAB, перейдите к знаменателю. Перейти дозволено и кликнув мышью в поле для ввода знаменателя. Как только формула написана, кликните указателем мыши в любом месте документа, панель инструментов закроется, ввод дроби будет закончен. Дабы отредактировать дробь, двукратно нажмите на ней левой кнопкой мыши.
3. Если при открытии меню «Вставка» -> «Объект», в списке вы не нашли инструмента Microsoft Equation, его нужно установить. Запустите установочный диск, образ диска либо файл дистрибутива Word. В появившемся окне инсталлятора выберите «Добавить либо удалить компоненты. Добавление либо удаление отдельных компонентов» и нажмите «Дальше». В дальнейшем окне подметьте пункт «Расширенная настройка приложений». Нажмите «Дальше». В дальнейшем окне обнаружьте пункт списка «Средства Office» и нажмите на плюсик слева. В развернувшемся списке, нас волнует пункт «Редактор формул». Кликните на значок рядом с надписью «Редактор формул» и, в открывшемся меню, нажмите «Запускать с моего компьютера». Позже этого нажмите «Обновить» и дождитесь пока пройдет установка нужного компонента.
Разная форма записи дробей может вызывать неудобство. Во-первых, не неизменно комфортно оперировать с десятичными формами, во-вторых, они зачастую отражают менее точные значения. И в этом случае вы можете преобразовать такую дробь в типичный вид.
Инструкция
1. Обратите внимание на то, что речь идет именно о реформировании десятичной дроби в типичную форму. Обратное действие не неизменно может иметь место, что связано с возникающей в некоторых случаях необходимостью округления: если в условиях данной задачи вы обязаны оперировать только точными значениями, придется оперировать только с обыкновенной формой дроби.
2. Запомните одно качество дроби, к которому сводятся все допустимые реформирования, проводимые с этой формой записи числа. Оно гласит, что умножение либо деления числителя и знаменателя на одно и то же число не приводит к изменению дроби. Причем не главно, в какой форме вы записываете число: в очевидной либо же как синус угла либо и совсем обозначив его переменной х либо у.
3. Не забывайте и о том, что в случае с десятичной дробью вы неизменно сразу можете записать ее знаменатель: это будет 10, 100, 1000 и т.д. Число нулей определяется числом знаков позже запятой. Остается осознать, что записать в числителе.
4. Выпишите в числитель все цифры десятичной дроби. Если это 0,75, то в числителе будет стоять 75, если 1,35 – 135, соответственно.
5. Приступайте к последующим реформированиям, если таковые допустимы. Это может требоваться для удачного решения задачи. Но если даже вам довольно примитивно преобразовать десятичную дробь в обычную форму, не останавливайтесь на одном действии. Учтите, что правила правильной математической записи требуют соблюдения 2-х правил. Во-первых, полученная дробь не должна сокращаться. Во-вторых, если числитель огромнее знаменателя, отменнее записать дробь в ее третье форме – смешанного числа.
6. Используйте качество дроби для того, дабы проверить вероятность сокращения. Чем поменьше знаменатель, тем поменьше вариантов вам придется перебирать. Если это 10, то проверьте, делится ли числитель на 2, 5, 10. Если 100 – на 2, 4, 5 и другие делители 100.
Видео по теме
Число , которое записано в виде целой и дробной частей, называют числом в смешанной записи. Для комфорта произношения почаще каждого это длинное наименование уменьшают до формулировки «смешанное число». Такое число имеет равную себе неправильную дробь , в которую его легко перевести.
Вам понадобится
- Смешанное число, бумага, ручка, 3 яблока, ножик.

Инструкция
1. Если вы не слишком отлично понимаете суть смешанного числа, неукоснительно возьмите бумагу и ручку, дабы не запутаться и все сделать положительно. На каждый случай приготовьте 3 яблока и ножик. Считается, что тема дробей в математике одна из самых трудных. Школьники начинают их проходить с 3-го класса и непрерывно, на всем дальнейшем ярусе обучения, возвращаются к аналогичным задачам, которые годично, раз за разом оказываются всё больше трудными.
2. Запишите смешанное число. Возможен, оно выглядит так: 2 3/4 (это то же самое, что и 2+3/4). Читается запись как «две целых три четвертых». Тут цифра 2 – это целая часть смешанного числа, а «три четвертых» – дробная часть. Для наглядности представьте его в виде 2-х целых яблок и еще одного, от которого осталось три четверти, а одну четверть, скажем, теснее съели.
3. Дабы смешанное число перевести в неправильную дробь , умножьте знаменатель его дробной части на целую часть. В данном случае это: 4х2=8. Вернитесь к наглядному примеру с яблоками. Разрежьте весь из 2-х целых плодов на четыре равных части. Позже этой операции частей также окажется восемь.
4. Дальнейшая операция: к полученному произведению прибавьте числитель дробной части смешанного числа. То есть к 8 прибавьте 3. Получится: 8+3=11. И сейчас к теснее имеющимся восьми яблочным кускам добавьте три сходственных ломтика от того яблока, которое первоначально оставалось неполным. Каждого окажется одиннадцать долек.
5. Заключительное действие: запишите получившуюся сумму на место числителя неправильной дроби. При этом знаменатель дробной части оставляйте без метаморфозы. Вывод в этом примере окажется таким: 11/4. Читается эта неправильная дробь как «одиннадцать четверых». И если вы вновь обратитесь к яблокам, то увидите, что всякий из ломтиков является четвертью от целого яблока, а каждого ломтиков одиннадцать. То есть когда вы их соберете совместно, вы здесь же получите одиннадцать четвертинок яблока.
Видео по теме
Все измерения выражаются числами, скажем, длина, площадь и объем в геометрии, расстояние и скорость в физике и т.д. Не неизменно итог получается целым, так возникают дроби. Существуют разные действия с ними и методы их реформирования, в частности, дозволено обыкновенную дробь превратить в десятичную.
Инструкция
1. Дробь – это запись вида m/n, где m принадлежит множеству целых чисел, а n – естественных. Причем если m>n, то дробь является неправильной, из нее дозволено выделить целую часть. При умножении числителя m и знаменателя n на одно и то же число итог остается постоянным. На этом правиле основаны все операции реформирования. Таким образом, дозволено превратить обыкновенную дробь в десятичную, подобрав соответствующий множитель.
2. Десятичную дробь отличает знаменатель, кратный десяти. Такая запись подобна разрядам целых чисел, идущая по возрастанию справа налево. Следственно для перевода обычной дроби надобно вычислить такой всеобщий показатель для ее делимого и делителя, дабы конечный содержал только десятичные, сотые, тысячные и т.п. доли.Пример: переведите дробь? в десятичный вид.
3. Подберите такое число, дабы итог его умножения на знаменатель был кратен 10. Рассуждения ведите от обратного: дозволено ли превратить число 4 в 10? Результат: нет, так как 10 не делится нацело на 4. Тогда 100? Да, 100 делится на 4 без остатка, в результате получается 25. Умножьте числитель и знаменатель на 25 и запишите результат в десятичном виде:? = 25/100 = 0,25.
4. Не неизменно дозволено воспользоваться способом подбора, существует еще два метода. Тезис их использования фактически один и тот же, различается лишь запись. Один из них – постепенное выделение десятичных знаков. Пример: переведите дробь 1/8.
5. Рассуждайте дальнейшим образом: 1/8 не имеет целой части, следственно, она равна 0. Запишите эту цифру и поставьте позже нее запятую; Умножьте 1/8 на 10, получите 10/8. Из этой дроби дозволено выделить целую часть, равную 1. Впишите ее позже запятой. Продолжите работу с образовавшимся остатком 2/8; 2/8*10 = 20/8. Целая часть равна 2, остаток – 4/8. Промежуточный результат – 0,12; 4/8*10 = 40/8. Из таблицы умножения следует, что 40 нацело делится на 8. На этом ваши расчеты закончены, итоговый результат – 0,125 либо 125/1000.
Из этой дроби дозволено выделить целую часть, равную 1. Впишите ее позже запятой. Продолжите работу с образовавшимся остатком 2/8; 2/8*10 = 20/8. Целая часть равна 2, остаток – 4/8. Промежуточный результат – 0,12; 4/8*10 = 40/8. Из таблицы умножения следует, что 40 нацело делится на 8. На этом ваши расчеты закончены, итоговый результат – 0,125 либо 125/1000.
6. И, наконец, 3-й способ – деление в столбик. Весь раз, когда вам доводится разделять меньшее число на большее, спускайте «сверху» нуль (см. рис).
7. Дабы превратить неправильную дробь в десятичную, необходимо вначале выделить целую часть. Скажем: 25/3 = 8 1/3. Запишите целую часть 8, поставьте запятую и переведите дробную часть 1/3 одним из описанных выше методов. К сожалению, не существует числа, кратного 10, которое делось бы на 3 без остатка. В сходственной обстановки применяется так называемый период, когда безмерно повторяющуюся цифру записывают в круглых скобках:8 1/3 ? 8,…;1/3*10 = 10/3 ? 8,3…, остаток = 1/3;1/3*10 = 10/3 ? 8,33…, остаток = 1/3;и т.д. до бесконечности.Результат: 8 1/3 = 8,3….3 = 8,(3).
Видео по теме
Стержневой спецификой человеческого интеллекта является способность к абстрактному мышлению. Одной из наивысших форм абстракции в человеческом мире является число. Выделяют несколько категорий чисел, различающихся свойствами. Особенно привычными и зачастую используемыми в повседневной жизни являются целые и действительные числа. Как водится, числа записываются в десятичной системе счисления. Действительные числа обозначаются десятичными дробями. Одним из недостатков записи дробных чисел в виде десятичных дробей является их ограниченная точность. Когда точность особенно главна, числа записывают в виде дробей (пары числитель-знаменатель). В ряде случаев дроби крайне комфортны, но арифметические операции с ними больше трудны, чем с десятичными числами. Скажем, дабы вычесть дробь с различными знаменателями , надобно совершить несколько математических действий.
Вам понадобится
- Калькулятор либо лист бумаги с ручкой.
Инструкция
1. Приведите дроби к одному знаменателю. Помножьте числитель и знаменатель первой дроби на знаменатель 2-й. Помножьте числитель и знаменатель 2-й дроби на знаменатель первой. Скажем, если начальные дроби равны 6/7 и 5/11, то дроби, приведенные к всеобщему знаменателю, будут равны 66/77 и 35/77. В данном случае числитель и знаменатель первой дроби были помножены на число 11, а числитель и знаменатель 2-й дроби – на число 7.
2. Произведите вычитание дробей. Вычтите из числителя первой дроби числитель 2-й дроби. Запишите полученное значение в качестве числителя результирующей дроби. В качестве знаменателя итога подставьте всеобщий знаменатель, полученный на предыдущем шаге. Так, при вычитании из дроби 66/77 значения дроби 35/77, получится итог 31/77 (из числителя 66 был вычтен числитель 35, а знаменатель оставлен бывшим).
3. Произведите сокращение дроби-итога, если это нужно. Подберите крупнейший всеобщий делитель, чудесный от 1 для числителя и знаменателя результирующей дроби. Поделите на него числитель и знаменатель. Запишите новые значения в качестве числителя и знаменателя итоговой дроби. Наибольшего всеобщего делителя, чудесного от 1 может и не существовать. В этом случае оставьте в качестве итога начальную дробь .
Этапы урока | Содержание урока | Примечание | Деятельность учителя | Деятельность учащихся | 1.Орг.момент. 2.Актуализация знаний. 3.Повторение. 4.Работа по теме. 5.Физминутка. 6.Работа с книгой. 7.Итог урока. Рефлексия. 8.Домашнее задание. | Чтение учителем стихотворения об осени. Проверяет готовность к уроку. Как называются числа на листочках? Что показывает знаменатель дроби? Что показывает числитель дроби? Прочитайте дроби и назовите числитель и знаменатель. Как найти разность дробей с одинаковыми знаменателями? Как найти разность дробей с разными знаменателями? А теперь проверим эти правила при вычислении. Решить примеры с дробями, узнаете автора первого учебника математики на Руси. Как фамилия автора учебника? Дополни дроби до единицы.
Вычислите: 1- ; 1- ; 1- 1 — ; 1- ; 4 — ; Какой из примеров вызывает у вас затруднения? Сейчас потренируемся в решении упражнений по данной теме. Заполни пропуски. 5 — = 4 = 4 9 — = 8 — = Вывод. № 946, №947 Самостоятельная работа по карточке. Что нового узнали? Что вспомнили на уроке? Что понравилось? Что показалось сложным? Оцените свою работу «смайликом» я узнаю ваше настроение от урока. Спасибо за урок. С.232 № 947(4-5-6) | Учащиеся готовы к уроку. На партах осенние листочки. Обыкновенные дроби. На сколько равных частей разделили целое. Сколько равных частей взяли. Учащиеся читают дроби. Чтобы найти разность дробей одинаковыми знаменателями надо из числителя первой дроби вычесть числитель второй дроби. Надо привести их к общему знаменателю. Учащиеся решают примеры. Ответы подставляют в таблицу с шифром. Магницкий. Учащиеся выполняют у доски Последний пример. Надо целое число превратить в неправильную дробь, а потом вычитать. Работу выполняют коллективно у доски. Взаимопроверка. |
Сложение и вычитание дробей с отрицательными числами
Как только вы научитесь
складывать и вычитать положительные дроби
, вы можете расширить метод, включив в него отрицательные дроби.
Обратите внимание, что:
— 2 3 такой же как — 2 3 а также 2 — 3
— 2 — 3 упрощается до 2 3
Когда вы складываете или вычитаете отрицательную дробь, вы обычно хотите учитывать числитель как отрицательный.Метод тот же, за исключением того, что теперь вам может потребоваться добавить отрицательные или положительные числители.
Пример 1:
Найдите сумму.
9 5 + ( — 4 3 )
LCM 5 а также 3 является 15 .
Чтобы сложить дроби с разными знаменателями, переименуйте дроби с общим знаменателем.
9 5 знак равно 9 × 3 5 × 3 знак равно 27 15 — 4 3 знак равно — 4 × 5 3 × 5 знак равно — 20 15
Так,
9 5 + ( — 4 3 ) знак равно 27 15 + ( — 20 15 )
Поскольку знаменатели совпадают, сложите числители.
знак равно 27 + ( — 20 ) 15 знак равно 7 15
Пример 2:
Найдите разницу.
— 7 10 — 2 15
LCM 10 а также 15 является 30 .
Чтобы вычесть дроби с разными знаменателями, переименуйте дроби с общим знаменателем.
— 7 10 знак равно — 7 10 × 3 3 знак равно — 21 год 30 2 15 знак равно 2 15 × 2 2 знак равно 4 30
Так,
— 7 10 — 2 15 знак равно — 21 год 30 — 4 30
Поскольку знаменатели одинаковы, вычтите числители.
— 21 год 30 — 4 30 знак равно — 21 год — 4 30
Упрощать. Мы получили:
— 25 30 или же — 5 6
Калькулятор дробей
Учитесь складывать, вычитать, умножать и делить дроби. Сократите дроби до наименьших значений, упростите, сравните и упорядочите дроби. Преобразуйте дроби в десятичные дроби и проценты, работайте со смешанными числами и неправильными дробями и решайте для X в уравнениях дробей с помощью онлайн-калькуляторов дробей CalculatorSoup ® .
Сократите дроби до наименьших значений, упростите, сравните и упорядочите дроби. Преобразуйте дроби в десятичные дроби и проценты, работайте со смешанными числами и неправильными дробями и решайте для X в уравнениях дробей с помощью онлайн-калькуляторов дробей CalculatorSoup ® .
Операции с дробями и манипуляции
Калькулятор дробей
Операции над правильными и неправильными дробями.Включает формулы для сложения, вычитания, умножения и деления дробей.
Сложение и вычитание дробей.
Сложите или вычтите до 10 дробей за раз и посмотрите, как найти ответ.
Смешанные числа новые решения
Смешанные числа, целые числа и дроби .Операции с целыми числами, целыми числами, смешанными числами, правильными дробями и неправильными дробями. Показывает уравнения и результаты работы калькулятора.
Смешанные фракции новые решения
(То же, что и для смешанных номеров)
Упрощение дробей
Преобразование неправильных дробей в смешанные числа.Упростите правильные и неправильные дроби, показывая работу и ответ в виде дроби или смешанного числа.
Упрощение калькулятора сложных дробей
Упростите дроби, задав числители и знаменатели любых двух смешанных чисел (смешанные дроби), правильные дроби, неправильные дроби или целые числа.
Калькулятор комплексных дробей новый
Сложение, вычитание, умножение и деление сложных дробей, содержащих смешанные числа, дроби или целые числа.
Десятичная дробь
Преобразование десятичной дроби в дробь.
Дробь в десятичную новые решения
Преобразует дробь в десятичную.
Доля к процентам
Преобразование дробей в проценты.
Процент в фракцию
Преобразование процента в дробь.
Наименьший общий знаменатель ( LCD )
Находит ЖК-дисплей дробей, целых и смешанных чисел. Показывает дроби и эквивалентные дроби с ЖК-дисплей .
Наименьшее общее кратное ( LCM )
Находит LCM целых и целых чисел.
Наибольший общий коэффициент ( GCF )
Находит GCF набора чисел, показывающих работу с использованием разложения на множители, разложения на простые множители и алгоритма Евклида.
Калькулятор соотношения
Решает задачи соотношения и пропорции для пропущенного значения соотношения в форме A: B = C: D (или эквивалентного A / B = C / D). Сравните два отношения эквивалентности: ИСТИНА или ЛОЖЬ.
Сравните два отношения эквивалентности: ИСТИНА или ЛОЖЬ.
Калькулятор отношения к дроби новый
Преобразование отношений в дроби.Введите частичное или частичное отношение к целому и найдите дробные эквиваленты.
Ratio Simplifier
Упростите и уменьшите соотношение в форме A: B. Показывает работу с шагом.
Золотое сечение
Введите одно значение в формулу золотого сечения (A + B: A = A: B), и другие значения будут сгенерированы с геометрическим представлением.
Эквивалентные дроби
Создает набор дробей, эквивалентных заданной дроби, смешанному числу или целому числу.
Неправильные дроби для смешанных чисел
Преобразуйте неправильные дроби в смешанные числа и посмотрите, как выполняется преобразование. Упростите дроби и сведите к минимуму.
Смешанные числа в неправильные дроби
Преобразуйте смешанные числа в неправильные дроби и посмотрите, как выполняется преобразование.
Преобразование смешанных чисел в десятичную
Преобразуйте смешанные числа, дроби или целые числа в десятичные числа и просмотрите работу, связанную с преобразованием.
Смешанные числа в процентах
Преобразуйте смешанные числа, дроби или целые числа в проценты и проследите за работой, связанной с преобразованием.
Порядок дробей
Упорядочивание и сортировка дробей, целых и смешанных чисел, чтобы определить, равны ли они, больше или меньше друг друга ( = или > или <). Показывает проделанную работу и преобразует входные данные в эквивалентные дроби с ЖК-дисплей .
Сравнение дробей
Сравнение дробей, целых и смешанных чисел, чтобы показать равенство или неравенство ( = или < или > ).Показывает входные данные, преобразованные в эквивалентные дроби с ЖК-дисплей .
Решение для X в дробях
Решить для неизвестных X , таких как X / 12 = 4/16 . Этот калькулятор может решить для X в долях как равенства и неравенства: <или ≤ или> или ≥ или = .Показывает работу по перекрестному умножению.
Оценка сумм и различий
Оцените суммы и разности для положительных собственных дробей, n / d, где n ≤ d и 0 ≤ n / d ≤ 1. Включает таблицу дробей для дробей порядка половин, четвертей, восьмых и шестнадцатых с их десятичными эквивалентами.
Усреднение дробей новинка
Вычисляет среднее значение набора дробей.Находит среднее значение положительных и отрицательных, правильных и неправильных дробей, целых и смешанных чисел. Включает возможность показать работу, связанную с вычислением результата.
Включает возможность показать работу, связанную с вычислением результата.
Таблица фракций
Дроби в порядке от 0 до 1, от половин до шестнадцатой. Включает десятичные эквиваленты дробей.
Строка числа дробей
Дробные части размером с шестнадцатую.
Преобразование дробей, десятичных знаков и процентов
Конвертер десятичных дробей в дробные
Конвертер десятичных чисел в проценты
Конвертер дробей в десятичные
Конвертер дробей в проценты
Конвертер процентов в десятичные
Конвертер процентов в доли
Конвертер смешанных чисел в десятичную
Конвертер смешанных чисел в проценты
Смешанные числа в неправильные дроби
Неправильные дроби для смешанных чисел
Калькулятор эквивалентных дробейИспользование калькулятора
Найдите эквивалентные дроби.Введите дробь, смешанное число или целое число, чтобы получить дроби, эквивалентные введенному вами значению. Примеры записей:
- Дробь — как 2/3 или 15/16
- Смешанное число — например, 1 1/2 или 4 5/6
- Целое число — например, 5 или 28
Что такое эквивалентные дроби?
Эквивалентные дроби — это дроби с разными числами, представляющие одну и ту же часть целого. У них разные числители и знаменатели, но их дробные значения одинаковы.
У них разные числители и знаменатели, но их дробные значения одинаковы.
Например, представьте дробь 1/2. Это означает половину чего-то. Вы также можете сказать, что 6/12 — это половина, а 50/100 — половина. Они представляют собой одну и ту же часть целого. Эти эквивалентные дроби содержат разные числа, но означают одно и то же: 1/2 = 6/12 = 50/100
Как найти эквивалентные дроби
Умножьте числитель и знаменатель дроби на одно и то же целое число. Пока вы умножаете верхнюю и нижнюю часть дроби на одно и то же число, вы не измените значение дроби и получите эквивалентную дробь.
Пример эквивалентных дробей
Найдите дроби, эквивалентные 3/4, умножив числитель и знаменатель на одно и то же целое число:
\ (\ dfrac {3} {4} \ times \ dfrac {2} {2} = \ dfrac {6} {8} \)
\ (\ dfrac {3} {4} \ times \ dfrac {3} {3} = \ dfrac {9} {12} \)
\ (\ dfrac {3} {4} \ times \ dfrac {4} {4} = \ dfrac {12} {16} \)
\ (\ dfrac {3} {4} \ times \ dfrac {5} {5} = \ dfrac {15} {20} \)
\ (\ dfrac {3} {4} \ times \ dfrac {6} {6} = \ dfrac {18} {24} \)
Следовательно, все дроби эквивалентны:
\ (\ dfrac {3} {4} = \ dfrac {6} {8} = \ dfrac {9} {12} = \ dfrac {15} {20} = \ dfrac {18} {24} \)
Обратите внимание, что если вы уменьшите все эти дроби до наименьших членов, они будут равны 3/4.
Для получения дополнительной информации о дробях см. Наш Калькулятор дробей, Упростите калькулятор дробей и Калькулятор смешанных чисел.
Калькулятор упрощенных дробей
Использование калькулятора
Преобразование неправильных дробей в смешанные числа в простейшей форме. Этот калькулятор также упрощает правильные дроби, сокращая их до наименьших значений и показывая объем работы.
Этот калькулятор также упрощает правильные дроби, сокращая их до наименьших значений и показывая объем работы.
Для упрощения дроби должно быть:
- Число, которое делится на числитель и знаменатель, чтобы его можно было уменьшить, или
- Числитель должен быть больше знаменателя (неправильная дробь), чтобы его можно было преобразовать в смешанное число.
Что такое неправильная дробь?
Неправильная дробь — это любая дробь, числитель которой больше знаменателя.Примеры неправильных дробей: 16/3, 81/9, 525/71.
Как преобразовать неправильную дробь в смешанное число
- Разделим числитель на знаменатель
- Запишите результат целого числа
- Используйте остаток как новый числитель над знаменателем. Это дробная часть смешанного числа.
Пример: преобразование неправильной дроби 16/3 в смешанное число.
- Разделим 16 на 3: 16 ÷ 3 = 5 с остатком от 1
- Результат целого числа 5
- Остаток равен 1. При 1 в числителе и 3 в знаменателе дробная часть смешанного числа равна 1/3.
- Смешанное число 5 1/3. Итак, 16/3 = 5 1/3.
По возможности, этот калькулятор сначала сокращает неправильную дробь до наименьшего члена, прежде чем найти форму смешанного числа.
Пример: преобразование неправильной дроби 45/10 в смешанное число.
Связанные калькуляторы
Дополнительное объяснение факторинга чисел для нахождения наибольшего общего множителя (GCF) см. В Калькулятор наибольшего общего коэффициента.
Если ваши неправильные дробные числа большие, вы можете использовать
Длинное деление с калькулятором остатков, чтобы найти целые числа и остатки при упрощении дробей вручную.
Чтобы выполнять математические операции с дробями, прежде чем вы их упрощаете, попробуйте наш Калькулятор дробей. Этот калькулятор также превратит неправильные дроби в смешанные числа.
Банкноты
Этот калькулятор выполняет расчет сокращения быстрее, чем другие калькуляторы, которые вы можете найти. Основная причина в том, что он использует алгоритм Евклида для уменьшения дробей, как показано на Математический форум.
Рационалов (числа со знаком, включая дроби)
Рационалы (числа со знаком, включая дроби)
Напомним, что целые числа — это положительные и отрицательные целые числа и ноль. Когда между целыми числами включены дроби и завершающие или повторяющиеся десятичные знаки, полная группа чисел называется рациональными числами . Это числа со знаком, включая дроби.Более техническое определение рационального числа — это любое число, которое может быть записано как дробь, где числитель является целым числом или целым числом, а знаменатель — натуральным числом. Обратите внимание, что дроби могут быть помещены в числовую линию, как показано на Рисунке 1
. Числовая строка, показывающая целые числа и дроби.Дроби могут быть как отрицательными, так и положительными. Отрицательные дроби обычно записываются следующим образом:
Хотя все они равны.
Правила для знаков при сложении целых чисел применимы и к дробям. Помните: Чтобы сложить дроби, вы должны сначала получить общий знаменатель.
Добавьте следующее.
Правила для знаков при сложении целых чисел также применимы к смешанным числам.
Добавьте следующее.
Правила для знаков при вычитании целых чисел применимы и к дробям. Помните: Чтобы вычесть дроби, вы должны сначала получить общий знаменатель.
Помните: Чтобы вычесть дроби, вы должны сначала получить общий знаменатель.
Вычтите следующее.
Правила для знаков при вычитании целых чисел также применимы к смешанным числам. Помните: Чтобы вычесть смешанные числа, вы должны сначала получить общий знаменатель. Если заимствование из столбца необходимо, остерегайтесь простых ошибок.
Вычтите следующее.
Проблемы, подобные предыдущим, обычно легче всего решить, сложив число с большим абсолютным значением наверху, вычтя и сохранив знак числа с большим абсолютным значением.
Правила для знаков при умножении целых чисел применимы и к дробям. Помните: Чтобы умножить дроби, умножьте числители, а затем знаменатели. По возможности всегда упрощайте до минимальных условий.
Умножьте следующее.
Можно отменить при умножении положительной и отрицательной дробей. Просто отмените, как вы это делаете при умножении положительных дробей, но обратите особое внимание на соответствующие знаки.Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Помните: Отсутствие знака означает, что понимается положительный знак.
Умножьте следующее.
Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Помните: Перед умножением смешанных чисел вы должны сначала изменить их на неправильные дроби.
Умножьте следующее.
Следуйте правилам знаков при делении целых чисел, чтобы получить правильный знак. Помните: При делении дробей сначала инвертируйте делитель, а затем умножайте.
Разделите следующее.
Следуйте правилам знаков при делении целых чисел, чтобы получить правильный знак. Помните: Перед тем, как делить смешанные числа, вы должны сначала изменить их на неправильные дроби. Затем вы должны инвертировать делитель и умножить.
Разделите следующее.
|
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, т. Е. 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически преобразуются в дроби, то есть 1,45 .
Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых и дробных чисел: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичные дроби в дроби: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.

 Сложение дробей
Сложение дробей

 Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
 (3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.
(3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.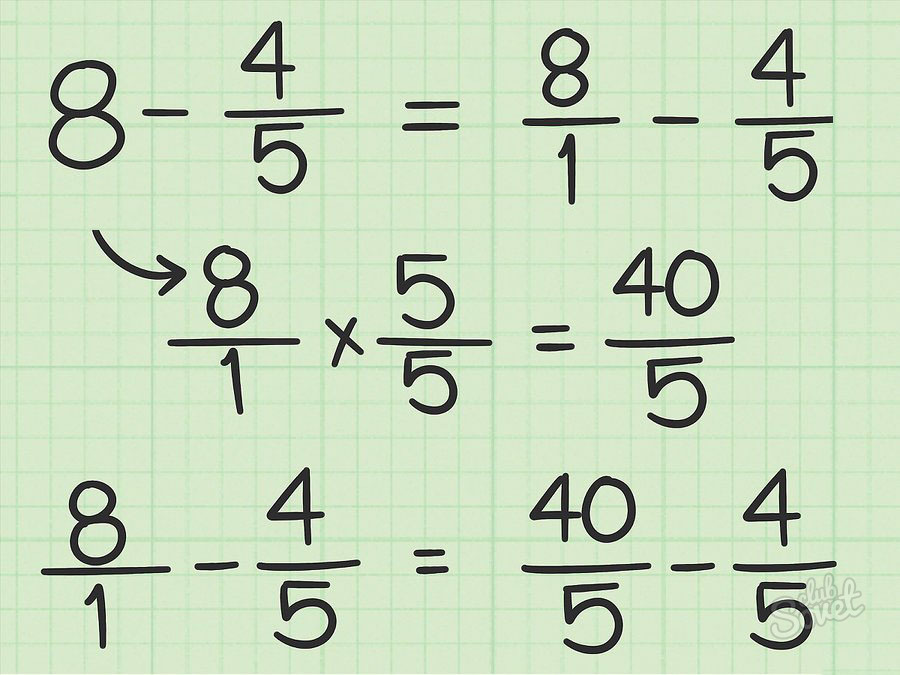 Поэтому все, что нам нужно сделать, – это вычесть 17 из 24 . Мы получаем 7 и дописываем к ней знаменатель, получаем 7 15 .
Поэтому все, что нам нужно сделать, – это вычесть 17 из 24 . Мы получаем 7 и дописываем к ней знаменатель, получаем 7 15 .
 Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065 — 13 62 = (1064 + 1) — 13 62
Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065 — 13 62 = (1064 + 1) — 13 62

 Получим \(1 = \frac{7}{7}\)
Получим \(1 = \frac{7}{7}\) Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху. 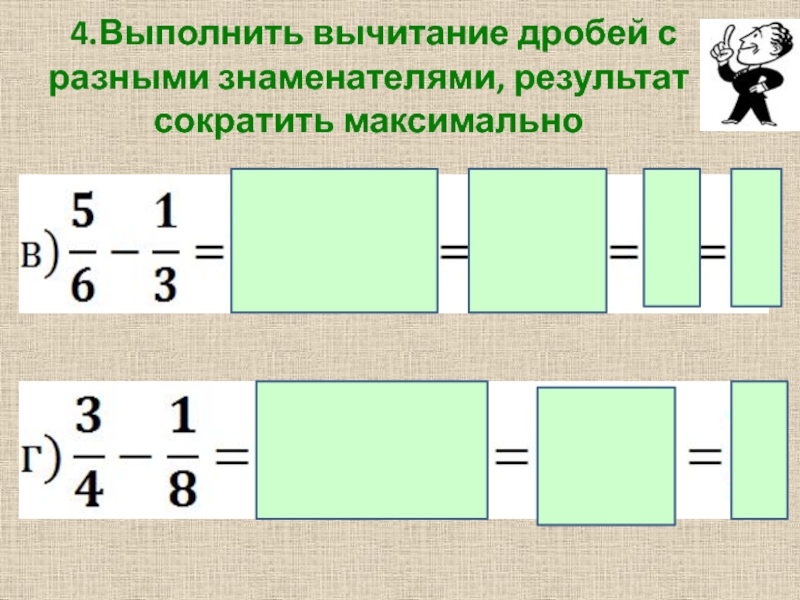 На языке Зенона это выглядит так:
На языке Зенона это выглядит так: Смотрим.
Смотрим. ..
..