Сложение и вычитание десятичных дробей
Тема: Сложение и вычитание десятичных дробей
Чтобы научиться правильно выполнять сложение десятичных дробей, достаточно выучить правило, состоящее всего из трех слов.
Три слова такие: запятая под запитой. Это самое важное, что следует помнить при сложении десятичных дробей. Складывая десятичные дроби, мы записываем их так, чтобы запятые в слагаемых находились строго одна под другой. Если после запятой в одном слагаемом цифр меньше, чем в другом, можно недостающие цифры дополнить нулями (а можно и не делать этого). В остальном сложение десятичных дробей практически ничем не отличается от сложения натуральных чисел — темы, которую проходили еще в начальной школе.
Запомните!
Если исходные десятичные дроби имеют разное количество знаков (цифр) после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Итак, ещё раз коротко основные правила сложения:
- уравниваем количество знаков после запятой;
- записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом;
- выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел;
- ставим в ответ запятую под запятыми.
Рассмотрим на примерах, как происходит сложение десятичных дробей.
Чтобы сложить 5,7 и 6,8, записываем их запятая под запятой. Затем складываем цифры по разрядам и в полученном ответе сносим запятую все по тому же правилу — запятая под запятой.
При сложении 2,256 и 0,74 числа записываем так, чтобы запятая находилась под запятой. Поскольку во втором числе после запятой два знака, а в первом — три, недостающий один знак в конце второго числа дополняем нулем (но его можно и не писать). После этого складываем числа, не обращая внимания на запятую (то есть к 2256 прибавляем 740).
Как обычно, сложение десятичных дробей начинаем с их записи таким образом, чтобы запятая стояла точно под запятой. Первым удобнее записать число, у которого количество цифр после запятой больше. Чтобы уравнять количество знаков после запятой в обоих слагаемых, во втором третьей цифрой после запятой записываем нуль. Складываем 52462 и 4980, не обращая внимания на запятую. В ответе сносим запятую под запятой.
Чтобы сложить десятичные дроби, записываем их «запятая под запятой». Складываем 4821 и 3179, не обращая внимания на запятую. После этого сносим запятую под запятой. Поскольку в десятичной дроби после запятой нули на конце не пишут, окончательный ответ 8.
Чтобы к натуральному числу прибавить десятичную дробь, можно в записи натурального числа в конце приписать запятую и столько нулей, сколько нужно (в данном примере — три). Затем складываем 35000 и 3146 и сносим запятую.
Сложение начинаем с записи десятичных дробей по правилу «запятая под запятой». Затем недостающий знак после запятой у числа 8,3 дополняем нулем. Складываем 374 и 830. В ответ сносим запятую под запятой.
Затем недостающий знак после запятой у числа 8,3 дополняем нулем. Складываем 374 и 830. В ответ сносим запятую под запятой.
Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.
Правило вычитания десятичных дробей
1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!
Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.
2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.
3) Вычитаем числа, не обращая внимания на запятую.
4) Сносим запятую под запятыми.
Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:
9,7-3,5=6,2.
Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:
23,45 — 1,5=21,95.
Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:
63,5-8,921=54,579.
Задания для самостоятельного решения:
1. Вычислите:
а) 10,3 – 8,17; б) 9,432 – 8,32; в) 7,3 + 0,865;
г) 4,1 – 2,74; д) 2,031 – 1,05; е) 3,6 + 0,55
2. Выполните сложение:
1,08 + 5,1 + 0,988 =
3. Решите уравнение:
Решите уравнение:
х +3,72 = 8
4. Вычислите выражение:
12,36 + ((11,31 + 0,03) — 1,38) — 3, 04 =
5. Решите задачу:
В первый день магазин продал 87,5 кг сахара, а во второй – на 9,85 кг больше. Сколько килограммов сахара продал магазин за два дня?
8-12. Сложение и вычитание десятичных дробей
Устный счет
Это надо знать
Сложение десятичных дробей выполняется поразрядно.
Правило сложения десятичных дробей:
1) в дробях уравниваем количество знаков после запятой;
2) записываем дроби друг под другом так, чтобы цифры одинаковых разрядов были одна под другой, запятая под запятой;
3) выполняем сложение по разрядам, ставим запятую под запятыми.
Примеры:
Найти сумму чисел: а) 12,25 + 2,56; б) 69,78 + 4,568; в) 4,321 + 15.
Законы сложения:
1. Переместительный закон
От перемены мест слагаемых сумма не меняется.
a + b = b + a
2. Сочетательный закон
От перемены места расстановки скобок сумма не меняется.
(a + b) + c = a + (b + c)
Вычитание десятичных дробей выполняется поразрядно.
Правило вычитания десятичных дробей:
1) в дробях уравниваем количество знаков после запятой;
2) записываем дроби друг под другом так, чтобы цифры одинаковых разрядов были одна под другой, запятая под запятой;
3) выполняем вычитание по разрядам, ставим запятую под запятыми.
Примеры:
Найти разность чисел: а) 12,25 — 2,56; б) 69,78 — 4,568; в) 24,321 — 15.
Видеоурок
youtube.com/embed/utTpUEuE-LM»>Домашнее задание
К уроку 8 (на 13.09)
П. 2.1
1 уровень (учебник)
№ 2.2
№ 2.7
2 уровень (сборник задач)
№ 1.25 стр. 9
Найдите число, которое больше десятичной дроби 11,063 на:
№ 1.21 (3-6) стр. 8
Найдите сумму:
К уроку 9 (на 14.09)
П. 2.1
1 уровень (учебник)
№ 2.11
№ 2.18
2 уровень (сборник задач)
№ 1.22 (1-4) стр. 8
Выполните сложение:
№ 1.23 стр. 9
№ 5.12 стр.
Сумма двух последовательных четных чисел равна 978. Найдите эти числа.
К уроку 10 (на 15.09)
П. 2.2
1 уровень (учебник)
№ 2.29
№ 2.30
2 уровень (сборник задач)
№ 1.26 стр. 9
Используя законы сложения, найдите сумму:
1) 4,83 + 6,669 + 3,331 + 5,17;
2) 9,6099 + 15,03 + 4,07 + 0,9001;
3) 351,75 + 30,048 + 0,25 + 0,952;
4) 6,094 + 6,099 + 3,006 + 2,001.
№ 1.39 стр. 11
Расположите числовые выражения A, B, C, D в порядке убывания их значений, если:
A = 12,9086 + 5093,1;
B = 129,086 + 5093,1;
C = 12,9086 + 5,0931;
D = 12,9086 + 509,31.
№ 5.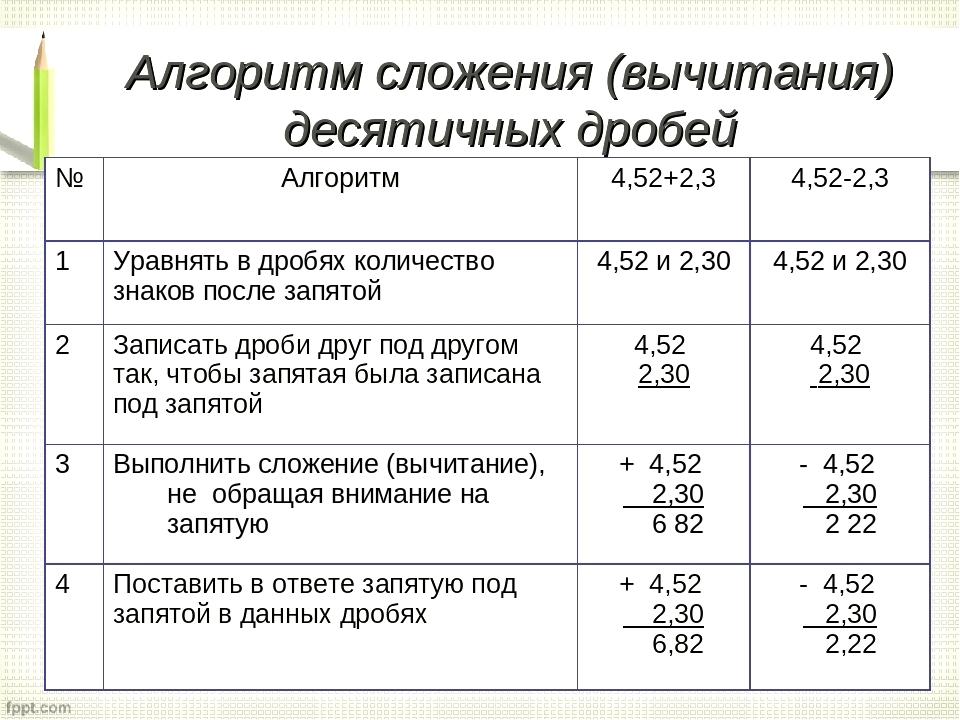 13 стр. 120
13 стр. 120
Сумма двух последовательных нечетных чисел равна 2044. Найдите эти числа.
К уроку 11 (на 16.09)
П. 2.3
1 уровень (учебник)
№ 2.41
№ 2.42
2 уровень (сборник задач)
№ 1.27 стр. 9
Найдите разность:
1) 197,364 — 0,364; 2) 51,0098 — 51; 3) 2673,48 — 73,48; 4) 6,4957 — 0,0957.
№ 1.40 стр. 11
Расположите числовые выражения P, T, K, M в порядке возрастания их значений, если:
P = 0,0298 — 0,00043;
T = 0,0298 — 0,0043;
K = 0,00298 — 0,000043
M = 0,298 — 0,0043.
№ 5.46 стр. 125
Доберман съедает порцию корма за 7 мин, а чау-чау ту же порцию — за 5 мин. За какое время, не конфликтуя, собаки съедят одну порцию корма вдвоем?
К уроку 12 (на 19. 09)
09)
П. 2.3
1 уровень (учебник)
№ 2.60
№ 2.57 (1-4)
2 уровень (сборник задач)
№ 1.29 стр. 9
Найдите значения выражения:
1) 25 — 24,39; 2) 95 — 0,62; 3) 100 — 99,99; 4) 3,489 — 2; 5) 791,54 — 91; 6) 304,89 — 4,89.
№ 1.37 стр. 11
Найдите значение выражения:
1) 9,604 — 5,21 — 0,809;
2) 99,009 — 9,09 — 9,9;
3) 72,6012 — 0,0012 — 32,6;
4) 315,06403 — 5,064 — 100,003.
№ 3.1 (1, 2) стр. 76
Решите уравнение:
1) х + 7,293 = 18,293;
2) 50,101 + у = 49.
Онлайн урок: Сложение и вычитание десятичных дробей по предмету Математика 5 класс
Десятичные дроби используют в самых различных сферах деятельности человека.
Они значительно упрощают вычисления и измерения.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Десятичные дроби удобны при решении профессиональных и бытовых задач.
Важным преимуществом десятичных дробей является то, что математические действия, производимые с ними, схожи по своей сути с арифметическими действиями, которые можно совершать с натуральными числами.
Десятичные дроби можно сравнивать, складывать, вычитать, умножать и делить, возводить в степень.
На данном уроке рассмотрим правила сложения и вычитания десятичных дробей.
Узнаем, как складывать и вычитать десятичные дроби столбиком.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Выясним, как на координатной прямой можно отметить десятичную дробь, не переводя ее в обыкновенную дробь.
Рассмотрим пример решения составной текстовой задачи на сложение и вычитание десятичных дробей арифметическим и алгебраическим способом.
Рассмотрим правила сложения десятичных дробей на примере.
Разберем простую арифметическую задачу.
На детский праздник купили 2,250 кг шоколадных конфет и 3,550 кг карамели.
Сколько всего конфет купили на детский праздник?
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Решение:
Кратко запишем условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Чтобы найти ответ на поставленный вопрос (найти общее количество конфет), необходимо сложить шоколадные конфеты и карамель вместе.
Схематически изобразим условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сложим десятичные дроби 2,250 и 3,550.
Сложение десятичных дробей можно свести к сложению смешанных чисел, которые соответствуют этим дробям.
Десятичной дроби 2,250 соответствует смешанное число \(\mathbf{2\frac{250}{1000}}\).
Десятичной дроби 3,550 соответствует смешанное число \(\mathbf{3\frac{550}{1000}}\).
Нам известно, как найти сумму двух смешанных чисел.
Сложим целые части отдельно, дробные- отдельно.
\(\mathbf{2\frac{250}{1000} + 3\frac{550}{1000} = 2 + \frac{250}{1000} + 3 + \frac{550}{1000} = (2 + 3) + (\frac{250}{1000} + \frac{550}{1000}) =}\)
\(\mathbf{= 5 + \frac{800}{1000} = 5\frac{800}{1000}}\) (кг) всего конфет купили для детского праздника.
Ответ: \(\mathbf{5\frac{800}{1000} = 5,800}\) (кг).
Такой же ответ можно получить, не обращая десятичные дроби в смешанные числа.
Выясним, как и по каким правилам складывают десятичные дроби.
Так как запись десятичных дробей основана на позиционной системе счисления, в которой значение каждого числового знака зависит от позиции (от места) в числе, десятичные дроби удобно складывать поразрядно.
В связи с этим, чтобы сложить дроби, записанные в десятичной форме, необходимо убедиться, что в числах одинаковое количество разрядов после запятой.
Сложение десятичных дробей практически не отличается от сложения натуральных чисел, удобнее всего выполнять операцию сложения в столбик, записывая соответствующие разряды друг под другом.
Чтобы сложить две десятичные дроби столбиком, необходимо соблюдать следующие правила:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
- Уравнять в слагаемых количество цифр после запятой, дописав нужное количество нулей к одной из дробей.

- Записать слагаемые друг под другом так, чтобы разряды второго слагаемого располагались строго под соответствующими разрядами первого слагаемого, а запятая под запятой.
- Сложить поразрядно числа, не обращая внимание на запятую так же, как выполняется сложение столбиком натуральных чисел.
- Поставить в полученной сумме запятую под запятыми слагаемых.
Используя данный алгоритм сложения десятичных дробей, решим задачу про конфеты, рассмотренную в начале нашего урока.
Вспомним условие задачи.
2,250 кг шоколадных конфет
3,550 кг карамельных конфет
Общее количество конфет- ? кг
Решение:
Найдем общее количество конфет, купленных на праздник, сложив две десятичные дроби 2,250 и 3,550.
Количество десятичных знаков в данных дробях одинаково, поэтому сразу запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге операция сложения двух десятичных дробей выглядит так:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
2,250 + 3,550 = 5,800 (кг) конфет купили для детского праздника
Ответ: 5,800 (кг).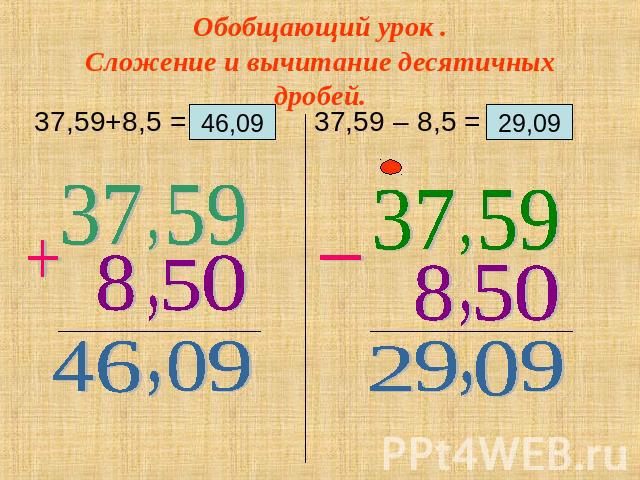
При сложении десятичных дробей получился результат такой же, как при сложении смешанных чисел, которые этим дробям соответствуют.
Как видите, операция сложения десятичных дробей мало отличается от сложения натуральных чисел, важно только верно расположить разряды и десятичные запятые слагаемых.
Встречаются случаи, когда приходится складывать десятичные дроби, в которых различное количество десятичных знаков.
Если после запятой в одном из слагаемых десятичных знаков меньше, чем в другом, количество знаков нужно уравнять, недостающие разряды следует заменить нулем.
После этого десятичные дроби складывают.
Рассмотрим поясняющий пример.
Найдем сумму десятичных дробей 0,434 и 0,28.
В первой десятичной дроби 0,434 после запятой три десятичных знака (разряд десятых, сотых, тысячных).
Во второй десятичной дроби 0,28 после запятой два десятичных знака (разряд десятых и сотых, отсутствует разряд тысячных).
Уравняем количество десятичных знаков.
Допишем нуль справа от десятичной запятой после самой правой ненулевой цифры (в разряде тысячных).
В итоге получим десятичную дробь 0,280, равную дроби 0,28.
Столбиком запишем дроби 0,434 и 0,280 так чтобы одноименные разряды и десятичные запятые находились строго друг под другом.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Далее выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
При сложении сотых получается двузначное число 11, поэтому единицу запишем под чертой, а свободный десяток перенесем в старший разряд.
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге операция сложения двух десятичных дробей 0,434 и 0,280 будет выглядеть так:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сложение десятичной дроби и натурального числа.
Иногда приходится находить сумму десятичной дроби и натурального числа.
По сути, чтобы сложить натуральное число с десятичной дробью, необходимо это натуральное число и целую часть десятичной дроби сложить, а дробную часть оставить без изменений.
При сложении десятичной дроби и натурального числа в конце натурального числа можно поставить десятичную запятую и приписать столько нулей, сколько содержится десятичных знаков в дроби.
Данные действия не изменят значение натурального числа.
Рассмотрим поясняющий пример, решим простую задачу на сложение.
С первого участка собрали 60 т зерна, а со второго на 16,8 т больше.
Сколько тонн зерна собрали со второго участка?
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Решение:
Запишем кратко условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Из условия задачи известно, что со второго участка собрали зерна больше, чем с первого, т.е. получается со второго поля убрали столько же, сколько и с первого, да еще 16,8 т.
Схематично изобразим условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Такая задача, в которой одно число увеличивают на какое-нибудь другое число (задача на увеличение на некоторое количество единиц), решается всегда сложением.
Сложим натуральное число 60 с десятичной дробью 16,8.
Для этого прибавим к целой части десятичной дроби натуральное число, а дробную часть оставим прежней.
Целая часть десятичной дроби 16,8 равна 16, прибавим к ней 60, получим число 76, поставим запятую и припишем дробную часть заданной десятичной дроби.
16,8 + 60 = 76,8 (т) зерна собрали со второго участка.
Ответ: 76,8 (т).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сложение десятичных дробей с обыкновенной дробью (смешанным числом).
- Сложение десятичных дробей с обыкновенной дробью (смешанным числом) можно свести к сложению обыкновенных дробей (смешанных чисел).
Для этого десятичную дробь необходимо представить в виде обыкновенной дроби.
- Сложение десятичных дробей с обыкновенной дробью (смешанным числом) можно свести к сложению десятичных дробей, представив обыкновенную дробь (смешанное число) в виде десятичной дроби.
Для примера сложим смешанное число и десятичную дробь.
Найдите сумму \(\mathbf{1\frac{2}{10} + 0,5}\).
Первый способ.
Переведем десятичную дробь в обыкновенную.
\(\mathbf{0,5 = \frac{5}{10}}\)
Теперь сумму смешанного числа \(\mathbf{1\frac{2}{10}}\) и обыкновенной дроби \(\mathbf{\frac{5}{10}}\) найдем по правилу сложения смешанного числа и обыкновенной дроби.
Сложим смешанное число и правильную дробь, найдем только сумму дробной части смешанного числа и этой дроби, целую же часть смешанного числа при этом оставим без изменений.
\(\mathbf{1\frac{2}{10} + \frac{5}{10} = 1 + \frac{2}{10} + \frac{5}{10} = 1 + (\frac{2}{10} + \frac{5}{10}) = 1 + \frac{7}{10} = 1\frac{7}{10}}\)
Переведем смешанное число \(\mathbf{1\frac{7}{10}}\) в десятичную дробь.
\(\mathbf{1\frac{7}{10} = 1,7}\)
Ответ: 1,7.
Второй способ.
Представим смешанное число в виде десятичной дроби.
\(\mathbf{1\frac{2}{10} = 1,2}\)
Теперь сумму десятичной дроби 1,2 и десятичной дроби 0,5 найдем по правилу сложения десятичных дробей.
Сумму чисел 1,2 и 0,5 запишем столбиком, располагая соответствующие разряды друг под другом, запятая под запятой.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Ответ: 1,7.
Вычисляя сумму первым и вторым способом, получили одинаковые ответы, следовательно, рассмотренные нами способы нахождения суммы десятичной дроби и обыкновенной дроби (смешанного числа) равноправны.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Рассмотрим правила вычитания десятичных дробей.
Так как десятичная дробь- это десятичная запись обыкновенной дроби, вычитание двух десятичных дробей можно свести к разности соответствующих обыкновенных дробей.
Рассмотрим пример вычисления десятичных дробей.
Задача
Провод длинной 15,45 м разрезали на две части.
Длина первой части провода 5,20 м.
Какова длина второй части провода?
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Решение:
Кратко запишем условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Две части провода вместе представляют собой целый провод.
Длина первой части провода- это известное слагаемое.
Длина второй части провода- это неизвестное слагаемое.
Схематически изобразим условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Найдем разность двух десятичных дробей 15,45 и 5,2.
Представим заданные десятичные дроби в виде смешанных чисел.
Десятичной дроби 15,45 соответствует смешанное число \(\mathbf{15\frac{45}{100}}\).
Десятичной дроби 5,2 соответствует смешанное число \(\mathbf{5\frac{2}{10}}\).
Приведем дроби к общему знаменателю.
Десятичная дробь 15,45 содержит два десятичных знака (разряд десятых и разряд сотых).
Десятичная дробь 5,2 содержит один десятичный знак (разряд десятых).
Чтобы уравнять количество знаков после запятой, запишем нуль в дроби 5,2 после разряда десятых.
Получим число 5,20, равное 5,2.
Десятичная дробь 5,20 соответствует смешанному числу \(\mathbf{5\frac{20}{100}}\).
После того, как мы уравняли знаменатели дробных частей смешанных чисел, можно приступать к вычитанию.
\(\mathbf{15\frac{45}{100} — 5\frac{20}{100} = (15 + \frac{45}{100}) — (5 + \frac{20}{100}) = (15 — 5) + (\frac{45}{100} — \frac{20}{100}) = 10\frac{25}{100}}\)
Переведем смешанное число \(\mathbf{10\frac{25}{100}}\) в десятичную дробь.
\(\mathbf{10\frac{25}{100} = 10,25}\) (м) длина второй части провода
Ответ: 10,25 (м).
Такой же ответ можно получить, не переводя десятичные дроби в смешанные числа.
Так же как при сложении, десятичные дроби удобно вычитать в столбик.
Операция вычитания десятичных дробей столбиком очень похожа на вычитание натуральных чисел аналогичным способом.
Выполняя вычитание десятичных дробей столбиком, необходимо соблюдать несложные правила:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
- Уравнять количество десятичных знаков в уменьшаемом и вычитаемом (если это требуется), дописав необходимое количество нулей к одной из дробей.
- Вычитаемое записать под уменьшаемым в столбик так, чтобы соответствующие их разряды находились строго друг под другом, запятая под запятой.
- Выполнить вычитание столбиком так, как вычитают натуральные числа (не обращая внимание на запятые).
- В полученной разности поставить запятую так, чтобы она находилась строго под запятыми уменьшаемого и вычитаемого.

Воспользуемся данным алгоритмом при решении задачи.
Вспомним задачу про провод, рассмотренную выше.
Кратко запишем условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Две части провода вместе представляют собой целый провод.
Длина первой части провода- это известное слагаемое.
Длина второй части провода- это неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Найдем разность двух десятичных дробей 15,45 и 5,2.
Уравняем количество знаков в уменьшаемом и вычитаемом, для этого в дробную часть десятичной дроби 5,2 в разряд сотых запишем нуль.
Получим число 5,20, равное 5,2.
Запишем уменьшаемое 15,45 и вычитаемое 5,20 столбиком так, чтобы соответствующие их разряды находились строго друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Вычтем дроби, не обращая внимание на десятичные запятые.
В полученной разности запятую поставим строго под запятыми, стоящими в уменьшаемом и вычитаемом.
Вычитание десятичных дробей столбиком будет выглядеть так:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В итоге получаем:
15,45 – 5,20 = 10,25 (м) длина второй части провода.
Ответ: 10,25 (м).
При вычитании десятичных дробей получился результат такой же, как при вычитании смешанных чисел, которые этим дробям соответствуют.
Операция вычитания десятичных дробей практически не отличается от вычитания натуральных чисел, важно только верно расположить разряды и десятичные запятые уменьшаемого и вычитаемого.
Вычитание десятичной дроби из натурального числа.
Вычитание десятичной дроби из натурального числа удобней выполнять в столбик.
Натуральное число в таком случае лучше представить в виде десятичной дроби, заменив дробную часть нулями.
Рассмотрим пример.
Периметр треугольника равен 34 см.
Сумма двух его сторон равна 23,1 см.
Найдите длину его третьей стороны.
Сделаем условный рисунок.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Пусть a, b, c— стороны треугольника, Р— это периметр треугольника- сумма длин трех его сторон.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Представим натуральное число 34 в виде десятичной дроби.
Вычитаемая дробь имеет один знак в дробной части, поэтому после натурального числа 34 поставим десятичную запятую, а после нее запишем один нуль, получим число 34,0 (тридцать четыре целых ноль десятых).
Выполним вычитание десятичных дробей 34,0 и 23,1 столбиком.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Так как из нуля единица не вычитается, займем десяток единиц из старшего разряда, при этом в нем на один десяток единиц станет меньше.
В итоге получаем:
c = 34 – 23,1 = 10,9 (см)- длина третьей стороны треугольника.
Ответ: с = 10,9 (см).
Вычитание натурального числа из десятичной дроби.
Чтобы вычесть натуральное число из десятичной дроби, необходимо это натуральное число вычесть из целой части уменьшаемой десятичной дроби, при этом дробную часть десятичной дроби необходимо оставить без изменений.
Пример.
Решим уравнение 59,3 – х = 18.
Найдем значение неизвестного х, при котором данное уравнение обратиться в верное равенство.
В заданном уравнении неизвестное является вычитаемым.
Чтобы найти вычитаемое (х), необходимо из уменьшаемого вычесть разность.
59,3 – х = 18
х = 59,3 – 18
Вычтем из десятичной дроби натуральное число по правилу: из целой части десятичной дроби 59,3 вычтем число 18, получим число 41, а дробную часть оставим без изменений.
х = 41,3
Проверка:
В исходное уравнение 59,3 – х = 18 вместо неизвестного х подставим найденное число х = 41,3.
59,3 – 41,3 = 18
Выполним вычитание столбиком двух десятичных дробей 59,3 и 41,3.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
18,0 = 18 (получили верное равенство, значит корень уравнения найден верно).
Ответ: х = 41,3.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и наоборот.
Первый способ.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и обыкновенной (смешанного числа) из десятичной можно свести к разности двух обыкновенных дробей (к разности двух смешанных чисел).
Для этого десятичную дробь нужно представить в виде обыкновенной дроби (смешанного числа) и выполнить вычитание двух обыкновенных дробей (смешанных чисел).
Второй способ.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и обыкновенной (смешанного числа) из десятичной можно свести к разности двух десятичных дробей.
Для этого обыкновенную дробь (смешанное число) нужно представить в виде десятичной дроби и выполнить вычитание двух десятичных дробей.
Рассмотрим пример.
Найдите значение выражения \(\mathbf{27\frac{35}{100} — 6,11}\).
Решение №1.
Переведем десятичную дробь 6,11 в смешанное число.
\(\mathbf{6,11 = 6\frac{11}{100}}\)
Подставим в исходное выражение вместо десятичной дроби 6,11 полученное смешанное число \(\mathbf{6\frac{11}{100}}\).
Найдем разность двух смешанных чисел.
\(\mathbf{27\frac{35}{100} — 6\frac{11}{100} = (27 — 6) + (\frac{35}{100} — \frac{11}{100}) = 21 + \frac{24}{100} = 21\frac{24}{100}}\)
Решение №2.
Представим смешанное число \(\mathbf{27\frac{35}{100}}\) в виде десятичной дроби.
\(\mathbf{27\frac{35}{100} = 27,35}\)
Подставим в исходное выражение вместо смешанного числа \(\mathbf{27\frac{35}{100}}\) соответствующую ему десятичную дробь 27,35.
Найдем разность двух десятичных дробей: 27,35 – 6,11.
Выполним вычитание столбиком.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В результате получили десятичную дробь 21,24.
Находя значение выражения \(\mathbf{27\frac{35}{100} — 6,11}\) первым и вторым способом, получили один и тот же ответ, что доказывает равенство этих двух способов вычисления.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Математические операции сложения и вычитания часто приходятся использовать при решении уравнений и различных задач.
Для одной и той же задачи может существовать несколько верных способов ее решения.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Выбрав верную логику рассуждения, можно значительно упростить и ускорить процесс решения текстовой задачи.
Попробуем решить составную текстовую задачу на сложение и вычитание десятичных дробей арифметическим и алгебраическим способом.
При решении задач тем и другим способом необходимо учитывать и соблюдать основные свойства и правила математических операций, применять известные правила упрощения и преобразования выражений.
Задача.
В трехкомнатной квартире, площадью 51,5 м2, первая комната имеет площадь 10,5 м2, площадь второй комнаты на 12,3 м2 больше площади первой.
Какова площадь третьей комнаты?
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Решим данную задачу арифметическим способом (составлением выражения).
Запишем кратко условие задачи.
Площадь первой комнаты- 10,5 м2
Площадь второй комнаты- 10,5 + 12,3 м2
Площадь третьей комнаты- ? м2
Общая площадь квартиры- 51,5 м2.
Чтобы найти площадь третьей комнаты, необходимо из общей площади трехкомнатной квартиры вычесть площадь первой и второй комнаты.
Составим выражение:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Найдем значение полученного выражения.
Данное выражение содержатся сразу несколько арифметических операций и скобки.
Определим порядок действий в данном выражении, используя правила, которые определяют порядок выполнения действий в математических выражениях.
1) Это выражение содержит скобки, следовательно, первым делом выполним действия в них.
Найдем сумму двух десятичных дробей 10,5 и 12,3 столбиком.
Количество десятичных знаков в десятичных дробях одинаково, поэтому сразу запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Поразрядно выполним сложение, в полученной сумме поставим десятичную запятую так, чтобы она находилась под запятыми слагаемых.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Оставшиеся за скобками действия- это действия первой ступени (сложение и вычитание), они выполняются по порядку следования слева направо.
2) Найдем разность десятичных дробей 51,5 и 10,5.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
3) Найдем разность значений, которые были получены во втором и первом действии, т.е. из десятичной дроби 41,0 вычтем десятичную дробь 22,8.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В результате получим:
51,5 – 10,5 – (10,5 + 12,3) = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Эту же задачу можно решить арифметическим способом, но по действиям.
Запишем кратко условие задачи.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Площадь третьей комнаты- ? м2
Общая площадь квартиры- 51,5 м2.
В этом случае решение заданной задачи будет состоять из следующих этапов:
- Найдем площадь второй комнаты (данное действие мы выполняли, решая задачу первым способом).

- Сложив результат, полученный в первом действии, с площадью первой комнаты, определим общую площадь двух комнат- первой и второй вместе.
- Из площади всей трехкомнатной квартиры вычтем общую площадь первой и второй комнат.
1. 10,5 + 12,3 = 22,8 (м2) площадь второй комнаты.
2. Чтобы высчитать площадь второй комнаты, выполним сложение двух десятичных дробей столбиком:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
10,5 + 22,8 = 33,3 (м2) площадь первой и второй комнат вместе.
3. Чтобы высчитать площадь третьей комнаты, выполним вычитание двух десятичных дробей столбиком:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
51,5 – 33,3 = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Решим задачу алгебраическим способом.
Кратко запишем условие задачи.
Площадь первой комнаты- 10,5 м2
Площадь второй комнаты- 10,5 + 12,3 м2
Пусть х м2 площадь третьей комнаты
Зная, что площадь всей квартиры равна 51,5 м2, составим уравнение.
10,5 + (10,5 + 12,3) + х = 51,5
Упростим уравнение: выполним действие в скобках, т.е. найдем сумму чисел 10,5 и 12,3, полученный результат сложим с первым слагаемым. (данные действия мы уже выполняли, решая задачу арифметическим способом).
10,5 + (10,5 + 12,3) = 10,5 + 22,8 = 33,3
В итоге получаем, что целое выражение 10,5 + (10,5 + 12,3) тождественно равно 33,3.
Подставим в исходное уравнение вместо суммы трех десятичных дробей результат их суммы: 33,3.
Получим простое уравнение с неизвестным слагаемым.
33,3 + х = 51,5
х = 51,5 – 33,3
х = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Все три способа решения задачи равноправны и дают одинаковый результат.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сложение и вычитание десятичных дробей. Решение задач на сложение и вычитание десятичных дробей.
- Альфашкола
- Статьи
- Сложение и вычитание десятичных дробей
Для того чтобы сложить или вычесть две и более десятичных дроби воспользуемся правилом столбика. Запишем десятичные запятые так, чтобы они находились одна под другой, то есть были в одном столбике. Сотни должны находиться под сотнями, десятки под десятками. Двадцать пять сотых – это ноль целых, две десятых и 5 сотых. Девять десятых – 0 целых и девять десятых. Ниже расписаны классы целых, десятых и сотых.
Запишем десятичные запятые так, чтобы они находились одна под другой, то есть были в одном столбике. Сотни должны находиться под сотнями, десятки под десятками. Двадцать пять сотых – это ноль целых, две десятых и 5 сотых. Девять десятых – 0 целых и девять десятых. Ниже расписаны классы целых, десятых и сотых.
\(0,25=0+0,2+0,05\)
\(0,9=0+0,9\)
\(2,25=2+0,2+0,05\)
\(3,102=3+0,1+0,002\)
Разобрались с этим, двигаемся дальше.
Задача 1. Сложить две дроби \(0.25\) и \(0,9\).
Решение. Запишем запятые в один столбик, затем складываем по отдельности каждую цифру.
Ответ: \(1,15\).
Распространенная ошибка, заключается в том, что \(5\) прибавляется к \(9\). Сотые приравниваются с десятками, а так делать нельзя, \(5\) – сотые части, \(9\) – десятые. Позиция значения места в столбике должна быть строгой, и основываться на десятичной запятой.
Позиция значения места в столбике должна быть строгой, и основываться на десятичной запятой.
Бывают случаи, когда у десятичных чисел не одинаковое количество цифр после запятой, тогда можно добавить ноль справа.
Задача 2. Вычесть две дроби 0,92 и 0,7.
Решение. Добавим один ноль справа у дроби 0,7 для удобства вычисления:
Ответ: \(0,22\).
Когда мы прибавляем десятичную дробь к натуральному числу, то в конце числа ставим запятую и столько нулей, сколько нам необходимо, чтобы приравнять цифры.
Выводы. При сложении и вычитании десятичных дробей в столбик существуют следующие правила:
- запятая располагается строго под запятой;
- если нужно приравнять цифры, то справа добавляются нули у десятичного числа, а у натурального числа ставится в конце запятая и добавляется необходимое количество нулей.

- в ответ записывается запятая под запятой;
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Оксана Николаевна Хаустова
Репетитор по математике
Стаж (лет)
Образование:
Саратовский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Готовлю к ВПР и ОГЭ по русскому языку. Учитель первой категории. Имею большой опыт работы с детьми. На своих уроках стараюсь легко и доступно преподносить материал. Надеюсь, что полученные знания помогут выполнять текущие контрольные работы, а также в дальнейшем успешно сдать ОГЭ по предмету.
Готовлю к ВПР и ОГЭ по русскому языку. Учитель первой категории. Имею большой опыт работы с детьми. На своих уроках стараюсь легко и доступно преподносить материал. Надеюсь, что полученные знания помогут выполнять текущие контрольные работы, а также в дальнейшем успешно сдать ОГЭ по предмету.
Анастасия Сергеевна Черная
Репетитор по математике
Стаж (лет)
Образование:
Кубанский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов. Подготовка к ОГЭ, ЕГЭ (базовый и профильный). Люблю математику за то, что она развивает аналитическое и критическое мышление
Системно-деятельностный подход
Информационно-развивающий и репродуктивный методы
Подробное и доступное объяснение, уважительное отношение, индивидуальный подход
Умею находить подход к ученикам любого уровня подготовки.
Подготовка к ОГЭ, ЕГЭ (базовый и профильный). Люблю математику за то, что она развивает аналитическое и критическое мышление
Системно-деятельностный подход
Информационно-развивающий и репродуктивный методы
Подробное и доступное объяснение, уважительное отношение, индивидуальный подход
Умею находить подход к ученикам любого уровня подготовки.
Наталья Николаевна Шарапова
Репетитор по математике
Стаж (лет)
Образование:
Челябинский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике с 1 по 11 класс. Подготовка к ОГЭ/ЕГЭ, профиль до 70 баллов. Репетитор по информатике для 7-9 классов. Люблю математику и информатику, потому что просто люблю. Если бывает трудно, то предлагаю идти вместе. Когда человек не один, то всегда легче и интереснее. Заодно и вспомним, что забыл и выясним, что не знал. До встречи!
Подготовка к ОГЭ/ЕГЭ, профиль до 70 баллов. Репетитор по информатике для 7-9 классов. Люблю математику и информатику, потому что просто люблю. Если бывает трудно, то предлагаю идти вместе. Когда человек не один, то всегда легче и интереснее. Заодно и вспомним, что забыл и выясним, что не знал. До встречи!
Похожие статьи
- Площадь параллелепипеда
- Факультет Социологии (НИУ ВШЭ)
- РУДН: факультет ветеринарии
- Задачи на числа и их свойства
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 3)
- Задачи на движение по воде
- Как вести себя со сложными подростками?
- Интересные факты об устройстве Вселенной
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
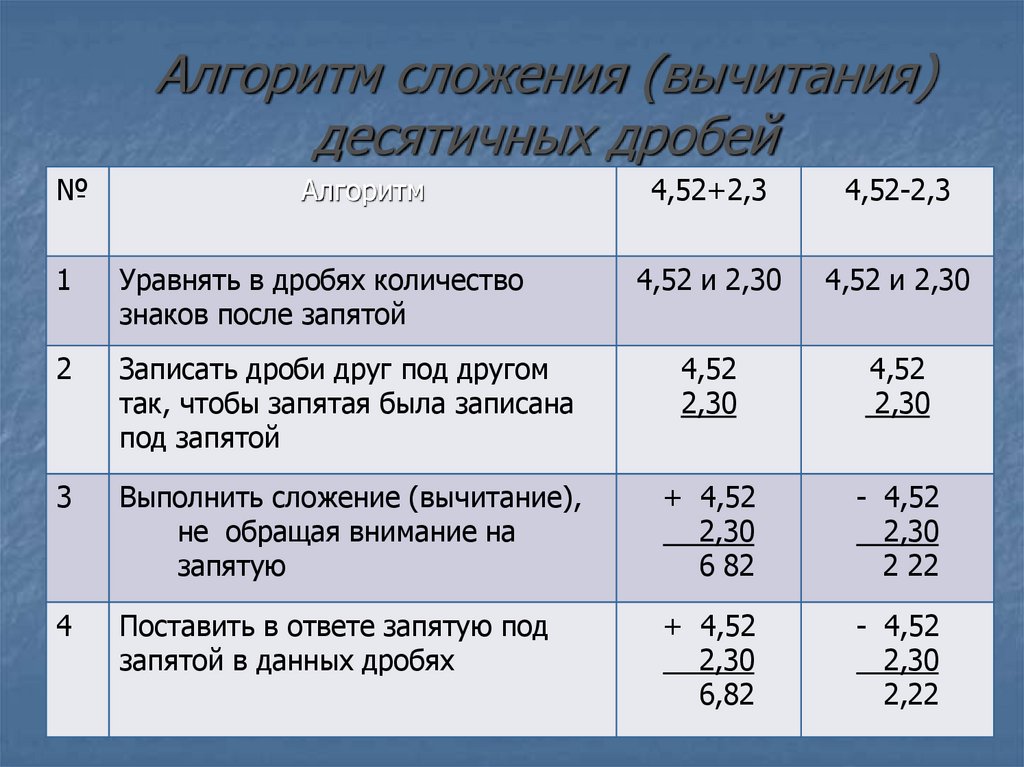
Алгоритм сложения (вычитания) десятичных дробей
Прозвенел звонок веселый,
Мы начать урок готовы!
Будем думать, рассуждать
И друг другу помогать!
2.
 Не бойся, когда не знаешь: страшно, когда знать не хочется
Не бойся, когда не знаешь: страшно, когда знать не хочется3. Алгоритм сложения (вычитания) десятичных дробей
1) Записать дроби в столбик друг под другом так,чтобы запятая была под запятой.
2) Уравнять в дробях количество цифр после
запятой нолями.
3) Выполнить сложение (вычитание), не обращая
внимания на запятые.
4) Поставить в ответе запятую под запятыми.
4. Алгоритм умножения десятичных дробей
1) Записать дроби в столбик друг под другом,не обращая внимания на запятые
(как натуральные числа).
2) Выполнить умножение, не обращая внимания
на запятые.
3) В ответе отделить запятой справа столько
цифр, сколько их было после запятых в обоих
множителях вместе.
5. Алгоритм деления десятичных дробей
1)Определить сколько цифр после запятой в
делителе (число на которое делим).
2) В делимом и делителе перенести запятую
вправо на столько цифр, сколько их после
запятой в делителе.
3) Выполнить деление столбиком на
натуральное число.

4) После окончания деления целой части
поставить в частном (в ответе) запятую и
продолжить деление (при необходимости к
остатку от деления приписать ноль).
6. Проверь себя
2,193 + 15,7 = 17,89370,4 – 5,631 = 64,769
35 – 16,4 = 18,6
206,4 · 0,9 = 185,76
0,45 · 1,3 = 0,585
0,004 · 0,28 = 0,00112
4,96 : 0,4 = 12,4
0,153 : 0,15 = 1,02
8 : 2,5 = 3,2
7. Задание 2. Зашифрована фамилия великого математика. Ответы замените буквами и узнаете его фамилию
Е Р П Е Л К6,155 1,24 90,34 25,4 1,712 4,05
Иоганн Кеплер –
великий немецкий
математик, физик и
астроном
Годы жизни: 1571-1630
Задание 3.
а) В таблице приведены нормативы по бегу на 30 метров
для обучающихся 9-х классов.
Мальчики
Девочки
Отметка
«отл.»
«хор.»
«удовл.»
«отл.»
«хор.»
«удовл.»
Время, секунды
4,6
4,9
5,3
5,0
5,5
5,9
Какую отметку получит девочка, пробежавшая
эту дистанцию за 5,3 секунды?
В ответе укажите номер правильного варианта.

1) Отлично
2) Хорошо
3) Удовлетворительно
4) Норматив не выполнен
Задание 3.
б) В таблице даны результаты забега мальчиков 7 класса
на дистанцию 60 м. Зачет выставляется при условии, что
показан результат не хуже 10,5 с.
Номер дорожки
I
II
III
IV
Время (в секундах)
10,6
9,7
10,1
11,4
Укажите номера дорожек, по которым бежали мальчики,
получившие зачет.
В ответе укажите номер правильного варианта.
1) только I
2) только II
3) I, IV
4) II, III
Задание 4. Найдите ошибки
В примерах выполнены действия с десятичными дробями.
Проверьте решение и если верно, то ставьте знак «+»,
если неверно, поставьте знак «–».
Примеры с ошибками реши в тетради правильно!
1)
2)
3)
4)
5)
3,17·10=31,7
8,5·100=8500
0,146·10=1,46
0,2·1000=200
9,172·100 =9172
6) 24,5:10=0,245
7) 30,2:100=0,302
8) 1,75:10=17,5
9) 88,5:100=8,85
10) 6,3:1000=0,0063
Задание 4.
 Проверь себя
Проверь себя1)
2)
3)
4)
5)
3,17·10=31,7
8,5·100=8500
0,146·10=1,46
0,2·1000=200
9,172·100 =9172
6) 24,5:10=0,245
7) 30,2:100=0,302
8) 1,75:10=17,5
9) 88,5:100=8,85
10) 6,3:1000=0,0063
13. Правило 1. Умножение десятичной дроби на 10, 100, 1000 и т.д.
• Чтобы десятичную дробь умножить на 10, 100, 1000 ит.д., надо в записи дроби перенести запятую вправо
на 1, 2, 3 и т.д. цифры, приписав при необходимости
нули справа.
Правило 2.
Деление десятичной дроби на 10, 100, 1000 и т.д.
• Чтобы десятичную дробь разделить на 10, 100, 1000 и
т.д., надо в записи дроби перенести запятую влево
на 1, 2, 3 и т.д. цифры, приписав при необходимости
нули слева.
Задание 5.
Найдите значение выражения, содержащего несколько
действий. Поставьте скобки так, чтобы получился
пример по заданному порядку действий:
1) Деление
2) Сложение
3) Умножение
4) Вычитание
3,8 – 2,736 : 0,76 + 0,04 · 0,45=
Самостоятельно.

1) Вычитание 2) Деление
3) Умножение
4) Сложение
Проверь себя и оцени
3,8 – (2,736 : 0,76 + 0,04) · 0,45 = 2,162
1) 2,736 : 0,76 = 3,6
2) 3,6 + 0,04 = 3,64
3) 3,64 · 0,45 = 1,638
4) 3,8 – 1,638 = 2,162
Оценка ______
Проверь себя и оцени
(3,8 — 2,736) : 0,76 + 0,04 · 0,45 = 1,418
1) 3,8 — 2,736 = 1,064
2) 1,064 : 0,76 = 1,4
3) 0,04 · 0,45 = 0,018
4) 1,4 + 0,018 = 1,418
Оценка ______
Запись ответа в бланках на ОГЭ и ЕГЭ
I , 4 I 8
Запишите печатными буквами свою фамилию
Д Р О З Д И K
Домашнее задание 22.03.17г. _____________________________________________
1) Платеж за потребление холодной и горячей воды за месяц осуществляется по
установленным в ЖКХ тарифам. Общая сумма платежа складывается из сумм по
каждому из двух тарифов. Квитанция на оплату содержит следующую таблицу.
Вычислите общую сумму платежа за указанный в таблице расход воды.
Виды услуг
Показания счетчика
Расход
воды (м3)
Тариф
(размер платы в рублях за 1 м3)
текущие
предыдущие
Холодная вода
00546
00538
23,32
Горячая вода
00329
00324
98,76
Сумма к
оплате
ИТОГО:
2) Платеж за потребление электроэнергии осуществляется по двухтарифному счетчику
(день, ночь).
 Тариф зависит от времени суток. Общая сумма платежа складывается из
Тариф зависит от времени суток. Общая сумма платежа складывается изсумм по каждому из двух тарифов. Квитанция на оплату содержит следующую таблицу.
Вычислите общую сумму платежа за указанный в таблице расход электроэнергии.
Тарифная
зона
Показания счетчика
Расход
электроэнергии
(кВт.ч)
Тариф
(размер платы
в рублях за 1 кВт.ч)
текущие
предыдущие
День
9632
9546
3,81
Ночь
6231
5937
0,95
ИТОГО:
Сумма к
оплате
Ответьте на вопросы анкеты
Если «да», то ставьте «+»,
если «нет», поставьте «–».
1. Довольны ли вы тем, как прошел урок?
2. Было ли вам интересно?
3. Сумели ли вы проверить свои знания?
4. Научились ли вы видеть и находить ошибки?
5. Пригодится ли вам справочный материал?
6. Вы с интересом будете выполнять домашнее задание?
7. Трудно ли научиться выполнять действия с
десятичными дробями?
Выбери цвет для самооценки
Зеленый: Урок полезен, всё понятно!
Желтый: Лишь кое-что чуть-чуть неясно.

Красный: Ёщё придется потрудиться.
Синий:
Да, трудно всё-таки учиться, но
уметь считать мне пригодится.
о
1,5
а
0,1
и
м
0,9
0,4
На земном шаре обитают птицы –
безошибочные составители
прогноза погоды на лето. Название
этих птиц вы прочтете, если
расположите эти дроби в порядке
возрастания.
г
1,36
Ф
н
л
0,92
0,03
0,012
Фламинго из песка строят гнезда в форме усеченного
конуса, в которые откладывают яйца. Высота гнезда
зависит от того, каким будет лето: сухим или дождливым.
Если лето будет дождливым, то гнезда строятся высокими,
чтобы их не могла затопить вода, если засушливым — то
более низкими.
Алгоритм решения уравнений
1) Раскрыть скобки в уравнении, если они есть.
2) Перенести слагаемые с переменной в левую часть
уравнения, а слагаемые без переменной – в правую
часть уравнения, изменив при этом их знаки
на противоположные.
3) Привести подобные слагаемые в левой и правой части
(вычислить).

4) Найти корень уравнения (значение переменной).
5) Записать ответ.
Алгоритм решения задачи
с помощью составления уравнения
1) Неизвестную величину обозначить буквой
2) Используя условие задачи, составить уравнение
3) Решить составленное уравнение
4) Ответить на вопрос задачи.
5) Записать ответ.
Как вычитать десятичные дроби. Правило сложения и вычитание десятичных дробей
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику Истоминой Н.Б.
Тренажер к учебнику Н.Я. Виленкина
Способы вычитания десятичных дробей
Вычитать десятичные дроби можно двумя способами.
Первый способ аналогичен вычитанию натуральных чисел столбиком.
Давайте рассмотрим этот способ на примере. Даны десятичные дроби: 45,68 и 4,1, определим: чему равна их разность?
Даны десятичные дроби: 45,68 и 4,1, определим: чему равна их разность?
Сначала уравняем количество знаков после запятой. Для этого справа к десятичной дроби 4,1 припишем ноль и получим 4,10. Значение десятичной дроби при этом не меняется, т.к. десятичную разделительную запятую мы не переносили.
Далее расположим десятичные дроби друг под другом и, начиная с самого крайнего правого столбца, будем вычитать цифры нижнего ряда из цифр верхнего ряда. В конце не забываем поставить запятую.
В результате этих операций мы получим разность десятичных дробей.
Все просто и понятно. Единственное затруднение может возникнуть, если при вычитании разряд числа уменьшаемого меньше разряда числа вычитаемого.
Рассмотрим еще один пример вычитания десятичных дробей.
Даны десятичные дроби: 23,18 и 3,2.
Сначала выравняем количество разрядов и получим: 23,18 и 3,20.
Запишем десятичные дроби в столбик друг под другом/
Начиная с правого крайнего ряда, вычитаем цифры нижнего ряда из цифр верхнего ряда. Если из цифры 1 вычесть цифру 2, то получим отрицательное число. Поэтому мы берем десяток единиц из соседнего разряда и получается, что производим вычитание числа 2 из числа 11.
В результате имеем:
Если из цифры 1 вычесть цифру 2, то получим отрицательное число. Поэтому мы берем десяток единиц из соседнего разряда и получается, что производим вычитание числа 2 из числа 11.
В результате имеем:
Алгоритм вычитания десятичных дробей:
1. Выравниваем десятичные дроби по количеству цифр после запятой.
2. Записываем десятичные дроби в столбик друг под другом.
3. Производим вычитание десятичных дробей по правилам вычитания натуральных чисел, не обращая внимания на наличие десятичной запятой.
4. После окончания вычитания, не забываем поставить десятичную запятую.
Второй способ вычитания десятичных дробей
Этот способ более сложен, менее нагляден и требует небольшого опыта. Зато он более быстр, поскольку здесь нет необходимости записывать числа в столбик и уравнивать количество знаков после запятой.
Самое главное в этом методе запомнить правило: десятые доли числа можно вычитать только из десятых долей, сотые — из сотых и т. д. Если в каком-либо разряде уменьшаемое меньше вычитаемого, то десяток единиц берем из соседнего слева разряда.
д. Если в каком-либо разряде уменьшаемое меньше вычитаемого, то десяток единиц берем из соседнего слева разряда.
Рассмотрим пример. Заданы десятичные дроби: 5,13 и 3,4.
Вычитаем сотые доли, получаем 3.
Вычитаем десятые доли. В данном пример нам необходимо взять десять единиц из соседнего разряда, т.к. при вычитании десятых долей, уменьшаемое меньше вычитаемого.
5,13 — 3,4 = 1,73
И как обычно, результаты вычитания нужно проверить сложением. Для нашего примера, это:
Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.
Правило вычитания десятичных дробей
1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!
Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.
2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.
3) Вычитаем числа, не обращая внимания на запятую.
4) Сносим запятую под запятыми.
Примеры на вычитание десятичных дробей .
Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:
2) 23,45 — 1,5
Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:
23,45 — 1,5=21,95.
Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:
Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:
63,5-8,921=54,579.
4) 2,8703 — 0,507
Чтобы вычесть эти десятичные дроби, записываем их так, чтобы запятая второго числа расположилась точно под запятой первого. В первом числе после запятой четыре цифры, во втором — три, поэтому второе число дополняем после запятой нулем в конце. После этого вычитаем эти числа, как обычные натуральные, не учитывая запятую. В полученном результате записываем запятую под запятыми:
2,8703 — 0,507 = 2,3663.
5) 35,46 — 7,372
Вычитание десятичных дробей начинаем с записи чисел таким образом, чтобы запятые находились одна под другой. Дополняем нулем после запятой первое число, чтобы в обоих дробях после запятой было по три цифры. Затем вычитаем, не обращая внимания на запятую. В ответе сносим запятую под запятыми:
35,46 — 7,372 = 28,088.
Чтобы из натурального числа вычесть десятичную дробь, в его записи в конце ставим запятую и приписываем необходимое количество нулей после запятой. Зачем вычитаем, не беря во внимание запятую. В ответ сносим запятую ровно под запятыми:
Зачем вычитаем, не беря во внимание запятую. В ответ сносим запятую ровно под запятыми:
45 — 7,303 = 37,698.
7) 17,256 — 4,756
Этот пример на вычитание десятичных дробей выполняем аналогично. В результате получили число с нулями после запятой в конце. Их в ответе не пишем: 17,256 — 4,756 =12,5.
Дата: 25.02.16г. Утверждаю:
Тема: Вычитание десятичных дробей
Цели:
Сформировать у учащихся знания о вычитании десятичных дробей
Развивать у учащихся интеллект и познавательный интерес
Осуществлять трудовое воспитание
Оборудование: учебник, классная доска
Тип урока : комбинированный
Метод: работа с отстающими
Ход урока :
Приветствие
Проверка отсутствующих
Проверка домашнего задания
Фронтальный опрос
Объяснение нового материала:
Также как и сложение, вычитание десятичных дробей производим по правилам
натуральных чисел.
Основные правила вычитания десятичных дробей.
Уравниваем количество знаков после запятой.
Записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом.
Выполняем вычитание десятичных дробей, не обращая внимания на запятые, по правилам вычитания в столбик натуральных чисел.
Ставим в ответе запятую под запятыми.
Если вы чувствуете себя уверенно в десятичных дробях и хорошо понимаете, что называется десятыми, сотыми и т.д., предлагаем вам попробовать другой способ вычитания (сложения) десятичных дробей без их записи в столбик. Другой способ вычитания десятичных дробей , как и сложение, основывается на трёх основных правилах.
Вычитают десятичные дроби справа налево . То есть, начиная с самой правой цифры после запятой.
При вычитании большей цифры из меньшей, у соседа слева меньшей цифры занимаем десяток.
Как обычно, рассмотрим пример:
Вычитаем справа налево с самой правой цифры. У нас самая правая цифра в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Вот их и вычитаем. 1 − 1 = 0. Получилось 0, значит, на месте сотых нового числа пишем ноль.
У нас самая правая цифра в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Вот их и вычитаем. 1 − 1 = 0. Получилось 0, значит, на месте сотых нового числа пишем ноль.
Десятые вычитаем из десятых. 2 — в первом числе, 3 — во втором числе. Так как из 2 (меньшего) мы не можем вычесть 3 (большее), занимаем десяток у соседа слева для 2. У нас это 5. Теперь мы не из 2 вычитаем 3, а из 12 вычитаем 3.
12 − 3 = 9.
На месте десятых нового числа пишем 9. Не забываем, что после занятия десятка из 5, мы должны вычесть из 5 единицу. Чтобы это не забыть ставим над 5 пустой кружок.
И наконец, вычитаем целые части. 14 — в первом числе (не забудьте, что мы из 5 вычли 1), 8 — во втором числе. 14 − 8 = 6
Запомните!
Во втором числе самая правая цифра это 2 (сотые), а в первом числе сотых нет в явном виде. Поэтому, к первому числу справа от 9 добавляем ноль и вычитаем согласно основным правилам.
Такие арифметические вычислительные действия, как сложение и вычитание десятичных дробей , необходимы для того, чтобы, оперируя дробными числами получать искомый результат. Особая важность проведения этих операций состоит в том, что во многих сферах деятельности человека меры многих сущностей представлены именно десятичными дробями . Поэтому для осуществления определенных действий со многими предметами материального мира требуется складывать или вычитать именно десятичные дроби . Следует заметить, что на практике эти операции используются практически повсеместно.
Особая важность проведения этих операций состоит в том, что во многих сферах деятельности человека меры многих сущностей представлены именно десятичными дробями . Поэтому для осуществления определенных действий со многими предметами материального мира требуется складывать или вычитать именно десятичные дроби . Следует заметить, что на практике эти операции используются практически повсеместно.
Процедуры сложения и вычитания десятичных дробей по своей математической сути осуществляется практически точно так же, как аналогичные операции для целых чисел. При ее осуществлении значение каждого разряда одного числа нужно записывать под значением аналогичного разряда другого числа.
Подчиняется следующим правилам:
Сначала необходимо произвести уравнивание количество тех знаков, что располагаются после запятой;
Затем нужно произвести запись десятичных дробей друг под другом таким образом, чтобы содержащиеся в них запятые располагались строго друг под другом;
Осуществить процедуру вычитания десятичных дробей в полном соответствии с теми правилами, которые действуют для вычитания целых чисел. При этом не нужно обращать никакого внимания на запятые;
При этом не нужно обращать никакого внимания на запятые;
После получения ответа запятую в нем нужно поставить строго под теми, которые имеются в исходных числах.
Операция сложения десятичных дробей осуществляется в соответствии с теми же правилами и алгоритмом, которые описаны выше для процедуры вычитания.
Пример сложения десятичных дробей
Две целых две десятых плюс одна сотая плюс четырнадцать целых девяносто пять сотых равняется семнадцать целых шестнадцать сотых.
2,2 + 0,01 + 14,95 = 17,16
Примеры сложения и вычитания десятичных дробей
Математические операции сложения и вычитания десятичных дробей на практике используются чрезвычайно широко, причем они нередко касаются многих предметов окружающего нас материального мира. Ниже приводится несколько примеров таких вычислений.
Пример 1
Согласно проектно-сметной документации, для строительства небольшого производственного объекта требуется десять целых пять десятых кубометров бетона. Используя современные технологии возведения зданий, подрядчикам без ущерба для качественных характеристик сооружения удалось использовать для проведения всех работ всего девять целых девять десятых кубометров бетона. Размер экономии составляет:
Используя современные технологии возведения зданий, подрядчикам без ущерба для качественных характеристик сооружения удалось использовать для проведения всех работ всего девять целых девять десятых кубометров бетона. Размер экономии составляет:
Десять целых пять десятых минус девять целых девять десятых равно ноль целых шесть десятых кубометра бетона.
10,5 – 9,9 = 0,6 м 3
Пример 2
Двигатель, устанавливаемый на старую модель автомобиля, потребляет в городском цикле восемь целых две десятых литра топлива на сто километров пробега. Для нового силового агрегата этот показатель составляет семь целых пять десятых литров. Размер экономии составляет:
Восемь целых две десятых литра минус семь целых пять десятых литра равно ноль целых семь десятых литра на сто километров пробега в городском режиме движения.
8,2 – 7,5 = 0,7л
Операции сложения и вычитания десятичных дробей применяются чрезвычайно широко, и их осуществление не составляет никаких проблем. В современной математике эти процедуры отработаны практически идеально, и ими практически все хорошо владеют еще со школьной скамьи.
В современной математике эти процедуры отработаны практически идеально, и ими практически все хорошо владеют еще со школьной скамьи.
Цели урока:
- формирование знаний о правилах сложения и вычитания десятичных дробей и умения применять их в простейших случаях;
- развитие умений сравнивать, выявлять закономерности, обобщать;
- воспитание самостоятельности при выполнении заданий.
Оборудование: компьютер, проектор, магнитные доски для учащихся, индивидуальные разноуровневые карточки.
Структура урока:
1. Организационный момент.
2. Активизация ранее полученных знаний.
3. Изучение нового материала.
4. Первичное закрепление изученного материала.
5. Тест.
6. Постановка домашнего задания.
7. Подведение итогов урока.
ХОД УРОКА
I. Организационный момент
Проверяется готовность класса к уроку.
Отмечается, что учащиеся недавно познакомились с
понятием «десятичная дробь», научились читать
и сравнивать десятичные дроби. На уроке будет
рассмотрен вопрос о том, как складывать и
вычитать десятичные дроби. Записывается тема
урока. Слайд 1.
На уроке будет
рассмотрен вопрос о том, как складывать и
вычитать десятичные дроби. Записывается тема
урока. Слайд 1.
II. Активизация ранее полученных знаний
Коль скоро речь сегодня пойдет о десятичных дробях, давайте вспомним:
- Какие из этих дробей можно записать в виде десятичных:
Слайд 2. (Учащиеся называют дроби).
Представьте дроби в виде десятичных. (Учащиеся показывают на магнитных досках) .
Еще раз вспомним, какие дроби можно записать в
виде десятичных. (Ученики дают ответ).
Представьте в виде десятичных дробей:
Слайд 3. (На магнитных досках учащиеся показывают записи).
- Читаем числа:
0,62; 7,321; 21,0001; 63,01246. Слайд 4.
III. Изучение нового материала
– Ребята, а какой из приведенных
примеров касается сегодняшней темы. (Учащиеся
отвечают, что последний).
– Давайте запишем этот пример в тетрадь и
найдем сумму.
Давайте запишем этот пример в виде десятичных дробей.
Тот же самый результат мы получим, складывая числа в столбик.
– Что мы с вами получили? (Сумму десятичных
дробей).
– Давайте проговорим, как мы это сделали. Слайд
6.
– Хорошо!
Ученикам предлагается найти сумму десятичных дробей, у которых разное количество цифр после запятой 6,23 + 173,3. Учащимся задается вопрос: «Как действовать в этом случае?». (Учащиеся отвечают, что в слагаемых разное количество знаков после запятой).
– Как же быть? (Нужно уравнять, дописав нуль справа у второго слагаемого).
6,32 + 173,7 = 6,32 + 173,70
А теперь можно записать числа в столбик и найти сумму.
Алгоритм сложения десятичных дробей дополняется и выглядит следующим образом:
– А как найти разность двух десятичных дробей? (Точно так же).
Алгоритм дополняется и выглядит так:
– Итак, как сложить или вычесть десятичные дроби?
Алгоритм повторяется учащимися и появляется
на экране.
IV. Первичное закрепление полученных знаний
1. Вычислим устно (примеры учащимся предлагаются на табличках, а ответы – на магнитных досках):
2. Решение упражнений.
№1213 (а, г, б), №1214 (а, д, е), №1219 (в, е, л).
Примеры решаются у доски с комментариями . Слайд 7.
V. Тест
– Итак, а сейчас мы проверим, как вы
запомнили правила сложения и вычитания
десятичных дробей.
Устно повторяется еще раз алгоритм.
Учащимся предлагаются карточки трех типов (Приложение 3 )
Ответы учащиеся демонстрируют на табличках.
При успешном выполнении заданий у всех
учащихся на табличках должно быть написано
слово «плюс». Слайд 8.
VI. Подведение итогов урока
– Что вам понравилось на сегодняшнем уроке?
– Что не понравилось?
– Чему мы с вами научились на уроке? (Складывать
и вычитать десятичные дроби).
– Какой способ нам позволит это сделать быстро? (Сложение
и вычитание «в столбик»).
– А как это сделать?
Учащиеся проговаривают алгоритм.
VII. Постановка домашнего задания
– Пользуясь этим алгоритмом дома, вы
выполните следующие задания: № 1255 (а, г, е), №1256 (е,
з), а также ознакомитесь с пунктом
параграфом 32 учебника. Сравните алгоритм,
предложенный в учебнике, с нашим.
– Урок окончен.
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробейСложение и вычитание десятичных дробей
Назад на страницу с десятичными дробями Назад к математике 187A страница Назад к математике Страница отдела электронная почта Вопросы и предложения
|
Сложение и вычитание десятичных дробей — методы, примеры
Сложение и вычитание десятичных дробей выполняется так же, как сложение и вычитание целых чисел с учетом того, что десятичная точка должна быть на месте. Длину десятичных чисел можно регулировать, добавляя или удаляя нули из десятичной части. Давайте узнаем больше о сложении и вычитании десятичных дробей в этой статье.
Длину десятичных чисел можно регулировать, добавляя или удаляя нули из десятичной части. Давайте узнаем больше о сложении и вычитании десятичных дробей в этой статье.
| 1. | Что такое сложение и вычитание десятичных дробей? |
| 2. | Как складывать и вычитать десятичные дроби с целыми числами? |
| 3. | Часто задаваемые вопросы о десятичном сложении и вычитании |
Что такое сложение и вычитание десятичных дробей?
Сложение и вычитание десятичных дробей включает обычные правила сложения и вычитания. Единственные моменты, о которых следует позаботиться, — это десятичные знаки после запятой. Числа должны быть записаны в столбцах в соответствии с их разрядами до и после запятой. Таблица десятичных разрядов показывает, что разряды до десятичной точки начинаются с десятков, сотен и т. д.; тогда как значения места после запятой начинаются с десятых, затем сотых и так далее. Давайте поймем это с помощью добавления десятичных чисел, объясненных в следующем разделе.
д.; тогда как значения места после запятой начинаются с десятых, затем сотых и так далее. Давайте поймем это с помощью добавления десятичных чисел, объясненных в следующем разделе.
Сложение десятичных знаков
Сложение десятичных знаков выполняется, начиная с правой стороны, а затем мы двигаемся влево, добавляя каждый столбец. Например, добавим 12,5 + 14,9, выполнив следующие действия.
- Шаг 1: Напишите числа одно под другим так, чтобы они были выровнены в соответствии со своими разрядными значениями, а десятичная точка располагалась одна под другой.
- Шаг 2: Теперь сложите десятичные числа, чтобы получить сумму. В данном случае 12,5 + 14,9= 27,4
Теперь давайте разберемся с вычитанием десятичных дробей в следующем разделе.
Вычитание десятичных дробей
Вычитание десятичных дробей выполняется так же, как вычитание целых чисел. Нам просто нужно правильно записать числа в соответствии с их разрядными значениями. Давайте разберемся в этом с помощью примера, приведенного ниже.
Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: Вычесть указанные десятичные дроби: 15,8 — 2,7
Решение: Давайте вычтем эти десятичные числа, используя следующих шагов.
- Шаг 1: Напишите числа одно под другим так, чтобы большее число было сверху, а меньшее — под ним.
- Шаг 2: Теперь вычтите десятичные числа, начиная со столбца десятых, переходя к столбцу единиц, а затем к столбцу десятков. Скопируйте десятичную дробь, как она есть. В этом случае 15,8 — 2,7 = 13,1
Сложение и вычитание в отличие от десятичных дробей
«В отличие от десятичных дробей» — это те десятичные числа, которые имеют разное количество цифр после запятой. Например, 3,45 и 7,831 «не похожи на десятичные числа», потому что 3,45 имеет два числа после запятой, а 7,831 — три числа после запятой. Другими словами, в отличие от десятичных дробей говорят, что они имеют разную длину. Операции сложения и вычитания удобно выполнять даже с такими непохожими десятичными дробями. Нам просто нужно преобразовать «непохожие десятичные числа» в «подобные десятичные числа», написав нули в тех местах, где длина десятичных чисел не одинакова. Таким образом, десятичные цифры в каждом из чисел становятся равными, и числа легче складывать или вычитать. Давайте разберемся в этом с помощью следующего примера.
Операции сложения и вычитания удобно выполнять даже с такими непохожими десятичными дробями. Нам просто нужно преобразовать «непохожие десятичные числа» в «подобные десятичные числа», написав нули в тех местах, где длина десятичных чисел не одинакова. Таким образом, десятичные цифры в каждом из чисел становятся равными, и числа легче складывать или вычитать. Давайте разберемся в этом с помощью следующего примера.
Пример: Сложите десятичные числа 24, 32,1, 0,08, 0,5 и 4,003
Решение: Сложим эти числа, выполнив следующие действия.
- Шаг 1: Здесь каждое из чисел должно иметь одинаковое количество десятичных цифр.
- Шаг 2: Для этого перепишем числа следующим образом: 24.000, 32.100, 0.080, 0.500 и 4.003. Следовательно, сумма данных десятичных чисел равна 60,683 .
Как складывать и вычитать десятичные дроби с целыми числами?
При сложении или вычитании десятичного и целого числа целое число преобразуется в десятичное число. Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, целое число 5 записывается в десятичной форме как 5,0. Давайте разберемся в этом с помощью следующих примеров.
Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, целое число 5 записывается в десятичной форме как 5,0. Давайте разберемся в этом с помощью следующих примеров.
Пример: Добавить 15 + 12,56
- Шаг 1: Обратитесь к цифре, приведенной выше, и поставьте десятичную запятую после 15 и напишите после нее два нуля, чтобы оба числа стали как десятичные.
- Шаг 2: Теперь сложите десятичные числа и найдите сумму, используя обычные правила сложения. Следовательно, 15 + 12,56 = 27,56 .
Давайте поймем это с помощью вычитания.
Пример: Вычесть 6 — 2,25
- Шаг 1: Обратитесь к приведенному выше рисунку и поставьте десятичную запятую после 6 и напишите после нее два нуля, чтобы оба числа стали как десятичные дроби.
- Шаг 2: Теперь вычтите десятичные числа и найдите разницу, используя обычные правила вычитания.
 Следовательно, 6 — 2,25 = 3,75
Следовательно, 6 — 2,25 = 3,75
Важные моменты при сложении и вычитании десятичных знаков
- Значение десятичного числа не меняется при размещении нуля после десятичных цифр. Например, 5 можно записать как 5,00 9.0042
- Несмотря на то, что мера времени и угла представлена в десятичном формате, их нельзя складывать или вычитать как десятичные дроби.
☛ Похожие темы
- Сложение и вычитание десятичных дробей
- Сложение и вычитание десятичных знаков. Рабочие листы 6 класс
- Сложение и вычитание десятичных дробей 5 класс
- Деление десятичных дробей
- Умножение десятичных дробей
Примеры десятичного сложения и вычитания
Пример 1: Добавьте 0,2 + 0,22 + 0,222 + 0,2222, используя правила десятичного сложения и вычитания.
Решение:
Данные десятичные дроби будут преобразованы в одинаковые десятичные дроби путем размещения необходимого количества нулей после десятичных дробей, так чтобы каждое число имело одинаковое количество десятичных дробей.
 Их можно записать следующим образом.
Их можно записать следующим образом.∴ Сумма заданных десятичных знаков равна 0,8642
Пример 2: Найдите разницу между 7847 и 78,47, используя концепцию сложения и вычитания десятичных знаков.
Решение:
Число 7847 записывается в десятичной форме как 7847,00. Теперь вычитание можно выполнить следующим образом.
Следовательно, 7847 — 78,47 = 7768,53
Пример 3: Запишите истину или ложь относительно десятичного сложения и вычитания.
а.) 20 + 12,17 = 32,17
а.) 10 + 69,32 = 69,42
Решение:
а.)
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки заучивания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Запись на бесплатный пробный урок
Практические вопросы по сложению и вычитанию десятичных дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о десятичном сложении и вычитании
Как складывать и вычитать десятичные дроби?
Сложение и вычитание десятичных дробей выполняется с использованием обычных правил сложения и вычитания. Единственное, что нужно иметь в виду, это количество цифр после запятой и то, что десятичная точка должна быть правильно размещена в сумме или разнице. Числа должны быть записаны в столбцы в соответствии с их разрядами до и после запятой, а затем они сложены или вычтены.
Единственное, что нужно иметь в виду, это количество цифр после запятой и то, что десятичная точка должна быть правильно размещена в сумме или разнице. Числа должны быть записаны в столбцы в соответствии с их разрядами до и после запятой, а затем они сложены или вычтены.
Каково правило сложения и вычитания десятичных знаков?
Правило сложения и вычитания десятичных знаков связано с десятичной точкой. Например, чтобы сложить 56,12 + 10,14, нам нужно выровнять эти числа одно под другим так, чтобы десятичная точка встала на место и все числа были записаны в соответствии со значениями разряда. В результате получится 66,26. В случае, если они не похожи на десятичные числа, нам нужно преобразовать их в одинаковые десятичные числа, написав соответствующее количество нулей после запятой, чтобы десятичные разряды стали равными. Например, 34,25 + 12,986 можно записать как 34,250 + 12,986 и сумма будет 34,250 + 12,986 = 47,236
Как складывать и вычитать десятичные дроби с целыми числами?
Чтобы складывать и вычитать десятичные дроби с целыми числами, нам нужно преобразовать целое число в десятичное число. Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, если нам нужно сложить 8 + 4,321, то мы можем записать целое число 8 в десятичной форме как 8,000, а затем прибавить его к 4,321. После этого числа можно сложить и записать как 8.000 + 4.321 = 12.321
Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, если нам нужно сложить 8 + 4,321, то мы можем записать целое число 8 в десятичной форме как 8,000, а затем прибавить его к 4,321. После этого числа можно сложить и записать как 8.000 + 4.321 = 12.321
Как складывать десятичные числа?
Для сложения любых двух десятичных чисел мы используем следующие шаги. Давайте разберемся в этом на примере. Например, добавим 23,12 + 4,23
- Шаг 1: Напишите числа одно под другим так, чтобы они были выровнены в соответствии со своими разрядными значениями, а десятичная точка располагалась одна под другой.
- Шаг 2: Теперь сложите десятичные числа, чтобы получить сумму. В этом случае будет 23,12 + 4,23 = 27,35
Как вычитать десятичные числа?
Чтобы вычесть любые два десятичных числа, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, давайте вычтем 44,32 — 3,6
Например, давайте вычтем 44,32 — 3,6
- Шаг 1: Запишите числа одно под другим так, чтобы они были выровнены в соответствии с их разрядами, а десятичная точка располагалась одна под другой.
- Шаг 2: Теперь вычтите десятичные числа, чтобы получить разницу. В этом случае будет 44,32 — 03,60 = 40,72
Как сложить десятичное число и целое число?
Чтобы прибавить десятичное число к целому числу, нужно преобразовать целое число в десятичное. Например, добавим 5 и 3,236. Здесь мы меняем 5 на 5.000 и получаем 5.000 + 3.326 = 8.326
Как умножить два десятичных знака?
Умножение десятичных дробей на целые числа аналогично умножению целых чисел. Разница только в расположении десятичной точки. Для умножения десятичных дробей на целые числа можно выполнить следующие шаги:
- Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
- Шаг 2: После умножения подсчитайте количество знаков после запятой в данных десятичных числах.
 Предположим, что множимое имеет 2 числа после запятой, а множитель имеет 1 число после запятой, тогда мы сложим эти 2 + 1 = 3. Итак, мы поместим десятичную дробь в произведении через 3 знака справа. Например, 0,04 × 0,2 = 0,008
Предположим, что множимое имеет 2 числа после запятой, а множитель имеет 1 число после запятой, тогда мы сложим эти 2 + 1 = 3. Итак, мы поместим десятичную дробь в произведении через 3 знака справа. Например, 0,04 × 0,2 = 0,008
Как разделить десятичную дробь на другую десятичную?
Чтобы разделить десятичное число на десятичное число, нам нужно преобразовать делитель в целое число, а затем продолжить деление. Например, если нам нужно разделить 13,8 ÷ 0,6, мы будем использовать следующие шаги.
- Шаг 1: Делимое равно 13,8, а делитель 0,6. Нам нужно изменить делитель на целое число, и поэтому мы умножим его на 10, чтобы десятичная точка сместилась вправо, и оно стало целым числом. Это означает, что 0,6 × 10 = 6
- Шаг 2: Нам нужно обращаться с делимым так же, как мы обращались с делителем. Значит, делимое тоже умножим на 10. Это означает, что будет 13,8 × 10 = 138. Другими словами, нам нужно переместить обе десятичные точки вправо, пока делитель не станет целым числом.
 Следовательно, 138 ÷ 6 = 23, .
Следовательно, 138 ÷ 6 = 23, .
Скачать БЕСПЛАТНЫЕ учебные материалы
Сложение и вычитание десятичных дробей Рабочий лист
Сложение и вычитание десятичных дробей
Горячая математикаЧтобы сложить два десятичных числа, сначала проверьте, имеют ли они одинаковое количество цифр справа от десятичной точки. Если это не так, добавляйте нули справа от одного из чисел, пока они не появятся.
Затем напишите одно число поверх другого, выровняв десятичные запятые по вертикали. Складывайте, как если бы вы делали это с целыми числами, и опускайте десятичную точку прямо вниз.
Пример 1:
Добавлять 13.492 а также 7,8 .
Напишите два лишних нуля в конце 7,8 , и напишите числа вертикально.
13.
4
9
2
+
7. 8
0
0
_
8
0
0
_
Теперь добавьте.
1
1
3
1
.
4
9
2
+
7
. 8
0
0
_
2
1
.
2
9
2
8
0
0
_
2
1
.
2
9
2
Ответ 21.292 .
Аналогичный метод работает для вычитания.
Пример 2:
Вычесть 7,8 из 13.492 .
Напишите два лишних нуля в конце 7,8 , и напишите числа вертикально.
13. 4 9 2 — 7. 8 0 0 _
Теперь вычтите.
1
3.
4
9
2
−
7.
8
0
0
_
5. 6
9
2
6
9
2
Ответ 5.692 .
6.4: Сложение и вычитание десятичных дробей
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48867
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады 9043X через OpenStax
Цели обучения
- понять метод сложения и вычитания десятичных дробей
- уметь складывать и вычитать десятичные дроби
- уметь пользоваться калькулятором для сложения и вычитания десятичных дробей
Логика метода
Рассмотрим сумму 4.
 37 и 3.22. Заменив каждую десятичную дробь на дробь, получим
37 и 3.22. Заменив каждую десятичную дробь на дробь, получим\(4 \dfrac{37}{100} + 3 \dfrac{22}{100}\) Выполнив сложение, получим
\(\begin{array} { rcl} {4,37 + 3,22 = 4 \dfrac{37}{100} + 3 \dfrac{22}{100}} & = & {\dfrac{4 \cdot 100 + 37}{100} + \dfrac{3 \ cdot 100 + 22}{100}} \\ {} & = & {\dfrac{437}{100} + \dfrac{322}{100}} \\ {} & = & {\dfrac{437 + 322} {100}} \\ {} & = & {\dfrac{759}{100}} \\ {} & = & {7 \dfrac{59}{100}} \\ {} & = & {\text{семь и пятьдесят девять сотых}} \\ {} & = & { 7,59} \end{массив}\)
Таким образом, \(4,37 + 3,22 = 7,59\).
Метод сложения и вычитания десятичных дробей
При написании предыдущего сложения мы могли записать числа столбцами.
\(\begin{array} {r} {4.37} \\ {\underline{+3.22}} \\ {7.59} \end{array}\)
Это согласуется с нашим предыдущим результатом. Исходя из этого наблюдения, мы можем предложить метод сложения и вычитания десятичных чисел.
Метод сложения и вычитания Десятичные дроби
Чтобы складывать или вычитать десятичные дроби:Выровняйте числа по вертикали так, чтобы десятичные точки располагались друг под другом, а соответствующие десятичные разряды находились в одном столбце.

Сложите или вычтите числа, как если бы они были целыми числами.
Поместите десятичную точку в результирующую сумму или разность непосредственно под другими десятичными точками.Набор образцов A
Найдите следующие суммы и разности.
\(9,813 + 2,140\)
Решение
\(\begin{array} {r} {9,813} \\ {\underline{+2,140}} \\ {11,953} \end{array}\ ) Десятичные точки выровнены в одном столбце.
Набор образцов A
\(841,0056 + 47,016 + 19,058\)
Решение
\(\begin{array} {r} {841,0056} \\ {47,016\under \ } 19.058\ \ }} \end{array}\)
Чтобы обеспечить правильное выравнивание столбцов, мы можем написать 0 в конце чисел 47.016 и 19.0,058 без изменения их значений.
Образец набора A
\(1,314 — 0,58\)
Решение
\(\begin{array} {r} {1,314} \\ {\underline{-0,58\}} \endline{-0,58\}} {массив}\) Напишите 0 в разряде тысячных.

Образец набора A
\(16.01 — 7.053\)
Решение
\(\begin{array} {r} {16.01\ \ } \\ {\underline{-7.053}} {массив}\) Напишите 0 в разряде тысячных.
Набор образцов A
Найдите сумму 6,88106 и 3,5219 и округлите ее до трех знаков после запятой.
Решение
\(\begin{array} {r} {6,88106} \\ {\underline{+3,5219\ \ }} \end{array}\) Запишите 0 в десятитысячной позиции.
Нам нужно округлить сумму до тысячных. Так как цифра в позиции сразу справа равна 9, а 9>5, мы получаем
10,403
Образец набора A
У Венди есть 643,12 доллара на текущем счете. Она выписывает чек на 16,9 долларов.2. Сколько стоит ее новый баланс на счете?
Решение
Чтобы найти новый баланс счета, нам нужно найти разницу между 643,12 и 16,92. Из 643,12 вычтем 16,92.
Выписав чек на 16,92 доллара, Венди теперь имеет остаток на своем расчетном счете в размере 626,20 доллара.

Набор для практики A
Найдите следующие суммы и разности.
\(3,187 + 2,992\)
- Ответить
6.179
Набор для практики A
\(14,987 — 5,341\)
- Ответить
9,646
Набор для практики A
\(0,5261 + 1,0783\)
- Ответить
1.6044
Набор для практики A
\(1.06 — 1.0535\)
- Ответить
0,0065
Набор для практики A
\(16 521,07 + 9 256,15\)
- Ответить
25 777,22
Набор для практики A
Найдите сумму 11,6128 и 14,07353 и округлите ее до двух знаков после запятой.
- Ответить
25,69
Калькуляторы
Калькулятор может быть полезен для нахождения сумм и разностей десятичных чисел.
 Однако калькуляторы с восьмиразрядным дисплеем нельзя использовать при работе с десятичными числами, содержащими более восьми цифр, или когда сумма дает более восьми цифр. На практике восьмиразрядный десятичный знак встречается редко. Есть несколько недорогих калькуляторов, которые могут обрабатывать 13 знаков после запятой.
Однако калькуляторы с восьмиразрядным дисплеем нельзя использовать при работе с десятичными числами, содержащими более восьми цифр, или когда сумма дает более восьми цифр. На практике восьмиразрядный десятичный знак встречается редко. Есть несколько недорогих калькуляторов, которые могут обрабатывать 13 знаков после запятой.Набор образцов B
Используйте калькулятор, чтобы найти каждую сумму или разницу.
42.0638 + 126.551
Решение
Дисплей считывает Тип 42.0638 42.0638 Пресс + 42.0638 Тип 126.551 126.551 Пресс = 168,6148 Сумма 168,6148.

Набор образцов B
Найдите разницу между 305,0627 и 14,29667.
Решение
Дисплей считывает Тип 305.0627 305.0627 Пресс — 305.0627 Тип 14.29667 14.29667 Пресс = 290.76603 Разница 290,76603
Набор образцов B
51,07 + 3 891,001786
Решение
Поскольку 3 891,001786 содержит более восьми цифр, мы не сможем использовать калькулятор с восьмизначным дисплеем для выполнения этого сложения. Однако мы можем найти сумму вручную.
\(\begin{array} {r} {51.070000} \\ {\underline{3891.
 001786}} \\ {3942.071786} \end{array}\)
001786}} \\ {3942.071786} \end{array}\)Сумма равна 3 942,071786.
Тренировочный набор B
Используйте калькулятор для выполнения каждой операции.
\(4,286 + 8,97\)
- Ответить
13.256
Практический набор B
\(452.0092 — 392.558\)
- Ответить
59.4512
Практический набор B
Найдите сумму 0,095 и 0,001862
- Ответить
0,096862
Практический набор B
Найдите разницу между 0,5 и 0,025
- Ответить
0,475
Практический набор B
Найдите сумму 2 776,00019 и 2 009,00012.
- Ответить
Поскольку каждое число содержит более восьми цифр, использование некоторых калькуляторов может оказаться бесполезным.
 Складывая их по «ручной технологии», получаем 4 785,00031
Складывая их по «ручной технологии», получаем 4 785,00031
Упражнения
В следующих 15 задачах выполните каждое сложение или вычитание. Используйте калькулятор, чтобы проверить каждый результат.
Упражнение \(\PageIndex{1}\)
\(1,84 + 7,11\)
- Ответить
8,95
Упражнение \(\PageIndex{2}\)
\(15.015 — 6.527\)
Упражнение \(\PageIndex{3}\)
\(11.842 + 28.004\)
- Ответить
39.846
Упражнение \(\PageIndex{4}\)
\(3.16 — 2.52\)
Упражнение \(\PageIndex{5}\)
\(3,55267 + 8,19664\)
- Ответить
11.74931
Упражнение \(\PageIndex{6}\)
\(0,9162 — 0,0872\)
Упражнение \(\PageIndex{7}\)
\(65.512 — 8.3005\)
- Ответить
57.
 2115
2115
Упражнение \(\PageIndex{8}\)
\(761.0808 — 53.198\)
Упражнение \(\PageIndex{9}\)
\(4,305 + 2,119 — 3,817\)
- Ответить
2,607
Упражнение \(\PageIndex{10}\)
\(19.1161 + 27.8014 + 39.3161\)
Упражнение \(\PageIndex{11}\)
\(0,41276 — 0,0018 — 0,00011\)
- Ответить
0,41085
Упражнение \(\PageIndex{12}\)
\(2,181 + 6,05 + 1,167 + 8,101\)
Упражнение \(\PageIndex{13}\)
\(1,0031 + 6,013106 + 0,00018 + 0,0092 + 2,11\)
- Ответить
9.135586
Упражнение \(\PageIndex{14}\)
\(27 + 42 + 9,16 — 0,1761 + 81,6\)
Упражнение \(\PageIndex{15}\)
\(10,28 + 11,111 + 0,86 + 5,1\)
- Ответить
27.
 351
351
Для следующих 10 задач решите, как указано. Калькулятор может быть полезен.
Упражнение \(\PageIndex{16}\)
Сложите 6,1121 и 4,916 и округлите до 2 знаков после запятой.
Упражнение \(\PageIndex{17}\)
Добавьте 21,66418 и 18,00184 и округлите до 4 знаков после запятой.
- Ответить
39.6660
Упражнение \(\PageIndex{18}\)
Вычесть 5,2121 из 9,6341 и округлить до 1 знака после запятой.
Упражнение \(\PageIndex{19}\)
Вычесть 0,918 из 12,006 и округлить до 2 знаков после запятой.
- Ответить
11.09
Упражнение \(\PageIndex{20}\)
Вычесть 7,01884 из суммы 13,11848 и 2,108 и округлить до 4 знаков после запятой.
Упражнение \(\PageIndex{21}\)
Баланс текущего счета составляет 42,51 доллара США. Чек выписан на 19,28 доллара.
 Что такое новый баланс?
Что такое новый баланс?- Ответить
23,23 $
Упражнение \(\PageIndex{22}\)
Баланс текущего счета составляет 82,97 доллара США. Один чек выписан на 6,49 доллара, а другой на 39,95 доллара. Что такое новый баланс?
Упражнение \(\PageIndex{23}\)
Человек покупает гамбургер на 4,29 доллара и расплачивается за него 10-долларовой купюрой. Сколько сдачи получает этот человек?
- Ответить
5,71 $
Упражнение \(\PageIndex{24}\)
Мужчина покупает канцтовары на 6,43 доллара и расплачивается за них купюрой в 20 долларов. Получив сдачу, он понимает, что забыл купить ручку. Если общая цена ручки составляет 2,12 доллара, и он ее покупает, сколько осталось от 20-долларовой купюры?
Упражнение \(\PageIndex{25}\)
Женщина начинает запись фильма на свой видеомагнитофон со счетчиком ленты, установленным на 21.
 93. В фильме работает 847,44 счетчика ленты. Каковы окончательные показания счетчика ленты?
93. В фильме работает 847,44 счетчика ленты. Каковы окончательные показания счетчика ленты?- Ответить
869,37
Упражнения для обзора
Упражнение \(\PageIndex{26}\)
Найдите разницу между 11 206 и 10 884.
Упражнение \(\PageIndex{27}\) 92\).
Упражнение \(\PageIndex{29}\)
Найдите значение \(8 \dfrac{1}{3} \cdot \dfrac{36}{75} \div 2 \dfrac{2}{5}\).
- Ответить
\(\dfrac{20}{9} = \dfrac{5}{3}\) или \(2 \dfrac{2}{9}\)
Упражнение \(\PageIndex{30}\)
Округлите 1,08196 до сотых.
Эта страница под названием 6.4: Сложение и вычитание десятичных знаков распространяется по лицензии CC BY, автором, ремиксом и/или куратором являются Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Теги

5.3: Сложение и вычитание десятичных знаков
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22489
- Дэвид Арнольд
- Колледж Редвудс
- Поместите добавляемые числа в вертикальном формате, совместив десятичные точки.
- Сложите числа, как если бы они были целыми числами.
- Поместите десятичную точку в ответе в тот же столбец, что и десятичные точки над ней.
- Ответ
5,893
- Ответить
10,91 $
- Ответ
25,56
- Ответ
51.156
- Поместите числа, которые нужно вычесть, в вертикальном формате, выровняв десятичные точки.
- Вычитание чисел, как если бы они были целыми числами.
- Поместите десятичную точку в ответе в тот же столбец, что и десятичные точки над ней.
- Ответ
19,81
- Ответ
6.
 444
444- Сложите величины десятичных чисел.
- Префикс общего знака.
- Ответ
−89,55
- Вычтите меньшую величину из большей величины.
- Ставьте префикс перед знаком десятичного числа с большей величиной.
- Ответ
−2,26
- Ответить
12.816
- Ответ
−9,06
- Ответить
−11,42
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Арнольд
- Лицензия
- CC BY-NC-SA
- Показать страницу Содержание
- нет
- Теги

Сложение десятичных знаков
Сложение десятичных чисел очень похоже на сложение целых чисел. Например, предположим, что нас просят добавить 2,34 и 5,25. Мы могли бы изменить эти десятичные числа на смешанных дробей и добавить.
\[ \begin{align} 2,34 + 5,25 & = 2 \frac{34}{100} + 5 \frac{25}{100} \\ & = 7 \frac{59}{100} \end{aligned }\nonumber \]
Однако мы также можем выровнять десятичные числа по их десятичным точкам и добавить по вертикали, как показано ниже.
\[ \begin{array}{r} 2.34 \\ + 5.25 \\ \hline 7.59 \end{array}\nonumber \]
Обратите внимание, что эта процедура выравнивания дает тот же результат: «семь и пятьдесят девять сотых». ” Это мотивирует следующую процедуру сложения десятичных чисел.
Добавление десятичных знаков
Чтобы добавить десятичные числа, выполните следующие действия:
Пример 1
Добавьте 3,125 и 4,814.
Решение
Расположите числа в вертикальном формате, выровняв их по десятичным точкам. Добавьте, затем поместите десятичную точку в ответе в тот же столбец, что и десятичные точки, которые появляются над ответом.
\[ \begin{array}{r} 3,125 \\ +4,814 \\ \hline 7,939 \end{array}\nonumber \]
Таким образом, 3,125 + 4,814 = 7,939.
Упражнение
Добавить: 2,864 + 3,029
Пример 2
У Джейн в кошельке 4,35 доллара. У Джима в кошельке 5,62 доллара. Если они суммируют свои деньги, какова общая сумма?
Решение
Расположите числа в вертикальном формате, выровняв десятичные точки, затем сложите.
\[ \begin{array}{r} \$ 4.35 \\ + \$ 5.62 \\ \hline \$ 9.97 \end{array}\nonumber \]
Упражнение
У Алисы в кошельке 8,63 доллара, а у Джоанны имеет 2,29 доллара. Если они объединят сумму своих денег, какова будет сумма?
Прежде чем рассматривать другой пример, давайте вспомним важное наблюдение.
Важное замечание
Добавление нулей в конец дробной части десятичного числа не меняет его значения. Точно так же удаление нулей в конце десятичного числа не меняет его значения.
Например, мы можем добавить два нуля в конце дробной части числа 7,25, чтобы получить 7,2500. Числа 7,25 и 7,2500 идентичны, как показывает следующий аргумент:
\[ \begin{aligned} 7,2500 & = 7 \frac{2500}{10000} \\ & = 7 \frac{25}{100} \\ & = 7.25 \end{aligned}\nonumber \]
Пример 3
Добавьте 7.5 и 12.23.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем завершающий ноль для улучшения выравнивания столбцов.
\[ \begin{array}{r} 7,50 \\ +12,23 \\ \hline 19,73 \end{array}\nonumber \]
Следовательно, 7,5 + 12,23 = 19,73.
Упражнение
Добавить: 9,7 + 15,86
Пример 4
Найдите сумму: 12,2+8,352 + 22,44.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем нули в конце, чтобы улучшить выравнивание столбцов.
Обратите внимание, что мы добавляем нули в конце, чтобы улучшить выравнивание столбцов.
\[ \begin{array}{r} 12,200 \\ 8,352 \\ + 22,440 \\ \hline 42,992 \end{array}\nonumber \]
Следовательно, 12,2+8,352 + 22,44 = 42,992.
Упражнение
Добавить: 12,9+4,286 + 33,97
Вычитание десятичных чисел
Вычитание десятичных чисел происходит почти так же, как сложение десятичных чисел.
Вычитание десятичных чисел
Чтобы вычесть десятичные числа, выполните следующие действия:
Пример 5
Вычтите 12,23 из 33,57.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце, затем вычтите. Обратите внимание, что мы вычитаем 12,23 из 33.57.
Обратите внимание, что мы вычитаем 12,23 из 33.57.
\[ \begin{array}{r} 33,57 \\ -12,23 \\ \hline 21,34 \end{array}\nonumber \]
Следовательно, 33,57 − 12,23 = 21,34.
Упражнение
Вычесть: 58,76 − 38,95
Как и при сложении, мы добавляем нули в конце дробной части десятичных чисел, чтобы облегчить выравнивание по столбцам.
Пример 6
Найдите разницу: 13,3 − 8,572.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем нули в конце дробной части числа 13.3, чтобы улучшить выравнивание по столбцам.
\[ \begin{array}{r} 13,300 \\ -8,572 \\ \hline 4,728 \end{array}\nonnumber \]
Следовательно, 13,3 − 8,572 = 4,728.
Упражнение
Вычесть: 15,2 − 8,756
Сложение и вычитание десятичных чисел со знаком
Мы используем те же правила для сложения десятичных чисел со знаком, что и для сложения целых чисел.
Сложение двух десятичных знаков с одинаковыми знаками
Чтобы сложить два десятичных знака с одинаковыми знаками, выполните следующие действия:
Пример 7
Упрощение: −3,2+(−18,95).
Решение
Чтобы добавить подобные знаки, сначала добавьте величины.
\[ \begin{array}{r} 3.20 \\ +18.95 \\ \hline 22.15 \end{array}\nonumber \]
Префикс общего знака. Следовательно, −3,2+(−18,95) = −22,15
Упражнение
Упростим: −5,7 + (−83,85)
Мы используем то же правило, что и для целых чисел, при добавлении десятичных дробей с разными знаками.
Сложение двух десятичных знаков с разными знаками
Чтобы сложить два десятичных знака с разными знаками, выполните следующие действия:
Пример 8
Упростить: −3 + 2,24.
Решение
Чтобы добавить разные знаки, сначала вычтите меньшую величину из большей величины.
\[ \begin{array}{r} 3,00 \\ -2,24 \\ \hline 0,76 \end{array}\nonnumber \]
Ставьте префикс перед знаком десятичного числа с большей величиной. Следовательно, -3 + 2,24 = -0,76.
Упражнение
Упрощение: −8 + 5,74
Вычитание по-прежнему означает, что прибавляется к противоположному .
Пример 9
Упрощение: −8,567 − (−12,3).
Решение
Вычитание нужно сначала заменить на сложение, добавив обратное.
\[−8,567 − (−12,3) = −8,567 + 12,3\номер \]
У нас разные знаки. Во-первых, вычесть меньшую величину из большей величины.
\[ \begin{array}{r} 12.300 \\ − 8.567 \\ \hline 3.733 \end{array}\nonumber \]
Ставьте префикс перед знаком десятичного числа с большей величиной. Отсюда:
\[ \begin{align} −8,567 − (−12,3) & = −8,567 + 12,3 \\ & = 3,733 \end{aligned}\nonumber \]
Упражнение
Упрощение: −2,384 − (− 15.2)
Порядок операций требует, чтобы мы сначала упрощали выражения, содержащиеся в круглых скобках.
Пример 10
Упростить: −11,2 − (−8,45 + 2,7).
Решение
Сначала нам нужно добавить в скобках. Поскольку у нас разные знаки, вычтите меньшую величину из большей величины.
\[ \begin{array}{r} 8,45 \\ − 2,70 \\ \hline 5,75 \end{array}\nonnumber \]
Префикс знака числа с большей величиной. Следовательно,
Следовательно,
\[−11,2 − (−8,45 + 2,7) = −11,2 − (−5,75)\nonnumber \]
Вычитание означает сложение противоположного.
\[−11,2 − (−5,75) = −11,2+5,75\номер \]
Опять же, у нас разные знаки. Вычесть меньшую величину из большей величины.
\[ \begin{array}{r} 11.20 \\ − 5.75 \\ \hline 5.45 \end{array}\nonumber \]
Префикс знака числа с большим значением.
\[ −11,2+5,75 = −5,45\не число \]
Упражнение
Упрощение: −12,8 − (−7,44 + 3,7)
Письмо по математике
Решение предыдущего примера должно быть записано следующим образом:
\[ \begin{aligned} −11,2 − (−8,45 + 2,7) & = −11,2 − (−5,75) \\ & = − 11,2+5,75 \\ & = −5,45 \end{aligned}\nonumber \]
Любая черновая работа, такая как вычисления в вертикальном формате в предыдущем примере, должна выполняться на полях или в блокноте.
Пример 11
Упростить: −12,3 −|− 4,6 − (−2,84)|.
Решение
Сначала мы упрощаем выражение внутри полос абсолютного значения, берем абсолютное значение результата, а затем вычитаем.
\[ \begin{align} -12,3 — |-4,6 -(-2,84)| ~ \\ = -12,3 -|-4,6 + 2,84| ~ & \textcolor{red}{ \text{ Добавить противоположное.}} \\ = -12,3 -|-1,76| ~ & \textcolor{red}{ \text{ Добавить: } -4,6 + 2,84 = -1,76.} \\ = -12,3-1,76 ~ & \textcolor{red}{ |-1,76|=1,76.} \\ =- 12,3 + (-1,76) ~& \textcolor{red}{ \text{ Добавить противоположное.}} \\ = -14,06 ~ & \textcolor{red}{ \text{ Добавить: } -12,3 + (-1,76) = -14.06.} \end{выровнено}\nonumber \]
Упражнение
Упрощение: −8,6 −|− 5,5 − (−8,32)|
Упражнения
В упражнениях 1-12 добавьте десятичные дроби.
1. \(31,9 + 84,7\)
2. \(9,39 + 7,7\)
3. \(4 + 97,18\)
4. \(2,645 + 2,444\)
5,000 4 + 87,502\)
6. \(23,69 + 97,8\)
7. \(95,57 + 7,88\)
\(95,57 + 7,88\)
8. \(18,7+7\)
9. \(52,671 + 5,97\)
10. \(9,696 + 28,2\)
11. \(4,76 + 2,1\)
12. \(1,5 + 46,4\)
4 с
- -2 В упражнении , вычесть десятичные дроби.
13. \(9 − 2,261\)
14. \(98,14 − 7,27\)
15. \(80,9 − 6\)
16. \(9,126 − 6\)
17 \55,672 − 3,3\)
18. \(4,717 − 1,637\)
19. \(60,575 − 6\)
20. \(8,91 − 2,68\)
21. \(45,8)
21. \(45,8)
22. \(8,210 − 3,7\)
23. \(8,1 − 2,12\)
24. \(7,675 − 1,1\)
В упражнениях 25–64 сложите или вычтите десятичные дроби, как указано.
25. \(−19,13 − 7\)
26. \(−8 − 79,8\)
27. \(6,08 − 76,8\)
28. \(5,76 − 36,8\)
290,0 \(−34,7+(−56,214)\)
30. \(−7,5+(−7,11)\)
31. \(8,4+(−6,757)\)
32. \(−1,94 + 72,85 \)
33. \(−50,4+7,6\)
34. \(1,4+(−86,9)\)
35. \(−43,3+2,2\)
36. \(0,08 + (−2,33)\)
37. \(0,19 − 0,7\)
\(0,19 − 0,7\)
38. \(9 − 18,01\)
39. \(−7 − 1,504\)
9
9 40. \(−4,28 − 2,6\)
41. \(−4,47 + (−2)\)
42. \(−9+(−43,67)\)
43. \(71,72 − (− 6)\)
44. \(6 − (−8,4)\)
45. \(−9,829 − (−17,33)\)
46. \(−95,23 − (−71,7)\)
47. \(2,001 − 4,202\)
48. \(4 − 11,421\)
49. \(2,6 − 2,99\)
50. \(3,57 − 84,21\)
51. \(-4,560 − 2,335\)
52. \(−4,95 − 96,89\)
53. \(−54,3 − 3,97\)
54. \(−2 − 9000
\) 0 0000853. 55. \(−6,32 + (−48,663)\)
56. \(−8,8+(−34,27)\)
57. \(−8 − (−3,686)\)
58. \(− 2,263 — (-72,3)\)
59. \(9,365 + (-5)\)
60. \(-0,12 + 6,973\)
61. \(2,762 — (-7,3)\)
62. \(65,079 — (-52,6)\)
63. \(-96,1+(-9,65)\)
64. \(-1,067 + (-4,4)\)
В упражнениях 65-80 упростите данное выражение.
65. \(−12,05 − |17,83 − (−17,16)|\)
66. \(15,88 −|− 5,22 − (−19,94)|\)
67. \(−6,4 + |9,38 − (−9,39)|\)
\(−6,4 + |9,38 − (−9,39)|\)
68. \(−16,74 + |16,64 − 2,6|\)
69. \(−19,1 − (1,51 − (−17,35))\)
70. \(17,98 − (10,07 − (−10,1))\)
71. \(11,55 + (6,3 − (−1,9))\)
72. \(−8,14 + (16,6 − (−15,41))\)
73 \(−1,7 − (1,9 − (−16,25))\)
74. \(−4,06 − (4,4 − (−10,04))\)
75. \(1,2 + |8,74 − 16,5|\)
76. \(18,4 + |16,5 − 7,6|\)
77. \(−12,4 − |3,81 − 16,4|\)
78. \(13,65 − |11,55 − (−4,44)|\)
79. \(−11,15 + (11,6 − (−16,68))\)
80. \(8,5 + (3,9 − 6,98)\)
81. Крупные банки . Рыночная капитализация четырех крупнейших банков страны (по состоянию на 23 апреля 2009 г.)
| JPMorgan Chase & Co | 124,8 миллиарда долларов |
| Уэллс Фарго и Ко | 85,3 миллиарда долларов |
| Goldman Sachs Group Inc. | 61,8 миллиарда долларов |
| Банк Америки | 56,4 миллиарда долларов |
Какова общая стоимость четырех крупнейших банков страны? Associated Press Times-Standard 22. 04.09
04.09
82. Зеркало телескопа. Недавно запущенный телескоп Herschel имеет зеркало диаметром 11,5 футов, в то время как зеркало Хаббла имеет диаметр 7,9 фута.футов в диаметре. Насколько больше зеркало Гершеля в диаметре, чем зеркало Хаббла?
83. Средняя температура . Средние температуры в Сакраменто, штат Калифорния, в июле составляют высокую дневную температуру 93,8 градусов по Фаренгейту и низкую ночную температуру 60,9 градусов по Фаренгейту. Как меняется температура днем и ночью? Подсказка: Формулу для сравнения температур см. в разделе 2.3.
84. Средняя температура . Средние температуры в июле в Реддинге, штат Калифорния, составляют высокую дневную температуру 9 градусов тепла.8,2 градуса по Фаренгейту и низкая ночная температура 64,9 градуса по Фаренгейту. Как меняется температура днем и ночью? Подсказка: Формулу для сравнения температур см. в разделе 2.3.
85. Чистая стоимость . Чистая стоимость определяется как активы за вычетом обязательств. Активы — это все ценности, которые могут быть конвертированы в наличные деньги, а пассивы — это сумма долгов. General Growth Properties, владельцы торгового центра Bayshore Mall, имеют активы в размере 29,6 млрд долларов и обязательства в размере 27 млрд долларов и обанкротились. Какова была чистая стоимость General Growth Properties до банкротства? Times-Standard 17.04.2009
Чистая стоимость определяется как активы за вычетом обязательств. Активы — это все ценности, которые могут быть конвертированы в наличные деньги, а пассивы — это сумма долгов. General Growth Properties, владельцы торгового центра Bayshore Mall, имеют активы в размере 29,6 млрд долларов и обязательства в размере 27 млрд долларов и обанкротились. Какова была чистая стоимость General Growth Properties до банкротства? Times-Standard 17.04.2009
86. Виноградная дробилка . Предварительный отчет Калифорнийского департамента продовольствия и сельского хозяйства показывает, что в 2009 году штат произвел 3,69 миллиона тонн винного винограда. Это немного меньше рекордного 2005 года — 3,76 миллиона тонн. На сколько тонн не дотянула до рекорда давка 2009 года? Ассошиэйтед Пресс-Таймс-Стандард Калифорнийский урожай винограда подскочил на 23% в 2009 году.
87. Оборот . В обзоре вакансий и текучести кадров Министерства труда говорится, что в январе 2010 года работодатели наняли около 4,08 миллиона человек, а 4,12 миллиона человек были уволены или иным образом покинули свои рабочие места. На сколько больше людей потеряло работу, чем было принято на работу? Превратите свой ответ в целое число. Ассошиэйтед Пресс-Таймс-Стандарт 03/10/10 Количество вакансий в январе резко увеличилось до 2,7 млн человек.
На сколько больше людей потеряло работу, чем было принято на работу? Превратите свой ответ в целое число. Ассошиэйтед Пресс-Таймс-Стандарт 03/10/10 Количество вакансий в январе резко увеличилось до 2,7 млн человек.
Answers
1. 116.6
3. 101.18
5. 91.502
7. 103.45
9. 58.641
11. 6.86
13. 6.739
15. 74.9
17. 52.372
19. 54,575
21. 35,3
23. 5,98
25. −26,13
27. -70,72
29.0009 33. −42.8
35. −41.1
37. −0,51
39. −8.504
41. −6,47
43. 77,72
45. 7.501
47. –2.201998
45. 7.50147,201
45. 7.501
47. 0,39
51. −6,895
53. −58,27
55. −54,983
57. -4,314
59. 4,365
61. 10.062
63. –105,75
999999999999999999999999999999999999999999999999999999999999999999999999979н0н. 12. 37
37
69. −37.96
71. 19.75
73. −19.85
75. 8.96
77. −24.99
79. 17.13
81. 328,3 млрд.
83. -32,9 градусов по Фаренгейту
85. 2,6 млрд. Долл.
Эта страница под заголовком 5.3: Добавление и вычитание десятичных знаков распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована Дэвидом Арнольдом.
Сложение и вычитание десятичных дробей — 3-й класс математики
Сложение и вычитание десятичных дробей — это то же самое, что и сложение целых чисел, но с небольшим отличием. 😉
Давайте рассмотрим
При сложении чисел без десятичных знаков начинают с самого правого место значение .
Затем переместить из справа до слева .
Совет: Перед добавлением убедитесь, что Единицы поместили цифры в ряд вверх, одну над другой.
Иногда, когда мы добавляем, нам приходится перегруппировываться.
Посмотрите ниже.
Перегруппируйте, когда сумма в столбце больше 9.
Совет: иногда при вычитании трехзначных чисел также приходится перегруппировать .
👉 Это происходит, когда мы вычитаем большую цифру из меньшей цифры.
Взгляните:
Отличная работа с этим обзором. ⚡️ Теперь научимся складывать десятичных знаков !
Как складывать десятичные дроби
Способ сложения десятичных дробей почти такой же, как как добавление 3 — цифр. Давайте разберемся на примере. Первый шаг состоит в том, чтобы записать это уравнение в столбец формы . . Затем начало добавление из самое правое (👉) место значение. В этом уравнении мы начинаем с сотых места . Затем двигаемся влево и складываем все через разряд сотни. Сумма равна 735,96 или 735 и 96 сотых. Отличная работа! Давайте попробуем другую задачу. Сначала запишите уравнение в столбец формы . Убедитесь, что десятичные точки совпадают. Совет: Десятичные точки должны быть над каждый другой , иначе вы получите неправильный ответ! 👍 Добавьте, начиная с , наименьшее разрядное значение справа (👉). 🤔 Почему мы всегда начинаем с прибавления справа? 👉 При сложении иногда нужно перегруппироваться в более высокое разрядное значение. Таким образом, нет смысла сначала добавлять большие числа, так как к ним можно добавить больше от перегруппировки. 🤓 Мы видим, что сумма сотых цифр равна 12. Это двузначное число… Что нам делать? 🤔 Да, мы перегруппировываемся. Это означает, что мы переносим 1 на в десятый столбец и пишем 2 в сотом разряде. Похоже, нам нужно перегруппировать для всех разрядных значений. Так давайте. 😃 Совет : Мы добавляем десятичные дроби, так что не забудьте до напишите десятичную точку ваш ответ Эти сложения не имеют того же числа из десятичных цифр . Если мы напишем их в столбце форме, у нас есть пробелы. Но ничего страшного. Когда a число равно , отсутствует в разряде, мы можем написать a вместо , чтобы помочь нам отслеживать вещи 902. Совет : Выстройте десятичных точек! Теперь мы можем сложить все цифры, начиная с самое правое место значение . The way to subtract decimals is almost the same as subtracting 3 — цифра чисел. Мы используем столбцовую форму и вычитаем по одному столбцу за раз! Давайте попробуем. 😺 Давайте воспользуемся формой столбец . Выстроив десятичные точки, мы видим, что количество десятичных цифр неодинаково. 😃 Мы можем добавить нулей , чтобы помочь нам следить за вещами. Теперь, вычтите из самое правое место значение . В данном случае это сотые места.
315,25 + 420,71 = ?
 ✅
✅ Сложение с перегруппировкой
475,83 + 957,69 = ?


Другой пример
15,2 + 4,23 = ?
 😃
😃 15.2 + 4.23 = 19.43 ✅
Subtracting Decimals

13,5 — 1,29 = ?