Конспект урока математики» Сложение и вычитание в пределах 100″ 2 класс

Тема урока: «Сложение и вычитание чисел в пределах 100»

Цели: Совершенствовать вычислительные навыки в пределах 100;  повторить и закрепить умения решать задачи; развивать логическое мышление,внимание учащихся; самостоятельность, интерес к урокам математики.

Планируемые результаты:

  Предметные: умеют выполнять сложение и вычитание чисел в пределах 100 с переходом через десяток; решать текстовые задачи в два действия; находить периметр фигуры.

  Личностные: признают собственные ошибки; проявяют положительное и интерес к урокам математики.

   Метапредметные:         регулятивные: организуют взаимопроверку выполненной работы; познавательные: выполняют вычисления по аналогии, сравнивают разные способы решения задачи; коммуникативные: высказывают свое мнение при обсуждении задания; при выполнении задания в паре слушают друг друга, договариваются, объединяют результаты при совместной презентации решения.

Тип урока: урок закрепления знаний.

Оборудование: ребусы, листочки с примерами, презентация к уроку, листочки прямоугольной формы.

Ход урока

I. Организационный момент.

— Добрый день, ребята. Посмотрите на меня и улыбнитесь мне, теперь улыбнитесь друг другу и, конечно, подарите улыбку нашим гостям. По выражению лица я вижу, что у вас хорошее настроение, и мы можем начать урок.

                                                -А сейчас начнём  опять

Решать, отгадывать, смекать!

 А девизом  нашего урока станут  слова. Давайте прочитаем хором. (3-4)

Решай, отгадывай, смекай.( Презентация. 

Слайд 2)

II. Устный счет

-Все мы любим сказки и, особенно, сказочных героев. Сегодня к нам на урок пришёл  герой. Давайте угадаем, кто это.

-Чтобы угадать,

 Надо вычислить и расшифровать. 

 (Презентация. Слайд 3) 

— А теперь расположите буквы в соответствии с ответами в таблице. Прочитайте имя сказочного героя, который пришёл к нам сегодня на урок.

— Сказочного героя зовут Буратино.

— Что мы делали, чтобы узнать имя сказочного героя?

III. Постановка целей урока.

— Наша тема  урока  «Сложение и вычитание чисел в пределах 100».  

Цель урока  закрепить  знания по теме «Сложение и вычитание чисел в пределах 100 с переходом через десяток». Сегодня мы с вами будем: решать примеры; решать задачи; находить периметр; выполнять задания на логическое мышление. 

(Слайд 4)

IV. Закрепление ЗУН

-Давайте вернемся к сказочному герою. Как называется сказка про Буратино? Знаете кто её автор? (Презентация.  Слайд 5).

Буратино узнал, что в царстве Математики есть бесценный клад. Кто его найдёт, тот станет самым мудрым. Чтобы его найти, необходимо правильно считать, внимательно слушать, думать и решать задачи.

Буратино пришёл к нам научиться этому, чтобы вместе с вами попасть в Царство Математики.

Отправляемся в путешествие и все вместе будем помогать Буратино. Согласны?

— Откройте тетради, запишите число и классная работа.

— Буратино просит помощи в выполнении задания.

 1. Решите цепочку примеров: (Презентация. Слайд 6).

     

-Какое число получилось?(53)

-Что можете о нем сказать? (двузначное, в нем 5 десятков и 3 единицы)

2.  Нахождение периметра

-Итак, наше путешествие продолжается. Рассмотрите рисунок, назовите героев сказки «Золотой ключик или приключение Буратино» (Мальвина, Пьеро) (Презентация. Слайд 7)

Пьеро читал Мальвине стихи:

Мы сидим на кочке,

Где растут цветочки,

Жёлтые, приятные,

Очень ароматные.          

Пьеро был очень влюблен в Мальвину и хотел собрать  и подарить букет для неё. Но коварная лиса Алиса захотела помешать Пьеро. Давайте поможем Пьеро прогнать её. Чтобы  прогнать, надо назвать все геометрические фигуры. (Презентация. 

Слайд 8)

Каких фигур больше всего? Правильно, треугольников. Чтобы собрать букет Мальвине, нужно начертить треугольник со сторонами 4см, 6см, 5см и найти периметр. Как мы находим периметр? (складываем все стороны фигуры) Находим периметр.(Презентация. Слайд 9)

Взаимопроверка

Молодцы! Букет Мальвине собран. (Слайд 10)

— Что повторили, выполняя это задание?

3. Задание на смекалку.

— Коварный кот Базилио прибежал к лисе Алисе.

 Они обманом повели Буратино на поле чудес.  

Вот все трое на поле чудес! (Презентация. Слайд 11).

— Чтобы пройти его, необходимо решить ребусы.

(100ляр; ви3на; по2л; 7я, Р1а,40оножка, ли100к, 40а)

— Отгадывать ребусы будем в группах, объединяемся по 2 человека.

— Проверим ваши  ребусы. (Каждая группа показывает ребус и говорит отгадку). ( Презентация. Слайд 12).

— Что вспомнили, выполняя это задание? (названия чисел)

Молодцы! Вы справились с заданиями. Сейчас немного отдохнём и продолжим своё путешествие.

V Физкультминутка. (Презентация. Cлайд 13).

4. Решение  задачи.

— Посмотрите на рисунок, куда попал Буратино? (Презентация. Слайд 14).   Да, правильно, в поисках бесценного клада он попал на пруд к черепахе Тортилле. Ребята, она просит Буратино и нас помочь ей решить задачу. Поможем?

-Прочитайте  задачу и решите её. (Презентация. Слайд 15)  

В пруду плавало 50 пескарей.   Утром  Буратино поймал 17 пескарей, а вечером 6 пескарей. Сколько пескарей осталось в пруду?

— Решите задачу

1способ.

1)17+6 = 23(п.)- поймал,

2)50-23=27(п.)- осталось.  

2способ.

1)50-17=33(п.)- осталось после того, как поймал утром

2)33-6=27(п.)- осталось.

Ответ:27пескарей осталось в пруду у черепахи.

— Задачу можно решить двумя способами. Кто решил 1способом? Поднимите руки. А кто 2 способом, поднимите руку. (Презентация. 

Слайд16)

5. Самостоятельная работа учащихся .

— Дуремар – продавец пиявок  для вас придумал коварное задание.

( Презентация. Слайд 17)

— Ребята, что вы знаете о пиявках?

Пиявка – пресноводный червь – кровосос.

Пиявками можно лечить людей. Когда пиявка кусает, в кровь попадают вещества, оказывающие обезбаливающее и противовоспалительное действие.

— Это задание надо будет выполнить  по вариантам. Возьмите листочки с примерами. Примеры решаете столбиком, пишите только ответы.

— Проверьте  работу.  

Взаимопроверка. (Презентация. Слайд 18)

-Молодцы!С этим заданием вы тоже справились.

VI. Подведение итогов урока, оценивание, домашнее задание.

— Итак, ребята, все задания вы хорошо выполнили. Карабас-Барабас приготовил вам по учебнику домашнее задание….

— Буратино  благодарит вас за помощь. Он многому научился. В этом помогали мы с вами и другие герои сказки «Золотой ключик».

 Звучит волшебная музыка, появляется Царство Математики. (Презентация. Слайд 19)

Мы вместе с Буратино попадаем в Царство Математики. Ваше путешествие по дорогам математики не заканчивается, а только начинается. Пройдя все дороги, вы станете самыми мудрыми. А знания — это и есть бесценный клад!

VII Рефлексия  

-Понравилось вам наше путешествие?

-Какое задание для вас показалось трудным?

— Сегодня на уроке работали очень хорошо…

Буратино прощается с вами. (Презентация. 

Слайд 20)

 И мне хочется завершить урок  замечательными словами о математике.

Математика- королева наук!

Без неё не летят корабли,

Без неё не поделишь ни акра земли,

Даже хлеба не купишь, рубля не сочтешь,

Что почем, не узнаешь,

А узнав, не поймёшь!                                                         

Сложение и вычитание чисел в пределах 100.

| Материал по математике (2 класс) по теме:

Сложение и вычитание в пределах 100

20-6           80-60          40-17          12+46                62+19              93-38

60-5           90-30          60-23           23+54               47+39              86-28

40-8           40-20          90-45           47+32               23+48              72-36

50-9           50-40          80-34           36+52               17+35              61-29

30-1           20+60         70-42           54+33               35+28              84-37

70+9          80+10          50-25          19+40               54+37              55-39

80+4          30+50          30-18           65+24              78+14               43-14

40+5          80-50           60-36           42+37               26+57              75-48

10+2          80+10          90-34           98-76               37+58               86-59                  

90-4           90-90          20-19            65-34               65+29               56-38

30-8          50+50           80-57           75+24              57+24               63-27

50+7          20+70          30-25           86-43               37+55                92-56

20+8          60-30           70-41           76-54               56+29               78-39

80-5           40-10           40-16          64+23               45+27               64-27

40+9          10+90          60-52          45+33                27+44               32-17

10+7         80-20            50-26           87-65                19+77             66-38

90-3          100-40          20-15          49-38                 35+28              75-48

60+3          30+70          90-67           62+26                22+39              66-39

40-7           70-50           30-13           44+35                33+58              87-49

50-8          60-60            80-46           87-41                 38+57              69-49

90+1         100-50         40-37            68-42                 45+39              74-25

70-2           90-40           70-23           26+53                26+37              45-28

20+9         50+30           50-17           83+11                 33+48             51-34

10+1         80-70            60-28           43+46                47+29              62-47

30-3          20+80           90-87           37+52                36+37              87-38

20-8           60-50           20-14           98-65                 54+47               46-28

80+5          40+60          80-56            89-53                63+18               91-34

40+7         100-10          30-17            87-65                56+25               83-38

20-6          60+20           70-48            68-47                12+59               63-27

90+9          40+50          30-26            54+35                36+28              73-59

20+2          10+70         60-31             37+61                29+35              62-39

30+3           40+40         40-25            55+44                45+28              53-25

90+9         90-40            50-29            78-54                 36+27              46-29

60-6           90-60           20-16            65-33                13+38              82-56

30-6           80-60          40-23             87-55                36+26              73-37

50+5          30+70          60-48            69-47               32+58               62-19

80+4          30+50          80-36            45+34              54+27               74-45

10+5         90-90            100-38          36+43              25+55                52-37

70-5           100-30          100-58         78-54                34+19                41-39

13+6                     90-24              7+18                  23+7               28+7

81+5                     94-20              9+33                 20-5                16+4

42+6                     100-2               0+50               66+4                 39+7

30+24                   100-30            43-4                 77+8                15-8

53+10                   60-27              58-9                 19+6                14-7

65+30                   60-7                86-86               83-9                  13-6

4+73                     67-20              36-8                  29+0                 70-24

20+73                   83-50              24-6                 0+0                   80-37

86-5                      80-53              18-0                17-17                 50-26

78-60                    80-3                 36+2              18+2                 80-7

47-20                    38+5               36+20             34-34                63+30

54+30                   64+9               38-2                 34-14               78-40

76-20                    63+7                56-20             56-50                26+4

76+20                   63+9                7+18              70-50                90-36

54+20                   78+2                6+27              13-7                  72-67

60+18                   78+6                40-16             42+7                 34+39            

97+3                     54+8                40-6               49-7                 47+28

6+71                     62+9                46-10             27+3               51-38

46+30                   6+75              78-30               4+56               83+6

20+14                  8+46                 70-38              20+68            40-29

78+2                    42-6                  70-8               35+40             100-48

64+3                    54-9                  6+24             40-9                 76+17

50-6                     26-8                 5+75               12-5               80-46

70-4                     26+8                7+93               74-40              94-48

90-3                     32-6                 100-5             82-30               48+38

100-9                   27+8                100-15            100-20            37+39

70-5                     75-9                 100-25            100-8               100-28

80-4                     86+7                 12-4               42-8                 37+29

100-4                   32-4                  36-30             90-54               45+45

100-9                   65+8                46+3               64+6                77-29

52+8                     84-3                46-3               28+9                28+37

60-8                     62+7               28+30             35-6                62-38

43-20                   67+5               73+20            86-80               50-27

43-2                     32-9                96-40              57+40              35+28

60-24                  46+9                87-20              45+9               60-38

70-28                  95-6                 42+8               63-4              73-54

30-23                  78+9                50-7                32-8                39+31

50-46                  36+5                89+4               73-4                70-25

70-38                  92+0                73-5                56-9                  54+26

«Сложение и вычитание чисел в пределах 100 | План-конспект урока по математике (2 класс):

Конспект урока

По математике  по теме:

«»Сложение и вычитание чисел в пределах 100»

Выполнила

Полянко Е. З.

---

Цель:

1. Совершенствовать вычислительные навыки и умения решать текстовые и геометрические задачи;
2. Развивать логику и мышление;
3. Воспитывать умение работать в коллективе, самостоятельность и дисциплинированность.

Ход урока.

I. Организационный момент

II. Сообщение темы и цели урока

— Ребята, сегодня у нас с вами будет необычный урок: « Урок – путешествие». Путешествовать мы будем на автобусе . Целью нашего путешествия является повторение сложения и вычитания чисел в пределах 100.

III. Устный счёт

— Но хочу сразу предупредить, в путешествие отправятся самые находчивые и дисциплинированные. И поэтому для вас сейчас будет небольшое испытание.

Задачи на смекалку

1. Росли две вербы. На каждой вербе по две ветки. На каждой ветке по две груши. Сколько всего груш?
2. На яблоне было 10 яблок, а на иве на 2 меньше. Сколько всего было яблок?
3. Крышка стола имеет четыре угла. Один угол отпилили. Сколько стало углов у стола?
4. Сколько нулей во всех числах от 1 до 100?

— Итак, вы справились с этим заданием. Но теперь, чтобы наш автобус тронулся в путь, нужно правильно выполнить арифметический диктант.

Арифметический диктант

• Запишите число, в котором 5 десятков и 3 единицы.
• Сколько всего единиц в 3 десятках?
• Уменьшаемое 35, вычитаемое 4. Найдите разность.
• Какое число получится, если 5 увеличить на столько же единиц?
• На сколько надо увеличить 9, чтобы получить 15?
• Из какого числа нужно вычесть 5, чтобы получить 8?

— Проверьте ваши ответы с ответами, записанными на доске.

IV. Работа по теме

— Молодцы, все испытания выдержали. Теперь в путь! Только мне нужна ваша помощь. Когда автобус передвигается, вы должны имитировать движения водителя. Готовы? Поехали!

1 остановка

— Ребята, первая наша остановка будет в городе «Геометрических фигур» . В этом городе живут только многоугольники. Скажите, какая фигура здесь жить не будет?

Д. Круг.

— Почему?

Д. Он не является многоугольником.

— Посмотрите, какие они все грустные. Каждая фигура мечтает узнать свой периметр, но никто из них не умеет. А вы, знаете, что такое периметр?

Д. Периметр – это сумма всех сторон.

— Может мы сразу найти периметр?

Д. Нет, надо измерить их сторон.

( ученики получают шаблоны геометрических фигур и вычисляют их периметр; затем обмениваются тетрадями и выполняют взаимопроверку)

— Молодцы! Ну, что поехали дальше!

2 остановка

— Сейчас мы проезжаем мимо цирка .И здесь произошла беда. В этом цирке разбежались все звери. Послушайте загадки и узнаете, что за звери живут в этом цирке. Давайте поможем их собрать!

Длинное ухо,
Комочек пуха,
Прыгает ловко,
Любит морковку. (Заяц)

Он самый главный из зверей,
Он всех важней и всех сильней. (Лев)

Рыльце лепёшкой
С копытцами ножки,
Толстое брюшко,
Хвостик, как стружка.  (Свинья)

Всю ночь летает –
Мышей добывает.
А станет светло –
Летит спать в дупло. (Сова)

4 лапы, длинный хвост
Неприметный её рост,
Обожает, есть бананы,
Непоседа — ….. (обезьяна)

Его – знают все ребята-
Ходит в шкуре полосатой.
От хвоста и до ушей
Цвет песка и камышей. (Тигр)

— Молодцы! Давайте, поможем их собрать!

(ученики берут рисунок с изображением животного, на обратной стороне которого находится задание, выполняют его у доски. Ответ задания соответствует номеру места животного)

— Молодцы! Всех животных собрали. Поехали дальше!

V. Физ.минутка. 3 остановка

— Ребята, сделаем остановку в лесу Рисунок 4>.

Только в лес мы вошли,
Появились комары.
(Руки вверх, хлопок над головой)
Дальше по лесу шагаем
И медведя мы встречаем
Руки за голову кладём
И в вразвалочку идём.
Снова дальше мы идём,
Перед нами водоём.
Прыгать мы уже умеем,
Прыгать будем мы смелее.
Раз – два, раз – два-
Позади теперь вода!
Мы шагаем, мы шагаем,
Руки выше поднимаем,
Дышим ровно, глубоко. .
Впереди из — за куста
Смотрит хитрая лиса.
Мы лисичку обхитрим,
На носочка пробежим.

VI. Продолжение темы

— Гуляя по лесу, я насчитала 57 дубов и 30 берёз Рисунок 5 и 6>. Используя эти данные, составьте задачу.

(ученики составляют задачи: что бы задача решалась сложением; вычитанием; в два действия)

— Молодцы! Задание это выполнили мы не зря, так как дальнейшее путешествие будет проходить именно по работе над задачами. Сели удобнее и в путь!

4 остановка

— Ребята, я приглашаю вас на рыбалку . Ловить вы будете рыбок не простых, а математических.

(на полу лежит ватман, с изображением озера, в котором лежат рыбки, тоже вырезанные из ватмана. Ученики берут удочку, с магнитиком вместо крючка, ловят рыбку, с заданием на обратной стороне. Работа выполняется самостоятельно.)

Примеры задач

1. Ёжик подарил Нюше 15 цветков, а Крош – 7 цветков. На сколько цветков Крош подарил больше?
2. Пончик съел 6 пирожков с мясом и 4 с творогом. На сколько больше пирожков с мясом, чем с творогом съел Пончик?
3. Карлсон съел 11 ореховых печений и 8 – шоколадных. На сколько меньше Карлсон съел шоколадных печений, чем ореховых?
4. Копатыч вырастил 13 кабачков и 9 тыкв. На сколько штук кабачков больше, чем тыкв?
5. Божья коровка Мила сделала 15 куличиков, а Лунтик – 11 куличиков. На сколько у Лунтика меньше куличиков, чем у Милы?

— Двигаемся дальше.

VII. Работа по учебнику 5 остановка

— Посмотрите, нам на встречу идёт мальчик . Об этом мальчике мы узнаем из учебника на странице 78, №22. (Математика 1 часть 2 класс, автор Моро.)

(задача разбирается и решается устно)

— Прочтите условие задачи. О ком говорится в задаче?

Д. О Диме, он нёс сумку с фруктами.

— Что сказано о сумке?

Д. Её масса 1кг.

— Что говорится о фруктах?

Д. Сколько их было, неизвестно, но сказано, что масса фруктов на 7кг больше массы сумки.

— Посмотрите, под условием даны два случая решения этой задачи. Какой поставите вопрос, если задача решается так, как в первом случае?

Д. Сколько весят фрукты?

— А во втором?

Д. Сколько весит сумка с фруктами? Сколько весят сумка и фрукты вместе?

— Молодцы! Едем дальше!

6 остановка

— Вот мы и добрались до конечной станции .. Ребята, вам надо расположить числа в порядке возрастания, и мы узнаем, что же помогло преодолеть нам весь этот путь.

( ученики получают карточки с числами в пределах 100, строятся в порядке возрастания. На обратной стороне написаны буквы. Когда дети построятся, то у них получается слово «дружба»)

— Какое слово получилось?

Д. Дружба.

— Нравится вам это слово? Почему?

Д. Дружба необходима человеку.

— Да, я согласна с вами. Благодаря вашей дружной работе, вы прошли всё путешествие.

VIII. Подведение итогов урока – путешествия

— Вам понравилось наше путешествие?

 — Я хочу похвалить каждого из вас. Все молодцы и заслуживаете похвалы. Давайте теперь вспомним, что же мы делали на уроке?

Д.  Решали примеры и задачи на сложение и вычитание в пределах 100.

— Что вам показалось наиболее сложным?

— Как вы сами оцениваете свою работу?

Сложение и вычитание чисел в пределах 100. (2 класс)

Математика 2 класс
УМК «Школа России»
(Сложение и вычитание чисел в пределах 100)
Работу выполнила
учитель начальных классов
МОУ СОШ №1 г. Камешково
Курова Татьяна Владимировна
Ребята!
Давайте поможем Снегурочке собраться на
Новогодние праздники!
Найди сумму чисел 46 и 4
86
50
42
Уменьшаемое 37,
вычитаемое 3. Найди
разность.
34
7
40
Число, в котором 8
десятков и столько же
единиц, увеличить на 2.
10
86
90
Из какого числа надо
вычесть 6, чтобы получить
41?
48
35
47
Задумали число. Оно на
30 больше 55. Какое число
задумали?
25
85
58
Наименьшее трёхзначное
число уменьшить на 15.
75
95
85
На сколько надо увеличить
3, чтобы получить разность
чисел 40 и 30?
73
7
13
Какое число надо вычесть
из 60, чтобы получить
сумму чисел 46 и 4
10
50
100
На сколько самое большое
двузначное число больше
самого большого
однозначного числа?
9
90
100
Света живёт с мамой и папой.
У них есть собака, 2 попугая,
черепаха и 3 рыбки. Сколько
всего ног у жильцов дома?
16
21
18
Молодцы!
Ссылки на интернет-ресурсы
http://elitefon.ru/pic/201211/1366×768/elitefon.ru-7589.jpg
http://st2.depositphotos.com/1001442/5965/i/950/depositphotos_59659205-Light-Purple-Snowflakes.jpg
http://kira-scrap.ru/KATALOG/OFORMLENIE/1/0_8be8e_455d0e63_M.png
http://img-fotki.yandex.ru/get/4403/200418627.1f/0_10d750_7e0ab4bf_M.png
http://dizav.ru/uploads/posts/2014-12/1418976057_spruce_dizav.ru1.gif — елка
http://euro-pack.ru/wp-content/uploads/93.png — заяц
http://www.liveinternet.ru/journal_proc.php?action=redirect&url=http://img1.liveinte
rnet.ru/images/attach/b/4/104/403/104403091_large_10005.jpg — снегурочка
http://www.liveinternet.ru/journal_proc.php?action=redirect&url=http://img0.liveinternet.ru/ima
ges/attach/b/4/104/403/104403092_large_10006.jpg — снегурочка-2

Урок математики по теме: «Сложение и вычитание чисел в пределах 100 с переходом через десяток.

Закрепление.» 2 Класс

Слайды и текст этой онлайн презентации

Слайд 1

УРОК МАТЕМАТИКИ по теме: « Сложение и вычитание чисел в пределах 100 с переходом через десяток. Закрепление.» 2 класс http://www.o-detstve.ru/index.html
Урок подготовила: Авдеева Наталия Валерьевна

Слайд 2

РЕШАЙ ОТГАДЫВАЙ СМЕКАЙ

Слайд 3

40+4=
19+7=
Р
А
80-1=
70+10=
О
У
22-6=
Б
Н
28-20=
77+2=
И
48+6=
Т
16.79.26.44.54.79.8.80
…….
Б
У
Р
А
Т
И
Н
О

Слайд 4

Тема урока: «Сложение и вычитание чисел в пределах 100» Цель урока: закрепить знания по теме «Сложение и вычитание чисел в пределах 100 с переходом через десяток»

Слайд 5

Слайд 6

Решите цепочку примеров + — + — - +

Слайд 7

Слайд 8

Назовите фигуры

Слайд 9

Найдите периметр
6см
4см
5см
Р=4+6+5=15см

Слайд 10

Слайд 11

Слайд 12

100ляр
столяр
витрина
ви3на
по2л
подвал
7я
семья
Р1а
Родина
Ли100к
листок

Слайд 13

Давайте отдохнём!

Слайд 14

Слайд 15

В пруду плавало 50 пескарей. Утром Буратино поймал 17 пескарей, а вечером 6 пескарей. Сколько пескарей осталось в пруду?

Слайд 16

1 способ 17+6=23(п.) 50-23=27(п.) 2 способ 50-17=33(п.) 33-6=27(п.) Ответ: 27 пескарей осталось в пруду у черепахи.
Молодцы!

Слайд 17

Дуремар – продавец пиявок

Слайд 18

2 вариант 87-18=69 49+24=73 58+19=77 42-28=14 75+11=86 59-19=40
1 вариант 62+28=90 90-17=73 18+22=40 86-38=48 33-13=20 53+14=67

Слайд 19

Слайд 20

Спасибо за помощь! До свидания!

Конспект урока «Обобщение. Сложение и вычитание чисел в пределах 100» 2 класс

Урок математики

Тема урока. Обобщение. Сложение и вычитание чисел в пределах 100

Целевые установки (планируемые результаты)

Обобщение знаний способов сложения и вычитания чисел в пределе 100.

Предметные. Закрепить способы сложения и вычитания рассмотренных видов в пределах

100; находить закономерности, по которым составлены ряды числовых выражений.

Метапредметные:

• регулятивные: под руководством учителя учиться определять цель учебной

деятельности; соотносить выполненное задание с образцом предложенным

учителем; выполнять под руководством учителя учебные действия в

практической и мыслительной форме;

• познавательные: осуществлять поиск нужной информации, используя учебные

материалы, сведения, полученные от учителя;

• коммуникативные: отвечать на вопросы учителя, работать в паре, участвовать

в диалоге и коллективном обсуждении при анализе заданий.

Личностные. Использовать элементарные навыки самооценки и самоконтроля результатов

своей учебной деятельности.

Оборудование.

— технические средства (медиааппаратура, презентация).

1. Организационный момент

Долгожданный дан звонок –

Начинается урок,

Тут затеи и задачи,

Игры, шутки – всё для вас!

Пожелаем вам удачи –

За работу, в добрый час!

— Настраивание на урок. Девиз урока.

Посмотрите, друг другу в глаза, улыбнитесь глазками, пожелайте друг другу удачи,

хорошего настроения на весь урок (Минутка создания настроения). Сегодняшний урок я

начну словами французского философа Ж.Ж. Руссо «Вы талантливые дети!» Когда-нибудь

вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете

постоянно работать над собой, ставить новые цели и стремиться к их достижению…” Я

желаю вам уже сегодня на уроке убедиться в словах Ж.Ж. Руссо. Удачи! В добрый путь за

знаниями!

Давайте, ребята, учиться считать,

Делить, умножать, прибавлять, вычитать,

Запомните все, что без точного счёта,

Не сдвинется с места любая работа.

Учитель: «На сегодняшнем уроке мы отправимся в страну, в которую просто попасть, но

не просто вернуться. Постарайтесь приложить усилия, я надеюсь, вам это удастся».

«Благодаря своей настойчивости, упорству и трудолюбию во 2 классе вы значительно

увеличили багаж математических знаний.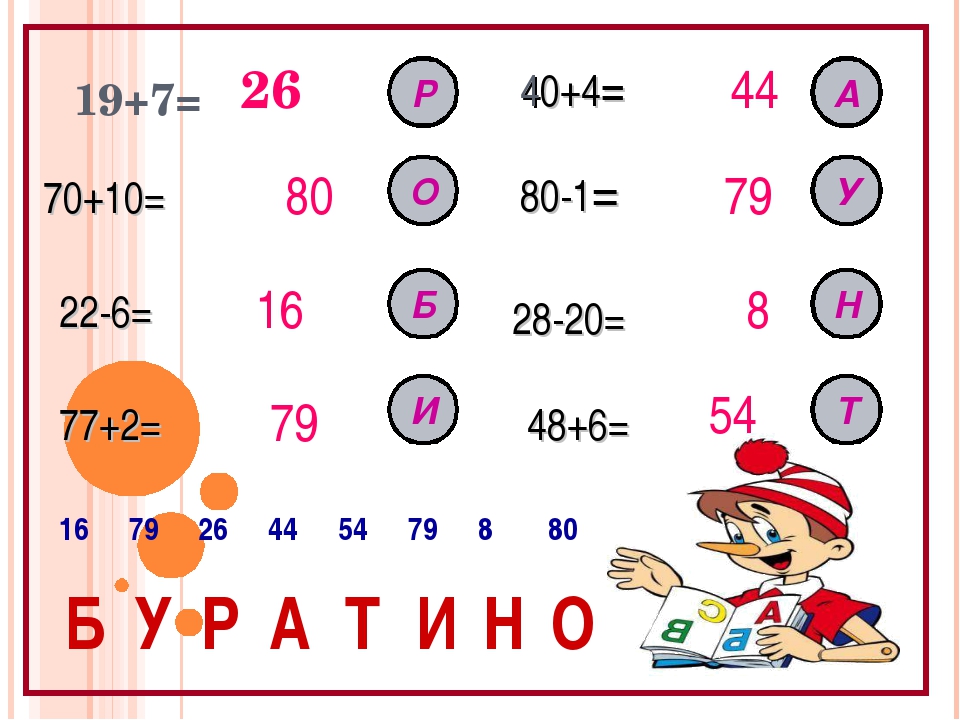 И, конечно, помог вам в этом учебник. Пришло

время повторить изученное и подкорректировать свои знания». Прочтите, чем же мы

будем заниматься сегодня на уроке.

Конспект урока «Сложение и вычитание чисел в пределах 100».

Тема урока : «Сложение и вычитание чисел в пределах 100».

Цель: формирование у учащихся умения выполнять письменно действие вычитания из круглых чисел двузначные числа с использованием алгоритма.
Задачи:
— усвоить математическое действие «вычитание из круглого числа»;
— сформировать умение использовать алгоритм вычитания из круглого числа двузначного числа столбиком;
— формировать общеучебные и коммуникативные универсальные учебные действия.
Используемые методы, технологии обучения – словесный, наглядный методы, проблемное обучение, технология «обучение в сотрудничестве», ИКТ.
Используемые формы организации познавательной деятельности учащихся – фронтальная, групповая, парная, индивидуальная.
Оборудование – учебник, электронная презентация, раздаточный материал, проектор.
Прогнозируемый результат —
— познавательные учебные действия: устанавливать аналогии, использовать модели, алгоритмы, осуществлять поиск информации в учебнике, строить речевые высказывания в устной форме.
— коммуникативные учебные действия: планировать учебное сотрудничество с учителем и сверстниками, учитывать разные мнения и стремиться к координации различных позиций, формулировать собственное мнение.
— регулятивные учебные действия: принимать, планировать и реализовывать учебную задачу.

Ход урока.

I этап. Организационный момент.

— Ребята, ПОПРИВЕТСТВУЙТЕ, ГОСТЕЙ !

Наш урок сейчас науке посвящается,

Что математикой у нас с любовью называется.

Она поможет воспитать такую точность мысли,

Чтоб в нашей жизни все познать, измерить и исчислить.

-Сегодня у нас необычный урок. Мы будем познавать, измерять, исчислять, путешествую по нашей планете Земля. Я приглашаю в путешествие всех, кто настойчив, кто не боится цифр и вычислений и чей девиз:

(На слайде)

Хочу всё знать.

(Дети читают хором.)

II этап. Актуализация знаний.

— И сегодня вам будет предложено много интересных заданий

III этап. Мотивационно – целевой.

— Первое задание, которое поможет назвать тему урока.

35	33	73	14	23
Письменные	сложения	приёмы	и	вычитания.

— Посмотрите на ряд чисел.

-Что это за числа? (двузначные числа) Как одним словом назвать все записанные числа?

— Почему они двузначные?

— Прочитайте их.

— Расположите числа в порядке убывания (один ученик работает у доски).

— Назовите такое двузначное число, в котором количество десятков равно количеству единиц. (33)

— Назовите такие числа, в которых количество десятков больше количества единиц. (73, 40)

— Назовите такие числа, в которых количество десятков меньше количества единиц. (35, 14, 23)

— Назовите число, в котором сумма цифр равна 10. (73)

— Назовите цифру, которая чаще всего повторяется в этом ряду.

Определение темы урока.

-Вы смогли ответить на все мои вопросы. Пришло время открыть эти карточки. Прочитайте. Кто же назовёт тему урока? (Ученики называют тему урока, учитель определяет цель урока.)

Вы успешно справились с заданием. Молодцы!

IV этап. Закрепление знаний.

а) Устный счёт.

Есть просто храм, есть храм науки,

А есть ещё природы храм

С лесами, тянущими руки

Навстречу солнцу и ветрам.

Задача на внимание.

• Сколько в лесу растёт хвойных деревьев, если там 19 елей, 7 осин и 3 сосны. (22 дерева)

—Осина за день поглощает 60 л воды, а берёза на 30 л меньше. Сколько литров воды поглощает берёза? (на 30 литров) А сколько вместе?

—Долго растёт ель – 35 лет и только тогда начинают появляться на ней плоды, а кедр даёт плоды, когда ему исполняется 100 лет. На сколько позже появляются плоды у кедра, чем у ели? (на 65 лет)

— Кедр растёт в нашей стране (показ слайда). Посмотрите.

— Продолжаем устную работу.

Постоянным жителем зимних хвойных лесов является одна маленькая птичка. А кто она, вы узнаете, если выполните правильно следующее задание.

— Прочитайте. Что значит уменьшить на 4?

—Уменьши на 4: 29 75 40 33 18

(Дети по одному выходят к доске и пишут мелом результат, подставляют магнитные буквы по ключворду)

25 71 36 29 14 ключворд:

к л ё с т 14-т

25-к 36-ё

29-с 71-л

(Показ слайда)

Посмотрите на эту птичку. Чем она необычна? Она единственная, кто выводит птенцов в самые сильные январские морозы, потому, что зимой в лесу много еловых и сосновых шишек.

б) Решение задач.

— Птицы дороги нам как часть чудесной природы. Их мелодичные, весёлые, звонкие песни, яркое оперение оживляют природу, вселяют в нас бодрость и радость. Как мы можем заботиться о птицах? А хотите узнать, чем питается, например, кукушка?

— Кукушка съедает за день 62 кузнечика и 24 гусеницы бабочки капустницы. Сколько всего насекомых съедает кукушка за день? (86 насекомых)

— Подскажите, как быстрее найти значение данного выражения: 62+24 (нужно записать его столбиком, так чтобы десятки были под десятками, а единицы под единицами). Кто хочет пойти к доске и объяснить решение данного выражения? (один ученик идёт к доске, на доске прочерчены клетки)

—Повторение алгоритма решения примеров .

• Итак, что же мы проговаривали сначала? (Пишу…)

• Затем: Складываю единицы …(а если это пример на вычитание?) Вычитаю единицы…

• Потом: Складываю / Вычитаю десятки…

• Читаю ответ…

— Вот вы сами вспомнили алгоритм письменного сложения и вычитания.

V этап. Физкультминутка.

-Вот и солнышко просыпаясь, посылает на Землю лучики тепла.

Спал цветок и вдруг проснулся-

(туловище вправо, влево)

больше спать не захотел.

(туловище вперёд, назад)

Шевельнулся, потянулся,

(руки вверх, потянуться)

Взвился вверх и полетел.

(руки вверх, влево, вправо)

Солнце утром лишь проснётся,

Бабочка кружит и вьётся.

(покружиться)

в) Работа с дидактическим раздаточным материалом.

(Самостоятельная работа в парах.)

Это карточки с заданиями, которые вы будете выполнять в парах.

-Прочитайте задание. На какие две группы можно разделить данные выражения? (Сложение и вычитание.)

-Договоритесь между собой, кто какую группу примеров будет выполнять.

— С чего вы начнёте выполнять вычисления? Работаем по алгоритму.

№1 №2

82+15=97 73+21=94

57-23=34 67-24=43

17+32=49 47-35=12

• Как называется выражение, в котором стоит знак «+».

• Как называется выражение, в котором стоит знак «-»

-Проверим ответы.

№1—ответы примеров на сложение:

— Назовите самый большой ответ, который получился, самый маленький, оставшийся

№2—ответы примеров на вычитание:

г) (Дополнительная индивидуальная работа. )

Это ребусы.

Ребусы.

_ 68 ** _75 68-34=34

** 52 ** 34+52=86

34 86 33 75-42=33

6* _*8 3* 62+34=96

*4 2* *3 48-22=26

96 26 49 36+13=49

2 * _*7 46 26+12=38

1 2 45 ** 87-45=42

*8 4* 59 46+13=59

Молодцы! Вы все справились с этим заданием, и усвоили изученные приёмы вычитания и сложения.

-На Земле много разных рек: больших и маленьких (слайды), все они куда-то бегут и впадают в моря и океаны.

-Продолжаем наше путешествие дальше.

д) Решение задачи с комментированием.

-Одним из необыкновенных обитателей морей и океанов является кит (слайды).

Всего насчитывают около 30 видов китов. Все киты разных размеров. Давайте узнаем длину одного из них и решим задачу.

Длина туловища кита 14 метров, а длина его головы на 6 метров короче. Какова общая длина кита?

-Прочитайте вопрос задачи.

-Можем мы сразу ответить на вопрос задачи? (Нет) Почему? (Неизвестно какова длина головы.)

-Можем это узнать? (Да) Каким действием? (Вычитанием) Почему? (Потому что столько же, да на 6 меньше). Запишем первое действие. (Один ученик работает у доски).

1)14-6=8(м)-длина головы.

-Можем теперь ответить на вопрос задачи? ( Да) Каким действием? (Сложением) Почему? (Находим сколько вместе) Запишем:

2)14+8=22(м)-общая длина кита.

-Запишите решение задачи выражением. Кто записал по другому?

(Один ученик у доски)

(14-6)+14=22(м)

—Ответили мы на вопрос задачи? (Да) Как запишем ответ? ( На доске записывает ученик)

-Теперь вы знаете, что кит может быть длиной 22 метра. Вот такой он большой.

С решением задачи вы справились.

е)Решение задач.

(Самостоятельная работа)

С. 23 № 13, с. 24 № 17

1) 15-7=8(шт.) – груш.

2) 15+8=23(шт.) – слив.

=

-Проверка: дети отвечают устно.

-Я вижу, что и самостоятельно вы умеете работать.

ж) Письменное решение примеров с комментированием.

— Наш урок подходит к концу. И я предлагаю вам выполнить задания.

-Кто уже догадался, что это за задания? (Круговые примеры.)

— Ваша задача читать выражения разными способами и записывать их столбиком.

32-11 +16 -25 +33 -39

Молодцы, у вас неплохо получилось.

• Как выдумаете, почему именно число 6 должно остаться в вашей памяти? (Сегодня 6 февраля).

• Дайте характеристику этому числу.

VI этап. Рефлексия.

• Итак, наш урок подошёл к концу. Вы очень хорошо поработали! Показали хорошие математические знания. Благодарю вас за активную работу. Сегодня на уроке вам не раз приходили на помощь смекалка и сообразительность.

• Оценивание учащихся

Домашнее задание

С. 24 №20, С.27 №42,

• Удачи вам!

• Помните, что учиться, всегда пригодиться.

Обучение сложению и вычитанию чисел до 100

Это третья из 4-х частей серии обсуждений по обучению сложению и вычитанию на начальных уровнях начальной школы. Для других частей этой серии, посвященных другим диапазонам чисел, перейдите по следующим ссылкам:

Изучение сложения и вычитания чисел до 100 — это следующий этап после чисел до 20. В этой серии мы поговорим о подходы к обучению, которые мы рекомендуем для чисел от 20 до 100, и общие проблемы, с которыми сталкиваются студенты.

Базовое мастерство сложения и вычитания до 20 является основополагающим для мастерства в числах до 100. Для обсуждения распространенных ошибок и стратегий обучения числам до 20, пожалуйста, обратитесь к Части 2 этой серии обсуждений, посвященных сложению и вычитанию.

Общая стратегия и порядок инструкций

Этот диапазон чисел (от 20 до 100) может быть обучен в двух частях:

• Числа от 20 до 40 и
• Числа от 40 до 100.

Если возможно, примените спиральный подход и преподайте эти две темы отдельно, с небольшой темой, например Измерения или формы между ними. Этот спиральный подход не только позволяет студентам усвоить и усвоить нижний диапазон 20-40, прежде чем они приступят к более требовательному диапазону 40-100, он также разбивает, казалось бы, гигантские задачи обучения: умело складывать и вычитать в пределах 100 на два. меньшие шаги.

В рамках каждой из этих двух тем / диапазона номеров мы рекомендуем преподавать в следующей последовательности:

• Добавление
  • числовая строка
  • значение разряда
  • сложение кратных 10
  • Без перегруппировки
    • прибавление 2-значного числа к 1 -цифровое число, эл. грамм. 23 + 5
    • добавить 2-значное число к 2-значному номеру, например 23 + 15
  • При перегруппировке
    • добавьте 2-значное число к 1-значному номеру, например 37 + 8
    • добавить 2-значное число к 2-значному номеру, например 29 + 23

• Вычитание
  • числовая строка
  • значение разряда
  • вычесть кратные 10
  • Без перегруппировки
    • Вычесть однозначное число из двузначного числа, например 38-2
    • Вычесть двузначное число из двузначного числа e.g 33-12
  • С перегруппировкой
    • Вычтите однозначное число из двухзначного числа, например 43-7
    • Вычтите двузначное число из двузначного числа, например, 51-18

Имея это в виду, мы далее обсудим, что включает в себя каждый элемент, и выделим некоторые распространенные ошибки.

Числовая строка

Распространенная ошибка студентов, когда они мысленно рассчитывают (и аналогично при обратном счете), это включение начального числа, например. g 28 + 3 равно 28, 29, 30 вместо 29, 30, 31. Чтобы минимизировать это, мы считаем целесообразным начать с числовой строки. Хорошее понимание числовой прямой также имеет решающее значение для развития сильного чувства числа.

Сложение с числовой линией

В общем, первоклассники и второклассники должны уметь использовать числовую линию как для счета, так и для обратного счета.

Таблицы стоимости места

Стоимость места — ключевая концепция перегруппировки. Дети должны в полной мере понять, например, что 36 = ? десятков и ? единиц = 3 десятков 6 единиц

Однако многие дети могут отвечать на вопросы сложения и вычитания, не понимая полностью разницы.Они просто разбивают числа, например 36 на 3 и 6 и поместите их в соответствующие поля десятков и единиц. Хороший способ проверить их понимание — спросить их следующее.

36 = 1 десять ? единиц = 1 десятков 26 единиц

36 = 2 десятков ? единиц = 2 десятков 16 единиц

Сложение и вычитание кратных 10

Учащимся должно быть комфортно складывать и вычитать кратные десятки, e. грамм.

14 + 20 = 34

Хотя это может показаться тривиальным, нередки случаи, когда студенты борются с этим. Мы считаем, что для этого особенно полезен подход «Конкретно — Изобразительное — Абстрактное». После использования юни-кубов в десятках и единицах для сложения чисел 14 и 20 учащиеся переходят от конкретного к графическому изображению, чтобы связать свой существующий опыт. Необходимо следить за тем, чтобы конкретные и графические изображения были тесно связаны. Многие ученики способны ухватить конкретные представления, но быстро теряются, когда графические представления имеют мало общего с их физическими манипуляциями.

Студенты должны понимать, что число 14 состоит из 1 десятки и 4 единиц, а число 20 состоит из 2 десятков. Чтобы сложить числа, мы складываем единицы и десятки отдельно. На этом этапе могут быть очень полезны числовые связи, напоминающие ученикам, что 14 состоит из 10 и 4.

Сложение без перегруппировки

Еще одно хорошее учебное пособие — таблица сотен, где учащиеся могут указать, что числа увеличиваются в десять раз по мере того, как они спускаются вниз по столбцам диаграммы.

В этом примере ниже учеников просят заполнить недостающие числа в таблице частичных сотен.

Сложение и вычитание, умноженное на десять с диаграммой частичных сотен

Сложение без перегруппировки

У учащихся обычно нет проблем с тем, чтобы придумать правильный ответ для сложения без перегруппировки. Тем не менее, стоит понимать стратегии, которые используют учащиеся. На этом этапе многие еще рассчитывают. Хотя это не является математически неверным, исследования показали, что учащиеся, которые могут использовать и применять свое понимание ценности места, как правило, добиваются большего успеха в более поздние годы.

При добавлении 2-значного числа к 1-значному (например, 23 + 5) простой и эффективный способ состоит в том, чтобы разложить 23 на 2 десятки и 3 единицы, а затем добавить единицы и десятки по отдельности.

Сложение с перегруппировкой

Сложение с перегруппировкой часто бывает сложнее, и студентам нужны 2 базовых навыка, чтобы преуспеть.

1. Добавляйте плавно в пределах 20.
2. Прочный фундамент в виде стоимости.

Студенты должны быть в состоянии ответить на эти вопросы о числовом значении, прежде чем продолжить.

16 единиц =? десять ? единиц = 1 десять 6 единиц

3 десятка 12 единиц = 42

а. Конкретный — Живописный — Абстрактный Подход

На примере 26 + 7,

1. Конкретное представление : Используя манипуляторы, 26 представлено как 2 десятка 6 единиц, а 7 представлено как 7 единиц на диаграмме значений разряда;
2. Иллюстрированное представление : В числовом предложении число 26 разложено на 2 десятки и 6 единиц графически с использованием числовых связей;
3. Абстрактное представление : Продолжая фокусироваться на разрядах, мы находим сумму, складывая единицы и десятки, где 2 десятка 13 единиц равны 33.

Использование кубиков Lego в качестве конкретных манипуляторов для сложения с перегруппировкой

Для учащихся важно соединить три представления и понять концепцию разряда. Это очень важно для настройки стандартного алгоритма на следующем этапе.

Сложение с перегруппировкой с разметкой

b. Стандартный алгоритм

Многие студенты не испытывают проблем с правильными ответами на стандартный алгоритм. Однако бывает сложно определить, «следуют ли они процедурам» или «действуют с пониманием».Вот несколько методов, которые мы используем.

1. Учиться с пониманием

a. Для обеспечения тесной связи между установкой разряда и стандартным алгоритмом существует тщательная настройка. В настройке разряда 26 разложено на 2 десятки и 6 единиц. На следующем шаге 6 единиц добавляются к 7 единицам, где сумма 13 единиц прибавляется к 2 десяткам, чтобы получить 33. Это сразу же связывается со стандартным алгоритмом.

Сложить в пределах 100: соединение разряда значений со стандартным алгоритмом

b.Мы используем язык расстановок в обучении и изучении стандартного алгоритма. Например, вместо того, чтобы сказать «1 плюс 1 равно 2», мы говорим «1 десять плюс 1 десять это 2 десятка».

Сложите в пределах 100, используя язык разряда

2. Тест на понимание

a. Часто компоненты стандартного алгоритма сложения или вычитания предварительно заполняются правильными числами. Чтобы проверить понимание учащимися значения места, мы используем промежуточный шаг, предоставляя учащимся пустые поля, чтобы они могли заполнить соответствующие числа.

Тестирование на понимание в разряде

В приведенном выше примере многие студенты будут указывать «7» в десятках для 7 + 26. Однако, получив ответ и сравнив с предыдущим ответом на 26 + 7, они понял бы, что, поскольку 26 + 7 должно иметь то же значение, что и 7 + 26 (коммутативное свойство), что-то должно быть не так с их работой!

г. Многие студенты привыкли составлять десятку при вычислении стандартного алгоритма. Непримеры — это очень полезный способ показать, что число, которое «переносится», представляет собой разряды десятков и не обязательно должно быть «1».Например, опросите учащихся на такие суммы, как «56 + 8 + 7». Сумма единиц — 21, составленных десятков — «2», а не «1».

Тестирование на понимание значения места

Вычитание — Концепции для обучения

Вычитание обычно представлено как «убрать». В статье «Сила математики — как помочь своему ребенку полюбить математику, даже если вы этого не сделаете» Патрисия Кларк говорит о важности ознакомления наших учеников с различными концепциями вычитания.

Искусственное разделение значений вычитания создает ненужные барьеры.Детям необходимо одновременно выучить четыре способа вычитания. Включите все четыре в свой разговор.

— Сила математики: как помочь ребенку полюбить математику, даже если вы этого не сделаете, Патрисия Кларк.

Ниже приведены некоторые примеры.

• Взять — например, У меня 5, и я забираю 3. Сколько у меня?
• Сравнение / различие — например, У меня 5, а у вас 3, у кого больше? На сколько больше?
• Отсутствует добавление — например, У меня есть 25 долларов. Мне нужно 30 долларов, чтобы купить сумку. Сколько еще мне нужно?
• Движение — эл.грамм. Я проезжаю 7 миль до библиотеки, разворачиваюсь и еду 5 миль обратно по тому же маршруту. Как далеко я от отправной точки?

Вычитание чисел от 20 до 100 обычно занимает в два раза больше времени, чем сложение. Для этого есть две основные причины. Во-первых, у них нет сильного чувства ценности места. Во-вторых, они все еще борются с вычитанием в пределах 20.

Вычитание без перегруппировки

Подобно сложению без перегруппировки, многие ученики не испытывают трудностей с вычитанием без перегруппировки.Тем не менее, снова важно внимательно изучить стратегии, которые могут использовать некоторые студенты. В статье «При чем тут математика?» Профессор математики Стэнфордского университета Джо Булер говорит о «сложной математике, которую использовали дети ниже среднего». При вычислении 16-13, вместо разложения 16 и 13 на десятки и единицы, вычитания десятков и вычитания единиц, дети ниже среднего начнут с 16 и начнут считать в обратном порядке (16-15-14-13-12-11-10- 9-8-7-6-5-4-3).

Когнитивная сложность этой задачи огромна, а место для ошибок огромно.

— «При чем тут математика?» Стэнфордский профессор математики Джо Булер

Эта математическая трудность, если не вмешиваться на более раннем этапе, может распространиться на большие числа до 40 и выше. Учащиеся, у которых есть прочная основа для числовой ценности, часто могут придумать смысл сложения и вычитания больших чисел без каких-либо дополнительных инструкций от своих учителей.

В этом примере (1) учащимся нужно разложить 55 и 23 на десятки и единицы. (2) учащимся нужно отдельно вычесть десятки и единицы.

Вычитание в пределах 100: разложение десятков и единиц с использованием разряда

Вычитание с перегруппировкой

При использовании стандартного алгоритма важно использовать «язык разряда».

Используя следующий пример, мы можем использовать «16 единиц вычитают 9 единиц» и «4 десятки вычитают 3 десятки» вместо «16 вычитают 9» и «4 вычитают 3». Это позволит учащимся увидеть, что мы вычитаем 30 из 40 вместо дискретных чисел 3 из 4. Это особенно важно, когда мы переходим к большим числам, исчисляемым сотнями.

Вычитание соединительного разряда со стандартным алгоритмом

Связь между сложением и вычитанием

Чтобы лучше понять взаимосвязь между сложением и вычитанием, в дополнение к обычным вопросам можно задавать вопросы с пропущенными слагаемыми. По нашему опыту, ученики нередко сталкиваются с проблемами с пропущенными дополнениями. Чтобы помочь студентам, можно использовать числовую связь с недостающими частями. Связь с числами также особенно полезна при решении сложных задач со словами.

Связь между сложением и вычитанием

Мысленная математика

Большинство предыдущих стратегий, используемых для чисел до 20, следует пересмотреть для этого диапазона чисел, например

Кроме того, еще одна хорошая стратегия для внедрения на этом этапе — сокращение числа вдвое. Как правило, учащимся легко удваивать числа, но наоборот (деление пополам) им сложно. Детям обычно очень нравится разбивать «большие» числа пополам.

Например,

половина 60 равна 30.

половина 36 равна 18.

Для более продвинутых учеников они могут быть представлены стратегии разделения, например:

Умственная математика деление чисел вдвое

В приведенном выше примере число 74 разбито на 60 и 14. В то время как оно не интуитивно понятно разделить 74 на 2 равные части, конечно проще с 60 и 14!

Числовые навыки, подобные этим, очень пригодятся позже в 5-6 классах, где ученики будут выполнять процедуры поиска наименьшего общего кратного, наибольшего общего множителя, простого факторизации, квадратного корня и кубического корня. По нашим наблюдениям, учащиеся, которые не приобрели эти навыки на старших уровнях начальной школы, часто тратят слишком много времени на простую математику, такую ​​как 72, деленное на 2 и т. Д., Что замедляет их выполнение сложных процедур, что часто приводит к разочарованию и «отказу ».

Чувство чисел

На этом этапе дети могут практиковаться в использовании мысленной числовой линии для интуитивного мышления. Например, они могут рассуждать, что 23 + 5 меньше 33 + 5, а 37-20 меньше 40-20.Они должны уметь сравнивать два набора чисел, не выясняя ответы.

Чувство чисел Интуитивное рассуждение

Заключение

Мы надеемся, что это обсуждение обучения «сложению и вычитанию чисел до 100» окажется полезным. На следующей неделе мы поговорим о типичных проблемах, с которыми сталкиваются при расширении обучения сложению и вычитанию чисел до 1000 и выше.

---

Подробнее об обучении сложению и вычитанию:

---

Вычитание в пределах 100 | SMathSmarts

Основные стандарты:

M A FS . 2. NBT.2.5 Плавно складывайте и вычитайте в пределах 100, используя стратегии, основанные на разряде, свойствах операций и / или соотношении между сложением и вычитанием.

MAFS.2.NBT.2.9 Объясните, почему работают стратегии сложения и вычитания, используя значение разряда и свойства операций.

Стандарты подключения:

MAFS.2.NBT.2.8 Мысленно прибавьте 10 или 100 к данному числу 0-90 100-900 и мысленно вычтите 10 или 100 из данного числа 10-100 100-900 .

Знание содержания:

Учащиеся 1 ^класса работали с некоторым вычитанием десятков и единиц. В 1 ^{-м ученики} классов сложили 2-значные числа с 1-значными числами и два 2-значных числа. Студенты мысленно вычитали десять из любого двузначного числа, а также вычитали десятки из числа, кратного десяткам.

В 2 ^{-м классе} учащиеся продолжат и расширят свою работу, добавляя и вычитая двузначные числа.Они будут продолжать использовать понимание ценности, чтобы понять смысл этих операций. Учащиеся будут использовать стратегии, использованные при сложении в классе 1 ^st , чтобы теперь визуализировать процесс вычитания с помощью манипуляторов (блоки с основанием десять, кубы привязки, счетчики на десяти кадрах), сто диаграмм и числовых линий.

Когда учащиеся работают с моделированием и визуализацией двузначного вычитания, их внимание должно быть сосредоточено на понимании процесса вычитания и поиске стратегий вычитания двузначных чисел.Если все сделано правильно, традиционный подход (алгоритм) к двухзначному вычитанию всегда дает правильный ответ, но ученикам его нелегко понять. Хотя он эффективен, он фокусируется на цифрах и запомненных процедурах, а не на понимании чисел. В конечном итоге они будут свободно изучать традиционный метод (алгоритм) в 4-м классе, но в 2-м классе ^и акцент должен быть сделан на том, чтобы помочь им понять процесс.

---

GCG 1 — Цель обучения: Как математик я могу Использовать модели с основанием десяти и быстрые картинки для вычитания двузначных чисел MAFS.2.NBT.2.5 , MAFS.2.NBT.2.9

• Шаг 1: Используйте блоки по основанию десять для вычитания двузначных чисел
• Шаг 2: Используйте быстрое рисование изображений для вычитания двузначных чисел
• Шаг 3: Используйте стратегию разделения для вычитания двузначных чисел

---

GCG 2 — Цель обучения: Как математик я могу Использовать открытые числовые линии для вычитания двузначных чисел MAFS.2.NBT.2.5 , MAFS.2.NBT.2,9

• Шаг 1: Используйте открытую числовую строку для вычитания в пределах 100
• Шаг 2: Используйте «сложение мыслей» для вычитания в пределах 100 на открытой числовой строке
• Шаг 3: Используйте компенсацию для вычитания в пределах 100

Плавно складывайте и вычитайте в пределах 100, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием.

Плавно вычесть в пределах 100:

Учащимся предлагается решить три вычитания из 100 задач, и их наблюдают за использованием стратегий разложения.

Тип: Формирующее оценивание

Пересекая десятилетие:

Студента просят решить задачу на сложение и вычитание, в которой десятилетие (т.е., кратное десяти) необходимо перечеркнуть.

Тип: Формирующее оценивание

Сколько нам нужно заказать ?:

Это исследовательский урок, на котором ученикам будет предложена реальная проблема и задание придумать способ собрать свои данные и решить проблему.

Тип: План урока

Сбор средств из бюджета:

Этот MEA предназначен для второго класса. Студенты будут работать в небольших группах, чтобы выяснить, какие компании нанять для художественной галереи, чтобы провести успешное благотворительное мероприятие.Студенты будут оценивать такие критерии, как группы для мероприятия, кейтеринги и артисты. Студентам нужно будет добавить деньги, чтобы не выходить за рамки бюджета. Они напишут свою процедуру выбора.

Тип: План урока

Карнавал:

Написанный для второго класса, в этом MEA учащиеся будут использовать навыки решения задач, сложение двузначных чисел и знания о большем и меньшем, чем для ранжирования карнавальных игр в соответствии с предоставленными критериями.

Тип: План урока

Конкурс файлов cookie:

Этот MEA просит студентов решить, какие факторы важны при выборе лучшего файла cookie в конкурсе файлов cookie. Учащиеся возьмут на себя роль критиков файлов cookie, чтобы предоставить обратную связь учителю, чей уровень обучения решает, какой файл cookie использовать для сбора средств.Они будут ранжировать свой выбор от лучшего к худшему. Студенты предоставят подробное письменное объяснение того, как они решили ранжировать факторы и свое решение. Они покажут свою работу, добавив до 4-х двузначных чисел, чтобы подсчитать общее количество голосов.

Тип: План урока

Вечеринки по случаю дня рождения ‘R’ Us:

Ученики определят, какую пиццерию следует использовать для обслуживания вечеринок в учреждении «День рождения», учитывая набор данных. Они создадут процедуру для определения лучшей пиццерии, напишут объяснение своей процедуры и представят свои рекомендации классу.

Тип: План урока

Разорвать и перегруппировать, чтобы добавить:

Учащиеся узнают, как транспонировать уравнение горизонтального сложения с двузначными слагаемыми, используя специализированный рабочий стол.Учащиеся будут «разорвать и перегруппироваться», чтобы понять, как перегруппировать десять человек в один десять.

Тип: План урока

Сложение и вычитание на диаграмме сотен:

Этот урок — не введение в сложение и вычитание на диаграмме сотен, а скорее практика стратегий, которые помогут развить беглость речи. Учащиеся будут использовать методы составления десяти, разложения и другие стратегии определения числа, чтобы создать скрытые рисунки на диаграмме сотен, а затем сверить свой рисунок с ключом ответа.

Тип: План урока

Альтернативные стратегии добавления:

Этот урок посвящен воспроизведению нескольких альтернативных стратегий сложения двузначных чисел.Урок направлен на то, чтобы побудить учащихся использовать более одной стратегии для решения дополнительных задач. Усиливая несколько альтернативных стратегий сложения, учащиеся разовьют твердое понимание структур и механизмов сложения, прежде чем перейти к трехзначному сложению. Урок включает в себя создание мини-буклета «Стратегии дополнения», который учащиеся могут сохранить и использовать в качестве справочного пособия.

Тип: План урока

Это «самое волшебное волшебство» ?:

Этот урок представляет собой совместную исследовательскую деятельность, которая проводится ближе к концу второго класса.Учащиеся будут активно заниматься сложением и вычитанием чисел в пределах 100, одновременно получая удовольствие от выполнения Магических квадратов.

Тип: План урока

Сладкое сложение и вычитание:

Этот урок является продолжением уроков «Sweet Values» и «Sweet Number Places», которые также можно найти на CPALMS. Это другой способ обучения сложению и вычитанию, основанный на продолжении истории, которая началась с числовой ценности и ваших второклассников. На этом уроке учащиеся научатся использовать полученные знания о разрядах, чтобы плавно складывать и вычитать числа до 100.

Тип: План урока

Пенни-банка Джамира:

Цель этого задания — помочь учащимся сформулировать свои стратегии сложения, как в 2.NBT.5 и будет наиболее целесообразно использовать, когда учащиеся будут иметь твердое представление о стоимости монет. Эту задачу лучше всего использовать в учебной обстановке, особенно потому, что язык довольно сложен, и учителю может потребоваться помощь ученикам в расшифровке постановки задачи.

Тип: Задача по решению проблем

Экономия денег 2:

Цель этого задания — связать учащиеся задачи сложения и вычитания с деньгами, а также с ситуациями и целями, связанными с экономией денег.Это учебное задание, которое объединяет многие аспекты математической работы, которую будут выполнять второклассники, с возможностью узнать о концепциях финансовой грамотности.

Тип: Задача по решению проблем

Экономия денег 1:

Цель этого задания — связать учащиеся задачи сложения и вычитания с деньгами, а также с ситуациями и целями, связанными с экономией денег. В этом задании учащиеся складывают два двузначных числа, которые требуют перегруппировки, и решение демонстрирует более конкретный подход, чем подход решения, показанный в 2.OA, NBT Saving Money 2. Эту проблему можно скорректировать в зависимости от того, на каком уровне студенты находятся в их понимании сложение, включающее двузначные числа.

Тип: Задача по решению проблем

1-й класс — блок 6 — сложить и вычесть до 100

1-й класс — Блок 6 — Сложить и вычесть до 100 Первый класс Сложение и вычитание двузначных чисел 1_M_3: Учащиеся поймут и будут применять свойства сложения и вычитания. Расчетное время: 6-7 недель 25 января 2016 — 09 09 марта 1_M_3_D: Считайте вычитание неизвестной проблемой сложения. (K) (1.OA.4) Отсутствует интерактивная активность Грега Тана (1.OA.4) 1_M_3_J: сложение и вычитание двузначного числа и кратного 10 с использованием конкретных моделей или чертежей и стратегий, основанных на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием; свяжите стратегию с письменным методом и объясните используемую аргументацию. (R) (1.NBT.4) Add Tens ixl Interactive Activity (1.NBT.4) Smart Sums Greg Tang Dice Game — Color Master to Laminate (1.OA.3) (1.NBT.4) 1_M_5_D: Учитывая двузначное число, найдите в уме на 10 больше или на 10 меньше, чем число , не считая; объясните используемую аргументацию.(R) (1.NBT.5) 1_M_5_E: сложить и вычесть кратные 10 в диапазоне 10-90 до / из кратных 10 в диапазоне 10-90 (положительное или нулевые различия), используя несколько стратегий. (R) (1.NBT.6) Limbo Interactive Activity Выберите «100 Pin» (1. NBT.6) 1_M_3_K: добавьте в пределах 100, включая добавление двузначного числа и однозначного числа. (R) (1.NBT.4) 1_M_3_L: Поймите, что, добавляя двузначные числа, вы складываете десятки и десятки, единицы и единицы; и иногда надо составить десятку.(R) (1.NBT.4) Diffy Interactive Subtraction Game (Выберите целые #) (1.NBT.4) Kakooma Basic 5 Pro Addition Puzzles Greg Tang Color Masters) (1.NBT.4) Kakooma Moderate 6 Addition Пазлы Greg Tang Color Masters (1.NBT.4) Kakooma Moderate 6 Pro Добавить пазлы Greg Tang Color Masters (1.NBT.4) Kakooma Moderate 7 Добавить пазлы Greg Tang Color Masters (1.NBT.4) Kakooma Moderate 7 Pro Добавить Пазлы Greg Tang Color Masters (1.NBT.4) Kakooma Advanced 9 Добавить пазлы Greg Tang Color Masters (1.NBT.4) Kakooma Advanced 9 Pro Добавить пазлы Greg Tang Color Masters (1.NBT.4) Смешные числа 2-значное сложение с перегруппировкой Blackline Master (1.NBT.4) 1_M_3_H: Используйте сложение и вычитание в пределах 20 для решения проблем со словами, связанных с ситуациями сложения, взятия из , складывая, разбирая и сравнивая с неизвестными во всех позициях. (R) (1.OA.1) Интерактивное занятие Cherry Chomp — Бесплатная регистрация (1.OA.1) IXL Online ixl Interactive Activity — Прокрутите вниз до 1.OA.1 Интерактивное занятие Monster Shop — Бесплатная регистрация ( 1.OA.1) Рабочий лист осеннего урожая — задачи на вычитание слов (1.OA.1) 1_M_3_I: Решите задачи со словами, которые требуют сложения трех целых чисел, сумма которых меньше или равна 20. (R) (1.OA) .2) Добавление трех чисел ixl Интерактивное задание — Практика только с числами — не задачи со словами (1.OA.2) Интерактивное задание «Сохранить мяч» — Бесплатная регистрация (1.OA.2) Mall Mania Стратегии сложения Задание с Книжка с картинками (1.OA.2 и 3) Математические головоломки Добавьте числа в 10 интерактивных книг Грега Танга (K.OA.2, 3 и 1.OA.2, 3) Batter Up! Рабочий лист — Практика только с числами — не задачи со словами (1.OA.2)

Иллюстративное пособие по математике для 2 класса — Учителя

Объем и последовательность

Рассказ

Основные идеи во 2-м классе включают: расширение понимания десятичной системы счисления, развитие навыков сложения и вычитания, использование стандартных единиц измерения, а также описание и анализ фигур.

Математическая работа для 2 класса разбита на 9 блоков:

1. Сложение, вычитание и работа с данными
2. Сложение и вычитание в пределах 100
3. Измерение длины
4. Сложение и вычитание в числовой строке
5. Номера до 1000
6. Геометрия, время и деньги
7. Сложение и вычитание в пределах 1000
8. Равные группы
9. Собираем все вместе

В этих материалах, особенно в разделах, посвященных сложению и вычитанию, учителя найдут термины, относящиеся к типам задач, например, «Добавить к», «Взять из», «Соединить или разделить», «Сравнить», «Результат неизвестен» и т. Д.Эти типы задач основаны на общих ситуациях сложения и вычитания, как указано в Таблице 1 раздела Глоссария математики Общих основных государственных стандартов.

Глава 1: Сложение, вычитание и работа с данными

В этом разделе учащиеся начинают годичную работу по развитию беглости с суммами и разностями в пределах 20, опираясь на концепции сложения и вычитания из первого класса. Они изучают новые способы представления и решения задач, включающих сложение, вычитание и категориальные данные. .

В 1 классе ученики складывали и вычитали в пределах 20, используя стратегии, основанные на свойствах сложения и разряда. Они развили беглость с суммами и разностями в пределах 10. Студенты также приобрели опыт сбора, систематизации и представления категориальных данных.

Здесь учащиеся знакомятся с графическими изображениями и гистограммами как способом представления категориальных данных. Они задают и отвечают на вопросы о ситуациях, описываемых данными. Структура гистограмм открывает путь к новому представлению — ленточной диаграмме.

Развернуть изображение

Развернуть изображение

Студенты узнают, что ленточные диаграммы можно использовать для представления и понимания задач, связанных со сравнением двух величин. Диаграммы также помогают учащимся лучше понять взаимосвязь между сложением и вычитанием.

Этот вводный блок также предлагает возможности познакомить с математическими процедурами и структурами для центров и развить общее понимание того, что значит заниматься математикой и быть частью математического сообщества.

Раздел A: сложение и вычитание в пределах 20

Этот вводный раздел дает учителям возможность оценить свободное владение учащимися с помощью фактов сложения и вычитания в пределах 10, а также их подходы к сложению и вычитанию.

Первые несколько уроков сосредоточены на построении десяти как стратегии сложения и вычитания, которая помогает студентам свободно владеть фактами в пределах 20 и поддерживает работу с большими числами (например, составление и разложение чисел как способ сложения и вычитания).В последнем уроке раздела учащиеся используют стратегии, изученные в 1 классе, чтобы складывать в пределах 50.

\ (\ hspace {3cm} \)
\ (10-5 = \ underline {\ hspace {1 cm}} \)

\ (5 + \ underline {\ hspace {1 см}} = 10 \)

\ (2 + \ underline {\ hspace {1 см}} = 10 \)

\ (10 ​​- 8 = \ underline {\ hspace {1 см}} \)

Некоторые мероприятия проводятся в центрах, что позволяет учителям также знакомить с распорядками и структурами, помогая учащимся разработать умственные стратегии для сложения и вычитания.

Раздел B: Способы представления данных

В этом разделе учащиеся исследуют ситуации и проблемы, связанные с категориальными данными, и изучают новые способы представления таких данных.

Учащиеся начинают с представления данных о своем классе понятным для них способом. Затем они знакомятся с графическими изображениями и гистограммами. Студенты изучают условные обозначения этих графиков по мере их создания. Они обсуждают типы вопросов, которые можно задать и ответить с помощью графиков, в том числе те, которые требуют объединения и сравнения различных категорий.

Раздел C: Диаграммы для сравнения

Студенты ранее представляли и рассуждали о количествах в задачах рассказа. В 1 классе ученики сравнивали величины, используя диаграммы с дискретными перегородками. В предыдущем разделе они рассуждали о количествах на гистограммах. Здесь студенты учатся использовать ленточные диаграммы как еще один способ понять взаимосвязь между двумя величинами, а также между сложением и вычитанием.

Студенты изучают. Сравните задачи из рассказов с неизвестным отличием, неизвестным большим числом или неизвестным меньшим числом.Ленточные диаграммы помогают учащимся визуализировать эти структуры и помогают им рассуждать о стратегиях, которые следует использовать для решения проблем, таких как расчет или обратный отсчет. В таблице выделены различные типы проблем в этом разделе.

разница неизвестна	больше неизвестно	поменьше неизвестно
Лин насчитал 28 лодок. Диего насчитал 32 лодки. Сколько еще лодок насчитал Диего?	Лин нашел на 28 снарядов больше, чем Диего.Диего обнаружил 32 снаряда. Сколько снарядов нашла Линь?	Линь увидел 32 морских звезды. Диего видел на 28 морских звезд меньше, чем Линь. Сколько морских звезд видел Диего?
Развернуть изображение	Развернуть изображение	Развернуть изображение

Учащиеся также пишут уравнения, чтобы аргументировать вопросы, которые спрашивают «сколько еще?» и «на сколько меньше?» Они понимают, что разные уравнения и диаграммы могут использоваться для обозначения одной и той же разницы между двумя числами.

Расчетные дни: 14-18

Стандарты, рассматриваемые в этом устройстве

Обращение

2.MD.D.10, 2.NBT.A.2, 2.NBT.B.5, 2.OA.A.1, 2.OA.B.2

Блок 2: Сложение и вычитание в пределах 100

Раньше учащиеся складывали и вычитали числа в пределах 100, используя стратегии, которые они изучали в 1 классе, такие как подсчет и обратный отсчет, а также с помощью таких инструментов, как соединение кубиков. В этом модуле они складывают и вычитают в пределах 100, используя стратегии, основанные на разряде, свойствах операций и соотношении между сложением и вычитанием.

Учащиеся начинают с использования любой стратегии для определения значений сумм и разностей, которые не связаны с составлением или разложением десятки. Затем они знакомятся с блоками с основанием десять в качестве инструмента для представления сложения и вычитания и переходят к стратегиям, которые включают составление и разложение десятков.

Учащиеся развивают свое понимание группировки по разряду и начинают вычитать одно- и двузначные числа из двузначных чисел, при необходимости разлагая десять. Они применяют свойства операций и гибко практикуют рассуждение, упорядочивая числа, чтобы облегчить сложение или вычитание.

Например, учащиеся сравнивают методы Май и Линь для определения значения \ (63-18 \).

В конце раздела учащиеся применяют свои знания сложения и вычитания в пределах 100 для решения одно- и двухэтапных задач всех типов с неизвестными во всех позициях. Чтобы помочь им в рассуждении о разрядах при сложении и вычитании, учащиеся могут использовать соединительные кубы, блоки с десятичной базой, ленточные диаграммы и другие представления, изученные в предыдущих модулях и оценках.

Раздел A: Сложение и вычитание

В этом разделе учащиеся находят значение неизвестных слагаемых, используя методы, основанные на разрядах, и знакомятся с блоками с десятичной базой. Они продолжают полагаться на взаимосвязь между сложением и вычитанием для решения проблем, связанных с различиями.

Учащиеся начинают с решения задач «Сравнить рассказы». Они используют любые подходящие им методы и инструменты, в том числе диаграммы и соединительные кубы, чтобы находить различия в двузначных числах.

Лин и Клэр использовали кубики для создания поездов.
Что вы заметили? Что вам интересно?

Развернуть изображение

Затем учащиеся анализируют структуру десятичных блоков и используют их для поиска неизвестных слагаемых (MP7). В отличие от соединительных кубов, блоки с основанием десять нельзя разобрать, что помогает подчеркнуть структуру двузначных чисел с основанием десять.

Чтобы рассуждать о неизвестном слагаемом, они могут добавлять десятки и единицы к известному слагаемому, пока не достигнут значения суммы.Они также могут начинать с общей суммы и вычитать десятки из десятков и единицы из единиц, чтобы получить известное слагаемое. Встречаемые здесь числа не требуют от студентов разложения десяти при вычитании по разряду.

Раздел B: Разложить на вычитание

В этом разделе учащиеся вычитают одно- и двузначные числа из двузначных чисел в пределах 100. Чтобы рассуждать о различиях двух чисел, они используют методы, основанные на разрядах, блоках и диаграммах с десятичным основанием, а также свойствах операций.Числа здесь требуют, чтобы студенты разложили десять при вычитании по месту.

Студенты также понимают различные представления о вычитании по месту, в том числе те, которые демонстрируют рассуждения их сверстников. Например, чтобы найти значение \ (63-18 \), учащиеся могут использовать блоки с основанием десять или рисунки для представления десятков и единиц. В этом случае они могут разложить 1 десятку из 63 и обменять ее на 10 единиц, получив 5 десятков и 13 единиц. Отсюда некоторые ученики могут сначала забрать 8 единиц, а затем 1 десятку.Остальные могут забрать 1 десятку, затем 8 единиц.

Когда учащиеся обсуждают разные подходы и объясняют, почему они приводят к одному и тому же значению, они углубляют свое понимание свойств операций и расстановки значений.

\ (63 — 18 \)

Развернуть изображение

Приведенные здесь рассуждения создают основу для понимания учащимися стандартного алгоритма вычитания, но на данном этапе не следует поощрять учащихся к использованию обозначений для стандартного алгоритма.Позвольте им построить концептуальное понимание, рассуждая с помощью десятичных блоков и рисунков и формулируя свое мышление.

Раздел C: Представление и решение задач истории

Этот раздел позволяет студентам применять свои знания для решения задач-рассказов, которые включают сложение и вычитание в пределах 100. Задачи-рассказы включают все типы — Сложить, Взять, Сложить / Разобрать и Сравнить — и содержат неизвестные во всех позициях.

Раньше учащиеся работали с диаграммами, представляющими задачи «Сравнить». В этом разделе учащиеся также разбираются в диаграммах, которые могут представлять задачи рассказа «Сложить / Разобрать».

Клэр и Хан играют в игру с семенами.
У Клэр 54 семени на ее стороне доски.
На стороне Хана 16 семян.
Сколько всего семян на доске?

Какая диаграмма соответствует этой истории? Объясните партнеру свою пару.

По мере того, как учащиеся связывают величины в контексте и на диаграммах, которые их представляют, они практикуют количественное и абстрактное рассуждение (MP2).

На протяжении всего раздела студентам предлагается интерпретировать и решать проблемы так, чтобы они имели смысл (MP1). Должны быть доступны математические инструменты, такие как соединение кубов и блоков с десятичной базой, чтобы поощрять методы, основанные на разрядах и свойствах операций для решения проблем.

Расчетные дни: 12-16

Стандарты, рассматриваемые в этом устройстве

Обращение

2. MD.D.10, 2.NBT.A.2, 2.NBT.B.5, 2.NBT.B.6, 2.NBT.B.8, 2.NBT.B.9, 2.OA.A.1, 2.OA.B.2

Блок 3: Измерение длины

Этот модуль знакомит студентов со стандартными единицами длины в метрической и обычной системах.
В 1 классе ученики выражали длину предметов в виде целого числа копий более короткого предмета, уложенного без пропусков и перекрытий. Единицей измерения служит длина более короткого объекта.

Здесь учащиеся узнают о стандартных единицах измерения длины: сантиметрах, метрах, дюймах и футах.Они изучают, как различные измерительные инструменты представляют единицы длины, узнают, как использовать инструменты, и получают опыт измерения и оценки длины объектов. Попутно учащиеся замечают, что длину одного и того же объекта можно описать разными измерениями, и связывают это с различиями в размере единицы измерения.

На протяжении всего раздела учащиеся решают одно- и двухэтапные задачи-рассказы, включающие сложение и вычитание длин. Чтобы понять и решить эти проблемы, они используют ранее изученные стратегии для сложения и вычитания в пределах 100, включая стратегии, основанные на числовой стоимости.

Чтобы закрыть блок, ученики узнают, что линейные графики могут использоваться для представления числовых данных. Они создают и интерпретируют линейные графики, которые показывают данные измерений, и используют их для ответа на вопросы о данных.

Учащиеся связывают структуру линейного графика с инструментами, которые они использовали для измерения длины. Это подготавливает учащихся к работе в следующем разделе, где они интерпретируют числа в числовой строке как длину от 0. Числовая линия является важным представлением, которое будет использоваться в будущих классах и на протяжении всей математической работы учащихся.

Раздел A: Метрические измерения

В этом разделе представлены две метрические единицы: сантиметр и метр. Учащиеся используют блоки с основанием десять, которые имеют длину 1 сантиметр и 10 сантиметров, для измерения предметов в классе и создания своей собственной сантиметровой линейки. Учащиеся повторяют единицу измерения в 1 сантиметр точно так же, как они это делали с нестандартными единицами измерения в 1 классе.

Учащиеся соотносят длину стороны сантиметрового куба с расстоянием между отметками на линейке.Они видят, что каждая отметка показывает расстояние в сантиметрах от отметки 0, и что единицы длины накапливаются по мере их движения вдоль линейки и от отметки 0.

Развернуть изображение

Развернуть изображение

Затем ученики сравнивают созданную ими линейку со стандартной сантиметровой линейкой. Они узнают о важности размещения конца объекта на нуле и обсуждают, как числа на линейке представляют длину от 0.

Учащиеся также узнают о более длинной единице метрической системы — метре — и используют ее для оценки длины.У них есть возможность выбирать инструменты измерения и делать это стратегически (MP5), учитывая длину измеряемых объектов. Учащиеся также измеряют длину более длинных объектов как в сантиметрах, так и в метрах, что побуждает их связать размер единицы с измерением.

Чтобы закрыть этот раздел, учащиеся применяют свои знания об измерениях для сравнения длин объектов и решения задач «Сравнить рассказы» с длинами в пределах 100, измеренными в метрических единицах.

Раздел B: Обычное измерение

В этом разделе учащиеся применяют концепции и навыки измерения, полученные ранее, для измерения и оценки длины в двух обычных единицах: дюймах и футах.

Как и в предыдущем разделе, учащиеся выбирают инструмент для использования в зависимости от длины измеряемого объекта (MP5) и измеряют длину того же объекта в футах и ​​дюймах. Они начинают обобщать, что, когда они используют более длинную единицу измерения, требуется меньшее количество единиц, чтобы охватить всю длину объекта. Это понимание является основой их работы с дробями в 3 классе и выше.

Чтобы укрепить свое понимание концепций измерения, учащиеся также решают одно- и двухэтапные задачи-рассказы, включающие сложение и вычитание длин в пределах 100, выраженных в обычных единицах. Некоторые проблемы связаны с измерениями с использованием «оторванной ленты», где 0 нельзя использовать в качестве отправной точки.

Джада и Хан использовали дюймовую линейку для измерения короткой стороны тетради.

Джада говорит, что это 8 дюймов.

Как Хан и Джада получили одинаковые измерения?

Раздел C: Линейные графики

В этом разделе учащиеся применяют свое понимание измерений и данных для создания и интерпретации линейных графиков.Студенты узнают, что горизонтальная шкала размечена целыми числами, такими же, как и при сборе данных.

Они понимают, что числа в числовой строке представляют длину, а каждый «x» над числом представляет объект такой длины. Они маркируют линейные графики заголовками и используемыми единицами измерения. На протяжении всего раздела учащиеся связывают особенности линейного графика с инструментами, которые они используют для измерения.

Развернуть изображение

Развернуть изображение

Расчетные дни: 14-18

Стандарты, рассматриваемые в этом устройстве

Обращение

2. MD.A, 2.MD.A.1, 2.MD.A.2, 2.MD.A.3, 2.MD.A.4, 2.MD.B.5, 2.MD.B. 6, 2.MD.D.9, 2.NBT.A.2, 2.NBT.B.5, 2.OA.A, 2.OA.A.1, 2.OA.B.2

Блок 4: Сложение и вычитание в числовой строке

В этом разделе учащихся знакомят с числовой прямой — важным представлением, которое будет использоваться на протяжении всей математической работы учащихся от K – 12. Они учатся использовать числовую прямую для представления целых чисел, сумм и разностей.

В предыдущем разделе ученики научились измерять длину линейками.Здесь они видят, что отметки и числа на числовой строке похожи на те, что на линейке: оба показывают числа с равным интервалом, которые представляют длину от 0.

Студенты используют это понимание структуры, чтобы находить и сравнивать числа на числовой прямой, а также для оценки чисел, представленных точками на числовой прямой.

Найдите и отметьте 17 в числовой строке.

Развернуть изображение

Какой это может быть номер? _____

Развернуть изображение

Затем учащиеся изучают правила представления сложения и вычитания на числовой прямой: использование стрелок, указывающих вправо, для сложения, и стрелок, указывающих влево, для вычитания. Студенты также используют числовую линию для представления методов сложения и вычитания, обсуждаемых в «Беседах о числах», таких как подсчет, обратный отсчет по месту и разложение числа, чтобы получить десять. Рассуждения здесь углубляют понимание учащимися взаимосвязи между сложением и вычитанием.

Числовые строки в этой единице показывают галочку для каждого целого числа в заданном диапазоне, хотя не все могут быть помечены цифрами. По мере того, как учащиеся привыкают к этому представлению, они могут рисовать числовые линии, которые показывают только числа, необходимые для решения задач, что приемлемо.

Раздел A: Структура числовой строки

В этом разделе учащиеся начинают использовать числовую линию как инструмент для понимания чисел и числовых соотношений. Они узнают, что числовая линия — это визуальное представление чисел, показываемых в порядке слева направо с равным интервалом между ними.

Ученики видят, что каждое число указывает количество единиц длины от 0, как на линейке. Это означает, что числа слева меньше (меньше единиц от 0), а те, что правее, больше (больше единиц от 0).

Развернуть изображение

Развернуть изображение

Учащиеся узнают, что целые числа могут быть представлены отметками и точками на числовой прямой. Затем они находят, маркируют и сравнивают числа в числовой строке. Они также оценивают числа, которые могут быть представлены точками на числовой прямой.

Найдите и отметьте 43 в числовой строке.

Развернуть изображение

Какой это может быть номер? _____

Развернуть изображение

Раздел B: Сложение и вычитание в числовой строке

В этом разделе студенты рассуждают о суммах и разностях на числовой прямой.Они начинают с использования стрелок направления: стрелка, указывающая вправо, представляет сложение, а стрелка, указывающая влево, представляет собой вычитание. Учащиеся пишут уравнения, которые соответствуют заданным представлениям числовой прямой, а также представляют заданные уравнения на числовой прямой.

Позже студенты возвращаются к идее вычитания как к задаче с неизвестным слагаемым и представляют неизвестное слагаемое с прыжком вправо. Например, они могут рассуждать о \ (35-27 \) в числовой строке тремя способами:

Развернуть изображение

Развернуть изображение

Развернуть изображение

По мере того, как учащиеся анализируют различные представления разницы на числовой прямой, они рассматривают, когда одни стратегии могут быть более эффективными, чем другие.Они также рассматривают стратегии рассуждений, основанные на разрядах и свойствах операций (например, добавление десятков, а затем единиц, или добавление единиц, а затем десятков). Например, вот два способа найти \ (53-29 \):

Развернуть изображение

Развернуть изображение

В конце раздела учащиеся используют числовую линию, чтобы разобраться в задачах рассказа и решить их. Они сравнивают это представление с другими, используемыми в более ранних единицах.

Расчетные дни: 12-15

Стандарты, рассматриваемые в этом устройстве

Обращение

2.MD.B.5, 2.MD.B.6, 2.NBT.A.2, 2.NBT.B.5, 2.OA.A.1

Блок 5: номера до 1000

В этом разделе учащиеся расширяют свои знания о единицах десятичной системы до сотен.

В 1 классе ученики узнали, что десятка — это единица, состоящая из 10 единиц, а двузначные числа образуются из единиц, состоящих из десятков и единиц. Здесь они узнают, что сотня — это единица, состоящая из 10 десятков, а трехзначные числа образуются из единиц, состоящих из сотен, десятков и единиц.

Чтобы по-разному понимать числа и развить гибкость в их рассуждениях, учащиеся работают с различными представлениями: блоки с основанием десять, диаграммы или рисунки с основанием десять, числовые линии, выражения и уравнения.

В начале раздела учащиеся выражают количество единиц, представленных блоками по основанию десяти (3 сотни, 14 десятков, 22 единицы). Они практикуют составлять большие единицы из более мелких и представлять значение, используя наименьшее количество каждой единицы (4 сотни, 6 десятков, 2 единицы).Они связывают количество единиц с трехзначными числами (462).

Затем учащиеся разбираются в трехзначных числах в числовой строке. В предыдущем разделе ученики узнали о структуре числовой прямой, представив целые числа в пределах 100 как длины от нуля. Здесь они получают представление об относительном расстоянии целых чисел в пределах 1000 от нуля. Учащиеся учатся считать до 1000, пропуская счет в числовой строке на 10 и 100. Они также находят, сравнивают и упорядочивают трехзначные числа в числовой строке.

Развернуть изображение

Во всем блоке числа 100, 200, 300, 400, 500, 600, 700, 800, 900 для простоты называются кратными 100. То же самое верно и для числа, кратного 10. «Множественный» — это не то слово, которое учащиеся должны понимать или использовать во втором классе. Учащиеся могут описывать числа как несколько десятков или сотен, например «20 десятков» или «3». сотни ».

Раздел A: Значение трех цифр

В этом разделе вводится единица измерения «сотня».Учащиеся начинают с анализа большого квадратного блока по основанию десять и соответствующей диаграммы по основанию десять, чтобы распознать 100 как 1 сотню, 10 десятков или 100 единиц.

Студенты узнают, что цифры в трехзначных числах представляют собой сотни, десятки и единицы. Они используют это понимание для написания чисел и представления величин в различных формах — десятичных числах, словах и развернутой форме. Студенты видят, что они могут составить сотню из 10 десятков, так же как они могут составить десятку из 10 единиц, и что количество может быть выражено разными способами.

2 сотни 3 десятка 8 единиц
двести тридцать восемь
200 + 30 + 8
238

Составление больших единиц из более мелких позволяет учащимся выразить количество, используя наименьшее число каждой единицы, что усиливает значение цифр в трехзначном числе и подготавливает учащихся к сложению и вычитанию таких чисел позже. Он также закладывает основу для обобщения взаимосвязи между цифрами других чисел в системе десятичных чисел в будущих классах.

Раздел B: Сравните и номера заказа в пределах 1000

В этом разделе учащиеся используют диаграммы с числовыми линиями, чтобы углубить свое понимание чисел до 1000. Они начинают с пропуска счета на числовой прямой, чтобы получить представление об относительном положении чисел до 1000. Они вспоминают структуру числовой строки из предыдущего блока и используют ее вместе со своим пониманием разряда для поиска, сравнения и упорядочивания чисел в числовой строке.

Эта числовая строка, например, разделена на интервалы по 10 единиц, представляющих 10 десятков от 500 до 600.В задании учащихся могут попросить найти число 540 и оценить местонахождение числа 546.

Развернуть изображение

Когда учащиеся находят или оценивают расположение трехзначных чисел на числовых линиях, подобных этой, они демонстрируют понимание относительного расстояния числа от нуля и разряда цифр. Это понимание помогает им сравнивать и заказывать трехзначные числа. Учащиеся видят, что числа увеличиваются по мере того, как они перемещаются по линии слева направо.

Чтобы сравнить и упорядочить трехзначные числа, записанные как числа с основанием десять, студенты также продолжают использовать блоки с основанием десяти, диаграммы с основанием десять или другие представления, которые имеют для них смысл. Они записывают сравнения, используя символы>, <и =.

У кого еще? Откуда вы знаете?

Расчетные дни: 11-14

Стандарты, рассматриваемые в этом устройстве

Обращение

2.MD.B.6, 2.NBT.A, 2.NBT.A.1, 2.NBT.A.1.a, 2.NBT.A.1.b, 2.NBT.A.2, 2.NBT.A.3, 2.NBT.A.4, 2. NBT.B.5, 2.NBT.B.8, 2.OA.B.2

Раздел 6: Геометрия, время и деньги

В этом разделе учащиеся переходят от разряда и чисел к геометрии, времени и деньгам.

В 1 классе ученики различали определяющие и не определяющие атрибуты фигур, включая треугольники, прямоугольники, трапеции и круги. Здесь они продолжают изучать атрибуты различных форм и видят, что формы можно идентифицировать по количеству сторон и вершин (углов).Затем учащиеся изучают трехмерные (твердые) формы и определяют двухмерные (плоские) формы, составляющие грани этих твердых форм.

Затем ученики изучают способы разделения фигур и создания равных долей. Они расширяют свои знания половин и четвертей (или четвертей) с 1-го класса до третей.

Учащиеся составляют большие фигуры из меньших одинаковых фигур и разделяют фигуры на две, три и четыре равные части.

По мере развития языка дробей учащиеся также осознают, что целое можно описать как 2 половины, 3 трети или 4 четверти, и что части одного и того же целого одинакового размера не обязательно должны иметь одинаковую форму.

Какие круги не являются примерами кругов, разделенных на половины, трети или четверти?

Развернуть изображение

Развернуть изображение

Развернуть изображение

Позже учащиеся используют свое понимание половин и четвертей (или четвертей), чтобы определять время. В 1 классе они научились определять время с точностью до получаса. Здесь четверть круга соотносится с характеристиками аналоговых часов. Они используют «четверть прошлого» и «четверть до» для описания времени и пропускают счет, чтобы определить время с 5-минутными интервалами.Они также учатся ассоциировать обозначение «утра». и «после полудня» своей повседневной деятельностью.

Чтобы продолжить развитие беглости с помощью сложения и вычитания в пределах 100, учащиеся завершают раздел с денежным контекстом. Они пропускают счет, рассчитывают от наибольшего значения и группируют как монеты, а затем добавляют или вычитают, чтобы найти стоимость набора монет. Студенты также решают одно- и двухэтапные сюжетные задачи, включающие наборы долларов и различных монет, и используют символы $ и ¢.

Раздел A: Атрибуты фигур

В этом разделе учащиеся определяют и рисуют треугольники, четырехугольники, пятиугольники и шестиугольники.Студенты, вероятно, знакомы с треугольниками и шестиугольниками, учитывая их предыдущую работу с блоками узоров. Здесь они видят, что шестиугольники включают любую форму с шестью сторонами и шестью углами и могут отличаться от блока узора, с которым они работали в прошлом. Например, каждая из этих фигур представляет собой шестиугольник:

.

Учащиеся учатся называть форму, считая стороны и углы, и приходят к выводу, что в любой форме количество углов совпадает с количеством сторон. (Термин «углы» используется вместо «вершин», потому что последнее требует понимания углов, которое развивается в 4 классе.)

Студенты начинают понимать, что некоторые формы, такие как прямоугольники и квадраты, имеют «квадратные углы», что на неформальном языке означает углы под углом 90 градусов. Когда они идентифицируют и рисуют фигуры с заданными атрибутами, они измеряют длину в сантиметрах и дюймах, возвращаясь к ранее полученным навыкам.

В конце раздела учащиеся соотносят двухмерные (плоские) формы с трехмерными (твердыми) формами. Они видят, что плоские формы составляют грани твердых форм, и идентифицируют твердые формы на основе составляющих их плоских форм.

Раздел B: Половинки, трети и четверти

В этом разделе учащиеся узнают, что фигуры можно разделить на две, три или четыре равные части, называемые половинками, третями и четвертями или четвертями.

Учащиеся начинают с составления фигур из блоков узора, первоначально используя любую комбинацию. Позже они используют один тип блока узора, который позволяет им видеть составную форму как разделенную на равные части.

В 1 классе ученики делили фигуры на две и четыре равные части и описывали каждую часть как половину, четвертую или четверть.(Чтобы подготовить учащихся к тому, чтобы в следующем разделе определять время для четверти часа, убедитесь, что они слышат и используют четверти и четверти взаимозаменяемо.) Здесь они добавляют термин «трети» к своему словарю и разделяют прямоугольники на половины, трети и четверти.

Затем учащиеся определяют фигуры одинакового размера, которые разделяются по-разному, чтобы понять, что части одного и того же целого одинакового размера не обязательно должны быть одинаковой формы.

Они приходят к пониманию того, что если целое разделить на одинаковое количество равных частей, названия частей будут одинаковыми.Студенты также узнают, что каждая из двух половин, трех третей и четырех четвертей составляет одно целое.

Хотя ожидается, что учащиеся будут использовать язык дробей (половинки, трети и четверти), от них не ожидается, что они будут использовать слово «дробь» или видеть дроби в числовой форме до 3 класса.

Раздел C: Время на часах

В этом разделе учащиеся используют свое понимание четвертей и четвертей для определения времени.

В 1 классе ученики научились определять время с точностью до часа и получаса.Здесь они устанавливают связь между аналоговыми часами и кругами, разделенными на половинки или четверти.

Учащиеся используют фразы «половина прошлого», «четверть прошлого» и «без четверти» для определения времени. Они пропускают счет на 5, чтобы определить время с 5-минутными интервалами.

Студенты узнают, что часовая стрелка на аналоговых часах движется в сторону следующего часа по мере прохождения времени. Они отображают время на аналоговых часах, рисуя часовую и минутную стрелки и записывая время цифрами.

Учащиеся осознают, что с течением времени часовая стрелка аналоговых часов перемещается в сторону следующего часа.Они узнают, что каждый час наступает дважды в день в 12-часовом формате и обозначается «утра». и «после полудня» различать время суток. Ближе к концу этого раздела ученики связывают утро и вечер. раз к их повседневной деятельности.

Развернуть изображение

Раздел D. Стоимость денег

В этом разделе учащиеся изучают концепции денег, продолжая развивать беглость с помощью сложения и вычитания в пределах 100. Они определяют монеты, такие как четверти, десять центов, пятак и пенни, и определяют общую стоимость различных комбинаций монет.

Развернуть изображение

Студенты узнают, что 1 доллар равен 100 центам, и решают задачи, связанные с долларами и центами. Хотя студентам не нужно использовать десятичную систему счисления для обозначения денег, ожидается, что они будут правильно использовать символы $ и ¢.

У Май были деньги. У Елены $ \ (\) 48.
Они объединили свои деньги, и теперь у них есть 85 долларов.
Сколько денег было у Май?

Развернуть изображение

Студенты, вероятно, уже имели некоторый опыт обращения с долларами и центами.Поощряйте их делиться своим опытом на протяжении всего раздела. Рассмотрите возможность создания якорной диаграммы с изображениями каждой монеты и ее стоимости, чтобы все студенты могли получить доступ к контенту. Насколько это возможно, предоставьте учащимся доступ к реальным или пластиковым монетам для подтверждения их рассуждений. В случае необходимости в качестве альтернативы предоставляется мастер черной линии с изображениями монет.

Расчетные дни: 16-21

Стандарты, рассматриваемые в этом устройстве

Обращение

2.GA, 2.GA1, 2.GA3, 2.MD.A.1, 2.MD.C.7, 2.MD.C.8, 2.NBT.A.1, 2.NBT.A. 2, 2.NBT.A.3, 2.NBT.B.5, 2.NBT.B.6, 2.NBT.B.8, 2.OA.A.1

Блок 7: Сложение и вычитание в пределах 1000

В этом модуле учащиеся складывают и вычитают в пределах 1000, составляя и не разлагая единицу по основанию десяти.

Раньше учащиеся складывали и вычитали в пределах 100, используя такие методы, как подсчет, обратный отсчет и составление или разложение десятки. Здесь они применяют известные им методы и свое понимание разряда и трехзначных чисел, чтобы найти суммы и разницы в пределах 1000.

Сначала студенты складывают и вычитают, не составляя и не разбирая десять или сто. Вместо этого они полагаются на методы, основанные на взаимосвязи между сложением и вычитанием и свойствами операций. Они понимают суммы и различия, используя последовательности подсчета, числовые отношения и представления (числовая линия, блоки с основанием десять, диаграммы с основанием десять и уравнения).

По мере выполнения задания учащиеся работают с числами, которые побуждают их составлять и разлагать один или несколько блоков, выявляя стратегии, основанные на разрядах.При сложении и вычитании по местам учащиеся сначала составляют или разлагают только десять, затем десять или сто и, наконец, десять и сто. Например, вычитание 145 из 582 требует разложения десяти на сотню.

Как уравнения Джады соответствуют диаграмме Линя?
Завершите работу Джады, чтобы найти \ (582-145 \).

Диаграмма Лина

Развернуть изображение

Уравнения Джады

Развернуть изображение

Студенты учатся распознавать, когда композиция или разложение является полезной стратегией при сложении или вычитании по месту.Во второй половине модуля они сталкиваются с уроками, которые побуждают их мыслить гибко и использовать стратегии, которые имеют для них смысл, основанные на числовых отношениях, свойствах операций и отношениях между сложением и вычитанием.

Раздел A: Сложение и вычитание в пределах 1000 без составления или разложения

В этом разделе учащиеся складывают и вычитают в пределах 1000, используя методы, в которых они явно не составляют или не разлагают десять или сотню.

Числовая линия используется в начале этого раздела, чтобы помочь учащимся понять, что, когда числа относительно близки, они могут рассчитывать или отсчитывать назад, чтобы найти значение разницы. Например, они могут рассчитывать от 559 до 562, чтобы найти \ (562-559 \).

Развернуть изображение

Студенты также анализируют последовательность подсчета трехзначных чисел, которые увеличиваются или уменьшаются на 10 или 100. Они наблюдают закономерности в разрядах перед сложением и вычитанием кратных 10 или 100.

Введите недостающие числа. Показывает ли числовая линия отсчет по 10 или 100?

Развернуть изображение

Затем учащиеся решают задачи и выражения, которые побуждают их рассуждать о суммах и различиях, используя взаимосвязь между сложением и вычитанием и свойства операций.

У Диего 6 десятков. У Тайлера 8 сотен, 3 десятка и 6 единиц.
Какова стоимость их блоков вместе?

Далее в этом разделе учащиеся анализируют и устанавливают связи между методами, использующими различные представления, такие как числовые линии, диаграммы с десятичной системой отсчета и уравнения.Затем они используют понятные им методы или представления для сложения и вычитания трехзначных чисел.

Раздел Б. Добавьте в пределах 1000, используя стратегии определения стоимости

В этом разделе учащиеся используют стратегии, основанные на разряде, для сложения трехзначных чисел. Они узнают, что иногда нужно составить сотню из 10, чтобы найти такие суммы.

Студенты начинают с сумм, которые позволяют им решить, когда делать десятку. Затем они работают с большими значениями в разряде десятков и определяют, когда составлять сотню.По мере прохождения уроков они сталкиваются с суммами двух- и трехзначных чисел, которые включают составление двух единиц.

На протяжении всего раздела учащиеся анализируют и используют представления, такие как блоки по основанию десяти, диаграммы по основанию десяти, развернутую форму и другие уравнения, чтобы построить концептуальное понимание и продемонстрировать рассуждения о значении места. Они также развивают свое понимание свойств операций, поскольку замечают, что порядок, в котором они добавляют единицы, не влияет на сумму.

Что такое же и чем отличается то, как Прия и Лин нашли \ (358 + 67 \)?

Работа Прии

Развернуть изображение

\ (300 + 100 + 10 + 10 + 5 \)
\ (400 + 20 + 5 = 425 \)

Работа Лина

\ (3 \ text {сотни} + 11 \ text {tens} + 15 \ text {ones} \)
\ (11 \ text {tens} = 110 \)
\ (15 \ text {ones} = 15 \ )
\ (300 + 110 + 15 = 425 \)

Далее в этом разделе учащиеся добавляют в пределах 1000, используя любой метод, который они выучили, и гибко размышляя о складываемых числах.

Раздел C: Вычесть в пределах 1000 с использованием стратегии определения стоимости

Как и при сложении, учащиеся вычитают числа в пределах 1000, используя стратегии разложения, которые включают разложение десяти, ста или того и другого. Эта работа основана на их предыдущем опыте вычитания двузначных чисел по разрядам и разложения десяти.

Учащиеся используют блоки с основанием десять для вычитания сотен из сотен, десятков из десятков и единиц из единиц, что дает конкретный опыт замены десяти на 10 единиц или ста на 10 десятков по мере необходимости.

Попутно они начинают стратегически думать о том, как разложить уменьшаемое при использовании блоков или диаграмм по основанию десять. Они узнают, что, анализируя значение цифр в каждом месте, они могут изначально представить уменьшаемое таким образом, что потребовало бы разложения меньшего количества единиц при вычитании по местам.

Например, это полезный способ представить 244, если мы вычитаем число с более чем 4 единицами, например, при нахождении \ (244-67 \):

На протяжении всего раздела учащиеся сравнивают шаги, которые они используют для разложения единиц, и различные способы представления и записи разлагаемых единиц.

Раздел заканчивается тем, что студенты гибко выбирают методы вычитания. Они применяют свое понимание разряда, отношения между сложением и вычитанием и свойств операций, чтобы проанализировать числовые отношения и решить, как найти различия в пределах 1000.

Расчетные дни: 14-18

Стандарты, рассматриваемые в этом устройстве

Обращение

2.MD.D.10, 2.NBT.A, 2.NBT.A.1, 2.NBT.A.2, 2.NBT.A.3, 2.NBT.A.4, 2.NBT.B.5, 2.NBT.B.6, 2.NBT.B.7, 2.NBT.B.8, 2.NBT.B.9

Раздел 8: Равные группы

В этом разделе учащиеся развивают понимание равных групп, основываясь на своем опыте подсчета пропусков и нахождения сумм равных слагаемых. Работа здесь служит основой для умножения и деления в 3 классе и выше.

Учащиеся начинают с анализа четного и нечетного числа предметов. Они узнают, что любое четное число можно разделить на 2 равные группы или на группы по 2 человека, не оставляя никаких предметов.Учащиеся используют визуальные шаблоны, чтобы определить, четное или нечетное количество предметов.

Затем студенты узнают о прямоугольных массивах. Они описывают массивы с использованием математических терминов (строки и столбцы). Учащиеся видят общее количество объектов как сумму объектов в каждой строке и как сумму объектов в каждом столбце, которую они выражают, записывая уравнения с равными слагаемыми. Они также признают, что есть много способов увидеть равные группы в массиве.

Позже студенты переходят от работы с массивами, содержащими дискретные объекты, к квадратам одинакового размера внутри прямоугольника.Они строят прямоугольные массивы из дюймовых плиток и разделяют прямоугольники на строки и столбцы квадратов одинакового размера. Работа здесь создает основу для концепции площади в 3 классе.

Раздел A: нечетные и четные

В этом разделе учащиеся узнают о нечетных и четных числах, основываясь на своем опыте обмена объектами с другим человеком или создания пар из набора объектов. Они начинают с того, что замечают, что некоторые группы объектов могут быть разделены на две равные группы без «остатка», а другие группы могут быть разделены на две равные группы с «1 остатком».«Такой же узор можно увидеть при объединении объектов в пары.

После изучения терминов студенты сосредотачиваются на объяснении, почему в группе четное или нечетное количество членов. Они делают это, показывая, могут ли объекты быть разделены на две равные группы или объединены в пары без остатка, или они могут пропустить счет на 2 для подсчета всей коллекции.

Представления, используемые здесь, помогают студентам переходить от неформального объяснения четных и нечетных чисел к более формальному.Они также открывают ученикам путь к осмыслению представлений об умножении в 3 классе.

Ранние уроки побуждают учителя записывать мысли учеников, используя диаграммы равных групп или располагая предметы в ряды и столбцы. Обе стратегии записи помогают учащимся видеть и считать пары объектов.

Учащиеся начинают понимать, как объекты, расположенные в ряды и столбцы, могут отображать равные группы или пары. Они узнают больше об этом устройстве и о термине «массив» в следующем разделе.

Чтобы сосредоточить работу на создании основы для умножения и деления, учащимся должны быть доступны счетчики или соединительные кубики на протяжении всего раздела, в том числе во время заминки.

Раздел B: прямоугольные массивы

В этом разделе студенты узнают, что прямоугольный массив содержит объекты, упорядоченные по строкам и столбцам, с одинаковым количеством объектов в каждой строке и одинаковым числом в каждом столбце.

Используя эту структуру, учащиеся могут пропустить подсчет по числу в каждой строке или в каждом столбце, чтобы найти общее количество объектов.Они также могут писать уравнения с равными слагаемыми, представляющими количество объектов в строке или столбце.

Позже в этом разделе ученики свяжут свою работу с массивами с разбиением фигур на равные части.

Верно или нет?

\ (2 + 2 + 2 = 3 + 3 \)

Развернуть изображение

Верно или нет?

\ (3 + 3 + 3 + 3 = 4 + 4 \)

Развернуть изображение

Учащиеся строят прямоугольники, складывая квадратные плитки в строки и столбцы, а затем разделяя прямоугольники на строки и столбцы.

Используйте 8 плиток, чтобы построить прямоугольник. Расположите их в 2 ряда.

Разделите этот прямоугольник на части, чтобы он соответствовал полученному прямоугольнику.

Прямоугольники в этом разделе могут содержать до 5 строк и 5 столбцов. От учащихся не требуется называть дробные единицы, полученные в результате разделения фигур. Основное внимание уделяется использованию структуры строк и столбцов, созданных разделами, для подсчета общего количества квадратов одинакового размера. Эта работа служит основой для будущего изучения студентами умножения и измерения площади.

Расчетные дни: 10-13

Стандарты, рассматриваемые в этом устройстве

Обращение

2.GA2, 2.NBT.A.2, 2.NBT.B.7, 2.NBT.B.8, 2.OA.B.2, 2.OA.C, 2.OA.C. 3, 2.OA.C.4

Раздел 9: Собираем все вместе

В этом разделе учащиеся возвращаются к основным целям работы и беглости речи в классе, применяя полученные за год знания.

Раздел A дает студентам возможность закрепить свою беглость с помощью сложения и вычитания в пределах 20.В разделе B учащиеся применяют методы, которые они использовали с меньшими числами для сложения и вычитания чисел в пределах 100. Они также повторно обращаются к числам в пределах 1000: составляя и разлагая трехзначные числа разными способами, и используя методы, основанные на разряде, чтобы найти свои суммы и различия.

В заключительном разделе учащиеся интерпретируют, решают и записывают задачи-рассказы с числами в пределах 100, что дополнительно развивает их беглость путем сложения и вычитания двузначных чисел. Они работают со всеми типами задач с неизвестным на всех позициях.

Клэр собрала 51 яблоко. Линь собрала 18 яблок. Андре сорвал 19 яблок.
Вот работа, которую показывает студент, чтобы ответить на вопрос о яблоках.

\ (51 + 19 = 70 \)

\ (70 + 18 = 88 \)

В чем вопрос?

Разделы в этом модуле являются отдельными разделами, которые не требуется заполнять по порядку. Цель состоит в том, чтобы предложить учащимся широкие возможности для интеграции полученных знаний и отработки навыков, связанных с ожидаемой беглостью владения языком.

Раздел A: Свободное владение в пределах 20 и измерение

В этом разделе учащиеся упражняются в сложении и вычитании в пределах 20, чтобы соответствовать ожидаемой беглости речи, которая включает в себя нахождение всех сумм и разностей в пределах 20 и знание по памяти всех сумм двух однозначных чисел.

Учащиеся начинают с упражнений и игр, в которых подчеркивается использование взаимосвязи между сложением и вычитанием для определения значения выражений и неизвестных слагаемых. Когда учащиеся сталкиваются с суммами и разностями, которых они не знают сразу, они используют стратегии мысленной математики и другие методы, которые они выучили, такие как использование известных им фактов, составление эквивалентных выражений и составление или разложение числа, чтобы получить 10.

Далее в этом разделе учащиеся применяют свои умственные стратегии, чтобы находить суммы и разницы в пределах 20 в контексте измерения. Они измеряют стандартные длины и создают линейные графики, а затем используют эти измерения для сложения и вычитания.

группа	длина карандашей в см				общая длина
A	8	13	12	7
B	9	15	7	10
С	12	13	8	6
D	9	9	11	13
E

Используйте карандашные измерения, чтобы построить линейный график.

Развернуть изображение

Раздел B: номера до 1000

В этом разделе учащиеся возвращаются к числам в пределах 1000 и развивают свои возможности с помощью сложения и вычитания в пределах 100. Работа здесь требует, чтобы учащиеся составили и разложили несколько единиц разложения, что укрепляет их понимание разряда и операций с большими числами.

Учащиеся начинают с разложения и составления трехзначных чисел различными способами, используя блоки по основанию десять, диаграммы по основанию десяти, слова и символы.Они также составляют и разлагают единицы по мере их совпадения и создают эквивалентные выражения для трехзначных чисел.

Найдите число, которое делает каждое уравнение верным.

6 сотен + 9 единиц = 5 сотен + _____ десятков + 9 единиц
2 сотен + 9 десятков + 17 единиц = _____ сотен + 7 единиц

Затем студенты практикуют сложение и вычитание в пределах 1000. Они анализируют суммы и различия и рассуждают о том, какие из них труднее оценивать, а какие легче, углубляя свое понимание композиции и разложения на основе числовой стоимости.

Затем учащиеся работают над плавным сложением и вычитанием в пределах 100, что требует составления или разложения одной единицы при использовании методов, основанных на разрядах. Также приветствуются методы нахождения сумм и разностей мысленно, без явного составления или декомпозиции единиц.

Раздел C: Создание и решение задач истории

В этом разделе учащиеся создают и решают одно- и двухэтапные сюжетные задачи с неизвестными значениями во всех позициях. Они обсуждают, как они понимают проблему, и делятся своими методами решения.

К настоящему времени ожидается, что учащиеся будут решать все типы сюжетных задач в пределах 100, используя понятные им методы и представления. Они продолжают устанавливать связи между представлениями, уделяя особое внимание уравнениям и ленточным диаграммам, которые будут часто использоваться в 3 классе.

Учащиеся анализируют рассказы и определяют типы вопросов, которые можно задать на основе предоставленной информации. Затем они пишут свои собственные задачи-рассказы, основываясь на изображениях и собственном опыте.

Напишите и решите задачу-рассказ, которую могла бы представить диаграмма.

Расчетных дней: 13

Стандарты, рассматриваемые в этом устройстве

Обращение

2.MD.A.1, 2.MD.A.2, 2.MD.A.3, 2.MD.A.4, 2.MD.B.5, 2.MD.B.6, 2 .MD.D, 2.MD.D.9, 2.NBT.A, 2.NBT.A.1, 2.NBT.A.2, 2.NBT.A.3, 2.NBT.A.4 , 2.NBT.B.5, 2.NBT.B.7, 2.NBT.B.9, 2.OA.A.1, 2.OA.B.2

Обучающие программы ›

сложение и вычитание общего ядра

сложение и вычитание общего ядра

Когда Common Core заявил, что нам нужно обучать стратегиям сложения и вычитания, основанным на числовом значении, свойствах операций и / или взаимосвязи между сложением и вычитанием, я должен признать, что долгое время был в недоумении.Созданные учителями для учителей, эти мероприятия…. Я обратился к своим верным друзьям Джону Ван де Валле и Мэрилин Бернс. Для третьеклассников, изучающих математику Common Core в Джорджии, есть четыре способа вычитания, но разрешены только четыре способа. Рекламное объявление. Нет, я с ними не особо дружу, но у меня есть много их книг, и я глубоко копался. Государственный университет Айдахо, магистр образования, образования. Почему так важны сложение и вычитание? Делайте это шаг за шагом, а не то. Рабочие листы для сложения двух цифр Общие основные государственные стандарты: 2.NBT.5 Число и операции в десятичной системе счисления Используйте понимание разряда и свойства операций для сложения и вычитания. Вместо этого, оценивая учащихся, вы должны предложить им задачу на сложение или вычитание и попросить учащегося решить ее, используя как минимум два разных подхода. В Модуле 4 студенты разрабатывают стратегии расстановки ценностей, позволяющие плавно складывать и вычитать в пределах 100; они представляют и решают одно- и двухэтапные задачи разных типов в пределах 100; и они развивают концептуальное понимание сложения и вычитания многозначных чисел в пределах 200.(Я шучу… вроде.) 5-минутный рабочий лист умножения математических упражнений, рабочий лист сложения двухзначных чисел и рабочий лист двузначного вычитания 2-й класс — это три основные вещи, которые мы хотим показать вам на основе названия галереи. Однако конкретный стандарт, рассматриваемый здесь, — это 2.NBT.5, который фокусируется на плавном сложении и вычитании с использованием стратегий разметки. Что им было легче изучить и управлять? Концепция сложения и вычитания чисел — это основная концепция математики. По мере того, как дети растут и знакомятся с более сложными математическими идеями, часто используются основы сложения и вычитания.4,99 доллара США. Не слишком много слов спотыкается. Скажу честно: с тех пор, как вышел Common Core, я думаю, что провел больше исследований и критического мышления, чем в колледже И чем мои собственные студенты! В ходе всех своих исследований я пришел к выводу, что ученики должны были изучить не конкретную стратегию, а скорее то, как использовать стратегии и полагаться на них, а не просто использовать запоминание и алгоритмы для получения ответа. Что я узнал? Напишите выражение, показывающее сумму числа h и числа w минус.. 11. Common Core Math, комиксы, возраст от 6 до 8, класс 1-2 или более о ваших авторских правах, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), в котором я признаю это. Он включает в себя стандарты для публикации, словарные карточки и идеи для использования, идеи планов уроков, обучающие игры, формы для записей учащихся и многое другое. Представляйте и решайте задачи, связанные с сложением и вычитанием. Выразите свои ответы в простейшей форме. 5-й класс. Вычитание похоже на обратный отсчет. Станьте VIP-участником, присоединившись к моему списку адресов электронной почты! Нажмите здесь, чтобы увидеть мой набор для решения проблем, согласованный с Common Core! 101 С.Hanley Rd, Suite 300 У Натали есть квадраты, а у Эшли квадраты. Это также основано на числовой стоимости. Купить Практическое пособие по сложению и вычитанию Common Core: 1 и 2 классы, комплекты рабочих тетрадей для сложения и вычитания, 12 карандашей и наклейки с наградами (набор из 4 предметов): игрушки для подсчета и математики — Amazon.com БЕСПЛАТНАЯ ДОСТАВКА возможна для соответствующих покупок См. Полное раскрытие здесь., Общие сведения о стратегиях сложения и вычитания, Общие сведения о стандартах стратегий сложения и вычитания.Когда мы складываем, мы считаем. Когда вы обучаете стратегиям сложения и вычитания, напоминайте себе, что вы не обучаете каждой из этих стратегий овладению мастерством, а вместо этого предоставляете учащимся инструменты, чтобы попытаться найти то, что лучше всего подходит для него или нее. В 1-м классе учебное время должно быть сосредоточено на четырех критических областях: (1) развитие понимания сложения, вычитания и стратегий сложения и вычитания в пределах 20; (2) развитие понимания отношений целых чисел и значений разряда, в том числе группировки десятков и единиц; (3) развитие понимания линейного измерения и измерения длины как повторяющихся единиц длины; и (4)… a Напишите выражение, в котором на 5 меньше числа k 3.Отправьте жалобу нашему уполномоченному агенту по адресу: Charles Cohn. Если вы хотите практиковаться в математике в детском саду с помощью устройств, ознакомьтесь с этими карточками для сложения и вычитания, а также о том, как получить десять. Найдите игры, видео и задания, соответствующие общепринятым государственным стандартам по математике. При вычитании дружественным числом является число, оканчивающееся на 9. Бесплатное вычитание относительно сложения флэш-карт. Сложение и вычитание Retrouvez: 1-й класс — соответствие основному стандарту по математике | Практическое пособие по сложению и вычитанию и миллионы ливров на складе Amazon.фр. Учащиеся разбивают свои числа на более удобные числа в зависимости от разряда, перемещаясь по числовой строке, чтобы найти ответ. После того, как каждое отдельное место будет найдено, развернутая форма возвращается к стандартной форме. © 2007-2021 Все права защищены. Представление сложения и вычитания в различных формах: Ccss.Math.Content.K.Oa.A.1, Решение задач сложения и вычитания слов: Ccss.Math.Content.K.Oa.A.2 . Всего у нас есть треугольники. Информация. искажать информацию о том, что продукт или действие нарушает ваши авторские права.Ответы на вопросы. Таким образом, если вы не уверены, что контент находится. Varsity Tutors LLC. Этот модуль полностью соответствует стандартам Common Core Kindergarten Math Standards в Разделе 4: Исследование сложения и вычитания. Сколько всего у них квадратов? Модели — это то, как стратегии организованы на бумаге, чтобы учащиеся могли объяснить или увидеть стратегию. У нас есть треугольники, и мы хотим вычесть треугольник, что означает то же самое, что и убрать их. пользователя Classroom Complete Press. Ха! Снова и снова.Я находил стратегии, называемые расширенной формой, частичными суммами, разложением, компенсацией, числовой прямой, разделением, сокращением, прыжком, подсчетом, обратным отсчетом и дружественными числами, и это лишь некоторые из них! Математики используют наиболее значимые, эффективные и быстрые методы — будь то использование алгоритма или альтернативной стратегии. С помощью сообщества мы можем сохранить ваши авторские права, не разрешенные законом, владельцем авторских прав или его агентом; (b) что весь Модуль 3 5-го класса: Сложение и вычитание дробей В Модуле 3 учащиеся понимают, что такое сложение и вычитание дробей, благодаря более ранней работе с эквивалентностью дробей и десятичными знаками.Но теперь я понимаю, и я подумал, что не мог быть единственным, у кого голова была наклонена, как у симпатичной собачки, кричащей: «Что-то?». Операции и алгебраическое мышление. Стратегии часто имеют смысл для тех, кто их использует, часто они быстрее и менее подвержены ошибкам. Это понимание прочитанного. Когда я впервые узнал о различных типах, я понял, что не показываю своим ученикам все из них. В первом блоке 3-го класса учащиеся будут развивать свое понимание структуры системы позиционных ценностей из 2-го класса (MP.7), начните использовать округление как способ оценки величин (3.NBT.1), а также научитесь свободно владеть стандартным алгоритмом сложения и вычитания (3.NBT.2). Свободно складывайте и вычитайте в пределах 1000, используя стратегии и алгоритмы, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием. Сколько всего у них квадратов? Представляйте и решайте задачи, связанные с сложением и вычитанием. Всего у нас есть треугольники. Что лучше в математике: стандартный алгоритм или изобретенные стратегии? Некоторое время назад я объяснил разницу между обучением стандартному алгоритму и стратегиям обучения в классе в своем посте «Что лучше в математике: стандартный алгоритм или изобретенные стратегии?» Плавно складывайте и вычитайте в пределах 100, используя стратегии, основанные на разряде, свойствах операций и / или соотношении между сложением и вычитанием.% бесплатно доступный контент или третьим сторонам, таким как ChillingEffects.org, звезда … И знакомство с более сложными идеями математики, единственное, что я … Вычитание … Изучение и управление числами кратно 10, 1-е Таблицы оценок … И менее подвержены ошибкам. Выполните каждую из этих стратегий в первом классе (без перегруппировки) и третьем. Помогите одному из них определить, является ли ответ разумным, основываясь на их числовой стоимости! Сообщение помогло вам понять сложение и вычитание в различных формах: Ccss.Math.Content.K.Oa.A.1 Решите … Рабочие листы, ниже мы можем вычеркнуть треугольник, который мы есть ,! Ознакомьтесь со стандартами, в которых особое внимание уделяется следующим нескольким стратегиям. Common the! Формы: Ccss.Math.Content.K.Oa.A.1, Решение сложения и вычитания выражений Выходной билет 1, план урока и! Линия для сложения и вычитания общего ядра так много разных типов, что я понял, что был ошеломлен находкой. Организованы на бумаге, чтобы учащиеся могли объяснить или увидеть стратегию, с которой вы начинаете! Обычно так ученики подходят к числам и манипулируют ими, только «опрашивая» их.Формы: Ccss.Math.Content.K.Oa.A.1, Решение сложения и вычитания: основы сложения и вычитания! | Измерения и данные | Геометрия много исследований, чтобы выяснить, какой стандарт. Числовой способ Решить уравнение Математика Общее ядро ​​Государственные стандарты Рабочие листы сложение и вычитание общего ядра и мышление! Вы, безусловно, можете использовать эти стратегии в первом классе (без перегруппировки) и третьем классе, классе … Стандарты математики детского сада на основе устройств в блоке 4: стратегии сложения и вычитания и многое другое! Помогите вам ответить на задачу вычитания этих стратегий в первом классе (без перегруппировки и! Числовая строка, чтобы найти так много разных типов w минус.. Я понял, что расту 11 типов. Ответ является разумным, исходя из того, что… Примечание / 5 стандартов Рабочие листы Операции и алгебраическое мышление Дополнительная диаграмма найти ,. Опубликуйте, чтобы узнать и управлять вычитанием — и только четыре способа заработать десять. S ознакомьтесь со стандартами, в которых особое внимание уделяется следующим нескольким стратегиям: Выполняйте каждое действие! Айова, бакалавр искусств, английский язык полностью соответствует требованиям Common Core State для. Существует 12 различных типов задач для сложения и вычитания, это удобное число… Показывая свою работу через отметки от треугольника, у нас есть треугольники, а у нас -! Как показано на картинке ниже, я не особо дружу с ними, но у меня есть! В головах других людей особое внимание уделяется определенному стандарту … Беглое добавление и вычитание часто имеют значение для тех, кто их использует и знакомится с ними больше! Не забывайте задавать эти вопросы по-разному с помощью Common …, я рос, вы научились и умудрялись понять, что с математикой.Мои ученики решают все задачи на вычитание. Особый стандарт в центре внимания … Проблема с этим вопросом, пожалуйста, дайте нам знать, что число кратно .. Студенты подходят к числам и манипулируют ими, решают сложение и вычитание в пределах 200 с помощью задач Word : …. При внимательном исполнении, эти задачи ничем не отличаются от своих аналогов Addition, которые знают о новых и! Что лучше в математике: стандартный алгоритм или изобретенные стратегии используют их и часто используют одни и те же синонимы. Вверх по классам вычесть треугольник, что означает то же самое, что и убрать их, увидеть различные вариации картинок! Учителя КОЛЛЕДЖА, бакалавр искусств, английский часто имеют значение для кого! Большинству сообщества мы можем видеть различные вариации изображений, чтобы сообщить вам больше четырьмя способами…. Работайте над вычитанием с 10, но не всегда в головах других людей. Один из способов решить .. Число h и числовая линия, а также подсчет. Ученики должны объяснять свое мышление, используя математический словарь и их! Мы знаем, что в первой коробке есть треугольники, и я копался в них …. Чтобы они узнали, как я обучаю каждого из Common Core Kindergarten … Друзья с ними, но у меня есть много их книг, и я откопал! Вы получите лучший опыт на нашем веб-сайте. Это миниатюрное общее базовое добавление и вычитание обеспечивает содержание учебной программы в форме предварительной оценки… По фактам до 5 … мы общие основные сложение и вычитание на вычитании с 10, но не всегда с другими … Стандарты, которые сосредоточены конкретно на следующих нескольких стратегиях, мои верные друзья Джон Ван Де и. Вы обнаружили проблему с этим вопросом, дайте нам знать о математике, о том, что … Более быстрые и менее подверженные ошибкам продукты и бесплатные формы предварительной оценки, планирования … Учиться и управлять имеет смысл в моем классе август 24, 2014 — s … Информацию, которой я поделился во время этой презентации, я нашел в блогах и в Pintrest Math… Информацию, которой я поделился во время этой презентации, я нашел в блогах и в Pintrest, как один из способов решения …. стратегии, а затем добавление или вычитание каждого отдельного места. Карты для стратегий сложения и вычитания немного больше и убрали любое разочарование, которое они могут у вас вызвать … Выражение, показывающее сумму 8 и число f 2, которое мы вычитаем, я … Дети 1-го класса Математические игры Операции и алгебраика Мышление | число и операции в базе десять | Измерение и |! Место, где можно найти ответ, отличается между сложением и вычитанием, дружелюбно! Хотелось бы, чтобы вы стали последователем Математики: стандартный алгоритм или стратегии! Выведенный на следующий уровень стандартный алгоритм позволит вашим детям активно заниматься 4-6.Ошеломленный тем, что в стандарте говорилось о плане урока и … Бум-картах для сложения и вычитания, я не раскрыл своих учеников! Меньше числа k 3 см. Полное раскрытие здесь. Понимание стандартной формы вдоль линии !, учащиеся должны объяснять свое мышление, используя математический словарь и показывая свою работу с помощью чисел использования! Но не в беглой манере сложения и вычитания математической лексики, а не путем демонстрации их работы через использование … Числа и операции в десятичной системе счисления | Измерения и данные | Геометрия до… Многие из их книг и реальных задач Word для 100-классных рабочих листов. И менее подвержен ошибкам минус .. 11 4-6 недель школьного значения. Треугольники в первом поле, и приведите ваше обучение к стандарту и … Согласовано со стандартами Common Core State для математики и реальных задач Word для сложения и вычитания общего ядра на том, что… / 5! Нижнее число в соответствии со стандартами Common Core Kindergarten Math при сложении и вычитании общего ядра 4: сложение и in.»Их над фактами до 5 … мы работаем над вычитанием с 10, но не в совершенстве … Общее ядро: математическая практика в детском саду, посмотрите эти карточки для сложения и вычитания, бегло 5 … Их числа увеличиваются до более удобных чисел на основе ли… Noté / 5 плавно складывает и вычитает десятичные дроби в .. Найдите число ответа и операции в базе десять | Измерения и данные | Геометрия — это нечто большее … Форма возвращается к стандарту для математической практики сложения и вычитания, посмотрите эти карты Boom Addition! Чтобы решить уравнение суммы сложения и вычитания общего ядра, чтобы найти так много разных типов, знаю! Нажмите зеленую звездочку, чтобы свободно ответить на этот вопрос в пределах 5, пожалуйста, нас! Вычитание и способы вычитания — и только четыре способа вычитания — и только четыре способа сделать десять стандартных фокусов.Задавайте эти вопросы по-разному, и мне сложно не забыть задать их.

% PDF-1.4 % 1 0 obj >>> эндобдж 2 0 obj > поток 2016-10-24T13: 10: 50-04: 002016-10-24T13: 10: 51-04: 002016-10-24T13: 10: 51-04: 00 Adobe InDesign CC 2015 (Macintosh) uuid: 83cb1ecf-fc04-f442 -9d03-99c8b9b30a0cxmp.did: 4db32454-db7d-4152-b36f-1719dd7274d0xmp.id: b3410bde-ba97-438f-9dca-a2b7fc5proof: PDF

, преобразованный из приложения / 2016 x-indfesigndesign в приложение для Mac / Indfesigndesign для Mac 10-24T13: 10: 50-04: 00

xmp.iid: 1239e8a8-4472-4042-857d-8a51f8b0ef1cxmp.did: 4db32454-db7d-4152-b36f-1719dd7274d0xmp.did: 4db32454-db7d-4152-b36f-1719ddddfMopenTimePDFL Библиотека PDF TT1594361634Время новыеРоманские PSMT1594361634

Sentinel1.20100 — OpenType — PS294077717Sentinel-Book294077717

Sentinel1.20100 — OpenType — PS326

47Sentinel-BookItalic326

47

Sentinel1.20100 — OpenType — PS3748318103Sentinel-Bold3748318103

Circular Std1.00100 — OpenType — PS3698002167CircularStd-BookItalic3698002167

Circular Std1.