Вычитание дробей с разными знаменателями – примеры, правила (5 класс, математика)
4.2
Средняя оценка: 4.2
Всего получено оценок: 270.
4.2
Средняя оценка: 4.2
Всего получено оценок: 270.
Вычитание дробей само по себе достаточно сложная задача, а уж вычитание дробей с разными знаменателями и вовсе порой ставит учеников 5 класса в ступор. Поэтому стоит разобраться в этой теме подробнее раз и навсегда.
Вычитание дробей
Вычитание дробей возможно только при одинаковых знаменателях.
Если вычитаемое больше уменьшаемого, то результатом станет отрицательное число.
При вычитании дробей мы создаем новую дробь, в числителе которой будет разность числителей изначальных дробей, а знаменатель останется прежним.
Следующим преобразованием будет вычисление разности в числителе.
Вычитание дробей с разными знаменателями
Если у дробей разные знаменатели, то необходимо первым делом привести дроби к общему знаменателю.
Для этого нужно воспользоваться правилом дробей.
Основное свойство дробей заключается в том, что при умножении числителя и знаменателя дроби на одно и то же число, значение дроби не изменится. Это обусловлено тем, что по факту дробь является не законченной операцией деления, а умножение делителя и делимого на одно и то же число не изменит частное.
Как найти общий знаменатель?
Общей знаменатель это НОК или наименьшее общее кратное. Наименьшее общее кратное двух и более чисел, это число, которое делится на каждое из них.
Для нахождения наименьшего общего кратного ряда простых чисел, нужно просто перемножить их между собой.
$$НОК=3*5*7=105$$
Но что будет, если в ряде будет три сложных числа?
18,15,25 – найдем для этого ряда НОК.
Для этого, каждое из чисел нужно разложить на простые множители.
$$18=2*3*3$$
$$15=3*5$$
$$25=5*5$$
Для того, чтобы найти НОК нужно перемножить простые множители чисел, которые еще не встречались.
Начнем с числа 2. Двойка встречалась только в простых множителях числа 18, вычеркнем ее.
$$НОК=2*…$$
Следующее число 3. Вычеркиваем одну тройку из разложения числа 18 и из разложения числа 15.
$$НОК=2*3…$$
У нас осталась еще одна тройка в разложении числа 18.
$$НОК=2*3*3…$$
Теперь посмотрим, какое число осталось в разложении 15. Это 5:
$$НОК=2*3*3*5…$$
Вычеркиваем одну 5 из разложения числа 15 и одну из разложения числа 25. Осталось одно число, множители которого не зачеркнуты: это 25, где осталась одна 5. Добавим ее в НОК и получим окончательное значение:
$$НОК=2*3*3*5*5=450$$
Так нужно действовать с любым рядом чисел, для которых необходимо найти НОК.
Пример
Теперь рассмотрим пример вычитания дробей с разным знаменателем. Найдем следующую разность:
$${37\over{81}}-{91\over{180}}$$
- Первым шагом нам нужно найти будущий общий знаменатель, который будет являться НОК(81,180)
Разложим на простые множители число 81
81=3*3*3*3
Разложим на простые множители число 180
180=2*2*3*3*5
Значит, для того, чтобы получить НОК нам необходимо домножить 81 на 5*2*2 или домножить 180 на 3*3.
Второй вариант немного проще, поэтому используем его:
180*3*3=180*9=1620
Для того, чтобы сложное число умножить на 9 необязательно умножать. Можно упростить вычисления следующим образом: умножить число на 10 и вычесть это же число. То есть: 180*9=180*10-180=1800-180=1620
- Теперь приведем каждую из дробей к общему знаменателю:
$${37\over{81}}={{37*20}\over{81*20}}={{740}\over{1620}}$$
$${91\over{180}}={{91*9}\over{180*9}}={{809}\over{1620}}$$
- Вычтем получившиеся значения:
$${{740}\over{1620}}-{{809}\over{1620}}={{740-809}\over{1620}}=-{{69}\over{1620}}$$ – получилось отрицательно число, но в этом нет ничего страшного. Просто изначально уменьшаемое было меньше вычитаемого
Что мы узнали?
Мы узнали, как правильно вычитать дроби с разными знаменателями, поговорили о том, как находить НОК и решили небольшой пример.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Милана Черникова
7/10
Никита Свирский
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 270.
А какая ваша оценка?
Сложение и вычитание дробей с разными знаменателями
Чтобы сложить или вычесть две дроби с разными знаменателями, нужно сначала привести их к общему знаменателю, после чего вычислить сумму или разность дробей с полученными одинаковыми знаменателями.
Приведение дробей к наименьшему общему знаменателю
Чтобы дробь привести к новому знаменателю, надо и числитель дроби, и ее знаменатель умножить на один и тот же множитель. Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Приводить несколько дробей к наименьшему общему знаменателю можно следующим образом:
1) найти наименьшее общее кратное знаменателей этих дробей, это и будет наименьший общий знаменатель этих дробей;
2) разделить наименьший общий знаменатель на знаменатели дробей, чтобы найти для каждой дроби соответствующий множитель;
3) умножить числитель и знаменатель каждой дроби на найденный для нее множитель.
Калькуляторы для решение примеров и задач по математике
Лучшие математические приложения для школьников и их родителей, студентов и учителей. Подробнее …
Пример 1. Привести к наименьшему общему знаменателю дроби
3/5
,
7/15
,
9/100
.
Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 5, 15, 100 на простые множители:
5 = 5;
15 = 3*5;
100 = 2*2*5*5.
Выбираем число 100 и в его разложение добавляем множители из разложений чисел 5 и 15, которых еще нет в разложении: 2*2*5*5*3=300. Следовательно, наименьшее общее кратное равно 300.
Теперь разделим число 300 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
300:5=60 =>
3/5
=
3*60/5*60
=
180/300
;
300:15=20 =>
7/15
=
7*20/15*20
=
140/300
;
300:100=3 =>
9/100
=
9*3/100*3
=
27/300
.
Пример 2. Привести к наименьшему общему знаменателю дроби
1/12
,
1/60
,
1/80
.
Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 12, 60, 80 на простые множители:
12 = 2*2*3;
60 = 2*2*3*5;
80 = 2*2*2*2*5.
Выбираем число 80 и в его разложение добавляем множители из разложений чисел 12 и 15, которых еще нет в разложении: 2*2*2*2*5*3=240. Следовательно, наименьшее общее кратное равно 240.
Теперь разделим число 240 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
240:12=20 =>
1/12
=
1*20/12*20
=
20/240
;
240:60=4 =>
1/60
=
1*4/60*4
=
4/240
;
240:80=3 =>
1/80
=
1*3/80*3
=
3/240
.
Пример 3. Привести к наименьшему общему знаменателю дроби
1/13
,
1/8
,
1/5
.
Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 13, 8, 5 на простые множители:
13 = 13;
8 = 2*2*2;
5 = 5.
Выбираем число 13 и в его разложение добавляем множители из разложений чисел 8 и 5, которых еще нет в разложении: 13*2*2*2*5=520. Следовательно, наименьшее общее кратное равно 520.
Теперь разделим число 520 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
520:13=40 =>
1/13
=
1*40/13*40
=
40/520
;
520:8=65 =>
1/8
=
1*65/8*65
=
65/520
;
520:5=104 =>
1/5
=
1*104/5*104
=
104/520
.
Сложение дробей с разными знаменателями
Пример 1. Вычислить сумму
3/5
+
7/25
.
Чтобы найти сумму этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить сумму дробей с полученными одинаковыми знаменателями.
Найдем наименьший общий знаменатель этих дробей:
5 = 5;
25 = 5*5.
Следовательно, наименьший общий знаменатель равен 5*5 = 25.
3/5
+
7/25
=
3*5/5*5
+
7/25
=
15+7/25
=
22/25
.
Пример 2. Вычислить сумму
23/24
+
15/16
.
Чтобы найти сумму этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить сумму дробей с полученными одинаковыми знаменателями.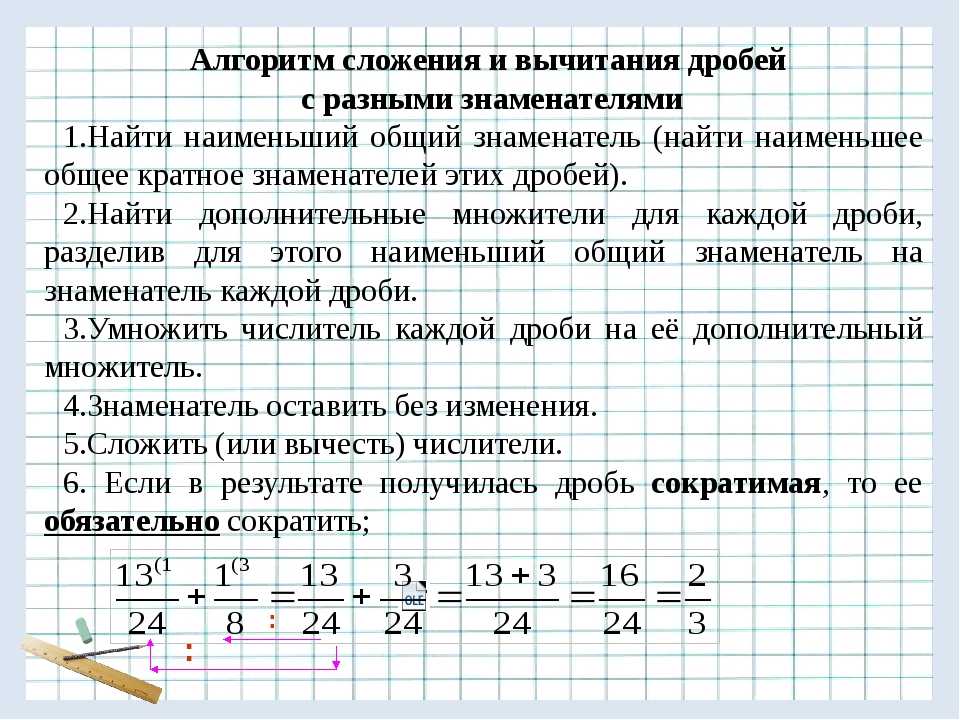
Найдем наименьший общий знаменатель дробей:
24 = 2*2*2*3;
16 = 2*2*2*2.
Следовательно, наименьший общий знаменатель равен 2*2*2*3*2=48.
23/24
+
15/16
=
23*2/24*2
+
15*3/16*3
=
46/48
+
45/48
=
46+45/48
=
91/48
= 1
43/48
.
Пример 3. Вычислить сумму
5/12
+
19/20
.
Найдем наименьший общий знаменатель дробей:
12 = 2*2*3;
20 = 2*2*5.
Следовательно, наименьший общий знаменатель равен 2*2*3*5=60.
5/12
+
19/20
=
5*5/12*5
+
19*3/20*3
=
25/60
+
57/60
=
25+57/60
=
82/60
= 1
22/60
= 1
11/30
.
Вычитание дробей с разными знаменателями
Рассмотрим вычитание дробей с разными знаменателями на примерах.
Пример 1. Вычислить разность
7/8
—
3/16
.
Чтобы найти разность этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить разность дробей с полученными одинаковыми знаменателями.
7/8
—
3/16
=
7*2/8*2
—
3/16
=
14/16
—
3/16
=
14-3/16
=
11/16
.
Пример 2. Вычислить разность
8/9
—
5/6
.
Найдем наименьший общий знаменатель дробей:
9 = 3*3;
6 = 2*3.
Следовательно, наименьший общий знаменатель равен 3*3*2=18.
8/9
—
5/6
=
8*2/9*2
—
5*3/6*3
=
16/18
—
15/18
=
16-15/18
=
1/18
.
Сложение и вычитание дробей с разными знаменателями в 3 этапа — Mashup Math
Как складывать и вычитать дроби с разными знаменателями?
Добро пожаловать в это бесплатное руководство, сопровождающее этот видеоурок «Сложение и вычитание знаменателей с отличающимися знаменателями», в котором вы узнаете ответы на следующие ключевые вопросы и информацию:
Сложение дробей
Subtracting Fractions
Unlike Denominators
How to add and subtract fractions with the same denominator
How to add and subtract fractions with different denominators
Этот Сложение и вычитание дробей с отличающимися знаменателями: полное руководство включает несколько примеров, пошаговое руководство, анимированный видео-мини-урок, а также бесплатный рабочий лист и ключ к ответу.
*Это руководство к уроку сопровождает наш анимационный ролик «Сложение и вычитание дробей с отличающимися знаменателями» на YouTube.
Хотите больше бесплатных уроков математики и видео? Подпишитесь на наш канал бесплатно!
Прежде чем вы научитесь складывать и вычитать дроби, вам нужно сначала понять некоторые ключевые термины.
Давайте начнем с рассмотрения разницы между числителем и знаменателем:
Поскольку 4/5 нельзя упростить дальше, вы можете заключить, что:
1/5 + 3/5 = 4/5
Но что делать, если знаменатели не совпадают?
Как складывать и вычитать дроби, если знаменатели разные?
Вы можете использовать следующий трехэтапный процесс для сложения и вычитания дробей (с общими знаменателями и без них).
ШАГ ПЕРВЫЙ: Найдите общий знаменатель.
ШАГ ВТОРОЙ: Сложите или вычтите числители.
ШАГ ТРЕТИЙ: При необходимости упростите результат.
Обратите внимание, что 3/27 можно упростить, так как числитель и знаменатель делятся на 3.
Вот и все!
Окончательный ответ:
Все еще запутались? Посмотрите анимированный видеоурок ниже:Посмотрите видеоурок ниже , чтобы узнать больше о сложении и вычитании дробей, а также о дополнительных задачах для свободной практики:
Есть мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)
Автор: Энтони Персико0108 MashUp Math .
Вы часто можете увидеть, как я с удовольствием разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Сложение и вычитание дробей с разными знаменателями
Результаты обучения
- Сложение и вычитание дробей с разными знаменателями
- Сложение и вычитание дробей с разными знаменателями, которые содержат переменные
- Идентифицировать и использовать дробные операции
После того, как мы преобразовали две дроби в эквивалентные формы с общими знаменателями, мы можем складывать или вычитать их, добавляя или вычитая числители.
Сложение или вычитание дробей с разными знаменателями
- Найдите ЖК-дисплей.
- Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.
- Сложение или вычитание дробей.
- Запишите результат в упрощенной форме.
Пример
Добавить: [latex]\Large\frac{1}{2}+\Large\frac{1}{3}[/latex]
Решение:
| [латекс]\Большой\фракция{1}{2}+\Большой\фракция{1}{3}[/латекс] | |
| Найдите ЖК-дисплей [латекс]2[/латекс], [латекс]3[/латекс]. | |
| Преобразование в эквивалентные дроби с помощью ЖК-дисплея [латекс]6[/латекс]. | [латекс]\Large\frac{1\cdot\color{red}{3}}{2\cdot\color{red}{3}} +\Large\frac{1\cdot\color{red}{2 }}{3\cdot\color{red}{2}}[/latex] |
| Упростите числители и знаменатели. | [латекс]\Большой\фракция{3}{6}+\Большой\фракция{2}{6}[/латекс] |
| Доп. | [латекс]\большой\фрак{5}{6}[/латекс] |
Помните, всегда проверяйте, можно ли упростить ответ. Поскольку [латекс]5[/латекс] и [латекс]6[/латекс] не имеют общих множителей, дробь [латекс]\большой\фрак{5}{6}[/латекс] нельзя сократить.
Попробуйте
Посмотрите следующее видео, чтобы увидеть больше примеров и пояснений о том, как сложить две дроби с разными знаменателями.
Попробуйте
Пример
Добавить: [latex]\Large\frac{7}{12}+\Large\frac{5}{18}[/latex]
Показать решение
Попробуйте
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.
Подумай об этом
Добавить [латекс]\Большой\фрак{3}{4}+\Большой\фрак{1}{6}+\Большой\фрак{5}{8}[/латекс]. Упростите ответ и запишите в виде смешанного числа.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.
Показать решение
Вычитание дробей
Когда вы вычитаете дроби, вы должны думать о том, есть ли у них общий знаменатель, как и при сложении дробей. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.
Пример
Вычесть: [латекс]\Большой\фрак{7}{15}-\Большой\фрак{19}{24}[/латекс]
Показать решение
Попробуйте
В следующем видео представлены еще два примера вычитания двух дробей с разными знаменателями.
Пример
Добавить: [latex]-\Large\frac{11}{30}+\Large\frac{23}{42}[/latex]
Показать решение
Попробуйте
Пример
Вычтите: [латекс]\Большой\фрак{1}{2}-\влево(-\Большой\фрак{1}{4}\вправо)[/латекс]
Показать раствор
Сложение и вычитание дробей, содержащих переменные
В следующем примере одна из дробей имеет в числителе переменную.