Видеоуроки. Математика. 6 класс. Сложение и вычитание дробей с разными знаменателям.

Видеоуроки. Математика. 6 класс. Сложение и вычитание дробей с разными знаменателям.

РАЗРАБОТКИ

Главная → Видеоуроки →  Математика. 6 класс. Сложение и вычитание дробей с разными знаменателям. 1  Видеоуроков в категории: 3 Видеоурок по математике «Сложение и вычитание смешанных чисел» 27.09.2015 Видеоурок «Сложение и вычитание дробей с разными знаменателями» 24.09.2015 Видеоурок «Основное свойство дроби. Сокращение дробей». 23.09.2015 1-3

ЕГЭ по математике Профильный уровень Задание 1     Задание 2 Задание 3     Задание 4 Задание 5     Задание 6 Задание 7     Задание 8 Задание 9     Задание 10 Задание 11     Задание 12 Задание 13     Задание 14 Задание 15     Задание 16 Задание 17     Задание 18 Задание 19     Задание 20 Задание 21 ГИА по математике Задача 1     Задача 2 Задача 3     Задача 4 Задача 5     Задача 6 Задача 7     Задача 8 Задача 9     Задача 10 Задача 11     Задача 12 Задача 13     Задача 14 Задача 15     Задача 16 Задача 17     Задача 18 Задача 19     Задача 20 Задача 21     Задача 22 Задача 23     Задача 24 Задача 25     Задача 26 Демонстрационные варианты ОГЭ по математике Математика. 5 класс. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. 10 — 11 класс. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.

Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Сложение и вычитание дробей с разными знаменателями исходя из основных требований ФГОС в процессе обучения.

Семенова Анна Николаевна,

Шаповал Светлана Александровна,

учителя математики

МАОУ «Гимназия «Гармония»,

Великий Новгород

Урок по теме: «Сложение и вычитание дробей с разными знаменателями» исходя из основных требований ФГОС в процессе обучения.

Предмет:МАТЕМАТИКА, 6 класс (УМК Виленкин Н.Я.) Тема урока:«Сложение и вычитание дробей с разными знаменателями» Тип урока:Урок открытия нового знания Цель: Образовательная: сформировать знания учащихся о сложении и вычитании дробей с разными знаменателями; Развивающая: Создание условий для развития познавательных универсальных учебных действий (самостоятельное создание алгоритмов деятельности при решении проблем; постановка и формулирование проблемы) средствами технологии развития критического мышления; Воспитательная: формировать навыки сотрудничества, взаимоподдержки, помощи «слабому» однокласснику в коллективном учебном труде; Деятельностная: формировать у учащихся умения самостоятельной исследовательской деятельности с постановкой учебной задачи и гипотезы;применять знания по математике в проблемных ситуациях; Задачи урока: Расширить понятийную базу учащихся за счет включения в нее новых элементов – алгоритма алгоритм сложения и вычитания дробей с разными знаменателями. Учить аргументировать и отстаивать свою точку зрения при решении математических заданий, используя алгоритм сложения и вычитания дробей с разными знаменателями. Развивать умение выделять существенную информацию, выдвигать гипотезу и обосновывать ее, извлекать необходимую информацию для решения нового вида задач. Воспитыватьспособность к самооценке, умение работать в группе Методы и методические приёмы: проблемный, частично поисковый, наглядный Оборудование для учителя:заранее приготовленные карточки, доска Литература для учащихся:учебник для общеобразовательных учреждений,М.: Мнемозина, 2013,Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, Этап урока (системно-деятельностный подход) Методический инструментарий Деятельность учителя Деятельность учащихся СТАДИЯ ВЫЗОВА Задачи: актуализация имеющихся у учащихся знаний, пробуждение познавательного интереса, определение темы и цели урока, определение затруднений 1. Самоопределение к учебной деятельности. Развитие регулятивных и познавательных УУД «Подводящий диалог» «Группировка» «Работа в парах» «Подводящий диалог» — Прослушайте, пожалуйста, высказывание канадского поэта Роберт Брингхерста: «Математика существует не для того, чтобы навязывать кому-либо тяжелую работу. Наоборот, она существует только для удовольствия. Для удовольствия тех, кто любит анализировать то, что он делает, или может сделать… » — Как вы относитесь к этим слова, согласны, нет? Объясните, почему? — Сегодня на уроке математики, участвуя в анализе проблемы, я, надеюсь, вы получите удовольствие от своей работы! Итак, начинаем работу. — Обратите внимание на доску (на доске магнитами прикреплены карточки с дробями). ; ; 0,75; ; 1,15; ; ; ; — Что вы видите перед собой? — А зачем нам вообще нужны дроби? — Как назывались дроби в первых учебниках? Почему? — Прочитайте прикреплённые к доске числа. — Что можно сделать с этими дробями с точки зрения математики? — Работа в парах Какие группы вы выделите? — С какими дробями мы с вами последнее время работаем? — Что мы умеем делать с обыкновенными дробями? — Как вы думаете, что бы вы ещё смогли делать с данными дробями? — Я надеюсь, что в конце урока вы сможете это сделать — Молодцы. Учащиеся высказывают своё мнение — дроби — результат измерения не всегда можно выразить целым числом — ломаные числа Читают числа — разделить их на группы — смешанные числа, десятичные дроби, обыкновенные дроби — обыкновенными дробями — сравнивать, сокращать, приводить к общему знаменателю — складывать, вычитать, умножать, делить

2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии. Развитие познавательных, личностных, регулятивных и коммуникативных УУД «Подводящий диалог» «Работа в парах» «Работа в парах» «Подведение к теме» — Таким образом, мы с вами выдели три группы дробей, одна из которой группа с обыкновенными дробями. 5 12 22 ; 63 ; 70 ; 32 66 84 90 48 — Что мы можем с этими дробями сделать в первую очередь? — Сократите дроби? Что получилось? — Что вы заметили? — Объясните почему. — Молодцы — Расположите дроби в порядке возрастания. — Объясните, как вы это делали? — Что такое несократимые дроби? — Я вам предлагаю решить примеры с данными обыкновенными дробями: + = + = — = — В чём заключается проблема? — Эту проблему мы и будем сегодня решать — А как вы думаете, что мы должны сделать, чтобы выполнить эти действия? Чуть позже мы проверим вашу гипотезу. Надеюсь, что в конце урока вы сможете решить данные примеры. — Сократить, сравнить, расположить в порядке возрастания или убывания. 1 ; 3 ; 7 ; 2 ; 3 4 9 3 — мы не можем сократить дробь — числитель и знаменатель взаимно-простые числа, те, у которых НОД равен 1 ; ; ; ; ; ; ; ; ; ; — необходимо привести дроби к общему знаменателю, дроби должны быть несократимыми — это дроби, которые больше нельзя сократить, то есть у которых числитель и знаменатель взаимно — простые числа — Мы не можем решить некоторые примеры, так как дроби имеют разные знаменатель, а мы умеем складывать и вычитать дроби только с одинаковыми знаменателями — Привести дроби к общему знаменателю. 3. Построение проекта выхода из затруднения Развитие познавательных и регулятивных УУД «Определяем тему урока» «Эпиграф» «Определяем цель урока» «Составление плана» -Сформулируйте тему урока — Эпиграфом нашего с вами сегодняшнего урока я хочу предложить слова американского писателя Джона Стейнбека «Человеку положено до всего добираться своим умом» — Как вы понимаете эти слова? Соотнесите с темой нашего урока? Мы пойдём с вами по этому пути, где вы самостоятельно будете продвигаться к истине. — Сформулируйте цель урока, помогут вам в этом слова – «целевые опоры»: Узнать: ………………… Уметь: ………………… Применять: ………….. -Запишите в тетрадь число и тему урока. — Что вам может помочь в достижении цели? — Составьте план действий. — «Сложение и вычитание дробей с разными знаменателями» Отвечают на поставленный вопрос Мы должны узнать алгоритм сложения и вычитания дробей с разными знаменателями; уметь использовать алгоритм и применять данные умения при решении задач. — уже известные алгоритмы и факты, основное свойство дроби, сложение и вычитание дробей с одинаковыми знаменателями, приведение дробей к общему знаменателю — чтобы научиться складывать и вычитать дроби с разными знаменателями, мы должны составить алгоритм сложения и вычитания дробей с разными знаменателями.

СТАДИЯ ОСМЫСЛЕНИЯ Задачи: получение новых знаний и соотнесение их с полученными раннее, формулирование собственного мнения по теме в виде нового правила 4. Реализация построенного проекта Развитие познавательных, личностных, регулятивных и коммуникативных УУД «2 – 4 — вместе» «Составим алгоритм» «Произносим алгоритм» Для реализации вашего плана я предлагаю работу в парах. На доске записаны 2 примера, вы выполняете их с соседом по парте, затем по хлопку вы разворачиваетесь к соседней парте и уже работаете вчетвером. Я даю вам 3 минуты на работу с соседом и 2 минуты на работу в 4. Задания: 11 + 5 = 14 21 5 — 9 = 6 14 При обсуждении складывается пошаговый алгоритм(учитель прикрепляет к доске заранее напечатанные пункты алгоритма) -Что является результатом вашей деятельности? — Какие этапы алгоритма вызвали у вас затруднения? Представитель одной из групп защищает проект, остальные дополняют его. При обсуждении складывается пошаговый алгоритм: чтобы сложить (вычесть) дроби с разными знаменателями надо: Привести дроби к общему знаменателю Выполнить сложение (вычитание) дробей Сократить результат (если можно) Выделить целую часть (если получилась неправильная дробь) — алгоритм сложения и вычитания дробей с разными знаменателями учащиеся отвечают на поставленный вопрос 5. Первичное закрепление во внешней речи Развитие познавательных, регулятивных и коммуникативных УУД «Решение упражнений и задач» — Что надо сделать, чтобы научиться применять новый алгоритм? — Для этой цели решите задачи из учебника №319 (а, б, в), 321 (г, д, е). — Мы достигли целей урока?  -Давайте докажем это себе и мне? — потренироваться. Решают в парах, каждый проговаривает соседу решение одной задачи по выбору. Ответы и ход решения сверяете с доской. У доски (с обратной стороны) решают 2 ученика, остальные —  в тетрадях. 6. Самостоятельная работа с самопроверкой по эталону Развитие познавательных, личностных, регулятивных и коммуникативных УУД «Самостоятель-ная работа» «Лови ошибку» «Рефлексия» — Я вам предлагаю самостоятельную работу на 5 минут Самостоятельная работа: Вычислите: + 0,75 За доской готовое решение. В решении некоторых примеров можно специально допустить ошибки (в зависимости от готовности класса к восприятию темы) После самопроверки самостоятельной работы организуется рефлексия: выясняется, какие ошибки были допущены, делается их анализ и исправление. -В чем было затруднение? Назовите причины затруднений? Учащиеся самостоятельно выполняют задание, после чего сравнивают решение с эталоном. Ученики, которые выполняют задание раньше всех остальных, получают дополнительные карточки с заданиями по данной теме.

7. Включение в систему знаний и повторение Развитие познавательных УУД «Самостоятель-ная работа» — Вы открыли новое знание. Какой следующий шаг вашей деятельности? — Правильно. Для этого предлагаю решить задачу №363 (дополнительно №336) из учебника. — Какие затруднения возникли при решении задачи? — Поднимите руки, кто самостоятельно и верно выполнил задание? — Применить новое знание для решения задач Один ученик решает задачу за доской, все остальные выполняют задание в тетради самостоятельно. Производят разбор возникших затруднений. РЕФЛЕКСИЯ Задачи: обобщение изученного, выводы, анализ результатов деятельности на уроке 8. Рефлексия деятельности на уроке Развитие познавательных и регулятивных УУД «Возврат к теме и целям» «Рефлексивный лист» — Над какой темой мы работали, какие цели ставили на уроке? — Вы достигли цели?  — Я, как учитель, ставила целью — построение алгоритма сложения и вычитания дробей с разными знаменателями. — Вы достигли этой цели?  — Сформулируйте алгоритм сложения и вычитания дробей с разными знаменателями. — Рассмотрим три примера, которые мы не смогли решить в начале урока. — А сейчас я вам предлагаю оценить свою работу на уроке, исходя из нашего алгоритма. На «Рефлексивном листе» поставьте себе «+» или «-» по пунктам алгоритма, оценив свои знания и умения: Знания и умения знаю/не знаю умею/не умею Привести дроби к общему знаменателю Выполнить сложение (вычитание) дробей Сократить результат (если можно) Выделить целую часть (если получилась неправильная дробь) — Вы все сегодня хорошо потрудились, скажем друг другу спасибо. Вспоминают тему и цель урока. — Достигли -Чтобы сложить (вычесть) дроби с разными знаменателями надо: Привести дроби к общему знаменателю Выполнить сложение (вычитание) дробей Сократить результат (если можно) Выделить целую часть (если получилась неправильная дробь) Домашнее задание «Дифференциро-ванное домашнее задание» — Ваше творческое домашнее задание заключается в том, что вы должны составит задачу по изученной нами теме (минимум 2 действия) и решить её. — Исходя из затруднений, вызванных данной темой, из предложенных номеров домашнего задания выберите минимум два, каждый номер соответствует определённому пункту алгоритма. У кого нет затруднений, выбирает любые два задания. Можно выполнить все задания. №283(ж,з,и) №360 (а, б) №271 (а, б) Выделить целую часть: 15 ; 23 ; 17 ; 48 7 4 3 13 Записывают домашнее задание

Адрес публикации: https://www. prodlenka.org/metodicheskie-razrabotki/410095-urok-po-teme-slozhenie-i-vychitanie-drobej-s-

Вычитание дробей с разными знаменателями

Звук:

Мы не можем вычесть два знаменателя, если у них нет ничего общего.

• Итак, как вычитать дроби с разными знаменателями, например ⁹ ⁄ ₂₈ — ¹³ ⁄ ₅₆ ?

Дроби говорят нам, сколько частей в целом.

Когда у дробей разные знаменатели , целое делится на разное количество частей. Поэтому детали будут разного размера.

Когда части не одного размера, мы не можем вычесть две дроби.

Например, посмотрите на разницу между ¹ / ₂ и ¹ / ₅ :

В первой модели целое разделено на 2 равные части. В другой модели целое разделено на 5 равных частей. Совершенно очевидно, что эти части не имеют одинакового размера из-за этих знаменателей.

Вот почему нельзя вычитать дроби с разными знаменателями — у них должен быть общий знаменатель.

Чтобы вычесть дроби с разными знаменателями, мы можем выполнить три простых шага:

Шаг первый

Найдите общий знаменатель. Умножьте числители на тот же коэффициент, который вы использовали для нахождения общего знаменателя.

Шаг второй

Вычтите числители. Оставьте знаменатель прежним.

Шаг третий

При необходимости упростите дробь.

Найдите минутку, чтобы применить эти шаги на практике. Посмотрите на пример ниже:

• Что такое ¹ / ₂ — ¹ / ₅ ?

Шаг первый

Найдите общий знаменатель.

Чтобы найти общий знаменатель, нам нужно найти наименьшее общее кратное двух знаменателей. Наименьшее общее кратное между 2 и 5 равно 10.

И 2, и 5 можно умножить на другие числа, чтобы получить 10. Кроме того, оба числа могут достигать 10 путем пропуска счета.

• Как изменить дроби так, чтобы обе дроби имели знаменатель 10?

Мы умножим верхнюю и нижнюю часть каждой дроби на коэффициент, необходимый для получения знаменателя 10.

Например, чтобы изменить знаменатель с ½ на 10, нам нужно будет умножить верхнюю и нижнюю часть на 5:

	1	х	5	=	5
	2	х	5	=	10

 

• Для ¹ / ₅ на что нужно умножить знаменатель 5, чтобы получить 10?

2! Умножьте верхнюю и нижнюю часть на 2.

	1	х	2	=	2
	5	х	2	=	10

 

Теперь обе дроби имеют общий знаменатель. Вы готовы к следующему шагу.

Шаг второй

Вычтите числители. Оставьте знаменатели одинаковыми.

Посмотрите теперь на модель дроби.

Теперь, когда ½ и ¹ / ₅ имеют одинаковый знаменатель, легко вычесть: 0102 5 — 2 = 3   10 10 = 10

 

Шаг третий

При необходимости упростите дробь.

³ / ₁₀ в самой простой форме. Числитель и знаменатель не могут делиться на общий множитель. Нам не нужно упрощать дробь.

Итак, ¹ / ₂ — ¹ / ₅ = ³ / ₁₀

Вы научились пользоваться карандаш и бумага, чтобы вычитать дроби с разными знаменателями. Вы также использовали модели для визуализации задач на вычитание.

Теперь используйте свои новые стратегии для решения практических задач и действий в

Понял? раздел.

Сложение и вычитание дробей с разными знаменателями

Нужно ли вашим учащимся больше практики с Дроби 5 класса? Вы ищете увлекательных, строгих математических заданий для 5-го класса , которые помогут учащимся практиковаться в сложении и вычитании дробей с разными знаменателями (без часов на подготовку!)? Не ищите дальше! Эти печатных И цифровых математических игр для 5-х классов удовлетворят потребности учащихся 5-х классов. Они идеально подходят для сложения и вычитания дробей.

Нажмите здесь, чтобы сэкономить 50% при покупке пакета всех математических игр для 5-го класса на весь год!

Есть 4 игры на сложение и вычитание дробей , которые помогут учащимся практиковать свои математические навыки в увлекательной игровой форме! Они соответствуют

5.NF.2. Эти задания по математике по спирали для 5-го класса отлично подходят для дополнительной практики или даже могут служить в качестве быстрой контрольной работы по математике в 5-м классе в конце раздела дроби 5-го класса. Они сделаны гибкими, чтобы вы могли использовать их по своему усмотрению!

ЧТО ВКЛЮЧЕНО? (ПЕЧАТЬ И ЦИФРОВОЙ)

• Упражнение: 1: Время кормления животных

Выберите букву правильного ответа. Учащиеся читают, чего хочет каждое животное (сколько еды в дробях), и решают, к какой коробке принадлежит животное. На каждой странице разные животные.

• Занятие 2: Выполним некоторые поручения

Учащиеся решают задачу со словами. Они читают задачу на сложение или вычитание дробей и решают, какую операцию использовать. Они записывают правильный ответ на каждой карточке с заданием.

• Занятие 3: Приготовим пирог!

Решите задачу. Каждая проблема со словами связана с добавлением или вычитанием дробей с разными знаменателями и связана с реальным миром благодаря использованию круга!

• Задание 4. Множественный выбор

Выберите единорога с правильным ответом. У каждого единорога есть своя задача на сложение и вычитание, которую учащиеся должны решить.

КАК РЕАЛИЗОВАТЬ:

Каждая из 4 игр содержит 11 задач (всего 44 вопроса).

• Цифровой: Первая задача всегда является примером для учащихся, чтобы они знали, что делать. Я бы порекомендовал ответить на 5 вопросов во время урока вместе, а остальные 5 дать учащимся для самостоятельного заполнения. Или назначьте все 10 после совместного просмотра первого примера слайда. Они предоставлены в Google Slides, поэтому вы можете назначить их в Google Classroom.

• Печать: Распечатайте карточки с заданиями и положите их в математический центр. Попросите учащихся записать ответы на предоставленном листе для записей. Учащиеся могут использовать ключ самопроверки для проверки своей работы. Вы можете выбрать между цветным и черно-белым вариантом.

ЗАЧЕМ КУПИТЬ?

• весело и увлекательно
• без подготовки
• 2 версии: печатная и цифровая (для использования с Google Slides)
• можно использовать лично или онлайн / дистанционно / дистанционно
• строгий
• 4 игры (44 карточки с заданиями)
• цветные и черно-белые
• ключи для ответов прилагаются
• простой в использовании формат

с, быстрые проверки , викторины, домашние задания, материалы для исправления, дополнительная практика, домашние задания, предварительные и последующие оценки, модульные тесты и многое другое. Их можно использовать с партнерами, независимо, в небольших группах, в математических центрах 5-го класса, в дистанционном обучении, для обогащения, исправления или в качестве спирального обзора математики 5-го класса.

✅4 игры в печатной и цифровой форме

✅40+ Google Slides и 40+ карточек с заданиями

✅ключи для ответов прилагаются

✅несколько версий для разных стилей обучения 0005

— ————————————————— ———————————————————

• Соответствует общему Core 5.NF.2

Решать текстовые задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи с разными знаменателями, например, используя визуальные модели дробей или уравнения для представления задачи. Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов. Например, распознайте неправильный результат 2/5 + 1/2 = 3/7, заметив, что 3/7 < 1/2 .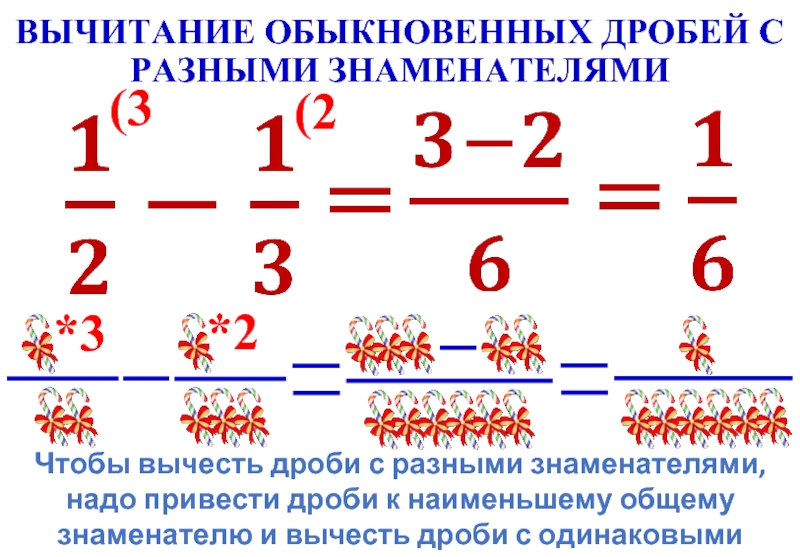

• Соответствует TEKS 5.3H

Быстро умножить трехзначное число на двузначное по стандартному алгоритму

• 9002 1 Согласуется с TEKS 5.3K

Добавить и плавно вычитать положительные рациональные числа

Это соответствует стандартам Флориды BEST (B.E.S.T.)

• MA.5.FR.2.1 Сложение и вычитание дробей с разными знаменателями, включая смешанные числа и дроби больше 1, с процедурной надежностью.
• MA.5.AR.1.2 Решение реальных задач на сложение, вычитание или умножение дробей, включая смешанные числа и дроби больше 1.

————— ————————————————— ——————————

Ищете другой уровень обучения?

Карточки с заданиями для 1-го класса

Карточки с заданиями для 2-го класса

3-й класс Карточки с заданиями

Карточки с заданиями для 4-го класса

Карточки с заданиями для 5-го класса

Карточки с заданиями по чтению

Дополнительные карточки с заданиями по математике для 5-го класса:

• График координат (5. G.1) 90 004
• Задачи по координатной графике (5.Ж.2)
• Геометрия (5.Ж.3)
• Иерархия форм (5.Ж.4)
• Преобразование единиц измерения (5.MD .1)
• Линейные графики (5.MD.2)
• Поиск объема (5.MD.3, 5.MD.4, 5.MD.5)
• Разрядное значение (5.MD.3, 5.MD.4, 5.MD.5) NBT.1)
• Десятичные степени (5.NBT.2)
• Чтение и запись десятичных знаков (5.NBT.3)
• Сравнение десятичных знаков (5.NBT.3)
• Округление десятичных знаков (5.NBT.4)
• Умножение 2-х цифр на 3-е (5.NBT.5)
• 2 цифры по 4 цифры Умножение (5.NBT.5)
• Умножение 3 цифр на 3 цифры (5.NBT.5)
• Длинное деление с остатком (5.NBT.6)
• Длинное деление без остатка индеры ( 5. NBT.6)
• Сложение и вычитание десятичных знаков (5.NBT.7)
• Словесные задачи на сложение и вычитание десятичных дробей (5.NBT.7)
• Сложение и вычитание смешанных чисел с разными знаменателями (5.NF.1)
• Сложение и вычитание дробей с разными знаменателями (5. NF.2)
• Дроби как деление (5.NF.3)
• Умножение дробей (5.NF.4)
• Умножение как масштабирование (5.NF.5)
• Умножить Словесные задачи со смешанными числами (5.NF.6)
• Деление дробей на целые числа (5.NF.7)
• Порядок действий (5.OA.1)
• Запись простых выражений (5.OA.2) 90 018
• График Числовой Выражения на координатной плоскости (5.OA.3)

Хотите преобразовать комнату, чтобы просмотреть этот стандарт?

Планировщик вечеринок Преобразование класса: сложение и вычитание дробей

———————————- ————————————————— ——————

Дополнительная информация:

Подпишитесь на меня и получайте уведомления о появлении новых продуктов.