Сложение и вычитание дробей с разными знаменателями

4

Средняя оценка: 4

Всего получено оценок: 286.

4

Средняя оценка: 4

Всего получено оценок: 286.

Дроби – это первое серьезное препятствие в курсе математики 5 класса. Если геометрическая часть преодолевается учениками без особых проблем, то понять, что складывать и вычитать можно не только целые числа, но и их части. Поэтому чтобы разобраться в сложении и вычитании дробей с разными знаменателями раз и навсегда поговорим о этой теме подробнее.

Что такое дробь?

На самом деле это очень интересный вопрос, поскольку именно он лежит в основе навыка сложения и вычитания дробей. В школьном курсе говорят, что дробь 5/7 означает, что пирог разделили на 7 частей и из них взяли 5. Это в общем-то верное определение, то слишком затянутое.

В учебники старших классов утверждают, что знак дроби заменяет знак деления. Что это значит? Это значит, что операцию деления не довели до конца, а просто заменили на дробь и уже с этой дробью стали производить какие-то манипуляции.

Приведем пример все с той же дробью:

$$5:7={5\over{7}}$$ – так это выглядит при записи в виде цифр.

Зачем это нужно?

Дело в том, что не всякое деление можно довести до конца, то есть может выйти либо деление с остатком, либо бесконечный результат. А потому в точных вычислениях используют подобные заменители, ведь пока вы не получили результат выражение будет считаться абсолютно точным.

В школьном курсе математики ставится задача научить учеников работать с дробями, чтобы облегчить точные расчеты в будущем.

Сложение дробей

Сложение и вычитание дробей процесс, который целиком и полностью зависит от числителя. Рассмотрим сложение двух дробей: ${5\over{7}} и {9\over{13}}$

Рассмотрим дроби, как операции деления, чтобы понять, зачем нужно перед сложением приводить дроби к одинаковым знаменателям:

$${5\over{7}}+{9\over{13}}=(5:7)+(9:13)$$ – дело в том, что при сложении дробей используется сочетательное свойство деления, которое говорит о том, что при делении двух слагаемых на одно и то же число, можно сначала сложить слагаемые, а потом сумму разделить на это число.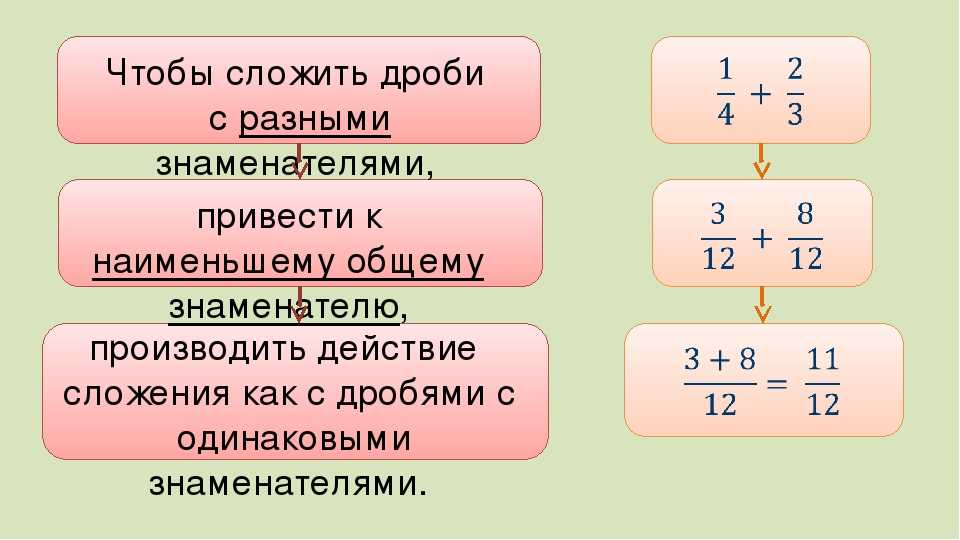

В виде формулы это выглядит так:

а:с+в:с=(а+в):с

Теперь становится ясно, зачем нужно приведение к одному знаменателю: иначе свойство работать не будет. А теперь доведем пример до конца:

$${5\over{7}}+{9\over{13}}$$ – каждый из знаменателей домножим на другой знаменатель.

В общем случае нужно найти НОК, но если НОК ищется для простых чисел, то достаточно перемножить их между собой.

Общий знаменатель в нашем случае: 7*13=91 – в первой дроби необходимо домножить числитель и знаменатель на 13, а во второй на 7.

$${5\over{7}}+{9\over{13}}={{5*13}\over{7}}+{{9*7}\over{13}}={{65+63}\over{91}}={128\over{91}}$$ – в нашем случае результатом стала неправильная дробь. Так как это конечный итог вычислений, то можно как выделить целую часть, так и оставить результат как есть.

Вычитание дробей

Если перед вами разность дробей с разными знаменателями, то смысл операций абсолютно не меняется, так как сложение и вычитания есть одна операция, которая называется математическое сложение.

Для примера разберем разность дробей:

$${1\over{3}}-{1\over{5}}$$ – оба знаменателя являются простыми числами, а потому общим знаменателем будущего результата будет число: 3*5=15

$${1\over{3}}-{1\over{5}}={5\over{15}}-{3\over{15}}={{5-3}\over{15}}={2\over{15}}$$ – как видите, изменилась лишь операция в числителе: вместо сложения стало вычитание при том же порядке действий.

Что мы узнали?

Мы поговорили о дробях. Узнали, что это такое, как складывать и вычитать дроби. Выяснили, почему для сложения и вычитания дробей с разными знаменателями, нужно сначала привести числа к одному знаменателю.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Физули Залбеков

  7/10

• Кирилл Девжеев

  9/10

• Ризван Яхьяев

  8/10

Оценка статьи

4

Средняя оценка: 4

Всего получено оценок: 286.

---

А какая ваша оценка?

Сложение и вычитание рациональных дробей с разными знаменателями / Рациональные выражения / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Рациональные выражения
5. Сложение и вычитание рациональных дробей с разными знаменателями

Чтобы сложить или вычесть рациональные дроби с разными знаменателями, нужно сначала привести эти дроби к общему знаменателю

, после чего воспользоваться правилами сложения или вычитания рациональных дробей с одинаковыми знаменателями.

или , где , , и — многочлены, причём многочлены и — ненулевые.

Здесь в качестве общего знаменателя выбрано выражение, равное произведению знаменателей данных дробей. Но произведение знаменателей данных дробей не всегда является наиболее удобным общим знаменателем. Помним, что при нахождении общего знаменателя обыкновенных дробей мы находили наименьшее общее кратное знаменателей, раскладывая их на простые множители. Аналогично для нахождения общего знаменателя рациональных дробей может оказаться удобным предварительно разложить знаменатели на множители.

Пример 1. Найдите сумму дробей и .

Решение:

Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен . Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей складываемых дробей, а каждая переменная взята с наибольшим показателем степени, с которым она входит в знаменатели дробей. Тогда дополнительным множителем к первой дроби будет одночлен , ко второй дроби — одночлен . Получаем:

Пример 2. Найдите разность дробей и .

Решение:

Чтобы найти общий знаменатель вычитаемых дробей, разложим знаменатель каждой дроби на множители:

Простейшим общим знаменателем служит выражение . Тогда дополнительный множитель к первой дроби — , ко второй дроби — . Получаем:

Пример 3. Упростите выражение .

Решение:

Представим выражение в виде дроби со знаменателем 1 и выполним вычитание дробей, учитывая то, что простейшим общим знаменателем дробей будет выражение . Получаем:

Обратите внимание, сумма и разность двух рациональных дробей являются рациональными дробями.

Советуем посмотреть:

Рациональные дроби

Основное свойство рациональной дроби

Сложение и вычитание рациональных дробей с одинаковыми знаменателями

Умножение и деление рациональных дробей. Возведение рациональной дроби в степень

Равносильные уравнения. Рациональные уравнения

Степень с целым отрицательным показателем

Свойства степени с целым показателем

Функция y=k/x и её график.

Рациональные выражения

Правило встречается в следующих упражнениях:

8 класс

Номер 127, Мерзляк, Полонский, Якир, Учебник

Номер 128, Мерзляк, Полонский, Якир, Учебник

Номер 129, Мерзляк, Полонский, Якир, Учебник

Номер 182, Мерзляк, Полонский, Якир, Учебник

Номер 184, Мерзляк, Полонский, Якир, Учебник

Номер 187, Мерзляк, Полонский, Якир, Учебник

Номер 189, Мерзляк, Полонский, Якир, Учебник

Номер 290, Мерзляк, Полонский, Якир, Учебник

Номер 298, Мерзляк, Полонский, Якир, Учебник

Номер 345, Мерзляк, Полонский, Якир, Учебник

---

Как складывать и вычитать отрицательные дроби

••• wutwhanfoto/iStock/GettyImages

Обновлено 13 марта 2018 г. знак. Процесс сложения и вычитания отрицательных дробей может быть простым, если вы помните о двух вещах. Отрицательная дробь, добавленная к другой отрицательной дроби, даст в результате отрицательную дробь. Вычитание отрицательной дроби из другой равносильно добавлению положительного дополнения к этой дроби.

Сделайте знаменатели (нижнюю часть дроби) одинаковыми, если они уже не совпадают. Вы можете складывать только половинки к половинкам, четверти к четвертям, десятые к десятым и так далее. Вычитание отрицательных дробей следует тому же методу.

Таким образом, если отрицательные дроби, которые вы складываете, не имеют одинаковых знаменателей, вы можете сделать это так.

-1/2, например, может быть записано как -2/4, -3/6, -4/8 и так далее. В каждом случае число вверху всегда вдвое меньше числа внизу. Все эти дроби означают половину количества.

Рассмотрим сложение и вычитание следующих отрицательных дробей.

• 1/4 + (-3/10) — 1/4 — (-3/10)

Первый пример — сложение отрицательных трех десятых с отрицательной одной четвертой. Второй – вычитание отрицательных трех десятых из отрицательной одной четвертой.

Метод: Вы не можете прибавлять одну четвертую к трем десятым, пока не приведете их обе к единому стандарту, чтобы у вас была общая точка отсчета, с которой вы могли бы работать. Вы можете только добавить лайк к лайку или вычесть лайк из лайка. Больше похоже на возможность сравнивать яблоки с апельсинами только тогда, когда вы хотя бы называете их фруктами.

Вам нужен общий знаменатель. Это будет наименьшее число, на которое будут делиться два знаменателя 4 и 10. Это будет 20.

Сохраните эквивалент дроби, используя этот общий знаменатель: 20.

(- 1/4) становится (- 5/20), потому что 5 составляет четверть от 20.

(- 3/10) становится (- 6/20). Знаменатель увеличился в 2 раза, поэтому верхняя часть числителя тоже должна удвоиться, чтобы дробь осталась прежней.

Теперь, когда общий знаменатель найден и отрицательные дроби выражены через этот новый знаменатель, отрицательные дроби можно складывать или вычитать.

При сложении отрицательных дробей складывать как обычно. Затем прикрепите к ответу знак «минус».

При вычитании отрицательных дробей вы, по сути, добавляете положительное дополнение к вычитаемой отрицательной дроби, потому что вычитание отрицательного числа или дроби равносильно добавлению положительного числа этой отрицательной дроби или числа. Два последовательных отрицательных знака «отменяют», давая положительный знак.

Сложение отрицательных дробей: (- 1/4) + (- 3/10) = — 5/20 + — 6/20 = — (11/20)

При вычитании: (- 1/4) — (- 3/10) = — 5/20 — (- 6/20) \= — 5/20 + 6/20 (два последовательных знака минус становятся знаком +) \= 1/20.

Статьи по теме

Ссылки

• Y-математика: сложение и вычитание дробей

Об авторе

Чарльз Эзеани пишет с 1998 года после изучения литературы на английском языке. Он был представлен в различных международных поэтических изданиях, таких как «Письма от души» и «Утешение ночи». Эзеани изучает электротехнику и электронику в Манчестерском столичном университете.

Вычитание дробей — Photomath

Изучение дробей

Мы освоили операции с целыми числами, и вы даже умеете складывать дроби! Но, конечно, мы не можем останавливаться на достигнутом.

Теперь пришло время научиться вычитать дроби — и вы можете быть более подготовлены, чем вы думаете!

Начнем.

Что значит вычитать дроби?

Вычитание дробей означает нахождение разницы хотя бы двух дробей. Как и при сложении дробей, нам понадобится наш старый друг: ЖК-дисплей.

Наименьший общий знаменатель, известный его друзьям как «LCD», является наименьшим общим кратным (НОК) всех знаменателей. Так, например, ЛКД чисел $$2$$ и $$3$$ равен $6$$, поскольку $6$$ — наименьшее общее кратное этих двух чисел. Вы получаете повесить его?

 Почему так полезно вычитание дробей?

К сожалению, математика — это не только целые числа. Когда мы не можем использовать целые числа, нам нужен другой набор чисел: рациональные числа. Рациональные числа (также известные как дроби) необходимы в жизни, поэтому вы начнете замечать их повсюду вокруг себя. Например, вы печете торт и отмерили $$\frac{6}{7}$$ стаканов муки. В рецепте сказано, что вам нужна чашка $$\frac{3}{4}$$. Хватит ли муки для пирога? (Мы очень на это надеемся!) Вы можете вычислить это, вычитая дроби:

$$\frac{6}{7}-\frac{3}{4}$$

Как вычитать дроби

Теперь, когда мы знаем, зачем нам нужно уметь вычитать дроби, давайте рассмотрим некоторые задачи. вместе.

Пример 1

---

Вычтите дроби:

$$\frac{3}{2} — \frac{1}{2}$$

Наши дроби имеют одинаковый знаменатель, $$2$$ — здорово! Это означает, что мы можем просто написать числители над этим общим знаменателем, включая наш оператор:

$$\frac{3-1}{2}$$

Вычесть числа из числителя:

$$\frac{2}{2}$$

О, привет: $$2$$ разделить на $$2$$ будет $$1$$, поэтому давайте упростим наш результат:

$$1$$

Отлично! Давайте попробуем другой пример.

Пример 2

---

Вычесть дроби:

$$\frac{2}{5}-\frac{1}{6}$$

О нет, у наших дробей разные знаменатели. Не волнуйтесь, мы все еще можем вычитать — нам просто нужно сначала найти наименьший общий знаменатель (LCD)! Чтобы найти ЖК, запишите знаменатели обеих дробей:

$$5, ~6$$

Запишите простые факторизации чисел:

$$\begin{gathered}5=5, && 6=2\times3 \end{gathered}$$

Хммм, числа $$5$$ и $$6$$ не имеют общих делителей. Это означает, что наш наименьший общий знаменатель будет произведением простых множителей каждого числа:

$${2\times3\times5}=30$$

Итак, наш LCD равен $30$$. Помните, что при сложении дробей мы не можем просто изменить знаменатель на $$30$$ — мы также должны обновить числители:

$$\frac{2\times6}{5\times6}-\frac{1\times5}{6\times5}$$

Умножьте числа внутри дробей, чтобы получить обновленные числители и знаменатели:

$ $\frac{12}{30}-\frac{5}{30}$$

Теперь, когда дроби имеют равные знаменатели, мы можем записать числители над одним знаменателем, не забывая включать знак вычитания:

$ $\frac{12-5}{30}$$

Все, что осталось сделать, это вычесть числа в числителе:

$$\frac{7}{30}$$

Так как дробь не может быть упрощена, это наш результат!

Отличная работа! Основываясь на этих примерах, давайте рассмотрим весь процесс в целом, чтобы вы могли решить больше проблем самостоятельно:

Резюме исследования

1. Найдите наименьший общий знаменатель (LCD), если это необходимо.