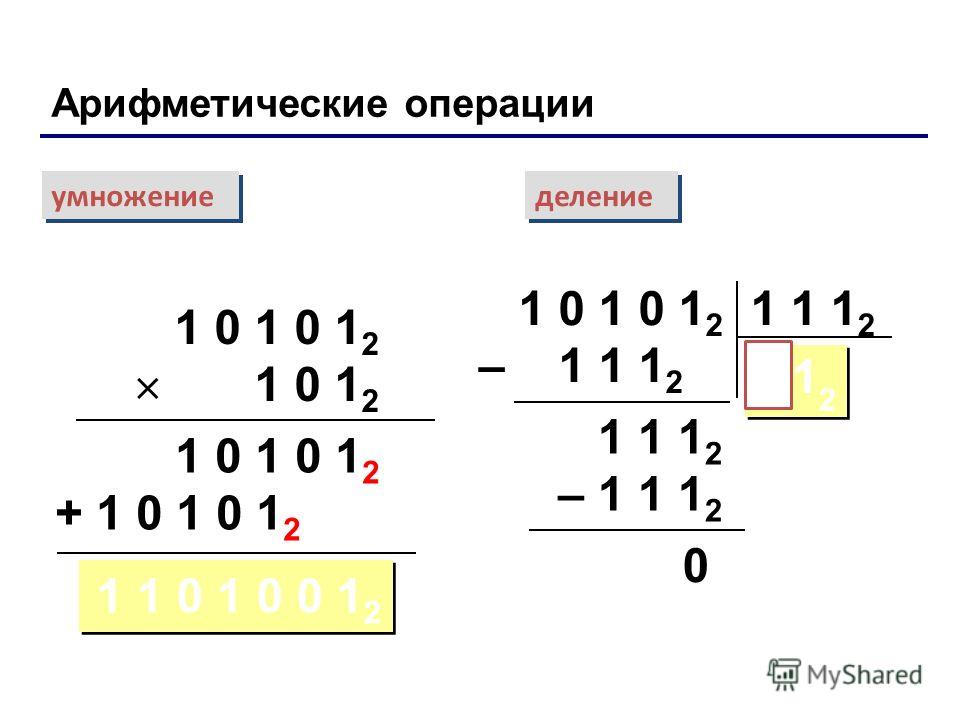
Ребенок никогда не запутается в порядке действий в примере после этого упражнения

Сначала скобочка, потом умножение – деление, потом сложение – вычитание. Чего уж проще?!

Но почти все дети в этом путаются. Особенно, когда дело доходит до длинных примеров.

Знаете, почему такое происходит?

Вот смотрите, когда дети начинаю изучать порядок действий, учитель просит их расписывать правильный порядок над выражением:

Это все очень хорошо и правильно на начальном этапе, и отлично работает на простых примерах вроде 2 + 3 * 4.

Дело в том, что, если в примере не более двух действий – циферки над примером действительно обозначают порядок действий.

То есть ребенок сначала выполнит умножение, а потом сложение – порядок действий будет “наоборот”, не по порядку.

Проблемы начинаются в тот момент, когда ребенок сталкивается с примерами вроде

4 + 1 * 3 – 2 + (6 – 8 : 2) + 1

Сначала умножение и деление, потом сложение и вычитание. А скобочки “рассматриваются как вложенные выражения”, так что их мы будем считать отдельно в первую очередь.

Ребенок делает как учили: пытается сначала посчитать скобочку, потому что она должна быть первой. Наталкивается на 8 деленное на 2 – и вот уже скобочка стала не первой, а внезапно второй…

Вот куда здесь ставить циферку первого действия, а куда циферку 2 – второго действия? Разрыв шаблонов.

А после скобочки еще находится умножение. А потом еще нужно разобраться, к какой части примера «присобачить» результаты скобочек и результаты умножения…

Понаблюдайте за детьми: почти все оказываются сталкиваются с одной и той же проблемой и все, как под копирку, высказывают одинаковые проблемы и допускают одинаковые ошибки в решении «длинных» примеров на порядок действий.

Если вы занимаетесь по программе Школы 21 века, конец второго класса – это уже километровые примеры, с которыми мучаются почти все дети.

Кто-то это перерастает и нарабатывает навык решения таких примеров, а кто-то до старости не может с этим справиться и только вздыхает: «Ну не математик я».

Секрет безошибочного порядка действий

Всех людей, которые ловко решают примеры на смешанные действия, отличает одно свойство. Точнее даже – навык.

Они умеют «видеть» или воспринимать числа, стоящие по обе стороны от знака умножения или деления не как «отдельно стоящие циферки», а как «единое число» (выраженное в такой странной форме).

Говоря наглядно, в нашем примере:

2 + 6 – 8 : 2

человек «видит» не четыре числа, а только три:

• Двойка
• Шестерка и
• 8:2, которые воспринимает как единое число.

Как правило, это неосознанное, невербализованное восприятие. Мозг мгновенно производит эту операцию, и человек не замечает её.

Этот навык вырабатывается долгим «нарешиванием» огромного количества длинных примеров. К старшей школе уже у многих детей есть.

Но можно попробовать ускорить события.

Предложу вам упражнение для отработки такого «видения».

Как научить ребенка никогда не ошибаться в порядке действий

Выполнить все упражнения ниже можно за 1 день, а в следующие дни только отрабатывать на «длинных» примерах.

Но лучше, если вы будете проходить весь цикл этих упражнений хотя бы неделю ежедневно – тогда навык закрепится лучше.

Уровень 1. Учимся «правильно видеть» умножение и деление.

Напишите на листе бумаги очень – очень длинный пример со всеми четырьмя действиями.

Пусть каждый пример будет длиной с целую страницу.

Подготовьте для занятия 4-5 таких страничек.

Числа можете писать «от балды» – считать его потом будет не обязательно… ну только если очень хочется 🙂

Очень длинный пример на разные действия

Скажите ребенку, что знаки умножения (•) и деления (:) как бы «склеивают» числа друг с другом. Эти «группы» – уже почти что самостоятельное число. Осталось только его сосчитать.

Возьмите ручку другого цвета и предложите ребенку обвести все группы «число – знак умножения/деления – число» в кружочки.

Обводим умножение и деление в кружочки, превращая их как-будто в единое число

Уже к концу первой страницы ребенок начнет «видеть» умножение и деление в примере совсем по-другому, но вы все же проделайте упражнение на нескольких страничках.

Уровень 2. Скобочки

Заготовьте точно такие же примеры длинной в 1 страницу (можно взять те же самые), только на этот раз пусть в примере будут не только все 4 знака, но и скобочки.

Расскажите ребенку, что скобочки – это еще один способ превратить несколько чисел в одно.

Теперь начнем выполнять упражнение.

Сначала ручкой другого цвета обведем все скобочки в кружочки:

Превращаем скобочки в “единое число”

Теперь возьмем ручку другого цвета и обведем все умножения и деления:

Превращаем умножение и деление в единое число

В некоторых случаях наши контуры скобочек и умножения – деления будут пересекаться. Так и скажите ребенку, что внутри одного «еще не посчитанного» числа есть другое «еще не посчитанное» число.

Теперь, когда обвели все группы в кружочки, Обратите внимание ребенка на то, что содержимое кружочков – почти уже готовые числа (вот такие длинные) – осталось только сосчитать.

Выполните упражнение – как и в прошлый раз – на нескольких страницах, каждая из которых будет длинным примером.

Уровень 3. Начинаем решать примеры

Теперь начинаем решать примеры.

Нам понадобятся не такие длинные примеры, как в прошлые разы. Пусть каждый будет не больше ширины листа.

В моем примере так:

Длинный пример на разные действия

Подберите простые числа, чтобы их удобно было считать в уме.

Снова обведём сначала все скобочки одним цветом:

Обвели все скобочки

а потом все группы с умножением / делением – другим:

Обвели все умножения и деления (в моем примере только умножения)

Начинаем считать С Начала Примера.

В школе учат расписывать под примером действия, начиная с «первых».

Приготовьтесь к этому расхождению.

Возможно, потом вам нужно будет специально натренировать ребенка выполнять эти школьные требования.

Итак, двигаемся по порядку и считаем.

Выполнили первое действие 2 + 2, получили 4

Под знаками будем записывать промежуточный результат накопительным итогом.

В моем примере в первом действии у нас результат 4, а во втором- 3:

От четверки из предыдущего действия отняли 1, накопительным итогом записали результат 3

Когда нам на пути попадается умножение или деление, отведённое в кружочек вместе со «своими числами», напоминаем ребенку, что это – как бы одно «склеенное» число, которое осталось только посчитать.

Добрались до кружочка с умножением, посчитали его. На первых порах можно подписать результат

На первых порах можно подписывать промежуточный результат и здесь. Но это быстро перестает быть удобным, так что ребенок начинает считать «склеенные» числа в уме и записывать только промежуточный результат сложения или вычитания:

Накопительным итогом посчитали результат

Продолжаем двигаться последовательно, записывая накопительным итогом результаты:

Двигаемся последовательно, записывая промежуточные результаты, пока не доберемся до скобочки (или нового умножения / деления)

… до тех пор, пока не подъедем до нового умножения / деления или до скобочки.

Когда подходим к скобочке, напоминаем ребенку, что содержимое скобочек – это как бы единое число, только еще не посчитанное.

Обсчитываем скобочку, производим действие с получившимся числом:

Превращаем скобочку в “единое число”

Если внутри скобочки что-то длинное, включающее умножение / деление – снова напоминаем, что они это почти что одно число.

В следующей скобочке сначала превращаем в единое число “внутренний кружочек”

Обсчитываем скобочку последовательно

Превращаем в число скобочку

Когда скобочку превратили в «совсем единое» число – производим с ним действие:

Производим действие с “накопленным” промежуточным результатом и числом, получившимся в скобочке

Решая такие примеры, ребенку имеет смысл пальцем вести по числам последовательно слева направо, указывая себе то действие, которое сейчас выполняется.

Прорешайте с ребенком 5-10 таких длинных примеров за одно занятие, чтобы запомнить принцип. И после повторяйте по 3-5 примеров ежедневно в течение недели, чтобы навык хорошо закрепился.

Этого в 98% случаев будет достаточно для того, чтобы проблема путаницы с порядком действий была решена окончательно и бесповоротно.

Правда, вас может настигнуть другая проблема: как «правильно» расписать пример в соответствии с требованиями школы: сначала все умножения, потом все скобочки… Но это уже другая – организационная – история, с которой вы разберетесь, если ребенок на самом деле умеет считать такие примеры правильно.

А у меня на сегодня всё.

Больших успехов вашим детям.

«Порядок выполнения действий в выражениях без скобок с действиями только одной ступени» | Учебно-методический материал по математике (2 класс) на тему:

Предмет: Математика 12.12. 2015

Тема: «Порядок выполнения действий в выражениях без скобок с действиями только одной ступени»

Класс: 2

Тип урока: открытие нового знания

Программа обучения: УМК «Перспектива» (учебник: Г. В Дорофеев,  Т.Н. Миракова. Математика. 2 класс в 2 частях)

Технологии: технологии проблемного, личностно-ориентированного, обучения, а также игровые, здоровьесберегающие и информационно-коммуникационные технологии.

Тема	Порядок выполнения действий в выражениях без скобок с действиями только одной ступени
Цели	Научить отличать действия первой ступени, действия второй ступени. Совершенствовать умение решать задачи.
Основное содержание темы, термины и понятия	Установление порядка выполнения действий в выражениях без скобок.
Планируемый результат	Предметные УУД: Научить устанавливать  порядок выполнения действий при вычислениях; находить примеры с действиями только первой ступени, второй ступени, обеих ступеней; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки. Личностные УУД: уметь проводить самооценку успешности учебной деятельности. Метапредметные УУД Регулятивные: уметь определять и формулировать цель на уроке с помощью учителя; проговаривать алгоритм  действий на уроке; работать по коллективно составленному плану в парах и группах;  планировать свои действия в соответствии с поставленной задачей; уметь применять правило о порядке выполнения действий. Коммуникативные: учиться формулировать связный ответ на поставленный вопрос; учиться умению совместно договариваться о правилах поведения и общения в паре, и следовать им. Познавательные: Выполнять под руководством учителя действия анализа, синтеза, обобщения при изучении нового понятия, разборе задачи, ознакомления с порядком выполнения действий.
Организация пространства
Межпредметные связи	Формы работы	Ресурсы
Математика. Литературное чтение (анализ текста задач)	Фронтальная работа, индивидуальная работа, работа в парах.	Учебник «Математика»для 2-го класса. Часть 1, Г.Ф. Дорофеев, Т.Н. Миракова — геометрические фигуры для математической игры «Великолепная семёрка» — тетрадь. — наглядный материал

        

Ход урока:

1. Мотивация (самоопределение) к учебной деятельности.

Прозвенел звонок и смолк-

Начинается урок.

Вы за парты тихо сели,

На меня все посмотрели.

Пожелайте успехов глазами

И вперёд за новыми знаниями!

— Работать сегодня мы будем коллективно и в парах. Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу)

2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии.

1. Чистописание.

— Установите закономерность и продолжите ряд: 11  12  23  34  45  56…

2. Математическая игра «Великолепная семёрка» (работа в парах)

— Из каких фигур вы сложили фигуру «Всадник»?

3. — Составьте поезд так, чтобы ответ предыдущего примера был равен числу следующего примера. Начинаем с примера на паровозике.

2. Задание на пробное действие. (На доске записаны примеры.)

Ваня и Аня решали примеры. Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?

19 – 8 + 5 =17 2 * 6 : 3 = 4 2 + 3 * 4 = 20

19 – 8 + 5 = 17 2 * 6 : 3 = 4 2 + 3 * 4 = 14

— Решите первый пример.

— Как выполняли действия?  (Сначала выполнили вычитание, а потом сложение.)

— Решите второй пример.

— Как выполняли действия. (Сначала выполнили умножение, а потом деление).

— Как решал третий пример Ваня? (Сначала выполнил сложение, а потом умножение).

— А как решала Аня? (Сначала выполнила умножение, а потом сложение).

4. Выявление места и причины затруднения.

— Как вы думаете, кто из ребят верно решил третий пример? Обоснуйте свой ответ. (Мы не можем определить, кто решил верно. )

— Чего мы не знаем?  (Мы не знаем, в каком порядке нужно выполнять действия в некоторых примерах.)

5. Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)

— Какая тема урока?  (Порядок выполнения действий.)

-Какова цель нашего урока? (Научиться устанавливать правильный порядок действий.)

6. Поиск решения проблемы.

— Откройте учебник на с. 97, прочитайте выделенное в рамочку.

Работа по слайду.

— Назовите арифметические действия первой ступени. Расположите их на нужной ступени.

— Назовите арифметические действия второй ступени.Расположите их на нужной ступени.

— Какая ступень выше? (Вторая)

— Сделайте вывод: какое действие надо выполнять первым? (умножение и деление)вторым? (сложение и вычитание)

— Мы получили новое знание. Проверим, правильно ли мы сделали выводы.

Сравним наше новое знание с научным в учебнике. Прочитайте на с.97выделенное в рамочку.

— Как вы думаете, кто верно решил третий пример: Ваня или Аня? Обоснуйте свой ответ. (Аня, т.к. в этом примере сначала надо выполнить действие умножения, а потом сложения)

7. Первичное закрепление с проговариванием во внешней речи

-Попробуем применить наше новое знание на практике.

(Коллективное выполнение с комментированием.)

— Выберите примеры с действиями только первой ступени.

-Как выполнять действия в первом столбике? (По порядку.)

— Выберите примеры с действиями только второй ступени.

-Как выполнять действия во втором столбике? (По порядку)

— Какие примеры остались? (примеры с действиями обеих ступеней)

— Как будем выполнять действия в третьем столбике?(Сначала выполним действие второй ступени, а затем первой ступени).

8. Физкультминутка

На горе стоит лесок

(круговые движения руками)

Он не низок не высок

(сесть, встать, руки вверх)

Удивительная птица подает нам голосок

(глаза и руки вверх, потянуться)

По тропинке два туриста

Шли домой издалека

(ходьба на месте)

Говорят:«Такого свиста,

Мы не слышали пока»

(плечи поднять)

9.  Включение в систему знаний повторение (на доске).

№3(с. 98).

— Объясни порядок действий в примерах. Вычисли.

10.Работа в парах  с самопроверкой по эталону.(Проверка по образцу на листочке, который находится у учителя.)

№5 (с. 98).

1 ряд – первую задачу.

2 ряд – вторую задачу.

3 ряд – третью задачу.

— Сравните условия и решения этих задач. Что можно заметить?

— Можно ли задачи назвать обратными? (Да)

(Ученик, решивший задачу первым, записывает решение и ответ на доске)

11. Рефлексия.

— Итак, над какой темой мы работали?

— Что нового узнали?

— В чём испытывали трудности? 

— Я поздравляю Вас, вы поднялись ещё на одну ступеньку знаний вверх Молодцы. Спасибо за урок.

---

12. Домашнее задание: правило на с. 97.

MathOnWeb — Электронная книга по алгебре — Pre-Algebra

• Факторы числа
• Наибольший общий делитель двух чисел
• Наименьшее общее кратное двух чисел
• Дроби и как их складывать, вычитать, умножать и делить
• Десятичная запись
• Экспоненциальное представление
• Порядок действий
• Невидимые кронштейны

---

1.

1 — Факторы числа

Числа, которые нас интересуют факторингом, натуральные числа 1, 2, 3, … Используется слово фактор как существительное и глагол. факторов (существительное) числа числа, которые делятся без остатка на число. Например, делителями числа 12 являются числа 1, 2, 3, 4, 6 и 12. (Обратите внимание, что наименьший множитель всегда равен 1, а наибольший множитель равен всегда само число.)

К коэффициенту (глагол) число означает его выражение как произведение меньших чисел. Например, мы можем разложить число 12 на множители. вот так: 12 = 3 · 4. Числа 3 и 4 называются факторами

. Другой способ размножения 12 выглядит следующим образом: 12 = 2 · 2 · 3. Теперь множители равны 2, 2 и 3. Каждый способ разложения числа на множители называется факторизацией .

Число, которое нельзя разложить на множители, называется 9.0026 простое число . Разложить число на , значит записать его как произведение простых чисел. Это также называется простой факторизацией .

Вот несколько примеров чисел в полностью факторизованной форме:

100 = 2 · 2 · 5 · 5

18 = 2 · 3 · 3

29 = 29       (29 — простое число)

---

Наибольший общий делитель (НОД) двух чисел

Если мы посмотрим на два или более числа, то у них будут общие множители. Например

множители 40 равны 1, 2, 4, 5, 8, 10, 20 и 40,

и множители 50 равны 1, 2, 5, 10, 25 и 50.

Мы показали общие факторы красным цветом. наибольший общий делитель является наибольшим из всех общие факторы. Наибольший общий делитель 40 и 50 равен 10. Вот еще несколько примеров величайших общих факторов:

GCF 24 и 30 равен 6

GCF 24, 30 и 33 равен 3

GCF 7 и 21 равен 7

GCF 7 и 13 равен 1

Вот процедура для нахождения наибольшего общего делителя двух или более числа. Проиллюстрируем числами 24 и 30. Разложите числа полностью и выстройте их множители. (Этим мы имеем в виду поставить общие множители друг под другом, и когда любое число отсутствует множитель, тогда оставьте для него место.)

Теперь легко увидеть факторы, общие для обоих чисел. Поскольку они оба имеют 2 и 3 общих наибольший общий делитель должен быть 2 · 3 = 6.

---

Наименьшее общее кратное (НОК) двух чисел

Кратные числа — это числа, которые имеют это число в качестве множителя. Например, числа, кратные 5, равны 5, 10, 15, 20, 25, …

. Если мы посмотрим на два или более числа, то у них будут общие кратные. Например

числа, кратные 3, равны 3, 6, 9, 12, 15, 18, 21, 24, 27, …

, а числа, кратные 4, равны 4, 8, 12, 16, 20, 24, 28, …

Мы показали красным цветом общие кратные чисел 3 и 4. Их 12, 24, … Самые маленькие из общее кратное называется наименьшим общим кратным . Вот еще несколько примеров наименьших общих кратных:

LCM 9 и 20 равен 180

LCM 2, 3 и 5 равен 30

LCM 7 и 21 равен 21

Вот процедура, чтобы найти наименьшее общее кратное двух или более числа. Проиллюстрируем числами 24 и 30. Разложите числа полностью и выстройте их множители. (Этим мы имеем в виду поставить общие множители друг под другом, и когда любое число отсутствует множитель, тогда оставьте для него место.)

Наименьшее общее кратное должно содержать все делители, которые в том или ином числе, но множители не используются дважды, когда они являются общими для обоих чисел. Выстроились вот так легко определить общие факторы. Наименьшее общее кратное должно быть 2 · 3 · 2 · 2 · 5 = 120,

Вам часто нужно найти факторы, которые каждый из исходных числа должны быть умножены, чтобы получить LCM. Выстроились вот так их легко заметить. Они просто отсутствуют факторы. В этом примере 24 нужно умножить на недостающие 5, и 30 нужно умножить на недостающие 2 · 2 или 4.

---

1.2 — Дроби и как их складывать, вычитать, умножать и делить

Обозначение дробей

Дроби (или обыкновенных дробей ) используются для описания части целого объекта. Существует несколько обозначений дробей:

a называется числителем , а b называется знаменателем . Обозначение означает, что мы разбиваем объект на b равных частей и у нас есть и таких штук. Часть или часть объекта, который у нас есть это / б . Например, если мы разобьем пирог на 4 равных куска и берем 1 кусок то у нас получается 1/4 часть пирога:

---

Эквивалентные дроби

Обратите внимание, что мы получаем одинаковое количество пирога как в предыдущем примере, если разделить пирог на 8 равных частей и получить 2 из них:

Такие дроби, как 1/4 и 2/8, имеющие одинаковое значение, называются эквивалентные дроби . Этот пример предлагает следующий метод для проверка на равенство двух дробей.

Две дроби равны , если умножить числитель и знаменатель одной дроби на то же целое число дает другая дробь.

Например, 4/5 и 24/30 эквивалентны, потому что мы можем начать с 4/5. и умножьте числитель и знаменатель на 6, чтобы получить 24/30:

Движение в обратном направлении (от 24/30 до 4/5) предполагает следующий метод. для сокращения дроби до младших членов или до простейшей эквивалентной дроби :

Приведение дроби к наименьшему члену или к простейшей эквивалентной дроби , полностью разложить как числитель, так и знаменатель (т. е. на простые числа). Затем сократите каждый множитель, который встречается как в числителе, так и в числителе. и знаменатель. Осталось простейшая эквивалентная дробь .

Например вот как уменьшить дробь 24/42 это самое простое эквивалентная дробь, а именно 4/7:

---

Неправильные дроби, смешанные дроби и длинное деление

Дробь, у которой числитель меньше знаменателя, называется правильной дробью и дробь, у которой числитель больше знаменателя, называется неправильная дробь . Пример неправильной дроби 7/4. Используя пример пирога, это означает, что вы сломали множество пирогов, каждый из которых разделен на 4 равные части, и у вас есть 7 таких частей:

Неправильные дроби иногда выражаются в виде смешанной дроби , которая представляет собой сумму целое число и правильная дробь, но без знака +. Например, 7/4 в обозначении смешанной дроби. выглядит так:

Обозначение смешанной дроби не используется в этой книге Algebra Help e или в программе Algebra Coach, потому что его слишком легко спутать с произведением целого числа на дробь. Вместо того, чтобы писать мы будем держать знак + и писать.

Длинное деление — это метод преобразования неправильной дроби в смешанную. Проиллюстрируем метод на дроби . Выполните следующие шаги:

• Установите формат длинного деления, а именно .
• Так как 5 в 9 идет 1 раз, напишите «1» над 9, напишите 1 × 5 или «5» ниже 9 и вычтите 5 из 9, чтобы получить разницу в 4, например:

• Затем опустите 2 следующим образом:
  Вот что мы на самом деле сделали: «1» и «5» находятся в десятки место, поэтому они на самом деле представляют числа 10 и 50, как показано здесь:
  Поэтому мы фактически показали, что .
• Теперь повторите весь процесс с остатком 42. Поскольку 5 в 42 идет 8 раз, напишите «8» над 2, напишите 8 × 5 или «40» ниже 42, и вычтите 40 из 42, чтобы получить остаток 2, например:

• Это показывает, что . Поскольку остаток 2 меньше делителя 5, это наш окончательный вариант. результат смешанной фракции.

---

Некоторые специальные дроби

Есть несколько специальных дробей, которые важно распознать:

• . Любое число n можно превратить в дробь, написав ее над знаменателем 1.
• . Все, что делится само на себя, равно 1. Мы называем это UFOO (a u seful f orm o f o ne). Подробнее об НЛО позже.
• Если числитель дроби кратен знаменателю то дробь равна целому числу. Примером является .
•  не определено для любого числителя n . Деление на ноль в математике запрещено.
• . Нулевой числитель не является проблемой. Эта дробь равна 0,
.

---

Сложение или вычитание дробей

На этом рисунке показано, что 2/8 пирога плюс 3/8 пирога равняются 5/8 пирога:

Дроби, имеющие одинаковые знаменатели, называются , как и дроби . Если подумать об этом примере, то следующая процедура добавления или вычитание одинаковых дробей очевидно:

Чтобы сложить или вычесть одинаковые дроби (дроби, имеющие общий знаменатель) , просто сложите или вычтите числители и приведите результат к общему знаменателю, так:

Но что, если дроби не имеют общего знаменателя? Ответ заключается в том, что они должны быть затем преобразованы к эквивалентным дробям, которые делают имеют общий знаменатель. Процедура проиллюстрирована на этом примере:

Шаги:

1. Найдите наименьшее общее кратное двух знаменатели 24 и 30. Применительно к дробям это число называется наименьшим общим знаменатель (ЖК-дисплей). В этом примере ЖК-дисплей равен 120,
.
2. Преобразуйте каждую дробь в эквивалентную дробь, имеющую ЖК 120 в знаменателе. Для этого в данном примере умножьте числитель и знаменатель первой дроби на 5, а числитель и знаменатель второй дроби на 4 (показаны красным).
3. Сложите числители и поместите над общим знаменателем.

Иногда есть еще один шаг. Результат всегда должен быть выражен как простейшая эквивалентная дробь, например:

Вот еще несколько примеров:

---

Умножение дробей

Умножение дробей производит новую фракцию. Умножьте числители, чтобы получить новый числитель и умножить знаменатели, чтобы получить новый знаменатель, так: Затем упростите, сократив новую дробь до наименьших членов. Чтобы умножить дробь на целое число, просто умножьте числитель дроби на целое число, чтобы получить новый числитель, например: Затем упростите, сократив новую дробь до наименьших членов.

Вот пример того, почему работает первая процедура. Предположим, что есть половина пирога (т. дробь 1/2), как показано слева. Теперь предположим, что вы взяли 2/3 из этой половины пирога. (Слово «из» переводится как математическая операция «умножить».) Это означает, что вы разрезаете половину пирога на 3 равные части и берете 2 из них. В результате получается 2/6 части пирога.

Вот пример того, почему вторая процедура работает. Предположим, вы съели 1/4 часть пирога. и что твой друг съел в 3 раза больше пирога, чем ты. Это означает, что ваш друг съел 3/4 пирога.

Вот еще несколько примеров умножения:

---

Обратные числа и деление дробей

Обратные числа играют важную роль при делении дробей. Говорят, что два числа или дроби равны 9.0026 обратны друг друга если их произведение равно 1. Например:

4/5 и 5/4 обратны, потому что

8 и 1/8 обратны, потому что

Деление дробей: Процедура заключается в замене деления на дробь на умножение на обратную дробь , например:

Обратите внимание, что вы берете обратная дробь на дне!

Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями. На первом шаге мы умножили эту дробь на UFOO числитель и знаменатель которого являются дробями. НЛО был выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого упрощение, оставившее только окончательное умножение дробей.

Пример 1: дробь, деленная на дробь :

---

Пример 2: дробь, деленная на число. Обратите внимание, что мы нарисовали одну разделительную линию. длиннее другого, чтобы вы могли сказать, какая дробь и какой это номер. Первый шаг — преобразовать целое число 4 в дробь 4/1. После нескольких шагов вы получите выражение, показанное синим цветом. Если сравнить это выражение с исходным вы заметите хороший ярлык. Число 4, на которое вы делите дробь, просто становится новый множитель в знаменателе дроби.

---

Пример 3: Число, разделенное на дробь. Проверьте действия. Этот пример сильно отличается от предыдущего!

---

1.3 — Десятичная запись

Слово десятичное означает десять . Десятичная система счисления знакома система, которая использует всего десять символов (цифр) для создания любого целого числа, независимо от того, насколько большой. Эти символы, конечно же, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.. (В отличие от двоичная система счисления использует только два символа 0 и 1 и шестнадцатеричная система счисления использует шестнадцать символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, чтобы создать любое число. Двоичный и шестнадцатеричный системы счисления, используемые в компьютерах.)

Для создания чисел больше 9 в десятичной системе используется разрядных значений . Например, диаграмма разрядности справа показывает, что 3528 означает 9. 0030

3528 = 3 · 1000 + 5 · 100 + 2 · 10 + 8 · 1 Это потому, что 3 стоит в разряде тысяч, а 5 — в разряде тысяч. разряд сотен, 2 в разряде десятков и 8 в разряде единиц место. Обратите внимание, что по мере того, как мы двигаемся справа налево в таблице разрядов, стоимость каждого места в десять раз превышает стоимость места вправо.

Если мы продолжим этот шаблон до справа , то мы получим показанная здесь расширенная диаграмма места:

Десятичная точка используется для отделения цифры в разряде единиц от цифры справа от него. Десятичное число 3528,74 означает:

---

Преобразование десятичных чисел в обозначение дроби:

Мы уже видели, что целые числа можно преобразовать в дроби. записи, просто поместив их над 1.

Десятичные числа с цифрами справа от запятой могут преобразовать в дробную форму, умножив их на УФО. Сначала определите разрядное значение самой правой цифры. Если разрядное значение — десятые, тогда умножьте на 10/10, если это сотые доли затем умножьте на 100/100 и т. д. Затем упростите числитель. Это превращает числитель в целое число. Вот некоторые примеры:

---

Экспоненциальное представление

Экспоненциальное представление является удобным сокращением для повторяющихся умножение. Экспоненциальное число b ⁿ означает умножить b раза на себя n раза:

b называется основанием , n называется показателем степени , а мы говорим что нас «повышение b до n ^th мощности» (кроме случаев, когда n равно 2, мы говорим, что «возводим в квадрат b » а когда n равно 3, мы говорим, что мы «возводим в куб b »).

Вот два примера:

3  ⁴ = 3 · 3 · 3 · 3 = 81

4  ³ = 4 · 4 · 4 = 64

Важно: во избежание путаницы убедитесь, что вы пишете показательную цифру аккуратно , с показателем меньше и выше , чем основание. Например, написал ли этот человек экспоненту 3  ⁴ или просто номер 34 ???

---

1.4 — Порядок действий

Выражение представляет собой набор чисел, которые объединяются с помощью таких операций, как как сложение, вычитание, умножение, деление, возведение в степень и т. д. Пример выражения:

4 + 5 · 2  ³ .

В этом выражении числа 4, 5, 2 и 3 объединяются операциями сложение, умножение и возведение в степень.

В выражениях часто используются скобки ( ) как символы группировки. В скобках содержится свои собственные подвыражения (таким образом создавая выражения внутри выражений). Пример:

3 (4 + 5) + 2.

Здесь подвыражение 4 + 5. Более сложный пример:

10 (3 (4 + 5) + 2)

Это предыдущее выражение, умноженное на 10. Это выражение содержит подвыражение который сам содержит подвыражение! Тогда возникает вопрос: в каком порядке мы выполняем эти операции? Ответ дан в этой таблице:

Порядок действий: Операция в скобках (круглые скобки) выполняется в первую очередь. Если есть вложенные скобки (скобки в скобках), то самые внутренние скобки делаются первыми. Затем возведение в степень . Затем умножение и деление слева направо. Затем сложение и вычитание слева направо.

Таким образом, приведенные выше примеры упрощаются следующим образом:

Пример: 4 + 5 · 2  ³ →   4 + 5 · 8 →   4 + 40 →   44

Пример: 3 (4 + 5) + 2 →   3 · 9 + 2 →   27 + 2 →   29

Пример: 10 (3 (4 + 5) + 2) →   10 (3 · 9 + 2) →   10 (27 + 2) →   10 · 29 →   290

Есть несколько сокращений, которые люди используют, чтобы запомнить таблица порядка операций. Один из них BEDMAS , что означает порядок: скобки, возведение в степень, деление и умножение, Сложение и вычитание.

Другой номер PEMDAS означает заказ: скобки, возведение в степень, Умножение и деление, Сложение и вычитание. Используйте любую аббревиатуру, которая вам больше нравится.

---

Невидимые кронштейны

Есть три места, где скобки обычно не отображаются, но вы должны представить, что они там есть. Одно место является показателем в экспоненте. Два других — числитель выше горизонтальная линия раздела и знаменатель под горизонтальной линией раздела. Вот два примера, показывающие выражения, первый с невидимыми скобками, а затем с видимыми скобками (показаны красным). Мы также показываем, что оценивают выражения.

Пример 1:

В этой экспоненте вы знаете, что «+2» находится в экспоненте вместе с «3». потому что оно написано меньше и выше основания и прямо возле «3». Это означает, что показатель степени должен быть равен «3+2» и должен храниться вместе, как если бы он был скобки вокруг него.

Пример 2:

В этой дроби вы знаете, что «+5» стоит в числителе вместе с «7». потому что это написано прямо рядом с «7», а разделительная линия проходит прямо через под оба. То же самое касается «+4» в знаменателе. Это означает, что в числителе «7+5», а в знаменателе «2+4», и оба должны быть вместе, как если бы вокруг них были скобки.

Примечание:

• Сравните следующие два примера с двумя приведенными выше. Разница лишь в том, что некоторые числа были немного перемещены или увеличены:
  Заключение: Аккуратность имеет значение!
• В приведенных выше примерах мы могли сказать, что число находится в показателе степени или в знаменателе с помощью насколько велика она была или где она была написана. Однако при вводе одного из этих выражений в В Algebra Coach (или в любой другой программе по алгебре) нельзя сделать числа меньше или больше. Все должно быть введено в одну строку, поэтому вы должны использовать квадратные скобки.

Математика с единицами измерения | GMAT Free

На GMAT, как и в реальном мире, многие числа имеют связанные с ними единицы измерения. Когда мы имеем дело с двумя числами, выраженными в единицах, если единицы одинаковы, мы можем складывать или вычитать как обычно. Однако, если единицы разные, то мы можем складывать или вычитать только в том случае, если единицы могут быть преобразованы в одинаковые единицы.

Например:

Некоторые единицы различаются, но могут быть преобразованы в общие единицы. Например,

Мы можем выполнить следующее сложение, только если сможем конвертировать яблоки в валюту США:

На GMAT вы столкнетесь с ситуациями, в которых вы будете использовать стандартное преобразование единиц измерения (например, 1 фут = 12 дюймов). ):

GMAT обычно не требует от вас знакомства с какой-либо конкретной системой единиц, кроме основных единиц измерения времени в секундах, минутах, часах, днях, неделях, месяцах и годах. Используются как единицы США, так и метрическая система, но когда вам нужно выполнить преобразование единиц, единицы будут предоставлены вам.

Пример, в котором требуется преобразование единиц измерения:

Чтобы выполнить это вычитание, нам нужно перевести две дроби в одни и те же единицы. Первый член равен

Оба умножения, встречающиеся в этой дроби, разрешены, поскольку они включают умножение на форму 1. Например, 3600 секунд равно 1 часу, поэтому дробь, умноженная на 1 час. в знаменателе просто кратно 1, что меняет единицы измерения.

Подставив эту дробь обратно в выражение, которое мы должны вычислить, мы получим:

На данный момент единицы измерения в обеих дробях одинаковы. Мы закончили преобразование единиц. Этот метод называется сокращением единиц или анализом размерностей.

Мы можем сделать важное замечание. На этом этапе этого конкретного вычисления мы можем исключить не только 90 131 единиц 90 132 здесь, но и 90 131 коэффициентов 90 132 . Дробь слева не нужно вычислять как есть; мы можем упростить его. Два множителя 10 сверху и снизу этой дроби сокращаются, что дает нам:

Кроме того, и числитель, и знаменатель имеют коэффициент 6, который мы можем сократить:

То, что нам нужно вычислить, было радикально упрощено! Вместо того, чтобы умножать 60 на 5280 и делить произведение на 3600, у нас есть только одно более простое деление. Мы можем закончить, разделив 528 на 6, используя деление в длинное число, чтобы получить:

Вы сможете выполнить множество упрощений, подобных этому, на GMAT. Ищите возможности аннулировать множители всякий раз, когда имеете дело с дробями.

Умножение и деление

При умножении или делении чисел на единицы они также умножаются или делятся.

Вот примеры, использующие одни и те же базовые единицы:

Хотя в физике имеют значение различные квадратные и кубические единицы, единственные квадратные и кубические единицы, которые вы, вероятно, встретите на GMAT, — это квадраты и кубы длины, соответствующие площади и объема соответственно.

Например, в случае прямоугольного тела:

Также возможно умножить или разделить число с единицами на скаляр (безразмерное число):

Так как показатели степени представляют умножение , операции с экспонентой применяются к единицам так же, как и умножение.