Умножение суммы на число. Правило и примеры
Умножить сумму на число можно двумя способами:
1) Чтобы умножить сумму на число, можно сначала выполнить сложение и полученный результат умножить на число.
Например, чтобы найти значение выражения:
(3 + 5) · 4,
можно сначала сложить числа 3 и 5:
3 + 5 = 8
и полученную сумму умножить на 4:
8 · 4 = 32, значит
(3 + 5) · 4 = 8 · 4 = 32.
2) Для умножения суммы на число, можно умножить каждое слагаемое на это число и полученные результаты сложить.
Например, чтобы найти значение выражения:
(3 + 5) · 4,
можно отдельно умножить число 3 и число 5 на 4:
3 · 4 = 12 и 5 · 4 = 20
и полученные произведения сложить:
12 + 20 = 32, значит
(3 + 5) · 4 = 3 · 4 + 5 · 4 = 12 + 20 = 32.
Данные способы умножения суммы на число можно легко проверить, посчитав количество звёздочек на картинке:
Не важно как мы будем их считать:
- пересчитывать все по порядку;
- считать количество звёздочек в строке и умножать полученный результат на количество строк;
- считать сначала количество жёлтых звёздочек, затем зелёных, и складывать полученный результаты.
При любом способе счёта получится ровно 32 звёздочки.
Умножение суммы на число можно представить в виде общей формулы:
(a + b) · c = a · c + b · c.
Данная формула выражает распределительный закон умножения.
Примеры
Пример 1. Найти значение каждого выражения двумя способами:
a) (3 + 8) · 2;
b) (6 + 3) · 5;
c) (1 + 4) · 3.
Решение:
a) (3 + 8) · 2 = 22;
- (3 + 8) · 2 = 11 · 2 = 22;
- (3 + 8) · 2 = 3 · 2 + 8 · 2 = 6 + 16 = 22.

b) (6 + 3) · 5 = 45;
- (6 + 3) · 5 = 9 · 5 = 45;
- (6 + 3) · 5 = 6 · 5 + 3 · 5 = 30 + 15 = 45.
c) (1 + 4) · 3 = 15;
- (1 + 4) · 3 = 5 · 3 = 15;
- (1 + 4) · 3 = 1 · 3 + 4 · 3 = 3 + 12 = 15.
Пример 2. Вычислить, удобным способом:
1) (4 + 6) · 5;
2) (32 + 13) · 2;
3) (4 + 3) · 5.
Решение:
1) (4 + 6) · 5 = 10 · 5 = 50;
2) (32 + 13) · 2 = 32 · 2 + 13 · 2 = 64 + 26 = 90;
3) (4 + 3) · 5 = 4 · 5 + 3 · 5 = 20 + 15 = 35.
Почему минус на минус дает плюс?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль.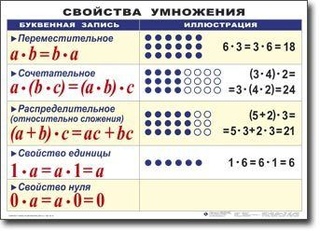 Это мы знаем из предыдущего переместительного закона:
Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Всё это приравняем к нулю:
(4 × (−2)) + ((−4) × (−2)) = 0
Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.
Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно поставим многоточие
−8 + … = 0
Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.
Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.
Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8
−8 + 8 = 0
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
Далее рассмотрим законы деления.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
12 : 4 = 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Порядок выполнения математических действий | интернет проект BeginnerSchool.
 ru
ruСегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.
Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.
Рассмотрим пример:
38 – (10 + 6) = 22;Итак, вспомним о том, что сначала вычисляются выражения в скобках
1) в скобках: 10 + 6 = 16;
2) вычитание: 38 – 16 = 22.
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5;
2) умножение: 5 × 4 = 20;
10 + 4 – 3 = 11, т.е.:
1) 10 + 4 = 14;
2) 14 – 3 = 11.
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7Порядок выполнения действий:
1) 18 ÷ 2 = 9;
2) 2 × 3 = 6;
3) 12 ÷ 3 = 4;
4) 9 – 6 = 3; т. е. слева направо – результат первого действия минус результат второго;
е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54, т.е.:1) выражение в скобках: 13 – 9 = 4;
2) умножение: 6 × 4 = 24;
3) сложение: 30 + 24 = 54;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Как сложить, вычесть, умножить и разделить 2 числа, каждое из которых содержит 100 цифр в C? (использование массивов)
Я пытаюсь написать код C для сложения, вычитания, умножения и деления 2 чисел, каждое из которых содержит 100 цифр. Это должно включать в себя использование массивов.
Может ли кто-нибудь дать мне какие-либо предложения, псевдокод или образец кода? Чтобы быть более ясным Пользователь введет 2 числа (целые числа) Каждое число может состоять из 100 или менее цифр, то есть целое число A может быть be 10, или 234, или 43582, или 23456788, или 23445667788 и т. д. То же самое для целого числа b. Теперь, взяв эти два целых числа, я должен выполнить арифметические операции сложения,вычитания, деления,умножения, модулей(%)
c arraysПоделиться Источник caitan correia 11 октября 2015 в 09:55
2 ответа
3
Вы можете попробовать использовать библиотеку GMP , как ответили на этот вопрос . Он может выполнять
Он может выполнять Bigint операций как в C , так и в C++ . Кроме того, если вы в порядке с кодом C++ для Bigint , вы можете проверить этот блог.
Поделиться Rahul Nori 11 октября 2015 в 10:53
1
Вы ищете подсказки по реализации арифметики произвольной точности. Начните читать эту статью: https://en.wikipedia.org/wiki/ произвольно-precision_arithmetic , затем поиск bignum c code с помощью поисковой системы, примеры реализаций легко найти. Избегайте полномасштабных пакетов, таких как gnu MP, потому что они слишком продвинуты и не являются правильной отправной точкой.
Поделиться chqrlie 11 октября 2015 в 10:53
Похожие вопросы:
Умножьте 2 очень больших числа на IOS
Я должен умножить 2 больших целых числа, каждое из которых состоит из 80+ цифр. Каков общий подход к такого рода задачам?
JQuery умножить и сложить
Допустим, у меня есть несколько чисел, которые я хочу умножить и сложить. var a = 5; var b = 10; var c = 2; var d = 3; Я хочу суммировать b и c, затем умножить это на a, а затем добавить d. Легко,…
Как сложить и вычесть 16-битные числа с плавающей запятой половинной точности?
Как сложить и вычесть 16-битные числа с плавающей запятой половинной точности? Скажем, мне нужно сложить или вычесть: 1 10000 0000000000 1 01111 1111100000 2-я форма дополнения.
Добавление двух разных цифр в c# (без использования BigInteger)
У меня есть задание C#. мне нужно сложить два числа. Первое число содержит около 100 цифр, таких как 12822429847264872649624264924626466826446692………… и второе число тоже со 100 цифрами или…
Как извлечь числа из списка массивов, сложить их и разделить на количество чисел в списке массивов?
Я смотрел онлайн-урок о массивах. Он научил меня ‘basics’ списков массивов: как создать список массивов. Поэтому мне было интересно, как можно создать список массивов из входных данных пользователей…
Он научил меня ‘basics’ списков массивов: как создать список массивов. Поэтому мне было интересно, как можно создать список массивов из входных данных пользователей…
Большие числа и тип данных
Если бы я хотел сложить два натуральных числа, каждое из которых содержит более 150 цифр, какой тип данных мне нужно было бы использовать? Правка: использование .Net 3.5
Как сложить или умножить цифры числа
Как говорится в названии, я хочу знать, можно ли сложить или умножить цифры числа в matlab напр.: для ряда 123456789 добавьте цифры, то есть 1+2+3+4+5+6+7+8+9 =>45 =>4+5 => 9 заранее…
Мне нужно написать программу C, которая добавляет два числа каждое из 100 + цифр?
Нужно написать программу C, которая добавляет два числа каждое из 100 + цифр.. Я не хочу, чтобы метод использования массивов делал это. Пожалуйста, подскажите мне, как хранить эти числа (по крайней…
Вычитание / деление двух списков цифр
Я хочу представить числа в виде списков цифр. Как я могу сложить, вычесть и разделить эти два числа, даже если они разного размера ? Например: 100-12 = 88 эквивалентно (1 0 0) минус (1 2) = ( 8 8)…
требуется ли компьютеру больше времени, чтобы умножить, разделить, вычесть, сложить два больших числа, чем меньшее число
Нам (людям) требуется больше времени, чтобы умножить, сложить, разделить и вычесть два больших числа, чем два маленьких. Требуется ли компьютеру больше времени для умножения 5 * 2 , чем, скажем,…
Правила сложения, вычитания, умножения чисел | fizmat.by
Тестирование онлайн
Сложение и вычитание
Сложение чисел
Результат сложения двух или более чисел называется суммой, а сами числа — слагаемыми.
Сумма двух отрицательных чисел. Складываем числа, аналогично положительным, записываем результат со знаком «минус». Например, (-6)+(-5,3)=-(6+5,3)=-11,3.
Например, (-6)+(-5,3)=-(6+5,3)=-11,3.
От перестановки мест слагаемых сумма не изменяется a+b=b+a.
Вычитание чисел
Результат действия называется разностью. Сами числа — уменьшаемое и вычитаемое.
Сложение положительного и отрицательного числа — это не что иное, как вычитание! Мало кто задумывается, что вычитание 7-2 можно представить в виде 7+(-2), получили сложение отрицательного и положительного числа. Для того, чтобы сложить два числа с противоположными знаками, необходимо от большего числа вычесть меньшее, а знак суммы должен совпадать со знаком большего числа.
Например, —8+3=—(8-3)=—5; или -7+45=+(45-7)=+38=38.
Умножение чисел
Результат умножения двух или более чисел называется произведением, а сами числа — множителями.
Умножить число а на b — значит найти сумму b слагаемых, каждое из которых равно a.
Например,
Произведение двух чисел одного знака есть число положительное. Например,
Произведение двух чисел с разными знаками есть число отрицательное. Например,
От перестановки множителей значение произведения не изменяется ab=ba.
1) Для любых натуральных чисел a и b верно равенство a+b=b+a. Это свойство называют переместительным (коммутативным) законом сложения, который формулируется так: от перестановки слагаемых значение суммы не изменяется.
2) Для любых натуральных a, b и c верно равенство (a+b)+с=a+(b+с). Это свойство называется сочетательным (ассоциативным) законом сложения, который формулируется так: значение суммы не изменится, если какую-либо группу слагаемых заменить их суммой.
1) Для любых натуральных чисел a и b верно равенство ab=ba. Это свойство называют переместительным законом умножения, который формулируется так: от перестановки множителей значение произведения не изменяется.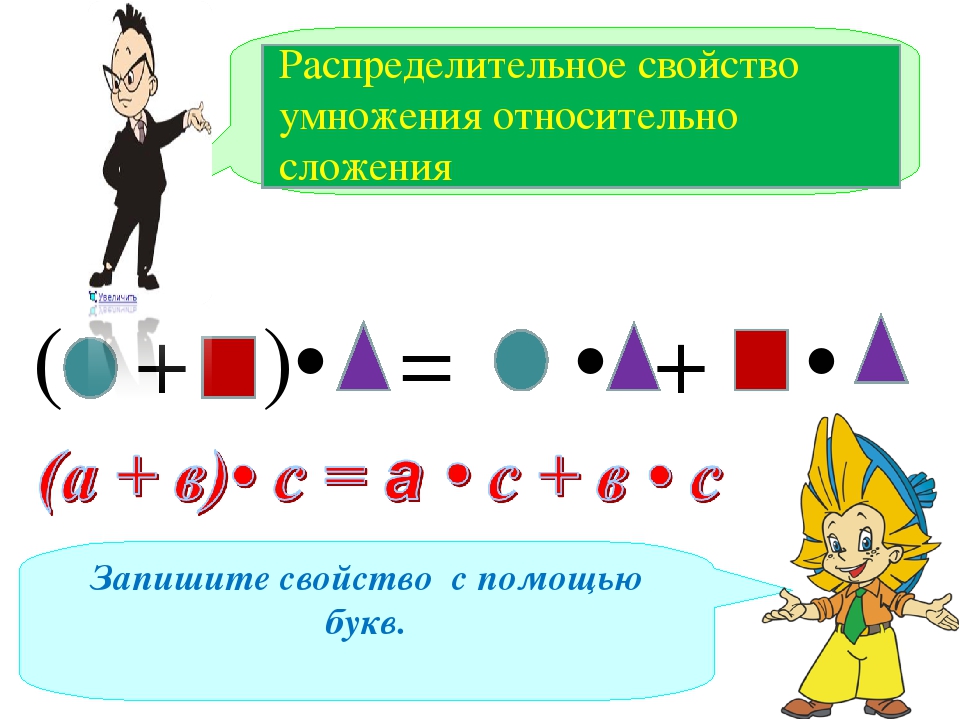
2) Для любых натуральных a, b и c верно равенство (ab)с=a(bс). Это свойство называют сочетательным законом умножения, который формулируется так: значение произведения не изменится, если какую-либо группу множителей заменить их произведением.
3) При любых значениях a, b и c верно равенство (a+b)с=aс+bс. Это свойство называют распределительным (дистрибутивным) законом умножения (относительно сложения), который формулируется так: чтобы умножить сумму на число, достаточно умножить каждое слагаемое на это число и сложить полученные произведения. Аналогично можно записать: (a-b)с=aс-bс.
Математические действия на английском языке
Наиболее употребительные простые дроби.Даже если ваша профессиональная деятельность никак не связана с точными науками, хотя бы основные математические действия на английском знать нужно. Они встречаются не только в специальной литературе, но и в фильмах, книгах, повседневной речи. В этой статье мы рассмотрим термины, связанные с арифметическими задачами, дробями, процентами. В конце я привожу озвученные карточки со основными словами на тему математики.
Обратите внимание, здесь рассматриваются только математические термины. Если вы ищете сведения о числительных, рекомендую эту статью: Числительные в английском языке.
Содержание:
Основные математические действия на английском: сложение, вычитание, умножение и деление
Наиболее употребительные математические термины относятся к арифметике. Обратите внимание, в русском языке у нас есть такие слова, как:
- Сложение, вычитание, деление, умножение – название действия.
- Складывать, вычитать, делить, умножать – глагол, обозначающий действие.
- Плюс, минус, разделить, умножить – название действия, которое мы используем в речи, когда читаем выражение, именно оно используется чаще всего.
В английском языке точно так же, поэтому представим арифметические действия в виде таблицы:
Название действия (сущ. ) ) | Название действия (глагол) | Используется в речи |
|---|---|---|
| Addition – сложение | Add – прибавлять | Plus – плюс |
| Subtraction – вычитание | Subtract – вычитать | Minus – минус |
| Multiplication – умножение | Multiply by – умножать на | Times – умножить |
| Division – деление | Divide by – делить на | Divided by – разделить |
| Equality – равенство | Equals to \ is equal to – равняться чему-то | Equals to \ is equal to \ is – равно |
Сама арифметическая задача (например, 2+2) называется problem (по-научному) или sum (разговорный вариант), решение или ответ – answer, а глагол “решать” – to solve (the problem).
Приведу примеры:
- 2+2=4 – Two plus two equals four.
- 7-2=5 – Seven minus two equals five.
Часто вместо equals или is equal to говорят просто is.
- 5×3=15 – Five times three is fifteen.
- 8÷4=2 – Eight divided by four is two.
Дроби на английском языке
Простые дроби – common fractions
Если у вас с математикой так же “прекрасно”, как у меня, напомню самое основное о дробях.
Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator). Напоминаю, числитель сверху, знаменатель снизу 🙂 Если число состоит из целого и дроби, например 1½, – это называется смешанная дробь или смешанное число (mixed numeral).
Числитель выражается количественным числительным, а знаменатель порядковым. Наиболее употребительные в речи дроби 1/2, 1/3, 1/4 в русском языке имеют не только “умные” называния “одна вторая”, “одна третья”, одна четвертая, но и простые: половина, треть, четверть. В английском точно так же.
- 1/2 – a half, one half.
- 1/3 – a third, one third.
- 1/4 – a quarter, one fourth.
- 1/5 – one fifth.
- 1/6 – one sixth.
- 2/3 – two thirds.
- 3/4 – three fourths.
- 1/8 – one eighth.
- 1/10 – a tenth.
- 1/100 – a hundredth.
- 1¼ – one and a quarter.
- 1½ – one and a half.
- 1¾ – one and three quarters.
Обратите внимание, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых).
Существительное, которое определяется дробью, используется с предлогом of:
- 3/4 mile – Three fourths of a mile.
- 1/4 bottle – A quarter of a bottle.
Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:
- 2 ½ miles – Two and a half miles.
- 1¼ bottles – One and a quarter bottles.
Десятичные дроби – decimal fractions, decimals
В английском в десятичных дробях (decimals) целое от дроби отделяется точкой (point), а не запятой, как у нас.
Ноль перед точкой называется zero или (британский вариант) nought. Ноль после точки может называться oh (как буква “o”), zero, nought. Лично я для простоты всегда говорю zero, потому что это слово проще выговорить и расслышать. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с “point”.
Целое число читается как обычное количественное числительное, например 45.1 – forty five point one. Но в дробной части каждая цифра читается отдельно тоже как количественное: 2. 45 – two point four five (а не two point forty five).
45 – two point four five (а не two point forty five).
Примеры:
- 0.1 – Point one, zero point one.
- 0.35 – Point three five, zero point three five.
- 1.25 – One point two five.
- 35.158 – Thirty five point one five eight.
- 15.05 – Fifteen point zero five.
Проценты в английском языке, трудности с числом глагола
Сотые доли могут выражаться с помощью процентов, тогда используется стандартный значок % и слово percent, всегда использующееся в единственном числе.
- 1% – One percent.
- 10% – Ten percent.
- 17% – Seventeen percent.
Трудность может вызвать число глагола в выражениях с процентами. Например:
- Twenty percent of the students are/is present. – 20% студентов присутствуют.
- The remaining twenty percent of the script has/have been rewritten. – Оставшиеся 20% сценария были переписаны.
В таких случаях глагол согласуется в числе с существительным после of:
- Twenty percent of the students are present (т. к. students – мн. число).
- The remaining twenty percent of the script has been rewritten (т. к. script – ед. число).
Возведение в степень в английском
Для обозначение степени используются выражения to the power of five, to the fifth power, raised to the power of five, raised to the fifth power. Для 2-ой и 3-ей степени используются термины “в квадрате” (squared) и “в кубе” (cubed).
- 32 – Three squared, three to the second power.
- 33 – Three cubed, three to the third power.
- 104 – Ten to the fourth power, ten to the power of four.
- 3024 – Thirty to the power of twenty four.

Квадратный корень называется square root:
- √16 = 4 – The square root of sixteen is four.
- √25 = 5 – The square root of twenty five is five.
Математические выражения со скобками
Круглые скобки называются parentheses (ед. число parenthesis) или, проще, round brackets. Если выражение стоит в скобках, и к нему применяется операция, используется слово quantity.
- (2+3)×4=24 – Two plus three quantity times four equals to twenty four.
- (3+5)2=64 Three plus five quantity squared is sixty four.
Карточки с английскими словами на тему “Математика”
Математические термины из этой статьи можно выучить с помощью карточек на Quizlet и PDF-карточек для распечатки.
| math (mathematics) | математика |
| do the math | считать (матем. действия) |
| problem (sum) | арифметическая задача |
| to solve | решать |
| answer | ответ |
| digit | цифра |
| number | число |
| odd number | нечетное число |
| even number | четное число |
| to add | прибавлять |
| to subtract | вычитать |
| to multiply by | умножать на |
| to divide by | делить на |
| to be equal to | равняться |
| plus | плюс |
| minus | минус |
| times | умножить |
| divided by | разделить |
| equals to | равно |
| common fractions | простые дроби |
| numerator | числитель |
| denominator | знаменатель |
| mixed number | смешанное число (дробь) |
| half | половина |
| quarter | четверть |
| decimals (decimal fractions) | десятичные дроби |
| point | точка (в дес. дробях) дробях) |
| percent | процент |
| to the power of five | в пятой степени |
| two squared | два в квадрате |
| two cubed | два в кубе |
| square root | квадратный корень |
| round brackets | круглые скобки |
| brackets | квадратные скобки |
| to round up the numbers | округлять числа |
Здравствуйте! Меня зовут Сергей Ним, я автор этого сайта, а также книг, курсов, видеоуроков по английскому языку.
Друзья! Меня часто спрашивают, но я не занимаюсь сейчас репетиторством. Если вам нужен репетитор, я рекомендую зайти на этот чудесный сайт. Здесь вы найдете учителей носителей и не носителей языка👅 для любых целей и на любой карман😄 Я сам прошел там более 100 уроков, рекомендую попробовать и вам!
Сначала умножить или сложить? Порядок обучения правилам операций
Когда дети сначала учатся сложению, вычитанию, умножению и делению, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Со временем математики разработали набор правил, называемых порядком операций, чтобы определить, какую операцию выполнять в первую очередь. Правила такие:
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
При упрощении выражения, такого как 12 ÷ 4 + 5 x 3 — 6, вы должны сначала вычислить 12 ÷ 4, поскольку порядок операций требует, чтобы вы начинали с левой стороны выражения и выполняли умножение или деление (в зависимости от того, что наступит раньше. ) перед сложением или вычитанием. После вычисления 12 ÷ 4 вы продолжаете движение слева направо в поисках умножения или деления. Итак, следующий шаг — вычислить 5 x 3. Теперь, когда все умножение и деление завершены, вы можете продолжить, добавляя или вычитая (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.
Шаги показаны ниже.
12 ÷ 4 + 5 x 3-6
3 + 5 x 3-6 (начиная с 12 ÷ 4 = 3)
3 + 15-6 (поскольку 5 x 3 = 15)
18-6 (поскольку 3 + 15 = 18)
12 (поскольку 18-6 = 12)
Группирующие символы, такие как круглые скобки (), квадратные скобки [] или фигурные скобки {}, позволяют определить порядок, в котором выполняются определенные операции. Посмотрите на это выражение:
6 + 4 x 7-3
6 + 28-3 (поскольку 4 x 7 = 28)
34-3 (поскольку 6 + 28 = 34)
31 (поскольку 34-3 = 31)
Что произойдет, если вы вставите скобки в выражение? Скобки позволяют определить, какая операция выполняется в первую очередь.Порядок операций гласит, что операции внутри круглых скобок выполняются перед операциями вне скобок. Что произойдет, если мы заключим в скобки 6 + 4?
(6 + 4) x 7 — 3
10 x 7 — 3 (6 + 4 = 10, которое выполняется первым, потому что оно заключено в круглые скобки)
70 — 3 (возобновляется нормальный порядок операций, и 10 x 7 = 70)
67 (поскольку 70 — 3 = 67)
Обратите внимание, что ответ значительно отличается от предыдущего.Что, если мы заключим в скобки 7–3?
6 + 4 x (7–3)
6 + 4 x 4 (На этот раз 7–3 заключено в скобки, поэтому мы сделаем это в первую очередь.)
6 + 16 (Если скобки не осталось , мы продолжаем умножение перед сложением.)
22 (так как 6 + 16 = 22)
Этот набор скобок дает еще один ответ. Итак, когда используются круглые скобки, правила порядка операций следующие:
- Операции в скобках.
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
Порядок работы: PEMDAS
Purplemath
Если вас просят упростить что-то вроде «4 + 2 × 3», естественно возникает вопрос: «Как мне это сделать? Потому что есть два варианта!» Я мог бы добавить первым:
4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18
. ..или я мог сначала умножить:
..или я мог сначала умножить:
4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10
Какой ответ правильный?
MathHelp.com
Кажется, ответ зависит от того, как вы смотрите на проблему.Но у нас не может быть такой гибкости в математике; математика не сработает, если вы не можете быть уверены в ответе или если можно вычислить одно и то же выражение, чтобы вы могли прийти к двум или более различным ответам.
Чтобы устранить эту путаницу, у нас есть некоторые правила приоритета, установленные, по крайней мере, еще в 1500-х годах, которые называются «порядком операций». «Операциями» являются сложение, вычитание, умножение, деление, возведение в степень и группирование; «порядок» этих операций указывает, какие операции имеют приоритет (о которых позаботятся) перед другими операциями.
Распространенным методом запоминания порядка действий является сокращение (или, точнее, «акроним») «PEMDAS», которое превращается в мнемоническую фразу «Пожалуйста, извините, моя дорогая тетя Салли». Эта фраза означает «круглые скобки, экспоненты, умножение и деление, сложение и вычитание» и помогает запомнить их порядок. Этот список показывает вам ранги операций: скобки опережают показатели, которые превосходят умножение и деление (но умножение и деление находятся в одном ранге), а умножение и деление превосходят сложение и вычитание (которые вместе находятся в нижнем ранге).Другими словами, приоритет:
- Круглые скобки (внутри них упростить)
- Экспоненты
- Умножение и деление (слева направо)
- Сложение и вычитание (слева направо)
Когда у вас есть несколько операций одного ранга, вы просто действуете слева направо. Например, 15 ÷ 3 × 4 не равно 15 ÷ (3 × 4) = 15 ÷ 12, а скорее (15 ÷ 3) × 4 = 5 × 4, потому что, двигаясь слева направо, вы попадаете в разделение подпишитесь первым.
Если вы не уверены в этом, проверьте это на своем калькуляторе, который был запрограммирован с иерархией порядка операций. Например, набрав указанное выше выражение в графическом калькуляторе, вы получите:
Используя приведенную выше иерархию, мы видим, что в вопросе «4 + 2 × 3» в начале этой статьи ответ 2 был правильным, потому что мы должны выполнить умножение, прежде чем выполнять сложение.
(Примечание: носители британского английского часто вместо этого используют аббревиатуру «BODMAS», а не «PEMDAS». BODMAS означает «скобки, порядки, деление и умножение, а также сложение и вычитание». и «порядки» совпадают с показателями, два акронима означают одно и то же. Кроме того, вы можете видеть, что буквы «M» и «D» поменяны местами в британо-английской версии; это подтверждает, что умножение и деление равны того же «звания» или «уровня».Канадцы, говорящие по-английски, разделяют разницу, используя BEDMAS.)
Порядок операций был определен, чтобы предотвратить недопонимание, но PEMDAS может создать свою собственную путаницу; некоторые студенты иногда склонны применять иерархию, как будто все операции в задаче находятся на одном «уровне» (просто идут слева направо), но часто эти операции не «равны». Во многих случаях это помогает решать проблемы изнутри, а не слева направо, потому что часто некоторые части проблемы находятся «глубже», чем другие части.Лучший способ объяснить это — привести несколько примеров:
Мне нужно упростить термин с показателем, прежде чем пытаться добавить 4:
Я должен упростить в круглых скобках, прежде чем я смогу провести экспоненту. Только после этого я смогу добавить 4.
4 + (2 + 1) 2 = 4 + (3) 2 = 4 + 9 = 13
Упростить 4 + [–1 (–2 — 1)]
2 .
Я не должен пытаться делать эти вложенные круглые скобки слева направо; этот метод слишком подвержен ошибкам. Вместо этого я постараюсь работать изнутри. Сначала я упрощу внутри фигурных скобок, затем упрощу внутри квадратных скобок и только потом займусь квадратом. После этого я наконец могу добавить 4:
4 + [–1 (–2 — 1)] 2
= 4 + [–1 (–3)] 2
= 4 + [3] 2
= 4 + 9
= 13
Использование квадратных скобок («[» и «]» выше) вместо скобок не имеет особого значения.Скобки и фигурные скобки (символы «{» и «}») используются, когда есть вложенные круглые скобки, как помощь в отслеживании того, какие круглые скобки к которым идут. Различные символы группировки используются только для удобства. Это похоже на то, что происходит в электронной таблице Excel, когда вы вводите формулу, используя круглые скобки: каждый набор скобок имеет цветовую кодировку, поэтому вы можете определить пары:
Упростить 4 (
–2 / 3 + 4 / 3 ).
Сначала я упрощу внутри скобок:
Итак, мой упрощенный ответ
8 / 3На следующей странице есть другие примеры работы ….
URL: https: // www.purplemath.com/modules/orderops.htm
При сложении и умножении одинаковы
При сложении и умножении одинаковы Дэвид А. УилерЭто еще одно небольшое эссе, представляющее собой увлекательное математическое упражнение; Надеюсь, вам это понравилось!
Когда сложение — это то же самое, что умножение? Другими словами, когда верно следующее?
х + у = х * у
Немного подумав, вы поймете, что {x, y} = {2,2} и {0,0} два решения проблемы, потому что:
2 + 2 = 2 * 2 = 4 0 + 0 = 0 * 0 = 0
Но есть ли другие решения? Чтобы выяснить это, нам нужно решить уравнение, используя небольшую алгебру:
х + у = ху 0 = ху - х - у 0 = (x-1) (y-1) - 1 (Вы запутались? См. Постскриптум ниже) 1 = (х-1) (у-1) 1 / (х-1) = у-1 у = 1 / (х-1) + 1
Итак, существует бесконечное количество решений с действительными числами; найти заданный y, просто вычислите y = 1 / (x-1) +1 (до тех пор, пока x не равно 1; в этом случае нет решения с действительными числами).2 +1 или -1 = х-1 х = 0 или 2
Теперь, вместо того, чтобы ограничиваться x = y, допустим любое значение x и y, но только если они оба целые. Существуют ли какие-либо другие решения для пар целых чисел с учетом этой вариации? Короткий ответ — нет — если вы ограничитесь целыми числами, 0 и 2 будут все, что возможно. Вот почему. Поскольку целые числа являются подмножеством действительных чисел, уравнение приведенное выше применяется:
у = 1 / (х-1) +1Итак, чтобы y было целым числом, 1 / (x-1) должно быть целым числом.Чтобы дробь производила целое число, когда наверху стоит единица, его знаменатель должен иметь абсолютное значение меньше единицы, поэтому:
| х-1 |
Это верно только для x = {0,1,2}. x не может быть 1, потому что
потребует, чтобы y было бесконечным.
Так что 0 и 2 также являются единственными целочисленными решениями.
Итог: существует бесконечное количество пар действительных чисел, где
сложение и умножение пары даст тот же ответ.
Но если вам требуется, чтобы пара имела одинаковое значение или оба
быть целыми числами, есть только два ответа: {0,0} и {2,2}.
К сожалению, некоторые люди присылали мне сообщения,
просят объяснить почему:
ху - х - у
такой же как:
(х-1) (у-1) - 1
Тск, тск! Жалуйтесь своим учителям алгебры, они
пропустил какой-то важный материал.
Оказывается, это несложно показать;
просто начните с «(x-1) (y-1)» и умножьте его.
Это два тривиальных выражения; ты можешь просто умножить
их так же, как вы умножаете многозначные числа:
х - 1
* у - 1
===============
-x + 1
ху -у
===============
ху -х -у + 1
Итак, (x-1) (y-1) - это , почти то же самое, что и xy-x-y, за исключением того, что
у него есть дополнительный «+1».Нет проблем, просто вычтите один, и он у вас есть.
Что означает, что:
ху - х - у = (х-1) (у-1) - 1
Теперь, честно говоря, я мгновенно узнал "xy-x-y" так же легко
переписывается как «(x-1) (y-1) -1»; Мне не нужно было «разбираться».
Но если вы не видели этого раньше, надеюсь, это вас убедит.
Если вам понравилась эта статья, возможно, вам понравятся мои статьи о
Проблема четырех четверок или
странные базы.
Не стесняйтесь видеть мою
домашняя страница на dwheeler.com.
Дэвид А. Уиллер, 10 сентября 2002 г.
Это Copyright (C) 2002-2005 Дэвид А. Уиллер.
Что означает слово «произведение» в математике?
Обновлено 19 декабря 2020 г.
Автор: Bert Markgraf
Произведение является результатом выполнения математической операции умножения. Когда вы умножаете числа, вы получаете их произведение. Другими основными арифметическими операциями являются сложение, вычитание и деление, а их результаты называются суммой, разностью и частным соответственно.У каждой операции также есть особые свойства, определяющие порядок расположения и комбинирования чисел. Для умножения важно знать об этих свойствах, чтобы вы могли умножать числа и комбинировать умножение с другими операциями, чтобы получить правильный ответ.
TL; DR (слишком долго; не читал)
Значение произведения в математике является результатом умножения двух или более чисел. Чтобы получить правильный продукт, важны следующие свойства:
- Порядок номеров не имеет значения.
- Группировка чисел в квадратные скобки не действует.
- Умножение двух чисел на множитель с последующим их сложением аналогично умножению их суммы на множитель.
- При умножении на 1 число не меняется.
Значение произведения числа
Произведение числа и одного или нескольких других чисел — это значение, полученное при умножении чисел. Например, произведение 2, 5 и 7 равно
2 × 5 × 7 = 70
Хотя произведение, полученное путем умножения определенных чисел, всегда одинаково, продукты не уникальны.Произведение 6 и 4 всегда равно 24, но равно как и произведение 2 и 12 или 8 и 3. Независимо от того, какие числа вы умножаете, чтобы получить произведение, операция умножения имеет четыре свойства, которые отличают ее от других основных арифметических операций. , Сложение, вычитание и деление разделяют некоторые из этих свойств, но каждое из них имеет уникальную комбинацию.
Арифметическое свойство коммутации
Коммутация означает, что условия операции можно менять местами, и последовательность чисел не влияет на ответ.Когда вы получаете произведение путем умножения, порядок, в котором вы умножаете числа, не имеет значения. То же самое и с сложением. Вы можете умножить 8 × 2, чтобы получить 16, и вы получите тот же ответ с 2 × 8. Точно так же 8 + 2 дает 10, тот же ответ, что и 2 + 8.
Вычитание и деление не имеют свойства коммутация. Если вы измените порядок чисел, вы получите другой ответ. Например,
8 ÷ 2 = 4 \ text {but} 2 ÷ 8 = 0,25
8 — 2 = 6 \ text {but} 2 — 8 = -6
Деление и вычитание не являются коммутативными операциями.
Свойство распределения
Распределение в математике означает, что умножение суммы на множитель дает тот же ответ, что и умножение отдельных чисел суммы на множитель с последующим сложением. Например,
3 × (4 + 2) = 18 \ text {и} (3 × 4) + (3 × 2) = 18
Сложение перед умножением дает тот же ответ, что и распределение множителя по числам на добавляется, а затем умножается перед сложением.
Деление и вычитание не обладают распределительным свойством.Например,
3 ÷ (4-2) = 1,5 \ text {but} (3 ÷ 4) — (3 ÷ 2) = -0,75
Вычитание перед делением дает другой ответ, чем деление перед вычитанием.
Свойство ассоциативности для продуктов и сумм
Свойство ассоциативности означает, что если вы выполняете арифметическую операцию более чем с двумя числами, вы можете связать или заключить в квадратные скобки два числа, не влияя на ответ. Продукты и суммы обладают ассоциативным свойством, а разности и частные — нет.
Например, если арифметическая операция выполняется с числами 12, 4 и 2, сумма может быть вычислена как
(12 + 4) + 2 = 18 \ text {или} 12 + (4 + 2) = 18
(12 × 4) × 2 = 96 \ text {или} 12 × (4 × 2) = 96
\ frac {12 ÷ 4} {2} = 1,5 \ text {while} \ frac {12} {4 ÷ 2} = 6
(12 — 4) — 2 = 6 \ text {while} 12 — (4 — 2) = 10
Умножение и сложение обладают ассоциативным свойством, а деление и вычитание — нет.
Операционные идентификаторы — разница и сумма по сравнению с продуктом и коэффициентом
Если вы выполняете арифметическую операцию с числом и рабочим идентификатором, число остается неизменным. Все четыре основных арифметических операции идентичны, но не одинаковы. Для вычитания и сложения тождество равно нулю. Для умножения и деления идентичность равна одному.
Например, для разницы 8 — 0 = 8. Число остается идентичным. То же самое и с суммой 8 + 0 = 8.Для продукта 8 × 1 = 8, а для частного 8 ÷ 1 = 8. Продукты и суммы имеют одинаковые основные свойства, за исключением того, что они имеют разные операционные идентичности. В результате умножение и его произведения обладают уникальным набором свойств, которые необходимо знать, чтобы получить правильные ответы.
Это не повторное добавление
Это не повторное добавлениеЕсли когда-либо и требовался веский аргумент в пользу того, что профессиональные математики должны интересоваться математическим образованием в K-12 и участвовать в этом процессе, этот пример должен предоставить его.Учителя, которые связываются со мной, делают это, потому что они искренне хотят знать, что я имею в виду, поскольку их самих учили, предположительно либо в учебных заведениях, либо по школьным учебникам, что умножение — это повторное сложение.
Начнем с основного факта. Умножение — это просто не повторное сложение, и рассказ молодым ученикам о том, что это такое, неизбежно приводит к проблемам, когда они впоследствии узнают, что это не так. Умножение натуральных чисел , безусловно, дает тот же результат , что и повторное сложение, но это не делает его одинаковым.Езда на велосипеде доставляет меня в офис примерно в то же время, что и машина, но эти два процесса очень разные. Сообщать учащимся неправду, полагая, что она может быть исправлена позже, редко бывает хорошей идеей. И говоря им, что умножение повторяется, сложение определенно требует отмены позже.
Сколько позже? Как только ребенок перейдет от умножения целых чисел к умножению на дроби (или произвольные действительные числа). В этот момент вам нужно рассказать другую историю.
«О, так умножение дробей — это РАЗНЫЙ вид умножения, не так ли?» — скажет смышленый ребенок, гадая, сколько еще раз вы собираетесь менять правила. Неудивительно, что так много людей в конечном итоге думают, что математика — это просто набор произвольных, нелогичных правил, которые нельзя понять, а просто нужно усвоить — только для того, чтобы вытащить коврик из-под них, когда правило, которое они только что выучили, заменяется на какое-то другое (казалось бы) произвольное, нелогичное правило.
Представление о том, что с числами есть только одна базовая операция (будь то целые числа, дроби или что-то еще), наверняка приведет к тому, что ученики будут считать, что числа — это просто аддитивная система и не более того. Почему бы не сделать это с самого начала?
Почему бы не сказать, что есть (по крайней мере) две основные вещи, которые вы можете делать с числами: вы можете складывать их и вы можете их умножать. (Здесь я не учитываю вычитание и деление, поскольку они просто противоположны сложению и умножению и, следовательно, не являются «основными» операциями.Это не значит, что обучить их несложно; это так.) Сложение и умножение — это всего лишь то, что вы делаете с числами — они идут в комплекте. Мы включаем их, потому что есть много полезных вещей, которые мы можем делать, когда можем складывать и умножать числа. Например, добавление чисел говорит вам, сколько вещей (или частей вещей) у вас есть при объединении коллекций. Умножение полезно, если вы хотите узнать результат масштабирования некоторой величины.
Вам не обязательно использовать эти приложения, но оба они просты и знакомы, и, на мой взгляд, они настолько хороши, насколько это возможно с точки зрения целесообразности.(Я думаю, что вам нужно представить простые повседневные примеры приложений. Обучать класс учеников начальной школы аксиоматическим областям целостности, вероятно, не лучшая идея! Эта колонка не является разглагольствованием в пользу «Новой математики», термина, который я использую здесь для обозначения популярной концепции отмененной ранее реформы образования, носящей это название.)
После того, как вы установили, что есть две различных (я не говорю несвязанных) полезных операций над числами, тогда станет самоочевидным, что повторное сложение — это не умножение, а просто сложение. — повторил!
Но теперь вы подготовили почву для того прекрасного момента, когда вы можете рассказать детям, а еще лучше, может быть, они сами откроют для себя этот чудесный трюк, заключающийся в том, что умножение дает вам сверхбыстрый способ вычисления суммы повторяемого сложения.Зачем лишать детей этого чудесного волшебства?
[Конечно, любой фокус теряет много, если посмотреть за кулисами. В самые ранние дни развития концепции числа, около 10 000 лет назад, существовали только целые числа, и, возможно, самым ранним предшественником того, что сейчас является умножением, действительно было повторное сложение. Но все это было 10 000 лет назад, и с тех пор многое изменилось. Мы не пытаемся понять, как работает iPod в терминах счётов, и мы не должны основывать нашу систему образования на том, что люди знали и делали в 8000 B.C.]
Математика полна примеров, когда что-то, относящееся к категории А, оказывается полезным для выполнения Б.
Возведение в степень дает быстрый способ повторного умножения — вау, это случилось снова! Это круто с математикой, что ли!
Антидифференциация оказывается быстрым способом вычисления интеграла. Боже, это так глубоко!
Я просто слышу, как некоторые ученики задаются вопросом: «Эй, сколько еще таких примеров? Это действительно очень интригует.Кажется, все это сочетается друг с другом. Здесь должно быть что-то глубокое. Мне нужно узнать больше «.
Я предполагаю, что причина нынешнего положения дел в том, что учителя (что на самом деле означает их учителей или авторов учебников, которые должны использовать эти учителя) чувствуют, что дети не смогут справиться с тем фактом, что есть две основных операции вы можете выполнять по числам. И они говорят им, что на самом деле существует только один, а другой — лишь его вариант.Но действительно ли мы считаем, что с двумя операциями сложнее договориться, чем с одной? Огромный скачок к абстракции связан с идеей абстрактных чисел, с которыми вы можете что-то делать. После того, как вы преодолели эту поистине потрясающую когнитивную пропасть, не имеет большого значения, сможете ли вы сделать одну абстрактную вещь с числами или с дюжиной или более.
Конечно, над числами можно выполнять не только две основные операции. Мгновение назад я упомянул третью базовую операцию: возведение в степень.Профессора математики в университетах отважно борются за то, чтобы избавить студентов от ложного убеждения, что возведение в степень — это «многократное умножение». Эй, если вы однажды можете запутать учеников ложью, почему бы не проделать тот же трюк снова? Я здесь дразню. Но с наилучшими намерениями привлечь внимание к чему-то, что, как мне кажется, нужно исправить.
И способ исправить это — убедиться, что, когда мы обучаем будущих учителей и когда авторы пишут или утверждают, что принимают учебники, мы все делаем это правильно.Мы, математики, несем здесь основную ответственность. Мы являемся признанными экспертами в области математических структур, включая различные системы счисления. («Системы» здесь включают в себя операции, которые могут быть выполнены с ними.) Наши профессиональные предшественники построили эти структуры. Они — часть нашего мировоззрения, вещи, которые мы так давно освоили в нашем образовательном путешествии, что они — вторая натура. Слишком долго мы молчаливо предполагали, что наши знания и понимание этих систем разделяются другими.Но это не так. У меня есть файл недоумевающих писем от квалифицированных учителей, свидетельствующих о пробеле.
В заключение я должен отметить, что я не пытался предписать , как учителя должны преподавать арифметику. Я не обученный учитель K-12, и у меня нет личного опыта, которым можно было бы воспользоваться. Но термин «преподавание математики» состоит из двух слов, и в первом у меня есть опыт. Это мое внимание здесь, и я полагаюсь на тех, кто имеет опыт преподавания.Безусловно, лучший путь вперед — это для двух групп специалистов, математиков и учителей, диалог — регулярно и часто.
А пока, учителя, пожалуйста, перестаньте говорить своим ученикам, что умножение — это повторное сложение.
Угол Девлина обновляется в начале каждого месяца.
Математик Кейт Девлин (электронная почта: [email protected]) является Исполнительный директор Центра изучения языка и информации Стэнфордского университета и Математик в выпуске выходного дня NPR.Последняя книга Девлина, Раскрытие преступлений с помощью математики: ЦИФРЫ ЗА НОМЕРАМИ, это книга-компаньон к хиту телевизионный криминальный сериал NUMB3RS, и написан в соавторстве с профессором Гэри Лорденом из Калифорнийского технологического института, ведущим советником по математике в этой серии. Он был опубликован в сентябре прошлого года издательством Plume.
Сложение, вычитание, умножение и деление целых чисел
Цели обучения
- Используйте сложение, вычитание, умножение и деление при вычислении целочисленных выражений
Работа с целыми числами и выполнение основных вычислений — основа всей математики.Предположим, вы помните, как выполнять сложение, вычитание, умножение и деление одной цифры. Для выполнения этих вычислений у вас часто будет под рукой калькулятор, но быстрое освежение знаний поможет вам лучше понять, как работать с числами, чтобы сложные уравнения были менее сложными.
Дополнение
пример
Добавьте: [латекс] 28 + 61 [/ латекс]
Решение
Чтобы сложить числа, состоящие из более чем одной цифры, часто проще записать числа вертикально в столбцы.
| Напишите числа так, чтобы цифры единиц и десятков располагались вертикально. | [латекс] \ begin {array} {c} \ hfill 28 \\ \\ \ hfill \ underset {\ text {____}} {+ 61} \ end {array} [/ latex] |
| Затем добавьте цифры в каждое значение разряда. Складываем единицы: [латекс] 8 + 1 = 9 [/ латекс] Складываем десятки: [латекс] 2 + 6 = 8 [/ латекс] | [латекс] \ begin {массив} {c} \ hfill 28 \\ \\ \ hfill \ underset {\ text {____}} {+ 61} \\ \ hfill 89 \ end {array} [/ latex] |
В предыдущем примере сумма единиц и сумма десятков были меньше [латекс] 10 [/ латекс].Но что будет, если сумма [латекс] 10 [/ латекс] или больше? Давайте воспользуемся нашей моделью base- [latex] 10 [/ latex], чтобы выяснить это.
На приведенном ниже рисунке снова показано добавление [латекса] 17 [/ латекса] и [латекса] 26 [/ латекса].
Когда мы складываем те, [latex] 7 + 6 [/ latex], мы получаем [latex] 13 [/ latex]. Поскольку у нас больше, чем [latex] 10 [/ latex], мы можем обменять [latex] 10 [/ latex] из них на [latex] 1 [/ latex] десять. Теперь у нас есть [латексные] 4 [/ латексные] десятки и [латексные] 3 [/ латексные] десятки.Не используя модель, мы показываем это как маленький красный [латекс] 1 [/ латекс] над цифрами в разряде десятков.
Когда сумма в столбце значений разряда больше [latex] 9 [/ latex], мы переносимся в следующий столбец слева. Перенос — это то же самое, что перегруппировка путем обмена. Например, [латекс] 10 [/ латекс] единиц за [латекс] 1 [/ латекс] десятку или [латекс] 10 [/ латекс] десяток за [латекс] 1 [/ латекс] сотню.
Сложить целые числа
- Напишите числа так, чтобы каждое разрядное значение было расположено вертикально.
- Сложите цифры в каждом значении разряда. Работайте справа налево, начиная с места единиц. Если сумма в разряде больше [latex] 9 [/ latex], переносится к следующему разряду.
- Продолжайте складывать каждое разрядное значение справа налево, добавляя каждое разрядное значение и перенося, если необходимо.
пример
Добавить: [латекс] 43 + 69 [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы цифры располагались вертикально. | [латекс] \ begin {array} {c} \ hfill 43 \\ \\ \ hfill \ underset {\ text {____}} {+ 69} \ end {array} [/ latex] |
| Добавьте цифры в каждом месте. Складываем единицы: [латекс] 3 + 9 = 12 [/ латекс] | |
| Запишите [латекс] 2 [/ латекс] в разрядах единиц суммы. Добавьте [latex] 1 [/ latex] десятку к разряду десятков. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {4} 3 \\ \ hfill \ underset {\ text {____}} {+ 69} \\ \ hfill 2 \ end {array} [/ латекс] |
| Теперь сложите десятки: [латекс] 1 + 4 + 6 = 11 [/ латекс] Запишите 11 в сумме. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {4} 3 \\ \ hfill \ underset {\ text {____}} {+ 69} \\ \ hfill 112 \ end {array} [/ латекс] |
Если слагаемые содержат разное количество цифр, будьте осторожны, чтобы выровнять соответствующие разрядные значения, начиная с единиц и двигаясь влево.
пример
Добавить: [латекс] 1,683 + 479 [/ латекс].
Покажи ответРешение
| Напишите числа так, чтобы цифры располагались вертикально. | [латекс] \ begin {array} {c} \ hfill 1,683 \\ \\ \ hfill \ underset {\ text {______}} {+ 479} \ end {array} [/ latex] |
| Добавьте цифры в каждое значение разряда. | |
| Складываем единицы: [латекс] 3 + 9 = 12 [/ латекс]. Напишите [latex] 2 [/ latex] в разряде единиц суммы и перенесите [latex] 1 [/ latex] десять в разряды десятков. | [латекс] \ begin {array} {c} \ hfill 1,6 \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ text {______}} {+ 479} \\ \ hfill 2 \ end {array} [/ latex] |
| Складываем десятки: [латекс] 1 + 7 + 8 = 16 [/ латекс] Напишите [латекс] 6 [/ латекс] в разряде десятков и отнесите [латекс] 1 [/ латекс] сотню к разряду сотен. | [латекс] \ begin {array} {c} \ hfill 1, \ stackrel {1} {6} \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ text {______}} {+ 479} \\ \ hfill 62 \ end {array} [/ latex] |
| Складываем сотни: [латекс] 1 + 6 + 4 = 11 [/ латекс] Напишите [латекс] 1 [/ латекс] в разряде сотен и перенесите [латекс] 1 [/ латекс] тысячу в разряды тысяч. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {1}, \ stackrel {1} {6} \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ текст {______}} {+ 479} \\ \ hfill 162 \ end {array} [/ latex] |
| Сложите тысячи [латекс] 1 + 1 = 2 [/ латекс]. Напишите [латекс] 2 [/ латекс] в разряде тысяч суммы. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {1}, \ stackrel {1} {6} \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ текст {______}} {+ 479} \\ \ hfill 2,162 \ end {array} [/ latex] |
Посмотрите видео ниже, чтобы увидеть еще один пример того, как сложить три целых числа, выровняв разряды.
Вычитание
Сложение и вычитание — обратные операции. Сложение отменяет вычитание, а вычитание отменяет сложение.
Мы знаем [латекс] 7 — 3 = 4 [/ латекс], потому что [латекс] 4 + 3 = 7 [/ латекс]. Знание всех фактов сложения чисел поможет при вычитании. Затем мы можем проверить вычитание, добавив. В приведенных выше примерах наши вычитания можно проверить сложением.
| [латекс] 7-3 = 4 [/ латекс] | потому что | [латекс] 4 + 3 = 7 [/ латекс] |
| [латекс] 13-8 = 5 [/ латекс] | потому что | [латекс] 5 + 8 = 13 [/ латекс] |
| [латекс] 43-26 = 17 [/ латекс] | потому что | [латекс] 17 + 26 = 43 [/ латекс] |
Чтобы вычесть числа с более чем одной цифрой, обычно проще записывать числа в столбцах вертикально, как мы это делали для сложения.Выровняйте цифры по разряду, а затем вычтите каждый столбец, начиная с единиц, а затем двигаясь влево.
Упражнение
Вычтите и проверьте, добавив: [латекс] 89 — 61 [/ латекс].
Покажи ответРешение
| Напишите числа так, чтобы цифры единиц и десятков располагались вертикально. | [латекс] \ begin {array} {c} \ hfill 89 \\ \ hfill \ underset {\ text {____}} {- 61} \ end {array} [/ latex] |
| Вычтите цифры в каждом значении разряда. Вычтите единицы: [латекс] 9 — 1 = 8 [/ латекс] Вычтите десятки: [латекс] 8–6 = 2 [/ латекс] | [латекс] \ begin {array} {c} \ hfill 89 \\ \ hfill \ underset {\ text {____}} {- 61} \\ \ hfill 28 \ end {array} [/ latex] |
| Проверить с помощью дополнения. [латекс] \ begin {array} {c} \ hfill 28 \\ \ hfill \ underset {\ text {____}} {+ 61} \\ \ hfill 89 \ end {array} \ quad \ checkmark [/ latex] |
Наш ответ правильный.
Вычесть целые числа
- Напишите числа так, чтобы каждое разрядное значение было расположено вертикально.
- Вычтите цифры в каждом значении разряда. Работайте справа налево, начиная с места единиц. Если цифра вверху меньше цифры внизу, при необходимости заимствуйте.
- Продолжайте вычитать каждое разрядное значение справа налево, при необходимости заимствуя.
- Проверить добавлением.
упражнение
Вычтите: [латекс] 43 — 26 [/ латекс].
В приведенном выше примере, если мы моделируем вычитание [latex] 26 [/ latex] из [latex] 43 [/ latex], мы бы заменили [latex] 1 [/ latex] десять на [latex] 10 [/ latex]. .Когда мы делаем это без моделей, мы говорим, что заимствуем [latex] 1 [/ latex] из разряда десятков и добавляем [latex] 10 [/ latex] в разряды единиц.
Упражнение
Вычтите и проверьте, добавив: [латекс] 207 — 64 [/ латекс].
Упражнение
Вычтите и проверьте, добавив: [латекс] 2,162 — 479 [/ латекс].
Покажи ответРешение
Наш ответ правильный.
Посмотрите видео ниже, чтобы увидеть еще один пример вычитания целых чисел путем выравнивания значений разряда.
Умножение
Чтобы умножать без использования моделей, вам необходимо знать все факты однозначного умножения. Убедитесь, что вы хорошо их знаете, прежде чем переходить к этому разделу. В таблице ниже показаны факты умножения.
В каждом поле показано произведение числа в левом столбце и числа в верхнем ряду. Если вы не уверены в продукте, смоделируйте его. Важно, чтобы вы запомнили любые числовые факты, которых вы еще не знаете, чтобы вы были готовы умножать большие числа.
| [латекс] x [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 1 [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 7 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 9 [/ латекс] |
|---|---|---|---|---|---|---|---|---|---|---|
| [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] |
| [латекс] 1 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 1 [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 7 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 9 [/ латекс] |
| [латекс] 2 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 10 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 14 [/ латекс] | [латекс] 16 [/ латекс] | [латекс] 18 [/ латекс] |
| [латекс] 3 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 9 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 15 [/ латекс] | [латекс] 18 [/ латекс] | [латекс] 21 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 27 [/ латекс] |
| [латекс] 4 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 16 [/ латекс] | [латекс] 20 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 28 [/ латекс] | [латекс] 32 [/ латекс] | [латекс] 36 [/ латекс] |
| [латекс] 5 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] 10 [/ латекс] | [латекс] 15 [/ латекс] | [латекс] 20 [/ латекс] | [латекс] 25 [/ латекс] | [латекс] 30 [/ латекс] | [латекс] 35 [/ латекс] | [латекс] 40 [/ латекс] | [латекс] 45 [/ латекс] |
| [латекс] 6 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 18 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 30 [/ латекс] | [латекс] 36 [/ латекс] | [латекс] 42 [/ латекс] | [латекс] 48 [/ латекс] | [латекс] 54 [/ латекс] |
| [латекс] 7 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 7 [/ латекс] | [латекс] 14 [/ латекс] | [латекс] 21 [/ латекс] | [латекс] 28 [/ латекс] | [латекс] 35 [/ латекс] | [латекс] 42 [/ латекс] | [латекс] 49 [/ латекс] | [латекс] 56 [/ латекс] | [латекс] 63 [/ латекс] |
| [латекс] 8 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 16 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 32 [/ латекс] | [латекс] 40 [/ латекс] | [латекс] 48 [/ латекс] | [латекс] 56 [/ латекс] | [латекс] 64 [/ латекс] | [латекс] 72 [/ латекс] |
| [латекс] 9 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 9 [/ латекс] | [латекс] 18 [/ латекс] | [латекс] 27 [/ латекс] | [латекс] 36 [/ латекс] | [латекс] 45 [/ латекс] | [латекс] 54 [/ латекс] | [латекс] 63 [/ латекс] | [латекс] 72 [/ латекс] | [латекс] 81 [/ латекс] |
Мы знаем, что изменение порядка сложения не меняет суммы.Мы видели, что [латекс] 8 + 9 = 17 [/ латекс] то же самое, что [латекс] 9 + 8 = 17 [/ латекс].
Верно ли это и для умножения? Давайте посмотрим на несколько пар факторов.
[латекс] 4 \ cdot 7 = 28 \ quad 7 \ cdot 4 = 28 [/ латекс]
[латекс] 9 \ cdot 7 = 63 \ quad 7 \ cdot 9 = 63 [/ латекс]
[латекс] 8 \ cdot 9 = 72 \ quad 9 \ cdot 8 = 72 [/ латекс]
При обратном порядке факторов продукт не изменяется. Это называется коммутативным свойством умножения.
Коммутативное свойство умножения
Изменение порядка факторов не меняет их произведение.
[латекс] a \ cdot b = b \ cdot a [/ латекс]
пример
Умножить:
[латекс] 8 \ cdot 7 [/ латекс]
[латекс] 7 \ cdot 8 [/ латекс]
Решение:
| 1. | [латекс] 8 \ cdot 7 [/ латекс] |
| Умножить. | [латекс] 56 [/ латекс] |
| 2. | [латекс] 7 \ cdot 8 [/ латекс] |
| Умножить. | [латекс] 56 [/ латекс] |
Изменение порядка факторов не приводит к изменению продукта.
Чтобы умножать числа, состоящие более чем из одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения и вычитания.
[латекс] \ begin {array} {c} \ hfill 27 \\ \ hfill \ underset {\ text {___}} {\ times 3} \ end {array} [/ latex]
Начнем с умножения [латекс] 3 [/ латекс] на [латекс] 7 [/ латекс].
[латекс] 3 \ раз 7 = 21 [/ латекс]
Мы пишем [латекс] 1 [/ латекс] на единицах товара. Переносим [latex] 2 [/ latex] десятки, написав [latex] 2 [/ latex] над разрядами десятков.
Затем мы умножаем [latex] 3 [/ latex] на [latex] 2 [/ latex] и добавляем [latex] 2 [/ latex] над разрядами десятков к изделию. Итак, [латекс] 3 \ times 2 = 6 [/ латекс], и [латекс] 6 + 2 = 8 [/ латекс]. Напишите [латекс] 8 [/ латекс] в разряде десятков продукта.
Изделие [латекс] 81 [/ латекс].
Когда мы умножаем два числа на разное количество цифр, обычно проще написать меньшее число внизу. Можно было бы написать и по-другому, но с этим проще работать.
пример
Умножение: [латекс] 15 \ cdot 4 [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы цифры [латекс] 5 [/ латекс] и [латекс] 4 [/ латекс] выстроились вертикально. | [латекс] \ begin {array} {c} \ hfill 15 \\ \ hfill \ underset {\ text {_____}} {\ times 4} \ end {array} [/ latex] |
| Умножьте [латекс] 4 [/ латекс] на цифру в разряде единиц [латекс] 15 [/ латекс]. [латекс] 4 \ cdot 5 = 20 [/ латекс]. | |
| Напишите [латекс] 0 [/ латекс] на единицах изделия и несите [латекс] 2 [/ латекс] десятки. | [латекс] \ begin {массив} {c} \ hfill \ stackrel {2} {1} 5 \\ \ hfill \ underset {\ text {_____}} {\ times 4} \\ \ hfill 0 \ end {массив } [/ latex] |
| Умножьте [латекс] 4 [/ латекс] на цифру в разряде десятков [латекс] 15 [/ латекс]. [латекс] 4 \ cdot 1 = 4 [/ латекс]. Добавьте [латекс] 2 [/ латекс] десятки, которые мы несли. [латекс] 4 + 2 = 6 [/ латекс]. | |
| Напишите [латекс] 6 [/ латекс] в разряде десятков продукта. | [латекс] \ begin {array} {c} \ hfill \ stackrel {2} {1} 5 \\ \ hfill \ underset {\ text {_____}} {\ times 4} \\ \ hfill 60 \ end {массив } [/ latex] |
пример
Умножение: [латекс] 286 \ cdot 5 [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы цифры [латекс] 5 [/ латекс] и [латекс] 6 [/ латекс] выстроились вертикально. | [латекс] \ begin {array} {c} \ hfill 286 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \ end {array} [/ latex] |
| Умножьте [латекс] 5 [/ латекс] на цифру в разряде единиц [латекс] 286 [/ латекс]. [латекс] 5 \ cdot 6 = 30 [/ латекс] | |
| Напишите [латекс] 0 [/ латекс] на единицах изделия и перенесите [латекс] 3 [/ латекс] на разряд десятков. Умножьте [латекс] 5 [/ латекс] на цифру в десятки место [латекс] 286 [/ латекс]. [латекс] 5 \ cdot 8 = 40 [/ латекс] | [латекс] \ begin {массив} {} \\ \ hfill 2 \ stackrel {3} {8} 6 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \\ \ hfill 0 \ end {array} [/ latex] |
| Добавьте [latex] 3 [/ latex] десятки, которые мы принесли, чтобы получить [latex] 40 + 3 = 43 [/ latex]. Напишите [латекс] 3 [/ латекс] в разряде десятков продукта и отнесите [латекс] 4 [/ латекс] к разряду сотен. | [латекс] \ begin {array} {c} \ hfill \ stackrel {4} {2} \ stackrel {3} {8} 6 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \ \ \ hfill 30 \ end {array} [/ latex] |
| Умножьте [латекс] 5 [/ латекс] на цифру в разряде сотен [латекс] 286 [/ латекс]. [латекс] 5 \ cdot 2 = 10 [/ латекс]. Добавьте [latex] 4 [/ latex] сотни, которые мы принесли, чтобы получить [latex] 10 + 4 = 14 [/ latex]. Напишите [латекс] 4 [/ латекс] в разряде сотен продукта и [латекс] 1 [/ латекс] в разряде тысяч. | [латекс] \ begin {array} {c} \ hfill \ stackrel {4} {2} \ stackrel {3} {8} 6 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \ \ \ hfill 1,430 \ end {array} [/ latex] |
Когда мы умножаем на число с двумя или более цифрами, мы умножаем на каждую из цифр отдельно, работая справа налево. Каждое отдельное произведение цифр называется частичным произведением.Когда мы пишем частичные продукты, мы должны убедиться, что выровнены значения позиций.
Умножение целых чисел
- Напишите числа так, чтобы каждое разрядное значение было расположено вертикально.
- Умножьте цифры в каждом значении разряда.
- Работайте справа налево, начиная с единиц в нижнем ряду.
- Умножьте нижнее число на цифру единиц в верхнем числе, затем на цифру десятков и так далее.
- Если продукт в разряде больше, чем [латекс] 9 [/ латекс], перейти к следующему разряду.
- Запишите частичные продукты, выровняв цифры в позиционных значениях с числами, указанными выше.
- Повторите эти действия для разряда десятков в нижнем числе, разряда сотен и так далее.
- Вставляйте ноль в качестве заполнителя с каждым дополнительным частичным продуктом.
- Работайте справа налево, начиная с единиц в нижнем ряду.
- Добавьте частичные продукты.
пример
Умножение: [латекс] 62 \ влево (87 \ вправо) [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы каждое место было расположено вертикально. | |
| Начните с умножения 7 на 62. Умножьте 7 на цифру 62 в разряде единиц. [латекс] 7 \ cdot 2 = 14 [/ латекс]. Напишите 4 в разряде единиц продукта и перенесите 1 в разряды десятков. | |
| Умножьте 7 на цифру в разряде десятков 62. [латекс] 7 \ cdot 6 = 42 [/ латекс]. Добавьте 1 десятку, которую мы несли. [латекс] 42 + 1 = 43 [/ латекс] латекс]. Запишите 3 в разряде десятков произведения и 4 в разрядах сотен. | |
| Первым частичным продуктом является [латекс] 434 [/ латекс]. | |
| Теперь напишите [latex] 0 [/ latex] под [latex] 4 [/ latex] на месте единиц следующего частичного продукта в качестве заполнителя, так как теперь мы умножаем цифру на разряды десятков [latex ] 87 [/ латекс] [латекс] 62 [/ латекс]. Умножьте [латекс] 8 [/ latex] на цифру в разряде единиц [latex] 62 [/ latex] [латекс] 8 \ cdot 2 = 16 [/ латекс]. Напишите [латекс] 6 [/ латекс] на следующем месте продукта, то есть на разряде десятков.Отнесите [латекс] 1 [/ латекс] к разряду десятков. | |
| Умножьте [latex] 8 [/ latex] на [latex] 6 [/ latex], цифру в разряде десятков [latex] 62 [/ latex], затем добавьте [latex] 1 [/ latex] десять. повезли получить [латекс] 49 [/ латекс]. Напишите [латекс] 9 [/ латекс] в разряде сотен продукта и [латекс] 4 [/ латекс] в разряде тысяч. | |
| Второй частичный продукт — [латекс] 4960 [/ латекс]. Добавьте частичные продукты. |
Продукт [латекс] 5,394 [/ латекс].
Если имеется три или более факторов, мы умножаем первые два, а затем умножаем их произведение на следующий коэффициент. Например:
| умножить | [латекс] 8 \ cdot 3 \ cdot 2 [/ латекс] |
| первое умножение [латекс] 8 \ cdot 3 [/ латекс] | [латекс] 24 \ cdot 2 [/ латекс] |
| затем умножить [латекс] 24 \ cdot 2 [/ латекс] | [латекс] 48 [/ латекс] |
В видео ниже мы суммируем концепции, представленные на этой странице, включая свойство умножения нуля, свойство идентичности умножения и свойство коммутативности умножения.м
Дивизион
Мы сказали, что сложение и вычитание — обратные операции, потому что одно отменяет другое. Точно так же деление — это операция, обратная умножению. Мы знаем [латекс] 12 \ div 4 = 3 [/ latex], потому что [латекс] 3 \ cdot 4 = 12 [/ latex]. При делении очень важно знать все факты о числах умножения.
Мы проверяем наш ответ на деление, умножая частное на делитель, чтобы определить, равно ли оно дивиденду.Мы знаем, что [latex] 24 \ div 8 = 3 [/ latex] правильно, потому что [latex] 3 \ cdot 8 = 24 [/ latex].
пример
Разделить. Затем проверьте умножением.
- [латекс] 42 \ div 6 [/ латекс]
- [латекс] \ frac {72} {9} [/ латекс]
- [латекс] 7 \ overline {) 63} [/ латекс]
Решение:
| 1. | |
| [латекс] 42 \ div 6 [/ латекс] | |
| Разделите [латекс] 42 [/ латекс] на [латекс] 6 [/ латекс]. | [латекс] 7 [/ латекс] |
| Проверить умножением. [латекс] 7 \ cdot 6 [/ латекс] | |
| [латекс] 42 \ квадратик \ галочка [/ латекс] |
| 2. | |
| [латекс] \ frac {72} {9} [/ латекс] | |
| Разделите [латекс] 72 [/ латекс] на [латекс] 9 [/ латекс]. | [латекс] 8 [/ латекс] |
| Проверить умножением. [латекс] 8 \ cdot 9 [/ латекс] | |
| [латекс] 72 \ квадратик \ галочка [/ латекс] |
| 3. | |
| [латекс] 7 \ overline {) 63} [/ латекс] | |
| Разделите [латекс] 63 [/ латекс] на [латекс] 7 [/ латекс]. | [латекс] 9 [/ латекс] |
| Проверить умножением. [латекс] 9 \ cdot 7 [/ латекс] | |
| [латекс] 63 \ квадратик \ галочка [/ латекс] |
Каким будет частное при делении числа на само себя?
[латекс] \ frac {15} {15} = 1 \ text {потому что} 1 \ cdot 15 = 15 [/ латекс]
Разделение любого числа [латекс] \ text {(кроме 0)} [/ latex] на само по себе дает частное [латекс] 1 [/ latex].Кроме того, любое число, деленное на [latex] 1 [/ latex], дает частное от числа. Эти две идеи изложены в разделе «Свойства единицы».
Разделение свойств одного объекта
| Любое число (кроме 0), разделенное само по себе, равно единице. | [латекс] a \ div a = 1 [/ латекс] |
| Любое число, разделенное на единицу, является одним и тем же числом. | [латекс] а \ div 1 = а [/ латекс] |
пример
Разделить. Затем проверьте умножением:
- [латекс] 11 \ div 11 [/ латекс]
- [латекс] \ frac {19} {1} [/ латекс]
Решение:
| 1. | |
| [латекс] 11 \ div 11 [/ латекс] | |
| Число, разделенное само по себе, — [латекс] 1 [/ латекс]. | [латекс] 1 [/ латекс] |
| Проверить умножением. [латекс] 1 \ cdot 11 [/ латекс] | |
| [латекс] 11 \ квадратик \ галочка [/ латекс] |
| 2. | |
| [латекс] \ frac {19} {1} [/ латекс] | |
| Число, разделенное на [латекс] 1 [/ латекс], равно самому себе. | [латекс] 19 [/ латекс] |
| Проверить умножением. [латекс] 19 \ cdot 1 [/ латекс] | |
| [латекс] 19 \ квадратик \ галочка [/ латекс] |
Предположим, у нас есть [latex] \ text {\ $ 0} [/ latex], и мы хотим разделить его между [latex] 3 [/ latex] людьми. Сколько получит каждый человек? Каждый получит [латекс] \ текст {\ $ 0} [/ латекс]. Ноль разделенный на любое число — [латекс] 0 [/ латекс].
Теперь предположим, что мы хотим разделить [latex] \ text {\ $ 10} [/ latex] на [latex] 0 [/ latex].Это означает, что нам нужно найти число, которое мы умножим на [latex] 0 [/ latex], чтобы получить [latex] 10 [/ latex]. Этого не может произойти, потому что [латекс] 0 [/ латекс] умноженное на любое число равно [латекс] 0 [/ латекс]. Деление на ноль равно undefined .
Эти две идеи составляют свойство деления нуля.
Подразделение свойств нуля
| Нуль, деленный на любое число, будет [латекс] 0 [/ латекс]. | [латекс] 0 \ div a = 0 [/ латекс] |
| Деление числа на ноль не определено. | [латекс] a \ div 0 [/ латекс] не определено |
Другой способ объяснить, почему деление на ноль не определено, — это вспомнить, что деление на самом деле является повторным вычитанием. Сколько раз мы можем убрать [latex] 0 [/ latex] из [latex] 10? [/ Latex] Поскольку вычитание [latex] 0 [/ latex] никогда не изменит общую сумму, мы никогда не получим ответа. Таким образом, мы не можем разделить число на [латекс] 0 [/ латекс].
пример
Разделить. Проверить умножением:
- [латекс] 0 \ div 3 [/ латекс]
- [латекс] \ frac {10} {0} [/ латекс]
Решение
| 1. | |
| [латекс] 0 \ div 3 [/ латекс] | |
| Ноль, деленный на любое число, равно нулю. | [латекс] 0 [/ латекс] |
| Проверить умножением. [латекс] 0 \ cdot 3 [/ латекс] | |
| [латекс] 0 \ квадратик \ галочка [/ латекс] |
| 2. | |
| [латекс] 10/0 [/ латекс] | |
| Деление на ноль не определено. | не определено |
Когда делитель или делимое состоит более чем из одной цифры, обычно проще использовать нотацию [latex] 4 \ overline {) 12} [/ latex]. Этот процесс называется длинным делением. Давайте поработаем над процессом, разделив [латекс] 78 [/ латекс] на [латекс] 3 [/ латекс].
| Разделите первую цифру делимого, [латекс] 7 [/ латекс], на делитель, [латекс] 3 [/ латекс]. | |
| Делитель [латекс] 3 [/ латекс] может входить в [латекс] 7 [/ латекс] два раза, так как [латекс] 2 \ times 3 = 6 [/ latex].Напишите [латекс] 2 [/ latex] над [latex] 7 [/ latex] в частном. | |
| Умножьте [латекс] 2 [/ латекс] в частном на [латекс] 2 [/ латекс] и запишите произведение [латекс] 6 [/ латекс] под [латекс] 7 [/ латекс]. | |
| Вычтите это произведение из первой цифры дивиденда. Вычтите [латекс] 7 — 6 [/ латекс]. Напишите разницу, 1, под первой цифрой делимого. | |
| Опустите следующую цифру делимого.Сбиваем [латекс] 8 [/ латекс]. | |
| Разделите [латекс] 18 [/ латекс] на делитель, [латекс] 3 [/ латекс]. Делитель [латекс] 3 [/ латекс] переходит в [латекс] 18 [/ латекс] шесть раз. | |
| Напишите [латекс] 6 [/ латекс] в частном над [латекс] 8 [/ латекс]. | |
| Умножьте [латекс] 6 [/ латекс] в частном на делитель и запишите произведение [латекс] 18 [/ латекс] под делимым. Вычтите [латекс] 18 [/ латекс] из [латекс] 18 [/ латекс]. |
Мы будем повторять процесс до тех пор, пока в дивиденде не останется цифр, которые нужно уменьшить. В этой задаче больше нет цифр, которые нужно сбивать, поэтому деление закончено.
[латекс] \ text {So} 78 \ div 3 = 26 [/ латекс].
Проверьте, умножив частное на делитель, чтобы получить дивиденд. Умножьте [латекс] 26 \ на 3 [/ латекс], чтобы убедиться, что продукт равен дивиденду, [латекс] 78 [/ латекс].
[латекс] \ begin {array} {c} \ hfill \ stackrel {1} {2} 6 \\ \ hfill \ underset {\ text {___}} {\ times 3} \\ \ hfill 78 \ end {массив } [/ латекс]
Да, поэтому наш ответ правильный.[латекс] \ галочка [/ латекс]
Деление целых чисел
- Разделите первую цифру делимого на делитель. Если делитель больше, чем первая цифра делимого, разделите первые две цифры делимого на делитель и т. Д.
- Напишите частное над дивидендом.
- Умножьте частное на делитель и запишите произведение под дивидендом.
- Вычтите этот продукт из дивиденда.
- Введите следующую цифру делимого.
- Повторяйте с шага 1 до тех пор, пока в дивиденде не останется цифр, которые нужно уменьшить.
- Проверьте, умножив частное на делитель.
На видео ниже мы показываем еще один пример использования деления в столбик.
пример
Разделить [латекс] 2,596 \ div 4 [/ латекс]. Проверить умножением:
Покажи ответРешение
Это равняется дивиденду, поэтому наш ответ правильный.
пример
Разделить [латекс] 4,506 \ div 6 [/ латекс].Проверить умножением:
Покажи ответРешение
Это равняется дивиденду, поэтому наш ответ правильный.
Посмотрите это видео, чтобы увидеть еще один пример того, как использовать длинное деление для деления четырехзначного целого числа на двузначное целое число.
Пока все проблемы с разделением решаются равномерно. Например, если бы у нас было [латексное] 24 [/ латексное] печенье и мы хотели бы сделать пакеты из [латексного] 8 [/ латексного] печенья, у нас были бы [латексные] 3 [/ латексные] пакеты.Но что, если бы было печенье [latex] 28 [/ latex], и мы хотели бы сделать пакеты из [latex] 8? [/ Latex] Начнем с файлов cookie [latex] 28 [/ latex].
Попробуйте разместить файлы cookie группами по восемь штук.
Остались группы [latex] 3 [/ latex] из восьми файлов cookie и [latex] 4 [/ latex] файлов cookie. Мы вызываем оставшиеся файлы cookie [latex] 4 [/ latex] и показываем их, записывая R4 рядом с [latex] 3 [/ latex]. (R означает остаток.)
Чтобы проверить это деление, мы умножаем [latex] 3 [/ latex] на [latex] 8 [/ latex], чтобы получить [latex] 24 [/ latex], а затем складываем остаток [latex] 4 [/ latex].
[латекс] \ begin {array} {c} \ hfill 3 \\ \ hfill \ underset {\ text {___}} {\ times 8} \\ \ hfill 24 \\ \ hfill \ underset {\ text {___} } {+ 4} \\ \ hfill 28 \ end {array} [/ latex]
пример
Разделить [латекс] 1,439 \ div 4 [/ латекс]. Проверить умножением.
Покажи ответРешение
Итак, [латекс] 1,439 \ div 4 [/ latex] — это [латекс] 359 [/ latex] с остатком [латекс] 3 [/ latex]. Наш ответ правильный.
пример
Разделите, а затем проверьте умножением: [латекс] 1,461 \ div 13 [/ латекс].
Покажи ответРешение
Наш ответ правильный.
Посмотрите видео ниже, чтобы увидеть еще один пример того, как использовать длинное деление для деления целых чисел, когда есть остаток.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Что такое повторное добавление? — Определение, факты и пример
Игры с повторяющимся сложением
Умножение как повторное сложениеСвязать умножение и сложение; умножение чисел можно рассматривать как многократное прибавление числа к самому себе.
охватывает общий основной учебный план 3.OA.1Играть сейчасУчитесь с помощью полной программы обучения математике K-5
Что такое повторяющееся добавление?При повторном сложении равные группы складываются вместе. Это также известно как умножение. Если то же число повторяется, мы можем записать это в форме умножения.
Например: 2 + 2 + 2 + 2 + 2
Здесь 2 повторяется 5 раз, мы можем записать это сложение как 5 × 2.
Точно так же, чтобы решить задачу умножения путем многократного сложения, мы многократно группируем и складываем одно и то же число снова и снова, чтобы найти ответ.
Вот несколько примеров повторного сложения.
Вот еще один пример повторного сложения, используемого для умножения в задачах со словами.
Есть 5 групп цыплят. В каждой группе по 3 цыпленка. Сколько всего цыплят?
Всего 5 групп.
В каждой группе по 3 цыпленка.
Добавьте, чтобы найти общее количество цыплят. 3 + 3 + 3 + 3 + 3 = 15 | Умножьте, чтобы найти общее количество цыплят. 5 × 3 = 15 |
Всего цыплят 15.
Поскольку умножение — это повторное сложение, каждое повторное сложение может быть записано двумя способами:
Например: 6 + 6 + 6 + 6 = 24 можно записать как 4 × 6 = 24, а также как 6 × 4 = 24
6 + 6 + 6 + 6 = 24 4 × 6 = 24 | 4 + 4 + 4 + 4 + 4 + 4 = 24 6 × 4 = 24 |
Повторное сложение также полезно при изучении фактов умножения.Например, если вы еще не знаете фактов 7 × 3, вам может быть проще вычислить 7 × 3, написав 3 + 3 + 3 + 3 + 3 + 3 + 3 или 7 + 7 + 7; а затем медленно добавляю. Это также может быть полезно с большими числами, такими как 5 × 40. Удобнее писать 40 + 40 + 40 + 40 + 40, а затем складывать десятки.
Интересные факты
|