Ментальная арифметика видео уроки бесплатно с нуля

Заинтересовала ментальная математика? Но не знаете, с чего начать? Специально для знакомства — наши лаконичные видеоуроки, которые вы можете посмотреть бесплатно в любое время!

Они подойдут родителям, которые планируют начать самостоятельное обучение детей счету. Полезны будут и для детей, дошкольников и младших школьников. А также всех-всех, кто хочет понять, как научиться считать быстро, с нуля, решать примеры и не бояться математики.

Посмотрите все уроки — это не займет много времени!

Подарите вашим детям увлекательный мир овладения счетом и решения задач!

Урок 1. Знакомимся с Абакусом

Узнайте, что такое ментальная арифметика, счеты Абакус, откуда они пошли и из каких элементов состоят.

Урок 2. Начинаем считать

Посмотрите это видео и через 1 минуту вы узнаете, как выполняется счет на Абакусе, как выставлять единицы, десятки и сотни.

Урок 3. Какими пальцами набирать

Это короткое видео расскажет, какими пальцами удобно работать на счетах и набирать цифры, напомнит принцип подсчета.

Урок 4. Учимся вычитать

Узнайте, как быстро решать примеры на вычитание, как набирать их на счетах и получать верный результат.

Урок 5.

Веселая ментальная карта

Сейчас вы увидите, что такое ментальная карта и как она используется в домашних условиях, при занятиях с ребенком.

Урок 6. Легко складываем и вычитаем большие числа

Этот видео-урок научит вашего ребенка работать с большими числами, уверенно складывать и вычитать, быстро решать разные примеры.

Урок 7. На чем потренироваться

Узнайте, какое приложение вы можете установить на планшет или телефон для тренировок в решении задач, как им пользоваться.

Урок 8. Быстрое руководство по Know Abacus

Познакомьтесь с приложением для начинающих и продолжающих освоение ментальной математики!

Урок 9. Легкое понимание состава числа 10

Веселое, игровое мини-видео научит вашего ребенка составу чисел, визуально закрепит в его памяти составляющие Десятки.

Урок 10. Уровни ментальной арифметики

Узнайте, что это такое и какая сложность уровней, какие примеры и задания туда входят.

Ментальная математика в домашних условиях

Ментальная Арифметика в Домашних Условиях (Методы и Занятия)

Как научить ментальной арифметике дома?

Вы решились научиться считать на счетах абакуса или соробана? Как научить ребенка ментальной арифметики дома?

Ментальная арифметика обучение дома?  Как именно считать и с чего начинать? Чтобы ответить на эти вопросы Вам просто необходимо прочитать азы ментальной арифметики.

Занятия в домашних условиях для ребенка будет сразу не так просты. Нужно будет набраться терпению и огромного усердия

Занятия не должны быть в хаотичном режиме! Постарайтесь решить в какое время будет проводиться систематические уроки. Теперь давайте ответим на вопросы:

Что же такое Ментальная Арифметика?

Это уникальная методика интеллектуального развития от 4 до 14 лет, в основе которой лежит многовековая система арифметических действий с помощью счета- абакус, соробан. На сегодняшний день действует около 6000  центров по более чем в 54 странах мира, основные из них: Китай, Казахстан, Япония, Турция, Малазия …

Открывать в человеке гения необходимо в детском возрасте, когда ум ребенка гибок и способен к трансформированию задатков в способности, те, в свою очередь, в таланты, и только тогда Вы получите гениального, успешного в любых делах и начинаниях ребенка!

Давайте составим  план урока:

1. Что такое абакус, соробан?
2. Расположение чисел
3. Как складывать?
4. Дополнительная литература

Что такое абакус?

Это внешний вид Абакуса.

Внешний вид Абакуса

Чем-то напоминает известные многим советские счеты с костяшками. Принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Абакус и счеты

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.

Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.

Теперь о том, как же располагаются числовые линейки.

расположение чисел на абакусе

Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?

Давайте посмотрим на примере.

Десятичные линейки рисовать не стала. То есть, крайняя правая линейка на  рисунке – это единицы.

Так будет выглядеть на абакусе число 3.

число-3-на-абакусе

Поднимаем к разделительной планке три костяшки на линейке единиц.

Попробуем взять двойное число, например, 15.

На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.

Получилось число 15!

Покажем теперь число для примера -53-на-абакусе На линейке десятков опускаем к разделителю верхнюю костяшку, которая означает 50. А на линейке единиц поднимаем с верху 3 костяшки. Получилось число 53!

А давайте чего-нибудь посущественнее наберем. Например, 6482!

На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?

Как складывать на абакусе?

А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14.

Откладываем на абакусе 33.

К трем десяткам прибавим еще один. Получим 4 десятка или 40.

прибавление одного десятка на абакусе

Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц.

В результате получилось 47! Результат мы получили верный!

Развить навыки быстрого счёта вы можете на бесплатном онлайн тренажёре здесь

Ментальная Арифметика научиться дома – Дополнительная литература

Вот по такой схеме на абакусе и считают. Показ был самого простого.  А ведь можно еще и вычитать, и умножать, и делить, и в степень возводить. И работать с огромными числами. Хотите знать больше? Пожалуйста!

Обратите внимание на книгу «Ментальная арифметика. Школа волшебников»  Она ориентирована на обучение детишек.

Рекомендуем вам приобрести:

Учебный материал для занятий дома

или

Методический комплект для родителей и педагогов 

Ментальная арифметика домашнее задание

Самая главная составляющая часть в обучении, не игнорируйте систематические каждодневные домашние задания, обязательно давайте их детям! Желательно заниматься дома не только Ментальной Арифметикой, но еще и Скорочтением.

У нас Вы можете найти упражнения для скорочтения. Более подробнее о скорочтении, Вы можете узнать  у нас в темах.

Ментальная математика в домашних условиях скачать бесплатно

Желаем Вам успехов в познании Ментальной Арифметики.

Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения

Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения

Ментальная арифметика – популярная методика гармоничного и равного развития обоих полушарий мозга. Методика одинаково подходит для детей и взрослых и заключается в обучении быстрому устному счету с применением специального инструмента, который называют абакусом или соробаном.

 

Научить детей ментальной арифметике в домашних условиях помогут видео уроки на сайте ВСЕ КУРСЫ ОНЛАЙН.

 

Строение и функции абакуса (соробана) 

 

Абакус – древние китайские счеты. Состоит из рамки, перекладины, спиц и косточек. Перекладина делит косточки горизонтально на 2 части. Нижние получили название «земных» (смотрят всегда вниз), верхние – «небесных» (смотрят вверх).  Косточки играют роль единиц, десятков и сотен. Сначала ученики осваивают простые арифметические действия (сложение и вычитание), затем сложные (умножение и деление). Следующий этап – счет без использования инструмента, в уме. Ученик двигает пальцами, представляя абакус, и решает примеры с многозначными числами. Инструмент можно запросто сделать самостоятельно, переконструировав обычные советские счеты. 

 

Основные принципы

 

• Считать правильно двумя руками, используя указательные и большие пальцы. 
• Поднимают кости всегда большим пальцем, опускают и двигают «небесные» косточки указательным. 
• Абакус нужно придерживать левой рукой.
• В правой руке всегда находится ручка для заметок и записей, обхваченная мизинцем, безымянным и средним пальцами.
• Сброс косточек в исходное положение делают, обхватив перекладину двумя рабочими пальцами и двигаясь справа налево.
   

 

 

Набор чисел

 

Крайний правый столбец предназначен для набора единиц, второй для десятков, третий для сотен, следующие для тысяч и так далее. Исходное положение означает ноль.  Поднятые нижние бусины – единицы от 1 до 4, десятки от 10 до 40 и аналогичные сотни, тысячи в зависимости от столбца. Верхние опущенные бусины обозначают числа, кратные пяти: 5, 50, 500, 5000 и т.д. по мере удаления столбцов. Цифра 7 – это 5+2. Значит нужно опустить небесную косточку и поднять две земных. Все остальные числа набирают по аналогичному принципу. Для тренировки хорошо использовать онлайн-тренажеры в Google или установить специальное приложение.

 

Правила

 

Правила имеют условные названия, которые образно иллюстрируют действия. Выполняются всегда в строгой последовательности.

1. «Просто» — поднятие нужного количества земных косточек, опускание небесной или то и другое одновременно.
2. «Брат» — когда первый пункт не работает и сумма выдает 5.
3. «Друг» — два числа, дающие 10.
4. «Друг + Брат» — совмещает два предыдущих правила, выполняется двумя руками.

 

Сложение (простое и с переходом на 10)

 

Самое простое действие, с которого начинают обучение.  Начинать первое знакомство можно в детском саду, начальной школе. Сначала следует научиться считать до 10. Затем решать примеры до 3. Следующий этап — сложение всех чисел без перехода на десятки. В качестве закрепляющих заданий эффективно использовать карточки с изображениями разных комбинаций на счетах. Например, найти правильный ответ на заданный пример.  При сложении за пределами десятка суммы необходимо разложить на простые составляющие. Состав десяти может иметь несколько комбинаций (1+9, 2+8, 3+7, 4+6, 5+5). 

 

Вычитание

 

Разницу считают подобно сумме, по правилам «просто», «брат», «друг», «друг+брат». Существует масса онлайн тренажеров и конструкторов заданий для закрепления арифметических навыков. Современные ученики обожают работать на компьютере, поэтому заставлять тренироваться даже не придется. Будущие математики сами с удовольствием будут выполнять нужные упражнения.

 

 

Умножение

 

Умножение (многократное сложение) можно выполнять несколькими различными методами. Самый простой и безошибочный был предложен Японским Комитетом по абакусу. Принцип напоминает умножение в столбик на бумаге, так же последовательно. Чтобы работать с двузначными числами (45*56), нужно учесть: ответ получится четырехзначным, и нужно будет уметь его прочитать. 

 

Деление

 

Деление производят по принципу многократного вычитания. Конечно, без выученной «на зубок» таблицы умножения приступать к действию не имеет смысла. Самый удобный метод разработан Такаши Койима в книге об использовании и теории японского абакуса. Главный плюс — использование привычной школьной терминологии: делимое, делитель, частное. Делимое находится правее центра, делитель левее, разделенные тремя-четырьмя свободными линейками.

 

 

Положительное влияние счета на абакусе

 

В Азии предмет входит в обязательную программу почти во всех учебных заведениях. С помощью простого девайса дети учатся умножать и делить многозначные числа без калькулятора. Существуют и другие сопутствующие бонусы.

• Развивается зрительная и слуховая память, повышается внимание и сосредоточенность.
• Активируется интуиция, сообразительность, смекалка.
• Возникает нестандартное мышление, самостоятельность, уверенность в принятии решений.
• Усиливаются творческие способности и предрасположенность к изучению иностранных языков.

 

Тренировочные упражнения

 

Благодаря японской методике родители имеют прекрасную возможность одновременно учить детишек счету и прокачивать ум и интеллект в целом. Европейцы подхватили идею и дополнили интерактивными технологиями: компьютерным тренажером (анзаном), флеш-картами и другими программами. Важно заниматься каждый день  в течение двух-трех лет , начиная с четырех-шестилетнего возраста.

В результате регулярных занятий повышается успеваемость в школе за счет улучшения памяти и повышения концентрации внимания. Ребенок легче запоминает новые слова, исторические даты и факты, теоремы и формулы. Одновременно развивается воображение и творческое мышление, способность нестандартно подходить к решению задач. 

 

Ментальная арифметика | Уроки счета на абакусе

Курс «Ментальная арифметика» предназначен для дошкольников и школьников. Возрастной диапазон – от 5 лет до 16 лет. Ментальная арифметика – это методика, активно способствующая интеллектуальному развитию детей, повышающая умственные способности и творческий потенциал за счёт устных арифметических вычислений и развития двухполушарного мышления.

Курсы ментальной арифметики развивают:

• Воображение.
• Творческие способности.
• Быстроту реакции.
• Нестандартный подход к любой ситуации.
• Креативность.
• Лидерские качества.
• Усидчивость и внимательность.
• Память.
• Интерес к изучению других дисциплин.
• Быстрый счёт в уме.

Навыки, развиваемые курсами ментальной арифметики в «Академии развития интеллекта AMAKids» – это отличный фундамент для дальнейшего развития вашего ребёнка! Изучение любой другой информации становится значительно более простым!

Зачем нужна ментальная математика для детей?

• Улучшается скорость реакции и работа памяти.
• Тренируется головной мозг.
• Быстро воспринимается новая информация.
• Возрастает уровень безопасности ребёнка в жизни.
• Повышается успеваемость по базовым школьным предметам.
• Результат со стопроцентной гарантией.

Ментальная арифметика – это методика, применяемая в нашей стране не так давно, но уже широко востребованная. Много людей желают узнать – а где и как она появилась? Возникновение ментальной математики принято связывать с изобретением древними китайцами счётами абак – это произошло более пяти тысячелетий назад. Затем эти счёты усовершенствовали японцы. Сегодня они носят имя «абакус», и мы используем их на занятиях в нашей школе ментальной арифметики «Академии развития интеллекта AMAKids».

Ментальная арифметика для детей – это система, не имеющая аналогов. Программа разделена на несколько фрагментов и выстроена таким образом, чтобы результат был максимальным:

• первое занятие начинается с того, что дети знакомятся как с физическими счётами, так с ментальными. На всех занятиях изучается сразу два типа вычислений;
• всего четырех недель регулярных занятий ментальной арифметикой хватит для того, чтобы ребёнок решал в уме примеры значительно быстрее любого взрослого человека;
• после двух месяцев занятий дети решают в уме примеры, декламируя при этом стихотворение вслух;
• через год ребёнок освоит все правила сложения и вычитания при счёте в уме;
• когда ребёнок закончит курс (это займет 2-2,5 года), он будет легко пользоваться всеми правилами умножения и деления при ментальном счёте.  

Курсы ментальной арифметики в «Академии развития интеллекта AMAKids» – это:

• Высококвалифицированные тренеры, которые прошли строгий конкурсный отбор и досконально знают все нюансы методики.
• Интересные и увлекательные занятия, которые проходят в игровой форме.
• Небольшие группы до 10 человек, что обеспечивает индивидуальный подход к каждому ребёнку.
• Красочные учебники.
• А также наша уникальная платформа, с помощью которой результат достигается в 2-3 раза быстрее.

Если вашему ребёнку исполнилось 5 лет, он умеет считать от 0 до 10 в прямом и обратном порядке, а также умеет соотносить цифру с количеством, то его уже можно записать на пробное занятие по ментальной арифметике в «Академии развития интеллекта AMAKids»! Первое же упражнение будет для вашего ребёнка шагом в мир удивительных возможностей! Наш сайт содержит максимально полную информацию о них!

Уроки ментальной арифметики проходят в игровой форме с тренером в центре AMAKids один раз в неделю. Длительность занятий зависит от возраста ребенка:

• Дети дошкольного возраста (5-6 лет) – 2 урока по 35 минут с веселой игровой переменкой!
• Дети школьного возраста – 2 урока по 45 минут.

Мы уверены, что родители заинтересованы в раскрытии потенциала своего ребёнка! Сделайте первый шаг к успешному будущему своего ребёнка, а «Академия развития интеллекта AMAKids» вам в этом поможет!

Ментальная арифметика: как и зачем решать 10 примеров в секунду

Ментальная арифметика: как и зачем решать 10 примеров в секунду

Умение быстро считать в уме развивает внимание, скорость обработки информации и даже творческое мышление. Дает ли этот навык ребёнку конкурентное преимущество в будущем? Станет ли шагом к успешной жизни или просто отнимет драгоценное время? Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике, рассказывает, в чем польза такого обучения.

Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике

Ментальная арифметика — программа развития умственных и творческих способностей, основанная на системе устного счета. Освоив ее, ребенок сможет решать арифметические задачи в уме всего за несколько секунд. Методика рекомендована для детей от 4 до 12 лет. Однако современные развивающие центры готовы обучать и более взрослых людей, как правило, с одной оговоркой — чем позднее начнешь, тем больше усилий потребуется.

Ментальная арифметика зародилась в Японии в ХVI веке. На начальных этапах обучения используются специальные счеты — абак или соробан. Счеты состоят из рамки, разделительной полосы, вертикальных спиц, верхних («небесных») и нижних («земных») косточек. Одна «небесная» косточка равна пяти «земным». Количество спиц варьируется от 13 до 31. При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма. Через некоторое время ребенок совершает вычисления на воображаемом абаке, а задачи решаются с помощью образов.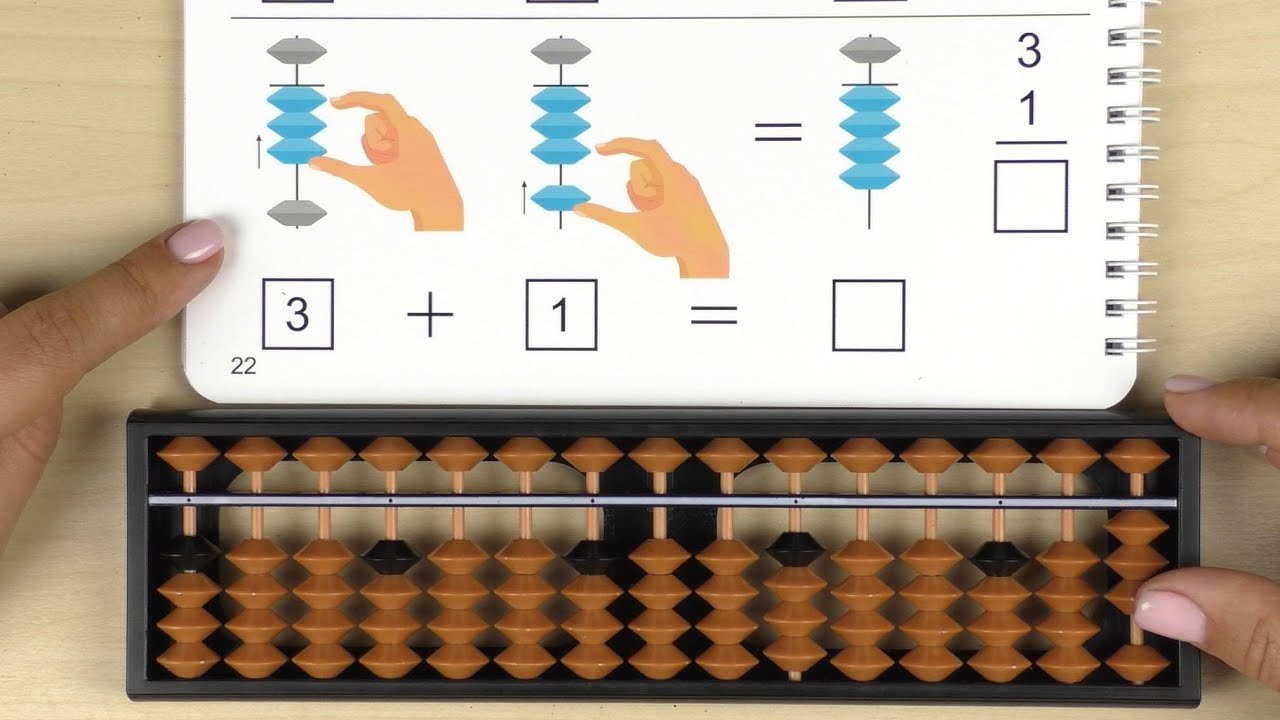

Формула интеллекта: логика плюс интуиция

Известно, что левое полушарие отвечает за логику, рациональность и анализ, а правое — за образность, целостность, интуицию, фантазию и воображение. Современная система образования уделяет больше внимания точным наукам. Время на танцы, рисование или занятие музыкой выделяется по остаточному принципу. Но даже если родителям удается найти золотую середину, возникает вопрос — как развить взаимосвязь работы обоих полушарий, чтобы максимально раскрыть потенциал ребенка?

Программа обучения метальной арифметики направлена на формирование устойчивых нейронных связей левого и правого полушарий. По мнению педагогов, именно этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.

Плюсы и минусы ментальной математики

Самый очевидный результат обучения — способность совершать арифметические действия с шестизначными числами за несколько секунд. Но сложно представить, зачем сегодня ребенку может понадобиться этот навык. Как утверждают педагоги по ментальной математике, быстрый счет в уме — это побочный эффект, а не цель. Основная задача обучения — добиться эффекта синергии от синхронной работы обоих полушарий мозга, который превосходит эффект от работы каждого полушария по-отдельности. Тогда вместе с математическими способностями в ребенке будут развиваться:

• усидчивость
• концентрация внимания
• фотографическая память
• воображение
• творческое мышление
• скорость обработки информации

Кроме возрастных ограничений, никаких противопоказаний к занятиям нет. Однако отзывы родителей говорят о том, что не все ученики наблюдают улучшение памяти и концентрации внимания, а у некоторых детей возникают проблемы с решением элементарных задач на логику.

Здесь стоит вспомнить простую истину о том, что каждый ребенок уникален. Менар — это одна из методик развития интеллекта, которая помогает выявить и раскрыть уникальные способности ребенка. Ребенок учится быстро усваивать новую информацию, формулировать мысли и делать выводы. Тем не менее, не стоит пренебрегать традиционными играми — шахматами, головоломками, ребусами. Поэтому, наблюдайте, пробуйте, анализируйте и выбирайте то, что подходит именно вам.

Как проходит обучение

Обучение состоит из 10 уровней, каждый из которых занимает до четырех месяцев. Полный курс длится 2−3 года. Занятия идут по два академических часа один раз в неделю, кроме этого дети должны потратить 15 минут на выполнение домашних заданий. Как правило, у каждого развивающего центра есть онлайн-платформы, которые позволяют более эффективно работать самостоятельно.

Самый главный инструмент — это абак. Также в процесс обучения включают настольные, подвижные игры, просмотр мультфильмов и физминутки. На первом этапе детей учат складывать и вычитать числа на абаке. В этот период тренируется мелкая моторика, пространственное и логическое мышление. Далее переходят на ментальную карту — картину с изображением абака. И на следующем этапе дети производят арифметические действия с помощью визуализации процесса. Таким образом, уже через год ребенок может делать вычисления в уме.

Как выбрать школу ментальной арифметики?

Результат обучения будет зависеть от трех участников процесса — ребенка, учителя и родителей. Но самое главное — правильно выбрать образовательный центр, где будут преподавать менар. Вот несколько простых правил:

• Запишитесь на пробное занятие. Оцените, насколько комфортно ребенку в новых условиях. Не упустите возможность пообщаться с другими родителями.
• Познакомьтесь с педагогом. Спросите, как готовят преподавателей ментальной арифметики? Контролирует ли головной офис методику преподавания, уровень знаний педагогов, проходят ли преподаватели аттестацию на профпригодность?
• Обратите внимание на количество учеников в группе. Только в небольших группах преподаватель может уделить необходимое время каждому ученику. Поэтому в младших группах занимаются 5−7 человек, в старших — 8−10.
• Сделайте анализ рынка. Стоимость обучения в пределах одного региона не может сильно отличаться. Слишком низкая цена может быть показателем недобросовестного подхода к подготовке персонала и разработке методики. Слишком высокая цена может быть связана с издержками, дорогой арендой или рекламой.

Самое главное — чтобы ребенку нравились. Ему должно быть интересно считать, несмотря на то что считать — может быть довольно скучным занятием. Если ребенку нравится, значит, преподаватель смог заинтересовать его. Кроме этого, чтобы оценить преподавателя, обычно спрашивают: через сколько появятся первые результаты? На какие способности влияет обучение? Что делают, чтобы ускорить обучение? Хороший педагог ответит на все вопросы.

Читайте также:

Ну и почерк! Почему детям всё-таки важно учиться красиво писать?

11 полезных советов для родителей от педагога по английскому языку

Зачем детям учить математику?

Фото: GRSI, Ann in the uk, NadyaEugene/Shutterstock.com

Есть ли детям польза от ментальной арифметики

Ментальная арифметика — это метод счета в уме, навеянный старинными счетными досками-абаками. На сайтах учебных центров пишут, что абак появился в Древнем Китае, но упорно называют его на латинский манер абакусом. На самом деле этим приспособлением пользовались по всему свету, его точное происхождение неизвестно. Но стереотип гласит, что азиаты сильнее всех в математике, так что почему бы не отдать лавры изобретателей китайцам. А с латинским суффиксом, как известно, любое слово звучит весомее.

Программа обучения ментальной арифметике обычно занимает два-три года и делится на несколько этапов. Сначала дети учатся считать на настоящем абаке. Далее вместо доски им дают ее изображение: глядя на рисунок во время вычислений, нужно представлять, как передвигаются костяшки. В конце концов у ребят забирают и картинку — на этой стадии они видят абак в уме и могут производить с ним те же операции, что и с настоящим. Выглядит это поразительно и немного пугающе: двигая в воздухе невидимые костяшки, крохи, многие из которых даже еще не ходят в школу, перелопачивают длинные ряды трехзначных чисел и за какие-то секунды дают правильный ответ.

Обучение ментальной арифметике начинается с настоящего абака

© China Photos/Getty Images

Что обещают родителям

Еще удивительнее, что, по заверениям учебных центров, быстрый счет в уме — всего лишь побочный эффект. Родителей убеждают, что ментальная арифметика развивает логическое мышление, аналитические навыки, увеличивает объем памяти, дети учатся визуализировать задачи, поэтому глубже их понимают, мыслят креативно, становятся более внимательными, лучше концентрируются, систематизируют знания, адаптируются к новым условиям и благодаря всему этому успешнее учатся в школе, причем пятерки они получают и по математике, и по всем остальным предметам.

В доказательство этих утверждений на сайте одной компании, которая продает по франшизе методику обучения ментальной арифметике, приведены результаты исследования некоей К. Васуки из Мадрасского университета в Индии. В нем участвовали две группы детей 8–12 лет по 160 человек в каждой. В первую отобрали ребят из классов ментальной арифметики первого уровня, во вторую — обычных мальчиков и девочек. За год дети пять раз прошли тесты на концентрацию, рабочую и ассоциативную память, креативность и еще несколько показателей. Вначале средние показатели в обеих группах были почти одинаковые, но под конец «ментальные счетоводы» заметно вырвались вперед.

Соревнования по ментальной арифметике в Индии в 2005 году

© AP Photo/Gautam Singh

Исследование Васуки выглядит так, будто выполнено по научным стандартам. Но кое-что в нем настораживает. Во-первых, чем дальше, тем труднее давались задания детям в контрольной группе. Почему за год они сдали почти по всем показателям, неясно. Во-вторых, ребят c IQ ниже среднего и из бедных и малообразованных семей почему-то не допустили до участия. В-третьих, при анализе результатов, судя по всему, не учтены другие факторы, например мотивация. Вдруг на курсы ментальной арифметики ходят те, кто в целом сильнее заинтересован в учебе? В-четвертых, статью об исследовании Васуки не удалось найти в рецензируемых научных журналах, то есть другие ученые его не проверяли. Наконец, к исследованию причастна компания, которая владеет правами на методику обучения, а это всегда подозрительно.

Помогает ли менар с математикой

Другие исследования дали не столь однозначные результаты. В США эффективность ментальной арифметики в течение года проверяли на учениках первых и вторых классов школ. Первоклашки вообще толком не справились с обучением, у ребят постарше дела шли чуть лучше, но этого все равно было недостаточно, чтобы заметно улучшить когнитивные навыки.

На эту тему

Авторы также прокомментировали работы коллег. Одни ученые утверждают, что ментальная арифметика развивает рабочую память, другие этого не обнаружили. Но даже если положительный эффект вправду есть, не исключено, что он проявляется лишь в лабораторных условиях или только у взрослых. У американских детей рабочая память лучше не стала. Авторы прямо написали, что в условиях обычной школы ментальная арифметика ничем не лучше других методик и точно не делает ребят умнее.

Двумя годами ранее тот же психолог Дэвид Барнер провел вместе с коллегами более продолжительное исследование в Индии. Тогда дети обучались ментальной арифметике не один, а три года. Выводы ученых гласили, что благодаря этой методике некоторые школьники, скорее всего, лучше справляются с арифметическими операциями, но результат, по-видимому, зависит от имеющихся способностей ребенка, а не от того, как он научился представлять и обращаться с объектами в рабочей памяти.

Развивает ли менар мозг

С влиянием ментальной арифметики на мозг ситуация еще более запутанная. В 2016 году китайские ученые подготовили обзор существующей научной литературы и пришли к выводу, что у мастеров менара и обычных детей при решении задач вправду задействуются разные области, также нашлись отличия в самой структуре мозга.

Но, во-первых, иногда эксперименты давали противоречивые результаты. Во-вторых, большинство исследований были краткосрочными: мозг — пластичная штука, поэтому неясно, сохраняются ли изменения спустя годы после обучения ментальной арифметике. В-третьих, не исключено, что именно особенности строения мозга привели детей в классы менара и позволили им достичь высот в этом деле. В-четвертых, в экспериментах участвовало мало детей — выводы надо делать осторожно.

Успехи в ментальной арифметике зависят от предварительной подготовки и квалификации преподавателей

© EPA/FRANCK ROBICHON

На сайтах учебных центров говорится, что ментальная арифметика гармонично развивает оба полушария мозга и налаживает между ними связь. Якобы поэтому у детей улучшается концентрация, увеличивается объем памяти, усиливаются творческие и аналитические способности. Но обо всем этом судить рано. В большинстве исследований проверяли только математические навыки — данных о том, как ментальная арифметика влияет на другие когнитивные навыки и успеваемость в школе, недостаточно. Также пока нельзя судить, меняется ли благодаря занятиям связность сетей мозга, отвечающих за разные функции.

Что о менаре думают учителя

Педагоги, как и ученые, не спешат превозносить ментальную арифметику. По словам заслуженного учителя России Леонида Звавича, устный счет — дело полезное, но есть масса приемов устного счета без абака и какой из них лучше, сказать сложно. Успехи ребенка в математике зависят прежде всего от того, какие у него были учителя, а любые развивающие занятия помогают подтянуть разные школьные предметы. «Если человек идет в школу, зная 100 стихотворений, он учится лучше, чем человек, который не знает ни одного», — считает Звавич.

На эту тему

Преподаватель математики, лауреат премии мэрии Москвы Александр Шевкин тоже думает, что всякое занятие, развивающее мышление, полезно и влияет на способности к обучению не по одному предмету. Но к ментальной арифметике он относится настороженно: «Это сильно распиаренный бизнес-проект. Под устную арифметику на русских счетах много денег не соберешь, а на загадочную ментальную арифметику получается. Ничего вредного в ней нет, а вот насколько нужна детям столь продвинутая техника устных вычислений, пусть решают родители. Я бы не стал переоценивать влияние этой методики, так как помню высказывание известного популяризатора правильных способов обучения математике Дьердя Пойи: «Можно научить дельфина крутить мяч на носу, но поможет ли это ему ловить рыбу?»

Сергей Рукшин, профессор РГПУ имени Герцена и учитель знаменитых математиков Григория Перельмана и Станислава Смирнова, оценивает ментальную арифметику еще более скептически: «Мне не известно ни одного исследования, доказательно обосновывающего преимущества этой методики, ее влияние на отдаленные результаты ребенка. В самом деле, нельзя же считать нынешние успехи китайской и японской экономики следствием того, что пять тысяч лет назад они начали применять счетные приспособления, аналогичные используемым в обучении «ментальной арифметике». А именно такие аргументы попадаются в рекламе. Гораздо важнее осознать следующее: многие современные родители не находят времени и душевных сил для личных занятий с собственным ребенком. Любое внимание, общение, обучение развивает личность ребенка и его способности. Ребенок развивается, чему бы его ни учили. А что касается «ментальной арифметики» — ничего личного, только бизнес».

Вероятно, кое-какая польза от ментальной арифметики все же есть, особенно если ребенку тяжело дается математика. Вдобавок на занятиях вырабатывается привычка трудиться — в жизни она пригодится, а целеустремленные сверстники — это хорошая компания и, возможно, новые друзья: ничто так не сближает, как общее дело. Но не стоит ждать от ментальной арифметики чудес: представляя в уме счетную доску, ребенок не приобретет цвет индиго.  

Марат Кузаев

записаться на урок — Amakids

Головной мозг человека разделен на левое и правое полушарие. Исследования показывают, что форма двух полушарий похожа, но функции у них разная. Левое полушарие имеет тесные связи с работой языка, абстрактного мышления и логического мышления. Правое полушарие имеет дело с объектом мышления: изображение, формы, творческое мышление и интуиция.

Большинство людей считают, что функции левого полушария преобладают над функциями правого полушария, а физиологи и психологи считают, что потенциал правого полушария должен использоваться больше. Идеальным методом является одинаковое использование обоих полушарий.

Альберт Эйнштейн, всемирно известный ученый и мыслитель, шокировал научное сообщество, когда предложил «теорию относительности». С помощью творчества и воображения правого полушария, он представлял взаимодействие пространства и времени в его сознании и преодолел ограничение в трех измерениях. В то же время, он также использовал дедукцию и логику левого полушария, чтобы доказать и выяснить научную и математическую ценность теорий. Поэтому, когда левое и правое полушария головного мозга объединяются и эффективно используются вместе, результаты могут быть поразительными.

Все мы хотим, чтобы наш ребенок был успешным человеком! Как воспитать своего ребенка таким? — эти вопросы занимают каждого любящего родителя.

Курсы ментальная арифметика

На сегодняшний день, много центров и клубов, предлагающих развивающие занятия для детей. Все они предлагают одностороннее развитие ребенка — это музыка, творчество, подготовка к школе, театральные студии, шахматы и т.д. Во всем этом сложно разобраться, что же лучше подойдет нашему ребенку, что бы стать разносторонне развитым, ведь заниматься абсолютно всем невозможно.

На самом деле ему необходимо научиться извлекать их из памяти нужную информацию в нужный момент, уметь оценивать, анализировать, делать выводы – и, самое, главное! – достигать поставленных целей. Самым эффективным инструментом в любых руках для достижения поставленных целей является Интеллект. Ведь это нечто большее, чем книжная ученость, умение петь, играть в шахматы или умение хорошо сдавать тесты. Это умение пользоваться своими знаниями. А эффективный интеллект – это способность получать, обрабатывать и использовать знания с максимальным эффектом, способность действовать в направлении желаемых целей.

Курс ментальной арифметики направлен на развитие интеллектуальных способностей , дети закладывают твердую основу для дальнейших академических успехов и развития личности. В результате освоения программы ментальная арифметика ребенок, например, может сложить пятизначные числа за несколько секунд, но это не единственный результат.

 

Благодаря ментальной арифметике развивается и улучшается:

• Концентрация внимания
• Фотографическая память
• Точность и быстрота реакции
• Уверенность в себе
• Творческое мышление
• Слух и наблюдательность
• Воображение и представление
• И как следствие успехи в учебе.

В начале обучения основная часть работы заключается в интенсивном использовании ребенком счетов Абакус (Соробан). На всех стадиях обучения ребенок использует обе руки для операций с косточками счетов, стимулируя работу обоих полушарий головного мозга. Дети постигают все 4 вида математических операций сложение, вычитание, умножение и деление. При равном участии обоих полушарий головного мозга процесс обучения и размышления становится гораздо более эффективным. На каждой тренировке постепенно ослабляется привязка ребенка к счетам и стимулируется его собственное воображение, благодаря чему уже через несколько занятий, он сможет производить простейшие расчеты в уме, лишь представляя Абакус (Соробан) перед собой и мысленно совершая движения косточками (так называемая работа с воображаемыми счетами).

Ребенок, обучаемый по программе ментальная арифметика, начинает решать математическую задачу, воспринимая числа как картинки, так как каждое конкретное число будет вызывать у него ассоциацию соответствующего изображения на косточках счетов.

Развивающий центр для детей AMAKids предлагает курс ментальной арифметики для детей в возрасте от 4 до 16 лет. Группы формируются по возрастам. Для младшей группы длительность обучения составляет 2,5 года, а для старшей – 2 года. Каждый месяц формируется и начинает обучаться новый класс желающих. Но присоединиться к уже начавшей занятия группе – невозможно.

Все, что не обходимо для процесса обучения, а именно счеты, учебные материалы и тетради, уже включено в стоимость курса.

Первая возрастная категория детей – это 4-6 лет, вторая – 7-10 лет, третья 11-16 лет. Класс младшей группы состоит из 4-6 человек, старшие допускает 6-10 человек. Дети обязательно проходят пробное занятие. Это нужно для того, чтобы сформировать равные группы. Основное требование для учеников – умение считать до 10.

Периодичность занятий удобная. Это по 2 урока в день 1 раз в неделю. Но ежедневная домашняя тренировка должна быть не менее 15 минут. Постепенно ребенок накапливает навыки. Каждый день тренируется одно правило.

Для домашних занятий ребенку нужен доступ к компьютеру. Он получает логин и пароль для входа в программу вместе с рабочими материалами и счетами Абакус (Соробан) еще вначале занятий.

Для младшей группы обязательно участие родителей в тренировках, контроль правильности выполнения домашнего задания. Для старшей группы участие родителей не обязательно, но в расписании ребенка желательно выделить определенное время для тренировок, привязанное к режимному моменту (например, перед ужином). Ощутимые результаты и одновременную работу двух полушарий мозга вы сможете увидеть через 2-3 месяца регулярных занятий. После успешного прохождения программы обучения ребенок получает соответствующий сертификат нашего центра.

Занятия по нашей методике помогут раскрыть и выразить экстраординарные способности каждого ребенка, развить креативность через инновационное обучение.

 

Мэрилин Бернс: ментальная математика | Scholastic

Каждый день в мире взрослых мы сталкиваемся с ситуациями, требующими сложения, вычитания, умножения или деления. Мы придумываем подсказки в ресторанах, решаем, когда уйти из дома, чтобы попасть в кино вовремя, оцениваем цену товара на распродаже, отслеживаем, что мы тратим, делая покупки в супермаркете, удваиваем и уменьшаем вдвое рецепты и т. Д. . По крайней мере половину времени мы делаем эти расчеты, когда мы на улице, без ручки и бумаги под рукой, а это значит, что мы должны думать мысленно.Поскольку мыслить в уме — это такой важный жизненный навык, он должен играть регулярную роль в вашем обучении математике в классе.

Математика без карандашей

Когда я хочу поработать со студентами умственные математические навыки, мы делаем то, что я называю «математикой за столом». Идея простая. Попросите студентов убрать все и положить руки на стол. Ни бумаги, ни карандаша, ни манипуляторов, ни книг. Затем представьте им проблему, которую нужно решить в их голове. Вот как это сделать:

Чтобы поддержать детей и убедиться, что это возможность для обучения, а не тестовая ситуация, сделайте решение проблемы усилием класса.Предложите учащимся поделиться своими идеями и услышать мнение своих одноклассников. Тем временем ведите инструктаж и записывайте идеи студентов на доске. Запись дает вам возможность продемонстрировать учащимся, как математически представить их мышление. Когда вы это сделаете, вы обнаружите, что учащиеся быстро привыкнут к рутинной математике за столом. Затем вы можете использовать его для всего урока математики или его части, чтобы решать различные задачи по математике.

Ментальная математика в действии

Для практической математики подходят всевозможные задачи, если их можно решить мысленно.Даже задачи, которые не сразу кажутся подходящими для ментальной математики, можно превратить в практические задачи. Например, задача умножения 148 x 21 не подходит, если цель — найти точный ответ. Но представить это как задачу оценивания — хороший вызов для четвероклассников. Попробуйте написать на плате такую ​​задачу:

Какой ответ ближе всего к продукту?
148 x 21 = 1 000
2 000
3 000
4 000
5 000

Дайте учащимся несколько минут, чтобы они могли спокойно подумать.Затем попросите их повернуться и поговорить с партнером или небольшой группой. Проведите обсуждение в классе, призывая учащихся делиться идеями. Поощряйте их объяснять свои мысли. Математически изобразите идеи на доске. Например, если ученик предлагает, что 1000 не может быть ближайшим, потому что 148 умножить на 10 равно 1480, напишите на доске «148 x 10 = 1480». Продолжайте обсуждение, пока все ученики не поделятся идеями и не поймут, почему 3000 — лучшая оценка. Даже если учащиеся разделяют ту же идею, им полезно объяснить ее своими словами.

В качестве дополнительного задания попросите студентов объяснить на бумаге решение проблемы. Студенты могут выбрать умножение, чтобы найти точный ответ. Они также могут относиться к тому, что вы записали на доске.

Правильный ответ

Для некоторых задач точный ответ — цель. Спросите у первоклассников, как они вычислили бы сумму двух однозначных чисел, например, 6 + 7, — это хороший способ сосредоточить внимание учащихся на различных стратегиях сложения.Или дайте задание на сложение с двумя двузначными числами, например, 26 + 57, и попросите учащихся объяснить, как они находят сумму.

Чтобы разнообразить практику сложения, дайте ученикам двузначное число и попросите их вычислить, сколько еще нужно, чтобы получить 100. Или дайте им большее число, 578 или 1375, и спросите их, как они могли бы переименовать его в сумма двух меньших чисел или, при необходимости, сумма трех меньших чисел. Несмотря на то, что все эти проблемы требуют точных ответов, учащиеся могут найти решения разными способами. Услышав идеи других, студенты расширяют свой собственный репертуар для вычислений, что помогает поддерживать их чувство числа и повышает гибкость.

Некоторые задачи не требуют от учащихся выполнения одного конкретного вычисления, но задействуют их в нескольких вычислениях для проверки различных возможностей. Например, перечислите семь различных величин и попросите студентов придумать числовое предложение, в котором используются три из них. Вот пример, в котором деньги используются в качестве контекста:

В числовом предложении используются три следующих значения: $ 1.50, 2, 3,75 доллара, 50 центов, 6, 3 доллара, 75 центов. Что может быть числовым предложением? Одно из возможных решений: 3,00 доллара США ÷ 2 = 1,50 доллара США.

Деньги предоставляют полезный контекст для решения многих проблем. Вот некоторые проблемы, для которых есть несколько правильных решений.

• Как вы могли потратить ровно 100 долларов, купив две вещи по разной цене?
• Как вы могли потратить ровно 100 долларов, купив три вещи по разным ценам?
• Как вы могли потратить ровно 100 долларов, купив три вещи по разной цене, если одна из них стоит 39 долларов?

Некоторые задачи не требуют вычислений, но все же способствуют интересным обсуждениям, которые помогают учащимся лучше понять числа.

Число округлено до 1 200. Какой может быть номер?

или:

Я записал число с одним нулем, но не могу вспомнить, что это было. Я знаю, что это было от 500 до 800. Какое могло быть число?

Для всех задач поощряйте студентов объяснять свои рассуждения, даже если они дают правильные ответы. Слишком часто учащиеся узнают, что учителя просят их только объяснить, когда они ошибаются. В практической математике объяснения всегда важны для всех учащихся.

Отслеживание математического мышления

Слишком часто ученики рассматривают работу с бумагой и карандашом просто как время для отработки навыков. Конечно, есть время для практики вычислений с использованием бумаги и карандаша, но также полезно подумать о работе с бумагой и карандашом более широко. Письмо учащихся также должно быть средством, позволяющим им отслеживать свое мышление. Студенты, занимающиеся записью в результате практической математики, подтверждают это.

Mental Math is Test Prep

Чтобы подготовить учеников к стандартным тестам, большинство учителей раздают практические буклеты.В следующий раз вместо этого попробуйте математику за столом. Напишите проблему на доске, но не записывайте варианты ответов. Вместо этого проведите обсуждение за столом, пока класс не придет к согласию с решением. Затем отправьте ответы. Затем обсудите другие варианты, которые были неправильными, и поговорите — опять же, положив руки на стол — о том, какие ошибки могут привести к выбору неправильного ответа. Ваши ученики будут поражены их умственной силой!

7 практических советов по ментальной математике (которые может использовать ЛЮБОЙ!)

Скорее всего, вы слышали о ментальной математике — способности делать вычисления в уме — и о том, как важно для детей ее выучить.Но почему это важно? Потому что ментальная математика связана с ЧУМСТВОМ ЧИСЛА: способность манипулировать числами в голове различными способами для выполнения вычислений. В свою очередь было доказано, что чувство числа предсказывает успехи студента в алгебре. По сути, то, что мы делаем с переменными в алгебре, аналогично тому, что учащиеся могут научиться делать с числами в младших классах.

Люди с пониманием чисел гибко используют числа . Они могут разбирать их и складывать различными способами для проведения расчетов.Это очень похоже на умение «ИГРАТЬ» словами, чтобы составлять интересные предложения, или умение играть с аккордами и мелодиями, чтобы сочинять песни.

Но ментальная математика / числовое чутье не только для «математических гениев» — как раз наоборот! Выучить основы этого сможет КАЖДЫЙ, и это значительно упростит изучение математики и алгебры! Мы ожидаем, что наши дети выучат много английских слов и смогут складывать эти слова разными способами в предложения, так почему бы не ожидать, что они сделают то же самое с числами? И они могут, если им показывают основы и показывают примеры того, как это происходит. Итак, давайте перейдем к практической части этого письма: математические стратегии для ВСЕХ.

1. «Девятка».

   Чтобы прибавить 9 к любому числу, сначала прибавьте 10, а затем вычтите 1. В моих книгах по Math Mammoth я рассказываю детям эту сюжетную линию, где девять очень сильно хотят равняться 10… поэтому он спрашивает это другое число в качестве «единицы». Другое число становится на единицу меньше. Например, мы меняем сложение 9 + 7 на 10 + 6, что намного проще решить.

   Но эта «хитрость» расширяется.Можете ли вы придумать простой способ сложить 76 + 99? Измените его на 75 + 100. Как насчет 385 + 999?

   Как бы вы сложили в голове 39 + 28? Пусть 39 станет 40… что уменьшает 28 до 27. Теперь сложение составляет 40 + 27. Еще один способ — подумать о компенсации: 39 — это на единицу меньше 40, а 28 — на два меньше, чем 30. Итак, их сумма на три меньше чем 70.

2. Двухместные + 1.

   Поощряйте детей запоминать двойные числа от 1 + 1 до 9 + 9. После этого у них под рукой появляется множество других фактов сложения: те, которые мы можем назвать «двойные плюс еще один».Например, 5 + 6 — это просто на единицу больше, чем 5 + 5, или 9 + 8 — это просто на единицу больше, чем 8 + 8.

3. Используйте факты сложения при сложении больших чисел.

   Как только вы узнаете, что 7 + 8 = 15, вы также сможете делать все эти сложения в уме:

   • 70 + 80 это 15 десятков, или 150
   • 700 + 800 это 15 сотен, или 1500
   • 27 + 8 — это 20, а 15, то есть 35. Или подумайте так: поскольку 7 + 8 на пять больше, чем десять, то 27 + 8 на пять больше, чем следующие десять.
4. Вычесть сложением.

   Это очень важный принцип, основанный на связи между сложением и вычитанием. Детям действительно не нужно запоминать факты вычитания как таковые, если они могут использовать этот принцип. Например, чтобы найти 8-6, подумайте: «Шесть плюс какое число дает 8?» Другими словами, подумайте о сложении отсутствующего числа 6 + ___ = 8. Ответ на это также является ответом на 8 — 6.

   Этот принцип особенно удобен с вычитаниями, такими как 13-7, 17-8, 16-9 и другими основными фактами вычитания, где уменьшаемое значение находится между 10 и 20.Но вы также можете использовать его во множестве других ситуаций. Например, число 63–52 легче решить сложением: 52 + 11 дает 63, поэтому ответ на 63–52 — 11.

5. Пять умноженное на число.

   Теперь обратим внимание на умножение. Вот изящный трюк, о котором вы, возможно, не знали. Чтобы найти любое число в 5 раз, сначала умножьте это число на десять, а затем возьмите половину этого числа. Например, 5 × 48 можно найти, умножив 10 × 48 = 480 и взяв половину результата, что дает нам 240.Конечно, вы также можете использовать эту стратегию для таких фактов умножения, как 5 × 7 или 5 × 9.

6. Четыре и восемь чисел.

   Если вы умеете удваивать числа, значит, у вас это уже есть! Чтобы найти четырехкратное число, удвойте это число дважды. Например, что такое 4 × 59? Сначала найдите удвоение 59, что составляет 118. Затем удвойте это, и вы получите 236.

   Точно так же восемь раз число означает просто три раза удвоение. Например, найти 8 × 35 означает удвоить 35, чтобы получить 70, удвоить 70, чтобы получить 140, и (еще раз) удвоить 140, чтобы получить 280.Однако лично я бы преобразовал 8 × 35 в 4 × 70 (вы удваиваете один множитель и делите второй вдвое), что легко решить до 280.

7. Умножить на части.

   Эта стратегия очень проста и фактически является основой стандартного алгоритма умножения. Вы можете мысленно найти 3 × 74, умножив 3 × 70 и 3 × 4 и сложив результаты. Получаем 210 + 12 = 222. Другой пример: 6 × 218 — это 6 × 200, а 6 × 10 и 6 × 8, что составляет 1200 + 60 + 48 = 1308.

Я надеюсь, что эти небольшие стратегии или принципы вдохновят вас не только на то, чтобы научить своих детей большему количеству мысленных вычислений, но также и на их использование в повседневной жизни. Играть с числами никогда не поздно!

Мария Миллер

---

Статья изначально опубликована на HomeschoolMagazine.com.

6 ментальных математических стратегий | Советы и рекомендации для студентов

Когда у них нет под рукой манипуляторов или рабочих документов, учащиеся должны чувствовать себя комфортно, выполняя основную математику в уме.

К счастью, может сделать любой ребенок, если он знает правильные советы и уловки .

Вот шесть умственных математических стратегий, которым можно научить ваших учеников. Вы дадите им уверенность, что они отложат калькулятор и начнут решать проблемы самостоятельно!

Округление до десяти

Работа с партиями по 10 значительно упрощает сложение и вычитание, потому что не требуется заимствование или перенос. Студенты могут максимально использовать это, округляя суммы в сумме до ближайших 10.

Уловка состоит в том, чтобы сохранить «лишние» числа, используемые для округления, а затем вычесть их в конце.Смоделируйте это для своих учеников с помощью числовой речи. Например, если сумма 57 + 48, ваш мыслительный процесс может быть:

• Я округлю эти числа до 60 + 50, потому что их легче сложить.
• Но я должен иметь в виду, что я дал себе дополнительные 5 для округления (3, чтобы превратить 57 в 60, и дополнительные 2, чтобы превратить 48 в 50). Когда я доберусь, мне придется вычесть эти 5 из своего окончательного ответа.
• Моя округленная сумма: 60 ​​+ 40 = 110.
• Минус 5 = 105.

Работать слева направо

На бумаге мы учим студентов решать многозначные суммы справа налево, начиная с единиц и заимствуя / перегруппировывая по мере необходимости.

Но если они делают это мысленно, они могут работать наоборот и не беспокоиться об отслеживании заимствований и перегруппировок. Возьмем для примера 34 + 17:

• Сначала мы складываем 3 и 4 в столбце десятков, получая 40.
• Теперь мы добавляем 4 и 7 в столбец единиц, что дает нам 11.
• Добавьте 11 к 40, и мы получим 51.

Используйте приемы умножения

Запоминание таблиц умножения является серьезным математическим препятствием для большинства учащихся начальной школы, но становится намного проще, когда они запоминают следующие «уловки»:

• Любое количество умноженное на 1 остается неизменным.
• К любому числу, умноженному на 10, добавляется ноль.
• Любое число до 9 умноженное на 11 — это одна и та же цифра, повторяемая дважды (например, 99).

Вместе эти приемы мгновенно дают учащимся 60 фактов умножения, которые могут быть вычислены автоматически — без запоминания.

Увеличьте десятичную дробь, чтобы легко найти процентное значение

Вычислить 10% чаевых в ресторане — одна из самых цитируемых задач по математике. К счастью, для этого есть чит, который легко запомнить.

Все, что нужно студентам, — это переместить десятичную запятую на одну позицию назад, в результате чего получится ровно 10% от исходной суммы. Таким образом, 25 долларов превращаются в 2,50 доллара, а 7,50 доллара в 75 центов.

Как только они овладеют навыками, учащиеся могут использовать много 10%, чтобы быстро вычислить и другие проценты.Им нужно только удвоить его, чтобы получить 20%, или уменьшить вдвое, чтобы получить 5%. Сложите эти два вместе, и у них будет 25%.

Розничная терапия внезапно становится намного проще!

Сделайте предположения

В повседневной жизни математические вычисления в уме редко должны быть точными на 100%. Если это так, мы все равно тянемся за калькулятором или листом бумаги.

Скажите своим ученикам, что можно подойти к более сложной математической задаче, «угадывая» ответ.

Это может означать, что нужно просто работать с высшими разрядами в сумме и использовать это для вычисления, что ответ будет «около» определенного числа.Затем они могут проверить ответ с помощью тренировки.

Разбери проблему

Глядя на некоторые из этих математических стратегий в уме, вы можете задаться вопросом, почему они, кажется, используют гораздо больше шагов, чем подход из учебника. Разве это не сбивает с толку, когда ученики размышляют над этим в уме?

На самом деле, наоборот . Вместо того, чтобы сразу переходить к окончательному решению, учащиеся добьются гораздо большего успеха, если они разделят большую проблему на ряд более мелких, а затем будут систематически их решать.

Помните, маловероятно, что этот процесс будет происходить естественным образом для всех. Лучший способ научить этому — моделировать числовую речь, когда вы сами решаете проблему. Подумайте вслух и четко привлеките внимание к каждому шагу, через который вы проходите, чтобы прийти к окончательному решению.

Совет: потренируйтесь в этом сами перед тем, как стать моделью в классе. Многие мыслительные движения, которые вы делаете, могут быть настолько интуитивными и быстрыми (в конце концов, вы же учитель математики), что вы даже не узнаете их, пока не замедлитесь и не начнете делать заметки!

Нужна дополнительная помощь, чтобы отточить умственную математику ваших учеников?

Наш ассортимент онлайн-программ обучения математике был разработан с педагогической точки зрения, чтобы отточить умственную математику и беглость фактов с помощью увлекательных мероприятий, таких как живые соревнования и динамичные игры.Подпишитесь на бесплатную пробную версию и узнайте, почему их любят 5 миллионов студентов по всему миру.

Оттачивайте умственную математику своих учеников с помощью наших программ онлайн-обучения

Изучите программы

Стратегии сложения умственной математики для свободного владения математическими фактами

Свободное владение математикой — это гораздо больше, чем просто скорость и точность. Истинная беглость также включает гибкость и правильное использование стратегии. Когда мы применяем мысленный математический подход к математическим фактам, мы поощряем студентов мыслить гибко, которые способны построить собственное понимание и использовать это понимание для решения более сложных задач.

Мы знаем, что способность гибко мыслить более эффективно, чем запоминание математических фактов. Это было глубоко изучено многими исследователями-математиками. Но иногда, когда мы начинаем обучать стратегиям, мы «обучаем» стратегиям запоминания. Например: «Каждый раз, когда вы видите числа, которые отличаются на 1, вы можете использовать стратегию удвоения плюс один». Вместо того, чтобы «обучать» стратегиям, в идеале мы хотим, чтобы учащиеся открывали их и строили собственное понимание.Лучший способ добиться этого — много-много работать с манипуляторами. И да, даже если вы преподаете старшие классы, ваши ученики должны использовать манипуляторы!

Тем не менее, иногда все же полезно иметь руководство по тому, к каким стратегиям направлять наших учеников.

Ниже я выделил семь различных стратегий сложения в уме, которые вы можете смоделировать в своем классе, чтобы помочь учащимся развить свое понимание. Я также включил видео для некоторых из них.

Рассчитывая — Рассчитывая на — это начальная математическая стратегия в уме. Подсчет означает, что вы начинаете с наибольшего числа в уравнении, а затем начинаете считать. Например, в уравнении 5 + 3 вы хотите, чтобы учащиеся начинали с цифры «5» в голове, а затем считали «6, 7, 8». Это сделано для того, чтобы учащиеся не считали «1, 2, 3, 4, 5… .,6, 7, 8». Студенты также должны понимать свойство коммутативности сложения: если уравнение выглядит так: «2 + 6», им все равно следует начинать с большего числа (в данном случае 6) и считать «7, 8».”

Вот видео, которое объяснит эту стратегию более подробно, или найдите модуль для обучения счету по стратегии ЗДЕСЬ.

Дубли — Дубли не обязательно является стратегией , а скорее набором фактов, которые легко усвоить и запомнить. Двойники вокруг нас; представьте себе пальцы рук и ног — 5 + 5, колеса автомобиля — 2 + 2 или яйца в коробке — 6 + 6. Создание прочного фундамента для парных занятий поможет студентам в следующей стратегии — «Двойные игры плюс один».

Найдите модуль для обучения двойным фактам ЗДЕСЬ.

Near Doubles — Эта стратегия является естественным продолжением парных игр. Это включает использование известного факта и построение на нем. Например, чтобы решить 5 + 6, ученик может подумать: «Я знаю, что 5 + 5 дает 10, а еще один — 11». Эту стратегию лучше всего смоделировать с десятью кадрами, поэтому ее так легко увидеть! И помните, мы должны дать нашим ученикам возможность ВИДЕТЬ математику, чтобы они могли углубить свое понимание!

Вот видео, которое объясняет стратегию близких удвоений более подробно или найдите модуль для обучения фактам близких удвоений ЗДЕСЬ.

Сделай десятку — Сделай десятку — это математическая стратегия в уме, в которой учащиеся используют числовые комбинации, составляющие десять, для установления связей и отношений с другими фактами. Сначала ученики должны выучить числовые комбинации, которые составляют 10. Затем они могут уверенно использовать эти комбинации. Например, чтобы решить 8 + 5, ученик может подумать: «Я могу взять два из 5 и передать их 8, чтобы получилась десятка, а затем сложить оставшиеся 3, чтобы получить 13.«Десять кадров — отличный способ проиллюстрировать эту стратегию.

Вот видео, в котором более подробно объясняется, как сделать десять стратегию или найти модуль для обучения сделать десять ЗДЕСЬ.

Получение кратных десяти — Эта стратегия является естественным продолжением создания десяти. Чтобы сделать кратными десяти , мы можем использовать числовые комбинации, которые составляют десять (6 + 4, 7 + 3 и т. Д.). Это помогает нам понять, что такие выражения, как 26 + 4, будут делиться на десять.Десять фреймов — отличный способ смоделировать мыслительный процесс. Например, когда мы моделируем 26 + 4 с десятью кадрами, легко видеть, что мы можем сдвинуть 4 точки, чтобы полностью заполнить три десяти кадра и получить 30.

Найдите модуль для обучения стратегии умножения десяти ЗДЕСЬ.

Сложение слева направо — Сложение слева направо — это мощная математическая стратегия для сложения чисел, состоящих из двух или более цифр. Понимание поставленной ценности является ключевым моментом, так как студенты будут группировать десятки, а затем единицы.Например, чтобы решить 24 + 53, мы сначала сложим 20 + 50, чтобы получить 70, затем 4 + 3, чтобы получить 7, и, наконец, 70 + 7, чтобы получить 77. Сложение слева направо важно для обучения ДО того, как учащиеся научатся традиционный алгоритм. Это связано с тем, что сложение слева направо сосредоточено на концептуальном понимании, а не на запоминании серии шагов.

Вот видео, в котором более подробно объясняется сложение слева направо, или найдите модуль для обучения сложению слева направо ЗДЕСЬ.

Разбить на части / Разобрать — Разбиение слагаемого по разряду — мощная математическая стратегия для сложения чисел, состоящих из двух или более цифр.Хотя это похоже на сложение слева направо, некоторые студенты предпочитают его, потому что только одно добавление разлагается по разряду, а не оба. Например, чтобы решить 43 + 35, мы могли бы сначала разложить 35 на 30 и 5. Мы начинаем с добавления 43 + 30, чтобы получить 73, а затем оставшиеся 5, чтобы получить 78.

Вот видео, которое объясняет стратегию разделения на части более подробно или найдите раздел для обучения разделению ЗДЕСЬ.

Я надеюсь, что этот пост помог вам составить план обучения математическим стратегиям в вашем классе! Я знаю, что если вы не учились таким образом, это будет непростой переход.

Если вам нужна дополнительная поддержка по обучению стратегиям сложения в классе, ознакомьтесь с этим комплектом стратегий сложения умственной математики, который включает блоки для всех стратегий, которые обсуждались выше.

Как преподавать ментальную математику: стратегии и задания

Хотите верьте, хотите нет, но подавляющее большинство математических вычислений, которые мы делаем ежедневно, взрослые, состоит из элементарной математической математики в уме. В продуктовом магазине мы используем мысленную математику при оценке стоимости товаров.В тренажерном зале мы подсчитываем количество минут, потраченных на поднятие тяжестей или на эллиптическом тренажере. Даже вне нашей профессии мы ежедневно используем мысленную математику для решения обычных задач.

В то время как взрослые умеют использовать мысленную математику в повседневной деятельности, детям необходимо развивать свои собственные математические навыки с нуля. Даже более важно, чем взрослые, дети должны укреплять умственные математические навыки, чтобы укрепить свои многообещающие математические навыки, поскольку умственная математика пригодится, чтобы упростить и ускорить решение математических уравнений и задач.

Зачем изучать ментальную математику?

Короче говоря, когда дети развивают умственные математические навыки, они:

• Получить более глубокое понимание математики, помимо простого запоминания
• Развивать логическое мышление и рассуждать
• Изучите навыки, которые улучшат математические навыки во всех классах
• Осваивайте навыки, которые они сохранят на всю жизнь, независимо от их профессии!

Очевидно, что ментальная математика имеет значение, но для того, чтобы уроки ментальной математики приносили пользу вашему ребенку, ее нужно делать последовательно каждый день или неделю. Если вы ищете занятия, которые помогут вам научиться обучать своего ребенка стратегиям мысленной математики, давайте рассмотрим несколько быстрых и простых способов включить мысленные математические упражнения в учебный распорядок вашего ребенка!

---

Программа «Талантливые и одаренные» со скидкой 60% этой осенью! Совершенствуйте свои математические навыки и готовьте своего ребенка к успеху с помощью увлекательных математических игр, видео и уроков, которые понравятся вашему ребенку!

---

Умственная математическая деятельность для детей младшего возраста

Классическая ментальная математическая игра: Свинья

Возможно, вы даже помните игру «Свинья» из детства! С небольшими изменениями вы можете сделать для своего ребенка игру «Свинья», которая подойдет детям даже в первом классе.

Используя всего один кубик, каждый игрок по очереди бросает кубик и ведет текущий счет выпавшей суммы. В свой ход игрок бросает кубик и записывает число. Они могут бросать столько раз, сколько хотят, мысленно следя за суммой во время броска.

Если игрок выбрасывает 1, он теряет всю текущую сумму, и следующий игрок получает ход. Если игрок хочет прекратить бросание в свой ход, просто попросите его или ее записать сумму, чтобы они могли добавить ее к сумме, которую они бросают в свой следующий ход.Затем ребенок передает кубик своему противнику. Первый игрок, набравший в сумме 25 побед! Для детей постарше увеличьте это число до 50 или 100, используя два кубика!

Соревнования по ментальной математике

Все становится веселее, когда ты делаешь соревнование! Эта веселая и универсальная игра отлично подходит для детей от начального до 3-го класса! Поскольку задачи можно адаптировать к возрасту вашего ребенка, эта игра отлично подходит для детей, которые только начинают развивать умственные математические навыки, или для детей старшего возраста, оттачивающих свои способности.

Чтобы играть, убедитесь, что у вас есть белая доска с маркерами для сухого стирания. Просто напишите на доске несколько математических предложений (например, те, которые посвящены сложению и удалению). Установите таймер от 30 секунд до минуты, чтобы ваш ребенок работал над проблемами, чтобы найти ответы. За каждую задачу, которую ваш ребенок решит, он получает 1 балл. За каждую ошибку вы получаете балл. После всех раундов, в которых хочет играть ваш ребенок, побеждает тот, у кого больше очков!

Mental Math Twister

Если вы хотите научиться преподавать мысленную математику второклассникам, ответ — сыграйте в Twister! Отлично подходит для небольшой группы детей, эта игра отлично подходит для друзей, братьев и сестер вашего ребенка, небольшого класса или даже всей семьи! Начните с однозначных чисел, но для старших 2-х или 3-х классов переходите к 2-значным числам, чтобы сыграть в увлекательную игру Twister.

Для начала вам понадобится подготовленный коврик Twister для этой веселой игры. Чтобы использовать коврик максимально эффективно, просто напишите числа на стикерах и прикрепите их к каждому цветному кружку на мате. На коврике каждый цвет должен представлять один и тот же ответ. Например, каждый желтый кружок представляет ответ «4», а каждый синий кружок может представлять ответ «6». Аналогичным образом, используя небольшой кусок стикера, отметьте значения ответов соответствующим цветом на счетчике.

Чтобы играть, попросите детей встать сбоку от коврика.Покрутите вертушку, чтобы увидеть, что и куда должен двигаться ваш ребенок. Вместо того, чтобы вызывать цвет при вращении, вместо этого создайте простую математическую задачу, которая равна числу, на которое они должны приземлиться. Например, если прядильщик говорит: «Правая рука, синяя», скажите детям: «Правая рука, 3 + 3». Поскольку ответ — 6, они кладут правую руку на синий кружок.

Так как эта игра может быть изменена в соответствии с потребностями вашего ребенка, вы можете переключить ее, чтобы бросить вызов детям, чтобы они добавляли двойные или двойные плюс 1! Благодаря такому количеству способов игры ваши дети будут двигаться и скручиваться, одновременно совершенствуя свои математические навыки!

---

Если вы ищете еще больше способов развить умственные математические навыки вашего ребенка, математические головоломки и онлайн-игры — отличный способ продолжить обучение вашего ребенка. Ознакомьтесь со всеми нашими математическими ресурсами, доступными в AppStore и на сайте kidsacademy.mobi!

Учебные материалы, рабочие листы и задания по ментальной математике

Выберите ваше местоположение

Выбор страны и штата поможет нам предоставить вам наиболее подходящие учебные ресурсы для ваших учеников.

Страна Австралия Соединенные Штаты Соединенное Королевство Афганистан Иландские острова Албания Алжир Американское Самоа Андорра Ангола Ангилья Антарктика Антигуа и Барбуда Аргентина Армения Аруба Австралия Австрия Азербайджан Багамы Бахрейн Бангладеш Барбадос Беларусь Бельгия Белиз Бенин Бермуды Бутан Боливия, Многонациональное Государство Сабациона и Герцеговина Бонавия Остров Буве Бразилия Британская территория в Индийском океане Бруней-Даруссалам Болгария Буркина-Фасо Бурунди Камбоджа Камерун Канада Кабо-Верде Каймановы острова Центральноафриканская Республика Чад Чили Китай Кокосовые острова (острова Килинг) Колумбия Коморские острова Конго Конго, Демократическая Республика Острова Кука Коста-Рика Кот д’Ивуар Хорватия Куба Кюрасао Кипр Чешская Республика Дания Джибути Доминика Доминиканская Республика Эквадор Египет Сальвадор Экваториальная Гвинея Эритрея Эстония Эфиопия Фолклендские (Мальвинские) острова Фарерские острова Фиджи Финляндия Франция Французская Гвиана Французская Полинезия Французский Южный Террит страны Габон Гамбия Грузия Германия Гана Гибралтар Греция Гренландия Гренада Гваделупа Гуам Гватемала Гернси Гвинея Гвинея-Бисау Гайана Гаити Остров Херд и острова Макдональд Святой Престол (государство-город Ватикан) Гондурас Гонконг Венгрия Исландия Индия Индонезия Иран, Исламская Республика Ирак Ирландия Остров Мэн Израиль Италия Ямайка Япония Джерси Иордания Казахстан Кения Кирибати Корея, Корейская Народно-Демократическая Республика, Республика Кувейт Кыргызстан Лаосская Народно-Демократическая Республика Латвия Ливан Лесото Либерия Ливия Лихтенштейн Литва Люксембург Макао Македония, бывшая югославская Республика Мадагаскар Малави Малайзия Мальдивы Мали Мальта Маршалловы острова Мартиник Мавритания Маврикий Майотта Мексика Микронезия, Федеративные Штаты Молдовы, Республика Монако Монголия Монголия Черногория Монтсеррат Марокко Мозамбик Мьянма Намибия Науру Непал Нидерланды Новая Каледония Новая Зеландия Никарагуа Нигер Нигерия Ниуэ Остров Норфолк Северные Марианские острова Норвегия Оман Пакистан Палау Палестина , Государство Панама Папуа-Новая Гвинея Парагвай Перу Филиппины Питкэрн Польша Португалия Пуэрто-Рико Катар Румыния Российская Федерация Руанда Сен-Бартелеми Остров Святой Елены, Вознесения и Тристан-да-Кунья Сент-Китс и Невис Сент-Люсия Сен-Мартен (французская часть) Сен-Пьер и Микелон Сент-Винсент и Гренадины Самоа Сан-Марино Сан-Томе и Принсипи Саудовская Аравия Сенегал Сербия Сейшельские острова Сьерра-Леоне Сингапур Синт-Мартен (голландская часть) Словакия Соломоновы острова Сомали Южная Африка Южная Джорджия и Южные Сандвичевы острова Южный Судан Испания Шри-Ланка Судан Суринам Свальбард и Ян-Майен Свазил Швеция Швейцария Сирийская Арабская Республика Тайвань, провинция Китая Таджикистан Танзания, Объединенная Республика Таиланд Тимор-Лешти Того Токелау Тонга Тринидад и Тобаго Тунис Турция Туркменистан Острова Теркс и Кайкос Тувалу Уганда Украина Объединенные Арабские Эмираты Соединенное Королевство Соединенные Штаты Внешние малые острова США Уругвай Узбекистан Вануату Венесуэла, Бол ivarian Республика Вьетнам Виргинские острова, Британские Виргинские острова, U. С. Уоллис и Футуна Западная Сахара Йемен Замбия ZimbabweState Австралийская столичная TerritoryNew Южная WalesNorthern TerritoryQueenslandSouth AustraliaTasmaniaVictoriaWestern AustraliaAlabamaAlaskaAmerican SamoaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict Из ColumbiaFederated Штатов MicronesiaFloridaGeorgiaGuamHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarshall IslandsMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaNorthern Mariana IslandsOhioOklahomaOregonPalauPennsylvaniaPuerto RicoRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirgin IslandsVirginiaWashingtonWest VirginiaWisconsinWyoming

Math 4 — Закон.01: Ментальная математика: сложение и вычитание

Временной интервал

2 академических часа по 30 минут каждое

Сводка

На этом уроке ученики будут использовать умственные математические навыки сложения и вычитания, умножая числа, кратные десяти, и корректируя (компенсация).Эти предлагаемые стратегии следует обсудить в двух отдельных уроках.

Материалы

• 7 книг
• счетчиков на каждую пару учеников
• 2 табурета / стула одинаковой высоты

Дополнительные ресурсы

«Психическая математика в средних классах», Публикации Дейла Сеймура, 1987 г.

Фон для учителей

Счет в голове — это практический жизненный навык. Множество видов повседневного вычислительные задачи можно решить мысленно. Мысленный расчет дает краеугольный камень для всех процессов оценки, позволяющий использовать множество альтернатив нестандартные методы или стратегии поиска ответов. Мысленное вычисление побуждает учащихся думать о числах и развитии числовых соотношений сильное чувство чисел и математическая уверенность. Опрос Национального Оценка успеваемости по математике показала, что большинство детей не осознавая, что мысленный расчет часто является наиболее удобным методом поиска решение.Большинство студентов утверждали, что либо бумага и карандаш, либо калькулятор был необходим для определения решений.

Было бы полезно, если бы студенты имели опыт работы с совместимыми числа, в данном случае пары чисел, которые «составляют десять».

Предполагаемые результаты обучения

1. Продемонстрируйте положительное отношение к математике.
2.Станьте решателями математических задач.
3. Рассуждайте математически.
4. Общайтесь математически.
5. Сделайте математические связи.
6. Представляйте математические ситуации.

Инструкционные процедуры

Урок первый: Компенсация (компенсация)
Приглашение учиться
Дайте одному ученику 4 книги, а другому ученику 3 книги.Спросите: «Если возьмете часть книг от одного ученика и отдать другому ученику делает это изменить общее количество книг? Как эта идея может помочь вам складывать числа? »

Инструкционные процедуры:

1. Студенты работают в парах. Попросите каждого ученика отсчитать определенное количество счетчики и найдите сумму. Определите, сколько счетчиков потребуется для сделать одну группу кратной 10. Переместите это количество жетонов из одной группы к другой группе.Это изменит общую сумму? (Нет) Повторить это действие несколько раз с разным количеством счетчиков.
2. Дайте ученикам задачу на сложение и попросите их сделать десятки. добавив совместимый номер в одно из дополнений. Вернитесь и вычтите такая же сумма из другого дополнения для компенсации. Затем добавьте два скорректированных добавляет.
3. Потренируйтесь торговать числами, чтобы получилась ровная группа десятков. для облегчения вычислений.Задачи для практики:

29 + 62	37 + 69
28 + 45	43 + 49
49 + 26	55 + 19

Урок второй: балансирующее вычитание (компенсация)
Приглашение к обучению
Попросите двух учеников разного роста продемонстрировать идею о том, что если вы добавляете одинаковую сумму как к числу, которое вы вычитаете, так и к числу вы начали, разница будет такой же.

Спросите, кто выше и примерно какая разница в росте? Дайте более низкий ученик — небольшой табурет / стул, на котором можно стоять. (Этот ученик должен сейчас быть выше). Многие студенты поймут, что разница изменился, когда более низкому ученику было на чем опереться. Чтобы сохранить разница такая же, более высокому ученику понадобится что-то такого же размера стоять на. Как вы можете использовать эту идею для вычитания чисел?

Инструкционные процедуры

1. Студенты должны понимать вычитание при переименовании.Напишите простое вычитание проблема на плате. Попросите учащихся отсчитать первое количество счетчиков. и вычтите второе число. (например, 6-2 = 4).
2. Используйте ту же задачу и добавьте «1» к каждому из чисел.
   (например, 7-3 = 4). Что случилось с разницей, когда мы переименовали проблему добавив одинаковое количество к обоим числам? (остался прежним). Попробуйте добавить «2» к каждому из исходных чисел. Три. Четыре. Есть ли разница оставайся таким же?
3. Дайте учащимся несколько задач на вычитание, используя балансирующее вычитание. стратегия.Убедитесь, что учащиеся понимают, что мы хотим «сделать десятки» с числом, которое мы вычитаем (вычитаем), а не с тем, которое мы вычитаем от (minuend). Гораздо проще вычесть красивую четную группу десятков из другой номер B без займа и т. д.
   Задачи для практики:

65 — 49	44–28
43-19	81–58
72–29	71–47

Добавочные номера

Возможные расширения / адаптации / интеграция
Используйте эти стратегии, чтобы найти сумму и разность трех- и четырехзначных чисел.

Домашнее задание и семейные связи
Попросите учащихся научить члена своей семьи новому способу мысленного сложения или вычитания и верните записку с указанием общего математического опыта между член семьи и студент.

План оценки

Попросите учащихся написать инструкции о том, как применять только что приобретенные навыки узнал в своих журналах.

Создано: 29.08.2003
Обновлено: 05.02.2018

58825

.