2 = 9
256 – 9 = 247

Если не закончить работу алгоритма, то в левом столбце будут сплошные нули, и поскольку 0 – чётное число, к нарастающей сумме добавлять ничего не будет нужно. Поэтому, как только мы получаем в левом столбце единицу, в третьем столбце появляется ответ.

Доказательство

Почему это работает? Можно сказать, что это обычное двоичное длинное умножение. Но мы приведём более длинное объяснение, которое будет заодно и более общим.

Обозначим число в левом столбце A, во втором – B, нарастающую сумму – R, а ответ – P. Следовательно

(A*B) + R = P

Тогда, если A чётное, то есть k, для которого A=2k. Перепишем уравнение:

(2k*B) + R = P

Или, что то же самое:

(k*2B) + R = P

Если мы заменим A половиной его значения, а B – удвоенным значением, и назовём их A’ и B’, то:

(A’*B’) + R = P

То есть, если A чётное, мы уполовиним первое число и удвоим второе, и наше уравнение верно.

А если нечётное? Тогда A=2k+1

A*B + R = P

(2k+1)*B + R = P

2k*B + B + R = P

2k*B + (B+R) = P

K*2B + (B+R) = P

A’*B’ + (B+R) = P

И опять мы обозначили половину A через A’ и удвоенное B через B’.

Наше уравнение верно, если мы:

• добавили число из второго столбца к нарастающей сумме
• уполовинили первый столбец
• удвоили второй

Видно, что наше уравнение остаётся сбалансированным при выполнении шагов нашего алгоритма.

Когда мы доходим до нуля, то имеем:

0 * B + R = P

Или R=P. Наша нарастающая сумма равна нужному результату.

Обобщение 1: возведение в степень

Попробуем подсчитать 2¹³. При возведении в степень мы перемножаем числа, а не складываем, поэтому мы усовершенствуем наш алгоритм:

заменим сложение умножением
заменим удвоение возведением в квадрат

степень   база
======   ====
  13      2 ->     1
   6      4        2
   3     16 ->
   1    256 ->    32
   0  65546     8192
                ^^^^

Нарастающее произведение начинается с 1. 13 – нечётное, поэтому умножаем второй столбец на нарастающее произведение, получая 2. Теперь мы уполовиним 13 и возведём 2 в квадрат.

6 – чётное, не умножаем нарастающее произведение. Уполовиним 6 и возведём в квадрат 4, получим 16.

3 – нечётное, умножаем 16 на наше нарастающее произведение, получим 32. Уполовиним первый столбец и возведём в квадрат второй.

Последний шаг: 1 – нечётное, умножаем 256 на 32, получаем 8192, что и является ответом.

Доказательство этого алгоритма такое же, как и у прошлого, просто теперь наше уравнение выглядит так:

B^A*R=E

Обобщение 2: матрицы

Но этот алгоритм можно использовать не только для возведения чисел в степень – он работает и для матриц. Наше нарастающее произведение начинается с единичной матрицы, а во второй столбец пишется матрица, чью степень нам надо получить. И всё работает.

Далее идёт функция, написанная на языке Python. Она работает для любой неотрицательной степени, и «базы» любого типа, поддерживающего ассоциативное умножение. e, где e – неотрицательное целое. Начинаем с # нарастающего произведения I, так что эта функция будет # работать и с числами, и с матрицами result = I while e > 0: if is_odd(e): result *= b b *= b e = e / 2 return result

Этого даже не нужно понимать, достаточно знать, что она работает для матриц.

Ссылки

• www.google.co.uk/search?q=russian+peasant+multiplication
• www.google.co.uk/search?q=Ethiopian+multiplication
• www.google.co.uk/search?q=Ancient+Egyptian+multiplication
• en.wikipedia.org/wiki/Ancient_Egyptian_multiplication

Тренажер: умножение в столбик — intmag24.ru

75,00 ₽

Примеры в столбик на умножение. Выбор первого и второго множителей: однозначные, двузначные и трехзначные.  С ответами. Для решения  на компьютере (в Excel без печати).

Артикул: i-13739 Категория: Для учебы Метки: 3 класс, 4 класс, Примеры в столбик

• Описание
• Детали
• Отзывы (0)

Описание

Тренажер на умножение в столбик – программа, которая формирует примеры на умножение в столбик, чтобы решать их на компьютере (не распечатывая).

Программа написана в Excel с помощью макросов. С помощью генератора примеров можно создать неограниченное число примеров. Можно выбрать

уровень сложности: задать отдельно первый и второй множители — однозначные, двузначные или трехзначные числа.

• При нажатии кнопки «Начать» запускается счетчик (обнуляется), который подсчитывает количество решенных примеров, в том числе  правильных и решенных с ошибкой.
• При нажатии кнопки «Новый пример» формируется новый пример на умножение в столбик. При этом статистика правильных и неправильных примеров сохраняется.
  При нажатии кнопки «Проверить» программа проверяет правильность решения примеров.

Записывать ответ можно с помощью клавиатуры или кнопок (для удобства в карточке есть кнопки с цифрами, которые можно использовать при выборе ответа).

Тренажер примеров на умножение в столбик по математике удобен, так как не нужно заранее покупать задачники и пособия по математике с примерами.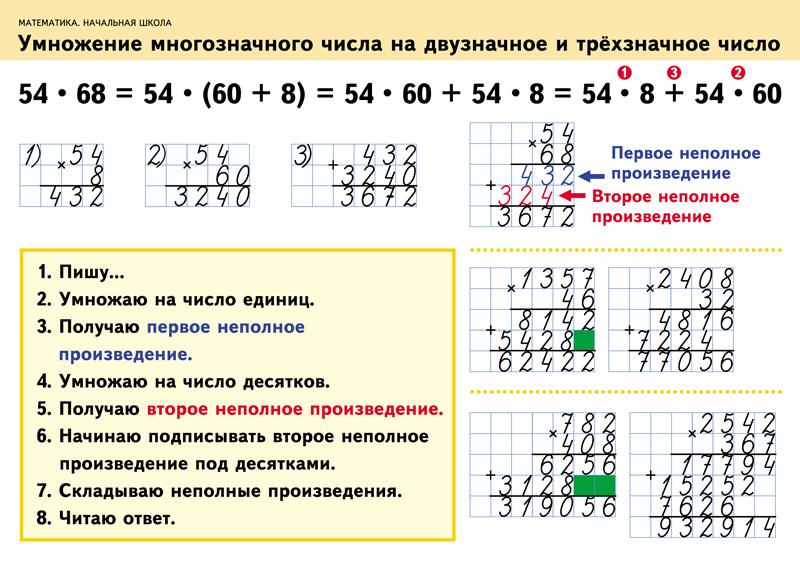

Можно скачать файл и решать примеры в любое время независимо от подключения к интернету.

Если Вы хотите посмотреть принцип работы программы, можете скачать программу «Тренажер счета в пределах 10» бесплатно.

Другие программы на умножение в столбик:

• Умножение в столбик (простое)
• Умножение в столбик 2 (с клеткой)

Другие программы, которые помогут закрепить навыки счета:

• • Деление в столбик (простое)
  • Деление в столбик 2 (с клеткой)
  • Деление в столбик 3 (со словами для самоконтроля)
  • Тренажер: деление в столбик» — решение на компьютере (без печати)

• • Сложение и вычитание в столбик (простое)
  • Сложение и вычитание в столбик 2 (с клеткой)
  • Сложение и вычитание в столбик 3 (со словами для самоконтроля)
  • Тренажер на сложение и вычитание в столбик — решение на компьютере (без печати)

На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Умножение в столбик

  75,00 ₽В корзину

• Умножение в столбик 2 (с клеткой)

  Оценка 5.00 из 5

  85,00 ₽В корзину

• Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски

  Оценка 5.00 из 5

  120,00 ₽В корзину

• Задачи на движение (разные виды)

  100,00 ₽В корзину

• Тренажер: сложение и вычитание в столбик

  70,00 ₽В корзину

• Умножение и деление в столбик

  Оценка 4.67 из 5

  100,00 ₽В корзину

• Деление в столбик 2 (с клеткой)

  Оценка 5.00 из 5

  85,00 ₽В корзину

• Сложение и вычитание в столбик

  Оценка 5. 00 из 5

  70,00 ₽В корзину

• Сложение и вычитание в столбик 2 (с клеткой)

  80,00 ₽В корзину

• Деление в столбик

  75,00 ₽В корзину

• Порядок действий в пределах 1000 (все действия)

  90,00 ₽В корзину

• Раскрытие скобок и порядок действий до 1000 (сложные примеры)

  130,00 ₽В корзину

Обзор умножения матриц

| Round Plus

Обзор

Матрицы — это способ группировки чисел, организованный в строки и столбцы. Матрицы часто используются как способ представления нескольких уравнений в более удобном для организации формате, однако для решения этих систем уравнений мы должны иметь возможность выполнять матричные операции, такие как умножение.

Строки и столбцы

Приведенная ниже матрица является примером матрицы [3×2]. Матрицы описываются в форме [RxC], где R представляет количество строк матрицы, а C представляет количество столбцов матрицы.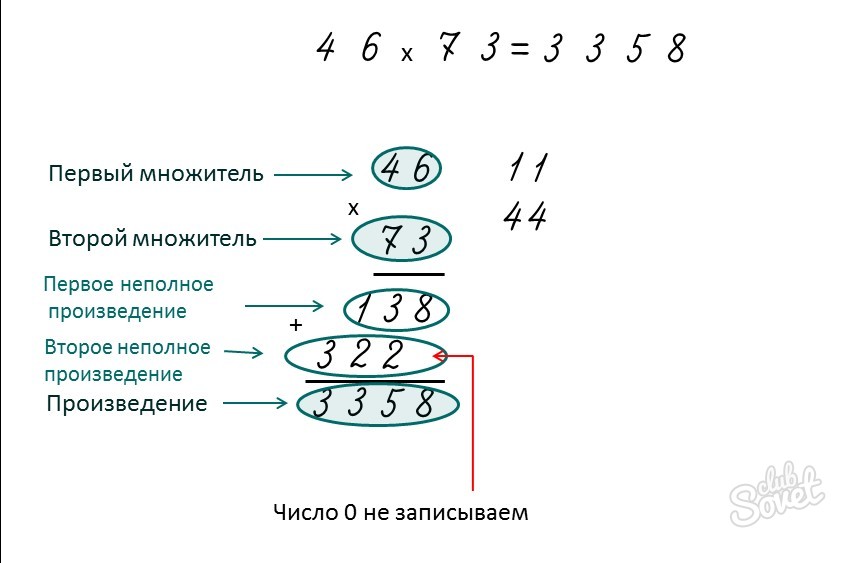

Приведенная выше матрица имеет размер [3×2], так как имеет 3 строки и 2 столбца.

Умножение на скаляр

Любую матрицу можно умножить на так называемую скалярную величину. В этом случае скаляр представляет собой действительное число, умноженное на всю матрицу. Например:

Умножение матриц

Также можно перемножать две матрицы вместе, однако матрицы можно перемножать только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы. Если две матрицы соответствуют этому критерию, их можно перемножить. Результатом будет третья матрица с таким же количеством строк, как и в первой матрице, и таким же количеством столбцов, как во второй матрице.

Пример

Можно ли перемножать следующие матрицы? Каковы будут размеры ответа?

1. [2×3] * [2×2]
2. [3×2] * [2×2]
3. [2*3] * [3*1]

Ответ

1. Мы не можем умножать эти матрицы, потому что матрица 1 три столбца, а матрица 2 имеет только две строки.

2. Мы можем перемножить эти матрицы, потому что матрица 1 имеет два столбца, а матрица 2 — 2 строки. Результирующая матрица будет иметь столько строк, сколько матрица 1, и столбцов, как матрица 2, поэтому она будет [3×2].

3. Мы можем перемножить эти две матрицы, потому что матрица 1 имеет три столбца, а матрица 2 — три строки. Результатом будет [2×1].

Примечание: Это упражнение должно было показать, что порядок имеет значение при умножении двух матриц. Попробуйте изменить порядок любого из приведенных выше примеров и посмотрите, изменится ли результат.

Правила умножения матриц

Как только мы узнаем, можно ли перемножить две матрицы, пришло время выполнить это умножение. Умножение двух матриц также известно как «точечный продукт». Каждое число в матрице ответов является результатом умножения одной из строк матрицы 1 на один из столбцов матрицы 2.

Чтобы найти первую строку, первый столбец матрицы ответов, умножьте первую строку матрицы 1 на первый столбец матрицы 2. Чтобы найти строку 1, второй столбец матрицы ответов, умножьте первую строку матрицы 1 на второй столбец матрицы 2. При умножении строки на столбец совпадающие термины умножаются и складываются.

Пример: Найдите скалярное произведение двух матриц

Матрица 1 состоит из двух столбцов, а матрица 2 состоит из двух строк, поэтому их можно перемножить. Ответ будет состоять из двух строк, поскольку в матрице 1 две строки и три столбца, поскольку в матрице 2 три столбца. Таким образом, ответ будет [2×3].

Допустим, мы сначала хотим найти верхний левый угол матрицы ответов (отмеченный X). Поскольку место, которое мы хотим найти, находится в строке 1 столбца 1, мы должны умножить строку 1 первой матрицы на столбец 1 второй матрицы. Строка и столбец, которые необходимо умножить, отмечены стрелками.

При умножении строки и столбца мы умножаем первое число в строке на первое число в столбце, умножаем второе число в строке на второе число в столбце и складываем результат.

Чтобы найти нижний левый угол матрицы ответов, мы повторяем тот же процесс. Поскольку точка, которую мы ищем, находится во второй строке и первом столбце матрицы ответов, мы должны умножить вторую строку первой матрицы на первый столбец второй матрицы.

Процесс повторяется снова для строки 2, столбца 2:

После умножения всех строк и столбцов, как показано в предыдущих шагах, матрица ответов завершена.

‍

Как умножить два столбца в Google Sheets

Изучение того, как использовать формулы в Google Таблицах, поможет вам более эффективно вычислять данные. Это также может сэкономить вам много времени, особенно когда вам нужно умножить два столбца. Однако эти формулы могут показаться сложными. Но как только вы освоите их, они сделают вашу жизнь намного проще.

В этой статье мы покажем вам, как использовать формулу для умножения двух столбцов в Google Sheets и другие функции умножения.

Основы формулы умножения

Чтобы формула в Google Sheets работала, она должна иметь некоторые знаки, которые вы должны запомнить. Первый из них, лежащий в основе каждой формулы, — это знак равенства (=). Чтобы ваша формула была действительна и показывала цифры, напишите этот знак в начале.

Далее, чтобы умножить числа, вы будете использовать знак звездочки (*) между ними. Наконец, чтобы получить сумму и завершить формулу, нажмите «Ввод».

Умножение двух столбцов

Чтобы умножить два столбца в Google Sheets, вам сначала нужно вставить данные. Наиболее эффективным способом является использование формулы массива.

Предположим, вы хотите получить умноженное значение данных из столбцов A и B. Выберите ячейку, в которой должна появиться сумма. Выполните следующие действия, чтобы успешно применить формулу:

1. Сначала напишите знак равенства (=) в выбранной ячейке.
   
   
2. Затем введите ARRAYFORMULA( .
   
   
3. Кроме того, вы можете нажать Ctrl + Shift + Enter или Cmd + Shift + Enter для пользователей Mac. Google Таблицы автоматически добавляют формулу массива. Замените ‘)’ на ‘(‘ в конце формулы и выполните следующий шаг.
   
   
4. Теперь перетащите вниз ячейки в первом столбце, который вы хотите умножить.
   
   
5. Затем введите «*», чтобы убедиться, что вы умножаете.
   
   
6. Перетащите вниз ячейки из другого столбца.
   
   
7. Наконец, нажмите «Ввод», чтобы применить формулу.
   
   
8. В выбранном вами столбце будут показаны умноженные значения.
   

Создав формулу массива, вы не сможете удалить или изменить отдельный массив. Однако вы можете полностью удалить массив. Просто дважды щелкните ячейку, в которую вы ввели формулу, и удалите содержимое. Он автоматически удалит все суммы из столбца.

Получение суммы умноженных значений

Если вам по какой-то причине нужно получить сумму умноженных значений, есть также простой способ сделать это. Просто убедитесь, что вы выполнили следующие шаги:

1. Сначала выполните описанные выше шаги, чтобы умножить ячейки.
2. Теперь выберите ячейку, в которую вы хотите получить сумму умноженного значения.
3. Введите здесь знак равенства (=).
4. Затем напишите ‘СУММПРОИЗВ(’.
5. Затем выберите ячейки, которые вы хотите просуммировать. (Это будут ячейки с формулой массива).
6. Наконец, нажмите «Ввод», чтобы получить сумму.

Умножение между столбцами

Если у вас есть два отдельных столбца с данными и вам нужно их перемножить, выполните следующие действия:

1. Сначала выберите ячейку, в которой вы хотите, чтобы отображалась сумма.
2. Введите знак равенства (=).
3. Затем щелкните ячейку из первого столбца.
4. Теперь введите «*».
5. Затем выберите ячейку из другого столбца.
6. Наконец, нажмите «Ввод».
7. Номер появится в выбранной вами ячейке.

Чтобы все значения отображались в столбце, щелкните маленький квадратик в правом нижнем углу умноженного значения. Вы должны иметь возможность перетащить его вниз по столбцу. Таким образом, все продукты будут отображаться в ячейках.

Умножение с одинаковым числом

Если вам нужно умножить ячейки с одинаковым числом, для этого тоже есть специальная формула. Вам придется использовать нечто, называемое абсолютной ссылкой. Это представлено символом доллара ($). Взгляните на этот Google Sheet. В столбце A есть некоторые данные, которые мы хотим умножить на три.

Но мы не хотим делать это вручную для каждой ячейки. Это отнимает много времени, особенно если ячеек с числами гораздо больше, чем здесь. Чтобы умножить A2 на B2, вам просто нужно ввести следующее:

1. В ячейке, в которую вы хотите получить умноженное значение, напишите знак равенства (=). Мы напечатаем это в C2.
2. Теперь либо щелкните A2, либо введите его рядом с «=».
3. Затем напишите «*».
4. После этого щелкните B2 или введите его.
5. Нажмите «Ввод».
6. Номер должен появиться там, где вы хотите.

Теперь вы можете попробовать перетащить значение вниз, чтобы получить умноженное значение для всех ячеек. К сожалению, это не сработает, и вы просто получите ноль во всех ячейках.

Чтобы продукт отображался в ячейках, вам нужно будет применить другую формулу. Вот почему вам придется использовать абсолютную ссылку. Хотя это звучит сложно, это не так. Потерпите нас.

1. Выберите ячейку, в которой должно появиться значение.
2. Теперь запишите знак равенства (=).
3. Нажмите на ячейку, которую вы хотите умножить.
4. Введите ‘*.’
5. Затем щелкните ячейку, которую вы хотите использовать для умножения всех ячеек. Например, Б2.
6. Вставьте «$» перед буквой и числом, обозначающим. Это должно выглядеть так: «$B$2».
7. Нажмите «Ввод», чтобы завершить формулу.
8. Нажмите на маленький квадрат в правом нижнем углу формулы.
9. Перетащите его вниз по столбцу, чтобы значения появились во всех ячейках.

Когда вы пишете «$» перед буквой и числом, представляющим ячейку, вы сообщаете Google Таблицам, что это абсолютная ссылка.