Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень 8 класс онлайн-подготовка на

113. Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень.

При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним. Например:

27+37=2+37=57.

Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:

ac+bc=a+bc,

где а, b и с — многочлены, причем с — ненулевой многочлен.

Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

Вычитание рациональных дробей выполняется аналогично сложению:

ac-bc=a-bc.

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

Пример 1. Сложим дроби:

3a-7b15ab+2a+2b15ab=3a-7b+2a+2b15ab=5a-5b15ab=5(a-b)15ab=a-b3ab.

Пример 2. Вычтем дроби:

a2+95a-15-6a5a-15=a2+9-6a5a-15=a-325a-3=a-35.

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.

Пример 3. Сложим дроби x4a3b+56ab4.

Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен 12а³b⁴. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей.

Дополнительные множители к числителям и знаменателям этих дробей соответственно равны 3b³и 2a².

Имеем

x4a3b+56ab4=x∙3b3+5∙2a212a3b4=3b3x+10a212a3b4.

Пример 4. Преобразуем разность a+3a2+ab-b-3ab+b2.

Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:

a+3a2+ab-b-3ab+b2=a+3a(a+b)-b-3b(a+b).

Простейшим общим знаменателем служит выражение ab(a+b). Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.

Имеем:

a+3a(a+b)-b-3ba+b=a+3b-b-3aaba+b=ab+3b-ab+3aaba+b=3a+baba+b=3ab.

Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.

Пример 5. Упростим выражение a-1-a2-3a+1

Представим выражение a-1 в виде дроби со знаменателем 1 и выполним вычитание дробей:

a-1-a2-3a+1=a-11-a2-3a+1=a-1a+1-a2-3a+1=a2-1-a2+3a+1=2a+1.

Умножение и деление дробей. Возведение дроби в степень.

При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например: 23∙45=2∙43∙5=815.

Таким же образом перемножают любые рациональные дроби:

ab∙cd=acbd,

где а, b, с и d — некоторые многочлены, причем b и d — ненулевые многочлены. Это равенство выражает правило умножения рациональных дробей

:

чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.

Пример 6. Умножим дроби a34b2∙6ba2.

Воспользуемся правилом умножения дробей:

a34b2∙6ba2=a3∙6b4b2∙a2=6a3b4a2b2=3a2b.

Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:

ab∙cd∙mn=acbd∙mn=acmbdn.

Выясним теперь, как выполняется возведение рациональной дроби в степень.

Рассмотрим выражение abn, являющейся n-й степенью рациональной дроби ab и докажем, что

abn=anbn.

По определению степени имеем

abn=ab·ab∙…∙ab (n раз).

Применяя правило умножения рациональных дробей и определение степени, получим

ab·ab∙…∙ab=a∙a∙…∙ab∙b∙…∙b=anbn.

Следовательно, abn=anbn.

Из доказанного тождества следует правило возведения рациональной дроби в степень:

чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.

Пример 7. Возведем дробь 2a2b4 в третью степень.

Воспользуемся правилом возведения в степень:

2a2b43=(2a2)3(b4)3=8a6b12.

Деление дробей

При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например: 38:25=38∙52=1516.

Так же поступают при делении любых рациональных дробей:

ab:cd=ab∙dc=adbc,

где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.

Это равенство выражает правило деления рациональных дробей:

чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

Пример 8. Разделим дроби 7a2b3:14ab.

Воспользуемся правилом деления дробей:

7a2b3:14ab=7a2b3·b14a=7a2b14ab3=a2b2.

Деление дробных чисел. Деление обыкновенных дробей: правила, примеры, решения

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры.

Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей.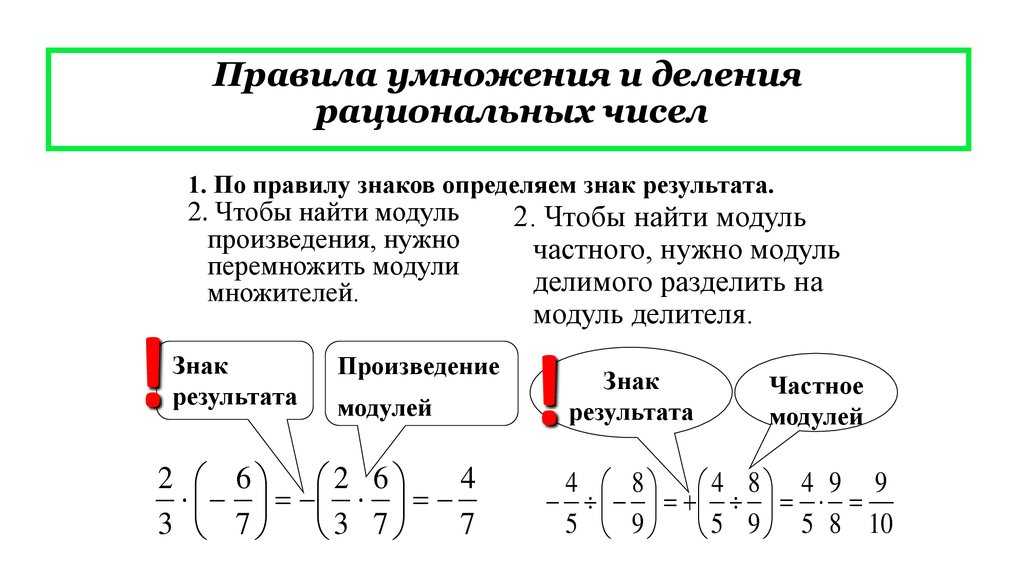

То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».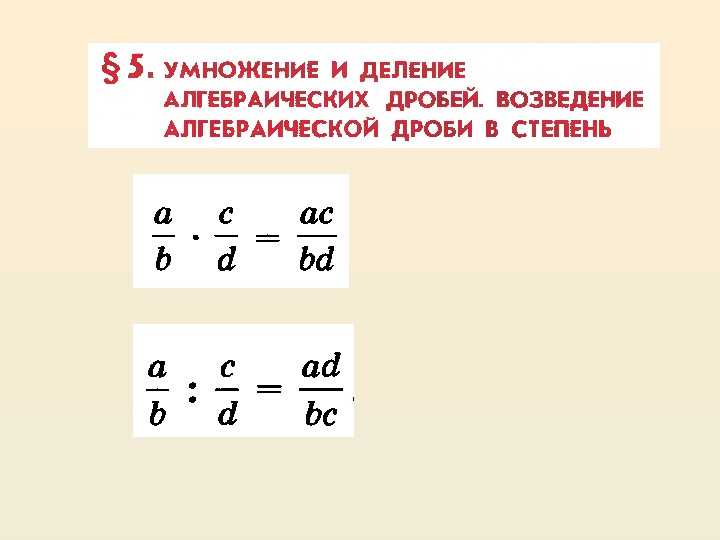

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Умножение дробей

151. По определению умножения, умножение на дробь — это взятие части множимого столько раз, сколько одинаковых частей единицы в множителе. (Статья 88.) Теперь знаменатель дроби показывает, на какие части предполагается разделить целостную единицу; а числитель показывает, сколько из этих частей принадлежит данной дроби. Следовательно, при умножении на дробь множимое должно быть разделено на такие части, которые обозначены знаменателем; и затем одна из этих частей должна быть повторена столько раз, сколько требует числитель.

Предположим, что $a$ нужно умножить на $\frac{3}{4}$.

Четвертая часть $a$ равна $\frac{a}{4}$.

Это $3$, умноженное на $\frac{a}{4} + \frac{a}{4} + \frac{a}{4} = \frac{3a}{4}$. (Статья 145 )

Опять же, предположим, что $\frac{a}{b}$ нужно умножить на $\frac{3}{4}$.

Одна четвертая часть $\frac{a}{b}$ равна $\frac{a}{4b}$. (Статья 135.)

Это $3$, умноженное на $\frac{a}{4b}+\frac{a}{4b}+\frac{a}{4b}=\frac{3a}{4b}$, искомое произведение.

Подобным образом любое дробное множимое можно разделить на части, умножив знаменатель; и одна из частей может повторяться, умножая числитель. Тогда имеем следующее правило:

152. ЧТОБЫ УМНОЖИТЬ Дроби, ПЕРЕМНОЖИТЕ ЧИСЛИТЕЛИ ВМЕСТЕ, ПОЛУЧИТЕ НОВЫЙ ЧИСЛИТЕЛЬ, И ЗНАМЕНАТЕЛИ ВМЕСТЕ, ПОЛУЧИТЕ НОВЫЙ ЗНАМЕНАТЕЛЬ.

Бывший. 1. Умножьте $\frac{3b}{c}$ на $\frac{d}{2m}$. Произведение $\frac{3bd}{2cm}$.

2. Умножить $\frac{a + d}{y}$ на $\frac{4h}{m — 2}$. Произведение $\frac{(4ah+4dh)}{(my — 2y)}$.

153. Метод умножения тот же, когда нужно умножить более двух дробей.

Перемножьте вместе $\frac{a}{b}, \frac{c}{d}$ и $\frac{m}{y}$. Произведение $\frac{acm}{bdy}$.

Для ix $\frac{a}{b}\cdot\frac{c}{d}$ равно последнему артикулу $\frac{ac}{bd}$, а это в $\frac{m}{y }$ равно $\frac{acm}{bdy}$.

2. Мульт. $\frac{3 + b}{n}, \frac{1}{h}$ и $\frac{d}{r + 2}$.

154. Умножение иногда можно сократить, отбрасывая равные множители из числителей и знаменателей.

1. Умножьте $\frac{a}{r}$ на $\frac{h}{a}$ и $\frac{d}{y}$. Произведение $\frac{dh}{ry}$.

Здесь а, находящееся в одном из числителей и в одном из знаменателей, может быть опущено. Если его сохранить, произведение будет $\frac{adh}{ary}$. Но это снижено до более низких сроков, согласно ст. 142, станет как раньше $\frac{dh}{ry}$.

Необходимо, чтобы множители, отбрасываемые из числителей, были в точности равны тем, которые отбрасывались из знаменателей. В последнем примере существо в двух числителях и только в одном знаменателе должно быть сохранено в одном из числителей.

2. Умножьте $\frac{a + d}{y}$ на $\frac{my}{ah}$. Произведение $\frac{am + dm}{ah}$.

Здесь, хотя одна и та же буква а стоит в одном из числителей и в одном из знаменателей, но так как она не стоит в в каждом члене числителя, ее нельзя сокращать.

3. Умножьте $\frac{am + d}{h}$ на $\frac{h}{m}$ и $\frac{3r}{5a}$.

Если при выполнении этих сокращений обнаружится какая-либо трудность, то лучше произвести умножение, не опуская ни одного из множителей; и впоследствии сократить произведение до более низких условий.

155. При перемножении дроби и целого числа числитель дроби умножается на целое число. Знаменатель не меняется; кроме случаев, когда деление знаменателя заменено умножением числителя, согласно ст. 136.

Таким образом, $a\cdot\frac{m}{y} = \frac{am}{y}$. Для $a = \frac{a}{1}$; и $\frac{a}{1}\cdot\frac{m}{y} = \frac{am}{y}$.

Итак, $r\cdot\frac{x}{d}\cdot\frac{h + 1}{3} = \frac{hrx + rx}{3d}$. И $a\cdot\frac{1}{b} = \frac{a}{b}$. Следовательно,

156. ДРОБЬ УМНОЖАЕТСЯ НА ВЕЛИЧИНУ, РАВНУЮ ЕЕ ЗНАМЕНАТЕЛЮ, BT ОТНОСЯ ИЗ ЗНАМЕНАТЕЛЯ.

Таким образом, $\frac{a}{b}\cdot b = a$. Для $\frac{a}{b}\cdot b = \frac{ab}{b}$. Но буква $b$, стоящая и в числителе, и в знаменателе, может быть опущена (статья 142).

Итак, $\frac{3m}{a — y}\cdot(a — y) = 3m$.

По такому же принципу дробь умножается на любое число в знаменателе с коэффициентом , путем вычитания этого множителя.

Таким образом, $\frac{a}{by}\cdot y = \frac{ay}{by}= \frac{a}{b}$. И $\frac{h}{24}\cdot 6 = \frac{h}{4}$.

157. Из определения умножения на дробь следует, что то, что обычно называют составной дробью , есть произведение двух или более дробей. Таким образом, $\frac{3}{4}$ из $\frac{a}{b}$ равно $\frac{3}{4}\cdot\frac{a}{b}$. Ибо $\frac{3}{4}$ из $\frac{a}{b}$ есть $\frac{1}{4}$ из $\frac{a}{b}$, взятое трижды, т.е. , $\frac{a}{4b}+\frac{a}{4b}+\frac{a}{4b}$. Но это то же самое, что $\frac{a}{b}$, умноженное на $\frac{3}{4}$. (Статья 151.)

Следовательно, приводить сложную дробь к простой, это то же самое, что умножать дроби друг на друга.

Бывший. 1. Уменьшите $\frac{2}{7}$ из $\frac{a}{b+2}$. Ответ $\frac{2a}{7b+14}$.

2. Сократите $\frac{2}{3}$ из $\frac{4}{5}$ из $\frac{b + h}{2a — m}$. Ответ $\frac{8b + 8h}{30a — 15m}$.

3. Сократите $\frac{1}{7}$ из $\frac{1}{3}$ из $\frac{1}{8 — d}$. Ответ $\frac{1}{168 — 21d}$.

158. Выражение $\frac{2}{3}a, \frac{1}{5}b, \frac{4}{7}y, \& c$. эквивалентны $\frac{2a}{3}, \frac{b}{5}, \frac{4y}{7}$. Для $\frac{2}{3}a$ это $\frac{2}{3}$ числа a, что равно $\frac{2}{3}\cdot a=\frac{2a}{3 }$.(Статья 155.)

Метод перекрестного умножения — формула, вывод, примеры

В математике мы перемножаем члены уравнения крестом, чтобы определить неизвестные значения. Метод перекрестного умножения в основном используется для идентификации неизвестной переменной в уравнении. В методе перекрестного умножения мы умножаем числитель первой дроби и знаменатель второй дроби, числитель второй дроби и знаменатель первой дроби данного выражения или дроби. Метод перекрестного умножения — это способ решения уравнения, в котором неизвестная переменная входит в состав двух равных дробей. Используя перекрестное умножение, мы можем сравнить две дроби, чтобы найти, какая из них больше, а какая меньше. Когда две дроби составляют уравнение, произведения числителя с одной стороны и знаменателя с другой стороны равны. Это свойство равенства величин в форме произведения называется методом перекрестного умножения.

Пусть a/b = c/d — выражение. Теперь формула перекрестного умножения выглядит следующим образом:

 

Примечание. Метод перекрестного умножения неприменим, если какой-либо из знаменателей равен нулю, т. е. b и d = 0.

Как решить перекрестное умножение?

Следуйте шагам, приведенным ниже, при использовании метода перекрестного умножения.

Шаг 1: Сначала умножьте числитель в левой части дроби на знаменатель в правой части дроби.

Шаг 2: Затем умножьте числитель в правой части дроби на знаменатель в левой части дроби.

Шаг 3: Теперь приравняйте оба произведения.

Шаг 4: Наконец, найдите переменную.

Пример: Решите: (m + 1)/3 = 4/9.

Решение:

Дано: (m + 1)/3 = 4/9.

Путем умножения крестом получаем;

⇒ (м + 1) × 9= 4 × 3

⇒ 9m + 9 = 12

⇒ 9m = 12 – 9 = 3

Теперь разделите обе части уравнения на 9.

⇒ 9m/9 = 3/9

⇒ m 1/3

Следовательно, значение «m» равно 1/3.

Перекрестное умножение с переменными в обеих частях

Предположим, что у нас есть одна и та же переменная, присутствующая в обеих частях уравнения. Теперь мы можем применить метод перекрестного умножения для определения переменной. Давайте рассмотрим несколько примеров, чтобы лучше понять.

Пример: Решите: (x – 1)/2 = 8/(x – 1).

Решение:

Дано: (x – 1)/2 = 8/(x – 1) 

Перемножая, получаем;

(х – 1) × (х – 1) = 2 × 8

⇒ (х – 1) ² = 16 1) = +4

⇒ x = 4 + 1 = 5

(или)

⇒ (x – 1) = –4

⇒ x = –4 + 1 = –3

Отсюда значение x равно –3 или 5.

Перекрестное умножение для сравнения дробей

Используя перекрестное умножение, мы можем сравнить две дроби, чтобы найти, какая из них больше, а какая меньше, или проверить, эквивалентны ли две дроби или нет. У нас есть два метода сравнения дробей.

Способ 1:

Например, предположим, что 5/8 эквивалентно 10/24.

Примечание. Две дроби называются эквивалентными, если в результате перекрестного умножения обеих дробей получаются равные значения. То есть произведение в левой части (LHS) должно быть равно произведению в правой части (RHS).

5/8 = 10/24

Перемножая крест-накрест, мы получаем;

5 × 24 = 10 × 8

120 = 80

Здесь произведение в левой части, т. е. 120, не равно произведению в правой части, т. е. 80. Значит, наше утверждение неверно.

Отсюда можно сделать вывод, что 5/8 не эквивалентно 10/24.

Метод 2:

Выполните шаги, указанные ниже, чтобы сравнить дроби, если две дроби имеют разные знаменатели:

• Шаг 1: Сначала умножьте знаменатели обеих дробей, чтобы получить один и тот же знаменатель.
• Шаг 2: Теперь, чтобы получить числитель первой дроби, умножьте числитель одной дроби на знаменатель другой.
• Шаг 3: Опять же, чтобы получить числитель второй дроби, умножьте знаменатель первой дроби на числитель другой дроби.
• Шаг 4: Теперь сравните две новые дроби.

Пример: Сравните 2/3 и 4/9.

Решение:

Умножьте знаменатели, то есть 3 и 9, чтобы получить;

3 × 9 = 27

Итак, 27 — общий знаменатель двух дробей.

Теперь нам нужно найти числители обеих дробей.

Итак, перекрестным умножением:

2 × 9 = 18

4 × 3 = 12

Итак, две дроби равны 18/27 и 12/27.

Теперь, если мы сравним обе дроби, то увидим, что 18 больше 12, следовательно,

27/12 < 27/18

⇒ 9/4 < 2/3.

Итак, 4/9 меньше 2/3.

Решенные примеры квадратных уравнений

Пример 1: Решите 13/5 = a/2.

Решение:

Дано: 13/5 = a/2

Перемножая крест-накрест, мы получаем;

⇒ 13 × 2 = a × 5

⇒ 26 = 5a

Теперь разделите обе части уравнения на 5.

⇒ 26/5 = 5a/5

⇒ a = 26/5

2 Следовательно, значение «а» равно 26/5.

Пример 2: Сравните 4/7 и 3/4.

Решение:

Умножьте знаменатели, то есть 7 и 4, чтобы получить;

7 × 4 = 28

Итак, 28 — общий знаменатель двух дробей.

Теперь нам нужно найти числители обеих дробей.

Итак, перекрестным умножением:

4 × 4 = 16

7 × 3 = 21

Итак, две дроби равны 16/28 и 21/28.

Теперь, если мы сравним обе дроби, то увидим, что 21 больше 16, следовательно,

16/56 < 21/56

⇒ 4/7 < 3/4.

Итак, 4/7 меньше 3/4.

Пример 3: Решите: 3/(x+6) = 5/8.

Решение:

Дано: 3/(x+6) = 5/8

Путем перекрестного умножения получаем

3 × 8 = 5 × (x + 6)

= 5x + 30

⇒ 5x = 24 – 30 = –6

Теперь разделите обе части уравнения на 5.

⇒ 5x/5 = –6/5

⇒ x = –6/5

Следовательно, значение «x» равно –6/5.

Пример 4: Если стоимость 10 манго составляет рупий. 350, то сколько будет стоить два десятка таких манго?

Решение:

Учитывая, что стоимость 10 манго = ₨ 350

Итак, стоимость 1 манго = 350/10  ————— (1)

Пусть стоимость двух десятков манго, то есть 24 манго будут «х».

Итак, стоимость 1 манго = x/24————— (1)

Из уравнений (1) и (2)

350/10 = х/24

Путем перекрестного умножения получаем;

350 × 24 = 10 × x

⇒ x = (350 × 24)/10

⇒ x = 840

Следовательно, стоимость двух дюжин манго составляет 840 фунтов стерлингов.

900 Найти эквивалентно ли 6/7 36/42 или нет.

Решение:

Две дроби называются эквивалентными, если перекрестное умножение обеих дробей дает равные значения.

6/7 = 36/42

Применяя перекрестное умножение, мы получаем;

6 × 42 = 36 × 7

252 = 252

Поскольку оба значения равны, обе дроби эквивалентны.

Следовательно, 6/7 эквивалентно 36/42.

Часто задаваемые вопросы о перекрестном умножении

Вопрос 1: Что подразумевается под перекрестным умножением?

Ответ:

Когда две дроби составляют уравнение, произведения числителя с одной стороны и знаменателя с другой стороны равны. Это свойство равенства величин в форме произведения называется методом перекрестного умножения. Метод перекрестного умножения неприменим, если какой-либо из знаменателей равен нулю, т. е. b и d ≠ 0,

Если a/b = c/d , то ad = bc .

Вопрос 2. Как найти переменную с помощью перекрестного умножения?

Ответ:

Умножить числитель первой дроби на знаменатель второй дроби, числитель второй дроби и знаменатель первой дроби данного выражения или дроби и приравнять товары. Наконец, найдите переменную.