Умножения десятичных дробей правила: Умножение десятичной дроби на десятичную дробь — урок. Математика, 5 класс.

admin

§ Умножение десятичных дробей

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

  • Геометрия: начальная школа
  • Действия в столбик
  • Деление с остатком
  • Законы арифметики
  • Периметр
  • Порядок действий
  • Разряды и классы. Разрядные слагаемые
  • Счет в пределах 10 и 20

Математика 5 класс

  • Взаимно обратные числа и дроби
  • Десятичные дроби
  • Натуральные числа
  • Нахождение НОД и НОК
  • Обыкновенные дроби
  • Округление чисел
  • Перевод обыкновенной дроби в десятичную
  • Площадь
  • Проценты
  • Свойства сложения, вычитания, умножения и деления
  • Среднее арифметическое
  • Упрощение выражений
  • Уравнения 5 класс
  • Числовые и буквенные выражения

Математика 6 класс

  • Масштаб
  • Модуль числа
  • Окружность. Площадь круга
  • Отношение чисел
  • Отрицательные и положительные числа
  • Периодическая дробь
  • Признаки делимости
  • Пропорции
  • Рациональные числа
  • Система координат
  • Целые числа

Алгебра 7 класс

  • Алгебраические дроби
  • Как применять формулы сокращённого умножения
  • Многочлены
  • Одночлены
  • Системы уравнений
  • Степени
  • Уравнения
  • Формулы сокращённого умножения
  • Функция в математике

Геометрия 7 класс

  • Точка, прямая и отрезок
  • Что такое аксиома и теорема

Алгебра 8 класс

  • Квадратичная функция. Парабола
  • Квадратные неравенства
  • Квадратные уравнения
  • Квадратный корень
  • Неравенства
  • Системы неравенств
  • Стандартный вид числа
  • Теорема Виета

Алгебра 9 класс

  • Возрастание и убывание функции
  • Нули функции
  • Область определения функции
  • Отрицательная степень
  • Среднее
    геометрическое

Алгебра 10 класс

  • Иррациональные числа

Алгебра 11 класс

  • Факториал

Теоретически между теорией и практикой разницы практически нет.

Но практика показывает, что она есть. Йоги Бера

на главную

Введите тему

Русский язык Поддержать сайт

Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби

Умножение десятичных дробей происходит в три этапа.

  • Десятичные дроби записывают в столбик и умножают как обыкновенные числа.

  • Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.

  • В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.

Пример:


  • Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11 мы рассматриваем как 311, а 0,01 как 1.

  • Получили 311. Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй — два. Общее количество цифр после запятых:

    2 + 2 = 4

  • Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.

    У нас не хватает одной цифры, поэтому приписываем слева один ноль.

Запомните!

При умножении любой десятичной дроби на 10; 100; 1000 и т. д. запятая в десятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.

Примеры:

  • 70,1 · 10 = 701
  • 0,023 · 100 = 2,3
  • 5,6 · 1 000 = 5 600

Запомните!

Чтобы умножить десятичную дробь на 0,1;    0,01;    0,001 и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.

Считаем и ноль целых!

Примеры:

  • 12 · 0,1 = 1,2
  • 0,05 · 0,1 = 0,005
  • 1,256 · 0,01 = 0,012 56

Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби

на натуральное целое число, дробь

В данной публикации мы рассмотрим, каким образом десятичную дробь можно умножить на натуральное целое число или другую десятичную дробь. Также разберем примеры для закрепления теоретического материала.

  • Умножение десятичной дроби на натуральное число
    • Делитель – 10, 100, 1000, 10000 и т.д.
    • Делитель – любое число
  • Произведение десятичных дробей

Умножение десятичной дроби на натуральное число

Делитель – 10, 100, 1000, 10000 и т.д.

Чтобы умножить десятичную дробь на натуральное число 10, 100, 1000 и т.д., просто переносим запятую-разделитель вправо на столько нулей, сколько содержит это число.

Пример 1

3,67 ⋅ 10 = 36,7

Объяснение: Т.к. в числе 10 всего один ноль, то и запятую переносим на одну позицию вправо.

Пример 2

3,67 ⋅ 100 = 367

Объяснение: Т.к. в числе 100 два нуля, то запятую переносим на две позиции.

Пример 3

0,357 ⋅ 10 = 3,57

Объяснение: В числе 10 один ноль, следовательно, десятичный разделитель сдвигаем на одну позицию.

Пример 4

0,0043 ⋅ 1000 = 4,3

Объяснение: В числе 1000 три нуля, значит разделитель сдвигаем на три позиции.

Примечание: если количество нулей и, соответственно, позиций переноса разделителя больше, чем цифр после запятой, значит дописываем оставшиеся нули в конце полученного результата. Это работает и в обратную сторону (см. Пример 7 ниже).

Пример 5

3,67 ⋅ 1000 = 3670

Объяснение: В числе 1000 три нуля, следовательно разделитель переносим на две позиции и дописываем один ноль в конце найденного числа.

Делитель – любое число

Чтобы умножить десятичную дробь на любое натуральное целое число, отбрасываем запятую и выполняем умножение, как будто имеем дело не с дробью, а с обычным числом. Затем отсчитываем с конца полученного результата столько цифр, сколько было в дробной части исходной десятичной дроби, и ставим в этом месте запятую.

Пример 6: найдем произведение чисел 5,68 и 8.

Решение:

Убираем запятую в числе 5,68 и умножаем его на 8:
568 ⋅ 8 = 4544

Отсчитываем две цифры с конца и добавляем запятую-разделитель, т.е.:

5,68 ⋅ 8 = 45,44

Примечание: Если десятичная дробь меньше 1 (т.е. целая часть равна 0), то отбросив запятую, мы не учитываем при умножении ноль/нули, которые идут в начале.

Пример 7: умножим число 0,089 на 7.

Решение:

Убираем запятую в числе 0,089 и, отбросив нули, умножаем его на 7:
89 ⋅ 7 = 623

Здесь обратная ситуация рассмотренной ранее в Примере 5. С конца отсчитываем 3 цифры, ставим запятую и добавляем ноль слева от нее, т.е.:

0,089 ⋅ 7 = 0,623

Произведение десятичных дробей

Чтобы умножить одну десятичную дробь на другую, выполняем практически те же самые действия, что и описанные в разделе выше – убираем запятые, на этот раз в обеих дробях, и умножаем их как обычные числа. Затем отсчитываем с конца найденного результата столько цифр, сколько их было вместе в дробных частях обоих множителей, и пишем запятую.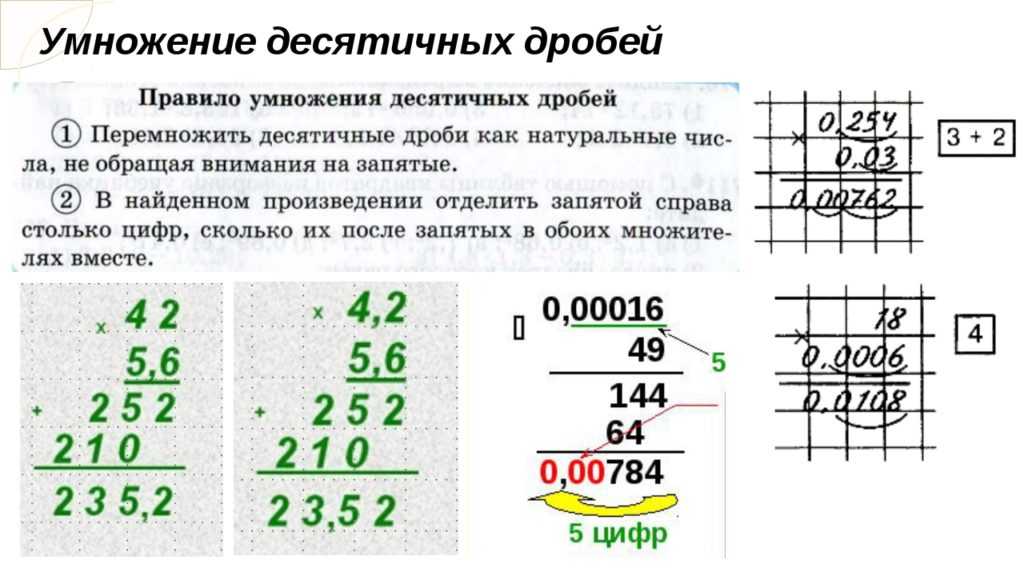

Пример 8: найдем, сколько будет 5,615 ⋅ 2,14.

Решение:

5615 ⋅ 214 = 1201610

Отсчитать с конца нужно 5 цифр, т.к. в первом множителе после запятой было три цифры, во втором – две (5 = 3 + 2). Т.е.:

5,615 ⋅ 2,14 = 12,01610 = 12,0161

Пример 9: вычислим, сколько будет 0,24 ⋅ 3,17.

Решение:

24 ⋅ 317 = 7608

Отсекаем запятой 4 цифры с конца и получаем ответ – 0,7608.

Числа — Умножение десятичных дробей — Первый взгляд

Числа — Умножение десятичных дробей — Первый взгляд
Дом | Учитель | Родители | Глоссарий | О нас

Чтобы умножить десятичные числа:

  1. Умножить числа так, как если бы они были целыми числами.
  • Выстроить цифры справа — не выравнивают десятичные точки .
  • Запуск справа, умножьте каждую цифру верхнего числа на каждую цифру нижнего нижнее число, как и с целыми числами.
  • Добавить товары.
  1. Поставьте запятую в ответе, начиная справа и двигаясь количество знаков, равное сумме десятичных знаков в обоих числах умноженный.

Помощь с домашним заданием | Предварительная алгебра | Номера Отправить эту страницу другу по электронной почте
Поиск







  ·   Умножение десятичных дробей












Первый Взгляд   В Глубина   Примеры   Тренировка

Умножение десятичных дробей

Умножение десятичных дробей

Умножение десятичных дробей

Показать рекламу

Скрыть рекламу
О рекламе

Умножьте без десятичной точки, затем снова вставьте ее в нужное место!

Как умножать десятичные числа

Просто выполните следующие действия:

  • Умножайте как обычно, игнорируя десятичные точки.
  • Затем поставьте в ответе запятую — в нем будет столько знаков после запятой, сколько двух исходных чисел вместе взятых.

Другими словами, просто подсчитайте, сколько чисел после запятой в обоих числах , которые вы умножаете, тогда в ответе должно быть столько же чисел после и десятичной запятой.

 

Пример: умножить 0,03 на 1,1

начать с:

 		 0,03 × 1,1

умножить без десятичной точки:

   3 × 11 = 33

0.03 имеет 2 десятичных знака ,
и 1.1 имеет 1 десятичный знак ,
поэтому ответ имеет 3 десятичных знака :

   0,033

 

См. анимацию умножения десятичных знаков

Как это работает?

Потому что, когда вы умножаете без десятичной точки, вы действительно сдвигаете десятичную точку вправо до убери с дороги :

Оригинал: 1 ход: 2 хода: 3 хода:
0,03 × 1,1     0,3  × 1,1     3.

admin

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

2024 © Все права защищены.