Урок для 4 класса по теме: «Письменное умножение двух чисел, оканчивающихся нулями»
Тема: « Письменное умножение двух чисел, оканчивающихся нулями»
Цель: познакомить с письменными приемами умножения двух многозначных чисел, оканчивающихся нулями; совершенствовать вычислительные навыки.
Задачи: научить работать по алгоритму «Умножение двух чисел, оканчивающихся нулями»; развивать вычислительные навыки, совершенствовать умения решать задачи; развивать интерес к предмету, математическую речь учащихся, логическое мышление.
Оборудование:
Учебник «Математика», 4 класс, ч.2.
Мультимедийная установка
Презентация к уроку
Карточки с заданиями для индивидуальной работы.
Ход урока
Организационный момент.
1. Эмоциональный настрой.
— Одна хорошая минута сделала одно хорошее дело,
Десять хороших минут сделали десять хороших дел.
А сколько хороших дел можно сделать за целый урок? (45)
— Молодцы!
— Я желаю всем сегодня сделать много хороших дел и девиз нашего урока « Математику учить – ум точить» (2 слайд)
— Повернитесь друг к другу, пожелайте удачи, добра… Ребята, а что нужно человеку, чтобы быть успешным, жизнерадостным, здоровым? Положительные эмоции, хорошие знания. Улыбнитесь друг другу. Итак, ребята, я хочу, чтобы вы сегодня получили только положительные эмоции от своих результатов, от урока.
2. Устный счет.
— У нас сегодня урок необычный. И начать я хочу с высказывания: « Математика – гимнастика ума». Как вы его понимаете? Давайте подумаем, что же мы должны будем сделать сегодня, чтобы гимнастика принесла нам пользу? Нам предстоит много думать, решать, повторять. Да, да! Мы будем как спортсмены на тренировке, ведь нам предстоит много работы, чтобы повторить пройденный материал и научиться новому. Спортсмены тренируют свои мышцы, а мы будем тренировать свой мозг. У каждого спортсмена есть свой тренер, который составляет специальную программу, подбирает упражнения, и сегодня нашими тренерами будут наши гости.
Да, да! Мы будем как спортсмены на тренировке, ведь нам предстоит много работы, чтобы повторить пройденный материал и научиться новому. Спортсмены тренируют свои мышцы, а мы будем тренировать свой мозг. У каждого спортсмена есть свой тренер, который составляет специальную программу, подбирает упражнения, и сегодня нашими тренерами будут наши гости.
( слайд 3)
— Итак, каждый спортсмен с вами проведет тренировку. В течение урока мы будем фиксировать успех ваших достижений в виде оценок. Для начала небольшая разминка и проведет ее бегун. ( слайд 4).
— А задание называется : «Реши цепочку». Тот кто первым решит эту цепочку, тот окажется победителем в беге.
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 = 23997
Ответ ( 5 слайд)
— А теперь задание усложняется. И беговые упражнения переходят в беговую эстафету. Главная задача этого задания выполнить все правильно и как можно быстрее. Работа в парах. Решаем пример, передаем на следующую парту, какой ряд быстрее решит примеры, тот победитель. (Слайд 6)
Работа в парах. Решаем пример, передаем на следующую парту, какой ряд быстрее решит примеры, тот победитель. (Слайд 6)
(Задания на карточках)
240*2+520:2-250:10+24*100 = ? (3115)Ответ (Слайд 7)
Новая тема
— Молодцы! Бегать вы умеете. А теперь у нас в гостях следующие спортсмены. Кто это ? ( Хоккесты) (Слайд 8)
— Пока мы с бегуном бегали, в гости к нам пришел новый тренер . Это оккеист. А вы знаете, чтобы играть в хоккей, нужен каток. Но он не достроен. У него необходимо построить ограждение и наложить искусственный лед. А для этого необходимо найти периметр и площадь катка, если известно, что длина 1200 метров, а ширина в 2 раза меньше.
1) 1200: 2= 600 (м) – ширина
2) (1200+600)*2= 3600 (м) – периметр
3) 1200*600= ?
— Вот встает проблема, как же найти площадь катка, если мы не умеем решать эту задачу. На прошлом уроке мы учились решать примеры, в котором одно число, оканчивающееся нулями. А сейчас нам встретился пример, в котором оба числа оканчиваются нулями. Значит , что мы будем изучать сегодня на уроке? Правильно! Мы будем учиться решать примеры, где оба числа оканчиваются нулями. Назовите тему нашего урока: Письменное умножение чисел, оканчивающихся нулями. И цель нашего урока: научиться решать такие примеры.
На прошлом уроке мы учились решать примеры, в котором одно число, оканчивающееся нулями. А сейчас нам встретился пример, в котором оба числа оканчиваются нулями. Значит , что мы будем изучать сегодня на уроке? Правильно! Мы будем учиться решать примеры, где оба числа оканчиваются нулями. Назовите тему нашего урока: Письменное умножение чисел, оканчивающихся нулями. И цель нашего урока: научиться решать такие примеры.
Перед тем как научиться решать примеры, сделаем физкультурную паузу.
Вот любимая зарядка,
Выполняем по порядку.
Быстро встаньте, улыбнитесь,
Выше, выше потянитесь,
Ну-ка плечи распрямите,
Поднимите, опустите,
Влево, вправо повернулись,
Рук коленями коснулись,
Сели – встали, сели – встали,
Вы, надеюсь, не устали?
Надо всем свободно встать
И спокойно подышать.
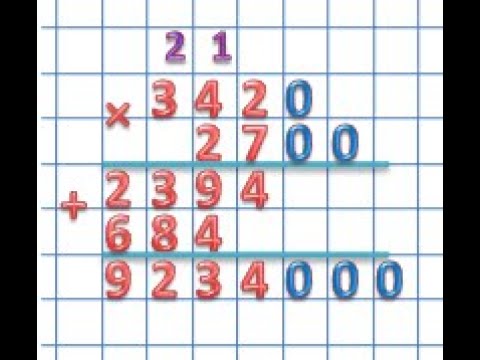
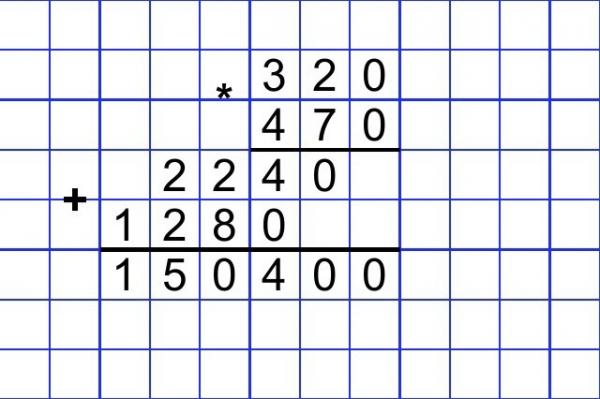
Объяснение учителя как решать пример, в котором два числа оканчиваются нулями.
1200 — Сколько сотен в числе 1200?
* 600 — Число 600 раскладываем на множители. Как это можно сделать?
_____ (6*100). А теперь считаем 12 сотен *6*100=7200сотен=720000
720000
— Используя наши знания, оформляем письменную запись. (Запись в столбик).
-Значит сделаем вывод, чтобы найти произведение круглых чисел, надо выполнить умножение, не глядя на нули, а затем приписать столько нулей, сколько в обоих множителях.
-Молодцы. Прекрасно справились с заданием, значит наши хоккеисты не останутся без хоккейного корта.
— А сейчас откройте учебники. Прочитаем правило на с.11. И следующими тренерами будут у нас шахматисты.
А как вы знаете, что шахматистам приходится выполнять разные вычисления, и они будут тренировать нас решать примеры на с. 11 № 55. Все решают в тетрадях, а один на доске.
11 № 55. Все решают в тетрадях, а один на доске.
_Молодцы! Справились и с этим заданием.
— И последнее задание, которое нам скинули с неба парашутисты, это задание на смекалку. С. 10. № 54.
-Молодцы!!! Прекрасно справились со всеми заданиями.
Итог урока.
— Скажите, какая проблема встала перед нами, когда мы решали задачу?
— Как вы думаете, справились ли с этой проблемой?
— Что самое трудное показалось вам на уроке?
— Если на следующем уроке в самостоятельной работе встретятся такие же примеры, вы справитесь с ними?
— Молодцы! Вы хорошо потрудились, и получили за это свои результаты. А чтобы достичь высот в математике, необходимо как альпинистам взбираться на гору знаний, медленно шаг за шагом не торопясь, дружно. И тогда, у вас будут высокие результаты. И подводя итог, я хочу сказать спасибо всем за хорошую плодотворную работу на уроке, за поддержку одноклассников и взаимопонимание на всем уроке.
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
0 · 1000 + 25000 – 5000 : 5 – 3000: 1000 =
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
240*2+520:2-250:10+24*100 = ?
№п/п | Этапы урока | Деятельность учителя | Деятельность учащихся | Формируемые УУД |
1. | Самоопределение к деятельности. /2 мин/ Цель: мотивация учащихся к учебной деятельности на личностно-значимом уровне | Создаёт условия для возникновения внутренней потребности включения в деятельность. Прозвенел звонок – начинается урок. Повернитесь друг к другу, пожелайте удачи, добра… улыбнитесь. Учитель предлагает занять свои рабочие места. — Много лет тому назад один античный мудрец сказал: «Не для школы, а для жизни мы учимся». — В чём же заключалась его мудрость? — А для чего вы учитесь? — Для чего вы учите математику? — Очень ли важен урок математики? — Тогда я желаю вам удачи! Будем двигаться дальше за новыми знаниями Девиз нашего урока: « С малой удачи начинается большой успех». — Как вы понимаете данное высказывание? — Вы с ним согласны? Не будем терять времени. | Стоят в круге. Включаются в учебную деятельность. Поддерживают диалог. Хором дополняют реплику учителя. Диалог в круге. — Положительные эмоции, внимание других, доброе отношение окружающих, хорошие знания и т.д. Объясняют смысл высказывания. Садятся за парты. | Личностные УУД: самоопределение. |
2. | Актуализация знаний. /5 мин/ Цель: готовность мышления и осознания потребности к построению нового способа действий. | Ведёт подводящий диалог. ( Активизирует у учащихся мыслительные операции, внимание, память) — Посмотрите внимательно на экран и предложите работу, которую мы можем выполнить. -Какую закономерность вы установили, исследуя первое выражение? -Предлагаю, прежде чем вы назовёте произведение, объяснить приём умножения. 1) 6·9= 54 2) 26·3 3) 139·0 4) 264·10 5) 92· 100 6) 523·300 ( По мере поступления ответов на экране появляются результаты рассуждения) (Слайд 3) | Участвуют в диалоге. — Можно посчитать треугольники. — Можно выявить закономерность. 1) табличное умножение 2) внетабличное умножение ( разбиваем на разрядные слагаемые) 3) умножение на нуль 4) увеличение числа в 10 раз, приём умножения на 10 5) приём умножения на 100 6) затрудняются | Познавательные УУД: — общеучебные; — логические. Коммуникативные УУД: умение вступать в диалог и участвовать в коллективном обсуждении проблемы. |
3. | Постановка учебной задачи. Создание проблемной ситуации. /5 мин/ Цель: выявление места и причины затруднения, постановка цели урока. | 1. Ведёт побуждающий диалог. — Почему вы затруднились назвать произведение в 6 треугольнике? Побуждает к осознанию темы и цели урока. — Как вы думаете, какова же тема нашего урока? (Слайд 4) — Я предлагаю вам два варианта решения данной проблемы. 2. Стимулирует к деятельности. Предлагает два варианта: — Первый: сама покажу вам приём умножения. Второй – на основе ранее полученных знаний попробуете решить сами. — Какой вариант выберете вы и почему? | Участвуют в диалоге. — Не можем, так как с этим приёмом умножения ещё не знакомы (умножение на числа, оканчивающееся нулями) Формулируют тему урока. -Умножение многозначных чисел на числа, которые оканчиваются нулями. Дети предпочитают «открывать» новое знание сами. | Познавательные УУД: — постановка и формулирование проблемы; — поиск и выделение необходимой информации. Регулятивные УУД: целеполагание. Коммуникативные УУД: умение выражать свои мысли. |
4 | « Открытие» детьми нового знания. /9 мин/ Цель: построение детьми нового способа действий и формирование способности к его выполнению. | 1. Организует деятельность. — Великий Сократ говорил о том, что научиться играть на флейте можно только, играя самому. -Так и вы можете научиться умножать такие числа, думая только своей головой и пытаясь решить самостоятельно. (Слайд 5) — У кого есть предположения, как можно его вычислить? — Хорошо, если вычислим на калькуляторе, получим готовый ответ, мы пополним копилку наших знаний? — Вы предложили устно выполнить вычисления. Как именно? — Какой закон математики вы применили? ( Слайд 6) — Всегда ли устно можно быстро и правильно выполнить умножение многозначного числа, учитывая то, что числа могут быть достаточно большими? — Какой способ мы можем ещё использовать? — Умеем мы это правильно делать? — Дайте более точную формулировку темы нашего урока. — Какую учебную задачу вы поставите перед собой? ( Слайд 7) 2.Предлагает записать пример столбиком самостоятельно и решить его. — Где мы можем проверить правильность наших рассуждений? — Откройте учебники на стр.75, внимательно рассмотрите образец и сравните со своим решением. — Я прошу поднять руку тех ребят, которые выполнили умножение так, как показано в учебнике. — Молодцы. Значит, вы умеете применять ранее полученные знания. — Открытые вами знания позволили закончить выполнение задания, сформулированного в начале урока? (Слайд 8) — Сейчас объясним приём умножения на доске. 3. Вызывает к доске ученика, верно решившего пример. — У кого другая запись? 4. Организует работу в парах по составлению алгоритма умножения. — Чтобы правильно решать такие примеры, нужно знать алгоритм решения. — Что такое алгоритм? — Сейчас мы его составим. У вас на партах карточки, на которых напечатаны действия алгоритма. Работая и обсуждая в парах, вы разложите карточки в нужном порядке. Выводит алгоритм на экран. (Слайд 9) | Выдвигают гипотезы: — устно — на калькуляторе — столбиком. -Нет. Объясняют приём умножения. 523·300= 523·(3·100)= 523·3·100=156900 — Сочетательный закон. — Не всегда. — Решение столбиком. -Нет. Дети формулируют тему и учебную задачу урока:«Письменное умножение на числа, оканчивающиеся нулями». — Мы должны научиться умножать письменно многозначные числа /в столбик /на числа, которые оканчиваются нулями. Пытаются решить пример самостоятельно. — В учебнике. Дети открывают учебники и сравнивают своё решение с образцом. Называют произведение в треугольнике. Объясняют приём умножения. — Выполняем умножение, не глядя на нули, а затем к результату приписываем столько нулей, сколько содержится во втором множителе. — Пошаговое выполнение действий. Открывают конверты. Располагают карточки в нужном порядке. Одна пара зачитывает. 1.Второй множитель записываю так, чтобы нули остались в стороне. 2.Умножаю многозначное число на число, не обращая внимания на нули. 3.К полученному результату приписываю нули. 4.Читаю ответ. | Познавательные УУД: — построение логической цепи рассуждений; — самостоятельное создание способов решения проблем поискового характера. Коммуникативные УУД: — инициативное сотрудничество в поиске и сборе информации со сверстниками и учителем. |
5. | Первичное закрепление с проговарива- нием. /5 мин/ Цель: зафиксировать способ письменного умножения на числа, оканчивающиеся нулями. | 1.Организует работу по закреплению нового знания. Фронтальная работа с проговариванием вслух. — Закрепим полученные знания, выполнив письменное умножение с объяснением на доске. (с.75 № 369 – 1 строчка ) К доске вызывает сначала «сильного» ученика, затем — «слабого». — Понятен ли вам этот вычислительный приём? — Как проверить, что вы его усвоили? Даёт инструктаж по выполнению задания. — У каждого из вас имеется карточка. На ней записаны примеры. (735 ·500 6307 · 40) Предлагаю спрогнозировать предполагаемый результат: в верхнем углу карточки вы видите круг. Закрасьте его зелёным цветом, если вы уверены в своих силах. Жёлтым цветом – если сомневаетесь. Красным цветом – если вам нужна помощь. Кому нужна помощь, обращайтесь к алгоритму. Критерий оценки – правильность счёта, безошибочность. А теперь приступим. — Передайте карточку соседу. Выводит ответы к заданию на экран. (Слайд 10) — Если нет ошибок, закрасьте нижний круг зелёным цветом, если есть ошибки – жёлтым. — Верните карточку владельцу. — Совпал ли ваш прогноз с результатом? | Два ученика работают у доски, остальные – в тетради. — Решить примеры самостоятельно. Прогнозируют результат и выполняют задание. Взаимопроверка по готовым ответам с доски. Ответы детей. (Мой прогноз совпал с результатом, был уверен и правильно выполнил. Мой прогноз не совпал с результатом, я был уверен, что справлюсь, но допустил ошибку). | Коммуникативные УУД: умение выражать свои мысли. Регулятивные УУД: овладение алгоритмом умножения. |
6. | Взаимоконтроль с проверкой по эталону. /3 мин/ Цель: тренировать способность к самоконтролю и самооценке, проверить способность к умножению многозначных чисел на числа, оканчивающиеся нулями. | Регулятивные УУД: -прогнозирование; -самоконтроль; -коррекция. Коммуникативные УУД: учебное сотрудничество. | ||
7. | Физминутка. /1 мин/ | Комплекс «Красивая осанка» 1. «Поза дерева». Упражнение выполняется стоя или сидя за столом, ноги вместе, стопы прижаты к полу, спина прямая. Сделать спокойный вдох и выдох, плавно поднять руки вверх, ладонями друг к другу, пальцы вместе. Потянуться всем телом. Дыхание произвольное, спокойное. Держать позу 15-20 секунд. Плавно опустить руки и расслабиться. 2. «Поза статуи». Выполняется сидя или стоя, руки опущены. Завести руки за спину, соединить ладони. Затем, вывернув сложенные руки пальцами вверх, расположить кисти так, чтобы мизинцы по всей длине касались позвоночника. Локти приподнять, спина прямая, плечи обязательно отвести назад. | ||
8. | Включение нового в систему знаний и повторения. /7 мин/ Цель: — закрепление умения решать текстовые задачи; — применение нового способа действия; — создание ситуации успеха. | 1. Организует индивидуальную работу с последующей проверкой в группе и самопроверкой по эталону. Внимание на экран. (Слайд 11) Перед вами 3 задания. — Какое из них далеко от темы нашего урока? А) 736·300 6 324· 50 Б) 6 895+ 72 456 + 658 В) 784 · 600 + 2 907 · 30 Осталось 3 задания. — Выберите себе то, которое для вас более интересно и которое вы в силах выполнить. Выполните его. / Учитель проходит по классу, наблюдает, какой уровень выбрал каждый из учащихся и кладёт рядом с его работой фишку (цвет фишки – уровень сложности выбранного задания)/ — Ребята, попрошу вас собраться в группы в соответствии с выполненным заданием. — Садитесь на свои места, посмотрите внимательно на экран и сверьте свою работу с образцом. (Слайд 12) 2. Организует работу над задачей. — Вернёмся к учебнику. Задача № 370. — Прочитайте задачу. — О чём говорится в задаче? — Что известно? — Как звучит вопрос задачи? Выделите главные слова и сделайте краткую запись задачи. (Слайд 13) М. – 8900 пар Ж.- ? в 2 раза , чем мужской 40000 пар Д. -? — Сколько пар мужской обуви продали? (8900) — Женской обуви? (Не знаем точно, но в 2 раза больше, чем мужской). — Что можно узнать, используя эти данные? (Найти сколько пар женской обуви продали) -Как? Запишите и вычислите.(8900*2= 17800) — Можем ли теперь ответить на вопрос задачи? (Нет) -Почему? (Нужно найти, сколько продали мужской и женской вместе) Найдите. (890+1780= 26700) — Теперь можем ответить на главный вопрос задачи? (Да). -Решите (40000 — 26700=13300) -Запишите ответ. | Анализируют и делают вывод, что лишнее задание Б. — Лишнее задание Б, так как оно не подходит к теме нашего урока. Оно подошло бы к теме – сложение многозначных чисел. Формулируют уровень сложности заданий и конкретизируют их. А – выполнить умножение столбиком, В — вспомнить порядок действий и вычислить Выбирают и выполняют задание. Собираются в группы по цвету фишек с целью взаимопроверки. Сверяют решение с образцом на слайдах. Исправляют ошибки и фиксируют затруднения. Дети отвечают на вопросы учителя по содержанию задачи. 1 ученик записывает решение задачи на доске. | Познавательные УУД: — анализ с целью выделения главных признаков; — умение осознанно строить речевое высказывание в устной форме; — выделение и поиск необходимой информации. Коммуникативные УУД: — умение достаточно полно и чётко выражать мысли; -интегрирование в группы и продуктивное взаимодействие. Регулятивные УУД: — планирование; — контроль; — коррекция; — самооценка. |
9. | Рефлексия учебной деятельности. / 3 мин/ Цель: — оценивание результатов собственной деятельности; — осознание метода построения границ применения нового знания. | Благодарит ребят за работу. — Вспомните девиз нашего урока. (Слайд 14) — Огромное трудолюбие и ваша тяга к знаниям помогла нам сделать на уроке открытие. Эта удача приблизила ещё на один шаг каждого из вас к успеху. — Какая тема нашего урока? (Слайд 15) — Какую учебную задачу мы ставили перед собой? (Слайд 16) — Чему новому научились? Над чем ещё надо поработать? (Слайд 17) — Достигли мы успеха? В память о нашем уроке, чтобы вы ничего не забыли — домашнее задание. Проводит инструктаж домашнего задания. С. 75 № 369 (2) – обязательно для всех, № 373 – предлагаю тем, кто не боится трудностей. Оценивание работы учащихся. (Слайд 19) — Я прошу подняться тех детей, которые считают, что их объём работы на уроке можно оценить. — Почему ты так считаешь? ВЫСТАВЛЕНИЕ ОЦЕНОК Всем спасибо за урок. (Слайд 20) | Проговаривают девиз урока. « С малой удачи начинается большой успех». Умножение многозначных на числа, оканчивающиеся нулями. — Научиться умножать письменно на числа, оканчивающиеся нулями. -Достигли. Записывают задание в дневники. Тот, кто поднялся, анализирует и оценивает свою работу на уроке. Высказывают своё мнение. | Регулятивные: — оценка того, что усвоено, осознание качества и уровня усвоения. Познавательные: — умение структурировать знания. Коммуникативные УУД: — аргументировать свои высказывания. |
Видеоурок: Умножение двузначных чисел: метод столбца
Расшифровка видеозаписи
Умножение двузначных чисел: метод Метод столбца
В этом видео мы узнаем как использовать стандартный письменный метод или алгоритм для умножения двузначного числа другим двузначным числом. И куда надо, туда идем перегруппироваться, чтобы помочь нам найти ответ.
Представим, что мы хотим
умножьте вместе 35 и 24. Теперь мы знаем, что можем разделить
35 на 30 и пять. И если мы хотим умножить 35 на
однозначное число, такое как четыре, нам просто нужно убедиться, что оба
части умножались на четыре: пять раз четыре, а затем 30 раз четыре. Теперь с вопросом, который мы
добрались сюда, мы не умножаем 35 на однозначное число. Нам нужно умножить его на
двузначное число. И так же, как мы можем думать о 35 как
30 и пять, мы можем разделить число, которое мы умножаем на 24, на 20 и
четыре. Таким образом, а также убедитесь, что мы
умножаем пять на четыре и 30 на четыре, нам нужно убедиться, что мы тоже умножаем
обе части 35 на 20 тоже.
И так же, как мы можем думать о 35 как
30 и пять, мы можем разделить число, которое мы умножаем на 24, на 20 и
четыре. Таким образом, а также убедитесь, что мы
умножаем пять на четыре и 30 на четыре, нам нужно убедиться, что мы тоже умножаем
обе части 35 на 20 тоже.
Другими словами, нам нужно выяснить
что такое пять умножить на 20, а также то, что будет 30 умножить на 20. Теперь эта диаграмма не такая, как мы
найти ответ. Мы нарисовали это здесь, потому что
это полезный способ показать нам, что нам нужно делать. Чтобы найти ответ, нам нужно
умножьте каждую часть числа 35 на каждую часть числа 24. Надеюсь, вы видите наши четыре
стрелки, что нам нужно сделать четыре умножения. Так это именно то, что мы собираемся
сделать сейчас, как мы используем метод столбца. Это будет связано с отработкой
ответы на четыре отдельных умножения, а затем сложение произведений в
конец, чтобы найти общую сумму.
Для нашего первого примера давайте
используйте эти цветные заголовки столбцов, а также мы будем использовать разные цвета для нашего
цифры. Итак, 35 — это три десятки и пять.
те. И мы хотим умножить это на 24
это две десятки и четыре единицы. Теперь, как мы сказали в начале,
нам нужно умножить обе части числа 35 на обе части числа 24. Итак, нам нужно сделать четыре
умножения. И для начала умножим
все на четыре единицы в 24. Итак, во-первых, что пять раз
четыре? Мой простой для начала
с: пять раз четыре равно 20. И мы можем написать число 20 тогда
под знаком равенства как первое из наших четырех умножений. И просто чтобы мы помнили, что мы
сделано, мы можем отметить сделанное нами умножение сбоку, которое было
пять раз четыре.
А теперь посмотрите, что еще нам нужно умножить на четвертую часть 24? Нам нужно умножить эту цифру здесь тоже на четыре. Теперь было бы очень легко смотреть при этом и думать про себя, что трижды четыре, потому что вы можете видеть цифра три. Нам нужно умножить на четыре. Но мы должны помнить, что это цифра три стоит в разряде десятков. Нам нужно найти ответ на 30 раза четыре. Теперь мы можем использовать идею из трех четверок, чтобы помочь нам, хотя. Мы знаем, что три четверки 12. Итак, три десятки умножить на четыре. будет таким же, как 12 10, то есть 120. Теперь, если мы остановимся на момент, вы можете видеть, что мы уже сделали? Мы умножили все в число 35, это пять и 30, на цифру четыре в 24.
Далее нам нужно умножить
все по десяткам части 24. И начинаем с пяти раз
20. Теперь снова, если мы посмотрим на эти
цифр, может показаться, что мы умножаем пять на два. Но мы видим, что наша цифра
два в разряде десятков. Это пять раз две десятки. Но опять же, мы можем использовать факты, которые мы
уже знают, чтобы помочь нам. Пять умножить на два будет 10, так что пять лотов
из двух десятков должно быть 10 10, что равно 100. Пять раз по 20 равно 100. Таким образом, после умножения пяти на 20,
самое последнее, что нам нужно сделать, это умножить 30 на 20.
Теперь снова, если мы посмотрим на эти
цифр, может показаться, что мы умножаем пять на два. Но мы видим, что наша цифра
два в разряде десятков. Это пять раз две десятки. Но опять же, мы можем использовать факты, которые мы
уже знают, чтобы помочь нам. Пять умножить на два будет 10, так что пять лотов
из двух десятков должно быть 10 10, что равно 100. Пять раз по 20 равно 100. Таким образом, после умножения пяти на 20,
самое последнее, что нам нужно сделать, это умножить 30 на 20.
Теперь из четырех разных
умножения, которые мы делаем, когда используем умножение столбцов, это последнее
наверное самый хитрый. Это не потому, что они
особенно большие числа или что-то в этом роде. Просто потому, что, вероятно,
с которым проще всего ошибиться. Мы могли бы просто посмотреть на три и
два и думать, что три умножить на два равно шести, но мы должны помнить, что оба
эти цифры стоят в разряде десятков. Это 30 умножить на 20. Но мы все равно могли бы использовать этот факт
три раза два шесть, чтобы помочь нам здесь. Если трижды два будет шесть, то
три десятки, умноженные на два, будут такими же, как шесть десятков или 60, а три десятки
умноженное на две десятки снова будет в 10 раз больше. Это будет так же, как 60 10s или
600.
Это 30 умножить на 20. Но мы все равно могли бы использовать этот факт
три раза два шесть, чтобы помочь нам здесь. Если трижды два будет шесть, то
три десятки, умноженные на два, будут такими же, как шесть десятков или 60, а три десятки
умноженное на две десятки снова будет в 10 раз больше. Это будет так же, как 60 10s или
600.
Вы видите там узор в
наши вопросы и ответы? Значит 30 умножить на 20 равно
600. Итак, мы умножили обе части
35 на четыре в 24. А потом мы умножили обе части
из 35 на 20 из 24. Теперь все, что нам нужно сделать, это найти
каков общий продукт. В нашей колонке у нас есть только
эти нули, поэтому мы можем поставить ноль на место единиц. Если мы добавим десятки, мы получим два
и два, а затем два нуля, так что всего четыре десятки. И если мы добавим сотни, мы
получил один плюс один плюс шесть. Итак, восемь сотен. Итак, можно сказать, что произведение
35 и 24 — это 840. Попробуем попрактиковаться.
метод столбца теперь с некоторыми вопросами.
Итак, восемь сотен. Итак, можно сказать, что произведение
35 и 24 — это 840. Попробуем попрактиковаться.
метод столбца теперь с некоторыми вопросами.
Рассчитайте следующее: 29 умножить на 64 равно чему.
В этом вопросе нам дается пару двузначных чисел, которые нужно перемножить вместе, и мы получаем действительно большую подсказку, поскольку как это сделать, потому что способ, которым этот расчет изложен, написание обоих чисел друг над другом. Это означает, что цифры находятся в столбцы. Один из способов описать это как столбчатый метод. И, написав числа, как это помогает нам разделить их на десятки и единицы. Обе части числа 29нужно умножить на обе части числа 64. Составим план всех умножения, которые нам нужно будет сделать.
Итак, для начала мы собираемся
нужно умножить каждую часть числа 29 на четыре единицы в числе 64, так что получится девять
четыре раза, а затем 20 раз четыре.
Далее нам нужно умножить 20 на
четыре. Помните, эта цифра два не
иметь значение два. Это разряд десятков. Это стоит 20. Опять же, мы можем использовать удвоение, чтобы помочь
нас.
Тогда наш ответ будет 10
раз больше. И мы знаем, что найти номер
это в 10 раз больше, чем другое, мы просто сдвигаем цифру на одно место в
влево, поэтому 120 становится 1200. Итак, теперь мы умножили каждую часть
числа 29 на единицы, а затем на десятки числа 64. Чтобы найти общий ответ, мы
просто нужно добавить эти частичные продукты вместе. Итак, для начала, если мы добавим наш
единицы, мы видим, что цифра равна шести, а все остальные цифры равны нулю. Итак, у нас их шесть. В столбце десятков у нас есть несколько
больше о чем подумать. У нас есть три десятки плюс восемь десятков.
плюс еще четыре десятки.
Итак, теперь мы умножили каждую часть
числа 29 на единицы, а затем на десятки числа 64. Чтобы найти общий ответ, мы
просто нужно добавить эти частичные продукты вместе. Итак, для начала, если мы добавим наш
единицы, мы видим, что цифра равна шести, а все остальные цифры равны нулю. Итак, у нас их шесть. В столбце десятков у нас есть несколько
больше о чем подумать. У нас есть три десятки плюс восемь десятков.
плюс еще четыре десятки.
Как бы вы добавили эти
быстро? Возможно, мы могли бы поставить три и
четыре вместе, чтобы сделать семь 10s. И мы знаем, что восемь десятков плюс
восемь десятков будут 16 десятками. Итак, если мы добавим восемь десятков к семи
10s, будет 15 10s. Значит, нам нужно обменять
10 из 15 10 на 100, а затем пять 10. Добавляя сотни, мы получили
пять сотен плюс еще две сотни. Это семь сотен.
Какой номер может заменить вопросительный знак в этом расчете? Завершите расчет, чтобы решить Это.
Расчет, упомянутый в
вопрос вот в чем. Похоже, что метод столбца имеет
используется для умножения пары двузначных чисел. 33 умножить на 30. О! У нас здесь пропущена цифра. Там знак вопроса. И первая часть этой задачи
спрашивает нас, какое число может заменить этот вопросительный знак. Теперь мы могли бы посмотреть на это
расчет и сказать себе: «Возможных ответов много. Недостающая цифра может быть чем угодно
от нуля до девяти». Но вы знаете, это неправда
потому что нам дали еще одну информацию. Мы видим, что кто-то уже
начали искать ответ на это умножение, и они уже нашли
частичный продукт 132,
Но вы знаете, это неправда
потому что нам дали еще одну информацию. Мы видим, что кто-то уже
начали искать ответ на это умножение, и они уже нашли
частичный продукт 132,
Теперь, когда мы используем столбец
метод, как этот, обычно первое, что мы делаем, это умножаем все на
единицы во втором номере. Итак, для начала умножим
трое из 33 — те, что во втором номере; тогда мы умножим 30 на 33 на
те, что во втором номере. Затем мы делаем то же самое, это
время, умноженное на десятки во втором числе, так что будет четыре
вообще умножения. Но ты видишь, как это
выставляется расчет? Есть место только для двух частичных
товары. Другими словами, человек, который
выработка ответа умножит 33 за один раз. Итак, 33 умножить на
которых мы, конечно, в данный момент не знаем, а затем 33, умноженные на
десятки. Итак, 33 умножить на 30.
Итак, 33 умножить на 30.
Теперь, когда мы знаем, что происходит
в этом расчете мы можем использовать его, чтобы узнать наше недостающее число: в 33 раза больше, чем
дает нам ответ 132. Теперь важная цифра, которую нам нужно
подумайте о вот цифра два. На какую цифру мы могли бы умножить нашу
три единицы, что дало бы нам ответ, оканчивающийся на два? Ну, очевидно, два меньше, чем
три. Это не кратно трем, поэтому мы
нужно думать о двузначном числе, которое заканчивается на два. И мы знаем, что трижды четыре
равно 12, а 12 оканчивается на двойку. Посмотрим, будет ли 33 умножить на четыре.
правильный. Как мы уже говорили, три раза четыре равно
12. Это то же самое, что раз 10 и два
те. А поскольку трижды четыре равно 12,
мы знаем, что три десятки, умноженные на четыре, должны быть 12 десятками. У нас есть один 10, а внизу
нам нужно не забыть включить, так что это 13 10s. А вот и наш номер 132.
А вот и наш номер 132.
Расчет явно 33 раза 34, а наша недостающая цифра — четыре. Наконец, нас просто попросили завершить расчет, чтобы решить его. Сколько будет 33 умножить на 34? Ну, мы разобрались с первым частичный продукт, так что теперь нам просто нужно отработать второй. Нам нужно умножить 33 на десятки цифра 34. Другими словами, 33 умножить на 30. Теперь мы знаем это число, которое мы умножение на 30 — это всего 10 лотов из трех. Так почему бы нам не умножить 33 на три, а затем использовать это, чтобы помочь? Трижды три девять, и три десятки умножить на три — девять десятков или 90. Итак, если 33 умножить на три будет 99, то 33 умножить на три 10 будет то же самое, что 99 10, что равно 990.
Итак, мы умножили 33 на четыре. Затем мы умножили 33 на 30. Теперь нам просто нужно сложить эти два
частичные продукты вместе. Две единицы плюс ноль единиц равно двум
те. Три десятки плюс девять десятков равно 12.
10s, что равно 100 и двум единицам. Тогда 100 плюс девять сотен равно 10 100.
плюс тот, который мы обменяли, равен 11 100, что равно 1100. И мы можем просто написать, что 1000
прямо в тысячное место. Это был интересный вопрос
потому что, помимо использования метода столбца, мы должны были использовать то, что мы знали о нем, чтобы
помогите найти пропущенную цифру. Номер, который заменяет
вопросительный знак в подсчете равен четырем, а 33 умножить на 34 — это 1122.
Три десятки плюс девять десятков равно 12.
10s, что равно 100 и двум единицам. Тогда 100 плюс девять сотен равно 10 100.
плюс тот, который мы обменяли, равен 11 100, что равно 1100. И мы можем просто написать, что 1000
прямо в тысячное место. Это был интересный вопрос
потому что, помимо использования метода столбца, мы должны были использовать то, что мы знали о нем, чтобы
помогите найти пропущенную цифру. Номер, который заменяет
вопросительный знак в подсчете равен четырем, а 33 умножить на 34 — это 1122.
Эти вопросы заставили нас задуматься
там хорошая практика. Но прежде чем мы закончим это видео,
давайте рассмотрим одну ошибку, которую нам действительно нужно избегать. Это довольно легко сделать, как
Что ж. Здесь мы видим, что эта девушка
пытается умножить 26 на 14, и в итоге у нее получается 40.
ей. 26 умножить на 14 будет 40? Здесь она ошиблась, и это
очень легко сделать ошибку. Можете ли вы определить, что это такое? Если мы начнем с конца и будем работать
назад, мы можем видеть, что она на самом деле правильно сложила эти цифры. Четыре плюс восемь плюс шесть плюс два
равно 20. Затем две десятки плюс две десятки
то, что она обменяла, равно 40, значит, она правильно выполнила эту часть добавления.
26 умножить на 14 будет 40? Здесь она ошиблась, и это
очень легко сделать ошибку. Можете ли вы определить, что это такое? Если мы начнем с конца и будем работать
назад, мы можем видеть, что она на самом деле правильно сложила эти цифры. Четыре плюс восемь плюс шесть плюс два
равно 20. Затем две десятки плюс две десятки
то, что она обменяла, равно 40, значит, она правильно выполнила эту часть добавления.
Проблема должна быть связана с
умножение в начале. Первый неполный продукт, который она получила
ей 24. И мы видим, откуда она взялась
из. Она начала с умножения на
единиц, а шесть раз четыре единицы — это 24. Далее она умножает эту цифру
два на четыре. И ты видишь, что она
Выполнено? Она присвоила этой цифре значение
два. Дважды четыре восемь, но мы
знайте, что эта цифра два не стоит двух. Это стоит 20. Это в разряде десятков.
Это стоит 20. Это в разряде десятков.
Значит, она должна была размножаться 20 на четыре, что дает ответ 80. Теперь действительно легко ошибиться сделать, и эта девушка продолжала делать все это время. Но это то, что нам нужно избегать. Вместо шестикратного одного она надо было посчитать шесть раз по 10. И вместо двух раз по одному она должен был найти ответ на 20 умножить на 10, что дает нам совсем другое результат. Всегда будьте осторожны со своим местом ценность.
Итак, что мы узнали из этого видео? Мы научились пользоваться стандартный письменный метод умножения пары двузначных чисел.
Как умножать десятичные дроби | Математика 4-го класса
Обзор десятичных дробей
Десятичные дроби — это числа с десятичной точкой, например 1,5.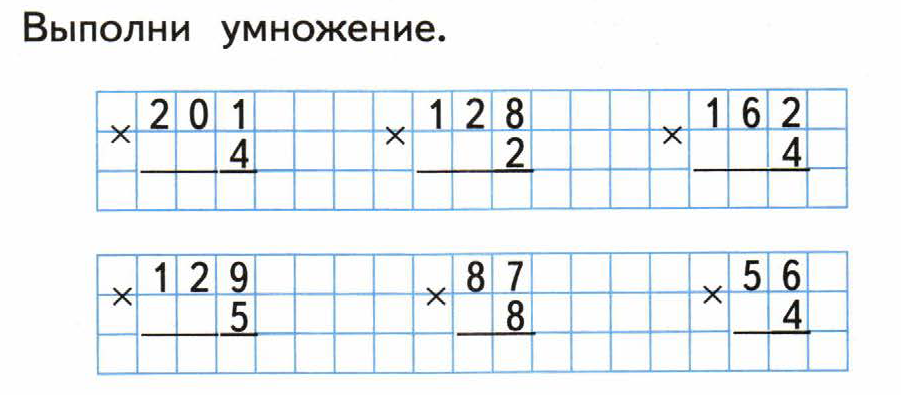
Целые числа — это положительные числа, такие как 1, 2 и 3. Они не имеют дробных или десятичных частей.
Умножение десятичных дробей очень похоже на умножение целых чисел.
Вам просто нужно позаботиться о десятичной точке в конце.
Давайте узнаем, как это сделать на нескольких примерах.
Умножение десятичных дробей
7,3 × 5 = ?
Сначала запишите эти коэффициенты в виде столбца :
Совет: Коэффициенты — это числа, которые вы перемножаете, чтобы получить произведение .
Начните с умножения 5 на 3.
Ответ: 15. Запишем 5 в качестве первого числа и перенесем 1 на 7.
Затем умножаем 5 на 7.
5 умножаем на 7 равно 35.
Затем прибавляем 1 что мы перенесли. Получается 36.
Наконец, мы должны выяснить, где для поставить десятичную точку .
У нас есть 1 цифра справа от десятичной точки в наших коэффициентах.
…итак, сдвигаем десятичную дробь влево на 1 цифру в произведении.
Вот наш окончательный ответ:
5 × 7,3 = 36,5 ✅Подумайте о умножении децималов
TIP: 7. . При делении числа на 10 его десятичная точка сдвигается на один разряд влево. Мы можем переписать нашу задачу выше так: Вот почему умножение десятичных дробей аналогично умножению целых чисел (5 × 73) и сдвигу десятичной точки в конце (365 ÷ 10). Сначала запишите коэффициенты в виде столбца. Затем мы умножаем каждую цифру нижнего множителя на каждую цифру верхнего множителя, начиная с 6, на 2. Получаем 12. Мы записываем 2 внизу и переносим 1 поверх 8. Далее умножаем 6 на 8. Произведение равно 48, затем прибавляем 1, которую мы перенесли. Это дает нам 49. Мы пишем 9 внизу и переносим 4 вверху 2. Следующие цифры для умножения — 6 и 2. Мы получаем 12 и добавляем 4. Получается 16. Мы пишем 16 внизу, рядом с 9 и 2. Следующее, что нужно сделать, это умножить 4 на цифры числа вверху. Начнем с 4 х 2. Но прежде чем мы решим это, сначала напишите ноль под 2! Зачем добавлять 0? 🤔 Поскольку 4 в нашем нижнем множителе на одну позицию выше, чем 6 рядом с ней, ее произведение также должно быть на одну позицию выше. Затем мы записываем результат 4 x 2 рядом с 0. Затем мы умножаем 4 x 8. Это дает нам 32. Мы записываем 2 под 6. Затем мы переносим 3 поверх 2. Теперь последние цифры для умножения 4 и 2. 4 × 2 равно 8. Затем мы добавляем 3, которые мы перенесли из предыдущих цифр. Это дает нам 11. Мы пишем 11 рядом с 2. Предпоследний шаг — сложение чисел: Последний шаг — запись десятичной точки. Есть две цифры справа от десятичной точки в наших факторах. Итак, мы сдвигаем десятичную точку на две цифры влево в нашем окончательном ответе. Отлично. Хорошо, вы почти закончили. Давайте вместе рассмотрим еще один пример. Давайте запишем эти числа в виде столбца. Начнем с умножения верхнего множителя на каждую цифру нижнего множителя, начиная с наименьшего, 1. Итак, умножаем 1 × 7. Далее умножаем 1 × 2. Теперь умножаем 1 × 8. После этого умножаем 1×1. Теперь мы переходим к следующей цифре в нижнем множителе, 3. Мы добавляем 0 в область ответа на новой строке для этой цифры. Затем умножаем 3 × 7. Ответ равен 21. Итак, пишем 1 внизу. Затем мы переносим 7 поверх 2. Обратите внимание, что мы сначала написали 0 под 7, а затем написали 1 рядом с ним. Во-вторых, мы умножаем 3 × 2 и добавляем переносимую часть. В-третьих, умножаем 8 на 3. 8 × 3 равно 24. Мы пишем 4 под 1 и переносим 2 наверх 1. Наконец, мы умножаем 3 на 1. 3 × 1 равно 1, и мы добавляем 1, которую мы перенесли. Это дает нам 5. Мы пишем 5 рядом с 4. Обратите внимание, что над ним нет числа. Чтобы потом не запутаться при добавлении, можно написать ноль выше 5. Теперь мы добрались до последней цифры в 2.31. Это 2. Поскольку теперь это третья цифра в нашем нижнем множителе, мы добавляем два нуля в зону произведения для цифры! Умножим 2 на 7. Произведение 2 × 7 равно 14. Мы пишем 4 внизу после нулей и переносим 1 на верх 2. Следующие числа, которые нужно умножить, это 2 и 2. Ответ 4, но нам нужно добавить 1, которую мы перенесли. Получается 5. Следующая цифра, которую нужно умножить на 2, это 8. 2 × 8 равно 16. Мы пишем 6 в области произведения и переносим 1. Последнее умножение, которое нам нужно сделать, это 2 × 1. Произведение, которое мы получаем, равно 2. Затем мы добавляем 1, которое мы перенесли. Получается 3. Напишите 3 рядом с 6. Над ним нет цифр. Чтобы помочь, вы можете написать нули над ним. Теперь добавим все. 3
3 5 × 7,3 = 5 × 73 / 10
Пример 2
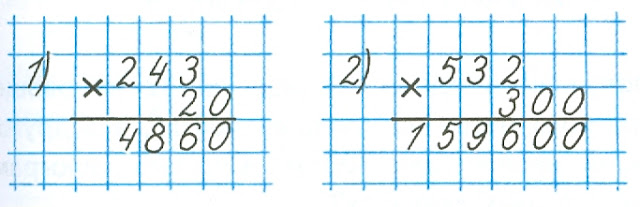
28,2 × 4,6 = ?


28,2 × 4,6 = 129,72
Окончательный пример
18,27 × 2,31 = ?



 (Слайд 2)
(Слайд 2)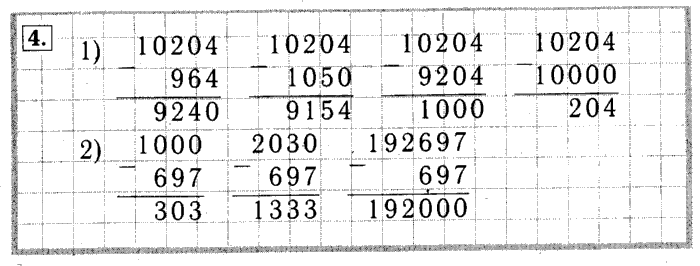







 Дыхание произвольное. Удерживать позу 20-30 секунд, затем медленно вернуться в исходное положение. Для снятия напряжения рук погладить запястья, встряхнуть кистями рук и спокойно подышать.
Дыхание произвольное. Удерживать позу 20-30 секунд, затем медленно вернуться в исходное положение. Для снятия напряжения рук погладить запястья, встряхнуть кистями рук и спокойно подышать. Проверьте своё решение с решением товарищей.
Проверьте своё решение с решением товарищей.

 (Слайд 18)
(Слайд 18)