Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.
Error in links file
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
| Расскажи друзьям vpr-klass или впр-класс Презентации Детские презентации Презентации по математике Демо-варианты: Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География Математика Русский язык |  com (впр-класс) com (впр-класс) Последние новости ГИА и ЕГЭ 2017. ЕГЭ по математике. КДР по математике. Математика 1-4 класс. Математика 5-6 класс. Алгебра и геометрия 7-9 класс. Алгебра и геометрия 10-11 класс. ГДЗ, решебники по математике, алгебре, геометрии. Онлайн калькуляторы по математике. Генераторы случайных примеров и задач по математике. Презентации. Другие школьные предметы. Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. | Интересно Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. Видео уроки |
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap.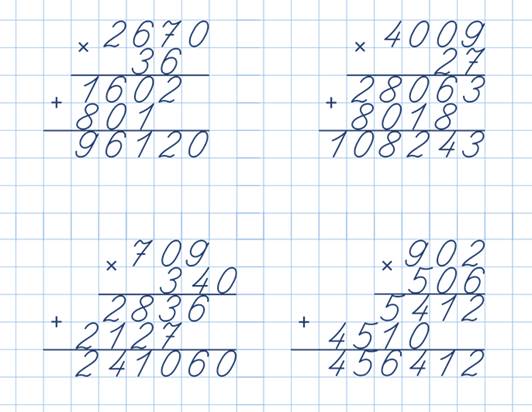 xml
xml
Онлайн калькулятор. Умножение столбиком.
Этот онлайн калькулятор поможет вам понять, как складывать, вычитать, умножать и делить целые числа и десятичные дроби столбиком. Калькулятор сложения, вычитания, умножения и деления столбиком очень просто и быстро вычислит сумму, разность, произведение и частное и выдаст подробное решение задачи.
Содержание
- Калькулятор для сложения, вычитания, умножения и деления столбиком
- Калькулятор умножение столбиком
- Как умножать столбиком
- Калькулятор умножения столбиком
Калькулятор для сложения, вычитания, умножения и деления столбиком
с остатком
Ввод данных в калькулятор для сложения, вычитания, умножения и деления столбиком
В онлайн калькулятор можно вводить натуральные числа или десятичные дроби.
Дополнительные возможности калькулятора для сложения, вычитания, умножения и деления столбиком
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Инструкция использования калькулятора для сложения, вычитания, умножения и деления столбиком
Для сложения, вычитания, умножения или деление целых чисел и десятичных дробей столбиком выполните следующие действия:
- введите значения чисел;
- выберите
- «+» — для сложения столбиком,
- «-» — для вычитания столбиком,
- «×» — для умножения столбиком,
- «÷» — для деления столбиком;
- нажмите кнопку ( «=» ).
Сложение, вычитание, умножение и деление столбикомСложение и вычитание в столбикУмножение в столбикДеление в столбикДеление в столбик с остаткомОстаток при деленииНОД и НОК двух чиселРазложение числа на множителиКалькулятор квадратных корнейПоказать все онлайн калькуляторы Упражнения. Сложение двух натуральных чисел.Упражнения. Вычитание двух натуральных чисел.Упражнения. Сложение и вычитание двух натуральных чисел.Упражнения. Изучение таблицы умножения.Упражнения. Умножение однозначных и двухзначных натуральных чисел.
Этот онлайн калькулятор поможет вам понять как умножить целые числа и десятичные дроби столбиком. Калькулятор умножения столбиком очень просто и быстро вычислит произведение и выдаст подробное решение задачи.
Калькулятор умножение столбиком
с остатком
Ввод данных в калькулятор умножение столбиком
В онлайн калькулятор можно вводить натуральные числа или десятичные дроби.
Дополнительные возможности калькулятора умножения столбиком
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Инструкция использования калькулятора для умножения столбиком
Для вычисления достаточно ввести числа (целые иди десятичные дроби) и нажать кнопку «=».
Сложение, вычитание, умножение и деление столбикомСложение и вычитание в столбикУмножение в столбикДеление в столбикДеление в столбик с остаткомОстаток при деленииНОД и НОК двух чиселРазложение числа на множителиКалькулятор квадратных корнейПоказать все онлайн калькуляторы Упражнения. Сложение двух натуральных чисел.Упражнения. Вычитание двух натуральных чисел.Упражнения. Сложение и вычитание двух натуральных чисел. Упражнения. Изучение таблицы умножения.Упражнения. Умножение однозначных и двухзначных натуральных чисел.Упражнения. Умножение однозначных и трехзначных натуральных чисел.Упражнения. Умножение двух двухзначных натуральных чисел.Упражнения. Умножение двухзначных и трехзначных натуральных чисел.Упражнения. Умножение двух трехзначных натуральных чисел.Упражнения. Умножение двух натуральных чисел.Упражнения. Деление двух натуральных чисел.Упражнения. Вычисления с двумя натуральными числами.Упражнения. Остаток от деления.Упражнения. Наибольший общий делитель.Упражнения. Наименьшее общее кратное.Упражнения. Признаки делимости на 2Упражнения. Признаки делимости на 3Упражнения. Признаки делимости на 4Упражнения. Признаки делимости на 5Упражнения. Признаки делимости на 6Упражнения. Признаки делимости на 9Упражнения. Признаки делимости на 10Упражнения. Признаки делимости на 2, 3, 5, 6, 9, 10Упражнения. Среднее арифметическое.Показать все онлайн упражнения
Упражнения. Изучение таблицы умножения.Упражнения. Умножение однозначных и двухзначных натуральных чисел.Упражнения. Умножение однозначных и трехзначных натуральных чисел.Упражнения. Умножение двух двухзначных натуральных чисел.Упражнения. Умножение двухзначных и трехзначных натуральных чисел.Упражнения. Умножение двух трехзначных натуральных чисел.Упражнения. Умножение двух натуральных чисел.Упражнения. Деление двух натуральных чисел.Упражнения. Вычисления с двумя натуральными числами.Упражнения. Остаток от деления.Упражнения. Наибольший общий делитель.Упражнения. Наименьшее общее кратное.Упражнения. Признаки делимости на 2Упражнения. Признаки делимости на 3Упражнения. Признаки делимости на 4Упражнения. Признаки делимости на 5Упражнения. Признаки делимости на 6Упражнения. Признаки делимости на 9Упражнения. Признаки делимости на 10Упражнения. Признаки делимости на 2, 3, 5, 6, 9, 10Упражнения. Среднее арифметическое.Показать все онлайн упражнения
Этот калькулятор деление столбиком онлайн может разделить столбиком два числа, выдавая подробное объяснение как учили в школе.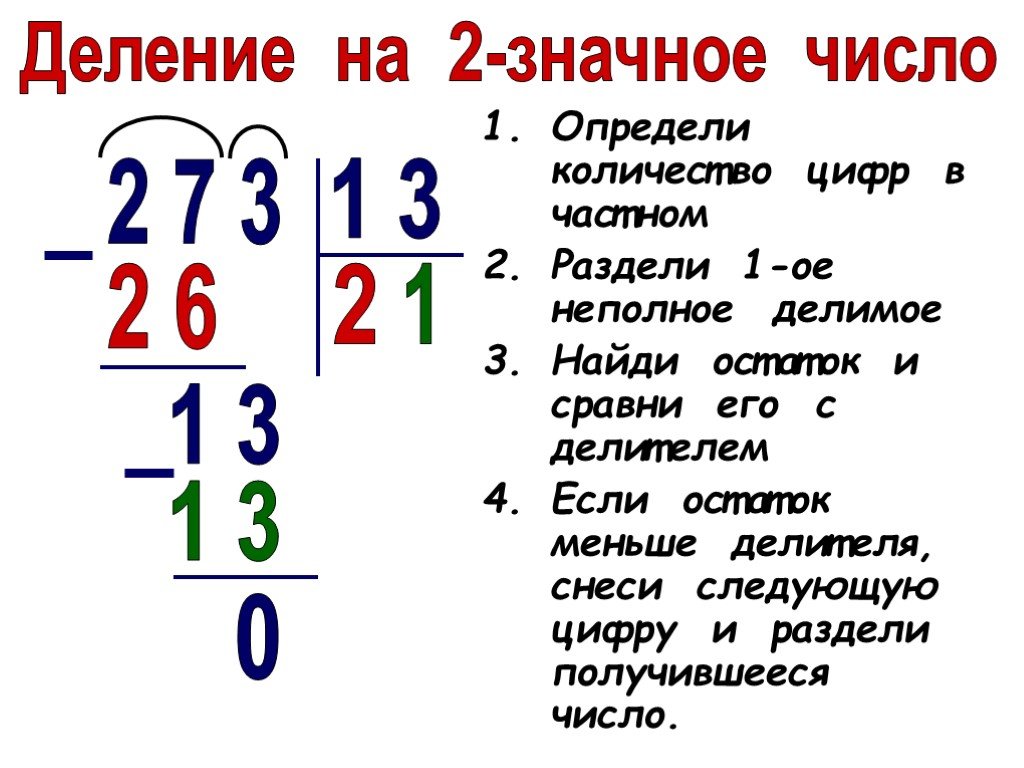 Поддержка чисел с запятыми и результата с остатком.
Поддержка чисел с запятыми и результата с остатком.
| Поставить LIKE | и поделиться ссылкой |
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме
Просто введите делимое в поле 1 и делитель в поле 2 и нажмите кнопку «Рассчитать». Для получения подробного ответа нажмите «Показать как оно получилось».
Разделить одно число на другое всегда считается самой сложной из ряда задач сложения, вычитания, умножения и деления. Это происходит потому что не существует операции «прямого деления», а все существующие на данный момент алгоритмы основаны на так называемом «подборе ответа». То есть придумывается число, которое затем умножают на делитель и в дальнейшем сравнивают его с делимым числом. Если они равны, то ответ считается найденным. Однако не всегда это удается. В таких случаях отыскивается ответ, который при умножении на делитель, дает результат максимально похожий на делимое но меньше его. Затем они вычитаются и все что остается называется остатком.
Затем они вычитаются и все что остается называется остатком.
Последние 20 расчетов на этом калькуляторе
- Деление 0.0625÷27 Выполнен: 2019-12-05 14:20 МСК
- Деление 16560÷920 Выполнен: 2019-12-05 13:31 МСК
- Деление 4÷40000 Выполнен: 2019-12-05 13:29 МСК
- Деление 21474÷3 Выполнен: 2019-12-05 13:13 МСК
- Деление 1540÷4 Выполнен: 2019-12-05 13:02 МСК
- Умножение 109 *407 Выполнен: 2019-12-05 12:53 МСК
- Деление 0.469÷0.09 Выполнен: 2019-12-05 12:51 МСК
- Деление 381÷5 Выполнен: 2019-12-05 12:44 МСК
- Деление 400÷25 Выполнен: 2019-12-05 12:07 МСК
- Умножение 16*25 Выполнен: 2019-12-05 12:04 МСК
- Деление 132÷264 Выполнен: 2019-12-05 11:11 МСК
- Деление 3600÷1000 Выполнен: 2019-12-05 10:32 МСК
- Деление 300÷15 Выполнен: 2019-12-05 10:30 МСК
- Деление 2700÷135 Выполнен: 2019-12-05 10:29 МСК
- Деление 240472÷496 Выполнен: 2019-12-05 10:14 МСК
- Сложение 1846353829+10364689 Выполнен: 2019-12-05 08:56 МСК
- Деление 206÷16 Выполнен: 2019-12-05 08:41 МСК
- Деление 8811÷111 Выполнен: 2019-12-05 07:41 МСК
- Деление 3060÷20 Выполнен: 2019-12-05 07:40 МСК
- Деление 10000001000÷2 Выполнен: 2019-12-05 07:36 МСК
Сообщите нам о возникшей проблеме в результате расчета на этом калькуляторе.
| Ваша оценка? |
Попробуйте новый сайт: Перейти
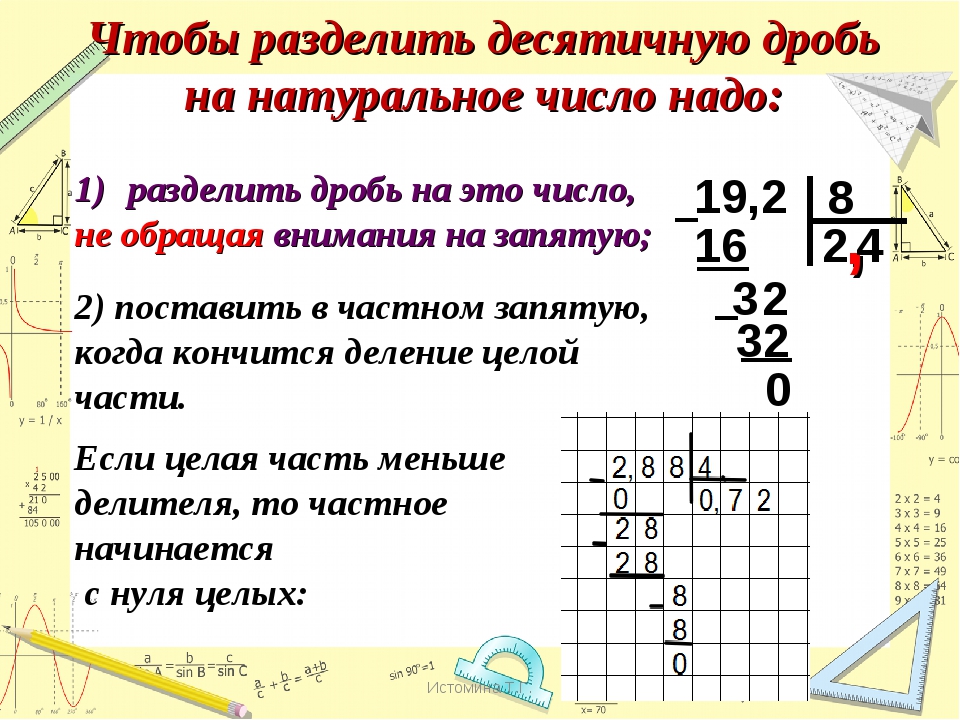
Как умножать столбиком
Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.
Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить 846 на 5:
Умножить 846 на 5 – значит, сложить 5 чисел, каждое из которых равно 846. Для этого достаточно взять сначала 5 раз по 6 единиц, потом 5 раз по 4 десятка и наконец 5 раз по 8 сотен.
5 раз по 6 единиц = 30 единиц, т. е. 3 десятка. Пишем 0 под чертой на месте единиц, а 3 десятка запоминаем. Для удобства, чтобы не запоминать можно написать 3 над десятками множимого:
5 раз по 4 десятка = 20 десятков, прибавляем к ним ещё 3 десятка = 23 десятка, т. е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:
е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:
5 раз по 8 сотен = 40 сотен, прибавляем к ним ещё 2 сотни = 42 сотни. Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:
Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить 3826 на 472:
Умножить 3826 на 472 – значит, сложить 472 одинаковых числа, каждое из которых равно 3826. Для этого надо сложить 3826 сначала 2 раза, потом 70 раз, потом 400 раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.
2 раза по 3826 = 7652. Пишем полученное произведение под чертой:
Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением. Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.
Умножаем 3826 на 7. Это будет второе частичное произведение (26782):
Умножаем множимое на 4. Это будет третье частичное произведение (15304):
Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение (1 805 872):
Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:
Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.
Например, необходимо вычислить 23 000 · 4500. Сначала умножим 23 на 45, не обращая внимание на нули:
И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится 103 500 000.
Калькулятор умножения столбиком
Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку
Просто введите множимое и множитель и нажмите кнопку Вычислить
.
Не секрет, что знакомство с математикой начинается с важнейшей науки о числах — арифметики. Как утверждал великий ученый М. В. Ломоносов, с арифметикой мы входим «во врата учености», именно с нее начинается нелегкий, но заманчивый путь познания мира. Эта наука изучает числа и действия над ними. Одним из таких действий над цифрами является умножение столбиком. Без ясного понимания последовательности действий при совершении умножения двух чисел в математике нельзя двигаться дальше. Следует знать, что числа, которые умножаются, называются множителями, а полученный результат — произведением. В числах имеются разряды, самый маленький — единицы, затем десятки, после них сотни и т. д. Если вы умножаете в столбик, расположите оба множителя друг над другом, чтобы совпадали разряды чисел. Большее число расположите в верхней строке, меньшее — в нижней. Если оба множителя или один из них имеют на концах нули, то числа располагают так, чтобы цифры наименьшего разряда (кроме 0) находились в одном столбике. Нули в поле поэтапных операций не заносятся, они переносятся под черту в конечный результат. Это делается потому, что при умножении любого числа на 0, все равно получается 0. Слева от множителей ставим «х». Умножение в столбик — поразрядное умножение. Это значит, что каждый разряд 1-го множителя, начиная с последней цифры, умножается на последнюю цифру 2-го множителя. Следующей строкой будет результат умножения верхнего числа (1-го множителя) на следующую цифру нижнего числа (2-го множителя). Следует помнить, что полученный после умножения на вторую цифру результат, следует размещать под второй цифрой полученного результата от первого умножения. Поэтапные произведения (разрядные) складываются по разрядам, результат заносится под черту, начиная с самой правой стороны. Слева от полученных произведений, которые складываются, ставим «+».
Нули в поле поэтапных операций не заносятся, они переносятся под черту в конечный результат. Это делается потому, что при умножении любого числа на 0, все равно получается 0. Слева от множителей ставим «х». Умножение в столбик — поразрядное умножение. Это значит, что каждый разряд 1-го множителя, начиная с последней цифры, умножается на последнюю цифру 2-го множителя. Следующей строкой будет результат умножения верхнего числа (1-го множителя) на следующую цифру нижнего числа (2-го множителя). Следует помнить, что полученный после умножения на вторую цифру результат, следует размещать под второй цифрой полученного результата от первого умножения. Поэтапные произведения (разрядные) складываются по разрядам, результат заносится под черту, начиная с самой правой стороны. Слева от полученных произведений, которые складываются, ставим «+».
Онлайн калькулятор поможет вам быстро и правильно выполнить умножение столбиком. умножение
ГДЗ Математика 3 класс Петерсон на Решалка
ГДЗ Математика 3 класс Петерсон
авторы: Петерсон.
издательство: «Ювента» 2014 год
Задачи
- ЧАСТЬ 1
- 1 урок. Множество и его элементы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 2 урок. Способы задания множеств
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 3 урок.
 Равные множества. Пустое множество.
Равные множества. Пустое множество.- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 4 урок. Диаграмма Эйлера-Венна. Знаки ∈ и ∉
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 5 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 6 урок. Подмножество. Знаки ⊂ и ⊄
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 7 урок.
 Решение задач
Решение задач- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 8 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 9 урок. Персечение множеств. Знак ∩
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 10 урок. Свойства операции пересечения множеств
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 11 урок.
 Решение задач
Решение задач- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12 урок. Объединение множеств. Знак U
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 13 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 14 урок. Свойства операции объединения множеств
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 15 урок.
 Разбиение множеств на части по свойствам (классификация)
Разбиение множеств на части по свойствам (классификация)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 16 урок. Как считать люди научились
- 1
- 2
- 3
- 4
- 5
- 17 урок. Система счисления
- 1
- 2
- 3
- 4
- 18 урок. Многозначные числа
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 19 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 20 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 21 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 22 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 23 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 24 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 25 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 26 урок. Умножение на 10, 100, 1000 …
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 27 урок. Умножение круглых чисел
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 28 урок.
 Деление на 10, 100, 1000 …
Деление на 10, 100, 1000 …- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 29 урок. Деление круглых чисел
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 30 урок. Единицы длины
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 31 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 32 урок. Единицы массы. Грамм
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 33 урок. Единицы массы. Тонна. Центнер
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- ЗАДАЧИ ДЛЯ ВСЕХ — ВСЕХ — ВСЕХ
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 1 урок. Множество и его элементы
- ЧАСТЬ 2
- 1 урок.
 Умножение на однозначное число
Умножение на однозначное число- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 2 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 3 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 4 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 5 урок.
 Деление на однозначное число
Деление на однозначное число- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 6 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 7 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 8 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 9 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 10 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 11 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 12 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 14 урок.
 Преобразование фигур
Преобразование фигур- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 15 урок. Симметрия
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 16 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 17 урок. Симметричные фигуры
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 18 урок.
 Меры времени. Календарь
Меры времени. Календарь- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 19 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 20 урок. Таблица мер времени
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 21 урок.
 Часы
Часы- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 22 урок. Сравнение, сложение и вычитание единиц времени
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 23 урок. Переменная
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 24 урок.
 Выражение с переменной
Выражение с переменной- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 25 урок. Верно и неверно. Всегда и иногда
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 26 урок. Равенство и неравенство
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 27 урок.
 Уравнения
Уравнения- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 28 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 29 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 30 урок. Формулы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 31 урок.
 Формула объема прямоугольного параллелепипеда
Формула объема прямоугольного параллелепипеда- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 32 урок. Формула деления с остатком
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 33 урок. Решение зада с помощью формул
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 1 урок.
- ЧАСТЬ 3
- 1 урок.
 Скорость. Время. Расстояние
Скорость. Время. Расстояние- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 2 урок. Формула пути
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 3 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 4 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 5 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 6 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 7 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 8 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 9 урок.
 Умножение на двузначное число
Умножение на двузначное число- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 10 урок. Формула стоимости
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 11 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 12 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 13 урок.
 Умножение на трехзначное число
Умножение на трехзначное число- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 14 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 15 урок. Формула работы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 16 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 17 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 18 урок. Формула произведения
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 19 урок. Способы решения составных задач
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 20 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 21 урок.
 Умножение многозначных чисел
Умножение многозначных чисел- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Задачи на повторение
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 1 урок.
Решебники к учебнику по математике за 3 класс под авторством Петерсон Л. С. станут полезными в качестве вспомогательного пособия для школьников, а также педагогов и родителей. Выполнение упражнений с контролем по ГДЗ происходит эффективнее, третьеклассник сможет подтянуть свои оценки и лучше изучить дисциплину.
С. станут полезными в качестве вспомогательного пособия для школьников, а также педагогов и родителей. Выполнение упражнений с контролем по ГДЗ происходит эффективнее, третьеклассник сможет подтянуть свои оценки и лучше изучить дисциплину.
Домашние задания доступно и быстро
Чтобы подготовиться к занятию, контрольной или другой итоговой работе, а также просто проверить свои знания и закрепить пройденный материал, теперь не нужно будет просиживать часами за тетрадями. ГДЗ по математике за 3 класс Петерсона содержат несколько частей с примерами, уравнениями, практическими задачами и тестами. Также учебник позволит качественнее подготовиться к разным аттестациям, научиться давать объективную оценку своим знаниям и повышать свой уровень.
Онлайн-сервис «Решалка» предлагает исключительно правильные ответы, ведь все материалы неоднократно вручную проверяли квалифицированные педагоги и методисты, которые имеют большой опыт. Искать нужные упражнения в ГДЗ по математике за 3 класс довольно просто. Лишь несколько кликов помогут перейти с одного тематического раздела на другой, изучить задания. Весь материал изложен в доступной форме для третьеклассников.
Лишь несколько кликов помогут перейти с одного тематического раздела на другой, изучить задания. Весь материал изложен в доступной форме для третьеклассников.
Рекомендуется не заниматься бездумным переписыванием предложенных компетентными авторами верных ответов, а воспользоваться сервисом для изучения пройденных, но плохо усвоенных на уроках тем.
Кому пригодятся готовые решения?
Наиболее востребованное это пособие учениками, которые занимаются изучением математики по учебнике Петерсона. В 3 классе ГДЗ поможет быстрее справляться с выполнением заданных на дом устных и письменных упражнений, а также ответственно готовиться к занятиям без многочасового сидения над учебниками.
Домашние задания не будут больше причиной стресса и волнений, ведь готовые ответы по математике за третий класс помогут раскрепоститься, стать увереннее и отвечать на любые тематические вопросы, решать примеры и упражнения. А проверить себя всегда можно на онлайн-сервисе «Решалка».
Как умножать в Excel с помощью специальной вставки
Смотреть видео – Как умножать в Excel с помощью специальной вставки
youtube.com/embed/Fw5hnfTA3SY?feature=oembed&autoplay=1″ src=»data:text/html;https://www.youtube.com/embed/Fw5hnfTA3SY?feature=oembed&autoplay=1;base64,PGJvZHkgc3R5bGU9J3dpZHRoOjEwMCU7aGVpZ2h0OjEwMCU7bWFyZ2luOjA7cGFkZGluZzowO2JhY2tncm91bmQ6dXJsKGh0dHBzOi8vaW1nLnlvdXR1YmUuY29tL3ZpL0Z3NWhuZlRBM1NZLzAuanBnKSBjZW50ZXIvMTAwJSBuby1yZXBlYXQnPjxzdHlsZT5ib2R5ey0tYnRuQmFja2dyb3VuZDpyZ2JhKDAsMCwwLC42NSk7fWJvZHk6aG92ZXJ7LS1idG5CYWNrZ3JvdW5kOnJnYmEoMCwwLDApO2N1cnNvcjpwb2ludGVyO30jcGxheUJ0bntkaXNwbGF5OmZsZXg7YWxpZ24taXRlbXM6Y2VudGVyO2p1c3RpZnktY29udGVudDpjZW50ZXI7Y2xlYXI6Ym90aDt3aWR0aDoxMDBweDtoZWlnaHQ6NzBweDtsaW5lLWhlaWdodDo3MHB4O2ZvbnQtc2l6ZTo0NXB4O2JhY2tncm91bmQ6dmFyKC0tYnRuQmFja2dyb3VuZCk7dGV4dC1hbGlnbjpjZW50ZXI7Y29sb3I6I2ZmZjtib3JkZXItcmFkaXVzOjE4cHg7dmVydGljYWwtYWxpZ246bWlkZGxlO3Bvc2l0aW9uOmFic29sdXRlO3RvcDo1MCU7bGVmdDo1MCU7bWFyZ2luLWxlZnQ6LTUwcHg7bWFyZ2luLXRvcDotMzVweH0jcGxheUFycm93e3dpZHRoOjA7aGVpZ2h0OjA7Ym9yZGVyLXRvcDoxNXB4IHNvbGlkIHRyYW5zcGFyZW50O2JvcmRlci1ib3R0b206MTVweCBzb2xpZCB0cmFuc3BhcmVudDtib3JkZXItbGVmdDoyNXB4IHNvbGlkICNmZmY7fTwvc3R5bGU+PGRpdiBpZD0ncGxheUJ0bic+PGRpdiBpZD0ncGxheUFycm93Jz48L2Rpdj48L2Rpdj48c2NyaXB0PmRvY3VtZW50LmJvZHkuYWRkRXZlbnRMaXN0ZW5lcignY2xpY2snLCBmdW5jdGlvbigpe3dpbmRvdy5wYXJlbnQucG9zdE1lc3NhZ2Uoe2FjdGlvbjogJ3BsYXlCdG5DbGlja2VkJ30sICcqJyk7fSk7PC9zY3JpcHQ+PC9ib2R5Pg==»> Специальная функция вставки Excel может сэкономить много времени. Одной из его функций являются «Операции», которые позволяют нам быстро выполнять математические вычисления (такие как сложение, вычитание, умножение и деление) в диапазоне ячеек.
Одной из его функций являются «Операции», которые позволяют нам быстро выполнять математические вычисления (такие как сложение, вычитание, умножение и деление) в диапазоне ячеек.
В этом уроке я покажу вам, как умножать в Excel, используя специальные опции операторов вставки. Они пригодятся, если вы хотите избежать применения формул или использования вспомогательных столбцов.
Предположим, у вас есть набор данных, как показано ниже. Это цифры прогноза продаж, и вам нужно увеличить эти значения прогноза на 10%.
Один из способов (длинный и утомительный) сделать это — использовать вспомогательный столбец и сначала вычислить новые значения по формуле, а затем вставить новые значения вместо старых.
Еще один (быстрый и потрясающий) способ — использовать функцию «Специальная операция вставки».
В этом руководстве рассматриваются:
Вот шаги для умножения в Excel с использованием специальных операций вставки:
- Скопируйте значение в ячейку E2 (1.
 1) [Используйте свою любимую комбинацию клавиш — Control + C].
1) [Используйте свою любимую комбинацию клавиш — Control + C]. - Выберите весь диапазон, который нужно умножить (B3:B14).
- Перейдите на главную страницу -> Буфер обмена -> Вставить -> Специальная вставка.
- Откроется специальное диалоговое окно Вставить.
Быстрый способ — использовать сочетание клавиш Alt + E + S.
- Откроется специальное диалоговое окно Вставить.
- В диалоговом окне «Специальная вставка» выберите «Умножить».
Шаги 3 и 4 можно выполнить с помощью сочетания клавиш Alt + E + S + M. - Нажмите OK.
- Если вы не используете значение в ячейке E2, вы можете удалить его.
Это заменит старые номера новыми номерами.
Что делать, если у вас есть числа в результате формулы
Никаких проблем!! Этот трюк работает как с числами, так и с формулами.
Предположим, у вас есть формула A1+A2 в ячейке, и вы хотите умножить результат на число 1,1 (которое находится в ячейке E2). Выполните те же действия, что указаны выше, и вы получите желаемый результат. Однако обратите внимание, что когда вы используете математические операции с формулой, она вставляется как часть формулы (см. ниже)
Выполните те же действия, что указаны выше, и вы получите желаемый результат. Однако обратите внимание, что когда вы используете математические операции с формулой, она вставляется как часть формулы (см. ниже)
Что делать, если вы хотите изменить только каждое N-е значение?
Да, можно!!
Предположим, вы хотите пересмотреть цифры прогноза только для четвертого квартала (в то время как остальные цифры должны быть такими же). Это можно сделать с помощью функции «Специальная операция вставки» с помощью этого изящного совета.
Вместо одного значения используйте диапазон из четырех значений (как показано ниже):
Скопируйте эти четыре ячейки вместо одной и выполните те же шаги, что описаны выше. Это работает путем умножения первых 3 значений на 1, четвертого на 1,1 и так далее.
Крутой трюк, не так ли!!
Вам также могут понравиться следующие учебные пособия по Excel:
- 10 очень точных способов очистки данных в электронных таблицах Excel.

- 24 ежедневных проблемы с Excel и их быстрое исправление.
- Более 200 сочетаний клавиш Excel.
- Показать формулы в Excel вместо значений.
- Общие сведения об абсолютных, относительных и смешанных ссылках на ячейки в Excel.
- Как транспонировать данные в Excel.
- Что такое оператор пересечения в Excel и как его использовать
- Как выполнять вычитание в Excel (вычитание ячеек, столбца, даты/времени)
- Вычисление процентного изменения в Excel (формула увеличения/уменьшения на %)
- Как умножить столбец на число в Excel (2 простых способа)
Длинное умножение (ключевой этап 2)
Что такое длинное умножение?
Длинное умножение — это метод умножения чисел.
Длинное умножение включает в себя запись чисел, которые нужно умножить, одно под другим, поэтому цифры располагаются в столбцах. Таким способом можно умножать множество чисел любой длины.
Реальный пример выполнения длинного умножения
Делать длинное умножение легко.
Умножьте приведенные ниже числа.
Пошаговая инструкция:
Напишите числа, которые вы хотите умножить, одно под другим.
Найдите самую правую цифру нижнего числа (в столбце единиц).
Найдите самую правую цифру верхнего числа (в столбце единиц).
Умножьте нижнюю цифру (4) на верхнюю цифру (5).
5 × 4 = 20
Проверьте, является ли ответ из шага 4 равным 9 или меньше: № . 20 — это , а не 9 или меньше.
- Если Нет , ответ будет состоять из двух цифр.

- Напишите цифру справа под столбцом (под чертой).
- Перенести левую цифру в столбец слева.
Переместите цифру влево в верхнем числе.
- Умножьте нижнюю цифру (4) на верхнюю цифру (2).
2 × 4 = 8
- Добавьте к ответу любые несущие числа.
8 + 2 = 10
Проверьте, является ли ответ из шага 7 равным 9 или меньше: № . 10 — это , а не 9 или меньше.
- Если Нет , ответ будет состоять из двух цифр.
- Напишите цифру справа под столбцом (под чертой).
- Перенести левую цифру в столбец слева.
Переместите цифру влево в верхнем числе.
Слева больше нет цифр.
Напишите переносимую цифру под чертой.
Напишите 0 справа в новой строке под линией.
Переместите цифру влево в нижнем числе (в столбце десятков).
Найдите самую правую цифру верхнего числа (в столбце единиц).
Умножьте нижнюю цифру (1) на верхнюю цифру (5).
5 × 1 = 5
Проверьте, является ли ответ из шага 4 равным 9 или меньше: Да . 5 равно 9 или меньше.
- Если Да , напишите число под чертой слева от 0.
Переместите цифру влево в верхнем числе.
Умножьте нижнюю цифру (1) на верхнюю цифру (2).
2 × 1 = 2
Проверьте, является ли ответ из шага 17 равным 9 или меньше: Да . 2 равно 9 или меньше.
- Если Да , напишите номер под чертой.
Переместите цифру влево в верхнем числе.
Слева больше нет цифр.
Используйте длинное сложение, чтобы добавить два числа под линией.
Ответ:
Решение 25 × 14 равно 350.
Слайды урока
Ползунок ниже показывает еще один реальный пример того, как делать длинное умножение. Откройте слайдер в новой вкладкеЧасти умножения
- Числа, которые вы перемножаете, составляют множителя .
- Результатом умножения чисел является произведение на .

Порядок умножения
Порядок умножения чисел не имеет значения. Например:
2 × 3 = 6
Если поменять местами 2 и 3, получится то же самое:
3 × 2 = 6
Это коммутативное свойство умножения — изменение порядка не меняет результат.
Цифры и разрядность
Числа состоят из цифр. В десятичной дроби цифры могут принимать значения от 0 до 9. Значение цифр зависит от их разрядности. Разрядное значение — это место в числе, на котором стоит цифра. Разрядные значения включают сотни, десятки и единицы. Например,
123 состоит из:
- 1 сотня
- 2 десятка
- 3 единицы
То есть:
Значение каждого места в 10 раз больше, чем значение справа от него. Сотня — это 10 раз по десятку, десятка — это 10 раз по единице. Та же система применяется к правому десятичному знаку:
Сотня — это 10 раз по десятку, десятка — это 10 раз по единице. Та же система применяется к правому десятичному знаку:
Разрядное значение и столбцы в длинном умножении
Длинное умножение зависит от разрядности. Цифры верхнего числа умножаются на цифры нижнего числа. Сначала используется самая правая цифра нижнего числа, затем одна левая, затем следующая левая. Из-за разрядности каждая цифра слева в 10 раз больше, чем цифра справа от нее. Когда используется цифра слева от нижнего числа, каждый ответ будет в 10 раз больше, чем ответы, сгенерированные самой правой цифрой нижнего числа. Чтобы обозначить это, 0 нужно добавить в конце ответа:
Добавление 0 делает каждый ответ в 10 раз больше места (10 в 10 раз больше, чем 1, 200 в 10 раз больше, чем 20 и т. д.) Когда используется следующая левая цифра нижнего числа, необходимо добавить два нуля:
Местное значение и перенос
Цифры в десятичной системе идут от 0 до 9. Числа от 0 до 9 могут быть записаны только с использованием значения разряда единиц.
Числа от 0 до 9 могут быть записаны только с использованием значения разряда единиц.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Чтобы записать числа после 10, необходимо использовать разряд десятков:
10, 11, 12…
1 в разряде десятков в 10 раз больше, чем 1 в столбце единиц. Точно так же числа до 99 используют разряды десятков и единиц. После 100 также необходимо использовать разряд сотен:
100, 101, 102…
где 100 это 10 десятков. В каком месте мы находимся, как только цифра в этом разряде становится больше 9, нам нужно представить большее число, поместив цифры в разрядное значение слева.
Вот почему при выполнении длинного умножения, если числа в любом столбце умножаются и становятся больше 9, цифра помещается под столбцом слева от него:
Игры на умножение для детей онлайн
Обзор умножения
Термин «умножение» является производным от слова «множественный». Слово «литературный» означает «много», а операция «умножение» увеличивает число во «много» раз. Подобно «сложению», «умножение» является формой повторного сложения.
Слово «литературный» означает «много», а операция «умножение» увеличивает число во «много» раз. Подобно «сложению», «умножение» является формой повторного сложения.
Уравнение умножения выглядит как следующее выражение:
4 x 7 = 28
Мультипликационный мультипликатор продукт
Различные математические символы используются в качестве операторов умножения, таких как крест (x), звездочка (*) или точка (. ).
После того, как дети приобретут навыки восприятия чисел и счета сотнями, продвинутые математические операции «умножение» и «деление» усваиваются путем беглого сложения и вычитания чисел.
Математические игры для обучения умножению
Развивая применимость сложения и вычитания, интерактивные математические игры для умножения предназначены для развития математических навыков, основанных на умственных вычислениях и остром наблюдении.
1. Обучение и результат
Применение знаний для решения математических головоломок, рутинных вычислений или загадок проявляется в абстрактном мышлении и математической логике. С практикой и пониманием языка игры на умножение оттачивают концепцию объединения объектов из разных групп в единую группу. В эклектичной манере тщательно разработанные игры с использованием визуальных приемов и умственных стратегий воспитывают основные понятия математических операций, чтобы преуспеть в математике.
С практикой и пониманием языка игры на умножение оттачивают концепцию объединения объектов из разных групп в единую группу. В эклектичной манере тщательно разработанные игры с использованием визуальных приемов и умственных стратегий воспитывают основные понятия математических операций, чтобы преуспеть в математике.
Ожидаемые результаты обучения перечислены ниже:
- Введение в основы продвинутых основных математических операций для решения сложных задач с умножением
- Исследование методов умножения с использованием различных визуальных моделей и методов для реализации концепции
- Идентификация числовых величин и построение математических выражений с помощью множимого и умножение с использованием математических символов для решения текстовых задач и получения произведения
- Понимание процесса умножения больших чисел до 4 цифр, дробей и десятичных знаков
- Корреляция значения «умножения» как основного математического навыка в области геометрии, физики и смежных областях
2.
 Требуемые математические навыки:
Требуемые математические навыки:
Уровень сложности продвинутого математического навыка «умножение» выше, чем сложение и вычитание. Поскольку этот процесс сродни многократному сложению, необходимым условием является свободное владение числовым смыслом для понимания чисел в сотнях и тысячах, а также «сложение». Понимание языка и численные рассуждения с точки зрения приоритета операторов играют важную роль в фундаментальном понимании концепции «умножения».
3. Участие:
Увлекательные обучающие игры для SplashLearn, соответствующие учебной программе «общие базовые математические стандарты», дают детям возможность оттачивать вычислительные навыки во время занятий в классе или на дому.
Подробные рабочие листы с полезными вопросами предназначены для расширения возможностей домашних заданий по математике. Благодаря привлекательному тематическому интерфейсу, мотивирующему и применяющему сложные методы работы с числами, игры существенно повышают уверенность детей в том, что они преуспеют в математике.
Манипуляции, используемые для обучения умножению
1. Модель массива с использованием счетчиков:
Использование счетчиков для обучения умножению является эффективным методом, позволяющим легко понять концепцию. Поскольку счетчики используются для понимания основных математических навыков «сложение» и «вычитание», объяснение процесса умножения как «повторяющегося сложения» с использованием счетчиков очень удобно.
Также расположение счетчиков для умножения аналогично массиву с одинаковым количеством элементов в каждой строке и столбце. Соответствующая модель умножения известна как модель массива.
Например:
- Умножьте 4 и 7, используя счетчики:
Эталонное изображение: Расположение счетчиков в виде массива с 4 строками и 7 столбцами для умножения чисел
2. База 10 блоков:
Использование различных визуальных моделей для понимания математической операции позволяет построить когнитивную модель и углубить обучение для младших классов. Блоки с основанием 10 для умножения очень четко относятся к концепции и упрощают изучение умножения двузначных чисел.
Блоки с основанием 10 для умножения очень четко относятся к концепции и упрощают изучение умножения двузначных чисел.
Числа разбиваются на блоки из единиц «единиц», десятков (набор из десяти «единиц») и сотен (набор из десяти «десятков»).
Например,
47 может быть записано как: 4 «десятка» + 7 «единиц»
полученные в каждой строке или столбце.
Эталонное изображение: Расположение блоков с основанием 10 для представления умножения двух чисел
3. Модель площади
Другой визуальной моделью для понимания процесса умножения является модель площади. Стратегия в основном относится к геометрическим фигурам для перевода всей площади в совокупность плиток единичной площади. Чтобы умножить два числа, числа называются длиной и шириной прямоугольной формы. Дальнейшее разложение чисел на кратные десяткам и единицы снижает общую сложность.
Например:
Умножить 74 на 16
Числа можно разложить как: 74 = 70 + 4 и 16 = 10 + 6
Числа присваиваются прямоугольникам, и соответствующая площадь оценивается и добавляется для вычисления произведения как 1184
Прогрессия умножения с классами
В 3 классе основные аспекты умножения развиваются в процессе многократного сложения. Использование техники восприятия чисел, определение числовых элементов и построение математического выражения или написание таблицы умножения является основным навыком для соответствующего уровня. Кроме того, позиционирование математической операции «умножение» как агрегирования элементов в группах одинакового размера оттачивает навык наблюдения, позволяющий умело моделировать проблему с использованием абстрактных понятий.
Использование техники восприятия чисел, определение числовых элементов и построение математического выражения или написание таблицы умножения является основным навыком для соответствующего уровня. Кроме того, позиционирование математической операции «умножение» как агрегирования элементов в группах одинакового размера оттачивает навык наблюдения, позволяющий умело моделировать проблему с использованием абстрактных понятий.
В 4 классе распределительное свойство умножения используется для уменьшения сложности умножения больших чисел. Используя более простые методы, такие как умножение однозначных чисел и чисел, кратных 10, большие числа разлагаются на сумму меньших чисел. Каждое слагаемое умножается на множитель отдельно, а сумма произведений оценивается как произведение двух чисел.
В 5 классе знания, полученные в предыдущих классах, распространяются на умножение дробей и десятичных чисел. Кроме того, развиваются продвинутые методы умножения двузначного числа на трехзначное число. Концепции подтверждаются областями применения, такими как геометрия, преобразование метрических единиц и другие.
Концепции подтверждаются областями применения, такими как геометрия, преобразование метрических единиц и другие.
Поощрение математических рассуждений и обучение детей с помощью веселых игр способствует лучшему обучению и развитию способностей.
Методики обучения умножению
1. Свойства умножения
Основные свойства умножения используются для простого решения сложных задач. Этими свойствами по отношению к случайным числам «a» и «b» являются:
- Свойство мультипликативной идентичности
- х 1 =
- Коммуникативное имущество
- а х б = б х а
- Ассоциативное имущество
- а x b = (a1 x a2) x b = a1 x (a2 x b)
- Распределительное имущество
- a x B ➔ a x (b +c) ➔ a x b + a x c
Математические выражения, обрамленные математическими символами и числами, решаются с использованием вышеуказанных свойств для упрощения вычислений.
2. Умножение на основе навыков сложения
- Умножение с картинками – Самый простой способ понять умножение – с картинками. Этот метод очень эффективен при умножении двух однозначных чисел. Изображения классифицируются как множимое и множитель. Сумма общего количества картинок равна произведению двух чисел. Основные канцелярские принадлежности, такие как цветные карандаши или карандаши, также можно использовать для обучения такому умножению.
- Например: умножьте 4 на 4
- Результат 16, оценивается повторным сложением объектов с помощью картинок
- Составление предложения на умножение . Словесные задачи на умножение можно решить, идентифицируя числовые значения и формируя допустимое математическое выражение с использованием математических символов. Математические операторы или символы, используемые в таком выражении, представляют собой либо просто крест умножения (x), либо сложение (+), вычитание (–) или деление (/).

- Например, умножьте первое нечетное двузначное число на следующее двузначное число .
- Уравнение будет: 11 x 12
- Сложение чисел на линейной диаграмме для умножения — метод умножения на линейной диаграмме аналогичен подсчету с пропуском. Начальное число — это множимое, и каждый «пропуск» значения множителя определяет произведение.
На следующем рисунке показано умножение числа «3» на разные числа на линейной диаграмме, позволяющей легко составить таблицу умножения.
- Связь между умножением и делением – Связь умножения с делением очень похожа на связь сложения и вычитания. Различные модели умножения, такие как модель «массива», используются в «делении» как модели разделения.
Любое действительное математическое выражение с умножением может быть воспроизведено как уравнение «деления» для вычисления неизвестного значения.
Например: определить произведение 45 и 32
Математическое выражение будет:
45 x 32 =?
45 x 32 = 1440 (используя модель «площадь»)
Уравнение можно записать следующим образом с оператором деления: 1440/45 =?
3.
 Умножение с использованием таблиц
Умножение с использованием таблиц
Развитие фундаментальных знаний, касающихся умножения как многократного сложения, полезно при написании таблиц умножения. Таблица умножения — это структурированный список чисел, в котором каждое число является произведением постоянного множителя и множителей от 1 до 10. Таблицы умножения также полезны при решении задач на деление.
Используя таблицу умножения, дети могут запомнить произведение однозначных и двузначных чисел на другие числа для быстрого счета.
4. Умножение на основе множителя
Знание числа, разрядной системы и кратных 10 способствует использованию быстрых математических приемов для решения текстовых задач и загадок. Умножение дробей и десятичных чисел требует концепции умножения чисел и оценки правильного места десятичной точки, а также свободного владения навыками «деления».
Число, кратное 10, например 1000, может быть записано как 103. Чтобы умножить число, например 380 на 1000, математическое выражение будет таким: x 104 = 380 000
Приложение :
Понятие «умножение» развивается у детей в течение юных лет с помощью сложения и вычитания. Базовый математический навык применяется при визуализации модели в случае группировки и подсчета для оценки продукта. Благодаря значительному вкладу в смежные области, такие как интерпретация данных, измерение физических величин, эта концепция очень полезна для понимания математики, связанной с наукой и физикой.
Базовый математический навык применяется при визуализации модели в случае группировки и подсчета для оценки продукта. Благодаря значительному вкладу в смежные области, такие как интерпретация данных, измерение физических величин, эта концепция очень полезна для понимания математики, связанной с наукой и физикой.
SplashLearn Игры на умножение. Рабочий лист
Самое важное учение — высвободить способность мозга к запоминанию. Концепции умножения с помощью тщательно подобранных словесных задач и математических головоломок связаны со счетом и группировкой. Игры SplashLearn, разработанные в соответствии с учебным планом «общие базовые математические стандарты», признаны универсальным средством домашнего обучения, помогающим преуспеть в математике при обучении в классе.
Склонность к поощрению абстрактного мышления и математических рассуждений предотвращает потерю навыков во время летних каникул и способствует обучению математике. Легко планируйте и планируйте ежедневные математические упражнения, используя исчерпывающие рабочие листы, и отслеживайте производительность с помощью функции оценки панели мониторинга в реальном времени.

 Равные множества. Пустое множество.
Равные множества. Пустое множество. Решение задач
Решение задач Решение задач
Решение задач Разбиение множеств на части по свойствам (классификация)
Разбиение множеств на части по свойствам (классификация)

 Деление на 10, 100, 1000 …
Деление на 10, 100, 1000 …
 Умножение на однозначное число
Умножение на однозначное число Деление на однозначное число
Деление на однозначное число
 Преобразование фигур
Преобразование фигур Меры времени. Календарь
Меры времени. Календарь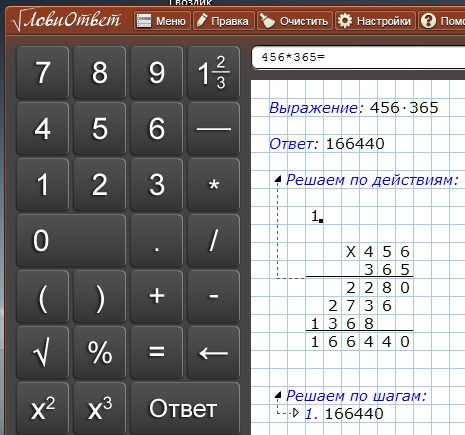 Часы
Часы Выражение с переменной
Выражение с переменной Уравнения
Уравнения Формула объема прямоугольного параллелепипеда
Формула объема прямоугольного параллелепипеда Скорость. Время. Расстояние
Скорость. Время. Расстояние
 Умножение на двузначное число
Умножение на двузначное число Умножение на трехзначное число
Умножение на трехзначное число
 Умножение многозначных чисел
Умножение многозначных чисел 1) [Используйте свою любимую комбинацию клавиш — Control + C].
1) [Используйте свою любимую комбинацию клавиш — Control + C].