Карточки для тренировки по теме «Сложение и вычитание в столбик трехзначных чисел». — «Семья и Школа»
Содержание
Приёмы устного счета для быстрого вычисления в уме
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 — это дважды умножить на 2;
-
умножить на 6 — это значит умножить на 2, а потом на 3;
-
умножить на 8 — это трижды умножить на 2;
-
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 — это дважды разделить на 2;
-
разделить на 6 — это сначала разделить на 2, а потом на 3;
-
разделить на 8 — это трижды разделить на 2;
-
разделить на 9 — это дважды разделить на 3.

Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.

- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
-
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
-
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.

-
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
УМНИКИ И УМНИЦЫ: ПРИМЕРЫ (ТРЕНАЖЕРЫ)
👌ГОТОВИМСЯ К ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЕ
Выполни по действиям:
602 630 – 297 480 : 37 · 69 + 8 653 =
424 410 : 47 – 261 + 608 · 34 =
3 807 · 98 + ( 550 701 – 82 989 ) : 64 =2 603 · 58 + ( 100 000 – 19 975 ) : 75 =
170 604 : 36 + ( 60 700 – 358 · 47 ) =
( 258 270 + 8 090 · 67 – 366 860 ) : 48 =
Реши уравнения:
у — 584= 425 856- с = 412
х + 147 = 231 к — 4523 = 2354
4824 : у = 12 х : 220 = 700
15 х у = 255 а х 28 = 1680
Реши задачи:
😼Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
😼Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
😼С одного аэродрома одновременно в противоположных направлениях вылетели два самолёта. Один летел со скорость 420 км/ч, скорость другого на 80 км/ч меньше. Какое расстояние будет между ними через 3 часа?
😼Из гнезда одновременно в противоположных направлениях полетели две ласточки. Через 20 с расстояние между ними было 680 м. чему равна скорость одной из ласточек, если другая летела со скоростью
16 м/с?
😼Два мальчика одновременно вышли навстречу друг другу из своих домов. Один мальчик шёл со скоростью 50 м/мин, а другой со скоростью 65 м/мин. Через сколько минут они встретятся, если расстояние между домами 1035 м?
😼С двух льдин расстояние между которыми 1785 дм, одновременно навстречу друг другу поплыли два белых медведя . Скорость первого медведя 27 дм/с. С какой скоростью плыл второй медведь, если они встретятся через 35 с.?
Скорость первого медведя 27 дм/с. С какой скоростью плыл второй медведь, если они встретятся через 35 с.?
😼Два автомобиля ехали с одинаковой скоростью. Один из них проехал 400 км, а другой — 480 км. Сколько часов был в пути каждый автомобиль, если первый был в пути на 2 часа меньше чем второй?
😼Два шофера возили зерно. Один из них сделал 3 рейса, другой — 5 рейсов за день. Второй шофер перевез на 30 т зерна больше, чем первый. Сколько зерна перевез каждый из шоферов по отдельности, если каждый рейс перевозилось одинаковое количество зерна?
😼Грузовики возили с базы муку в два разных магазина. В первый магазин отвезли 3 грузовика муки, а во второй 5. Сколько центнеров муки отправили в каждый магазин по отдельности, если в первый магазин отправили муки на 40 центнеров меньше, чем во второй?
👌ДЕЛЕНИЕ НА ДВУЗНАЧНОЕ ЧИСЛО
| 6519 : 53 = | 1127 : 49 = | 4872 : 87 = | 288 : 24 = |
| 2805 : 33 = | 5037 : 73 = | 2812 : 76 = | 2870 : 35 = |
| 4268 : 44 = | 18228 : 28 = | 1450 : 25 = | 735 : 15 = |
243:14 3912:12 6405:15 10104:12
6372:12 10914:34 3945:15 7800:24
👌УМНОЖЕНИЕ НА ТРЕХЗНАЧНОЕ ЧИСЛО
👌УМНОЖЕНИЕ НА ДВУЗНАЧНОЕ ЧИСЛО
👌ВЕЛИЧИНЫ
1. Вырази в миллиметрах.
Вырази в миллиметрах.
53 см =……..мм 6 м 46 см = ………мм
3 м 5 дм 8 мм = ……….мм 6 м 4 дм 8 мм = ……….мм
38 см =……..мм 7 м 26 см = ……мм
2. Переведи.
9000 м = ….. км 6040 м = ….. км ….. м 5001 м = ….. км …..м 730 см = ….. дм ….. см
306 мм = ….. см ….. мм 9005 мм = ….. м ….. мм
730 мм = ….. см
….. мм 39 см = ….. дм ….. см
527 см =
….. дм….. 39 мм =
….. см ….. мм
7030 мм =
….. м ….. мм 65200 м = …… км …… м
10 см, 20 мм, 9 дм, 11 км, 43 см, 8 мм, 5 м, 62 м, 7 дм.
1. Вырази в центнерах.
6 т 4 ц
5 т 200 кг 84000кг
2. Вырази
в тоннах.
2600 ц
57000 кг 69000ц
3.
Сравни.
329т… 331 ц
673ц… 375т
1000 кг… 1т
340 кг. .. 304 ц
.. 304 ц
901кг… 899 ц 871кг… 817 ц
4.
Переведи.
4000 г =… кг 26 т65 ц = … ц
62 т 5 ц = … ц 30 ц = … кг
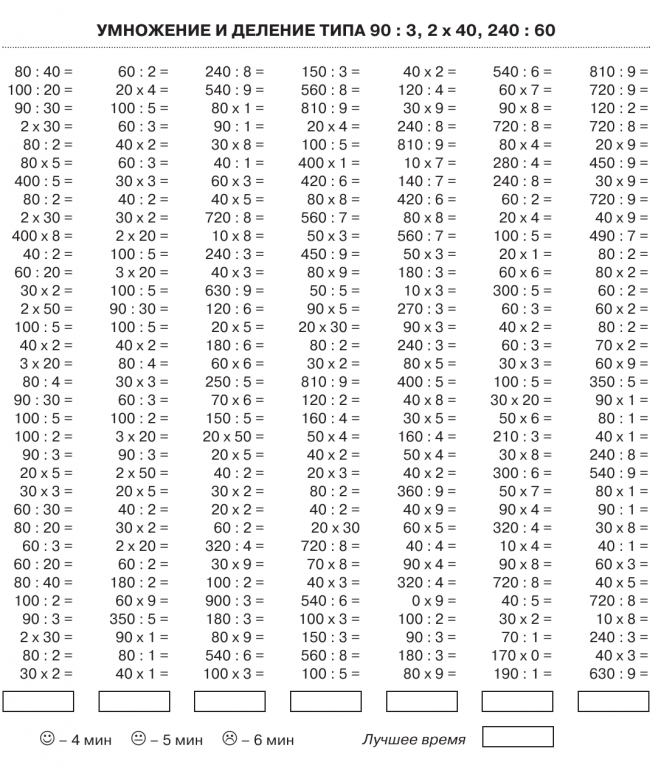
УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
Раздели заданные многозначные числа на однозначное число.
| 1) | 8 | 36830 | 5 | 39809 | 7 | 9314 | 1 | 16548 | 4 | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | . .. | … | … | ||||||
| 2) | 7885 | 1 | 69616 | 8 | 12964 | 7 | 90369 | 9 | 6912 | 4 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| 3) | 9396 | 9 | 10126 | 1 | 50301 | 9 | 18819 | 9 | 22536 | 3 | |||||
. .. .. | … | … | … | … | … | … | … | … | |||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| 4) | 5055 | 3 | 71010 | 9 | 75042 | 9 | 83862 | 9 | 13820 | 5 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | . .. | … | … | … | ||||||
| 5) | 52025 | 5 | 15230 | 2 | 14100 | 6 | 17346 | 7 | 2188 | 1 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| 6) | 25092 | 4 | 8126 | 2 | 16236 | 6 | 21352 | 2 | 23988 | 4 | |||||
. .. .. | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
ЕДНИЦЫ ИЗМЕРЕНИЯ ПЛОЩАДИ
И ПЕРЕВОД ВЕЛИЧИН
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
УМНОЖЕНИЕ И ДЕЛЕНИЕ КРУГЛЫХ МНОГОЗНАЧНЫХ ЧИСЕЛ
РЕШИ
ДЕЛЕНИЕ ДВУЗНАЧНОГО НА ОДНОЗНАЧНОЕ
ДЕЛЕНИЕ ДВУЗНАЧНОГО ЧИСЛА
НА ДВУЗНАЧНОЕ
УМНОЖЕНИЕ И ДЕЛЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ
ПИСЬМЕННОЕ ДЕЛЕНИЕ ТРЕХЗНАЧНОГО ЧИСЛА
НА ОДНОЗНАЧНОЕ
нажми сюда
👇
Видео «Письменное деление»
Примеры для тренировки: 855 : 5 568 : 2 879 : 3
526 : 2 724 : 4 655 : 3
847 : 7 966 : 6 968 : 4
жми сюда и решай
👇
Письменное деление
Умножение: целые числа
Умножение можно рассматривать как многократное добавление. Итак, если вы умножаете число
а
по другому номеру
б
, это то же самое, что добавить число
а
снова и снова
б
раз. (Или добавление
б
снова и снова
а
раз). Например:
Итак, если вы умножаете число
а
по другому номеру
б
, это то же самое, что добавить число
а
снова и снова
б
раз. (Или добавление
б
снова и снова
а
раз). Например:
3 × 5 знак равно 5 + 5 + 5 знак равно 15 3 × 5 знак равно 3 + 3 + 3 + 3 + 3 знак равно 15
Другой способ думать об умножении целых чисел а × б состоит в том, чтобы визуализировать объекты, расположенные в виде прямоугольника, с а ряды и б столбцы.
3 × 5
Обратите внимание, что есть 15 точки на рисунке.
Стандартный алгоритм
Чтобы умножить многозначное число на однозначное с помощью стандартного алгоритма, напишите два числа друг над другом так, чтобы единицы были выровнены по вертикали, а многозначное число — сверху.
127 × 3 _
Умножьте цифру единиц верхнего числа на нижнее число. Запишите разряд единиц результата. Если результат больше 10 , несите цифру десятков, как при сложении.
Здесь, 7 × 3 знак равно 21 , так
1 2 2 7 × 3 _ 1
Теперь умножьте разряд десятков верхнего числа на нижнее число и прибавьте полученную цифру к результату. Здесь,
2
×
3
знак равно
6
, а потом добавляем
2
получить
8
. С
8
меньше чем
10
, мы не должны нести на этот раз.
Здесь,
2
×
3
знак равно
6
, а потом добавляем
2
получить
8
. С
8
меньше чем
10
, мы не должны нести на этот раз.
1 2 2 7 × 3 _ 8 1
Наконец, умножьте разряд сотен верхнего числа на нижнее число. Здесь, 3 × 1 знак равно 3 .
1 2 2 7 × 3 _ 3 8 1
Так, 127 × 3 знак равно 381 .
Чтобы умножить два многозначных числа , напишите число с большим количеством цифр сверху. Например, чтобы умножить 29 по 543 , мы пишем
543 × 29 _
Сначала умножьте верхнее число на разряд единиц нижнего числа, как описано выше. 3 × 9 знак равно 27 , так что запишите 7 и нести 2 :
5 4 2 3 × 2 9_ 7
4 × 9 36, плюс 2 является 38 , поэтому запишите 8 и несите 3 :
5 3 4 2 3 × 2 9_ 8 7
5 × 9 является 45 , плюс 3 является 48 . Больше нет цифр для переноса, так что записывайте 48 .
5 2 4 2 3 × 2 9_ 4 8 8 7
Далее нам нужно умножить верхнее число на разряд десятков нижнего номера. Поскольку мы на самом деле умножаем на
20
, не по
2
, мы записываем
0
в качестве заполнителя.
5 4 3 × 29_ 4887 0
3 × 2 является 6 , поэтому запишите 6 .
5 4 3 × 2 9_ 4887 6 0
4 × 2 является 8 , поэтому запишите 8 .
5 4 3 × 2 9_ 4887 8 6 0
5 × 2 является 10 , и больше нет цифр для переноса, поэтому запишите 10 .
5 4 3 × 2 9_ 4887 10 860
Последним шагом является добавление двух результатов.
5 4 3 × 29_ 4887 + 10 860 _ 13947
Так, 543 × 29знак равно 13947 .
Как и сложение, умножение коммутативный для действительных чисел (т. а × б знак равно б × а ; порядок не имеет значения) и ассоциативный (то есть, ( а × б ) × с знак равно а × ( б × с ) ; группировка не имеет значения.) См. Свойства умножения для большего.
Шаблон плана урока Direct Instruction — Математика — Шаблон плана урока Direct Instruction
Шаблон плана урока Direct Instruction
Общая информация
Название урока: Умножение на многозначные числа Предмет(ы): математика Класс/Уровень/Настройка: 5-й Необходимые навыки/предварительные знания: Разрядное значение, факты умножения, умножение на однозначные числа
Стандарты и цели
Государственный/национальный академический стандарт(ы):
NBT. 5.A Умножение многозначных целых чисел Цели обучения: Учащиеся смогут решать задачи на умножение 4-значного числа на 2-значное, используя стандартный алгоритм с вероятностью 75%.
точность.
5.A Умножение многозначных целых чисел Цели обучения: Учащиеся смогут решать задачи на умножение 4-значного числа на 2-значное, используя стандартный алгоритм с вероятностью 75%.
точность.
Технология материалов
SmartBoard Диаграммная бумага Интерактивные тетради. Выходные билеты iPad
SAMR Уровень: Увеличение Использование активности SmartBoard, которую я также могу нажать в Google Classroom как физическое лицо или партнер деятельность позволяет практиковаться и получать немедленную обратную связь от меня.
Требования к языку
Особые способы использования учащимися академического языка (лексика, функции, дискурс, синтаксис) для участия
в учебных задачах посредством чтения, письма, прослушивания и/или разговора, чтобы продемонстрировать свое понимание. Языковые функции: Содержание и языковая направленность учебной задачи представлены активными глаголами в результатах обучения.
Словарь: Многозначное, разрядное значение, единицы, десятки, сотни, тысячи, множитель, произведение, умножение, перегруппировка, стандартный алгоритм, место держатель (или нулевой заполнитель), частичное произведение, множимое
Дискурс и/или синтаксис: Обсуждение: учащиеся будут участвовать в беседах о числах по поводу умножения, чтобы улучшить свои навыки устной речи. Синтаксис: учащиеся ведут интерактивные записные книжки с математическими таблицами и заметками.
Запланированная языковая поддержка: Студенты будут иметь очередь и время для разговора во время упреждающего набора, чтобы повторить то, что мы сделали вчера с умножением 4- цифра однозначными числами
Учебные стратегии и учебные задачи
Упреждающий набор: Описание занятия/Действия учителя и ученика Вопрос к учащимся: Что вы помните? со вчерашнего дня? (умножение 4-значного числа на 1-значное числа)
Обсуждение всей группой
Повернитесь и обсудите вопрос с партнером
Обсуждение всей группой
Поставьте цель обучения на день самостоятельно слова Процедуры представления новой информации и/или моделирования: Описание занятия/Действия учителя и ученика Лексика: повторение вчерашних слов (многозначное число, фактор, произведение, разрядное значение, единицы, десятки, сотни, тысячи, умножить, стандарт алгоритм, перегруппируйтесь) Познакомить с новыми словарными словами: место держатель (или нулевой заполнитель), частичный продукт, множимое Следующие определения будут поставлены на якорная диаграмма: Заполнитель: при умножении на число в разряде десятков (или сотен) необходимо добавить
Повернитесь и поговорите с напарником, чтобы просмотреть вчерашнее словарный запас
Скопируйте новые словарные слова в свои интерактивный блокнот
Скопируйте проблемы, которые я моделирую, в свои интерактивный блокнот
Что дальше? (7 х 4)
Что такое 7 х 4? (28) Я смоделирую как ты пишешь
вниз по 8 в столбце сотен и нести
2 Что будет дальше? (7 х 2)
Что такое 7 х 2? (14) смоделирую как вам нужно
добавить 2 к 14, чтобы получить 16, а 4 идет в
столбец тысяч и 1 идет в десятке
столбец тысяч Теперь, что мне нужно сделать? (поставить заглушку
нуль)
Что дальше? (9х 5)
Что такое 9 х 5? (45) Я смоделирую как ты пишешь
5 в столбце десятков и нести 4 Какой следующий шаг? (9 х 0)
Что такое 9 х 0? (0) смоделирую как вы добавите
4 вы перенесли на ноль и записали 4 в
столбец сотен Что будет дальше? (9 х 4)
Что такое 9 х 4? (36) Я смоделирую, как ты пишешь
6 в столбце тысяч и нести 3 Какой следующий шаг? (9 х 2)
Что такое 9 х 2? (18) смоделирую как вы добавите
от 3 до 18, чтобы получить 21 и написать 1 в десятке
столбец тысяч и 2 в сотне
тысяч столбец Что мы делаем, когда закончим
умножение? (добавьте 2 цифры) буду моделировать
добавление 2 чисел, показывающих, как это так
важно, чтобы у них все было в порядке
правильно Независимая студенческая практика:
Описание занятия/Действия учителя и ученика Я буду ходить и наблюдать за студентами, как
они работают над деятельностью Google Classroom. я
поможет, ответит на вопросы и прояснит
заблуждения по мере необходимости.
я
поможет, ответит на вопросы и прояснит
заблуждения по мере необходимости.
Учащиеся будут работать в Google Classroom на своих iPad для завершения самостоятельной работы. Они будут сможет продемонстрировать свой уровень понимание стандартного алгоритма и
На активности будут следующие проблемы: 5284 х 94 6301 х 32 2833 х 81 4025 х 40 3536 x 67
умножение многозначных чисел.
Кульминация или завершение процедуры/мероприятия: Описание занятия/Действия учителя и ученика Выходной билет Ученики продемонстрируют свои знания о стандартный алгоритм и умножение на 4 проблемы. 2039 х 23 4937 х 35 7251 х 44 1490 x 53
Учащиеся заполняют выходной билет показать свои знания об умножении и стандартный алгоритм.
Дифференцированное обучение
Подумайте, как приспособиться к потребностям каждого типа учащихся. Убедитесь, что вы предоставляете конкретное содержание
приспособления, которые помогают удовлетворить различные потребности в обучении.
Эффективный счёт в уме или разминка для мозга / Хабр
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899.
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400; 3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68.
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
600 : 25 = (600 : 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600.
Теперь не кажется невозможным умножить в уме 625 на 53:
625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = = (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125.2 = 17000 + 19000 + 2000 + 25 = 38025.
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
M = 10m + n, K = 10a + 10 - n.
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001.
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
48 x 42 = 2016.
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. 2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
Умножение вектора на матрицу
Горячая математикаЧтобы умножить вектор-строку на вектор-столбец, вектор-строка должен иметь столько столбцов, сколько строк имеет вектор-столбец.
Определим произведение матрицы
А
и вектор Икс в котором количество столбцов в
А
равно количеству строк в Икс .
Так что если А является м × н матрица, то произведение А Икс определяется для н × 1 столбцы векторов Икс . Если мы позволим А Икс знак равно б , тогда б является м × 1 вектор-столбец. Другими словами, количество строк в А определяет количество рядов в изделии б .
Общая формула для матрично-векторного произведения:
А Икс знак равно [ а 11 а 12 ⋯ а 1 н а 21 а 22 ⋯ а 2 н ⋮ ⋮ ⋮ ⋮ а м 1 а м 2 ⋯ а м н ] [ Икс 1 Икс 2 ⋮ Икс н ] знак равно [ а 11 Икс 1 + а 12 Икс 2 + ⋯ + а 1 н Икс н а 21 Икс 1 + а 22 Икс 2 + ⋯ + а 2 н Икс н ⋮ а м 1 Икс 1 + а м 2 Икс 2 + ⋯ + а м н Икс н ]
Пример :
Находить
А
у
куда
у
знак равно
[
2
1
3
]
и
А
знак равно
[
1
2
3
4
5
6
7
8
9
]
.
По определению количество столбцов в А равно количеству строк в у .
А у знак равно [ 1 2 3 4 5 6 7 8 9 ] [ 2 1 3 ]
Сначала умножьте ряд 1 матрицы по столбцу 1 вектора.
[ 1 2 3 ] [ 2 1 3 ] знак равно [ 1 ⋅ 2 + 2 ⋅ 1 + 3 ⋅ 3 ] знак равно 13
Далее умножить ряд
2
матрицы по столбцу
1
вектора.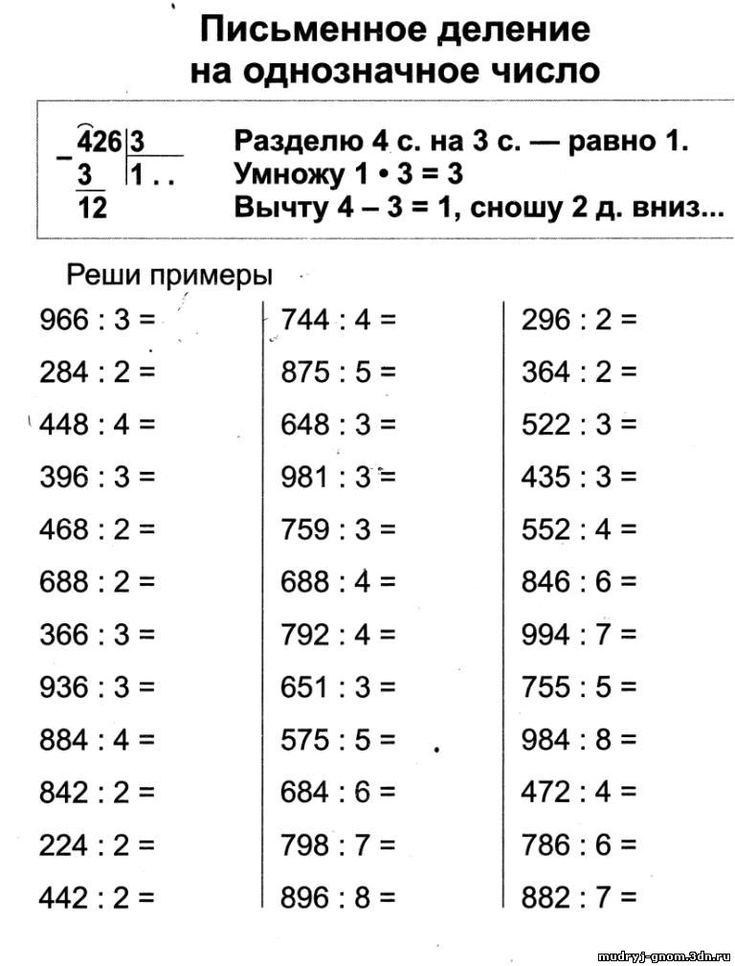
[ 4 5 6 ] [ 2 1 3 ] знак равно [ 4 ⋅ 2 + 5 ⋅ 1 + 6 ⋅ 3 ] знак равно 31
Наконец, умножьте ряд 3 матрицы по столбцу 1 вектора.
[ 7 8 9 ] [ 2 1 3 ] знак равно [ 7 ⋅ 2 + 8 ⋅ 1 + 9 ⋅ 3 ] знак равно 49
Записав произведение матрицы на вектор, мы получим:
А у знак равно [ 13 31 49 ]
Загрузите наши бесплатные приложения для обучения и книги для подготовки к экзаменам
| Умножение и массивы.
 Имеет ли значение порядок? math club
Имеет ли значение порядок? math clubВсех с Новым годом. Мое решение состоит в том, чтобы писать больше сообщений в блоге. Снимаю по 2 в месяц. Мне часто задают вопросы по электронной почте, и я собираюсь начать использовать эти вопросы и ответы в качестве блогов. Я надеюсь, что это поможет сделать этот материал актуальным для всех вас. Первый из них касается рассмотрения массивов как математического инструмента и «правил» в отношении массивов и математических выражений. И затем, через пару недель, у меня есть один на Fractions, готовый к запуску.
Давайте начнем здесь. Этот вопрос от моего бывшего ученика, который сейчас работает учителем первого курса. Она «встряхивает» его на собраниях своей команды, задавая такие вопросы, как этот:
Привет, доктор Фолкнер,
На сегодняшнем собрании возник вопрос о «порядке» массива. В нашей рабочей тетради для детей прямо указано, что первое число в умножении — это количество строк, а второе — количество столбцов. Например, 3X4 будет 3 строки по 4 столбца. Всегда.
Например, 3X4 будет 3 строки по 4 столбца. Всегда.
Я не знаю, существует ли определенный порядок создания массива умножения или нет. Я возражал против (но я мог ошибаться!) Лучшая причина, которую я получил от моей команды, чтобы объяснить, почему это были строки, а затем столбцы, заключалась в том, что именно так это будет, когда они вычислят площадь (что не имело смысла и не имело смысла). меня не удовлетворил).
Во всяком случае, я надеялся, что вы сможете пролить свет на эту проблему для меня. Если я прав, мне хорошо, если нет, я научу лучше в следующем году 🙂
Спасибо, TM
Я часто слышу этот вопрос, и здесь есть несколько вопросов. Мой короткий ответ заключается в том, что я на стороне ТМ в этом вопросе — это искусственная идея о том, что абстрактная задача на умножение ДОЛЖНА всегда представлять определенную вещь. У команды ТМ есть один достойный аргумент, но дело не в том, что мы будем жестко решать проблемы с площадями, а в том, что это относится к матрицам в алгебре. Давайте посмотрим на несколько вещей здесь.
Давайте посмотрим на несколько вещей здесь.
Сначала подумаем о Практический стандарт № 2 – Абстрактное и количественное обоснование (* полную версию практического стандарта 2 см. ниже). Заблаговременное создание жестких «правил» для учащихся (3 × 4 всегда означает количество строк и столбцов) затрудняет для вас и класса взаимодействие с практическим стандартом № 2. Если вы уже сказали мне, что все означает заранее, почему я должен останавливаться и думать, что означают эти абстракции в моем общении с другими? Короче, я бы не стал. Мне просто нужно запомнить, что учитель сказал, что это всегда строки, а это всегда столбцы. Сама идея этого практического стандарта состоит в том, чтобы понять, что цифры сами по себе ЯВЛЯЮТСЯ абстракцией. Они абстрактны. Только контекст действительно оживляет их. Как я слышал, некоторые люди говорят, что «числа — это прилагательные». Я думаю, это помогает. Итак, 3 и 4 — это прилагательные, описывающие что-то. ЕСЛИ вы хотите передать, что 3×4 означает для вас 3 строки x 4 столбца, напишите это. Это побуждает вас и класс помнить, что «следить за своими единицами» действительно важно и полезно. Вы можете сказать что-то вроде «У меня есть привычка сначала писать свои строки, поэтому я знаю, что когда я пишу 3 x 4, я имею в виду строки x столбцы. Если я знаю, что общаюсь с кем-то еще, мне нужно, чтобы мои единицы были там». И что-то вроде этого «Помните, что 3 и 4 — это просто прилагательные, дескрипторы. Что они описывают? Ну, мы не знаем этого, пока мы не контекстуализируем их. Вот почему единицы так важны, они помогают нам связать эти абстрактные дескрипторы с вещами, которые они описывают. Синий говорит вам, ну, не очень много. А ведь синяя корова говорит о многом! То же и с числительными…»
Это побуждает вас и класс помнить, что «следить за своими единицами» действительно важно и полезно. Вы можете сказать что-то вроде «У меня есть привычка сначала писать свои строки, поэтому я знаю, что когда я пишу 3 x 4, я имею в виду строки x столбцы. Если я знаю, что общаюсь с кем-то еще, мне нужно, чтобы мои единицы были там». И что-то вроде этого «Помните, что 3 и 4 — это просто прилагательные, дескрипторы. Что они описывают? Ну, мы не знаем этого, пока мы не контекстуализируем их. Вот почему единицы так важны, они помогают нам связать эти абстрактные дескрипторы с вещами, которые они описывают. Синий говорит вам, ну, не очень много. А ведь синяя корова говорит о многом! То же и с числительными…»
Мы могли бы также рассмотреть, являются ли сами массивы просто абстракциями и не очень конкретными. Массив — это не совсем то же самое, что реальный контекст, верно? Массив — это математический инструмент для понимания выражения умножения, но на самом деле он не такой конкретный. Что обозначают строки и столбцы? Строки и столбцы ради строк и столбцов? Они являются инструментом для организации размышлений о том, что такое умножение. Если мы хотим думать о них как о более конкретных, нам нужно сделать их более конкретными через контекст. Коллега из Эшвилла, Тима Уильямс, в настоящее время размышляет о том, как важно помнить, что многие из наших математических инструментов не так конкретны, как они должны быть для некоторых студентов. Она прислала мне эту фотографию, чтобы напомнить нам, что для многих студентов Инструмент Массива должен быть более конкретным, и что этот конкретный уровень должен существовать некоторое время для некоторых студентов. Легкое междометие для поддержки мышления всех учащихся. Таким образом, это приводит нас к рассмотрению Практический стандарт № 5 Стратегически используйте соответствующие инструменты. Видите ли вы, что, заранее определяя, что представляет собой данная задача, мы отговариваем учащихся от размышлений о том, что значит использовать такой математический инструмент, как массив (№5)? Вместо того, чтобы думать «хорошо, так что же представляет моя 3 на моем рисунке и как массив помогает мне понять это», ученика будут думать «хорошо, учитель сказал, что это всегда ряды — я не знаю, почему но это всегда так».
Что обозначают строки и столбцы? Строки и столбцы ради строк и столбцов? Они являются инструментом для организации размышлений о том, что такое умножение. Если мы хотим думать о них как о более конкретных, нам нужно сделать их более конкретными через контекст. Коллега из Эшвилла, Тима Уильямс, в настоящее время размышляет о том, как важно помнить, что многие из наших математических инструментов не так конкретны, как они должны быть для некоторых студентов. Она прислала мне эту фотографию, чтобы напомнить нам, что для многих студентов Инструмент Массива должен быть более конкретным, и что этот конкретный уровень должен существовать некоторое время для некоторых студентов. Легкое междометие для поддержки мышления всех учащихся. Таким образом, это приводит нас к рассмотрению Практический стандарт № 5 Стратегически используйте соответствующие инструменты. Видите ли вы, что, заранее определяя, что представляет собой данная задача, мы отговариваем учащихся от размышлений о том, что значит использовать такой математический инструмент, как массив (№5)? Вместо того, чтобы думать «хорошо, так что же представляет моя 3 на моем рисунке и как массив помогает мне понять это», ученика будут думать «хорошо, учитель сказал, что это всегда ряды — я не знаю, почему но это всегда так». Видите ли вы также, как это напрямую влияет на целеустремленность ученика и, следовательно, влияет на его способность придумывать веские аргументы в пользу своего рисунка?
Видите ли вы также, как это напрямую влияет на целеустремленность ученика и, следовательно, влияет на его способность придумывать веские аргументы в пользу своего рисунка?
Затем это влияет на Практический стандарт #3 Создание обоснованных аргументов и критика рассуждений других . Когда мы учим студентов строить аргументы, мы должны помнить, что «потому что так сказал учитель» не является жизнеспособным аргументом. С другой стороны, , «потому что на моем рисунке вы можете видеть здесь, что 3 представляет мои столбцы, а 4 представляет мои строки» — действенный аргумент, связывающий учащихся с числовым выражением, с которым они работают. Этот аргумент ( 3 для моих столбцов и 4 для моих строк ) является «неправильным» только в контексте произвольного «правила» учителей. Это связано с тем, как мы хотим, чтобы учащиеся взаимодействовали со своими моделями/чертежами/математическими инструментами и как мы хотим, чтобы они могли выразить словами то, что они представляют, когда они учатся строить жизнеспособные аргументы.
Одна из причин, по которой мне нравится вопрос ТМ, заключается в том, что, на мой взгляд, она так четко борется с этими стандартами. Будучи молодым учителем (или пожилым, как многие из нас, если на то пошло!), здорово иметь привычку думать о математике, которую вы преподаете, таким образом, чтобы она соответствовала стандартам практики. TM выясняет, что значит стратегически использовать подходящие инструменты (в данном случае массивы), и пытается создать жизнеспособный аргумент, чтобы представить ее команде*.
Площадь и матрицы и практический стандарт № 4 Модель с математикой — А как насчет аргументов команды? Есть ли весомый аргумент в пользу их позиции? Я не верю их аргументу о том, что «вот что мы будем делать с площадью, так что привыкайте к этому сейчас». Почему площадь всегда должна быть представлена таким образом? По какой-то причине мы застряли на идее, что длина и ширина — это разные вещи. Они действительно обе длины. Если вы хотите назвать большую длину шириной, вы, конечно, можете это сделать, но это немного нематематическая уловка. Возможно, мы можем просто сказать, что это повседневное использование, которое не очень хорошо помогает нам в мире математики. В представлении площади и 3, и 4 являются длинами. Мы можем увидеть, просто взглянув на него, какая сторона длиннее, нам не нужно называть это как-то по-другому. Расположение 3 и 4 в определенном контексте определяет ориентацию прямоугольника. Здесь мы собираемся использовать наше математическое выражение для моделирования внутреннего дворика, который мы хотим построить (Практический стандарт № 4). Что касается вашей входной двери, у вас может быть внутренний дворик 3 × 4 или внутренний дворик 4 × 3. Может быть, один лучше подходит и избегает стока, может быть, один лучше смотрится с потоком переднего двора. Оттуда студентов можно попросить продемонстрировать свои идеи для внутреннего дворика, а затем объяснить, какое математическое выражение они хотят использовать для его описания и почему. О, и кстати, здесь я говорю в метрах или ярдах, а не в футах.
Возможно, мы можем просто сказать, что это повседневное использование, которое не очень хорошо помогает нам в мире математики. В представлении площади и 3, и 4 являются длинами. Мы можем увидеть, просто взглянув на него, какая сторона длиннее, нам не нужно называть это как-то по-другому. Расположение 3 и 4 в определенном контексте определяет ориентацию прямоугольника. Здесь мы собираемся использовать наше математическое выражение для моделирования внутреннего дворика, который мы хотим построить (Практический стандарт № 4). Что касается вашей входной двери, у вас может быть внутренний дворик 3 × 4 или внутренний дворик 4 × 3. Может быть, один лучше подходит и избегает стока, может быть, один лучше смотрится с потоком переднего двора. Оттуда студентов можно попросить продемонстрировать свои идеи для внутреннего дворика, а затем объяснить, какое математическое выражение они хотят использовать для его описания и почему. О, и кстати, здесь я говорю в метрах или ярдах, а не в футах.
Ранние исследования с PS #4 (Моделирование математики) могут быть довольно простыми: В начальных классах это может быть так же просто, как написать уравнение сложения для описания ситуации (PS #4). В нашем примере с патио мы использовали простое выражение умножения для моделирования нашего патио. Если мы заранее установим «правило» для таких ситуаций («длина» всегда стоит на первом месте, а «ширина» — на втором), мы отобьем у учащихся желание связывать значение с их контекстом и математическим выражением, которое они хотят использовать для моделирования этой ситуации. контекст.
В нашем примере с патио мы использовали простое выражение умножения для моделирования нашего патио. Если мы заранее установим «правило» для таких ситуаций («длина» всегда стоит на первом месте, а «ширина» — на втором), мы отобьем у учащихся желание связывать значение с их контекстом и математическим выражением, которое они хотят использовать для моделирования этой ситуации. контекст.
Для протокола: я случайно оказался на собрании в NCDPI и смог проконсультироваться по этому вопросу с представителями старшей школы и начальной математики. Они оба согласны с аргументами, которые я привел выше. Они также согласны с тем, что было бы искусственным говорить, что именно так мы всегда должны относиться к области. Они, однако, упомянули, что есть один достойный аргумент в пользу этой позиции. То есть, когда мы добираемся до алгебры, существует формальное понимание того, что первое числительное/прилагательное/множитель в выражении умножения действительно представляет строку в матрице, а второе числительное/прилагательное/множитель представляет столбец. Но это еще не достаточное основание, чтобы сделать это «правилом» в начальных классах. Давайте снова обратимся к Стандарту практики № 4. В пояснении к этому стандарту написано «Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов». Ключевым моментом здесь является то, что их нельзя обобщать или делать формальными до более поздних классов. Когда вы формируете идеи в виде правил слишком рано, вы снижаете способность учащихся вести дискуссии и описывать свои мысли. Вы также наносите ущерб их способности думать о разнице между абстрактным выражением (3 x 4), инструментом для представления его значения (массив — строки и столбцы) и тем, что вы, возможно, хотите, чтобы оно представляло (патио).
Но это еще не достаточное основание, чтобы сделать это «правилом» в начальных классах. Давайте снова обратимся к Стандарту практики № 4. В пояснении к этому стандарту написано «Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов». Ключевым моментом здесь является то, что их нельзя обобщать или делать формальными до более поздних классов. Когда вы формируете идеи в виде правил слишком рано, вы снижаете способность учащихся вести дискуссии и описывать свои мысли. Вы также наносите ущерб их способности думать о разнице между абстрактным выражением (3 x 4), инструментом для представления его значения (массив — строки и столбцы) и тем, что вы, возможно, хотите, чтобы оно представляло (патио).
Мы хотим вести подобные беседы с юными учениками, а установление правила сверху вредит вашим усилиям вести хорошую математическую беседу. Говоря учащимся : «Когда вы будете учиться в старшей школе, вы увидите, что математики имеют понятную привычку использовать первое произведение для представления строк, но здесь мы сосредоточимся на том, можете ли вы описать свою модель и связать ее с числами, которые ее представляют. » сильно отличается от высказывания «первым фактором всегда является строка, а вторым фактором всегда является столбец».
Говоря учащимся : «Когда вы будете учиться в старшей школе, вы увидите, что математики имеют понятную привычку использовать первое произведение для представления строк, но здесь мы сосредоточимся на том, можете ли вы описать свою модель и связать ее с числами, которые ее представляют. » сильно отличается от высказывания «первым фактором всегда является строка, а вторым фактором всегда является столбец».
Не стесняйтесь добавлять комментарии и мысли к тому, что, как я надеюсь, является жизнеспособным аргументом в пользу того, что мы НЕ должны иметь привычку представлять 3 x 4 как «Всегда ряды, а затем столбцы», а вместо этого представлять это как возможность работать над стандартами практики . 2, 3, 4 и 5 .
*Постскриптум. Как и ТМ, я борюсь со стандартами, когда пишу это. Я отправил это сообщение в блог некоторым коллегам, и они предложили мне провести более четкое различие между практическими стандартами 4 (модели) и 5 (инструменты).
Это то, что мой коллега Темпл Валковиак предложил мне рассмотреть в отношении моей интерпретации Стандарта 4 (модели) и 5 (инструменты) (что я и сделал и внес изменения в свой блог выше: ).
Темпл утверждает, что вопрос ТМ больше касается Стандарта 5, чем 4:
Вот почему… согласно определению CCSS-M, моделирование с помощью математики — это когда мы используем математику для моделирования реальных ситуаций. Как написано в вашем сообщении в блоге, похоже, что они боролись только с массивами, отсутствующими в каком-либо реальном контексте. Итак, я мог бы сказать: «ТМ выясняет, что значит стратегически использовать соответствующие инструменты (в данном случае массивы) в своем классе, и она пытается создать жизнеспособный аргумент, чтобы представить ее команде».
CCSS.Math.Practice.MP2 Рассуждать абстрактно и количественно.
Подкованные в математике учащиеся понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представить ее символически и манипулировать репрезентирующими символами, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на свои референты. — и способность контекстуализировать , чтобы при необходимости сделать паузу в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
— и способность контекстуализировать , чтобы при необходимости сделать паузу в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
CCSS.MATH.PRACTICE.MP5 Стратегически используйте соответствующие инструменты.
Подкованные в математике учащиеся рассматривают имеющиеся инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
CCSS.Math.Practice.MP3 Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
Подкованные в математике учащиеся понимают и используют установленные предположения, определения и ранее установленные результаты при построении аргументов.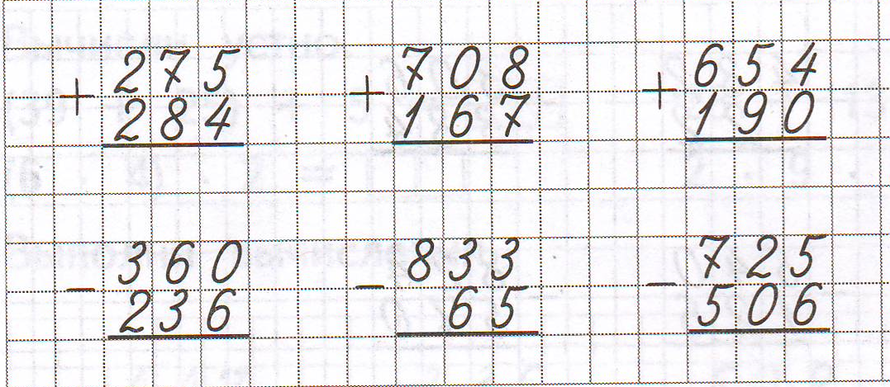 Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент.
Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.MP4 Модель с математикой.
Подкованные в математике учащиеся могут применять известные им математические знания для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра.



 2 = 17000 + 19000 + 2000 + 25 = 38025.
2 = 17000 + 19000 + 2000 + 25 = 38025.