Алгоритмы письменного умножения и деления многозначных чисел
Алгоритмы письменного умножения и деления многозначных чисел.
Этапы изучения темы:
умножение и деление на однозначное число;
умножение и деление на двузначные и трехзначные разрядные числа;
умножение и деление на двухзначные и трехзначные числа.
Умножение и деление изучаются одновременно на каждом этапе, но сначала – умножение, затем – деление.
На каждом этапе наряду с умножением и делением натуральных чисел изучается умножение и деление величин на число.
Частные случаи:
Умножение
-первый и второй множитель оканчиваются нулями 87600*4,376*240
-нули в середине второго множителя 875*304
-различные сочетания этих случаев 170*230, 1630*103
Деление:
-частное оканчивается нулями 227200:4=56800
-нули в середине частного 72450:7=10350.
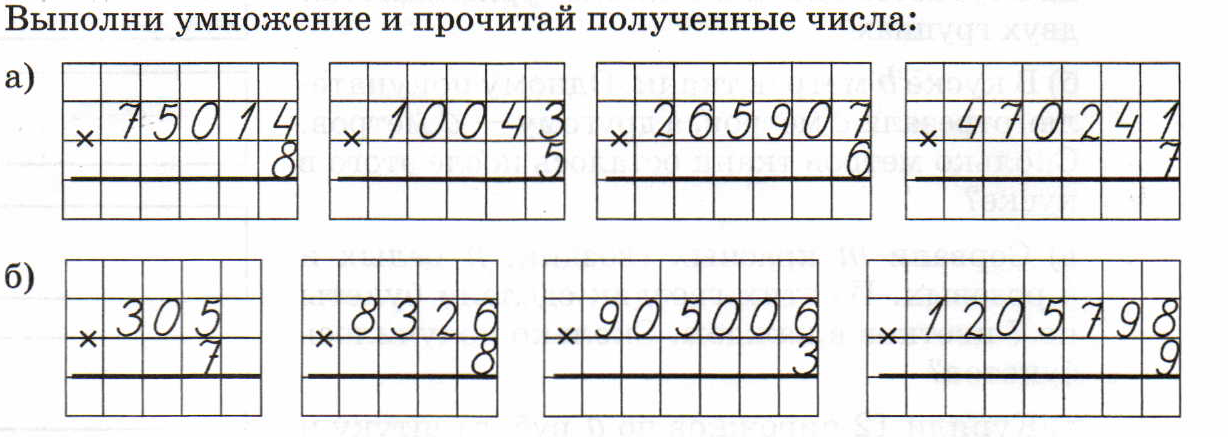
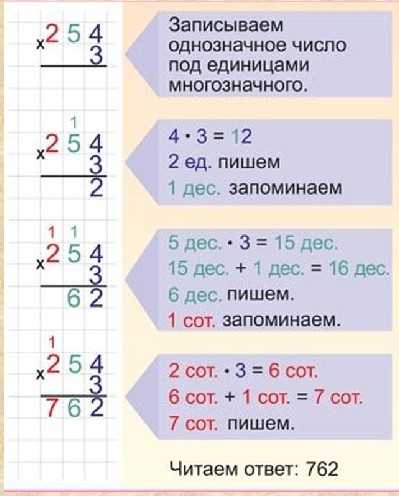
Умножение многозначных чисел на однозначное число
К письменному приему обращаемся только тогда, когда устно решить трудно.
54879*5
А лгоритм:
-записать числа в столбик (однозначное число под единицами многозначного)
-умножить единицы I множителя на II множитель, результат записать по единицами;
-умножить десятки I множителя на II, результат записать под десятками;
-аналогичные действия проделать со всеми основными разрядами I множителя;
-прочитать полученный результат.
Далее, опираясь на алгоритм, дети решают аналогичные выражения, при этом фиксируют словами каждую операцию (комментируют). Выражения подбираются в усложняющейся последовательности:
-увеличивается I множитель 284*3 2934*5 28751*7
-I множитель содержит нули (частный случай).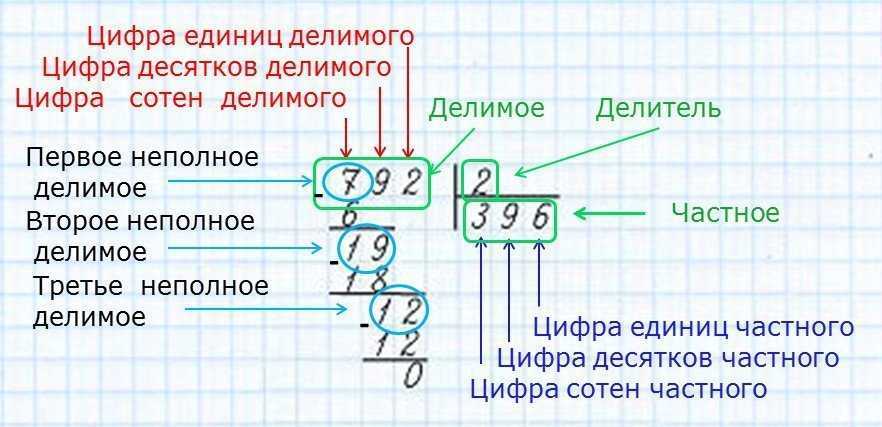
На освоение алгоритма умножения – задания на нахождение преднамеренно допущенных ошибок.
Например: 7056 8539 5700
8 2 9
56408
II этап умножение на двузначные и трехзначные разрядные числа
621*30. Используя свойство а*(в*с), показываем детям целесообразность записи 621*(3*10) 621
30
Особое внимание заслуживают выражения, где оба множителя заканчиваются нулями.
Устно: 300*50 (3 сот * 5)*10=15 сот*10=150 сот=15000.
Письменно: аналогично вышеприведенному случаю 7800
30
234000
Вывод: сначала решать без нулей, затем посчитать сколько их и приписать.
7тыс*30=~210000= в ответе не меньше 6 цифр.
При выполнении умножения «в столбик» обязательно делать прикидку.
III этап умножения на двухзначное и трехзначное число
87*64, 286*374
А лгоритм:
1.Записать числа в столбик, единицы под единицами; десятки под десятками.
2.Умножить I множитель на единицы II множителя – получится I неполное произведение, результат записать под единицами.
3.Умножить I множитель на десяток II множителя – получится II полное произведение, записать результат на один разряд влево, под десятки.
4.Далее действия повторяются.
5.Сложить все неполные произведения.
6.Записать и прочитать полученный результат.
Новое понятие «неполное произведение».
Закрепление:
-расписать 286*374
-по плану решения составить пример 84*6+84*30
-сравнить 138*14 и 138*40 алгоритмы.
-376*4+376*10 на какое число умножаем?
-решить удобным способом:
32*2*50= 73*6*3+73*2=
54*80+54*20= 83*16+17*16=
Частные случаи умножения чисел, содержащих нули.
Умножение чисел, оканчивающихся нулями, знакомы детям =больше самостоятельности.
158
4003
Эти виды выражений трудны для детей. (Сдвиг цифр на 2 или 3 цифры влево). Использовать «нерациональный» способ! Пока слабые дети не будут ориентированы.
158
4003
474
000 000
000
63648 632
632474
После вводится умножение величин выражений в 2 наименованиях.
Закрепление: аналогично.
Деление многозначных чисел.
I этап – деление на однозначное число.
Алгоритм:
1.Записать пример в столбик.
2.Выбрать первое неполное делимое. Определить количество цифр в частном.
3.Методом подбора найти первую цифру частного.
4.Проверить правильность выбора первой цифры частного, умножив её на делитель.
5.Полученное число сравнить с I неполным делимым (с помощью вычитания).
6.Получившийся остаток сравнить с делителем:
а)если остаток
б)если остаток = делимому, то допущена ошибка при подборе цифры частного (цифру увеличить)
в)остаток = 0, деление закончено (в одном случае)
г)(в другом) 0 является промежуточным результатом, надо снести цифру исходного делимого и получить II неполное делимое.
7.II неполное делимое сравнить с делимым:
а)если оно = делителя, то произвести подбор второй цифры частного
б)если оно
8.Аналогично подбираются следующие цифры частного.
9.Записать и назвать полученный результат.
Постепенно примеры усложняются: увеличивается число разрядов в делимом (3,4,5,6 значные числа)
Частные случаи: (в записи частного встречается 0)
22720:4=5680 – полностью весь алгоритм и последнее 0:4=0. Частное…
4254:6=709 – дети часто пропускают 0.
Для предупреждения ошибок:
-определить количество цифр в частном;
-проверка умножением;
-проверка неправильным решением примеров.
На этом же этапе решаем примеры на деление с остатком и деление однородных величин.
II этап. Деление на двухзначные и трехзначные разрядные числа
Письменные приемы:
4980:60
480
180
180
Делимое 498 десятков =в частном 2 цифры. Здесь перемешивать деление с остатком и без остатка.
Частные случаи: Дети могут разобрать аналогично предыдущему. Так же и деление на разрядные трехзначные числа.
III этап. Деление на двухзначное и трехзначное число.
а)деление трехзначного числа на двухзначное, цифра после одной пробы, в частном однозначное число
315 : 63=5
Чтобы найти цифру частного округлим делитель ближайшим разрядным числом (60)=31:6…
б)деление четырех, пяти, шестизначных чисел на двухзначное, цифра частного после одной пробы
3456:54=64
в)деление трехзначного числа на двухзначное = однозначное (несколько проб) 464:58=8 (9 много)
г)деление четырехзначного, пятизначного, шестизначного числа без остатка и с остатком 4042:47=
делитель округлять в меньшую сторону!
Прием деления на трехзначное число аналогично.
Математика Письменное сложение трехзначных чисел
Материалы к уроку
Конспект урока
42. Письменное сложение трехзначных чисел
|
Организационный этап
Мы – умные! |
||||||||||||
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Ребята, сегодня на уроке мы будем путешествовать с нашим любимым сказочным героем, а с каким вы узнаете, решив примеры и расположив ответы в порядке возрастания. Молодцы, ребята! Это Золушка. Без вашей помощи она не сможет попасть на бал во дворец. Давайте ей поможем. Для этого нужно выполнить все задания. |
||||||||||||
|
Устный счёт
Золушка должна перемыть всю посуду, вычистить дом, полить грядки. Ей нужно помочь. Задание Запишите число, следующее за числом 100, 399, 999, 580, 209, 429. Проверьте себя. 101, 400, 1000, 581, 210, 430 Задание Запишите число, которое состоит из семи сотен и восьми единиц…….708 Задание Запишите самое большое трехзначное число и представьте его в виде суммы разрядных слагаемых. Проверьте себя. 999 = 900 + 90 + 9 |
||||||||||||
|
Задание Решите примеры. 345 + 600 = 780 – 300 = 510 + 80 = 325 + 434 = Все ли примеры у вас получилось решить? Давайте проверим 345 + 600 = 945 780 – 300 = 480 510 + 80 = 590
Конечно, ребята! Такой пример как 325 + 434 мы еще не решали. Сегодня на уроке мы будем учиться складывать трехзначные числа. |
||||||||||||
|
Когда устно сложение трехзначных чисел выполнить сложно, действия выполняют письменно. Нужно сложить триста двадцать пять и четыреста тридцать четыре Читаем ответ: семьсот пятьдесят девять. Задание Давайте поможем Золушке с пошивом платьев. У нее перепуталась вся тесьма. Если при сложении получается семьсот восемьдесят, то эта тесьма от фиолетового платья,
Чтобы танцевать на балу, нужно выучить движения танцев. Для этого сделаем разминку. |
||||||||||||
|
Этап усвоения новых знаний
Задание Решите задачу. Перед отъездом на бал мачеха приказала Золушке посадить триста двадцать шесть кустов белых роз и двести сорок семь кустов красных роз. Сколько всего кустов роз нужно посадить Золушке? Проверьте себя. Чтобы узнать, сколько всего кустов роз нужно посадить Золушке, нам нужно 326 кустов белых роз и 247 кустов красных роз сложить. 326 Ответ: Золушке нужно посадить 573 куста роз. Задача Золушке нужно было полить двести сорок пять кустов клубники и сто семнадцать кустов малины. Сколько всего кустов необходимо полить Золушке? Решите задачу самостоятельно. Проверьте себя. 245 Ответ: Золушке нужно полить 362 куста. |
||||||||||||
|
Задание
Проверьте себя.
Задание А вот и тетушка волшебница.
|
||||||||||||
|
Задание Спускаясь по лестнице, Золушка пробежала триста пятьдесят семь ступенек, потом она бежала еще двести шестьдесят три ступеньки и потеряла туфельку, в одной туфельке она пробежала двести восемьдесят пять ступенек до конца лестницы. Проверьте себя. 1) 357 + 263 = 620 ступенек до потерянной туфельки. Ответ: лестница во дворце состоит из 905 ступенек. Задание Принц в поисках невесты надевал потерянную туфельку двумстам сорока одной девушке в первом королевстве, трёмстам семидесяти шести девушкам во втором королевстве и двумстам семидесяти пяти девушкам в третьем королевстве. Сколько девушек хотело стать принцессами? Проверьте себя. 1) 241 + 376 = 617 девушек примерили туфельку в первых двух королевствах. Ответ: 892 девушки хотели стать принцессами. |
||||||||||||
|
Итог урока
Сегодня на уроке мы познакомились с приемами письменного сложения трехзначных чисел. Давайте вспомним алгоритм сложения трёхзначных чисел. Записываем единицы под единицами, десятки под десятками, сотни под сотнями
Рефлексия
Ребята, если вам всё понятно, нарисуйте звёздочку красного цвета, Спасибо, ребята, за урок. До новых встреч! |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Трехзначное умножение с нулевыми образовательными ресурсами Обучение K12, арифметика, целые числа и операции, планы уроков математики, упражнения, эксперименты, помощь на дому
Аудио:
Мэри работает в местном цветочном магазине. В магазине 105 цветочных горшков по 19 цветов в каждом горшке. Сколько цветов в цветочном магазине во всех горшках?
В магазине 105 цветочных горшков по 19 цветов в каждом горшке. Сколько цветов в цветочном магазине во всех горшках?
Давайте поможем Мэри с ее задачей по математике.
Мэри работает в местном цветочном магазине. В магазине 105 цветочных горшков с 19цветы в каждом горшке. Сколько цветов в цветочном магазине во всех горшках?
Чтобы решить эту задачу, можно было бы складывать, но умножение происходит гораздо быстрее.
105 x 19 =
Сначала сформулируйте задачу и выровняйте цифры:
| 1 | 0 | 5 | |||
| х | 1 | 9 | |||
Начните с умножения цифр в столбце единиц: 5 x 9 = 45.
Двузначное число нельзя записать в разряде единиц, поэтому запишите 5 в разряде единиц, а 4 перенесите в разряд десятков:
| 4 | |||||
| 1 | 0 | 5 | |||
| х | 1 | 9 | |||
| 5 |
Умножьте разряд десятков на 9: 0 x 9 = 0. Теперь прибавьте 0 + 4 = 4. Запишите четыре в разряде десятков. Помните, что любое число, умноженное на ноль, равно нулю, но переносимое число все равно должно быть добавлено к сумме. Всегда сначала умножайте, а затем добавляйте переносимое число:
Теперь прибавьте 0 + 4 = 4. Запишите четыре в разряде десятков. Помните, что любое число, умноженное на ноль, равно нулю, но переносимое число все равно должно быть добавлено к сумме. Всегда сначала умножайте, а затем добавляйте переносимое число:
| 4 | |||||
| 1 | 0 | 5 | |||
| х | 1 | 9 | |||
| 4 | 5 |
Затем умножьте разряд сотен: 1 x 9 = 9. Запишите 9 в разряде сотен:
| 4 | |||||
| 1 | 0 | 5 | |||
| х | 1 | 9 | |||
| 9 | 4 | 5 |
Теперь вы повторите эти шаги и умножите разряд десятков в числе 19 на каждое число в 105. .
.
| 4 | |||||
| 1 | 0 | 5 | |||
| х | 1 | 9 | |||
| 9 | 4 | 5 | |||
| 1 | 0 | 5 | 0 |
Теперь сложите частичные произведения вместе:
| 4 | |||||
| 1 | 0 | 5 | |||
| х | 1 | 9 | |||
| 9 | 4 | 5 | |||
| + | 1 | 0 | 5 | 0 | |
| 1 | 9 | 9 | 5 |
1995 цветков на всех растениях вместе взятых.
Другой пример покажет, как умножить трехзначное число на другое трехзначное число с нулем в обоих числах.
305 х 102 =
| 3 | 0 | 5 | |||
| х | 1 | 0 | 2 | ||
Выполните те же действия, что и выше:
Умножьте разряд единиц, 5 x 2 = 10, напишите 0 и перенесите 1.
Умножьте десятки в числе 305 и единицы в числе 102, 0 x 2 = 0 и добавьте остаток 1. 0 + 1 = 1, поэтому напишите 1 в разряде десятков.
Умножьте сотни в числе 305 и единицы в числе 102: 3 x 2 = 6. Запишите 6 в разряде сотен.
| 1 | |||||
| 3 | 0 | 5 | |||
| х | 1 | 0 | 2 | ||
| 6 | 1 | 0 |
*При умножении важно записывать нули. Они так же важны, как и любые другие числа, и их нельзя пропускать.
Они так же важны, как и любые другие числа, и их нельзя пропускать.
Затем умножьте разряд десятков в числе 102 на каждую цифру в числе 305.
Что вы заметили в значении разряда десятков в числе 102? Это 0. Помните, что все числа, умноженные на 0, дадут вам произведение 0.
Не забудьте включить заполнитель 0 в разряд единиц, так как теперь вы умножаете цифры в разряде десятков. Как вы можете видеть ниже, следующая строка нашего произведения состоит из нулей:
| 1 | |||||
| 3 | 0 | 5 | |||
| х | 1 | 0 | 2 | ||
| 6 | 1 | 0 | |||
| 0 | 0 | 0 | 0 |
Последний шаг — умножить цифру в разряде сотен в числе 102 на каждую цифру в числе 305.
Начните с 1 в числе 102 и умножьте его на разряд единиц, десятков и сотен в числе 305.
Теперь должно быть два нуля-заполнителя, так как мы сейчас умножаем разряд сотен. Нули-заполнители очень важны!
| 1 | |||||
| 3 | 0 | 5 | |||
| х | 1 | 0 | 2 | ||
| 1 | 6 | 1 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| + | 3 | 0 | 5 | 0 | 0 |
| 3 | 1 | 1 | 1 | 0 |
После умножения сложите каждое частичное произведение: 305 x 102 = 31 110.
Обсудите с родителями или учителем:
- Какие шаги необходимо выполнить, чтобы умножить трехзначное число на однозначное?
- Какое особое правило важно помнить при умножении на 0?
Теперь потренируйтесь умножать числа в Понял? раздел .
Числа до 3 цифр — определение, разрядное значение, расширенная форма
3-значные числа начинаются со 100 и заканчиваются на 999. остальные 3 цифры могут быть любым числом от 0 до 9. Изучение трехзначных чисел является строительным блоком для более высоких цифр. Давайте узнаем больше о важности, формировании и значении чисел до 3 цифр.
| 1. | Что такое трехзначные числа? |
| 2. | Разрядное значение трехзначных чисел |
3. | Расширенная форма трехзначных чисел |
| 4. | Общие ошибки чисел до 3 цифр |
| 5. | Операции с числами до 3 цифр |
| 6. | Часто задаваемые вопросы о номерах до 3 цифр |
Что такое трехзначные числа?
3-значные числа — это числа, состоящие только из 3-х цифр. Они начинаются со 100 и продолжаются до 999. Например, 673, 104, 985 — трехзначные числа. Следует отметить, что первая цифра трехзначного числа не может быть нулем, потому что в этом случае оно становится двузначным числом. Например, 045 становится 45.
Разрядное значение трехзначных чисел
Значение каждого трехзначного числа можно найти, проверив разрядное значение каждой цифры. Рассмотрим число 243. Говорят, что первая крайняя правая цифра стоит на месте единиц, поэтому она будет умножена на 1. Следовательно, произведение равно 3 × 1 = 3. Тогда второе число равно 4, а поскольку оно стоит на разряде десятков, оно умножается на 10. Следовательно, значение равно 4 × 10 = 40. Третье число 2 стоит на разряде сотен. Таким образом, 2 умножается на 100, и его значение равно 2 × 100 = 200. Следовательно, число равно 200 + 40 + 3 = 243, 9.0005
Тогда второе число равно 4, а поскольку оно стоит на разряде десятков, оно умножается на 10. Следовательно, значение равно 4 × 10 = 40. Третье число 2 стоит на разряде сотен. Таким образом, 2 умножается на 100, и его значение равно 2 × 100 = 200. Следовательно, число равно 200 + 40 + 3 = 243, 9.0005
Разложение трехзначного числа : В трехзначном числе используются три разряда – сотни, десятки и единицы. Давайте возьмем один пример, чтобы понять это лучше. Здесь 465 — это трехзначное число и оно раскладывается в виде суммы трех чисел. Так как 5 на разряде единиц, 60 на разряде десятков и 400 на разряде сотен.
Значение нуля в трехзначных числах: Число ноль не дает никакого вклада в трехзначное число, если оно расположено в позиции, где слева от него нет других ненулевых чисел. Так чем же 303 отличается от 033 или даже 003? В 033 значения равны (0 × 100) + (3 × 10) + (3 × 1) = 0 + 30 + 3 = 33, что означает, что число на самом деле становится двузначным числом, т. е. 33, или в в случае 003 оно становится однозначным числом, т. е. 3. В этих двух примерах ноль не вносит никакого вклада в число, поэтому числа также могут быть выражены как 33 или 3.
е. 33, или в в случае 003 оно становится однозначным числом, т. е. 3. В этих двух примерах ноль не вносит никакого вклада в число, поэтому числа также могут быть выражены как 33 или 3.
Расширенная форма трехзначных чисел
Расширенная форма трехзначного числа может быть выражена и записана тремя различными способами. Рассмотрим трехзначное число 457. Число 457 можно записать в одной форме как 457 = (4 × сотни) + (5 × десятки) + (7 × единицы). Вторым способом число 457 можно записать как 457 = (4 × 100) + (5 × 10) + (7 × 1). И, наконец, число 457 можно разложить в виде 457 = 400 + 50 + 7. Все три способа записи чисел в развернутом виде верны. Запись трехзначного числа в развернутой форме помогает узнать составные части числа.
В основном разделение или расширение трехзначного числа помогает нам лучше понять трехзначное число. Разделив, мы узнаем количество сотен, десятков и единиц, доступных в трехзначном числе.
Важные примечания о трехзначных числах
- 100 — наименьшее трехзначное число, а 999 — наибольшее трехзначное число.

- Трехзначное число не может начинаться с 0.
- 10 десятков составляют 1 сотню, которая является наименьшим трехзначным числом, а 10 сотен составляют тысячу, которая является наименьшим 4-значным числом.
- Трехзначное число также может иметь два нуля, но два нуля должны стоять на десятках, а единицы — на, например, 100, 200, 300, 400. Следует отметить, что нули не могут стоять на сотнях. место, потому что в этом случае он становится двузначным числом. Например, 067 становится 67.
Общие ошибки чисел до 3-х цифр
Некоторые распространенные ошибки наблюдаются при записи или чтении трехзначного числа. Эти ошибки в чтении и интерпретации трехзначного числа часто понимаются как какое-то другое число. В процессе чтения, записи и интерпретации трехзначного числа необходимо правильно интерпретировать разрядное значение цифр. Ниже мы перечислили три распространенные ошибки, которые часто допускают дети при написании трехзначных чисел.
- Заблуждение 1 : Дети делают ошибки в определении чисел, когда в разряде единиц или десятков стоит ноль. Пример: Когда студентов просят прочитать 130 и 103, они могут запутаться. Это помогает им моделировать числа с помощью блоков Base-10. Таким образом, они могут явно видеть значение разряда десятков и единиц.
- Заблуждение 2 : Когда студентов просят написать «сто двадцать три», ученики часто сначала пишут 100, а затем добавляют к нему 23, в результате чего получается число «10023» Факт: Это заблуждение возникает из-за поверхностного понимания разрядных значений. Используя блоки с основанием 10 или счеты, покажите детям, что цифра имеет разные значения в зависимости от ее положения.
- Заблуждение 3 : Иногда, когда детей просят составить наименьшее трехзначное число из трех цифр, содержащих ноль, дети помещают ноль в крайнее левое положение. Факт: Это неверно.
 Ноль не может находиться в разряде сотен, если мы создаем трехзначное число. Например: самое маленькое трехзначное число, в котором используются все цифры 5, 0 и 7, — это 507, а не 057 9.0264
Ноль не может находиться в разряде сотен, если мы создаем трехзначное число. Например: самое маленькое трехзначное число, в котором используются все цифры 5, 0 и 7, — это 507, а не 057 9.0264
Операции с числами до трех цифр
Четыре арифметические операции сложения, вычитания, умножения и деления удобно выполнять над трехзначными числами. В процессе выполнения этих арифметических действий должно правильно совпадать разрядное значение соответствующего числа. Ошибка в сопоставлении разрядного значения может привести к неправильным ответам. Здесь мы рассмотрим простое упражнение с использованием трехзначных чисел, чтобы помочь нам понять закономерность изменения каждой из цифр сотого разряда, разряда десятков и разряда единиц. Эта деятельность должна помочь в лучшем понимании обучения, необходимого для трехзначных чисел.
Предложите учащимся пропустить счет до 10 и до 100, чтобы научиться бегло обращаться с трехзначными числами .
 Сначала начните со 100. Затем начните с любого случайного трехзначного числа, например 136.
Сначала начните со 100. Затем начните с любого случайного трехзначного числа, например 136.Помогите детям заметить закономерность: при пропуске счета до 10 цифра в разряде единиц не меняется. Точно так же при пропуске счета на 100 цифры в разряде единиц и разряде десятков не меняются .
Используйте сетку из 100 квадратов для развития беглости речи . Пусть учащиеся заметят, что перемещение на одну строку вверх или вниз равнозначно пропуску счета на 10. Перемещение столбцов (влево или вправо) увеличивает или уменьшает числа на 1.
Часто детям дают трехзначное число и просят найти наибольшее и наименьшее трехзначное число, используя все цифры. Хитрость здесь заключается в том, чтобы расположить все цифры в порядке убывания, чтобы найти наибольшее число. 909:25 Чтобы найти наименьшее число, расположите все цифры в порядке возрастания . Но имейте в виду, что если ноль является одной из цифр, его нельзя ставить слева.
 Например. Используя цифры 7, 3 и 6, самое большое число — 763 (цифры в порядке убывания), а наименьшее число — 367 (цифры в порядке возрастания). Используя цифры 4, 0 и 8, наибольшее число будет 840, а наименьшее трехзначное число — 408, а не 048.
Например. Используя цифры 7, 3 и 6, самое большое число — 763 (цифры в порядке убывания), а наименьшее число — 367 (цифры в порядке возрастания). Используя цифры 4, 0 и 8, наибольшее число будет 840, а наименьшее трехзначное число — 408, а не 048.
Наименьшее трехзначное число
Наименьшее трехзначное число — 100, потому что предшествующее ему число — 99, двузначное число. Трехзначные числа начинаются со 100 и заканчиваются на 999.
Наибольшее трехзначное число
Наибольшее трехзначное число — 999, потому что за ним следует 1000, четырехзначное число. Трехзначные числа начинаются со 100 и заканчиваются на 999.
☛ Статьи по теме
- Числа до 2 цифр
- Номера до 4 цифр
- Числа до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- Номера до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
Примеры трехзначных чисел
Пример 1: Сколько существует трехзначных чисел?
Решение:
Всего 900 трехзначных чисел.
 Это можно рассчитать, используя следующий метод.
Это можно рассчитать, используя следующий метод.- Шаг 1: Запишите самое большое и самое маленькое трехзначное число. Мы знаем, что самое большое трехзначное число — 999. Наименьшее трехзначное число — 100.
- Шаг 2: Найдите разницу между ними. Их разница 999 — 100 = 899 .
- Шаг 3: Добавьте 1 к разнице. Это означает 899 + 1 = 900. Следовательно, всего 900 трехзначных чисел.
Пример 2: Решите головоломку: сложите наименьшее двузначное число с наименьшим однозначным числом. Вычтите сумму из на единицу меньше, чем наибольшее трехзначное число.
Решение:
Наименьшее двузначное число = 10. Наименьшее однозначное число = 1. Сумма этих двух чисел равна 10 + 1 = 11. На единицу меньше, чем наибольшее трехзначное число, равно 998. Вычтя 11 из 998, получим. 998 — 11 = 987.
Пример 3: Найдите наибольшее трехзначное число, которое является полным квадратом.

Решение: Наибольшее трехзначное число, являющееся полным квадратом, равно 961, потому что 31 2 = 961.
перейти к слайдуперейти к слайдуперейти к слайду
Помогите ребенку визуализировать, как работают числа!
Наша методология основана на визуальном обучении. Почувствуйте разницу, которую создают более 5000 визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по числам до 3 цифр
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о номерах до 3 цифр
Сколько существует трехзначных чисел?
Всего существует 900 трехзначных чисел. К ним относятся от наименьшего трехзначного числа — 100 до самого большого трехзначного числа — 999. Числа за пределами этих трехзначных чисел являются четырехзначными числами, а числа меньше трехзначных чисел являются двузначными числами.
Какое самое большое трехзначное число?
Самое большое трехзначное число — 999. Если к нему добавить еще 1, оно станет четырехзначным, т. е. 1000.
Если к нему добавить еще 1, оно станет четырехзначным, т. е. 1000.
Какова сумма трех самых больших трехзначных чисел?
Три самых больших трехзначных числа — это 997, 998, 999. Их сумма равна 2994, т. е. 997 + 998 + 999 = 2994.
Какое самое маленькое трехзначное число?
Число 100 — наименьшее трехзначное число. Если из него вычесть 1, получится двузначное число. Всего существует 900 трехзначных чисел, из которых число 100 является наименьшим трехзначным числом.
Сколько существует четных трехзначных чисел?
Всего имеется 900 трехзначных чисел. Из них половина — четные числа, а оставшаяся половина — нечетные числа. Следовательно, есть 900/2 = 450 четных трехзначных чисел.
Может ли трехзначное число иметь два нуля?
В трехзначном числе может быть два нуля. Два нуля должны быть в разряде десятков и разряде единиц. Некоторыми примерами трехзначных чисел с двумя нулями являются 100, 200, 300 и 400. Следует отметить, что разряд сотен в трехзначном числе не может иметь число 0, потому что это сделает его двузначным.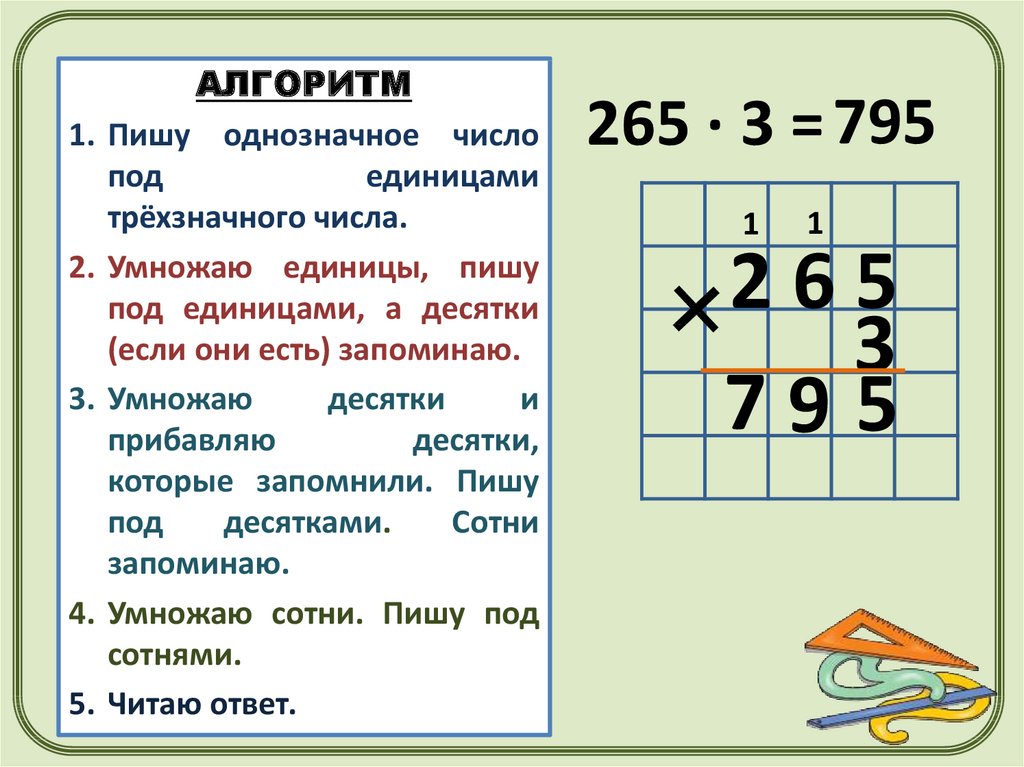


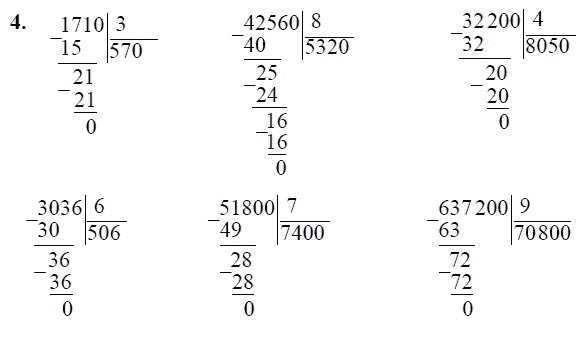 Как и при вычислениях с двузначными числами используют запись в столбик. Сложение выполняют поразрядно, начиная с единиц.
Как и при вычислениях с двузначными числами используют запись в столбик. Сложение выполняют поразрядно, начиная с единиц.



 Из скольких ступенек состоит лестница во дворце?
Из скольких ступенек состоит лестница во дворце?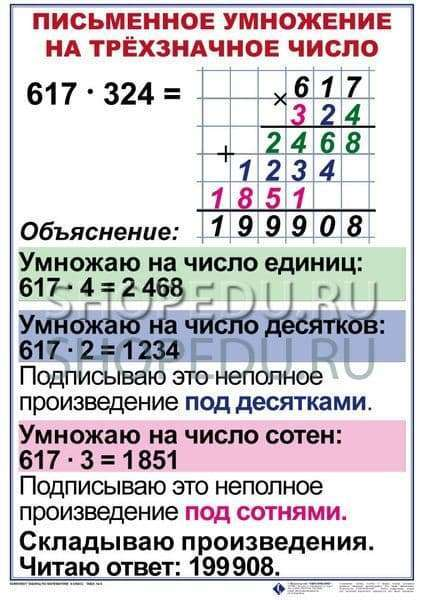
 Ноль не может находиться в разряде сотен, если мы создаем трехзначное число. Например: самое маленькое трехзначное число, в котором используются все цифры 5, 0 и 7, — это 507, а не 057 9.0264
Ноль не может находиться в разряде сотен, если мы создаем трехзначное число. Например: самое маленькое трехзначное число, в котором используются все цифры 5, 0 и 7, — это 507, а не 057 9.0264 Сначала начните со 100. Затем начните с любого случайного трехзначного числа, например 136.
Сначала начните со 100. Затем начните с любого случайного трехзначного числа, например 136.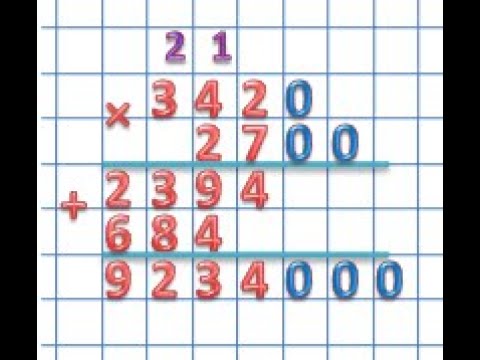 Например. Используя цифры 7, 3 и 6, самое большое число — 763 (цифры в порядке убывания), а наименьшее число — 367 (цифры в порядке возрастания). Используя цифры 4, 0 и 8, наибольшее число будет 840, а наименьшее трехзначное число — 408, а не 048.
Например. Используя цифры 7, 3 и 6, самое большое число — 763 (цифры в порядке убывания), а наименьшее число — 367 (цифры в порядке возрастания). Используя цифры 4, 0 и 8, наибольшее число будет 840, а наименьшее трехзначное число — 408, а не 048.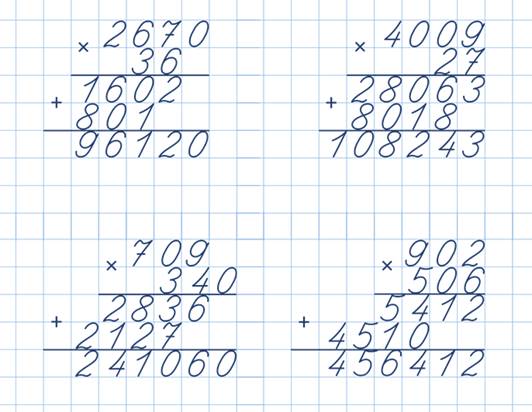 Это можно рассчитать, используя следующий метод.
Это можно рассчитать, используя следующий метод.