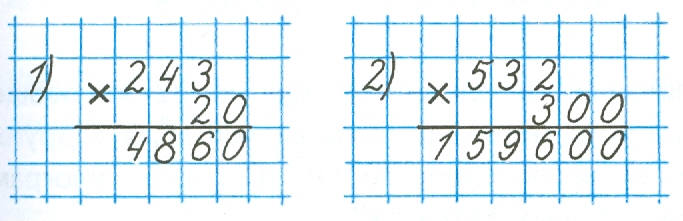
Математика Письменное умножение двух многозначных чисел, оканчивающихся нулями
Материалы к уроку
41. Письменное умножение двух многозначных чисел, оканчивающихся нулями.ppt
26.10 MBСкачать41. Письменное умножение двух многозначных чисел, оканчивающихся нулями.doc
45.5 KBСкачать
Конспект урока
|
41. Письменное умножение двух многозначных чисел, оканчивающихся нулями
|
|
Организационный этап
Как картинка из книжки старинной, Н. Гумилев |
|
Сегодня на уроке мы будем учиться решать примеры на умножение, где оба числа оканчиваются нулями. А также отправимся в путешествие по загадочной стране — Египту. Величество и таинственность Египетских пирамид привлекают ученых и туристов уже не одну сотню лет. Каждый пытается найти ответы на неразрешимые вопросы. По подсчетам французской археологической экспедиции, найдено около 118 пирамид. Этап подготовки учащихся к активному сознательному усвоению знаний
Запишите и решите уравнения.
1 вариант Сумма неизвестного числа и 219 равна произведению чисел 118 и 3. |
|
2 вариант Частное неизвестного числа и числа 2 равна произведению чисел 118 и 3. Проверьте себя.
Х+219=118·3 Х+219=354 Х=354-219 Х=135
Х·2=118·3 Х·2=354 Х=354:2 Х=177 А впереди нас ждет египетский математический диктант. Записываем только ответы. 1. Считается, что самая высокая пирамида – это пирамида Хеопса. Высота пирамиды 146 метров. Сколько это дм? 2. Пирамиды сложены из каменных блоков гигантского размера и массы, доходящей до 200 тонн. 200 тонн — это сколько кг? 3. Многие пирамиды состоят из каменных блоков. Найдите объем одного каменного блока, если его стороны равны 9 м, 3 м, 6 м. 4. По записям египтян строительство одной пирамиды занимало 20 лет. 5. Облицовка пирамиды состоит из каменных плит. Одна плита весит 20 тонн. На одной из таких пирамид установлено 144 тысячи таких плит. Сколько тонн весит 144 плиты? 6. Основание самой большой пирамиды — Хеопса, Проверьте себя и оцените свои успехи.
200 тонн — это 200000 кг Объем одного каменного блока 162 м³ 20 лет — это 240 мес. 144 плиты весит 2880 т 50 000 м² — это 5 га |
|
Работа над новым материалом
Давайте попробуем тоже построить свои пирамиды. Для этого нужно сделать кое-какие вычисления. 160 • 20 = 1600 • 300 = На прошлом уроке мы учились решать примеры, в которых одно число оканчивалось нулями. А сейчас нам встретились числовые выражения, в которых оба числа оканчиваются нулями. Посмотрите на примеры и скажите, как вычислить. Вторые множители раскладываем на 2 и 10, 3 и 100, используя сочетательный закон умножения. Решение этих же примеров можно записать в столбик. Как вы думаете, как это сделать? 160 • 20 = Умножение многозначных чисел, которые оканчиваются нулями, записывают так: сначала выполняем умножение, не учитывая нули: 16·2 получим 32, а затем приписываем столько нулей, сколько в обоих множителях вместе. Читаем ответ: 3200. 1600 • 300 = Выполняем умножение, не учитывая нули: 16·3 получим 48, а затем приписываем столько нулей, сколько в обоих множителях вместе. 160 • 20 = 160 • (20 • 10) = 160 • 2 • 10 = 3200 1600 • 300 = 1600 • (3 • 100) = 160 • 3 • 100 = 480000 |
|
Закрепление материала
Как можно умножить числа, которые оканчиваются нулями? Запомните! При умножении чисел, оканчивающихся нулями, сначала выполняют умножение, не учитывая нули, а затем приписывают столько нулей, сколько в обоих множителях вместе.
Решите числовые выражения, выполнив действие столбиком. 3 600 • 60 870 • 300 6800 • 400 35 000 • 50 790 • 900 28 000 • 700 Проверьте себя.
870 • 300 = 261 000 6800 • 400 = 2720000 35 000 • 50=1750000 790 • 900 = 711000 28 000 • 700= 19600000 |
|
Самостоятельная работа
Я приглашаю вас прокатиться на кораблях по реке Нил.
Решите задачу. Из двух городов навстречу друг другу отправились два корабля. Один шел 6 часов со скоростью 28 км/ч. А второй прошел до встречи вторую часть пути, пройденного первым. С какой скоростью шел второй корабль? Самостоятельно составьте схему к задаче и решите ее. Давайте проверим
Во втором действии узнаем, сколько км до встречи прошел 2 корабль: 168:2=84 (км) В третьем действии определим скорость 2 корабля: 84:6=14 (км/ч) Ответ: скорость второго корабля 14 км/ч. Пока корабли плывут, покажите свою смекалку. 1) Фараон Рамсес и его слуга пришли на пристань, чтобы встретить корабль в 8 ч 30 мин. У пристани они встретились без пятнадцати девять. Сколько минут был в пути Фараон? Фараон был в пути 15 минут. Так как без пятнадцати девять – это 8 часов 45 мин.
Хафра – старший брат. Тутатхамон – средний брат Хуву – младший брат
Этап подведения итогов
Вот и наше путешествие подошло к завершению. И мы должны подвести итоги. Какое открытие мы совершили сегодня? Что узнали?
Рефлексия
Молодцы! Вы хорошо потрудились, и получили за это свои результаты. |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Б) Умножение на числа, оканчивающиеся нулями — Мегаобучалка
Следует отметить, что при изучении умножения, многозначных чисел на числа, оканчивающиеся нулями, вычисления обязательно опираются на случаи умножения и деления на числа 10, 100,1000. Эти случаи умножения и деления уже рассматривались с детьми при изучении еще нумерации многозначных чисел. Теперь к этим случаям умножения и деления обязательно следует вернуться. Причем их не целесообразно разделять, как это предлагают авторы учебников.
Теоретической основой вычислительного приема, используемого при умножении на числа, оканчивающиеся нулями, является правило умножения числа на произведение. Это правило является для детей новым. Его рассмотрению следует уделить внимание. Однако, по сравнению с другими правилами, при раскрытии его сути достаточно использовать только числовой материал.
Приведем вариант разговора с детьми, который может быть таким.
Учитель. Прочитайте выражение и вычислите его значение 2 • (3 • 4)
Дети. Число 2 умножить на произведение чисел 3 и 4. Чтобы вычислить значение, надо найти произведение (выполнить действие в скобках), получаем 12, а затем 2 умножить на 12, получим 24.
Учитель. Давайте запишем.
2 •(3•4) = 2 • 12=24.
А теперь давайте попробуем умножить число 2 на произведение чисел 3 и 4 по-другому. Умножим вначале число 2 на первый множитель 3. А затем, что надо сделать?
Дети. Полученный результат умножить на второй множитель 4.
Полученный результат умножить на второй множитель 4.
Учитель. Верно, то есть, 2 • (3 • 4) = (2 • 3) • 4 = 6 • 4 = 24.
Ответ мы получили один и тот же. О чем это говорит?
Дети. Рассуждения ведем верно.
Учитель. А теперь давайте попробуем число 2 умножить на второй множитель:
2 • (3 • 4) = (2 • 4) • 3 = 8 • 3 = 24.
Видим, что результат один, значит, рассуждали верно. Давайте обобщим и сделаем вывод, как можно умножать число на произведение.
Дальнейшая работа над правилом продолжается в том же плане, как и для всех других:
— формируем умение применять все три способа вычислений;
— учим выделять удобный способ;
— учим применять правило для вычислений.
Затем переходим к рассмотрению случаев умножения многозначных чисел на числа, оканчивающиеся нулями. Начинаем с устного приема, чтобы показать ход рассуждений. Например:
12 • 40 = 12 • (4 • 10) = (12 • 4) • 10 = 48 • 10 = 480.
Подводим детей к выводу, что фактически умножаем 12 на 4 и приписываем столько нулей, сколькоих во втором множителе. Затем дается задание объяснить решение примера:
306 • 90 = 306 • (9 • 10) = (306 • 9) • 10 = 2754 • 10 = 27 540.
После этого переходим к рассмотрению письменного умножения на числа, оканчивающиеся нулями, т.е. к записи в столбик.
Предлагаем решить пример. 583 • 70. Выясняем, что устно решить трудно, Надо записать столбиком. Как это сделать? Это покажет ход рассуждений. 583 • 70 = 583 • (7 • 10) = (583 • 7) • 10 = 4081 • 10 = 40810.
Значит, 583 будем умножать на 7, а полученный результат умножим на 10. Отсюда запись: второй множитель 70 пишем так, чтобы цифра 7 стояла под цифрой 3.
583 583
Х х
7 70
4 081 41 810
Рассуждения: 583 умножим на 7, получим 4081 и приписываем ноль, получаем 40 810.
Отдельно выделяется и рассматривается случай, когда оба множителя оканчиваются нулями. Начинаем опять с устного приема, чтобы уяснить ход рассуждений.
Начинаем опять с устного приема, чтобы уяснить ход рассуждений.
30 • 50 = 3 дес. • (5 • 10) = (3 дес. • 5) • 10 = 150 дес. = 1500.
800 • 60 = 8 сот. • (6 • 10) = 48 сот. • 10 = 48 000.
2600 • 60 и т.д.
Подмечаем с детьми, что практически надо перемножить значащие части чисел и приписать столько нулей, сколько их в двух множителях вместе.
Такие примеры записываются в строчку и решаются устно. При письменном умножении запись делается в столбик, причем эта запись должна отражать ход рассуждений.
2600 4250 1860
х 80 х 70 х 300
208000 297500 558000
Следует обратить внимание на тот факт, что после ознакомления с новым приемом вычисления, где надо один из множителей представлять в виде произведения, учащиеся начинают путать этот прием умножения числа на произведение с приемом умножения числа на сумму.
1. Чтобы предупредить такие ошибки надо предлагать учащимся упражнение на сравнение соответствующих приемов вычисления. Например:
Например:
15 • 60= 15•(б • 10) = (15 •6) • 10 = 90 •10=900.
15 • 14 =15•(10+4)== 15• 10 + 15 • 4 = 150 + 60 = 210.
В) Умножение на двузначное и трехзначное число
Теоретическая основа вычислительных приемов, используемых при рассмотрении этих случаев умножения — правило умножения числа на 4 сумму, которое предварительно изучается.
Рассмотрение случаев умножения на двузначное число полезно начать с устного приема, чтобы показать ход рассуждений:
14•13 =14•(10+3)= 14 • 10 + 14 • 3 = 140 + 42 = 182.
Затем целесообразно усложнить задание. 67 • 45 = 67 • (40 + 5) = 67 • 40 + 67 • 5 = 2680 + 335 =3015.
Устно выполнить трудно, можно предложить сделать вычисления письменно.
67 67 2680
х х +
40 5 335
2680 335 3015
В ходе этих рассуждений подводим детей к выводу, что надо найти два неполных произведения и их сложить, то есть данное число умножаем на число десятков второго множителя; затем это число умножаем на число единиц второго множителя. Полученные результаты складываем. Если устно умножать трудно, лучше записать столбиком. Умножать начинаем с единиц. Показываем ход рассуждений при этом.
Полученные результаты складываем. Если устно умножать трудно, лучше записать столбиком. Умножать начинаем с единиц. Показываем ход рассуждений при этом.
Х 45
+2680
Умножаем 67 на 5, получим 335 единиц. Теперь умножим 67 на 40. Для этого умножаем 67 на 4 и полученное число умножим на 10, получаем 2680. Обращаем внимание, что 335 и 2680 — это неполные произведения. Число 3015 — полное произведение, или окончательный результат.
Обращаем внимание учащихся на то, что второе неполное произведение — это результат умножения на круглые десятки, поэтому всегда в нем на месте единиц стоит 0, его обычно не пишут. Это неполное произведение указывает на количество десятков в нем, его и начинают записывать под десятками первого неполного произведения.
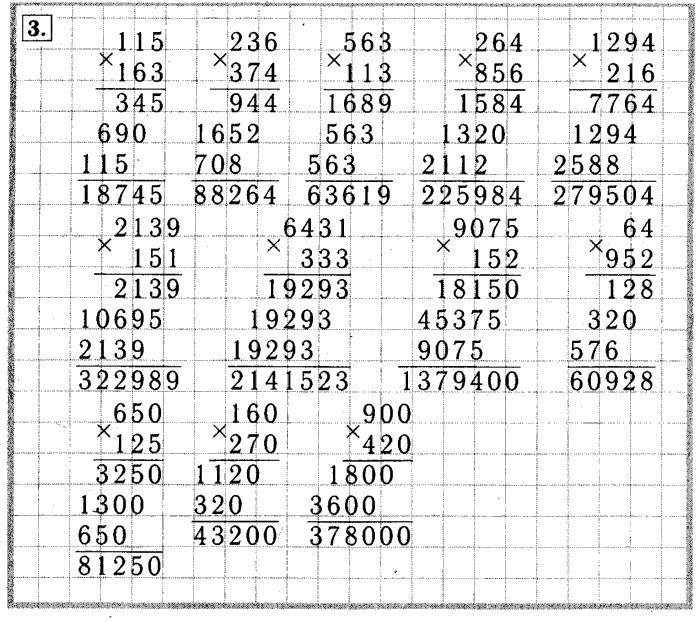
Таким образом, рассуждения ведем так: 67 умножим на 5 единиц, получаем 335 единиц — первое неполное произведение. Теперь 67 умножим на 4 десятка, получаем 268 десятков — второе неполное произведение.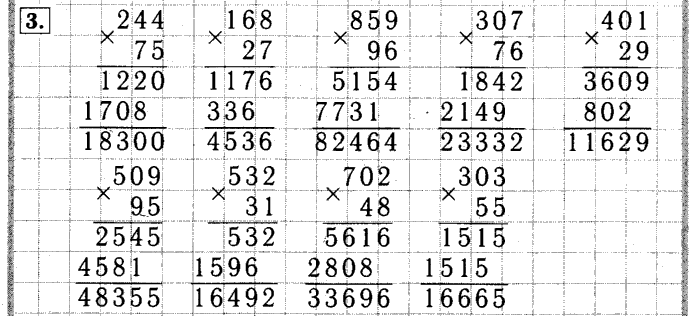 Складываем.
Складываем.
При умножении на трехзначное число следует подвести детей к выводу, что рассуждения в принципе те же, только здесь будет добавляться только третье неполное произведение, а значит, третье слагаемое — какое-то количество сотен. Третье неполное произведение начинаем записывать под сотнями первого неполного произведения.
Практика показывает, что для того чтобы выработать прочные навыки безошибочных вычислений, нужно прорешать значительно количество упражнений и необходима достаточная тренировка. Кроме того, успех зависит и от того, насколько прочны знания учащихся таблицы умножения и как уверенно дети овладели навыками сложения двух-трех чисел.
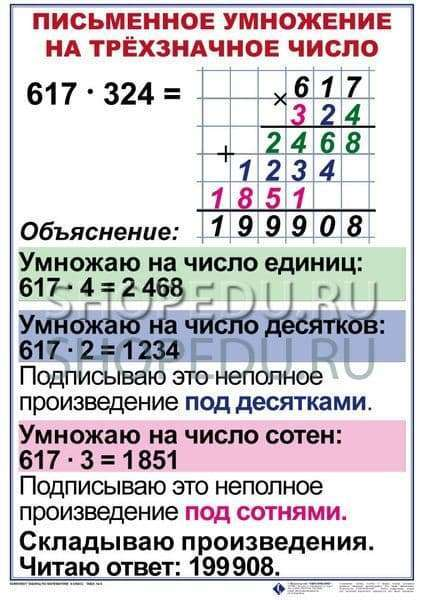
После того как рассмотрены общие случаи умножения на двузначное и трехзначное число, рассматриваются частные случаи умножения, а именно случаи умножения чисел с нулями в середине второго множителя, Фактически здесь учащиеся встречаются с тем же самым приемами вычислений, но с некоторыми особенностями.
Например, 829 • 703. Для первого такого примера целесообразно показать детям более подробную запись:
Для первого такого примера целесообразно показать детям более подробную запись:
829
х
703
+
После обсуждения дети подводятся к выводу, что второе неполное произведение здесь можно убрать. Отсюда приходим к записи:
Х 703
+5803
Такой подход позволит предупредить возникновение у детей ошибок в записи второго неполного произведения для аналогичных случаев.
Умножение на числа, выходящие за пределы трехзначных (4-хзначные, 5-значные и др.) по существу не отличаются от умножения на трехзначное число. Поэтому, овладев навыками умножения на трехзначное число, ученики смогут овладеть умением умножать многозначные числа на любое число.
И опять после рассмотрения всех случаев умножения многозначных чисел вводится умножение составных именованных чисел, выраженных в метрических мерах. Здесь умножение целесообразно выполнять одним способом: составное именованное число заменяется простым, выполняют действие над отвлеченными числами, а затем полученное простое именованное число заменяют составным.
7 м 85 см·18 = 141 м 30 см 4 ц 90 кг • 26 = 127ц 40 кг
Х 18
+785
См)
При изучении всех случаев умножения прежде всего необходимо добиться понимания вычислительного приема, после чего вести работу по формированию вычислительных навыков. А для этого надо своевременно и разумно сокращать объяснение решения и переходить к кратким пояснениям. Большее значение в этом имеет тщательно подобранная система тренировочных упражнений.
Алгоритмы письменного умножения и деления многозначных чисел
Алгоритмы письменного умножения и деления многозначных чисел.
Этапы изучения темы:
умножение и деление на однозначное число;
умножение и деление на двузначные и трехзначные разрядные числа;
умножение и деление на двухзначные и трехзначные числа.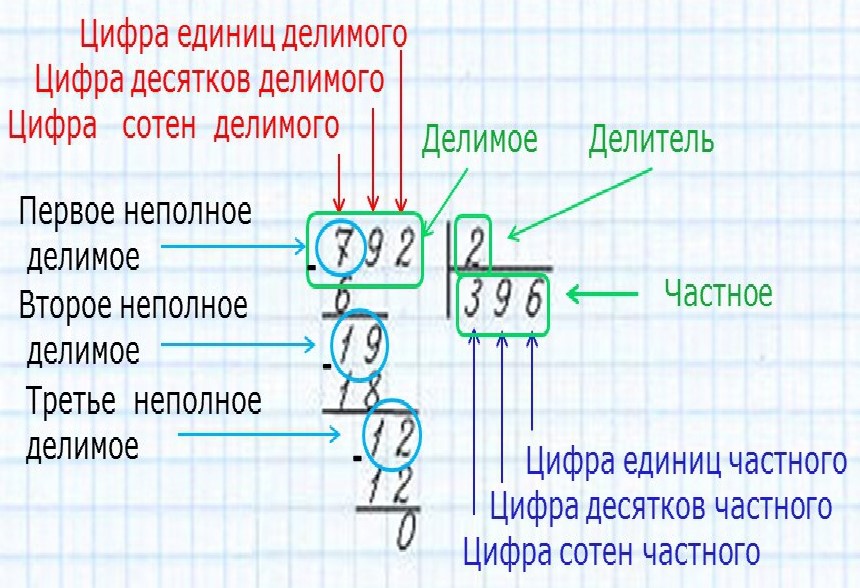
Умножение и деление изучаются одновременно на каждом этапе, но сначала – умножение, затем – деление.
На каждом этапе наряду с умножением и делением натуральных чисел изучается умножение и деление величин на число.
Частные случаи:
Умножение
-первый и второй множитель оканчиваются нулями 87600*4,376*240
-нули в середине второго множителя 875*304
-различные сочетания этих случаев 170*230, 1630*103
Деление:
-частное оканчивается нулями 227200:4=56800
-нули в середине частного 72450:7=10350.
Умножение многозначных чисел на однозначное число
К письменному приему обращаемся только тогда, когда устно решить трудно.
54879*5
А лгоритм:
-записать числа в столбик (однозначное число под единицами многозначного)
-умножить единицы I множителя на II множитель, результат записать по единицами;
-умножить десятки I множителя на II, результат записать под десятками;
-аналогичные действия проделать со всеми основными разрядами I множителя;
-прочитать полученный результат.
Далее, опираясь на алгоритм, дети решают аналогичные выражения, при этом фиксируют словами каждую операцию (комментируют). Выражения подбираются в усложняющейся последовательности:
-увеличивается I множитель 284*3 2934*5 28751*7
-I множитель содержит нули (частный случай).
На освоение алгоритма умножения – задания на нахождение преднамеренно допущенных ошибок.
Например: 7056 8539 5700
8 2 9
56408
II этап умножение на двузначные и трехзначные разрядные числа
621*30. Используя свойство а*(в*с), показываем детям целесообразность записи 621*(3*10) 621
30
Особое внимание заслуживают выражения, где оба множителя заканчиваются нулями.
Устно: 300*50 (3 сот * 5)*10=15 сот*10=150 сот=15000.
Письменно: аналогично вышеприведенному случаю 7800
30
234000
Вывод: сначала решать без нулей, затем посчитать сколько их и приписать.
7тыс*30=~210000= в ответе не меньше 6 цифр.
При выполнении умножения «в столбик» обязательно делать прикидку.
III этап умножения на двухзначное и трехзначное число
87*64, 286*374
А лгоритм:
1.Записать числа в столбик, единицы под единицами; десятки под десятками.
2.Умножить I множитель на единицы II множителя – получится I неполное произведение, результат записать под единицами.
3.Умножить I множитель на десяток II множителя – получится II полное произведение, записать результат на один разряд влево, под десятки.
4.Далее действия повторяются.
5.Сложить все неполные произведения.
6.Записать и прочитать полученный результат.
Новое понятие «неполное произведение».
Закрепление:
-расписать 286*374
-по плану решения составить пример 84*6+84*30
-сравнить 138*14 и 138*40 алгоритмы.
-376*4+376*10 на какое число умножаем?
-решить удобным способом:
32*2*50= 73*6*3+73*2=
54*80+54*20= 83*16+17*16=
Частные случаи умножения чисел, содержащих нули.
Умножение чисел, оканчивающихся нулями, знакомы детям =больше самостоятельности.
158
4003
Эти виды выражений трудны для детей. (Сдвиг цифр на 2 или 3 цифры влево). Использовать «нерациональный» способ! Пока слабые дети не будут ориентированы.
Использовать «нерациональный» способ! Пока слабые дети не будут ориентированы.
158
4003
474
000 000
000
63648 632
632474
После вводится умножение величин выражений в 2 наименованиях.
Закрепление: аналогично.
Деление многозначных чисел.
I этап – деление на однозначное число.
Алгоритм:
1.Записать пример в столбик.
2.Выбрать первое неполное делимое. Определить количество цифр в частном.
3.Методом подбора найти первую цифру частного.
4.Проверить правильность выбора первой цифры частного, умножив её на делитель.
5.Полученное число сравнить с I неполным делимым (с помощью вычитания).
6.Получившийся остаток сравнить с делителем:
а)если остаток
б)если остаток = делимому, то допущена ошибка при подборе цифры частного (цифру увеличить)
в)остаток = 0, деление закончено (в одном случае)
г)(в другом) 0 является промежуточным результатом, надо снести цифру исходного делимого и получить II неполное делимое.
7.II неполное делимое сравнить с делимым:
а)если оно = делителя, то произвести подбор второй цифры частного
б)если оно
8.Аналогично подбираются следующие цифры частного.
9.Записать и назвать полученный результат.
Постепенно примеры усложняются: увеличивается число разрядов в делимом (3,4,5,6 значные числа)
Частные случаи: (в записи частного встречается 0)
22720:4=5680 – полностью весь алгоритм и последнее 0:4=0. Частное…
Частное…
4254:6=709 – дети часто пропускают 0.
Для предупреждения ошибок:
-определить количество цифр в частном;
-проверка умножением;
-проверка неправильным решением примеров.
На этом же этапе решаем примеры на деление с остатком и деление однородных величин.
II этап. Деление на двухзначные и трехзначные разрядные числа
Письменные приемы:
4980:60
480
180
180
Делимое 498 десятков =в частном 2 цифры. Здесь перемешивать деление с остатком и без остатка.
Частные случаи: Дети могут разобрать аналогично предыдущему. Так же и деление на разрядные трехзначные числа.
III этап. Деление на двухзначное и трехзначное число.
Деление на двухзначное и трехзначное число.
а)деление трехзначного числа на двухзначное, цифра после одной пробы, в частном однозначное число
315 : 63=5
Чтобы найти цифру частного округлим делитель ближайшим разрядным числом (60)=31:6…
б)деление четырех, пяти, шестизначных чисел на двухзначное, цифра частного после одной пробы
3456:54=64
в)деление трехзначного числа на двухзначное = однозначное (несколько проб) 464:58=8 (9 много)
г)деление четырехзначного, пятизначного, шестизначного числа без остатка и с остатком 4042:47=
делитель округлять в меньшую сторону!
Прием деления на трехзначное число аналогично.
Числа до 3 цифр — определение, разрядное значение, расширенная форма
3-значные числа начинаются со 100 и заканчиваются на 999. оставшиеся 3 цифры могут быть любым числом от 0 до 9. Изучение трехзначных чисел является строительным блоком для более высоких цифр. Давайте узнаем больше о важности, формировании и значении чисел до 3 цифр.
Изучение трехзначных чисел является строительным блоком для более высоких цифр. Давайте узнаем больше о важности, формировании и значении чисел до 3 цифр.
| 1. | Что такое трехзначные числа? |
| 2. | Разрядное значение трехзначных чисел |
| 3. | Расширенная форма трехзначных чисел |
| 4. | Общие ошибки чисел до 3 цифр |
| 5. | Операции с числами до 3 цифр |
| 6. | Часто задаваемые вопросы о числах до 3 цифр |
Что такое трехзначные числа?
3-значные числа — это числа, состоящие только из 3-х цифр. Они начинаются со 100 и продолжаются до 999. Например, 673, 104, 985 — трехзначные числа. Следует отметить, что первая цифра трехзначного числа не может быть нулем, потому что в этом случае оно становится двузначным числом. Например, 045 становится 45.
Например, 045 становится 45.
Разрядное значение трехзначных чисел
Значение каждого трехзначного числа можно найти, проверив разрядное значение каждой цифры. Рассмотрим число 243. Говорят, что первая крайняя правая цифра стоит на месте единиц, поэтому она будет умножена на 1. Следовательно, произведение равно 3 × 1 = 3. Тогда второе число равно 4, а поскольку оно стоит на разряде десятков, оно умножается на 10. Следовательно, значение равно 4 × 10 = 40. Третье число 2 стоит на разряде сотен. Таким образом, 2 умножается на 100, и его значение равно 2 × 100 = 200. Следовательно, число равно 200 + 40 + 3 = 243, 9.0005
Разложение трехзначного числа : В трехзначном числе используются три разряда – сотни, десятки и единицы. Давайте возьмем один пример, чтобы понять это лучше. Здесь 465 — это трехзначное число и оно раскладывается в виде суммы трех чисел. Так как 5 на разряде единиц, 60 на разряде десятков и 400 на разряде сотен.
Значение нуля в трехзначных числах: Число ноль не дает никакого вклада в трехзначное число, если оно расположено в позиции, где слева от него нет других ненулевых чисел. Так чем же 303 отличается от 033 или даже 003? В 033 значения равны (0 × 100) + (3 × 10) + (3 × 1) = 0 + 30 + 3 = 33, что означает, что число на самом деле становится двузначным числом, т. е. 33, или в в случае 003 оно становится однозначным числом, т. е. 3. В этих двух примерах ноль не вносит никакого вклада в число, поэтому числа также могут быть выражены как 33 или 3.
Расширенная форма трехзначных чисел
Расширенная форма трехзначного числа может быть выражена и записана тремя различными способами. Рассмотрим трехзначное число 457. Число 457 можно записать в одной форме как 457 = (4 × сотни) + (5 × десятки) + (7 × единицы). Вторым способом число 457 можно записать как 457 = (4 × 100) + (5 × 10) + (7 × 1). И, наконец, число 457 можно разложить в виде 457 = 400 + 50 + 7. Все три способа записи чисел в развернутом виде верны. Запись трехзначного числа в развернутой форме помогает узнать составные части числа.
Все три способа записи чисел в развернутом виде верны. Запись трехзначного числа в развернутой форме помогает узнать составные части числа.
В основном разделение или расширение трехзначного числа помогает нам лучше понять трехзначное число. Разделив, мы узнаем количество сотен, десятков и единиц, доступных в трехзначном числе.
Важные примечания о трехзначных числах
- 100 — наименьшее трехзначное число, а 999 — наибольшее трехзначное число.
- Трехзначное число не может начинаться с 0.
- 10 десятков составляют 1 сотню, которая является наименьшим трехзначным числом, а 10 сотен составляют тысячу, которая является наименьшим 4-значным числом.
- Трехзначное число также может иметь два нуля, но два нуля должны стоять на десятках, а единицы на разряде, например, 100, 200, 300, 400. Следует отметить, что нули не могут стоять на сотнях. место, потому что в этом случае он становится двузначным числом. Например, 067 становится 67.
Общие ошибки чисел до 3-х цифр
Некоторые распространенные ошибки наблюдаются при записи или чтении трехзначного числа. Эти ошибки в чтении и интерпретации трехзначного числа часто понимаются как какое-то другое число. В процессе чтения, записи и интерпретации трехзначного числа необходимо правильно интерпретировать разрядное значение цифр. Ниже мы перечислили три распространенные ошибки, которые часто допускают дети при написании трехзначных чисел.
Эти ошибки в чтении и интерпретации трехзначного числа часто понимаются как какое-то другое число. В процессе чтения, записи и интерпретации трехзначного числа необходимо правильно интерпретировать разрядное значение цифр. Ниже мы перечислили три распространенные ошибки, которые часто допускают дети при написании трехзначных чисел.
- Заблуждение 1 : Дети делают ошибки в определении чисел, когда в разряде единиц или десятков стоит ноль. Пример: Когда студентов просят прочитать 130 и 103, они могут запутаться. Это помогает им моделировать числа с помощью блоков Base-10. Таким образом, они могут явно видеть значение разряда десятков и единиц.
- Заблуждение 2 : Когда студентов просят написать «сто двадцать три», ученики часто сначала пишут 100, а затем добавляют к нему 23, в результате чего получается число «10023» Факт: Это заблуждение возникает из-за поверхностного понимания разрядных значений.
 Используя блоки с основанием 10 или счеты, покажите детям, что цифра имеет разные значения в зависимости от ее положения.
Используя блоки с основанием 10 или счеты, покажите детям, что цифра имеет разные значения в зависимости от ее положения. - Заблуждение 3 : Иногда, когда детей просят составить наименьшее трехзначное число из трех цифр, содержащих ноль, дети помещают ноль в крайнее левое положение. Факт: Это неверно. Ноль не может находиться в разряде сотен, если мы создаем трехзначное число. Например: самое маленькое трехзначное число, в котором используются все цифры 5, 0 и 7, — это 507, а не 057 9.0084
Операции с числами до трех цифр
Четыре арифметические операции сложения, вычитания, умножения и деления удобно выполнять над трехзначными числами. В процессе выполнения этих арифметических действий должно правильно совпадать разрядное значение соответствующего числа. Ошибка в сопоставлении разрядного значения может привести к неправильным ответам. Здесь мы рассмотрим простое упражнение с использованием трехзначных чисел, чтобы помочь нам понять закономерность изменения каждой из цифр сотого разряда, разряда десятков и разряда единиц.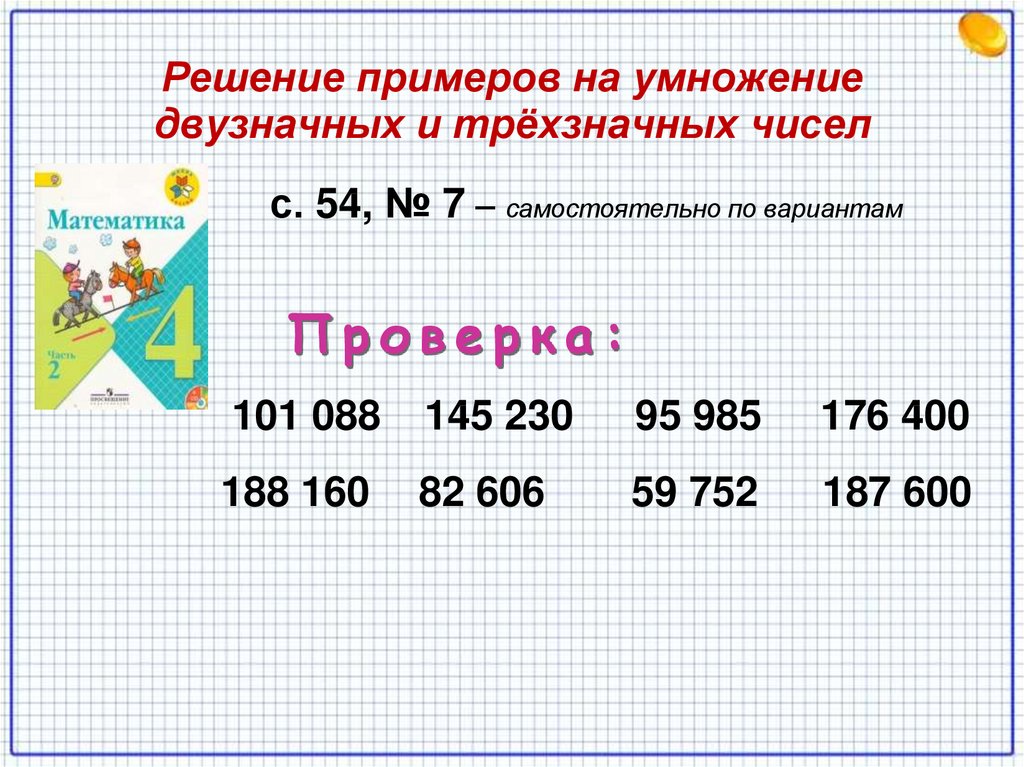 Эта деятельность должна помочь в лучшем понимании обучения, необходимого для трехзначных чисел.
Эта деятельность должна помочь в лучшем понимании обучения, необходимого для трехзначных чисел.
Предложите учащимся пропустить счет до 10 и до 100, чтобы улучшить беглость с трехзначными числами . Сначала начните со 100. Затем начните с любого случайного трехзначного числа, например 136.
Помогите детям заметить закономерность: при пропуске счета до 10 цифра в разряде единиц не меняется. Точно так же при пропуске счета на 100 цифры в разряде единиц и разряде десятков не меняются .
Используйте сетку из 100 квадратов, чтобы развить беглость речи . Пусть учащиеся заметят, что перемещение на одну строку вверх или вниз равнозначно пропуску счета на 10. Перемещение столбцов (влево или вправо) увеличивает или уменьшает числа на 1.
Часто детям дают трехзначное число и просят найти наибольшее и наименьшее трехзначное число, используя все цифры.
 Хитрость здесь заключается в том, чтобы расположить все цифры в порядке убывания, чтобы найти наибольшее число.
Хитрость здесь заключается в том, чтобы расположить все цифры в порядке убывания, чтобы найти наибольшее число.
Чтобы найти наименьшее число, расположите все цифры в порядке возрастания . Но имейте в виду, что если ноль является одной из цифр, его нельзя ставить слева. Например. Используя цифры 7, 3 и 6, самое большое число — 763 (цифры в порядке убывания), а наименьшее число — 367 (цифры в порядке возрастания). Используя цифры 4, 0 и 8, наибольшее число будет 840, а наименьшее трехзначное число — 408, а не 048.
Наименьшее трехзначное число
Наименьшее трехзначное число — 100, потому что предшествующее ему число — 99, двузначное число. Трехзначные числа начинаются со 100 и заканчиваются на 999.
Наибольшее трехзначное число
Наибольшее трехзначное число — 999, потому что за ним следует 1000, четырехзначное число. Трехзначные числа начинаются со 100 и заканчиваются на 999.
☛ Похожие статьи
- Числа до 2 цифр
- Номера до 4 цифр
- Числа до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- Номера до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
Примеры трехзначных чисел
Пример 1: Сколько существует трехзначных чисел?
Решение:
Всего 900 трехзначных чисел.
 Это можно рассчитать, используя следующий метод.
Это можно рассчитать, используя следующий метод.- Шаг 1: Запишите самое большое и самое маленькое трехзначное число. Мы знаем, что самое большое трехзначное число — 999. Наименьшее трехзначное число — 100.
- Шаг 2: Найдите между ними разницу. Их разница 999 — 100 = 899 900 84.
- Шаг 3: Добавьте 1 к разнице. Это означает 899 + 1 = 900. Следовательно, всего 900 трехзначных чисел.
Пример 2: Решите головоломку: сложите наименьшее двузначное число с наименьшим однозначным числом. Вычтите сумму из на единицу меньше, чем наибольшее трехзначное число.
Решение:
Наименьшее двузначное число = 10. Наименьшее однозначное число = 1. Сумма этих двух чисел равна 10 + 1 = 11. На единицу меньше, чем наибольшее трехзначное число, равно 998. Вычтя 11 из 998, получим. 998 — 11 = 987.
Пример 3: Найдите наибольшее трехзначное число, которое является полным квадратом.

Решение: Наибольшее трехзначное число, являющееся полным квадратом, равно 961, потому что 31 2 = 961.
перейти к слайдуперейти к слайдуперейти к слайду
Помогите ребенку наглядно представить, как работают числа!
Наша методология основана на визуальном обучении. Почувствуйте разницу, которую создают более 5000 визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по числам до 3 цифр
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о номерах до 3 цифр
Сколько существует трехзначных чисел?
Всего существует 900 трехзначных чисел. К ним относятся от наименьшего трехзначного числа — 100 до самого большого трехзначного числа — 999. Числа за пределами этих трехзначных чисел являются четырехзначными числами, а числа меньше трехзначных чисел являются двузначными числами.
Какое самое большое трехзначное число?
Самое большое трехзначное число — 999. Если к нему добавить еще 1, оно станет четырехзначным, то есть 1000.
Если к нему добавить еще 1, оно станет четырехзначным, то есть 1000.
Какова сумма трех самых больших трехзначных чисел?
Три самых больших трехзначных числа — это 997, 998, 999. Их сумма равна 2994, т. е. 997 + 998 + 999 = 2994.
Какое самое маленькое трехзначное число?
Число 100 — наименьшее трехзначное число. Если из него вычесть 1, получится двузначное число. Всего существует 900 трехзначных чисел, из которых число 100 является наименьшим трехзначным числом.
Сколько существует четных трехзначных чисел?
Всего имеется 900 трехзначных чисел. Из них половина — четные числа, а оставшаяся половина — нечетные числа. Следовательно, есть 900/2 = 450 четных трехзначных чисел.
Может ли трехзначное число иметь два нуля?
В трехзначном числе может быть два нуля. Два нуля должны быть в разряде десятков и разряде единиц. Некоторыми примерами трехзначных чисел с двумя нулями являются 100, 200, 300 и 400. Следует отметить, что разряд сотен в трехзначном числе не может иметь число 0, потому что это сделает его двузначным. количество. Например, 098 становится 98.
количество. Например, 098 становится 98.
Какое наименьшее трехзначное число делится на 4?
Наименьшее трехзначное число — 100, и мы знаем, что оно делится на 4, потому что 100/4 = 25. Следовательно, мы можем сказать, что 100 — это наименьшее трехзначное число, которое делится на 4.
Какие 3 Числовое число имеет наибольшее количество факторов?
Трехзначное число с наибольшим количеством делителей — 840. Делители числа 840 могут быть перечислены как 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70, 84, 105, 120, 140, 168, 210, 280, 420 и 840.
Скачать БЕСПЛАТНО учебные материалы
Скачать БЕСПЛАТНУЮ электронную книгу о концепциях
Скачать БЕСПЛАТНО Советы и рекомендации
Скачать БЕСПЛАТНО рабочие листы
| · = | ||||||||||||||||||||
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа в столбик (видео по математике)
Чтобы попрактиковаться и быстро научиться, вы также можете попробовать умножать числа в столбик.
Умножение больших чисел, запись их в строку рано или поздно становится довольно сложным и утомительным процессом. Гораздо проще использовать специальный алгоритм умножения в столбик: не надо держать цифры в голове и что-то запоминать. Вы можете делать пометки над колонкой, чтобы всегда видеть, как числа нужно перевести. Если вы пытаетесь научить ребенка таким образом, очень важно, чтобы таблица умножения отскакивала от его зубов, иначе процесс затянется надолго, а сам малыш сделает много ошибок, которые будут тянуться в строка на протяжении всего примера. Читайте внимательно статью и берите такой алгоритм на вооружение.
Запишите пример в строку и посмотрите: какой из множителей меньше? Меньший будет ниже в столбце умножения, а больший множитель будет вверху.
Напишите пример так, как показано на рисунке ниже.
- Напишите большее число сверху.
- Слева поставить знак умножения в виде креста.
- Запишите меньшее число ниже.

- Проведите прямую линию под образцом.
Если в примере есть множитель, оканчивающийся на ноль или более нулей, то его следует записать так:
- Нули для примера нужно вынести.
- Запишите цифры под цифрами.
В этом случае вы просто оборачиваете это количество нулей сразу в ответ. Если и первый множитель, и второй имеют нули, то сложите их количество и запишите в ответ.
Теперь начнем расчет следующим образом:
- Вы умножаете все верхнее число на последнюю цифру нижнего. Помните, что умножение последних нулей не выполняется.
- Чтобы вам было удобнее, запишите номера, которые нужно перевести, вверху всего примера. Позже их можно будет просто стереть, но при этом не придется запоминать переносные номера.
- Как только вы закончите вычисление, запишите полученное число под чертой.
Как только вы умножите верхнее число на последнюю цифру нижнего числа и запишете свой ответ, начните умножать следующее.
По такому же принципу умножаем все верхнее число на вторую цифру с конца нижнего. Также запишите передаточные числа, однако ответ следует записывать под первым решением, но сдвигая запись на одну клетку влево. У вас получится столбец с линией, выступающей влево.
Как вы уже догадались, нужно умножить верхнее число на все цифры нижнего, начиная с конца. Каждый раз запись ответа перемещается на одну ячейку влево.
Умножьте все числа таким образом. Теперь снова нарисуйте линию под столбцом. Поставьте знак добавления между всеми решениями.
Теперь все, что вам нужно сделать, это сложить стопку, что вы уже должны уметь делать:
- Сложите все числа, которые находятся на одной вертикальной линии.
- Если число получилось двузначным, то вы переносите число десятков на следующую вертикальную черту.
Под одними номерами вообще не будет других — в этом случае вы просто записываете этот номер в ответ. Не забудьте передать в ответ все нули, которые стоят в конце множителей.
Не забудьте передать в ответ все нули, которые стоят в конце множителей.
Умножение в столбик очень удобно и быстро, особенно если нужно умножать большие числа. Вы можете легко проверить правильность умножения, просто разделив ответ на один из множителей. Для этого воспользуйтесь калькулятором, либо методом деления уголка. Поначалу такое умножение занимает значительную долю времени, но с опытом все действие происходит буквально за пару секунд.
Если в процессе решения задачи нам потребуется умножать натуральные числа, удобно использовать для этого готовый метод, который называется «умножение столбцов» (или «умножение столбцов»). Это очень удобно, так как с его помощью можно свести умножение многозначных чисел к последовательному умножению однозначных.
Основы умножения в столбцах
Для выполнения вычисления в столбце нам понадобится таблица умножения. Важно запомнить его наизусть, чтобы считать быстро и качественно.
Также нужно будет запомнить, какой результат мы получим при умножении натурального числа на ноль.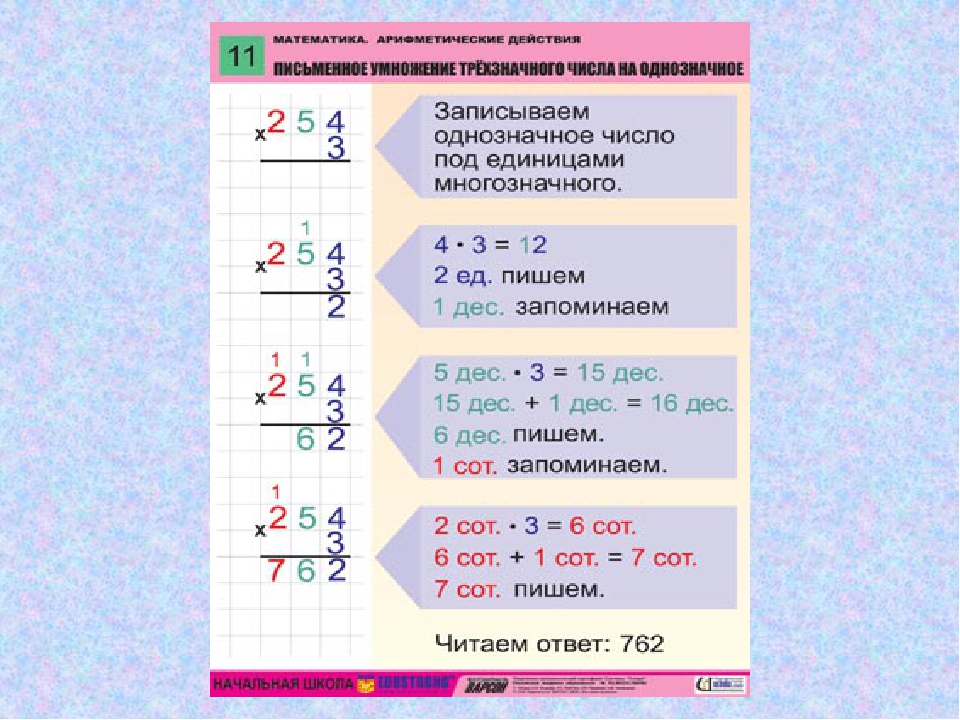 Это часто видно на примерах. Нам понадобится свойство умножения, которое буквально записывается как 0 = 0 (а — любое натуральное число).
Это часто видно на примерах. Нам понадобится свойство умножения, которое буквально записывается как 0 = 0 (а — любое натуральное число).
Чтобы лучше понять, как умножать в столбик, рекомендуем повторить тот же метод сложения. Одним из этапов вычислений будет именно сложение промежуточных результатов, и знание этого метода пригодится при сложении чисел.
Также важно уметь сравнивать натуральные числа и помнить, что такое место.
Как всегда, начнем с того, как правильно писать исходные цифры. Нам нужно взять два множителя и записать их один под другим так, чтобы все ненулевые числа располагались друг под другом. Проведем под ними горизонтальную черту, разделяющую ответ, и добавим с левой стороны знак умножения.
Пример 1
Например, для расчета и 71 , 550 45 002 и 534 000 4 300 запишем следующие столбцы:
Далее нам нужно разобраться с процессом умножения. Сначала посмотрим, как правильно умножить многозначное натуральное число на однозначное, а потом посмотрим, как умножать многозначные числа друг на друга.
Если для решения задачи нам нужно перемножить два натуральных числа, одно из которых однозначное, а второе многозначное, то можно воспользоваться методом столбца. Для этого выполним последовательность шагов, которую поясним сразу на примере. Во-первых, давайте возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Пример 2
Условие: вычислить 45 027 3 .
Раствор
Запишем множители так, как предполагает метод умножения столбцов. Однозначный множитель помещаем под последним знаком многозначного. Мы получили такую запись:
Далее нам нужно выполнить последовательное умножение цифр многозначного числа на указанный множитель. Если получаем число меньше десяти, сразу вписываем его в поле ответа под горизонтальной чертой, строго под вычисляемой цифрой. Если в результате получилось 10 и более, то под нужной цифрой указываем только значение единиц от полученного числа, а десятки запоминаем и прибавляем на следующем шаге к старшей цифре.
На конкретных числах процесс будет выглядеть так:
1. Умножаем 7 на 3 (семёрку мы взяли из разряда единиц первого многозначного множителя): 7 3 = 21. Получили число больше десяти, значит, пишем цифру 1 с правого края (значение единичного разряда числа 21), а двойку запоминаем. Наша запись становится такой:
2. После этого умножаем значения десятков первого множителя на второй и прибавляем к результату два оставшихся от предыдущего этапа. Если после этого получается меньше 10, то вводим значения соответствующей цифры, если больше — вводим значение единицы и переносим десятки дальше. В нашем примере нам нужно умножить 2 на 3, будет 6. Складываем десятки, оставшиеся от последнего умножения (от числа 21, как мы помним): 6 + 2 = 8. Восемь меньше десяти, а значит, на следующую цифру ничего переносить не нужно. Пишем 8 в нужном месте и получаем:
3. Далее действуем таким же образом. Теперь нам нужно умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если вы запомнили число на предыдущем этапе, прибавьте его к результату, сравните с десятью и запишите на нужное место.
Порядок действий тот же: если вы запомнили число на предыдущем этапе, прибавьте его к результату, сравните с десятью и запишите на нужное место.
Здесь нужно умножить 3 на 0. По правилам умножения результатом будет 0 . Ничего добавлять не будем, так как на предыдущем этапе число было меньше 10. Получившийся ноль тоже меньше десяти, поэтому запишем его на месте под горизонтальной чертой:
4. Перейти к следующей категории — умножить тысячи. Продолжаем расчеты по алгоритму, пока не закончатся числа в многозначном множителе.
Осталось умножить 5 на 3 и получить 15 . Результат больше 10, пишем пять и запоминаем десять:
Нам нужно просто умножить 4 на 3, будет 12. Прибавляем к результату единицу, взятую из предыдущего расчета. 13 больше 10, пишем 3 в нужном месте и сохраняем единицу.
У нас больше не осталось цифр для умножения, но одна еще есть в наличии. Мы просто напишем его под горизонтальной чертой слева от всех уже имеющихся цифр:
Процесс подсчета столбиком завершен. Мы получили шестизначное число, которое является правильным решением нашей задачи.
Мы получили шестизначное число, которое является правильным решением нашей задачи.
Ответ: 45 027 3 = 135 081.
Чтобы было понятнее, мы представили алгоритм умножения многозначного натурального числа на единственное в виде диаграммы. Здесь правильно отражена суть процесса подсчета, но не учтены некоторые нюансы:
Что делать, если условие задачи содержит многозначное число, оканчивающееся нулем (или несколькими нулями подряд)? Давайте рассмотрим пример шаг за шагом. Чтобы было проще, давайте позаимствуем числа из предыдущей задачи и просто добавим пару нулей к исходному многозначному множителю.
Решение
Сначала напишите числа правильно.
После этого проводим вычисления, игнорируя нули справа. Возьмем результаты из предыдущей задачи, чтобы лишний раз не считать:
Завершающим этапом решения является переписывание нулей в многозначном числе под горизонтальной чертой в области результатов. Нам нужно добавить 2 лишних нуля:
Нам нужно добавить 2 лишних нуля:
Это число и будет ответом на нашу задачу. Это завершает умножение столбцов.
Ответ: 4 502 700 3 = 13 508 100 .
Этот способ вполне подходит для тех случаев, когда оба множителя являются многозначными натуральными числами. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим записи с нулями.
Пример 4
Условие: вычислить сколько будет 207 8 063 .
Раствор
Начнем, как всегда, с правильного обозначения факторов. Более удобен способ записи, при котором множитель с большими знаками количества находится вверху. Итак, сначала напишем 8063, а под ним 207. Если количество символов в множителях одинаковое, то порядок записи значения не имеет. В нашей задаче нам нужно расположить числа первого множителя под номерами второго справа налево:
Начинаем последовательно перемножать значения цифр. В этом случае мы получим результаты, которые называются неполными продуктами.
В этом случае мы получим результаты, которые называются неполными продуктами.
1. Первый шаг заключается в том, что нам нужно перемножить значения единиц в первом и втором множителе. В нашем случае это 3 и 7. Делаем все так же, как мы уже объясняли в предыдущем пункте (если нужно, читаем еще раз). В итоге получаем первый неполный продукт, который является промежуточным результатом:
2. Второй шаг — умножение десятков. Умножаем первый множитель столбиком на значение разряда десятков второго множителя (при условии, что он не равен 0). Результат пишем под чертой под разрядом десятков. Если во втором множителе вместо десятков стоит 0, то сразу переходим к следующему этапу.
3. Дальнейшие действия выполнить аналогично, умножая по очереди значения искомых разрядов (если они не равны 0). Вводим результаты под чертой.
Итак, нам нужно умножить 8063 на сотни значений в 207 (т.е. два). Мы получили второй некомплектный товар, пишем его так:
Мы получили все необходимые нам некомплектные работы. Их количество равно количеству цифр во втором множителе (кроме 0). Последнее, что нам осталось сделать, это добавить две работы в столбец, используя одинаковые обозначения. Цифры никуда не переписываем: они остаются с тем же сдвигом влево. Подчеркиваем их дополнительной горизонтальной чертой и ставим слева плюс. Складываем по уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10, и прибавляем их на следующем шаге). Наша задача будет:
Их количество равно количеству цифр во втором множителе (кроме 0). Последнее, что нам осталось сделать, это добавить две работы в столбец, используя одинаковые обозначения. Цифры никуда не переписываем: они остаются с тем же сдвигом влево. Подчеркиваем их дополнительной горизонтальной чертой и ставим слева плюс. Складываем по уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10, и прибавляем их на следующем шаге). Наша задача будет:
Семизначное число, полученное под чертой, является результатом умножения нужных нам исходных натуральных чисел.
Ответ: 8063 207 = 1669041.
Процесс умножения двух многозначных чисел столбцов также можно представить в виде наглядной схемы:
Для лучшего закрепления материала приведем решение еще одного примера .
Пример 5
Условие: умножить 297 на 321.
Решение
Начнем с правильного обозначения множителей.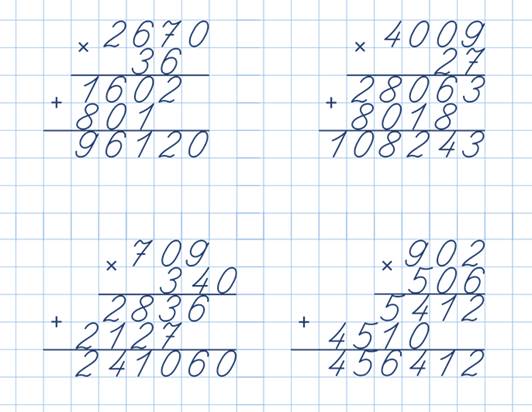 Количество знаков в них одинаковое, поэтому порядок написания особого значения не имеет:
Количество знаков в них одинаковое, поэтому порядок написания особого значения не имеет:
1. Первый этап — умножаем 297 на 1, что находится в разряде единиц второго множителя.
2. Затем таким же образом умножаем первый множитель на 2, что в десятках второго множителя. Получаем второй неполный продукт.
Онлайн-игра-симулятор «Умножение в столбик» помогает научиться умножать дву- и трехзначные числа. Эта игра предназначена для детей от 7 до 10 лет. Умножение чисел столбиком – это программа по математике для 3 класса школы. Но ничего сложного в этом действии нет, поэтому умножение в столбик можно освоить и раньше.
Как научиться умножать в столбик?
В игре три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трехзначного числа на трехзначное число (числа от 100 до 999) и перемешивание. В миксе трехзначное число умножается на двузначное число или двузначное число умножается на трехзначное число.
Чтобы правильно умножать дву- и трехзначные числа, нужно знать и хорошо.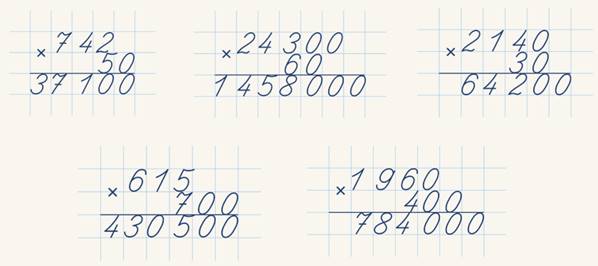
Надеюсь, вы помните, что числа, которые умножаются друг на друга, называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Я также верю, что вы знаете, что в числах есть цифры: единицы (наименьшие), десятки, сотни, тысячи…
Итак, приступим. Начинать умножение в столбик нужно, располагая множители таким образом, чтобы числа с одинаковыми цифрами оказывались друг под другом: единицы под единицами, десятки под десятками и так далее. На следующем шаге берем цифру из единиц второго множителя и умножаем ее по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записывается в верхней строке под соответствующей категорией.
За каждый правильный ответ начисляется 1 балл. Неверно — снимается 3 балла.
Если вам понравилась эта игра, обязательно поделитесь ею с друзьями. В конце концов, им она тоже может понравиться 🙂
Эта игра разработана и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.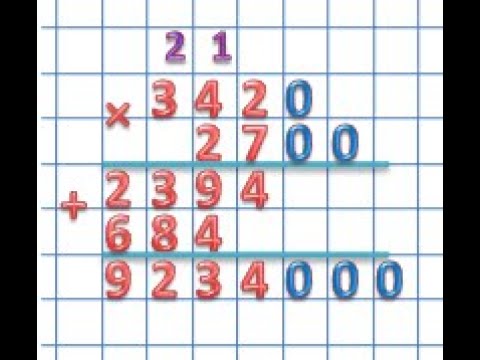
Умножение в столбик позволяет быстро выдать решение примеров даже с многозначными числами. Чтобы считать, нужно всего лишь знать наизусть таблицу умножения.
Как умножать в столбик
Как и при сложении и вычитании в столбик, при умножении числа записываются одно под другим. Каждая цифра на своем месте: единицы под единицами, десятки под десятками и т. д. Внизу проводится горизонтальная черта, под ней пишется ответ.
Возьмем числа 78 и 12. Для лучшего понимания: вверху пишем 78, внизу 12. Начнем с единицы меньшего числа, то есть с числа 2.
Сначала считаем 8×2=16. Число получилось больше 10, значит, как дополнение, пишем последнюю цифру (6), и держим в уме единицу. Теперь переходим к десятке, то есть считаем 7×2 = 14. Единицу мы помнили, значит, теперь прибавляем ее к результату, получается 14+1=15. Число 5 пишется под десятками, а 1 переходит в новый разряд — сотни. Другими словами, под горизонтальной чертой следует написать «156».
Давайте перейдем к следующей категории. Теперь наш ответ будет записан иначе: последняя цифра ответа должна быть ровно под десятками, то есть под цифрой 5. Получается, что каждое последующее промежуточное число сдвинуто на 1 цифру влево.
Считаем 8×1=8. Число меньше 10, пишем 8 под пятеркой в числе «156». Мы считаем 7×1=7. Семёрка переходит в разряд сотен, то есть её следует писать под единицей в ответе «156». Под шестеркой ничего не пишется; для удобства можно поставить туда ноль.
Складываем полученное выражение в столбик: 156 + 78. К 6 (0) ничего не прибавляем, а значит, переписываем его в прежнем виде. Затем посчитайте 5+8=13, напишите 3, имея в виду единицу. Наконец, 1 + 7 = 8, прибавляем единицу — получается 9.
Итак, ответ: 936.
Лучше тренироваться на листе в клеточку, чтобы привыкнуть к расположению цифр множители
Таким же образом умножаются и другие многозначные числа.
Если в множителях есть нули, то они не перемножаются, а просто переносятся в правую часть итогового ответа.
Варианты карт
Для наглядности можно распечатать карточки с примерами. разные уровни сложности. Так детям будет легче запомнить принцип счета. Примеры для практики можно использовать как при изучении умножения в первый раз, так и для повторения после каникул.
Поначалу решение примеров будет занимать много времени, но постепенно скорость будет увеличиваться. Даже если у вас есть калькулятор, лучше считать вручную: это развивает умственную деятельность.
Фотогалерея: карточки-примеры к уроку
Видео: умножение чисел в столбик
Постоянная практика – залог успеха, и со временем вы сможете научиться умножать в уме даже большие числа. Но начинать лучше с простых примеров, постепенно повышая уровень сложности.
Умножение на 1000 — Математика с мамой
Опубликовано Математика с мамой
Умножение на 1000- Чтобы умножить число на тысячу, переместите каждую цифру на три разряда влево.

- Чтобы умножить 2 на 1000, цифра «2» перемещается на три позиции влево.
- «2» перемещается из столбца единиц в столбец тысяч.
- В столбцах сотен, десятков и единиц нет цифр, поэтому в каждом из этих столбцов записан ноль.
- 2 x 1000 = 2000.
- Умножение целого числа на одну тысячу равносильно добавлению трех цифр нуля в конце этого числа.
Чтобы умножить число на 1000, переместите все его цифры на три позиции влево.
Умножение целого числа на 1000 равносильно добавлению трех нулей в конце числа.
- Чтобы умножить число на 1000, все цифры этого числа перемещаются на три столбца разряда влево.
- Мы умножим десятичное число 7,04 на 1000.
- Цифра «7» перемещается из столбца единиц в столбец тысяч.
- Цифра «0» перемещается из столбца десятых в столбец сотен.
- Цифра «4» перемещается из столбца сотых в столбец десятков.

- В столбце единиц измерения нет цифр между цифрой «4» и десятичной точкой, поэтому вместо нее ставится «0».
- 7,04 х 1000 = 7040.
Чтобы умножить число на 1000, переместите каждую цифру в этом числе на три столбца разряда влево .
Все цифры в исходном номере остаются в том же порядке.
Чтобы умножить целое число на тысячу, достаточно просто добавить три нулевых цифры в конце этого целого числа.
Вот пример умножения целого числа на 1000.
В приведенном выше примере цифра 2 была перемещена на три позиции влево . Он переместился из столбца единиц в столбец тысяч .
Поскольку ни в столбце сотен, ни в столбце десятков, ни в столбце единиц больше нет цифр, мы пишем ноль в каждом пробеле, чтобы показать, что они равны нулю.
Возможно, вы уже обнаружили, что 2 x 1000 = 2000, «прибавив три нуля». Это работает только при умножении целых чисел.
При обучении умножению на 1000 лучше сначала показать цифры, перемещающиеся по трем столбцам разряда. Это то, что происходит на самом деле, потому что 1000 состоит из 10 х 10 х 10, что равносильно умножению на 10 три раза.
Каждый раз, когда мы умножаем на десять, мы перемещаем нашу цифру на один разрядный столбец влево, потому что наши столбцы разрядных значений находятся в базе десяти и представляют собой умножение на десять.
Большинство людей по-прежнему будут «добавлять три нуля» при умножении целого числа на 1000, и это самый простой и лучший способ умножить целое число на 1000, так как это можно сделать быстро и в уме.
Этот трюк следует демонстрировать после показа цифр, перемещающихся в столбцах их позиционных значений, и следует подчеркнуть, что это работает только с целыми числами.
Важно понимать, как работает умножение на 1000, потому что не все числа, которые мы будем умножать, будут целыми числами.
Вот пример умножения десятичного числа на 1000:
Чтобы умножить десятичное число 0,05 на 1000, мы переместим 5 на три знака влево . Мы перемещаем его из столбца сотых в столбец десятков . Мы должны убедиться, что мы показываем, что столбец единиц равен нулю, записывая ноль в этом месте.
Мы перемещаем его из столбца сотых в столбец десятков . Мы должны убедиться, что мы показываем, что столбец единиц равен нулю, записывая ноль в этом месте.
Если слева от десятичной точки нет цифр, мы всегда пишем одну цифру нуля перед десятичной точкой, чтобы показать это.
При умножении числа, состоящего из более чем одной цифры, на 1000, нам нужно убедиться, что мы перемещаем каждую цифру на три позиции влево .
Например:
Начнем с перемещения 3 на три позиции левее . Мы перемещаем его из столбца десятых в столбец сотен . Затем может следовать 9. Мы перемещаем 9 из столбца сотых в столбец десятков .
Мы должны убедиться, что мы показываем, что столбец единиц равен нулю, записывая ноль в этом месте.
Итак, 0,39 х 1000 = 390.
Мы можем видеть цифры в исходном числе, а именно «3» и «9».’, остаются в том же порядке в ответе и что они по-прежнему находятся рядом друг с другом.
Нам нужно быть более осторожными при работе с числами, в которых между двумя другими цифрами стоит ноль.
Например:
Мы должны убедиться, что мы перемещаем каждую цифру в 7.04 на три позиции влево, включая ноль . Мы перемещаем 7 из столбца единиц в столбец тысяч , мы перемещаем 0 из столбца десятых.0302 в столбец сотен и мы перемещаем 4 из столбца сотых в столбец десятков .
Поскольку в столбце единиц больше нет цифр, мы должны вписать ноль, чтобы показать, что он равен нулю.
Цифры в ответе расположены в том же порядке, что и цифры в исходном вопросе. У нас есть «7», за которым следует «0», за которым следует «4».
Мы можем использовать это, чтобы быстро и мысленно умножать числа на 1000.
Мы знаем, что при умножении на 1000 любые цифры в столбце единиц переместятся в столбец тысяч.
У нас есть «7» в столбце единиц, поэтому мы знаем, что при умножении на 1000 ответ будет 7 тысяч с чем-то.


 Это сколько месяцев?
Это сколько месяцев?  Для вас новое задание:
Для вас новое задание: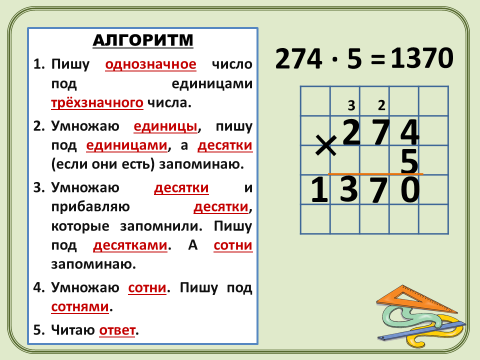
 Поэты древности называли Египет «подарком Нила». Без сомнения Нил является одной из величайших рек мира. Именно благодаря этой реке Египет обязан своей историей.
Поэты древности называли Египет «подарком Нила». Без сомнения Нил является одной из величайших рек мира. Именно благодаря этой реке Египет обязан своей историей.
 А, чтобы достичь высот в математике, необходимо взбираться на гору знаний медленно, шаг за шагом, не торопясь, дружно. Спасибо всем за хорошую плодотворную работу на уроке.
А, чтобы достичь высот в математике, необходимо взбираться на гору знаний медленно, шаг за шагом, не торопясь, дружно. Спасибо всем за хорошую плодотворную работу на уроке.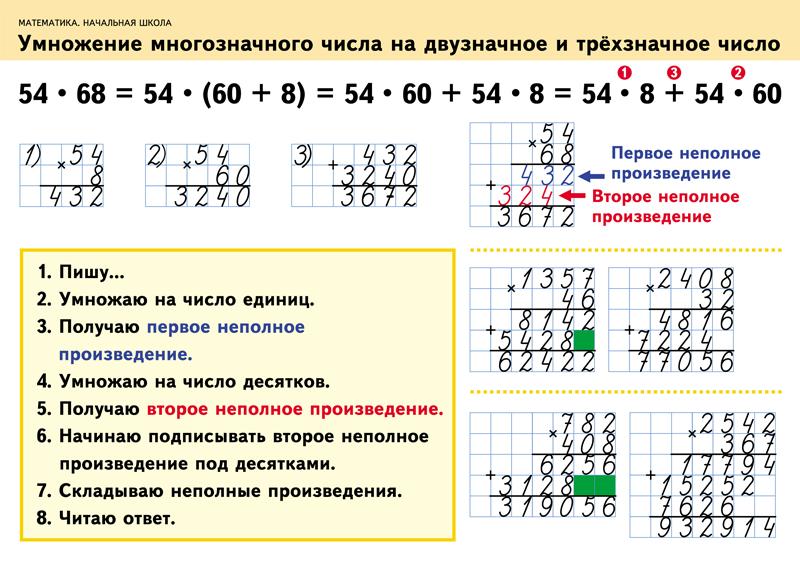 Используя блоки с основанием 10 или счеты, покажите детям, что цифра имеет разные значения в зависимости от ее положения.
Используя блоки с основанием 10 или счеты, покажите детям, что цифра имеет разные значения в зависимости от ее положения. Хитрость здесь заключается в том, чтобы расположить все цифры в порядке убывания, чтобы найти наибольшее число.
Хитрость здесь заключается в том, чтобы расположить все цифры в порядке убывания, чтобы найти наибольшее число.  Это можно рассчитать, используя следующий метод.
Это можно рассчитать, используя следующий метод.
 Проверьте это сами!
Проверьте это сами!