Умножение столбиком примеры: § Умножение в столбик. Как умножать в столбик

Содержание

3 класс — Умножение чисел в столбик. Двузначные на однозначные, задачи. Свойства и примеры

Дата публикации: 12 апреля 2017.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Скачать:Умножение в столбик. Двузначные числа на однозначные (PDF)

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Математика 1-4 классов, Г.В. Дорофеев, электронное учебное пособие к учебникам

3 КЛАСС. ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.1

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.

	44		31		89		50		21
x	8	x	4	x	0	x	8	x	6
	…		…		…		…		…

	46		67		46		35		81
x	6	x	9	x	6	x	7	x	2
	…		…		…		…		…

	73		89		60		63		33
x	7	x	1	x	4	x	1	x	8
	…		…		…		…		…

	47		27		12		61		79
x	4	x	1	x	4	x	3	x	0
	…		…		…		…		…

	51		97		33		88		76
x	3	x	0	x	4	x	4	x	3
	…		…		…		…		…

	29		37		59		86		30
x	3	x	7	x	2	x	7	x	0
	…		…		…		…		…

	85		25		90		16		71
x	6	x	5	x	7	x	9	x	3
	…		…		…		…		…

	79		52		50		73		20
x	7	x	4	x	3	x	3	x	7
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.2

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.

	79		49		74		79		31
x	7	x	5	x	2	x	3	x	7
	…		…		…		…		…

	95		82		19		17		25
x	6	x	3	x	1	x	1	x	5
	…		…		…		…		…

	71		85		96		16		31
x	6	x	7	x	1	x	9	x	4
	…		…		…		…		…

	39		64		10		55		10
x	9	x	6	x	2	x	0	x	2
	…		…		…		…		…

	75		90		83		25		24
x	1	x	2	x	8	x	8	x	4
	…		…		…		…		…

	91		54		80		68		20
x	5	x	5	x	2	x	1	x	0
	…		…		…		…		…

	11		90		26		11		62
x	6	x	1	x	6	x	2	x	3
	…		…		…		…		…

	61		19		74		27		51
x	3	x	0	x	8	x	2	x	8
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.3

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.

	44		16		24		99		65
x	5	x	2	x	8	x	8	x	6
	…		…		…		…		…

	94		66		61		62		63
x	0	x	1	x	8	x	2	x	4
	…		…		…		…		…

	50		53		79		41		73
x	2	x	8	x	9	x	7	x	5
	…		…		…		…		…

	23		96		11		75		48
x	1	x	3	x	5	x	1	x	0
	…		…		…		…		…

	10		92		37		28		46
x	4	x	1	x	3	x	1	x	9
	…		…		…		…		…

	56		65		95		97		42
x	3	x	6	x	5	x	3	x	4
	…		…		…		…		…

	31		10		48		43		76
x	1	x	7	x	3	x	2	x	6
	…		…		…		…		…

	63		14		58		80		41
x	9	x	0	x	3	x	3	x	8
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.4

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.

	31		31		17		34		81
x	0	x	0	x	6	x	7	x	7
	…		…		…		…		…

	89		72		42		27		71
x	4	x	6	x	4	x	1	x	5
	…		…		…		…		…

	73		35		96		11		19
x	6	x	3	x	7	x	3	x	4
	…		…		…		…		…

	34		76		79		12		13
x	9	x	9	x	7	x	2	x	6
	…		…		…		…		…

	27		66		99		60		86
x	9	x	0	x	2	x	2	x	6
	…		…		…		…		…

	64		49		92		55		58
x	3	x	5	x	2	x	5	x	3
	…		…		…		…		…

	97		31		70		42		38
x	8	x	2	x	8	x	8	x	6
	…		…		…		…		…

	24		83		15		71		40
x	8	x	9	x	7	x	9	x	4
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.5

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.

	40		45		41		26		41
x	8	x	1	x	3	x	5	x	9
	…		…		…		…		…

	67		58		37		83		82
x	4	x	2	x	5	x	9	x	7
	…		…		…		…		…

	79		15		81		33		19
x	6	x	0	x	6	x	5	x	7
	…		…		…		…		…

	95		46		34		21		35
x	9	x	5	x	2	x	0	x	2
	…		…		…		…		…

	46		25		91		57		68
x	4	x	9	x	3	x	4	x	7
	…		…		…		…		…

	86		13		73		81		20
x	9	x	2	x	8	x	4	x	3
	…		…		…		…		…

	31		74		63		60		49
x	4	x	0	x	2	x	4	x	1
	…		…		…		…		…

	35		22		37		28		17
x	8	x	7	x	2	x	7	x	1
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.1
ANSWERS.


Умножи числа в столбик. Двузначное на однозначное.

	44		31		89		50		21
x	8	x	4	x	0	x	8	x	6
	352		124		0		400		126

	46		67		46		35		81
x	6	x	9	x	6	x	7	x	2
	276		603		276		245		162

	73		89		60		63		33
x	7	x	1	x	4	x	1	x	8
	511		89		240		63		264

	47		27		12		61		79
x	4	x	1	x	4	x	3	x	0
	188		27		48		183		0

	51		97		33		88		76
x	3	x	0	x	4	x	4	x	3
	153		0		132		352		228

	29		37		59		86		30
x	3	x	7	x	2	x	7	x	0
	87		259		118		602		0

	85		25		90		16		71
x	6	x	5	x	7	x	9	x	3
	510		125		630		144		213

	79		52		50		73		20
x	7	x	4	x	3	x	3	x	7
	553		208		150		219		140

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.2
ANSWERS.


Умножи числа в столбик. Двузначное на однозначное.

	79		49		74		79		31
x	7	x	5	x	2	x	3	x	7
	553		245		148		237		217

	95		82		19		17		25
x	6	x	3	x	1	x	1	x	5
	570		246		19		17		125

	71		85		96		16		31
x	6	x	7	x	1	x	9	x	4
	426		595		96		144		124

	39		64		10		55		10
x	9	x	6	x	2	x	0	x	2
	351		384		20		0		20

	75		90		83		25		24
x	1	x	2	x	8	x	8	x	4
	75		180		664		200		96

	91		54		80		68		20
x	5	x	5	x	2	x	1	x	0
	455		270		160		68		0

	11		90		26		11		62
x	6	x	1	x	6	x	2	x	3
	66		90		156		22		186

	61		19		74		27		51
x	3	x	0	x	8	x	2	x	8
	183		0		592		54		408

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.3
ANSWERS.


Умножи числа в столбик. Двузначное на однозначное.

	44		16		24		99		65
x	5	x	2	x	8	x	8	x	6
	220		32		192		792		390

	94		66		61		62		63
x	0	x	1	x	8	x	2	x	4
	0		66		488		124		252

	50		53		79		41		73
x	2	x	8	x	9	x	7	x	5
	100		424		711		287		365

	23		96		11		75		48
x	1	x	3	x	5	x	1	x	0
	23		288		55		75		0

	10		92		37		28		46
x	4	x	1	x	3	x	1	x	9
	40		92		111		28		414

	56		65		95		97		42
x	3	x	6	x	5	x	3	x	4
	168		390		475		291		168

	31		10		48		43		76
x	1	x	7	x	3	x	2	x	6
	31		70		144		86		456

	63		14		58		80		41
x	9	x	0	x	3	x	3	x	8
	567		0		174		240		328

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.4ANSWERS.


Умножи числа в столбик. Двузначное на однозначное.

	31		31		17		34		81
x	0	x	0	x	6	x	7	x	7
	0		0		102		238		567

	89		72		42		27		71
x	4	x	6	x	4	x	1	x	5
	356		432		168		27		355

	73		35		96		11		19
x	6	x	3	x	7	x	3	x	4
	438		105		672		33		76

	34		76		79		12		13
x	9	x	9	x	7	x	2	x	6
	306		684		553		24		78

	27		66		99		60		86
x	9	x	0	x	2	x	2	x	6
	243		0		198		120		516

	64		49		92		55		58
x	3	x	5	x	2	x	5	x	3
	192		245		184		275		174

	97		31		70		42		38
x	8	x	2	x	8	x	8	x	6
	776		62		560		336		228

	24		83		15		71		40
x	8	x	9	x	7	x	9	x	4
	192		747		105		639		160

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.5
ANSWERS.


Умножи числа в столбик. Двузначное на однозначное.

	40		45		41		26		41
x	8	x	1	x	3	x	5	x	9
	320		45		123		130		369

	67		58		37		83		82
x	4	x	2	x	5	x	9	x	7
	268		116		185		747		574

	79		15		81		33		19
x	6	x	0	x	6	x	5	x	7
	474		0		486		165		133

	95		46		34		21		35
x	9	x	5	x	2	x	0	x	2
	855		230		68		0		70

	46		25		91		57		68
x	4	x	9	x	3	x	4	x	7
	184		225		273		228		476

	86		13		73		81		20
x	9	x	2	x	8	x	4	x	3
	774		26		584		324		60

	31		74		63		60		49
x	4	x	0	x	2	x	4	x	1
	124		0		126		240		49

	35		22		37		28		17
x	8	x	7	x	2	x	7	x	1
	280		154		74		196		17

Умножение в столбик.

Умножение и деление столбиком

В третьем классе начальной школы дети начинают изучать внетабличные случаи умножения и деления. Числа в пределах тысячи – материал, на котором происходит овладение темой. Программа рекомендует операции деления и умножения трехзначных и двузначных чисел производить на примере однозначных. В ходе работы над темой учитель начинает формировать у детей такой важный навык, как умножение и деление столбиком. В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.

Что является основой умножения

Главные положения, на которых строится алгоритм умножения многозначного числа на многозначное, являются теми же, что при действиях на однозначное. Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.

Первым правилом является поразрядность операций. Второе заключается в использовании таблицы умножения в каждом разряде.

Необходимо учесть, что эти основные положения усложняются при выполнении действий с многозначными числами.

Записанный ниже пример позволит понять, о чем идет речь. Допустим, необходимо 80 х 5 и 80 х 50.

В первом случае ученик рассуждает так: 8 десятков необходимо повторить 5 раз, получатся тоже десятки, и их будет 40, так как 8 х 5 = 40, 40 десятков – это 400, значит, 80 х 5 = 400. Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.

Чтобы найти значение второго выражения, тоже необходимо воспользоваться табличным случаем и 8 х 5. Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.

В результате совместных усилий педагога и детей становится ясно, что для умножения многозначного числа на многозначное необходимо умение применять сочетательный закон, при котором один из множителей заменяется произведением (80 х 50 = 80 х 5 х 10 = 400 х 10 = 4000)

Кроме того, возможен путь, когда используется распределительный закон умножения относительно сложения или вычитания. В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.

Исследовательская работа детей

Ученикам предлагается достаточно большое количество примеров подобного вида. Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.

Учитель делает это, преследуя две цели. Во-первых, дети осознают, отрабатывают основные пути выполнения операции умножения на многозначное число. Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.

Этапы изучения умножения на многозначное число.

В методических рекомендациях изучение указанной темы происходит в несколько этапов. Они должны следовать один за другим, давая возможность школьникам понять весь смысл изучаемого действия. Перечень этапов открывает учителю общую картину процесса подачи материала детям:

самостоятельный поиск учениками способов нахождения значения произведения многозначных множителей;
для решения поставленной задачи используется сочетательное свойство, а также умножение на единицу с нулями;
отработка навыка умножения на круглые числа;
использование при вычислениях распределительного свойства умножения относительно сложения и вычитания;
операции с многозначными числами и умножение в столбик.

Следуя указанным этапам, учитель постоянно должен обращать внимание детей на тесные логические связи ранее изученного материала с тем, что осваивается в новой теме. Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.

Задачи изучения умножения в курсе начальной школы

Учитель, преподавая математику, точно знает, что наступит момент, когда у четвероклассников возникнет вопрос о том, как решать столбиком умножение многозначных чисел. И если он вместе с учениками на протяжении трех лет обучения – во 2, 3, и 4 классах – целенаправленно и вдумчиво изучал конкретный смысл умножения и все вопросы, которые связаны с этой операцией, то трудностей в освоении рассматриваемой темы у детей возникнуть не должно.

Какие же задачи ранее были решены учениками и их преподавателем?

Освоение табличных случаев умножения, то есть получение результата в один шаг. Обязательным требованием программы является доведение навыка до автоматизма.
Умножение многозначного числа на однозначное. Результат получается путем многократного повторения шага, которым дети уже владеют в совершенстве.
Умножение многозначного числа на многозначное осуществляется благодаря повторению шагов, обозначенных в пункте 1 и 2. Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.

Использование свойств умножения

Перед тем как на последующих страницах учебников начнут появятся примеры умножения столбиком, 4 класс должен очень хорошо научиться пользоваться для рационализации вычислений сочетательным и распределительным свойством.

Путем наблюдений и сопоставлений ученики приходят к выводу, что сочетательное свойство умножения для нахождения произведения многозначных чисел используется только тогда, когда один из множителей можно заменить произведением однозначных чисел. А это возможно не всегда.

Распределительное свойство умножения в этом случае выступает как универсальное. Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.

Алгоритм записи действия умножения в столбик

Запись умножения столбиком является самой компактной из всех существующих. Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.

Детям предлагается самостоятельно составить последовательность действий при выполнении умножения. Знание этого алгоритма станет залогом успешного формирования навыка. Поэтому учителю не нужно жалеть времени, а постараться приложить максимум усилий к тому, чтобы порядок выполнения действий при умножении в столбик был усвоен детьми на «отлично».

Упражнения для формирования навыка

Прежде всего нужно отметить, что примеры умножения в столбик, предлагаемые детям, от урока к уроку усложняются. После знакомства с умножением на двузначное число дети учатся выполнять действия с трехзначными, четырехзначными числами.

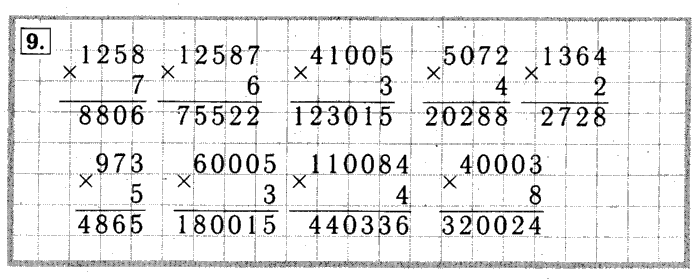
Для отработки навыка предлагаются примеры с готовым решением, но среди них преднамеренно размещают записи с ошибками. Задача учеников состоит в том, чтобы обнаружить неточности, объяснить причину их появления и исправить записи.

Теперь при решении задач, уравнений и всех других заданий, где надо выполнять умножение многозначных чисел, от учеников требуется оформление записи столбиком.

Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»

Большое внимание на уроках, посвященных изучению указанной темы, уделяется развитию таких познавательных действий, как нахождение разных способов решения поставленной задачи, выбор наиболее рационального приема.

Использование схем для проведения рассуждений, установление причинно-следственных связей, анализ наблюдаемых объектов на основе выделенных существенных признаков – еще одна группа формируемых познавательных умений при изучении темы «Умножение в столбик».

Обучение детей способам деления многозначных чисел и оформлению записи столбиком осуществляется только после того, как дети научатся умножать.

ГДЗ по Алгебре 7 класс: Макарычев

Готовые домашние задания для 7 класса по алгебре Макарычева

Если в прошлом к решебникам относились скептически, то сегодня они стали важным дополнением учебного процесса. Пособиями с готовыми ответами активно пользуются не только ученики, но и их родители, которые хотят проконтролировать своих детей.

ГДЗ от Ответкина это не просто краткие материалы для списывания. Наш сайт не имеет аналогов, потому что здесь вы можете найти подробный алгоритм решения задач, несколько вариантов ответов, комментарии, благодаря которым можно понять трудную тему.

Что такое Ответкин?

Это актуальная база данных. В других решебниках школьники вынуждены сверять номера, тратить дополнительное время на поиск нужного ответа. Но на нашем портале мы разместили только свежие ГДЗ к актуальным учебникам, по которым учатся в школах Российской Федерации.
Подробные решения. Практически к каждому заданию на Ответкине есть короткий ответ и подробный, с алгоритмом выполнения примера, комментариями к нему. Когда нет времени и нужно быстро ответить на уроке, ученик может воспользоваться кратким решением, но если нужно разобраться с непонятной темой – помогут пояснения.
Бесплатный помощник. Наш сайт бесплатно помогает учащимся и их родителям контролировать правильность выполнения домашней работы. Это позволяет сэкономить деньги на репетиторах.
Несколько вариантов ответа. Видя альтернативные способы решения – школьник понимает механизм выполнения задачи, ему становятся понятны важные нюансы, которые он пропустил или не усвоил на уроке.
Удобный поиск по сайту. Учебное пособие с пояснениями можно просматривать как с компьютера, так с мобильного телефона. Чтобы быстро найти определенный номер нужно лишь ввести его в строку поиска. Кроме того, в личном кабинете сохраняется история просмотров, с помощью которой удобно возвращаться к предыдущим заданиям.

ГДЗ от Ответкина становятся незаменимы в конце четверти или учебного года, когда нужно быстро повторить пройденный материал, подтянуть успеваемость.

Уникальные подробные решения с пояснениями Ответкина

С 7 класса школьники начинают изучать новый для них раздел математики – алгебру. Это важный, но не простой предмет, который тесно связан с экономикой, информатикой, физикой и другими точными науками.

Нередко семиклассники теряются при выполнении разнообразных алгебраических задач. Теперь им нужно решать уравнения не только с одной, но и двумя переменными, строить графики функций, осуществлять разложение многочленов на множители. Далеко не каждый учитель может объяснить эти сложные темы простым и понятным для детей способом. Поэтому родители ломают голову, где бы найти хорошего репетитора, как проверить домашнее задание ребенку, когда сам уже забыл пройденную школьную программу.

С решением этих проблем помогает Ответкин. Он дает возможность узнать правильный ответ и его разные варианты, понять алгоритм выполнения примера.

Почему наш сайт достойная альтернатива занятиям с репетитором?

Это быстро и бесплатно. Использование учебного пособия с пояснениями позволяет родителям сэкономить деньги. Ученикам не нужно тратить дополнительное время на дорогу к репетитору и обратно домой. В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
Это удобно. Репетитор занимается с ребенком в назначенное время, поэтому все вопросы школьник вынужден откладывать до следующего дополнительного занятия. А решебником можно воспользоваться в любой момент, как находясь на уроке в школе, так и дома.
Ответкин приучает к самостоятельности. Готовые домашние задания на нашем сайте — это не просто материалы для списывания, а подробное объяснение важных нюансов школьной программы. Практически каждый номер содержит не только несколько вариантов ответа, на и комментарии, с помощью которых можно восполнить пробелы в знаниях алгебры.

Если говорить о видеоуроках, то они не могут сравниться с нашим порталом по эффективности, удобству и актуальности данных. Нередко спикеры объясняют материал 7 класса, не имея опыта преподавания в школе. Они могут говорить много, но без конкретики, не дают подсказок к выполнению домашней работы. Видеоролики нужно проматывать несколько раз, тратить 30-40 минут на усвоение одной только темы. В то время как школьник, возможно, хочет уточнить несколько важных нюансов, а не прослушивать материал всего урока.

Как пользоваться сайтом и открывать нужную задачу с комментариями?

Наша команда сделала Ответкин максимально удобным для пользователей. Мы учли, что семиклассники часто просматривают готовые домашние задания в мобильном телефоне. В отличие от других сайтов у нас все материалы размещены на узком полотне, выполнены красивым понятным шрифтом, который комфортно читать со смартфона.

Подсказки как пользоваться сайтом:

Чтобы найти нужное задание введите его в строку быстрого поиска. Ознакомьтесь с кратким вариантом ответа, который откроется на новой странице. Если вы хотите увидеть подробный алгоритм решения задачи с разными вариантами – зарегистрируйтесь на нашем сайте.
Вы можете выбрать один из двух, наиболее удобный для вас вариант авторизации. Первый – через социальные сети. Рядом с кнопкой «Войти» нажмите на социальную сеть, например, гугл аккаунт. Подтвердите вход, дайте свое согласие, что ознакомлены с правилами пользования сайтом. Второй вариант – регистрация с нуля с использованием почтового ящика. Напишите адрес вашей почты и ждите письма со ссылкой для активизации аккаунта. Перейдите по ссылке и пользуйтесь сайтом.
После авторизации вам откроется доступ в личный кабинет. По умолчанию вам будет предоставлена бесплатная подписка, где будет видно количество оставшихся ответов. Каждые сутки пользователь может открывать не более трех заданий. Открытые решения будут храниться в личном кабинете в течение 24 часов, которые можно просматривать неограниченное количество раз.
Если пользователь желает получить большее число открываний в сутки – ему стоит приобрести подписку на платной основе сроком на месяц. В этом случае в личном кабинете исчезнет реклама. В профиле будет видно сколько дней еще действует платная подписка.

Для удобства, чтобы пользователь быстро сориентировался в задании – на белом фоне изображен краткий ответ для записи в тетрадь, на цветном фоне отображена теория и подробные пояснения к номеру. Но даже краткие решения на нашем сайте более подробные, чем в других ГДЗ.

Решебник алгебры седьмого класса к учебнику Ю.Н. Макарычева, Н.Г. Миндюка, К.И. Нешкова, С.Б. Суворова

Решения с пояснениями по алгебре за 7 класс составлены на основе учебника Макарычева 2013 года, который соответствует Федеральным государственным образовательным стандартам. Номера в пособии с готовыми домашними заданиями соответствуют нумерации учебника.

Алгебра седьмого класса содержит 5 глав, состоящих из 16 параграфов, которые в свою очередь в общей сложности разбиты на 46 подпунктов. К каждой теме помимо теории есть практические упражнения. Для коллективного решения предусмотрены «задачи-исследования» и задания для работы в парах. В конце каждого параграфа, для закрепления изученного материала размещены контрольные вопросы. По уровню подготовки среди упражнений есть обязательные, а также повышенной сложности, которые выполняют на добровольной основе.

Готовые домашние задания по алгебре от Ответкина направлены на усвоение следующих тем и понятий:

Числовые выражения, сравнение их значений и преобразование.
Уравнение, решение задач с его помощью, линейные уравнения с одной и двумя переменными, графики и системы линейных уравнений. Линейные неравенства с двумя переменными. Способ подстановки и способ сложения.
Функция, линейная функция и ее график, вычисление функции по формуле.
Статистические характеристики: медиана, среднее арифметическое, мода, размах.
Степень, умножение и деление степеней.
Стандартный вид одночлена и многочлена. Умножение одночленов, одночлена на многочлен, многочлена на многочлен. Возведение одночлена в степень. Сложение и вычитание многочленов. Преобразование целого выражения в многочлен. Разложение многочлена на множители.
Квадрат суммы и квадрат разности. Возведение в квадрат разности и суммы двух выражений. Разложение на множители разности квадратов, суммы и разности кубов.

Подробные ответы с комментариями по алгебре за 7 класс помогут школьникам вспомнить пройденный материал: различные действия с дробями и целыми числами, решение текстовых задач, поиск корня уравнения. Но главное, решебник станет надежным советчиком в изучении новых тем, которые впервые вводятся с 7 класса. Это операции с многочленами, решение системных уравнений с двумя переменными, построение графиков функций.

Мы уверены, что учебное пособие от Ответкина поможет полюбить новый предмет – алгебру. С его помощью школьники разберутся в пропущенных темах, подтянут успеваемость, будут уверены в правильности выполнения упражнений.

Умножение матриц — MathBootCamps

Хотя сложение или вычитание матриц относительно просто, умножение матриц сильно отличается от большинства математических операций, которые вы изучали ранее. Здесь мы рассмотрим хороший способ умножения двух матриц и некоторые важные свойства, связанные с ним. Вы также узнаете, как узнать, когда умножение не определено.

Содержание:

Умножение двух матриц: «строки попали в столбцы» (анимация этого)
Умножение матриц не всегда определено
Умножение матриц не является коммутативным

Примеры умножения матриц
Краткое описание свойств

Умножение двух матриц: «строки попадают в столбцы»

Чтобы понять общую схему умножения двух матриц, подумайте «строки попадают в столбцы и заполняют строки». Рассмотрим следующий пример.

Первая строка «соответствует» первому столбцу, что дает нам первую запись продукта. Обратите внимание, что поскольку это произведение двух матриц 2 x 2 (количество строк и столбцов), результатом также будет матрица 2 x 2. Мы рассмотрим, как размер матрицы влияет на это позже в статье.

Теперь первая строка «соприкасается» со второй колонкой, заполняя строку продукта.

Закончились столбцы для «попадания», теперь работаем со второй строкой.

Осталось вычислить последнюю запись. Вторая строка теперь «поразит» второй столбец.

Наконец, нам просто нужно выполнить арифметические действия, чтобы получить окончательный ответ.

Анимация этого процесса

Вы можете увидеть анимацию этого процесса здесь. Звука нет — так что не беспокойтесь о поиске наушников!

Вскоре мы увидим еще пару примеров, но сначала нам нужно обсудить, как размер матрицы влияет на результат умножения. На самом деле бывают случаи, когда из-за размера матрицы умножение не определено.

Умножение матриц не всегда определено

При умножении матриц размер двух задействованных матриц определяет, будет ли произведение определено. Вы также можете использовать размеры, чтобы определить результат умножения двух матриц. Напомним, что размер матрицы — это количество строк на количество столбцов. Приведенные выше матрицы были 2 x 2, поскольку каждая из них имела 2 строки и 2 столбца.

Как видите, размеры матриц не обязательно должны быть одинаковыми, вам просто нужно, чтобы совпадали средние два числа, когда вы записываете размеры рядом. В противном случае продукт не определен.

Подумайте вот о чем: если, например, матрица A имеет размер 3 x 4, то произведение A и самой себя не будет определено, так как внутренние числа не будут совпадать. Это всего лишь один пример того, как умножение матриц ведет себя не так, как вы могли бы ожидать.

Умножение матриц не коммутативно

Из начальной школы вы знаете, что произведение (2)(3) = (3)(2). Неважно, в каком порядке вы умножаете числа, результат один и тот же. Это не работает вообще для матриц. Только в особых случаях можно сказать, что АВ = ВА. Так что в целом следует считать, что они не равны. Может быть даже так, что AB определено, а BA не определено!

Даже если произведение определено, маловероятно, что результаты для AB и BA будут одинаковыми.

Примеры перемножения матриц

Теперь, когда мы рассмотрели некоторые важные свойства умножения матриц, давайте рассмотрим пару примеров.

Пример

Найдите произведение AB, где:
$A = \left[\begin{array}{cc} -5 & 3\\ -4 & -1\\ \end{array}\right]$
и
$ B = \left[\begin{массив}{cc} 1 & -1\\ 2 & 6\\ \end{массив}\right]$

Решение

Помните, что строки пересекаются со столбцами и заполняют строки. Здесь каждая матрица имеет размер 2 x 2, поэтому результатом будет матрица 2 x 2.

$\begin{align} AB &= \left[\begin{array}{cc} -5 & 3\\ -4 & -1\\ \end{array}\right] \left[\begin{array} {cc} 1 & -1\\ 2 & 6\\ \end{массив}\right]\\ &= \left[\begin{массив}{cc} -5(1) + 3(2) & -5 (-1) + 3(6)\\ -4(1) +(-1)(2) & (-4)(-1)+(-1)(6)\\ \end{массив}\right ]\\ &= \boxed{\left[\begin{array}{cc} 1 & 23\\ -6 & -2\\ \end{массив}\right]}\end{align}$

Пример

Найдите произведение AB, где:

$A = \left[\begin{array}{cccc} -2 & -1 & 0 & 0 \\ 1 & 2 & 1 & 1\\ \end{array}\right ]$
и
$B = \left[\begin{array}{cccc} 3 & 1 & 1 & 2 \\ -1 & -1 & 0 & 1\\ \end{array}\right]$

Решение

Здесь у нас есть матрица 2 x 4, умноженная на матрицу 2 x 4. Внутренние номера этих размеров не совпадают, поэтому:

$\boxed{AB \text{не определено}}$

Пример

Найдите произведение AB, где:
$A = \left[\begin{array}{cc} 1 & 2\\ -2 & 0\\ 3 & 1\\\end{array}\right]$

и
$B = \left[\begin{array}{cc} 4 & 0\\ 0 & 1\\ \end{array}\right]$

Решение

Произведение матрицы 3 x 2 и матрицы 2 x 2. Внутренние числа совпадают, поэтому продукт определен. В результате получится матрица 3 х 2.

$\begin{align} AB &= \left[\begin{array}{cc} 1 & 2\\ -2 & 0\\ 3 & 1\\\end{array}\right]\left[\begin {array}{cc} 4 & 0\\ 0 & 1\\ \end{array}\right]\\ &= \left[\begin{array}{cc} 1(4) + 2(0) & 1 (0) + 2(1)\\ -2(4) + 0(0) & -2(0) + 0(1)\\ 3(4) + 1(0) & 3(0) + 1( 1)\\\end{массив}\right]\\ &= \boxed{\left[\begin{array}{cc} 4 & 2\\ -8 & 0\\ 12 & 1\\\end{массив }\right]}\end{выравнивание}$

Резюме

Всегда помните следующее при перемножении двух или более матриц.

Строки попадают в столбцы и заполняют строки.
Умножение матриц не всегда определено – сначала проверьте размеры матриц!
Умножение матриц вообще не является коммутативным.

Подпишитесь на нашу рассылку!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.

Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), сообщающие о новинках!

Как умножать матрицы? С Примерами

Умножение матриц является одной из фундаментальных, но продвинутых концепций матриц. Вы должны быть осторожны при умножении матриц. Это не так просто, как кажется. Вы должны хорошо знать все основные понятия, такие как, что такое матрица, строки и столбцы в матрице, как представлять матрицу и как умножать матрицы.

Снова в школу: Матрицы — это группы чисел, переменных, символов или выражений в прямоугольной таблице с различным количеством строк и столбцов. Это прямоугольные массивы с различными операциями, такими как сложение, умножение и транспонирование. Элементами матрицы являются числа или элементы, составляющие матрицу. Горизонтальные элементы матриц — это строки, а вертикальные — столбцы.

Количество строк и столбцов можно изобразить с помощью переменных. Например, пусть количество строк в матрице K равно «m», а количество столбцов — «n». Таким образом, мы можем представить матрицу K как [K] _{м х п} . Матрица представлена в квадратных скобках «[]» с произведением ее строк и столбцов в нижнем индексе.

До 1812 года человечеству не было известно умножение матриц. Филипп Мари Бине, французский математик, изобрел умножение матриц в 1812 году для описания линейных карт с матрицами. Он обнаружил, что умножение матриц является бинарной операцией. Две матрицы перемножаются, образуя одну матрицу.

Далее в этой статье вы узнаете правила и основные принципы умножения матриц.

Что такое умножение матриц?

Во введении к этой статье вы прочитали, что умножение матриц — это бинарная операция. Это означает, что всякий раз, когда вы находите произведение двух или более матриц, ответом является единственная матрица, следующая за исходными матрицами. Для перемножения двух матриц проверяется их совместимость. Это означает, что две матрицы должны следовать набору правил для умножения.

Эти параметры совместимости описаны ниже:

Значение количества столбцов в матрице один должно быть равно значению количества строк в матрице 2.
Если вышеуказанное условие не выполняется, матрицы нельзя перемножать.
Если матрицы являются квадратными матрицами одного порядка, их можно умножать друг на друга.
Квадратную матрицу 2 x 2 нельзя умножить на квадратную матрицу 3 x 3. Ее можно умножить на другую квадратную матрицу 2 x 2.

Давайте рассмотрим пример, чтобы лучше понять это:

Пример 1: Предположим, у нас есть две матрицы, K и L. Порядок матриц задан как m x n и n x o соответственно. Выяснить, можно ли перемножать матрицы?

Решение: Дано

Матрица 1 = [ K ] _{m x n}

Матрица 2 = [ L ] _{n x o}

Мы видим, что количество столбцов в матрицах равно количеству строк K матрица L. Следовательно, две матрицы можно перемножить.

Результирующая матрица: Матрица, полученная путем умножения двух матриц, является результирующей матрицей. Эта матрица может быть представлена как:

Название матрицы в квадратных скобках
Произведение количества строк матрицы 1 на количество столбцов матрицы два в порядке.

Снова обратимся к приведенному выше примеру:

Мы знаем, что K и L совместимы с умножением. Таким образом, результирующая матрица, скажем, D, будет = [D] _{m x o}, где m = количество строк матрицы один и o = количество столбцов матрицы 2.

Пример 2: Матрица [ K ] _{2 x 4} умножается на матрицу [ X ] _{4 х 2} . Если [ Y ] результирующая матрица, то каков порядок Y.

Решение: Нам дано

Матрица 1 = [ K ] _{2 x 4}

Матрица 2 = [ X ] _{4 x 2}

Поскольку количество столбцов матрицы K равно количеству строк матрицы X, K и X можно перемножить. Следовательно,

Матрица Y = [ Y ] _{2 x 2}

Порядок матрицы Y равен 2 x 2. Y — квадратная матрица.

Ориентация двух матриц также является решающим фактором для определения произведения матриц. Если есть две матрицы, K и L, то чтобы найти произведение K и L, вы должны сначала написать матрицу K, а затем написать матрицу L. Если вы запишете матрицу L перед матрицей K, вы получите совершенно другую матрицу . Коммутативный закон не применяется при умножении матриц. Это означает, что KL ≠ LK.

Теперь, когда мы разобрались с правилами умножения двух матриц, давайте научимся умножать матрицы.

Как умножать матрицы?

Давайте изучим пошаговую процедуру умножения двух матриц. Поначалу это может показаться вам запутанным, но когда вы освоитесь, перемножать матрицы так же просто, как намазать маслом свой тост.

Шаг 1: Проверьте совместимость предоставленных матриц. Если они несовместимы, оставьте умножение.

Шаг 2: Возьмите первую строку матрицы 1 и умножьте ее на первый столбец матрицы 2. Затем умножьте первую строку матрицы 1 на 2-й столбец матрицы 2. Теперь умножьте первую строку матрицы 1 на 3-й столбец матрицы 2 и так далее. Полученные из них значения заполнят первую строку матрицы продукта.

Шаг 3: Теперь возьмите вторую строку матрицы 1 и умножьте ее на первый столбец матрицы 2 и выполните те же шаги, что и для 2. Это заполнит вторую строку матрицы произведения.

Шаг 4: Продолжайте эти шаги, выполняя каждую строку, пока не будет получена матрица произведения.

Под умножением строк и столбцов мы подразумеваем, что элементы, присутствующие в этих строках и столбцах, будут умножены. Не забудьте умножить соответствующие элементы, а затем добавить продукты, чтобы найти элемент матрицы продукта.

Если вы не уверены в шагах, посмотрите на пример пошагового решения ниже:

Пример: Найдите произведение матриц, приведенных ниже:

K = и L =

Решение:

Шаг 1: Матрица K имеет порядок 1 x 4, а матрица L имеет порядок 4 x 2. Поскольку количество столбцов матрицы K соответствует количеству строк матрицы L, поэтому матрицы совместимы для умножения. Полученная матрица имеет порядок 1 x 2.

Шаг 2: Поскольку K имеет только 1 строку, умножьте ее на первый столбец матрицы L следующим образом: (2 x 4) + (4 x 5) + (1 x 4) + (7 x 3) = 51. Обратите внимание, как 1-й элемент строки умножается на 1-й элемент столбца 1, аналогично 2-му, 3-му и 4-му. Затем они складываются вместе, чтобы получить результирующий матричный элемент.

Шаг 3: Теперь аналогичным образом умножьте 1-ю строку на второй столбец матрицы L. Результат будет (2 x 3) + (4 x 2) + (1 x 9) + (7 x 6) = 65. .

Шаг 4: Разместите результат в матрице продуктов. Предположим, что [ X ] — результирующая матрица; следовательно, X = [51 65].

Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).

Как умножить матрицу 2 x 2

Для умножения матриц 2 x 2 вы должны хорошо знать шаги, описанные в предыдущем разделе. Поскольку мы перемножаем 2 квадратные матрицы одного порядка, нам не нужно проверять совместимость в этом случае. Помните, что матрица произведения также будет иметь тот же порядок, что и квадратная матрица. Давайте решим пример, чтобы понять, как умножить матрицу 2 x 2.

Пример: Умножить квадратную матрицу на

A = и B =

Шаг 1: Умножая первую строку матрицы A на первый столбец матрицы B. Получаем (2 x 1) + (9 x 3) = 29. Теперь умножаем первую строку матрицы A со вторым столбцом матрицы B. Получаем (2 x -4) + (9 x 7) = -8 + 63 = 55.

Шаг 2: Повторим шаг 1, но изменим строку матрица A. Первый и второй столбцы матрицы B будут умножены на строку 2 матрицы A. Результатом будет

(3 x 1) + (-7 x 3) = 3 – 21 = -18, и (3 x -4) + (-7 х 7) = -12 – 49= -61

Шаг 3: Разместите результаты правильно

Следовательно, результирующая матрица C =

Точно так же вы можете решать квадратные матрицы, такие как 3 x 3, 4 x 4 и так далее.

Как умножить столбец на число в Excel (2 простых способа)

Хотя Excel является мощным инструментом анализа данных, многие пользователи используют его для основных арифметических операций.

Одним из распространенных требований является умножение всего столбца на число (постоянное значение).

В этом уроке я покажу вам два простых способа умножить целый столбец с заданным числом .

Итак, приступим!

Это руководство охватывает:

Умножение столбца на число с помощью формулы (жесткое кодирование значения в формуле)

Предположим, у меня есть набор данных, как показано ниже, где у меня есть имена торговых представителей в столбце A и их текущие значения продаж в столбце B.

Я хочу рассчитать их план продаж на следующий год, который будет на 10% выше их текущих продаж.

По существу это означает, что я хочу увеличить все значения в столбце B на 10 % (т. е. умножить эти значения на 1,1 или 110 %)

Жестко закодировать значение в формуле

Ниже приведена формула для умножения 110 % на значения во всем столбце B2 (используйте эту формулу в ячейке C2):

 =B2*110%

Приведенная выше формула даст вам результат умножения значения в ячейках B2 на 110%.

Но мы также хотим получить результат, когда все значения в столбце B умножаются на одно и то же число.

Для этого выделите ячейку C2, поместите курсор в правую нижнюю часть выделения, удерживайте левую клавишу мыши и перетащите вниз. Это скопирует одну и ту же формулу для всех ячеек в столбце C.

Кроме того, вы также можете скопировать ячейку C2 и вставить ее в ячейки под ней (подойдет простое сочетание клавиш Control +C и Control + V).

Обратите внимание, что результат формулы является динамическим. Поэтому, если вы измените значения в столбце B, результат соответственно обновится. Если вы не хотите, чтобы это было динамически, а вместо этого хотите статические значения, вы можете преобразовать формулу в значения.

Умножить весь столбец на значение в ячейке

В приведенном выше примере я жестко закодировал значение 110% в формуле.

Другой вариант — иметь значение, на которое я хочу умножить весь столбец, в отдельной ячейке и использовать ссылку на ячейку вместо жесткого кодирования фактического значения в формуле.

Преимущество этого метода в том, что если я изменю значение в ячейке, формулы автоматически обновятся.

Ниже у меня есть тот же набор данных, и у меня есть новый целевой процент продаж в ячейке E2.

Ниже приведена формула, которая даст мне новый план продаж:

 =B2*$E$2

Чтобы умножить весь столбец, вам нужно скопировать ячейку с формулой и вставить ее во все ячейки столбца. . Это также скопирует формулу и даст вам правильный результат.

Как это работает?

Хитрость этого метода заключается в использовании знаков доллара в ссылке на ячейку, содержащую число, на которое мы хотим умножить весь столбец (в данном примере это $E$2).

Когда вы добавляете знак доллара перед номером строки и алфавитом столбца, это гарантирует, что при копировании этой формулы в другие ячейки ссылка не изменится.

В нашей формуле часть формулы $E$2 не изменится, в то время как A2 станет A3, если формула будет скопирована в ячейку C3, и станет A4, если формула будет скопирована в ячейку C4, и так далее.

Примечание. Если вы используете Excel для Microsoft 365, где у вас есть доступ к динамическим массивам, вы можете просто использовать формулу =B2:B13*E2. Не нужно копировать для всего столбца, сама формула рассыпает результат на весь диапазон.

Несколько столбцов с номером с использованием специальной вставки

Другой метод, который можно использовать для быстрого умножения всего столбца с заданным числом, — использование специальной техники вставки.

Предположим, у вас есть набор данных, как показано ниже, где я хочу умножить число в ячейке E2 на весь набор данных в столбце A.

Ниже приведены шаги для этого:

Скопируйте все значения в столбце B и вставьте его в столбец C. Мы делаем это, поскольку умножение специальной вставки будет применено к столбцу C, и мы также сохраним исходные значения в столбце B.

Скопируйте ячейку E2 (вы можете выбрать ее и использовать Control + C, или вы можете щелкнуть ее правой кнопкой мыши, а затем нажать «Копировать».

Выделите все ячейки в столбце A, с которыми вы хотите умножить номер

Щелкните правой кнопкой мыши выбранные ячейки и выберите параметр «Специальная вставка».

Приведенные выше шаги мгновенно изменят все значения в столбце A и дадут вам результат после умножения этих чисел на значение в ячейке E2.

В результате вы получаете статические значения (по сравнению с формулой, которую вы получаете в методе до этого)

Когда вы закончите с умножением, вы можете удалить значение в ячейке E2 (если хотите).

При использовании этого метода важно отметить, что когда вы умножаете весь столбец с помощью специального метода вставки, он также копирует форматирование из ячейки E2. Поэтому, если вы зададите цвет ячейки для ячейки E2 и используете этот метод, все ячейки в столбце A также будут скопированы в него. Чтобы избежать этого, вы также можете выбрать параметр «Значение» в диалоговом окне «Специальная вставка» на шаге 4 9. 0003

Вот два простых метода, которые можно использовать для умножения целого столбца на число в Excel.

Надеюсь, этот урок был вам полезен.

Другие учебные пособия по Excel, которые могут оказаться полезными:

Как копировать и вставлять формулы в Excel без изменения ссылок на ячейки
Как применить формулу ко всему столбцу в Excel (5 простых способов)
Как выделить весь столбец Столбец (или строка) в Excel — ярлык
Применить условное форматирование на основе другого столбца в Excel
Как скопировать и вставить столбец в Excel?

Power BI Умножьте измерения на примерах

6 сентября 2021 г. 2 сентября 2021 г.

В этом учебном пособии по Power BI мы узнаем все о Power BI Измерение, умноженное на . Также мы обсудим:

Измерение Power BI, умножение двух столбцов с использованием DAX

Измерение Power BI, умножение на 100
Измерение Power BI, умножение двух столбцов из разных таблиц
Power BI Измерение умножения столбца на измерение

Power BI Измерение умножения

В Power BI в DAX нет функции умножения. Мы используем арифметическую функцию (Звездочка) ‘ * ’ для умножения.

Когда мы передаем любой аргумент в виде строки, он автоматически преобразуется в числа.

давайте рассмотрим пример, здесь мы возьмем два аргумента в виде строк.

 Умножение = "5"*"10"

Power BI Измерение умножения

Power BI Измерение умножения двух столбцов с использованием DAX

В Power BI оператор умножения возвращает значение умножения двух чисел.

Синтаксис умножения:

 ( * )

Например, мы создали простую таблицу, как показано ниже:

Power BI Measure умножить два столбца

Теперь создадим показатель для расчета умножение двух значений:

 Умножение = РАСЧЕТ(СУММ('Таблица'[значение-1])) * СУММ('Таблица'[значение-2])

Power BI Измерение умножить на

Мы можем вычислять умножение не только положительных чисел, но и отрицательных, как показано в таблице.

Вот как вычислить умножение с помощью Power BI Measure.

Считать количество мер Power bi с фильтром

Мера Power BI, умноженная на 100

Теперь мы увидим, как создать меру, которая вернет результат, умноженный на 100.

Для этого здесь мы создали таблицу, подобную приведенной ниже. :

Измерение Power BI умножить на 100

Теперь мы создадим меру, которая будет вычислять, если год больше или равен 2020, то сумма инвестиций умножится на 100. В противном случае она останется прежней.

 Сумма прибыли = IF(SELECTEDVALUE('Таблица инвестиций'[Год]) >= 2020, ВЫЧИСЛИТЬ (SELECTEDVALUE('Таблица инвестиций'[Инвестиции]) * 100, ФИЛЬТР('Таблица инвестиций', 'Таблица инвестиций'[Год] >= 2020)), SELECTEDVALUE('Таблица инвестиций'[Инвестиции]))

Показатель Power BI умножить на 100

За исключением тех лет (которые меньше 2020), все суммы были увеличены, т.е. умножены на 100 от суммы инвестиций.

Вот как вычислить Меру Power BI, умножить на 100.

Прочитать функцию Countif в Мере Power BI

Меру Power BI, умножить два столбца из разных таблиц

Теперь мы увидим, как вычислить умножение между двумя столбцы из разных таблиц. Вот пошаговые инструкции по реализации этого.

Шаг 1:

Например, мы создали две простые таблицы. Один основан на идентификаторе продукта и количестве. Другой основан на деталях продукта, таких как идентификатор, имя и цена.

Таблица 1 – Таблица продуктов

Вычислить меру, умножив ее на два столбца

Таблица 2 – Сведения о продукте Информация.

В Power BI выберите представление модели > Таблица продуктов > дополнительные параметры > управление взаимосвязью

Измерьте умножение двух столбцов из разных таблиц в Power BI

Откроется страница управления взаимосвязью. Нажмите на Новый . Здесь мы создадим связь между ProductID (из таблицы Product) и ID (сведения о продукте). Затем нажмите OK .

Измерение умножения двух столбцов из разных таблиц в Power BI

Теперь мы можем видеть, что между этими двумя таблицами создается связь, подобная этой: создайте меру для вычисления умножения двух столбцов из разных таблиц.

 Мера = SUM('Таблица продуктов'[Количество])* SUM('Сведения о продукте'[Цена])

Мера Power BI умножает два столбца из разных таблиц

Мы видим, что мера вычислила общую сумму путем умножения цены и количество продуктов из двух разных таблиц.

Вот как с помощью меры Power BI выполнить расчет для умножения двух столбцов из разных таблиц .

Чтение оператора Power bi Measure Switch

Power BI Measure, умножить столбец на Measure

Теперь мы увидим, как создать меру, которая возвращает умножение столбца в Power BI. Для этого мы создали простую таблицу, основанную на идентификаторе продукта, количестве, цене за единицу, прибыли, как показано ниже:

Показатель Power BI умножить столбец на показатель

Сначала мы создадим показатель, который будет вычислять общую цену продукта.

общая цена = SUM('Таблица товаров'[Количество]) * SUM('Таблица товаров'[Цена за единицу]) и общая цена (мера).

 Новая мера = СУММ ( 'Таблица продуктов', [общая цена] * СУММА ( [прибыль])) )

Умножить столбец на показатель с помощью показателя Power BI

Вот как мы можем умножить столбец на показатель с помощью показателя Power BI .

Вам могут понравиться следующие учебные пособия по Power BI:

Разделение показателя Power BI
Дата измерения Power BI
Измерение суммы Power BI
Измерение мощности Bi по категориям
Измерение Power BI IF с примерами
Вычитание меры Power bi

Заключение

Из этого руководства по Power BI мы узнали следующие темы:

Что такое Power BI Measure Multiple?
Как выполнить умножение между двумя столбцами с помощью DAX в измерении Power BI?
Как вычислить показатель Power BI, умноженный на 100?
Как оценить умножение двух столбцов из разных таблиц в Power BI Measure?
Как рассчитать столбец умножения на показатель с помощью меры Power BI?

Бхавана Ратор

Бхавана Ратор — Microsoft MVP (3 раза в Office Apps & Services) и увлеченный консультант по SharePoint, имеющий около 10 лет опыта работы в сфере ИТ в отрасли, а также в технологиях .

Net. Ей нравится делиться своим техническим опытом на сайтах EnjoySharePoint.com и SPGuides.com

Умножение матриц в Excel (5 примеров)

Матрица — важный инструмент, который ежедневно используется в статистике и научных исследованиях. Электронные таблицы Excel сами по себе представляют собой очень большие матрицы, содержащие 1 048 576 строк и 16 384 столбца. Неудивительно, что Excel предоставляет несколько полезных инструментов для матричных операций. В этой статье мы сосредоточимся на 9Умножение матриц 0146 в Excel с разными примерами разных сценариев.

Скачать практическую рабочую тетрадь

Как выполнить умножение матриц?

5 подходящих примеров для умножения матриц в Excel

1. Матричное умножение двух массивов

2. Умножьте один столбец на один массив строк

3. Умножение массива одной строки и одного столбца в Excel

4. Вычислить квадрат матрицы из умножения матриц

Умножение матрицы на скаляр.

Ошибки при умножении матриц в Excel

Ограничение умножения матриц в Excel

Вывод

Статьи по Теме

Загрузить рабочую тетрадь

Вы можете загрузить книгу, содержащую все примеры, использованные в этой статье, из поля ниже.

Как выполнять умножение матриц?

Во-первых, давайте сосредоточимся на том, как на самом деле работает умножение матриц. Если есть две матрицы размерности i x j и j x k каждый элемент первой строки будет умножен на элементы их соответствующих входных номеров из первого столбца второй матрицы. Затем все добавленные результаты будут указывать значение элемента первой строки и первого столбца результирующей матрицы, взяв номер строки из первой матрицы и номер столбца из второй. Это будет продолжаться 90 146 i x k 90 147 раз и приведет к матрице 90 146 i x k 90 147.

Давайте возьмем пример, где мы добавляем две матрицы A и B.

Каждая запись из первой строки матрицы A будет умножаться на соответствующие записи из первого столбца матрицы B. Тогда результат даст нам значение 1×1 умноженной матрицы, скажем, C. В этом примере это будет 1 *4+2*6+3*8=40.

Тот же процесс повторяется для 1-й строки из A и 2-го столбца из B, 2-й строки из A и 1-го столбца из B, 2-й строки из A и 2-го столбца из B.

Наконец, результат будет выглядеть примерно так.

Это произведение матрицы А и В.

5 подходящих экземпляров для умножения матриц в Excel

Excel имеет встроенную функцию МУМНОЖ для умножения матриц. Эта функция принимает в качестве аргументов два массива. Мы можем использовать матрицы в качестве массивов аргументов в этой функции, чтобы получить желаемый результат.

1. Матричное умножение двух массивов

Возьмем две отдельные матрицы A и B. В Excel мы будем рассматривать их как массивы для умножения матриц.

Шаги:

Сначала выберите ячейки, в которые вы хотите поместить свою матрицу.

Затем запишите следующую формулу.

=МУМНОЖ(B5:D7,B10:D12)

Теперь на клавиатуре нажмите Ctr+Shift+Enter . Вы получите результат матрицы AxB.

Вы можете сделать то же самое для матрицы BxA, введя матрицу B в качестве первого и матрицу A в качестве второго аргумента ММУЛЬМ функция.

Подробнее: Как умножить 3 матрицы в Excel (2 простых метода)

2. Умножение одного столбца на массив одной строки

Возьмем следующий набор данных с матрицами, содержащими только один столбец и одну строку.

Перемноженная матрица AxB будет результатом умножения матриц с одним столбцом и одной строкой.

Шаги:

Сначала выберите диапазон ячеек для перемножаемой матрицы.

Затем запишите следующую формулу.

=МУМНОЖ(B5:B7,B10:D10)

Наконец, нажмите Ctrl+Shift+Enter на клавиатуре. У вас получится результирующая матрица.

Подробнее: Как умножить несколько ячеек в Excel (4 метода)

Аналогичные показания

Как умножать столбцы в Excel (9Полезные и простые способы)
Умножение двух столбцов в Excel (5 самых простых способов)
Как использовать функцию умножения в Excel (с 3 альтернативными методами)
Если ячейка содержит значение, умножьте его с помощью формулы Excel (3 примера)

3. Умножение массива одной строки и одного столбца в Excel

Для того же набора данных, который использовался в предыдущем методе, матричное умножение BxA будет означать умножение матриц из одной строки и одного столбца.

Шаги:

Сначала выберите ячейку. Это умножение даст только одно значение, поэтому выберите здесь одну ячейку.

Затем введите следующую формулу.

=МУМНОЖ(B10:D10,B5:B7)

Теперь нажмите Ctrl+Shift+Enter на клавиатуре. Вы получите желаемый результат.

Подробнее: Формула умножения в Excel (6 быстрых подходов)

4. Вычисление площади матрицы путем умножения матриц

Вернемся к матрицам на примерах, использованных в первом примере. Здесь мы воспользуемся умножением матриц, чтобы определить квадраты матриц A и B.

Шаги:

Выберите диапазон ячеек для вашей квадратной матрицы.

Теперь запишите следующую формулу.

=МУМНОЖ(B5:D7,B5:D7)

Теперь нажмите Ctrl+Shift+Enter на клавиатуре. У вас получится квадрат матрицы А.

Можно заменить диапазон матрицы A на диапазон матрицы B (B10:D12) и получить квадрат матрицы B тоже.

Подробнее: Что такое формула умножения в Excel для нескольких ячеек? (3 направления)

Аналогичные показания

Как умножить столбец на число в Excel (4 простых метода)
Умножение на проценты в Excel (4 простых способа)
Как умножить столбец в Excel на константу (4 простых способа)
Умножение двух столбцов, а затем суммирование в Excel

5. Умножение матрицы на скаляр

Когда матрица умножается только на число, все элементы матрицы умножаются на это число. Это также может быть достигнуто в Excel.

Для демонстрации я использую здесь матрицу A и умножаю ее на 7.

Шаги:

Выберите диапазон ячеек для перемножаемой матрицы.

Затем введите в поле следующую формулу.

=B5:D7*G7

Нажмите Ctrl+Shift+Enter на клавиатуре.

Подробнее: Как умножать в Excel: столбцы, ячейки, строки и числа

Ошибки при умножении матриц в Excel

Существует несколько ошибок, с которыми вы можете столкнуться при выполнении умножения матриц в Excel.

Из них #ЗНАЧЕНИЕ! Ошибка может возникнуть, если количество столбцов в первом массиве и количество строк во втором массиве не совпадают.

Вы получите ту же ошибку, если в ячейке массива есть хотя бы одно нечисловое значение.

Если вы выберете больше значений, чем выглядит ваша предполагаемая матрица умножения, у вас будет ошибка #N/A , но только в дополнительных выбранных вами ячейках.

Подробнее: Как делить и умножать в одной формуле Excel (4 способа)

Ограничение умножения матриц в Excel

Если вы используете Excel 2003 или более раннюю версию, существует ограничение на умножение матриц размером 71×71. Но для более поздних версий вы можете выполнять операцию столько, сколько позволяет электронная таблица, ограничиваясь только оперативной памятью вашей системы.

Заключение

Это были разные ситуации, в которых вы можете выполнять умножение матриц в Excel. Надеюсь, вы нашли эту статью полезной и информативной. Если у вас есть какие-либо вопросы или предложения для нас, сообщите нам об этом ниже.

Дополнительные руководства, подобные этим, см. на веб-сайте Exceldemy.com .

Связанные статьи

Как составить таблицу умножения в Excel (4 метода)
Умножение одной ячейки на несколько ячеек в Excel (4 способа)
Как рассчитать ковариационную матрицу в Excel (с помощью простых шагов)
Создание тренировочной матрицы в Excel (3 простых метода)
Как создать матрицу прослеживаемости в Excel
Создание корреляционной матрицы в Excel (2 удобных подхода)

Как написать агрегатную функцию умножения на языке SQL — Java, SQL и jOOQ.

Все знают агрегатную функцию SQL SUM() (и многие также знают ее вариант оконной функции). При запросе базы данных Sakila мы можем получить ежедневный доход (используя синтаксис PostgreSQL):


С р КАК (
  ВЫБРАТЬ
    CAST (дата_платежа AS DATE) AS дата,
    количество
  ОТ оплаты
)
ВЫБРАТЬ
  свидание,
  SUM (сумма) AS daily_revenue,
  SUM (СУММА (сумма)) OVER (ORDER BY date) AS cumulative_revenue
С р
СГРУППИРОВАТЬ ПО дате
ЗАКАЗАТЬ ПО дате

Результат будет выглядеть примерно так:

дата |daily_revenue |cumulative_revenue
-----------|---------------|----
2005-05-24 |290,92 |29,92
2005-05-25 |573,63 |603,55
2005-05-26 |754,26 |1357,81
2005-05-27 |685,33 |2043,14
2005-05-28 |804.04 |2847.18
2005-05-29 |648,46 |3495,64
2005-05-30 |628.42 |4124.06
2005-05-31 |700,37 |4824,43
2005-06-14 |57,84 |4882,27
...

То же самое с умножением

Это уже весьма полезно. Однако очень редко нам нужно объединять несколько значений не в сумму (через сложение), а в произведение (через умножение). Недавно я наткнулся на такой случай на Stack Overflow. Вопрос хотел достичь следующего результата:

накопленный коэффициент даты
---------------------------------------
10 января 1986 г. ноль 1000
13 января 1986 г. -0,026595745 973.4042548
14 января 1986 г. 0,005464481 978,7234036
15 января 1986 г. -0,016304348 962,7659569
1986-01-16 0 962,7659569
1986-01-17 0 962,7659569
1986-01-20 0 962,7659569
1986-01-21 0,005524862 968,0851061
1986-01-22 -0,005494506 962,765957
1986-01-23 0 962.765957
1986-01-24 -0,005524862 957,4468078
1986-01-27 0,005555556 962,7659569
1986-01-28 0 962.7659569
1986-01-29 0 962,7659569
1986-01-30 0 962,7659569
1986-01-31 0,027624309 989,3617013
1986-02-03 0,016129032 1005,319148
1986-02-04 0,042328041 1047,872338
1986-02-05 0,04568528 1095,744679

Если бы это была электронная таблица Microsoft Excel, столбец НАКОПЛЕННОЕ просто начинался бы с 1000 и имел бы следующую формулу во всех остальных строках:

накоплено (i) = накоплено (i - 1) * (1 + фактор)

Другими словами (значения усечены для простоты):

1000,0 = начало
 973,4 = 1000,0 * (1 - 0,026)
 978,7 = 973,4 * (1 + 0,005)
 962,7 = 978,7 * (1 - 0,016)
 962,7 = 962,7 * (1 - 0,000)
 962,7 = 962,7 * (1 - 0,000)
 962,7 = 962,7 * (1 - 0,000)
 968,0 = 962,7 * (1 + 0,005)
 . ..

Это захватывающе, потому что нам требуется не только мультипликативная агрегация, но даже кумулятивная мультипликативная агрегация. Итак, еще одна оконная функция. Но, к сожалению, SQL не предлагает MUL() агрегатная функция, даже если бы ее было относительно просто реализовать. У нас есть два варианта:

Реализация пользовательской агрегатной функции (следите за будущим сообщением в блоге)
Использование трюка путем суммирования логарифмов вместо непосредственного умножения операндов

Мы реализуем последнее на данный момент. Загляните на этот крутой сайт Википедии о логарифмических тождествах, которому мы будем слепо доверять. В середине имеем:

б ^х * б ^у = б ^{х + у}

Что приводит к:

log _b (x * y) = log _b (x) + log _b (y)

Как это круто? И поэтому:

x * y = b ^{log _b (x) + log _b (y)}

Таким образом, мы можем определить любое умножение в терминах множества возведений в степень по некоторому основанию (скажем, 9). 1111 e ) и логарифмы по некоторому основанию (например, e ). Или в SQL:

х * у = EXP (LN (х) + LN (у))

Или, как агрегатная функция:

МУЛЬМ(х) = ЕХР(СУММ(LN(х)))

Хе! Таким образом, наша первоначальная проблема может быть очень легко решена с помощью этого, как показано в моем ответе на переполнение стека:


ВЫБРАТЬ
  свидание,
  фактор,
  1000 * (EXP(СУММ(LN(1 + ОБЪЕДИНЕНИЕ(множитель, 1)))
       БОЛЕЕ (ЗАКАЗАТЬ ПО дате)) - 1) КАК НАКОПЛЕНО
ИЗ т

И мы получаем хороший результат, как показано ранее. Возможно, вам придется заменить LN() на LOG() в зависимости от вашей базы данных.

Внимание: отрицательные числа

Попробуйте запустить это:


ВЫБЕРИТЕ ЛН(-1)

Ты получишь:

Ошибка SQL [2201E]: ОШИБКА: невозможно логарифмировать отрицательное число

Логарифмы определены только для строго положительных чисел, если только ваша база данных не поддерживает обработку комплексных чисел. В случае чего одно нулевое значение все равно нарушило бы агрегацию. Но если ваш набор данных содержит только строго положительные числа, все будет в порядке — плюс-минус некоторые ошибки округления с плавающей запятой. Или вы выполните некоторую обработку знаков, которая выглядит следующим образом:


С v(i) КАК (ЗНАЧЕНИЯ (-2), (-3), (-4))
ВЫБРАТЬ
  КЕЙС
    КОГДА СУММА (СЛУЧАЙ, КОГДА i < 0, ТОГДА -1 КОНЕЦ) % 2 < 0
    ТОГДА -1
    ИНАЧЕ 1
  END * EXP(SUM(LN(ABS(i)))) умножение1
С в;

С v(i) КАК (ЗНАЧЕНИЯ (-2), (-3), (-4), (-5))
ВЫБРАТЬ
  КЕЙС
    КОГДА СУММА (СЛУЧАЙ, КОГДА i < 0, ТОГДА -1 КОНЕЦ) % 2 < 0
    ТОГДА -1
    ИНАЧЕ 1
  END * EXP(SUM(LN(ABS(i)))) умножение2
С в;

Вышеуказанная доходность

умножение1
--------------------
-23,999999999999993


умножение2
--------------------
119,99999999999997

Достаточно близко.

Внимание: ноль

Попробуйте запустить это:


ВЫБЕРИТЕ ЛН(0)

Ты получишь:

Ошибка SQL [2201E]: ОШИБКА: невозможно взять логарифм нуля

Ноль отличается от отрицательных чисел. Произведение с нулевым операндом всегда равно нулю, поэтому мы должны уметь с этим справляться. Мы сделаем это в два этапа:

Исключить нулевые значения из фактической агрегации, использующей EXP() и LN()
Добавить дополнительное выражение CASE , которое проверяет, равен ли какой-либо из операндов нулю

Первый шаг может не понадобиться в зависимости от того, как ваш оптимизатор базы данных выполняет второй шаг.


С v(i) КАК (ЗНАЧЕНИЯ (2), (3), (0))
ВЫБРАТЬ
  КЕЙС
    КОГДА СУММА (СЛУЧАЙ, КОГДА i = 0, ТОГДА 1 КОНЕЦ) > 0
    ТОГДА 0
    КОГДА СУММА (СЛУЧАЙ, КОГДА i < 0, ТОГДА -1 КОНЕЦ) % 2 < 0
    ТОГДА -1
    ИНАЧЕ 1
  END * EXP(SUM(LN(ABS(NULLIF(i, 0))))) умножение
С в;

Добавочный номер: DISTINCT

Вычисление произведения всех значений DISTINCT требует повторения ключевого слова DISTINCT в 2 из 3 приведенных выше сумм:


С v(i) КАК (ЗНАЧЕНИЯ (2), (3), (3))
ВЫБРАТЬ
  КЕЙС
    КОГДА СУММА (СЛУЧАЙ, КОГДА i = 0, ТОГДА 1 КОНЕЦ) > 0
    ТОГДА 0
    КОГДА СУММА (ОТЛИЧНЫЙ СЛУЧАЙ, КОГДА i < 0, ТОГДА -1 КОНЕЦ) % 2 < 0
    ТОГДА -1
    ИНАЧЕ 1
  END * EXP(SUM(DISTINCT LN(ABS(NULLIF(i, 0))))) умножение
С в;

Результат сейчас:

умножение |
---------------|
6 |

Обратите внимание, что первый SUM() , который проверяет наличие значений NULL , не требует ключевого слова DISTINCT , поэтому мы опускаем его для повышения производительности.

Расширение: оконные функции

Конечно, если мы сможем эмулировать агрегатную функцию PRODUCT() , мы хотели бы также превратить ее в оконную функцию. Это можно сделать, просто преобразовав каждое отдельное SUM() в оконную функцию:


С v(i, j) КАК (
  ЗНАЧЕНИЯ (1, 2), (2, -3), (3, 4),
         (4, -5), (5, 0), (6, 0)
)
ВЫБЕРИТЕ i, j,
  КЕЙС
    КОГДА СУММА (СЛУЧАЙ, КОГДА j = 0, ТОГДА 1 КОНЕЦ)
      БОЛЕЕ (ПОРЯДОК ПО i) > 0
    ТОГДА 0
    КОГДА СУММА (СЛУЧАЙ, КОГДА j < 0, ТОГДА -1 КОНЕЦ)
      ПРЕВЫШЕНИЕ (В ПОРЯДКЕ ПО i) % 2 < 0
    ТОГДА -1
    ИНАЧЕ 1
  КОНЕЦ * EXP(СУММ(LN(ABS(NULLIF(j, 0))))
    OVER (ORDER BY i)) умножение
С в;

Результат сейчас:

я |j |умножение |
--|---|--------------------|
1 | 2 |2 |
2 |-3 |-6 |
3 | 4 |-23,999999999999993 |
4 |-5 |119,99999999999997 |
5 | 0 |0 |
6 | 1 |0 |

Так круто! Совокупный продукт становится все больше и больше, пока не достигнет нуля, после чего он остается равным нулю.

3 класс — Умножение чисел в столбик. Двузначные на однозначные, задачи. Свойства и примеры

3 КЛАСС. ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.1

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

3 КЛАСС.

Умножение в столбик.

Что является основой умножения

Исследовательская работа детей

Этапы изучения умножения на многозначное число.

Задачи изучения умножения в курсе начальной школы

Использование свойств умножения

Алгоритм записи действия умножения в столбик

Упражнения для формирования навыка

Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»

ГДЗ по Алгебре 7 класс: Макарычев

Готовые домашние задания для 7 класса по алгебре Макарычева

Что такое Ответкин?

Уникальные подробные решения с пояснениями Ответкина

Почему наш сайт достойная альтернатива занятиям с репетитором?

Как пользоваться сайтом и открывать нужную задачу с комментариями?

Решебник алгебры седьмого класса к учебнику Ю.Н. Макарычева, Н.Г. Миндюка, К.И. Нешкова, С.Б. Суворова

Популярные решебники

Умножение матриц — MathBootCamps

Умножение двух матриц: «строки попадают в столбцы»

Анимация этого процесса

Умножение матриц не всегда определено

Умножение матриц не коммутативно

Примеры перемножения матриц

Пример

Решение

Пример

Решение

Пример

Решение

Резюме

Подпишитесь на нашу рассылку!

Как умножать матрицы? С Примерами

Как умножить столбец на число в Excel (2 простых способа)

Умножение столбца на число с помощью формулы (жесткое кодирование значения в формуле)

Жестко закодировать значение в формуле

Умножить весь столбец на значение в ячейке

Несколько столбцов с номером с использованием специальной вставки

Power BI Умножьте измерения на примерах

Power BI Измерение умножения

Power BI Измерение умножения двух столбцов с использованием DAX

Мера Power BI, умноженная на 100

Меру Power BI, умножить два столбца из разных таблиц

Power BI Measure, умножить столбец на Measure

Заключение

Умножение матриц в Excel (5 примеров)

Загрузить рабочую тетрадь

Как выполнять умножение матриц?

5 подходящих экземпляров для умножения матриц в Excel

1. Матричное умножение двух массивов

2. Умножение одного столбца на массив одной строки

3. Умножение массива одной строки и одного столбца в Excel

4. Вычисление площади матрицы путем умножения матриц

5. Умножение матрицы на скаляр

Ошибки при умножении матриц в Excel

Ограничение умножения матриц в Excel

Заключение

Связанные статьи

Как написать агрегатную функцию умножения на языке SQL — Java, SQL и jOOQ.

То же самое с умножением

Внимание: отрицательные числа

Внимание: ноль

Добавочный номер: DISTINCT

Расширение: оконные функции

Добавить комментарий Отменить ответ