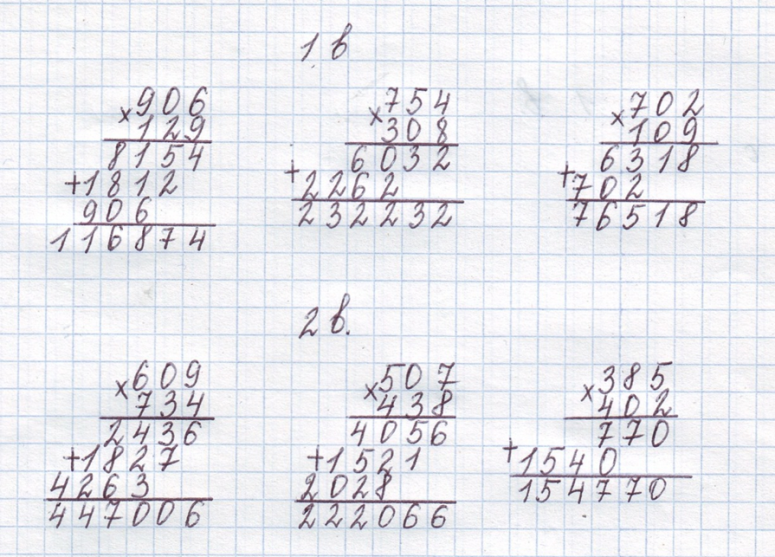Умножение на однозначное число в столбик / Умножение / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Умножение
5. Умножение на однозначное число в столбик

А теперь научимся умножать трёхзначные и двузначные числа на однозначное число в столбик.

Запоминаю порядок:

---

Умножение двузначного числа

Например, 42 • 2 = ?

	×	4	2
			2
		8	4

Сначала умножаем единицы: 2 • 2 = 4 и записываем под единицами.

Потом умножаем десятки: 4 • 2 = 8 и записываем под десятками.

Получили 8 десятков и 4 единицы — 84.

Рассмотри алгоритм умножения двузначного числа на однозначное число:

---

Умножение трёхзначного числа

Например, 174 • 3 = ?

	×	1	7	4
				3
		5	2	2

Рассмотри алгоритм умножения трёхзначного числа на однозначное число:

---

 

Советуем посмотреть:

Табличное умножение

Внетабличное умножение

Умножение суммы на число

Умножение на числа, оканчивающиеся нулями

Свойства умножения

Умножение

Правило встречается в следующих упражнениях:

3 класс

Страница 100, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 63, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 64, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 65, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 66, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 67, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 76, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 76. Урок 27, Петерсон, Учебник, часть 1

Страница 50. Урок 20, Петерсон, Учебник, часть 2

4 класс

Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 8, Моро, Волкова, Рабочая тетрадь, часть 1

5 класс

Номер 40, Мерзляк, Полонский, Якир, Учебник

Номер 42, Мерзляк, Полонский, Якир, Учебник

Номер 3, Мерзляк, Полонский, Якир, Учебник

Номер 1, Мерзляк, Полонский, Якир, Учебник

---

Умножение в столбик.

Распределительный, переставной, связующий законы умножения

Что такое умножение? Компоненты действия умножения

Умножение – это арифметическое действие, заключающееся в нахождении суммы одинаковых слагаемых.

Компоненты или названия чисел при умножении: множимое, множитель, произведение. Число, являющееся слагаемым, называется множимым; число, показывающее, сколько таких одинаковых слагаемых, называется множителем. Результат действия, то есть число, найденное при умножении, называется произведением. Множимое и множитель иногда называют одним словом сомножители.

Запись действия умножения:

Необходимо умножить 4 на 5. В математике запись будет выглядеть: 4×5 = 20. Знак умножения «×» или «·»

Чтобы умножить 4 на 5, необходимо 5 раз добавить число 4 или найти сумму пяти одинаковых слагаемых (числа 4).

4 + 4 + 4 + 4 + 4 = 20

В этом случае 4 будет множеным, 5 – множителем, 20 – произведением.

В буквенном выражении между множеным и множителем принято не ставить знак умножения:

Правила, свойства и законы умножения

Есть 3 основных закона умножения: переместительный, сочетательный и распределительный. Иногда их называют свойствами, например распределительное свойство умножения.

Переместительный закон умножения

От перестановки множимого и множителя произведение не меняется.

То есть, если мы переставим местами множители, то результат умножения останется без изменений. 5×6 = 6×5

В буквенном выражении переместительный закон умножения можно записать следующим образом (a, b, c – сомножители):

 

Сочетательный закон умножения

Произведение не изменится, если любую группу рядом множителей заменить их произведением.

То есть при умножении нескольких чисел можно объединять или соединять (от этого название закона) их в группы.

Распределительный закон умножения

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и образовавшиеся произведения добавить

(5 + 2 +3) × 7 = 5 × 7 + 2 × 7 + 3 × 7 = 35 + 14 +21 = 70

Распределительный закон также можно использовать при вычитании:

(9 – 6) × 5 = 9 × 5 – 6 × 5 = 45 – 30 = 15

Умножение произведения на число и числа на произведение

Чтобы умножить произведение нескольких чисел на определенное число, достаточно один из множителей произведения умножить на это число, оставив другие сомножители без изменения. Умножая число на произведение, достаточно умножить данное число на один из множителей произведения.

Например, 25 × (13 × 4) = (25 × 4) × 13 = 100 × 13 = 1300

Правило действует и для большего количества множителей: 20 × (9 × 5 × 12) = (20 × 5) × 9 × 12 = 100 × 9 × 12 = 10800

Умножение на 0: правило

Свойство умножения на нуль:

При умножении любого числа на 0 произведение будет равно 0. То есть, если множимое или множитель равны нулю, то произведение также будет равно нулю.

0 × 0 = 0

5 × 0 = 0

0 × 86 = 0

0 × b = 0 при любом значении переменной b

Умножение на 1

1 × b = b при любом значении переменной b

Правило: при умножении на единицу получим второй сомножитель, который не равен 1. Если множимое равно единице, то произведение равно множителю. Если множитель равен единице, то произведение будет равно множимому.

1 × 1 = 1

1 × 47 = 47

256 × 1 = 256

Умножение на 10, на 100 и т.д.

При умножении натурального числа на 10, 100, 1000 и т.д., необходимо приписать к этому числу справа столько нулей, сколько их есть в числе, на которое умножаем.

49 × 10 = 490

325 × 1000 = 325000

Умножение многоцифровых чисел

Умножим трехзначное число на однозначное 354 × 3

Мы можем разложить 354 на следующие слагаемые: 300 + 50 + 4 и умножить каждый разряд на 3 (согласно распределительному закону умножения): (300 + 50 + 4) × 3 = 300 × 3 + 50 × 3 + 4 × 3 = 900 + 150 +12 = 1062

Второй способ – выполнение умножения, начиная с низших разрядов. 354×3 – начинаем с умножения единиц: 4×3 = 12, записываем 2, а 1 десяток запоминаем, чтобы добавить его к произведению десятков. 5 десятков умножаем на 3, получим 15 десятков + 1 десяток = 16 десятков, записываем 6, а десять десятков или 1 сотню запоминаем, чтобы добавить в разряд сотен. В разряде сотен умножаем 3 сотни на 3, получим 9 сотен и добавляем еще 1 сотню = 10 сотен. Результат умножения: 1062

Умножение в столбик: умножение трехзначного числа на трехзначное

Пример 1. Необходимо умножить 423 × 334

Выполняя умножение в столбик, сначала умножаем множимое на единицы множителя: 423×4 = 1692, данное число называется первым промежуточным произведением. Далее нам необходимо умножить множимое на десятки множителя: 423×3 = 1269 (второе промежуточное произведение). Умножим множимое на разряд сотен: 423×3 = 1269 (третье промежуточное произведение).

При записи умножения в столбик первое промежуточное произведение записываем под разрядом единиц, второй – под разрядом десятков, третий – под разрядом сотен. После этого добавляем промежуточные произведения поразрядно, начиная с разряда единиц.

Калькулятор умножения в столбик

Пример 2. Необходимо умножить 126 × 209.

Сначала начинаем умножение с разряда единиц: умножаем 126 на 9, получим 1134; записываем, начиная с разряда единиц. В этом примере используем правило умножения на 0 и запишем промежуточное произведение в виде трех нулей, справа налево, начиная с разряда десятков. Умножив 126 на 2, получим 252 и запишем, начиная с сотен.

Подытожим основные правила умножения в столбик:

При умножении в столбик сначала находим первое промежуточное произведение – для этого умножаем множимое на разряд единиц множителя. Промежуточное произведение следует начинать подписывать под той разрядной единицей, на которую выполняется умножение. То есть, если мы умножаем разряд единиц (9 из предыдущего примера), то промежуточное произведение записываем так, чтобы последняя цифра промежуточного произведения была под разрядом единиц. Далее умножаем множимое на разряд десяток множителя. Последняя цифра второго промежуточного произведения должна быть под разрядом десятков (в нашем примере под 0). Третий шаг – умножаемое множимое на разряд сотен множителя и записываем промежуточное произведение. После этого добавляем промежуточные произведения по правилу добавления в столбик.

Умножение в столбик на натуральные числа, оканчивающиеся нулями

Для упрощения действия следует выполнить умножение в столбик без учета нулей, а до произведения чисел справа нужно дописать столько нулей, сколько их есть во всех множителях вместе.

Например, 5600 × 230

При умножении в столбик мы записали 56×23, в результате получили 1288 и дописываем справа три нуля, результат умножения – 1288000

Проверка умножения

Чтобы проверить правильность умножения нужно:

• Переставить местами множители и выполнить действие умножения. Если результат будет одинаковым, то действие выполнено правильно.
• Разделить произведение на один из множителей. Если в результате получим второй множитель, то действие исполнено правильно. О делении натуральных чисел читайте в следующем уроке

Как быстро умножать большие числа?

Существует несколько способов быстрого умножения, рассмотрим их с помощью примеров.

Умножение на число, близкое к единице определенного разряда (до 10, 100, 1000 и т.д.).

206 × 98 = 206 × (100 – 2) = 206 × 100 – 206 × 2 = 20600 – 412 = 20188

9103 × 1004 = 9103 × (1000 + 4) = 9103000 + 36412 = 9139412

В данном типе примеров мы расписываем приближенное число к единице определенного разряда как сумму или разность чисел (98 = 100 – 2; 1004 = 1000 + 4), а также используем распределительный закон умножения.

Умножение на 9, 99, 999 и т.д.

Правило: Чтобы умножить на число, записанное девятками (9 или 99, или 999 и т.д.), нужно к множимому приписать справа столько нулей, сколько девяток в множителе, и от результата вычесть множимое.

685 × 9 = 6850 – 685 = 6165

32 × 99 = 3200 – 32 = 3168

27 × 999 = 27000 – 27 = 26973

Умножение двузначного числа на 11

При умножении двузначного числа на 11 следует учесть, сумма цифр данного числа меньше 10, больше или равна десяти.

Чтобы умножить двузначное число, сумма цифр которого меньше 10, на 11, нужно между цифрами числа написать сумму его цифр.

63 × 11 = 693

25 × 11 = 275

Чтобы умножить на 11 двозначное число, сумма цифр которого больше или равна 10, нужно между цифрой десятков, увеличенной на 1, и цифрой единиц написать избыток суммы цифр числа сверх 10.

76 × 11 = 836

7+6=13 > 10 , поэтому результат будет: цифру десятков увеличиваем на 1, записываем 7+1 = 8, между цифрами 7 и 6 прописываем 3 (7+6-10=3), цифру единиц – 6 записываем без изменений. В результате получим произведение 836

Умножение чисел до 20

Если для умножения чисел до 10 можно использовать таблицу умножения, то для выполнения расчетов с двузначными числами в пределах 20 следует воспользоваться алгоритмом, описанным ниже.

Умножим 14 на 17

• К одному из чисел добавляем количество единиц второго: 14 + 7 = 21
• Полученное число умножаем на 10: 21×10 = 210
• Добавляем произведение единиц двух чисел: 210 + 4×7 = 238

14 × 17 = (14 + 7) × 10 + 4 × 7 = 238

Правильность этого метода можно доказать и проверить: 14 × 17 =

(10 + 4 ) × (10 + 7) = 10 × 10 + 10 × 4 + 10 ×7 + 4 × 7 = 10 × (10 + 4 + 7) + 4 × 7 = 238

В этом случае число 10 считается опорным числом.

Знак умножения на клавиатуре

Чаще всего знак умножения отображают крестиком «×» или точкой «·», реже используют звездочку «*».

На клавиатуре можно набрать знак звездочки* сочетанием клавиш Shift+8

Если вам нужен знак ×, можно использовать символ Unicode (Вставка/Символы), код: 00D7. Код 00B7 — отображает знак «·»

T \]

Чтобы выполнить сложение матрицы с , две матрицы должны иметь одинаковые размеры. Это означает, что они должны иметь одинаковое количество строк и столбцов. В этом случае просто добавьте каждый отдельный компонент, как показано ниже.

Например

\[A + B = \begin{pmatrix} 1 & -5 & 4 \\ 2 & 5 & 3 \end{pmatrix} + \begin{pmatrix} 8 & -3 & -4 \\ 4 & -2 & 9 \end{pmatrix} = \begin{pmatrix} 1 + 8 & -5 — 3 & 4 — 4 \\ 2 + 4 & 5 -2 & 3 + 9Т \]

Матричное скалярное умножение Раздел

 

Чтобы умножить матрицу на скаляр, также известное как скалярное умножение , умножьте каждый элемент матрицы на скаляр.

Например…

\[ 6*A = 6 * \begin{pmatrix} 1 & -5 & 4\\ 2 & 5 & 3 \end{pmatrix} = \begin{pmatrix} 6 * 1 & 6 * -5 & 6 * 4\\ 6 * 2 и 6 *5 и 6 * 3 \end{pmatrix} = \begin{pmatrix} 6 & -30 & 24 \\ 12 & 30 & 18 \end{pmatrix}\]

Чтобы умножить два вектора одинаковой длины, нужно взять скалярное произведение , также называемое внутренним произведением .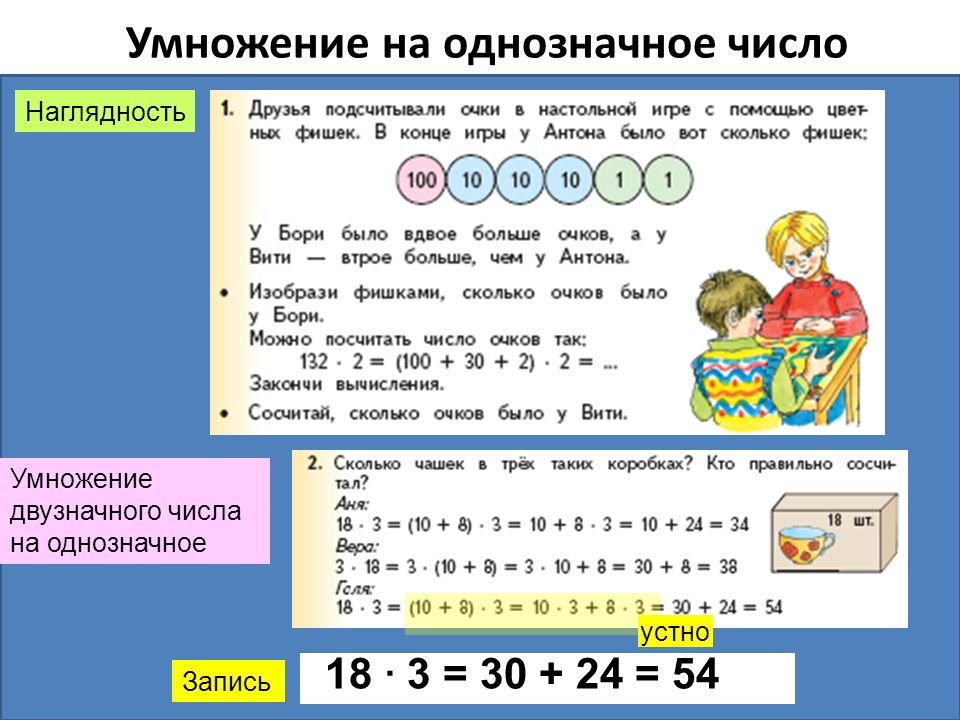 Это делается путем умножения каждой записи в двух векторах вместе, а затем сложения всех продуктов.

Например, для векторов x и y скалярное произведение рассчитывается ниже

\[ x \cdot y = \begin{pmatrix} 1 & -5 & 4 \end{pmatrix} * \begin{pmatrix} 4 & -2 & 5 \end{pmatrix} = 1*4 + (-5 )*(-2) + 4*5 = 4+10+20 = 34\]

Умножение матриц Раздел

 

Чтобы выполнить умножение матриц , первая матрица должна иметь такое же количество столбцов, сколько строк во второй матрице. Количество строк полученной матрицы равно количеству строк первой матрицы, а количество столбцов полученной матрицы равно количеству столбцов второй матрицы. Таким образом, матрицу 3 × 5 можно умножить на матрицу 5 × 7, получив матрицу 3 × 7, но нельзя умножить матрицу 2 × 8 на матрицу 4 × 2. Чтобы найти элементы в результирующей матрице, просто возьмите скалярное произведение соответствующей строки первой матрицы и соответствующего столбца второй матрицы. T\).

Умножение – Элементарная математика

Как с картинкой, так и с выражениями, это не что иное, как чудо, что 4 × 3 = 3 × 4. Дети, конечно, могут переставлять объекты, сгруппированные как 3 + 3 + 3 + 3, чтобы показать эквивалентность 4 + 4 + 4, но требует перестановки и не является «очевидной».

Но если одно и то же печенье разложить на подносе рядами и столбцами, то совершенно очевидно, что как бы мы ни держали поднос, количество печенья одинаково. Даже если у нас есть предпочтения в отношении того, как мы обозначаем первые две картинки ниже (настаивая, например, на том, что одна имеет размер 4 × 3, а другая — 3 × 4, чего математики не делают), у нас нет способа сделать такое изображение. задание для последнего лотка. 4 × 3 просто равно 3 × 4, хотя обозначения не совпадают.

Если мы описываем картинку «три тарелки, по четыре печенья на каждой», используя повторяющееся выражение сложения, то 4 + 4 + 4 более «естественно» использовать, чем 3 + 3 + 3 + 3. Но если мы опишем эту картинку с помощью выражение умножения, 3 × 4 и 4 × 3 одинаково правильно; нет математически предпочтительного порядка записи выражений умножения.[1].

Для младших школьников полезно и возможно развить представление об умножении, которое выдержит переход от целых чисел к дробям и десятичным дробям. Конечно, также полезно увидеть, как умножение может упростить вычисление, которое в противном случае потребовало бы повторного сложения, но оно не должно быть первичным образом умножения и, по этой причине, предпочтительно не его первым образом.

В Подумай о математике! умножение связано прежде всего с рядами и пересечениями, а довольно рано связано с «сочетаниями» (в том числе и простыми парами) вещей: улицами и проспектами, гласными и согласными в двухбуквенных словах и т. д. Идея повторного сложения также представлена, но позже, как пример другой задачи, которую решает умножение.

Учитывая количество строк и столбцов в прямоугольном массиве, умножение сообщает нам, сколько элементов в массиве, не заставляя нас считать их один за другим или многократно добавлять (или пропускать счет) элементы в каждой строке или столбце. Когда элементы в строках и столбцах представляют собой квадраты, выровненные из стороны в сторону, умножение подсчитывает эти квадраты и, следовательно, дает нам площадь прямоугольника. Это изображение отлично работает даже для дробей и объясняет алгоритм умножения дробей.

Если прямоугольник размером три на четыре разместить «на уровне» в одну сторону, он будет состоять из 3 строк и 4 столбцов  ; если мы повернем его на 90 градусов, строки станут столбцами, а столбцы станут строками, поэтому в нем будет 4 строки и 3 столбца . Если он держится под наклоном, нет правила, указывающего, какие строки называть, а какие столбцы, но в любом случае это не имеет значения; количество квадратов внутри него одинаково. Также не имеет значения, в каком порядке мы обозначаем ширину и длину прямоугольника: 3 × 4 и 4 × 3 обозначают один и тот же прямоугольник, независимо от того, как прямоугольник держат. Два выражения, 3 × 4 и 4 × 3, называют одно и то же число. Комбинации: сколько возможных блоков можно составить ровно из трех цветов и четырех форм? (Предположим, что каждый блок одного цвета и все блоки одного размера. ) Вопросы такого рода предполагают другой образ (и использование) умножения.

На самом деле, умножение подходит для любой ситуации, когда элементы одного набора соединяются по порядку с элементами другого набора. Здесь элементы одного набора являются началами «слов», а элементы другого набора — окончаниями.

Намек на связь с алгоритмом умножения.

См. статью об умножении и делении для полной разработки алгоритма многоразрядного умножения, показывающего, как он является точной записью показанных здесь моделей пересечения/площади.

В отличие от сложения, которое объединяет только одинаковые количества (сотни с сотнями, единицы с единицами), умножение образует все пары (3 × 7, 3 × 40, 3 × 200, 80 × 7, 80 × 40, 80 × 200)

Для целей выполнения многозначного умножения изображение «пересечения», показанное выше, неудобно, потому что оно рассеивает частичные произведения таким образом, что это мешает на последнем шаге сложения. . Для понимания того, как организовать вычисления, удобнее использовать табличное представление комбинаций, а также знакомит с моделью массива/площади.

Такой взгляд на многозначное умножение лежит в основе ведического умножения в Индии. Это может быть увлекательной культурной побочной темой для учащихся, которые научились умножать многозначные числа.

Массивы и таблица умножения

В начале второго класса дети могут решать подобные задачи и получать от них удовольствие.

Вот две красные буквы и три синие буквы: A, I, S, N, T . Сколько двухбуквенных слов вы можете составить, начиная с красной буквы и заканчивая синей буквой?

Сколько двухблочных башен именно такой формы можно построить из этих блоков?
Вот два примера: . Сколько других вы можете сделать?

Дети могут проводить опыты, создавая актуальные комбинации, а также изобретать собственную систему записи этих комбинаций. В случае двухбуквенных слов достаточно просто написать слова. Что касается башен, дети могут нарисовать их или указать сочетания цветов более абстрактным способом. Когда количество вариантов достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все варианты.

Пересечения как модель для составления организованного списка

Когда количество возможностей больше, как в задаче о блочной башне, дети склонны пропускать комбинации или дублировать их, если только они не систематизированы.

Вот один из способов визуализировать пары в этих двух экспериментах. Каждое пересечение представляет собой комбинацию. Сам символ × связан с изображением пересечения, пересечением линий.

Дети могут «провести» пальцем по «улице А» и «проспекту Н» и обозначить светофор на этом перекрестке «ан». например, top. Когда второклассники впервые проводят эти эксперименты, они учатся составлять систематические списки, а не умножать. Но мы видим, к чему это ведет: пересечения сами по себе перечисляют комбинации, которые ищут дети, и помогают им понять, как организовать эти списки; количество пересечений можно найти путем умножения, и дети получают предварительный просмотр этих идей умножения.

Таблицы как модель для составления организованного списка

Таблицы одинаково хороши для представления комбинаций и организации задачи их перечисления. Ячейки внутри таблицы (старательно избегая путаницы с ячейками «заголовка» над каждым столбцом и слева от каждой строки) снова показывают, как умножение отвечает на вопрос «сколько пар можно составить?»

Математика широко использует обе структуры — таблицы и пересекающиеся линии.

Умножение часто представляется в виде массивов смежных квадратов — «модель площади» умножения — или массивов точек или других мелких объектов. Первые визуально больше похожи на внутренности столов; последние визуально больше похожи на пересечения. Якорь

Построение основных фактов

Первые шаги

Когда мы видим одинаковые тройки чисел — 3, 5, 15; 4, 3, 12; 2, 5, 10; 6, 4, 24 — всплывающие в разных контекстах, они начинают казаться знакомыми еще до каких-либо сознательных усилий по их запоминанию. На самом деле, сфокусированные, преднамеренные усилия, которые кажутся необходимыми для некоторых троек (например, 7, 8, 56), могут быть связаны именно с тем, что существует так мало естественных контекстов, в которых эти тройки иначе появляются. Многие внешкольные занятия помогают построить таблицу умножения на 5: опыт определения времени в минутах на часах, обращения с монетами, наблюдения за своими руками. Следующие идеи представляют несколько контекстов для одних и тех же основных фактов, чтобы разнообразить практику (чтобы она оставалась интересной и создавала богатое разнообразие образов), чтобы к тому времени, когда дети пытаются запомнить факты умножения, они уже были хорошо знакомы с наиболее распространенными. те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).

Удвоение и деление пополам

В первом классе дети учатся удваивать ([[арифметика в уме|в уме]) все целые числа до 12. Второклассники практикуют эти основные удвоения, используя их, наряду с развитием своих представлений о разрядном значении , удваивать (мысленно) целые числа до 50. В этих классах дети также учатся находить половину четных чисел, получающихся в результате такого удвоения.

Малые массивы

В Подумай о математике! , вторая половина второго класса дает учащимся большой опыт работы с небольшими массивами, из которых они могут запоминать небольшие факты умножения. В одном из упражнений учитель может поднять такой массив и спросить: «Сколько строк? Сколько столбцов? Сколько маленьких квадратиков?»

Учащиеся, которые еще не умеют правильно складывать, могут использовать сложение или пропустить счет, чтобы определить количество квадратов. Связывание размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.

Затем учитель может держать тот же массив в этой ориентации и задавать те же вопросы.

Строки и столбцы меняются местами, но количество квадратов остается прежним.

Учитель может устроить из этого веселую игру, меняя набор поддерживаемых массивов (2×3, 3×3, 4×5 и т. д., но не более 5 строк или столбцов, потому что большие числа слишком сложны). узнавать без утомительного подсчета), и учащиеся довольно быстро запоминают, сколько квадратов в этих знакомых прямоугольниках.

Тот факт, что прямоугольник, расположенный горизонтально или вертикально, имеет одинаковое количество маленьких квадратов внутри, дает наглядное представление о том, почему умножение является коммутативным.

Пересекающиеся вертикальные и горизонтальные линии дают еще один образ для умножения — 2 вертикальные линии пересекают 3 горизонтальные линии в 6 пересечениях — и еще один контекст для репетиции фактов. Они могут рисовать их или играть с прозрачными картами, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки, чтобы непосредственно подсчитать их предсказания. С картами с прорезями в них тоже интересно играть. Дети выбирают пару и, как и в случае с диапозитивами, пытаются изобразить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку поверх другой, чтобы убедиться, что их предсказание было верным. Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.

Пересечения для пояснения умножения на 0 и 1. «Представьте себе крошечный городок с тремя дорогами, идущими с востока на запад…» Проведите пальцем по воздуху горизонтально, чтобы объяснить, что означает «восток-запад». Затем «нарисуйте» еще две дороги с востока на запад прямо в воздухе, чтобы дети могли представить их в уме. Позже вы или ребенок нарисуете их на доске. «…и только одна дорога, идущая с севера на юг».

В воздухе укажите пальцем дорогу с севера на юг.

«Давайте нарисуем карту этого крошечного городка. Вот дороги с востока на запад.

Нарисуйте неправильную границу города, а в ней нарисуйте три параллельные горизонтальные линии от одной стороны города к другой (и продолжайте немного выходить за границу города, чтобы указать, что они продолжают идти в соседние регионы).

«На карте дороги выглядят как три горизонтальные линии. Кто хотел бы нарисовать дорогу с севера на юг?»

Можно снова указать направление пальцем в воздухе, но не прямо на карте. Пригласите кого-нибудь порисовать.

«Город поставил светофор на каждом перекрестке (укажите на перекрестки). Сколько там светофоров?»

Играйте с изображением.

«А что, если бы город построил еще одну дорогу с востока на запад? Сколько пересечений получится?»

Умножение любого числа на 1 дает это число; умножение любого числа на 0 дает 0. Дети, которых учат этим просто правилам для запоминания, без некоторого понимания часто искажают правила, путая их друг с другом. (Что дает 1 умножение числа на 1 или число?) Изображение крошечного городка помогает понять, почему 1 умножение на любое число дает это число. (При наличии только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)

Карты с 0-5 слотами также могут быть особенно полезными. Когда карта с одним вертикальным слотом помещается поверх карты с тремя горизонтальными слотами, три пересечения появляются как единственные «окна» через пару карт. Изменение того, какая карта находится сверху или какая вертикальная, а какая горизонтальная, не имеет значения. Если одна карта имеет один слот, количество пересечений будет соответствовать количеству слотов на другой карте, когда они наложены друг на друга (и другие слоты перпендикулярны одному слоту). Изображение слота особенно ясно показывает, почему умножение на 0 всегда дает 0.

Этот урок дает прекрасную возможность использовать слова горизонтальный и вертикальный в контексте и связать их использование в качестве направлений на картах с востоком, западом, севером и югом как направлениями на земле. (См. «Горизонтальный» и «Вертикальный», чтобы узнать о распространенных путаницах в отношении идей, которые представляют эти слова.)

Построение таблицы умножения

Ученический проект для второго класса: учащиеся используют сетку, которая организована как таблица умножения, но не имеет строки или столбец для нуля. Используя лист бумаги в форме буквы L, они выбирают часть сетки; в правом нижнем углу выделения они пишут количество захваченных квадратов (что равно площади прямоугольника, если каждый маленький квадрат представляет собой одну квадратную единицу площади).

Обратите внимание, что число вверху, ближайшее к синей границе, указывает ширину зеленого прямоугольника, количество столбцов квадратов; число слева, ближайшее к синей границе, дает высоту зеленого прямоугольника и количество строк в нем.

Если мы переместим границу прямо вниз на один шаг, мы добавим новую строку без изменения количества квадратов в строке.

Таким образом, скажем, что 6 (количество квадратов в предыдущем прямоугольнике, 2×3) плюс 3 (количество квадратов в новом ряду) равно 9(количество квадратов в новом прямоугольнике). Другой способ описать новый прямоугольник — 3×3. Итак, 2×3 + 3 = 3×3.

Этот прямоугольник имеет одинаковую ширину и высоту, так что это квадрат. Поэтому число в углу (количество крошечных квадратов внутри него) называется квадратным числом.

Ход по диагонали — один шаг «на юг» и один шаг «на восток» (или один шаг вниз и один шаг вправо) — дает другое квадратное число.

Два диагональных шага на юго-восток дают еще один квадратный номер.

Интересно, если начать с квадратного числа (в данном случае 16) и сделать один шаг на северо-восток

или юго-запад

полученное число ровно на 1 меньше квадратного числа, с которого вы начали. Этот пример показывает, что прямоугольник 3×5 содержит на один квадрат меньше, чем прямоугольник 4×4. См. статью о разнице квадратов, чтобы узнать больше об этом интригующем шаблоне и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.

Симметрия таблицы умножения

Подсчет квадратов в прямоугольниках позволяет понять, почему 3×4 = 4×3. Оба способа описания этого прямоугольника . И даже если мы решим зарезервировать одну из этих нотаций для , а другую нотацию для , они все равно будут равны.

Поскольку умножение коммутативно, т. е. 2×6 = 6×2 и 3×5 = 5×3 и т. д., таблица умножения симметрична по диагонали северо-запад-юго-восток. Эта диагональ, желтая на этих иллюстрациях, содержит квадратные числа.

Избавившись от отвлекающих цифр и стрелок, мы видим три области: диагональ с квадратными цифрами, зеленую область с другими товарами и белую область с теми же номерами, что и в зеленой области.

Это очень хорошая новость для тех, кто пытается запомнить факты умножения! (См. Сколько фактов нужно выучить? ниже.)

Умножение на 10 и 100

Строится: 7 палочек — это 70 маленьких кубиков

Умножение на 5 и 50

Дети, которые умеют умножать на 10 и могут взять половину, могут затем использовать эти навыки, чтобы умножить на 5. Например, 7×5 — это половина 7×10, значит, это 35. В конечном счете, 7 × 5 следует просто распознавать сам по себе — один из «основных фактов», — но двухэтапная процедура (умножение на 10 и затем взятие половины результата) также полезно знать, и хорошая связь, чтобы установить с 5-кратные факты. Точно так же, зная, что 50 — это половина 100, мы можем видеть, что 50 семерок — это половина 100 семерок, поэтому 50 × 7 — это половина 100 × 7: мы можем умножить любое число на 50, умножив его на 100, а затем взяв половину.