Как правильно умножать натуральные числа столбиком

Оглавление

Время чтения::  10 минут

622

Умножение натуральных чисел в столбик – это способ, который позволит перемножить без калькулятора любые многозначные числа. Чтобы пользоваться таким методом на практике, нужно знать правила его применения. Рассмотрим подробнее умножение разных чисел в теории и на примерах.

Основные закономерности умножения столбиком

Есть ряд математических правил, которые нужно помнить, чтобы успешно пользоваться таким методом умножения:

• Во-первых, нужно знать наизусть таблицу умножения, и, не задумываясь использовать ее.
• Во-вторых, не стоит забывать правила умножения на нуль. Нуль часто встречается в двух и трехзначных числах, а значит, будет выступать в качестве одного из множителей.
• Помним, что \[x \times 0=0\]
• Под x мы понимаем любое натуральное число.
• Прежде, чем решать примеры на умножение в столбик, стоит вспомнить правила сложения в столбик и потренироваться суммировать числа.
• Повторить понятие разряда и сравнения любых натуральных цифр.

Как записывать множители при решении примеров на умножение столбиком

Залогом правильного решения задачи будет умение правильно записывать выражение столбиком. Здесь придерживаемся следующих правил:

1. В качестве первого множителя записывается цифру, которая имеет больший разряд.
2. Во второй строке (под первым множителем) записывается второй множитель. Здесь важно строго соблюдать закономерность сопоставления разрядов. Это значит, что десятки пишутся под десятками, единицы под единицами, и никак иначе.
3. Записав все множители друг под другом, нужно подвести горизонтальную черту, которая отделит их от ответа.

Рассмотрим на примере, как записать такое выражение.

На примере мы видим, как соблюдаются разряды при умножении четырехзначной цифры на трехзначную.

Теперь, чтобы научиться умножать в столбик, потребуется разобраться, как происходит умножение и как записывается результат. Начнем с умножения многозначного множителя на однозначный.

Как происходит умножение двузначных чисел в столбик на однозначные

Если требуется решить пример на умножение многозначного натурального числа на однозначное, легко можем применить данный метод. Процесс решения сразу рассмотрим ниже.

Разберем алгоритм действий:

1. Записываем множители в столбик, строго соблюдая разряды. Единицы пишем под единицами, следовательно, 2 под 4.
2. Перемножаем их по порядку, так же соблюдая разряд. Сначала перемножаем на 2 единицы, потом десятки, потом сотни. Полученный результат вписываем под чертой.

Здесь стоит отметить, что в образце приведены числа, при перемножении которых результат не превысил 10. В том случае, если при перемножении мы получаем двузначный ответ, то записываем только единицы. Десятки запоминаем и прибавляем к результату, который получится при перемножении следующего разряда. Если количество разрядов закончилось, а остались неучтенные десятки, они просто вписываются крайней левой цифрой.

Умножение в столбик с нулями

Если нам потребуется решить пример по математике, где один из множителей имеет на конце нули, действовать придется несколько иначе. Рассмотрим на конкретном примере.

Условие: нам нужно умножить 5400 на 7.

Первым делом нужно правильно записать выражение:

\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\\ \end{array} \\ \hline \begin{array}{r} \end{array} \end{array}\]

Здесь нужно обратить внимание на то, что под нулями множитель не записывается.

Следующий этап решения примера в столбик – умножение без учета нулей.

\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\quad\\ \end{array} \\ \hline \begin{array}{r} 378 \quad \end{array} \end{array}\]

Теперь вспоминаем, что у нас осталось два неучтенных нуля. Их просто переносим вниз за черту.

\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\quad\\ \end{array} \\ \hline \begin{array}{r} 37800 \end{array} \end{array}\]

В итоге получаем: 5400×7=37800

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как умножать столбиком, если в примере два многозначных числа

Чтобы понять, как умножать в столбик многозначные числа, возьмем задание и рассмотрим алгоритм его решения. Предположим, нам нужно умножить 8063 на 207.

Решение:

1. Первое действие – записывать множители правильно. Первым записывается множитель, имеющий больше разрядов. В нашем случае – 8063. Под ним записывается второй множитель – 207. Не забываем о строгом соблюдении разрядов. Если нам придется решать примеры, в которых оба множителя имеют равное количество разрядов, записывать их можно в любом порядке.
2. Следующий шаг – перемножение единиц. Это значит, что умножаем 3 на 7, потом 6 на 7, и так далее все разряды первого множителя на единицы второго. Полученный результат будет считаться промежуточным. В некоторых источниках его называют неполным произведением.
   
3. Следующий этап – перемножение десятков. Так как во втором множителе мы имеем нуль в десятках, его просто пропускаем. Согласно правилам, при умножении на нуль все равно получим нуль.
   
4. Следующий этап – перемножение сотен. В итоге мы получим второе неполное произведение или второй промежуточный результат. Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.
   В итоге мы получили два неполных произведения. Задания на умножение столбиком содержат столько промежуточных результатов, сколько разрядов во втором множителе. У нас получилось два, так как в десятках мы имеем нуль, и его пропускаем. Если бы вместо него была любая другая натуральная цифра, мы бы записали три неполных произведения друг под другом со сдвигом влево.
   
5. Завершающий этап – сложение всех полученных промежуточных результатов. Для этого не нужно переписывать их в отдельный пример. Достаточно просто вписать слева знак суммы – плюс и подвести дополнительную черту.

   Под чертой будем записывать полученное в итоге сложения семизначный результат, который и будет ответом.

Таким образом, можно записать выражение:

8063×207=1669041

Можно сказать, что для быстрого и верного решения заданий на умножение в столбик нужно на отлично знать таблицу умножения, помнить правила сложения в столбик, а также помнить основные математические термины.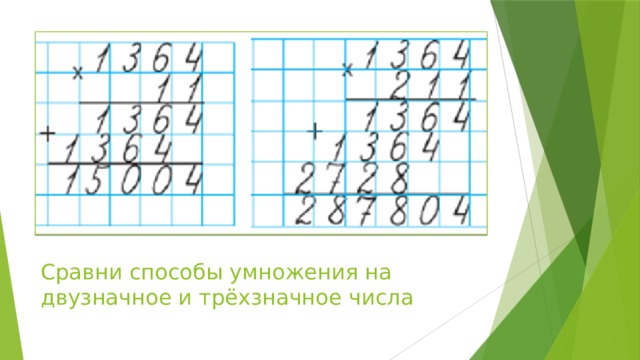

Под основными терминами понимаются следующие:

• Однозначное число – это число, состоящее из одной цифры (например, 6).
• Двухзначная цифра – это та, в составе которой два натуральных числа (например, 28), и т.д.
• Разряд – это позиция, которую занимает число в комбинации с другими числами. Разряд отсчитывается с конца.
• Разряд единиц – это концовка любого многозначного числа. Перед ним находится разряд десятков, далее разряд сотен, и т.д.

Например, число 4657.

7 – разряд единиц;

5 – разряд десятков;

6 – разряд сотен;

4 – разряд тысяч.

Определение

Умножение – это арифметическое действие, в процессе которого перемножаются два составляющих – множители. Результат данного действия называется произведением.

Чтобы разобраться, как решать умножение в столбик, нужно помнить и основные правила этого математического действия.

1. Перестановка мест множителей не влияет на результат.
   \[x \times y=y \times x\]
2. Произведение трех и более множителей будет иметь идентичное значение, даже если любую группу заменить произведением.
   \[x \times y \times z=(x \times y) \times z\]
3. Умножение на нуль всегда дает нуль.

Есть еще одна категория примеров, на которую стоит обратить внимание. Это перемножение множителей, на конце каждого из которых есть нули. В таких примерах часто допускаются ошибки. Независимо от количества нулей на конце многозначных натуральных чисел, нужно действовать в последовательности, описанной на примере ниже.

Пример умножения чисел столбиком

Пример

Условие: 34500×230

Первым делом нужно записать пример в столбик таким образом, чтобы натуральные числа, отличные от нуля, расположились друг под другом.

\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\end{array}\]

После того, как мы записали пример в столбик, мы можем просто перемножить множители в соответствие с
правилами перемножения многозначных чисел, без учета нулей.

В ходе вычислений у нас должно получиться два неполных, или промежуточных результата.

\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline\end{array}\]

Последний этап – сложение двух промежуточных результатов и переписывание справа нулей. Нулей мы напишем столько, сколько имеют оба множителя, а именно, три.

\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array} \\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline7935000\end{array}\]

В итоге получаем, что 34 500×230=7 935 000

Анализируя вышеперечисленный пример, можно сказать, что перемножить в столбик можно любые без исключения числа, если руководствоваться правилами математики. Умножение двузначных чисел в столбик – это школьная программа, освоив которую, примеры научится решать любой ребенок, ученик четвертого класса.

Умножение двузначных, трехзначных и многозначных чисел столбиком. Как умножать в столбик?

Для решения произведения двух положительных целых чисел, одно из которых является однозначным, а другое — многозначным, используйте метод столбцов. Для расчета используйте приведенную выше последовательность действий.

Основные понятия

Для записи чисел принято использовать эти десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Их можно использовать для создания любого натурального числа.

Название числа напрямую связано с количеством цифр.

• Однозначное — состоит из одного знака.
• Двузначное — из двух.
• Трехзначное — из трех и так далее.

Разряд — это позиция, в которой находится число в наборе данных. Обычно принято считать их с конца.

Единицы — это точка, на которой заканчивается каждое число. Цифра «десятки» предшествует цифре «единицы». Цифра сотни предшествует цифре десятки. На место пропущенной цифры всегда можно поставить ноль.

• Например, в числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.

Умножение — это арифметическая операция с двумя аргументами — множителями. Результат их умножения называется произведением.

Выясните, по каким предметам вы отстаете, а затем проработайте их без формул и скучных лекций.

Свойства умножения

1. От перестановки множителей местами произведение не меняется.
   • a × b = b × a
2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
   • a × b × c = (a × b) × c = a × (b × c)

Самое главное — знать таблицу умножения. Это сделает процесс подсчета гладким и быстрым.

Важно помнить правило, что при умножении в столбцах с нулями получается ноль:

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик, давайте рассмотрим шаги:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т.
   д.
3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни. Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
5. Складываем то, что нашли и получаем ответ.

Занимайтесь по 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.

Умножение двузначных, трехзначных и многозначных чисел столбиком

В этом посте мы рассмотрим правила и практические примеры умножения натуральных чисел (двух, трех и четырехзначных чисел) с помощью столбцов.

Чтобы найти произведение двух целых положительных чисел, можно использовать умножение в столбик.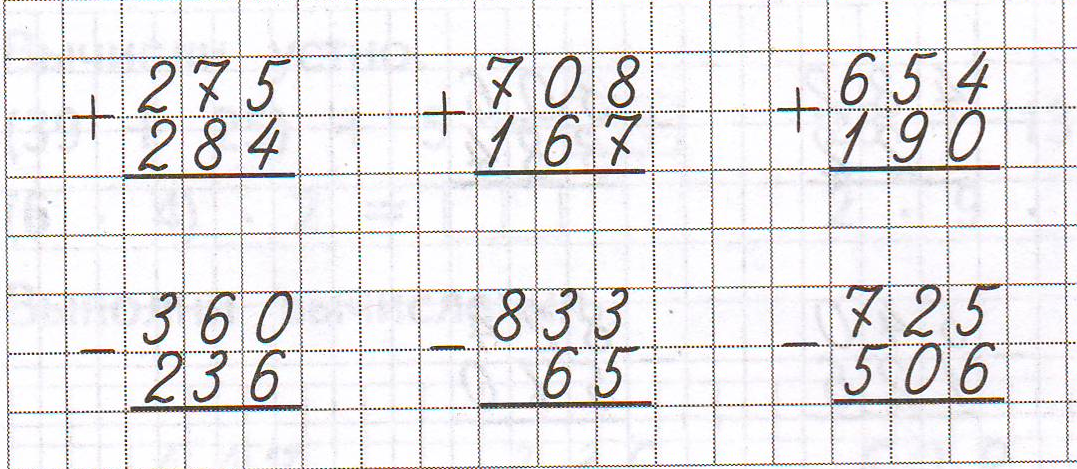 Для этого:

1. Пишем первый множитель (начинаем с того, у которого больше разрядов).
2. Под ним записываем второй множитель (с новой строки). При этом важно, чтобы одинаковые разряды обоих чисел были расположены строго друг под другом (десятки под десятками, сотни под сотнями и т.д.)
3. Под сомножителями чертим горизонтальную линию, которая будет отделять их от результата.
4. Начинаем выполнять умножение:
   • Крайнюю правую цифру второго множителя (разряд – единицы) поочередно умножаем на каждую цифру первого числа (справа налево). При этом если ответ оказался двузначным, в текущем разряде оставляем последнюю цифру, а первую переносим в следующий, сложив со значением, полученным в результате умножения. Иногда в результате такого переноса в ответе появляется новый разряд.
   • Затем переходим к следующей цифре второго множителя (десятки) и выполняем аналогичные действия, записывая результат со сдвигом на один разряд влево.
5. Получившиеся числа складываем и получаем ответ. Правила и примеры сложения чисел в столбик мы рассмотрели в отдельной публикации.

Примеры умножения в столбик

Пример 1

Умножьте двузначное число на однозначное, например, 32 на 7.

В этом случае второй множитель состоит только из одной цифры — единицы. Умножьте 7 на каждую цифру первого множителя по очереди. В данном случае произведение 7 и 2 равно 14. В ответе мы оставляем цифру 4 в ее текущем положении (единицы) и прибавляем единицу к результату умножения 7 на 3 (7⋅3+1=22).

Пример 2

Найдите произведение двузначного и трехзначного чисел: 416 и 23.

• Записываем множители друг под другом (в верхней строке – 416).
• Поочередно умножаем цифру 3 числа 23 на каждый разряд числа 416, получаем – 1248.
• Теперь умножаем 2 на каждую цифру 416, и полученный результат (832) записываем под числом 1248 со смещением на один разряд влево.
• Остается только сложить числа 832 и 1248, чтобы получить ответ, который равняется 9568.

Публикации по теме:

• Таблица сложения чисел
• Таблица умножения чисел
• Таблица деления чисел
• Таблица вычитания чисел
• Расчеты с процентами
• Чему равна промилле и как обозначается
• Простые и взаимно простые числа
• Позиционные системы счисления
• Квадраты натуральных чисел
• Кубы натуральных чисел
• Единицы измерения времени
• Единицы измерения длины
• Единицы измерения массы
• Единицы измерения объема
• Сложение двузначных, трехзначных и многозначных чисел столбиком
• Свойства сложения чисел с примерами
• Свойства вычитания чисел с примерами
• Свойства умножения чисел с примерами
• Свойства деления чисел с примерами
• Вычитание двузначных, трехзначных и многозначных чисел столбиком
• Что такое натуральные числа

Примеры умножения двузначных чисел

Чтобы лучше понять умножение двузначных чисел в столбик, рассмотрите следующие примеры решения в столбик.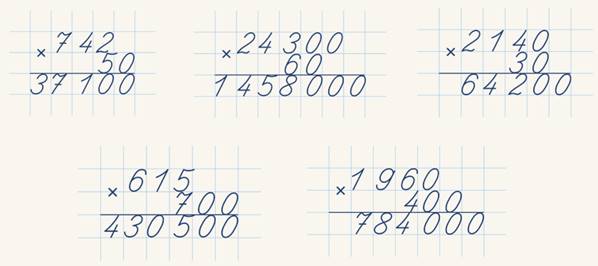 Рассмотрев каждый пример, вы узнаете, как это сделать более подробно:

Пример 1

Умножение 15 на 37. Пошаговый алгоритм умножения в столбик:

Пример 2

Умножьте 23 на 79. Пошаговый алгоритм умножения столбиком:

Умножение столбиком трехзначных чисел

Для умножения трехзначных чисел в столбик все действия выполняются одинаково, алгоритм не меняется.

Пекарня «Горячий хлеб» испекла 345 буханок ржаного хлеба, 568 буханок белого хлеба и 875 сладких булочек. Сколько буханок они испекут за месяц (31 день), если каждый день они будут выпекать одинаковое количество?

Давайте вкратце рассмотрим эту проблему.

Умножение столбиком многозначных натуральных чисел

Вы уже догадались, что каждое число нужно умножить на 31 и сложить произведения.

Запишите все вычисления в столбцы. Давайте напишем объяснения правильно. Посмотрите, как написана запись в тетради ученика 4-го класса.

Решение задач с многозначными числами

Можно ли решить эту проблему другим способом?

Сначала сложите количество всех хлебобулочных изделий, выпеченных за один день, а затем умножьте полученное число на 31.

Какой метод вам больше нравится? Второй метод можно назвать рациональным, поскольку он намного короче и удобнее.

Решите проблему мебельной фабрики самостоятельно. Запишите его вкратце. Запишите свои вычисления в столбик в тетради, объясните свои пояснения и ответьте правильно. Сравните свои записи с примером.

Проблема

Мебельная фабрика за один день произвела 122 стола и 475 стульев. Сколько столов и стульев будет произведено в феврале (28 дней)?

Вы много работали. Молодец! Давайте вернемся к долгоживущим животным, с которых мы начали наш урок.

Это интересно! Гренландские киты находятся под угрозой исчезновения. Некоторые киты живут до 200 лет. Ученые установили, что киту-рекордсмену было 211 лет. Тигровый питон — это очень крупная неядовитая змея, которая может лазать по деревьям. В неволе питоны живут около 20-25 лет, но в дикой природе они могут доживать до 100 лет. Черепахи живут в среднем 20-50 лет, но есть некоторые виды, которые при благоприятных условиях могут жить до 200 лет!

Решите юмористическую задачу о черепахе.

Проблема сообразительности

Сначала сложите количество всех хлебобулочных изделий, выпеченных за один день, а затем умножьте полученное число на 31.

Ответ: Черепаха не найдет свой панцирь на берегу, потому что она хочет переплыть реку три раза. Таким образом, он окажется на противоположном берегу.

На этом уроке мы научились умножать в столбик, решать задачи с многозначными числами и правильно формулировать решение.

2-Digit by 2-Digit Multiplication Song | 4–5 классы

Описание видео:

Следуйте за Стэном в его доме и дворе, пока он решает задачи на умножение 2 на 2 цифры со своими лучшими друзьями Беном и Стеллой. Они научат вас, как выполнять длинное умножение с двумя цифрами, а плюшевая игрушка Стэна прольет свет на то, что делать с десятичными числами.

2-Digit by 2-Digit Multiplication Song Lyrics:

СТИХ ПЕРВЫЙ
Вот как вы умножаете пятьдесят девять на двадцать пять;
Пять раз девять — сорок пять; нести четыре и писать пять.
Пять раз пять — двадцать пять;
, затем добавьте четыре и двадцать девять.
Мы пишем ноль, когда умножаем десятки.
Дважды девять — восемнадцать;
пишут восьмерку, но несет один.
Пять раз два равно десяти;
, затем добавьте единицу, и вы получите одиннадцать.
Сложите числа, и это будет продукт.
Я сказал: «Сложите числа, и это будет произведение».

ПРИПЕВ
Нам нужно писать ноль, когда мы умножаем десятки.
Сложите числа и получите продукт.

СТИХ ВТОРОЙ
Сейчас на сцену выходит двадцать три раза по девятнадцать.
Трижды девять — двадцать семь;
пишите семерку, несите десятки.
Дважды девять — восемнадцать; сложите два и получите двадцать.
Тогда пишем ноль, когда… умножаем десятки.
Трижды один — три — два раза один — два —
и теперь мы знаем, что делать…
сложите два числа, а затем
получите четыреста тридцать семь.
Сложите два числа и затем
получите четыреста тридцать семь.
сложите два числа, а затем…
ПОСЕТИТЕ NUMBEROCK.COM

МОСТ
Когда мы делаем длинное умножение
, мы проверяем его с помощью обратной операции.
Продукт становится дивидендом.
Делитель — это множитель или множимое.
Затем вычисляем с точностью, делаем длинное деление;
, если частное является другим множителем,
, то мы знаем, что получили правильный ответ.

КОНЦОВКА
Я чучело, и я здесь, чтобы сказать вам, что…
Если числа содержат десятичные дроби, дополнительная работа минимальна.
Просто умножьте все, как раньше,
, и останется еще один шаг.
Подсчитайте количество знаков после запятой,
затем сдвиньте влево в произведении столько пробелов;
, где стоит десятичная точка,
и каждый пробел слева делится на десять.

Подробнее

Эта песня предназначена для стандартов обучения TEKS и Common Core как для 4-го, так и для 5-го класса. Ознакомьтесь с соответствующими стандартами здесь или углубитесь в длинное умножение здесь.

Если вы заинтересованы в том, чтобы получить идеи о том, как спланировать надежный урок рассказывания в соответствии со стандартами, мы рекомендуем ознакомиться с рекомендациями Instructure для общих основных стандартов 4.NBT.5 и 5.NBT.5. Эти страницы помогают разбить стандартный язык, указать соответствующий классу уровень строгости для каждой концепции и предлагают различные предложения для занятий (начальные уроки), которые помогают учащимся достичь своих учебных целей.

Чтобы продолжить просмотр библиотеки математических видеоматериалов Numberock, нажмите здесь. Чтобы получить доступ к растущей библиотеке премиум-контента Numberock, нажмите здесь.

4.NBT.5 5.NBT.5
 

Двузначное умножение стало проще! — Caffeine Queen Teacher

Умножение двузначных чисел — сложная задача, требующая много практики и повторения (и повторения и повторения). В прошлом я преподавал множество методов, включая ящик, частичные произведения, решетку и традиционный алгоритм.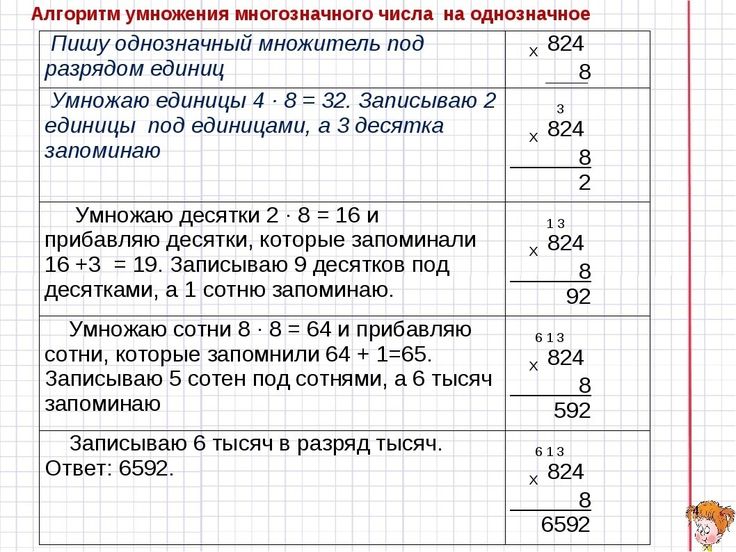

Некоторые учащиеся быстро и легко адаптируются к целому ряду методов, в то время как другие с трудом усваивают даже один метод.

Многие учащиеся (и большинство родителей) с облегчением концентрируются на стандартном алгоритме. Стандартный алгоритм — это традиционный метод, которым пользуется большинство людей.

К 5-му классу в большинстве штатов требуется, чтобы учащиеся свободно владели стандартным алгоритмом. На протяжении многих лет я провел много поисков и не смог найти графический органайзер, который приносил бы пользу моим ученикам, испытывающим затруднения.

Некоторым моим ученикам было трудно выучить шаги и выполнить их в правильном порядке. Я понял, что мои борцы, как правило, были визуальными и практическими учениками, поэтому я разработал графический органайзер, чтобы помочь студентам с алгоритмом.

Щелкните, чтобы получить БЕСПЛАТНЫЙ набор навыков стратегии умножения!

Визуальный органайзер для умножения на 2 цифры

Этот органайзер представляет собой метод, который учителя могут использовать для обучения традиционному алгоритму. Органайзер удобный для студентов  и использует форм и цветов , чтобы помочь учащимся выполнять шаги по порядку.

Во время обучения я постоянно говорю: «Кружки идут к кругам» или «Квадраты идут к квадратам». Это побуждает учащихся искать следующий шаг в этой конкретной форме. Эти утверждения помогают учащимся помнить, куда класть их продукты, когда они решают задачи на умножение. Например, учащиеся выполняют каждый шаг для красных кругов, прежде чем перейти к синим квадратам.

Как видно на картинках, органайзеры используют не только формы, но и цвета. Цвета и формы могут быть добавлены или удалены в зависимости от уровня адаптации, в котором нуждаются ваши ученики.

Цвета и формы помогают новичкам. По мере того, как учащиеся становятся более опытными, цвета могут быть удалены или даже добавлены учащимися, если это необходимо. Маркеры также можно использовать, чтобы подчеркнуть и сфокусировать внимание на конкретных шагах, которые необходимо укрепить учащимся.

Якорная диаграмма визуальной стратегии

FYI — приведенная выше якорная диаграмма — это винтаж — 2014 года, но вы поняли идею. Первоначально в этих наборах использовались треугольники, а не пятиугольники. Мне показалось, что треугольники не дают ученикам достаточно места для письма, поэтому форму заменили на пятиугольники.

 

2-значное умножение с использованием органайзера фигур

Я ОБОЖАЮ эти карманные диаграммы C-Line , которые можно приобрести в магазинах для учителей, Wal-Mart или Amazon. Вы просто вставляете страницу в карманную таблицу и ВУАЛЯ! Ламинировать не надо.

Это пластиковый футляр, который можно использовать для маркеров с сухим стиранием. Студенты часто пользуются ими.

Ученикам нравится использовать карманные рукава, потому что маркеры с сухим стиранием позволяют легко писать и стирать, не беспокоясь об ошибках.

Органайзеры и рабочие листы для умножения двузначных чисел

Мне было трудно найти рабочие листы без перегруппировки. Я хотел, чтобы мои ученики сосредоточились на стандартном алгоритме умножения без дополнительного шага перегруппировки.

Когда учащиеся освоятся с умножением без перегруппировки, они готовы к изучению этого дополнительного шага. Перегруппировка должна пройти гладко после того, как вы потратите время на решение проблем без перегруппировки и изучения процесса двузначного умножения.

Выделение или раскрашивание начальной точки помогает учащимся запомнить, с чего начать.

Эти наборы органайзеров для умножения Shape Math содержат множество практических страниц, поэтому используйте столько страниц, сколько нужно вашим ученикам. Кроме того, наборы облегчают дифференциацию в зависимости от уникальных потребностей учащихся.

Моим ученикам обычно требовалась дополнительная практика и МНОГО повторений, поэтому в исходный набор включено множество различных рабочих листов с перегруппировкой.

Кроме того, в набор входят три графических органайзера разного размера. Первый и самый большой органайзер занимает целую страницу. На других страницах есть четыре органайзера; другая страница содержит девять пустых органайзеров. Эти страницы идеально подходят для вас (или ваших учеников) для решения задач. Мои ученики любят составлять рабочие листы друг для друга и быть «учителем».

Страница ниже свернута, что является простым приспособлением для студентов, которые перегружены просмотром целой страницы задач.

Страница свернута для учащихся, которые перегружены объемом работы, которую от них ожидают.

Рабочие листы размеров , цветов и рабочих листов упрощают дифференциацию и создание лесов. Эти наборы для умножения и деления Shape Math — мои любимые, они протестированы учащимися и одобрены учителями!

После того, как учащиеся научатся решать задачи на умножение с перегруппировкой и без нее, учащиеся готовы решать задачи без графического органайзера. Два рабочих листа на миллиметровой бумаге включены, чтобы помочь им перейти к независимости.

 

Если вы также обучаете делению, вам понравится этот комплект, который сэкономит ваше время!

Советы по обучению учащихся двухэтапному умножению

В коротком (5-минутном) видеоролике ниже показано, как я обучаю учащихся двузначному умножению с помощью шаблона Shape Multiplication.

Нажмите, чтобы посетить Учителя Платите учителям и узнайте больше!

Хотите узнать больше?

Если вы хотите узнать больше об этой новой стратегии умножения (а также о стратегиях деления!), вот несколько статей, которые вы можете прочитать:

Рабочие листы дифференцированного умножения:

Все ресурсы по умножению  – Ознакомьтесь все ресурсы умножения, которые я предлагаю в моем магазине учителей, платных учителям.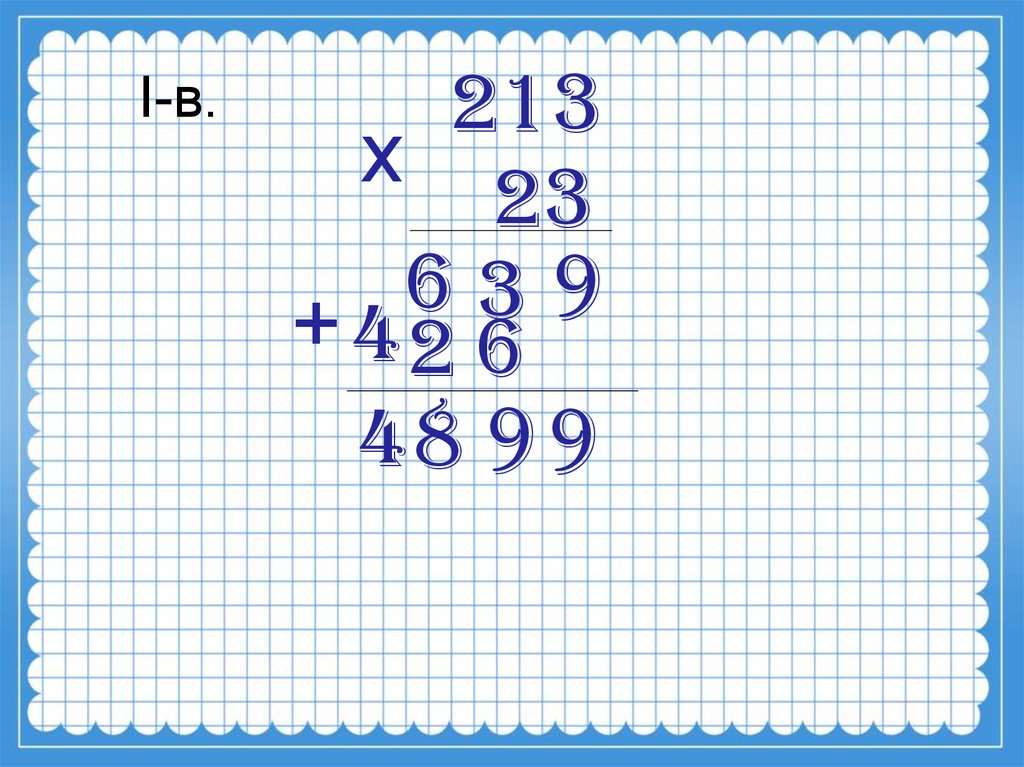

Двузначное умножение — дифференцированная стратегия обучения многозначному умножению с использованием органайзеров и рабочих листов, чтобы помочь учащимся визуализировать процесс умножения.

2-значное и 3-значное умножение — этот метод многозначного (3-х 2-значного) умножения использует цвета и формы для визуальной, конкретной стратегии.

Статьи об умножении:

3 идеи для обучения многозначному умножению . Вот 3 идеи FAST для обучения многозначному умножению. Эти вмешательства просты и быстры для занятых учителей.

Рабочие листы по умножению 2-значных чисел: дифференцированные . Ниже представлен визуальный метод обучения умножению 2-значных чисел с использованием дифференцированных визуальных подсказок, которые помогут учащимся добиться успеха в обучении.

Двузначное умножение стало проще!

– Вот как использовать организаторы двузначного умножения и рабочие листы.