Онлайн калькулятор. Умножение столбиком — «Семья и Школа»
Содержание
Умножение чисел столбиком. 5 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Тема урока:
Умножение чисел столбиком
5 класс
С.М. Никольский и др.
Учитель Чернышова Анна
Владимировна
2. Цели урока:
Систематизировать, расширить и
углубить знания по данной теме.
Развивать
наблюдательность,
умение
анализировать,
вычислительные навыки.
Искать наиболее рациональные
пути решения задач.
3. Этапы урока:
1. Повторение.
2. Изучение нового материала.
3. Решение упражнений и задач.
Самопроверка.
4. Математическая эстафета
5. Подведение итогов урока.
6. Домашнее задание.
Повторение:
(a b) с=a (b с)
a (b+с)=a b+ a с
a (b-с)=a b- a с
Переместительный закон
Сочетательный закон
Распределительный закон
Повторение:
a 0=0
При умножении любого числа на
нуль всегда будет нуль
a 1=а
При умножении любого числа на
единицу всегда получаем это
число
Рассмотрим выражение:
25 ∙ 589 ∙ 5 ∙ 125 ∙ 2 ∙ 4 ∙ 8 = ?
Чтобы найти значение этого выражения, не
обязательно перемножать все числа в столбик:
достаточно
воспользоваться
сочетательным
законом умножения.
Объединим попарно некоторые множители:
(25 ∙ 4) ∙ 589 ∙ (5 ∙ 2) ∙ (125 ∙ 8) = 100 ∙ 589 ∙
10 ∙ 10000 = 589 ∙ 10000000 = 589000000
Вычисление
произведения
однозначного и многозначного
чисел,
и
тем
более двух
многозначных чисел, требует
применения не только таблицы
умножения,
но
и
законов
сложения и умножения.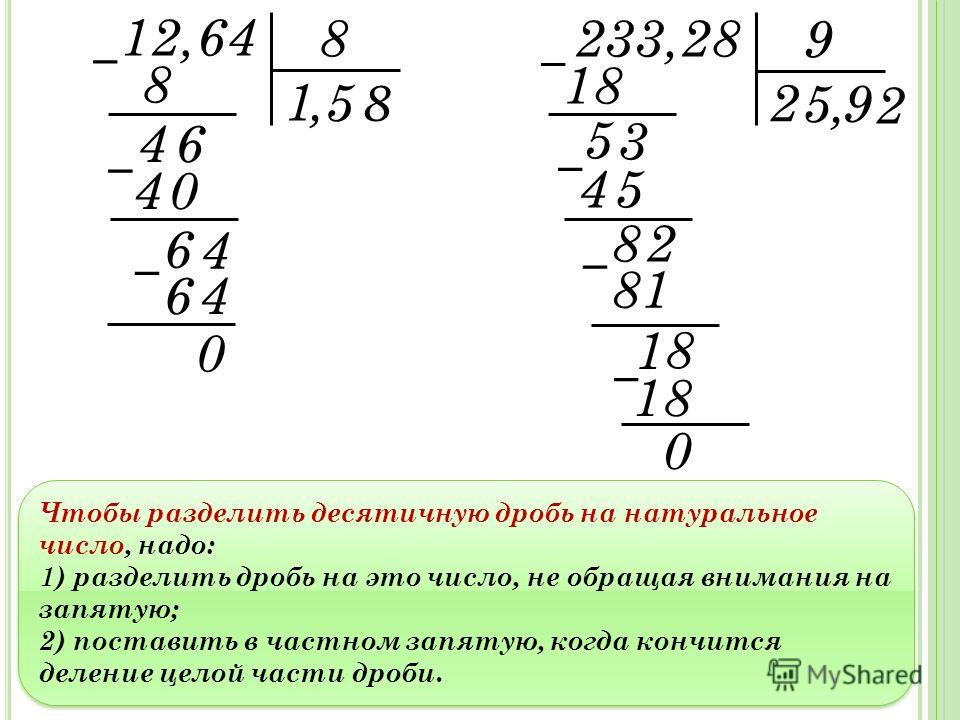
Вычислим произведение 723 ∙ 5 = ?
Можно представить число 723 в виде суммы
разрядных слагаемых, и каждое из этих
слагаемых умножить на 5, а затем сложить
полученные результаты.
723 ∙ 5 = (700 + 20 + 3) ∙ 5 = 700 ∙ 5 + 20 ∙ 5+
+ 3 ∙ 5 = 3500 + 100 + 15 = 3615
Можно записать вычисление значения
этого выражения столбиком:
При умножении трёх на пять получаем пятнадцать.
Пять записываем в разряд единиц, единицу прибавляем
в разряд десятков. При умножении двух на пять
получаем десять, плюс единица, которую мы запомнили,
получаем в разряде десятков единицу, единицу
добавляем к разряду сотен. При умножении семи на пять
получим тридцать пять, плюс один – тридцать шесть.
Ответ: 3615.
Рассмотрим ещё одно выражение: 329 ∙ 34 = ?
Запишем это произведение в столбик:
Сначала умножаем целиком верхнее число на
последнюю цифру нижнего числа, т.е. на 4. Результат
справа налево.

Переходим к умножению числа 329 на 3.
Умножаем по тем же правилам, что и в
предыдущем вычислении.
Результат умножения на вторую цифру необходимо
записывать под второй цифрой результата первого
действия умножения.
Полученные числа под чертой складываем
по правилам сложения в столбик.
Упражнение:
Вычислите: 3256 ∙ 25 = ?
Решение: вычислим данное произведение в столбик:
Ответ: 81400.
Задача:
Пете ко Дню рождения надо было купить конфет. Он
купил конфеты трёх видов: «Батончики», «Мишка на севере»,
«Грильяж». «Батончиков» он купил 56 штук, «Мишек на
севере» – в 15 раз больше, чем «Батончиков», а «Грильяжа»
на 50 конфет больше, чем «Батончиков». Сколько всего
конфет купил Петя?
Решение:
1) 56 ∙ 15 = 840 (шт.) – «Мишка на севере».
2) 56 + 50 = 106 (шт.) – «Грильяж».
3) 56 + 840 + 106 = 1002 (шт. ) – всего.
) – всего.
Ответ: 1002 штуки.
Математическая эстафета:
1 столбик
2 столбик
3 столбик
1) 12 10=
1) 15 10=
1) 17 10=
2) 24 2=
2) 31 3=
2) 71 9=
3) 42
х 12
3) 22
х 33
3) 53
х 31
4) 101
х 332
4) 101
х 648
4) 101
х 458
Домашнее задание:
Классная работа:
Проработать
презентацию, прочитать
параграф 1. 10 с.34-35,
выполнить задание
письменно слайд 14.
Домашняя работа: с.36
№143 письменно
Спасибо за урок!
English Русский Правила
Умножение в столбик. Умножение и деление столбиком
В третьем классе начальной школы дети начинают изучать внетабличные случаи умножения и деления. Числа в пределах тысячи – материал, на котором происходит овладение темой. Программа рекомендует операции деления и умножения трехзначных и двузначных чисел производить на примере однозначных. В ходе работы над темой учитель начинает формировать у детей такой важный навык, как умножение и деление столбиком. В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
Что является основой умножения
Главные положения, на которых строится алгоритм умножения многозначного числа на многозначное, являются теми же, что при действиях на однозначное. Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.
Первым правилом является поразрядность операций. Второе заключается в использовании таблицы умножения в каждом разряде.
Необходимо учесть, что эти основные положения усложняются при выполнении действий с многозначными числами.
Записанный ниже пример позволит понять, о чем идет речь. Допустим, необходимо 80 х 5 и 80 х 50.
В первом случае ученик рассуждает так: 8 десятков необходимо повторить 5 раз, получатся тоже десятки, и их будет 40, так как 8 х 5 = 40, 40 десятков – это 400, значит, 80 х 5 = 400. Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Чтобы найти значение второго выражения, тоже необходимо воспользоваться табличным случаем и 8 х 5. Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
В результате совместных усилий педагога и детей становится ясно, что для умножения многозначного числа на многозначное необходимо умение применять сочетательный закон, при котором один из множителей заменяется произведением (80 х 50 = 80 х 5 х 10 = 400 х 10 = 4000)
Кроме того, возможен путь, когда используется распределительный закон умножения относительно сложения или вычитания. В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
Исследовательская работа детей
Ученикам предлагается достаточно большое количество примеров подобного вида. Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.
Учитель делает это, преследуя две цели. Во-первых, дети осознают, отрабатывают основные пути выполнения операции умножения на многозначное число. Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.
Этапы изучения умножения на многозначное число.
В методических рекомендациях изучение указанной темы происходит в несколько этапов. Они должны следовать один за другим, давая возможность школьникам понять весь смысл изучаемого действия. Перечень этапов открывает учителю общую картину процесса подачи материала детям:
- самостоятельный поиск учениками способов нахождения значения произведения многозначных множителей;
- для решения поставленной задачи используется сочетательное свойство, а также умножение на единицу с нулями;
- отработка навыка умножения на круглые числа;
- использование при вычислениях распределительного свойства умножения относительно сложения и вычитания;
- операции с многозначными числами и умножение в столбик.

Следуя указанным этапам, учитель постоянно должен обращать внимание детей на тесные логические связи ранее изученного материала с тем, что осваивается в новой теме. Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.
Задачи изучения умножения в курсе начальной школы
Учитель, преподавая математику, точно знает, что наступит момент, когда у четвероклассников возникнет вопрос о том, как решать столбиком умножение многозначных чисел. И если он вместе с учениками на протяжении трех лет обучения – во 2, 3, и 4 классах – целенаправленно и вдумчиво изучал конкретный смысл умножения и все вопросы, которые связаны с этой операцией, то трудностей в освоении рассматриваемой темы у детей возникнуть не должно.
Какие же задачи ранее были решены учениками и их преподавателем?
- Освоение табличных случаев умножения, то есть получение результата в один шаг. Обязательным требованием программы является доведение навыка до автоматизма.

- Умножение многозначного числа на однозначное. Результат получается путем многократного повторения шага, которым дети уже владеют в совершенстве.
- Умножение многозначного числа на многозначное осуществляется благодаря повторению шагов, обозначенных в пункте 1 и 2. Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Использование свойств умножения
Перед тем как на последующих страницах учебников начнут появятся примеры умножения столбиком, 4 класс должен очень хорошо научиться пользоваться для рационализации вычислений сочетательным и распределительным свойством.
Путем наблюдений и сопоставлений ученики приходят к выводу, что сочетательное свойство умножения для нахождения произведения многозначных чисел используется только тогда, когда один из множителей можно заменить произведением однозначных чисел. А это возможно не всегда.
Распределительное свойство умножения в этом случае выступает как универсальное. Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Алгоритм записи действия умножения в столбик
Запись умножения столбиком является самой компактной из всех существующих. Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.
Детям предлагается самостоятельно составить последовательность действий при выполнении умножения. Знание этого алгоритма станет залогом успешного формирования навыка. Поэтому учителю не нужно жалеть времени, а постараться приложить максимум усилий к тому, чтобы порядок выполнения действий при умножении в столбик был усвоен детьми на «отлично».
Упражнения для формирования навыка
Прежде всего нужно отметить, что примеры умножения в столбик, предлагаемые детям, от урока к уроку усложняются. После знакомства с умножением на двузначное число дети учатся выполнять действия с трехзначными, четырехзначными числами.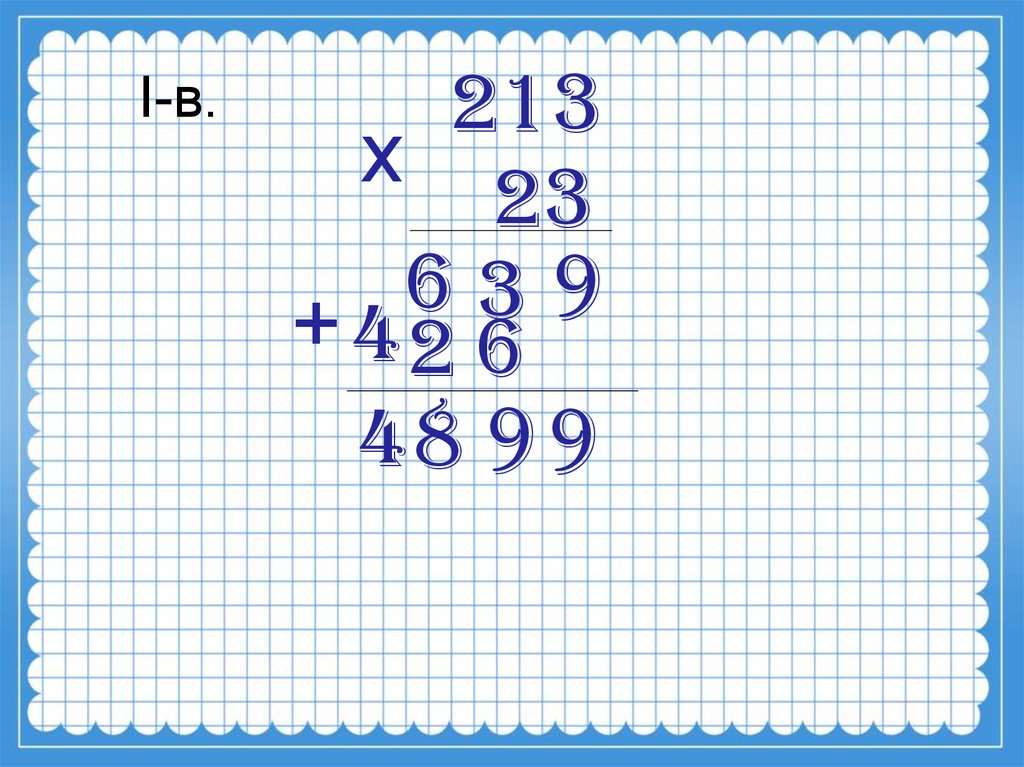
Для отработки навыка предлагаются примеры с готовым решением, но среди них преднамеренно размещают записи с ошибками. Задача учеников состоит в том, чтобы обнаружить неточности, объяснить причину их появления и исправить записи.
Теперь при решении задач, уравнений и всех других заданий, где надо выполнять умножение многозначных чисел, от учеников требуется оформление записи столбиком.
Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»
Большое внимание на уроках, посвященных изучению указанной темы, уделяется развитию таких познавательных действий, как нахождение разных способов решения поставленной задачи, выбор наиболее рационального приема.
Использование схем для проведения рассуждений, установление причинно-следственных связей, анализ наблюдаемых объектов на основе выделенных существенных признаков – еще одна группа формируемых познавательных умений при изучении темы «Умножение в столбик».
Обучение детей способам деления многозначных чисел и оформлению записи столбиком осуществляется только после того, как дети научатся умножать.
Умножить на процент — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Дополнительно… Меньше
Примечание: Если вам нужно найти процент от суммы или найти процент изменения между двумя числами, вы можете узнать больше в статье Расчет процентов.
Допустим, вам нужно уменьшить или увеличить еженедельные расходы на еду на 25%. Чтобы рассчитать сумму, используйте формулу для вычитания или добавления процента.
В этом примере столбец B содержит текущую потраченную сумму, а столбец C – процент, на который эту сумму нужно уменьшить. Вот формула, которую вы можете ввести в ячейку D2, чтобы добиться этого:
.
=В2*(1-С2)
В этой формуле 1 соответствует 100%. Значения в скобках вычисляются первыми, поэтому значение C2 вычитается из 1, что дает нам 75%. Результат умножается на B2, чтобы получить результат 56,25 за неделю 1.
Чтобы скопировать формулу из ячейки D2 вниз по столбцу, дважды щелкните маленький зеленый квадратик в правом нижнем углу ячейки D2. Вы получаете результаты во всех других ячейках без повторного ввода или копирования и вставки формулы.
К увеличьте сумму на 25%, просто замените знак + в формуле в ячейке D2 на знак минус ( — ):
=В2*(1+С2)
Затем снова дважды щелкните маркер заполнения.
Умножить весь столбец чисел на процент
Рассмотрим пример таблицы, такой как на рисунке, в которой у нас есть несколько чисел, которые нужно умножить на 15 процентов. Даже если в столбце содержится 100 или 1000 ячеек данных, Excel все равно может обработать их за несколько шагов.
Вот как это сделать:
Введите в столбец числа, которые нужно умножить на 15%.

В пустой ячейке введите процентное значение 15 % (или 0,15), а затем скопируйте это число, нажав Ctrl + C.
Выберите диапазон ячеек A1:A5 (перетаскивая столбец вниз).
Щелкните правой кнопкой мыши выделенную ячейку и выберите Специальная вставка (не , а щелкните стрелку рядом с Специальная вставка ).
Щелкните Значения > Умножьте , затем щелкните OK .
В результате все числа умножаются на 15%.
Совет: Вы также можете умножить столбец, чтобы вычесть процент. Чтобы вычесть 15%, добавьте знак минус перед процентом и вычтите процент из 1, используя формулу =1- n % , где n — это процент. Чтобы вычесть 15%, используйте формулу
Чтобы вычесть 15%, используйте формулу
=1-15% .
Умножить весь столбец чисел на процент
В этом примере у нас есть всего несколько чисел, которые нужно умножить на 15 процентов. Даже если в столбце содержится 100 или 1000 ячеек данных, Excel в Интернете все равно может обработать их за несколько шагов. Вот как:
Введите =A2*$C$2 в ячейку B2. (Обязательно включите в формулу символ $ перед C и перед 2.)
Символ $ делает ссылку на ячейку C2 абсолютной, что означает, что при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали символы $ в формуле и перетащили формулу в ячейку B3, Excel в Интернете изменит формулу на =A3*C3, что не сработает, так как в ячейке C3 нет значения.
org/ListItem»>
Перетащите формулу из ячейки B2 в другие ячейки столбца B.
Совет: Вы также можете умножить столбец, чтобы вычесть процент. Чтобы вычесть 15%, добавьте знак минус перед процентом и вычтите процент из 1, используя формулу =1- n %, где
n — это процент. Таким образом, чтобы вычесть 15%, используйте 9.0005 =1-15% как формула.
Как умножать ячейки и числа в Excel с помощью 3 методов
- Вы можете умножать в Excel, используя несколько различных методов.
- В Excel легко умножить два числа, но вы также можете перемножить множество разных ячеек и чисел или умножить столбец значений на константу.
- Посетите домашнюю страницу Business Insider, чтобы узнать больше.
Умножение значений — одна из наиболее часто выполняемых функций в Excel, поэтому неудивительно, что это можно сделать несколькими способами.
Вы можете использовать любой метод, который лучше всего подходит для того, что вы пытаетесь выполнить в своей электронной таблице на Mac или ПК.
Вот несколько простейших вариантов выполнения умножения.
Ознакомьтесь с продуктами, упомянутыми в этой статье:
Microsoft Office 365 Home (от $99,99 в Best Buy)
MacBook Pro (от $1299,99 в Best Buy)
Lenovo IdeaPad 130 (от $299,99 в Best Buy)
9029 9013 Самый простой способ сделать это — умножить числа в одной ячейке с помощью простой формулы.
Например, если вы введете «=2*6» в ячейку и нажмете Enter на клавиатуре, вы должны увидеть в ячейке «12».
Самый простой способ умножить числа — использовать звездочку. Дэйв Джонсон/Business InsiderВы также можете перемножить две разные ячейки.
1. В ячейке введите «=»
2. Щелкните ячейку, содержащую первое число, которое нужно умножить.
3. Введите «*».
4. Щелкните вторую ячейку, которую нужно умножить.
5. Нажмите Enter.
Вы можете ссылаться на ячейки в формуле умножения, щелкая их. Дэйв Джонсон/Business Insider
Как умножать ячейки и числа с помощью формулы ПРОИЗВЕД
Вы не ограничены умножением только двух ячеек — вы можете умножать до 255 значений одновременно, используя формулу ПРОИЗВЕД.
Используя эту формулу, вы можете умножать отдельные ячейки и числа, разделяя их запятыми, и умножать ряды ячеек с помощью двоеточия.
Например, в формуле «=ПРОИЗВ(A1,A3:A5,B1,10)» — Excel умножит (A1 x A3 x A4 x A5 x B1 x 10), поскольку A3:A5 указывает, что следует умножить A3 , А4 и А5.
Помните, что порядок этих ячеек и чисел не имеет значения при умножении.
Как умножить столбец значений на константу
Предположим, у вас есть ряд чисел и вы хотите умножить каждое из них на одно и то же значение.
1. Настройте столбец чисел, которые вы хотите умножить, а затем поместите константу в другую ячейку.
2. В новой ячейке введите «=» и щелкните первую ячейку, которую нужно умножить.
3 . Введите имя ячейки, содержащей константу, добавив «$» перед буквой и цифрой. Знак доллара превращает его в абсолютную ссылку, поэтому он не изменится, если вы скопируете и вставите его в электронную таблицу.
$ — это мощный инструмент для ссылки на ячейки в формуле. Дэйв Джонсон/Business Insider
4. Нажмите Enter.
5. Теперь вы можете скопировать и вставить это в дополнительные ячейки, чтобы выполнить умножение на другие числа. Самый простой способ сделать это — перетащить ячейку за правый нижний угол, чтобы скопировать ее.
Когда вы копируете формулу вниз по столбцу чисел, вы можете умножать набор чисел на другой набор или на константу. Дэйв Джонсон/Business Insider
Дэйв Джонсон/Business Insider
Четыре способа объединения и разделения ячеек в Microsoft Excel для очистки данных и форматирования
Как заблокировать ячейки в Microsoft Excel, чтобы люди, которым вы отправляете электронные таблицы, не могли изменить определенные ячейки или данные
Как расположить данные в электронной таблице Excel в алфавитном порядке по столбцам или строкам, а также с помощью сочетаний клавиш
Как встроить видео YouTube в презентацию PowerPoint, в зависимости от версии PowerPoint
Дэйв Джонсон
Внештатный писатель
Дэйв Джонсон — журналист, пишущий о потребительских технологиях и о том, как индустрия трансформирует спекулятивный мир научной фантастики в современную реальную жизнь.
Умножение десятичных дробей на натуральные числа. 5 класс. Урок-игра – конспект урока – Корпорация Российский учебник (издательство Дрофа – Вентана)
авторы: Печенкина Наталья Николаевна, учитель математики МКОУ школа-интернат №1 г.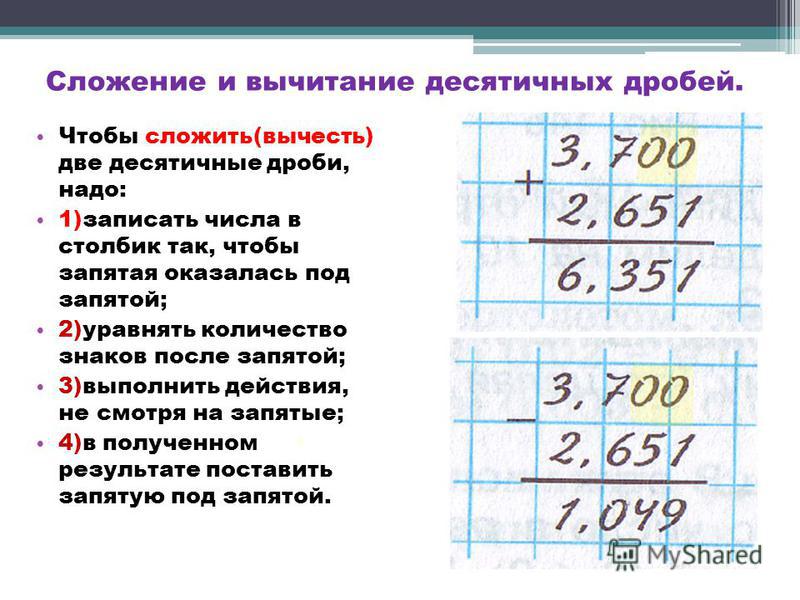 Кирова
Кирова
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Тип урока: урок получения новых знаний и умений.
Урок игра-путешествие.
Цель урока: изучить правило умножения десятичных дробей на натуральные числа, первичное закрепление правила.
Задачи урока:
- Образовательные: повторение правил действий над десятичными дробями (сложение, вычитание), вывод правила умножения десятичных дробей на натуральное число, начать формировать умения и навык умножения десятичных дробей на натуральные числа.
- Развивающие: коррекция логического и творческого мышления на основе развивающих упражнений; коррекция внимания и памяти в процессе выполнения коррекционных упражнений, продолжить развивать способности к самоконтролю учащихся, кругозор, коммуникативные способности.

- Воспитательные: продолжить воспитание ответственного отношения к делу, организованности, аккуратности, интереса к предмету; воспитывать культуру математической речи и записей.
Использованные источники:
- Математика. 5 класс. Г.К. Муравин, О.В. Муравина
- Математика 5, Н.Я. Виленкин, В.И Жохов, А.С. Чесноков, С.И. Шварцбурд
- Математика. 5-11 классы. Электронное пособие.
1. Организационный момент
Включает в себя приветствие учащихся класса, проверку отсутствующих.
2. Актуализация знаний
Работа в парах по карточкам с проверкой ответов по таблице соответствия.
Мы с вами пятый год плаваем по бескрайнему морю Математики в поисках истины и знаний. Сегодня мы отправимся в далекое путешествие за сокровищами. Как вы думаете, какие сокровища вы можете найти на уроке математики?
– Правильно, самыми ценными сокровищами, добытыми на уроке являются знания. Если вы будете внимательны, то без труда овладеете кладом! А ещё сегодня на уроке мы побываем на охоте – «Охоте за пятерками». Но для этого нам необходимо взять с собой оружие – знания и умения, внимательность и смекалку.
Если вы будете внимательны, то без труда овладеете кладом! А ещё сегодня на уроке мы побываем на охоте – «Охоте за пятерками». Но для этого нам необходимо взять с собой оружие – знания и умения, внимательность и смекалку.
Напоминаю вам, что вы уже знакомы с натуральными числами, то есть числами, которые используют для счета предметов и дробными числами, среди которых выделяют десятичные дроби. При этом вы умеете выполнять арифметические действия над теми и другими числами. Давайте вспомним, как удобно складывать и вычитать десятичные дроби?
– Правильно, столбиком. Не забывайте, что при сложении столбиком целую часть записывают под целой, а дробную под дробной, при этом запятая оказывается под запятой. Итак, начнем нашу охоту с небольшой самостоятельной работы (3 минуты):
|
1 вариант |
2 вариант |
Ответы: |
|
1,5 + 2,7 |
2,3 + 1,9 |
4,2 – Е |
|
10,5 – 8,6 |
6 – 4,1 |
1,9 – Н |
|
3 + 5,8 |
9,8 – 1 |
8,8 – П |
|
22,45 – 13,05 |
4,7 + 4,7 |
9,4 – Е |
|
27,4 + 27,4 |
100,67 – 45,87 |
54,8 – Р |
Выпишите ответы в порядке возрастания, то есть от самого маленького числа к самому большому и составьте слово с помощью таблицы соответствия. Вы получили фамилию известного математика Джона Непера, который в 17 веке ввел в обозначение десятичных дробей запятую. До этого времени целую и дробную части разделяли более сложным знаком – (0). Например: 5(0)6 или 78(0)65
Вы получили фамилию известного математика Джона Непера, который в 17 веке ввел в обозначение десятичных дробей запятую. До этого времени целую и дробную части разделяли более сложным знаком – (0). Например: 5(0)6 или 78(0)65
3. Мотивация
Итак, складывать и вычитать десятичные дроби вы умеете хорошо, а какие действия вы ещё не умеете выполнять с десятичными дробями?
– Конечно же, умножать: умножать на натуральные числа и друг на друга, но обо всем по порядку! Сегодня я постараюсь показать вам как важно уметь умножать десятичные дроби на натуральные числа и делать это правильно. А вы постарайтесь понять, запомнить и научиться применять правило умножения десятичных дробей.
– Итак, к какой цели мы помчимся с вами по волнам сегодняшнего урока?
(Дети отвечают: наша цель научиться выполнять умножение десятичных дробей на натуральные числа.)
Пусть это будет целью вашего сегодняшнего путешествия.
Поднять носы и паруса, наше путешествие считаю открытым!
4. Новый материал
Итак, запишите в тетради число, «Классная работа» и тему нашего урока: «Умножение десятичных дробей на натуральные числа».
И вот мы уже подплыли к острову Блестящих вычислений.
Пожалуйста, вычислите ответ к задачам:
Задача 1. Масса каждого из трех сундуков равна 23 кг. Сколько весят все три сундука?
23 + 23 + 23 = 23 · 3 = 69 (кг) – весят три сундука
Задача 2. Масса каждого из трех ларцов равна 2,3 кг. Сколько весят все три ларца?
2,3 + 2,3 + 2,3 = 6,9 (кг)
Давайте запишем в тетради:
|
Задача 1 |
Задача 2 |
|
23 + 23 + 23 = 23 · 3 = 69 (кг) |
2,3 + 2,3 + 2,3 = 6,9 (кг) |
– Заметим, что ответы к обеим решенным задачам очень похожи друг на друга, как и сами задачи.
Мы отплываем от острова Вычислений, так как справились с его заданиями на отлично!
И сразу же попадаем на остров Несложных вопросов, хотя будет ли сложен вопрос для такой дружной команды умных матросов с таким отличным капитаном – помощником?
Как короче записать сумму 2,3 + 2,3 + 2,3?
Итак, вы опять на высоте! Абсолютно верно, эту сумму можно заменить произведением 3·2,3. Поэтому допишем во второй столбик
|
Задача 1 |
Задача 2 |
|
23 + 23 + 23 = 23 · 3 = 69 (кг) |
2,3 + 2,3 + 2,3 = 6,9 (кг) 3 · 2,3 = 6,9 (ответ мы уже знаем) |
– Молодцы команда! Но этот остров коварен, он не отпускает нас просто так, нас закручивает Трудное течение!
Чем отличаются примеры? А чем отличаются ответы? Попробуйте сами рассказать, как можно было получить ответ к этой задаче и как можно было быстро вычислить его?
Прекрасно, умнички! А сейчас давайте всё же узнаем четкое правило умножения десятичных дробей на натуральные числа, ведь десятичные дроби бывают разными. Откройте, пожалуйста, учебник на странице 204.
Откройте, пожалуйста, учебник на странице 204.
Правило: чтобы умножить десятичную дробь на натуральное число надо
- умножить её на это число не обращая внимания на запятую,
- отделить в полученном произведении справа столько цифр, сколько их после запятой в исходной десятичной дроби.
– Обращаю ваше внимание на схему, которая появилась на доске. Этот пример– схема будет сопровождать нас всё путешествие. А особое внимание обратите на правый край этого примера – посмотрите, он выровнен, потому что мы умножаем десятичные дроби, не обращая внимания на запятую, как обычные натуральные числа.
Давайте выполним задания №1306 стр. 205, используя новое правило (решения на доске с проговариванием правила):
- 8,9 · 6 = 53,4
- 3,75 · 12 = 45
- 0,075 · 24 = 1,8
- 10,45·42 = 438,9
5.
 Физкультминутка
ФизкультминуткаДинамическая игра: Внимание, внимание, мы приближаемся к острову Неисправленных ошибок. SOS, SOS. Чтобы не сесть на мель нам надо потрудиться!!! Каждый должен приложить свои усилия, торопитесь исправить ошибки! (на пол хаотично выкладываются примеры с пропущенными знаками, дети подбегают, наклоняются, поднимают пример, исправляют в нем ошибку, с помощью маркеров, и крепят к доске с помощью магнитов. Проверку проводят гости-эксперты, которые, как и дети вспомнили правило умножения десятичных дробей).
6. Остров Успеха
А мы плавно подплываем к острову Успеха. Здесь всё зависит от вас, от вашей внимательности, от вашей сосредоточенности, от вашего желания. Я отпускаю вас в свободное плавание и желаю вам счастливого пути, но буду все время рядом, чтобы помочь и ответить на все ваши вопросы. А также прошу вас не забывать о том, как важна точность в расчетах и со мной соглашаются даже писатели детских стихов (указать на стенд со стихом). Маршрут дальнейшего плавания указан на доске.
Маршрут дальнейшего плавания указан на доске.
Дети приступают к самостоятельному решению в тетради:
- №1306 д) –м)
- №1309
- №1307
- 8№1330
7. Домашнее задание
«Авось да как-нибудь до добра не доведут».
– А как вы думаете, что означают эти слова?
(Каждое действие должно быть обдуманным, просчитанным, тогда и результат будет успешным.)
Пусть эти слова будут девизом при выполнении домашних заданий.
П. 34, стр. 204, прочитать и выучить правило умножения десятичных дробей на натуральные числа, №1330 (доделать), 1308.
Творческое задание: сочинить рассказ о приключениях на острове “Десятичных дробей” или сказку, персонажами которой были бы десятичные дроби и другие числа.
8. Подведение итогов
Настало время подвести итоги нашего урока:
Чему мы научились за время путешествия? Что нового мы узнали? (правило и ещё раз его проговариваем).
Удалось ли справиться с целью, поставленной в начале урока?
Отметьте свое настроение, полученное на уроке – путешествии на корабле с помощью одного из 3 смайликов. Вы можете подойти, приклеить смайлик и идти на следующий урок.
Общие базовые стандарты: CCSS.Math.Content.HSN-VM.C.8
- Главная /
- Общие основные стандарты /
- Математика
Стандарты
- О
- Средняя школа: номер и количество
- О
- Вещественная система счисления
- Величины
- Комплексная система счисления
- Векторные и матричные величины
- Средняя школа: Алгебра
- Средняя школа: Функции
- Средняя школа: Моделирование
- Средняя школа: геометрия
- Средняя школа: статистика и вероятность
- 8 класс
- 7 класс
- 6 класс
- 5 класс
- 4 класс
- 3 класс
- 2 класс
- 1 класс
- Детский сад
Количество векторов и матриц HSN-VM.
 C.8
C.8- Стандарт
- Примеры заданий
- Выровненные ресурсы
8. Сложите, вычтите и умножьте матрицы соответствующих размеров.
Это говорит само за себя.
И сложение, и вычитание матриц невероятно просты. Если ваши ученики прогуляли урок в тот день, когда вы преподавали сложение и вычитание матриц, они, вероятно, были бы правы, если бы просто догадались, как это делать. Естественно, они ответственные дети и никогда бы не подумали о том, чтобы бросить такой увлекательный урок, как ваш.
Правило состоит в том, чтобы просто складывать или вычитать числа, которые находятся в одном и том же месте. Таким образом, число в верхнем левом углу прибавляется или вычитается из числа в верхнем левом углу.
Учащиеся должны понимать одно важное понятие о сложении и вычитании матриц разных размеров. Это невозможно сделать. Матрицы должны иметь одинаковое количество строк и столбцов для выполнения этих конкретных операций.
Вот несколько примеров.
Дополнение
Вычитание
Что касается умножения, мы должны быть с вами откровенны. Это довольно сложно.
Вот как работает умножение: двигаемся по верхней строке первой матрицы и вниз по второй строке второй. Умножьте элементы, а затем сложите их.
Нет, мы не шутим. Мы не настолько жестоки, чтобы шутить над чем-то вроде этого.
Итак, прежде чем мы начнем, для умножения количество столбцов первой матрицы должно равняться количеству строк второй. В противном случае они не могут быть умножены.
Возможно, сначала вы захотите поосторожнее со студентами и начнете с квадратных матриц.
Сначала мы перемещаемся по верхнему ряду по мере продвижения вниз по первому столбцу. Ответ идет в верхней строке, первый столбец.
3 × 2 + 5 × 8 = 46
Теперь верхний ряд, второй столбец.
3 × 6 + 5 × 9 = 63
Это наши два числа для верхней строки. Теперь мы перейдем к нижней строке этой первой матрицы, начиная с первого столбца.
Теперь мы перейдем к нижней строке этой первой матрицы, начиная с первого столбца.
1 × 2 + 4 × 8 = 34
И, наконец, посчитаем нижнюю строку, второй столбец.
1 × 6 + 4 × 9 = 42
Это означает, что наша результирующая матрица равна .
Учащиеся должны знать, что это не так уж и плохо, как только они освоятся. Есть две хитрости. Первый — это физическое перемещение пальцев по матрицам и вниз, чтобы мы знали, какие числа нужно умножать и складывать. Во-вторых, знать, куда поместить ответ. Просто посмотрите, какую строку вы умножили на какой столбец, и это будет ответом.
Наконец, учащиеся должны знать не только, как выполнять эти функции, но и как обращаться за помощью, если она им понадобится. Матрицы — друзья, но с ними не всегда легко ужиться.
Вот краткое видео о перемножении матриц.
Сверла
Чему равна сумма следующих матриц?
- (А) (Б) (В) (Г)
Правильный ответ:
Объяснение ответа:
Помните, добавлять легко.
 Вы просто добавляете записи, которые занимают одни и те же места, и ставите суммы в это место. Складывать и вычитать не так уж и безумно. Мы должны следить за умножением.
Вы просто добавляете записи, которые занимают одни и те же места, и ставите суммы в это место. Складывать и вычитать не так уж и безумно. Мы должны следить за умножением.Вычесть.
- (А) (Б) (В) (Г)
Правильный ответ:
Объяснение ответа:
Помните, что мы вычитаем числа в одном и том же месте, а затем записываем то, что получается. Итак, наша верхняя строка 10 – 3 = 7, за которой следуют 2 – 6 или -4. Нижняя строка 4 – (-1), что равно 5, затем 6 – 0, что равно 6. Наш ответ всегда должен быть того же размера, что и две матрицы, с которых мы начали, поэтому (C) и (D) не равны. верно.
Чему равна сумма следующих матриц?
- (А) (Б) (В) (Г)
Правильный ответ:
Объяснение ответа:
Если мы складываем две матрицы, все, что нам нужно сделать, это объединить числа в соответствующих местах, и это наш ответ. Мы можем выполнить базовые арифметические действия (надеюсь), поэтому в итоге получим (C) в качестве ответа.

Можно ли перемножать следующие матрицы?
- (A) Нет, потому что их размерности не совпадают (B) Да, потому что размерности перемножаемых матриц не имеют значения (C) Да, потому что количество строк в первой матрице равно количеству столбцов в вторая матрица (D) Нет, потому что матрицы нельзя перемножать
Правильный ответ:
Да, потому что количество строк в первой матрице равно количеству столбцов во второй матрице
Объяснение ответа:
Мы говорили вам, что перемножать матрицы сложно. Поскольку умножение матриц происходит путем умножения строк на столбцы, количество строк в первой матрице должно совпадать с количеством столбцов во второй матрице.
То же, что и ?
- (A) Да, из-за коммутативного свойства умножения (B) Нет, потому что строки умножаются на столбцы (C) Нет, потому что строки умножаются вместе (D) Нет, потому что столбцы умножаются вместе
Правильный ответ:
Нет, потому что строки умножаются на столбцы
Объяснение ответа:
Мы можем сделать быстрый расчет, чтобы перепроверить.
 Если у нас есть , первое число будет aw + на . Если бы матрицы были перевернуты по порядку, первое число было бы wa + cx . Поскольку на не обязательно должно равняться cx , порядок имеет значение, поскольку строки умножаются на столбцы. Это также прелюдия к следующему стандарту.
Если у нас есть , первое число будет aw + на . Если бы матрицы были перевернуты по порядку, первое число было бы wa + cx . Поскольку на не обязательно должно равняться cx , порядок имеет значение, поскольку строки умножаются на столбцы. Это также прелюдия к следующему стандарту.Чему равно произведение следующих матриц?
- (А) (Б) (В) (Г)
Правильный ответ:
Ответ Пояснение:
Если мы умножим первую строку на первый столбец, мы получим 3 × 2 + 5 × -7 = -29. Если мы продолжим умножать как таковые (или просто остановимся на этом), мы сможем сказать, что (С) является правильным ответом. Видеть? Это не слишком сложно, правда? Во всяком случае, пока нет.
Чему равно произведение следующих матриц?
- (A) Перемножить эти матрицы вместе невозможно (B) (C) (D)
Правильный ответ:
Ответ Пояснение:
Во-первых, мы знаем, что эти две матрицы можно перемножить, потому что количество строк совпадает с количеством столбцов второй.
 Если мы умножим первую строку на первый столбец, мы получим 3 × 2 + 5 × 3 +6 × -6 = -15. Первая строка, умноженная на второй столбец, равна 3 × -1 + 5 × 6 + 6 × 0 = 27. Этого достаточно, чтобы указать нам на (B).
Если мы умножим первую строку на первый столбец, мы получим 3 × 2 + 5 × 3 +6 × -6 = -15. Первая строка, умноженная на второй столбец, равна 3 × -1 + 5 × 6 + 6 × 0 = 27. Этого достаточно, чтобы указать нам на (B).Как решить следующую проблему?
- (A) Невозможно выполнить эту функцию (B) (C) (D)
Правильный ответ:
Ответ Объяснение:
Квадрат матрицы равен . Умножение первой строки и первого столбца дает нам -4 × -4 + 2 × 3 = 22. Если бы мы продолжали умножать, мы бы получили (C) в качестве матрицы.
Чему равно произведение следующих матриц?
- (A) Перемножить эти матрицы вместе невозможно (B) (C) (D)
Правильный ответ:
Ответ Объяснение:
Перемножить эти матрицы можно, потому что строки и столбцы совпадают. Если мы умножим 2 × 5 + 0 × 6 + 4 × 1 = 14. Тогда первая строка, умноженная на второй столбец, будет 2 × 4 + 0 × 3 + 4 × -2 = 0. Поскольку это все еще было в первом row, мы знаем, что для каждой строки результирующей матрицы требуется два столбца.
 Единственная матрица, которая удовлетворяет всем этим, это (B).
Единственная матрица, которая удовлетворяет всем этим, это (B).Как решить следующую проблему?
- (A) Выполнение этой функции невозможно (B) (C) (D)
Правильный ответ:
Выполнение этой функции невозможно
Объяснение ответа:
На самом деле мы пытаемся умножить . Матрицы имеют 2 строки и 3 столбца, и мы умножаем их вместе. Дело в том, что мы не можем этого сделать. Строки и столбцы не совпадают, поэтому возвести матрицу в квадрат невозможно.
Совмещенные ресурсы
- ACT Math 5.5 Алгебра среднего уровня
- ACT Math 5.2 Алгебра среднего уровня
- Матричные операции
Видео
- ПРЕДЫДУЩИЙ СТАНДАРТ
- СЛЕДУЮЩИЙ СТАНДАРТ
Дополнительные стандарты средней школы: количество и количество — векторные и матричные количества
- HSN-VM.A.1
- HSN-VM.
 B.4
B.4 - HSN-VM.C.7
- HSN-VM.C.10
- HSN-VM.B.5
- HSN-VM.C.8
- HSN-VM.C.11
- HSN-VM.A.3 6666 .C.6
- HSN-VM.C.9
- HSN-VM.C.12
- Сложение и вычитание матриц
- Шаг 1: Убедитесь, что можно перемножить две матрицы (количество столбцов в первой должно быть таким же, как количество строк во второй).

- Шаг 2: Элементы каждой строки первой матрицы следует умножить на элементы каждого столбца второй матрицы.
- Шаг 3: Добавьте продукты.
- \(\color{синий}{\begin{bmatrix}0 и 2 \\-2 и -5 \end{bmatrix}\begin{bmatrix}6 и -6 \\3 и 0 \end{bmatrix} }\)
- \(\color{blue}{\begin{bmatrix}3 & -1 \\-3 & 6\\-6&-6 \end{bmatrix}\begin{bmatrix}-1 & 6 \\ 5 и 4\end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}0 & 5 \\-3 & 1\\-5&1 \end{bmatrix}\begin{bmatrix}- 4 и 4 \\-2 и -4\end{bmatrix}}\)
- \(\color{синий}{\begin{bmatrix}5 и 3&5 \\1 и 5&0 \end{bmatrix}\begin{bmatrix}-4 и 2 \\-3 & 4\\3&-5 \end {bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}4 и 5 \\-4 и 6\\-5&-6 \end{bmatrix}\begin{bmatrix}4 и 6 \ \6& 2\\-4&1 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-2 & -6 \\-4 & 3\\5&0 \\4&-6\ end{bmatrix}\begin{bmatrix}2 & -2&2 \\-2 &0&-3 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}6 & 0 \\ -27 и 12 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-8 и 14 \\33 & 6\\ -24&-60\end{bmatrix}}\)
- \(\color{blue}{\begin {bmatrix}-10 и -20 \\10 и -16\\ 18&-24\end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-14 & -3 \\- 19 и 22 \end{bmatrix}}\)
- \(\color{blue}{Undefined}\)
- \(\color{blue}{\begin{bmatrix}8 & 4&14\\-14 & 8&- 17\\10&-10&10 \\20&-8&26\end{bmatrix}}\)
9
.2
Если бы мне пришлось обучать Common Core, я бы тоже использовал Shmoop.
Аристотель
Наблюдаемый гравитационный эффект между действиями Общего Ядра является результатом их деформации Шмуптайма.
Альберт Эйнштейн
Как умножить матрицу? (+ БЕСПЛАТНЫЙ рабочий лист!)
Вот пошаговое руководство по умножению матриц. Упражнения могут помочь вам измерить свои знания об умножении матриц.
См. также
Пошаговое руководство по умножению матриц
Умножение матриц – Пример 1:
\(\begin{bmatrix}-5 & -5 \\-1 & 2 \end{bmatrix}\)\(\begin{bmatrix}-2 & -3 \\ 3 и 5 \end{bmatrix}\)
Решение:
Умножьте строки первой матрицы на столбцы второй матрицы. \(\begin{bmatrix}(-5)(-2)+(-5)(3) & (-5)(-3)+(-5)(5) \\(-1)(-2) +(2)(3) & (-1)(-3)+(2)(5) \end{bmatrix}= \begin{bmatrix}(10)+(-15) & (15)+(-25 ) \\(2)+(6) & (3)+(10) \end{bmatrix}=\begin{bmatrix}-5 & -10 \\8 & 13 \end{bmatrix}\)
Умножение матриц – Пример 2:
\(\begin{bmatrix}-4 & -6&-6 \\0 & 6&3 \end{bmatrix}\begin{bmatrix}0 \\-3 \\0 \end{bmatrix}\)
Решение :
Умножьте строки первой матрицы на столбцы второй матрицы. \(\begin{bmatrix}(-4)(0)+(-6)(-3)+(-6)(0) \\(0)(0)+(6)(-3)+(3 )(0) \end{bmatrix}=\begin{bmatrix}0+18+0 \\0-18+0 \end{bmatrix}=\begin{bmatrix}18 \\-18 \end{bmatrix}\)
Умножение матриц – Пример 3:
\(\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}\)\(\begin{bmatrix}2 &4 \\-2 & 1 \end{ bmatrix}\)
Решение :
\(\begin{bmatrix}(1) (2)+(3)(-2) & (1) (4)+(3) (1) \\(2) (2)+ (4) )(-2) & (2) (4)+(4) (1) \end{bmatrix}=\begin{bmatrix}(2)+(-6) & (4)+(3) \\(4 )+ (-8) & (8)+(4) \end{bmatrix}=\begin{bmatrix}-4 & 7 \\-4 & 12 \end{bmatrix}\)
Умножение матриц – пример 4:
\(\begin{bmatrix}2 & -1&-1 \\3 & 1&5 \end{bmatrix}\begin{bmatrix}-2 \\-1 \\4 \end{bmatrix}\)
Решение :
Умножьте строки первой матрицы на столбцы второй матрицы. \(\begin{bmatrix}(2)(-2)+(-1)(-1)+(-1) (4)\\(3)(-2)+(1)(-1)+( 5) (4) \end{bmatrix}=\begin{bmatrix}(-4)+(1)+(-4)\\(-6)+(-1)+(20) \end{bmatrix}= \begin{bmatrix}-7 \\13 \end{bmatrix}\)
\(\begin{bmatrix}(2)(-2)+(-1)(-1)+(-1) (4)\\(3)(-2)+(1)(-1)+( 5) (4) \end{bmatrix}=\begin{bmatrix}(-4)+(1)+(-4)\\(-6)+(-1)+(20) \end{bmatrix}= \begin{bmatrix}-7 \\13 \end{bmatrix}\)
Упражнения для умножения матриц
Решить.
Реза
Реза — опытный преподаватель математики и эксперт по подготовке к экзаменам, который обучает студентов с 2008 года.



 Вы просто добавляете записи, которые занимают одни и те же места, и ставите суммы в это место. Складывать и вычитать не так уж и безумно. Мы должны следить за умножением.
Вы просто добавляете записи, которые занимают одни и те же места, и ставите суммы в это место. Складывать и вычитать не так уж и безумно. Мы должны следить за умножением.
 Если у нас есть , первое число будет aw + на . Если бы матрицы были перевернуты по порядку, первое число было бы wa + cx . Поскольку на не обязательно должно равняться cx , порядок имеет значение, поскольку строки умножаются на столбцы. Это также прелюдия к следующему стандарту.
Если у нас есть , первое число будет aw + на . Если бы матрицы были перевернуты по порядку, первое число было бы wa + cx . Поскольку на не обязательно должно равняться cx , порядок имеет значение, поскольку строки умножаются на столбцы. Это также прелюдия к следующему стандарту. Если мы умножим первую строку на первый столбец, мы получим 3 × 2 + 5 × 3 +6 × -6 = -15. Первая строка, умноженная на второй столбец, равна 3 × -1 + 5 × 6 + 6 × 0 = 27. Этого достаточно, чтобы указать нам на (B).
Если мы умножим первую строку на первый столбец, мы получим 3 × 2 + 5 × 3 +6 × -6 = -15. Первая строка, умноженная на второй столбец, равна 3 × -1 + 5 × 6 + 6 × 0 = 27. Этого достаточно, чтобы указать нам на (B). Единственная матрица, которая удовлетворяет всем этим, это (B).
Единственная матрица, которая удовлетворяет всем этим, это (B). B.4
B.4 