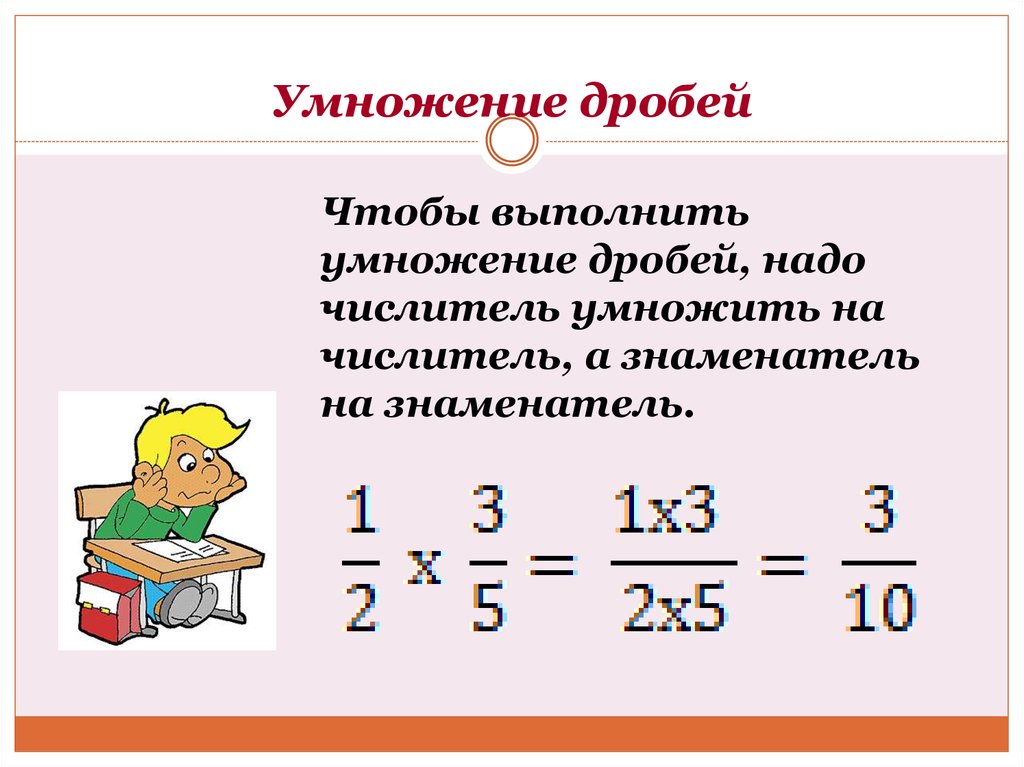
Умножение обыкновенных дробей — урок. Математика, 6 класс. — «Семья и Школа»
Содержание
Отрицательные дроби. Действия с отрицательными дробями
- Сложение и вычитание
- Умножение и деление
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7),
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
| — | 2 | = | -2 | = | 2 | . |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример.
| — | 2 | + (- | 1 | ) | . |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Умножение дробей и смешанных чисел. Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)Поделиться:
 Введите свой запрос: | ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть.Как умножать смешанные числа
Что такое смешанные числа
Смешанное число — это целое число и правильная дробь, представленные вместе.
Обычно представляет собой число между любыми двумя целыми числами.
Посмотрите на данное изображение, оно представляет собой дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число.
Некоторые другие примеры смешанных чисел:
Части смешанного числа
Смешанное число образуется путем объединения трех частей: целого числа, числителя и знаменателя. Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число.
Преобразование смешанных чисел в неправильные дроби
- Умножить целое число на знаменатель дроби.
- Прибавьте ответ, полученный на шаге 1, к числителю дроби.
- Запишите ответ, полученный на шаге 2, над знаменателем.
Предположим, нам нужно преобразовать $2\frac{2}{3}$ в неправильную дробь.
Шаг 1 : Умножаем 3 на 2, получаем 3$\умножить на 2 = 6$.
Шаг 2 : Складываем 6 и 2, получаем 6$ + 2 = 8$
Шаг 3: Полученная дробь равна $\frac{8}{3}$.
Умножение смешанного числа на целое число
Шаг 1: Преобразуйте смешанное число в неправильную дробь.
Шаг 2: Перепишите целое число в виде дроби со знаменателем 1.
Шаг 3: Умножьте две дроби, умножая числители и знаменатели отдельно.
Шаг 4: При необходимости преобразуйте его в упрощенную форму.
Предположим, нам нужно перемножить 3 и $2\frac{1}{2}$.
$2\frac{1}{2}=\frac{2\times2+1}{2}=\frac{5}{2}$
$3\times\frac{5}{2}=\frac {3}{1}\times\frac{5}{2}=\frac{15}{2}=7\frac{1}{2}$
Умножение смешанного числа на дробь
Шаг 1 : Преобразуйте смешанное число в неправильную дробь.
Шаг 2: Умножьте числители дроби и умножьте знаменатели дроби.
Шаг 3: При необходимости преобразовать в упрощенную форму.
Предположим, нам нужно перемножить $\frac{2}{5}$ и $3\frac{1}{2}$.
$3\frac{1}{2}=\frac{3\times2+1}{2}=\frac{7}{2}$
$\frac{2}{5}\times\frac{ 7}{2}=\frac{14}{10}=\frac{7}{5}=1\frac{2}{5}$
Умножение двух смешанных чисел
Шаг 1: Преобразование смешанных чисел числа в неправильные дроби.
Шаг 2: Умножьте две дроби, раздельно умножив числители и знаменатели.
Шаг 3: При необходимости преобразуйте его в упрощенную форму.
Например: умножьте $4\frac{1}{2}$ и $3\frac{1}{3}$.
$4\frac{1}{2}=\frac{4\times2+1}{2}=\frac{9}{2}$
$3\frac{1}{3}=\frac{3 \times3+1}{3}=\frac{10}{3}$
$4\frac{1}{2}\times3\frac{1}{3}=\frac{9}{2}\times \frac{10}{3}=\frac{90}{6}=15$
Заключение
В этой статье мы узнали об умножении смешанных чисел. Смешанные числа также известны как смешанные дроби. Чтобы прочитать больше таких информативных статей о других концепциях, посетите наш веб-сайт. Мы в SplashLearn стремимся сделать обучение интересным и интерактивным для всех учащихся.
Решенные примеры
1. Умножьте $5\frac{3}{7}$ на мультипликативное значение, обратное $7\frac{3}{5}$ .
Решение: $5\frac{3}{7}=\frac{5\times7+3}{7}=\frac{38}{7}$
$7\frac{3}{5} =\frac{7\times5+3}{5}=\frac{38}{5}$
Мультипликативное значение, обратное $\frac{38}{5}$ равно $\frac{5}{38} $.
Продукт $= \frac{38}{7}\times\frac{5}{38}=\frac{5}{7}$
2. Эмма идет 5 2 3 миль в день. Какое расстояние она преодолеет за 9 дней?
Решение: Расстояние, пройденное Эммой за 1 дней $= 5\frac{2}{3}$ миль $=\frac{17}{3}$ миль.
Расстояние, пройденное Эммой за 9 дней $= 9\times\frac{17}{3}= 51$ миль
3. Умножьте $6\frac{2}{5}\times\frac{3} {4}$ .
Решение: $6\frac{2}{5}=\frac{6\times5+2}{5}=\frac{32}{5}$
$\frac{32}{5}\times \frac{3}{4}=\frac{32\times3}{5\times4}=\frac{96}{20}=\frac{24}{ 5}=4\frac{4}{5}$
Практические задачи
1
Какой из этих шагов является первым шагом к умножению смешанных чисел?
Вычисление НОК знаменателей
Умножение числителей
Умножение знаменателей
Преобразование смешанных чисел в неправильные дроби
Правильный ответ: Преобразование смешанных чисел в неправильные дроби
Преобразование смешанных чисел в неправильные дроби
Первым шагом к умножению смешанных чисел является преобразование их в неправильные дроби.
2
При умножении $10\frac{1}{6}$ на $2\frac{2}{11}$ получаем ____.
целое число
смешанное число
правильная дробь
отрицательное число
Правильный ответ: смешанное число
$10\frac{1}{6}\times\frac2{2}{11}=\frac{61} {6}\times\frac{24}{11}=\frac{244}{11}=22\frac{2}{11}$, т. е. смешанное число
3
Значение $4\frac{2}{9}\times1\frac{1}{7}$:
$1\frac{52}{63}$
$2\frac{52} {63}$
$4\frac{52}{63}$
$\frac{61}{63}$
Правильный ответ: $4\frac{52}{63}$
$4\frac{2 {9}\times1\frac{1}{7}=\frac{38}{9}\times{8}{7}=\frac{304}{63}=4\frac{52}{63} $
Часто задаваемые вопросы
Требуются ли одинаковые знаменатели при умножении двух или более смешанных чисел ?
Нет. Нам не нужны одинаковые знаменатели для умножения двух или более смешанных чисел. Мы даже можем умножать непохожие дроби.
Как еще называют смешанные числа?
Другое название смешанных чисел — смешанные дроби.
Всегда ли произведение смешанного числа на другое смешанное число является смешанным числом?
Нет. Смешанное число всегда больше 1. Таким образом, произведение 2 чисел больше 1 всегда будет больше 1, т. е. смешанное/целое число.
Умножение смешанных дробей – шаги, правила, примеры
LearnPracticeDownload
Операция умножения любых двух смешанных дробей называется умножением смешанных дробей. Смешанные дроби можно определить как дробь, состоящую из целого числа и правильной дроби. Это еще один способ представления неправильной дроби. В этой статье мы узнаем больше об этапах и примерах умножения смешанных дробей.
| Умножение смешанных дробей с одинаковыми знаменателями | |
| 2. | Умножение смешанных дробей с разными знаменателями |
3. | Умножение смешанных и правильных дробей |
| 4. | Умножение смешанных дробей на целые числа |
| 5. | Часто задаваемые вопросы по умножению смешанных дробей |
Умножение смешанных дробей с одинаковыми знаменателями
Умножение смешанных дробей с одинаковыми знаменателями определяется как операция умножения двух смешанных дробей с одинаковым знаменателем. Обратите внимание на следующие моменты, которые следует учитывать при умножении смешанных дробей.
- Смешанная дробь \(a\dfrac{b}{c}\) также может быть записана как + (b/c).
- Чтобы преобразовать смешанное число в неправильную дробь, нужно умножить целое число на знаменатель и прибавить результат к числителю правильной дроби, сохранив знаменатель. Например, чтобы преобразовать \(1\dfrac{3}{5}\) в неправильную дробь, мы умножаем 1 и 5, т. е. 1 × 5 = 5, и результат прибавляем к 3, т. е. 5 + 3 = 8. Таким образом, неправильная дробь равна 8/5.
- Чтобы преобразовать неправильную дробь в смешанное число, нужно разделить числитель неправильной дроби на ее знаменатель. Частное становится целой частью числа, остаток становится числителем правильной дроби, а знаменатель остается прежним. Например, чтобы преобразовать 17/5 в смешанное число, мы сначала разделим 17 на 5 и получим частное как 3, а остаток как 2. Таким образом, смешанное число равно \(3\dfrac{2}{5}\) .
Давайте рассмотрим пример, чтобы понять умножение смешанных дробей с одинаковыми знаменателями.
Пример: Перемножьте смешанные дроби \(2\dfrac{2}{7}\) и \(3\dfrac{1}{7}\).
- Шаг 1: Преобразуйте заданные смешанные дроби \(2\dfrac{2}{7}\) и \(3\dfrac{1}{7}\) в неправильные дроби. т. е. \(2\dfrac{2}{7}\) = 16/7 и \(3\dfrac{1}{7}\) = 22/7.
- Шаг 2: Числители и знаменатели этих дробей умножаются отдельно. т. е. (16 × 22) / (7 × 7).
- Шаг 3: Сократите общие делители, если они существуют в числителе и знаменателе. В этом примере нет общих множителей.
- Шаг 4: Выполните расчет. (16 × 22) / (7 × 7) = 352/49.
- Шаг 5: Если результат, полученный на предыдущем шаге, представляет собой неправильную дробь, преобразуйте ее в смешанную дробь. т. е. 352/49 = \(7\dfrac{9}{49}\).
В этом примере нет общих множителей.Умножение смешанных дробей с разными знаменателями
Умножение смешанных дробей с разными знаменателями определяется как умножение двух смешанных дробей с разными знаменателями, например \(1\dfrac{2}{9}\) и \(2\dfrac{1}{4}\).
Шаги для умножения смешанных дробей остаются одинаковыми независимо от одинаковых или разных знаменателей, как обсуждалось в предыдущем разделе. Давайте возьмем пример умножения смешанных дробей, чтобы понять это лучше.
Пример: Перемножим две смешанные дроби \(1\dfrac{2}{9}\) и \(2\dfrac{1}{4}\), имеющие разные знаменатели.
\(1\dfrac{2}{9}\) × \(2\dfrac{1}{4}\)
= (11/9) × (9/4) [При преобразовании их в неправильные дроби ]
= (11 × 9) / (9 × 4)
= 11/4 [путем исключения общих множителей]
= \(2\dfrac{3}{4}\) [путем преобразования в смешанный дробь]
Таким образом, значение \(1\dfrac{2}{9}\) × \(2\dfrac{1}{4}\) равно \(2\dfrac{3}{4}\) .
Умножение смешанных дробей и правильных дробей
Давайте рассмотрим пример, чтобы понять шаги умножения смешанных дробей и правильных дробей.
Пример: Умножьте дробь 1/5 на \(3\dfrac{1}{3}\).
Мы должны выполнить (1/5) × \(3\dfrac{1}{3}\).
- Шаг 1: Преобразуем заданную смешанную дробь в неправильную дробь. т. е. \(3\dfrac{1}{3}\) = 10/3.
- Шаг 2: Теперь мы умножим данную дробь 1/5 на дробь, полученную на предыдущем шаге. т. е. (1/5) × (10/3).
- Шаг 3: Чтобы умножить (1/5) × (10/3), мы умножим числители и знаменатели дробей. т. е. (1 × 10) / (5 × 3).
- Шаг 4: Чтобы упростить это, мы уменьшим общие множители в числителе и знаменателе, что даст нам 2/3.
- Шаг 5: После выполнения расчета получаем в результате 2/3.
- Шаг 6: Если результатом предыдущего шага является неправильная дробь, мы преобразуем ее обратно в смешанную дробь.
Умножение смешанных дробей на целые числа
Операндами при умножении смешанных дробей на целые числа являются смешанная дробь и умножаемое целое число. Целое число можно записать в формате дроби, предполагая, что знаменатель равен 1. Например, 5 можно записать как 5/1. Шаги умножения смешанных дробей на целые числа будут очень похожи на предыдущий раздел. Давайте возьмем пример, чтобы понять это.
Пример: Умножьте смешанную дробь \(2\dfrac{1}{6}\) на целое число 3.
\(2\dfrac{1}{6}\) × 3
= (13/6) × (3/1) [О преобразовании смешанной дроби в неправильную дробь и записи всего числа через дробь]
= (13 × 3) / (6 × 1)
= 13/2 [Отмена общих множителей и вычисление]
= \(6\dfrac{1}{2}\) [Преобразование результата обратно в смешанная дробь]
Так мы делаем умножение смешанных дробей на целые числа.
Статьи по теме Умножение смешанных дробей
Ознакомьтесь с этими статьями, посвященными умножению смешанных дробей.
- Смешанные фракции
- Неправильные дроби
- Правильная дробь
- Дроби
Умножение смешанных дробей Примеры
Пример 1. Умножьте смешанные дроби \(2\dfrac{1}{8}\) и \(4\dfrac{2}{6}\).
Решение: Мы будем следовать шагам умножения смешанных дробей, чтобы решить вопрос. Преобразуем смешанные дроби в неправильные дроби. т. е. \(2\dfrac{1}{8}\) = 17/8 и \(4\dfrac{2}{6}\) = 26/6 = 13/3. Теперь перемножим полученные неправильные дроби 17/8 и 13/3.
(17/8) × (13/3)
= (17 × 13) / (8 × 3)
= 221/24
= \(9\dfrac{5}{24}\)
Таким образом, произведение \(2\dfrac{1}{8}\) и \(4\dfrac{2}{6}\) равно \(9\dfrac{5}{24}\).
Пример 2: Дейзи проходит \(5\dfrac{1}{2}\) км каждый день. Какое расстояние она преодолеет за сентябрь?
Решение: Расстояние, пройденное Daizy за 1 день = \(5\dfrac{1}{2}\) км.
В сентябре месяце 30 дней. Таким образом, чтобы вычислить общее расстояние, пройденное ею в сентябре месяце, воспользуемся понятием умножения смешанных дробей на целые числа.\(5\dfrac{1}{2}\) × 30
= (11/2) × (30/1)
= (11 × 30) / (2 × 1)
= 11 × 15
= 165
Таким образом, всего за сентябрь она преодолела 165 км.
В сентябре месяце 30 дней. Таким образом, чтобы вычислить общее расстояние, пройденное ею в сентябре месяце, воспользуемся понятием умножения смешанных дробей на целые числа.перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по умножению смешанных дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по умножению смешанных дробей
Как решать умножение смешанных дробей?
Умножение смешанных дробей осуществляется путем их преобразования в неправильную дробь с последующим умножением соответствующих числителей и знаменателей по отдельности и упрощением.
Например, \(3\dfrac{5}{7}\) × \(1\dfrac{2}{3}\)
= (26/7) × (5/3)
= (26 × 5) / (7 × 3)
= 130/21
= \(6\dfrac{4}{21}\)
Как умножать смешанные дроби на целые числа?
Для умножения смешанных дробей на целые числа мы запишем целое число в дробной форме, написав в знаменателе 1 и заменив смешанную дробь на неправильную, а затем умножив две дроби. Например, \(1\dfrac{2}{3}\) × (7/1)
= (5/3) × (7/1)
= (5 × 7) / (3 × 1)
= 35/3 = \(11\dfrac{2}{3}\)
Как умножать смешанные дроби на неправильные дроби?
Смешанные дроби сначала преобразуются в неправильную дробь с последующим умножением результата на заданную неправильную дробь. Окончательный результат упрощается и преобразуется обратно в смешанную дробь, если это неправильная дробь.
Например, \(2\dfrac{1}{8}\) × (26/17) 90 183
= (17/8) × (26/17)
= 13/4
= \(3\dfrac{1}{4}\)
Как умножать смешанные дроби с одинаковыми знаменателями?
Умножение смешанных дробей с одинаковыми знаменателями осуществляется путем преобразования смешанных дробей в неправильные с последующим умножением числителей и знаменателей по отдельности и упрощением для получения результата.
Например, \(4\dfrac{2}{3}\)× \(3\dfrac{1}{3}\)
= (14/3) × (10/3)
= (14 × 10) / (3 × 3)
= 140/9
= \(15\dfrac{5}{9}\)
Как умножать смешанные дроби с разными знаменателями?
Умножение смешанных дробей с разными знаменателями можно легко умножить так же, как обычное умножение смешанных дробей.
Калькулятор дробей онлайн (с подробным решением)
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
+−×÷
=
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅
+ 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅
+ 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели.
Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅
6⋅
=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅
+ 1116=11116
См.
такжеУмножение смешанных чисел Образовательные ресурсы K12 Обучение, арифметика, дроби и операции, математика Планы уроков, упражнения, эксперименты, помощь на дому
Аудио:
Новый щенок проходит 1,5 мили в день. Если он гуляет 5 дней в неделю, какое расстояние щенок проходит за 5 дней?
Дроби являются частью целого и могут использоваться для обозначения части другой части.
Когда вы хотите найти часть другой части, вы умножаете. Слово «из» является ключевым словом, используемым для определения того, когда следует использовать умножение. Когда целое число и дробь используются для обозначения суммы, например 1½, это называется «смешанным числом» или «смешанной дробью». Умножение смешанных чисел и дробей немного отличается от умножения дробей меньше единицы, например ½ x ½. Тем не менее, некоторые из шагов одинаковы.
Посмотрите два видео об умножении смешанных чисел, дробей и целых чисел.
Ответьте на следующие вопросы в своем математическом журнале:
- Какие два шага показаны для умножения дроби на целое число, например, 4 x 1/2?
- Как умножить смешанное число на другое смешанное число? Какие шаги включены?
- Что делать , а не при умножении дроби и смешанного числа, как показано на видео?
После просмотра первого видео, Песня «Умножение дробей на целые числа» группы NUMBEROCK, ответьте на вопрос №1.
Теперь посмотрите видео Real Math Solutions Multiplying Fractions — Multiplying Mixed Numbers by a Fraction и ответьте на вопросы 2–3:
и дроби выполняются следующим образом:
- Преобразуйте все смешанные числа или целые числа в неправильные дроби.
- Умножьте числители.
- Умножьте знаменатели.
- Сократите ответ и при необходимости преобразуйте обратно в смешанное число.
Если у вас есть целое число и вы хотите преобразовать его в дробь, напишите целое число в числителе и 1 в знаменателе.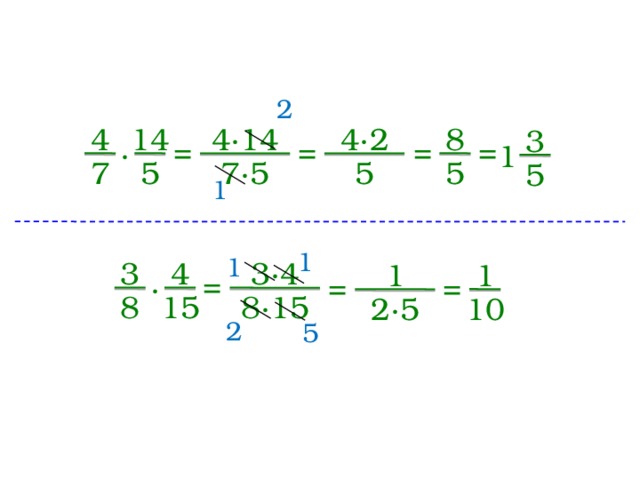
Например, неправильная дробь 5 записывается как 5 ⁄ 1 . Все целые числа имеют 1 в качестве знаменателя при преобразовании в дробь.
Пример: В начале урока вам была предложена задача со словами:
Новый щенок проходит 1,5 мили в день. Если он гуляет 5 дней в неделю, какое расстояние щенок проходит за 5 дней?
Используйте приведенную ниже диаграмму, чтобы визуализировать содержание вопроса. Если щенок проходит 1,5 мили каждый день и повторяет это в течение 5 дней, мы получаем 5 равных групп по 1,5 мили.
| 1½ | 1½ | 1½ | 1½ | 1½ |
Поскольку умножение — это многократное сложение, вместо сложения смешанных чисел вы хотите их умножить.
| 1 | 1 | х | 5 | = | |||||||
| 2 |
Шаг 1.
Преобразуйте все смешанные или целые числа в неправильные дроби.
| 1 | 1 | х | 5 | = | → | 3 | х | 5 | = | ||
| 2 | 2 | 1 |
Шаг 2. Умножьте числители.
| 3 | х | 5 | = | 15 | |||||||
| 2 | 1 | ? |
Шаг 3. Умножьте знаменатели.
| 3 | х | 5 | = | 15 | |||||||
| 2 | 1 | 2 |
Шаг 4.
Сократите ответ и при необходимости преобразуйте обратно в смешанное число.
Разделите 15 на 2 и получите 7½. Щенок прошел в общей сложности 7,5 миль за 5 дней.
В своем математическом журнале напишите ответы на следующие вопросы:
- Как записать целое число в виде неправильной дроби?
- Объясните, как умножать два смешанных числа.
- Где еще вы можете столкнуться с такими проблемами в повседневной жизни?
Теперь переходим к Понял? Раздел для завершения интерактивной практики с умножением смешанных чисел.
Как складывать смешанные дроби с разными знаменателями?
Дроби могут быть определены как числа, которые могут быть представлены в виде A/B , где A и B — целые числа, а B не должен быть равен нулю.
В дроби верхняя часть называется Числитель , а нижняя часть называется знаменателем .
Примеры: 1/2, 4/5, -2/3 и т. д.
Смешанные дробиСмешанные дроби можно определить как дроби, состоящие из двух частей, одна из которых называется целой частью, а другая называется дробная часть.
Пример: 1×(1/2), где 1 — целая часть числа, а другая — дробная часть, равная 1/2.
Сложение смешанных дробей
Чтобы сложить смешанные дроби, сначала преобразуйте смешанную дробь в простые дроби, используя следующий метод:
Учитывая, что 5×(2/3) является смешанной дробью, теперь, чтобы преобразовать ее в простую дробь, нам нужны числитель и знаменатель.
Формула для нахождения числителя
Умножьте целую часть числа на знаменатель смешанной части и добавьте числитель смешанной части.
Таким образом, числитель = 5×3 + 2 = 17
Знаменатель будет таким же, поэтому знаменатель = 3
Следовательно, смешанная дробь преобразуется в простую дробь 5×(2/3) = 17/3
Теперь сложите дроби по следующей процедуре:
Сложение дробей Для сложения дробей существует правило, которое гласит, что знаменатели дробей, которые нужно сложить, должны быть равны.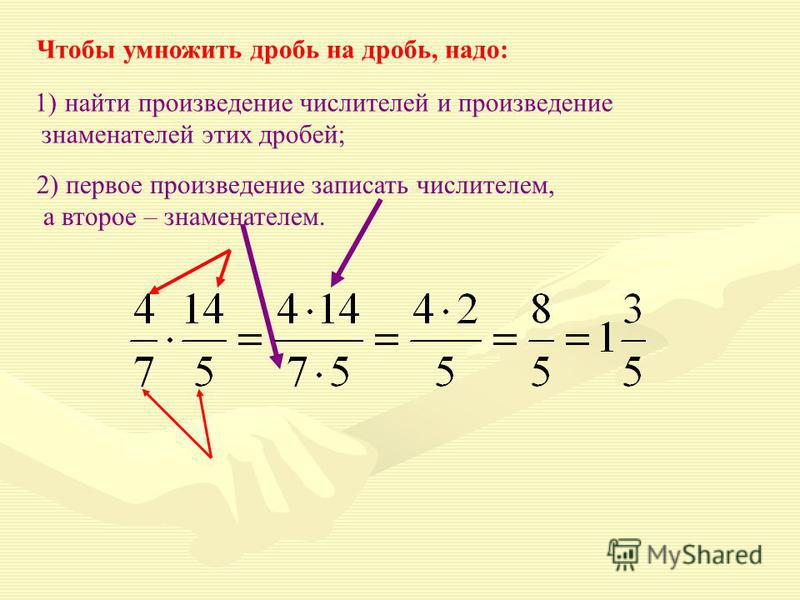
Если знаменатели дроби не равны, сделайте их равными, взяв наименьшее общее кратное (НОК) знаменателей.
Как найти LCM?
Чтобы найти НОК чисел (здесь знаменатели), мы будем использовать метод деления.
Давайте разберемся с этим методом на примере, возьмем два числа 4 и 15 для нахождения НОК методом деления.
Шаг 1: Составьте таблицу, состоящую из левой и правой частей, в правой части укажите числа, НОК которых мы находим.
Шаг 2: Теперь начните с наименьшего числа (не 1) и проверьте, имеет ли любое число из заданных чисел это кратное. В примере 2 — это множитель 4, поэтому используйте его, чтобы разделить 4 в следующей строке.
Шаг 3: Теперь во второй строке 2 осталось 15, только множитель 2 равен 2, поэтому разделите его на 2.
Шаг 4: Теперь у нас есть 1, 15 в следующей строке, поэтому 3 — это множитель 15, поэтому делим 15, результат равен 1, 5.
Шаг 5: Теперь 5 — это множитель 5, поэтому делим 5, результат 1, 1.
Шаг 6: Процесс завершен, так как мы получаем 1 для всех чисел, теперь умножаем все числа в левой части, которые равны 2,2,3,5, так что их кратно 60.
Сложение смешанных дробей с разными знаменателями
Шаги для сложения смешанных дробей с разными знаменателями:
Шаг 1: Преобразование смешанных дробей в простые дроби.
Шаг 2: Найдите НОК знаменателей.
Шаг 3: Разделите НОК на знаменатель каждого добавляемого числа.
Шаг 4: Умножьте числитель на частное ( найденное на предыдущем шаге).
Шаг 5: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
Шаг 6: Знаменатель будет LCM.
Пример
Возьмем 2 смешанные дроби с разными знаменателями, 1×(1/3), 4×(5/8).
Шаг 1: Преобразование смешанных дробей в простые дроби путем умножения целой части на знаменатель и добавления числителя, чтобы получить числитель простой дроби и знаменатель будут одинаковыми.
Таким образом, 1×(1/3) = 4/3
и 4×(5/8) = 37/8
Шаг 2: Нахождение НОК из 3 и 8
95 5 Шаг 3: Разделите LCM на знаменатель каждого числа, которое необходимо добавить.
LCM = 24, поэтому разделите его на каждое число (знаменатель)
24/3 = 8 частное 1
24/8 = 3 частное 2
Шаг 4: числитель частное (найдено на предыдущем шаге).
Числители 4 и 37, поэтому умножьте их на соответствующие частные.
4×8 = 32
37×3 = 111
Шаг 5: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
32 + 111 = 143, что является числителем.
Шаг 6: В знаменателе будет LCM, т.е. 24.
Ответ: 143/24
Возьмем пример 1/2, 2/3
Шаг 1: Возьмите две дроби для сложения 1/2 и 2/3
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первое число со знаменателем второго числа, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×3 + 2×2 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
2×3 = 6, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/6.
Примеры вопросов
Вопрос 1: Сложите заданные смешанные дроби 2×(1/7) и 3×(1/7).
Ответ:
Преобразуйте эти дроби в простые дроби так, чтобы 2×(1/7) = 15/7 и 3×(1/7) = 22/7.
В данном вопросе знаменатели равны, поэтому просто сложите числители, и знаменатель будет равен 7.
Складывая числители 15 + 22 = 37
Знаменатель = 7
Ответ = 37/7.
Вопрос 2. Найдите НОК 4, 7, 12.
Ответ:
Вопрос 3: Сложите заданные смешанные дроби 1×(1/2), 1×(1/3) и 1×(1/5).
Ответ:
Шаг 1: Преобразуйте смешанные дроби в простые, так что 1×(1/2) = 3/2
1×(1/3) = 4/3 и 1× (1/5) = 6/5.
, поэтому дроби равны 3/2, 4/3 и 6/5.
Шаг 2: Нахождение LCM 2,3,5
LCM мы получили 30.
Шаг 3: Разделите LCM на знаменатель каждого числа, которое нужно добавить.
LCM = 30, поэтому разделите его на каждое число (знаменатель)
30/2 = 15 частное 1
30/3 = 10 частное 2
30/5 = 6 частное 3
66 Шаг 4:
Умножьте числитель на частное (найденное на предыдущем шаге).Числитель 3, 4, 6, поэтому умножьте их на соответствующие частные.
3×15 = 45
4×10 = 40
6×6 = 36
Шаг 5: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
45 + 40 + 36 = 121, что является числителем.
Шаг 6: В знаменателе будет LCM, то есть 30.
Ответ: 121/30.
Вопрос 4: Сложите данные смешанные дроби 1×(2/13), 2×(1/2) методом перекрестного умножения.
Ответ:
Шаг 1: Преобразование смешанных дробей в простые, так что Шаг 2: Взяв 15/13 и 5/2
Шаг 3: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель второго числа и аналогичным образом умножим числитель второго числа со знаменателем первого числа и сложите оба члена, чтобы получить числитель.
