правило, примеры, как умножить числа с разными знаками
В данной статье рассмотрим правила умножения отрицательных и положительных чисел. Применим теорию в решении практических задач.
Правило умножения чисел с разными знаками
Определение 1Для того, чтобы произвести действие умножения чисел с разными знаками, необходимо перемножить модули заданных чисел и полученному результату присвоить знак минус.
Запишем указанное правило в виде равенства. Пусть заданы любое действительное положительное число a и любое действительное отрицательное число –b. Тогда правило умножения будет выглядеть следующим образом: a·(-b) =-(|a|·|b|). Если задано отрицательное число –a и положительное число b, справедливо будет равенство: (-a)·b=-(|a|·|b|).
Правило перемножения чисел с различными знаками в полной мере соответствует свойствам действий с действительными числами. Опираясь на них, возможно продемонстрировать, что для любых действительных положительных чисел a и b будет справедливой следующая цепочка равенств: a·(-b) +a·b=a·((-b)+ b)=a·0=0. Эта цепочка является доказательством того, что a·(- b)
Эта цепочка является доказательством того, что a·(- b)
Отметим, что рассматриваемое правило перемножения чисел с различными знаками распространяется не только на действительные числа, но и рациональные и целые. Такой вывод можно сделать, опираясь на то, что действия с рациональными и целыми числами имеют те же свойства, что мы использовали при доказательстве правила.
По сути, умножение чисел с различными знаками по правилу, указанному выше, приводит к перемножению положительных чисел.
Примеры умножения чисел с разными знаками
Пример 1Необходимо выполнить умножение отрицательного числа -5 на положительное число 8.
Решение
Согласно правилу умножения чисел с различными знаками, перемножим модули заданных множителей.
|-5|= 5 и |8| = 8, тогда перемножение натуральных чисел 5 и 8 даст в результате число 40.
Присвоим данному результату знак минус, получим: -40
Кратко решение можно записать так: (-5)·8 =-(5·8) =-40.
Ответ: (-5)·8 =-40.
Пример 2Необходимо произвести умножение чисел 0,(2) и -214.
Решение
Первым шагом переведем периодическую десятичную дробь в обыкновенную (первый множитель), затем выполним переход от смешанного числа к неправильной дроби (второй множитель), применим далее правило умножения чисел с разными знаками и тогда получим: 0,2·-214= 29·-94= -29 ·94= -12
Ответ: 0,2·-214=-12.
Отдельно приведем пример умножения чисел с разными знаками, когда один из множителей или оба – иррациональные числа, которые записаны в виде корней, логарифмов и пр. В таких случаях ответ зачастую представляется в виде числового выражения.
Пример 3Необходимо выполнить умножение sin3 на -1,3.
Решение
Используем правило умножения чисел с разными знаками, чтобы преобразовать равенство: sin3·(-1,3) =-(1,3·sin3).
Никак более упростить выражение мы не сможем, оно и будет являться ответом.
Ответ: sin3·(-1,3)=-(1,3·sin3).
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Урок 4. Частные методики умножения двузначных чисел до 30
Преимуществом трех способов умножения двузначных для устного счета, описанных в прошлом уроке, состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако, эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.
Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.
Умножать на 11 таким способом можно любые двузначные числа. Для наглядности приведены примеры:
81 * 11 = 8 (8+1) 1 = 891
68 * 11 = 6 (6+8) 8 = 748
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа — об этом читайте в данной статье, а также в книге «Система быстрого счета по Трахтенбергу».
Квадрат суммы, квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
232= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529
692 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
152 = (1*(1+1)) 25 = 225
252 = (2*(2+1)) 25 = 625
852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Умножение чисел до 20
1 шаг. Для примера возьмём два числа – 16 и 18. К одному из чисел прибавляем кол-во единиц второго – 16+8=24
2 шаг. Полученное число умножаем на 10 – 24*10=240
3 шаг. Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
Методика умножения чисел до 20 очень проста:
Если записать короче, то:
16*18 = (16+8)*10+6*8 = 288
Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода.
Последнее выражение и является демонстрацией описанного выше метода.
По сути, этот метод является частным способом использования опорных чисел (о которых будет сказано в следующем уроке). В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100… Подробнее о методе использования опорного числа читайте в следующем уроке.
Опорное число
Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8. Для того, чтобы узнать их произведение, нужно совершить следующие операции:
15*18
- К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.

- Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
- К 230 прибавляем произведение 5*8. Ответ: 270.
Подробнее о методике использования опорного числа для счета в уме читайте в следующем уроке.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Cтатистика На весь экран
Евгений Буянов
← 3 Традиционное умножение5 Опорное число →
Правило вероятности умножения | Теорема умножения о вероятности
Правило умножения вероятности определяет условие между двумя данными событиями. Для двух событий, A и B, связанных с пространством выборки S, A ∩ B обозначает события, в которых произошли оба события. Это также известно как теорема умножения в вероятности. Вероятности двух заданных событий перемножаются, чтобы получить вероятность того, что эти события произойдут одновременно.
Для двух событий, A и B, связанных с пространством выборки S, A ∩ B обозначает события, в которых произошли оба события. Это также известно как теорема умножения в вероятности. Вероятности двух заданных событий перемножаются, чтобы получить вероятность того, что эти события произойдут одновременно.
| 1. | Что такое правило умножения вероятности? |
| 2. | Правило умножения формулы вероятности |
| 3. | Правило умножения вероятностного доказательства |
| 4. | Правило умножения вероятности для n событий |
| 5. | Вероятностное правило умножения Примеры |
| 6. | Часто задаваемые вопросы о правиле умножения вероятности |
Что такое правило умножения вероятности?
Правило вероятности умножения гласит, что всякий раз, когда событие является пересечением двух других событий, то есть события A и B должны произойти одновременно.
Правило умножения вероятности для зависимых событий
Если исход одного события влияет на исход другого, то такие события называются зависимыми событиями. Иногда возникновение первого события влияет на вероятность второго события. Из теоремы имеем P(A ∩ B) = P(A) P(B | A), где A и B — независимые события.
Правило умножения вероятности для независимых событий
Если исход одного события не влияет на исход другого, то такие события называются независимыми событиями. Правило умножения вероятности для зависимых событий может быть распространено на независимые события. Имеем P(A ∩ B) = P(A) P(B | A), поэтому, если события A и B независимы, то P(B | A) = P(B), и, таким образом, приведенное выше теорема сводится к P(A ∩ B) = P(A) P(B). Это означает, что вероятность того, что оба события произойдут одновременно, является произведением их соответствующих вероятностей.
Это означает, что вероятность того, что оба события произойдут одновременно, является произведением их соответствующих вероятностей.
Правило умножения формулы вероятности
Правило умножения вероятности гласит, что вероятность того, что события A и B произойдут вместе, равна вероятности того, что B произойдет, умноженной на условную вероятность того, что A произойдет при условии, что B произойдет.
- Правило умножения можно записать как P(A∩B)=P(B)⋅P(A|B).
- Общее правило умножения вероятности можно получить простым способом, просто умножив обе части уравнения условной вероятности на знаменатель.
Правило умножения вероятностного доказательства
Вероятность пересечения двух событий, А и В, получается с использованием свойств условной вероятности.
- Мы знаем, что условная вероятность события A при условии, что произошло B, обозначается P(A|B) и определяется как: P(A|B) = P(A∩B)P(B), где , Р(В)≠0.
 P(A∩B) = P(B)×P(A|B) …….(1)
P(A∩B) = P(B)×P(A|B) …….(1) - P(B|A) = P(B∩A)P(A), где P(A) ≠ 0. P(B∩A) = P(A)×P(B|A)
- Так как P(A∩B) = P(B∩A), P(A∩B) = P(A)×P(B|A) ……..(2)
- Из (1) и (2) P(A∩B) = P(B)×P(A|B) = P(A)×P(B|A), P(A) ≠ 0,P( Б) ≠ 0. Следовательно, полученный таким образом результат известен как правило умножения вероятности.
- Для независимых событий A и B P(B|A) = P(B). Уравнение (2) можно изменить следующим образом: P(A∩B) = P(B) × P(A)
Правило умножения вероятности для n событий
Теперь, чтобы получить правило умножения вероятности для n событий, распространение теоремы умножения вероятности на n событий для n событий A 1 , A 2 , … , A n , имеем P(A 1 ∩ A 2 ∩ … ∩ A n ) = P(A 9 ) 7 2 | A 1 ) P(A
Для n независимых событий теорема умножения сводится к виду0098 ) … P(A n ).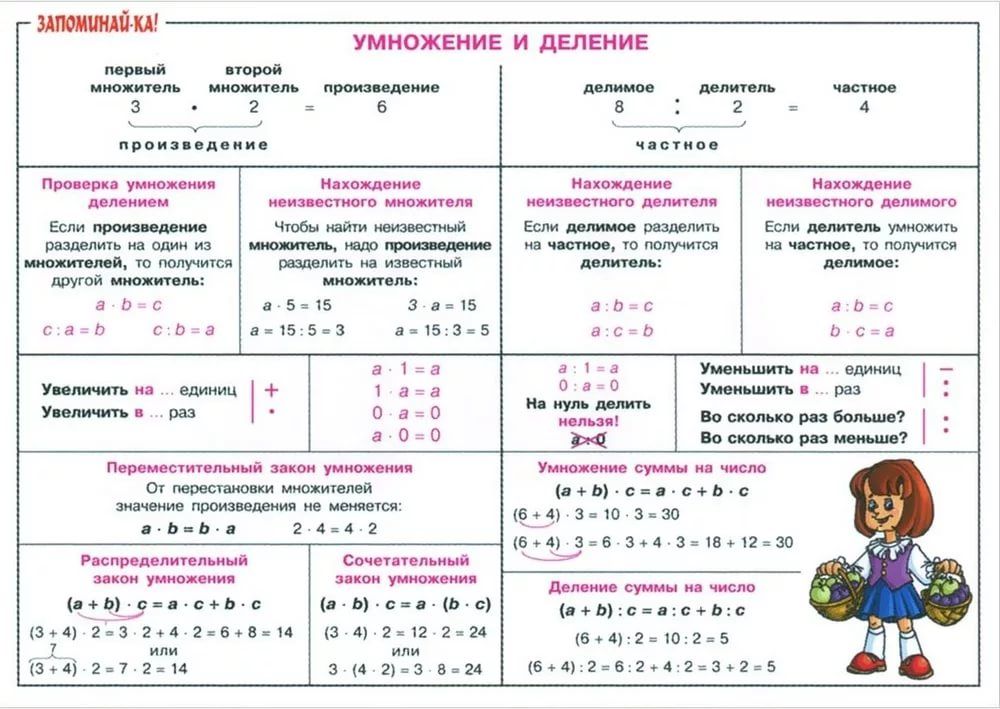
Связанные темы
Следующие связанные темы помогают лучше понять правило умножения вероятности.
- Вероятность и статистика
- Вероятностные правила
- Взаимоисключающие события
- Независимые события
- Биномиальное распределение
- Формула Байе
- Формула распределения Пуассона
Правило вероятностей умножения Примеры
Пример 1: Какова вероятность того, что на обычном шестигранном кубике выпадет 5, а затем 2?
Решение:
Пространство выборки = {1, 2, 3, 4, 5, 6}
Всего событий = 6
Вероятность получения 5 = 1/6
Вероятность получения 6 = 1 /6
Применение правила умножения вероятности для независимых событий,
P(получение 5, а затем 2 ) = (1/6).(1/6) = 1/36.
Следовательно, вероятность выпадения 5, а затем 2 на обычном шестигранном кубике равна 1/36.

Пример 2: Две карты выбираются без замены первой карты из колоды. Найти вероятность выбора короля, а затем выбора ферзя.
Решение:
Всего событий = 52
Поскольку первая карта не заменена, события зависимы.
Вероятность выбора короля = P(K) = 4/52
Вероятность получения дамы = P(Q) = 4/51 (одна карта, взятая первой, не была заменена)
P(король и тогда ферзь) = P(K).P(Q|K)
=4/52 . 4/51 = 16/2652 = 1/166.
Таким образом, вероятность выбора короля, а затем ферзя равна 1/166.
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по правилу умножения вероятности
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о правиле умножения вероятности
Что такое теорема умножения вероятности?
Согласно теореме умножения вероятности, вероятность одновременного возникновения двух событий A и B равна произведению вероятности другого события при условии, что произошло первое.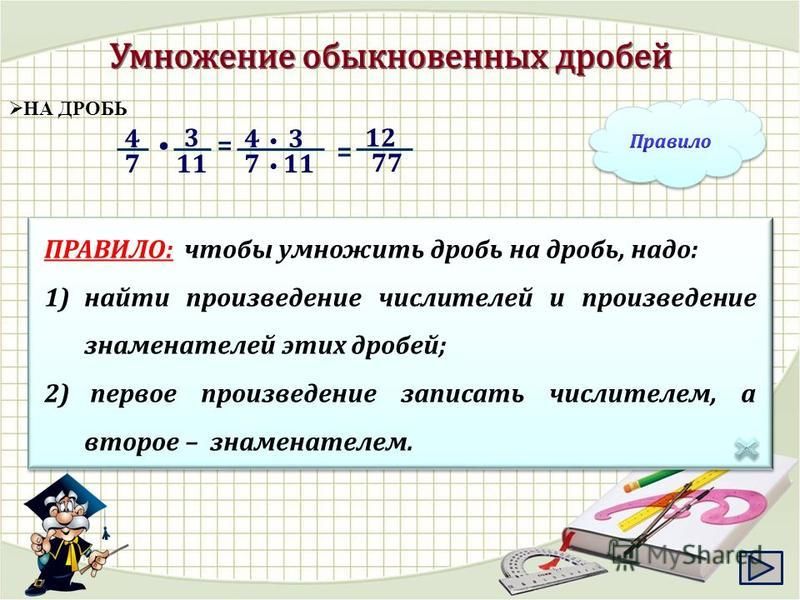 Это называется теоремой умножения вероятности.
Это называется теоремой умножения вероятности.
Почему мы используем правило умножения в вероятности?
Используя правило умножения, мы можем рассчитать вероятность того, что события A и B произойдут вместе, при условии, что события A и событие B происходят по отдельности.
Как найти вероятность 3 событий, используя правило умножения вероятности?
В случае трех событий, A, B и C, правило умножения задается как вероятность пересечения P(A и B и C) = P(A)P(B|A)P(C |А и Б).
Как использовать правило умножения вероятности?
В случае, если одновременно происходят два события, просто умножьте вероятность первого события на второе. Например, если вероятность события А равна 2/7, а вероятность события В равна 5/7, то вероятность того, что оба события произойдут одновременно, вычисляется с использованием правила умножения вероятности, т. е. (2/7) *(5/7) = 10/49.
Правило умножения используется для расчета вероятности какого типа?
Правило умножения вычисляет вероятность одновременного возникновения нескольких событий, используя известные вероятности отдельных событий.
Что такое правило умножения вероятности для зависимых событий?
В случае зависимых событий, применяя правило умножения вероятности, вероятность событий определяется как P(A и B)=P(A)⋅P(B | A), где A и B происходят одновременно
Что такое правило умножения вероятности для независимых событий?
Если A и B являются двумя независимыми событиями, то согласно правилу умножения вероятность того, что оба события произойдут одновременно, определяется как P(A и B)=P(A)⋅P(B)
Скачать учебные материалы БЕСПЛАТНО
Рабочий лист правила умножения
Счет по правилу умножения
Счет — очень сложная область математики, но он также очень важен для понимания приложений в реальной жизни, а затем и для определения вероятностей. В этой статье мы изучим один конкретный метод, используемый при подсчете: правило умножения.
[adsenseWide]
Правило умножения
Представьте, что вы пытаетесь угадать чей-то пароль. Если вы знаете, что пароль состоит из 5 букв или цифр, можно представить, что вы просто угадываете все 5 сразу. Но мы могли бы также представить, что вы угадываете первую букву или цифру, затем вторую, затем третью и так далее. В конце концов, результат тот же, но то, как мы думаем об этом, отличается.
Но мы могли бы также представить, что вы угадываете первую букву или цифру, затем вторую, затем третью и так далее. В конце концов, результат тот же, но то, как мы думаем об этом, отличается.
Если вы можете представить процесс в виде таких шагов, то мы можем применить правило умножения. Чтобы найти общее количество возможных паролей, мы сначала подумаем, сколько вариантов есть для первого символа, сколько для второго и так далее. Затем мы умножаем их, чтобы найти общее количество возможностей.
Пример – пароли
Пароль состоит из 5 символов и состоит из букв и цифр. Сколько различных паролей возможно?
Мы будем думать о количестве возможностей для каждого персонажа индивидуально.
Мы знаем, что пароль состоит из букв и цифр. Некоторые наблюдения по этому поводу:
- В алфавите 26 букв.
- Для любого символа существует 10 возможных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- В пароле прописные и строчные буквы считаются разными, поэтому для любого символа может быть 26 + 26 = 52 возможных буквы.

Для первого символа это означает, что всего 10 + 52 = 62 возможности.
Для следующего символа у нас еще есть 62 возможности. Не было никаких указаний на то, что пароль не может использовать одну и ту же букву или цифру дважды. На самом деле, у каждого персонажа есть одинаковое количество возможностей. Заполнив это и применив правило умножения, мы имеем:
Пример – пароли пересмотрены
Пароль состоит из 5 символов, состоит из букв и цифр и не содержит повторяющихся символов. Сколько различных паролей возможно?
Этот вопрос почти идентичен первому, за исключением одной части: нет повторяющихся символов. Обратите внимание на такие формулировки!!
Это говорит вам, что после того, как вы использовали одну цифру или букву, вы не можете использовать ее снова. Таким образом, количество вариантов для первого символа по-прежнему равно 62. Но теперь вы использовали 1 из символов, поэтому для следующего можно выбрать только 61. Этот шаблон продолжается после того, как каждый выбор сделан.
Этот шаблон продолжается после того, как каждый выбор сделан.
Пример – покупка сэндвичей
В гастрономе клиенты могут приготовить себе сэндвич. Они могут выбрать один из трех видов хлеба (пшеничный, белый и ржаной), два вида сыра (американский или проволоне), четыре вида мяса (индейка, ростбиф, ветчина и салями) и соус (обычный майонез, острый майонез, барбекю). Используя эти ингредиенты, сколько разных бутербродов можно приготовить?
Приложения
В самом деле, вы можете думать о любой проблеме счета как о настоящей проблеме приложения — если вы когда-либо видели рекламу, в которой говорится «более 15 000 различных разновидностей» чего-то подобного, значит, вы видели счет в использовать!
Когда вы думаете о счете, возникают и другие интересные проблемы. Например, сколько 4-значных банковских пин-кодов возможно? (ответ: 10 000 — можете ли вы использовать правило умножения, чтобы выяснить, почему?) Используя другое правило, называемое принципом голубя, мы можем сказать, что это означает, что в любой группе из более чем 10 000 человек по крайней мере двое ДОЛЖНЫ иметь один и тот же номер контакта.

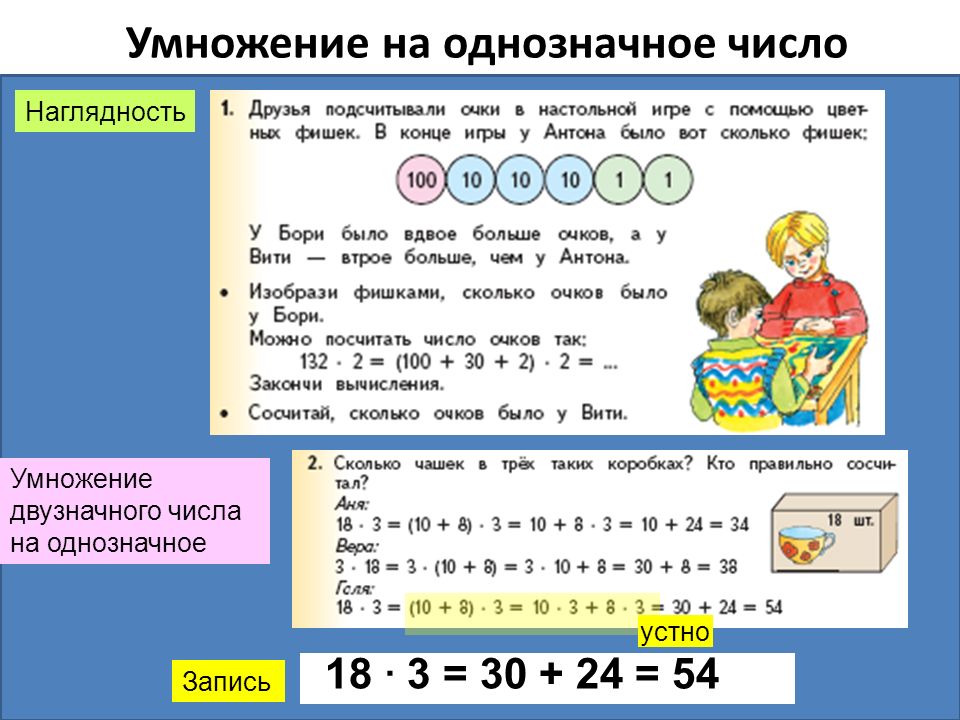 P(A∩B) = P(B)×P(A|B) …….(1)
P(A∩B) = P(B)×P(A|B) …….(1)