Все школьные темы по математике для 6 класса | Wika
Loading
Навигация по разделам
- Обыкновенные дроби
- Десятичные дроби
- Натуральные числа
- Решение уравнений
- Координаты на плоскости
- Рациональные числа
- Умножение и деление обыкновенных дробей
- Отношения и пропорции
- Раскрытие скобок при упрощении
- Признаки делимости
Обыкновенные дроби
Определение прямой и обратной пропорциональной зависимости
Разложение числа на простые множители
Простые числа в математике
Как правильно сравнивать дроби с разными знаменателями
Нахождение дроби от числа
Как правильно складывать дроби с разными знаменателями
Основные сведения о признаках делимости чисел 2,4,5,10,25
Доказательство делимости числа на 3 и 9 — что важно знать
Объяснение дробных выражений для 6 класса
Основные сведения о взаимно обратных числах в математике
Десятичные дроби
Правило умножения десятичных дробей на натуральные числа
Как вычитать дроби с разными знаменателями
Натуральные числа
Умножение отрицательных чисел
Решение уравнений
Как решать задачи на составление уравнений
Координаты на плоскости
Основные сведения о столбчатых диаграммах
Рациональные числа
Сложение отрицательных чисел
Правила вычитания отрицательных чисел
Основные сведения о сложении чисел с разными знаками
Коэффициент в математике
Умножение и деление обыкновенных дробей
Как найти число по заданному значению его дроби
Как применять распределительной свойство умножения для решения задач
Отношения и пропорции
Составление и решение пропорций в математике
Что нужно знать об отношении двух чисел в математике за 6 класс
Длина окружности и площадь круга
Раскрытие скобок при упрощении
Как правильно раскрывать скобки в математических выражениях
Признаки делимости
Основные сведения о делимости произведения
Конспект урока математики по теме «Умножение дробей» | План-конспект урока по математике (6 класс):
Тема урока. Умножение дробей.
Умножение дробей.
Дата проведения. 16.11.2017г.
Тип урока: комбинированный.
Цели урока:
- образовательная: вывод правил умножения обыкновенных дробей; выработка
умений по применению полученных знаний.
- развивающая: развитие логического мышления, познавательного интереса, любознательности, умение анализировать, наблюдать и делать выводы. воспитательная: воспитание самостоятельности, самооценки, активности, умения работать в группах
Задачи урока:
- отработать навыки умножения дробей, применяя методы самоконтроля, самоанализа своей учебной деятельности;
- подвести обучающихся к самостоятельному формулированию правила умножения смешенного числа на натуральное число и отработать навык его применения;
- выявить пробелы в знаниях учащихся по данной темес целью их дальнейшей коррекции;
- способствовать расширению кругозора путем введения новых терминов из других предметов;
- развивать логическое мышление путем составления модели правил умножения дробей, логических цепочек, и т.
 д.;
д.; - развивать самостоятельную деятельность учащихся через выполнения индивидуальных заданий.
По завершении урока учащийся должен:
Знать: правило умножения дроби на натуральное число; дроби на дробь, умножение смешанных чисел, умножения смешанного числана натуральное число рациональным способом.
Уметь: умножать дробь на натуральное число, дробь на дробь, умножать смешанные числа,умножать смешанное числона натуральное число рациональным способом.
Оборудование:
- учебник математики 6-й класс, автор Н.Л. Виленкин;
- презентация;
- раздаточный материал;
- мультимедийный экран, проектор;
- оценочные листы.
План урока.
- Организационный момент (1 мин)
- Постановка цели (2 мин)
- Актуализация знаний (5 мин)
- Работа по теме (6 мин)
- Физминутка (1 мин)
- Работа по теме урока (4 мин)
- Изучение нового материала (6 мин)
- Отработка навыков (14 мин)
- Проверка знаний (5 мин)
- Рефлексия (1 мин)
Ход урока
Этапы | Ход урока | Время | ||||||||||||||||||||||||||||||||||||
I Орг. Цель: психологическая установка на урок. | — Здравствуйте, ребята. Сегодня нам предстоит серьезно потрудиться, мне хочется, чтобы от работы на уроке вы получили удовлетворение. Ведь успех – это состояние души. Девизом сегодняшнего урока я предлагаю слова: (слайд) «Человеческий ум, «растянутый» новой идеей, никогда не сможет вернуться к своим прежним размерам». — А сейчас не будем больше терять времени, оглядываться назад и будем вместе, двигаться только вперед! | 1 мин | ||||||||||||||||||||||||||||||||||||
II Сообщение темы, целей | — Откройте тетради, запишите число и тему нашего урока… (слайд ) — Ой, что случилось с презентацией? Все буквы рассыпались. Помогите определить тему нашего урока. ( Ребята называют тему из рассыпанных букв «Умножение дробей») — Спасибо. Запишем ее в тетрадь.(слайд ) Для вас эта тема новая? — Нет. — А как по вашему, зачем мы ее опять записали? — Что бы ни забыть и закрепить. — Тогда скажите, какую цель мы перед собой поставим? — Отработать (закрепить) правила умножения дробей. Отработать знания и умения, связанные с правилами умножения дробей:
— А также – Внимание!
— Ребята, у вас на столах лежат оценочные листы (слайд ), где записаны все этапы нашего урока. Ваша задача оценить свою работу на каждом этапе урока и поставить себе баллы, по одному за каждый правильный ответ. Оценка за урок будет зависеть от набранных баллов.
| 2 мин | ||||||||||||||||||||||||||||||||||||
III Актуализация знаний | — Начнем с актуализации знаний.(слайд ) Если вы правильно решите примеры, то сможете назвать фамилию ученого-математика. А, внимательно послушав сообщение сказать, что нового он ввел в математику. 7/13 * 39/56 = у 3 1/9 * 2 1/7= е 12/13 * 26/27= д 3 3/8 * 1 1/15= п 4/11 * 4 7/12= н 6/7 * 2 13/18= а
— И так, какая фамилия у нас получилась? (Пеануд) — Поставьте себе в оценочный лист баллы. И послушаем сообщение из истории дробей. Из которого вы должны будете сказать, что же нового Пеануд ввел в математику. — Современное обозначение дробей берет своё начало в древней Индии; дробная черта появилась в записи дробей лишь около 300 лет назад. — Кто может сказать, что же нового ввел в математику Максим Пеануд? — Название “числитель” и “знаменатель”.
| 5 мин | ||||||||||||||||||||||||||||||||||||
IV Работа по теме урока. Цель: отработка и систематизация знаний по теме. 2.Индивидуальная работа | — У меня на столе лежат карточки с заданиями разных цветов(слайд).Решив правильно красную карточку, сможете набрать4 балла, синюю –3балла, а зеленую -2 балла. Эти баллы вы занесете в оценочный лист. Ваша задача выбрать себе карточку по своим возможностям и решить предложенные в ней задания. — 2 балла (зеленая карточка)
— 3балла (синяя карточка)
— 4балла(красная карточка)
— Кто справился с заданиями, проверяет себя по карточке-информатору. И выставляет себе баллы в оценочный лист следующим образом (слайд 10): у кого красная карточка — ставят себе столько баллов, сколько правильных заданий было решено; у кого синяя – на 1 балл меньше от правильно решенных заданий; у кого зеленая – в 2 раза меньше правильно решенных заданий. | 5-6 мин | ||||||||||||||||||||||||||||||||||||
V Физкультминутка | — Ребята, улыбнитесь. Передайте своему товарищу мысленно положительные эмоции, поделитесь капелькой теплоты, добра. | 1мин | ||||||||||||||||||||||||||||||||||||
VI Работа по теме урока (продолжение) 3. Найти ошибку. | — И так, приступим к следующему этапу, на котором нам предстоит вспомнить правила, с помощью которых выполнялись предложенные задания (слайд). — На экране вы видите записанные правила, которые содержат ошибки. Ваша задача найти их и исправить. 1). Чтобы умножить дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменений. 2). Произведением двух дробей является дробь, числитель которой равен произведению знаменателей, а знаменатель – произведению числителей. 3).Чтобы умножить смешанные числа, надо сначала записать их в виде правильных дробей, а затем воспользоваться правилом умножения дробей. (слайд) 4). Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют умножением дробей. (слайд) — Молодцы, нашли все ошибки. — Выставляем себе по одному баллу за каждую найденную ошибку. | 4-5 мин | ||||||||||||||||||||||||||||||||||||
4.Изучение нового Цель: изучить правило умножения N числа на смешанное. | — ( слайд). А сейчас, ребята, я хочу предложить вам немного подумать как же проще (рациональней) можно умножить натуральное число на смешанное число, попытаться смоделировать это правило, найдя закономерность при умножении этих чисел. — Например, нам нужно умножить следующие числа: 2* 4 — Как бы вы стали их умножать? — Перевести смешанное число в неправильную дробь, а затем умножить. — Верно, по изученным правилам это возможно. = 2 * = = = 8 — Может еще, кто предложит свой способ умножения? — … — Посмотрите внимательно на пример и ответ.(слайд) — Что было, а что стало с целой частью, с числителем и знаменателем? — Целую часть и числитель умножили на N число, а знаменатель не изменился.(слайд) Правильно заметили, но перед тем, как сформулировать правило, давайте еще раз проверим, выполняется ли эта закономерность при других числах. Умножив двумя способами числа… которые предложите вы сами. Одно – N число, др. – смешанное число. Будут ли у нас одинаковые результаты? — Учащиеся придумывают числа и двое выполняют решение у доски каждый своим способом. Приходят к выводу, что ответы получились одинаковые, но вторым способом намного быстрее и проще, т.е.- рациональней. Формулируют правило,(слайд ) и один записывает его модель на доске.(слайд ) — Чтобы умножить смешанное число на N число, надо его целую часть и числитель умножить на это число, а знаменатель оставить без изменения. — Оказывается, есть и научное обоснование этому правилу. С помощью распределительного закона умножения, который мы повторяли на прошлом уроке. Давайте это разберем устно. Может, у кого-то из вас получиться обосновать это правило с помощью распределительного закона умножения? ( слайд) (Ребята с учителем доказывают правило с помощью распределительного закона умножения) — Молодцы! Поставьте себе по баллу за каждое верное задание выполненное у доски или верный устный ответ. | 5-6 мин | ||||||||||||||||||||||||||||||||||||
5.Угадай слово | — Приступим к закреплению полученных знаний. А помогут нам в этом, уникальные животные. — На островах Тихого океана живут черепахи – гиганты. Они такой величины, что дети могут кататься, сидя у них на панцире. Узнать название самой крупной в мире черепахи поможет нам следующие задание. (слайд) -Выполните умножение дробей. — Из волшебной коробочки вы должны достать букву и перемножив соответствующие числа из таблицы, определить на какое место ее вписать.
— Итак, как называется самая крупная в мире черепаха? — Дермохелис. — Вы ребята хорошо справились со всеми примерами. Поставьте баллы в свой оценочный лист. | 10-12 мин | ||||||||||||||||||||||||||||||||||||
6. Проверка знаний | — В завершении нашего урока проведем небольшой контроль знаний, что позволит понять достигли мы поставленной в начале урока цели. — Каждому из вас будет предложена карточка, где выполнив задания по цепочке нужно ответить на вопрос. А после поделиться с классом тем,что нового вы узнали, выполняя это задание. — Решаем прямо в карточке и вставляем пропущенные числа. Карточка 1.
Карточка 2
Карточка 3
— Поменяйтесь карточками и проверьте решение друг у друга. Ответы записаны на доске. За каждый верный ответ – 1 балл. (слайд) — Выставляем баллы в оценочные листы. Карточки с решением сдаем. — Послушаем, что вы узнали о животных выполняя задание.(слайд) (Ребята делятся своими ответами) | 5-8 мин | ||||||||||||||||||||||||||||||||||||
VII Домашнее задание | — Запишем домашнее задание | 1 мин | ||||||||||||||||||||||||||||||||||||
VIII Итог урока. | — (слайд). Подсчитаем баллы, которые вы заработали за урок и ставим себе оценку по следующим критериям: (слайд ) От 4 до 6 – оценка «3» От 7 до 9 – оценка «4» От 10 и выше – оценка «5». — Выберите смайлики, которые дадут понять как вам было на уроке. Вам было на уроке: Легко Обычно Трудно — Молодцы! Наш урок я хочу закончить словами…(слайд) Поверь, лишь тот знаком С душевным наслаждением, Кто приобрёл его Трудами и терпеньем. (В. Гете) — Спасибо за урок. До свидания. | 1 мин | ||||||||||||||||||||||||||||||||||||
Отрицательные дроби, десятичные знаки и проценты
Точно так же, как целые числа могут быть положительными или отрицательными,
дроби,
десятичных знака и проценты также могут быть положительными или отрицательными. До сих пор вы, вероятно, видели
только как положительные, либо со знаком плюс (+) перед
, либо вообще без знака, подразумевая, что они положительные. Однако дроби, десятичные числа,
и проценты также могут быть отрицательными. «Правила» сложения, вычитания, умножения и деления положительных и отрицательных чисел, о которых мы говорили на страницах
все еще применяются.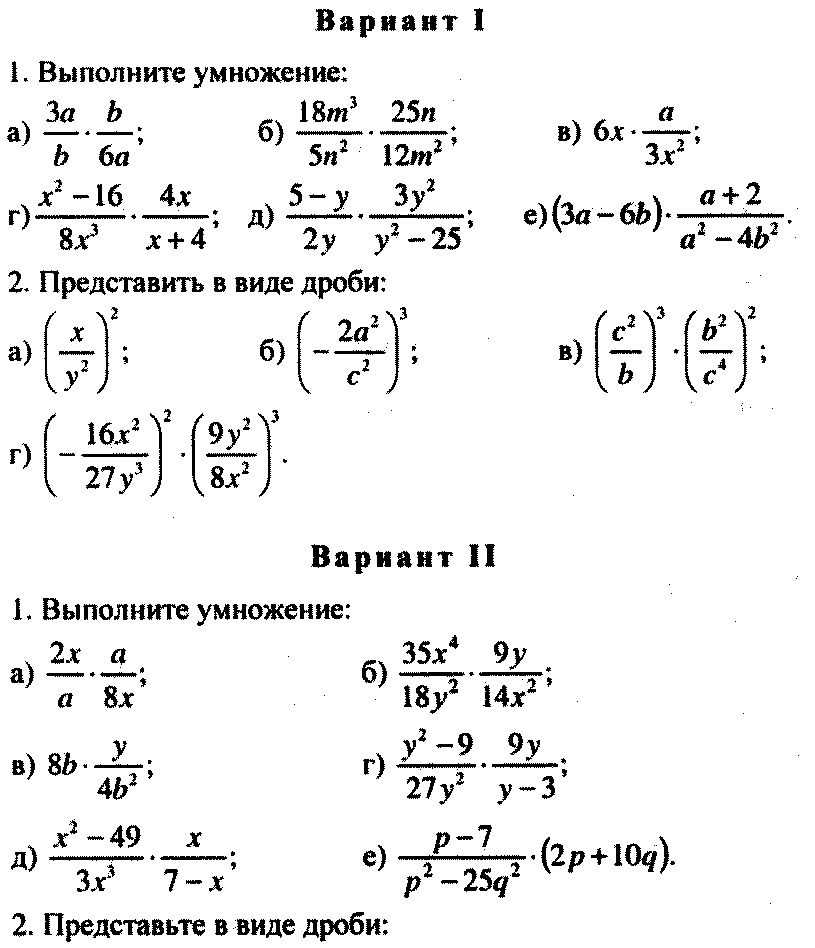
десятичными знаками и процентами, когда они отрицательные.
Отрицательные дроби
С отрицательными дробями поступают так же, как и с целыми отрицательными числами, и число
также можно вычислить на числовой прямой. Например, возьмем следующую задачу
и ее решение:
Это соответствует обычному правилу сложения положительных чисел с отрицательными числами — начните с 9.0003 на отрицательное число и считать вперед (сложение). Итак, для этой задачи мы найдем
-1/4 на числовой прямой и сосчитаем оттуда вперед 3/4, например:
Когда мы закончим счет вперед (сложение), мы получим +2/4. Наш ответ теперь положительный
, потому что сейчас мы находимся на положительной (правой) стороне нуля. Каждая ячейка, на которую мы перемещали
с четвертями.
 Наконец, мы заканчиваем наш ответ на 2/4.
Наконец, мы заканчиваем наш ответ на 2/4.Давайте попробуем другой пример. Это немного сложнее.
Эта задача следует тому же правилу, что и вычитание отрицательного числа
из положительного числа. Вместо вычитания минуса мы превращаем два знака
в знак сложения, например:
Затем мы должны сложить две дроби вместе, например:
Таким образом, мы получаем ответ 5/5, который в упрощенном виде равен 1,9.0011
Давайте попробуем последний пример. Это сложно, поэтому будьте внимательны. Вот проблема
:
Помните, мы превращаем знак минус и минус перед 2 2/3 в знак плюс
Красная точка над -1 1/3 показывает, что именно с этого мы начинаем нашу проблему. Синяя стрелка
, ведущая счет вперед, показывает, что мы добавляем 2 2/3 к исходному числу.
После прибавления 2 2/3 наш ответ равен 1 1/3. Это показано синим кружком
вокруг 1/3, следующей за 1 (что означает 1 1/3).
Умножение и деление дробей также работает так же, как умножение и деление
целых положительных и отрицательных чисел.
Например, если у вас возникла проблема
Вы заметите, что одна дробь положительна, а другая — отрицательна. Напоминая
правила умножения и деления положительных и отрицательных чисел, вы бы
поняли, что положительное число, умноженное на отрицательное число, дает отрицательное число.
отрицательным, когда закончите, например:
Отрицательные десятичные дроби
Отрицательные десятичные числа также работают как целые положительные и отрицательные числа, но, как и в случае с дробями
, они представляют части чисел. Десятичная задача с отрицательными числами
Десятичная задача с отрицательными числами
может выглядеть так:
-0,55 + 2,45 = ____
Чтобы решить эту задачу, вы должны следовать обычным правилам добавления положительного числа
к отрицательному числу. Правило гласит, что вы должны пересчитать вперед
(или добавить) сумму положительного числа. С десятичными дробями это иногда бывает сложно,
, поэтому, чтобы облегчить себе задачу, вы можете просто вычесть отрицательное число
2,45 – 0,55 = ____
Выполнив обычное вычитание, вы получите 1,90 в качестве окончательного ответа. Это число
положительно, потому что большее число (2,45) было положительным.
Вот еще один пример:
-7,89 – (-3,45) = ____
Чтобы решить эту задачу, вы должны следовать обычным правилам вычитания
отрицательного числа из другого отрицательного числа. Во-первых, вы меняете минус и
отрицательный знак в знак сложения, поэтому ваша проблема гласит:
-7,89 + 3,45 = ____
Обычно после этого шага вы будете считать вперед (прибавлять) второе число к первому числу
. Однако из-за десятичных дробей было бы очень сложно сосчитать
Однако из-за десятичных дробей было бы очень сложно сосчитать
вперед от -7,89. Следовательно, вы просто вычтете два числа, например:
7,89 – 3,45 = 4,44
Теперь вернитесь к уравнению, которое говорит -7,89.+ 3,45 = _____. Какое число больше,
отрицательное число или положительное число? Как видите, отрицательное число
больше. Следовательно, наш ответ будет отрицательным, поэтому наш окончательный ответ будет
-4,44.
Давайте попробуем вместе решить еще одну десятичную задачу. На этот раз наша проблема выглядит так:
-6,43 – 5,94 = ____.
Чтобы решить эту задачу, вы должны следовать обычным правилам вычитания
положительного числа из отрицательного числа. В правилах сказано, что начиная с первых
отрицательное число (в данном случае -6,43) считать в обратном порядке (или вычесть) второе число
(в данном случае 5,94). Однако с десятичными числами это становится намного сложнее.
, следуя этому методу, вы можете просто сложить два числа вместе (6,43 + 5,94)
, а затем, поскольку они оба являются отрицательными числами, вы поставите знак минус перед
перед своим ответом.
Чтобы решить эту задачу, 6,43 + 5,94 = 12,37, а затем поставить знак минус перед
ответа, например: -12,37. Готово!
Отрицательные проценты
Очень редко вы встретите отрицательные проценты; тем не менее, мы все же покажем вам
несколько коротких примеров на случай, если вы увидите проблему с отрицательным процентом. В
реальной жизни отрицательные проценты часто используются при работе с деньгами, фондовым рынком,
и стоимостью предметов. Например, в задачах со словами
вам могут приходить отрицательные проценты вот так:
Акции AKL сегодня утром стартовали с отметки $53,99. Он упал на 1,59.% в 10:00, но затем
вырос на 2,4% около 14:00 сегодня днем. В целом, какой процент получило или потеряло это акционерное общество
Решение: Процент, который «упал» или уменьшился, означает, что у вас отрицательный процент.
Процент, который «вырос» или увеличился, означает, что у вас положительный процент. Чтобы решить
эту задачу, вы должны объединить два процента, написав числовое уравнение.
Это уравнение будет выглядеть так: -1,59% + 2,4% = ____. Это работает очень похоже на добавление
и вычитание положительных и отрицательных десятичных чисел. Вам было бы очень трудно
считать вперед от -1,59, поэтому вы можете поменять местами числа и вычесть.
В вашей новой задаче будет указано, что 2,4% – 1,59% = ____. После вычитания вы получите
0,81%; это ваш окончательный ответ.
Попробуем еще один пример работы с отрицательными процентами. Оценка Марси по математике
началась с 80%. После одного теста он упал на 14%, а к концу семестра 9%.0003 он вырос на 20%. Какова была общая прибыль или убыток Марси?
Решение: еще раз обратите внимание, что это включает понижение или уменьшение процента, а затем
увеличение процента, поэтому наше уравнение будет выглядеть следующим образом:
-14% + 20% = ____.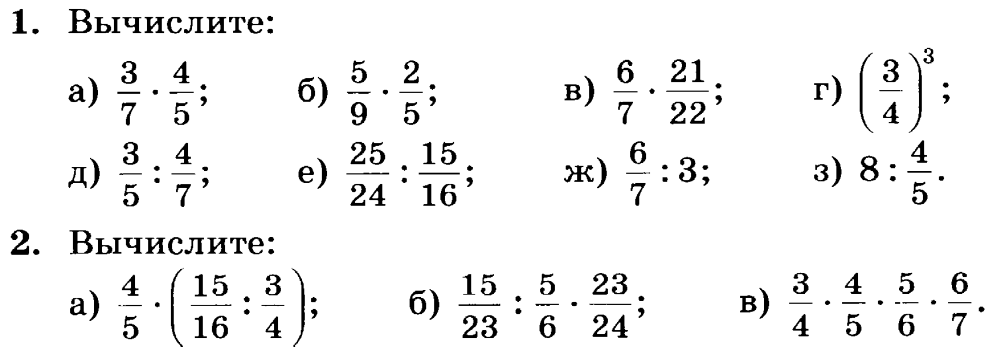
Чтобы решить эту проблему, вы можете начать с -14 и считать вперед 20, что даст
+6%. Итак, ваш ответ — прибавка в ее оценке на 6%.
Тест «Отрицательные дроби, десятичные числа и проценты»
Вот несколько задач, которые помогут вам попрактиковаться в работе с положительными и отрицательными числами.
Выполните их самостоятельно, а затем сверьтесь с нашими ответами.
| 1. -3/4 + 1/2 | 2. -4,5 – 2,8 | 3. 8/9 – (-2/9) |
| 4. 80% + (-30%) | 5. 5,9 – (-2,34) | 6. -90% + 50% |
| 7. -7/10 + (-1/10) | 8. -9,2 – (-2,4) -9,2 – (-2,4) | 9. -3/5 – 4/5 |
| 10. -0,35 + (-1,35) |
Решения
| 1. -1/4 | 2. -7,3 | 3. 10/9 или 1 1/9 |
| 4. 50% | 5. 8.24 | 6. -40% |
| 7. -8/10 | 8. -6,8 | 9. -7/5 или -1 2/5 |
| 10. -1,70 |
Калькулятор отрицательной или положительной дроби
Калькулятор отрицательных и положительных дробей цель 2 математические задачи практика 7-й класс | ответы на NC издание алгебры 1 | решение квадратных корней | рабочий лист по алгебре для 8 класса | онлайн алгебра 1 книга (техас) | весы ти-83 | ти 84 графических изображений | бесплатная печатная математика рациона с использованием данных для семиклассника | «множители 250»
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 д.;
д.;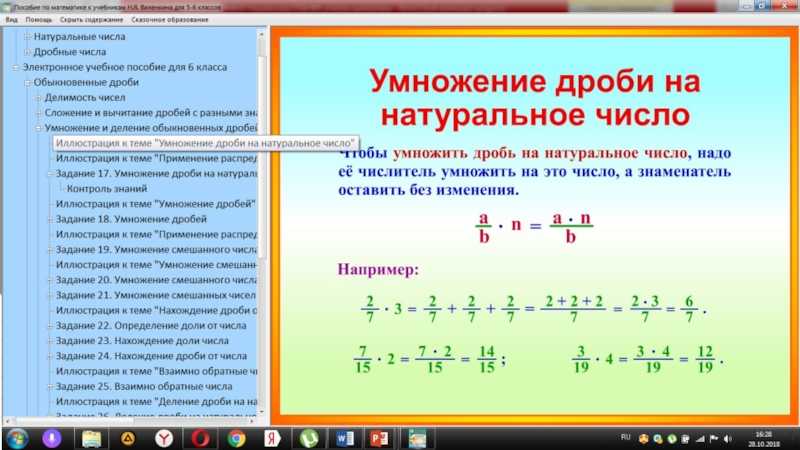 момент
момент Мы ее уже изучали на прошлых уроках.
Мы ее уже изучали на прошлых уроках. Актуализация знаний
Актуализация знаний
 Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный-математик Максим Пеануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.
Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный-математик Максим Пеануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение. После, вы получите карточку – информатор, в которой будет записан верный ответ и приведено решение. Т.о. вы сможете проверить себя, а так же проверить правильность записи решения.
После, вы получите карточку – информатор, в которой будет записан верный ответ и приведено решение. Т.о. вы сможете проверить себя, а так же проверить правильность записи решения.
 (слайд )
(слайд ) Давайте найдем это значение:
Давайте найдем это значение: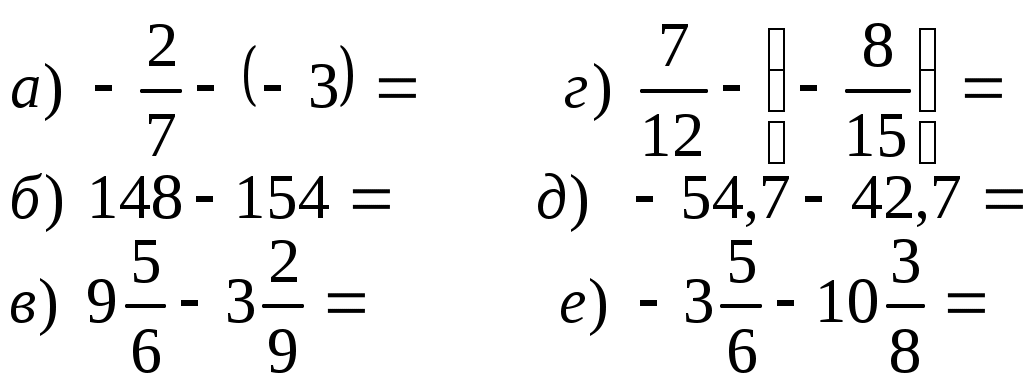
 (По одному примеру обучающиеся решают у доски с комментариями, а оставшиеся примеры делят между собой, выбирая из коробочки буквы).
(По одному примеру обучающиеся решают у доски с комментариями, а оставшиеся примеры делят между собой, выбирая из коробочки буквы). (слайд)
(слайд) Какой кошке поклонялись древние индейцы?
Какой кошке поклонялись древние индейцы? (слайд)
(слайд) 01.2002
01.2002  Может кто-нибудь показать мне дорогу? Мне очень нужна помощь от вас, ребята, для завтрашнего задания. Пожалуйста, ответьте.
Может кто-нибудь показать мне дорогу? Мне очень нужна помощь от вас, ребята, для завтрашнего задания. Пожалуйста, ответьте. Однако, если вам нужна помощь с математикой на долгосрочной основе, вам следует проверить Алгебратор, это то, что я сделал в своей Алгебре 2, и я должен сказать, что это так здорово! Это дешевле, чем услуги частного учителя, и вы можете использовать его в любое время. Использовать его несложно, даже если вы никогда не пробовали подобную программу. Я бы посоветовал вам купить его как можно скорее и забыть о репетиторах по математике. Вы не пожалеете!
Однако, если вам нужна помощь с математикой на долгосрочной основе, вам следует проверить Алгебратор, это то, что я сделал в своей Алгебре 2, и я должен сказать, что это так здорово! Это дешевле, чем услуги частного учителя, и вы можете использовать его в любое время. Использовать его несложно, даже если вы никогда не пробовали подобную программу. Я бы посоветовал вам купить его как можно скорее и забыть о репетиторах по математике. Вы не пожалеете! Этот продукт настолько классный, что помог мне резко улучшить свои оценки. Это не только помогло мне с домашним заданием, но и научило решать проблемы. Вы ничего не теряете и получаете все, покупая это блестящее программное обеспечение.
Этот продукт настолько классный, что помог мне резко улучшить свои оценки. Это не только помогло мне с домашним заданием, но и научило решать проблемы. Вы ничего не теряете и получаете все, покупая это блестящее программное обеспечение. Как я мог приобрести эту программу? Не могли бы вы дать мне ссылку, которая могла бы привести меня к более подробной информации об этом программном обеспечении?
Как я мог приобрести эту программу? Не могли бы вы дать мне ссылку, которая могла бы привести меня к более подробной информации об этом программном обеспечении? Algebrator — действительно отличная программа для алгебры. Я использовал его на нескольких занятиях по алгебре — алгебре среднего уровня, алгебре 1 и алгебре колледжа. Я просто вводил проблему из рабочей книги, и, нажимая «Решить», появлялось пошаговое решение. Программа настоятельно рекомендуется.
Algebrator — действительно отличная программа для алгебры. Я использовал его на нескольких занятиях по алгебре — алгебре среднего уровня, алгебре 1 и алгебре колледжа. Я просто вводил проблему из рабочей книги, и, нажимая «Решить», появлялось пошаговое решение. Программа настоятельно рекомендуется.