Умножение обыкновенных дробей Арифметика
Привет, мой друг, тебе интересно узнать все про умножение обыкновенных дробей, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое умножение обыкновенных дробей , настоятельно рекомендую прочитать все из категории Арифметика
умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.
Умножение обыкновенной дроби на дробь
Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей.
Чтобы умножить дробь на дробь, надо:
- числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
- знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;
Пример.
Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби .
Пример.
Умножение дроби на натуральное число
Чтобы дробь умножить на натуральное числонужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.
Если в результате умножения получилась неправильная дробь, не забудьте превратить ее в смешанное число, то есть выделить целую часть.
Умножение смешанных чисел
Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.
Другой способ умножения дроби на натуральное число
Иногда при расчетах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.
Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.
Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про умножение обыкновенных дробей Надеюсь, что теперь ты понял что такое умножение обыкновенных дробей и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Умножение обыкновенных дробей на натуральное число
«Человек подобендроби, числитель
которой есть то, что
человек представляет
собой, а знаменатель
– то, что он о себе
думает. Чем большего
человек о себе
мнения, тем больше
знаменатель, а значит,
тем меньше дробь»
Л. Н. Толстой
2. Выполним устно
1. Разбей дроби на группы, укажи признак5 8 6 3 15 4 2 7 11
;
;
;
;
;
;
;
;
7 12 5 4 21 3 6 9 11
.

3. Выполним устно
2. Назовите обыкновенные дроби в видедесятичных: :
1
3
а) 1 ; б) 1 ; в) ; г)
2
5
4
4
3. Вычислите:
а) 3 + 0,15
4
б)
2
25
· 0,3
4. Выразите метры в сантиметрах:
а) 3 м = … см
5
б)
4
5
м = … см
4. Выполним устно
5. Замените сумму произведением.а) 2+2+2+2+2+2
2
2
2
б) 5 + 5 + 5
в) a+ a + a + a
6. Замените произведение суммой.
а) 6 ∙ 2
3
б) 4 ∙ 5
в) b ∙ 3
5. Задача 1.
2Черепаха за 1 мин проползает
м.
9
Какое расстояние она преодолеет
за 4 мин.?
6. Тема урока: «Умножение обыкновенных дробей на натуральное число»
7. Учение о дробях всегда считалось трудным. У немцев сохранилась пословица: «ПОПАСТЬ В ДРОБИ» Как вы думаете, что она означает?
Попасть в тяжёлое, трудное положение.2
Черепаха за 1 мин проползает 9 м.
Какое расстояние она преодолеет за 4 мин?
1м
2
2
2
2
2
·4= 9 + 9 + 9 + 9 =
9
2+2+2+2
2·4
=
=
9
9
2
2·4
·4=
9
9
8
9
Чтобы умножить
дробь на натуральное число, надо ее
числитель умножить на это число, а
знаменатель оставить тем же.

а
b
·m=
a·m
b
10. Найдите произведение
31)
∙ 3;
4 4
5
∙ 6;
5
8
∙ 5;
3
2) 5 ∙ 7 ;
5
1
∙
9;
3
0∙ ;
17
3) 7 ∙ 36;
12
5
12∙ 6 ;
1
12 ∙ 12
Вопрос.
А разве нельзя сначала сократить, а
потом записывать ответ?
7
12
.
36
=
7 ∙ 36
12
1
3
=
21
12. Найди ошибку
31. Найдите произведение: 16 4
3
А) ;
4
Б)
12
16
В)
3
48
.
5
2. Найдите произведение: 23
46
А)
115
;
46
Б) 2 1 ;
2
В) 5 .
2
13. Решить задачу № 430 страница 71 учебника
Математический диктантПроверьте себя:
1 вариант
1.
2
·3
17
2.
2
3
3.
3
8
4.
2
53
5.
3
13
·5
·4
·
·
8
2
=
6
17
=
10
3
=
3
2
=
16
53
=
6
13
=3
1
3
=1
1
2
2 вариант
1.

3
·4
13
2.
2
5
3.
5
·3
12
4.
2
41
·
9
5.
3
7
·
2
·7
=
12
13
=
14
5
=
5
4
=
18
41
=
6
7
=2
4
5
=1
1
4
15. Заполнить пропуски в тексте:
Чтобы умножить дробь нанатуральное число, надо ………. дроби
………… на это число, а знаменатель
……………. прежним.
16. Домашнее задание
1. Прочитать пункт 13 до задачи 2.2. Выучить правило умножения
обыкновенной дроби на натуральное число
на стр. 69.
3. Решить в тетради № 427, № 432, № 479.
Дополнительно
2
6
11
3
22
7
24
7
6
5
3
1
2
Х
5
12
2
3
1
6
4
5
8
5
2
8
3
3
4
3
2
3
Урок в 5 классе Умножение обыкновенных дробей
Конспект урока по математике в 5 классе
Тема урока: Умножение обыкновенных дробей.
Тип урока: Урок открытия нового знания.
Цели:
Деятельностная цель: формирование у учащихся способностей к самостоятельному построению новых способов действия на основе метода рефлексивной самоорганизации.
Образовательная цель: расширение понятийной базы по теме «Действия с обыкновенными дробями»:
вывести правило умножения дробей, сформировать умение умножать обыкновенные дроби и смешанные числа.
В ходе урока учащиеся смогут:
— самостоятельно сформулировать правило умножения обыкновенной дроби на натуральное число;
-применить правило при решении упражнений.
Планируемые результаты:
Личностные результаты: формировать устойчивый познавательный интерес, умение работать в парах.
Метапредметные результаты.
Коммуникативные УУД: ученик получит возможность вступать в обсуждение, аргументируя свою точку зрения, используя адекватные языковые средства для отображения своих чувств, мыслей, мотивов и потребностей; развивать умение договариваться и приходить к общему решению в совместной деятельности на основе взаимоуважения к партнёру по работе.
Регулятивные: ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.
Познавательные: записывать выводы в виде правил «если…, то…».
Предметные результаты:
Формулировать правило умножения обыкновенных дробей и смешанных чисел.
Применять правило умножения обыкновенных дробей и смешанных чисел при решении заданий.
Учебное оборудование: мультимедийный проектор, компьютер, экран, раздаточный материал.
Ресурсы:
1. Алгоритм умножения обыкновенной дроби на натуральное число ( каждый пункт правила на отдельной табличке).
2. Задание по группам.
3. Бумага, маркеры.
4.Презентация «Умножение обыкновенных робей».
1.Этап мотивации.
Цель этапа: включение учащихся в деятельность на личностно-значимом уровне
— Здравствуйте!
Проверьте все ли у вас готово к уроку: дневник, учебник, тетрадь, ручка, карандаши. У каждого из вас лежит дополнительный материал, по мере необходимости вы будете на уроке его использовать.
2. Актуализация знаний
Цель этапа: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося
Устная работа. Слайд 1.
-Как называются данные числа?
4/5, 3/8, 11/5, 12/7.
Как называются первые две дроби? Какие дроби называются правильными?
Другие две дроби. Какие две дроби называются неправильными?
-Сократить дроби:
18/21, 15/40, 12/36, 5/15.
Сравнить дроби:
Повторяем правило сравнения дробей.
½ и ¼, 5/8 и 5/9, 9/8 и 5/8, 11/16 и 4/15.
Вычислить:
а)1/5+ 2/5, 1/6 +2/6, 3/10-5/20, 7/8 + 3/5
б) Задача: (краткая запись задачи на доске ).
Ребята все вы смотрели мультфильм « Ми- Ми – мишки». Вот однажды Лисичка решила возле дома сделать клумбу и посадить красивые цветы. Клумба получилась прямоугольной формы. Чтобы рассчитать сколько нужно семян Лисичке нужно знать площадь участка. Как найти площадь клумбы, если известно, что её ширина 4/5м, а длина 3м ?.
— Какое выражение можно составить для решения задачи?
— Сможем ли мы найти значение этого выражения?
Дают ответы:
Умножение 4/5·3. А мы можем это вычислить?
— Не умеем умножать дроби. Возможен ответ « да », гипотезу записать на доске, проверить решение в конце урока
3. Постановка проблемы.
Цель этапа: сформулировать проблему, тему и цели урока.
-Почему не смогли решить задачу?
-Почему не смогли выполнить умножение дробей?
-Как вы думаете, какая тема урока сегодня будет?
-Запишите число и тему урока.
-Какие цели поставим на сегодняшний урок? Чему вы хотели бы сегодня научиться?
— А как мы поймем научились мы умножать обыкновенные дроби или нет?
Давайте вместе проговорим, чему мы должны научиться на уроке.
По мере постановки учащимися учебных задач учитель записывает их на доску.
-вывести правило умножения обыкновенных дробей и смешанных чисел;
-применять это правило при выполнении примеров и решении задач.
— Не умеем умножать обыкновенные дроби.
Умножение обыкновенных дробей.
вывести правило умножения обыкновенных дробей и смешанных чисел;
-применять это правило при выполнении примеров и решении задач
Записывают число, тему урока в тетради.
4. Открытие учениками нового знания.
Цель этапа: организовать решение проблемной ситуации.
Сегодня мы поработаем в парах. Постарайтесь вывести правило умножения обыкновенных дробей сами. У вас на партах лежат рабочие листы по теме. Выполните задание. Попробуйте сформулировать правило. Если это задание у вас вызовёт затруднение, то можно обратиться к учебнику. Задания по рядам. Два вида карточек.
После работы в парах: группы представляют отчет о проделанной работе на формате А3. По каждому заданию заслушивается одна из групп, другая дополняет ответ.
— Давайте, сравним полученные алгоритмы и попробуем выбрать более рациональный.
Формулируем правило. Сравниваем вывод детей с правилом в учебнике.
Ещё раз расскажите правило своему соседу.
Выполняют задания в рабочих листах.
Озвучивают выводы.
Читают правило в учебнике.
Записывают формулу в тетради.
(физкультминутка)
Раз, два, три, четыре, пять. (Прыжки на месте.)
Прибавляю, отнимаю (Наклоны туловища влево-вправо.)
Математику я знаю, (Повороты туловища влево-вправо.)
И поэтому с утра
Я кричу: «Ура! Ура!» (Хлопаем в ладоши.)
Раз, два, три, четыре, пять! (Шагаем на месте.)
Все умеем мы считать! (Хлопаем в ладоши.)
Отдыхать умеем тоже (Прыжки на месте.)
Руки за спину положим, (Спрятали руки за спину.)
Голову поднимем выше (Руки на поясе, голову подняли выше.)
И легко — легко подышим… (Громкий вдох-выдох.)
Все умеем мы считать
Раз, два, три, четыре, пять —
Все умеем мы считать.
Раз! Подняться потянуться. (Под счет учителя дети выполняют потягивания.)
Два! Согнуться, разогнуться.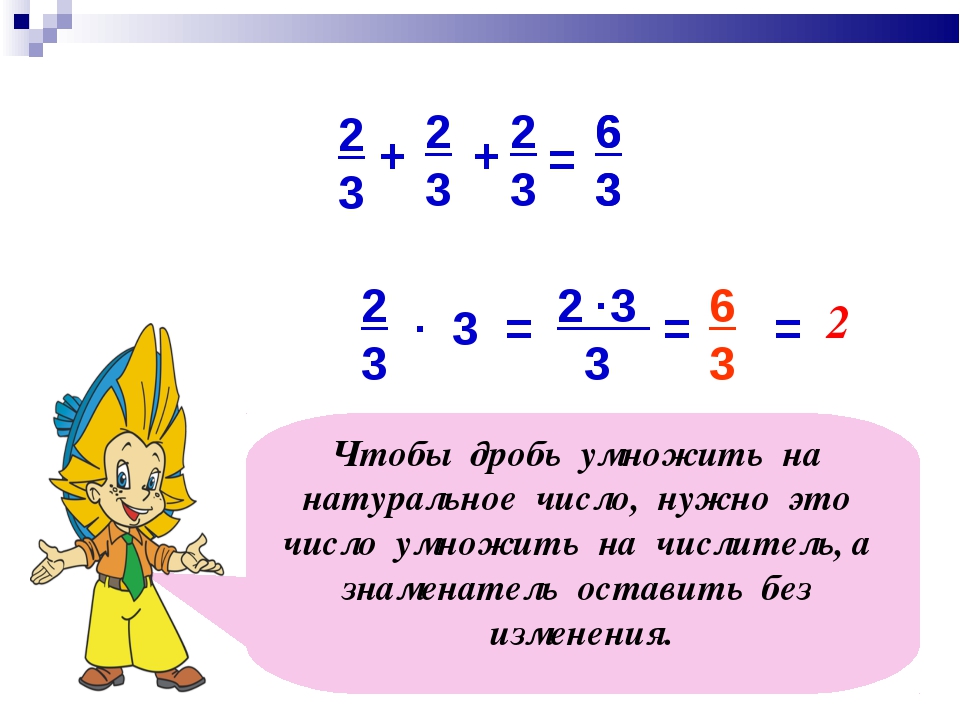 (Наклоны. Повороты туловища.)
(Наклоны. Повороты туловища.)
Три! В ладоши три хлопка,
Головою три кивка. (Движения головой.)
На четыре — руки шире. (Хлопки в ладоши.)
Пять — руками помахать. (Движения руками.)
Шесть — за парту тихо сесть.
5. Этап закрепления изученного материала. Первичное закрепление
Цель этапа: организовать решение и объяснение задания.
А сейчас мы будем работать по правилу. Решим № 969, 974. В последнем номере делаем вывод о том, как можно умножить смешанные числа.
Каким правилом мы пользовались при умножении дробей?
Учащиеся решают задания у доски с комментарием.
Дети проговаривают правило (несколько человек).
6.Самостоятельная работа с самопроверкой
Цель этапа: создать условия для самостоятельного решения и нахождения ошибок в работе.
Самостоятельная работа.
1.Запишите алгоритм умножения обыкновенных дробей.
Чтобы умножить обыкновенные дроби надо:
1. Числитель первой дроби умножить на ____________________ ,
2. _____________________ умножить на знаменатель второй,
_____________________ умножить на знаменатель второй,
3. если можно ____________________,
4. выполнить _________________ в числителе и в знаменателе
5. Запишите это правило на математическом языке (формулой).
2. Используя правило, выполни умножение обыкновенных дробей.
Ребята, а теперь Вам предстоит творчески поработать.
Перед вами примеры и дана таблица с ответами. Решив примеры, вы находите в таблице правильный ответ и соответствующую ему букву.
Т | А | В | Ю | Л | И | К | Ё | Л | Н | Ь | П | С |
12 | 5/9 | 6 | 7/9 | 9 | 3 8 | 10/3 | 2/3 | 9 | 8 | 2/7 | 3/5 | 1/3 |
1) 2/3•9 2) 2/3•5/6 3) 4/10•5/6 4) 3/4•1/2
5) 3/5•15 6) 4/3•3/6 7) 1/3•10 (Василек)
Нарисуйте конечный ответ». За быстрый и правильный ответ 5 баллов.
За быстрый и правильный ответ 5 баллов.
Математический диктант.
Выполняют самостоятельную работу и математический диктант
7.Этап контроля и оценки. Итог урока (рефлексия деятельности)
Цель этапа: осознание уч-ся своей учебной деятельности, самооценка результатов деятельности своей и всего класса
-Какая задача стояла перед нами в начале урока?
— Можно ли считать, что мы сами вывели это правило?
-Что нам помогло?
— Где можно применить новые знания?
— Оцените свою работу на уроке. Работу класса.
Дают ответы на вопросы
-Да
Рабочие листы и учебник.
Анализируют работу на уроке через самооценку
Заполняют листы самооценки
Отметьте своё эмоциональное состояние на забавных рожицах.
В журнал выставляются оценки за урок.
«Закончить урок мне хочется словами Л.Н. Толстого: «Человек есть дробь. Числитель — это сравнительно с другими — достоинства человека; знаменатель – это оценка человеком самого себя. Увеличить своего числителя – свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя – свое мнение о самом себе, и этим уменьшением приблизиться к совершенству.”
Увеличить своего числителя – свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя – свое мнение о самом себе, и этим уменьшением приблизиться к совершенству.”
Домашнее задание
1.Выучить правило умножения обыкновенных дробей.
2. Прочитать материал § 9.4.
3.Выполнить № 983, № 990.
Записывают домашнее задание
Рабочий лист №1.
Выполните умножение по указанному алгоритму: 4/5 м · 3 м
1. Выразите метры в сантиметрах и найдите значение выражения.
2. Полученный результат запишите в квадратных метрах.
3. Запишите полученный результат в виде обыкновенной дроби (если надо сократите дробь).
Решите задачи.
1. Автомашина движется со скоростью 60 км/ч. Какой путь прошла
автомашина за 3 ч? За 2/3 ч?
Оформляем решение в тетради. Проверяем (самопроверка).
2. Найдите площадь листа бумаги прямоугольной формы с измерениями 2/5м и 3/4м.
Сильным учащимся контрольный модуль из коллекции ЭОР.
Ответьте на вопрос: как выполнить умножение обыкновенных дробей?
Подготовьте и оформите отчет вашей группы.
Рабочий лист №2.
Выполните умножение по указанному алгоритму: 4/5 м · 3 м
1. Выразите метры в сантиметрах и найдите значение выражения.
2. Полученный результат запишите в квадратных метрах.
3. Запишите полученный результат в виде обыкновенной дроби (если надо сократите дробь).
Найдите площадь куска ткани прямоугольной формы шириной 2/5м и длиной 5 м.
Найдите площадь листа бумаги прямоугольной формы с измерениями 3/5м и 7/8м.
Похожи ли условия задачи? Сравни алгоритм решения. Если затрудняетесь решить вторую задачу, то прочитай вывод на странице 208-209.
Ответьте на вопрос: как выполнить умножение обыкновенных дробей?
Подготовьте и оформите отчет вашей группы.
Карточка с самостоятельной работой.
1.Запишите алгоритм умножения обыкновенных дробей.
Чтобы умножить обыкновенные дроби надо:
1. Числитель первой дроби умножить на ____________________ ,
Числитель первой дроби умножить на ____________________ ,
2. _____________________ умножить на знаменатель второй,
3. если можно ____________________,
4. выполнить _________________ в числителе и в знаменателе
5. Запишите это правило на математическом языке (формулой).
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/404073-urok-v-5-klasse-umnozhenie-obyknovennyh-drobe
Умножение дробей онлайн с решением. Калькулятор умножения дробей.
Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели, первое произведение записать числителем, а второе знаменателем.
Правила умножения дробей
Произведение двух дробей равно дроби. В числителе которой произведение числителей, а в знаменателе произведение знаменателей.
Как умножать обыкновенные дроби
Для умножения обыкновенных дробей нужно найти произведение числителей и произведение знаменателей. Первое произведение записать числителей а второе знаменателем.
Разберём пример: умножим дроби 1/4 × 1/3. Для этого перемножим числители 1 × 1 = 1 и знаменатели 4 × 3 = 12 в итоге у нас получится дробь 1/12
Как умножать натуральное число на дробь
Чтобы умножить дробь на натуральное число нужно числитель умножить на это число а знаменитель оставить без изменения.
Как умножать 3 и более дробей
При умножении 3 и более дробей мы пользумеся теми же правилами что и при умножении двух дробей.
Разберём пример: умножим правильную дробь 1/4 на натуральное число 5 и на смешанную дробь 3 целые 1/8.
Перед умножением нужно смешанную дробь перевести в неправильную 3 целые 1/8 = 25/8. Затем перемножить числители 1*5*25 = 125 и знаменатели 4*8 = 32. Полученное записать в виде дроби 125/32. При необходимости сократить и перевести в смешанную дробь.
Как умножить смешанную дробь на целое число
Чтобы умножить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем числитель неправильной дроби умножить на целое число. Знаменатель оставить без изменения.
Знаменатель оставить без изменения.
Разберём пример: умножим смешанную дробь 2 целые 1/4 на целое число 6.
Перед умножением нужно смешанную дробь перевести в неправильную 2 целые 1/4 = 9/4. Затем умножить числитель неправильной дроби на целое число 9*6 = 54 а знаменатель останется без изменения 4. При необходимости сократить и перевести в смешанную дробь.
Как перемножить смешанные дроби
Чтобы перемножить смешанные дроби, нужно их перевести в неправильные. Затем перемножить числители и знаменатели.
Разберём пример: умножим смешанную дробь 1 целая 2/5 на смешанную дробь 2 целые 1/3.
Переведём смешанные дроби в нерпавильные 1 целая 2/5 = 7/5 и 2 целые 1/3 = 7/3. Затем перемножим числители 7*7 = 49 и знаменатели 5*3 = 15. Получится дробь 49/15. При необходимости сократить и перевести в смешанную дробь.
Урок математики 5 класс Умножение обыкновенных дробей | План-конспект урока по математике (5 класс):
Тема урока: Умножение обыкновенных дробей.
Тип урока: изучение нового материала.
Цель: Создать ситуацию, при которой обучающиеся смогут вывести правило умножения дробей. Сформировать умение умножать обыкновенные дроби.
Планируемые результаты:
Личностные результаты: формировать устойчивый познавательный интерес, уважение к личности и её достоинству, доброжелательное отношение к окружающим, проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные результаты.
Коммуникативные УУД: оформлять свои мысли в устной форме; слушать и понимать речь других; ученик получит возможность вступать в обсуждение, аргументируя свою точку зрения, используя адекватные языковые средства для отображения своих чувств, мыслей, мотивов и потребностей; развивать умение договариваться и приходить к общему решению в совместной деятельности на основе взаимоуважения к партнёру по работе.
Регулятивные: ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно, определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке;
работать по коллективно составленному плану;
оценивать правильность выполнения действия на уровне адекватной оценки;
планировать своё действие в соответствии с поставленной задачей;
вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение
Познавательные: записывать выводы в виде правил , ориентироваться в своей системе знаний :отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке
Предметные результаты:
- Формулировать правило умножения обыкновенных дробей
- Применять правило умножения обыкновенных дробей при решении заданий.

Учебное оборудование: мультимедийный проектор, компьютер, экран,
Ресурсы: презентация «Умножение обыкновенных дробей».
Ход урока
1.Этап мотивации
Здравствуйте дети! Садитесь! Здравствуйте уважаемые гости! Прозвенел уже звонок, Начинаем наш урок. Все на месте, все в порядке. Книга, ручка и тетрадка, Карандаш, линейка тут? Все готовы, знанья ждут.
Я рада приветствовать Вас на уроке математики |
2. Актуализация знаний
-Вспомним, какие числа мы изучаем ? (У. обыкновенные дроби) -А что называется дробью в математике? (У. Дробь – это число, состоящее из одной единицы или состоящее из нескольких частей единицы) -Артём Фролов нашёл человека, который впервые ввёл понятие обыкновенная дробь в математике и нас с ним сейчас познакомит (Артём рассказывает со слайдом 2) Прочитай ,Эсмира, что написано на слайде (У. Как Вы понимаете это высказывание? (пример ответа ученика) Я понимаю это так: если человек знает куда идти, то он осилит дорогу, также и в математике, если ты мыслишь, то встречаясь с проблемой, всегда сможешь найти способ её решения!) -Абсолютно точно! А давайте это высказывание возьмём девизом нашего сегодняшнего урока! Мы будем мыслить, рассуждать, исследовать и только так получать знания по математике -А теперь наступило время вспомнить, что уже мы знаем об обыкновенных дробях: 1. Виды обыкновенных дробей. 2.Что называют сокращением дробей 3.Основное свойство дроби 4.Как сравнить дроби с одинаковым знаменателем 5.Как сравнить дроби с одинаковыми числителями 6.как сравнить дроби с разными знаменателями 7.Как сложить дроби с одинаковым знаменателем 8 Как сложить дроби с разными знаменателями 9. Как вычесть дроби с одинаковым знаменателем 10.Как вычесть дроби с разными знаменателями -Теорию повторили, посмотрим , а как у нас обстоит дело с практикой? (Решаем устно упражнения со слайда)
| Слайд 2 Слайд3 Устная работа. Слайд 4 1.Сократить дроби: 2. Представьте натуральное число в виде дроби: 2; 5; 7; 15; 28 . Слайд 5. 3.Замените сумму произведением: а) 2+2+2+2+2+2; б) 2/5 +2/5 +2/5; в) a + a + a + a. 4.Замените произведение суммой: а) 6 *2; б) 3/4* 5; в) b* 3. Вычислить: 1/6+ 2/9= 3/4 -1/8= 3/5-2/7= 1/8 + ¼= 1/17*5= 2/5*3/7= –дети затрудняются решить эти примеры, но могут предположить ответ. |
3.Постановка проблемы.
-Почему не смогли выполнить умножение дробей? (не умеем умножать) -Как вы думаете, какая тема урока сегодня будет? (Умножение обыкн. дробей) -Запишите число и тему урока. -Какие цели поставим на сегодняшний урок? Чему вы хотели бы сегодня научиться? (-вывести правило умножения обыкновенных дробей ; -применять это правило при выполнении примеров и решении задач. | на доске |
4.Открытие учениками нового знания.
Попробуйте решить пример 1/17*5 , основываясь на ваши знания:? (Заменить умнож. сложением) -Ребята, я вам предлагаю поработать в парах. Попробуйте сами вывести правило умножения обыкновенных дробей на натуральное число. Если это задание у вас вызовёт затруднение, то можно обратиться к учебнику. ———————————————————————————————————————— -Кто может сформулировать правило умножения обыкновенной дроби на натуральное число?
(После работы в парах, формулируем правило. Сравниваем вывод детей с правилом в учебнике. ) -Ещё раз расскажите правило своему соседу. (рассказывают) -А теперь решим нашу проблему другим способом. (К доске вызываю ученика) Представим число 5 в виде дроби Что получаем. __________________ Сделаем вывод. -А как же умножить дроби 2/5*3/7? Ребята, не спешите перемножать числители и знаменатели: записав их произведения, посмотрите, нельзя ли сократить. Например,———————————————- Осталось составить алгоритм умножения обыкновенных дробей(запись на буквах) Молодцы!!! Вы совершили очередное открытие в математике. |
5.Этап закрепления изученного материала.
Первичное закрепление(самостоятельная работа с проверкой по эталону)
А сейчас мы будем закреплять данное правило. №889 «Солнышко» Решение в тетради самостоятельно с самопроверкой (по слайду)
Каким правилом мы пользовались при умножении дробей? Хорошо! Молодцы ребята! | Сайт 6 Слайд7 |
Физминутка
Раз – подняться, потянуться, Два – согнуться, разогнуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире. Пять – руками помахать, Шесть – за парту сесть опять |
6.Самостоятельная работа с самопроверкой
Слайд 8,9 |
7.Этап включения нового в систему знаний и повторения
Слайд 10,11 | В Простоквашино дяде Фёдору выделили земельный участок. Кот Матроскин решил отдать участок прямоугольной формы, длина которого 4/5 км и ширина 3/7км, под пастбище для коровы Мурки с телёнком. Какова площадь пастбища? |
8.Этап контроля и оценки.
Итог урока (рефлексия)
-Какая задача стояла перед нами в начале урока? — Можно ли считать, что мы сами вывели это правило? -Что нам помогло? — Где можно применить новые знания? — Оцените свою работу на уроке. Заполните оценочные листы Рефлексия Ребята, послушайте притчу: Шел мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановил и задал каждому по вопросу. У первого он спросил: « Что ты делал целый день?» и тот ответил с ухмылкой, что целый день возил проклятые камни. У второго спросил мудрец, и тот ответил, что добросовестно выполнял свою работу. А третий улыбнулся и сказал, что он принимал участие в строительстве храма. — Давайте оценим, как каждый из вас работал сегодня на уроке. — Кто работал как первый человек? — Кто работал как второй человек, работал добросовестно? — Кто работал как третий человек, принимал участие в строительстве храма? | Оформление оценочного листа |
9.Домашнее задание по уровням
П.4.9, №894, Творческое задание – придумать задачу на умножение Спасибо за урок | Слайд 12 Слайд 13 |
6 класс.
 Математика. Умножение обыкновенных дробей — Умножение обыкновенных дробейКомментарии преподавателя
Математика. Умножение обыкновенных дробей — Умножение обыкновенных дробейКомментарии преподавателяЧтобы узнать, сколько литров сока в 5 бутылках, нужно умножить на 5, то есть найти сумму пяти слагаемых каждое из которых равно . Выполним сложение. Для этого сложим числители, а знаменатель оставим тем же. Сложить пять троек – это то- же самое, что 3 умножить на 5. Итак, в пяти бутылках литров сока или 3 литра.
Задача №2. Длина прямоугольника дм, а ширина дм. Чему равна площадь прямоугольника?
Рассмотрим квадрат со стороной 1 дм.
Разделим одну сторону на 3 одинаковые части и возьмем 2 такие части.
Другую же сторону разделим на 5 одинаковых частей и возьмем 4 такие части. При таком делении квадрат будет состоять из 15 равных частей, а прямоугольник – из 8. Значит, его площадь дм2. С другой стороны, площадь прямоугольника равна произведению длины на ширину. Получим равенство:
Значит, его площадь дм2. С другой стороны, площадь прямоугольника равна произведению длины на ширину. Получим равенство:
Пройденный путь – это произведение скорости и времени. Найдем произведение и.
Представим каждое смешанное число в виде неправильной дроби. Выполним умножение: найдем произведение числителей и знаменателей, полученную дробь сократим на 12. В результате получим . Выделим целую часть. Итак, велосипедист проедет км.
источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/umnozhenie-i-delenie-obyknovennyh-drobej/umnozhenie-obyknovennyh-drobey?seconds=0&chapter_id=339
источник видео — http://www.youtube.com/watch?v=o92eTsVxdbM
источник видео — http://www.youtube.com/watch?v=ou3YhsAe-LM
источник видео — http://www.youtube.com/watch?v=KeJCpi-clqg
источник презентации — http://prezentacii.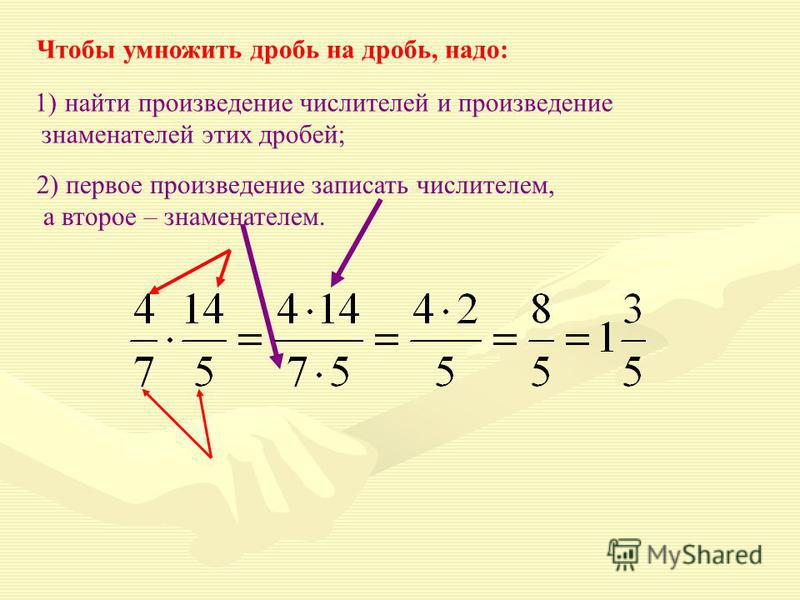 com/matematike/5186-umnozhenie-obyknovennyh-drobey.html
com/matematike/5186-umnozhenie-obyknovennyh-drobey.html
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут.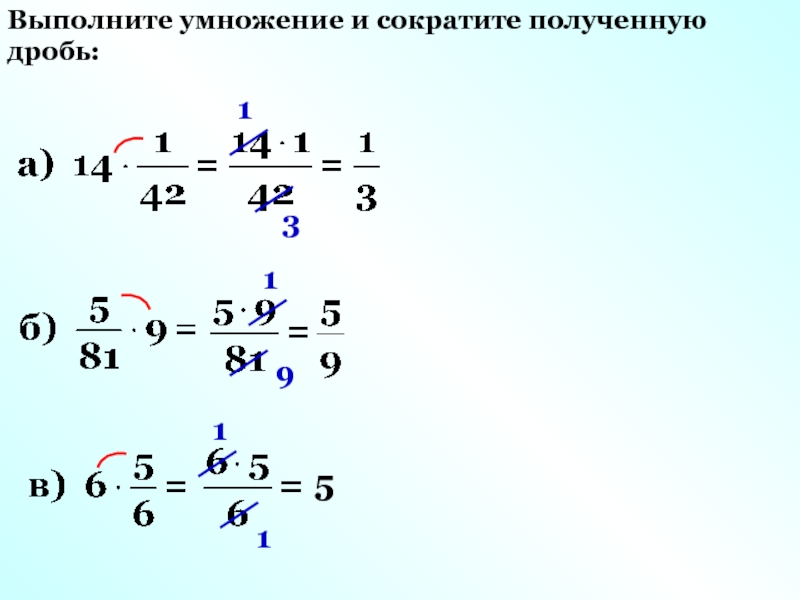 Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Что такое умножение дроби на целое число?
Умножение дроби на целое число Мы знаем, что умножение — это повторное сложение. Итак, умножение дроби на целое число эквивалентно сложению дроби целое число раз.
Например:
3 x 14 может отображаться как,
Алгебраически это означает, что 3 x 1 4 = 1 4 + 1 4 + 1 4 = 1 + 1 + 1 4 = 3 4
Рассмотрим произведение 5 x 2 3.
Это эквивалентно сложению 23,5 раза. Поскольку повторное сложение может быть выполнено умножением, это можно сделать, умножив числитель на 5.
То есть 5 x 23 = 5×24 = 103
Другой способ взглянуть на это — рассмотреть целое число 5 как дробь со знаменателем 1. Чтобы умножить две дроби, умножьте числители и знаменатели по отдельности, а затем запишите их произведения как числители и знаменатели соответственно.
5 x 23 = 51 + 23 = 5x21x3 = 103
Так как произведение представляет собой неправильную дробь, преобразуйте ее в смешанное число.Разделите 10 на 3. Частное равно 3, а остаток равен 1.
Таким образом, 103 = 313.
Это можно четко определить в геометрической интерпретации, как показано:
Пример:
Екатерина делает торт, для которого ей нужно использовать три четверти стакана масла. Если она решит испечь три торта, какое количество масла потребуется?
Если она решит испечь три торта, какое количество масла потребуется?
Для трех лепешек количество используемого масла должно быть в 3 раза больше трех четвертей стакана масла.
3 x 34 = 31 x 34 = 3x31x3 = 94
Преобразует неправильную дробь в смешанное число.
9 ÷ 4 = Q 2 R 1
Таким образом, 94 = 21 4
Следовательно, для нового рецепта потребуется 2 с четвертью стакана масла.
Интересный факт:
|
Пример: 5 x 62 3
Сначала преобразуем 62 3 в неправильную дробь.
623 = (6×3) +23 = 203
Итак, 5 x 623 = 5 x 203 = 51 x203 = 1003
Теперь преобразуем 1003 в смешанную дробь.
120 ÷ 3 = 33 р 1
Таким образом, 1003 = 3313
Умножение обыкновенных дробей Арифметика
Умножение обыкновенных дробей будет рассмотрено в нескольких возможных вариантах.
Умножение обыкновенной дроби на дробь
Это простейший случай, когда вам нужно использовать следующие правила для умножения дробей .
Чтобы умножить дробь на дробь , необходимо:
- умножить числитель первой дроби на числитель второй дроби и записать их произведение в числитель новой дроби;
- знаменатель первой дроби, умноженный на знаменатель второй дроби, и их произведение, записанное в знаменателе новой дроби;
Пример.
Перед тем, как умножать числители и знаменатели, проверьте, можно ли уменьшить дробь. Уменьшение дробей при расчетах значительно облегчит ваши расчеты.
Пример.
Умножение дроби на натуральное число
Чтобы умножить дробь на натуральное число, вам нужно умножить числитель дроби на это число, а знаменатель дроби оставить неизменным.
Если результатом умножения является неправильная дробь, не забудьте превратить ее в смешанное число, то есть выбрать целую часть.
Умножение смешанных чисел
Чтобы умножить смешанные числа, вы должны сначала превратить их в неправильные дроби, а затем умножить их в соответствии с правилом умножения обычных дробей.
Другой способ умножения дроби на натуральное число
Иногда в расчетах удобнее использовать другой способ умножения обыкновенной дроби на число.
Чтобы умножить дробь на натуральное число, знаменатель дроби должен быть разделен на это число, а числитель должен остаться прежним.
Как видно из примера, этот вариант правила удобнее использовать, если знаменатель дроби делится без остатка на натуральное число.
Как умножить дроби: 7 удивительных упражнений, которые стоит попробовать
Поздравляем! Вы преуспели в обучении умножению (за шесть простых шагов). Но теперь пора научить ваших учеников умножать дроби. Глубокие вдохи. Учителя и ученики могут утверждать, что эта концепция более устрашающая, чем переход от вычитания и сложения к умножению. К счастью, существуют стратегии, которые должны упростить понимание умножения дробей — и мы собрали их для вас в виде четкого руководства. В этой статье вы найдете: Но сначала быстро напомним. Что такое умножение? Проще говоря, умножение складывает одно и то же число снова и снова . Хорошие новости для ваших учеников: если они могут складывать, они могут умножать! Вместо того, чтобы писать 1 + 1 + 1 + 1 , есть гораздо более быстрый способ чтобы написать эту сложную задачу: 1 × 4 .Вот несколько примеров: Кредит: Класс мисс Жираф Помимо умножения целых чисел, вы также можете умножать на целые числа, десятичные дроби и, сегодня, дробей . Определение трех типов дробей Дробь обычно состоит из двух частей:
К счастью, существуют стратегии, которые должны упростить понимание умножения дробей — и мы собрали их для вас в виде четкого руководства. В этой статье вы найдете: Но сначала быстро напомним. Что такое умножение? Проще говоря, умножение складывает одно и то же число снова и снова . Хорошие новости для ваших учеников: если они могут складывать, они могут умножать! Вместо того, чтобы писать 1 + 1 + 1 + 1 , есть гораздо более быстрый способ чтобы написать эту сложную задачу: 1 × 4 .Вот несколько примеров: Кредит: Класс мисс Жираф Помимо умножения целых чисел, вы также можете умножать на целые числа, десятичные дроби и, сегодня, дробей . Определение трех типов дробей Дробь обычно состоит из двух частей:- Числитель — верхнее число , которое указывает, сколько частей (целого) у вас есть.
- Знаменатель — нижнее число , которое относится к общему количеству частей, составляющих целое.

- Умножение числителей ( верхних числа )
- Умножение знаменателей ( нижние числа )
- При необходимости упростите или уменьшите дробь
 Давайте вместе рассмотрим пример! Модели площадей для дробного умножения Модель площадей, идеально подходящая для учащихся, обучающихся наглядно в вашем классе, эффективно иллюстрирует, как выглядит одна часть, умноженная на другую (или «из»). Как вы можете видеть на иллюстрации ниже, создавая модель площади умножить дробь легко:
Давайте вместе рассмотрим пример! Модели площадей для дробного умножения Модель площадей, идеально подходящая для учащихся, обучающихся наглядно в вашем классе, эффективно иллюстрирует, как выглядит одна часть, умноженная на другую (или «из»). Как вы можете видеть на иллюстрации ниже, создавая модель площади умножить дробь легко:- Нарисуйте дроби, которые вы умножаете, в отдельных прямоугольниках, каждый используя свой цвет
- Объедините рисунки в один прямоугольник, используя новый цвет для частей, которые перекрывают друг друга
- Чтобы написать произведение, спросите себе два вопроса:
- Сколько коробок имеют оба цвета? Это будет ваш числитель
- Сколько всего ящиков? Это будет ваш знаменатель.
Умножение дробей? Это не большая проблема. Сделайте верхний раз верхний поверх нижнего раза нижний. И прежде чем попрощаться, не забудьте упростить!
Сделайте верхний раз верхний поверх нижнего раза нижний. И прежде чем попрощаться, не забудьте упростить!
Solve : 2 × ⁄₁₃ Записываем целое число как дробь : ²⁄₁ × ⁵⁄₁₃ Умножение числителей : 2 × 5 = 10 Умножаем знаменатели : 1 × 13 = 13 Новая дробь : ¹⁰⁄₁₃
Примечание : Если учащиеся борются с целыми числами, объясните, что они могут рассматривать целое число как верхнее число, а нижнее число всегда равно единице. Умножение неправильных дробей Кредит: Miranda Weenusk Вы умножаете неправильные дроби так же, как и правильные. Однако иногда ученики могут получать неправильные дроби. Возьмем для примера эту задачу:
Однако иногда ученики могут получать неправильные дроби. Возьмем для примера эту задачу:Решить : ⁵⁄₃ × ⁷⁄₆ Умножение числителей : 5 × 7 = 35 Умножить знаменатели : 3 × 6 = 18 Новая дробь : ³⁵⁄₁₈
Если учащиеся знакомы со смешанными дробями, они могут изменить неправильную дробь на смешанную.В данном случае это смешанное число будет 1 ⁄₁₈, но вы можете узнать больше о смешанных числах ниже! Умножение смешанных дробей Прежде чем научить студентов умножать дроби на смешанные числа, им необходимо знать три шага:- Преобразование любых смешанных дробей в неправильные дроби
- Умножение неправильных дробей
- Преобразование конечного произведения обратно в смешанное число
- Найти новый числитель — Умножить целое число на знаменатель, затем прибавить к нему исходный числитель.

- Оставить тот же знаменатель — знаменатель не изменится.
M в конечном итоге A dd D enominator
Шаг второй, умножьте неправильные дроби, как мы проиллюстрировали перед этим разделом.Шаг третий: преобразуйте неправильную дробь обратно в смешанное число. Вот небольшой стишок, который поможет вашим ученикам запомнить, как это делать:С неправильной дробью дивизия это акция!
Предоставлено: шоу и рассказ Хизер Давайте воспользуемся примером, изображенным ранее: ⁄₅. Если деление — это действие, то вам нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток. Пять переходит в 16 трижды равномерно , в сумме получается 15.Это означает, что целая числовая часть смешанного числа будет три . Но оно не делилось идеально, что вы можете увидеть по остатку от на . Таким образом, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕). Как выглядит смешанная дробь, это 3 ⅕ . Для более наглядного пошагового руководства по умножению смешанных чисел посмотрите это четырехминутное видео из Khan Academy: И это то, что вам нужно знать при умножении дробей и смешанных чисел. Две основные ошибки, которые делают ученики при умножении дробей Хотя некоторые ученики быстро усваивают уроки умножения дробей, другие могут столкнуться с трудностями при использовании этих новых концепций. Более ранние учителя улавливают эти заблуждения, тем скорее ученики смогут извлечь уроки и исправить свои ошибки. к практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для от детского сада до 8-го класса» — это одни из наиболее распространенных заблуждений в отношении обучения умножению дробей. 1. Вера в то, что целые числа имеют тот же знаменатель, что и дроби в задаче Группа из восьми экспертов гида признала, что это заблуждение может побудить учащихся взять задачу, такую как 4 — ⅜, и переписать ее как ⁄₈ — ⅜, поскольку неправильный ответ ⅛.
Как выглядит смешанная дробь, это 3 ⅕ . Для более наглядного пошагового руководства по умножению смешанных чисел посмотрите это четырехминутное видео из Khan Academy: И это то, что вам нужно знать при умножении дробей и смешанных чисел. Две основные ошибки, которые делают ученики при умножении дробей Хотя некоторые ученики быстро усваивают уроки умножения дробей, другие могут столкнуться с трудностями при использовании этих новых концепций. Более ранние учителя улавливают эти заблуждения, тем скорее ученики смогут извлечь уроки и исправить свои ошибки. к практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для от детского сада до 8-го класса» — это одни из наиболее распространенных заблуждений в отношении обучения умножению дробей. 1. Вера в то, что целые числа имеют тот же знаменатель, что и дроби в задаче Группа из восьми экспертов гида признала, что это заблуждение может побудить учащихся взять задачу, такую как 4 — ⅜, и переписать ее как ⁄₈ — ⅜, поскольку неправильный ответ ⅛. При представлении смешанного числа учащиеся с таким неправильным представлением могут добавить целое число в числитель, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁄₇ = ⁴ ⁄₃ × ⁶⁄₇ = ²⁴⁄₂₁. Помощь учащимся в понимании взаимосвязи между смешанными числами и неправильными дробями, а также в том, как переводить одно в другое, имеет решающее значение для работы с дробями. Как помочь своим ученикам Избегайте соблазна взорвать базовые уроки. Найдите время, которое нужно вашим ученикам, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами и как преобразовать их из одного в другое. Кредит: Однажды в творческом классе 2. Оставить знаменатель неизменным Учащиеся могут совершить ошибку, забыв умножить равные знаменатели. Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей.Например, они могут увидеть × ⅓ и неправильно ответить вместо ²⁄₉. Как помочь своим ученикам В практическом руководстве члены экспертной группы предлагают «объяснить концептуальную основу умножения дроби, используя единичные дроби (например, ½ × ½ = половина половины = ¼)».
При представлении смешанного числа учащиеся с таким неправильным представлением могут добавить целое число в числитель, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁄₇ = ⁴ ⁄₃ × ⁶⁄₇ = ²⁴⁄₂₁. Помощь учащимся в понимании взаимосвязи между смешанными числами и неправильными дробями, а также в том, как переводить одно в другое, имеет решающее значение для работы с дробями. Как помочь своим ученикам Избегайте соблазна взорвать базовые уроки. Найдите время, которое нужно вашим ученикам, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами и как преобразовать их из одного в другое. Кредит: Однажды в творческом классе 2. Оставить знаменатель неизменным Учащиеся могут совершить ошибку, забыв умножить равные знаменатели. Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей.Например, они могут увидеть × ⅓ и неправильно ответить вместо ²⁄₉. Как помочь своим ученикам В практическом руководстве члены экспертной группы предлагают «объяснить концептуальную основу умножения дроби, используя единичные дроби (например, ½ × ½ = половина половины = ¼)». В частности, учителя могут показать что проблема ½ × ½ на самом деле спрашивает, что такое ½ от ½, что подразумевает, что произведение должно быть меньше любой умножаемой дроби. Вербализация этого заблуждения полезна, но визуализация его особенно эффективна.Войдите во фракционную стену ! Дробные стены — отличный способ помочь учащимся увидеть, как в данном случае выглядит абстрактная половина из половины (т. Е. Одна четверть).
В частности, учителя могут показать что проблема ½ × ½ на самом деле спрашивает, что такое ½ от ½, что подразумевает, что произведение должно быть меньше любой умножаемой дроби. Вербализация этого заблуждения полезна, но визуализация его особенно эффективна.Войдите во фракционную стену ! Дробные стены — отличный способ помочь учащимся увидеть, как в данном случае выглядит абстрактная половина из половины (т. Е. Одна четверть).Теперь вы знаете о проблемах многих учеников, когда учились умножать дроби, что дальше? Давайте рассмотрим, как закрепить уроки дроби — и почему рабочие листы могут быть не лучшей стратегией.Поболтайте со своей суперзвездой @ rudstony4 в эти выходные! Посмотрите вместе на Стену дробей … спросите их о нашей ключевой лексике … НОМЕРАТОР, ЗНАЧИТЕЛЬ, СМЕШАННОЕ ЧИСЛО, ЭКВИВАЛЕНТ … сколько они могут вам объяснить ?! #rudstonmaths pic.twitter.com/V02vgd9SYV
— Класс 4 (@ Rudstony4) 1 февраля 2019 г.
 Смерть рабочих листов? Доктор Стивен Камарата, специалист по развитию детей и отклонениям в развитии, считает, что естественное любопытство детей сводится на нет. В эссе для журнала Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.
Смерть рабочих листов? Доктор Стивен Камарата, специалист по развитию детей и отклонениям в развитии, считает, что естественное любопытство детей сводится на нет. В эссе для журнала Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.Но данные о достижениях в США по сравнению с остальным миром говорят об обратном. По иронии судьбы, по мере того, как все больше и больше листов вводятся в ранние и ранние классы и становятся все более механическими, скучная домашняя работа вынуждает развивающиеся умы, успеваемость учащихся в США продолжает снижаться.Источник: Источник: NAEP Data Explorer, Национальный центр статистики образования. В отчете исследовательского центра Pew указано снижение и без того мрачных оценок достижений в США. Д-р Камарата подчеркнул:
Только 34% четвероклассников и 27% восьмиклассников были оценены как хорошо владеющие математикой в 2011 году, и этот показатель снизился до 33% для четвероклассников и 25% для восьмиклассников в 2015 году (последние данные Невозможно положительно повлиять на эти результаты: в настоящее время более двух третей четвероклассников и трое из четырех восьмиклассников не владеют математикой .Означает ли это, что школы должны обходиться без рабочих листов? Не обязательно. Корреляция — это не причинно-следственная связь. Фактически, многие учителя и ученики добились успеха с рабочими таблицами. Однако преподаватели должны понимать, что образование быстро меняется — от рабочих листов к классным технологиям. Итак, вот несколько творческих способов научить умножению дробей — без рабочих листов! 7 Интересные примеры для обучения студентов умножению дробей 1. Prodigy Prodigy — это бесплатная математическая игра по учебной программе, которую используют более миллиона учителей и 50 миллионов студентов по всему миру.Он предлагает материалы по всем основным математическим темам с 1-го по 8-й класс. Что касается умножения дробей, Prodigy может помочь студентам научиться:Это 38-е место в мире.
- Умножать дробь на целое число
- Умножать две дроби
- Умножать целое число на пропущенную дробь
- Умножать две дроби с помощью словесных задач
- И многое другое
 Игра Prodigy отправит ваших учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези. 2. Переверните дроби Кредит: MathFileFolderGames Для этого задания разделите учащихся на группы по четыре человека. Затем они разделятся на команды по два человека, одна из которых будет игроком А, а другая — игроком Б. Раздайте каждой группе колоду перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12). на картинке выше каждый ученик рисует карточку с числителем (над карандашом) и карточку со знаменателем (под карандашом).Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. После того, как они ответят, игроки Б. сделают то же самое. В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы они выполнили столько, сколько они смогут. Попросите учащихся сдать листы с ответами после задания. отметьте, или ответьте на 10+ вопросов вместе в классе. Примечание : Вы также можете назвать эту игру «Slam-it fractions», заменив карты и карандаши на домино. 3. Умножение дробей BINGO Кредит: jimmiehomeschoolmom Каждый ученик получает заполненную дробью карточку бинго вместе с небольшими листами бумаги (или «фишками бинго») с соответствующими задачами умножения дробей. Когда вы говорите «ИДТИ» , »Они могут начать решать каждую задачу одну за другой, кладя фишку поверх правильной дроби. Вам решать, хотите ли вы, чтобы они завершили линию или всю карточку бинго. Вы также можете выбрать, будут ли ответы на карты бинго упрощенными.Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом решать каждую проблему и вместе решать, как их решать. Примечание : Вы можете использовать этот и последующие примеры в качестве формирующих оценок для оценки успеваемости учащихся и раннего выявления неправильных представлений. 4. Задачи со словами
Игра Prodigy отправит ваших учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези. 2. Переверните дроби Кредит: MathFileFolderGames Для этого задания разделите учащихся на группы по четыре человека. Затем они разделятся на команды по два человека, одна из которых будет игроком А, а другая — игроком Б. Раздайте каждой группе колоду перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12). на картинке выше каждый ученик рисует карточку с числителем (над карандашом) и карточку со знаменателем (под карандашом).Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. После того, как они ответят, игроки Б. сделают то же самое. В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы они выполнили столько, сколько они смогут. Попросите учащихся сдать листы с ответами после задания. отметьте, или ответьте на 10+ вопросов вместе в классе. Примечание : Вы также можете назвать эту игру «Slam-it fractions», заменив карты и карандаши на домино. 3. Умножение дробей BINGO Кредит: jimmiehomeschoolmom Каждый ученик получает заполненную дробью карточку бинго вместе с небольшими листами бумаги (или «фишками бинго») с соответствующими задачами умножения дробей. Когда вы говорите «ИДТИ» , »Они могут начать решать каждую задачу одну за другой, кладя фишку поверх правильной дроби. Вам решать, хотите ли вы, чтобы они завершили линию или всю карточку бинго. Вы также можете выбрать, будут ли ответы на карты бинго упрощенными.Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом решать каждую проблему и вместе решать, как их решать. Примечание : Вы можете использовать этот и последующие примеры в качестве формирующих оценок для оценки успеваемости учащихся и раннего выявления неправильных представлений. 4. Задачи со словами Задачи со словами — прекрасный способ сделать уроки математики актуальными для жизни ваших учеников. Умение умножать дроби может показаться им чуждым, но простая история может полностью изменить их точку зрения. примерно дроби, но математика в целом. Вот пример задачи со словами:Пятиклассники сегодня очень много размышляли над математикой. ❤️Они работали над концептуальным пониманием умножения дроби на целое число.@svmimac @BuenaVistaWCSD pic.twitter.com/Bg7HapJc82
— Келлианна Боксер (@BVBockser) 25 января 2019 г.
У вас есть ½ пакета чипсов в шкафу, но вы съели ½ из них после обеда. Сколько всего пакета вы съели? (Не сокращайте свой ответ до самых простых слов.)
Конечно, это простой пример. Но секунду назад эта дробь была просто числом выше и ниже короткой линии. Однако теперь эта «повседневная» проблема слов сделала умножение дробей применимым к реальной жизни. 5. Война фракций Предоставлено: Шерри Фишер Это упражнение для двух человек адаптировано из карточной игры «Война». Примечание : Многие учителя отходят от решения задач на основе скорости, потому что это не обязательно демонстрирует понимание учащимися.В вашем классе также могут быть дети, которые нервничают из-за необходимости быстро заниматься математикой и поэтому не успевают. Итак, лучше всего оценить свой класс, прежде чем играть в эту версию. Сидя бок о бок, у каждого ученика будет половина колоды карт фракций (которую вы можете скачать здесь). Положив стопку карт лицом вниз, каждый ученик одновременно вытянет карту . Первый ученик, умноживший на две фракции правильно добавляют эти карты в свою колоду. Учащийся выигрывает, если у него в руке оказывается вся колода карт фракций или у него есть большинство карт по прошествии, например, 20 минут.Более того, быстрое мышление на месте этого упражнения с дробями может помочь улучшить умственные математические навыки ваших учеников. В качестве альтернативы вы можете запустить версию этой игры, позволяющую всем играть против вас. Кому не нравится возможность перехитрить своего учителя !? Разделите класс на пять групп. Вы перейдете в первую группу и встретитесь с одним вопросом, прежде чем переходить ко второй группе и так далее. Помните: цель этой версии не в том, чтобы отвечать перед учениками, а в том, чтобы помочь им развить математические способности.Это позволяет учащимся отвечать коллективно, чтобы не выделять детей, которые могут испытывать трудности с умственной математикой. 6. Пищевые фракцииДети любят поесть — это не секрет! Так почему бы не включить это в свой план урока? Учительница в твите выше заставила своих детей попрактиковаться в умножении дробей, преобразовывая рецепты вкусной еды.Вы можете попросить каждого ученика выбрать свою любимую еду и умножить ингредиенты, чтобы накормить весь класс. Также может помочь стимул! Например, после того, как все переработали свою любимую еду, выберите безопасную закуску, которая понравится классу. Найдите оригинальный рецепт. Теперь пусть ваши ученики поработают вместе над умножением ингредиентов, и, если они сделают это правильно, весь класс получит домашнюю (или купленную в магазине) выпечку! 7) Вымпел с умноженной дробью Кредит: Математические леса Вырежьте листы бумаги в форме ленты или треугольника для каждого ученика.Вверху напишите «Я могу умножить…» Ниже вы будете включать:Удивительно, как дети увлекаются, когда речь идет о ЕДА! Цель: найти любимый рецепт, а затем рассчитать каждый ингредиент для всех 90 пятиклассников! Им это нравится! Подлый способ попрактиковаться в умножении дробей. 😉 @Falcons_BMS #FalconsInFlight pic.twitter.com/M6Rg7zaXXQ
— Эмили Либберт (@EmilyLibbert) 24 января 2019 г.
- Модель площади, иллюстрирующую дроби, которые они умножают
- Сама задача умножения (с местом для демонстрации их работы)
- Пробел в внизу с надписью «Мой продукт сокращается до …»
Читайте дальше: Как разделить дроби за 3 простых шага
Тема — умножение и деление смешанных дробей. Деление смешанных чисел. Деление дробей с использованием натурального числа
В этой статье мы проанализируем умножение смешанных чисел . Сначала мы объявим правило умножения смешанных чисел и рассмотрим применение этого правила в примерах решения. Далее поговорим об умножении смешанного числа и натурального числа.Наконец, мы узнаем, как умножить смешанное число на обыкновенную дробь.
Навигация по страницам.
Умножение смешанных чисел.
Умножение смешанных чисел можно свести к умножению обыкновенных дробей. Для этого просто переводите смешанные числа в неправильные дроби.
Запишем правило умножения смешанных чисел :
- Во-первых, перемноженные смешанные числа необходимо заменить неправильными дробями;
- Во-вторых, нужно воспользоваться правилом умножения дроби на дроби.
Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.
Пример.
Произвести умножение смешанных чисел и.
Решение.
Во-первых, представьте перемноженные смешанные числа в виде неправильных дробей: и. Теперь мы можем заменить умножение смешанных чисел умножением обычных дробей:. Применяя правило умножения дробей, получаем. Получившаяся дробь несократимая (см. Приводимые и несократимые дроби), но она неверна (см. Правильные и неправильные дроби), поэтому для получения окончательного ответа остается выделить из неправильной дроби целую часть :.
Записываем все решение в одну строку :.
Ответ:
.
Для закрепления навыков умножения смешанных чисел рассмотрим решение другого примера.
Пример.
Выполните умножение.
Решение.
Веселые числа и равны дробям 13/5 и 10/9 соответственно. Потом . На этом этапе самое время вспомнить об уменьшении дроби: мы заменяем все числа в дроби их разложениями на простые множители и выполняем сокращение тех же множителей.
Ответ:
Умножение смешанного числа и натурального числа
После замены смешанного числа неправильной дробью, умножение смешанного числа и натурального числа сводится к умножению обыкновенной дроби и натурального числа.
Пример.
Умножьте смешанное число и натуральное число 45.
Решение.
Тогда смешанное число равно дроби. Замените числа в полученной дроби на их разложения на простые множители, произведите сокращение, а затем выберите целую часть :.
Ответ:
Умножение смешанного числа и натурального числа иногда удобно выполнять с помощью распределительного свойства умножения относительно сложения. В этом случае произведение смешанного числа и натурального числа равно сумме произведений целой части на данное натуральное число и дробной части на данное натуральное число, то есть.
Пример.
Рассчитайте произведение.
Тема урока: «Умножение и деление смешанных дробей»Цель: развить у студентов умение применять правила умножения и деления смешанных дробей;
развитие аналитического мышления студентов, формирование у студентов умения выделять главное и обобщать.
Задания: повторить правило умножения и деления обыкновенных дробей.
Проверьте навыки применения правила умножения и деления обыкновенных дробей,
правила умножения дроби на натуральное число и наоборот. Проверьте способность переводить неправильную дробь в смешанное число и наоборот.
Вывести новое правило и алгоритм умножения и деления смешанных чисел.
Разработайте новое правило по задачам.
Предметные результаты: алгоритм умножения и деления смешанных дробей (памятка)
Мета-субъектные и личностные результаты :
Нормативный УУД: постановка целей; план, получение результата
Когнитивный УУД: общеобразовательный, логический, постановка и решение задачи
Коммуникативный УУД: работа в парах
Оборудование: учебник математики 6 класс
Раздаточный материал.
Проектор.
Во время занятий:
I.Проблемная ситуация и обновление знаний
1. Опрос детей на повторение изученного материала по теме умножения и деления дробей (алгоритм выполнения, правило умножения дроби на натуральное число).
2. Иллюстрация примеров на проекторе. Виды обыкновенных дробей. Как смешать неправильную фракцию и обратно.
3. В конце опроса, самостоятельная работа, включающая примеры умножения и деления обыкновенных дробей и содержащая два примера умножения и деления смешанных дробей, где дети сталкиваются с проблемой.Правильные ответы для примирения со студентами отражаются на проекторе.
4. Обсуждение проблемы. Довести до темы урока.
II. Совместное открытие знаний.
1 / Предлагается обсуждение попарно, для озвучивания варианта решения проблемы. Версии написаны на школьной доске. Как узнать, какая версия правильная?
2 / Предложите студентам обратиться к учебнику по соответствующей теме.
3 / Выполните вводное чтение, найдите необходимый абзац и изучите его, чтобы составить алгоритм умножения и деления смешанных дробей.Контроль выполнения задания.
4 / Прослушивание версий составляет основной общий алгоритм. Переверните его на проекторе и раздайте ученикам в виде памятки.
III. Самостоятельное применение знаний
1 / Вернуться к задаче с решением примеров из самостоятельной работы и применением полученного алгоритма для их решения. Проверяйте попарно. Отобразите результаты на проекторе для проверки.
2 / Дайте задание из учебника. Контроль исполнения.
IV. Краткое содержание урока
Начните с проблемы, возникшей в начале урока, обсудите способы ее решения и результат.
Оценка успеваемости студентов.
Домашнее задание.
) и знаменатель знаменателя (получаем знаменатель произведения).
Формула умножения дробей:
Например:
Прежде чем приступить к умножению числителей и знаменателей, необходимо проверить возможность уменьшения дробей.Если вам удастся уменьшить дробь, то вам будет легче продолжать расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае сложения, переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанные):
- переводим смешанные дроби в неправильные дроби;
- умножить числители и знаменатели дробей;
- уменьшить дробь;
- , если вы получили неправильную дробь, конвертируйте неправильную дробь в смешанную.
Примечание! Чтобы умножить смешанную дробь на другую смешанную дробь, сначала нужно привести их к виду неправильных дробей, а затем умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Удобнее использовать второй способ умножения обыкновенной дроби на число.
Примечание! Чтобы умножить дробь на натуральное число, необходимо разделить знаменатель дроби на это число, а числитель оставить неизменным.
Из приведенного выше примера ясно, что этот вариант более удобен для использования, когда знаменатель дроби делится на натуральное число.
Многоэтажные фракции.
В средней школе часто встречаются трехэтажные (или более) дроби. Пример:
Чтобы привести такую дробь к обычному виду, используйте деление на 2 балла:
Примечание! При делении на фракции очень важен порядок деления.Будьте осторожны, запутаться легко.
Примечание, например:
При делении единицы на любую дробь получится такая же дробь, только в обратном порядке:
Практические советы по умножению и делению дробей:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность. Все расчеты производите аккуратно и четко, четко и четко. Лучше написать в черновике несколько лишних строк, чем запутаться в расчетах в уме.
2. В заданиях с разными типами дробей — переходите к форме обыкновенных дробей.
3. Уменьшаем все дроби до тех пор, пока уменьшать уже нельзя.
4. Многоэтажные дробные выражения задаются в виде обыкновенных, с делением на 2 балла.
5. Разделите единицу на дробь в уме, просто перевернув дробь.
Далее следуем правилу: умножаем первую дробь на дробь, обратную второй (то есть на обратную дробь, в которой числитель и знаменатель меняются местами).При умножении дробей числитель умножается на числитель, знаменатель — знаменатель.
Рассмотрим примеры деления смешанных чисел.
Деление смешанных чисел мы начинаем с перевода их в неправильные дроби. Затем делим полученные дроби. Для этого первую дробь умножьте на перевернутую вторую. 20 и 25 на 5, 3 и 9 — на 3. Получили неправильную дробь, значит надо.
Смешанные числа переводятся в неправильную дробь.Далее по правилу деления дробей первое число оставляем и умножаем на число, обратное второму. Уменьшаем 15 и 25 на 5, 8 и 16 — на 2. Из полученной неправильной дроби выделяем целую часть.
Заменяем смешанные числа на неправильные дроби и делим их. Для этого перепишем первую дробь без изменений и умножим на перевернутую вторую. Уменьшаем 18 и 36 на 18, 35 и 7 — на 7. В итоге получилась неправильная дробь. Изолируем от него всю деталь.
Как умножить смешанное число на натуральное. Доля. Умножение дробей обыкновенных, десятичных, смешанных
Еще одно действие, которое можно выполнить с обыкновенными дробями, — это умножение. Мы постараемся уточнить его основные правила при решении задач, покажем, как обыкновенная дробь умножается на натуральное число и как правильно выполнять умножение трех обыкновенных дробей и не только.
Сначала подготовим основное правило:
Определение 1.
Если мы умножим одну обыкновенную дробь, то полученная в результате дробь будет равна произведению исходных дробей, а знаменатель будет произведением их знаменателей. В алфавитной форме для двух дробей A / B и C / D это можно выразить как a b · c d = a · c b · d.
Давайте посмотрим на примере, как применить это правило. Предположим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда цифра фигуры составит 1 квадратный метр.Блок. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единице, мы обнаружим, что теперь он состоит из 32 прямоугольников (потому что 8 · 4 = 32). Соответственно, площадь каждого из них будет составлять 1 32 от площади всей фигуры, то есть 1 32 квадратных метра. единицы измерения.
Имеется раскрашенный фрагмент с партиями, равными 5 8 числовым единицам и 3 4 числовым единицам. Соответственно, чтобы вычислить его площадь, необходимо первую дробь умножить на вторую.Он будет равен 5 8 · 3 4 кв. единицы измерения. Но мы можем просто посчитать, сколько прямоугольников входит в фрагмент: их 15, значит, общая площадь составляет 15 32 квадратных единицы.
Так как 5 · 3 = 15 и 8 · 4 = 32, мы можем записать следующее равенство:
5 8 · 3 4 = 5 · 3 8 · 4 = 15 32
Является подтверждением сформулированных нами правил умножения обыкновенных дробей, которое выражается как a b · c d = a · c b · d. Действует так же, как правильные и неправильные дроби; С его помощью можно умножать дроби с разными и одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1.
Умножить 7 11 на 9 8.
Решение
Для начала вычисляем произведение числителей дробей, умножая 7 на 9. У нас получилось 63. Затем вычисляем произведение знаменателей и получаем: 11 · 8 = 88. Составим им два числа Ответ : 63 88.
Все решения можно записать как:
7 11 · 9 8 = 7 · 9 11 · 8 = 63 88
Ответ: 7 11 · 9 8 = 63 88.
Если в ответе у нас нехватка дроби, нужно увеличить расчет до конца и сделать его уменьшение. Если мы ошиблись дробью, необходимо выделить целую часть.
Пример 2.
Вычислить работу дробей 4 15 и 55 6.
Решение
Оспаривая приведенное выше правило, нам нужно умножить числитель на числитель, а знаменатель на знаменатель. Решение будет выглядеть так:
4 15 · 55 6 = 4 · 55 15 · 6 = 220 90
Получена фракция фракции, т.е.е. Имеет знак делимости на 10.
Выполняем нарезку дроби: 220 90 НОД (220, 90) = 10, 220 90 = 220: 10 90: 10 = 22 9. В результате у нас получилась неправильная дробь, из которой выделяем всю часть и получаем смешанное число: 22 9 = 2 4 9.
Ответ: 4 15 · 55 6 = 2 4 9.
Для удобства мы можем уменьшить начальные дроби перед выполнением действия умножения, для чего нам нужно привести дробь к форме A · C b · d.Разложим значения переменных на простые множители и уменьшим такие же.
Поясним, как это выглядит, используя конкретную задачу.
Пример 3.
Рассчитать работу 4 15 · 55 6.
Решение
Пишем расчеты по правилу умножения. Нас будет:
4 15 · 55 6 = 4 · 55 15 · 6
Поскольку оба 4 = 2 · 2, 55 = 5 · 11, 15 = 3 · 5 и 6 = 2 · 3, значит, 4 · 55 15 · 6 = 2 · 2 · 5 · 11 3 · 5 · 2 · 3.
2 · 11 3 · 3 = 22 9 = 2 4 9
Ответ : 4 15 · 55 6 = 2 4 9.
Числовое выражение, в котором происходит умножение обыкновенных дробей, обладает освобождающим свойством, то есть при необходимости мы можем изменить порядок множителей множителей:
a b · c d = c d · a b = a · c b · d
Как умножить обыкновенную дробь на натуральное число
Мы сразу записываем основное правило, а затем пытаемся объяснить его на практике.
Определение 2.
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. В этом случае знаменатель конечной дроби будет равен знаменателю исходной дроби. Умножение некоторой дроби a b на натуральное число N можно записать в виде формулы A b · n = a · n b.
Легко понять эту формулу, если вспомнить, что любое натуральное число можно представить в виде обыкновенной дроби со знаменателем, равным единице, то есть:
a b · n = a b · n 1 = a · n b · 1 = a · n b
Поясним нашу идею на конкретных примерах.
Пример 4.
Рассчитать работу 2 27 до 5.
Решение
В результате умножения числителя исходной дроби на второй множитель мы получаем 10. В силу упомянутых выше правил мы получим 10 27. Все решения приведены в этом посте:
2 27 · 5 = 2 · 5 27 = 10 27
Ответ: 2 27 · 5 = 10 27
Когда мы получаем натуральное число обычным выстрелом, вам часто приходится уменьшать результат или представлять его как смешанное число.
Пример 5.
Условие: Рассчитать работу с 8 по 5 12.
Решение
По приведенному выше правилу умножаем натуральное число на числитель. В результате получаем, что 5 12 · 8 = 5 · 8 12 = 40 12. Конечная дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
NOK (40, 12) = 4, следовательно, 40 12 = 40: 4 12: 4 = 10 3
Теперь осталось только выделить всю часть и написать готовый ответ: 10 3 = 3 1 3.
В этой записи можно увидеть все решение: 5 12 · 8 = 5 · 8 12 = 40 12 = 10 3 = 3 1 3.
Мы могли также уменьшить дробь с помощью разложения числителя и знаменателя до простых множителей, и результат оказался бы точно таким же.
Ответ: 5 12 · 8 = 3 1 3.
Числовое выражение, в котором натуральное число умножается на дробь, также имеет свойство движения, то есть расположение множителей не влияет на результат:
a b · n = n · a b = a · n b
Как произвести умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел.Это следует из самого определения этих понятий.
Благодаря знанию комбинирующих и подвижных свойств вы можете умножить три обыкновенные дроби и более. Допускается переставлять множители местами для большего удобства или раскрывать скобки, так будет легче посчитать.
Покажем на примере, как это делается.
Пример 6.
Умножение четырех обыкновенных дробей 1 20, 12 5, 3 7 и 5 8.
Решение: Для начала сделайте запись о работе.У нас будет 1 20 · 12 5 · 3 7 · 5 8. Нам нужно перемножить друг друга числа и все знаменатели: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5. · 7 · 8.
Перед тем, как приступить к умножению, мы можем легко облегчить нашу задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем уменьшить получившуюся готовую фракцию.
1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · (2 · 2 · 3) · 3 · 5 2 · 2 · 5 · 5 · 7 (2 · 2 · 2) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280
Ответ: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9 280.
Пример 7.
Умножение 5 чисел 7 8 · 12 · 8 · 5 36 · 10.
Решение
Для удобства мы можем сгруппировать кадр 7 8 с номером 8 и номер 12 с дробью 5 36, так как это будет очевидно в будущих версиях. В результате у нас будет:
7 8 · 12 · 8 · 5 36 · 10 = 7 8 · 8 · 12 · 5 36 · 10 = 7 · 8 8 · 12 · 5 36 · 10 = 7 1 · 2 · 2 · 3 · 5 2 · 2 · 3 · 3 · 10 = 7 · 5 3 · 10 = 7 · 5 · 10 3 = 350 3 = 116 2 3
Ответ: 7 8 · 12 · 8 · 5 36 · 10 = 116 2 3.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Умножить целое число на дробь — несложная задача. Но есть тонкости, в которых вы наверняка разбирались в школе, но с тех пор забыли.
Как умножить целое число на дробь — немного членов
Если вы помните, какой числитель является знаменателем, а какой правильный выстрел из неправильного — пропустите этот абзац. Он для тех, кто совсем забыл теорию.
В числителе указывается верхняя часть дроби — то, что делится. Знаменатель ниже. Это то, что мы разделяем.
Правильная дробь той, у которой числитель меньше знаменателя. Неправильно названная дробь, у которой числитель больше или равен знаменателю.
Как умножить целое число на дробь
Правило умножения целого числа на дробь очень простое — числитель умножается на целое, и знаменатель не касается знаменателя.Например: умножьте два на одну пятую — мы получим две пятых. Четыре умножить на три гекса — получится двенадцать шестнадцатое.
Сокращение
Во втором примере полученная дробь может быть уменьшена.
Что это значит? Примечание — и числитель, и знаменатель этой дроби делятся на четыре. Разделить оба числа на общий делитель и называется — уменьшить дробь. Получаем три четверти.
Неправильные дроби
Но предположим, что мы умножили четыре на два пятнадцать.Получилось восемь пятых. Это неправильная дробь.
Его необходимо привести в правильный вид. Для этого необходимо выделить его целиком.
Здесь нужно использовать деление по остатку. Получаем единицу и три в остатке.
Одно целое и три пятых, и вот наша правильная дробь.
Привести в правильную форму тридцать пять восьмых — задача немного сложнее. Число, близкое к тридцати семи, деленное на восемь, дает тридцать два.При делении получаем четыре. Берем из тридцати пяти тридцать два — получаем три. Итог: четыре целых и три восьмых.
Равенство числителя и знаменателя. А дальше все очень просто и красиво. При равенстве числителя и знаменателя получается просто единица.
В прошлый раз мы научились складывать и вычитать дроби (см. Урок «Сложение и вычитание дробей»). Самым сложным моментом в действиях было приведение дробей к общему знаменателю.
Теперь пора заняться умножением и делением. Хорошая новость в том, что эти операции выполнять даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной части.
Чтобы умножить две дроби, необходимо умножить их числа и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, нужно первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому мы будем рассматривать весь урок преимущественно по умножению.
В результате умножения может возникнуть (и часто действительно бывает) нехватка дроби — ее, конечно, нужно уменьшить. Если после всех разрезов дробь оказалась неверной, ее следует отнести к целой части.Но чего точно не будет при умножении, так это привести к общему знаменателю: никаких методов «кросс-старшего», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дроби на целую часть и отрицательную дробь
Если в махинациях есть целые части, их нужно переводить в неправильные — и только потом умножать по схемам выше.
Если в знаменателе в знаменателе или перед ним стоит минус, он может быть получен путем умножения или полностью удален в соответствии со следующими правилами:
- Плюс, минус дает минус;
- Два отрицания дают утвердительный ответ.
До сих пор эти правила выполнялись только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. По работе их можно обобщить, чтобы «сжечь» сразу несколько минусов:
- Минусы вытягиваю попарно, пока они полностью не исчезнут. В крайнем случае может выжить один минус — тот, кто не нашел пару;
- Если минусов нет, операция завершена — можно переходить к умножению. Если последний минус не зачеркивается, так как не нашел пары, переносим вне умножения.Получается отрицательная дробь.
Задание. Найдите значение выражения:
Все дроби переводятся в неправильные, а потом выносим минусы вне умножения. Что остается, умножайте по обычным правилам. Получаем:
Еще раз напоминаю, что минус, стоящий перед дробью с выделенной целой частью, относится ко всей дроби, а не только к ее части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они находятся в скобках. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более точной.
Уменьшение фракций «На лету»
Умножение — очень трудоемкая операция. Числа здесь довольно большие, и для упрощения задачи можно попробовать уменьшить дробь больше до умножения . Ведь по сути, числа и знаменатели дробей являются обычными множителями, и поэтому их можно разрезать, используя основное свойство дроби.Взгляните на примеры:
Задание. Найдите значение выражения:
По определению имеем:
Во всех примерах отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители уменьшились полностью. На их месте мало единиц, о которых, вообще говоря, писать нельзя. Во втором примере добиться полного сокращения не удалось, но общий объем вычислений все же уменьшился.
Однако ни в коем случае не используйте эту технику при сложении и вычитании дробей! Да, иногда встречаются похожие числа, которые хочется сократить. Вот смотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении дроби в числителе появляется сумма, а не произведение чисел. Следовательно, нельзя применить главное свойство дроби, потому что в этом свойстве речь идет об умножении чисел.
Других оснований для уменьшения дробей просто нет, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте осторожны.
) И знаменатель на знаменателе (получаем знаменатель работы).
Формула умножения дробей:
Например:
Прежде чем приступить к умножению чисел и знаменателей, необходимо проверить возможность сокращения дроби.Если получится сократить дробь, то вам будет легче проводить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае сложения, переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанные):
- превращаем смешанные дроби в неправильные;
- уменьшить числительные и знаменатели дробей;
- уменьшающая фракция;
- , если вы ошиблись дробью, мы преобразуем неправильную дробь в смешанную.
Примечание! Чтобы умножить смешанную дробь на другую смешанную дробь, вам нужно для начала привести их в виду неправильные дроби, а затем умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Удобнее использовать второй способ умножения обыкновенной дроби на число.
Примечание! Для умножения дроби на натуральное число знаменатель дроби должен быть разделен на это число, а числитель остается неизменным.
Из приведенного выше примера ясно, что этот вариант более удобен для использования, когда обозначение дроби делится без остатка на натуральное число.
Многоэтажные фракции.
В классах средней школы встречаются трехэтажные (или более) дроби. Пример:
Чтобы довести такую дробь до привычного представления, используйте деление после 2 баллов:
Примечание! При делении на дроби очень важен порядок деления.Будьте осторожны, здесь легко запутаться.
Примечание, например:
При делении единиц на любую дробь результат будет такая же дробь, только в обратном порядке:
Практические советы при умножении и делении дробей:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность. Все расчеты делайте аккуратно и аккуратно, сосредоточенно и четко. Лучше записать в черновиках несколько лишних строк, чем запутаться в расчетах в уме.
2. В задачах с разными типами дробей — переходите к видам обычных дробей.
3. Все фракции уменьшаются до невозможности разрезания.
4. Многоэтажные дробные выражения в виде обыкновенных, с делением через 2 точки.
5. Единицу дроби делим в уме, просто переворачивая дробь.
В курсах средней и старшей школы учащиеся сдали тему «Фруи». Однако это понятие намного шире, чем дано в процессе обучения.Сегодня понятие дроби встречается довольно часто, и не каждый может вычислить какое-либо выражение, например, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерения. Как показывает практика, часто встречаются примеры определения длины отрезка, объема прямоугольного прямоугольника.
Изначально студенты знакомятся с таким понятием, как доля. Например, если разделить арбуз на 8 частей, каждая получит каждый восьмой арбуз.Этот один из восьми и называется дробью.
Часть 1/2 от любого значения называется половиной; ⅓ — Третий; ¼ — Квартал. Записи вида 5/8, 4/5, 2/4 называются обыкновенными дробями. Обыкновенная дробь делится на числитель и знаменатель. Между ними есть признак дроби или дробный признак. Дробный объект можно нарисовать как в виде горизонтальной, так и в виде наклонной линии. В данном случае это означает знак деления.
Знаменатель показывает, насколько одинаковые акции разделены значением; А числитель — сколько взято одинаковых дробей.Числитель пишется над знаком дроби, знаменатель — под ним.
На координатном луче удобнее всего отображать обыкновенные дроби. Если один сегмент разделить на 4 равные доли, обозначить каждую дробь латинской буквы, то в результате можно получить отличный наглядный допуск. Итак, точка A показывает долю, равную 1/4 от всего сегмента единицы, а точка B отмечает 2/8 от этого сегмента.
Разновидности дробей
Плоды бывают обыкновенные, десятичные, а также смешанные.Кроме того, дробь можно разделить на правильную и неправильную. Эта классификация больше подходит для обычных фракций.
Под правильной дробью — число в числителе меньше знаменателя. Соответственно, неправильная дробь — это число, числитель которого больше знаменателя. Вторая форма обычно записывается в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная.Однако, если вам нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается этого выражения, то они понимают запись, в которой любое число представлено знаменателем дробного выражения которой может быть выражается единицей с несколькими нулями.Если дробь верна, то вся часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, вы должны сначала записать целую часть, отделив ее от дробной запятой, а затем написать дробное выражение. Необходимо помнить, что числитель после точки с запятой должен содержать столько цифровых символов, сколько нулей в знаменателе.
Пример . Представьте дробь 7 21/1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Для записи задания в ответ неправильная дробь некорректно, поэтому ее необходимо перевести в смешанное число:
- разделите числитель на существующий знаменатель;
- в конкретном примере неполное частное — целое число;
- , а остаток является числителем дробной части, а знаменатель остается неизменным.
Пример . Переведите неправильную дробь в смешанное число: 47/5.
Решение . 47: 5. Неполное частное равно 9, остаток = 2. Итак, 47/5 = 9 2/5.
Иногда необходимо представить смешанное число как неправильную дробь. Затем нужно использовать следующий алгоритм:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение добавляется в числитель;
- результат записывается в числитель, знаменатель остается неизменным.
Пример . Представьте смешанную форму как неправильную дробь: 9 8/10.
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение обыкновенных дробей
Над обыкновенными дробями можно выполнять различные алгебраические операции. Чтобы умножить два числа, нужно умножить числитель на числитель, а знаменатель на знаменатель. Более того, умножение дробей с разными знаменателями отличается от произведения дробных чисел с такими же знаменателями.
Бывает, что после нахождения результата нужно уменьшить дробь. В обязательном порядке нужно упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе является ошибкой, но и назвать ее правильным ответом тоже сложно.
Пример . Найдите произведение двух обыкновенных дробей: ½ и 20/18.
Как видно из примера, после нахождения работы получилась сокращенная дробная запись.И числитель, и знаменатель в данном случае делятся на 4, и получается ответ 5/9.
Умножение десятичных дробей
Произведение десятичных дробей по своему принципу сильно отличается от работы обыкновенной. Итак, умножение дробей выглядит следующим образом:
- две десятичные дроби должны быть записаны друг в друга так, чтобы крайние правые числа были друг к другу;
- надо записанные числа умножать, не смотря на запятые, то есть как натуральные;
- вычислить количество цифр после точки с запятой в каждом из чисел;
- в результирующем шаге после умножения результата необходимо подсчитать столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить разделительный знак;
- Если цифр в работе получилось меньше, то перед ними нужно написать столько нулей, чтобы покрыть эту сумму, поставить запятую и поставить целую часть равной нулю.
Пример . Вычислите работу двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, вам необходимо использовать правило умножения дробей:
- переводит смешанные числа в неправильные дроби;
- найдите произведение цифр;
- найти произведение знаменателей;
- записать полученный результат;
- максимальное упрощение выражения.
Пример . Найдите продукт 41 и 6 2/5.
Умножение числа на дробь (дроби на число)
Помимо нахождения работы двух дробей, смешанных чисел, существуют задания, где нужно умножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, вам нужно:
- записать число под дробью так, чтобы крайние правые числа оказались одно над другим;
- найти работу, не смотря на запятую;
- в полученном результате можно отделить целую часть дроби с помощью точки с запятой, считая справа то количество символов, которое стоит после запятой в дроби.
Чтобы умножить обыкновенную дробь на число, вы должны найти произведение числителя и натурального множителя. Если ответ представляет собой уменьшенную дробь, его следует преобразовать.
Пример . Рассчитываем работу 5/8 и 12.
Решение . 5/8 * 12 = (5 * 12) / 8 = 60/8 = 30/4 = 15/2 = 7 1/2.
Ответ : 7 1/2.
Как видно из В предыдущем примере необходимо было уменьшить полученный результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения смешанной формы и натурального множителя. Чтобы умножить эти два числа, вы следуете за целой частью смешанного множителя для умножения на число, умножаете числитель на то же значение, а знаменатель оставляете без изменений. При необходимости нужно легко упростить результат.
Пример . Найдите товар 9 5/6 и 9.
Решение . 9 5/6 x 9 = 9 x 9 + (5 x 9) / 6 = 81 + 45/6 = 81 + 7 3/6 = 88 1/2.
Ответ : 88 1/2.
Умножение множителей 10, 100, 1000 или 0,1; 0,01; 0,001.
Из предыдущего пункта следует следующее правило. Для умножения десятичной дроби, 10, 100, 1000, 10 000 и т. Д. Нужно сдвинуть запятую вправо на столько знаков числа, сколько нулей в множителе после единицы.
Пример 1. . Найдите продукт 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2. . Найдите товар 3.9 и 1000.
Решение . 3,9 х 1000 = 3900 х 1000 = 3900.
Ответ : 3900.
Если нужно умножить натуральное число на 0,1; 0,01; 0,001; 0,0001 и т. Д. Следует переместить левую запятую в получившемся продукте на такое количество знаков цифр, сколько нулей до единицы. При необходимости нулей записывают в достаточном количестве натуральным числом.
Пример 1. . Найдите продукт 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2. . Найдите продукт 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, поиск работы различных дробей не должен вызывать затруднений, кроме подсчета результата; В этом случае без калькулятора просто не обойтись.
Умножение — произведение, закон, пример и законы
Умножение часто описывается как повторяющееся сложение . Например, произведение 3 × 4 равно сумме 4 + 4 + 4 трех четверок. Закон, на котором это основано, — это закон распределения: a (b + c) = ab + ac. В этом случае закон применяется к 4 (1 + 1 + 1), что дает 4 (1) + 4 (1) + 4 (1) или 4 + 4 + 4.
Если один или оба множителя не являются натуральными числами , закон все еще применяется, 0.4 (1,2) = 0,4 (1) + 0,4 (0,1) + 0,4 (0,1), но члены суммы не просто «повторяются», и необходимы другие правила, такие как правила размещения десятичной точки.
Конечно, нельзя возвращаться к закону распределения каждый раз, когда он или она вычисляет продукт. Фактически, большая часть времени в младших классах школы посвящена построению таблицы умножения и ее запоминанию для последующего использования. Однако при применении этой таблицы к таким продуктам, как 12 × 23, явно используется закон распределения:
Здесь а равно 12; b равно 20; и c равно 3.
Говоря об умножении, используется несколько терминов. В 6 × 3 все выражение, записывается ли оно как 6 × 3 или как 18, называется произведением. Каждая шестерка и тройка называются множителями, множителями или, иногда, членами. Старые слова «умножаемое» (для 6) и «множитель» (для 3), которые делали различие между числом, которое умножается, и числом, которое производило умножение, вышли из употребления. Теперь «множитель» применяется к любому числу.
Умножение обозначается тремя способами: знаком «×», как в случае 6 × 3; с точкой в центре, как в 6 • 3; и написав числа рядом друг с другом, как в 5x, 6 (3), (6) (3) или (x + y) (x — y).Последний способ обычно предпочтительнее.
| Для всех номеров a, b и c | |
| ab — уникальный номер | закон о закрытии |
| ab = ba | коммутативный закон |
| а (bc) = (ab) c | ассоциативный закон |
| а • 1 = а | закон мультипликативной идентичности |
| Если ab = cb и b ≠ | закон об отмене |
| Из этих законов можно вывести еще три полезных закона: | |
| a • 0 = 0 | умножение на нулевое свойство |
| Если ab = 0, то a = 0, или b = 0, или и то, и другое. | Отсутствие делителей нуля |
| Факторы в продукте можно комбинировать в любом порядке. | обобщенное коммутативное свойство |
Умножение регулируется не только законом распределения, который связывает его со сложением, но и законами, которые применяются только к умножению. Эти законы представлены в таблице выше.
Поскольку арифметика выполняется с натуральными числами, необходимы некоторые дополнительные законы для обработки десятичных дробей, обыкновенных дробей и других чисел, которые не являются натуральными числами:
Десятичные дроби: умножайте десятичные дроби, как если бы они были натуральными числами.Поместите десятичную точку в произведении так, чтобы количество разрядов в произведении было суммой количества разрядов в множителях. Например, 3,07 × 5,2 = 15,964.
Дроби: Числитель произведения является произведением числителей; знаменатель произведения — произведение знаменателей. Например, (3/7) (5/4) = 15/28.
Числа со знаком: умножайте числа, как если бы они не имели знаков. Если один из двух факторов имеет знак минус, поставьте продукт знак минус.Если оба множителя имеют знак минус, напишите продукт без знака минус. Например, (3x) (- 2y) = -6xy; (-5) (- 4) = 20; (-x) 2 = x 2 ; и (5x) (x) = 5x 2 .
Степени одного и того же основания: чтобы умножить две степени одного и того же основания , сложите экспоненты. Например, 10 2 × 10 3 = 10 5 и x 2 × x = x 3 .
Одночлены: чтобы умножить два одночлена, переставьте множители. Например, (3x 2 y) (5xyz) = 15x 3 y 2 z.
Многочлены : Чтобы умножить два многочлена, умножьте каждый член одного из на каждый член другого, объединяя одинаковые члены. Например, (x + y) (x — y) = x 2 — xy + xy — y 2 = x 2 — y 2 .
Умножение — это модель для множества практических ситуаций. В одном у нас есть количество, a, групп по b вещей в каждой группе . Произведение ab представляет собой общее число. Например, семь коробок для яиц содержат всего 7 × 12 яиц. В других ситуациях мы имеем «прямое изменение» или пропорциональность: y = kx. Столько галлонов бензина из расчета на столько галлонов требует умножения, как и вычисление расстояния как , функция из , скорость и время, D = RT.
В отличие от сложения, в котором длина плюс длина равна другой длине, а длина плюс вес, бессмысленна, произведение двух количеств одного и того же типа или разных типов часто имеет смысл и имеет тип, отличный от обоих. Например, произведение двух одномерных мер, таких как длина, становится двумерной мерой, площадью. Умножение силы , такой как сила тяжести, на расстояние дает работу, которая представляет собой изменение количества энергии .Таким образом, хотя умножение тесно связано с вычислительным сложением, в приложении оно учитывает отношения более сложных измерений.
Хотя умножение обычно является операцией между числами, оно также может быть операцией между другими видами математических элементов. Умножение в более широком смысле подчиняется многим законам обычного умножения, но не обязательно всем из них.
Например, в «часовой арифметике» выполняются все основные законы, кроме отмены.В арифметике часов 3 × 4 = 3 × 8, потому что обе оставляют стрелки в одном и том же положении, но, конечно, 4 не равно 8. При умножении матриц коммутативность не выполняется.
Особенно интересным расширением идеи умножения является декартово произведение двух множеств. Если A = {1, 2, 3} и B = {x, y}, то A × B — это множество {(1, x), (1, y), (2, x), (2, y ), (3, x), (3, y)}, сформированный путем объединения каждого элемента A с каждым элементом B. Поскольку множества иногда используются в качестве основы для арифметики, декартовы произведения образуют важную связь между множествами и обычным умножением. .
Натуральное число: определение и примеры
Определения статистики> Натуральные числа и целые числа
Содержание (Щелкните, чтобы перейти к этому разделу)
- Натуральное число
- Целые числа
- Почему натуральное число — это целое число?
- Пример целых чисел
- Закрытые комплекты и целые
- Свойства целых номеров
Натуральные числа — это числа, которые мы используем для счета.Они целые, неотрицательных числа. Мы часто видим их представленными на числовой строке .
Линия на изображении выше начинается с 1 и увеличивается в значении до 5. Однако числа могут увеличиваться в значении бесконечно (обозначено пунктирной линией на изображении). Таким образом, натуральные числа могут продолжаться до бесконечности.
Набор натуральных чисел обычно обозначается символом ℕ . Например:
ℕ = {1, 2, 3, 4, 5, 6, 7…}
Набор натуральных чисел, включающий ноль, известен как целых чисел .Набор целых чисел обычно обозначается W . Например, это набор целых чисел:
Вт = {0, 1, 2, 3, 4, 5, 6, 7…}
Возможно, что сбивает с толку, некоторые авторы не включают ноль в набор целых чисел. В этом случае это то же самое, что и набор натуральных чисел.
Как упоминалось выше, натуральные числа должны быть целыми и положительными. Это имеет смысл по ряду причин, включая тот факт, что они считают числа.Допустим, учитель хочет подсчитать количество учеников в своем классе: она может сосчитать только всех детей.
Мы часто видим в статистике, публикуемой в Интернете, цифры, которые кажутся противоречащими «целостности» людей. Например, «средний размер семьи — 3,1 человека». Должно быть достаточно ясно, что невозможно иметь 0,1 человека, но это число является лишь средним. Среднее количество автомобилей на семью рассчитывается путем сложения общего количества автомобилей и деления на количество домашних хозяйств.После деления мы больше не работаем с натуральными числами. Скорее, у нас остается действительное число, в данном случае дробь.
Сумма или произведение натуральных чисел также являются натуральными числами. Например, 5 + 5 = 10 (все три из которых являются естественными) или 10 · 15 = 150.
Точно так же в физическом мире «натуральных» чисел нет смысла говорить, что у нас есть «что-то отрицательное». Скорее, мы говорим, что у нас есть ноль чего-то там, где его нет.Используя приведенный выше пример с учителем, если у учителя в настоящее время нет учеников в его классе, у него нет учеников; В реальном мире нет смысла иметь отрицательных учеников.
Полный набор целых чисел равен набору из неотрицательных целых чисел. Целые числа похожи на целые числа, за исключением того, что они также могут быть отрицательными или нулевыми. Например: -10, -3, 0, 1 5.
Статья по теме: Целочисленные последовательности (CalculusHowTo.com).
Несколько примеров целых чисел: 3, 15, 998, 2, 232, 589.
Все следующие числа являются , а не целыми числами :
- Десятичные : 0,1, 5,23, 15,999, 1,7 2 .
- Фракции : ½, 1/27, 2 ½, 99/100.
- Отрицательные числа: -10, -99, -521.
В теории множеств целые числа подчиняются нескольким правилам. Набор целых чисел:
Замкнут на сложение и умножение. Возьмите два целых числа a и b. Если вы сложите затем (a + b = c), то «c» также будет целым числом.То же верно и для умножения: a · b = d.
Давайте рассмотрим несколько конкретных примеров с числами вместо переменных:
Набор целых чисел не закрывается для деления и вычитания. Если a — целое число, то существует еще одно целое число b, которое дает нецелочисленное решение. В обозначениях это:
Где «b», «c» и «d» не целые числа.
Примеры :
- Вычитание:
6 и 10 — целые числа,
, но 7-9 = -2, что не является целым числом. - Раздел :
4 и 5 — целые числа, но 4/5 — не целые числа.
- Целые числа коммутативны для сложения и умножения. Вы не можете вычесть два целых числа в любом порядке и получить тот же результат.
В обозначениях: Для каждого a, b в множестве целых чисел a + b = b + a и a · b = b a.
Пример : 10 — 1 не то же самое, что 1 — 10. - Целые числа ассоциативны для сложения и умножения.Порядок добавления не важен (их можно сгруппировать в разном порядке).
Для любых a, b и c в наборе целых чисел a (b · c) = (a · b) · c и (a + b) + c = a + (b + c).

 Дорогу осилит идущий, а математику мыслящий!)
Дорогу осилит идущий, а математику мыслящий!)
 )
)

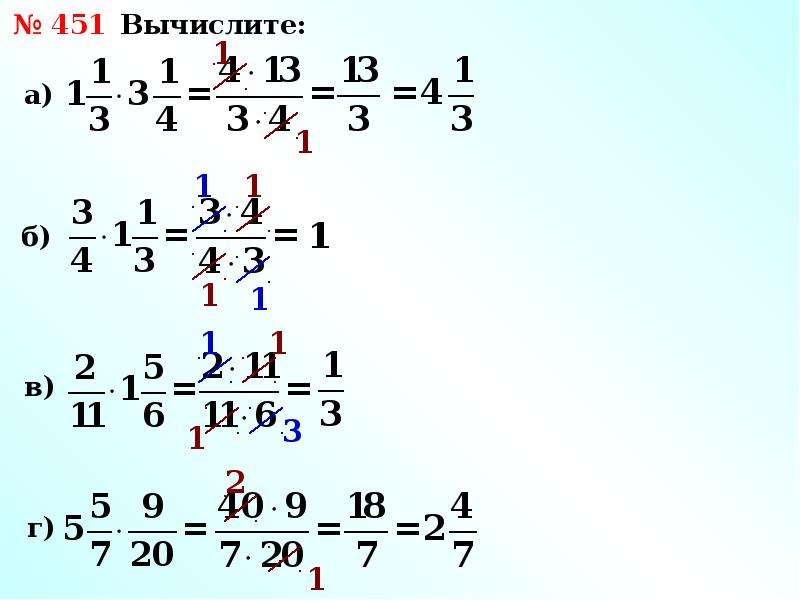


 Это 38-е место в мире.
Это 38-е место в мире.