Умножение дробей с разными знаменателями решение десятичных дробей с ответами

Умножение дробей с разными знаменателями решение десятичных дробей с ответами

1 2 3 4 5 6 7 8 9 0 . C

Ответить

98. 1 * 184.7 =

74.7 * 29.8 =

7.9 * 187.5 =

38.5 * 180.3 =

65.5 * 97.6 =

28.8 * 69 =

122.2 * 77.5 =

194.7 * 35 =

196.4 * 156.9 =

140 * 168.9 =

Попробуй другие онлайн тренажеры с дробями

Калькулятор дробей с разными знаменателями

Примеры дробей с разными знаменателями

Что такое часть от целого?

Тема «дробные числа» в математике одна из самых сложных для восприятия школьниками. Также эта тема очень большая, поскольку охватывает сразу несколько разделов. При изучении дробей в математике очень важно не упустить момент если ребенок что-то хоть немного недопонял или сомневается или не уверен

В данном случае главное объяснить где применяется

«дробная часть числа», а также наглядность примеров. Само слово «Дробь» уже подразумевает дробление, деление, часть от чего-то. В школьной программе к изучению дробей приступают только после изучения всех операций над целыми числами и начинают изучении дробей только в 4 классе. Вначале дети тренируются на простых операциях сложения и вычитания обыкновенных дробей. Затем, приступают к примерам сложнее на умножение дробей. Их также легко можно отработать на тренажёре умножения дробей

Но объяснить ребенку

что такое обыкновенные дроби и решать задания, и познакомиться с примерами решения дробей лучше гораздо раньше. Это сформирует пространственное представление и логическое мышление. Наш тренажер сложения дробей в этом, конечно, поможет. А в 5 классе изучении дробей со сверстниками не составит труда! Но если надо решить уже имеющуюся дробь, ту придет на помощь калькулятор решающий дроби

Как рассказать про часть, чтобы ребенок понял?

Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы. Правильные дроби – это дроби, в которых числитель меньше знаменателя Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя

Дробь — число не целое, оно обозначает количество долей целого

Обыкновенная дробь состоит из двух частей: числитель и знаменатель

Дроби бывают правильные и неправильные. У правильных дробей числитель меньше знаменателя. У неправильных дробей наоборот, числитель больше знаменателя, а значит любую неправильную дробь можно перевести в смешанную, выделив у нее целую часть и отняв ее из числителя

Познакомься с другими тренажерами курса

Меры измерения

Мер величин много и в них легко запутаться. Изучайте меры длины, времени и массы на тренажере

Скорей заниматься

Римские цифры

Множество примеров различной сложности помогут ребенку быстро запомнить римские цифры

Скорей заниматься

Задачи на объем, площадь, периметр

Решение задач на применение формул объем, площадь, периметр

Скорей заниматься

Обыкновенные дроби. Конспект — Kid-mama

Из этой статьи вы узнаете:

1. Что такое обыкновенные дроби.
2. Виды обыкновенных дробей
3. Преобразования дробей
4. Сравнение дробей
5. Основное свойство дроби. Сокращение дробей. Понятие о НОД.
6. Как приводить дроби к одному знаменателю. НОК
7. Сложение и вычитание дробей.
8. Умножение и деление дробей. Взаимно обратные числа и дроби.

 Что такое обыкновенные дроби. Виды дробей.

Дробь всегда означает какую то часть целого. Дело в том, что не всегда количество можно передать натуральными числами, то есть пересчитать: 1,2,3 и т.д.  Как, например, обозначить половину арбуза или четверть часа? Вот для этого и появились дробные числа, или дроби.

Для начала нужно сказать, что вообще дробей бывает два вида: обыкновенные дроби и десятичные дроби. Обыкновенные дроби записываются так:
Десятичные дроби записываются по другому:

Обыкновенные дроби состоят из двух частей: вверху — числитель, внизу — знаменатель. Числитель и знаменатель разделяет дробная черта. Итак, запомните:

Любая дробь — это часть целого. За целое обычно принимают  1 (единицу). Знаменатель дроби показывает, на сколько частей разделили целое (1), а числитель — сколько частей взяли. Если мы разрезали торт на 6 одинаковых частей ( в математике говорят долей ), то каждая часть торта будет равна 1/6. Если Вася съел 4 куска, то значит, он съел 4/6 .

С другой стороны, дробная черта — это не что иное, как знак деления. Поэтому дробь — это частное двух чисел — числителя и знаменателя. В тексте задач или в рецептах блюд  дроби записываются обычно так: 2/3,  1/2  и т.д. Некоторые дроби получили собственное название, например, 1/2 — «половина», 1/3 — «треть», 1/4 — «четверть»
А теперь разберемся, какие бывают виды обыкновенных дробей.

 Виды обыкновенных дробей

Обыкновенные дроби бывают трех видов: правильные, неправильные и смешанные:

Правильная дробь

Если числитель меньше, чем знаменатель, то такую дробь называют правильной, например:  Правильная дробь всегда меньше 1.

Неправильная дробь

Если числитель больше, чем знаменатель или равен знаменателю, такая дробь называется неправильной, например:

Неправильная дробь больше единицы(если числитель больше знаменателя) или равна единице (если числитель равен знаменателю)

Смешанная дробь

Если дробь состоит из целого числа (целая часть) и правильной дроби (дробная часть), то такая дробь называется смешанной, например:

Смешанная дробь всегда больше единицы.

 

 Преобразования дробей

В математике обыкновенные дроби часто приходится преобразовывать, то есть смешанную дробь превращать в неправильную и наоборот. Это необходимо для выполнения некоторых действий, например, умножения и деления.

Итак, любую смешанную дробь можно перевести в неправильную. Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:

Любую неправильную дробь можно превратить в смешанную.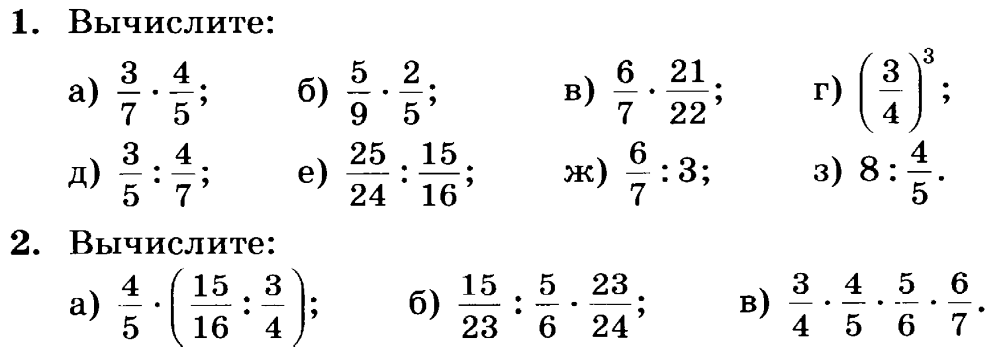 Для этого делят числитель на знаменатель (с остатком). Полученное число будет целой частью, а остаток — числителем дробной части, например:

При этом говорят: «Мы выделили целую часть из неправильной дроби».

Необходимо запомнить еще одно правило: Любое целое число можно представить в виде обыкновенной дроби со знаменателем 1, например:

Поговорим о том, как сравнивать дроби.

 Сравнение дробей

При сравнении дробей может быть несколько вариантов: Легко сравнивать дроби с одинаковыми знаменателями, гораздо сложнее — если знаменатели разные. А есть еще и сравнение смешанных дробей. Но не волнуйтесь, сейчас мы подробно рассмотрим каждый вариант и научимся сравнивать дроби.

Сравнение дробей с одинаковыми знаменателями

Из двух дробей с одинаковыми знаменателями, но разными числителями больше та дробь, у которой числитель больше, например:

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями, но разными знаменателями больше та дробь, у которой знаменатель меньше, например:

Сравнение смешанных и неправильных дробей с правильными дробями

Неправильная или смешанная дробь всегда больше правильной дроби, например:

Сравнение двух смешанных дробей

При сравнении двух смешанных дробей больше та дробь, у которой целая часть больше, например:

Если целые части у смешанных дробей одинаковые, больше та дробь, у которой дробная часть больше, например:

Сравнение дробей с разными числителями и знаменателями

Сравнивать дроби с разными числителями и знаменателями без их преобразования нельзя. Сначала дроби нужно привести к одному знаменателю, а затем  сравнить их числители. Больше та дробь, у которой числитель будет больше. А вот как приводить дроби к одинаковому знаменателю, мы рассмотрим в следующих двух разделах статьи статьи. Сначала мы рассмотрим основное свойство дроби и сокращение дробей, а затем непосредственно приведение дробей к одному знаменателю.

Основное свойство дроби. Сокращение дробей. Понятие о НОД.

Запомните: складывать и вычитать, а также сравнивать можно только дроби, у которых одинаковые знаменатели. Если знаменатели разные, то сначала нужно привести дроби к одному знаменателю, то есть так преобразовать одну из дробей, чтобы ее знаменатель стал таким же, как у второй дроби.

У дробей есть одно важное свойство, называемое также основным свойством дроби:

Если и числитель, и знаменатель дроби умножить или разделить на одно и то же число, то величина дроби при этом  не изменится:

Благодаря этому свойству мы можем сокращать дроби:

Сократить дробь — значит разделить и числитель, и знаменатель на одно и то же число(смотрите пример чуть выше). Когда мы сокращаем дробь, то можно расписать наши действия так:

Чаще же в тетради сокращают дробь так:

Но запомните: сокращать можно только множители. Если в числителе или знаменателе сумма или разность, сокращать слагаемые нельзя. Пример:

Нужно сначала преобразовать сумму в множитель:

Иногда, при работе с большими числами,  для того, чтобы сократить дробь, удобно найти наибольший общий делитель числителя и знаменателя (НОД)

Наибольший общий делитель (НОД) нескольких чисел — это наибольшее натуральное число, на которое эти числа делятся без остатка.

Для того, чтобы найти НОД двух чисел (например, числителя и знаменателя дроби), нужно разложить оба числа на простые множители, отметить одинаковые множители в обоих разложениях, и перемножить эти множители. Полученное произведение и будет НОД. Например, нам нужно сократить дробь:

Найдем НОД чисел 96 и 36:

НОД нам показывает, что и в числителе, и в знаменателе есть множитель12, и мы легко сокращаем дробь.

Иногда, чтобы привести дроби к одному знаменателю, достаточно сократить одну из дробей. Но чаще бывает необходимо подбирать дополнительные множители для обеих дробей .Сейчас мы рассмотрим, как это делается. Итак:

 Как приводить дроби к одному знаменателю. Наименьшее общее кратное (НОК).

Когда мы приводим дроби к одинаковому знаменателю, мы подбираем для знаменателя такое число, которое бы делилось и на первый, и на второй знаменатель (то есть было бы кратным обоим знаменателям, выражаясь математическим языком). И желательно, чтобы  число это было как можно меньшим, так удобнее считать. Таким образом, мы должны найти НОК обоих знаменателей.

Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:

Для того, чтобы найти НОК нескольких чисел, нужно:

1. Разложить эти числа на простые множители
2. Взять самое большое разложение, и записать эти числа в виде произведения
3. Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
4. Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:

Однако вернемся к нашим дробям. После того, как мы подобрали или письменно вычислили НОК  обоих знаменателей, мы должны умножить числители этих дробей на

дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:

 

Таким образом мы привели наши дроби к одному знаменателю — 15.

Сложение и вычитание дробей

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:

Сложение и вычитание смешанных дробей с одинаковыми знаменателями

Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью:

Пример 1:

Пример 2:

Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:

Вычитание проводится аналогично: целая часть вычитается из целой, а дробная — из дробной части:

Если дробная часть вычитаемого больше, чем дробная часть уменьшаемого, «занимаем» единицу из целой части, превращая уменьшаемое в неправильную дробь, а дальше действуем как обычно:

Аналогично вычитаем из целого числа дробь:

Как сложить целое число и дробь

Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:

Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:

Сложение и вычитание дробей  с разными знаменателями.

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как при сложении дробей с одинаковыми знаменателями (сложить числители):

При вычитании действуем аналогично:

Если работаем со смешанными дробями, приводим к одинаковому знаменателю их дробные части и далее вычитаем как обычно: целую часть из целой, а дробную — из дробной части:

 Умножение и деление дробей.

Умножать и делить обыкновенные дроби гораздо проще, чем складывать и вычитать, так как не нужно приводить их к одному знаменателю. Запомните простые правила умножения и деления дробей:

Чтобы умножить дробь на натуральное число, нужно числитель умножить на это число, а знаменатель оставить без изменений  

Например:

Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель — на знаменатель:

Например:

При умножении смешанных дробей нужно сначала записать эти дроби в виде неправильных дробей, а затем умножать как обычно: числитель умножить на числитель, а знаменатель на знаменатель:

Перед тем, как перемножать числа в числителе и знаменателе желательно сократить дробь, то есть избавиться от одинаковых множителей в числителе и знаменателе, как в нашем примере.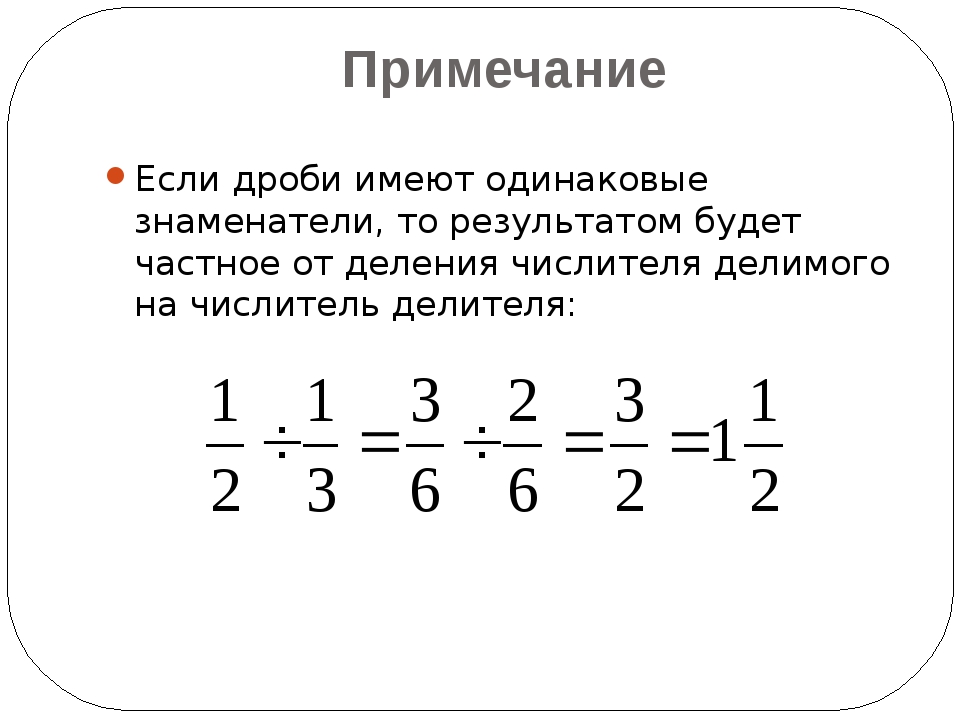

Чтобы  разделить дробь на натуральное число, нужно знаменатель умножить на это число, а числитель оставить без изменений:

Например:

Деление дроби на дробь

Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное делителю (обратную дробь).Что же это за обратная дробь?

Взаимно обратные числа и дроби.

Если мы перевернем дробь, то есть поменяем местами числитель и знаменатель, то получим обратную дробь. Произведение дроби и обратной ей дроби дает единицу. В математике такие числа называют взаимно обратными числами:

Например, числа — взаимно обратные, так как 

Таким образом, вернемся к делению дроби на дробь:

Чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю:

Например:

При делении смешанных дробей нужно так же, как и при умножении, сначала перевести их в неправильные дроби:

При умножении и делении дробей на целые натуральные числа, можно представлять эти числа так же в виде дробей со знаменателем 1.

И при делении целого числа на дробь  представляем это число в виде дроби со знаменателем 1:

 

Как умножать дроби за 3 шага [обновлено]

Как умножать дроби

Умножение дробей можно обсуждать в рамках трех основных категорий.

1. Умножение правильных дробей
2. Умножение неправильных дробей
3. Умножение смешанных чисел

Умножение правильных дробей

Правильная дробь – это дробь меньше единицы, у которой числитель меньше знаменателя.

Пример:

Чтобы умножить правильные дроби, вам нужно выполнить всего три простых шага

Шаг 1  – Умножить числители
Шаг 2 – Умножить знаменатели
Шаг 3 – Простейшая форма должны следовать этому шагу, только когда у нас есть общие множители для числителя и знаменателя.

В противном случае оставьте все как есть.)

Теперь давайте обсудим несколько простых примеров

Пример 01 :

Теперь давайте решим это, выполнив три простых шага, описанных выше.

Шаг 01  и  Шаг 02 (если вам трудно умножать, вы можете использовать таблицу умножения)

Шаг 03 –

Следуя шагу 01 и шагу 02, мы получили ответ 9005 На шаге 03 мы должны упростить дробь. Но в приведенном выше ответе мы видим, что нет общих множителей (число, которое делит и 2, и 15).

Таким образом, окончательный ответ будет

Пример 02 :

Шаг 01 и Шаг 02

Шаг 03

Теперь мы получили

в качестве ответа. Мы видим, что и 15, и 24 могут

разделить на 3 (3 — общий множитель)

Окончательный ответ будет

Пример 03 :

Шаг 01

и Шаг 02

Шаг 03 –

Для этого числителя и знаменателя у нас есть несколько общих делителей, таких как 2,3 и 6.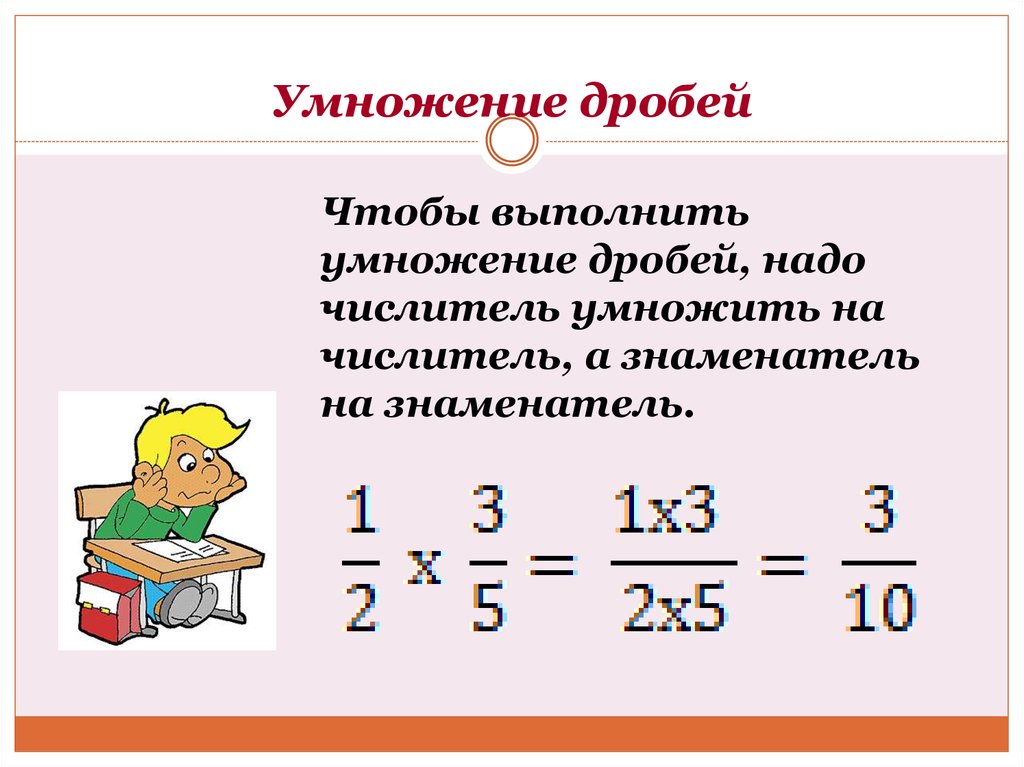

из этих делителей вы должны выбрать наибольший общий делитель (он также называется Наибольшим общим делителем — HCF)

Таким образом, окончательный ответ будет

Думайте, что вы не можете найти наибольший общий делитель,
, который равен 6 в приведенном выше примере. Не запутайтесь. Вы можете продолжить упрощать дробь с любым общим множителем, который вы помните.

Предположим, вы смогли найти только 2 в качестве общего множителя. Просто продолжайте с 2.

В нашей новой дроби

снова, мы можем видеть, что 3 является общим делителем.

Умножение неправильных дробей

Неправильная дробь — это дробь, у которой числитель больше знаменателя

Пример:

Чтобы умножить неправильную дробь, нужно выполнить всего три простых шага

Шаг 1 – Умножить числители
Шаг 2 – Умножить знаменатель в неправильную дробь
1 Шаг 3 смешанный номер

Теперь давайте обсудим несколько простых примеров

Пример 1 :

Шаг 01 и Шаг 02

Шаг 03 –

смешанное число. Существует несколько методов преобразования.

Позвольте мне объяснить вам простой метод.

В этом методе Вы должны использовать длинное деление. Разделить числитель на знаменатель.

Таким образом, окончательный ответ равен 9.0005

Пример 02 :

Шаг 01 и Шаг 02

Шаг 03 –

Разделите 63 на 12, тогда частное равно 5, а остаток равен 3.

Ответ

Умножение смешанных чисел

Число, представляющее собой сумму целого числа и правильной дроби, записанной таким образом, определяется как смешанные числа

Примеры:

Чтобы умножить смешанные числа, необходимо выполнить четыре простых шага.

Шаг 1 – Преобразуйте смешанное число в неправильную дробь
Шаг 2 – Умножьте числители
Шаг 3 – Умножьте знаменатели
Шаг 4 – Выразите ответ в виде смешанного числа

Пример 01 :

Шаг 01

Запишите каждое смешанное число в виде неправильной дроби.

Шаг 02 и Шаг 03

Умножить числитель на числитель и знаменатель на знаменатель

Шаг 04

Преобразование неправильной дроби в смешанное число

Пример 02 :

Общие множители можно удалить следующим образом.

Пример 03 :

Теперь вы знаете, как умножать дроби. Также вам нужно потренироваться,

• как умножать смешанные дроби с разными знаменателями
• как умножать дроби на дроби
• как делить и умножать дроби
• как умножить две дроби

Если у вас возникли трудности с умножением двух дробей, оставьте комментарий ниже.

Упражнение 01

Видео с вопросами: Умножение трех смешанных чисел

Стенограмма видео

Вычислить полтора раза по три и три четверти помножить на одну и семь девятых.

Эти номера считаются смешанными. А чтобы умножить три смешанных числа, нам нужно преобразовать их в неправильные дроби. Неправильная дробь — это дробь, у которой числитель — большее число, а знаменатель — меньшее число.

Итак, как мы сказали, чтобы умножить три смешанных числа, нам нужно преобразовать их в неправильные дроби, а затем умножить числители вместе, умножить знаменатели вместе, а затем упростить.

Итак, давайте начнем преобразовывать эти смешанные числа в неправильные дроби. Итак, полтора, давайте перепишем единицу так, чтобы она имела знаменатель, равный двум. Два больше двух равно одному.

А это полтора. Итак, нам нужно два на два с половиной. Итак, нам нужно добавить половину. Когда мы складываем дроби, мы добавляем числители и сохраняем знаменатели, если они одинаковы.

Получаем три половинки. Теперь продолжим. Три и три четверти, так как же мы можем переписать три как нечто большее, чем четыре? Что ж, мы можем взять четыре умножить на три и сделать из них 12, потому что полная противоположность, 12, разделенная на четыре, даст нам три.

Таким образом, 12 четвертей равны трем, а затем мы прибавляем три четверти. Итак, 12 плюс три равно 15. И мы сохраняем наш общий знаменатель, то есть пятнадцать четвертых.

Один и семь девятых, один мы можем переписать как девять на девять плюс семь девятых. Складываем числители и получаем 16, сохраняем знаменатель и получаем девять. Итак, у нас есть 16 девятых. Итак, как мы уже говорили ранее, нам нужно умножить все наши неправильные дроби, умножив все числители вместе и умножив все знаменатели вместе.

Трижды умножить на 15, умножить на 16, будет 720. И дважды четыре, умножить на девять, будет 72. Мы уменьшим это число и получим 10. Теперь мы можем сделать это другим способом. При умножении чисел мы можем упростить, прежде чем умножать числа.

Три можно упростить до девяти. Сколько раз три идет девять? Он входит в девять три раза, а затем входит в себя один раз. Итак, продолжаем искать.

Теперь у нас может возникнуть соблазн сказать, что двойка и четверка внизу могут упростить, но для упрощения это должно быть число из числителя и число из знаменателя.