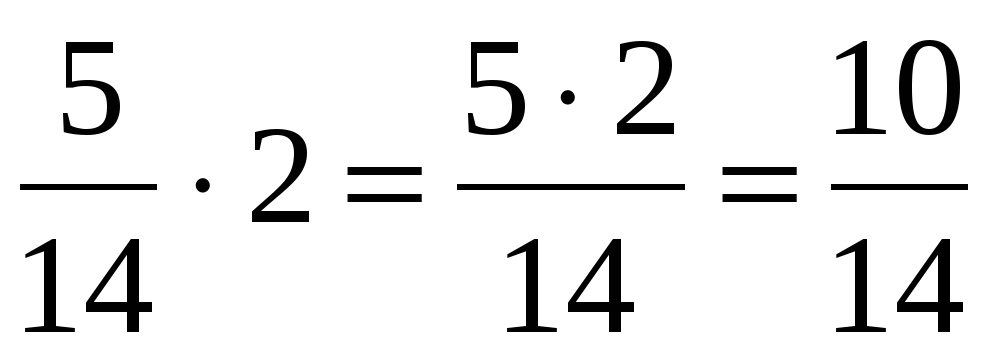.

Учитывая это, можно деление выполнять по следующему правилу.

Чтобы разделить одно число на другое, нужно делимое умножить на число, обратное делителю.

Пример 1.

.

Пример 2.

Пример 3.

.

10. Примеры на все действия с обыкновенными дробями. Решение примеров на все действия с дробями выполняют с помощью записи по отдельным действиям или записи цепочкой.

Пример. Вычислить:

Решение по частям.

Ответ. 1.

Пример вычисления цепочкой:

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

ГЛАВНАЯ СТРАНИЦА / МЕНЮ САЙТА / СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ 

1) привести данные дроби к наименьшему общему знаменателю; 2) сравнить (сложить, вычесть) полученные дроби — Студопедия

Поделись  

правило умножения обыкновенных дробей:

умножение дроби на дробь дает дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей.

То есть, умножению обыкновенных дробей a/b и c/d отвечает формула .

правило умножения обыкновенной дроби на натуральное число:

умножение дроби на натуральное число дает дробь, числитель которой равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби. С помощью букв правило умножения дроби a/b на натуральное число n имеет вид .

правило деления обыкновенной дроби на натуральное число:

Чтобы разделить дробь на натуральное число, нужно знаменатель умножить на это число, а числитель оставить без изменений.

Пример:

правило деления обыкновенных дробей:

чтобы разделить обыкновенную дробь a/b на дробь c/d нужно делимое умножить на число, обратное делителю. С помощью букв озвученное правило умножения обыкновенных дробей записывается так: .

Смешанное число – это число, равное сумме натурального числа

n и правильной обыкновенной дроби a/b, и записанное в виде . При этом число n называют целой частью числа, а число a/b называют дробной частью числа.

Чтобы из неправильной дроби выделить целую часть надо:

1. разделить с остатком числитель на знаменатель;

2. полученное неполное частное записываем в целую часть дроби;

3. остаток записываем в числитель дроби;

4. делитель записываем в знаменатель дроби

Чтобы представить смешанное число в виде неправильной дроби, нужно:

1. умножить его целую часть на знаменатель дробной части;

2. к полученному произведению прибавить числитель дробной части;

3. записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Пример:

правило сложения смешанного и натурального числа :

чтобы сложитьсмешанное число и натуральное число, надо к целой части смешанного числа прибавить данное натуральное число, а дробную часть оставить без изменения. Немного поясним это правило. Пусть нам нужно провести сложение смешанного числа и натурального числа n. Любое смешанное число равно сумме целой и дробной части, поэтому , а свойства сложения позволяют последнюю сумму переписать в виде .

Чтобы сложить смешанные дроби, надо:

1. привести дробные части этих чисел к наименьшему общему знаменателю;

2. отдельно сложить целые части и отдельно дробные части;

3. если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;

4. сократить полученную дробь.

Чтобы выполнить вычитание смешанных чисел, надо:

1. привести дробные части этих чисел к наименьшему общему знаменателю;
2. если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;
3. отдельно выполнить вычитание целых частей и отдельно дробных частей;
4. сократить полученную дробь.

Умножение смешанных чисел: Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.



Каковы правила умножения дробей?

Обновлено 21 декабря 2020 г.

Автор Lisa Maloney

Умножение — одна из самых простых операций, которые вы можете выполнять с дробями, потому что вам не нужно беспокоиться о том, имеют ли дроби одинаковые знаменатели или нет; просто перемножьте числители вместе, умножьте знаменатели вместе и упростите полученную дробь, если это необходимо. Однако есть несколько вещей, на которые следует обратить внимание, включая смешанные числа и отрицательные знаки.

Умножение по прямой

Первое и самое важное правило умножения дробей заключается в том, что вы умножаете только числитель × числитель и знаменатель × знаменатель. Если у вас есть две дроби 2/3 и 4/5, их перемножение даст новую дробь:

\frac{2 × 4}{3 × 5}

, что упрощается до:

\frac{8} {15}

На этом этапе вы бы упростили, если бы могли, но поскольку числа 8 и 15 не имеют общих множителей, дальнейшее упрощение этой дроби невозможно.

Другие примеры, включая умножение дробей, которые необходимо уменьшить, смотрите в видео ниже:

Знаки минуса

Если вы умножаете дроби с отрицательными членами, убедитесь, что вы несете эти отрицательные знаки по вашим расчетам. Например, если вам даны две дроби -3/4 и 9/6, вы должны перемножить их вместе, чтобы создать новую дробь:

\frac{-3 × 9}{4 × 6}

Какой получается:

\frac{-27}{24}

Поскольку −27 и 24 имеют общий множитель 3, вы можете разложить 3 как из числителя, так и из знаменателя, и у вас останется:

\frac{-9}{ 8}

Обратите внимание, что -9/8 представляет собой значение, сильно отличающееся от 9/8. Если бы этот отрицательный знак потерялся по пути, ваш ответ был бы неправильным.

Да, вы можете умножать неправильные дроби

Взгляните еще раз на только что приведенный пример. Вторая дробь 9/6 — неправильная дробь. Или, другими словами, его числитель был больше знаменателя. Это совсем не меняет того, как работает ваше умножение, хотя, в зависимости от вашего учителя или особенностей задачи, над которой вы работаете, вы можете предпочесть упростить результат последнего примера, который сам по себе является неправильной дробью, до смешанное число:

\frac{-9}{8} = -1 \, \frac{1}{8}

Умножение смешанных чисел

Это прекрасно ведет к обсуждению того, как умножать смешанные числа: Преобразовать смешанное число в неправильную дробь и умножить как обычно, как описано в последнем примере. Например, если вам дана дробь 4/11 и смешанное число 5 2/3 для умножения, вы должны сначала умножить целое число 5 на 3/3 (это число 1 в виде дроби). которое имеет тот же знаменатель, что и дробная часть смешанного числа), чтобы преобразовать его в дробь:

5 × \frac{3}{3} = \frac{15}{3}

Затем добавьте дробную часть смешанного числа, получив:

5 \,\frac{2}{3} = \frac{15}{3} + \frac{2}{3} = \frac{17}{3}

Теперь вы готовы перемножить две дроби вместе:

\frac{17}{3 } × \frac{4}{11}

Умножение числителя на знаменатель дает:

\frac{17 × 4}{3 × 11}

Что упрощается до:

\frac{68}{33}

Вы не можете больше упрощать члены этой дроби, но если хотите, вы можете преобразовать ее обратно в смешанное число:

2 \, \frac{2}{33}

Умножение обратно делению

Вот удобный трюк: если вы знаете, как умножать на дроби, вы уже знаете, как делить на дроби. Просто переверните вторую дробь вверх ногами и умножьте ее вместо того, чтобы делить. Итак, если у вас есть:

\frac{3}{4} ÷ \frac{2}{3}

Это то же самое, что написать:

\frac{3}{4} × \frac{3}{ 2}

, которые затем можно умножить как обычно.

Умножение дробей — УРОКИ МАТЕМАТИИ КЕЙТ

Вы видите ярлык, который мы могли бы использовать? Чтобы найти ответ без диаграммы, мы можем перемножить числители вместе (1 x 1 = 1) и умножить вместе знаменатели (2 x 4 = 8), чтобы получить ответ.

Давайте рассмотрим еще один пример, чтобы увидеть, применимо ли это сокращение. Допустим, у нас есть 2/3 умножить на 4/5. Это означает, что нам нужно 2/3 дроби 4/5. Начнем с картинки 4/5. 4/5 означает, что целое было разделено на 5 равных частей, и у нас есть 4 из 5 равных частей.

Если мы хотим найти 2/3 от 4/5, это означает, что нам нужно найти 2/3 заштрихованной части выше. Для этого мы можем разбить прямоугольник на 3 равные строки. Чтобы найти 2/3, нам нужны 2 строки из 3.

Так что же такое 2/3 от 4/5? Когда мы разделили коробку на 3 ряда, мы образовали прямоугольник размером 5 х 3. Это дает нам в общей сложности 15 равных частей. Нам нужны только 2/3 заштрихованной части, поэтому нам нужно подсчитать только то, что заштриховано в 2 из 3 рядов (внутри фиолетового прямоугольника, показанного выше). Мы видим, что это дает нам 8 одинаковых частей из 15: 8/15.

Вы видите ярлык? Чтобы найти ответ, мы можем перемножить числители вместе (2 х 4 = 8) и умножить знаменатели вместе (3 х 5 = 15).

​Как умножать дроби

Вам не нужно рисовать каждый раз, когда вы перемножаете две дроби. Вместо этого используйте ярлык. Чтобы умножить дроби вместе, вы просто умножаете прямо. Перемножьте числители вместе. Затем умножьте знаменатели вместе. Наконец, упростите свой ответ, если это необходимо.

​15 и 56 не имеют общих делителей, кроме 1, поэтому дробь не нужно упрощать. Вот пример, где дробь можно упростить:

.

Есть еще один вариант, который может быть проще. Вместо упрощения в конце можно упростить в начале. Если вы сначала упростите, может быть легче увидеть общие факторы с меньшими числами в начале.

Не имеет значения, упростите ли вы первое или последнее, в итоге вы получите один и тот же ответ. Выберите способ, который кажется вам самым простым.

Умножение дробей на целые числа

Что делать, если только одно число является дробью, а другое — целым числом? Превратите целое число в дробь, используя 1 в качестве знаменателя. Деление на 1 не меняет числа, поэтому любое целое число можно переписать с 1 в знаменателе. После того, как вы записали целое число в виде дроби, вы можете выполнить шаги по умножению дробей.

​Умножение на смешанное число

Одно или оба числа, которые вы умножаете, могут быть смешанными числами. Прежде чем умножать, запишите смешанное число как неправильную дробь.

Деление обычного числа на дробь. Деление дроби на натуральное число

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы. ..

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.

Кстати, у меня есть ещё парочка интересных сайтов для Вас. )

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.

Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:

1. Верхняя часть дроби называется числителем, а нижняя – знаменателем.
2. При делении числа называются так: делимое: делитель = частное

Как делить дроби: простые дроби

Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:

3/77: 1/11 = 3 /77 * 11 /1 = 3/7

Как делить дроби: смешанные дроби

Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:

10 2/3: 4/15 = 32/3: 4/15 = 32/3 * 15 /4 = 40/1 = 40

Как делить дробь на число

Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:

5/11: 7 = 5/11: 7/1 = 5/11 * 1/7 = 5/77

Как делить десятичные дроби

Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.

Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно, приведем следующий пример.

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками.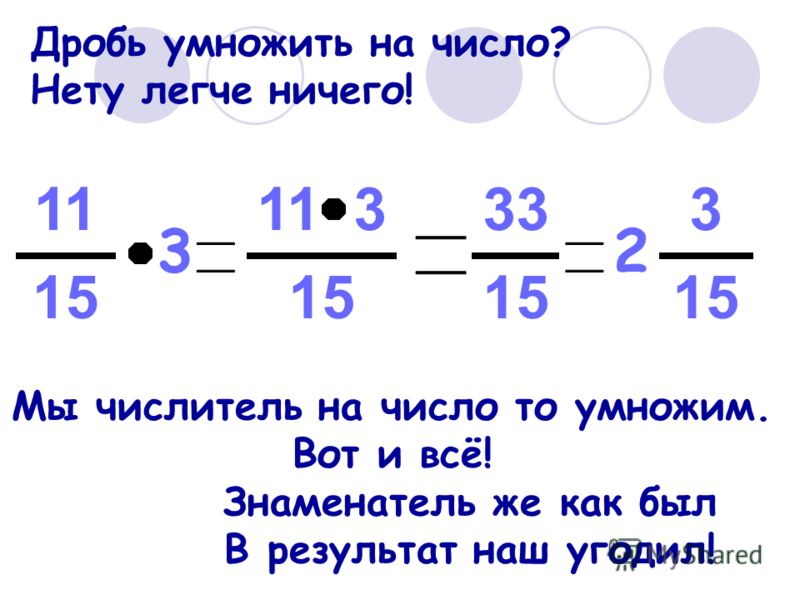 Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Что произойдет с целым числом, если его умножить на дробь, большую 1?

Числа — это математические цифры или значения, которые можно использовать для подсчета, измерения или выполнения других арифметических операций. Эти системы чисел включают целые числа, целые числа, натуральные числа, рациональные и иррациональные числа, простые числа и так далее. Система счисления — это стандартизированный способ представления чисел на различных носителях, включая цифры и язык. Он содержит широкий диапазон чисел, включая простые числа, нечетные числа, четные числа, рациональные числа, целые числа и так далее. В зависимости от используемой системы счисления эти числа могут быть представлены различными способами.

В системе счисления есть несколько типов чисел, таких как простые числа, нечетные числа, четные числа, рациональные числа, целые числа и так далее. Эти числа могут быть выражены с использованием этих цифр и слов. Например, целые числа, такие как 50 и 35, выраженные цифрами, также могут быть записаны как пятьдесят и тридцать пять.

Целые числа

Целые числа — это подмножество чисел, содержащее ноль и все положительные целые числа. Общее число варьируется от 0 до бесконечности. Эти числа обычно используются в повседневных расчетах, в основном для количественной оценки фундаментальных величин. Натуральные числа — это просто целые числа, включая ноль. Подмножество представлено целыми числами 0, 1, 2, 3, 4, 5,… Дроби, десятичные дроби и отрицательные целые числа не включаются в подмножество.

Положительные целые числа, также называемые счетными числами, представляют собой части целых чисел, содержащие ноль, например 0, 1, 2, 3, 4, 5 и т. д., тогда как отрицательные целые числа, дроби и десятичные дроби не включаются. К целым числам относятся 10, 11, 24, 50, 100, 1000 и так далее.

Дробь 

Дроби определяются как числовое число, представляющее часть целого.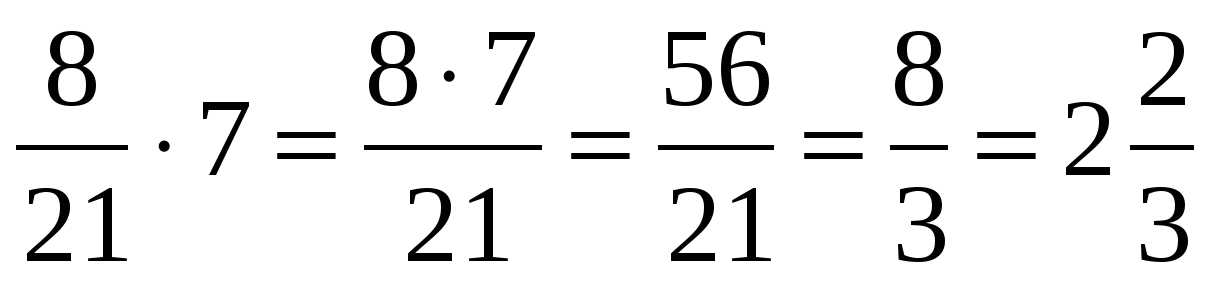 Дробь — это компонент или сектор любого количества, взятого из целого, где целое может быть любым числом, заданным значением или объектом. Все дроби имеют числитель и знаменатель, которые разделены горизонтальной чертой, называемой дробной чертой.

Что происходит с целым числом, если его умножить на дробь, большую 1?

Решение:  

Есть три условия, которые дают разные результаты, когда целое число умножается на дробь.

• Первый случай: Если мы умножим целое число на дробь больше 1, то результирующее значение станет больше. Пример: 5 — это целое число, и если его умножить на дробь больше 1, получится
9.0032

 = 5 × 4/3 

 = 5 × 1,33

 = 6,6666

Здесь целое число равно 5, но после умножения его на дробь, большую 1, результирующее значение становится больше.

• Второй случай: Если мы умножим целое число на дробь меньше 1, то его результирующее значение станет меньше. Пример: 5 — это целое число, и если мы умножим его на дробь меньше 1.

= 5 × 2/4 

= 5 × 0,5

= 2,5

Здесь целое число равно 5, но после умножения его на дробь меньше 1 результирующее значение становится меньше.

• Третий случай: Если умножить целое число на дробь, равную 1, то результирующее значение будет таким же, так как изменений не будет. Пример: 5 — это целое число, и если мы умножим его на дробь, то получится 1.

= 5 × 5/5

= 5 × 1

= 5, что равно целому числу.

Примеры вопросов

Вопрос 1: Сложить целое число 8 + 5/2 с дробью?

Решение:

Дано: 8 + 5/2

Здесь мы можем записать 8 как 8/1

= 8/1 + 5/2

5)/2  

= 13/2

Вопрос 2. Упростите 3/5 + 5/6

Решение:  

Здесь: 3/90 см 0 0 50 + 0 50 знаменателя 5 и 6 равны 30

= (18 + 25)/30

= 43/30

Вопрос 3: Упростите 6/2 + 5/8 + 2/9.

Решение:

Дано: 6/2 + 5/8 + 2/9

Здесь, взяв lcm знаменателя 2, 8, 9, получаем 72

= (216 +)/452

= 277/72

Вопрос 4: Умножить 8 × 9/2?

Решение:

Дано: 8 × 9/2

= 8 × 9/2

= 72/2

= 36

Вопрос 5: Если мы умножим целое число 6 на дробь большую 2, что получится?

Решение:

6 — это целое число, и если мы умножили его на фракцию больше 2,

= 6 × 7/3

= 6 × 2,33

= 13,998

. умножьте целое число 6 на дробь, большую 2, тогда результирующее значение станет больше.

Вопрос 6: В классе 50 учеников, 1/5 ^th из них смотрят мультфильмы. Сколько школьников не смотрят мультфильмы?

Решение:

Общее количество учащихся = 50,

Доля учащихся, смотрящих мультфильмы = 1/5 количество учеников, которые не смотрят мультфильмы = 50 – 10 = 40

Следовательно, количество учеников, которые не смотрят мультфильмы, равно 40.  

Умножение дроби на целое число: определение, части и примеры

Хотите знать, что такое дроби и целые числа?

И!

Как дроби умножаются на целое число?

Здесь мы обсудим два математических термина «Дроби» и «Целое число», а также как простым способом умножить дробь на целое число.

Что такое дробь?

Дробь — это не что иное, как числовое значение, представляющее часть целого.

Давайте лучше разберем дроби на примере.

Нарежьте пиццу, и вы получите часть.

Умножьте дробь на целое число всего за 2 шага

Хотите узнать, что такое дроби и целые числа?

И!

Как дроби умножаются на целое число?

Здесь мы обсудим два математических термина «Дроби» и «Целое число», а также как простым способом умножить дробь на целое число.

Что такое дробь?

Дробь — это не что иное, как числовое значение, представляющее часть целого.

Давайте лучше разберем дроби на примере.

Нарежьте пиццу, и вы получите часть.

Здесь

Верхнее число говорит о том, сколько у вас есть ломтиков.

Нижнее число показывает, на сколько частей одинакового размера была разделена вся пицца.

Части дроби

Дробь состоит из двух частей, а именно числителя и знаменателя.

Число, написанное над чертой, называется числителем. Числитель — это количество деталей, которые у нас есть.

Число, написанное под чертой, называется знаменателем. Знаменатель — это количество частей, на которые разбита вся единица.

Линия, которая разделяет числитель и знаменатель, называется «полосой дроби» или «винкулумом».

\[ \frac{Числитель}{Знаменатель} \]

Типы дробей

Правильная дробь: Дробь, значение числителя которой меньше значения знаменателя, называется правильной дробью. Например, \[ \frac{2}{7} \], \[ \frac{3}{10} \],\[ \frac{1}{2} \] и т. д. являются правильными дробями.

Неправильная дробь: Дробь, значение числителя которой больше или равно значению знаменателя, называется неправильной дробью. Например, 5/2, 8/5 и т. д. — неправильные дроби.

Смешанная фракция: Фракция, представляющая собой комбинацию целого и части, называется смешанной фракцией. Например, \[ 3\tfrac{1}{4} \] , \[ 2\tfrac{1}{2} \] и т. д. — смешанные дроби.

Что такое целые числа?

В математике целые числа — это просто числа, начинающиеся с 0. Например:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…. и так далее

Запомни!

Целые числа не включают отрицательные числа, дроби и десятичные дроби.

Вместо этого целые числа включают только положительные счетные числа.

Как умножить дробь на целое число за два шага?

Чтобы умножить дробь на целое число, выполните следующие два шага:

Шаг 1: Умножьте значения числителя.

Шаг 2: Оставьте знаменатель дроби прежним.

Пример:

Умножить \[ \frac{3}{2} \] x 5

Шаг 1: Умножение значений числителя дает:

3 x 5 = 15

Шаг 2: Оставить знаменатель дроби одинаковый. Соответственно, в знаменателе будет 2.

Теперь:

Новый числитель равен 15.

Знаменатель 2 остается прежним.

Отсюда \[ \frac{3}{2} \] x 5 = \[ \frac{15}{2} \]

Как умножить дробь на целое число за четыре шага?

Шаг 1: Преобразуйте целое число в дробь со знаменателем 1. (Мы делаем это, потому что все, что делится на 1, остается неизменным).

Шаг 2: Умножьте числители.

Шаг 3: Умножьте знаменатели.

Шаг 4: При необходимости упростите дробь.

Давайте разберемся на примере:

Умножьте \[ \frac{3}{2} \] на 8

Шаг 1: Преобразуйте целое число в дробь со знаменателем 1.

8 = \[ \фракция{8}{1} \]

Шаг 2: Умножьте числители.

3 8 = 24

Шаг 3: Умножьте знаменатели.

2 x 1 = 2

Следовательно,

Новая дробь равна \[ \frac{24}{2} \]

Шаг 4: Упростите дробь:

\[ \frac{24}{2} \] = 12 или \[ \frac{12}{1} \]

Как умножить смешанную дробь на целое число?

Ниже приведены шаги для умножения смешанной дроби на целое число:

Шаг 1: Преобразуйте смешанную дробь в неправильную дробь.

Шаг а: Умножьте целое число на неправильную дробь.

Примечание. Чтобы преобразовать смешанную дробь в неправильную, умножьте целое число на знаменатель, а затем добавьте результат или произведение, полученное с помощью числителя, чтобы получить новое значение числителя неправильной дроби. Значение знаменателя неправильной дроби будет таким же, как и раньше.

Пример:

Умножьте 3 x \[ 2\tfrac{5}{7} \]

Решение:

Шаг 1. Преобразование смешанной дроби в неправильную.

\[ 2\tfrac{5}{7} \]= \[ \frac{2 \times 7+5}{7} \]= \[ \frac{19}{7} \]

Шаг 2 : Умножение неправильной дроби, полученной на шаге 1, на целое число.

\[ 3\frac{19}{7} \] = \[ \frac{19 \times 3}{7} \] = \[ \frac{57}{7} \]

Следовательно, \[ 3 \times 2\tfrac{5}{7} \] = \[ \frac{57}{7} \] или \[ 8\tfrac{1}{7} \]

Как умножить дробь на Работа с целыми числами?

Когда дробь умножается на целое число, это работает как многократное сложение.

Давайте разберемся на примере:

Умножение \[ \frac{5}{7} \] на 2 равносильно \[ \frac{5}{7} \] + \[ \frac{5}{ 7} \]

Помните! \[ \frac{5}{7} \] x2 = \[ \frac{5}{7} \] x \[ \frac{2}{1} \]= \[ \frac{5×2}{7×1} \] = \[ \frac{10}{7} \]

Следовательно, доказано

Умножение целого числа на дробь Пример задачи

Предположим, что в корзине 10 апельсинов и \[ \frac{3}{ 5}\] из них кислые. Сколько апельсинов кислые?

Решение:

Нахождение \[ \frac{3}{5} \] на 10 аналогично \[ \frac{3}{5} \] x 10

Теперь выполните описанные выше действия для умножения.

\[ \frac{3}{5} \] \times 10 = \[ \frac{3}{5} \] x \[ \frac{10}{1} \] = \[ \frac{3 \times 10}{5 \times 1} \] = \[ \frac{30}{5} \] = 6

Следовательно, 6 апельсинов кислые.

Кто-нибудь из вас знал?

• Сложение и умножение любых двух целых чисел можно выполнять в любом порядке.

• Все числа, кроме 0, имеют непосредственное предшествующее или предшествующее число.

• Десятичная дробь либо заканчивается, либо продолжает повторяться. Например, \[ \frac{1}{4} \] = 0,25, \[ \frac{1}{7} \] = 0,142857142857. С другой стороны, десятичное разложение иррациональных чисел никогда не повторяется.