Таблица умножения: учить нельзя запомнить

Как всё было просто в нашем советском детстве: «Таблица умножения должна отскакивать от зубов!» — говорили мамам строгие учительницы. И вот второклашки всей страны твердили перед сном: «Пятью пять — двадцать пять. Шестью шесть — тридцать шесть». И хором за ними повторяла вся семья, от кота до бабушки. Была даже такая песенка у композитора Шаинского: «Дважды два — четыре. Это всем известно в целом мире!».

Современный ФГОС сходится с советскими школьными стандартами в главном: таблицу умножения школьник должен знать. А вот как именно он ее узнает? Тут-то и начинается самое интересное.

Все чаще можно услышать мнение, будто таблицу умножения можно не учить вовсе. Например, Монтессори подход подразумевает, что ребенок постепенно запомнит все главные примеры таблицы, просто сталкиваясь с ними в реальной жизни. То есть несколько раз умножит 7 на 8 и постепенно запомнит ответ: «56». Для реализации этого подхода требуется большое родительское терпение.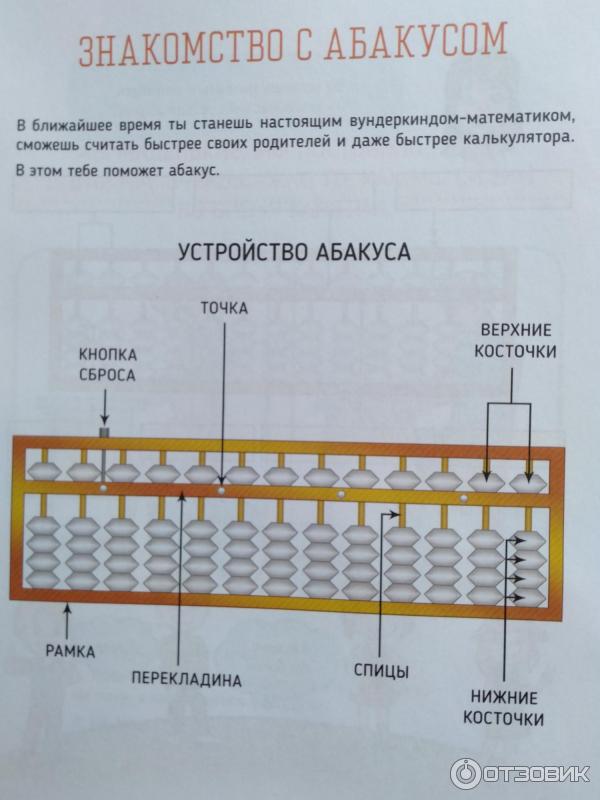 Да и в школе объясняться с учительницей, скорее всего, придется долго.

Так что большинство родителей и педагогов сходятся в том, что таблицу умножения лучше всего выучить, только в игре и ненасильственно, дать ребенку время на осознание самого принципа математического действия — умножения. И здесь в помощь различные техники и приемы. Мы собрали для вас лучшие способы, среди которых каждый может выбрать наиболее подходящий.

Таблица Пифагора

Раньше ее печатали на обороте копеечных тетрадок в клеточку, помните? Вот эта таблица — и есть настоящая таблица умножения, а не те цветные колонки примеров, что сегодня здесь и рядом кочуют по школьным плакатам. Большое преимущество таблицы Пифагора в том, что она позволяет увидеть закономерности в умножении! Например, что 1 на 8 и 8 на 1 — это одно и то же.

Самое лучшее, что можно придумать, так это дать ребенку заполнить такую таблицу самостоятельно, распечатав пустой бланк. Вас ждет много инсайтов, особенно если в школе вы сами пользовались только методом зубрежки!

Пробуйте и делитесь в комментариях своими впечатлениями: что нового вы заметили и узнали? А еще такую табличку можно заламинировать и превратить в многоразовый тренажер. Как в этом видео:

Умножение на 9 и другие хитрости

Для освоения сложного счета из таблицы существуют различные хитрости. Например, не всем взрослым известный прием с пальцами, который позволяет быстро научиться умножать на 9. Для этого нужно выставить перед собой все 10 пальцев обеих рук и загнуть тот по счету слева палец, который вам нужно умножить на 9.

Допустим, это 3 — и вы загибаете вниз третий палец. Слева остается 2 прямых пальца, а справа — 7. То есть 27. Вот и ответ! У «Фиксиков» есть даже мульсовет на эту тему:

На пальцах можно научиться умножать на 6,7 и 8.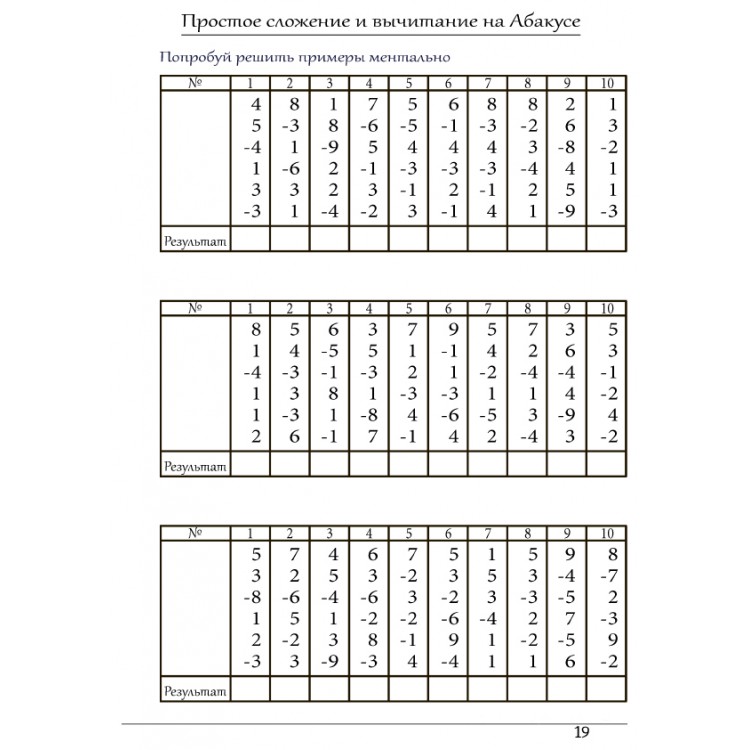 Смотрите:

Настольные игры

Игра — основной язык ребенка. Поэтому вместо «Давай учить таблицу умножения» скажите ему: «А давай поиграем!». Самые простые игры на умножение — с карточками. Вместо покупки готовых наборов всегда можно нарисовать свои или воспользоваться шаблонами, например, таким.

С карточками можно придумать десятки разных активностей. Разложить карточки с примерами и ответами на две группы картинками вверх и по очереди набирать по две карточки из каждой: пример плюс ответ. Если правильно составил пару, забираешь ее себе. Кто набрал больше пар — тот и выиграл. Можно играть с карточками как в мемо, можно устроить большой семейный чемпионат по умножению.

Есть и много хороших готовых игр про таблицу. Самые известные делает «Банда умников»: например, «Цветариум». А уж какое пространство для креатива открывается в изготовлении собственных настолок! Вот простой вариант: тщательно вымыть пластиковую кассету от десятка яиц, вклеить на дно картинки с цифрами от 1 до 9. Положить в кассету два шарика или маленьких кубика, закрыть и потрясти. Когда вы откроете крышку, каждый из кубиков окажется на каком-то числе. Кто первый назовет произведение двух этих чисел, тот и выиграл кон.

Под другим углом

Если вы чувствуете, что все приемы уже надоели ребенку, а задача с освоением таблицы умножения еще не решена, попробуйте посмотреть на нее под другим углом. Это полезно всем: и детям, и взрослым. Знаете ли вы, что в других странах мира умножают совершенно не так, как мы с вами привыкли — в столбик? Существуют и другие популярные способы, например, японский и итальянский. Попробуйте разобраться, как это работаете, и увлекательный совместный вечер с детьми вам обеспечен. Зачем это нужно? Чтобы влюбиться в математику, ее красоту и возможности, потренировать мозги и отлично провести время всей семьей. Итальянский способ умножения «решеткой»:

Японский способ умножения:

Рейтинг: 1/5 — 1 голосов

Что такое ментальная арифметика / TeachMePlease

В то время как большинство из нас жертвует навыком счёта в уме, некоторые люди развивают его с особым усердием с помощью ментальной арифметики. Они похожи на гениев, потому как совершают вычисления с многозначными числами быстрее, нежели калькулятор. Разбираемся, что это за методика, как проходит обучение и кто может заниматься по ней.

О методике

Ментальная арифметика — это одна из методик устного счёта без вспомогательных инструментов, которая задействует воображение.

Методика кажется новой, так как широкую известность она получила относительно недавно. На самом же деле техника древняя, её использование связывают с изобретением счётов суанпан в Китае, которые впервые упоминаются в книге «Восточная династия Хан» в 190 году н.э.

Под ментальной арифметикой подразумевают обучение вычислениям сначала с помощью деревянных счётов, абакуса, и постепенный переход к выполнению сложения, вычитания, умножения и деления в уме. Особенность методики – дети выполняют не абстрактные вычисления, они работают с цифрами через визуализацию и  воображение. Техника позволяет научиться скоростному счёту, что практически недостижимо с помощью классических школьных методов.

Несмотря на широкое распространение калькуляторов, занятия на абакусе до сих пор практикуются в азиатских странах. Вычисления на соробане, японской версии абакуса, изучают в начальных классах и частных учебных заведениях Японии. С его помощью детей учат системе десятичных чисел и счёту не абстрактно, а с помощью визуализации. Попутно учителя дают детям песенные инструкции, что воздействует на аудиальное восприятие.

После того как дети начинают уверенно использовать соробан, их учат совершать вычисления в уме при помощи воображаемой счётной доски. Это одна из причин, по которой японские родители отправляют детей к частным педагогам, преподающим данную методику.

Что такое абакус?

На занятиях для детей используют соробан — японскую версию абакуса. Название же «абакус» используется как обобщённое для всех видов счёт: от китайских до российских.

Абакус для занятий ментальной арифметикой представляет собой прямоугольник, разделённый тринадцатью вертикальными спицами по вертикали, и одной горизонтальной линией. На каждой спице находится по 5 косточек: 1 над горизонтальной перегородкой и 4 под ней.

Как проходит обучение?

Полная программа обучения длится от двух до трёх лет и разделена на несколько этапов. Во время учёбы дети чувствуют прогресс, так как после освоения новых навыков переходят на уровень выше.

На первом этапе дети учатся считать на абакусе. Сначала осваивают сложение и вычитание.

Следующая ступень — представление абакуса в уме. Вы могли видеть как дети считают, совершая непонятные действия руками в воздухе. Таким образом они передвигают воображаемые костяшки на воображаемых счётах.

Далее отрабатываются более сложные арифметические действия: умножение и деление.

Высшую ступень мастерства демонстрируют участники соревнований по ментальной арифметике, которые решают примеры с многозначными числами за несколько секунд.

Кто может научиться?

Программы ментальной арифметики, как правило, рассчитаны на детей от 4 до 16 лет. Правда, отзывы родителей говорят о том, что начинать лучше немного позже, оптимальный возраст 6–12 лет. Хотя вычисления в уме могут быть полезны для взрослых и в большей степени для пожилых людей.

Ребёнок, отправляющийся на занятие, обязательно должен уметь считать до 10. 

Также нужно учитывать, что придётся заниматься не только в классе, но и дома хотя бы по 15 минут ежедневно.

Если вы заинтересовались курсами ментальной арифметики для детей, предлагаем познакомиться с программами на TeachMePlease, и выбрать ту, которая подойдёт вам по местоположению, цене и условиям проведения занятий.

Ментальная арифметика. Умножение и деление

Форма проведения :

Дистанционная с автоматической проверкой

Краткое описание:

В процессе обучения Вы: — познакомитесь с целями и задачами методики; — тщательно изучите методику по теме «Умножение и деление», освоите технологию преподавания, используя подробный поурочный план; — научитесь выполнять арифметические действия на счётах Абакус; — научитесь выполнять арифметические действия в уме с большей скоростью; — научитесь вести занятия с использованием дистанционных образовательных технологий и ресурсов на сайте УМИУС; — получите все необходимые пособия для успешной работы. По результатам прохождения курса слушатели не только улучшат собственные навыки скорого устного счета, но и смогут проводить обучение по данной методике. Для этого мы предоставляем: — планы уроков, в которых подробно расписана каждая тема, как ее преподнести и как закрепить полученные знания; — методические материалы, такие как: рабочие тетради, сборники примеров, тексты, задания; — полезные в образовательном процессе сопутствующие материалы. Все материалы входят в содержание курса, имеют формат *pdf и доступны для скачивания.

Для кого этот курс:

педагог дополнительного образования, классный руководитель, молодые специалисты, выпускники педагогических вузов

Преподавательский состав:

Кокина Марина Викторовна

Занятия проводятся по дням:

Курс дистанционного формата. Обучение в любое удобное для Вас время.

Адрес и место обучения:

Бутлерова, 17Б

Рекомендовано Экспертным советом ДПО
ФИО	Место работы	Рекомендация	Рейтинг ОО
Моторо Наталья Павловна	ГАОУ ВО «Московский городской педагогический университет»	рекомендовано	не участвует в рейтинге
Старостина Мария Евгеньевна	ГБОУ Школа № 508	рекомендовано	281
Рощина Наталья Леонидовна	ГБОУ Школа № 37	рекомендовано	не участвует в рейтинге

Ментальная арифметика.

Умножение и деление

Я б в нефтяники пошел!

Пройди тест, узнай свою будущую профессию и как её получить.

Химия и биотехнологии в РТУ МИРЭА

120 лет опыта подготовки

Международный колледж искусств и коммуникаций

МКИК — современный колледж

Английский язык

Совместно с экспертами Wall Street English мы решили рассказать об английском языке так, чтобы его захотелось выучить.

15 правил безопасного поведения в интернете

Простые, но важные правила безопасного поведения в Сети.

Олимпиады для школьников

Перечень, календарь, уровни, льготы.

Первый экономический

Рассказываем о том, чем живёт и как устроен РЭУ имени Г. В. Плеханова.

Билет в Голландию

Участвуй в конкурсе и выиграй поездку в Голландию на обучение в одной из летних школ Университета Радбауд.

Цифровые герои

Они создают интернет-сервисы, социальные сети, игры и приложения, которыми ежедневно пользуются миллионы людей во всём мире.

Работа будущего

Как новые технологии, научные открытия и инновации изменят ландшафт на рынке труда в ближайшие 20-30 лет

Профессии мечты

Совместно с центром онлайн-обучения Фоксфорд мы решили узнать у школьников, кем они мечтают стать и куда планируют поступать.

Экономическое образование

О том, что собой представляет современная экономика, и какие карьерные перспективы открываются перед будущими экономистами.

Гуманитарная сфера

Разговариваем с экспертами о важности гуманитарного образования и областях его применения на практике.

Молодые инженеры

Инженерные специальности становятся всё более востребованными и перспективными.

Табель о рангах

Что такое гражданская служба, кто такие госслужащие и какое образование является хорошим стартом для будущих чиновников.

Карьера в нефтехимии

Нефтехимия — это инновации, реальное производство продукции, которая есть в каждом доме.

Ментальная арифметика. Умножение и деление (72 ч.)

Авторы курса: квалифицированные педагогические кадры, управленцы-практики в сфере дополнительного образования по курсу «Ментальная арифметика. Умножение и деление», фандрайзеры, ведущие разработчики курсов УМИУС — Величко Е. А., Кокина М. В., Кускевич Т. А., Чувилина М. А.
Целью реализации программы является повышение профессионального уровня в рамках имеющейся квалификации и формирование/приобретение, совершенствование профессиональных компетенций, необходимых слушателям в области освоения технологии ментального счета для развития интеллектуальных способностей учащихся.
Программа направлена на формирование у слушателей знаний и умений, необходимых для выполнения следующих видов профессиональной деятельности: — проведение дополнительных занятий для учащихся по программе «Ментальная арифметика. Умножение и деление».
В процессе освоения программы происходит формирование/приобретение, совершенствование полученных следующих профессиональных компетенций:

• способность использовать современные методы и технологии обучения и диагностики результатов обучения по программе «Ментальная арифметика. Умножение и деление»;
• способности работать с системой обеспечения качества и контроля эффективности учащихся по программе «Ментальная арифметика. Умножение и деление» посредством Личного кабинета на ресурсе https://umius.ru;
• готовность обучать учащихся умножению и делению на абакусе;
• способность самостоятельно развивать собственные навыки скоростного устного счета.

Данный курс может быть интересен: педагогам дополнительного образования, руководителем образовательных организаций, преподавателям СПО и ВО, учителям школ, воспитателям, логопедам, психологам, методистам и преподавателям частных образовательных организаций, а также всем заинтересованным лицам.
Последующее применение полученных знаний будет способствовать:

• Росту успеваемости у учащихся в образовательных учреждениях;
• Повышению эффективности образовательного процесса;
• Увеличению рейтинга ОУ за счет реализации востребованных программ;
• Увеличению степени участия родителей в жизни школы и школьников;
• Формированию лояльности родителей к образовательному учреждению;
• Формированию лояльности населения к Администрации ОУ, как к современным управленцам;
• Организации и проведению дополнительных масштабных мероприятий, таких как Государственные Чемпионаты по отдельной методике «Ментальная арифметика» на территории региона, района;
• Дополнительному источнику дохода для школ;
• Получению существенного превосходства ОУ перед иными коммерческими организациями, реализующими данную программу.

Почему стоит освоить преподавание ментальной арифметики:

1. Спрос на ментальную арифметику постоянно растет. Это перспективная программа.
2. Программу легко освоить в любом возрасте. Актуальна от 5 до 99 лет.
3. Низкая конкуренция в вашем городе из-за отсутствия специалистов и высокой стоимости обучения.
4. Легкий маркетинг. Программа у всех на слуху и не требует дополнительной раскрутки.
5. Свободный график работы. Собираете группы на удобное для вас время и день.
6. Минимальная дополнительная нагрузка. На одну группу необходимо всего 90 минут один раз в неделю.
7. Быстрая подготовка к уроку. Перед уроком не нужно думать, как преподать материал — все расписано до мелочей.
8. Отсутствие рутины. Занятия разнообразны и интересны не только для обучающихся, но и для педагогов.
9. Саморазвитие и личностный рост. Приобретение новых и актуальных компетенций.
10. Повышение успеваемости детей. И, как следствие, формирование лояльности окружающих.

Материалы, необходимые для прохождения курса:

• Тетрадь для записей, ручка;
• Счеты Абакус (Соробан).

Выдаваемый документ: удостоверение установленного образца.
Форма итоговой аттестации: тестирование.
Теги: ментальная арифметика; математика; Дошкольник; Младший школьник; Интеллектуальные способности; Развитие интеллектуальных способностей.

Содержание

• Уровень 1. Умножение
• Уровень 2. Умножение
• Уровень 3. Деление

Сообщество

Таблица Умножения

Существует много секретов, благодаря которым можно быстро и легко, с пониманием смысла, выучить таблицу умножения. Узнать о них и научиться премудростям быстрого счета можно на нашем экспресс-курсе «Таблица умножения за 15 уроков».

Занятия проходят 3 раза в неделю, продолжительностью 60 минут. 

Таблица умножения — почему это важно?

Знание таблицы умножения позволяет:

• Проводить вычисления с многозначными числами в уме или на бумаге без калькулятора
• Видеть глубокие связи в математике и развивать свою «математическую интуицию»

Но чаще всего, таблицу умножения учат потому, что этого требуют в школе, не задумываясь, что это таблица умножения, без преувеличения, является одной из основ математической науки. Без ее знания обучение математике и алгебре станет очень трудным, если не невозможным вовсе.

Таблица умножения нужна всем, ведь мы даже не замечаем того, что постоянно ее используем. В магазинах, дома и на производстве мы умножаем и делим числа, не приберегая к калькуляторам. Вот так уже на втором уроке!

На летних каникулах очень удобно учить таблицу умножения. Простые и логичные правила помогут вашему ребенку понять и надолго запомнить результат.

В таблице умножения главное понять ряд закономерностей, которые значительно упростят обучение. Для примера возьмём умножение на 6. Чтобы умножить 6 на четное число воспользуемся правилом: запишем сначала половину второго множителя, а потом сам множитель. Вот что получается:

• 6*4=24 — четыре/2 и четыре.
• 6*6=36 — шесть/2 и шесть.
• 6*8=48 — восемь/2 и восемь.

Для каждого случая умножения есть своя подсказка, благодаря которой ребенок с легкостью освоит всю таблицу.

НАШ КУРС ПОМОЖЕТ ВАШЕМУ РЕБЕНКУ РАЗВИТЬ И УКРЕПИТЬ ПАМЯТЬ, ОСВОИТЬ НАВЫКИ БЫСТРОГО СЧЁТА, КОТОРЫЕ ПОМОГУТ ЕМУ СОРИЕНТИРОВАТЬСЯ В НУЖНУЮ МИНУТУ.

Ответы на вопросы о нашем курсе ментальной арифметики

На какие разделы делится курс?

1. Уровень S
Длительность: 3 месяца
Программа: Знакомство с абакусом, его составляющие, правила работы с ним.
Результат: Дети узнают как правильно складывать и вычитать на абакусе. Активно развивается навык мелкой моторики: почерк, манипуляция с мелкими предметами. Первые заметные улучшения успеваемости в школе.

2. Уровень М
Длительность: 3 месяца
Программа: Закрепление навыков, изучение формул счета.
Результат: Ребенок начинает считать по формулам. Ощутимо улучшается память и концентрация внимания. Заметно лучше запоминаются стихотворения и виден прогресс в артикуляции речи.

3. Уровень А
Длительность: 5-6 месяцев
Программа: Доведение техник сложения и вычитания до автоматизма.
Результат: Дети могут посчитать любые примеры на сложение и вычитание за считанные секунды. Феноменально развиваются воображение, представление и фотографическая память.

4. Уровень R
Длительность: 5-6 месяцев
Программа: Подготовка к умножению на абакусе.
Результат: Молниеносный ментальный счет, доскональное знание и оперирование таблицей умножения, увеличение скорости счета. Значительно вырастает способность к аналитической деятельности, самостоятельность и заметно повышается самооценка.

5. Уровень T
Длительность: 5-6 месяцев
Программа: Умножение на абакусе.
Результат: Ребенок умножает на абакусе, используя уже изученные формулы. На этом этапе ребенок тратит минимальное время на решение любых арифметических задач в школе. Многие дети занимают призовые места на олимпиадах.

6. Уровень Y
Длительность: 5-6 месяцев
Программа: техника счета деления на абакусе.
Результат: Ребенок не только с легкостью подходит к решению любых задач как в школе, так и в жизни. Активно выражено стремление к лидерству, умение аргументировано отстаивать свою точку зрения, улучшается успеваемость по большей части предметов в школе.

 

Можно ли обучить своего ребенка самостоятельно?

Вы можете заниматься со своим ребенком индивидуально, пройдя обучение данной методике. Даже если вы решили заниматься сами, советуем проводить занятия в группе, поскольку групповые занятия развивают коммуникабельность, умение работать в команде.

 

Насколько эффективны эти занятия? Есть ли реальный прогресс?

Ментальная арифметика развивает творческое и аналитическое мышление, улучшает концентрацию внимания, фотографическую память, воображение, логику, а также наблюдательность и слух. Это не обычный счет в уме, ведь умение находить ответ на самые сложные примеры и задачи в считанные секунды развивает правое полушарие мозга, отвечающее за воображение и представление.

 

Не противоречит ли обучение ментальной арифметике школьной программе?

Обучение ментальной арифметике помогает ребенку лучше усваивать школьную программу. Во-первых, он развивает способности, связанные с памятью, воображением, логикой и мышлением. Во-вторых, помогает лучше понимать точные науки: математику, физику, геометрию. А в-третьих, придает уверенности детям. Когда ваш ребенок научится быстро считать и делать это лучше взрослого, он будет знать, что может научиться всему, нужно лишь постараться!

 

Ребенок может решать такие примеры на калькуляторе, зачем ему ментальная арифметика?

Абакус сложно сравнить с калькулятором, т.к. калькулятор вызывает леность ума, в то время как абакус заставляет мозг работать, что позволяет решать арифметические задачи со скоростью калькулятора. Кроме того, занятия ментальной арифметикой не только повышают скорость устного счета, но и развивают другие когнитивные способности ребенка (воображение, память, внимание, наблюдательность).

 

 

уловок и советов по умножению умножения, которые помогут быстрее вычислить в уме

Приемы умножения и советы в этом посте позволят вам выполнять вычисления в уме быстрее, чем калькулятор, находящийся в вашей голове. Существует множество умственных стратегий умножения, но описанные здесь стратегии умственного умножения могут применяться для умножения любого набора чисел. Изучение советов по умножению умственных способностей, приведенных в этом посте, будет похоже на обучение катанию на велосипеде. Как только вы выучите это, действительно очень трудно это забыть.

Прежде чем мы продолжим, вы, должно быть, освоили однозначное умножение. Обязательным условием является знание таблиц однозначного умножения от 1 x 1 до 9 x 9, прежде чем вы начнете умножать большие числа в уме. Если вы немного подзабыли, добавьте этот пост в закладки и сначала убедитесь, что вы запомнили свои однозначные таблицы умножения. Если вы хорошо умеете умножать однозначные числа, можете читать дальше.

Этот пост является второй частью серии «Уловки с умственной математикой».Настоятельно рекомендуется прочитать первый пост из этой серии — Уловки мысленной математики для скоростной математики, прежде чем приступить к изучению того, как выполнять мысленную математику при умножении.

Секрет умножения умножения

В первой части «Уловок ментальной математики» мы узнали, что математику в уме становится труднее выполнять, если вы считаете справа налево. Следовательно, секрет ментальной математики в том, чтобы делать обратное и вместо этого вычислять слева направо. Решая слева направо, вы начнете называть ответ до того, как закончите полный расчет.Вычисление слева направо сначала может показаться немного странным, но после небольшой практики это станет естественным. В этом посте мы увидим, как применить это к умственному умножению.

Что такое множимое и множитель?

Прежде чем мы перейдем к уловкам умножения для выполнения мысленных вычислений, давайте быстро определим, что такое множимое и множитель. Возьмем, к примеру, задачу умножения 43 x 23. Здесь число 43 — это множимое — число, которое умножается. Число 23 — это множитель — число, на которое умножается первое число.

В этом посте есть несколько приемов умножения для умственной математики. У каждого метода умственного умножения будет два примера. Первый пример, видимый всем, познакомит вас с уловкой умножения. Во втором примере, видимом только авторизованным пользователям, будут варианты, не описанные в первом примере. Так что войдите в систему или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту.

Уловки умножения для однозначного числа

Общее умножение умножения на однозначное умножение

Общий мысленный метод умножения — умножение слева направо.Хотя общий метод может применяться для любого числа, он работает лучше всего, когда числа не заканчиваются на 7, 8 и 9. У нас есть отдельный метод для чисел, заканчивающихся на 7, 8 и 9. А пока давайте применим умножение умножения умножить 5321 x 4.

Правило простое. Умножайте слева направо. По одной цифре за раз.

Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньше чисел, чтобы вызвать их и использовать позже. Вы сразу же начнете называть ответ с самого первого шага расчета.

Теперь попробуйте умножить 7142 на 6. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение в уме с округлением в большую сторону для однозначного множителя

Использование умственных приемов умножения после округления в большую сторону полезно, когда числа заканчиваются на 7, 8 или 9. Это значительно упрощает умножение. Давайте посмотрим, как применить это на примере. Умножить 68 x 3.

1. Округлите число

2. Умножить слева направо

3. Умножьте округленную сумму в большую сторону.

4.Вычтите числа из двух предыдущих шагов

Если вы попытаетесь сделать это так, как вы обычно делаете это на бумаге, вы поймете, что требуется больше времени, чем то, что вам нужно сейчас, чтобы сделать это в уме. Если у вас еще нет скорости, не волнуйтесь. Это придет с практикой. В конце есть практические упражнения и рабочие листы умственного умножения, которые вы можете скачать и практиковать.

Теперь вы попробуйте умножить 96 x 7. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение 2-значных чисел в уме

Общие приемы умножения

Давайте теперь посмотрим, как теперь умножать в уме двузначные числа.Уловки умножения, которые мы видели ранее, нужно немного изменить. Давайте посмотрим, как это сделать, на примере. Умножить 36 x 32.

1. Разбить множимое

2. Умножить слева направо

3. Сложите отдельные ответы, чтобы получить окончательный ответ

Вы можете решить ту же задачу, разбив множитель вместо множимого. Ваш выбор будет зависеть от того, что дает вам более простой процесс сложения на шаге 3. Постарайтесь выбрать число, которое имеет меньшую цифру, потому что в большинстве случаев это обычно приводит к добавлению меньших чисел.

Теперь вы попробуйте умножить 26 x 23. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Округление в большую сторону для 2-значного множителя

Как и в случае однозначных множителей, округление и умножение полезно, когда числа заканчиваются на 7, 8 или 9. Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99:

1. Округлить число

2. Умножьте округленное значение на сумму, округленную в большую сторону слева направо.

3. Вычтите два числа

Теперь попробуйте умножить 41 x 57.Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение умножения с использованием множителей

Как и округление в большую сторону, одна из уловок умножения состоит в том, чтобы разложить число на множители перед его умножением. Давайте посмотрим, как это сделать, попытавшись умножить 45 x 22.

1. Разложите на множители

.

2. Умножьте число на первый множитель (слева направо)

4. Умножьте произведение на второй множитель (слева направо)

В уловках умножения, которые мы видели ранее, вам нужно будет запомнить произведение первой цифры, чтобы добавить / вычесть произведение второй цифры.Однако при умножении с использованием множителей вы просто умножаете второй множитель на первое произведение, так что вам не нужно запоминать столько чисел при вычислении.

Теперь вы попробуете умножить 21 x 63 с помощью факторного метода. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Рабочие листы по уловкам умственного умножения

Ниже вы можете скачать рабочие листы в формате PDF, чтобы применить описанные приемы умножения.

Калькулятор для превращения в человека

Вы узнали основные приемы умножения. Но Мы лишь поцарапали поверхность, и нам предстоит еще многое рассказать. Если вы действительно хотите стать человеком-калькулятором и вывести свои математические навыки на новый уровень, то посмотрите это видео. В видео я поделюсь историей о том, как я на самом деле боролся с математикой и как я пришел туда, где я нахожусь сегодня. Вы узнаете секрет, который сократит вашу кривую обучения и ускорит ваш путь к математическому мастерству в уме.Чтобы посмотреть видео кликните здесь.

Заключение

Свои вопросы, пояснения и отзывы оставляйте в комментариях. Потребуется практика, прежде чем применение уловок умножения станет простым и легким. Поначалу вам будет сложно запомнить все числа в своей голове, когда вы будете считать. Но практика поможет вам улучшить кратковременную память на числа. Заставьте себя мысленно производить вычисления слева направо для повседневных вычислений и используйте калькулятор только для того, чтобы перепроверить свои числа.Чем больше вы практикуетесь, тем выше ваша скорость и способности.

случайных математических уловок (Часть 1): Умножение двузначных чисел | Тайсон Ву

Фото предоставлено: Unsplash

Пример 1

45 * 63 =?

Прежде чем искать лучший способ решения подобных проблем умножения, давайте посмотрим, как традиционный метод преподавания в начальной школе будет подходить к этому вопросу:

Вертикальная форма

Когда нам нужно выполнить умножение двух двузначных чисел в, мы можем интуитивно разделить их на две задачи умножения двузначного и однозначного числа.В приведенном выше примере обычный способ выполнения математических вычислений — разбить его на 45 * 60 + 45 * 3.

Проблемы возникают при обычной практике

Однако, когда нам приходится выполнять математические вычисления без карандаша и бумаги, мы не можем отметить какие-либо промежуточные результаты , и мы часто забываем результат 45 * 60, когда переходим к вычислению 45 * 3. Не говоря уже о том, что мы должны сложить два результата, чтобы получить окончательный ответ. Мы должны найти лучший способ, который меньше полагается на запоминание промежуточных результатов.

Метод

«Эмпирическое правило» выглядит так:

«Внешние * внутренние, десятки * десятки, единицы * единичные»

Вот объяснение:

• Умножьте две «внешние» цифры (4 и 3) и две «внутренние» цифры (5 и 6), затем сложите их: 4 * 3 + 5 * 6 = 42. Это первый промежуточный результат . Чтобы промежуточный результат не занимал ваши драгоценные места в памяти, вы можете напомнить себе число 42 жестом руки, то есть 4 слева и 2 справа.

Ваша рука должна выглядеть так.

• Двигаясь дальше, мы смотрим на две цифры десятков и умножаем их. 4 * 6 = 24. Снова посмотрите на свою руку и представьте себе число 24. Совместите крайнюю правую цифру с десяткой на руке и сложите их, как показано ниже. У вас должно получиться число 282 , и это число, которое следует сейчас запомнить:

Посмотрите на свою руку и представьте, что эти числа парят в воздухе

• Наконец, мы смотрим на две цифры на единицы и умножаем их.5 * 3 = 15. Помните промежуточный результат 282 ? Совместите крайнюю левую цифру 15 с крайней правой цифрой промежуточного результата и сложите их. И это окончательный ответ: 2835.

Это рассматривается как улучшенный способ умножения двузначных чисел, поскольку нам нужно только запомнить не более два простых промежуточных результата в любой момент. Кроме того, мы могли меньше запоминать с помощью жестов рук.

Пример 2

Давайте сделаем еще один пример:

79 * 23 =?

Число, которое проходит через вашу руку и голову, следует записывать следующим образом:

• Первый промежуточный результат «Outers * Inners» должен быть 39 .
• «Добавьте» 14 к первому промежуточному результату и получите 179.
• «Добавьте» 27 к 179, чтобы получить 1817.
• Готово!

Это то, что вы сделали в своей голове?

79 * 23 =?

Сначала ваша скорость вычислений с использованием этого трюка может быть немного медленной, но я могу гарантировать, что после небольшой практики вы сможете придумать ответ быстрее, чем ваш друг, который пытается ввести числа в калькулятор. чтобы получить результат. Это уловка, которую определенно стоит потренировать!

5 приемов для более быстрого умственного умножения

Теперь, когда мы изучили основы молниеносного умственного сложения, умственного вычитания и умственного умножения, пришло время обратить наше внимание на несколько советов, которые помогут вам развить свои навыки. следующий уровень.

Сегодня мы собираемся начать с изучения 5 советов, которые помогут вам быстро умножать числа в своей голове и стать волшебником мысленной математики в своей семье.

1. Как умножить на 5
2. Как возводить в квадрат числа, заканчивающиеся на 5
3. Как легко умножить девятки
4. Как умножить на 2
5. Как быстро удвоить и уменьшить вдвое

Купить сейчас

Как партнер Amazon и книжный магазин.org, QDT зарабатывает на соответствующих покупках.

Совет №1: как умножить на 5-ю степень

Бывают моменты в жизни, когда тебе просто везет. Оказывается, один из тех счастливых моментов случается каждый раз, когда вам нужно умножить одно число на другое, которое оказывается степенью 5. Например, скажем, вам нужно найти 36 x 5 (что, конечно же, , отвечает всем требованиям, поскольку 5 — это первая степень числа 5). Уловка состоит в том, чтобы признать тот факт, что 5 = 10/2.2 это конечно. Так как же это работает в этом случае? Уловка здесь состоит в том, чтобы распознать, что 25 = 100/4. И вообще, уловка со степенями 5 состоит в том, чтобы признать, что они всегда кратны 10, деленной на целое число. Это говорит нам, что 36 x 25 = 36 x 100/4. Поскольку мы можем быстро вычислить, что 36 x 100 = 3600, легко найти, что 36 x 25 = 3600/4 = 900.

Совет № 2: как возводить в квадрат числа, заканчивающиеся на 5

На этом наше веселье с пятерками не заканчивается. Мы уже говорили о том, как возводить числа в квадрат в уме раньше, но оказалось, что все становится намного проще, если возвести в квадрат двузначное число, которое заканчивается на 5.2 = 5625. Быстро и просто!

Совет № 3: как легко умножить партии девяток

Третий трюк на сегодня связан с умножением любого числа на 9, 99, 999 или любое другое число, которое на 1 меньше степени 10. Что делает все эти дикие 9 чисел особенными? В задаче типа 44 x 9 хитрость состоит в том, чтобы распознать, что 44 x 9 = 44 x (10 — 1). Распределительное свойство умножения говорит нам, что это то же самое, что и 44 x 10–44. А поскольку умножить на степень 10 легко, такой взгляд на проблему значительно упрощает ее решение.В частности, он говорит нам, что 44 x 9 = 44 x 10 — 44 = 440 — 44 = 440 — 40 — 4 = 396 (зоркие любители математики могут заметить здесь уловку, связанную с советами мысленного вычитания из ранее).

Если мы вместо этого пытаемся решить 44 x 99, уловка состоит в том, чтобы распознать, что это то же самое, что 44 x (100 — 1) = (44 x 100) — 44. Другими словами, в любое время, когда вы умножая на одно из этих чисел, состоящих из девяток, хитрость заключается в том, чтобы знать, что вы можете просто умножить другое число на следующую более высокую степень 10, а затем вычесть исходное число.Попробуйте, и вы увидите, насколько это быстрее.

Если вы пытаетесь решить 44 x 99, уловка состоит в том, чтобы распознать, что это то же самое, что 44 x (100 — 1) = (44 x 100) — 44.

Совет №4: как умножить на две степени

Вы можете использовать сегодняшний четвертый совет каждый раз, когда вы умножаете одно число на другое число, которое является степенью 2. Это означает, что каждый раз, когда вы умножаете какое-то число на 2, 4, 8, 16, 32, 64 и т. Д. на, это ваш билет к умственному математическому блаженству.3 или 12 x 2 x 2 x 2. Это означает, что мы можем быстро найти ответ, постоянно удваивая 12 три раза. Таким образом, первое удвоение 12 дает 24, второе удвоение приводит нас к 48, а третье удвоение дает 96. Итак, 12 x 8 = 96.

Совет 5: как удвоить и уменьшить вдвое, чтобы быстро умножить

Предыдущий трюк на самом деле является частным случаем сегодняшнего пятого и последнего (и я думаю, самого крутого) трюка, который вы можете использовать всякий раз, когда одно из умножаемых вами чисел четное. Допустим, вы умножаете 47 на 24.Поскольку 24 — четное число, давайте воспользуемся идеей удвоения и уменьшения вдвое, чтобы быстро решить эту проблему.

Что я имею в виду под удвоением и уменьшением вдвое? Уловка состоит в том, чтобы постоянно удваивать одно число, а другое уменьшать вдвое. В данном случае это означает, что мы превращаем задачу 47 x 24 в задачу 94 x 12, одновременно удваивая 47 и уменьшая вдвое 24. Затем мы можем сделать то же самое и превратить задачу в 188 x 6 и снова получить 376 x 3. На данный момент мы не можем удваивать и уменьшать вдвое дальше, поэтому нам просто нужно решить оставшуюся — гораздо проще! — задачу умножения, чтобы найти, что 47 x 24 = 376 x 3 = 1,128.

Заключение

Вам определенно понадобится попрактиковаться в этих техниках, чтобы освоиться (и быстро) их использовать, поэтому я настоятельно рекомендую вам придумывать некоторые задачи умножения, над которыми нужно работать. На это потребуется время и силы, но ваши старания непременно будут вознаграждены!

Хорошо, это все математические вычисления, которые у нас есть на сегодня.

Обязательно ознакомьтесь с моей аудиокнигой по мысленной математике под названием The Math Dude’s 5 Tips to Mastering Mental Math . А чтобы узнать больше о математике, посмотрите мою книгу The Math Dude’s Quick and Dirty Guide to Algebra .

Не забудьте стать поклонником Math Dude на Facebook, где вы найдете много отличных математических публикаций в течение недели. Если вы в Твиттере, подпишитесь и на меня. Наконец, присылайте свои математические вопросы мне через Facebook, Twitter или по электронной почте [email protected].

До следующего раза, это Джейсон Маршалл с Быстрые и грязные советы Math Dude, чтобы упростить математику . Спасибо за чтение, любители математики!

Образ мысленной математики от Shutterstock.

Уловки с умственной математикой: калькулятор не нужен!

Быстро! Что будет 14682 умножить на 5? Или 77 умножить на 14? Сможете ли вы возвести 75 в квадрат за три секунды?

Нет, не используй свои хитрости с калькулятором!

Вы не поверите, но есть быстрые и простые способы решить эти проблемы в уме, сэкономив время, бумагу и батареи калькулятора.

Если у вас есть ребенок, который борется с математикой, или вы просто кто-то, кто хочет улучшить свою математику, мы собираемся поделиться некоторыми умственными математическими приемами, которые сделают вашу жизнь намного проще!

Почему важна ментальная математика?

В таком нагруженном технологиями обществе, как наше, зачем вам нужны простые математические уловки? Почему ты не можешь просто положиться на свои хитрости с калькулятором?

Что ж, вот несколько веских причин.

Уловки с умственной математикой экономят время

Если вы сдаете SAT там, где нельзя пользоваться калькуляторами. Вместо того, чтобы тратить драгоценное время на умножение 1082 на 9 от руки, вы можете получить ответ вдвое быстрее и приложить усилия в другом месте.

Уловки с мысленной математикой, чтобы ваш мозг оставался острым

Да, эти таинственные новомодные калькуляторы бесполезны. Но когда вы слишком полагаетесь на технологии, вы просто чувствуете, что все начинает… спотыкаться.Верно? Это не может быть только я. Есть причина, по которой люди решают судоку, головоломки и кроссворды. Уловки с умственной математикой — это просто еще одно упражнение для мозга, и оно определенно стоит затраченных усилий.

Выглядит круче, чем уловки с калькулятором

Честно говоря, это впечатляет и заставляет почувствовать себя кем-то из фильма о Джеймсе Бонде, когда кто-то хочет знать, что такое 273 x 11, и вы можете небрежно сказать правильный ответ, прежде чем кто-то его напечатает. Это немного похоже на академический фокус.

Уловки мысленной математики, которые вы должны знать

Поскольку вы явно все еще читаете, это означает, что вам интересно узнать немного больше о секретном мире чисел. Из всех техник, которыми мы собираемся поделиться, главное запомнить ЭТО:

У каждого трюка есть свои правила, которые заставляют его работать, и вам нужно научиться с первого взгляда распознавать, когда число (или пара чисел) соответствует этим правилам.

Готовы? Давайте начнем!

Умножение двузначных чисел на 11

Вы ведь прекрасно знаете, как умножить на 10, не так ли? Просто добавьте 0 в конец числа! Так просто.Но подожди. А как насчет 11? Особенно, если это число вроде 67? Или 81?

Это кажется немного более сложным … но как только вы научитесь этому трюку, все будет проще простого. Считайте это разминкой для вашего мысленного математического калькулятора.

Вот шаги:

Посмотрите на число, которое вы умножаете на 11. (Итак, если вы умножаете 36 x 11, посмотрите на 36.) Сложите эти две цифры вместе. (3 + 6 = 9) Вставьте эту цифру между числом из шага 1. (396)

Просто, правда?

Но подождите.Что, если на шаге 2 вы получите что-то вроде 14? Или 18? Как вы справляетесь с подобным?

Ну, немного по-другому, но ненамного.

Давайте попробуем с 86 x 11.

1. Посмотрите на 86. (Звучит знакомо?)

2. Сложите эти две цифры вместе. (8 + 6 = 14)

Хорошо. Итак, теперь у вас есть две первые цифры, верно? У вас есть первая цифра из шага 1 (8, из 86)… и у вас есть первая цифра из шага 2.(1, из 14.)

Вот трюк. Вы собираетесь сложить первые цифры вместе.

3. Сложите первые цифры. (8 + 1 = 9)

Это первая цифра вашего ответа. После этого вы вернетесь к старым, знакомым шагам.

4. Вставьте вторую цифру из шага 2 посередине.

Середина чего именно?

Что ж, следите внимательно. Возьмите новую первую цифру из шага 3 (9), приклейте вторую цифру из шага 2 рядом с ней (4) и закройте второй цифрой из шага 1 (6).

Итак, ваш ответ — 946.

Умножение трехзначных чисел на 11

Итак, теперь вы можете умножить любое двузначное число на 11 в мгновение ока! (Или, может быть, два мигания глаза.)

А как насчет трехзначных чисел?

Процесс очень похож на двузначный… но с одной изюминкой.

Помните, как первый шаг двузначного процесса — это сложение ваших цифр? (Пример: если вы умножаете 26 на 11… 2 + 6 = 8.)

Вы можете подумать, что с трехзначным числом вы просто должны сложить все три числа вместе… но это не так.

Вместо этого представьте свое трехзначное число… ну, давайте представим его, как две сестры, ухаживающие за своим младшим братом.

(Останься со мной.)

Задача: умножить 317 x 11.

Итак, вот где появляется сестра. Число, на котором мы хотим сосредоточиться, — 317.

3 — это Threeresa. Она сестра с рыжими волосами и любит овсяное печенье.

7 — это Sevenie. Она высокая и гибкая, с редкими веснушками, читает допоздна.

Они оба собираются в парк со своим младшим братом Уаном. (Ему один год. Его родители кажутся странными именниками.)

Чтобы правильно умножить этих братьев и сестер, вам нужно сначала разделить их на части, но Одного нельзя оставлять одного. (Ради всего святого, он всего лишь ребенок!)

Так что разделите число на части… но одна из сестер всегда должна цепляться за Единую.

317

Во-первых, Триреза держит Единицу. Давайте сложим их вместе. (3 + 1 = 4)

Тогда у Семи есть Единица. (7 + 1 = 8)

Оба числа застревают посередине… итоговое число выглядит так:

Триреза, Триреза-холдинг-Уан, Семи-холдинг-Уан, Севени.

Или другими словами: 3, 4, 8, 7 -> 3487

Квадрат

Это действительно очень просто — сделать, запомнить и объяснить.

Для этого вам понадобится двузначное число, которое заканчивается на 5. 25, 55, 15, 95 — что угодно. Все они в игре.

Пара вещей, которые следует запомнить:

Ответ всегда, всегда, всегда заканчивается на 25. Вы всегда умножаете первую цифру на следующее по величине число.

Хотите знать, что это значит?

Итак, если вы возводите в квадрат 25, ваш первый шаг — умножить 2 на 3.

Квадрат 55? Умножить 5 x 6.

Квадрат 85? Умножьте 8 x 9.

Видите выкройку?

Затем просто добавьте 25 в конец. Шутки в сторону. Это НАСТОЛЬКО просто.

Умножение большого числа на 5

Ух ты. Это было просто, правда? Что ж, вот такой же простой.

Мы уже говорили об известном приеме умножения числа на 10. (Добавьте ноль).

Ну а если умножить на 5? И я говорю о большом числе, например, 2486 или 18067.

Вот простой двухэтапный прием, который может упростить задачу.

Разделите число на 2, умножьте на 10.

Верно? Итак, для 2486 разделите его на 2… что даст вам 1243.

Затем просто добавьте 0… и вы получите 12430.

Поговорим о мгновенном!

Умножение большого числа на 9

Один из простейших математических приемов, которым вы можете научиться, — это умножение большого числа на 9. Принцип действия аналогичен уловке №1. 4.

Допустим, вы умножаете 230 на 9. Выполните следующие действия:

Умножим 230 на 10.(2300) Вычтем 230. (2300-230 = 2070)

Просто добавьте ноль и вычтите само число. Вот и все!

Умножение по частям

Используя свой собственный математический калькулятор, вы можете проще умножать числа. Просто нужно делать по частям:

Чтобы найти ответ на 7 x 93, вам просто нужно мысленно умножить 7 x 90 и 7 x 3. Складывая результаты 630 + 21 = 651.

Другой пример: 6 x 215.Уловка будет 6 x 200, 6 x 10 и 6 x 5.

Получится 1200 + 60 + 30 = 1290.

Вычесть путем сложения

Это один из математических приемов, который покажет вам взаимосвязь между сложением и вычитанием.

Принцип этого трюка таков: вместо вычитания выясните, какое число вам нужно добавить, чтобы получить другое число. Совершенно непонятно? Вот пример.

Чтобы ответить, что такое 10-6, подумайте о числе, которое вам нужно прибавить к 6, чтобы получилось 10.Ответ будет 4.

Добавить 1 к двойным

Еще один из множества интересных математических приемов, которыми мы расскажем, — это прибавление единицы к двойным. Это очень простой трюк, которому дети могут легко научиться.

По сути, им просто нужно запомнить двойные числа, такие как 6 + 6, 8 + 8 и т. Д. Как только они это уже запомнили, они могут быстро ответить, что такое 6 + 7, потому что им просто нужно добавить 1.

Умножение чисел, оканчивающихся на ноль

При умножении чисел, оканчивающихся на ноль, вам просто нужно умножить первые числа и добавить нули после них.Для иллюстрации:

200 x 600 равно 2 x 6 = 12

Теперь, когда у вас уже есть базовое число, просто сложите все нули, которые вы посчитали от 200 до 600. Это будет четыре нуля после 12. Итак, ответ — 120 000. Очень просто!

Вычитание из 1000

Ваш мысленный математический калькулятор справится с этим, потому что это довольно просто. При вычитании любого числа из 1000 вычтите каждое число из 9, кроме последнего, которое следует вычесть из 10.

Вот пример:

1000–495 будет 9–4, 9–9 и 10–5.

Ответом будет 5, 0 и 5. Объедините их, и вы получите 505. Это ваш ответ на 1000 — 495.

Процент переворачивания

Какой самый быстрый способ найти процентное значение числа? Посчитайте в уме процентное соотношение, повернув его.

Пример:

Что такое 4% от 50? Это то же самое, что и 50% от 4.

Что делать, если число, которое вы пытаетесь найти, более сложное, например 17% от 23.

23% из 17 не легче, что бы вы тогда делали?

23% — это почти 25%, так что вы можете очень быстро получить приблизительную оценку — 4,25

Но у вас 2% скидка. Итак, что 1% от 17? 0,17

Удвойте, то есть 0,34

Вычтите это из 4,25, и вы получите 3,91.

Заключение

Не так уж ухмылка, правда? Калькулятор Человек.

И по мере того, как вы будете изучать все больше и больше этих математических приемов, вы станете еще лучше разбираться в числах, узнаете, как стать лучше в математике.

А теперь вперед — отточите свои мечи мысленной математики! Решите любую возникающую математическую задачу. Мы все болеем за вас.

4.3 6 голоса

Рейтинг статьи

Следующие две вкладки изменяют содержимое ниже.

Здравствуйте! Меня зовут Тодд. Я помогаю студентам строить жизнь своей мечты, обеспечивая учебу, стипендию и карьерный успех! Я бывший наставник в течение семи лет, получатель стипендии в размере 85000 долларов, участник Huffington Post, ведущий разработчик курсов SAT & ACT, ведущий подкаста по исследованию карьеры для подростков, и работал с тысячами студентов и родителей, чтобы обеспечить более светлое будущее в будущем. поколение.Я приглашаю вас присоединиться к моему следующему вебинару, чтобы узнать, как сэкономить тысячи + настроить вашего подростка на учебу, стипендию и карьерный успех!

Делайте математику в уме с помощью этих умственных математических уловок

Analog Week Аналоговая неделя Просто потому, что «для этого есть приложение», не означает, что вы должны его использовать. На этой неделе мы перейдем к аналогу, напоминая себе, что мы можем жить — и жить хорошо, — без смартфонов, и посмотреть, что стоит сохранить с того времени, когда мы все были подключены к сети 24 часа в сутки, 7 дней в неделю.

Вам, вероятно, не приходилось годами заниматься чистыми математическими вычислениями, но вы занимаетесь мысленными вычислениями каждый день. Или, может быть, вы гуглите математические задачи десять раз в день, потому что вы забыли, как выполнять любые математические операции, кроме вашей базовой таблицы умножения. Вот несколько быстрых клавиш, которые помогут вам делать больше математических расчетов в уме.

Вычислить проценты в обратном направлении

X% от Y = Y% от X. Вы всегда можете поменять местами эти проценты, если выполнение математических расчетов наоборот проще. Итак, 68% от 25 = 25% от 68 = 68/4 = 17.

Это упрощает многие вычисления, если запомнить проценты, равные базовым дробям:

• 10% = 1/10
• 12,5% = 1/8
• 16,666 …% = 1/6
• 20% = 1/5
• 25% = 1/4
• 33,333 …% = 1/3
• 50% = 1/2
• 66,666 …% = 2/3
• 75% = 3/4

Вычитание без заимствования цифр

Мысленное вычитание проще всего, когда вы можете вычитать каждую цифру без необходимости заимствования из следующего разряда.Если второе число имеет несколько больших цифр, чем первое, это усложняется. Чтобы избежать заимствования мест, вам нужно избавиться от этих больших цифр. Вот как это сделать:

Допустим, вы вычисляете 925-734. Разряд десятков немного усложняет задачу. Было бы проще вычислить 925-7 2 4, а затем отдельно вычесть эти дополнительные 10: 925-724 = 201 и 201-10 = 191. Вот ваш ответ.

G / O Media может получить комиссию

Сообщите, делится ли число без остатка на другое число

• Все (и только) кратные 2 заканчиваются на 0, 2, 4, 6 или 8.
• Все (и только) числа, кратные 3, содержат цифры, которые в сумме дают 3 (или другое кратное 3).
• Кратное 4: игнорировать все, начиная с сотен и выше. Разделите оставшееся двузначное число пополам. Затем запустите тест умножения на 2.
• Все (и только) числа, кратные 5, оканчиваются на 5 или 0.
• Кратные 6: Выполните тест 2 и тест 3.
• Кратное 7: есть несколько тестов, но все они сложнее, чем раскопки телефона. Это, наверное, самый простой:

Удвойте единицы и вычтите из десятков.Например, 1365 → 136− (2 × 5) = 126 → 12− (2 × 6) = 0. Если цепочка заканчивается на 0 или кратным 7, то исходное число делится на 7.

• Кратное 8: игнорировать все, начиная с разряда тысяч и выше. Оставшееся трехзначное число разделите пополам. Потом снова пополам. Затем запустите тест умножения на 2.
• Все (и только) числа, кратные 9, имеют цифры, которые в сумме дают 9 или кратное 9.
• Все (и только) кратные 10 оканчиваются на 0.
• Чтобы проверить делимость на большее число, попробуйте разложить на множители уменьшите его до однозначных чисел, затем запустите тесты, описанные выше, сохраняя все повторяющиеся множители вместе.Например, 60 = 2 * 2 * 3 * 5. Таким образом, все числа, кратные 60, также кратны 2 * 2, 3 и 5. Обратите внимание на 2 * 2; число, кратное 60, должно делиться на 4, а не только на 2. (150 делится на 2, но не на 4, поэтому оно не делится на 60).

Используйте эти ярлыки умножения

Чтобы умножить в уме, попробуйте превратить проблему в более легкую. Например:

• Как правило, удваивать числа проще. Поэтому при умножении на четное число сначала умножьте на половину этого числа, а затем на 2.
• Умножить на 5: сначала умножить на 10, затем разделить на 2.
• Умножить на 9: Умножить на 10 и вычесть число. Итак, 65 * 9 = (65 * 10) -65 = 650-65 = 585.
  
• Умножение однозначного числа x на 9: первая цифра — x -1. Вторая цифра — 9 минус первая цифра. Итак, 8 * 9 = 72.

Запомните простую арифметику

Чем больше вы запомните простых вычислений, тем больше вы сможете разбирать более крупные математические задачи. Если вы забыли свои таблицы умножения, освежите их.Приятно распознать число, кратное 12, и понять, что можно разделить большее число.

Найдите квадратное число, немного большее, чем самое большое из известных вам

Если вы знаете квадрат целого числа, вы можете легко найти квадрат следующего целого числа, сложив первый квадрат, первое корневое число и второе корневое число: x ² + x + ( x +1) = ( x +1) ².

Например, вы знаете, что 10² равно 100. Итак, 11² = 100 + 10 + 11 или 121.И 12² = 121 + 11 + 12 = 144. И 13² = 144 + 12 + 13 = 169. И так далее.

Чтобы возвести двузначное число в квадрат, сначала округлите его

Допустим, вам нужно возвести в квадрат 46. Сначала округлите его до ближайшего числа, кратного 10 (добавив 4), затем вычтите ту же сумму для получения нового числа, так что у вас есть 50 и 42. Затем умножьте эти два числа и затем добавьте квадрат суммы, которую вы округлили на: (в данном случае 4²). Итак, 46² = (50 * 42) + 4² = 2100 + 16 = 2116.

Между прочим, когда я мысленно проделал это, 50 * 42 мне все еще было немного сложно, поэтому я превратил его в 100 * 21.Сочетание умственных математических уловок действительно увеличивает вашу силу.

Если вы этого не усвоили, вот более подробное объяснение, которое может помочь.

Преобразование температур

Чтобы приблизительно преобразовать градусы Цельсия в градусы Фаренгейта, умножьте на 2 и прибавьте 30. Из градусов Фаренгейта в градусы Цельсия вычтите 30 и разделите на 2. (Чтобы более точно преобразовать C в F, умножьте на 1,8 и прибавьте 32).

Порядок важен: сложение / вычитание всегда ближе к стороне Фаренгейта преобразования.Если вы забыли порядок, вы знаете, что 32 ° F = 0 ° C, поэтому вы можете проверить свою формулу.

Или просто запомните, что комнатная температура составляет около 20–22 ° C или 68–72 ° F, а нормальная температура тела составляет около 36–37 ° C или 97–99 ° F, в зависимости от нескольких факторов.

Ваша годовая зарплата примерно в 2000 раз превышает вашу почасовую ставку

Для работы на полную ставку 1 доллар в час = 2000 долларов в год.

Ваша годовая зарплата — это ваша почасовая ставка, умноженная на количество отработанных часов в неделю, умноженное на 52 недели.40 * 52 — это 2080, но чтобы вычислить его мысленно, вы можете округлить до 2000, что является приблизительным значением. Удвойте почасовую ставку и добавьте три нуля. Итак, 25 долларов в час — это около 50 000 долларов в год. Или сделайте наоборот: возьмите трехзначную сумму своей зарплаты и уменьшите ее вдвое, и это примерно будет ваша почасовая ставка. Это будет как минимум две недели, если вам будут платить за каждый будний день в году.

Если вы хотите быть немного точнее, возьмите эту приблизительную сумму и сложите свою почасовую ставку, умноженную на 100. Это всего на два с половиной рабочих дня сверх вашей 52-недельной зарплаты.

Чтобы быть на больше , умножьте на 2 080 (40 * 52): умножьте на 2 000 и отложите полученную сумму. Затем умножьте свою почасовую ставку на 80 (удвойте, удвойте, удвойте , что и добавьте ноль). Добавьте это к приблизительной оценке, и вы получите свою 52-недельную зарплату.

Если вы хотите учесть оплачиваемый отпуск или другие особенности, воспользуйтесь этим календарем рабочих дней, где вы можете настроить числа и рабочие дни, пока не получите фактическое количество рабочих часов. Но я думал, что вы пришли сюда ради мысленной математики, .

Найдите больше горячих клавиш

Listverse предлагает несколько простых математических сокращений. В Википедии есть множество расширенных сокращений, которые охватывают арифметику, квадраты и кубы, корни и логарифмы. В документе «Лучшее объяснение» перечислены некоторые распространенные единицы преобразования, например «миль в час = футы в секунду * 1,5».

5 советов для более быстрого умножения умножения

Теперь, когда мы изучили основы молниеносного умственного сложения, умственного вычитания и умственного умножения, пора обратить наше внимание на несколько советов, которые помогут вам поднять свои навыки на новый уровень.

Сегодня мы собираемся начать с изучения 5 советов, которые помогут вам быстро умножать числа в своей голове и стать волшебником умственной математики в своей семье.

Совет №1: Умножение на 5 степеней
Бывают моменты в жизни, когда просто везет. Оказывается, один из тех счастливых моментов случается каждый раз, когда вам нужно умножить одно число на другое, которое оказывается степенью 5. Например, скажем, вам нужно найти 36 x 5 (что, конечно же, , отвечает всем требованиям, поскольку 5 — это первая степень числа 5).2 это конечно. Так как же это работает в этом случае? Уловка здесь состоит в том, чтобы распознать, что 25 = 100/4. И вообще, уловка со степенями 5 состоит в том, чтобы признать, что они всегда кратны 10, деленной на целое число. Это говорит нам, что 36 x 25 = 36 x 100/4. Поскольку мы можем быстро вычислить, что 36 x 100 = 3600, легко найти, что 36 x 25 = 3600/4 = 900.

Совет № 2: возведение чисел в квадрат, заканчивающиеся на 5
На этом наше веселье с пятерками не заканчивается. Мы уже говорили о том, как возводить числа в квадрат в уме раньше, но оказалось, что все становится намного проще, если возвести в квадрат двузначное число, которое заканчивается на 5.Вот уловка: каждый раз, когда вы возводите в квадрат двузначное число, которое заканчивается на 5, последние цифры ответа будут 25, а цифры перед ним даются путем умножения первой цифры числа на число, которое на единицу больше.

> Продолжите чтение на QuickAndDirtyTips.com

Уловки умножения умственной математики для детей

На этой странице вы узнаете несколько уловок, которые помогут вам

6-кратный стол

Умножение на 4 | Умножение на 8

Умножение на 9 или 99 или 999 | Умножение на 11

Умножение на удвоение и деление пополам

Вы можете использовать калькулятор, исследуя эти уловки.

x	0	1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	10	11	12
2	0	2	4	6	8	10	12	14	16	18	20	22	24
3	0	3	6	9	12	15	18	21	24	27	30	33	36
4	0	4	8	12	16	20	24	28	32	36	40	44	48
5	0	5	10	15	20	25	30	35	40	45	50	55	60
6	0	6	12	18	24	30	36	42	48	54	60	66	72
7	0	7	14	21	28	35	42	49	56	63	70	77	84
8	0	8	16	24	32	40	48	56	64	72	80	88	96
9	0	9	18	27	36	45	54	63	72	81	90	99	108
10	0	10	20	30	40	50	60	70	80	90	100	110	120
11	0	11	22	33	44	55	66	77	88	99	110	121	132
12	0	12	24	36	48	60	72	84	96	108	120	132	144

Работает только для четных чисел.

6×2 = 12

6×4 = 24

6×6 = 36

6×8 = 48

Число, на которое вы умножаете, всегда является числом в столбце единиц. 6×2 = 12

Столбец десятков всегда равен половине числа в столбце единиц.

Вернуться к началу

Умножение на 8 может быть получено путем трехкратного удвоения:

Пример:

Q.Что такое 742 х 8?
A. 742 x 2 = 1484
….. 1484 x 2 = 2968
….. 2968 x 2 = 5936

Ответ: 5936

Вернуться к началу

Джо и Кимберли

Держите обе руки перед собой ладонями к себе.

На что бы вы ни умножили (скажем, 8), согните этот палец.
(8-я слева направо)

Пальцы слева от согнутого пальца — это десятки (7), а справа — единицы (2).

Ответ 8 x 9 равен 72.

——————————

11 x 9 легко

12 умножить на девять — это просто мнемоника.

12 это 10 + 2

помню 2

2×9 = 18

просто вставьте 0 посередине

——————————

Вот еще одна хитрость

Независимо от того, что вы умножаете на 9, в ответе десятки всегда на единицу меньше.

например. 8x = 70 что-то 4x = 30 что-то и так далее

Сумма цифр в ответах таблицы умножения на 9 всегда дает 9.

(Десятки и единицы ВСЕГДА до 9!)

например. 7 x 9 = 60 что-то

6+? = 9

, поэтому 7x 9 = 63

Другой метод умножения на 9

Умножение на 9 в действительности умножает на 10, а убирая, вы умножаете.

Итак, 8 × 9 — это всего лишь 8 × 10-8, что составляет 80-8 или 72.

Давайте попробуем пример посложнее: 46 × 9 = 46 × 10–46 = 460–46 = 414.

Еще один пример: 68 × 9 = 680-68 = 612.

Умножение на 99 или 999 аналогично

Чтобы умножить на 99, вы умножаете на 100 и убираете, вы умножаете.

Итак, 46 × 99 = 46x 100 — 46 = 4600-46 = 4,554

Чтобы умножить на 999, вы умножаете на 1000 и убираете, вы умножаете.

38 × 999 = 38×1000-38 = 38000-38 = 37,962

Вернуться к началу

Таблицу одиннадцати умножений всегда было очень легко выучить до 9 x 11.

Вот способ умножить большие числа и на 11:

Чтобы умножить любое количество двух цифр на 11:
Пример:

В. Что такое 34 x 11?
A. Сложите первую и вторую цифры… 3 + 4 = 7;
…. Разместите ответ между первой и второй цифрами ….. 374

Ответ — 374.

NB. Когда сумма первой и второй цифр больше 9, увеличьте левое число на 1, которое нужно перенести.

Пример:

В. Что такое 98 x 11?
A. Сложите первую и вторую цифры … 9 + 8 = 17
…. Добавьте 1 к 9, чтобы получить 10
…. Поместите 7 между 10 и 8

Ответ 1078

Чтобы умножить любое количество трех цифр на 11:
Вы складываете пары чисел рядом друг с другом, за исключением чисел по краям.

Пример:

В. Что такое 324 x 11?

A. Запишите первую цифру … 3
……. сложите первую и вторую цифры … 3 + 2 = 5
……. сложите вторую и третью цифры .. 2 + 4 = 6
……. Запишите последнюю цифру ……….. 4

Ответ: 3564.

Работает ли он для всех трехзначных чисел?

Чтобы умножить любое четырехзначное число на 11:

Q.Что такое 3254 × 11?

A. Запишите первую цифру … 3
……. сложите первую и вторую цифры … 3 + 2 = 5
……. сложите вторую и третью цифры .. 2 + 5 = 7
……. сложите третью и четвертую цифры .. 5 + 4 = 9
……. запишите последнюю цифру ……….. 4

Ответ: 35794.

Помните, когда сумма первых и вторых цифр больше 9, увеличивайте левое число на 1, чтобы оно было перенесено.

Пример переноски:

В. Что такое 4657 × 11?

A. Запишите первую цифру … 4
……. сложите первую и вторую цифры … 4 + 6 = 10
……. сложите вторую и третью цифры .. 6 + 5 = 11
……. сложите третью и четвертую цифры .. 5 + 7 = 12
……. запишите последнюю цифру ……….. 7

Двигаясь справа налево, запишите 7

Обратите внимание, что 5 + 7 = 12

Запишите 2 и перенесите 1

6 + 5 = 11, плюс 1 у вас есть = 12

Итак, запишите 2 и перенесите 1

4 + 6 = 10, плюс 1, который у вас есть, = 11

Итак, запишите 1 и перенесите 1

К крайней левой цифре 4 прибавьте 1, которую вы несете

Итак, 4657 × 11 = 51 227

Вернуться к началу

Когда вы умножаете два числа и одно из них четное, вы можете разделить это число на два и умножить другое число на 2.Вы можете делать это снова и снова, пока не дойдете до умножения, которое вам будет легко делать.

В. Что такое 14 x 16?

A. Одно число удвоить, а второе число разделить вдвое

14 × 16 = 28 × 8

Для меня это все еще сложно, поэтому удвойте одно число и уменьшите вдвое другое число

28 × 8 = 56 × 4

Для меня это все еще сложно, поэтому удвойте одно число и уменьшите вдвое другое число

56 × 4 = 112 × 2

Теперь мне стало проще.

112 × 2 = 224

Вот еще один пример:

В. Что такое 12 × 15?

А. 12 × 15 = 6 × 30

6 × 30 с то же, что 6 × 3 с 0 в конце, поэтому ответ 180.

Вернуться к началу

.