Умножение и деление 1. Деление одинаковых чисел — урок. Математика, 3 класс.
Умножение \(1\). Умножение на \(1\)
\(·\) | \(1\) ↓ | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) ↓ | \(9\) |
\( 2\) | \(3\) | \(7\) | \(9\) | ||||||
\(2\) | \( 2\) | ||||||||
\(3\) | \(3\) | ||||||||
\(4\) | \(4\) | ||||||||
\(5\) | \( 5\) | ||||||||
\(6\) | \( 6\) | ||||||||
\(7\) | |||||||||
\(8\)→ | |||||||||
\(9\) |
Множители можно менять местами:
\(1 · 8 = 8 · 1 = 8\).
При умножении любого числа на \(1\) получается то число, которое умножили.
1⋅a=a⋅1, где \(a\) — любое число.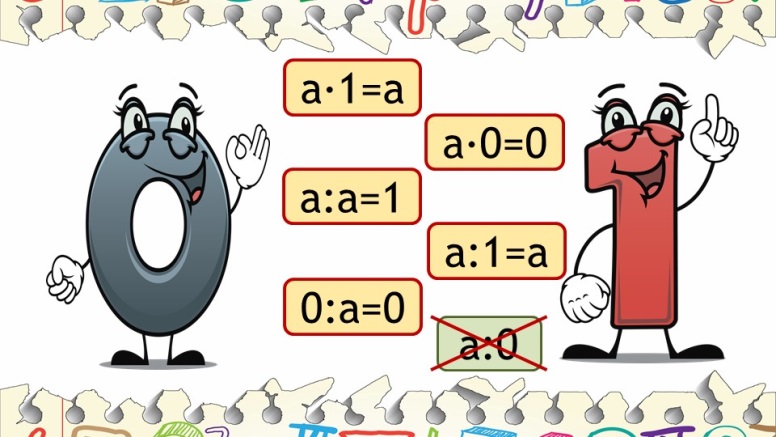
Деление на \(1\)
\(8 : 1 = 8\).
При делении любого числа на \(1\) получается то число, которое делили.
a:1=a, где \(a\) — любое число.
Деление одинаковых чисел
\(8 : 8 = 1\).
При делении любого числа, кроме нуля, на само это число получается \(1\).
a:a=1,a≠0, где \(a\) — любое число.
Умножение и деление с числом 1.
Тема: Умножение и деление с числом 1.
Цель урока: методом наблюдения учащиеся выведут правило умножения и деления на 1.
Ожидаемые результаты: : научатся выполнять деление с 1 на основе связи с действием умножения, повторят связи компонентов действий умножения и деления, табличные случаи умножения и деления. Находят значения выражений при умножении и делении на 1, составляют верные равенства и неравенства, решают примеры в столбик, комментируя, объясняя, выслушивая доводы одноклассников.
Ход урока
1.Организационный момент
— Я прошу улыбнуться тех, кто пришёл на занятие с хорошим настроением
— Я прошу поднять руку тех, кому нравится общаться с одноклассниками
— Если вы не любите конфликтовать и спорить по пустякам, то хлопните в ладоши
-Пожмите друг другу руки, если вы стараетесь уважительно относиться к людям
2. Актуализация знаний, умений и навыков.
Б) Если согласен с утверждением, ставь +, если нет, ставь -.
В неделе 7 дней.
После воскресенья наступает суббота.
В 1 сантиметре 100 миллиметров.
Сумма чисел 0 и 34 равна 0.
Произведение чисел 2 и 9 равно 18.
Если к 27 прибавить 6, получится 33.
Если сумма равна 44, а первое слагаемое – 20, то второе слагаемое 4.
Значение выражения 16 – 7 + 5 + 10 – 3 – 19 + 42 – 6 + 40 равно 87.
3.Работа по теме урока
Замените сложение умножением там, где возможно.
2+2+2+2+2 = 2 * 5
4+4+4+4 = 4 * 4
5+5+5+6 =
13+13 = 13 * 2
7+7+7 = 7 * 3
9+9+9+9+8+9+9 =
3+3+3+3 = 3 * 4
15+15+15 = 15 * 3
1+1+1+1 = 1*1
-Какой случай мы не изучали?
Целеполагание
-С какими случаями умножения мы будем знакомиться на уроке?
— Каковы цели нашего урока?
А) стр.46 №1- устно
-Что вы заметили при умножении 1 на число?
— Сколько раз берётся слагаемым число 1?
-Какой вывод можно сделать?
Вывод стр.46 1*а=а
3.Физминутка “Зарядка”
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
4.Работа по учебнику
А) стр.46 №2- письменно, составить по два взаимообратных равенства на умножение и деление.
Б) стр.47 №3- с объяснением
5.Закрепление изученного материала
А) стр.47 № 6 (1,2 столбик)- письменно, у доски
Б) стр.47 № 5(б)- составить и решить задачу по краткой записи
6.Домашнее задание
стр.46-47 формулы, № 5 (а)
7.Итог урока. Оценки
-Что нового узнали на уроке?
Чему учились?
Какие задания вызвали трудность?
А что было интересным?
Как вы оцениваете свою работу?
Рефлексия
Оценочная лесенка
Цель: развитие умений критериального оценивания
Детям предлагается лесенка ,на которой они должны поставить солнышко на той ступеньке, на которую поставили бы себя при выполнении заданий .
Умножение и деление числа на 1. Умножение и деление 0 на число. Умножение 1 на число.
Цель урока: закрепить знания и умения в делении и умножении числа на 1, 0 на число, умножении 1 на число.
Задачи урока:
- Закрепить табличное умножение и деление на 2, 3, 4, умение решать задачи.
- Развивать логическое мышление, внимание, память, вычислительные навыки, математическую речь.
- Воспитывать самостоятельность, активность, аккуратность при работе в тетрадях.
Просмотр содержимого документа
«Умножение и деление числа на 1. Умножение и деление 0 на число. Умножение 1 на число.»
___________
Математика
3 класс
Тема урока: Умножение и деление числа на 1. Умножение и деление 0 на число. Умножение 1 на число.
Цель урока: закрепить знания и умения в делении и умножении числа на 1, 0 на число, умножении 1 на число.
Задачи урока:
Закрепить табличное умножение и деление на 2, 3, 4, умение решать задачи.
Развивать логическое мышление, внимание, память, вычислительные навыки, математическую речь.
Воспитывать самостоятельность, активность, аккуратность при работе в тетрадях.
Оборудование: учебники, тетради, карточки, формулы, сигнальные карточки, цветные мелки.
Ход урока
Организационный момент.
Проверьте, все ли у вас готово к уроку?
У вас на партах лежат кружочки, цвета светофора. Посмотрите и покажите свое настроение. Если у вас сейчас грустное настроение покажите красный цвет, если среднее – то жёлтый, а если отличное – то зеленый.
Я надеюсь, что у вас настроение в конце урока улучшиться.

Итак, приступим к работе.
Актуализация опорных знаний
Ученик выучил таблицу умножения. На контрольной работе он выполнил задание. Давайте мы, сейчас сыграем роль учителей и проверим, правильно ли он выполнил задание.
43=12 24:3=8 14=1
4:1=1 45=20 240=24
53=15 02=2 9:3=3
Как вы думаете, знает ли ученик таблицу умножения.
Обратите внимание на ошибки ученика.
Что вы заметили?
Чтобы решить эти примеры понадобится ли таблица умножения?
Какие правила не знает ученик?
Сообщение темы и цели урока.
Как вы думаете, что мы на уроке будем закреплять?
Какова тема урока? (умножение деление 0 на число, 1 на число, числа на 1).
Давайте приступил к работе.
Повторение изученного материала.
Как умножить и делить число на 1?
При умножении или делении числа на 1 получается то же число.
Какое правило нужно знать, чтобы умножить любое число на 0?
При умножении 0 на любое число получается нуль.
Что если 0 делить на число?
При делении 0 на любое число получается нуль.
Можно ли делить на нуль?
На нуль делить нельзя.
Закрепление изученного материала.
Карточка
Вычислите.
а) 91 10:1 890 0:45
110 63:1 025 10
б) 560 451 0:19 0:99
70:1 18 41 300
У вас на партах лежат карточки по буквой А выполним у доски (желающие).

А теперь под буквой Б вы выполните самостоятельно.
Коллективная проверка с помощью красного и зеленого кругов.
С. 48 №6 б (у доски).
Прочитайте задачу.
Прочитайте условие задачи.
Прочитайте вопрос задачи.
О чем говорится в задаче?
Какие слова возьмем для краткой записи? (Бабушка и Маша)
Нам известно, сколько бабушка собрала груш? Сколько? (14)
Нам известно, сколько Маша собрала груш? Что известно?
Чтобы узнать, сколько груш собрала Маша, какое действие нужно выполнить?
Бабушка – 14 гр.
Маша — ? гр., в 2 раза М.
14:2=7 (гр.)
Ответ: 7 груш собрала Маша.
Физминутка.
У оленя дом большой,
Он сидит, глядит в окошко.
Зайка по полю бежит,
В дверь к нему стучит:
«Тук-тук, дверь открой,
Там в лесу охотник злой».
«Зайка, зайка, забегай!
Лапку мне давай».
Работа в парах.
Карточка.
Сравните.
250 0:5 18:3 23 15 10:2
181 19:1 16:4 116 15:3 0:5
201 120 73 121 0:15 151
Коллективная проверка
- Работа по вариантам.
Карточка
Реши примеры с остатком. Сделайте проверку.
1 вариант – 1 столбик, 2 вариант – 2 столбик.
9:4 16:5
8:3 6:4
15:6 18:5
20:3 17:7
Домашнее задание.
С. 49 №3б. Решить задачу.
Итог урока.
Что нового повторили?
Что закрепляли?
Какое задание вам больше понравилось?
Какое задание вызвало трудности?
Кто сегодня хорошо работал? Кому нужно постараться? (оценивание).
Возьмите круги, соответствующие вашему настроению и покажите мне.
Урок окончен. Спасибо за внимание.
«Умножение и деление. Умножение и деление с числами 1, 0. Деление на 0. Повторение, закрепление» | План-конспект урока по математике (3 класс) на тему:
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
Государственное казенное общеобразовательное учреждение города Москвы
Школа № 2124 «Центр развития и коррекции»
Урок математики в 3 «А» классе по теме:
«Умножение и деление. Умножение и деление с числами 1, 0.
Деление на 0. Повторение, закрепление»
Москва 2016
Урок математики в 3 классе по теме:
«Умножение и деление. Умножение и деление с числами 1,0.
Деление на 0. Повторение, закрепление»
Цель урока: закрепление знаний таблицы умножения и соответствующих случаев деления.
Задачи:
• повторение и закрепление знаний табличных случаев умножения и деления,
• способствовать воспитанию активности, самостоятельности, продолжить формирование коммуникативных навыков.
• участвовать в диалоге, в общей беседе, выполняя принятые правила речевого поведения, культуры речи; умение работать в группах, анализировать;
Тип урока – урок повторения, систематизации и обобщения знаний.
Формы работы учащихся: работа в парах, фронтальная.
ХОД УРОКА
Этапы. Содержание
I. Организационный момент (Цель: создать благоприятный эмоциональный микроклимат)
Семь раз отмерь, один раз отрежь!
— Что значит эта поговорка? Назовите имена числительные, которые вы услышали. В каких случаях мы их используем?
– Начнем урок математики.
– Какое сегодня число? (четное — нечетное)
– Какое число было три дня назад?
– Какой по счету день недели?
– Какой день недели будет послезавтра?
Развитие мелкой моторики (пальчиковая гимнастика)
– Откройте тетради, запишите дату сегодняшнего урока.
II. Устный счет
(Цель: продемонстрировать полученные знания)
Чтобы спорилась работа,
Начнем с «гимнастики ума»
1. Сыну 8 лет. Отец в 4 раза старше. Сколько лет отцу?(36)
2. С одной яблони собрали 18 кг яблок, а с другой на 4 кг меньше. Сколько кг яблок собрали со второй яблони?(14 кг)
3. Бабушке 60 лет. Внук в 10 раз моложе бабушки. Сколько лет внуку?(6)
4. Высота березы 9 метров, а дом на 3 метра выше. Какова высота дома?(12)
5. В деревне 28 деревянных домов, а каменных в 4 раза меньше. Сколько каменных домов в деревне?(7)
6. Сережа вырезал 5 геометрических фигур, а Оля в 3 раза больше. Сколько геометрических фигур вырезала Оля?
Блицопрос:
• В классе 5 девочек, а мальчиков – в 2 раза больше. Сколько мальчиков в классе? (10 мальчиков)
• У Димы 18 синих шаров и 6 красных. Во сколько раз синих шаров больше, чем красных? (В 3 раза)
• В 9 машинах 18 пассажиров, в каждой поровну. Сколько пассажиров в каждой машине? (2)
• 14 человек разместились в двухместные лодки. Сколько лодок понадобилось? (7)
• У портнихи 18м ткани. На пошив одного платья она израсходовала 3м ткани. Сколько платьев сшила портниха?(6)
• В 5 одинаковых банках 20л сока. Сколько литров сока в каждой банке? (4)
• Верёвку длиной 12м разрезали на 3 одинаковые части. Сколько метров верёвки в каждой части. (4)
III. Повторение, закрепление
Повторение, закрепление
— Ребята, найдите значение выражений. (слайд 1.)
— Проверка в парах (слайд 2)
IV. Физминутка
V. Работа с учебником с.85 №6 ( 3 ученика)
С.85 №2 (Задача)
VI. Рефлексия
– Наш урок заканчивается. Сегодня все замечательно трудились, выполнили много заданий.
– Что повторили на уроке? (Табличные случаи умножения и деления, решали задачи)
– Какое задание было интересным для вас?
– Какое оказалось самое трудное?
Резервное задание
— Ребята, а какие вы знаете геометрические фигуры? Назовите их свойства.
— А как вы думаете, на какую геометрическую фигуру похожа хоккейная площадка?
Давайте решим следующую задачу и запишем её в тетрадь:
Задача.
Длина хоккейной площадки 60 метров, а ширина 30 метров. Какова площадь хоккейной площадки?
Урок 62. табличное умножение и деление. умножение числа 2 и на 2 — Математика — 2 класс
Урок № 62. Табличное умножение и деление. Умножение числа 2 и на 2
Перечень вопросов, рассматриваемых в теме:
- Таблица умножения числа 2 и на 2.
- Чтение равенств таблицы умножения числа 2.
- Для чего знать таблицу умножения числа 2 и на 2.
Глоссарий по теме:
Умножение – это сложение одинаковых слагаемых. Знак умножения — *, х.
Компоненты умножения: первый множитель, второй множитель.
Результат умножения – произведение.
Переместительное свойство умножения – от перестановки мест множителей произведение не изменяется. С помощью букв переместительное свойство умножения записывают так: a • b = b • a.
Выражение – запись из букв и чисел, соединённых знаками арифметических действий.
Равенство – числа или выражения, которые соединены знаком равенства =.
Обязательная литература и дополнительная литература:
- Моро М.И., Бантова М.А. и др. Математика 2 класс. Учебник для общеобразовательных организаций М.
 ; Просвещение, 2017. – с.80
; Просвещение, 2017. – с.80 - М.И.Моро, С.И.Волкова. Для тех, кто любит математику 2 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 57
Теоретический материал для самостоятельного изучения
Гном посадил лук в 9 горшочков, по 2 луковицы в каждый. И задумался, сколько луковиц у него вырастет?
Гном стал рассуждать:
2 + 2 = 4
Заменим сумму одинаковых слагаемых умножением.
2 • 2 = 4
2 • 3 = 6
2 • 4 = 8
2 • 5 = 10
2 • 6 = 12
2 • 7 = 14
2 • 8 = 16
2 • 9 = 18
У гнома вырастет 18 луковиц.
Мы составили таблицу умножения числа 2. Первый множитель 2, второй множитель увеличивается на 1, произведение увеличивается на 2.
Мы уже знаем, что удобнее большее число умножить на меньшее. Пользуясь переместительным свойством умножения, составим таблицу умножения на 2.
Первый множитель увеличивается на 1, второй множитель одинаковый, 2. Произведение увеличивается на 2.
Таблицу умножения числа 2 можно читать так: дважды два – четыре, дважды три – шесть и т.д.
2 • 5 = 10
Равенство прочитаем так: 2 умножить на 5, получится 10. Или, дважды пять – десять.
Подумайте, для чего необходимо знать таблицу умножения?
Зная таблицу умножения, вы легко и быстро сможете выполнять вычисления в уме.
Необходимо помнить: таблица умножения помогает выполнять вычисления быстрее. Выучи ее наизусть.
Ответим на вопросы, поставленные в начале урока.
Таблицу умножения числа 2 можно составить на основе знания того, что умножение – сумма одинаковых слагаемых. Первый множитель число – 2, второй множитель увеличивается на 1, произведение увеличивается на 2.
Таблицу умножения на число 2 можно составить, пользуясь переместительным свойством умножения, где первый множитель увеличивается на 1, второй множитель 2, произведение увеличивается на 2.
Читать таблицу умножения числа 2 можно читать по-разному.
Знание таблицы умножения числа 2 и на 2 помогает быстрее выполнять вычисления и решать задачи.
Выполним несколько тренировочных заданий.
1. Вычислите.
2 • 4 + 2 2 • 3 + 2 2 • 2 + 2
2 • 4 – 2 2 • 3 – 2 2 • 2 – 2
Зная равенства таблицы умножения, найдем значение выражений. Помните, сначала выполняется действие умножение, а после – сложение и вычитание.
2 • 4 + 2 = 8 + 2 = 10 2 • 3 + 2 = 6 + 2 = 8 2 • 2 + 2 = 4 + 2 = 6
2 • 4 – 2 = 8 – 2 = 6 2 • 3 – 2 = 6 – 2 = 4 2 • 2 – 2 = 4 – 2 = 2
2. Сравните выражения
6 • 2 + 2 … 6 • 3
7 • 2 + 2 … 8 • 2
9 • 2 – 2 … 10 • 2
Для сравнения выражений будем использовать таблицу умножения на 2.
6 • 2 + 2 = 6 • 3
7 • 2 + 2 = 8 • 2
9 • 2 – 2 < 10 • 2
3. Решите задачу.
На каждую грядку посадили по 7 кустиков клубники. Сколько кустиков клубники на двух таких грядках?
Проверьте решение задачи:
7 • 2 = 14 (кус.)
Ответ: 14 кустиков клубники.
Урок 7. таблица умножения и деления с числом 3 — Математика — 3 класс
Математика
3 класс
Урок №7
Таблица умножения и деления с числом 3
Перечень вопросов, рассматриваемых в теме:
— В чём заключается принцип построения таблицы умножения с числом 3?
Глоссарий по теме:
Умножение – это сложение одинаковых слагаемых.
Компоненты умножения – первый множитель, второй множитель. Результат умножения – произведение.
В таблице умножения с числом 3 произведение увеличивается на 3.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 21.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 13-16.
Часть 1. М.; Просвещение, 2016. – с. 13-16.
Теоретический материал для самостоятельного изучения
Рассмотрим два числовых ряда.
- 8; 10; 12; 14; ___; ___.
- 9; 11; 13; 15; ___4 ___.
В первом ряду числа увеличиваются на 2. Можно продолжить этот ряд числа 16; 18.
Это числа чётные, числа из таблицы умножения с числом 2.
Во втором ряду числа тоже увеличиваются на 2. Можно продолжить ряд числами 17; 19.
Это числа нечётные. Они не делятся на 2 . Этих чисел нет в таблице умножения с числом 2.
Рассмотрим рисунок и составим выражение по рисунку.
3 + 3 + 3 + 3 = 12
Сложение одинаковых слагаемых можно заменить умножением.
3 + 3 + 3 + 3 = 3 ∙ 4 = 12
Мы число 3 взяли 4 раза, так на каждой тарелке лежит по 3 пирожка, таких тарелок 4.
Рассмотрим следующий рисунок и узнаем, сколько всего треугольников.
Посчитать количество треугольников можно разными способами.
1 способ.
В каждом ряду по 5 треугольников, таких рядов 3. Значит надо 5 взять 3 раза.
5 ∙ 3 = 15 (т.)
2 способ.
В каждом столбике 3 треугольника, таких столбиков 5. Значит надо 3 взять 5 раз.
3 ∙ 5 = 15 (т.)
От перестановки множителей произведение не изменяется.
5 ∙ 3 = 3 ∙ 5 = 15 (т.)
Мы составили к рисункам такие выражения:
3 ∙ 4 = 12 + 3
3 ∙ 5 = 15
Первый множитель 3, второй множитель увеличился на 1, потому что второй множитель показывает сколько раз нужно взять первый множитель. Поэтому произведение увеличилось на 3.
Сохраняя эту закономерность, запишем следующие примеры:
3 ∙ 6 = 18 +3
3 ∙ 7 = 21 +3
3 ∙ 8 = 24 +3
3 ∙ 9 = 27
Это есть таблица умножения числа 3.
Зная правила:
1. От перестановки слагаемых произведение не изменяется;
2. Если произведение разделить на известный множитель, то получим другой множитель;
составим примеры на умножение и деление:
4 ∙ 3 = 12; 12 : 3 = 4; 12 : 4 = 3;
5 ∙ 3 = 15; 15 : 3 = 5; 15 : 5 = 3;
6 ∙ 3 = 18; 18 : 3 = 6; 18 : 6 = 3;
7 ∙ 3 = 21; 21 : 3 = 7; 21 : 7 = 3;
8 ∙ 3 = 24; 24 : 3 = 8; 24 : 8 = 3;
9 ∙ 3 = 27; 27 : 3 = 9; 27 : 9 = 3.
Тренировочные задания.
1. Какое число пропущено в примерах?
☐ ∙ 3 = 9; ☐ ∙ 5 = 15; ☐ ∙ 7 = 21; ☐ ∙ 9 = 27.
Правильный ответ: 3
2 . Соедините линиями сумму чисел и произведение чисел.
3 + 3 + 3 + 3 + 3 | 3 + 3 + 3 | 3 + 3 + 3 + 3 + 3 + 3 + 3 | 3 + 3 + 3 + 3 | 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 |
3 ∙ 7 | 3 ∙ 5 | 3 ∙ 4 | 3 ∙ 8 | 3 ∙ 3 |
Правильный ответ:
3 + 3 + 3 + 3 + 3 | 3 + 3 + 3 | 3 + 3 + 3 + 3 + 3 + 3 + 3 | 3 + 3 + 3 + 3 | 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 |
3 ∙ 5 | 3 ∙ 3 | 3 ∙ 7 | 3 ∙ 4 | 3 ∙ 8 |
КСП по математике на тему Умножение и деление с числом 1 3 класс
Краткосрочное планирование № 1
Учитель:Нургалиева Ж.Б.
Предмет: Математика
Класс: 3
Дата проведения:
Тема урока: Умножение и деление с числом 1.
Цель:Уметь выполнять особые случаи умножения и деления с числом 1.
Ожидаемые результаты:
Ученики знают, называют, компоненты, умеют устно выполнять умножение и деление с числом 1(С-все учащиеся)
Ученики объяснять способ выполнения умножения и деления с числом 1. (В-большинство учащихся)
Ученики могут решать усложненные задания с применением знаний умножения и деления с числом 1.(А-отдельные учащиеся)
Этап урока | Время | Деятельность учителя | Деятельность ученика | Ресурсы |
Мотивационный Выйти на тему урока, создать мотивацию у учащихся, пробудить интерес | 10 мин | 1. выход на новую тему: «Как вы думаете, какие термины лишние?» | Ситуация успеха (Бодрячок – «Солнышко») Учащиеся выполняют упражнение Постановка целей урока детьми | Клип «Солнышко» Флипчарт |
Операционный Изучение нового материала с использованием новых подходов в обучении | 15 мин | Совместная выработка критериев успешности работы в группах Организовать работу группы: карточка Организует письменную работу. | 1. Работа с учебником с 46 №1-2. () 2.Работа в группах: изучить ресурс, выполнить постер: «Лови ошибку» 1∙6=7 15:15=0 35∙1=34 40∙1=41 15∙1=16 28:28=56 1∙8=7 1∙78=78 1.Просмотрите внимательно выражения. 2.Вспомните правило умножения и деления с числом 1. 3. Составьте постер по данным выражения. 4. Составьте краткий рассказ по выявлению ошибки, опираясь на постер. 5. Подготовьте три ответа на вопросы Что? Когда? и Почему? вы делали. | карточка |
Рефлексивный Закрепление изученного материала, систематизация знаний, контроль знаний Д/З | 17 мин | Организует работу в группе Наблюдение за выполнением заданий | Стратегия «Думай в группе и делись» Работа с учебником (с.47 № 4) | Карточки Дерево успеха |
3 мин | На выбор № 5 или №7 с.47-48. | Дети записывают домашнее задание в дневники. |
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/172379-ksp-po-matematike-na-temuumnozhenie-i-deleni
1.3: Умножение и деление целых чисел
Мы начинаем этот раздел с обсуждения умножения целых чисел.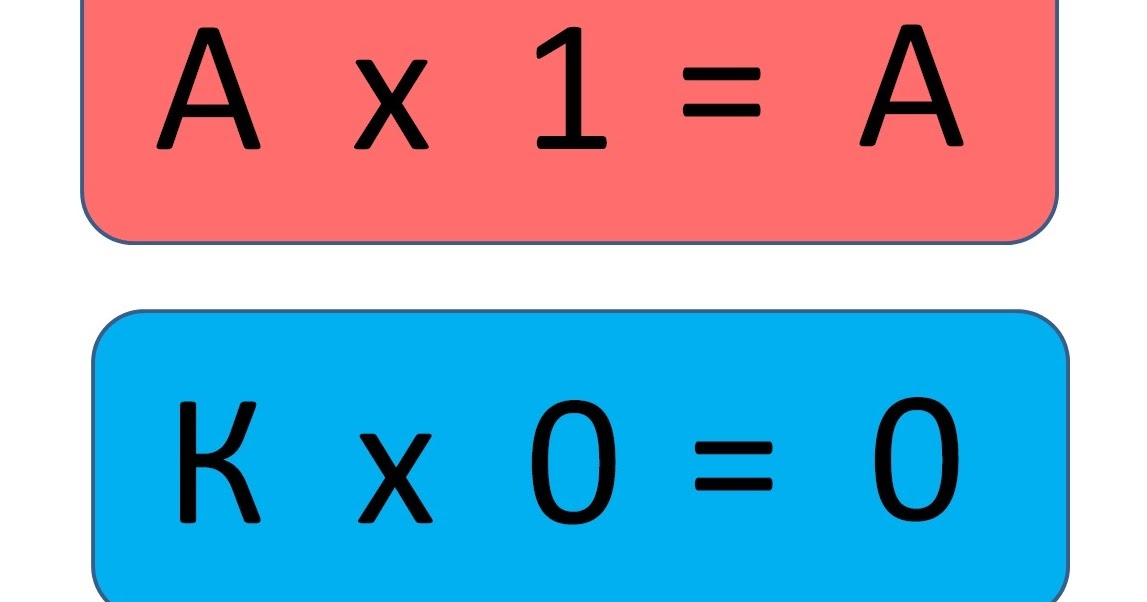 Первым делом нужно ввести различные символы, используемые для обозначения умножения двух целых чисел.
Первым делом нужно ввести различные символы, используемые для обозначения умножения двух целых чисел.
Математические символы, обозначающие умножение
| Символ | Пример | |
|---|---|---|
| × | раз символ | 3 × 4 |
| · | точка | 3,4 |
| () | скобки | (3) (4) или 3 (4) из (3) 4 |
Продукты и факторы
В выражении \ (3 · 4 \) целые числа 3 и 4 называются коэффициентами , а \ (3 · 4 \) называют произведением .
Ключ к пониманию умножения содержится в следующем утверждении.
Умножение эквивалентно повторному сложению.
Предположим, например, что мы хотим оценить продукт \ (3 · 4 \). Поскольку умножение эквивалентно повторному сложению, \ (3 · 4 \) эквивалентно сложению трех четверок. То есть
\ [3 \ cdot 4 = \ underbrace {4 + 4 + 4} _ {\ text {три четверки}} \ nonumber \]
Таким образом, \ (3 · 4 = 12 \). Вы можете визуализировать произведение \ (3 · 4 \) как сумму трех четверок на числовой прямой, как показано на рисунке 1.6.
Рисунок 1.6: Обратите внимание, что 3 · 4 = 4 + 4 + 4. То есть 3 · 4 = 12.Как и при сложении, порядок множителей не имеет значения.
\ [4 \ cdot 3 = \ underbrace {3 + 3 + 3 + 3} _ {\ text {четыре тройки}} \ nonumber \]
Таким образом, \ (4 · 3 = 12 \). Рассмотрим визуализацию \ (4 · 3 \) на рис. 1.7.
Рисунок 1.7: Обратите внимание, что 4 · 3 = 3 + 3 + 3 + 3. То есть 4 · 3 = 12. Доказательства на рисунках 1. 6 и 1.7 показывают нам, что умножение коммутативно. То есть
6 и 1.7 показывают нам, что умножение коммутативно. То есть
\ [3 · 4 = 4 · 3 \ nonumber \]
Коммутативное свойство умножения
Если a и b — любые целые числа, то
\ [а · Ь = Ь · а.\ nonumber \]
Мультипликативная идентичность
Обратите внимание на рисунок 1.8 (a), что пять единиц равны 5; то есть \ (5 · 1 = 5 \). С другой стороны, на рис. 1.8 (b) мы видим, что одна пятерка равна пяти; то есть 1 · 5 = 5.
Рисунок 1.8: Обратите внимание, что 5 · 1 = 5 и 1 · 5 = 5.Поскольку умножение целого числа на 1 дает это идентичное число, целое число 1 называется мультипликативным тождеством.
Свойство мультипликативной идентичности
Если \ (a \) — любое целое число, то
a · 1 = a и 1 · a = a.
Умножение на ноль
Поскольку \ (3 · 4 = 4 + 4 + 4 \), мы можем сказать, что произведение \ (3 · 4 \) представляет «3 набора по 4», как показано на рисунке 1.9, где три группы по четыре блока каждая заключена в овал.
Рисунок 1.9: Три набора из четырех: 3 · 4 = 12.Следовательно, \ (0 · 4 \) будет означать ноль наборов из четырех. Конечно, ноль наборов из четырех — это ноль.
Умножение на ноль.
Если a представляет любое целое число, то
\ (а · 0 = 0 \) и \ (0 · а = 0 \).
Ассоциативное свойство умножения
Как и сложение, умножение целых чисел ассоциативно. Действительно,
\ [\ begin {align *} 2 · (3 · 4) & = 2 · 12 \\ [4pt] & = 24 \ end {align *} \]
и
\ [\ begin {align *} (2 · 3) · 4 & = 6 · 4 \\ [4pt] & = 24. \ end {align *} \]
Ассоциативное свойство умножения.
Если a , b и c — любые целые числа, то
\ [a · (b · c) = (a · b) · c.\ nonumber \]
Умножение больших целых чисел
Подобно сложению и вычитанию больших целых чисел, нам также потребуется умножать большие целые числа. Опять же, мы надеемся, что алгоритм знаком из предыдущих курсовых работ.
Опять же, мы надеемся, что алгоритм знаком из предыдущих курсовых работ.
Пример 1
Упростить: \ (35 · 127 \).
Решение
Выровняйте числа по вертикали. Порядок умножения не имеет значения, но мы поставим большее из двух чисел поверх меньшего.Первым делом умножаем 5 на 127. Снова идем справа налево. Итак, 5 умножить на 7 равно 35. Мы записываем 5, затем переносим 3 в столбец десятков. Затем 5 умножить на 2 равно 10. Добавьте цифру переноса 3, чтобы получить 13. Запишите 3 и перенесите 1 в столбец сотен. Наконец, 5 умножить на 1 равно 5. Добавьте цифру переноса, чтобы получить 6.
Следующий шаг — умножить 3 на 127. Однако, поскольку 3 стоит в разряде десятков, его значение равно 30, поэтому мы фактически умножаем 30 на 126. Это то же самое, что умножить 127 на 3 и поставить 0 в конце. результата.
После сложения 0, 3 умножить на 7 будет 21. Мы записываем 1 и переносим 2 над 2 в столбце десятков. Затем 3 умножить на 2 равно 6. Добавьте цифру переноса 2, чтобы получить 8. Наконец, 3 умножения на 1 будет 1.
Осталось только добавить результаты.
Таким образом, 35 · 127 = 4, 445.
Альтернативный формат
Не помешает опустить завершающий ноль на втором этапе умножения, где мы умножаем 3 на 127.Результат будет выглядеть так:
В этом формате понимается ноль, поэтому нет необходимости иметь его физически. Идея состоит в том, что при каждом умножении на новую цифру мы отступаем от произведения на один пробел справа.
Упражнение
Упростить: 56 · 335
- Ответ
18 760
Деление целых чисел
Теперь перейдем к теме деления целых чисел.Сначала мы вводим различные символы, используемые для обозначения деления целых чисел.
Математические символы, обозначающие деление
| Символ | Пример | |
|---|---|---|
| ÷ | условное обозначение | 12 ÷ 4 |
| – | фракция пруток | \ (\ frac {12} {4} \) |
| \ (\ longdiv {-} \) | разделительная планка | \ (4 \ longdiv {12} \) |
Обратите внимание, что все следующие утверждения говорят об одном и том же; то есть «12, разделенное на 4, равно 3. ”
”
\ (12 \ div 4 = 3 \ quad \ text {или} \ quad \ frac {12} {4} = 3 \ quad \ text {или} \ quad 4 \ sqrt {12} \)
Коэффициенты, дивиденды и делители
В ведомости
\ (\ frac {3} {4) 12} \)
целое число 12 называется делимым , целое число 4 называется делителем , а целое число 3 называется частным . Обратите внимание, что это обозначение шкалы деления эквивалентно
.\ (12 \ div 4 = 3 \ quad \ text {и} \ quad \ frac {12} {4} = 3.\)
Выражение a / b означает « a , разделенное на b », но эта конструкция также называется дробью .
Определение: дробь
Выражение
\ (\ frac {a} {b} \)
называется дробью . Число \ (a \) сверху называется числителем дроби; число \ (b \) внизу называется знаменателем дроби.
Ключ к пониманию деления целых чисел содержится в следующем утверждении.
Деление эквивалентно повторному вычитанию.
Предположим, например, что мы хотим разделить целое число 12 на целое число 4. Это эквивалентно задаче вопроса «сколько четверок мы можем вычесть из 12?» Это можно визуализировать на числовой линейной диаграмме, например, на рисунке 1.10.
Рисунок 1.10: Деление — это повторное вычитание.Обратите внимание на рис. 1.10, что если мы вычтем три четверки из двенадцати, результат будет равен нулю. В символах,
\ (12- \ underbrace {4-4-4} _ {\ text {три четверки}} = 0.\)
Аналогично, мы также можем спросить: «Сколько групп из четырех человек в 12?» И расположить нашу работу, как показано на рис. 1.11, где мы можем видеть, что в массиве из двенадцати объектов мы можем обвести три группы по четыре; т.е. 12 ÷ 4 = 3.
Рисунок 1.11: Есть три группы по четыре из двенадцати. Обратите внимание, что на рисунках 1.10 и 1.11 деление (повторное вычитание) не оставляет остатка. Это не всегда так.
Это не всегда так.
Пример 2.
Разделить 7 на 3.
Решение
На рисунке 1.12, мы видим, что можем вычесть две тройки из семи, оставив остаток на единицу.
Рисунок 1.12: Деление с остатком.В качестве альтернативы, в массиве из семи объектов мы можем обвести две группы по три, оставив остаток по одному.
Рисунок 1.13: При делении семи на три остается один.Как на рис. 1.12, так и на рис. 1.13 показано, что есть две группы по три из семи, и одна осталась. Мы говорим: «Семь разделить на три — это два, а остаток — один.
Упражнение
Используйте метод числовой прямой и метод массива прямоугольников, чтобы разделить 12 на 5.
Раздел не коммутативен
Порядок деления целых чисел имеет значение. Например
12 ÷ 4 = 3,
, но 4 ÷ 12 — это даже не целое число. Таким образом, если a и b являются целыми числами, то a ÷ b не не должны быть такими же, как b ÷ a .
Деление не ассоциативное
Когда вы делите три числа, порядок, в котором они сгруппированы, обычно влияет на ответ.Например,
(48 ÷ 8) ÷ 2 = 6 ÷ 2
= 3,
но
48 ÷ (8 ÷ 2) = 48 ÷ 4
= 12.
Таким образом, если a , b и c являются целыми числами, ( a ÷ b ) ÷ c не обязательно должно совпадать с a ÷ ( b ÷ с ).
Деление на ноль не определено
Предположим, что нас просят разделить шесть на ноль; то есть нас просят вычислить 6 ÷ 0.На рисунке 1.14 у нас есть массив из шести объектов.
Рисунок 1.14: Сколько групп нулей вы видите? Теперь, чтобы разделить шесть на ноль, мы должны ответить на вопрос: «Сколько групп нулей мы можем обвести на рисунке 1.14?» Некоторые мысли дадут ответ: это бессмысленная просьба! Совершенно бессмысленно спрашивать, сколько групп нулей можно обвести в массиве из шести объектов на рис. 1.14.
1.14.
Дивизион по нулю
Деление на ноль — undefined .Каждое из выражений
\ (6 \ div 0 \ quad \ text {and} \ quad \ frac {6} {0} \ quad \ text {and} \ quad 0) \ overline {6} \)
— это undefined.
С другой стороны, имеет смысл спросить: «Что такое ноль делится на шесть?» Если мы создадим массив из нулевых объектов, а затем спросим, сколько групп из шести человек мы можем обвести, ответ будет «ноль групп из шести». То есть ноль, деленный на шесть, равняется нулю.
\ (0 \ div 6 = 0 \ quad \ text {and} \ quad \ frac {0} {6} = 0 \ quad \ text {and} \ quad 6 \ frac {0} {0} \)
Разделение больших целых чисел
Теперь мы кратко рассмотрим деление больших целых чисел с помощью алгоритма, который обычно называют длинным делением .Это не всестороннее обсуждение, а беглое обсуждение. Мы рассчитываем на то, что наши читатели сталкивались с этим алгоритмом на предыдущих курсах и знакомы с процессом.
Пример 3
Упростить: 575/23.
Решение
Мы начинаем с оценки, сколько 23 делится на 57, угадывая 1. Мы помещаем 1 в частное над 7, умножаем 1 на 23, помещаем ответ под 57, затем вычитаем.
\ (\ begin {array} {c} {23) \ frac {1} {575}} \\ {\ frac {23} {34}} \ end {array} \)
Поскольку остаток больше делителя, наша оценка слишком мала.Пробуем еще раз с оценкой 2.
\ (\ begin {array} {r} {2} \\ {2 3 \ longdiv {5 7 5}} \\ {\ frac {46} {11}} \ end {array} \)
Это алгоритм. Разделите, умножьте, затем вычтите. Вы можете продолжить, только если остаток меньше делителя.
Чтобы продолжить, опустите 5, прикиньте, что 115 разделенное на 23 равно 5, затем умножьте 5 на делитель и вычтите.
\ (\ begin {array} {c} {25} \\ {2 3 \ longdiv {5 7 5}} \\ {\ frac {46} {115}} \\ {\ frac {115} {0} } \ end {array} \)
Поскольку остаток равен нулю, 575/23 = 25.
Упражнение
Разделить 980/35
- Ответ
28
Приложение — счет прямоугольных массивов
Рассмотрим прямоугольный массив звезд на рис. 1.15. Чтобы подсчитать количество звезд в массиве, мы могли бы использовать грубую силу, считая каждую звезду в массиве по одной за раз, в общей сложности 20 звезд. Однако, поскольку у нас есть четыре ряда по пять звезд в каждом, умножение происходит намного быстрее: 4 · 5 = 20 звезд.
Рисунок 1.15: Четыре строки и пять столбцов. Рисунок 1.16: Площадь в квадратных единицах.Приложение — Площадь
На рис. 1.16 (a) изображен квадрат размером в один квадратный дюйм (1 из 2 ), по одному дюйму с каждой стороны. На Рисунке 1.16 (b) изображен квадрат размером в один квадратный фут (1 фут 2 ), по одному футу с каждой стороны. Оба эти квадрата являются мерой площади. Теперь рассмотрим прямоугольник, показанный на рисунке 1.17. Длина этого прямоугольника составляет четыре дюйма (4 дюйма), а ширина — три дюйма (3 дюйма).
Рисунок 1.17: Прямоугольник длиной 4 дюйма и шириной 3 дюйма.Чтобы найти площадь фигуры, мы можем подсчитать отдельные единицы площади, составляющие площадь прямоугольника, всего двенадцать квадратных дюймов (12 на 2 ). Однако, как мы это делали при подсчете звезд в массиве на рис. 1.15, гораздо быстрее заметить, что у нас есть три ряда по четыре квадратных дюйма. Следовательно, намного быстрее умножить количество квадратов в каждой строке на количество квадратов в каждом столбце: 4 · 3 = 12 квадратных дюймов.
Приведенный выше аргумент приводит к следующему правилу определения площади прямоугольника.
Площадь прямоугольника
Пусть L и W представляют длину и ширину прямоугольника соответственно.
Чтобы найти площадь прямоугольника, вычислите произведение длины и ширины. То есть, если A представляет площадь прямоугольника, тогда площадь прямоугольника определяется формулой
A = LW .
Пример 4
Прямоугольник имеет ширину 5 футов и длину 12 футов. Найдите площадь прямоугольника.
Решение
Замените L = 12 футов и W = 5 футов в формулу площади.
A = LW
= (12 футов) (5 футов)
= 60 футов 2
Следовательно, площадь прямоугольника составляет 60 квадратных футов.
Упражнение
Прямоугольник имеет ширину 17 дюймов и длину 33 дюйма.Найдите площадь прямоугольника.
- Ответ
561 квадратный дюйм
Упражнения
В упражнениях 1–4 используйте числовые линейные диаграммы, как показано на рис. 1.6, чтобы изобразить умножение.
1. 2 · 4.
2. 3 · 4.
3. 4 · 2.
4. 4 · 3.
В упражнениях 5-16 укажите свойство умножения, отображаемое данной идентичностью.
5.9,8 = 8,9
6,5 · 8 = 8 · 5
7. 8 · (5 · 6) = (8 · 5) · 6
8. 4 · (6 · 5) = (4 · 6) · 5
9. 6 · 2 = 2 · 6
10. 8 · 7 = 7 · 8
11. 3 · (5 · 9) = (3 · 5) · 9
12. 8 · (6 · 4) = (8 · 6) · 4
13. 21 · 1 = 21
14. 39 · 1 = 39
15. 13 · 1 = 13
16. 44 · 1 = 44
В упражнениях 17–28 умножьте заданные числа.
17,78 · 3
18.58,7
19. 907 · 6
20. 434 · 80
21 128 · 30
22 454 · 90
23 799 · 60
24. 907 · 20
25. 14 · 70
26. 94 · 90
27. 34 · 90
28. 87 · 20
В упражнениях 29-40 умножьте заданные числа.
29,237,54
30. 893 · 94
31. 691 · 12
32. 823 · 77
33. 955 · 89
34.714,41
35. 266 · 61
36. 366 · 31
37. 365 · 73
38. 291 · 47
39. 955 · 57
955 · 57
40. 199 · 33
41. Подсчитайте количество объектов в массиве.
42. Подсчитайте количество объектов в массиве.
43. Подсчитайте количество объектов в массиве.
44. Подсчитайте количество объектов в массиве.
В упражнениях 45–48 найдите площадь прямоугольника заданной длины и ширины.
45. L = 50 дюймов, W = 25 дюймов
46. L = 48 дюймов, W = 24 дюйма
47. L = 47 дюймов, W = 13 дюймов
48. L = 19 дюймов, W = 10 дюймов
В упражнениях 49-52 найдите периметр прямоугольника заданной длины и ширины.
49. L = 25 дюймов, W = 16 дюймов
50. L = 34 дюйма, W = 18 дюймов
51. L = 30 дюймов, W = 28 дюймов
52. L = 41 дюйм, W = 25 дюймов
53. Набор бус стоит 50 центов за дюжину. Сколько стоят (в долларах) 19 десятков наборов бусин?
54.Набор бусин стоит 60 центов за дюжину. Сколько стоит (в долларах) 7 десятков наборов бусин?
55. Если бы репетитор по математике работал 47 часов и получал 15 долларов за каждый час, сколько денег она заработала бы?
56. Если бы репетитор по математике работал 46 часов и получал 11 долларов за каждый час, сколько денег он заработал бы?
57. В одной дюжине 12 яиц, в одном брутто — 12 дюжин. Сколько яиц в партии брутто 24 шт.?
58. В одной дюжине 12 яиц, в одном брутто — 12 дюжин.Сколько яиц в партии брутто 11?
59. Если каждый кирпич весит 4 килограмма, каков вес (в килограммах) 5000 кирпичей?
60. Если каждый кирпич весит 4 фунта, каков вес (в фунтах) 2000 кирпичей?
В упражнениях 61–68 какое из следующих четырех выражений отличается от остальных трех?
61. \ (\ frac {30} {5} \), 30 ÷ 5, \ (5 \ longdiv {3 0} \), 5 ÷ 30
62. \ (\ frac {12} {2} \), 12 ÷ 2, \ (2 \ longiv {12} \), 2 ÷ 12
63.\ (\ frac {8} {2} \), 8 ÷ 2, \ (2 \ longdiv {8} \), \ (8 \ longdiv {2} \)
64. \ (\ frac {8} {4} \), 8 ÷ 4, \ (4 \ longdiv {8} \), \ (8 \ longdiv {4} \)
\ (\ frac {8} {4} \), 8 ÷ 4, \ (4 \ longdiv {8} \), \ (8 \ longdiv {4} \)
65. \ (2 \ longdiv {14} \), \ (14 \ longdiv {2} \), \ (\ frac {14} {2} \), 14 ÷ 2
66. \ (9 \ longdiv {54} \), \ (54 \ longdiv {9} \), \ (\ frac {54} {9} \), 54 ÷ 9
67. \ (3 \ longdiv {24} \), 3 ÷ 24, \ (\ frac {24} {3} \), 24 ÷ 3
68. \ (3 \ longdiv {15} \), 3 ÷ 15, \ (\ frac {15} {3} \), 15 ÷ 3
В упражнениях 69–82 упростите данное выражение.Если ответа не существует или он не определен, напишите «undefined».
69.0 ÷ 11
70. 0 ÷ 5
71,17 ÷ 0
72. 24 ÷ 0
73. 10 · 0
74. 20 · 0
75. \ (\ frac {7} {0} \)
76. \ (\ frac {23} {0} \)
77. \ (16 \ longdiv {0} \)
78. \ (25 \ longdiv {0} \)
79. \ (\ frac {0} {24} \)
80. \ (\ frac {0} {22} \)
81. \ (0 \ longdiv {0} \)
82.0 ÷ 0
В упражнениях 83–94 разделите заданные числа.
83. \ (\ frac {2816} {44} \)
84. \ (\ frac {1998} {37} \)
85. \ (\ frac {2241} {83} \)
86. \ (\ frac {2716} {97} \)
87. \ (\ frac {3212} {73} \)
88. \ (\ frac {1326} {17} \)
89. \ (\ frac {8722} {98} \)
90. \ (\ frac {1547} {91} \)
91. \ (\ frac {1440} {96} \)
92. \ (\ frac {2079} {27} \)
93. \ (\ frac {8075} {85} \)
94.\ (\ frac {1587} {23} \)
В упражнениях 95-106 разделите заданные числа.
95. \ (\ frac {17756} {92} \)
96. \ (\ frac {46904} {82} \)
97. \ (\ frac {11951} {19} \)
98. \ (\ frac {22304} {41} \)
99. \ (\ frac {18048} {32} \)
100. \ (\ frac {59986} {89} \)
101. \ (\ frac {29047} {31} \)
102. \ (\ frac {33264} {86} \)
103. \ (\ frac {22578} {53} \)
104. \ (\ frac {18952} {46} \)
105.\ (\ frac {12894} {14} \)
106. \ (\ frac {18830} {35} \)
\ (\ frac {18830} {35} \)
107. Бетонный тротуар уложен квадратными блоками размером 6 футов с каждой стороны. Сколько блоков будет на прогулке длиной 132 фута?
108. Бетонный тротуар выложен квадратными блоками размером 5 футов с каждой стороны. Сколько блоков будет на прогулке длиной 180 футов?
109. Одна лодка на остров может принять 5 человек. Сколько рейсов придется совершить лодке, чтобы переправить на остров 38 человек? (Подсказка: округлите свой ответ.)
110. На одной лодке на остров могут разместиться 4 человека. Сколько рейсов придется совершить лодке, чтобы переправить на остров 46 человек? (Подсказка: округлите ответ.)
111. Если уличные фонари расположены на расстоянии не более 145 футов друг от друга, сколько уличных фонарей потребуется для улицы протяженностью 4 мили, если предположить, что фонари есть на каждом конце улицы? (Примечание: 1 миля = 5280 футов)
112. Если уличные фонари расположены на расстоянии не более 70 футов, сколько уличные фонари потребуется для улицы протяженностью 3 мили, если предположить, что огни есть на каждом конце улицы? (Примечание: 1 миля = 5280 футов.)
113. Бетонный тротуар выложен квадратными блоками размером 4 фута с каждой стороны. Сколько блоков будет на прогулке длиной 292 фута?
114. Бетонный тротуар выложен квадратными блоками размером 5 футов с каждой стороны. Сколько блоков будет на прогулке длиной 445 футов?
115. На одной лодке на остров могут разместиться 3 человека. Сколько рейсов придется совершить лодке, чтобы переправить на остров 32 человека? (Подсказка: округлите свой ответ.)
116. Одна лодка на остров может принять 4 человека. Сколько рейсов придется совершить лодке, чтобы переправить на остров 37 человек? (Подсказка: округлите ответ.)
117. Если уличные фонари расположены на расстоянии не более 105 футов друг от друга, сколько уличные фонари потребуется для улицы протяженностью 2 мили, если предположить, что огни есть на каждом конце улицы? (Примечание: 1 миля = 5280 футов)
118. Если уличные фонари расположены на расстоянии не более 105 футов друг от друга, сколько уличных фонарей потребуется для улицы протяженностью 3 мили, если предположить, что фонари есть на каждом конце улицы? (Примечание: 1 миля = 5280 футов.)
Если уличные фонари расположены на расстоянии не более 105 футов друг от друга, сколько уличных фонарей потребуется для улицы протяженностью 3 мили, если предположить, что фонари есть на каждом конце улицы? (Примечание: 1 миля = 5280 футов.)
119. Написание статей . Эли пишет в среднем 4 статьи в день пять дней в неделю, чтобы поддержать продажи продукции. Сколько статей Илай пишет за неделю?
120. Пулемет . Зенитный пулемет калибра 0,50 может стрелять 800 выстрелов в минуту. Сколько выстрелов можно было выстрелить за три минуты? Associated Press Times-Standard 15.04.09
121. Круги . Плавательный бассейн в CalCourts составляет 25 ярдов в длину.Если пройти один круг вверх и обратно, сколько ярдов проплыл Венделл, сделав 27 кругов?
122. Холодильная мощность . Обычный холодильник будет работать около 12 часов в день и потреблять 150 Вт энергии каждый час. Сколько ватт мощности будет потреблять холодильник в течение дня?
123. Конское сено . Взрослые лошади должны съедать не менее 12 фунтов сена каждый день и могут есть гораздо больше в зависимости от своего веса. Сколько минимум фунтов съела бы лошадь за год?
124. Колледж стоит . После повышения платы за обучение на 662 доллара жители Калиформии, желающие поступить в Калифорнийский университет в качестве бакалавра, должны рассчитывать на предстоящий 2009-2010 учебный год заплатить 8700 долларов. Если стоимость не изменится в течение следующих нескольких лет, как сколько студент должен ожидать платить за четырехлетнюю программу обучения в школе UC?
125. Расходы нерезидентов . Студенты-нерезиденты, желающие поступить в колледж Калифорнийского университета, должны заплатить около 22000 долларов в следующем учебном году.Если предположить, что затраты останутся прежними, сколько может стоить четырехлетняя степень?
126. Студенческий налог . Мэр Провиденса, Род-Айленд, хочет обложить налогом своих 25000 студентов Университета Брауна по 150 долларов каждый, чтобы внести свой вклад в налоговые поступления, заявив, что студенты должны платить за ресурсы, которые они используют, так же, как жители города. Сколько долларов заработает майер?
Студенческий налог . Мэр Провиденса, Род-Айленд, хочет обложить налогом своих 25000 студентов Университета Брауна по 150 долларов каждый, чтобы внести свой вклад в налоговые поступления, заявив, что студенты должны платить за ресурсы, которые они используют, так же, как жители города. Сколько долларов заработает майер?
127. Новый айсберг . Новый айсберг, срезанный с ледника после столкновения с другим айсбергом, имеет размеры около 48 миль в длину и 28 миль в ширину.Какова примерная площадь нового айсберга? Associated PressTimes-Standard 27.02.10 2 Огромные айсберги вышли из берегов Антарктиды.
128. Солнечные батареи . Одна из солнечных панелей на Международной космической станции имеет длину 34 метра и ширину 11 метров. Если их восемь, какова общая площадь для сбора солнечной энергии?
129. Тротуар . Бетонный тротуар должен быть 80 футов в длину и 4 фута в ширину. Сколько будет стоить укладка тротуара из расчета 8 долларов за квадратный фут?
130. Тюки сена . Средний тюк сена весит около 60 фунтов. Если лошадь съедает 12 фунтов сена в день, сколько дней один тюк может кормить лошадь?
131. Солнечные пятна . Солнечные пятна, в которых магнитное поле Солнца намного выше, обычно встречаются парами. Если общее количество солнечных пятен составляет 72, сколько пар пятен существует?
Ответы
1. \ (2 \ cdot 4 = \ underbrace {4 + 4} _ {2 \ text {times}} = 8 \)
3. \ (4 \ cdot 2 = \ underbrace {2 + 2 + 2 + 2} _ {4 \ text {times}} = 8 \)
5.Коммутативное свойство умножения
7. Ассоциативное свойство умножения
9. Коммутативность умножения
11. Ассоциативное свойство умножения
13. Свойство мультипликативной идентичности
15. Свойство мультипликативной идентичности
17,234
19. 5442
21. 3840
23. 47940
25.980
27. 3060
29. 12798
31.8292
33. 84995
35. 16226
37. 26645
39. 54435
41. 64
43. 56
45. 1250 в 2
47. 611 в 2
49. 82 в
51,116 в
53. 9,50
55. 705
57. 3456
59. 20000
61,5 ÷ 30
63. \ (8 \ sqrt {2} \)
65. \ (14 \ sqrt {2} \)
67,3 ÷ 24
69.0
71. Не определено
73. 0
75. Не определено
77. 0
79. 0
81. Не определено
83. 64
85. 27
87. 44
89. 89
91,15
93. 95
95,193
97,629
99 564
101. 937
103. 426
105. 921
107. 22
109. 8
111. 147
113.73
115,11
117.102
119. 20 статей
121. 1350 ярдов
123. 4380 фунтов сена
125. 88 000 долларов США
127. 1344 миль 2
129. 2,560 долл. США
131. 36
Умножение и деление на числа от 0 до 1 — Умножение и деление — KS3 Maths Revision
Умножение на число от 0 до 1
Знак умножения можно заменить фразой «много».
Например:
\ (2 \ times 3 \) означает \ (2 \) лоты из \ (3 \) (\ ({= 6} \))
\ (6 \ times 8 \) означает \ (6 \) лотов \ (8 \) (\ ({= 48} \))
Итак, \ ({10} \ times \ frac {1} {2} \) означает \ ({10} \) много \ (\ frac {1} {2} \) (\ ({= 5} \))
И \ ({12} \ times \ frac {1} {3} \) означает \ ({12} \) много \ (\ frac {1} {3} \) (\ ({= 4} \))
Когда вы умножаете на число больше 1, ответ будет больше, чем исходное число. Но когда вы умножаете на число от 0 до 1, ответ будет меньше исходного числа.
Мы видели, что: \ ({10} \ times \ frac {1} {2} = {5} \)
Мы также знаем, что \ ({10} \ div {2} = {5} \)
Следовательно: \ ({10} \ times \ frac {1} {2} = {10} \ div {2} \)
Это показывает, что ‘\ (\ times ~ \ frac {1} {2} \ ) ‘то же самое, что’ \ (\ div ~ {2} \) ‘.
В общем:
\ [m \ times \ frac {1} {n} = m \ div n \]
Примеры
\ (8 \ times \ frac {1} {4} = 8 \ div 4 = 2 \) (поскольку ‘\ (\ times ~ \ frac {1} {4} \)’ совпадает с ‘\ (\ div ~ {4} \)’)
\ (20 \ times \ frac { 1} {5} = 20 \ div 5 = 4 \) (поскольку ‘\ (\ times ~ \ frac {1} {5} \)’ означает то же самое, что ‘\ (\ div ~ {5} \)’)
Деление на число от 0 до 1
Представьте, что у вас есть \ (10 \) плиток шоколада, которые вы хотите разделить с детьми.
Если вы дадите дочерним элементам \ (2 \) столбца каждый, у вас будет достаточно для \ (5 \) детей.
\ [10 \ div 2 = 5 \]
Если бы вы дали каждому дочернему элементу \ (\ frac {1} {2} \) полоску, у вас было бы достаточно для \ (20 \) детей.
\ [10 \ div \ frac {1} {2} = 20 \]
Шаблон
Вы видите, что происходит?
\ [10 \ div 2 = 5 \]
\ [10 \ div \ frac {1} {2} = 20 \]
При делении на целое число ответ будет меньше исходного числа.Когда вы делите на \ (\ frac {1} {2} \), ответ (\ ({20} \)) будет на больше, чем исходного числа (\ ({10} \)).
Когда вы делите на число больше 1, ответ будет меньше исходного числа. Но когда вы разделите на число от 0 до 1, ответ будет больше, чем исходное число.
Итак: \ (10 \ div \ frac {1} {2} = 20 \)
Аналогично: \ (10 \ div \ frac {1} {3} = 30 \) и \ (10 \ div \ frac {1} {4} = 40 \)
В целом: \ (m \ div \ frac {1} {n} = mn \)
- Вопрос
Q1.Что такое \ (10 \ div \ frac {1} {7} \)?
2 кв. Найдите значение \ (4 \ div \ frac {1} {3} \)
- Показать ответ
A1. \ ({10} \ div \ frac {1} {7} = {10} \ times {7} = {70} \)
A2. \ (4 \ div \ frac {1} {3} = 4 \ times 3 = 12 \)
Это полный урок с видео и упражнениями, показывающими, в первую очередь, общий ярлык для умножения и деления десятичных знаков на степень десяти: вы перемещаете десятичную точку на столько шагов, сколько нулей в числе 10, 100, 1000. и т.п. Затем я также показываю , откуда происходит этот ярлык, с помощью диаграмм значений разряда. На самом деле перемещение десятичной точки является своего рода иллюзией, и вместо этого цифр числа перемещаются в пределах диаграммы разряда. Это объяснение действительно может помочь студентам понять причину «трюка» с перемещением десятичной точки. Урок ниже объясняет этот ярлык более подробно, а также содержит различные виды упражнений, задачи со словами и даже забавную загадку для учащихся. 1. Умножить.
2. Давайте еще немного попрактикуемся.
3. А теперь попрактикуемся в использовании степени десяти.
4. Разделить.
5. Теперь попрактикуемся в использовании степени десяти.
6. Разделить. Подумайте о дробях в десятичные дроби или воспользуйтесь ярлыком. Сравните проблемы в каждой коробке! 7. Мешок с орехами весом 10 фунтов стоит.
72 доллара. 8. Найдите цену 100 шары для пинг-понга, если один мяч для пинг-понга стоит 0 долларов.89.
9. Разделите целые числа на 1000. Упростите окончательный ответ, отбросив любой конечный десятичный разделитель. нули.
10. Разделите целые числа на 10 и 100. 11. Найдите одну десятую от … а. $ 8 г. 25,50 $ г. $ 126 12. Найдите одну сотую из … а. $ 78 г. $ 4 г. $ 390 13. Пара обуви стоимостью 29 долларов была снижена на 3/10 ее цены.Какая новая цена? ( Подсказка: сначала найдите 1/10 цены. ) 14. Найдите цену со скидкой: а. На велосипед стоимостью 126 долларов скидка составляет 2/10 его цены. б. Сотовый телефон за 45 долларов со скидкой 5/100 от его цены. 15. Одна сотая определенного числа
составляет 0,03.Какой номер? 16. Какой пылесос оказывается дешевле? Модель B сейчас стоит 75 долларов, но вы получите скидку 1/4 его цены.
17. Пришло время для некоторых заключительная практика. Найдите недостающие числа. Сопоставьте букву каждой задачи с правильным ответом в квадратах и решить загадку. Есть два набора коробок. Первые блоки относятся к первому набору упражнений, а последние блоки относятся ко второму набору. Почему 7 не понял, о чем идет речь в 3.14?
Я также предлагаю бесплатные рабочие листы: Этот урок взят из книги Марии Миллер Math Mammoth Decimals 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. Математика Мамонт Десятичные 2 Самообучающийся рабочий текст для 5-6 классов, охватывающий четыре операции с десятичными знаками до трех десятичных знаков, с упором на десятичное умножение и деление. В книге также рассматриваются разряды, сравнение, округление, сложение и вычитание десятичных знаков. Есть много проблем с умственной математикой. Загрузить ($ 6.25) . Также доступен в печатном виде. => Узнайте больше и посмотрите бесплатные образцы! | |||||||||||||||||||||||||||||||
Умножение и деление KS2
Квадратного не было
Возраст от 7 до 11 лет
Уровень испытания
Миссис Морган, классная учительница, прикрепила числа на спинах троих детей. Используйте информацию, чтобы узнать, что это были за три числа.
Все цифры
Возраст от 7 до 11 лет
Уровень испытания
Это умножение использует каждую из цифр 0–9 только один раз и только один раз.Можете ли вы, пользуясь приведенной информацией, заменить в расчете звездочки на цифры?
Велосипедные квадраты
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы составить цикл пар, которые складываются в квадратное число, используя все числа в поле ниже, только один раз и только один раз?
утроение
Возраст от 7 до 11 лет
Уровень испытания
Можно ли заменить буквы на цифры? В каждом случае есть только одно решение?
Форма Время Форма
Возраст от 7 до 11 лет
Уровень испытания
Эти одиннадцать фигур обозначают разные числа.Можете ли вы использовать числовые предложения, чтобы понять, что они собой представляют?
Что вам нужно?
Возраст от 7 до 11 лет
Уровень испытания
Четыре из этих подсказок необходимы, чтобы найти выбранное число в этой сетке, и четыре верны, но не помогают в поиске числа. Сможете ли вы разобрать улики и найти номер?
Три кости
Возраст от 7 до 11 лет
Уровень испытания
Исследуйте сумму чисел на верхней и нижней гранях линии из трех кубиков.Что ты заметил?
Как это сделать?
Возраст от 7 до 11 лет
Уровень испытания
Это групповое задание побудит вас поделиться стратегиями вычислений и подумать о том, какая стратегия может быть наиболее эффективной.
Шаблоны таблиц сходят с ума!
Возраст от 7 до 11 лет
Уровень испытания
Практически все мы сделали выкройки таблиц на сотках, то есть сетках 10 на 10. В этой задаче рассматриваются узоры на квадратных сетках разного размера.
Путешествий в стране чисел
Возраст от 7 до 11 лет
Уровень испытания
Том и Бен посетили Numberland. Используйте карты, чтобы вычислить количество очков, набранных каждым из их маршрутов.
Карты заказа
От 5 до 11 лет
Уровень испытания
Эта задача предназначена для того, чтобы помочь детям выучить и использовать таблицу умножения на два и три.
Давайте разделим!
Возраст от 7 до 11 лет
Уровень испытания
Посмотрите на разные способы деления вещей.Что они имеют в виду? Как бы вы могли показать их на картинке, с вещами, с числами и символами?
Галька
Возраст от 7 до 11 лет
Уровень испытания
Поместите четыре камешка на песок в форме квадрата. Продолжайте добавлять как можно меньше камешков, чтобы удвоить площадь. Сколько дополнительных камешков добавляется каждый раз?
Сладости в коробке
Возраст от 7 до 11 лет
Уровень испытания
Сколько коробок разной формы вы можете создать для 36 конфет в один слой? Можно ли расположить конфеты так, чтобы конфеты одного цвета не находились рядом друг с другом в любом направлении?
Круглый и круглый круг
Возраст от 7 до 11 лет
Уровень испытания
Что произойдет, если вы присоединитесь к каждой второй точке этого круга? Как насчет каждого третьего балла? Попробуйте выполнить разные шаги и посмотрите, сможете ли вы предсказать, что произойдет.
Дайси Аррайлайв
От 5 до 11 лет
Уровень испытания
Посмотрите видео об этой игре. Вы можете выработать правила? Какие суммы кубиков можно получить и почему?
Зиос и Зептс
Возраст от 7 до 11 лет
Уровень испытания
На планете Вув есть два вида существ. У Zios 3 ноги, а у Zepts 7 ног. Великий исследователь планет Нико насчитал 52 ноги. Сколько зиосов и сколько зептов было?
Обильные номера
Возраст от 7 до 11 лет
Уровень испытания
48 называется избыточным числом, потому что оно меньше суммы его факторов (без самого себя).Можете ли вы найти более обширные числа?
Марка 100
Возраст от 7 до 11 лет
Уровень испытания
Найдите хотя бы один способ поставить несколько знаков операции (+ — x ÷), чтобы эти цифры равнялись 100.
Проблесковые огни
Возраст от 7 до 11 лет
Уровень испытания
Норри видит, как два огонька мигают одновременно, затем один из них мигает каждые 4 секунды, а другой — каждые 5 секунд. Сколько раз они мигают вместе за целую минуту?
Луны Вувв
Возраст от 7 до 11 лет
Уровень испытания
У планеты Вувв семь лун.Можете ли вы определить, сколько времени проходит между каждым суперзатмением?
Загадочная матрица
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы заполнить этот квадрат таблицы? Для его создания использовались числа 2-12, причем дважды использовалось только одно число.
Четыре ради добра
Возраст от 7 до 11 лет
Уровень испытания
Используйте 4 четыре раза с простыми операциями, чтобы получить ответ 12. Можете ли вы также получить 15, 16 и 17?
Квадраты умножения
Возраст от 7 до 11 лет
Уровень испытания
Сможете ли вы определить расположение цифр в квадрате, чтобы указанные продукты были правильными? Цифры от 1 до 9 можно использовать только один раз.
Факторные линии
Возраст от 7 до 14 лет
Уровень испытания
Расположите четыре карточки с цифрами на сетке в соответствии с правилами, образуя диагональную, вертикальную или горизонтальную линию.
Кубики в кубиках
Возраст от 7 до 14 лет
Уровень испытания
Начнем с одного желтого куба и построим вокруг него куб 3x3x3 с красными кубиками. Затем мы строим вокруг этого красного куба синие кубики и так далее. Сколько кубиков каждого цвета мы использовали?
Самый высокий и самый низкий
Возраст от 7 до 11 лет
Уровень испытания
Поместите знаки операции между числами 3 4 5 6, чтобы получить максимально возможное число и наименьшее возможное число.
Остатки
Возраст от 7 до 14 лет
Уровень испытания
Я думаю о числе. Мой номер кратен 5 и 6. Каким может быть мой номер?
Квадрат чисел
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы поместить числа от 1 до 8 в кружки, чтобы четыре вычисления были правильными?
Что быстрее?
Возраст от 7 до 11 лет
Уровень испытания
Что быстрее: до 30 единиц или до 300 десятков? Почему?
Что в коробке?
Возраст от 7 до 11 лет
Уровень испытания
В этой большой коробке все, что попадает в нее, умножается на то же число.Если вы знаете, какие числа выпадают, какое умножение может происходить в коробке?
Нечетные квадраты
Возраст от 7 до 11 лет
Уровень испытания
Придумайте число, возведите его в квадрат и вычтите начальное число. Номер, который у вас остался, четный или нечетный? Как изображения помогают это объяснить?
Лестницы вверх и вниз
Возраст от 7 до 11 лет
Уровень испытания
Один блок необходим для создания лестницы, ведущей вверх и вниз, с одной ступенькой вверх и одной ступенькой вниз.Сколько блоков потребуется, чтобы построить лестницу с 5 ступенями вверх и 5 ступенями вниз?
Правила Дивизиона
Возраст от 7 до 11 лет
Уровень испытания
Эта задача побуждает вас исследовать деление трехзначного числа на однозначное число.
Карточки для переноски
Возраст от 7 до 11 лет
Уровень испытания
Эти шестнадцать детей стоят в четыре ряда по четыре человека, один за другим. У каждого из них есть карточка с номером.Можете ли вы найти недостающие числа?
Сетка кратных
Возраст от 7 до 11 лет
Уровень испытания
Что общего у цифр, выделенных синим цветом на этой сотке? Что вы заметили в розовых цифрах? Как насчет закрашенных цифр в других квадратах?
Игра на множители и множители
Возраст от 7 до 16
Уровень испытания
Эта игра может заменить стандартные практические упражнения по поиску множителей и множителей.
Музыка для моих ушей
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы предсказать, когда вы будете хлопать и когда будете щелкать, если начнете этот ритм? Как насчет того, чтобы в это же время друг начал новый ритм?
Факторно-множественные цепи
Возраст от 7 до 11 лет
Уровень испытания
Вы видите, как работают эти множительные цепочки? Найдите цепочку, содержащую наименьшие возможные числа. Как насчет максимально возможных чисел?
Четыре Гоу
Возраст от 7 до 11 лет
Уровень испытания
Это испытание — игра для двух игроков.Выберите два числа, которые хотите умножить или разделить, затем отметьте свой ответ в числовой строке. Можно четыре подряд?
Изобразите пирамиду …
Возраст от 7 до 11 лет
Уровень испытания
Представьте себе пирамиду, состоящую из квадратных слоев маленьких кубиков. Если мы пронумеруем кубики сверху, начиная с 1, можете ли вы представить себе, какие кубики находятся непосредственно под этим первым кубом?
Игра Остатков
Возраст от 7 до 14 лет
Уровень испытания
Сыграйте в эту игру и посмотрите, сможете ли вы выяснить выбранный номер компьютера.
Какой символ?
Возраст от 7 до 11 лет
Уровень испытания
Выберите символ, который нужно вставить в числовое предложение.
Таблицы умножения Сдвиги
Возраст от 7 до 11 лет
Уровень испытания
В этом упражнении компьютер выбирает таблицу умножения и сдвигает ее. Можете ли вы каждый раз прорабатывать стол и смену?
Счетные винтики
Возраст от 7 до 14 лет
Уровень испытания
Какие пары зубцов позволяют цветному зубу касаться каждого зуба на другом зубце? Какие пары этого не допустят? Почему?
Зажги огни снова
Возраст от 7 до 11 лет
Уровень испытания
Каждый свет в этом интерактиве включается согласно правилу.Что происходит, когда вы вводите разные числа? Сможете ли вы найти наименьшее число, при котором загораются все четыре лампочки?
Следуй за числами
Возраст от 7 до 11 лет
Уровень испытания
Что происходит, когда вы складываете цифры числа, затем умножаете результат на 2 и продолжаете это делать? Вы можете попробовать разные числа и разные правила.
Любопытное число
Возраст от 7 до 11 лет
Уровень испытания
Можно ли расположить цифры от 1 до 3, чтобы получилось число, которое делится на 3, чтобы после удаления последней цифры оно превратилось в двухзначное число, делящееся на 2, и так далее?
Фактор Трек
Возраст от 7 до 14 лет
Уровень испытания
Factor Track — это не гонка, а игра мастерства.Идея состоит в том, чтобы объехать трассу за как можно меньше ходов, соблюдая правила.
Итак, время!
Возраст от 7 до 14 лет
Уровень испытания
Как вы решите, какой способ переворота и / или поворота сетки даст вам наибольшее количество очков?
Квадратное вычитание
Возраст от 7 до 11 лет
Уровень испытания
Посмотрите, что происходит, когда вы берете число, возводите его в квадрат и вычитаете свой ответ. Какой у вас номер? Вы можете доказать это?
Гамельнский крысолов
Возраст от 7 до 11 лет
Уровень испытания
Изучите различное количество людей и крыс, которое могло бы быть, если бы вы знали, сколько всего у них ног!
Умножить на 1
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы завершить этот расчет, заполнив недостающие числа? Сколько разных способов вы можете это сделать?
Умножить на 2
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы придумать несколько различных способов сбалансировать это уравнение?
Умножить на 3
Возраст от 7 до 11 лет
Уровень испытания
Попытайтесь уравновесить это уравнение.Можете ли вы найти разные способы сделать это?
Представьте свой метод
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы сопоставить эти методы расчета с их визуальным представлением?
Сравните расчеты
Возраст от 7 до 11 лет
Уровень испытания
Можете ли вы расположить эти четыре вычисления в порядке сложности? Как вы решили?
Y Вы также можете быть заинтересованы в этой подборке упражнений с веб-сайта STEM Learning, которые дополняют действия NRICH, указанные выше.
Дивизион ÷ | Основы арифметики
На этой странице представлены основные сведения о Дивизионе (÷) .
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение ( + ), Вычитание (-) и Умножение ( × ).
Дивизион
Обычный письменный символ деления — (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).
Деление — это противоположность умножения в математике.
Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять расчеты деления. Когда мы хорошо разбираемся в методе и правилах, мы можем без ошибок использовать калькулятор для более сложных вычислений.
Дивизион позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте посмотрим, как мы можем найти ответ на 10 ÷ 2 (десять, разделенные на два). Это то же самое, что «разделить» 10 сладостей между 2 детьми.У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ — 5.
Некоторые быстрые правила о делении:
Если вы разделите 0 на другое число, ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 сладостей, разделенных поровну между 2 детьми — каждый ребенок получает 0 сладостей.
Когда вы делите число на 0, вы вообще не делите (это большая проблема в математике). 2 ÷ 0 невозможно.У вас есть 2 сладости, но нет детей, чтобы разделить их между собой. Нельзя делить на 0.
При делении на 1 ответ будет таким же, как и число, которое вы делили. 2 ÷ 1 = 2. Две сладости, разделенные на одного ребенка.
Когда вы делите на 2, вы делите это число вдвое. 2 ÷ 2 = 1.
Любое число, разделенное на такое же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет, разделенных на двадцать детей — каждый ребенок получает по одной конфете.
Номера должны быть разделены в правильном порядке.10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять сладостей, разделенных на двоих детей, очень отличаются от двух сладостей, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ — это 1 ÷ 2. Одна конфета, разделенная на двоих детей. См. Нашу страницу Дроби для получения дополнительной информации.
Множественное вычитание
Так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.
Например:
Если у Джона есть 10 галлонов топлива в машине и он использует 2 галлона в день, сколько дней до того, как он закончится?
Мы можем решить эту проблему, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.
- В день 1 Джон начинает с 10 галлонов и заканчивается 8 галлонов. 10-2 = 8
- В день 2 Джон начинает с 8 галлонов и заканчивается 6 галлонов. 8-2 = 6
- В день 3 Джон начинает с 6 галлонов и заканчивается 4 галлонов. 6 — 2 = 4
- В день 4 Джон начинает с 4 галлонов и заканчивается 2 галлонов. 4–2 = 2
- В день 5 Джон начинает с 2 галлонов и заканчивается 0 галлонами. 2–2 = 0
У Джона заканчивается топливо на 5-й день.
Более быстрый способ выполнить этот расчет — разделить 10 на 2. То есть сколько раз 2 уходит в 10 или сколько партий по два галлона в десяти галлонах? 10 ÷ 2 = 5.
Таблица умножения (см. Умножение) может помочь нам найти ответ на простые вычисления деления.
В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (заштрихованный красным заголовок).Двигайтесь вниз по столбцу, пока не найдете искомый номер: 10 . Переместитесь по строке влево, чтобы увидеть ответ (заштрихованный красным заголовок) 5 .
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Мы можем выполнить другие простые вычисления деления, используя тот же метод.Например, 56 ÷ 8 = 7 . Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .
Если возможно, вам следует попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет решение простых вычислений умножения и деления.
Деление больших чисел
Вы можете использовать калькулятор для вычисления деления, особенно когда вы делите большие числа, которые труднее вычислить в уме.Однако важно понимать, как выполнять расчеты деления вручную. Это полезно, когда у вас нет под рукой калькулятора, но также важно для того, чтобы вы правильно использовали калькулятор и не допускали ошибок. Деление может показаться устрашающим, но на самом деле, как и в большинстве арифметических операций, оно логично.
Как и всю математику, проще всего понять, если мы рассмотрим пример:
Машине Дэйва нужны новые шины. Ему нужно заменить все четыре шины на машине, а также запасную.
Дэйв получил предложение от местного гаража на сумму 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?
Задача, которую нам нужно вычислить, — это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 перейдет в 480?
Условно мы пишем это как:
Мы работаем слева направо в логической системе.
Мы начинаем с деления 4 на 5 и сразу же решаем задачу. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.
Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 переходит в 4?».
Мы знаем, что 2 дважды переходит в 4 (4 ÷ 2 = 2), и мы знаем, что 1 переходит в 4 четыре раза (4 ÷ 1 = 4), но 5 не переходит в 4, потому что 5 больше 4.
Число, на которое мы делим (в данном случае 5), должно войти в число, на которое мы делим (в данном случае 4) целое количество раз. Как вы увидите, это необязательно должно быть точное целое число.
Поскольку 5 не переходит в 4, мы помещаем 0 в первый столбец (сотни). Для получения справки о столбцах сотен, десятков и единиц см. Нашу страницу с номерами .
| Сот | Десятки | Квартир | |
| 0 | |||
| 5 | 4 | 8 | 0 |
Затем мы переместимся вправо, чтобы включить столбец десятков.Теперь мы можем увидеть, сколько раз 5 переходит в 48.
5 переходит в 48, так как 48 больше 5. Однако нам нужно выяснить, сколько раз оно идет.
Если мы обратимся к нашей таблице умножения, то увидим, что 9 × 5 = 45 и 10 × 5 = 50 .
48 , число, которое мы ищем, находится между этими двумя значениями. Помните, что нас интересует целое число , умноженное на , что 5 переходит в 48. Десять раз — это слишком много.
Мы видим, что 5 переходит в 48 целое число (9) раз, но не совсем точно, с оставшимися 3.
9 × 5 = 45
48-45 = 3
Теперь мы можем сказать, что 5 делится на 48 девять раз, но с остатком 3. Остаток — это то, что остается, когда мы вычитаем найденное число из числа, на которое делим: 48-45 = 3 .
Итак, 5 × 9 = 45, + 3, чтобы получить 48.
Мы можем ввести 9 в столбец десятков в качестве ответа для второй части расчета и поставить остаток перед нашим последним числом в столбце единиц.Наше последнее число становится 30.
| Сот | Десятки | Квартир | |
| 0 | 9 | ||
| 5 | 4 | 8 | 30 |
Теперь разделим 30 на 5 (или узнаем, сколько раз 5 делится на 30). Используя нашу таблицу умножения, мы можем увидеть, что ответ — ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
| Сот | Десятки | Квартир | |
| 0 | 9 | 6 | |
| 5 | 4 | 8 | 30 |
Так как остатков нет, расчет закончен и мы получили ответ 96 .
Новые шиныДэйва будут стоить фунтов стерлингов 96 каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .
Отдел рецептов
Наш последний пример деления основан на рецепте. Часто во время готовки рецепты сообщают вам, сколько еды они собираются приготовить, например, чтобы накормить 6 человек.
Ингредиенты, указанные ниже, необходимы для изготовления 24 сказочных лепешек, однако мы хотим приготовить только 8 сказочных лепешек. Мы немного изменили ингредиенты для удобства этого примера (оригинальный рецепт на сайте BBC Food).
Первое, что нам нужно установить, это сколько восьмерок в 24 — используйте приведенную выше таблицу умножения или свою память.3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Следовательно, нам нужно разделить каждый ингредиент, указанный ниже, на 3, чтобы получить правильное количество смеси, чтобы сделать 8 сказочных лепешек.
Состав
- 120 г сливочного масла, размягченного при комнатной температуре
- 120 г сахарной пудры
- 3 яйца от кур на свободном выгуле, слегка взбитые
- 1 чайная ложка ванильного экстракта
- 120 г муки самоподнимания
- 1-2 столовые ложки молока
Масло сливочное, сахар и мука все одинаковые, 120гр.Следовательно, необходимо всего один раз проработать 120 ÷ 3, поскольку для этих трех ингредиентов ответ будет одинаковым.
Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, так как 3 больше 1. Затем мы смотрим, сколько умноженных на 3 получается 12. Используя таблицу умножения при необходимости мы можем увидеть, что 3 переходит в 12 ровно 4 раза по без остатка.
120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г масла, сахара и муки.
Исходный рецепт требует 3 яйца, и мы снова делим на 3. Итак, 3 ÷ 3 = 1, поэтому необходимо одно яйцо.
Следующий рецепт требует 1 чайная ложка (чайная ложка) ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 то же самое, что third (одна треть). Вам понадобится чайной ложки ванильного экстракта, хотя на самом деле сложно точно отмерить чайной ложки!
Оценка может быть полезной, а единицы измерения можно менять!
Мы можем взглянуть на это с другой стороны, если знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам.(Если вам нужна помощь с единицами измерения, см. Нашу страницу о системах измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 делится на 5 один раз (3), а 2 остается. 2 ÷ 3 — это то же самое, что и so, поэтому 5 мл, разделенное на 3, дает 1 ⅔ мл, что в десятичных дробях составляет 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, немного больше полутора миллилитров. Если у вас на кухне есть крошечные мерные ложки, вы можете быть очень точными!
Мы можем оценить ответ, чтобы убедиться, что мы правы.Три партии по 1,5 мл дают нам 4,5 мл. Итак, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшие оценки могут быть забавой и хорошей практикой для нашей ментальной арифметики.
Следующий рецепт требует 1-2 ст. Л. Молока. Это от 1 до 2 столовых ложек молока. У нас нет точного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.
Мы уже знаем, что 1 ÷ 3 — это, а 2 ÷ 3 -.Поэтому нам понадобится – столовой ложки молока, чтобы испечь восемь сказочных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому – столовой ложки равно 5–10 мл, что соответствует 1–2 чайным ложкам!
Связь между умножением и делением
Математика — очень логичная наука, построенная на правилах, принципах и отношениях. Математическое мышление основано на последовательном изучении процедур сначала с конкретными объектами, затем с визуальными моделями и только потом с абстрактными символами и понятиями.Такой систематический подход к обучению позволяет учащимся понять смысл математических операций и связь между ними.
Начиная с 3-го класса, «Счастливые числа» дают пошаговые объяснения умножения и деления, их связи со сложением и вычитанием, которые учащиеся освоили ранее, и того, как применять эти операции. Кроме того, студенты изучают связь между умножением и делением, поскольку эти операции обратны друг другу. Впоследствии они укрепляют и развивают эти знания при решении различных задач.В этой статье рассматривается, как Happy Numbers помогает учащимся изучить взаимосвязь между умножением и делением, чтобы они могли свободно выполнять эти операции.
1. Связанные факты об умножении и делении
Связь деления на число с умножением на одно и то же число
Самый простой способ установить связь между умножением и делением на интуитивном уровне — использовать модель массива, которая в равной степени подходит для обеих операций.«Счастливые числа» предлагает серию упражнений, которые приводят учащихся к концептуальному пониманию этой взаимосвязи.
В первом упражнении учащиеся сопоставляют факты умножения и деления, соответствующие одной и той же модели массива. Каждая из трех задач начинается с разделения. Например, на снимке экрана ниже показан третий массив, а результаты первых двух сохраняются в правом верхнем углу:
Если учащиеся отвечают неправильно, следующая подсказка напоминает им об интерпретации деления, которая позволяет им найти ответ:
Следующий шаг — завершение предложения умножения на основе того же представления массива:
Теперь студенты смотрят на результаты трех заданий и приходят к важному предположению:
Чтобы просмотреть упражнение полностью, перейдите по этой ссылке.
Деление на 3 связано с умножением на 3. Не только это, но и отношение верно для любого числа: Деление на число связано с умножением на то же число .
Это делает утверждение «Деление связано с умножением» более конкретным и может быть дополнительно детализировано, чтобы стать незамедлительно используемым инструментом.
Связанные факты умножения и деления состоят из связанных одинаковыми числами
Чтобы детализировать установленную выше взаимосвязь, Happy Numbers предлагает упражнения, привлекающие внимание студентов к числам, участвующим в двух операциях (делении и умножении), соответствующих одной и той же модели массива:
Учащиеся выделяют три пары чисел, и эта цветовая кодировка помогает составить утверждение:
Это утверждение затем позволяет студентам заполнить факты умножения, связанные с данным фактом деления.Например:
В случае неправильного ответа ученики получают напоминание:
В этих задачах используется один бланк, однако его размещение может быть разным. Он может быть в любом уравнении и в любом положении. Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Таким образом, учащиеся понимают, что оба связанных уравнения состоят из одних и тех же чисел. Это добавляет важную деталь к ранее установленным отношениям, и вместе они описывают очень практический факт:
Деление на число связано с умножением на одно и то же число.Два связанных уравнения состоят из одних и тех же чисел.
Пример: 14 ÷ 2 = 7, 7 × 2 = 14
Это подробное описание взаимосвязи между умножением и делением позволяет учащимся составить уравнение деления, связанное с данным уравнением умножения, и наоборот.
Чтобы привыкнуть к взаимосвязи, студенты работают над простыми задачами в пределах 100 : для данного уравнения деления они находят соответствующее уравнение умножения в таблице умножения.
Это делается в два этапа. Ответ на первую часть задания…
… позволяет учащимся ограничить поиск связанных фактов умножения таблицей умножения для одного числа (2 в этом примере).
В вышеуказанных упражнениях учащиеся не выполняют умножение или деление; вместо этого они развивают математическое мышление, чтобы обнаружить взаимосвязь между этими типами фактов, что поможет им решать проблемы в будущей деятельности.
Деление на 100 на основе связи между умножением и делением
К настоящему времени студенты искали только факт умножения, связанный с с учетом факта деления , и пришло время рассмотреть более практический случай, когда результат деления неизвестен.
Happy Numbers представляет эту задачу так, что она очень похожа на предыдущую с заданным фактом деления. Это помогает студентам понять, что связь между умножением и делением остается применимой и здесь:
… и соответствующий факт умножения можно найти в соответствующей таблице умножения (× 3 в этом примере):
Есть важная подсказка для тех, кому это нужно:
На приведенном выше снимке экрана другие коэффициенты в таблице умножения на 3 скрыты, чтобы подчеркнуть, что соответствующее предложение умножения можно идентифицировать без какой-либо информации об этом коэффициенте.
Итак, родственные предложения:
Здесь результат деления и один из множителей на самом деле являются одним и тем же числом , поэтому знание одного из них означает также знание другого:
Зная основной факт умножения 4 × 3 = 12, сразу следует, что 12 ÷ 3 равно 4.Чтобы просмотреть упражнение полностью, перейдите по этой ссылке.
Та же стратегия работает для поиска фактов деления, связанных с основными фактами умножения (то есть умножения двух однозначных чисел). Рассмотрим, например, умножение и деление на 7. В учебной программе «Счастливые числа» учащиеся сначала работают с фактами умножения × 7, а затем применяют взаимосвязь между делением и умножением для деления.Здесь подсказка напоминает им о взаимосвязи между умножением и делением:
В случае неправильного ответа предоставляется дальнейшая поддержка:
Студенты получают дополнительную поддержку при необходимости: таблицу × 7 можно сделать доступной, нажав кнопку справки.
Здесь достигается двойная цель: усвоение основных фактов и понимание взаимосвязи между умножением и делением.
Две пары связанных фактов умножения и деления
Для дальнейшего развития понимания учащимися этой взаимосвязи «Счастливые числа» вводит факт умножения, такой как 3 × 8 = 24, и показывает, как взаимосвязь между умножением и делением приводит к факту деления 24 ÷ 8 = 3.
Стоит упомянуть, что существует еще одна пара связанных фактов, состоящих из тех же трех чисел. Это связано с коммутативным свойством умножения: факты умножения в двух парах просто поменяли местами множители.Например:
3 × 8 = 24 8 × 3 = 24Каждое из уравнений умножения имеет свой собственный факт деления.
Эти пары фактов представляют собой обратные операции: первая — умножение на 8 и деление на 8, другая — умножение на 3 и деление на 3.Итак, отношения внутри каждой пары очень близкие, а все четыре факта связаны. Студенты узнают, что делитель в факте деления и один из факторов в факте умножения одинаковы. Кроме того, оба уравнения состоят из одних и тех же трех чисел.
2. Деление как проблема неизвестного фактора
Толкование и определение подкласса
В начальной школе деление обычно вводится с учетом двух его интерпретаций: нахождения количества групп и нахождения количества предметов в каждой группе.Оба они используют равное распределение объектов между несколькими группами, в то время как каждая интерпретация затрагивает свой вопрос.
Начнем с интерпретации деления как , находим количество групп , когда даны количество объектов в каждой группе и общее количество. Рассмотрим, например, задание из учебной программы «Счастливые числа»:
.Количество групп (ящиков) можно найти делением 10 ÷ 2 = ▢. При этом задачу можно представить и решить в виде уравнения для неизвестного количества групп: ▢ × 2 = 10.
Другая интерпретация деления — это нахождение количества объектов в каждой группе , когда даны общее количество и количество групп. Например:
Как и в предыдущем примере, неизвестное число можно найти любым способом: делением 12 ÷ 4 = ▢ или решением уравнения для неизвестного числа объектов в каждой группе: 4 × ▢ = 12. Из-за коммутативности При умножении коэффициенты можно поменять местами, чтобы неизвестный коэффициент оказался в первой позиции ▢ × 4 = 12, как и в первой интерпретации.
Таким образом, в обеих интерпретациях неизвестное можно найти, решив уравнение в той же форме:
▢ × делитель = дивиденд
, несмотря на различное значение неизвестного (количество групп или количество объектов в каждой группе). Итак, не имеет значения, какая из двух интерпретаций используется. Например, 120 ÷ 8: оба подразумевают одно и то же уравнение ▢ × 8 = 120 для нахождения частного. Две интерпретации разделения согласованы!
Дело в том, что нахождение неизвестного фактора на самом деле является определением подразделения .Точнее:
— Отдел находит неизвестный множитель из уравнения ▢ × делитель = делимое
или другими словами:
— Результат деления — это число, умноженное на делитель, чтобы получить дивиденд.
Прежде всего, это означает, что любой известный факт умножения дает факт деления. Например, зная, что 25 × 6 = 150, человек знает, что 150 ÷ 6 = 25. Этот источник фактов деления очень полезен до тех пор, пока студенты не овладеют стандартным алгоритмом деления.Фактически, мы использовали эту стратегию ранее для установления фактов деления, соответствующих основным фактам умножения в пределах 100.
Наиболее важным в понимании деления как нахождения неизвестного фактора является то, что оно охватывает все случаи деления действительных чисел, включая деление любого целого числа, даже если оно не приводит к частному целому числу.
Дробь как результат деления целых чисел
Не всегда можно разделить целые числа и получить результат целого числа (при делении на остаток получается пара целых чисел , а не единичное число ).Итак, набор целых чисел и операция деления расширены, чтобы это стало возможным. В игру вступают дроби, и интерпретация деления на основе равного распределения показывает, что результатом деления может быть дробь. Например, в задании из учебной программы «Счастливые числа» учащиеся делят 3 пирожных поровну на 4 тарелки
.Они работают в интерактивном режиме со всей необходимой поддержкой, чтобы получить следующий результат:
Выполнение ряда аналогичных заданий приводит учащихся к разумному выводу, что:
Результатом деления целого числа делимого на целое число делителя является дробьЛегко прийти к такому выводу, если понимать разделение как обнаружение неизвестного фактора.Давайте проверим, например, что 5, разделенное на 9, равно 5 ⁄ 9 . С точки зрения поиска неизвестного фактора это означает: убедитесь, что 5 ⁄ 9 удовлетворяет уравнению
▢ × 9 = 5, что верно: 5 ⁄ 9 × 9 = 5.
Умножение и деление как обратные операции
Часто говорят, что умножение и деление — обратные операции, но что именно это означает? Фактически, это сводится к полезному утверждению, которое является просто еще одним способом выразить взаимосвязь между умножением и делением, как обсуждалось выше.
Рассмотрим, например, деление числа m на 7. Соотношение между умножением и делением говорит о том, что умножение результата m ÷ 7 на делитель дает дивиденд m :
( м ÷ 7) × 7 = мИтак, , если число делится на 7, умножение частного на 7 отменяет деление на 7 , или для краткости: умножение на 7 является обратной операцией для деления на 7.На самом деле это верно для любого числа n ≠ 0 вместо 7:
Умножение на n отменяет деление на n ( n ≠ 0)Верно и наоборот:
Деление на n отменяет умножение на n ( n ≠ 0)Эти утверждения интуитивно понятны и полезны. Например, умножение на 10 (или более, обычно на соответствующую степень 10) с последующим делением упрощает умножение десятичной дроби до умножения целого числа:
Начиная с исходного выражения 3 × 2.3, студенты преобразовали его, умножив десятичный множитель на 10. Это также означает, что произведение умножается на 10 из-за ассоциативного свойства. Теперь ученики делят на 10, чтобы отменить умножение и таким образом получить требуемый исходный продукт.
Эта стратегия также применима к умножению и делению двух десятичных чисел.
Проверка деления с умножением
Это занятие с двойной целью.Первая цель — это, конечно, проверка расчета, что особенно важно, когда разделение «сложное» или когда вводятся новые приложения. Это довольно «сложно», если, например, деление в столбик выглядит так:
Решение можно проверить, проверив, истинно ли 957 × 3 = 2,871.
Пример нового применения деления — введение деления дроби на целое число.
Проверка результата 2 ÷ 1 ⁄ 3 = 6 путем проверки правильности 6 × 1 ⁄ 3 = 2 здесь важна для усиления концептуального понимания деления.
Возможный подход к задачам дробного деления
Сила отношения умножения / деления простирается за пределы начальной школы. Учащиеся 6 классов и старше могут использовать уравнение умножения с неизвестным фактором в качестве стратегии для решения задач деления на дроби. Давайте рассмотрим этот подход для двух стандартных типов задач со словами и задач с числовым делением.
Давайте начнем со словарной задачи, основанной на интерпретации деления как , нахождение неизвестного размера акций , когда указаны количество акций и общая сумма.
Это похоже на проблему с заданными целыми числами. Например, «Джим прополз 6 ярдов, что было 3 из его обычных ежедневных поездок. Как долго длится обычная ежедневная поездка? » Интерпретируется как проблема с заданной суммой — 6, заданным количеством акций — 3 и неизвестным размером доли . Исходная проблема часто интерпретируется таким же образом, хотя общая сумма является дробным числом (что неудивительно), а количество долей дробное. Студенты должны привыкнуть к последнему, что возможно на примере использования долей, таких как 2-галлонный резервуар: 1 галлон — это половина его, четверть галлона — это одна восьмая его объема и т. Д.
Задача решается разделением 1 ⁄ 2 ÷ 3 ⁄ 4 = ▢, при этом фактическое решение основано на модели, представляющей 1 ⁄ 2 как 2 ⁄ 4 и деление как 2 ⁄ 4 ÷ 3 ⁄ 4 = 2 ÷ 3 = 2 ⁄ 3 . Упрощение данных дробей до общего знаменателя работает для любой задачи деления на дроби. Однако это дополнительный шаг, от которого студенты могут научиться избавляться позже, когда умножение на обратную дробь заменяет прямое деление.
Давайте теперь рассмотрим альтернативную стратегию решения вышеуказанной проблемы.
Постановка задачи немедленно переводится как «Найдите всю длину поездки ▢, учитывая, что 3 ⁄ 4 из нее равны 1 ⁄ 2 ярдов». Поскольку 3 ⁄ 4 из ▢ равно 3 ⁄ 4 × ▢, это проблема неизвестного фактора
. 3 ⁄ 4 × ▢ = 1 ⁄ 2, относящееся (эквивалент) к задаче деления 1 ⁄ 2 ÷ 3 ⁄ 4 = ▢.
Чтобы найти неизвестный коэффициент, достаточно выделить out в уравнении
3 ⁄ 4 × ▢ = 1 ⁄ 2 . Этого легко добиться, умножив обе части уравнения на величину, обратную величине 3 ⁄ 4 , то есть на 4 ⁄ 3 . (Обратной величиной любой дроби является дробь, в которой числитель и знаменатель исходной дроби поменяны местами. Обратное значение дроби, умноженной на эту дробь, всегда равно 1.) Это умножение дает
и ответ на проблему:
▢ = 4 ⁄ 3 × 1 ⁄ 2 = 2 ⁄ 3Рассмотрим теперь другой тип словесной задачи.
Независимо от того, что данная сумма и размер долей являются дробными, это проблема нахождения неизвестного количества долей : 1 1 ⁄ 2 ÷ 2 ⁄ 5 = ▢.Исходная постановка проблемы также переводится в проблему с неизвестным фактором — количество долей, умноженное на размер доли, равняется заданной сумме:
▢ × 2 ⁄ 5 = 1 1 ⁄ 2В качестве альтернативы можно прийти к проблеме неизвестного фактора, начиная с проблемы деления и используя взаимосвязь между умножением и делением. Проблема неизвестного фактора решается, как указано выше, с использованием обратной дроби: 3 ⁄ 2 .
Как видите, задачи даже дробного деления можно понять и решить, связав их с умножением.
***
Happy Numbers предлагает учебную программу, в которой студенты последовательно изучают математические процедуры. Они увеличивают и углубляют знания с помощью описательных визуальных моделей, дополненных манипулятивной механикой и выразительной анимацией. Мгновенная обратная связь, интегрированная в виде подсказок, позволяет учащимся улучшить свою стратегию решения в данный момент и, таким образом, учиться на собственных ошибках.
Happy Numbers может стать отличным цифровым помощником на уроках математики! Готовы присоединиться? Зарегистрируйтесь в качестве преподавателя на сайте, чтобы начать бесплатный пробный период.
Отдел
Дивизион делится на равные части или группы.
Это результат «честного обмена».
Пример: есть 12 шоколадных конфет, и 3 друга хотят ими поделиться, как они делят шоколадные конфеты?
12 шоколадных конфет
12 шоколадных конфет, разделенных на 3
Ответ: 12 разделить на 3 равно 4.Они получают по 4 штуки.
Символы
÷ /
Мы используем символ ÷ или иногда символ / для обозначения деления:
Давайте использовать здесь оба символа, чтобы мы к ним привыкли.
Другие примеры
Вот еще несколько примеров:
Противоположность умножению
Деление — это , противоположное умножению .


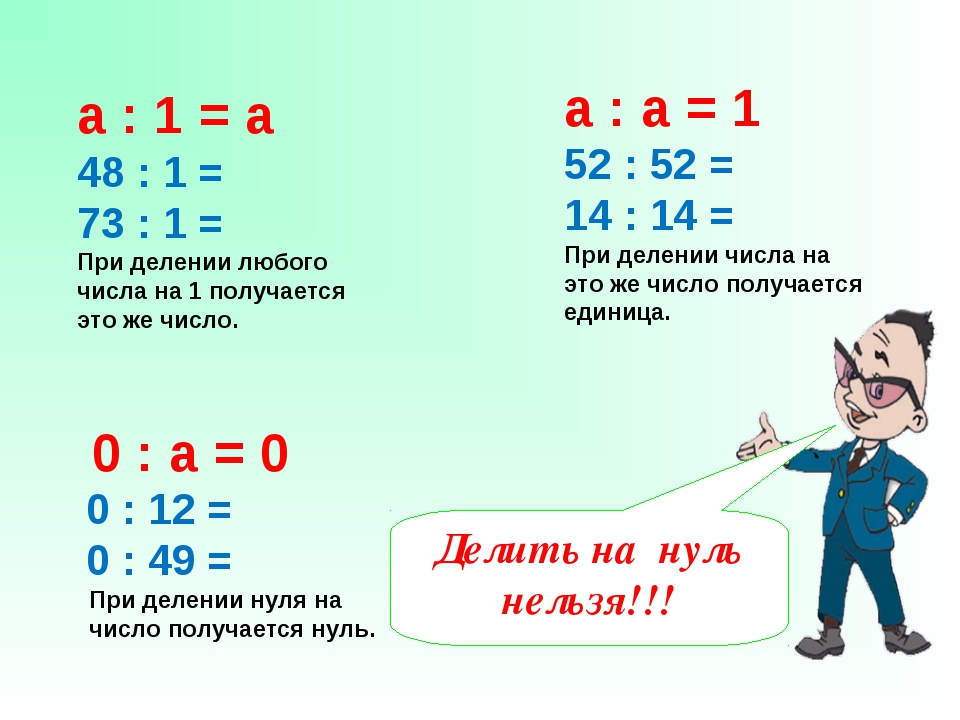 ; Просвещение, 2017. – с.80
; Просвещение, 2017. – с.80 Фрагмент по ИКТ «Соотнести понятия и их математические записи» по желанию, проверка по ключу на флипчарте,
Фрагмент по ИКТ «Соотнести понятия и их математические записи» по желанию, проверка по ключу на флипчарте,