Умножение и деление с числами 1,0. Деление нуля на число
Цель: познакомить с приёмом деления нуля на число; обобщить и закрепить знания таблицы умножения
Личностные результаты: умение анализировать результаты учебной деятельности, объяснять причины успеха или неуспеха в своей учёбе.
Оборудование: учебник «Математика 3 класс», тетради, таблички с формулами, карточки с заданиями, снежинки с заданиями и для рефлексии, новогодняя елка, компьютер и проектор, презентация.
Этапы урока | Деятельность учителя | Деятельность ученика | ||||||||||||
Организационный этап | Здравствуйте, ребята. Проверьте свою готовность к уроку, сядьте прямо. | Приветствуют учителя. | ||||||||||||
Мотивация | — Какой сейчас месяц? (декабрь) А что можно сказать о 31 декабря? (В ночь с 31 декабря на 1 января наступает Новый год!) — Кто самый желанный гость на новогоднем празднике? Конечно, Дедушка Мороз. — Ребята, посмотрите какую елочку нам принес Дедушка Мороз. Но чего-то не хватает. Даже не знаю чего. Как вы думаете? Конечно же, нам надо ее украсить. — Поможем дедушке морозу ее украсить? Для этого нам нужно выполнять разные задания на снежинках. Вы готовы отправиться в сказочную страну Деда Мороза? Для этого нам надо стать помощниками Деда Мороза. У вас на столах лежат шапочки помощников, давайте их оденем и отправимся в путешествие. — Ваша работа на уроке должна быть обязательно оценена. Поэтому для каждого из вас есть лист помощника Деда Мороза. | Отвечают на вопрос. | ||||||||||||
3. Актуализация знаний | — Снимает снежинку под номером 1. — Ребята, вы любите фокусы? — Показать вам фокус? Содержание фокуса. Попросить учеников задумать число (однозначное). Потом это число ученик должен умножить на 2, прибавить к результату 8, разделить результат на 2 и отнять задуманное число. В результате получается число 4. — Сейчас запишите число в черновиках и покажите партнеру по плечу. — Хотите услышать ответ? Ответ будет 4. — У вас получилось? Молодцы! — Оцените себя. Нарисуйте зеленый кружок в листе помощников Деда Мороза, если ошибки не было, если было — красный. Давайте вспомним, какие правила умножения на 1 и 0 мы уже изучили. ( Формулы-подсказки я повешу на доске. а ∙ 1 = а ,а ∙ 0 = 0) — Откройте свои тетради, запишите сегодняшнее число и классная работа. Снежинка № 2 Работа в группах. Расставьте примеры в 2 группы: — Почему так распределили? . Что вы заметили? Есть ли здесь лишний пример? Все ли примеры вы смогли решить? У кого возникли затруднения? Чем этот пример отличается от остальных? Если кто-то решил, то молодец. (Проверка и отметка в Листе Помощников Деда Мороза) | Отвечают дети (При умножении любого числа на 1 получается тоже самое число. При умножении любого числа на нуль получается нуль. — С ответом 4 и 5 | ||||||||||||
4. Постановка цели и задач урока. | Но почему не все смогли справиться с этим примером? — Здесь есть пример с 0. А от 0 можно ожидать разные фокусы. Это необычное число. Вспомните, что вы знаете про 0? — Посмотрите, какой он коварный: когда его прибавляют, он не изменяет число, а когда умножают, превращают его в 0. — Подходят ли эти правила к нашему примеру? — Итак, какова наша цель на этом уроке? Цель: _________________ — Что для этого надо? Задача: __________ Следовательно Тема урока:_____________ | -а·0=0, 0·а=0, 0+а=а -Нет — Цель урока: «Научиться решать такие примеры». — Задача « Узнать правило деления 0 на число» — Тема урока: «Умножение и деление с числами 1,0. Деление нуля на число». | ||||||||||||
5. Первичное усвоение новых знаний. | — Сколько получится в последнем примере? Как узнали? (Если дети ответили, то объясняют как решили. Если не ответили, то я объясняю) — Деление связано с умножением. На какое число надо умножить 9, чтобы получить 0? Вывод: При делении нуля на любое другое число, получается нуль. 0:b=0 Сравните свой вывод с тем, который есть в учебнике на стр. 85 (прочитайте и расскажите друг другу) — Итак, продолжаем выполнение заданий на снежинках. Снежинка № 3 Работа со словарем (в группе). Ребята, а вы знаете, что означает слово «Ноль»? Где мы можем узнать о значении этого слова? — Значит, какой вывод мы можем сделать? — Можно ли поделить ничего на ноль? — Какой вывод можно сделать? ПОМНИ, делить на нуль нельзя! Почему? Да потому, что какое бы число вы не умножали на 0, в ответе всегда будет 0 а:0 Физкультминутка «Снеговик» Немножко отдохнули. Продолжаем помогать Дедушке Морозу. | — На 0 (Представители групп зачитывают толкование слова ноль) — Ноль – ничего. — Нет — Ноль на число делить нельзя. | ||||||||||||
6. Первичная проверка понимания | Снежинка № 4 Работа в парах. — Кто уже чувствует в себе силу самостоятельно применить новые знания и получить звание «умников» и «умниц»? Кому нужна помощь? (Как правило, никому) — Сейчас снежинка предлагает поработать в парах. — Что нужно сделать в следующем задании? Подобрать знаки *, :, +, -. 1 вариант: 0 : 16= 16 * 0= 2 вариант 16 * 1= 16 * 0= Одна пара у доски. Проверяем по доске (взаимопроверка), оцениваем в листах Помощников Деда Мороза. (без ошибок – зеленый, 1 ошибка – желтый, 2 ошибки – красный. — Посмотрите, сколько у меня карандашей. Хотите узнать сколько? Давайте сосчитаем(48). Снежинка №5 Решение задачи. Ни один урок математики не обходится без решения задач. — Значит наша задача о чем? Решение задачи по карточкам У Маши есть 48 карандашей в коробках, 6 в каждом. Сколько у нее коробок с карандашами? А) Составление таблицы. — О чем идет речь? Какой вопрос задачи? — Прочитайте условие задачи и подумайте, как удобнее выполнить краткую запись. — Что такое 48? — 6? — Какая ещё графа должна быть в таблице? — Мы можем ответить на вопрос задачи? — Почему? — Как мы можем найти количество коробок? — Заполните таблицу, решите задачу и запишите ответ в группе.
Б) Проверка решения. 1) 48:6 = 8(кор.) Ответ: у Маши есть 8 коробок с карандашами. — Группы меняются местами и проверяют решение (по экрану). (Оценивание в листке Помощников Деда Мороза: задача решена – зеленый кружок, не решена – красный) | 1 вариант: 0:16= 0 16 *0= 0 2 вариант 16*1= 16 16*0= 0 — О карандашах — В таблице — Кол-во всех карандашей — Количество карандашей в 1 коробке — Количество коробок — Нет — Нужно найти. — Делением | ||||||||||||
7. Первичное закрепление. | Снежинка №6 Разноуровневые задания (самостоятельная работа по карточкам разного цвета) Найди ошибки, исправь и запиши правильно в свою тетрадь.
Самооценивание по образцу на экране. Доп.задача: («Проверь себя» (учебник, с. 84, 85). Проверка. Ответы записываю на доске: с. 84 — 1, 8, 12; с. 85 — 0, 0, 0.) |
| ||||||||||||
8. | 1в. Стр.85 № 6 1), № 8 (1,2 уравнения) 2в.Стр.85 № 6 2), № 8 (3,4 уравнения) | Записывают домашнее задание | ||||||||||||
9. Рефлексия (подведение итогов занятия) | — Какую цель мы сегодня поставили? — Достигли мы эту цель? -Какие правила вы узнали сегодня на уроке? -Какие правила повторили? -Какие задания ещё вызывают у вас затруднения? -За что вы можете себя похвалить? Оцените свою работу на уроке в листе Помощников Деда Мороза. Давайте нашу елочку украсим новыми снежинками. *Доволен своей работой на уроке. *Были отдельные моменты, когда я испытывал трудности. *Не доволен, много не сумел сделать. Ребята, мне очень понравилось с вами работать. Вы большие молодцы. Я вам желаю успехов. Спасибо за урок | Отвечают на вопросы — 5-6 зеленые кружочки -3-4 зеленые кружочки — 0-2 зеленые кружочки |
Умножение и деление на 1 и 0
Дружно за руки возьмемся
И друг другу улыбнемся.
А потом мы скажем дружно:
«Хорошо учиться нужно».
Познакомимся с умножением
и делением на 1 и 0,
научимся умножать
и делить на 1 и 0.
Сколько лет в яйце цыплёнку,
Сколько крыльев у котёнка,
Сколько в алфавите цифр,
Сколько гор проглотит тигр,
Сколько мышка весит тонн,
Сколько в стае рыб ворон,
Сколько зайцев съела моль,
Знает только цифра … !
Сколько лет в яйце цыплёнку,
Сколько крыльев у котёнка,
Сколько в алфавите цифр,
Сколько гор проглотит тигр,
Сколько мышка весит тонн,
Сколько в стае рыб ворон,
Сколько зайцев съела моль,
Знает только цифра НОЛЬ.
Сколько солнышек за тучкой,
Сколько стержней в авторучке,
Сколько у слона носов,
Сколько на руке часов?
Знает и собой гордится,
Цифра-столбик … .
Сколько солнышек за тучкой,
Сколько стержней в авторучке,
Сколько у слона носов,
Сколько на руке часов?
Знает и собой гордится,
Цифра-столбик ЕДИНИЦА.
0 1 2 3 4 5 6 7 8 9
Всё в математике, друзья,
Подчинено законам.
Законы эти важно знать,
Чтоб без ошибок вычислять.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
44-38= 6
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
21:7=3
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
2·4=8
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
15:3=5
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
18:9=2
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
36:9=4
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
5+2=7
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
3·3=9
0, 1, 2, Молодцы!
3, 4, 5, 6, 7, 8, 9
Что такое
умножение?
Умножение —
это сложение
одинаковых слагаемых.
Замените в следующих примерах
произведение суммой и запишите.
5·3=
5·2=
5·1=
5·0=
Проверьте себя.
5·3= 5+5+5
5·2= 5+5
5·1= ?
5·0= ?
5·1=?
1·5=1+1+1+1+1=5
Запомните!
Математический закон №1
При умножении
любого числа на 1,
получается то число,
которое умножали.
a·1= a
5·0=?
0·5=0+0+0+0+0=0
Запомните!
Математический закон №2
При умножении
любого числа на 0,
получается 0.
a·0= 0
a·1= a
·
a·0= a
·
Что такое
деление?
Деление —
это действие,
обратное умножению.
Запомните! а:а=
а:а=1
Запомните! а:1=а
а:1=
Запомните! 0:а=0
0:а=
При делении числа
на то же самое число
получается 1.
При делении числа на 1
получается то же самое число.
При делении 0 на любое число
х·5=0
х=00. 0·5=0
получается
5·1= 5
5:5= 1
5:1= 5
0:5= 0
Выполните вычисления.
91∙1=91
64+0=64
18∙0=0
1∙35=35
25+1=26
0∙36=0
72∙0=0
54∙1=54
31-0=31
0∙15=0
1∙76=76
98-1=97
Проверьте себя.
91∙1=91
64+0=64
18∙0=0
1∙35=35
25+1=26
0∙36=0
72∙0=0
54∙1=54
31-0=31
0∙15=0
1∙76=76
98-1=97
Найдите числовые выражения, при решении которых допущена ошибка.
Запишите эти выражения, сделав вычисления правильно.
1·15=15
3·0=3
19:19=1
23:1=1
26:26=1
12+0=0
17-0=17
Проверьте себя.
1·15=15
3·0=3
19:19=1
23:1=1
26:26=1
12+0=0
17-0=17
Проверьте себя.
1·15=15
3·0=0
19:19=1
23:1=1
26:26=1
12+0=0
17-0=17
Проверьте себя.
1·15=15
3·0=0
19:19=1
23:1=23
26:26=1
12+0=0
17-0=17
Проверьте себя.
1·15=15
3·0=0
19:19=1
23:1=23
26:26=1
12+0=12
17-0=17
а∙1=а
а∙0=0
а:а=1
а:1=а
0:а=0
а:0
Начальный курс алгебры 7
Начальный курс алгебры
Урок 7. Умножение и деление действительных чисел
WTAMU > Virtual Math La b > Начальная алгебра
Цели обучения
После завершения этого руководства вы сможете:
- Найдите обратное число.

- Умножить положительные и отрицательные числа.
- Разделить положительные и отрицательные числа.
- Умножить на ноль.
- Знайте, что деление на ноль не определено.
Введение
В этом руководстве рассматривается умножение и деление действительных чисел. числа и переплетения что с некоторым порядком работы и оценкой проблемы. Это также напоминает вам, что деление на 0 дает неопределенный ответ. В Другими словами, это большое нет, нет.
Я абсолютно уверен, что вы знакомы с умножение и деление, но иногда правила для отрицательных чисел (фу!) время от времени немного путаюсь. Итак, хорошо перейти их чтобы убедиться, что они у вас есть.
Учебник
Обратный мультипликатив
(или обратный)
Для каждого действительного числа а, кроме 0,
есть уникальный
реальное число такое
что
Другими словами, когда вы умножаете число на его
мультипликативный
обратный результат равен 1.
Более распространенный термин, используемый для обозначения мультипликативная обратная обратное .
Мультипликативная обратная или обратная величина действительного числа a (кроме 0) находится «переворачиванием» a вверх вниз. Числитель a становится знаменатель обратного числа на и в знаменатель числа а становится числителем принадлежащий обратное на .
Пример 1: Запишите обратную (или мультипликативную) обратный) из -3.
Обратная величина -3 равна -1/3 , так как -3(-1/3) = 1.
Когда вы берете обратное, знак оригинала
номер остается
нетронутый.
Помните, что вам нужно число, которое при умножении раз данный число, которое вы получите 1. Если вы меняете знак, когда берете взаимный, вы получите -1 вместо 1, а это нет-нет.
Пример 2: Запишите обратную (или мультипликативную) обратный) 1/5.
Обратная величина 1/5 равна 5 , так как 5(1/5) = 1.
Частное число действительных чисел
Если a и б настоящие
числа и
b не 0, тогда
Умножение или деление вещественного числа
Номера
Поскольку деление равносильно умножению на
взаимный, разделительный
и умножение имеют одинаковые правила знаков.
Шаг 1: Умножьте или
разделить их абсолютные
ценности.
Шаг 2. Введите правильный знак.
Если два числа имеют один и тот же знак , произведение или частное положительный .
Если они имеют противоположных знака , продукт или частное отрицательное .
Пример 3: Найдите произведение (-4)(3).
(-4)(3) = -12.
Произведение абсолютных значений 4 x 3 равно 12, и они иметь напротив знаков, поэтому наш ответ равен -12.
Пример
4: Найдите продукт.
*Мульт. число вместе
*мульт. ден. вместе
*(-)(-) = (+)
*Уменьшить дробь
Произведение абсолютных значений 2/3 x 9/10 равно 18/30 = 3/5 и они имеют тот же знак, поэтому мы получаем ответ 3/5.
Обратите внимание: если вам нужна помощь по дробям, перейдите к Tutorial. 3: Дроби
Пример 5: Найти продукт
Работая над этой задачей слева направо получаем:
*(3)(-2) = -6
*(-6)(-10) = 60
Пример
6: Разделить (-10)/(-2).
(-10)/(-2) = 5
Частное абсолютного значения 10/2 равно 5, и они имеют те же знаков, поэтому наш ответ равен 5.
Пример 7: Разделить.
*Разд. то же, что и мульт. к взаимный
*Множ. число вместе
*мульт. ден. вместе
*(+)(-) = —
*Уменьшить дробь
Отношение абсолютных значений 4/5 и 8 равно 4/40 =
1/10 и они
имеют противоположные знаки, поэтому наш ответ равен -1/10.
Обратите внимание: если вам нужна помощь с дробями, перейдите к Учебник 3: Дроби
Умножение на и
Деление на ноль
0 (когда a не равно 0)
Другими словами, ноль (0), умноженный на любое действительное число, равен нулю
(0) и ноль
(0), деленное на любое действительное число, кроме нуля (0), равно нулю (0).
Пример 8: Умножьте 0 (½).
0(½) = 0 .
Умножение любого выражения на 0 дает ответ от 0.
Пример 9: Разделить 0/5.
0/5 = 0 .
Деление 0 на любое выражение, отличное от 0 , дает ответ 0.
Деление на ноль
a/0 не определено
Ноль (0) не входит ни в какое число, поэтому всякий раз, когда вы
делят
нулем (0) ваш ответ не определен.
Пример 10: Разделить 5/0.
5/0 = не определено .
Деление на 0 дает неопределенный ответ.
Пример 11: Упростить.
Так как у нас есть несколько операций, происходящих в этом проблема, мы будем должны использовать порядок операций, чтобы убедиться, что мы получаем правильный отвечать.
*Оценка внутри абсолюта
значения
*Вычесть
*(-)/(-) = +
Пример
12: Оценить выражение
если x = -2 и y = — 4.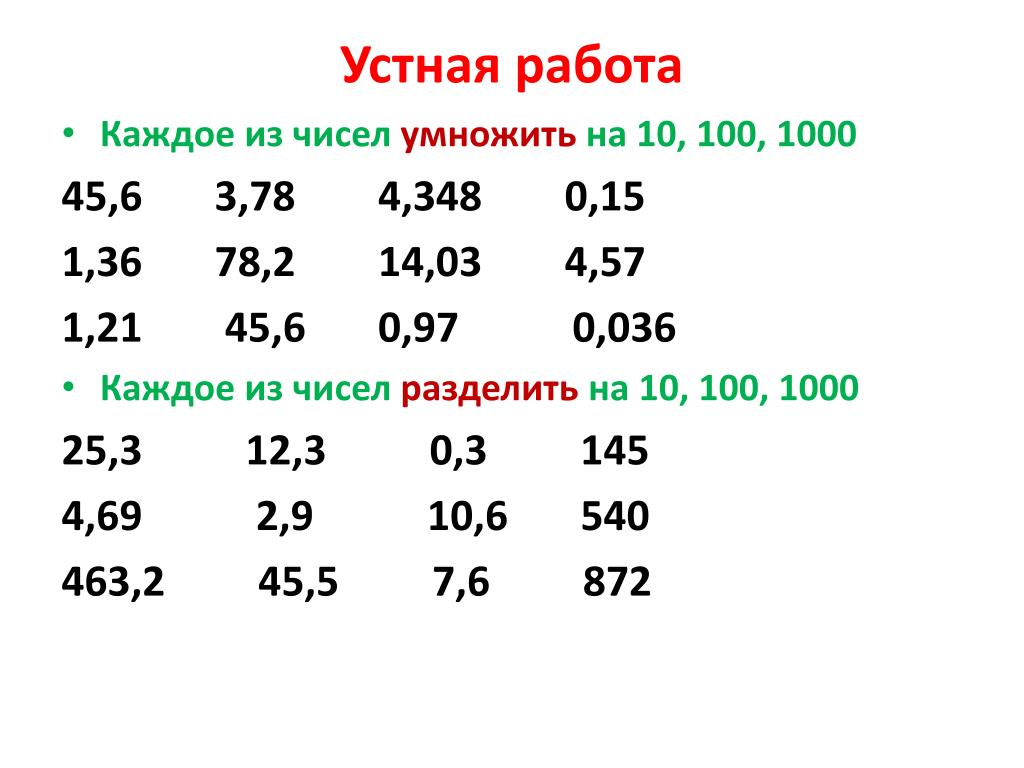
Для просмотра оценка выражение перейдите к Уроку 4: Введение в переменные выражения и уравнения.
Заглушка -2 для x и — 4 для и и упрощая получаем:
*Подставьте -2 для x и -4 для y
*Экспонента
*Умножьте
*Добавьте 9 0004
Практические задачи
Это практические задачи, которые помогут вам
следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы
эти
виды проблем. Математика работает так же, как
что-либо
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этого, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой задачи . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1а — 1в: Умножить.
1а. (-2)(-25)
(ответ/обсуждение
к 1а)
1б. (0)(-100)
(ответ/обсуждение
к 1б)
1в. (-2)(3)(5)
(ответ/обсуждение
к 1с)
Практика Задачи 2а — 2в: Разделить.

2а.
(ответ/обсуждение
к 2а)
2б.
(ответ/обсуждение
до 2b)
2c.
(ответ/обсуждение
к 2с)
Практика Задача 3а: Упростить.
3а.
(ответ/обсуждение
к 3а)
Практика Задача 4a: Оцените выражение, когда x = 5 и y = -5.
4а.
(ответ/обсуждение
к 4а)
Нужна дополнительная помощь по этим темам?
Следующие веб-страницы
что может помочь
вас в темах, которые были освещены на этой странице:
http://www. mathleague.com/help/integers/integers.htm#multiplyingintegers
mathleague.com/help/integers/integers.htm#multiplyingintegers
Эта веб-страница поможет вам умножить целые числа.
http://www.mathleague.com/help/posandneg/posandneg.htm#
умножение положительных и отрицательных чисел
Эта веб-страница посвящена умножению положительных и отрицательных чисел.
вместе.
http://www.mathleague.com/help/integers/integers.htm#dividingintegers
Эта веб-страница посвящена делению целых чисел.
http://www.mathleague.com/help/posandneg/posandneg.htm#
деление положительных и отрицательных чисел
Эта веб-страница посвящена делению положительных и отрицательных чисел.
Перейти к получению
Помощь за пределами
Классная комната в Учебнике 1: Как добиться успеха на уроке математики для
некоторый
больше предложений.
WTAMU > Виртуальная математическая лаборатория > Начальная алгебра
Последняя редакция Ким Сьюард от 25 июля 2011 г.
Авторское право на все содержимое (C) 2001–2011, WTAMU и Ким Сьюард. Все права защищены.
Почему деление на ноль не определено
Почему деление на ноль неопределенно Перейти к основному содержанию Перейти к основной навигации Перейти к нижнему колонтитулу В этом видео мы собираемся выяснить, почему деление на ноль не определено. Но сначала нам нужно ознакомиться с определением деления. Определение деления гласит, что если «а», деленное на «b», равно «с», а «с» уникально, то «b», умноженное на «с», равно «а». Итак, давайте что-нибудь сделаем — разделим два известных нам числа. Итак, допустим, что 6 разделить на 2 равно 3. Мы все можем с этим согласиться. Обратите внимание, мы можем сказать, что «c» уникален. 3 уникально, потому что мы знаем, что 3 — это единственное число, которое равняется 6, деленному на 2. Мы также можем выяснить, что означает вторая часть. Если мы умножим наше «b» на «с», то мы должны получить «а». Таким образом, наше «b» равно 2, умноженному на «c», что равно 3, равно «a», что равно нашим 6. Оба эти условия выполняются. Итак, это означает, что 6, деленное на 2, действительно равно 3. И мы также можем сказать, что это «определено», потому что оно удовлетворяет полному определению деления. Точно так же, если он удовлетворяет только одной части определения, это будет означать, что он «не определен». Давайте посмотрим на примеры с нулем в них и посмотрим, что с ними происходит. Итак, позвольте мне прояснить это, и давайте начнем с нуля, деленного на 1. Я собираюсь сказать, что это равно нулю, потому что 1, умноженный на ноль, равно нулю. Это удовлетворяет этой второй части определения.
Итак, допустим, что 6 разделить на 2 равно 3. Мы все можем с этим согласиться. Обратите внимание, мы можем сказать, что «c» уникален. 3 уникально, потому что мы знаем, что 3 — это единственное число, которое равняется 6, деленному на 2. Мы также можем выяснить, что означает вторая часть. Если мы умножим наше «b» на «с», то мы должны получить «а». Таким образом, наше «b» равно 2, умноженному на «c», что равно 3, равно «a», что равно нашим 6. Оба эти условия выполняются. Итак, это означает, что 6, деленное на 2, действительно равно 3. И мы также можем сказать, что это «определено», потому что оно удовлетворяет полному определению деления. Точно так же, если он удовлетворяет только одной части определения, это будет означать, что он «не определен». Давайте посмотрим на примеры с нулем в них и посмотрим, что с ними происходит. Итак, позвольте мне прояснить это, и давайте начнем с нуля, деленного на 1. Я собираюсь сказать, что это равно нулю, потому что 1, умноженный на ноль, равно нулю. Это удовлетворяет этой второй части определения. И эта первая часть, если вы подставите, скажем, 1, 2 или любое другое число, тогда оно не будет равно этому, поэтому мы можем фактически сказать, что «с» уникален. Таким образом, это удовлетворяет тому, что это на самом деле единственное число, которое вы можете положить туда, чтобы фактически равняться нулю. Мы можем сказать, что ноль, деленный на 1, равен нулю, и мы также можем сказать, что это также «определено». Наш следующий пример будет делением 1 на ноль. И многим нравится гадать, что это будет ноль. Итак, давайте попробуем это. Мы берем наше «b», которое равно нулю, и умножаем его на наше «c», которое равно нулю. Мы не понимаем, что такое «а», потому что, конечно, ноль, умноженный на ноль, не равен 1. Так что это не удовлетворяет этой части уравнения. Поскольку он не удовлетворяет хотя бы одной части этого определения, это означает, что он считается «неопределенным». Так что это не работает, и это означает, что он будет «неопределенным». Теперь, для нашего следующего примера, иногда мы сталкиваемся с этой идеей, когда у нас на самом деле ноль делится на ноль.
И эта первая часть, если вы подставите, скажем, 1, 2 или любое другое число, тогда оно не будет равно этому, поэтому мы можем фактически сказать, что «с» уникален. Таким образом, это удовлетворяет тому, что это на самом деле единственное число, которое вы можете положить туда, чтобы фактически равняться нулю. Мы можем сказать, что ноль, деленный на 1, равен нулю, и мы также можем сказать, что это также «определено». Наш следующий пример будет делением 1 на ноль. И многим нравится гадать, что это будет ноль. Итак, давайте попробуем это. Мы берем наше «b», которое равно нулю, и умножаем его на наше «c», которое равно нулю. Мы не понимаем, что такое «а», потому что, конечно, ноль, умноженный на ноль, не равен 1. Так что это не удовлетворяет этой части уравнения. Поскольку он не удовлетворяет хотя бы одной части этого определения, это означает, что он считается «неопределенным». Так что это не работает, и это означает, что он будет «неопределенным». Теперь, для нашего следующего примера, иногда мы сталкиваемся с этой идеей, когда у нас на самом деле ноль делится на ноль. Что ж, я думаю, все мы можем согласиться с тем, что мы, очевидно, можем поставить там ноль, и вторая часть будет определена. Поскольку у нас есть ноль, который представляет собой наше «b», умноженное на ноль, что является нашим «с», это равно нашему «а», которое равно нулю. Итак, эта часть работает. Ну, мы также можем поставить 5, если захотим, потому что ноль умножить на 5 равно нулю, так что это все еще работает для второй части. Мы действительно можем подключить туда что угодно. Мы можем сказать, что ноль над нулем равен х. У нас все еще есть нуль, умноженный на x, равный нулю. Но я имею в виду, что это первая часть, которая не удовлетворена. Потому что если мы можем сказать, что ноль, 5 или вообще любое число, это означает, что это «с» не уникально. Итак, в этом сценарии первая часть не работает. Итак, это означает, что это будет undefined. Таким образом, ноль, деленный на ноль, не определен. Итак, давайте назовем это так. Убедитесь, что когда вы сталкиваетесь с чем-то подобным, когда вы делите на ноль, убедитесь, что вы не записываете фактическое число или переменную вниз.
Что ж, я думаю, все мы можем согласиться с тем, что мы, очевидно, можем поставить там ноль, и вторая часть будет определена. Поскольку у нас есть ноль, который представляет собой наше «b», умноженное на ноль, что является нашим «с», это равно нашему «а», которое равно нулю. Итак, эта часть работает. Ну, мы также можем поставить 5, если захотим, потому что ноль умножить на 5 равно нулю, так что это все еще работает для второй части. Мы действительно можем подключить туда что угодно. Мы можем сказать, что ноль над нулем равен х. У нас все еще есть нуль, умноженный на x, равный нулю. Но я имею в виду, что это первая часть, которая не удовлетворена. Потому что если мы можем сказать, что ноль, 5 или вообще любое число, это означает, что это «с» не уникально. Итак, в этом сценарии первая часть не работает. Итак, это означает, что это будет undefined. Таким образом, ноль, деленный на ноль, не определен. Итак, давайте назовем это так. Убедитесь, что когда вы сталкиваетесь с чем-то подобным, когда вы делите на ноль, убедитесь, что вы не записываете фактическое число или переменную вниз.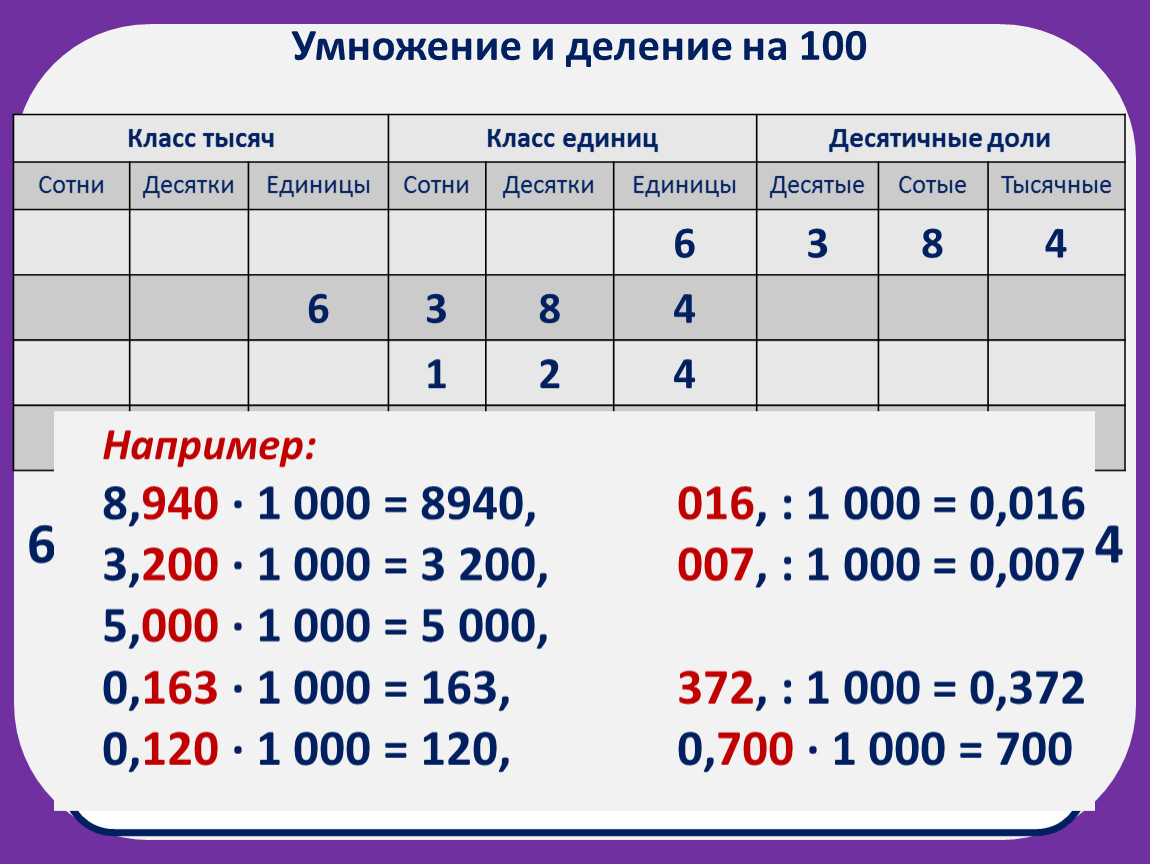

 В течении всего урока вы будете выполнять задания и оценивать себя (подписать фамилию и имя).
В течении всего урока вы будете выполнять задания и оценивать себя (подписать фамилию и имя).
 )
)


 )
)


 Информация о домашнем задании, инструктаж по его выполнению
Информация о домашнем задании, инструктаж по его выполнению

