Умножение дроби на целое число — Мегаобучалка
Следующим действием изучается умножение дроби на целое число. Умножение дроби на целое число определяется так же, как умножение целых чисел.
При изучении умножения дроби на целое число необходимо установить с учащимися определение действия умножения дроби на целое число как сложения равных слагаемых, из которых каждое равно множимому; показать тождественность умножения дроби на целое увеличению дроби в несколько раз, дать определение умножения дроби на 1; показать рациональный прием сокращения дроби, числитель которой представляет произведение, с которым учащиеся встречаются впервые при умножении дроби на целое; научить применять это действие к задачам; рассмотреть частные случаи умножения, например, умножение дроби на число, равное знаменателю; умножение смешанного числа на целое число. Приведенный перечень задач, стоящих при изучении умножения дроби на целое число, показывает, что каждый вопрос, кажущийся простым, требует тщательного изучения и как много возникает дополнительных задач в связи с данным вопросом.
Приведем пример плана урока на эту тему,
1) Проверка домашнего задания.
2) Устные упражнения на сложение и вычитание дробей.
3) Устные примеры на деление произведения на число:
4) Сокращение дробей:
5) Повторение определения умножения на целое число:
6) Определение умножения дроби на целое число:
7) Решение задач в одно действие на умножение дроби на целое »»
число. Например: 1 м3 сосновых дров весит т. Найти вес 2м3 этих
дров (в тоннах), 7 м3.
8) Сформулировать правило умножения дроби на целое число:
чтобы умножить дробь на целое число, достаточно числитель дроби умножить на это число, оставив прежний знаменатель.
9) Решение примеров на умножение дроби на целое число:
10) Составить задачи, при решении которых требовалось бы умножить.
11) Домашнее задание.
Приведенные в этом плане устные упражнения на деление произведения на число и сокращение дробей имеют цель подготовить учащихся к обоснованию сокращения дробей, в числителе которых стоит произведение. Учащиеся вспоминают, как разделить произведение на число и при сокращении дробей ведут следующие рассуждения: чтобы сократить дробь, надо числитель и знаменатель разделить на одно и то же число; в числителе стоит произведение; чтобы произведение разделить на число, достаточно один из множителей разделить на это число. Поэтому при сокращении дроби делим 10 и 25 на 5.
Учащиеся вспоминают, как разделить произведение на число и при сокращении дробей ведут следующие рассуждения: чтобы сократить дробь, надо числитель и знаменатель разделить на одно и то же число; в числителе стоит произведение; чтобы произведение разделить на число, достаточно один из множителей разделить на это число. Поэтому при сокращении дроби делим 10 и 25 на 5.
На следующем уроке следует предложить учащимся на нескольких примерах умножения дроби на целое число сравнить множимое и произведение по величине. Установить, что для дробей, как и для целых чисел, увеличить дробь в несколько раз — значит умножить ее на целое число. На основании рассмотрения примеров вида
делается вывод об изменении величины дроби с увеличением числителя или уменьшением знаменателя в данное число раз и дается частный прием умножения дроби на целое число, годный для случая, когда знаменатель дроби делится на данное целое число:
При изучении умножения смешанного числа на целое вначале рассматриваются два способа. Например:
Например:
Последние рассуждения показывают справедливость распределительного закона умножения относительно суммы, когда одно из слагаемых дробь. Рассматривается пример вида
и делается вывод, что при умножении смешанного числа на целое в большинстве случаев проще отдельно умножить целое и дробь на целое число.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление com/groups/DPVA.ru»>Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||
Умножение дроби на целое число
В этом уроке мы будем умножать дробь на целое число, включая смешанные числа и отрицательные значения.
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Тест:
Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!
Q1.В долях от миллиона, насколько больше людей проживает в Лидсе, чем Халл и Уэйкфилд вместе взятые?ABCD
В2. В магическом квадрате каждая строка, столбец и диагональ имеют одинаковую сумму. Что должно заменить вопросительный знак?ABCD
Q3. Периметр этого прямоугольника равен 12 м. Какая ширина (все измерения в метрах)?ABCD
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Тест:
Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!
Вот быстрый тест!
ABCD
Q2. В магическом квадрате каждая строка, столбец и диагональ имеют одинаковую сумму. Что должно заменить вопросительный знак?ABCD
Q3. Периметр этого прямоугольника равен 12 м. Какая ширина (все измерения в метрах)?ABCD
Эти слайды помогут вам выполнить некоторые задания урока. Если вам нужно повторно воспроизвести видео, нажмите значок «Возобновить видео». Если вас попросят добавить ответы на слайды, сначала загрузите или распечатайте рабочий лист. После того, как вы выполнили все задачи, нажмите «Далее» ниже.
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Тест:
Умножение дроби на целое число, включая смешанные числа и отрицательные значения.
Q1.Каков правильный ответ на это умножение?ABCD
Q2.Каков правильный ответ на это умножение, записанное как смешанное число в его простейшей форме?ABCD
Q3. Каков правильный ответ на это умножение, записанное как смешанное число в его простейшей форме?
Каков правильный ответ на это умножение, записанное как смешанное число в его простейшей форме?ABCD
Q4.Каков правильный упрощенный ответ на это умножение?ABCD
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Тест:
Умножение дроби на целое число, включая смешанные числа и отрицательные значения.
Q1.Каков правильный ответ на это умножение?ABCD
Q2.Каков правильный ответ на это умножение, записанное как смешанное число в его простейшей форме?ABCD
Q3.Каков правильный ответ на это умножение, записанное как смешанное число в его простейшей форме?ABCD
Q4.Каков правильный упрощенный ответ на это умножение?ABCD
Похоже, вы не прошли один из тестов.
Чтобы поделиться своими результатами с учителем, пройдите один из тестов.
Знаете ли вы, что упражнения помогают вашей концентрации и способности к обучению?
На 5 минут. ..
..
Перемещение:
Подниматься по лестнице
На месте:
Танцы
Расписание предметов
Рациональные отношения (числа со знаком, включая дроби)
Напомним, что целые числа — это положительные и отрицательные целые числа и ноль. Когда дроби и завершающие или повторяющиеся десятичные знаки между целыми числами включены, полная группа чисел называется
Числовая строка, показывающая целые числа и дроби.
Дроби могут быть как положительными, так и отрицательными. Отрицательные дроби обычно записываются следующим образом:
.Хотя они все равны.
Правила для знаков при сложении целых чисел применимы и к дробям. Помните: Чтобы складывать дроби, нужно сначала получить общий знаменатель.
Помните: Чтобы складывать дроби, нужно сначала получить общий знаменатель.
Добавьте следующее.
Правила для знаков при сложении целых чисел применимы и к смешанным числам.
Добавьте следующее.
Правила знаков при вычитании целых чисел применимы и к дробям. Помните: Чтобы вычесть дроби, вы должны сначала получить общий знаменатель.
Вычтите следующее.
Правила знаков при вычитании целых чисел применимы и к смешанным числам. Помните: Чтобы вычесть смешанные числа, вы должны сначала получить общий знаменатель. Если необходимо заимствование из колонки, будьте осторожны с простыми ошибками.
Вычтите следующее.
Задачи, подобные предыдущим, обычно проще всего решать, складывая число с большим абсолютным значением сверху, вычитая и сохраняя знак числа с большим абсолютным значением.
Правила знаков при умножении целых чисел применимы и к дробям. Помните: Чтобы умножить дроби, умножьте числители, а затем умножьте знаменатели. Всегда упрощайте до минимума, если это возможно.
Умножьте следующее.
Вы можете отменить при умножении положительных и отрицательных дробей. Просто отмените, как при умножении положительных дробей, но обратите особое внимание на соответствующие знаки. Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Помните: Отсутствие знака означает, что положительный знак понятен.
Умножьте следующее.
Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Помните: Прежде чем умножать смешанные числа, вы должны сначала преобразовать их в неправильные дроби.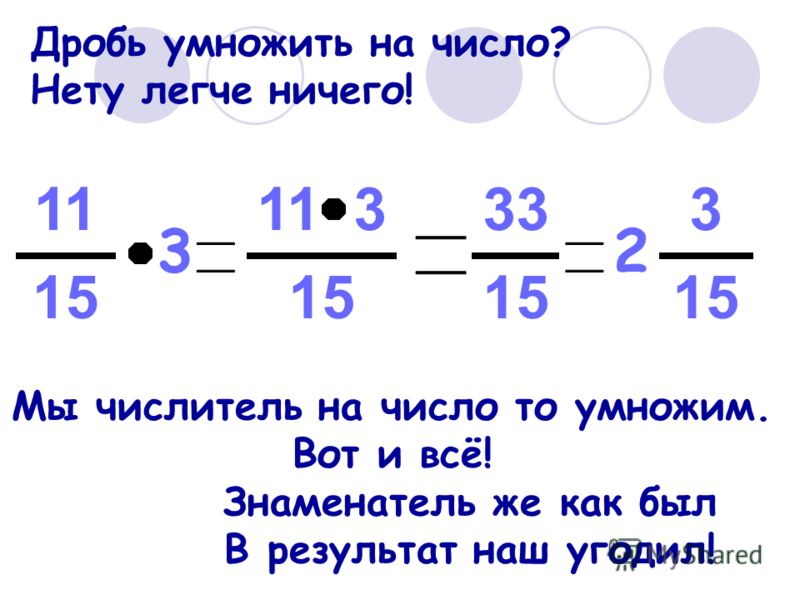

 Введите свой запрос:
Введите свой запрос: