Обыкновенные дроби и действия с ними — что это, определение и ответ

Доля – это часть от целого.

Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).

Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)

Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.

Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.

ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:

Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).

Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.

Например:

\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)

\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)

\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:

1. Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.

\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)

Например:

\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)

\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)

2. Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:

\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)

Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.

Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.

АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:

1. Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.

2. Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.

3. Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.

4. Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.

Например:

\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:

1. Обратные числа:

Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:

\(\frac{a}{1} = a : 1 = a\)

Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).

Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.

2. Умножение дробей:

Представим умножение дроби на число как сумму дробей:

\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)

Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:

\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)

3. Деление дробей:

Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.

Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:

\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)

Таким же образом делят дроби на дроби:

\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)

Презентация к уроку на тему:» Умножение дробей» 6 класс | Презентация к уроку по математике (6 класс):

Опубликовано 29.08.2019 — 14:08 — Сизова Юлия Сергеевна

Материал для урока.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Умножение дробей 6 класс Учитель: Сизова Ю.С.

Слайд 2

Какая часть фигуры закрашена? 3 2 4 3 8 7 9 8 ответ ответ ответ ответ

Слайд 3

Умножение обыкновенных дробей 5 5 4 • 7 = 5 4 • 7 = 5 28 = 5 3 НА НАТУРАЛЬНОЕ ЧИСЛО Правило ПРАВИЛО: чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения.

Слайд 4

Умножение обыкновенных дробей 7 4 • = • НА ДРОБЬ Правило ПРАВИЛО: чтобы умножить дробь на дробь, надо: найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем. 11 3 4 3 7 • 11 = 12 77

Слайд 5

СМЕШАННЫХ ЧИСЕЛ Умножение обыкновенных дробей • = • ПРАВИЛО: для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. 5 3 = 13 9 9 4 1 3 • 18 5 9 13 18 • 5 = 13 • • 1 2 5 = 26 5 = 5 1 5 Правило

Слайд 6

Выполни умножение 1) 2) 3) 4) = 15 28 = 16 33 = 24 65 = 15 56 3 4 5 7 · 12 1 3 2 5 · 2 3 8 11 · 5 8 3 7 · для проверки нажать =

Слайд 7

Подсказка 1 5 2 3 • 1 3 1 = 4 2 5 3 2 11 4 • = 22 5 = 1 2 3 4 • 1 2 1 = 6 5 11 3 • = 33 8 = 4 1 8 ответ ответ решение решение

Слайд 8

Математический диктант I вариант II вариант = 1 8 = 3 20 = 4 15 = 3 14 = = 2 3 = 2 3 = 8 25 = 2 15 = 7 12 3 14 1) · 2) 11 25 15 44 · 14 15 5 7 1) · 3) 13 20 16 39 · 4) 7 26 39 49 · 5) 8 9 15 16 6 25 · · 3) 22 35 28 55 · 2) 17 19 38 51 · 5) 7 8 12 49 14 15 · · 4) 18 25 5 27 · 1 5 1 5

Слайд 9

Справочный материал

По теме: методические разработки, презентации и конспекты

Презентация к уроку по теме «Умножение обыкновенных дробей»

Предназначена  для  урока  повторения  по  теме  «Умножение обыкновенных  дробей». ..

Презентация для урока по теме «Умножение двучлена на двучлен». 7 класс.

Презентацию можно использовать на стандартном уроке при объяснении и закреплении материала по данной теме….

Презентация к уроку по теме «Умножение и деление обыкновенных дробей»

Обобщение материала по теме «Умножение и деление обыкновенных дробей». Урок математики в 6-м классе. Данный урок позволяет формировать навыки выполнения арифметических действий с обыкновенными др…

Презентация к уроку по теме «Умножение десятичных дробей»

Данный урок проводиться в 5 классе по учебнику Виленкина Н.Я….

Презентация к уроку по теме «Умножение обыкновенных дробей», 6 класс

Данная презентация может быть использована при изучении темы «Умножение обыкновенных дробей» на уроках математике в 6 классе с целью ознакомления с новым материалом….

Презентация к уроку на тему: » Умножение десятичных дробей» 5 класс

Материал для урока….

Презентация к уроку по теме «Умножение рациональных чисел; урок 1»

Данная презентация посвящена началу изучения темы «Умножение рациональных чисел» и может быть использована для первого ознакомительного урока по данной теме. В презентации представлены:1. Пра…

Поделиться:

 

Умножение дробей Рабочие листы

1. Рабочие листы >
2. Математика >
3. Предварительная алгебра >
4. Дроби >
5. Умножение

Пройдите наши бесплатные рабочие листы по умножению дробей и выйдите победителем, умножая дроби с нюансами! Широкий выбор печатных форм, оснащенных ключами для ответов, помогает учащимся выполнять умножение дробей путем умножения дробей с использованием визуальных моделей, взаимного исключения и тематических задач; нахождение недостающих дробей; и более. Имея в своем распоряжении эти рабочие листы для умножения дробей, дети превосходят свои собственные установленные стандарты, вычисляя произведение дробей, смешанных чисел и целых чисел в два раза быстрее.

Наши инструменты для подготовки PDF-файлов подходят для учащихся 4, 5, 6 и 7 классов.

CCSS: 4. NF, 5.NF

Умножение дробей с использованием визуальных моделей печатные рабочие листы по умножению дробей помогают детям отличиться, блестяще выполняя умножение дробей с использованием числовых линий и других красочных иллюстраций.

Умножение дробей на числовом ряду

Что может быть лучше, чем числовые ряды, чтобы научить детей умножать дроби и целые числа? Начните свою тренировку с наших бесплатных рабочих листов, изучите прыжки и интервалы на диаграммах числовых линий и получите продукт!

Эксклюзивные онлайн-рабочие листы

Умножение единичных дробей на целые числа

В качестве первого шага к пониманию умножения дробей выполните эти упражнения на умножение единичных дробей и целых чисел. Запишите целые числа вместо числителя единичных дробей и упростите полученные таким образом дроби.

Умножение дробей на целые числа

После того, как учащиеся поймут основы умножения дробей на целые числа, уже не оглядываться назад! Помните, что нужно умножить целое число на числитель дроби, а знаменатель оставить как есть.

Умножение смешанных чисел на целые числа

Найдите набор бесплатных рабочих листов в формате PDF на умножение дробей, включающих смешанные числа и целые числа. Преобразуйте смешанное число в дробь и легко найдите произведение. Рекомендуется для детей 5-6 классов.

Умножение дробей | Рабочий лист №1

Чему равно произведение 2/3 и 4/5? Это 8/15! Решайте похожие упражнения и побейте рекорд, улучшив свои навыки умножения дробей. Числители и знаменатели в каждой задаче меньше 20, так что вы легко стартуете.

Умножение дробей | Рабочий лист № 2

Вот отличный дополнительный ресурс, часть наших бесплатных рабочих листов по умножению дробей, который помогает учащимся 4, 5 и 6 классов постепенно улучшать свои баллы, поэтому вычисление произведений двух дробей не составляет труда.

Умножение дробей путем перекрестного сокращения

Как бы просто ни было умножение дробей, вот кое-что, что сделает его еще проще: умножение дробей после перекрестного сокращения. Посмотрите, как юные ученики гордятся вами, определяя и вычеркивая кратные по диагонали в каждой паре дробей!

Умножение смешанных чисел

Благодаря нашим ресурсам умножение смешанных чисел не только не должно быть пугающим занятием, но и дети будут преобразовывать смешанные числа в дроби и находить произведения в два раза быстрее. Сократите ответ до наименьших условий везде, где это необходимо.

Умножение дробей. Сложные задачи. Листы

Внесите прилив энергии в свои математические занятия с этой обширной коллекцией рабочих листов по умножению дробей, наполненных увлекательными, энергичными задачами. Оставьте детей в напряжении с этим набором, и они будут размножаться, как ни в чем не бывало!

Умножение трех дробей

Этот рабочий лист по умножению трех дробей в формате pdf требует, чтобы дети находили произведение трех дробей и по возможности приводили к наименьшим числам. Добавьте к разнообразию, грандиозности и интриге свою практику умножения!

Умножение смешанных чисел и дробей | Рабочий лист №1

Пусть ученики 5-го, 6-го и 7-го классов удивят вас, перемножая смешанные числа и дроби со всеми ружьями! Преобразуйте смешанное число в неправильную дробь и продолжайте вычислять две дроби, как обычно.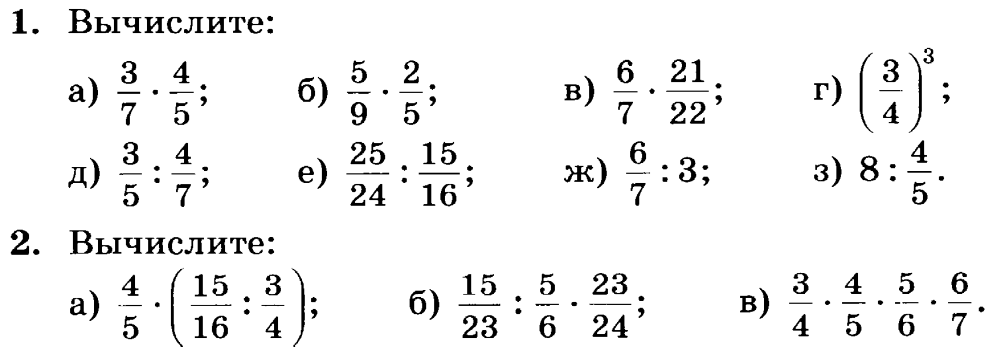

Умножение смешанных чисел и дробей | Рабочий лист № 2

Предложите учащимся попрактиковаться в этом печатном рабочем листе умножения дробей, который состоит из смешанных чисел и дробей, и вдохнуть новую жизнь, особенно в их вычислительные навыки. Используйте ключи ответов, чтобы проверить их решения.

Найдите недостающие дроби | Рабочий лист №1

Пусть ребенок не ошибется, когда столкнется с уравнениями умножения дробей! Этот бесплатный рабочий лист в формате pdf «Найди недостающие дроби», где дети заполняют недостающие дроби, чтобы закончить заданные уравнения, оставляет позади кучу умных и свежих учеников.

Найдите недостающие дроби | Рабочий лист № 2

Помогите учащимся 5-го, 6-го и 7-го классов умножить произведение на обратное заданному множителю или множителю, чтобы найти недостающие дроби. Завершение уравнений умножения должно стать гудящим с большим количеством действий!

6 класс Умножение дробей Рабочие листы с ответами

Умножение дробей упражнения для шестого класса

6-й класс Умножение дробей Рабочие листы с ответами — Умножение дробей Упражнения

состоят из следующих математических навыков для детей: умножение дроби с целыми числами, дроби числа словесные задачи, оценка произведений дробей и целых чисел , умножение двух дробей, умножение дробей, текстовые задачи, масштабирование целых чисел на дроби, масштабирование целых чисел на смешанные числа, умножение трех или более дробей и целых чисел, оценка произведений дробей, смешанных чисел и целых чисел, умножение смешанных чисел.

6

^th РАСПЕЧАТКИ ПО МАТЕМАТИКЕ

Лучшее из БЕСПЛАТНЫХ 6

^{-го класса} Рабочие листы по математике Категории

• • Целые числа
  • Умножение
  • Отдел
  • Показатель степени и квадратный корень
  • Теория чисел
  • Десятичные числа
  • Сложение и вычитание десятичных знаков
  • Умножение и деление десятичных дробей
  • Дроби и смешанные числа
• • Сложение и вычитание дробей
  • Умножение дробей
  • Разделить дроби
  • Целые числа
  • Операции с целыми числами
  • Смешанные операции
  • Рациональные числа
  • Решение проблем
  • Соотношение и пропорции
• • Проценты
  • Измерительные блоки
  • Денежная математика
  • Бытовая математика
  • Определение времени
  • График координат
  • Алгебраические выражения
  • Одношаговые уравнения
  • Решение и построение графиков неравенств
• • Двухшаговые уравнения
  • 2D-геометрия
  • Симметрия и трансформация
  • 3D-фигуры
  • Измерение геометрии
  • Данные и графики
  • Статистика
  • Вероятность

• ВСЕ 6

  КЛАССА ДЛЯ ЕЖЕДНЕВНЫХ ЗАДАНИЙ

  6

  Быстрая письменная ежедневная
         Math Practices
  • Тип ресурса: Печатные издания, Математические центры
  • Формат: Zip | 834 страницы
    2000+ вопросов с решениями
  • Цена: $75

   

• БЕСПЛАТНО 6

  ^-й КЛАСС ОНЛАЙН-ПРАКТИКА

Важные факты об умножении дробей для 6 класса

Укрепите свои навыки умножения и дроби 6 ^-го -классника с оригинальным запасом рабочих листов умножения дробей с ответами .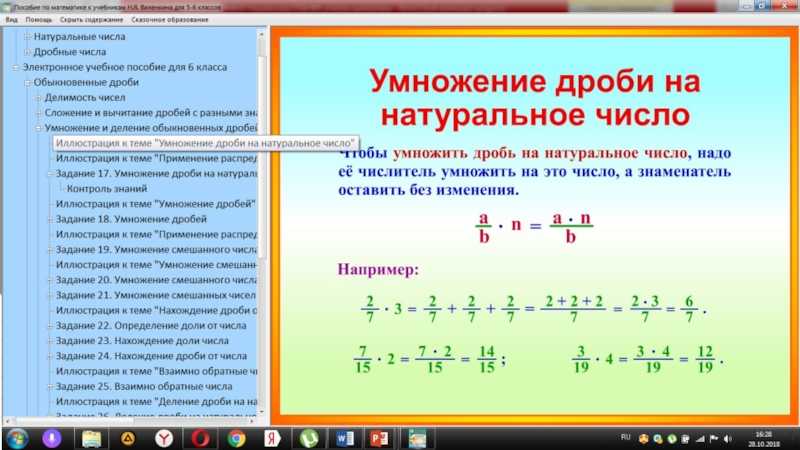 Наши упражнения на умножение дробей помогут вашим детям научиться самым простым способам умножать дроби целых чисел, умножать две дроби с помощью моделей, решать задачи на умножение дробей; умножать три и более дроби и целые числа и многие другие.

Эти интерактивные занятия помогут вашим детям развить математические способности, а также быстро освоить более сложные математические понятия, такие как предварительная алгебра, геометрия, даже тригонометрия и т. д. Тем не менее, это отличные навыки, жизненно важные для вашего ребенка. будущий математический успех ребенка.

Как помочь своим детям научиться эффективно умножать дроби?

В заявке , чтобы помочь вашим детям научиться эффективно умножать дроби , мы создали так много забавных дизайнов и упражнений, которые углубят чувство дроби вашего ребенка.

Одним из таких упражнений в нашем содержании является дробь с использованием моделей .