Действия с дробями: правила, примеры, решения

Данная статья рассматривает действия над дробями. Будут  сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида AB, где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.

Правила выполнения действий с числовыми дробями общего вида

Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 35, 2,84, 1+2·34·(5-2), 34+782,3-0,8, 12·2, π1-23+π, 20,5ln 3, то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.

Определение 1

Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:

• При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: ad±cd=a±cd, значения a, c и d≠0 являются некоторыми числами или числовыми выражениями.
• При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями.  Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
• При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим ab·cd=a·cb·d, где a, b≠0, c, d≠0 выступают в роли действительных чисел.
• При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: ab:cd=ab·dc.

Обоснование правил

Определение 2

Существуют следующие математические моменты, на которые следует опираться при вычислении:

• дробная черта означает знак деления;
• деление на число рассматривается как умножение на его обратное значение;
• применение свойства действий с действительными числами;
• применение основного свойства дроби и числовых неравенств.

С их помощью можно производить преобразования вида:

ad±cd=a·d-1±c·d-1=a±c·d-1=a±cd;ab±cd=a·pb·p±c·rd·r=a·ps±c·es=a·p±c·rs;ab·cd=a·db·d·b·cb·d=a·d·a·d-1·b·c·b·d-1==a·d·b·c·b·d-1·b·d-1=a·d·b·cb·d·b·d-1==(a·c)·(b·d)-1=a·cb·d

Примеры

В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.

Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.

Пример 1

Даны дроби 82,7 и 12,7, то по правилу необходимо числитель сложить, а знаменатель переписать.

Решение

Тогда получаем дробь вида 8+12,7. После выполнения сложения получаем дробь вида 8+12,7=92,7=9027=313. Значит, 82,7+12,7=8+12,7=92,7=9027=313.

Ответ: 82,7+12,7=313

Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:

82,7+12,7=8027+1027=9027=313

Пример 2

Произведем вычитание из 1-23·log23·log25+1 дроби вида 233·log23·log25+1.

Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что

1-23·log23·log25+1-233·log23·log25+1=1-2-233·log23·log25+1

Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.

Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.

Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.

Пример 3

Рассмотрим на примере сложения дробей 235+1 и 12. 

Решение

В данном случае общим знаменателем выступает произведение знаменателей. Тогда получаем, что 2·35+1. Тогда при выставлении дополнительных множителей имеем, что к первой дроби он равен 2, а ко второй 35+1. После перемножения дроби приводятся к виду 42·35+1.

Общее приведение 12 будет иметь вид 35+12·35+1. Полученные дробные выражения складываем и получаем, что

235+1+12=2·22·35+1+1·35+12·35+1==42·35+1+35+12·35+1=4+35+12·35+1=5+352·35+1

Ответ: 235+1+12=5+352·35+1

Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет.  В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.

Пример 4

Рассмотрим на примере 16·215 и 14·235, когда их произведение будет равно 6·215·4·235=24·245. Тогда  в качестве общего знаменателя берем 12·235.

Рассмотрим примеры умножений дробей общего вида.

Пример 5

Для этого необходимо произвести умножение 2+16 и 2·53·2+1. 

Решение

Следую правилу, необходимо переписать и в виде знаменателя написать произведение числителей. Получаем, что 2+16·2·53·2+12+1·2·56·3·2+1.  Когда дробь будет умножена, можно производить сокращения для ее упрощения. Тогда 5·332+1:1093=5·332+1·9310.

Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:

5·332+1:1093=5·332+1·9310

 После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что

5·332+1:1093=5·33·9310·2+1=5·210·2+1=32·2+1==3·2-12·2+1·2-1=3·2-12·22-12=3·2-12

Ответ: 5·332+1:1093=3·2-12

Данный пункт применим, когда число или числовое выражение может быть представлено в виде дроби, имеющую знаменатель, равный 1, тогда и действие с такой дробью рассматривается отдельным пунктом. Например, выражение 16·74-1·3 видно, что корень из 3 может быть заменен другим 31 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 16·74-1·3=16·74-1·31.

Выполнение действие с дробями, содержащими переменные

Правила, рассмотренные в первой статье , применимы для действий с дробями, содержащими переменные. Рассмотрим правило вычитания, когда знаменатели одинаковые.

Необходимо доказать, что A, C и D (D не равное нулю) могут быть любыми выражениями, причем равенство AD±CD=A±CD равноценно с его областью допустимых значений.

Необходимо взять набор переменных ОДЗ. Тогда  А, С, D должны принимать соответственные значения a0, c0 и d0.  Подстановка вида AD±CD приводит разность  вида a0d0±c0d0, где по правилу сложения получаем формулу вида a0±c0d0. Если подставить выражение A±CD, тогда получаем ту же дробь вида a0±c0d0. Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A±CD и AD±CD считаются равными.

При любом значении переменных данные выражения будут равны, то есть их называют тождественно равными. Значит это выражение считается доказываемым равенством вида AD±CD=A±CD.

Примеры сложения и вычитания дробей с переменными

Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это  незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.

Пример 6

Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.

Решение

1. Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2.  После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
2. Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:​​​​​​lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
   Сложение было выполнено. Видно, что можно произвести сокращение дроби.  Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2из формул сокращенного умножения. Тогда получаем, что
   lg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x
3.  Заданные дроби вида x-1x-1+xx+1 с разными знаменателями. После преобразования можно перейти к сложению.

Рассмотрим двоякий способ решения.

Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида

x-1x-1=x-1(x-1)·x+1=1x+1

Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.

В таком случае необходимо избавляться от иррациональности в знаменателе.

Получим:

1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1

Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда

x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1

Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.

В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби.

Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей  с добавлением дополниетльных множителей к числителям.

Пример 7

Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x

Решение

1.  Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
2. Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться  произведение вида x5·ln2x+1·2x-4. Отсюда x4
    является дополнительным множителем к первой дроби, а ln(x+1) ко второй. После чего производим вычитание и получаем, что:
   x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)
3.  Данный пример имеет смысл при работе со знаменателями дробями. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2.  Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.

После чего получаем, что

1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2

Ответ:

1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.

Примеры умножения дробей с переменными

При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.

Пример 8

Произвести умножение дробей x+2·xx2·ln x2·ln x+1 и 3·x213·x+1-2sin2·x-x.

Решение

Необходимо выполнить умножение. Получаем, что

x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)==x-2·x·3·x213·x+1-2×2·ln x2·ln x+1·sin (2·x-x)

Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x2, тогда получим выражение вида

3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x)

Ответ: x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)=3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x).

Деление

Деление у дробей аналогично умножению, так как первую дробь умножают на вторую обратную. Если взять к примеру дробь x+2·xx2·ln x2·ln x+1 и разделить на 3·x213·x+1-2sin2·x-x, тогда это можно записать таким образом, как

x+2·xx2·ln x2·ln x+1:3·x213·x+1-2sin(2·x-x), после чего заменить произведением вида x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)

Возведение в степень

Перейдем к рассмотрению действия с дробями общего вида с возведением в степень. Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей.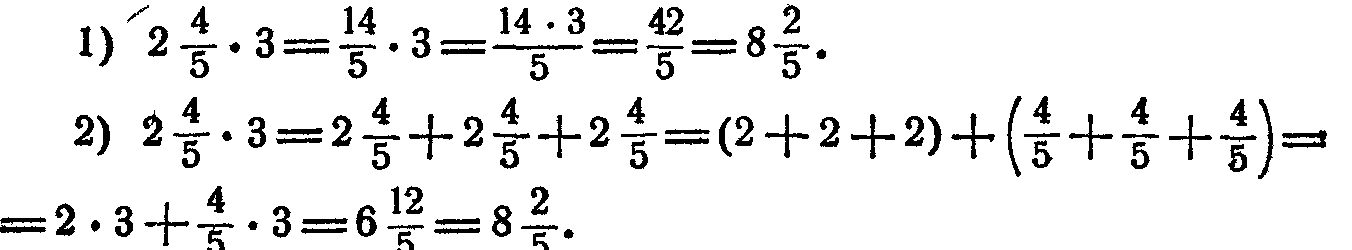 Но рекомендовано  использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:

x0,7-π·ln3x-2-5x+12,5==x0,7-π·ln3x-2-52,5x+12,5

Порядок выполнения действий с дробями

Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять  в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.

Пример 9

Вычислить 1-xcos x-1cos x·1+1x.

Решение

Так как имеем одинаковый знаменатель, то 1-xcos x и 1cos x, но производить вычитания по правилу нельзя, сначала выполняются действия в скобках, после чего умножение, а потом сложение. Тогда при вычислении получаем, что

1+1x=11+1x=xx+1x=x+1x

При подстановке выражения  в исходное получаем, что 1-xcos x-1cos x·x+1x. При умножении дробей имеем: 1cos x·x+1x=x+1cos x·x. Произведя все подстановки, получим 1-xcos x-x+1cos x·x. Теперь необходимо работать с дробями, которые имеют разные знаменатели. Получим:

x·1-xcos x·x-x+1cos x·x=x·1-x-1+xcos x·x==x-x-x-1cos x·x=-x+1cos x·x

Ответ: 1-xcos x-1cos x·1+1x=-x+1cos x·x.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

методика и ее реализация, примеры решения задач

Математика

12.11.21

13 мин.

Расчеты выполняются не только с натуральными целыми числами, но и с дробными. На уроках математики в 6 классе примеры умножения обыкновенных дробей изучаются более подробно. Для правильного вычисления необходимо применить определенную методику, которую разработали специалисты для этой цели. Они рекомендуют сначала приобрести базовые знания, а затем перейти к их практической реализации.

Оглавление:

• Общие сведения
• Виды обыкновенных дробей
• Работа со смешанными числами
• Правила сокращения
• Алгоритм умножения

Общие сведения

Процесс нахождения произведения двух обыкновенных дробных тождеств очень прост. Однако существуют «подводные камни», которые могут вызвать много ошибок. Чтобы этого не случилось, необходимо руководствоваться специальным алгоритмом, который предлагают ведущие преподаватели-специалисты.

Обыкновенная дробь имеет два компонента — числитель и знаменатель. Первый находится вверху и называется делимым, а второй — внизу. Последний называется делителем. Следует отметить, что дробный вид — представление частного, т. е. результата операции деления. Эта форма записи применяется для читабельной формы, поскольку иногда одно число не делится на другое.

Например, при делении 2 на 3 образуется десятичная бесконечная периодическая дробь. Ее можно записать в таком виде: 0,(6). Скобки означают, что число 6 повторяется бесконечное количество раз, так обозначается периодичность.

Однако бывают случаи, когда образуется десятичная непериодическая величина, а ее каким-то образом нужно записать с точностью до десятитысячной доли. Эта операция невозможна, поскольку после целой части будут следовать 10000 разрядов. Вот для ее записи и необходимо применять обыкновенную дробь.

Следует отметить, что умножать бесконечные непериодические дроби также проблематично. Их нужно преобразовать в обыкновенные величины, а далее применить соответствующий алгоритм. Чтобы воспользоваться методикой, требуется получить базовые знания. К ним относятся следующие:

1. Классификация обыкновенных дробных чисел.
2. Работа со смешанными дробями обыкновенного типа.
3. Сокращение.

Следует отметить, что каждый компонент необходимо подробно разобрать, поскольку от качественного изучения материала зависит скорость обучения. Если ученик не понял различия между правильной и неправильной дробями, то не имеет смысла переходить ко второму пункту. Это вызовет путаницу, а драгоценное время будет потрачено впустую.

Виды обыкновенных дробей

Классификация дробных выражений позволяет понять основные их свойства, методы конвертации и основные различия между собой. Они бывают трех типов: правильными, неправильными и смешанными. Для удобства необходимо записать дробь в математическом представлении «p/t», где р — числитель, а t — знаменатель.

Правильной дробью называется выражение, в котором числитель меньше знаменателя, т. е. выполняется условие p<t. Если величина «t» превышает «р», то дробное тождество является неправильным.

Однако при расчетах можно в учебниках (например, Виленкина Н. Я.) увидеть смешанное представление. Например, 6[2/3]. Последнее состоит из целой и дробной частей, причем последняя представлена в виде обыкновенного дробного значения. Эта форма записи применяется для конечного отображения результата, полученного при расчетах.

Математики рекомендуют всегда преобразовывать ответ в читабельный вид, чтобы им в дальнейшем могли воспользоваться другие люди. Далее требуется подробно разобрать работу со смешанными числовыми представлениями, поскольку в этом случае умножать обыкновенные дроби проблематично. Отсутствие конвертации может привести к возникновению множества ошибок при вычислениях.

Работа со смешанными числами

Для работы со смешанными числами также существует определенный алгоритм. Он имеет два направления: прямое и обратное преобразование. В первом случае выполняется конвертация смешанного дробного тождества в неправильную дробь обыкновенного типа. Он имеет следующий вид:

1. Написать величину: M[p/t].
2. Рассчитать значение числителя «Р» по такой формуле: Р=Мt+p.
3. Записать неправильную дробь: Р/t.

Следует отметить, что алгоритм преобразования неправильной обыкновенной величины выполняется строго в обратном порядке. Методика выглядит следующим образом:

1. Записать неправильное тождество обыкновенного дробного вида: Р/t.
2. Выделить целочисленную константу, разделив числитель на знаменатель: Р/t=M.
3. Вычислить новый числитель, который должен быть меньше знаменателя: р=Р-М*t.
4. Записать искомое значение: М[p/t].

Следует отметить, что при последнем действии дробную часть рекомендуется сократить. Эту операцию требуется делать постоянно, чтобы оптимизировать дальнейшие расчеты. Далее необходимо разобраться с методикой сокращения числителя и знаменателя.

Правила сокращения

Сокращение числителя и знаменателя необходимы для уменьшения объема вычислений. Например, требуется выполнить операцию умножения для двух дробных значений 44/55 и 90/100. Если оставить выражения в таком виде, то для вычисления произведения нужно оперировать с большими числами, а это очень неудобно. Следовательно, дроби нужно сократить. Для этой цели используется специальная методика. Она имеет такой вид:

1. Записать дробную величину.
2. Найти общий множитель для числителя и знаменателя.
3. Вынести величину, полученную в первом пункте.
4. Сократить дробь, записав результат.

Однако алгоритм нужно отработать на практике. Его реализация имеет такой вид:

1. 44/55 и 90/100.
2. 11 и 10 — общие множители для двух значений дробного вида.
3. (11*4)/(11*5) и (10*9)/(10*10).
4. 4/5 и 9/10.

Следует отметить, что выполнять любые арифметические операции с дробями обыкновенного вида, полученными на четвертом шаге алгоритма, удобнее, чем с их первоначальными значениями. На основании этого можно сделать вывод о том, что сокращение — вынужденная мера, используемая во всем мире для оптимизации вычислений. Далее можно переходить к самой методике умножения дробей в 6 классе.

Алгоритм умножения

Методика умножения дробных обыкновенных значений довольно проста. Однако в математике бывает всего три случая, которые на уроках не всегда поддаются объяснению (очень часто преподаватели не обращают на них внимания учеников):

1. Одинаковые знаменатели.
2. Равные между собой числители, но разные знаменатели.
3. Каждый элемент равен однотипному компоненту, т. е. числитель первой дроби эквивалентен числителю второй, а знаменатели также равны между собой.

На самом деле умножение простых дробей с разными знаменателями является одной и той же операцией, т. е. поиск решения осуществляется по одному принципу. Чтобы его объяснить, нужно разобрать методику выполнения. Она имеет следующий вид:

1. Записать две дроби.
2. Конвертировать смешанные числа в неправильные дробные числа.
3. Привести их к нормальному виду при помощи операции сокращения.
4. Сократить числитель и знаменатель одной величины на элементы неправильной дроби другого значения.
5. Перемножить числители и знаменатели.
6. Записать искомый результат, сокращая его при необходимости и переводя в правильную дробь.

Для понимания алгоритма нужно научиться решать задачи на умножение дробей с разными знаменателями для 6 класса. Например, необходимо перемножить 6[4/8] и 3[20/35]. Их произведение находится по следующей методике:

1. 6[4/8] и 3[20/35].
2. Конвертацию нужно выполнять только после приведения дробных величин к оптимальному виду: 6[4/8]=6[½] и 3[20/35]=3[4/7].
3. Перевод в неправильные дробные тождества: 13/2 и 25/7.
4. Сокращение между величинами невозможно, поскольку 25 не делится нацело на 2, а 13 на 7.
5. Перемножение: (13*25)/(2*7)=325/14.
6. Для сокращения нужно найти общий множитель для чисел 325 и 14 (минус — не делится, а плюс — делится): 2 (-), 3 (-), 4 (-), 5 (-), 6 (-), 7 (-), 8 (-), 9 (-). Невозможно сократить дробное выражение.
7. Запись в смешанной форме, руководствуясь методикой конвертации неправильного дробного значения в смешанное число: 23[(325−23*14)/14]=23[3/14].

Следует отметить, что каждый шаг методики необходимо оптимизировать. Для этого необходимо избавляться от лишних вычислений, постоянно сокращая дробные величины. Однако некоторые могут не понять, как влияет методика умножения на результат. Для этого нужно решить пример другим методом:

1. Для удобства сократить величины дробного вида: 6[½] и 3[4/7].
2. Перемножить целые и дробные части: 18[4/14].
3. Сократить: 18[2/7].

Следует отметить, что результаты не совпадают, поскольку последний способ является неверным. На основании этого можно сделать вывод о том, что требуется решать задачи по методике. Если не следовать правилам, то могут появиться ошибки при расчетах.

Таким образом, для выполнения операции произведения двух обыкновенных дробей необходимо использовать определенный алгоритм, а также уметь сокращать дробные величины и преобразовывать смешанные числа.

Умножение дробей на целые числа

3-й класс

Купить сейчас

4 класс

Купить сейчас

5-й класс

Купить сейчас

2 класс

Купить сейчас

15 сентября 2019 г. 1 комментарий

Учащиеся четвертого класса должны научиться умножать дроби. Ниже приведен общий основной стандарт.

4.NF.4 – Применение и расширение предыдущего понимания умножения для умножения дроби на целое число.

Вводя эту концепцию, я позаботился о том, чтобы связать уравнения с повторяющимся сложением и тем, как символ «x» означает «группы».

Работа с дробями может сбивать с толку, поэтому мы также использовали множество математических манипуляций, чтобы сделать эти уравнения более конкретными.

Не спешите обучать студентов приемам и приемам. Важно уделить время и показать учащимся, что означают эти уравнения. Ниже приведено быстрое упражнение, которое вы можете использовать перед тем, как перейти к умножению дробей. Эта деятельность включена в бесплатную загрузку в конце этого поста.

Различные способы представления дробей

На изображении выше мы рассмотрели различные способы представления дробей.

1. Мы можем нарисовать модель местности. (4/6)
2. Затем мы можем разбить дробь на единичные дроби, и она все равно будет равна той же сумме.
3. Мы можем записать единичные дроби в виде предложения с повторяющимся сложением. (1/6 + 1/6 + 1/6 + 1/6)
4. Затем мы можем взять повторяющееся сложение и заменить его уравнением умножения. (4 х 1/6)

Не забудьте показать свою работу!

Если вы подпишитесь на меня в Instagram, вы обнаружите, что я публикую то, над чем моя дочь и я работаем в течение недели.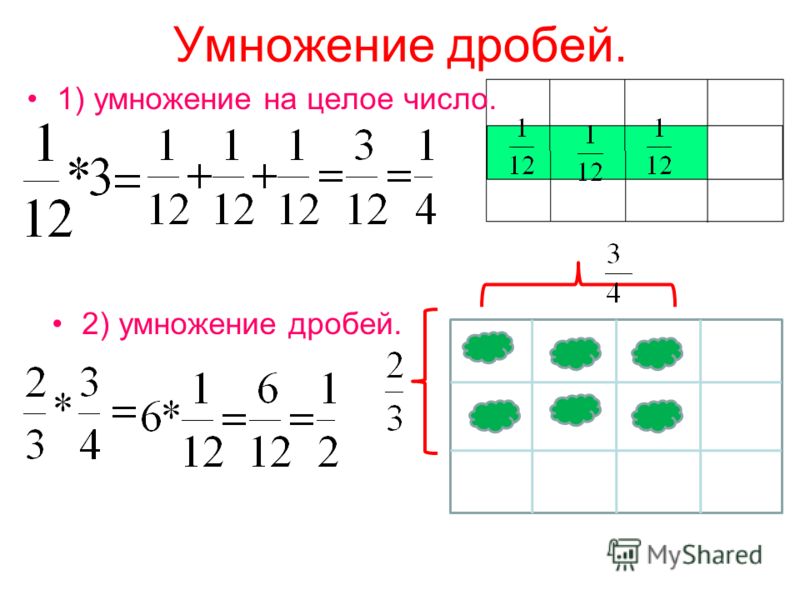 Она посещает виртуальную школу, а я ее тренер по обучению. Ниже пара фотографий, которые я разместил, пока мы работали над уроком.

Учащиеся могут продемонстрировать свою работу, записав дроби ( левое изображение ) или используя математические операции ( правое изображение ).

Прокрутите уравнение — бесплатная математическая игра

Я создал следующую игру, чтобы попрактиковаться в умножении дробей на целое число. Он также включает дроби больше единицы. Опять же, важно показать, что означают эти уравнения, либо написав предложение с повторяющимся сложением, либо используя математические манипуляции, либо нарисовав модели.

Вышеупомянутая игра включена в бесплатную загрузку.

Загрузите ресурсы

• Просто заполните форму ниже, чтобы получить бесплатных печатных форм . После того, как вы подтвердите подписку, бесплатные ресурсы, перечисленные в этом сообщении блога, будут отправлены на ваш почтовый ящик!
• Уже подписаны? Посетите библиотеку ресурсов!
Умножение дробей на целые числа

Занятия по математике для 3-го класса: распечатка и цифровая математика

Получите доступ к ТРЕМ печатным и цифровым математическим играм для повторения дробей!

Я хочу эту халяву!

Вам также могут понравиться эти публикации

Взаимодействие с читателями

Math Tech All Access

Получите мгновенный доступ ко всем ресурсам Math Tech Connections!

Вступай в клуб!

Интерактивные цифровые математические слайды

Все ресурсы

Привет, друзья!

Меня зовут Мариэла! Я преподаватель и основатель Math Tech Connections. Я начал создавать ресурсы для своих учеников, когда увидел, что обучение по учебнику не работает. Студентам нужны увлекательные, практические занятия! Моя цель — сэкономить ваше время с помощью качественных, соответствующих стандартам ресурсов, которые делают математику увлекательной. С более чем 900 ресурсов и более 60 000 отзывов учителей, я уверен, что вы найдете подходящий ресурс для вашего следующего урока. Обязательно присоединитесь к нашему списку адресов электронной почты, чтобы получать советы и еженедельные бесплатные подарки. 🙂

Оставайтесь на связи!

Управление согласием

Умножение дробей на целое число

Понятия о дробях изучаются на уровне 5-го класса, и многие темы очень абстрактны и трудны для понимания учащимися. Умножение дробей на целое число не обязательно должно быть одним из этих сложных понятий! С помощью схемы CRA (конкретно-репрезентативный-абстрактный) ваши учащиеся свяжут то, что они уже знают об умножении на  , с умножением дробей  , и в кратчайшие сроки добьются успеха!

Бетон Умножение дробей на целое число

Прежде чем вы начнете с дробей, закрепите у учащихся понимание того, что значит умножать. Дайте им кучу кубиков и попросите их смоделировать что-то очень простое, например, «4×3». Ваши пятиклассники должны быстро и легко смоделировать эту задачу. Спросите своих учеников о том, что они построили, и как они узнают, что это представляет собой уравнение.

Давай, доставай свои шаблоны. Они являются ИДЕАЛЬНЫМ представлением фракции. Пусть шестиугольник представляет собой целое, и пусть ваши ученики выяснят, какие блоки представляют 1/3 (ромб), 1/2 (трапеция) и 1/6 (треугольник). Как только ваши ученики соберутся со своими кубиками, они готовы начать! У вас нет блоков фракций под рукой? Дробные круги будут работать так же хорошо!

Спросите своих учеников: «Если бы 4 группы по 3 блока представляли 4×3, как мы могли бы представить 4 x 1/3?» Позвольте учащимся использовать блоки шаблона ромба для представления 4 групп по 1/3. Прелесть использования блоков заключается в том, что учащиеся могут собрать эти блоки вместе, чтобы увидеть как неправильную дробь, так и смешанное число, которое получается при умножении дробей.

**Эта ИЗОБРАЖЕНИЕ не является конкретной моделью, но если вы создаете эту модель из фрагментов дробей, ваши ученики работают на конкретном уровне! **

Репрезентативное умножение дробей на целое число

Как только ваши учащиеся смогут моделировать 4 x 1/3, вы хотите, чтобы они связали это понимание с репрезентативной моделью, такой как повторное сложение. Вы можете начать с того, что попросите своих учеников написать повторяющееся уравнение сложения для представления 4 x 3. Это легко для ваших учеников! Теперь попросите их использовать свои знания об умножении, чтобы написать повторяющееся уравнение сложения, представляющее 4 x 1/3.

Реферат Умножение дроби на целое число

Конкретные и репрезентативные этапы этого упражнения позволяют вашим учащимся ясно понять, что происходит при умножении дроби на целое число. После того, как ваши ученики познакомятся на конкретном и репрезентативном уровне, дайте им новое уравнение, такое как 4 x 2/8, и спросите своих учеников, что они *думают* о продукте.