Умножение дробей. Деление Дробей.

• Альфашкола
• Статьи
• Умножение и деление дробей

Любое натуральное число можно представить в виде обыкновенной дроби.

Для того чтобы умножить две дроби надо:

• перевести дроби в неправильные;
• перемножить их числители и записать результат в числитель;
• перемножить их знаменатели и записать результат в знаменатель;
• если можно сократить;

Пример 1. Умножить \(\frac{7}{8}\) и \(\frac{5}{6}\):

 

 

При делении дробей вторую дробь нужно перевернуть, то есть поменять местами числитель и знаменатель, а затем выполнить умножение:

                                                                                  

Две дроби называются взаимно обратными, если их произведение равно \(1\).

Пример: 3/4 и 4/3 являются взаимно обратными, так как в результате дают \(1\):

Также стоит помнить, что на ноль делить нельзя.

---

Задача 1. Умножить \(2\frac{5}{7} \) и \(2 \frac{8}{9}\).

Решение.

\(\frac{19}{7}*\frac{26}{9}\)=\(\frac{494}{63}\)\(=7\frac{53}{63}\)

Ответ: \(7\frac{53}{63}\).

Задача 2. Разделить \(2\frac{5}{6}\) и \(\frac{3}{4} \).

Решение. 

\(\frac{17}{6}:\frac{3}{4}\)\(=\frac{17*4}{6*3}=\frac{17*2}{3*3}=\frac{34}{9}=3\frac{7}{9}\)

Ответ: \(3\frac{7}{9}\).

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Вадим Вадимович Козлов

Репетитор по математике

Стаж (лет)

Образование:

Брянский государственный технический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Мария Валерьевна Загребина

Репетитор по математике

Стаж (лет)

Образование:

Удмуртский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Вера Петровна Любчак

Репетитор по математике

Стаж (лет)

Образование:

Университет штата Аризона

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ОГЭ по математике
• Репетитор по химии для подготовки к ОГЭ
• Подготовка к олимпиадам по химии
• Репетитор для подготовки к ЕГЭ по физике
• Подготовка к олимпиадам по физике
• Репетитор по грамматике русского языка
• Подготовка к олимпиадам по английскому языку
• Репетитор грамматики английского языка
• Подготовка к ЕГЭ по информатике
• Подготовка к ОГЭ по литературе

Похожие статьи

• Методы решения систем уравнений с двумя переменными
• Формулы по алгебре
• Углы правильного многоугольника. Формулы
• Как складывать числа в столбик?
• Эллипс
• Движение в противоположных направлениях
• Как построить график гиперболы?
• РУДН: прикладная математика и информатика (очно / заочно)

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

6 класс, умножение дробей, применение умножения дробей при решении задач

Дата публикации: 12 апреля 2017.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

---

Скачать:Умножение дробей. Текстовые задачи на умножение дробей (PDF)

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 6 класса
Тренажер к учебнику Н.Я. Виленкина
Тренажер к учебнику Г.В. Дорофеева и Л.Г. Петерсона

---

Умножение дробей

1. Решите примеры.

а) 3⁄10 * 1⁄6 =	б) 32⁄9 * 3⁄7 =	в) 2⁄3 * 5 * (2⁄6 — 1,7) =
г) 17⁄10 * 42⁄5 =	д) 36⁄13 * 22⁄7 =	е) 27⁄8 * 1 * ( 5⁄7 + 5,3 ) =

2. Решите задачу.
В магазине Саша купила 3 кг мандарин по цене 4³⁄₅ рубля за кг. Сколько денег потратила Саша?

3. Решите задачу.

Маляр красил коридор в больнице. На каждый метр он расходовал 2⁴⁄₈ литра краски. Сколько литров краски ему понадобилось, если длина коридора равна 12 метрам?

4. Найдите значения выражений.

а) 5 — 1 9⁄12 * 4 + 3⁄6 * 3 =	б) 2 2⁄7 * 3 7⁄8 — 2,5 =
г) 13 1⁄7 * 2 — 4 3⁄8 * 4 =	д) 3⁄8 * 1⁄4 =

5. Решите задачу.
Одна сторона прямоугольника равна ³⁄₈ метра, а вторя сторона – 1⁵⁄₇ метра. Найдите площадь прямоугольника.

6. Решите задачу.
Одна сторона прямоугольника равна ⁵⁄₉ см, а вторя сторона – длиннее первой в 2 раза. Найдите площадь прямоугольника.

7. Решите задачу.
Сторона куба равна 3⁷⁄₁₂ метра.

Чему равен объем куба?

8. Решите задачу.
Из города одновременно в одном направлении выехали 3 автомобиля. Скорость первого автомобиля – 40 ⁵⁄₆ км/ч, скорость второго автомобиля в 1,5 раза меньше, чем скорость первого автомобиля. А скорость третьего автомобиля – на 10 ⁵⁄₂₀ км/ч больше, чем скорость первого автомобиля. Найдите расстояние между автомобилями через 2 часа и через 4 часа после выезда из города.

9. Решите задачу.
Из двух сел одновременно навстречу друг другу вышли два пешехода. Скорость первого пешехода – 4 ²⁄₅ км/ч, а скорость второго – на ⁵⁄₉ км/ч. Каково расстояние между селами, если они встретились через 2 часа?

10. Решите задачу.
Грузовая машина весит 12 т, легковая машина – ¹⁄₈ от массы грузовика. Сколько весят 8 легковых автомобилей?

11. Решите задачу.
На тарелке лежало 64 конфеты. Коля съел ²⁄₈ части конфет, а Миша – ¹⁄₁₂ часть. Сколько конфет съели ребята?

12. Определите.

а) 3⁄10 от 5;	б) 2⁄9 от 8⁄18;	в) 2⁄3 от 4 3⁄8;
г) 40% от 21⁄5;	д) 70% от 15 2⁄9;	е) 0, 60 от 3 * (2⁄7 + 5,3).

4.4: Умножение дробей — Математика LibreTexts

Дроби дробей

Мы знаем, что дробь представляет собой часть целого числа. Например, две пятых одной единицы могут быть представлены как

\(\dfrac{2}{5}\) целого заштриховано.

Естественный вопрос: что такое дробная часть дробной величины, или что такое дробь дроби? Например, что такое \(\dfrac{2}{3}\) из \(\dfrac{1}{2}\)?

Мы можем предложить ответ на этот вопрос, используя изображение для изучения \(\dfrac{2}{3}\) из \(\dfrac{1}{2}\).

Сначала представим \(\dfrac{1}{2}\).

\(\dfrac{1}{2}\) всего заштриховано.

Затем разделите каждую из частей\(\dfrac{1}{2}\) на 3 равные части.

Каждая часть равна \(\dfrac{1}{6}\) целого.

Теперь возьмем \(\dfrac{2}{3}\) блока \(\dfrac{1}{2}\).

\(\dfrac{2}{3}\) из \(\dfrac{1}{2}\) равно \(\dfrac{2}{6}\), что сводится к \(\dfrac {1}{3}\).

Умножение дробей

Теперь спросим, ​​какая арифметическая операция \((+, — , \times , \div)\) даст \(\dfrac{2}{6}\) из \(\dfrac{2}{3}\ ) из \(\dfrac{1}{2}\)?

Обратите внимание, что если в дробях \(\dfrac{2}{3}\) и \(\dfrac{1}{2}\) умножить числители вместе и знаменатели вместе, мы получим точно \( \dfrac{2}{6}\).

\(\dfrac{2 \cdot 1}{3 \cdot 2} = \dfrac{2}{6}\)

Это сводится к \(\dfrac{1}{3}\), как и раньше.

Используя это наблюдение, мы можем предположить следующее:

Слово «из» переводится как арифметическая операция «раз».
Чтобы умножить две или более дроби, умножьте числители вместе, а затем умножьте знаменатели вместе. 2} \end{массив}} = \dfrac{3}{2}\) 9{16}} \end{array}} = \dfrac{1}{16}\)

Это означает, что \(\dfrac{2}{5}\) из \(\dfrac{5}{8}\ ) из \(\dfrac{1}{4}\) целой единицы равно \(\dfrac{1}{16}\) исходной единицы.

Тренировочный набор A

Выполните следующие умножения.

\(\dfrac{2}{5} \cdot \dfrac{1}{6}\)

Ответить

\(\dfrac{1}{15}\)

Тренировочный набор A

\(\dfrac{1}{4} \cdot \dfrac{8}{9}\)

Ответить

\(\dfrac{2}{9}\)

Тренировочный набор A

\(\dfrac{4}{9} \cdot \dfrac{15}{16}\)

Ответить

\(\dfrac{5}{12}\)

Тренировочный набор A

\((\dfrac{2}{3}) (\dfrac{2}{3})\)

Ответить

\(\dfrac{4}{9}\)

Практический набор A

\((\dfrac{7}{4}) (\dfrac{8}{5})\)

Ответить

\(\dfrac{14}{5}\)

Тренировочный набор A

\(\dfrac{5}{6} \cdot \dfrac{7}{8}\)

Ответить

\(\dfrac{35}{48}\)

Тренировочный набор A

\(\dfrac{2}{3} \cdot 5\)

Ответить

\(\dfrac{10}{3}\)

Тренировочный набор A

\((\dfrac{3}{10}) (10)\)

Ответить

\(\dfrac{15}{2}\)

Тренировочный набор A

\(\dfrac{3}{4} \cdot \dfrac{8}{9} \cdot \dfrac{5}{12}\)

Ответить

\(\dfrac{5}{18}\)

Умножение дробей путем деления общих множителей

Мы видели, что для умножения двух дробей мы умножаем числители вместе, затем знаменатели вместе, а затем, если необходимо, приводим к наименьшим слагаемым. Сокращение может быть утомительным, если числа в дробях большие. Например, 97} \end{array}} = \dfrac{3 \cdot 5}{8 \cdot 7} = \dfrac{15}{56}\)

Разделить 3 на 9 и 21, а 2 разделить на 10 и 16 Произведение представляет собой дробь, приведенную к наименьшим условиям.

Практическое руководство: процесс умножения путем деления общих множителей

Чтобы умножить дроби путем деления общих множителей, разделите множители, общие как для числителя, так и для знаменателя. Делимый множитель может стоять в любом числителе и в любом знаменателе.

Набор образцов A 96} \end{array}} = \dfrac{1 \cdot 1 \cdot 1}{9 \cdot 1 \cdot 6} = \dfrac{1}{54}\)

Практический набор B

Выполните следующие умножения.

\(\dfrac{2}{3} \cdot \dfrac{7}{8}\)

Ответить

\(\dfrac{7}{12}\)

Тренировочный набор B

\(\dfrac{25}{12} \cdot \dfrac{10}{45}\)

Ответить

\(\dfrac{25}{54}\)

Тренировочный набор B

\(\dfrac{40}{48} \cdot \dfrac{72}{90}\)

Ответить

\(\dfrac{2}{3}\)

Тренировочный набор B

\(7 \cdot \dfrac{2}{49}\)

Ответить

\(\dfrac{2}{7}\)

Тренировочный набор B

\(12 \cdot \dfrac{3}{8}\)

Ответить

\(\dfrac{9}{2}\)

Тренировочный набор B

\((\dfrac{13}{7}) (\dfrac{14}{26})\)

Ответить

1

Тренировочный набор B

\(\dfrac{16}{10} \cdot \dfrac{22}{6} \cdot \dfrac{21}{44}\)

Ответить

\(\dfrac{14}{5}\)

Умножение смешанных чисел

Умножение смешанных чисел Числа
Чтобы выполнить умножение, в котором есть смешанные числа, удобно сначала преобразовать каждое смешанное число в неправильную дробь, а затем умножить.

Набор образцов C

Выполните следующие операции умножения. Преобразуйте неправильные дроби в смешанные числа.

\(1 \dfrac{1}{8} \cdot 4 \dfrac{2}{3}\)

Преобразуйте каждое смешанное число в неправильную дробь.

\(1 \dfrac{1}{8} = \dfrac{8 \cdot 1 + 1}{8} = \dfrac{9}{8}\) 91} \end{array}} = \dfrac{3 \cdot 7}{4 \cdot 1} = \dfrac{21}{4} = 5 \dfrac{1}{4}\)

Набор образцов C

\(16 \cdot 8 \dfrac{1}{5}\)

Преобразование \(8 \dfrac{1}{5}\) в неправильную дробь.

\(8 \dfrac{1}{5} = \dfrac{5 \cdot 8 + 1}{5} = \dfrac{41}{5}\)

\(\dfrac{16}{1} \cdot \dfrac{41}{5}\).

Нет общих множителей для разделения.

\(\dfrac{16}{1} \cdot \dfrac{41}{5} = \dfrac{16 \cdot 41}{1 \cdot 5} = \dfrac{656}{5} = 131 \dfrac {1}{5}\) 91} \end{массив}}} \\ {} & = & {\dfrac{11 \cdot 3 \cdot 5}{8 \cdot 1 \cdot 1} = \dfrac{165}{8} = 20 \dfrac {5}{8}} \end{array}\)

Практический набор C

Выполните следующие умножения. Преобразуйте неправильные дроби в смешанные числа.

\(2 \dfrac{2}{3} \cdot 2 \dfrac{1}{4}\)

Ответить

6

Тренировочный набор C

\(6 \dfrac{2}{3} \cdot 3 \dfrac{3}{10}\)

Ответить

22

Тренировочный набор C

\(7 \dfrac{1}{8} \cdot 12\)

Ответить

\(85\dfrac{1}{2}\)

Тренировочный набор C

\(2 \dfrac{2}{5} \cdot 3 \dfrac{3}{4} \cdot 3 \dfrac{1}{3}\)

Ответить

30

Степени и корни дробей 92\)

Ответить

\(\dfrac{9}{100}\)

Тренировочный набор D

\(\sqrt{\dfrac{4}{9}}\)

Ответить

\(\dfrac{2}{3}\)

Тренировочный набор D

\(\sqrt{\dfrac{1}{4}}\)

Ответить

\(\dfrac{1}{2}\)

Тренировочный набор D

\(\dfrac{3}{8}\cdot\sqrt{\dfrac{1}{9}}\)

Ответить

\(\dfrac{1}{8}\)

Тренировочный набор D

\(9 \dfrac{1}{3} \cdot \sqrt{\dfrac{81}{100}}\)

Ответить

\(8 \dfrac{2}{5}\)

Тренировочный набор D

\(2 \dfrac{8}{13} \cdot \sqrt{\dfrac{169}{16}}\)

Ответить

\(8 \dfrac{1}{2}\)

Упражнения

Для следующих шести задач используйте диаграммы, чтобы найти каждую из следующих частей. Используйте умножение, чтобы проверить свой результат.

Упражнение \(\PageIndex{1}\)

\(\dfrac{3}{4}\) из \(\dfrac{1}{3}\)

Ответить

\(\dfrac{1}{4}\)

Упражнение \(\PageIndex{2}\)

\(\dfrac{2}{3}\) из \(\dfrac{3}{5}\)

Упражнение \(\PageIndex{3}\)

\(\dfrac{2}{7}\) из \(\dfrac{7}{8}\)

Ответить

\(\dfrac{1}{4}\)

Упражнение \(\PageIndex{4}\)

\(\dfrac{5}{6}\) из \(\dfrac{3}{4}\)

Упражнение \(\PageIndex{5}\)

\(\dfrac{1}{8}\) из \(\dfrac{1}{8}\)

Ответить

\(\dfrac{1}{64}\)

Упражнение \(\PageIndex{6}\)

\(\dfrac{7}{12}\) из \(\dfrac{6}{7}\)

​​​​

Для следующих задач найдите каждую часть, не используя схему.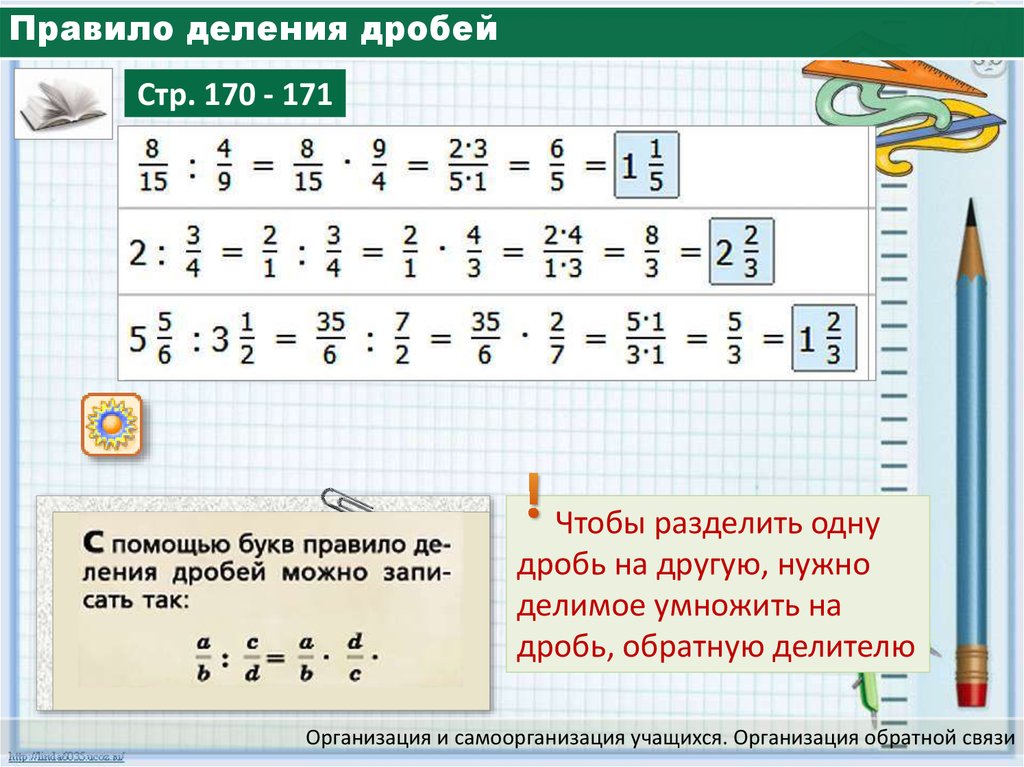

Упражнение \(\PageIndex{7}\)

\(\dfrac{1}{2}\) из \(\dfrac{4}{5}\)

Ответить

\(\dfrac{2}{5}\)

Упражнение \(\PageIndex{8}\)

\(\dfrac{3}{5}\) из \(\dfrac{5}{12}\)

Упражнение \(\PageIndex{9}\)

\(\dfrac{1}{4}\) из \(\dfrac{8}{9}\)

Ответить

\(\dfrac{2}{9}\)

Упражнение \(\PageIndex{10}\)

\(\dfrac{3}{16}\) из \(\dfrac{12}{15}\)

Упражнение \(\PageIndex{11}\)

\(\dfrac{2}{9}\) из \(\dfrac{6}{5}\)

Ответить

\(\dfrac{4}{15}\)

Упражнение \(\PageIndex{12}\)

\(\dfrac{1}{8}\) из \(\dfrac{3}{8}\)

Упражнение \(\PageIndex{13}\)

\(\dfrac{2}{3}\) из \(\dfrac{9}{10}\)

Ответить

\(\dfrac{3}{5}\)

Упражнение \(\PageIndex{14}\)

\(\dfrac{18}{19}\) из \(\dfrac{38}{54}\)

Упражнение \(\PageIndex{15}\)

\(\dfrac{5}{6}\) из \(2 \dfrac{2}{5}\)

Ответить

2

Упражнение \(\PageIndex{16}\)

\(\dfrac{3}{4}\) из \(3 \dfrac{3}{5}\)

Упражнение \(\PageIndex{17}\)

\(\dfrac{3}{2}\) из \(2 \dfrac{2}{9}\)

Ответить

\(\dfrac{10}{3}\) или \(3 \dfrac{1}{3}\)

Упражнение \(\PageIndex{18}\)

\(\dfrac{15}{4}\) из \(4 \dfrac{4}{5}\)

Упражнение \(\PageIndex{19}\)

\(5 \dfrac{1}{3}\) из \(9 \dfrac{3}{4}\)

Ответить

52

Упражнение \(\PageIndex{20}\)

\(1 \dfrac{13}{15}\) из \(8 \dfrac{3}{4}\)

Упражнение \(\PageIndex{21}\)

\(\dfrac{8}{9}\) из \(\dfrac{3}{4}\) из \(\dfrac{2}{3}\)

Ответить

\(\dfrac{4}{9}\)

Упражнение \(\PageIndex{22}\)

\(\dfrac{1}{6}\) из \(\dfrac{12}{13}\) из \(\dfrac{26}{36}\)

Упражнение \(\PageIndex{23}\)

\(\dfrac{1}{2}\) из \(\dfrac{1}{3}\) из \(\dfrac{1}{4}\)

Ответить

\(\dfrac{1}{24}\)

Упражнение \(\PageIndex{24}\)

\(1 \dfrac{3}{7}\) из \(5 \dfrac{1}{5}\) из \(8 \dfrac{1}{3}\)

Упражнение \(\PageIndex{25}\)

\(2 \dfrac{4}{5}\) из \(5 \dfrac{5}{6}\) из \(7 \dfrac{5}{7}\)

Ответить

126

Для решения следующих проблем найдите продукты. Обязательно уменьшайте.

Упражнение \(\PageIndex{26}\) ​​

\(\dfrac{1}{3} \cdot \dfrac{2}{3}\)

Упражнение \(\PageIndex{27}\)

\(\dfrac{1}{2} \cdot \dfrac{1}{2}\)

Ответ

\(\dfrac{1}{4}\)

Упражнение \(\PageIndex{28}\)

\(\dfrac{3}{4} \cdot \dfrac{3}{8}\)

Упражнение \(\PageIndex{29}\)

\(\dfrac{2}{5} \cdot \dfrac{5}{6}\)

Ответить

\(\dfrac{1}{3}\)

Упражнение \(\PageIndex{30}\)

\(\dfrac{3}{8} \cdot \dfrac{8}{9}\)

Упражнение \(\PageIndex{31}\)

\(\dfrac{5}{6} \cdot \dfrac{14}{15}\)

Ответить

\(\dfrac{7}{9}\)

Упражнение \(\PageIndex{32}\)

\(\dfrac{4}{7} \cdot \dfrac{7}{4}\)

Упражнение \(\PageIndex{33}\)

\(\dfrac{3}{11} \cdot \dfrac{11}{3}\)

Ответить

1

Упражнение \(\PageIndex{34}\)

\(\dfrac{9}{16} \cdot \dfrac{20}{27}\)

Упражнение \(\PageIndex{35}\)

\(\dfrac{35}{36} \cdot \dfrac{48}{55}\)

Ответить

\(\dfrac{28}{33}\)

Упражнение \(\PageIndex{36}\)

\(\dfrac{21}{25} \cdot \dfrac{15}{14}\)

Упражнение \(\PageIndex{37}\)

\(\dfrac{76}{99} \cdot \dfrac{66}{38}\)

Ответить

\(\dfrac{4}{3}\)

Упражнение \(\PageIndex{38}\)

\(\dfrac{3}{7} \cdot \dfrac{14}{18} \cdot \dfrac{6}{2}\)

Упражнение \(\PageIndex{39}\)

\(\dfrac{4}{15} \cdot \dfrac{10}{3} \cdot \dfrac{27}{2}\)

Ответить

12

Упражнение \(\PageIndex{40}\)

\(\dfrac{14}{15} \cdot \dfrac{21}{28} \cdot \dfrac{45}{7}\)

Упражнение \(\PageIndex{41}\)

\(\dfrac{8}{3} \cdot \dfrac{15}{4} \cdot \dfrac{16}{21}\)

Ответить

\(7\dfrac{13}{21}\) или \(\dfrac{160}{21}\)

Упражнение \(\PageIndex{42}\)

\(\dfrac{18}{14} \cdot \dfrac{21}{35} \cdot \dfrac{36}{7}\)

Упражнение \(\PageIndex{43}\)

\(\dfrac{3}{5} \cdot 20\)

Ответить

12

Упражнение \(\PageIndex{44}\)

\(\dfrac{8}{9} \cdot 18\)

Упражнение \(\PageIndex{45}\)

\(\dfrac{6}{11}\cdot 33\)

Ответить

18

Упражнение \(\PageIndex{46}\)

\(\dfrac{18}{19} \cdot 38\)

Упражнение \(\PageIndex{47}\)

\(\dfrac{5}{6}\cdot 10\)

Ответить

\(\dfrac{25}{3}\) или \(8\dfrac{1}{3}\)

Упражнение \(\PageIndex{48}\)

\(\dfrac{1}{9} \cdot 3\)

Упражнение \(\PageIndex{49}\)

\(5 \cdot \dfrac{3}{8}\)

Ответить

\(\dfrac{15}{8} =1 \dfrac{7}{8}\)

Упражнение \(\PageIndex{50}\)

\(16 \cdot \dfrac{1}{4}\)

Упражнение \(\PageIndex{51}\)

\(\dfrac{2}{3} \cdot 12 \cdot \dfrac{3}{4}\)

Ответить

6

Упражнение \(\PageIndex{52}\)

\(\dfrac{3}{8} \cdot 24 \cdot \dfrac{2}{3}\)

Упражнение \(\PageIndex{53}\)

\(\dfrac{5}{18} \cdot 10 \cdot \dfrac{2}{5}\)

Ответить

\(\dfrac{10}{9} = 1 \dfrac{1}{9}\)

Упражнение \(\PageIndex{54}\)

\(\dfrac{16}{15} \cdot 50 \cdot \dfrac{3}{10}\)

Упражнение \(\PageIndex{55}\)

\(5 \dfrac{1}{3} \cdot \dfrac{27}{32}\)

Ответить

\(\dfrac{9}{2} = 4 \drac{1}{2}\)

Упражнение \(\PageIndex{56}\)

\(2 \dfrac{6}{7} \cdot 5 \dfrac{3}{5}\)

Упражнение \(\PageIndex{57}\)

\(6 \dfrac{1}{4} \cdot 2 \dfrac{4}{15}\)

Ответить

\(\dfrac{85}{6} = 14 \drac{1}{6}\)

Упражнение \(\PageIndex{58}\) 92\)

Найдите каждое значение для следующих проблем. Сократите ответы до минимальных значений или преобразуйте их в смешанные числа.

Упражнение \(\PageIndex{71}\)

\(\sqrt{\dfrac{4}{9}}\)

Ответить

\(\dfrac{2}{3}\)

Упражнение \(\PageIndex{72}\)

\(\sqrt{\dfrac{16}{25}}\)

Упражнение \(\PageIndex{73}\)

\(\sqrt{\dfrac{81}{121}}\)

Ответ

\(\dfrac{9}{11}\)

Упражнение \(\PageIndex{74}\)

\(\sqrt{\dfrac{36}{49}}\)

Упражнение \(\PageIndex{75}\)

\(\sqrt{\dfrac{144}{25}}\)

Ответить

\(\dfrac{12}{5} = 2 \dfrac{2}{5}\)

Упражнение \(\PageIndex{76}\)

\(\dfrac{2}{3}\cdot\sqrt{\dfrac{9}{16}}\)

Упражнение \(\PageIndex{77}\) 92 \cdot \sqrt{\dfrac{36}{49}} \cdot \sqrt{\dfrac{64}{81}}\)

Упражнения для обзора

Упражнение \(\PageIndex{81}\)

Сколько тысяч в числе 342 810?

Ответить

2

Упражнение \(\PageIndex{82}\)

Найдите сумму 22, 42 и 101.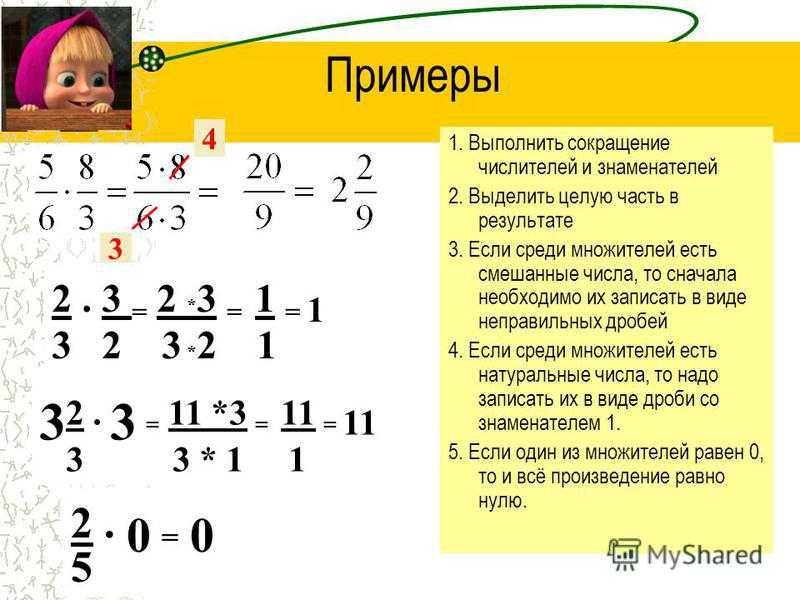

Упражнение \(\PageIndex{83}\)

Делится ли 634 281 на 3?

Ответить

да

Упражнение \(\PageIndex{84}\)

Является ли целое число 51 простым или составным?

Упражнение \(\PageIndex{85}\)

Сократить \(\dfrac{36}{150}\) до минимального значения

Ответить

\(\dfrac{6}{25}\)

Умножение правильных дробей — Математика с мамой

Опубликовано Математика с мамой

Умножение правильных дробей

0005

Поделиться в Google Classroom

ExampleVideoQuestionsLesson

Поделиться в Google Classroom

• Нахождение ¹ / ₂ из ¹ / ₃ то же самое, что и нахождение ¹ / ₂ × ¹ / ₃ × ¹ .
•   ¹ / ₃   означает разделить фигуру на 3 равные части.
• Теперь мы найдем половину этого числа, разделив его на две равные части.
• Теперь у нас есть 1 часть из 6 равных частей.
•   ¹ / ₂   ×   ¹ / ₃   =   ¹ / ₆  .
• Мы можем просто умножить числители

  Число в верхней части дроби над чертой.

  дробей, чтобы получить числитель ответа.
• Мы можем просто умножить

  знаменателяЧисло в нижней части дроби под чертой.

  дробей, чтобы получить знаменатель ответа.
• 1 × 1 = 1, что идет сверху.
• 2 × 3 = 6, который идет снизу.

Умножьте числители сверху, чтобы получить числитель ответа.

Умножьте знаменатели внизу, чтобы получить знаменатель ответа.

• У нас есть ¹ / ₂ × ¹ / ₃ .
• Умножьте числа на вершинах дробей (числители) вместе.
• 1 × 1 = 1, значит, 1 — это числитель в верхней части ответа.
• Умножьте числа в нижних частях дробей (знаменатели).
• 2 × 3 = 6, значит, 6 — знаменатель в нижней части ответа.
•   ¹ / ₂   ×   ¹ / ₃   =   ¹ / ₆  .

Как умножать правильные дроби

Правильная дробь — это дробь, у которой сверху меньшее число (в числителе), а внизу больше (в знаменателе).

Чтобы умножить правильные дроби, выполните следующие действия:

1. Умножьте числители над дробями.
2. Этот результат будет числителем в верхней части ответа.
3. Умножьте знаменатели нижних дробей.
4. Этот результат будет знаменателем внизу ответа.

Вот пример умножения дробей одной половины на одну треть.

Нас спрашивают: «Что такое ¹ / ₂   ×   ¹ / ₃  ?»

Числители — это числа над дробями. Мы умножаем числитель первой дроби на числитель второй дроби, чтобы получить числитель в верхней части нашего ответа.

1 × 1 = 1

Знаменатели – это числа в нижней части дробей. Мы умножаем знаменатель первой дроби на знаменатель второй дроби, чтобы получить знаменатель в нижней части нашего ответа.

2 × 3 = 6

¹ / ₂   ×   ¹ / ₃   =   ¹ / ₆  .

Вот еще один пример умножения правильных дробей с использованием описанных выше шагов.

У нас есть ¹ / ₄ × ¹ / ₃ .

Сначала умножаем числители.

1 × 1 = 1

Таким образом, 1 — это числитель в верхней части нашего ответа.

Далее умножаем знаменатели.

4 × 3 = 12

¹ / ₄   ×   ¹ / ₃   =   ¹ / ₁₂  .

В этом примере умножения правильных дробей мы имеем ² / ₅ × ² / ₃ .

Начнем с умножения числителей на вершинах двух дробей.

2 × 2 = 4

4 — это числитель в верхней части нашего ответа.

Затем мы умножаем два знаменателя в основаниях дробей вместе.

5 × 3 = 15

15 — знаменатель внизу нашего ответа.

² / ₅   ×   ² / ₃   =   ⁴ / ₁₅  .

В этом примере мы умножаем правильные дроби ¹ / ₅ × ³ / ₄ .

Умножая числители имеем:

1 × 3 = 3

Умножая знаменатели, имеем:

5 × 4 = 20

¹ / ₅   ×   ³ / ₄   =   ³ / ₂₀  .

Почему правильные дроби становятся меньше при их умножении?

Умножение дроби на правильную дробь всегда делает ее меньше.

Это связано с тем, что правильная дробь имеет меньшее число сверху в качестве числителя по сравнению с большим числом внизу в качестве знаменателя.