Правила деления дробей. Умножение простых и смешанных дробей с разными знаменателями

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно.

Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно.

С первого раза! Без калькулятора! И сделайте верные выводы. ..

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас. )

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.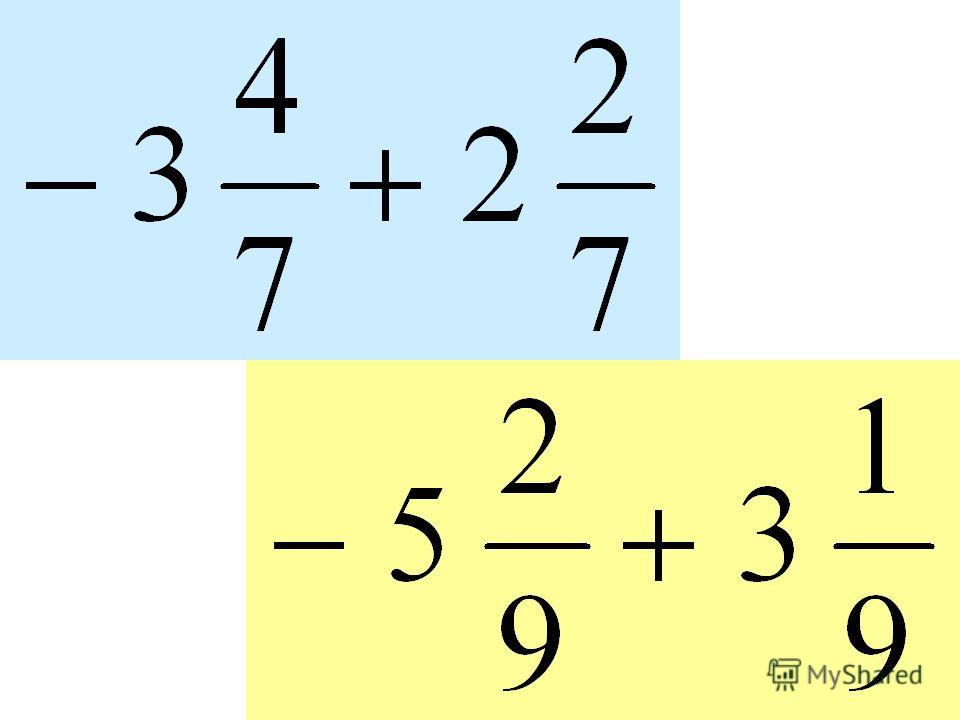

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

1. Чтобы поделить 1-ну дробь на вторую, необходимо делимое умножить на число, которое обратно делителю.

Для правильных и неправильных дробей правило деления следующее:

Чтобы поделить обыкновенную дробь, необходимо числитель делимого умножить на знаменатель делителя, а знаменатель делимого умножить на числитель делителя. Первое произведение берем числителем, а второе — знаменателем.

Деление дроби на дробь.

Чтобы разделить 1-ну обыкновенную дробь на вторую, не равную нулю, необходимо:

• числитель 1-ой дроби умножить на знаменатель 2-ой дроби и записать произведение в числитель полученной дроби;
• знаменатель 1-ой дроби умножить на числитель 2-ой дроби и записать произведение в знаменатель полученной дроби.

Иными словами, деление дробей переходит к умножению.

Чтоб поделить 1-ну дробь на вторую, необходимо делимое (1-ну дробь) умножить на обратную дробь делителю.

Деление дроби на число.

Схематически деление дроби на натуральное число выглядит так:

Чтобы поделить дробь на натуральное число, используют такой метод:

Выражаем натуральное число как неправильную дробь с числителем, который равен самому числу, а знаменатель равным 1-це.

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть.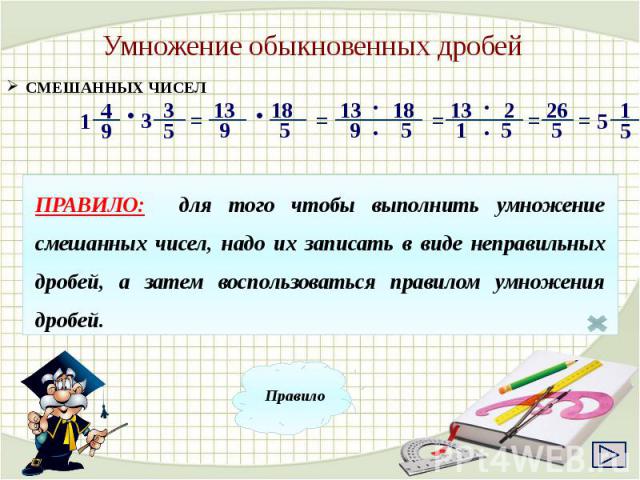 Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Дробь – это одна или более долей целого, за которое обычно принимается единица (1). Как и с натуральными числами, с дробями можно выполнять все основные арифметические действия (сложение, вычитание, деление, умножения), для этого нужно знать особенности работы с дробями и различать их виды. Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.

Как разделить простую дробь на натуральное число?
Обыкновенными или простыми называют дроби, записывающиеся в виде такого отношения чисел, при котором вверху дроби указывается делимое (числитель), а внизу – делитель (знаменатель) дроби. Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.

Для этого мы должны выполнить ряд действий:
Таким образом, если перед нами стоит задача разделить дробь на целое число, схема решения будет выглядеть примерно так:

Подобным образом можно разделить любую обыкновенную (простую) дробь на целое число.

Как разделить десятичную дробь на целое число?
Десятичная дробь — это такая дробь, которая получается вследствие деления единицы на десять, тысячу и так далее частей. Арифметические действия с десятичными дробями выполняются довольно просто.

Рассмотрим на примере как разделить дробь на целое число. Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.

Подводя итоги, остановимся на двух основных моментах, которые важны при выполнении операции деления десятичных дробей на целое число:

• для разделения десятичной дроби на натуральное число применяют деление в столбик;
  
• запятая ставится в частном тогда, когда закончено деление целой части делимого.
  

Применяя эти простые правила, всегда можно без особого труда разделить любую десятичную или простую дроби на целое число.

Умножение дробей | Преалгебра

Результаты обучения

• Использование диаграммы для моделирования умножения положительных и отрицательных дробей
• Умножение дробей и целых выражений, содержащих переменные

Модель может помочь вам понять умножение дробей. Мы будем использовать дробные плитки для моделирования [латекс]\большой\фрак{1}{2}\cdot \фрак{3}{4}[/латекс]. Чтобы умножить [латекс]\большой\фракция{1}{2}[/латекс] и [латекс]\большой\фракция{3}{4}[/латекс], подумайте [латекс]\большой\фракция{1}{ 2}[/latex] из [latex]\Large\frac{3}{4}[/latex].
Начните с тайлов дроби на три четверти. Чтобы найти половину от трех четвертей, нам нужно разделить их на две равные группы. Поскольку мы не можем разделить три плитки [latex]\Large\frac{1}{4}[/latex] поровну на две части, мы обмениваем их на плитки меньшего размера.

Мы видим, что [latex]\Large\frac{6}{8}[/latex] эквивалентен [latex]\Large\frac{3}{4}[/latex]. Взяв половину из шести плиток [latex]\Large\frac{1}{8}[/latex], мы получим три плитки [latex]\Large\frac{1}{8}[/latex], то есть [латекс] \Large\frac{3}{8}[/latex].

Следовательно,

[латекс]\Large\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}[/latex]

Пример

Используйте диаграмму к модели [латекс]\Большой\фрак{1}{2}\cdot \фрак{3}{4}[/латекс]

Решение:
Первый оттенок в [латекс]\Большой\фрак{3}{4} [/latex] прямоугольника.

Мы возьмем [латекс]\Large\frac{1}{2}[/latex] этого [латекса]\Large\frac{3}{4}[/latex], поэтому сильно заштрихуем [латекс] \Large\frac{1}{2}[/latex] заштрихованной области.

Обратите внимание, что [латекс]3[/латекс] из [латекс]8[/латекс] сильно затенены. Это означает, что [latex]\Large\frac{3}{8}[/latex] прямоугольника сильно затенены.
Следовательно, [latex]\Large\frac{1}{2}[/latex] из [latex]\Large\frac{3}{4}[/latex] равно [latex]\Large\frac{3}{ 8}[/латекс], или [латекс]{\большой\гидроразрыв{1}{2}\cdot \гидроразрыва{3}{4}}={\большой\гидроразрыва{3}{8}}[/латекс] .

Попробуйте

Используйте диаграмму для моделирования: [латекс]\Большой\фракция{1}{2}\cdot \фракция{3}{5}[/латекс]

Показать решение

Посмотрите на результат, который мы получили от модели в примере выше. Мы обнаружили, что [latex]\Large\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}[/latex]. Вы заметили, что мы могли бы получить один и тот же ответ, перемножив числители и умножив знаменатели?

	[латекс]\Large\frac{1}{2}\cdot \frac{3}{4}[/latex]
Умножьте числители и умножьте знаменатели.	[латекс]\Large\frac{1}{2}\cdot \frac{3}{4}[/latex]
Упрощение.	[латекс]\большой\фрак{3}{8}[/латекс]

Это приводит к определению дробного умножения. Чтобы умножить дроби, мы умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.

Умножение дробей

Если [latex]a,b,c,\text{ и }d[/latex] являются числами, где [latex]b\ne 0\text{ и }d\ne 0[/latex], затем

[latex]\Large\frac{a}{b}\cdot \frac{c}{d}=\frac{ac}{bd}[/latex]

Пример

Умножьте и запишите ответ в упрощенной форме: [latex]\Large\frac{3}{4}\cdot \frac{1}{5}[/latex]

Показать решение

Попробуйте

При умножении дробей сохраняются свойства положительных и отрицательных чисел. В качестве первого шага рекомендуется определить знак произведения. В следующем примере мы умножим два отрицательных значения, поэтому произведение будет положительным.

Пример

Умножьте и запишите ответ в упрощенной форме: [латекс]\большой-\frac{5}{8}\left(-\frac{2}{3}\right)[/latex]

Показать решение

Попробуйте

В следующем видео приведены дополнительные примеры умножения дробей и упрощения результата.

Пример

Умножьте и запишите ответ в упрощенной форме: [latex]\Large-\frac{14}{15}\cdot \frac{20}{21}[/latex]

Показать решение

 

Попробуйте

В следующем видео показан еще один пример умножения отрицательных дробей.

При умножении дроби на целое число может быть полезно записать целое число в виде дроби. Любое целое число, [латекс]а[/латекс], может быть записано как [латекс]\большой\фрак{а}{1}[/латекс]. Например, [latex]3=\Large\frac{3}{1}[/latex].

пример

Умножьте и запишите ответ в упрощенной форме:

1. [латекс]\Large{\frac{1}{7}}\normalsize\cdot 56[/latex]
2. [латекс]\Large{\frac{12}{5}}\normalsize\left(-20x\right)[/latex]

Показать раствор

Попробуйте

Посмотрите следующее видео, чтобы увидеть больше примеров умножения дроби и целого числа.

Дроби

Дробь , или дробное число используются для представления части целого. Дроби состоят из двух чисел: числитель (который стоит над чертой) и знаменатель (под чертой).

Знаменатель говорит вам о количестве равных частей, на которые что-то делится. Числитель говорит вам, сколько из этих равных частей рассматривается. Таким образом, если дробь состоит из пирога, знаменатель 5 говорит вам, что пирог был разделен на пять равных частей, из которых 3 (числитель) находятся в дроби. Иногда полезно представить, что разделительная линия (середина дроби) означает «из». Другими словами, также означает 3 из 5 равных частей от всего пирога.

Отрицательные дроби

Дроби могут быть отрицательными , а также положительными. (См. рисунок ниже.)

Однако отрицательные дроби обычно записываются следующим образом:

Сложение положительных и отрицательных дробей

Правила для чисел со знаком применимы и к дробям.

Пример 1

Добавьте следующее.

Вычитание положительных и отрицательных дробей

Правило вычитания чисел со знаком применимо и к дробям.

Пример 2

Вычтите следующее.

Умножение дробей

Чтобы умножить дроби, просто умножьте числители, а затем умножьте знаменатели. При необходимости уменьшите до самых низких условий.

Пример 3

Умножение.

Этот ответ пришлось сократить, потому что он не был самым низким. Поскольку целые числа также можно записать в виде дробей и т. д., проблему можно решить, заменив 3 на .

Раннее сокращение

Раннее сокращение при умножении дробей избавило бы вас от необходимости уменьшать ваши ответы после завершения умножения. Чтобы уменьшить, найдите число, которое делится без остатка на один числитель и один знаменатель. В этом случае 2 будет делиться на 2 без остатка в числителе 2 (проходит один раз) и в знаменателе 12 (проходит шесть раз). Таким образом,

Помните, вы можете делать раннее сокращение только тогда, когда умножаете дроби. Здесь также действуют правила умножения чисел со знаком.

Пример 4

Уменьшить, где это возможно, раньше, а затем умножить.

Умножение смешанных чисел

Чтобы умножить смешанные числа, сначала замените любое смешанное число на неправильную дробь. Затем умножьте.

Пример 5

Умножить.

Измените ответ, если он в форме неправильной дроби, обратно на смешанное число и при необходимости уменьшите. Помните, что здесь также применяются правила умножения чисел со знаком.

Деление дробей

Чтобы разделить дроби, инвертировать (перевернуть вверх дном) вторую дробь (ту, на которую «делится») и умножить. Затем уменьшить, если это возможно.

Пример 6

Разделить.

Здесь также применяются правила деления чисел со знаком.

Деление сложных дробей

Иногда задача на деление дробей может появляться в следующем виде (такие называются сложные дроби ).

Пример 7

Упрощение.

Предположим, что линия, разделяющая две дроби, означает «разделить на». Следовательно, эту задачу можно переписать следующим образом:

Теперь выполните ту же процедуру, что и в примере .

Деление смешанных чисел

Чтобы разделить смешанные числа, сначала преобразуйте их в неправильные дроби.