«Умножение обыкновенных дробей. Решение упражнений и задач».

Тема: «Умножение обыкновенных дробей. Решение упражнений и задач».

Образовательные: повторить, обобщить и систематизировать первоначальные значения учащихся по теме: «Умножение обыкновенных дробей», закрепить умения и навыки применения этих действий при решении задач и упражнений.

Развивающая: развивать логическое мышление и воображение, творческую и умственную активность, математическую речь, учить самостоятельно добывать знания, прививать интерес к математике, пробуждать к любознательности.

Коррекционно-развивающие: учить анализировать полученные данные и делать выводы, способствовать развитию внимания.

Воспитательная: воспитывать сознательное отношение к учебному труду, развивать самостоятельность, интерес к предмету, прививать аккуратность и трудолюбие.

Тип урока: урок обобщения и систематизации знаний, умений и навыков.

Формы работы учащихся: фронтальная, индивидуальная.

Ход урока

1. Организационный момент

Долгожданный дан звонок

Начинается урок.

Тут затеи и задачи,

Все для вас

Пожелаю вам удачи –

За работу в добрый час!

Давайте улыбнемся друг другу и с хорошим настроением начнем урок.

2. Проверка домашнего задания (3 слайд)
3. Актуализация опорных знаний учащихся (4 слайд)

 

1.Что такое дробь?

Дробь – это одна или несколько равных частей целого.

2.Что такое числитель и знаменатель дроби?

Числитель дроби показывает, сколько взяли равных частей.

Знаменатель – на сколько равных частей поделили целое.

3.Дроби можно поделить на…..?

Правильные и неправильные, сократимые и несократимые.

Правильная дробь – (числитель <знаменателя), меньше 1.

Неправильная дробь – (числитель> знаменателя), больше или равно 1.

4.Основное свойство дроби

Если числитель и знаменатель дроби умножить или поделить на одно и то же натуральное число, то величина дроби не изменяется.

Сократить дробь -значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.

5.Какие действия над дробями мы уже умеем выполнять?

Сложение, вычитание, умножение.

6.Как найти дробь от числа?

Чтобы найти дробь от числа, нужно данное число умножить на эту дробь.

4. Сокращение дробей, интерактивное упражнение (слайд)

5. Приведение дроби к другому знаменателю, интерактивное упражнение (слайд)

    

6. Самостоятельная работа (тест, слайд )

7. Физкультминутка (слайд 10)
8. Решение упражнений и задач 

№ 368

1. · 5 = = = = 1

3. 4 · 0,25 = = = = 1

10. · 2 = = = = 1

№ 390

І д. — ст.

ІІ д.- ст. 270 ст.

ІІІ д.- ? ст.

Решение

1. 270 · = = = = 60 (ст.) прочитал за І день
2. 60 · = = = = 80 (ст.) прочитал за ІІ день
3. 270 – 60 – 80 = 130 (ст.) – прочитал за ІІІ день

     Ответ: 130 страниц

Дополнительное  задание:       

№ 362

÷ = 1           Решение: 1 · = · =  = 1

= 1 ·

= 1

Ответ: 1

9. Домашнее задание: повторить § 9 №369 (2,3), №391
10.  Рефлексия

Наше занятие подходит к концу. Пожалуйста поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).

Вам для этого помогут слова:

1. Я узнал……
2. Я почувствовал…….
3. Я увидел…….
4. Я сначала испугался, а потом……..
5. Я заметил, что……
6. Я сейчас слушаю и думаю…..
7. Мне интересно следить за………

Наше занятие подходит к концу. Пожалуйста поделитесь с нами своим настроением.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

\\

 

 

Дробь – это одна или несколько равных частей целого/

 

Числитель дроби показывает, сколько взяли равных частей.

Знаменатель – на сколько равных частей поделили целое.

 

Правильные и неправильные, сократимые и несократимые.

Правильная дробь – (числитель <знаменателя), меньше 1.

Неправильная дробь – (числитель> знаменателя), больше или равно 1.

 

4.Основное свойство дроби:

Если числитель и знаменатель дроби умножить или поделить на одно и то же натуральное число, то величина дроби не изменяется.

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.

 

Сложение, вычитание, умножение.

 

Чтобы найти дробь от числа, нужно данное число умножить на эту дробь.

 

 

 

 

 

Таблица умножения

правила, примеры, решения, как умножить натуральное число на смешанную дробь

Данная статья дана для разбора смешанных чисел. Научимся выполнять умножения смешанных чисел и натурального числа.

Умножение смешанных чисел

Умножение смешанных чисел сводится к умножению обыкновенных дробей. Для этого нужно сделать перевод смешанных чисел в неправильные дроби.

Используем правила умножения смешанных чисел:

Определение 1

• Умножаемые смешанные числа нужно заменить неправильными дробями;
• Использование правила умножения дроби на дробь.

Рассмотрим решения на примерах.

Пример 1

Сделать умножение 357 и 1211.

Решение

Для начала умножаем смешанные числа в виде неправильных дробей: 357=3·7+57=267 и 1211=1·11+211=1311.

Умножение смешенных дробей заменяем умножением обыкновенных: 357·1211=267·1311.

После чего получим 267·1311=26·137·11=33877.

Дробь несократимая, поэтому выделяем целую часть:33877=43077.

В итоге получим 357·1211=267·1311=26·137·11=33877=43077.

Ответ: 357·1211=43077.

Чтобы закрепить знания умножения смешанных чисел, рассмотрим пример решения.

Пример 2

Произвести умножение 715·119.

Решение

Смешанные числа 715 и 119 можно представить в виде неправильных дробей: 135 и 109.

Получим, что 715·119=365·109=36·105·9.

Этот этап характеризуется применением правила сокращения дроби, тогда получим 36·105·9.

Мы раскладываем на простые множители и выполняем сокращение одинаковых множителей:

36·105·9=2·2·3·3·2·55·3·3=2·2·21=8

Ответ: 715·119=8.

Умножение смешенного и натурального числа

После того, как произведется замена неправильной дробью, умножение смешенного и натурального числа сводится к умножению обыкновенной дроби  и натурального числа.

Пример 3

Произвести умножение 2518 и 45.

Решение

Представляем смешанное число 2518 в виде неправильной дроби 4118, получим 2518·45=4118·45=41·4518. Необходимо заменить на простые множители и выделить целую часть:

41·4518=41·3·3·52·3·3=41·52=2052=10212

Ответ: 2518·45=10212.

Умножение смешенного и натурального числа рассматривается, как решение с распределительным свойством умножения относительно сложения. Получаем, что произведение смешанного  и натурального числа равно сумме произведений целой части на натурально число и дробной части на данное натуральное число, тогда получаем, что abc·n=a+bc·n=a·n+bc·n.

Пример 4

Вычислить 1038·8.

Решение

Необходимо заменить смешанное число суммой целой или дробной его части. Далее используем свойство распределительного умножения:

1038·8=10+38·8=10·8+38·8=80+3=83

Ответ: 1038·8=83.

Умножение смешанного числа и обыкновенной дроби

Умножение смешанного числа и обыкновенной дроби лучше представить в виде произведения обыкновенных дробей, умноженное на смешенное число неправильной дробью.

Пример 5

Умножить 323 на 415.

Решение

Заменим данное смешанное число 323 при помощи дроби 113, тогда получим, что 323·415=113·415=4·113·15=4445.

Ответ: 323·415=4445.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Умножение дроби на целые числа? Определение, примеры

Что такое целые числа?

Целые числа — это набор чисел, включающий все натуральные числа, а также 0. Например, 10, 18, 200 и т. д. 

Источник изображения

Что такое дробь?

Дроби часто называют числом между числами. Дроби — это числовые значения, которые представляют собой часть или часть целого. Например, посмотрите на пиццу ниже.

Эта пицца разрезана на 4 равные части. Таким образом, каждый кусок пиццы представляет собой 1 из 4 равных частей. Таким образом, математически мы можем представить каждую часть как $\frac{1}{4}$. Это число называется дробью.

В общем, когда целое разделено на равные части, каждая часть представляет собой часть целого, и мы записываем дроби как $\frac{a}{b}$, где a и b — действительные числа, а b не может быть равно нулю .

Число под чертой, представляющее общее количество равных частей, на которые делится целое, называется знаменателем. А число сверху, которое представляет количество рассматриваемых нами равных частей, называется числителем.

Умножение дробей на целые числа

Умножение двух чисел аналогично многократному сложению. Например,

2 раза по 4 или $2 \times 4$ равносильно добавлению числа «4» 2 раза.

Итак, умножение дробей на целые числа — это то же самое, что многократное сложение, когда мы складываем дробь столько же раз, сколько и целое число.

Например: попробуем перемножить 3 и $\frac{1}{4}$.

3 раза $\frac{1}{4}$ означает сложение дроби $\frac{1}{4}3$ раза.

Алгебраически это означает,

Мы можем решить это выражение визуально,

Источник

И наш ответ будет:

Но теперь давайте посмотрим, как мы можем обобщить это, не создавая модель каждый раз, когда мы хотим умножить целое число и дробь.

Умножение дробей с целыми числами

Сделаем это с помощью примера,

Умножим 5 и $\frac{3}{4}$.

Шаг 1: Преобразуйте 5 в дробную форму, применив 1 к знаменателю.

Шаг 2: Умножьте числитель на числитель и знаменатель на знаменатель.

И вуаля, у нас есть ответ.
В качестве дополнительного шага, если вы получили неправильную дробь, вы можете преобразовать ее в смешанное число.

Умножение смешанных дробей на целые числа

Умножение смешанных чисел на целые числа следует той же процедуре, только с дополнительным шагом.

Сделаем это на примере.

Как умножить 3 на $2\frac{1}{5}$?

Шаг 1: Преобразуйте смешанное число в неправильную дробь.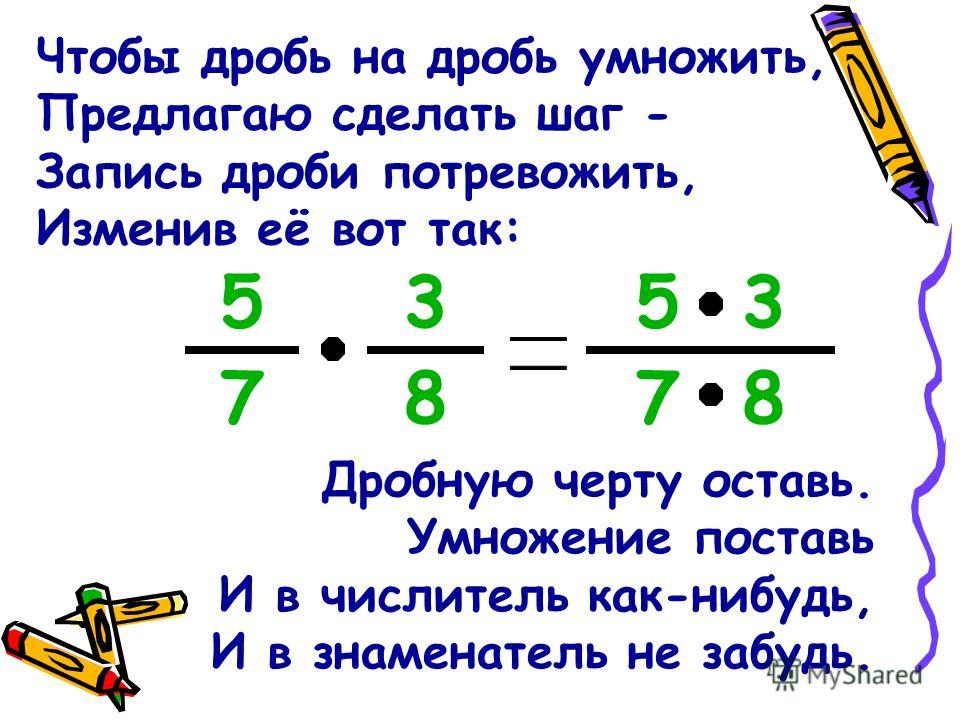

Шаг 2: Преобразуйте 3 в дробную форму, применив 1 к знаменателю.

Шаг 2: Умножьте числитель на числитель и знаменатель на знаменатель.

И после преобразования в неправильную дробь

Получим ответ:

Решенные примеры

Пример 1: Кэтрин готовит торт, для которого ей нужно три четверти чашки масла . Если она решит испечь три лепешки, сколько потребуется масла?

Решение : 

Количество лепешек $= 3$ 

Масло, необходимое для 1 лепешки $= \frac{3}{4}$ стаканов

Общее количество требуемого масла $= 3 \times { 3}{4} = \frac{9}{4} = 2\frac{1}{4}$ чашек

Пример 2. Найдите произведение целого числа 10 и смешанной дроби 523.  Решение : $10\times 5\frac{2}{3} = 10\times \frac{17}{3} = \frac{170}{3} = 56\frac{2}{3}$

Практические задачи

$8$$l$

$10$$l$

$9$$l$

$15$$l$

Правильный ответ: $9$$l$
Необходимое количество сока $= 15 \times \frac {3}{5} = \frac{45}{5} = $$9$$l$

$2\frac{2}{4}$ миль

$\frac{2}{5}$ миль

$2$ миль

$1\frac{1}{4}$ миль

Правильный ответ: $2\frac{2}{4}$ миль
Расстояние, пройденное за 10 дней $= 10 \times$ расстояния, пройденного за один день
$= 10 \times \frac{1}{4} = \frac{10}{4} = 2\frac{2}{4}$ миль

5

10

2

4

Правильный ответ: 4
Общее количество яблок $= 20$
Доля гнилых яблок $= \frac{1}{5}$
Количество гнилых яблок = 20 \times \frac{1}{5} = \frac{20}{5} = 4 яблока

Часто задаваемые вопросы

Как умножить дробь на целое число, используя числовую прямую?

Сначала мы отмечаем дробь на числовой прямой, а затем, чтобы умножить ее на целое число, прибавляем к той же дроби столько раз, сколько этого требует умножение.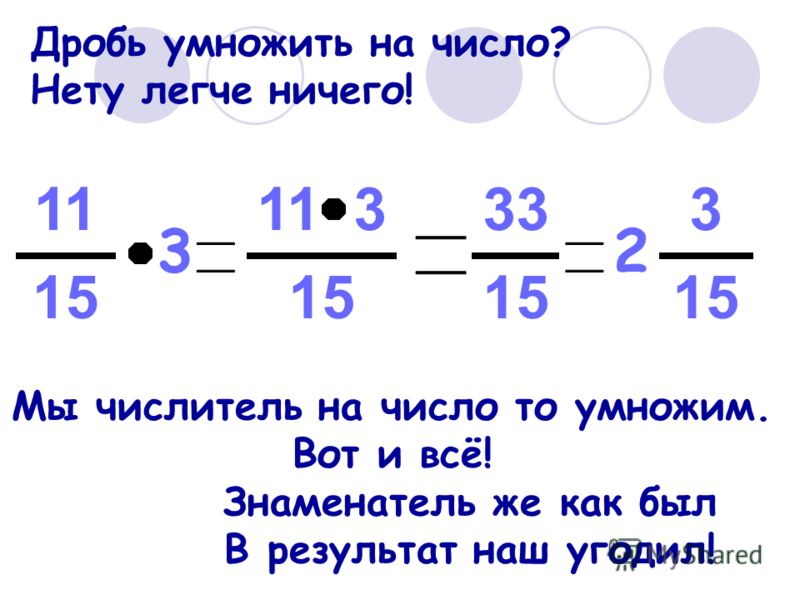

Каково произведение целого числа и смешанной дроби?

Произведением целого числа и смешанной дроби может быть смешанная дробь, неправильная дробь, правильная дробь или целое число.

Какое целое число дает тот же продукт, что и исходная дробь?

Число «1», умноженное на любую дробь, дает ту же дробь, что и ответ. Например, $1 \times \frac{3}{5} = \frac{3}{5}$.

Умножение дроби на целое число

Горячая математика

Чтобы умножить дробь на целое число, помните, что умножение — это многократное сложение.

Пример 1:

Умножить 1 7 ⋅ 3 .

Запишите умножение как сложение. Добавлять 1 7 три раза.

1 7 ⋅ 3 знак равно 1 7 + 1 7 + 1 7

Теперь нам просто нужно добавить дроби с одинаковыми знаменателями. Оставьте знаменатели одинаковыми и добавьте числители.

знак равно ( 1 + 1 + 1 ) 7 знак равно 3 7

Пример 2:

Умножить 5 ⋅ 3 16 .

5 ⋅ 3 16 знак равно 3 16 + 3 16 + 3 16 + 3 16 + 3 16 знак равно 5 ⋅ 3 16 знак равно 15 16

Другой способ подумать об этом — переписать целое число в виде дроби со знаменателем 1 .

5 ⋅ 3 16 знак равно 5 1 ⋅ 3 16

Затем умножьте числители а также знаменатели , по обычным правилам умножение дробей .

знак равно 5 ⋅ 3 1 ⋅ 16 знак равно 15 16

В некоторых случаях ваш ответ может быть больше, чем 1 , поэтому вы захотите переписать его как смешанное число . Возможно, вам также придется уменьшить дробь чтобы получить его в простейшей форме.

Пример 3:

Умножить 1 4 ⋅ 10 .

1 4 ⋅ 10 знак равно 10 4

И числитель, и знаменатель имеют общий делитель 2 .