Умножение натуральных чисел / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Умножение натуральных чисел
Умножение — одна из операций математики, предназначена для упрощения сложения одинаковых чисел.
Например: 4 + 4 + 4 = 4 · 3 = 12.
Умножение обозначают точкой «·» или крестиком «х».
Числа, которые умножаются, называют «множителями», результат умножения, называют «произведением»
Пример:
Алгоритм умножения чиселРазберем порядок умножения чисел на примере. Умножим число 25 на 16
1. Сначала записываем множители в столбик.
Второй множитель записывается под первым множителем так, что разряды второго множителя находились под соответствующими разрядами первого множителя, т. е. единицы второго множителя записываются под единицами первого, десятки под десятками и т.д. Снизу под записанными множителями проводится горизонтальная линия, а слева ставится знак умножения.
е. единицы второго множителя записываются под единицами первого, десятки под десятками и т.д. Снизу под записанными множителями проводится горизонтальная линия, а слева ставится знак умножения.
2. Производим последовательное умножение.
Сначала число, обозначающее разряд единиц класса единиц второго множителя последовательно умножаем на все разряды первого множителя.
Умножим цифру 6 на 5, получаем 30 — 3 десятка 0 единиц. 0 запишем под единицами, 3 «запомним». После этого 6 умножаем на цифру десятков первого множителя на 2, получаем 12. Прибавим к 12 получившиеся в предыдущем действии десятки, т.е. 3, в результате получаем 15. Поскольку разрядов в первом множителе больше нет., запишем число 15 под десятками. Первое неполное произведение 150.
3. Найдем второе неполное произведение. Последовательно умножим десятки второго множителя — 1 на все разряды первого слагаемого. Сначала 1 умножим на 5, получаем 5, запишем полученное произведение под десятками. После этого 1 умножаем на 2, получим 2, записываем 2 впереди 5. Второе неполное произведение 25. Поскольку мы умножали десяток второго слагаемого на первое слагаемое, запись второго неполного произведения 25 будет находиться под разрядом десятков. Получается «смещение» числа влево.
После этого 1 умножаем на 2, получим 2, записываем 2 впереди 5. Второе неполное произведение 25. Поскольку мы умножали десяток второго слагаемого на первое слагаемое, запись второго неполного произведения 25 будет находиться под разрядом десятков. Получается «смещение» числа влево.
4. Последовательно сложим цифры полученных неполных произведений по правилам сложения.
Свойства умножения натуральных чисел.1. Переместительное свойство умножения.
a · b = b · a
От перемены мест множителей произведение не изменится.
12 · 4 = 4 · 12
12 · 4 = 48
4 · 12 = 48
2. Сочетательное свойство умножения.
a · (b · c) = (a · b) · c
Произведение не зависит от группировки сомножителей.
2 · (3 · 6) = (2 · 3) · 6
2 · (3 · 6) = 36
1) 3 · 6 = 18; 2) 18 · 2 = 36
(2 · 3) · 6 = 36
1) 2 · 3 = 6; 2) 6 · 6 = 36
3.
a · (b + c) = ab + ac
При умножении числа на сумму двух других чисел, можно данное число умножить на каждое из слагаемых, а полученные результаты сложить.
3 · (5 + 4) = 3 · 5 + 3 · 4
3 · (5 + 4) = 27
1) 5 + 4 = 9; 2) 9 · 3 = 27
3 · 5 + 3 · 4 = 27
1) 3 · 5 = 15; 2) 3 · 4 = 12; 3) 12 + 15 = 27
4. Распределительное свойство умножения относительно вычитания
a · (b — c) = ab — ac
При умножении числа на разность двух других чисел, можно данное число умножить на уменьшаемое и на вычитаемое, а полученные результаты вычесть.
6 · (7 — 5) = 6 · 7 — 6 · 5
6 · (7 — 5) = 12
1) 7 — 5 = 2; 2) 2 · 6 = 12
6 · 7 — 6 · 5 = 12
1) 6 · 7 = 42; 2) 6 · 5 = 30; 3) 42 — 30 = 12
5. Свойство умножения единицы на натуральное число
Свойство умножения единицы на натуральное число
a · 1 = a
При умножении единицы на любое число, получим равное ему число.
1 · 76 = 76
6. Свойство умножения нуля на натуральное число
0 · a = 0
При умножении 0 на любое число, получим 0
0 · 123 = 0
Произведение всех натуральных чисел от 1 до называют факториал, записывают: , читают: «эн факториал». Следовательно, справедливо равенство:
= 123…
Пример:
3! = 123 = 6;
5! = 12345 =120.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 734, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 866, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1112, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 934, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 440, Мерзляк, Полонский, Якир, Учебник
Номер 441, Мерзляк, Полонский, Якир, Учебник
Номер 516, Мерзляк, Полонский, Якир, Учебник
Номер 572, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 1083, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 110, Мерзляк, Полонский, Якир, Учебник
Номер 201, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 1199, Мерзляк, Полонский, Якир, Учебник
Задание 252, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 580, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 594, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 612, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 797, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 884, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 12, Мерзляк, Полонский, Якир, Учебник
Номер 17, Мерзляк, Полонский, Якир, Учебник
Номер 78, Мерзляк, Полонский, Якир, Учебник
Номер 432, Мерзляк, Полонский, Якир, Учебник
Номер 528, Мерзляк, Полонский, Якир, Учебник
Номер 564, Мерзляк, Полонский, Якир, Учебник
Номер 706, Мерзляк, Полонский, Якир, Учебник
Номер 1006, Мерзляк, Полонский, Якир, Учебник
Номер 1033, Мерзляк, Полонский, Якир, Учебник
Умножение чисел столбиком
Технологическая карта урока.
Тема урока: Умножение натуральных чисел и его свойства.
Тип урока: урок систематизации и обобщения знаний и умений.
Оборудование: доска, задания для выполнения на уроке, интерактивная доска, проектор, карточки самооценивания, презентация.
Цели урока:
Обучающие: совершенствование навыка умножения натуральных чисел, применение рациональных приёмов вычислений. Продолжить работу над умножением натуральных чисел в столбик.
Развивающие: развивать умение анализировать,сравнивать, обобщать, делать выводы, развивать внимание, развивать устную речь.
Воспитательные: воспитывать умение высказывать свою точку зрения, слушать ответы других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству.
Методы:
По источникам знаний: словесные, наглядные;
По степени взаимодействия учитель-ученик: эвристическая беседа; интерактивный метод.
Относительно дидактических задач: подготовка к восприятию;
Относительно характера познавательной деятельности: активный метод, репродуктивный, частично- поисковый.
Планируемый результат.
УУД.
Личностные:умножают натуральные числа, используют свойства умножения, применяют рациональные приёмы для вычислений, формируют внимательность и аккуратность в вычислениях требовательное отношение к себе и к своей работе.
Познавательные: закрепляют навыки и умения применять алгоритмы при решении задач на умножение натуральных чисел и применение свойств умножения, систематизируют знания, обобщают и углубляют знания при решении задач по теме « Умножение натуральных чисел и его свойства», выбирают и формулируют познавательную цель, выражают смысл ситуации с помощью различных примеров.
Предметные: уметь в процессе реальной ситуации применять понятие умножение натуральных чисел и свойства умножения.
Регулятивные:
Самостоятельно формулируют познавательную цель и строят свои действия в соответствии с ней.
Планируют собственную деятельность, определяют средства для её осуществления.
Коммуникативные: регулируют собственную деятельность посредством речевых действий, умение слушать и вступать в диалог, воспитывать чувство взаимопомощи. Уважительное отношение к чужому умению, культуру учебного труда, требовательное отношение к себе и своей работе.
Технологическая карта урока математики в 5 классе
« Умножение натуральных чисел и его свойства».
Этап урока. | Задачи этапа. | Деятельность учителя. | Деятельность учеников. | Время. | Формируемые УУД | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.Организационный этап. | Создать благоприятный психологический настрой на работу. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Включаются в деловой ритм урока. | 1 | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности. Личностные: мотивация учения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Актуализация знаний Слайд№2-4. | Актуализация опорных знаний и способов действий. | 1. Организация устного счёта 60+9 =69 :3=23 -15=8 ∙12=96 :2=48 +12=60 2 Повторение теории 3. | Участвуют в работе по повторению: в беседе с учителем отвечают на поставленные вопросы. | 5 | Познавательные: структурирование собственных знаний. Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. Регулятивные: контроль и оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся. Слайд №5-6 | Обеспечение мотивации учения детьми, принятие ими целей урока. | Мотивирует учащихся, вместе с ними определяет тему и цель урока, акцентирует внимание учащихся на значимость темы. 1) 21∙10= 6) 4∙1000= 2) 100∙65= 7) 63∙100= 3) 34∙3= 8) 18∙7= 4) 27∙5= 9) 81∙3= 5) 316∙10= 10) 6∙23= Вопросы: 1) Посмотрите внимательно на выражения, на какие группы их можно разделить? 2) Какие примеры помогают быстрее вычислять? 2∙5=10 25∙4=100 5∙20=100 125∙8=1 000 125∙16=125∙8∙2=2 000 3) Вычислите и запомните! | Определяют тему и цели урока. Отвечают на вопросы учителя. Предлагают рациональные способы вычислений, и записывают в тетрадь основные примеры.(слайд №3) | 4 | Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.Применение знаний и умений в новой ситуации Слайд №7-8 | Показать разнообразие примеров на применение рациональных способов вычислений. | Организация и контроль за процессом решения примеров.
5) Какие свойства умножения можем применить при решении предложенных примеров?
Организация и контроль за процессом выполнения умножения в столбик вида: 467∙304 1) Посмотрите внимательно на выражения. Чем похожи примеры? 2) Что необходимо напомнить, друг другу, чтобы он избежал ошибок при вычислениях? 3) Выполните умножение в столбик 1) 467∙304=141968 2) 1208∙401=484408 3) 516∙309=159444 | Решают примеры (слайд№2).работают в парах над поставленными задачами. Проговаривают свойства умножения. На конкретных примерах учатся их применять. Выполняют задание на умножение натуральных чисел и применяют рациональные способы вычислений. Комментируют решения примеров. | 9 | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. Физкультминутка Слайд №9 | Смена деятельности. | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. «От улыбки хмурый день светлей» | Учащиеся сидят на месте и повторяют действия за учителем Учащиеся сменили вид деятельности и готовы продолжить работу | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6.Контроль усвоения, обсуждение допущенных ошибок и их коррекция. Слайд №10 | Дать качественную оценку работы класса и отдельных учащихся. | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. с/р на листочках самооценки
| Учащиеся анализируют свою работу, выражают в слух свои затруднения и обсуждают правильность решения примеров и задач. | 4 | Личностные: формирование позитивной самооценки, учатся принимать причины успеха (неуспеха). Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений. Регулятивные:умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7..Рефлексия. Слайд №11 | Дать количественную оценку работы учащихся. | Подводят итоги работы. Организуют обсуждение: Слайд №8.
| Учащиеся подводят итоги своей работы: Я сегодня понял… Я сегодня научился… Мне понравилось…, Мне не понравилось. Я не понял… | 2 | Регулятивные: оценивание собственной деятельности на уроке. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. Информация о домашнем задании. Слайд №12 | Обеспечение понимания детьми содержания и способов выполнения домашнего задания. | Даёт комментарий к домашнему заданию. П. 1.10, № 142 (3 ст.), № 143 (1 и 2 ст.) | Учащиеся записывают в дневники задание | 3 |
Лист самооценки
Фамилия | Результат | |
1 | Устный счет | |
2 | Закончи предложение | |
3 | Найдите значение выражения | |
4 | Вычисли и запомни | |
5 | Вычисли удобным способом | |
6 | Умножение столбиком | |
с/р в-1 | ||
1 | Вычислите удобным способом 25·96·4= 306·8·125= | |
2 | Торт в 3 раза дороже, чем 5 пирожных. | |
3 | Выполните умножение 5075·68 |
Фамилия | Результат | |
1 | Устный счет | |
2 | Закончи предложение | |
3 | Найдите значение выражения | |
4 | Вычисли и запомни | |
5 | Вычисли удобным способом | |
6 | Умножение столбиком | |
с/р в-2 | ||
1 | Вычислите удобным способом 4·316·25= 207·125·8= | |
2 | Бочка вмещает воды в 9 раз больше, чем 4 ведра. | |
3 | Выполните умножение 4075·84 |
7.Рефлексия
Притча.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
— Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.
— Кто работал как первый человек?
— Кто работал добросовестно?
— Кто принимал участие в строительстве храма своих знаний?
Конспект урока по теме: Умножение чисел столбиком | План-конспект урока по математике (5 класс) на тему:
УРОК № 22 (28. 09.16)
09.16)
Технологическая карта урока математики в 5 классе по теме: «Умножение чисел столбиком. Свойства умножения»
Тип урока: урок систематизации знаний
Форма урока: урок-практикум
Образовательная цель урока: совершенствование навыков умножения натуральных чисел с применением свойств умножения натуральных чисел; применение рациональных приёмов вычислений; продолжение работы над текстовыми задачами.
Деятельностная цель урока: формирование у обучающихся способностей к самостоятельному построению новых способов действий по теме: «Умножение чисел столбиком. Свойства умножения» на основе метода рефлексивной самоорганизации.
Планируемые результаты деятельности обучающихся:
Предметные: обучающиеся должны уметь применять правила умножения натуральных чисел, сложения, вычитания натуральных чисел, правило сравнения натуральных чисел; анализировать и осмысливать текст задачи, составлять план решения задачи (арифметическим способом).
Метапредметные: обучающиеся должны обнаруживать и формулировать учебную проблему; осуществлять самооценку и самокоррекцию учебной деятельности, саморефлексию; уметь понимать точку зрения другого, слушать.
Личностные: способность осуществлять самооценку на основе критерия успешности учебной деятельности, обучающиеся должны объяснять самому себе свои отдельные ближайшие цели саморазвития, понимать и осознавать социальную роль ученика; проявлять положительное отношение к урокам математики, интерес к способам решения новых учебных задач, понимать причины успеха или неуспеха в своей учебной деятельности.
Межпредметные связи: подготовка к изучению алгебры, геометрии и физики
Оборудование урока: учебник Математика,5 кл. С.М. Никольский, 2014 г., доска, рабочая тетрадь, карточки.
Дидактическая структура (этапы урока), время | Смысловой блок (содержание) | Методы и формы | Деятельность учителя | Деятельность ученика | Планируемый результат, формирование УУД |
1 Организационный момент, 1 мин. | Создание благоприятного психологического настроя на работу | Словесный Коллективная | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. — Добрый день. Ребята, проверьте свою готовность к уроку. Кто полностью готов, посмотрите на меня и улыбнитесь. | Включаются в деловой ритм урока. Проявление интереса к материалу изучения. | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности. Личностные: мотивация учения. |
II Работа над ошибками в к.р. №1 10 мин. | Контроль применения полученных знаний при решении примеров и задач | Словесный Индивидуальная | Контроль и анализ ошибок, допущенных детьми в примерах и задаче на контрольной работе от 27. | Представление собственного опыта, высказывание собственных мыслей | Личностные: оценивание усваиваемого материала |
III Актуализация субъектного опыта учащихся, 5 мин. | Повторение правил сложения и вычитания натуральных чисел. Проверка умений осуществлять переход от сложения к умножению. | Наглядный Парная | Организация актуализации требований к ученику с позиций учебной деятельности: устного счёта и повторения основных типов примеров на умножение натуральных чисел и свойств умножения. Графический диктант с взаимопроверкой
| Участвуют в работе по повторению: в беседе с учителем отвечают на поставленные вопросы. Демонстрируют знания, умения. | Познавательные: структурирование собственных знаний. Коммуникативные: организовывать учебное сотрудничество с учителем и сверстниками. Регулятивные: оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала |
IV Постановка цели и задач урока, 3 мин. | Мотивация учебной деятельности учащихся | Словесный Индивидуальная | Мотивирует учащихся на определение темы и цели урока, акцентирует внимание учащихся на значимость темы; обращает внимание на грамотность при написании даты и темы урока Математический диктант: 1.Сколько существует способов разложения числа 16 на два множителя? а) 3 способа; б) 2 способа; в) 4 способа. 2. В магазин привезли 8 коробок конфет по 7 кг каждая и 12 коробок печенья по 4 кг каждая. а)общий вес кондитерских изделий, привезенных в магазин; б) на сколько кг коробка с конфетами тяжелее коробки с печеньем; в) на сколько кг вес всех конфет больше веса всего привезенного печенья. 3. Точка B лежит на прямой между точками А и С. Длина отрезка АВ равна 8 см, а отрезок АС в 3 раза длиннее отрезка АВ. Длина ВС равна: б) 24 см; б) 16 см; в) 11 см. Вопросы:
| Записывают в тетрадь дату, определяют тему и цели урока. Выполняют самостоятельно, потом проверяют ответы. Отвечают на вопросы учителя. Предлагают рациональные способы вычислений и записывают в тетрадь основные | Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. |
V Применение изученного в новой ситуации, 5 мин. | Усвоение учениками нового способа действий | Наглядный и практичес- кий Парная | Организация и контроль над процессом решения примеров. Организует усвоения учениками нового способа действий с проговариваем во внешней речи. Организация работы в парах. 1.Какие свойства умножения можем применить при решении предложенных примеров?
— Пробуем решить несколько примеров. 2.Тренировочные упражнения по учебнику: № 141, 144. | Решают примеры , работают в парах над поставленными задачами. Проговаривают свойства умножения. На конкретных примерах учатся их применять. Выполняют задание на умножение натуральных чисел и применяют рациональные способы вычислений. Комментируют решения примеров. | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
VI Физкультминутка, 1 мин. | Смена деятельности, обеспечивающая эмоциональную разгрузку учащихся; профилактика утомления, нарушения осанки. | Практичес-кий Коллективная | Давайте немного отдохнём. Поднимает руки класс — это «раз». Повернулась голова – это «два». Руки вниз, вперёд смотри – это «три». Руки в стороны пошире развернули на «четыре», С силой их к груди прижать – это «пять». Всем ребятам надо сесть – это «шесть». | Учащиеся поднимаются с мест и повторяют действия за учителем. Учащиеся сменили вид деятельности и готовы продолжить работу. Получают эмоциональный заряд. Дети проводят подходящую физкультминутку с минимальной помощью учителя. | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. |
VII Обобщение и систематизация полученных знаний, 8 мин. | Продолжение формирования навыка применения правила умножения натуральных чисел. | Наглядный и практичес-кий Парная и групповая | Организация и контроль над процессом решения текстовой задачи под диктовку. ЗАДАЧА: На склад привезли 5 ящиков с красками, по 144 коробки в каждом ящике. В каждой коробке имеется 12 тюбиков краски. Сколько тюбиков краски привезли на склад всего?
В зависимости от предложенных вариантов строится дальнейший разбор и решение задачи. Решение:
Ответ: 8640 тюбиков. | Решают задачу, работают в парах над текстовой задачей. Обсуждают подходы для решения задачи. Выполняют краткую запись по условию задачи , отвечают на поставленные вопросы Комментируют действия для решения задачи. Учащиеся предлагают несколько вариантов первого действия к задаче. | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
VIII Контроль и самоконтроль, 7 мин. | Проверка усвоения полученных знаний, обсуждение допущенных ошибок | Наглядный Индивиду-альная | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. Каждому на парту дается тест. Из учебника № 142 дополнительно тем, кто закончил работу с тестом раньше. | Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения теста, примеров, задач. | Личностные: формирование позитивной самооценки, учатся принимать причины успеха (неуспеха). Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений. Регулятивные: умение самостоятельно анализировать правильность выполнения действий и вносить необходимые коррективы. |
IX Рефлексия, 3 мин. | Обеспечение осознания учащимися своей учебной деятельности на уроке. Соотнесение цели урока и результата. | Словесный Фронтальная | Организует фиксирование нового содержания, рефлексию, самооценку учебной деятельности. Организуют обсуждение:
| Ученики отвечают на вопросы.Рассказыва-ют, что узнали. Учащиеся подводят итоги своей работы: -Я сегодня понял… -Я сегодня научился… -Мне понравилось…, -Мне не понравилось. -Я не понял… | Регулятивные: уметь правильно оценивать собственную деятельность на уроке. Предметные: уметь читать буквенные выражения. |
X Информация о домашнем задании, 2 мин. | Обеспечение понимания детьми содержания и способов выполнения д/з | Словесный Коллективная | Даёт комментарий к домашнему заданию. п.1.10 разобрать, № 143 (1.2 ст.) | Учащиеся записывают задание в дневники |
5 класс.
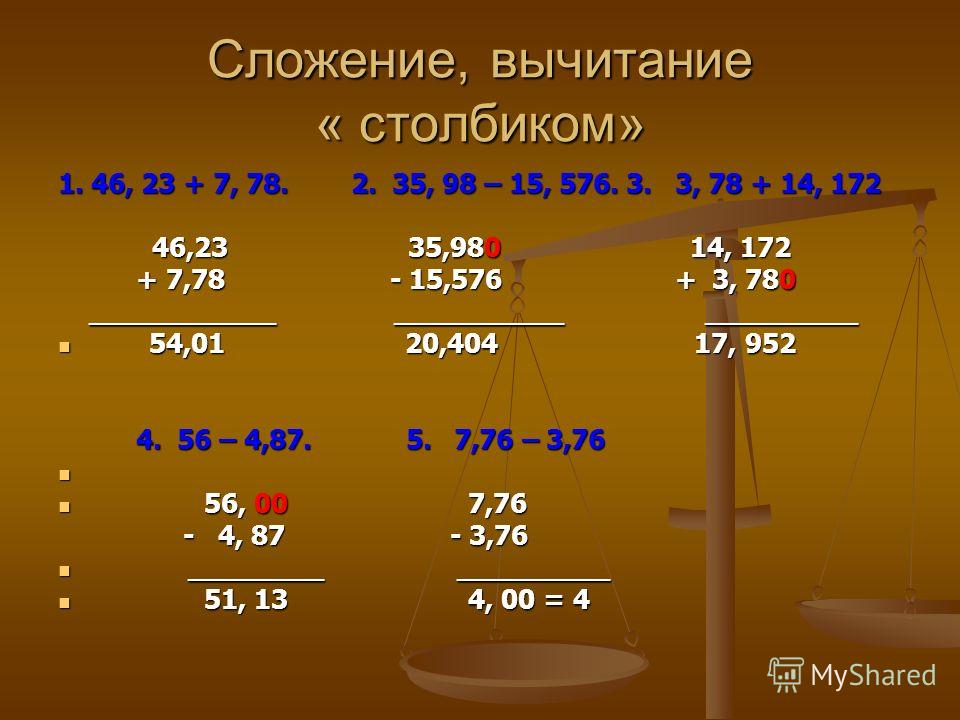 Математика. Никольский. Учебник. Ответы к стр. 36
Математика. Никольский. Учебник. Ответы к стр. 36Натуральные числа и нуль
Умножение чисел столбиком
Ответы к стр. 36
137. Какие законы используют при умножении столбиком?
Законы сложения и умножения: α + 0 = α, α • 0 = 0, α • 1 = α, таблица умножения.
138. Объясните, как выполнено умножение:
а) ×748 б) ×973 в) ×7050
6 50 7
4488 48650 49350
г) ×926 д) ×326 е) ×4830
38 502 4900
+ 7408 + 652 + 4347
2778 1630 1932
35188 163652 23667000
а) Умножение трёхзначного числа на однозначное.
б) Так как 973 • 50 = 973 • 5 • 10, то можно сначала умножить 973 на 5, а затем полученный результат умножить на 10, то есть приписать к нему справа нуль. Поэтому 5 пишем под 3, а ноль приписываем справа.
Поэтому 5 пишем под 3, а ноль приписываем справа.
в) Так как 7050 • 7 = 705 • 10 • 7, то можно сначала умножить 705 на 7, а затем полученный результат умножить на 10, то есть приписать к нему справа нуль. Поэтому 7 пишем под 5, а ноль приписываем справа.
г) Умножение трёхзначного числа на двухзначное.
д) Число 502 содержит цифру 0 при умножении на которую числа 326 получается 0. Поэтому эту строку в вычислениях можно опустить, а значение произведения 326 на 5 начать записывать справа налево под цифрой 5.
е) Так как 4830 • 4900 = 483 • 10 • 49 • 100 = 483 • 49 • 1000, то можно сначала умножить 483 на 49, а затем полученный результат умножить на 1000, то есть приписать к нему справа три нуля. Поэтому 9 пишем под 3, а нули приписываем справа.
139. Вычислите произведение чисел:
а) 12 • 10; б) 32 • 100; в) 65 • 1000;
г) 20 • 100; д) 300 • 1000; е) 1500 • 100;
ж) 10 • 190; з) 1000 • 20; и) 100 • 380;
к) 129 • 100; л) 1000 • 130; м) 2900 • 10.
а) 12 • 10 = 120;
б) 32 • 100 = 3200;
в) 65 • 1000 = 65 000;
г) 20 • 100 = 2000;
д) 300 • 1000 = 300 000;
е) 1500 • 100 = 150 000;
ж) 10 • 190 = 1900;
з) 1000 • 20 = 20 000;
и) 100 • 380 = 38 000;
к) 129 • 100 = 12 900;
л) 1000 • 130 = 130 000;
м) 2900 • 10 = 29 000.
140. Вычислите произведение чисел:
а) 24 • 2; б) 31 • 3; в) 52 • 4; г) 71 • 9;
д) 23 • 8; е) 9 • 18; ж) 65 • 4; з) 76 • 5;
и) 48 • 9; к) 8 • 34; л) 7 • 85; м) 9 • 78.
а) 24 • 2 = (20 + 4) • 2 = 20 • 2 + 4 • 2 = 40 + 8 = 48;
б) 31 • 3 = (31 + 1) • 3 = 30 • 3 + 1 • 3 = 90 + 3 = 93;
в) 52 • 4 = (50 + 2) • 4 = 50 • 4 + 2 • 4 = 200 + 8 = 208;
г) 71 • 9 = (70 + 1) • 9 = 70 • 9 + 1 • 9 = 630 + 9 = 639;
д) 23 • 8 = (20 + 3) • 8 = 20 • 8 + 3 • 8 = 160 + 24 = 184;
е) 9 • 18 = 9 • (10 + 8) = 9 • 10 + 9 • 8 = 90 + 72 = 162;
ж) 65 • 4 = (60 + 5) • 4 = 60 • 4 + 5 • 4 = 240 + 20 = 260;
з) 76 • 5 = (70 + 6) • 5 = 70 • 5 + 6 • 5 = 350 + 30 = 308;
и) 48 • 9 = (40 + 8) • 9 = 40 • 9 + 8 • 9 = 360 + 72 = 432;
к) 8 • 34 = 8 • (30 + 4) = 8 • 30 + 8 • 4 = 240 + 32 = 272;
л) 7 • 85 = 7 • (80 + 5) = 7 • 80 + 7 • 5 = 560 + 35 = 595;
м) 9 • 78 = 9 • (70 + 8) = 9 • 70 + 9 • 8 = 630 + 72 = 702.
141. Вычислите произведение чисел:
а) 132 • 5; б) 645 • 3; в) 5 • 418; г) 7 • 338;
д) 106 • 4; е) 401 • 6; ж) 4381 • 2; з) 7713 • 8;
и) 7 • 6204; к) 9 • 5007; л) 6 • 5769; м) 7 • 777.
а) ×132 б) ×645 в) ×418 г) ×338
5 3 5 7
660 1935 2090 2366
д) ×106 е) ×401 ж) ×4381 з) ×7713
4 6 2 8
424 2406 8762 61704
и) ×6204 к) ×5007 л) ×5769 м) ×777
7 9 6 7
43428 45063 34614 5439
142. Вычислите произведение чисел:
а) 23 • 11; б) 42 • 12; в) 22 • 33;
г) 53 • 31; д) 68 • 61; е) 64 • 24;
ж) 79 • 23; з) 72 • 25; и) 42 • 68;
к) 37 • 33; л) 74 • 15; м) 37 • 66;
н) 48 • 37; о) 54 • 29; п) 63 • 36.
а) ×23 б) ×42 в) ×22
11 12 33
+ 23 + 84 + 66
23 42 66
253 504 726
г) ×53 д) ×68 е) ×64
31 61 24
+ 53 + 68 + 256
159 408 128
1643 4148 1536
ж) ×79 з) ×72 и) ×42
23 25 68
+ 237 + 360 + 336
158 144 252
1817 1800 2856
к) ×37 л) ×74 м) ×37
33 15 66
+ 111 + 370 + 222
111 74 222
1221 1110 2442
н) ×48 о) ×54 п) ×63
37 29 36
+ 336 + 486 + 378
144 108 189
1776 1566 2268
143.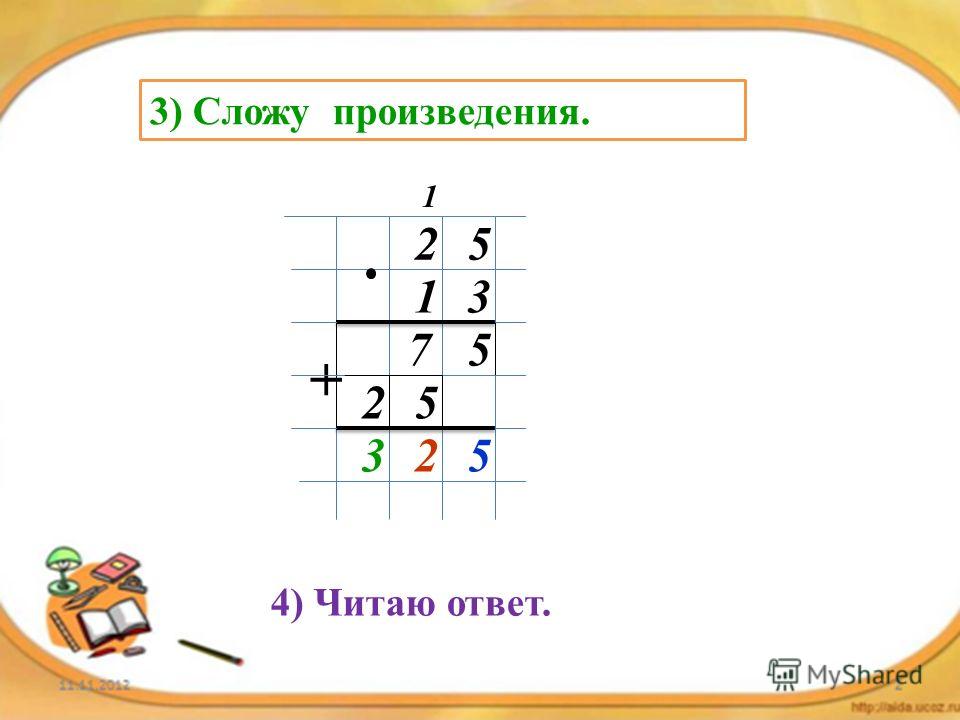 Вычислите произведение чисел:
Вычислите произведение чисел:
а) 86 • 49; б) 92 • 16; в) 88 • 97;
г) 951 • 18; д) 663 • 26; е) 847 • 64;
ж) 101 • 332; з) 302 • 648; и) 321 • 562;
к) 955 • 317; л) 861 • 242; м) 999 • 732;
н) 679 • 679; о) 125 • 125; п) 420 • 450.
а) ×86 б) ×92 в) ×88
49 16 97
+ 774 + 552 + 616
344 92 792
4214 1472 8536
г) ×951 д) ×663 е) ×847
18 26 64
+ 7608 + 3978 + 3388
951 1326 5082
17118 17238 54208
ж) ×332 з) ×648 и) ×321
101 302 562
+ 332 + 1296 642
332 1944 +1926
33532 195696 1605
180402
к) ×955 л) ×861 м) ×999
317 242 732
6685 1722 1998
+955 +3444 +2997
2865 1722 6993
302735 208362 731268
н) ×679 о) ×125 п) ×420
679 125 450
6111 625 +210
+4753 +250 168
4074 125 189000
461041 15625
144. Вычислите наиболее простым способом:
Вычислите наиболее простым способом:
а) 24 • 98 + 24 • 2; б) 305 • 199 + 305 • 1;
в) 49 • 18 + 18; г) 153 • 598 + 306.
а) 24 • 98 + 24 • 2 = 24 • (98 + 2) = 24 • 100 = 2400;
б) 305 • 199 + 305 • 1 = 305 • (199 + 1) = 305 • 200 = 61 000;
в) 49 • 18 + 18 = (49 + 1) • 18 = 50 • 18 = 900;
г) 153 • 598 + 306 = 153 • 598 + 153 • 2 = 153 • (598 + 2) = 153 • 600 = 91 800.
145. Выполните действие:
а) 325 • 40; б) 3508 • 250; в) 7380 • 420;
г) 3800 • 550; д) 48 • 9; е) 789 • 1020.
а) ×325 б) ×3508 в) ×7380
40 250 420
13000 +17540 + 1476
7016 2952
877000 3099600
г) ×3800 д) ×48 е) ×789
550 9 1020
+190 432 +1578
190 789
2090000 804780
Ответы по математике.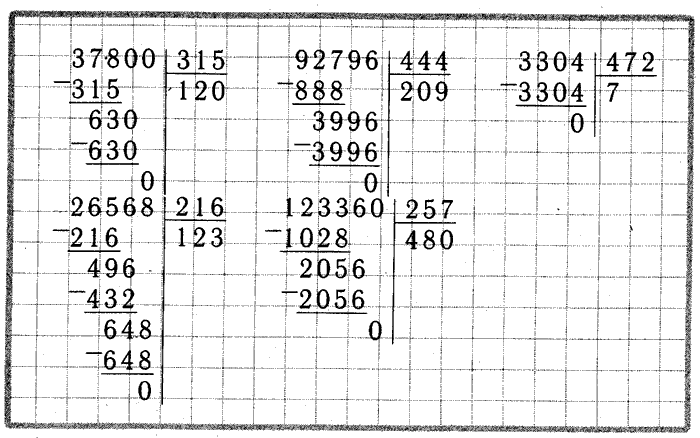 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Сложение столбиком 3 чисел. Сложение трехзначных чисел столбиком.
- Альфашкола
- Статьи
- Как складывать 3 числа в столбик?
Когда вы хотите сложить три числа, вы можете также сложить их столбиком. Сложение трех чисел происходит аналогично сложению двух чисел:
десятки цифр располагаются под десятками, сотни под сотнями и так далее. Затем складываем по столбцам, начиная со столбца справа. Сложение чисел столбиком можете почитать в статье Как складывать числа в столбик?
Пример 1. Сложите три числа: \(121+ 262+13\) в столбик.
Решение:
Ответ: \(396.\)
Также не забываем, если при сложении образуется число больше 9, то мы запоминаем десятки и складываем к следующему разряду
Пример 2. Сложите три числа: \(283+ 232+113\) в столбик.
Решение:
Ответ: \(628.\)
Пример 3. Сложите три числа: \(487+ 232+113\) в столбик.
Решение:
Ответ: \(832.\)
Пример 4. Сложите три числа: \(487+ 188+289\) в столбик.
Решение:
Ответ: \(964.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Олеся Гвидоновна Сиротенко
Репетитор по математике
Стаж (лет)
Образование:
Могилевский государственный университет им А. А. Кулешова
А. Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов. Занимаюсь подготовкой к сдаче ОГЭ, ЕГЭ. В преподавании считаю самым главным комфортную атмосферу и доверие. Помогаю ученикам не бояться ошибок. Считаю, что умение помочь ученику поверить в свои силы, увидеть свой потенциал — это миссия каждого учителя!
Юлия Анатольевна Шустова
Репетитор по математике
Стаж (лет)
Образование:
Тюменский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов. Приветствую всех желающих изучать химию — науку о веществах и превращениях! Однажды открыв для себя этот волшебный мир, вы захотите снова и снова узнавать его тайны. Я с удовольствием сделаю для вас эту науку простой и понятной , покажу ученику, что мир химии очень интересен и увлекателен!
Приветствую всех желающих изучать химию — науку о веществах и превращениях! Однажды открыв для себя этот волшебный мир, вы захотите снова и снова узнавать его тайны. Я с удовольствием сделаю для вас эту науку простой и понятной , покажу ученику, что мир химии очень интересен и увлекателен!
Тамара Анатольевна Меркулова
Репетитор по математике
Стаж (лет)
Образование:
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов. Математика – это ясный и логичный мир, который откроется вам, когда вы узнаете его поближе. Надеюсь, вам он тоже понравится, как нравится мне. Я помогу вам понять законы и правила математики, справиться с трудными и опасными местами там. Мы сможем спокойно и уверенно подготовиться к любым контрольным и экзаменам. Ни ОГЭ, ни ЕГЭ не будут для вас препятствием.
Надеюсь, вам он тоже понравится, как нравится мне. Я помогу вам понять законы и правила математики, справиться с трудными и опасными местами там. Мы сможем спокойно и уверенно подготовиться к любым контрольным и экзаменам. Ни ОГЭ, ни ЕГЭ не будут для вас препятствием.
Похожие статьи
- Объем куба
- Площадь произвольного четырехугольника
- НИУ ВШЭ (МИЭМ): Прикладная математика
- ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 1)
- ЕГЭ по математике, базовый уровень. Задачи с прикладным содержанием (вариант 3)
- Задачи на совместную работу (вариант 3)
- Задачи на прогрессии
- Два мира, живущие недалеко друг от друга
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Способы умножения.

- Авторы
- Руководители
- Файлы работы
- Наградные документы
Солдатова В.А. 1
1МБОУ СОШ №3 г.Тосно
Неизвестный Е.В. 1
1МБОУ СОШ №3 г.Тосно
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения. В школе мы изучаем таблицу умножения, а затем учимся умножать числа в столбик. Это не единственный способ умножения. На самом деле, существует несколько десятков способов умножения многозначных чисел.
Актуальность: В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» я выбрала тему проекта «Различные способы умножения».
Цель: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Задачи:
Найти и разобрать различные способы умножения.
Научиться демонстрировать некоторые способы умножения.
Рассказать о новых способах умножения и научить одноклассников ими пользоваться.
Основная часть
История появления таблицы умножения.
При раскопках здания в городе Нара, древней столице Японии, археологами была найдена деревянная табличка с фрагментом таблицы умножения. Из всех табличек, обнаруженных в Японии, найденная – самая древняя.
Из всех табличек, обнаруженных в Японии, найденная – самая древняя.
Каким же образом жители Японии впервые узнали о математической «запоминалочки»? Судя по тому, что иероглифы, которыми записаны цифры напоминают китайское письмо, скорее всего, она была просто скопирована из китайского учебника арифметики того времени. А откуда она взялась в Китае? Не исключено, что именно там ее впервые и придумали.
Эту версию подтверждает находка, сделанная китайскими археологами на юге страны. Там была обнаружена дощечка, на которой был фрагмент таблицы умножения, возраст которой ученые оценили в 2700 -3000 лет.
На основании этой находки ученые Китая предложили гипотезу, согласно которой впервые таблица умножения была составлена в Древнем Китае, а потом вместе с караванами проникли в Индию, а оттуда в страны Передней Азии и Европу. Однако этой версии противоречат многие находки, сделанные ранее. Например, в Индии в свое время были обнаружены более древние варианты таблицы умножения, возраст которых оценивается в 3000-3200 лет.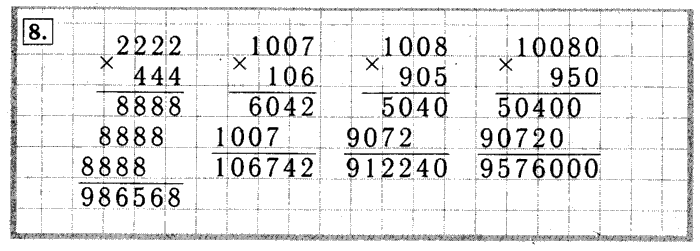
Самые старые в мире таблицы умножения были найдены при раскопках городов Древней Месопотамии. Они были нанесены с помощью клинописи на глиняные таблички, возраст которых составляет 5000 лет. Скорее всего, таблица умножения появилась где-то в тех краях.
Хотя не исключено также и то, что данная система устного счета появилась независимо в разных местах. Узнать имя гениального математика, который первым додумался записать результаты умножения в виде таблицы, скорее всего, не удастся. Это пришло в голову сразу нескольким людям. В европейской культуре автором таблицы умножения считается знаменитый греческий математик Пифагор. [1, с.78]
Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть ли не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
За тысячелетия развития математики было придумано множество способов умножения чисел, и все эти приемы соперничали друг с другом и усваивались с большим трудом. [2, с.16]
Давайте рассмотрим наиболее интересные и простые способы умножения.
Способы умножения
Русско-крестьянский способ умножения.
Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоений другого числа. Пример: 32 х 13
Пример: 32 х 13
|
Множимое =32 |
Множитель = 13 |
|
32 |
13 |
|
16 |
26 |
|
8 |
52 |
|
4 |
104 |
|
2 |
208 |
|
1 |
416 |
Таблица 1.
Деление пополам (см. левую половину Табл.1) продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число (правая часть Табл.1). Последнее удвоенное число и дает искомый результат.
Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение:( 32 х 13 ) = ( 1 х 416 ) [3, с.54]
Особо внимательные заметят «А как быть с нечетными числами, которые не кратны 2-м?».
Итак, пусть нам необходимо умножить два числа: 987 и 1998. Одно запишем слева, а второе — справа на одной строчке. Левое число будем делить на 2, а правое — умножать на 2 и результаты записывать в столбик. Если при делении возникнет остаток, то он отбрасывается.
Операцию продолжаем, пока слева не останется 1. Затем вычеркнем те строчки, в которых слева стоят четные числа и сложим оставшиеся числа в правом столбце. Это и есть искомое произведение. [3, с.67] Дана графическая иллюстрация по данному описанию. ( см. Таблицу 2.)
Это и есть искомое произведение. [3, с.67] Дана графическая иллюстрация по данному описанию. ( см. Таблицу 2.)
Таблица 2.
Квадрат Пифагора.
1 2 3
4 5 6
7 8 9
Это всем известный Квадрат Пифагора, отражающий мировую систему счисления, состоящую из девяти цифр: от 1 до 9. Выражаясь современным языком – это девяти разрядная числовая матрица, в которой цифры, являющиеся основой для дальнейших вычислений любой сложности расположены в порядке возрастания. Квадрат Пифагора называют и Эннеадой, а тройку цифр — триада. Можно рассматривать тройки цифр расположенные по горизонтали (123, 456, 789) и по вертикали(147, 258, 369). Причем, записанные таким образом, тройки цифр начинают обозначать уже особые числа, подчиняющиеся законам математической пропорции и гармонии.
Вспомним главное правило древнеегипетской математики, в котором сказано, что умножение производится при помощи удвоения и сложения полученных результатов; то есть каждое удвоение есть сложение числа с самим собой. Поэтому интересно посмотреть на результат подобного удвоения цифр и чисел, но полученному современным методом складывания « в столбик», известному даже в начальных классах школы. Это будет напоминать египетскую систему счисления, по сути, с разницей в том, что все цифры либо числа записываются в один столбик (без указания того или иного действия в соседнем столбике — как у египтян). [4, с.97]
Поэтому интересно посмотреть на результат подобного удвоения цифр и чисел, но полученному современным методом складывания « в столбик», известному даже в начальных классах школы. Это будет напоминать египетскую систему счисления, по сути, с разницей в том, что все цифры либо числа записываются в один столбик (без указания того или иного действия в соседнем столбике — как у египтян). [4, с.97]
Начнем с цифр, составляющих Квадрат Пифагора: от 1 – до 9.
1 2 3 4 5 6 7 8 9
2 4 6 8 10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
10 20 30 40 50 60 70 80 90
Цифра 1: обычный последовательный ряд цифр.
Цифра 9: левый столбик — четкий восходящий ряд («поток»).
правый столбик — четкий нисходящий ряд последовательных цифр. Условимся называть восходящим ряд, значения чисел в котором увеличиваются сверху вниз ; в нисходящем же – наоборот: уменьшаются значения чисел сверху вниз.
Условимся называть восходящим ряд, значения чисел в котором увеличиваются сверху вниз ; в нисходящем же – наоборот: уменьшаются значения чисел сверху вниз.
Цифра 2: в правом столбике повторяются четные цифры 2,4,6,8 («в периоде»).
Цифра 8: такой же повтор — только в обратном порядке- 8,6,4,2.
Цифры 4 и 6: четные цифры «в периоде» 4,8,2,6 и 6,2,8,4.
Цифра 5: подчиняется правилу сложения цифры 5- чередование 5 и 0.
Цифра 3: правый столбик — нисходящий ряд уже не цифр, а чисел, образующих тройки вертикальных рядов в квадрате Пифагора- 369, 258, 147. Причем, отсчет идет «из правого угла квадрата» или справа налево. Здесь также действует принятое выше правило восходящего — нисходящего ряда. Но восходящий ряд – это движение от тройки чисел 147 до тройки 369; нисходящий — от 369 до 147.
Цифра 7: восходящий ряд чисел 147,258,369 из «левого угла» или слева направо. Впрочем, все зависит от того, как изображена сама девятиразрядная числовая матрица — где поставить цифру 1.
Китайский способ умножения.
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:
Этот рисунок состоит из 10 линий (количество может быть любым)
Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
А эти линии обозначают число 13 (1 линия, отступ, 3 линии)
Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом: (пересечения на рисунке указаны точками)
Количество пересечений:
Верхний левый край: 2
Нижний левый край: 6
Верхний правый: 4
Нижний правый: 12
1) Пересечения в верхнем левом крае (2) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа
3) Пересечения в нижнем правом крае (12) – третье число ответа.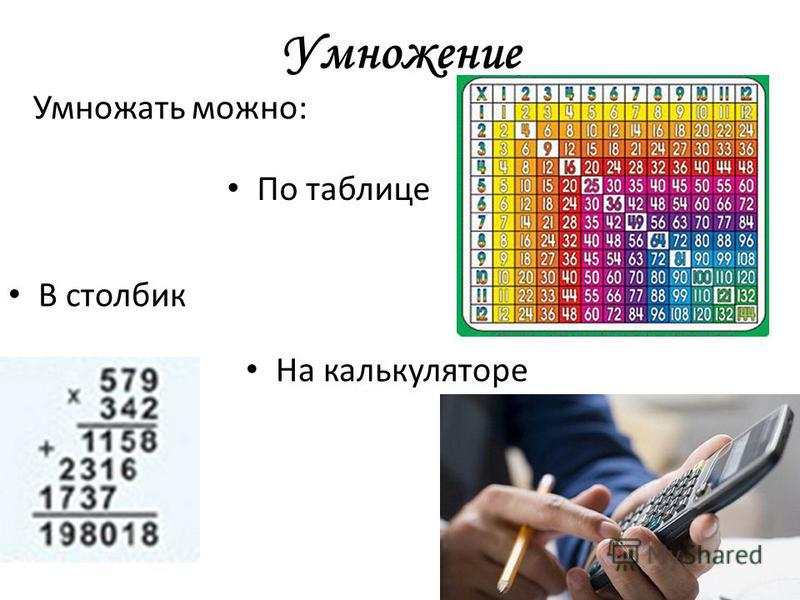
Получается: 2; 10; 12.
Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.
3(2+1)1(0+1)2
Ответ: 312 [5, с.48]
Итальянский способ умножения.
В Италии, а также во многих странах Востока, этот способ приобрел большую известность. [5, с.74]
Использование приема:
Например, умножим 6827 на 345.
Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
Умножаем число каждого ряда последовательно на числа каждой колонки.
т.е.
6*3 = 18. Записываем 1 и 8
8*3 = 24. Записываем 2 и 4
Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.
(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)
Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
Ответ: 2355315.
Таблица Оконешникова.
Рис.1. Таблица Оконешникова
Умножение не стоит на месте, о чем доказывает новый способ умножения, который разработал Василий Иванович Оконешников. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе и «теперь ребята смогут умножать и складывать в уме не только единицы, десятки, но также миллионы, триллионы и даже, не пугайтесь, секстиллионы с квадриллионами»При этом каждая кнопка делится еще на 9 квадратов, в которой записываются результаты перемножения числа данной кнопки на числа от одного до девяти, т.е. получаем своеобразную таблицу умножения. Данный метод имеет ограничение — умножение делается на однозначное число. Например, найдем произведение чисел 148 и 4.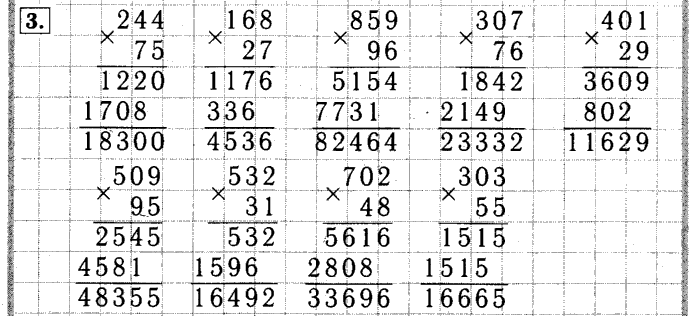 Для этого обратимся к квадрату соответствующему четверке, выбираем числа, соответствующие цифрам числа по порядку: единице, четверке, восьмерке. Получаем: 04 16 32. Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие складываем попарно: четверку с единицей, шестерку с тройкой.. Последняя цифра также без изменений. 0(4 + 1)(6+3)2 = 0592. Число 592 и есть результат умножения. Произведя расчет по методу Василия Ивановича Оконешникова при умножении многозначного числа на однозначное, этот метод достаточно прост и быстр, если имеется готовая таблица в уме или перед глазами. [8, с.32]
Для этого обратимся к квадрату соответствующему четверке, выбираем числа, соответствующие цифрам числа по порядку: единице, четверке, восьмерке. Получаем: 04 16 32. Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие складываем попарно: четверку с единицей, шестерку с тройкой.. Последняя цифра также без изменений. 0(4 + 1)(6+3)2 = 0592. Число 592 и есть результат умножения. Произведя расчет по методу Василия Ивановича Оконешникова при умножении многозначного числа на однозначное, этот метод достаточно прост и быстр, если имеется готовая таблица в уме или перед глазами. [8, с.32]
Индийский способ умножения.
В древней Индии применяли два способа умножения: сетки и галеры. На первый взгляд они кажутся очень сложными, но если следовать шаг за шагом в предлагаемых упражнениях, то можно убедиться, что это довольно просто.
Умножаем, например, числа 6827 и 345:
1. Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте. В предложенном примере можно использовать одну из этих сеток.
В предложенном примере можно использовать одну из этих сеток.
Сетка 1 Сетка 2
2. Выбрав сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Посмотри на этой схеме, как пишется произведение в соответствующей клетке.
Сетка 1
3. Посмотри, как выглядит сетка со всеми заполненными клетками.
Сетка 1
4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.
Сетка1
Посмотри, как из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315, которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315. [8, с.65]
Египетский способ умножения.
Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное перемножение на второй множитель (см. пример). Этот метод можно и сегодня встретить в очень отдаленных регионах.
Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное перемножение на второй множитель (см. пример). Этот метод можно и сегодня встретить в очень отдаленных регионах.
Разложение. Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число.
Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу значений:
1 x 2 = 2 2 x 2 = 4 4 x 2 = 8 8 x 2 = 16 16 x 2 = 32
Пример разложения числа 25: Кратный множитель для числа «25» — это 16; 25 — 16 = 9. Кратный множитель для числа «9» — это 8; 9 — 8 = 1. Кратный множитель для числа «1» — это 1; 1 — 1 = 0. Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1. [9, с.28]
[9, с.28]
Пример: умножим «13» на «238» . Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: ✔ 1 х 238 = 238 ✔ 4 х 238 = 952 ✔ 8 х 238 = 1904
13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 =1904 + 952 + 238 = 3094.
Заключение
Существует много различных, забавных и интересных способов умножения чисел, но не все они удобны в использовании. Из всех найденных мною необычных способов счета более интересным и простым показался мне «Итальянский способ».
Я показал некоторые способы умножения своим одноклассникам, и многие очень заинтересовались необычными вычислениями.
Работая над этим проектом, я пришла к выводу, что самый простой и привычный способ умножения, это тот, который мы изучаем в школе. А чтобы пользоваться этим способом, нужно всем знать наизусть таблицу умножения!
Список литературы и Интернет — ресурсы
1. 1. Арутюнян Е., Левитас Г. Занимательная математика. — М.: АСТ — ПРЕСС, 1999. — 368 с.1.2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. — ЛКИ ,2012.-208 с.1.3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140 с.1.4. Ликум А. Все обо всем. Т. 2. — М.: Филологическое общество «Слово», 1993. — 512 с.1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.1.6. Перельман Я.И. Занимательная арифметика. — М.: Русанова, 1994 – 205с.1.7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с. 1.8. Савин А.П. Математические миниатюры. Занимательная математика для детей. — М.: Детская литература, 1998 — 175 с.1.9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.2. Другие источники информацииИнтернет – ресурсы: 2.1. Корнеев А.А. Феномен русского умножения. История. [Электронный ресурс]
1. Арутюнян Е., Левитас Г. Занимательная математика. — М.: АСТ — ПРЕСС, 1999. — 368 с.1.2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. — ЛКИ ,2012.-208 с.1.3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140 с.1.4. Ликум А. Все обо всем. Т. 2. — М.: Филологическое общество «Слово», 1993. — 512 с.1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.1.6. Перельман Я.И. Занимательная арифметика. — М.: Русанова, 1994 – 205с.1.7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с. 1.8. Савин А.П. Математические миниатюры. Занимательная математика для детей. — М.: Детская литература, 1998 — 175 с.1.9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.2. Другие источники информацииИнтернет – ресурсы: 2.1. Корнеев А.А. Феномен русского умножения. История. [Электронный ресурс]
Приложение 1
Анкетирование
Мною было проведено анкетирование учащихся 5а класса, в котором приняли участие 25 человек.
На основании анкетирования выявлено, что все опрошенные умеют умножать традиционным способом, а вот о нетрадиционных способах умножения большинство ребят не знают. И есть желающие познакомиться с ними.
Вопросы в анкете были следующие:
Когда была неделя математики в нашей школе, видели ли вы мою стенгазету о разных способах умножения?
Рис.2. Круговая диаграмма. Опрос учащихся к 1-му вопросу
Ответ: да – 20 человек, нет – 5 человек.
Знаете ли вы нетрадиционные способы умножения? Приведите пример.
Рис.3. Круговая диаграмма. Опрос учащихся к 2-му вопросу
Ответ: знают – 7 человек, не знают – 18 человек.
Хотели бы вы научиться нетрадиционным способам умножения?
Рис.3. Круговая диаграмма. Опрос учащихся к 3-му вопросу
Ответ: хотят – 19 человек, не хотят – 6 человек.
Приложение 2
Сравнение результатов по вычислению примеров (по эффективности затраченного времени)
|
Время, за которое мне и моим одноклассникам удалось решить один и тот же пример разными способами |
||||
|
Китайский способ |
Таблица Оконешникова |
Итальянский способ |
Столбик |
|
|
Я |
56 секунд |
30 секунд |
25 секунд |
8 секунд |
|
Ученик №1 |
58 секунд |
32 секунд |
28 секунд |
10 секунд |
|
Ученик №2 |
1 минута 6 секунд |
50 секунд |
42 секунды |
10 секунд |
|
Ученик №3 |
1 минута 10 секунд |
56 секунд |
48 секунды |
11 секунд |
|
Ученик №4 |
1 минута 25 секунд |
1 минута |
55 секунд |
12 секунд |
Вывод: самым эффективным способом умножения является умножение столбиком.
Приложение 3
Моя работа на неделе математики в школе
Приложение 4
Памятка для учащихся
Просмотров работы: 3920
Количество строк и столбцов — Рабочие листы по математике
Количество строк и столбцов — Рабочие листы по математике — SplashLearnГлавная > Рабочие листы > Рабочие листы по математике > Количество строк и столбцов
Распечатайте этот рабочий лист, чтобы попрактиковаться в количестве строк и столбцов, как в математической легенде!
Распечатать
Присвоить классу
ПРЕДМЕТЫ И ТЕМЫ
Узнайте больше о рабочих листах с количеством строк и столбцов
Борьба с массивами может быть легко преодолена, если учащиеся будут практиковать эту концепцию весело и увлекательно! Визуальные элементы в содержании привлекают внимание учащихся и способствуют лучшему пониманию. Здесь учащиеся решают множество задач, используя объекты реального мира для извлечения информации.
Исследуйте потрясающие рабочие листы по умножению
Просмотреть все 371 рабочий лист
Умножение
Описание равных групп
Превратите математику в увлекательное занятие, потренировавшись описывать равные группы.
ПОДРОБНЕЕ
Умножение
Представление равных групп
В этом рабочем листе учащиеся попрактикуются в представлении равных групп.
ПОДРОБНЕЕ
Умножение
Решите, используя многократное сложение
Помогите своему ребенку повторить умножение, решая, используя многократное сложение.
ПОДРОБНЕЕ
Умножение
Найдите выражение умножения
Погрузитесь в этот увлекательный печатный лист, потренировавшись, чтобы найти выражение умножения.
ПОДРОБНЕЕ
Умножение
Представление равных групп с помощью умножения
Учащиеся должны представлять равные группы, используя умножение, чтобы улучшить свои математические навыки.

ПОДРОБНЕЕ
Умножение
Умножение с использованием равных групп
Распечатайте этот рабочий лист, чтобы попрактиковаться в умножении с использованием равных групп, как математическую легенду!
ПОДРОБНЕЕ
Умножение
Умножение с использованием равных групп
Помогите ребенку попрактиковаться в умножении с использованием равных групп.
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение
Строки и столбцы
Распечатайте этот рабочий лист, чтобы практиковать строки и столбцы, как математическую легенду!
ПОДРОБНЕЕ
Умножение
Массивы и их атрибуты
Распечатайте этот рабочий лист, чтобы попрактиковаться с массивами и их атрибутами, как с математической легендой!
ПОДРОБНЕЕ
Умножение
Выражения сложения и умножения
В этом рабочем листе учащиеся смогут попрактиковаться в выражениях сложения и умножения.

ПОДРОБНЕЕ
Умножение
Представление массивов с помощью выражений
Превратите математику в увлекательное занятие, решая задачи на представление массивов с помощью выражений.
ПОДРОБНЕЕ
Умножение
Умножение с использованием массивов
Изучите умножение со скоростью молнии, умножая с использованием массивов.
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение
Использование массивов для умножения
Дети должны использовать массивы для умножения, чтобы укрепить свои математические навыки.
ПОДРОБНЕЕ
Умножение
Работа с равными группами
Сосредоточьтесь на основных математических навыках с помощью этого забавного рабочего листа, решив работать с равными группами.
ПОДРОБНЕЕ
Умножение
Представление равных групп
Укрепите свои математические навыки, потренировавшись представлять равные группы.

ПОДРОБНЕЕ
Связанные игры
Просмотреть все 199 игр
Умножение
Подсчет строк и столбцов
Сделайте первый шаг к построению своего математического замка, потренировавшись считать строки и столбцы.
ПОДРОБНЕЕ
Умножение
Создание массивов
Наслаждайтесь чудом математики, учась создавать массивы.
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение
Понимание строк в массиве
Войдите в безумие математической мультивселенной, поняв строки в массиве.
ПОДРОБНЕЕ
Умножение
Понимание столбцов в массиве
Добавьте больше стрелок в математический колчан вашего ребенка, поняв столбцы в массиве.
ПОДРОБНЕЕ
Умножение
Представление массивов с помощью повторного сложения
Наслаждайтесь чудом математики, изучая, как представлять массивы с помощью многократного сложения.

ПОДРОБНЕЕ
Умножение
Нахождение суммы с помощью многократного сложения
Практикуйте суперсилу умножения, находя сумму с помощью многократного сложения.
ПОДРОБНЕЕ
Умножение
Создайте модель для данного предложения сложения
Дети должны создать модель для данных предложений сложения, чтобы попрактиковаться в умножении.
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение
Поиск равных групп и размер группы
Практикуйте сверхспособности умножения, учась находить равные группы и размер группы.
ПОДРОБНЕЕ
Умножение
Определение количества и размера групп
Примените свои знания об умножении, чтобы определить количество и размер групп.
ПОДРОБНЕЕ
Умножение
Создание равных групп
Упростите изучение умножения, создав равные группы.

ПОДРОБНЕЕ
Умножение
Пропустите счет, чтобы найти ответ
Используйте свои математические способности, чтобы пропустить счет, чтобы найти ответ.
ПОДРОБНЕЕ
Умножение
Представление равных групп с помощью многократного сложения
Дети должны представлять равные группы с помощью повторяющегося сложения, чтобы попрактиковаться в умножении.
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение
Использование многократного сложения для нахождения суммы
Наслаждайтесь чудом математической мультивселенной, изучая, как использовать многократное сложение для нахождения суммы.
ПОДРОБНЕЕ
Умножение
Моделирование сложения предложений с использованием равных групп
Добавьте больше стрелок в математический колчан вашего ребенка, моделируя сложение предложений с использованием равных групп.

ПОДРОБНЕЕ
Умножение
Поиск равных групп и размер группы
Практикуйте сверхспособности умножения, учась находить равные группы и размер группы.
ПОДРОБНЕЕ
Универсальное решение для всех потребностей обучения в классе.
Дайте вашему ребенку страсть и уверенность, чтобы безбоязненно учиться чему-либо самостоятельно
Родители, зарегистрируйтесь бесплатно
Учителя, используйте бесплатно
4417+
4413+
ПОХОЖИЕ ТЕМЫУмножение однозначных чисел | Символы, примеры, приемы
Введение Умножение — одна из четырех основных математических операций, а остальные три — сложение, вычитание и деление. Итак, что мы подразумеваем под умножением и как умножаются два числа в математике? Давайте узнаем.
Предположим, у нас есть 5 ручек в коробке. Мы называем это группой из 5 ручек. Теперь, если у нас есть еще одна коробка с 5 ручками, ее тоже можно назвать группой из 5 ручек. Получается две группы по 5 ручек в каждой.
Точно так же мы можем сказать, что если два попугая образуют группу, то 4 попугая образуют две группы по 2 попугая в каждой. Чтобы присутствовало 3 группы попугаев, нам потребуется 3 группы по 2 попугая в каждой.
Это можно представить как –
Одна группа ручек = 5 ручек
Две группы ручек = 5 ручек + 5 ручек = 10 ручек
Три группы ручек = 5 ручек + 5 ручек + 5 ручек = 15 ручек
Аналогично,
Одна группа попугаев = 2 попугая
Две группы попугаев = 2 попугая + 2 попугая = 4 попугая
Три группы попугаев = 2 попугая + 2 попугая + 2 попугая = 6 попугаев
Из приведенного выше примера видно, что в каждой группе одинаковое количество попугаев. Чтобы найти сумму групп, нам нужно снова и снова складывать одно и то же число.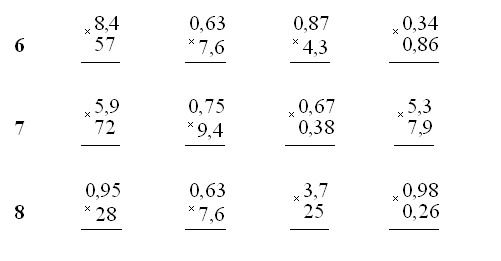
Это то, что мы умножение чисел. Таким образом, умножение чисел есть не что иное, как многократное сложение. Теперь, когда мы поняли, что мы подразумеваем под умножением, давайте разберемся с определением умножения в математических терминах.
Что такое умножение?Процесс нахождения произведения двух или более чисел называется умножением. Полученный таким образом результат называется продуктом . Предположим, вы покупаете 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Это также можно записать как 2 x 6 = 12
Символ умноженияОбратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.
Некоторые важные термины, используемые при умножении: –
Множимое – Число, которое нужно умножить, называется множимым.
Множитель — Число, на которое мы умножаем, называется множителем.
Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.
Связь между множителем, множимым и произведением может быть выражена как –
Множитель × Множитель = Произведение
Давайте разберемся с этим на примере.
Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.
Итак, мы выражаем это как 9 x 5, что дает нам 45.
Следовательно, 9 x 5 = 45
Здесь 9 равно множимое, 5 — множитель, 45 — произведение.
Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.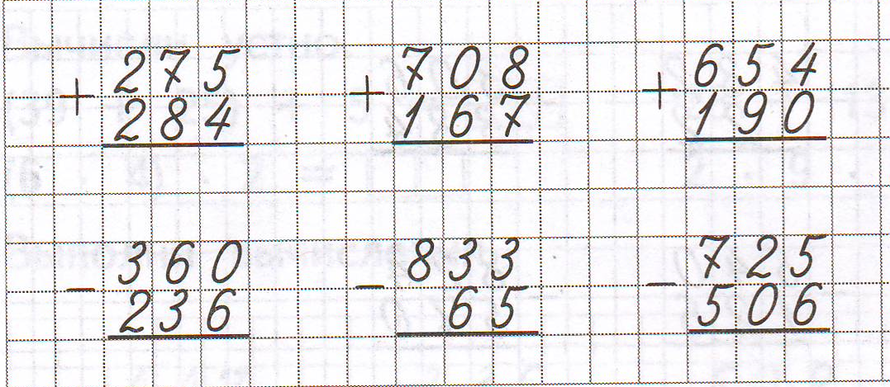
Возьмем пример.
Предположим, у нас есть 1 лист. Поскольку мы знаем, что умножение — это многократное сложение, давайте проверим, что мы получим после повторного прибавления 1. У нас будет,
1 лист
1 лист + 1 лист = 2 листа
1 лист + 1 лист + 1 лист = 3 листа
1 лист + 1 лист + 1 лист + 1 лист = 4 листа и так далее
Математически это можно записать как
1
1 + 1 = 1 x 2 = 2
1 + 1 + 1 = 1 x 3 = 3
1 + 1 + 1 +1 = 1 x 4 = 4 и т. д.
Из приведенного выше примера мы можно увидеть, что число при умножении на 1 даст результат как само число. Графически многократное добавление 1 можно изобразить как
Итак, мы имеем
1 x 1 = 1
2 x 1 = 2
3 x 1 = 3
4 x 1 = 4
5 x 1 = 5
6 х 1 = 6
7 х 1 = 7
8 х 1 = 8
9 x 1 = 9
10 x 1 = 10
Умножение числа на 2 Возьмем пример.
Предположим, у нас есть 2 листа. Поскольку мы знаем, что умножение — это многократное сложение, давайте проверим, что мы получим после повторного прибавления 2. У нас будет,
2 листа
2 листа + 2 листа = 4 листа
2 листа + 2 листа + 2 листа = 6 листьев
2 листа + 2 листа + 2 листа + 2 листа = 8 листьев
Математически это можно записать как
Из приведенного выше видно, что умножение на 2 — это пропуск числа 2. Графически это можно представить как –
Следовательно, мы имеем
2 x 1 = 2
2 х 4 = 8
2 х 3 = 6
2 х 4 = 8
2 х 5 = 10
2 х 6 = 12
2 х 7 = 14
2 х 7 = 14
16 х 8 0 = 14
2 х 8 0 9 = 18
2 x 10 = 20
Аналогично, для умножения 3 на однозначное число мы просто будем считать с пропуском на 3 и 4 соответственно.
Давайте проверим счет с пропуском на 5.
Умножение числа на 5Рассмотрим сетку ниже
В сетке выше начните с 5 и раскрасьте каждое пятое число.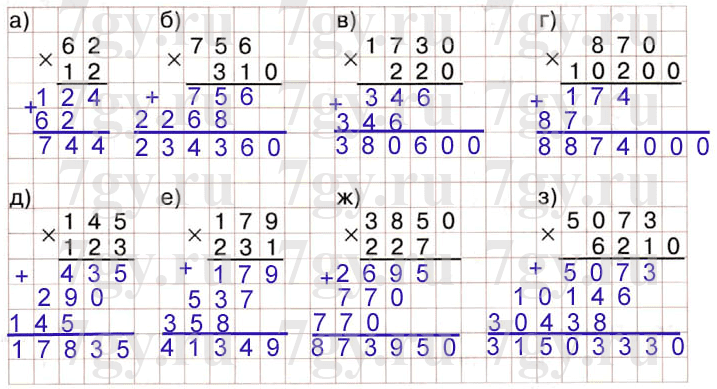 Что вы получите?
Что вы получите?
Выше мы видим, что цветные прямоугольники заканчиваются либо на 5, либо на 0. Это умножение числа на 5.
Используя счет с пропусками, мы можем записать это как
5
5 + 5 = 5 х 2 = 10
5 + 5 + 5 = 5 х 3 = 15
5 + 5 + 5 + 5 = 5 x 4 = 20 и т. д.
В приведенных выше примерах мы видим, что числа 1, 2 и 5 можно последовательно умножать на каждое число. Это представление умножения называется таблицей умножения. Давайте узнаем о них больше.
Что такое таблица умножения?Таблица умножения — это список кратных числа. Другими словами, он показывает произведение одного числа на другие числа. Итак, как нам получить таблицу умножения? Мы можем получить таблица умножения путем умножения данного числа на целые числа.
Итак, чтобы умножать однозначные числа, мы должны быть знакомы с таблицей умножения от 2 до 10. Запишем таблицы для однозначных чисел.
Таблица умножения однозначных чиселМы напишем каждую таблицу умножения множимого от 1 до 102 × 1 = 2
| 3 × 1 = 3 | 3 × 6 = 18 |
| 3 × 2 = 6 | 3 × 7 = 21 |
| 3 × 3 = 9 | 3 × 8 = 24 |
| 3 × 4 = 12 | 3 × 9 = 27 |
| 3 × 5 = 15 | 3 × 10 = 30 |
| 4 × 1 = 4 | 4 × 6 = 24 |
| 4 × 2 = 8 | 4 × 7 = 28 |
| 4 × 3 = 12 | 4 × 8 = 32 |
| 4 × 4 = 16 | 4 × 9 = 36 |
| 4 × 5 = 20 | 4 × 10 = 40 |
| 5 × 1 = 5 | 5 × 6 = 30 |
| 5 × 2 = 10 | 5 × 7 = 35 |
| 5 × 3 = 15 | 5 × 8 = 40 |
| 5 × 4 = 20 | 5 × 9 = 45 |
| 5 × 5 = 25 | 5 × 10 = 50 |
| 6 × 1 = 6 | 6 × 2 = 12 |
| 6 × 3 = 18 | 6 × 4 = 24 |
| 6 × 5 = 30 | 6 × 6 = 36 |
| 6 × 7 = 42 | 6 × 8 = 48 |
| 6 × 9 = 54 | 6 × 10 = 60 |
| 7 × 1 = 7 | 7 × 6 = 42 |
| 7 × 2 = 14 | 7 × 7 = 49 |
| 7 × 3 = 21 | 7 × 8 = 56 |
| 7 × 4 = 28 | 7 × 9 = 63 |
| 7 × 5 = 35 | 7 × 10 = 70 |
| 8 × 1 = 8 | 8 × 6 = 48 |
| 8 × 2 = 16 | 8 × 7 = 56 |
| 8 × 3 = 24 | 8 × 8 = 64 |
| 8 × 4 = 32 | 8 × 9 = 72 |
| 8 × 5 = 40 | 8 × 10 = 80 |
| 9 × 1 = 9 | 9 × 6 = 54 |
| 9 × 2 = 18 | 9 × 7 = 63 |
| 9 × 3 = 27 | 9 × 8 = 72 |
| 9× 4 = 36 | 9 × 9 = 81 |
| 9 × 5 = 45 | 9 × 10 = 90 |
Теперь, когда мы поняли, как умножаются однозначные числа, как их записать? Всегда ли мы используем табличный метод или мы можем написать их любым другим методом? Давайте узнаем.
Существует два метода умножения чисел, а именно метод расширенной записи и метод столбца.
Метод расширенной записиВ методе расширенной записи мы расширяем множимое в соответствии со значениями разряда, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Например, умножьте 8 на 4
Здесь разрядное значение 8 равно 8, поскольку это однозначное число. Поэтому мы просто запишем произведение 8 на 4 как
8 x 4 = 32
Аналогично, 7, умноженное на 6, будет записано как 7 x 6 = 42
Метод столбцаВ этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.
Давайте разберемся с ними один за другим
Умножение без перегруппировки Предположим, мы хотим умножить 2 на 4. Запишем это как
Запишем это как
Здесь важно отметить, что «О» над 2 в умножении приведенный выше пример представляет собой разрядное значение числа 2, которое является местом.
В приведенном выше примере у нас не было необходимости в перестановке, поскольку у нас было два однозначных числа, и полученное произведение также было однозначным числом. Но как поступить, если произведение не является однозначным числом? Вот тут-то и появляется концепция перегруппировки. Давайте выясним, что мы подразумеваем под перегруппировкой.
Умножение с перегруппировкойВ приведенном выше случае мы имеем небольшие умножения, которые ни на одном шаге не содержат двузначных результатов. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Предположим, мы хотим умножить 8 на 9. Из таблицы умножения мы получили значение 8, умноженное на 9, как 72. Но как это записывается? Если мы запишем это умножение в столбцовом методе, мы получим
Но как это записывается? Если мы запишем это умножение в столбцовом методе, мы получим
. Здесь важно отметить, что буква «T» выше представляет разряд десятков разряда. Мы видим, что поскольку полученное произведение было двузначным, следовательно, нам нужно переставить цифру 7 на разряд десятков. У нас есть
8 x 9 = 72.
Решенные примерыПример 1 У Алисы было 6 печенек. У ее брата было в 7 раз больше печенья, чем у нее. Сколько печенья было у ее брата?
Решение Нам сообщили, что у Алисы было 6 печенек. Также у ее брата было в 7 раз больше печенья, чем у нее. Нам нужно узнать количество печенья, доступное у брата Алисы. У нас есть –
Печеньки с Алисой = 6
Печеньки с ее братом = 7 раз 6
Обратите внимание, что, когда мы говорим a раз b, мы имеем в виду, что мы многократно добавляем a, b число раз, или, проще говоря, слов, мы умножаем a на b. поэтому, когда мы говорим, что печенья у брата Алисы в 7 раз больше, чем у Алисы, мы имеем в виду, что количество печений у брата Алисы равно 7 х 6.
Теперь из таблицы умножения мы знаем, что
7 x 6 = 42
Следовательно, количество файлов cookie с братом Алисы = 42
Раствор У нас есть
- Повторное сложение называется умножением.
- Процесс нахождения произведения двух или более чисел называется умножением.
- Результат, полученный при умножении двух чисел, называется произведением.
- Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
- Число, которое нужно умножить, называется множимым.

- Число, на которое мы умножаем, называется множителем.
- Связь между множителем, множимым и произведением может быть выражена как Множитель × Множное = Произведение
- Число, умноженное на 1, даст результат как само число.
- Число, умноженное на 5, всегда заканчивается либо на «0», либо на «5».
- Таблица умножения — это список кратных числа.
- В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ.
- В методе столбца мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим.
Умножение однозначных целых чисел на кратные 10 Рабочие листы по математике для 3-го класса
Вычитание двузначных и однозначных чисел Рабочие листы по математике для 1-го класса
Решение задач на умножение и деление (на тему Хэллоуина) Рабочие листы по математике
Просмотреть все рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Умножение – определение, формула, примеры
В математике умножение – это метод нахождения произведения двух или более чисел. Это основная арифметическая операция, которая довольно часто используется в реальной жизни. Умножение используется, когда нам нужно объединить группы одинакового размера. Давайте узнаем больше об умножении на этой странице.
| 1. | Что такое умножение? |
| 2. | Формула умножения |
| 3. | Как решать задачи на умножение? |
| 4. | Умножение с помощью числовой строки |
| 5. | Задачи на умножение слов |
| 6. | Часто задаваемые вопросы по умножению |
Что такое умножение?
Умножение — это операция, представляющая основную идею многократного сложения одного и того же числа. Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа .
Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа .
Пример: Если есть 6 коробок кексов и в каждой коробке 9 кексов, найдите общее количество кексов.
Решение: Мы можем решить этот вопрос сложением, но это займет больше времени, чтобы получить ответ. То есть 9+9+9+9+9+9=54 кекса. Другими словами, когда у нас есть большие числа для работы, полезно умножение.
Теперь давайте решим эту задачу с помощью умножения. Мы умножим количество коробок на количество кексов в каждой коробке. Если мы умножим 6 × 9, мы получим общее количество кексов, которое равно 6 × 9 = 54 кексов. Таким образом, мы видим, что получаем тот же результат за более короткий промежуток времени. Вот почему умножение также называют повторным сложением.
Символ умножения (×)
В математике используются разные символы. Символ умножения является одним из наиболее часто используемых математических символов. В приведенном выше примере мы узнали об умножении двух чисел 6 и 9. Если мы наблюдаем выражение умножения (6 × 9= 54), мы видим, что символ (× ) соединяет два числа и завершает данное выражение. Помимо символа креста (×), умножение также обозначается точкой срединной линии (⋅) и знаком звездочки ( *).
Символ умножения является одним из наиболее часто используемых математических символов. В приведенном выше примере мы узнали об умножении двух чисел 6 и 9. Если мы наблюдаем выражение умножения (6 × 9= 54), мы видим, что символ (× ) соединяет два числа и завершает данное выражение. Помимо символа креста (×), умножение также обозначается точкой срединной линии (⋅) и знаком звездочки ( *).
Формула умножения
Формула умножения выражается следующим образом: Множимое × Множитель = Произведение ; где:
- Множимое: первое число (множитель).
- Множитель: Второе число (коэффициент).
- Продукт: Конечный результат после умножения множимого и множителя.
- Символ умножения: ‘×’ (соединяет все выражение)
Давайте поймем формулу умножения с помощью следующего выражения.
7(множимое) × 5 (множитель) = 35 (произведение)
Используя эту основную концепцию умножения, давайте научимся решать задачи на умножение.
Как решать задачи на умножение?
При решении задач на умножение однозначные числа можно умножать простым способом с помощью таблиц умножения, но для больших чисел мы разбиваем числа на столбцы, используя соответствующие разряды, например, единицы, десятки, сотни, тысячи, и так далее. Есть два типа задач на умножение:
- Умножение без перегруппировки
- Умножение с перегруппировкой
Давайте разберем оба случая на примерах.
Умножение без перегруппировки
Умножение двух чисел без перегруппировки включает меньшие числа, когда нет необходимости выполнять перенос на следующее более высокое разрядное значение. Это базовый уровень, который может помочь учащемуся понять основы умножения, прежде чем перейти к более высокому уровню задач, включая перегруппировку. Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: умножьте 3014 на 2.
Решение:
- Шаг 1: Начните с разряда единиц.
 (2 × 4 = 8)
(2 × 4 = 8) - Шаг 2: Умножьте 2 на разряд десятков. (2 × 1 = 2)
- Шаг 3: Теперь умножьте 2 на цифру в сотнях. (2 × 0 = 0)
- Шаг 4: Теперь умножьте 2 на разряд тысяч. (2 × 3 = 6)
- Шаг 5: 3014 × 2 = 6028.
Чт Х Т О
3 0 1 4
× 2
6 0 2 8
Умножение с перегруппировкой
Умножение более двух чисел с перегруппировкой включает числа с двузначным произведением. В этом типе умножения нам нужно сделать перенос на следующее более высокое разрядное значение. Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: умножьте 2468 на 8
Решение: Давайте умножим 2468 × 8, используя приведенные ниже шаги, и попробуем связать их с числом, приведенным после шагов.
- Шаг 1: Начните с разряда единиц, то есть 8 × 8 = 64 единицы, что означает 6 десятков 4 единицы.
 Теперь перенесите 6 десятков в столбец десятков.
Теперь перенесите 6 десятков в столбец десятков. - Шаг 2: Умножьте 8 на разряд десятков, то есть 8 × 6 = 48 десятков. Теперь мы добавим это к переносу. Это означает, что 48 + 6 (перенос из шага 1) = 54. Перенесите 5 в столбец сотен.
- Шаг 3: Умножьте 8 на цифру в разряде сотен, то есть 8 × 4 = 32 сотни. Теперь давайте добавим это к переносу с предыдущего шага. Это означает, что 32 + 5 (перенос из шага 2) = 37. Мы снова перенесем 3 в столбец тысяч.
- Шаг 4: Умножьте 8 на разряд тысяч, то есть 8 × 2 = 16 тысяч. Итак, давайте снова добавим это к переносу, то есть 16 + 3 (перенос с шага 3) = 19
- Шаг 5: Следовательно, произведение 2468 × 8 = 19744.
Умножение с помощью числовой строки
Умножение на числовую прямую означает применение операции умножения к заданному набору чисел через числовую прямую. Числовая линия — это визуальное представление чисел на прямой линии. Мы знаем, что умножение также известно как многократное сложение. Итак, чтобы выполнить умножение на числовой прямой, мы начинаем с нуля и двигаемся к правой стороне числовой строки заданное количество раз.
Мы знаем, что умножение также известно как многократное сложение. Итак, чтобы выполнить умножение на числовой прямой, мы начинаем с нуля и двигаемся к правой стороне числовой строки заданное количество раз.
Пример: Умножьте 3 × 5, используя числовую прямую.
Решение: Обратите внимание на следующую числовую линию, чтобы увидеть работу 3 × 5 = 15. Мы начнем с 0 и будем двигаться вправо от числовой линии. Мы сформируем 3 группы по 5 равных интервалов. Это приведет нас к 15.
Приведенная выше числовая строка показывает, что 3 умножить на 5 равно 15. Представление также можно записать как 5 + 5 + 5 = 15. Оператор умножения выражается как 3 × 5 = 15.
Задачи на умножение слов
Задачи на умножение слов можно легко решить, внимательно наблюдая за ситуацией и находя решение. Давайте разберемся в теории реальных задач на умножение слов с помощью интересного примера.
Пример: В коробке 245 фруктов. Найдите количество фруктов в 4 таких ящиках, используя формулу умножения.
Найдите количество фруктов в 4 таких ящиках, используя формулу умножения.
Решение: Чтобы решить такие задачи на умножение слов, проще всего записать заданные параметры, а затем решить.
Дано:
Общее количество фруктов в одном ящике = 245
Количество ящиков = 4
Общее количество фруктов в 4 таких ящиках = 245 × 4.
Шаг 1: Начните с разряда единиц. Умножьте 4 × 5 = 20. Теперь перенесите 2 в столбец десятков.
Шаг 2: Умножьте 4 на цифру в разряде десятков, то есть 4 × 4 = 16. Теперь прибавьте это к переносу с предыдущего шага. 16 + 2 (перенос из шага 1) = 18. Отсюда перенесите 1 в столбец сотен.
Шаг 3: Умножьте 4 на разряд сотен, 4 × 2 = 8 сотен. 8 + 1 (перенос из шага 2) = 9.
Шаг 4: Следовательно, произведение 245 × 4 = 980.
H T O
1 2
2 4 5
× 4
9 8 0
Следовательно, общее количество фруктов в 4 таких коробках = 245 × 4 = 980. несколько советов и приемов, которые можно использовать при выполнении умножения.
несколько советов и приемов, которые можно использовать при выполнении умножения.
- При умножении порядок чисел не имеет значения. Так что выбирайте тот порядок, в котором вам удобнее. При использовании таблицы умножения, по сравнению с 9 × 4, учащиеся могут легче запомнить 4 × 9.
- При умножении трех чисел выберите два числа, которые легко умножаются. Например, умножение 5 × 17 × 2 будет затруднено, если мы попытаемся сначала умножить 5 × 17. Вместо этого умножение 5 на 2 дает 10, которые можно легко умножить на 17, чтобы получить 170.
- При умножении двузначного числа на однозначное иногда помогает разбить двузначное число по разрядности. Затем умножьте каждую часть и сложите. Например, 37 × 4 можно решить в уме, разбив 37 как 30 + 7. Тогда 30 × 4 = 120 и 7 × 4 = 28. Таким образом, окончательный ответ будет 120 + 28 = 148. Хотя это может показаться более утомительным, когда записано, гораздо легче решить в уме.
- Даже если вы не помните факт умножения, его можно легко вычислить в уме.
 Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Итак, ответ будет 170 — 17 = 153.
Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Итак, ответ будет 170 — 17 = 153.
☛ Статьи по теме
- Длинное умножение
- Калькулятор умножения
- Таблица умножения
- Рабочие листы с задачами на умножение
- Длинные рабочие листы умножения
- Рабочие листы умножения
Примеры умножения
Пример 1. Используйте трюки с умножением, чтобы решить следующую задачу на умножение слов.
Цена книги 48 долларов. Найдите цену 500 таких книг.Решение:
Цена одной книги = $48
Цена 500 книг = 500 × 48H T O
5 0 0
× 4 8
4 0 0 0
+2 0 0 0 x
2 4 0 0 0 _Цена таких 500 книг 24000 долларов.
Другой способ решить этот вопрос — просто умножить 48 на 5 и присоединить два нуля к окончательному ответу.
 Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.
Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.Пример 2. Решите следующую задачу на умножение слов.
Сколько будет 784 умножить на 44?Решение:
Используя формулу умножения, 784 умножить на 44 = 784 × 44
Следовательно, 784 умножить на 44 равно 34496.
Пример 3: Укажите истинность или ложность следующих утверждений, используя факты умножения.
а.) Умножение представляет собой основную идею многократного вычитания.
b.) Формула умножения выражается как: Множитель × Множитель = Произведение
Решение:
а.) Неверно, умножение представляет собой основную идею повторного сложения одного и того же числа.
b.) Правда, формула умножения выражается как: Множимое × Множитель = Произведение
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по умножению
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по умножению
Что означает умножение?
Умножение — это операция, представляющая основную идею многократного сложения одного и того же числа. Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа 9.0349 .
Используется, когда нам нужно объединить группы одинакового размера. Например, если в 5 корзинах по 4 яблока, то чтобы найти общее количество яблок, мы можем использовать умножение и решить как 5 × 4 = 20 яблок.Какая формула используется для выполнения умножения?
Формула, которую мы используем для выполнения умножения: «Множное × Множитель = Произведение». Например, 9 (множимое) × 5 (множитель) = 45 (произведение)
Например, 9 (множимое) × 5 (множитель) = 45 (произведение)
Каковы свойства умножения?
Различные свойства умножения приведены ниже.
- Коммутативное свойство умножения : Произведение двух чисел не изменится, если мы изменим порядок чисел. Это свойство умножения известно как коммутативное свойство умножения, которое представлено как A × B = B × A. Например, 12 × 13 = 13 × 12 = 156, .
- Ассоциативное свойство умножения : Произведение трех или более чисел не меняется при изменении группировки чисел. Это свойство умножения известно как ассоциативное свойство умножения, которое представлено как A × (B × C) = (A × B) × C = B × (A × C). Например, 12 × (13 × 5) = (12 × 13) × 5 = 13 × (12 × 5) = 780,
- Свойство идентичности умножения : Если любое число умножается на 1, произведением является само число. Например, 12 × 1 = 12. Здесь 1 — единица умножения.
- Нулевое свойство умножения : Если любое число умножается на 0, произведение всегда равно нулю.
 Это нулевое свойство умножения. Например, 12 × 0 = 0, .
Это нулевое свойство умножения. Например, 12 × 0 = 0, . - Распределительное свойство умножения : Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, полученному при умножении каждого слагаемого по отдельности на число. Это свойство также применимо к вычитанию и представляется как A × (B + C) = AB + AC или A × (B — C) = AB — AC. Например, 12 × (13 + 5) = (12 × 13) + (12 × 5) = 216,
Что такое символ умножения?
При выполнении умножения мы используем символ креста (×), который соединяет все выражение, этот символ (×) известен как символ умножения. Например, 7 умножить на 4 равно 28 можно представить как 7 × 4 = 28.
Какие части умножения?
Различные части умножения выражаются следующим образом. Давайте разберем это на примере: 6 × 4 = 24.
- Множественное (множитель): Множимое — это первое число.
 В этом случае 6 является множимым.
В этом случае 6 является множимым. - Множитель (Коэффициент): Множитель — это второе число. В данном случае множитель 4.
- Продукт: Конечный результат после умножения множимого и множителя. В этом примере 24 — это произведение.
- Символ умножения: ‘×’ (соединяет все выражение)
Приведите пример предложения с умножением.
Чтобы решить задачу на умножение, нам нужно записать ее в виде предложения на умножение. Например, что будет 36 умножить на 9? Мы знаем, что 36 умножить на 9 записывается в форме предложения умножения как 36 × 9 = 324. Здесь 36 и 9 — множители, а 324 — произведение. Таким образом, 36 умножить на 9 равно 324.
Как умножение связано со сложением?
Умножение представляет собой основную идею многократного сложения одного и того же числа. Это упрощает задачу повторного добавления. Например, , если есть 3 пачки карандашей и в каждой пачке по 6 карандашей, найдем общее количество карандашей. Мы можем решить этот вопрос сложением, то есть 6 + 6 + 6 = 18 карандашей. Однако когда нам приходится иметь дело с большими числами, умножение полезно. Теперь, если мы используем умножение для решения этой задачи, нам нужно умножить количество пачек на количество карандашей в каждой пачке. Это означает, что 3 × 6 = 18 карандашей. Таким образом, мы легко получаем тот же результат. Следовательно, умножение также называется повторным сложением.
Мы можем решить этот вопрос сложением, то есть 6 + 6 + 6 = 18 карандашей. Однако когда нам приходится иметь дело с большими числами, умножение полезно. Теперь, если мы используем умножение для решения этой задачи, нам нужно умножить количество пачек на количество карандашей в каждой пачке. Это означает, что 3 × 6 = 18 карандашей. Таким образом, мы легко получаем тот же результат. Следовательно, умножение также называется повторным сложением.
В чем разница между умножением и делением?
При умножении мы объединяем группы одинакового размера, а при делении делим или разделяем заданное число на равные группы. Умножение — это произведение двух или более чисел, где умножаемые числа являются множителями, а результат называется произведением. При делении число, на которое делится делимое, называется делимым, число, на которое делится делимое, называется делителем, а результат — частным.
Как умножение используется в повседневной жизни?
Умножение широко используется в нашей повседневной жизни. Например, мы можем рассчитать цену предметов в соответствии со ставкой за количество, мы можем найти правильное количество ингредиента, которое будет использоваться в приготовлении пищи, мы можем рассчитать стоимость нескольких предметов, когда известна стоимость 1 предмета, и так далее.
Например, мы можем рассчитать цену предметов в соответствии со ставкой за количество, мы можем найти правильное количество ингредиента, которое будет использоваться в приготовлении пищи, мы можем рассчитать стоимость нескольких предметов, когда известна стоимость 1 предмета, и так далее.
Каковы стратегии умножения?
Стратегии умножения — это различные способы изучения умножения. Например, умножение с помощью числового ряда, умножение с помощью таблицы стоимостных значений, разделение десятков и единиц, а затем их умножение по отдельности и так далее. Эти стратегии помогают учащимся понять концепцию умножения в более широкой перспективе.
Урок пятого класса Несколько способов умножения с несколькими цифрами
Модуль 2Урок 4Цель
Включение — вовлечение учащихся в процесс обучения
Введение в несколько способов умножения
15 учителям нравится этот урок
Распечатать урок
Цель
Учащиеся смогут использовать «стандартный» алгоритм с пониманием свойств операций и десятичной системы.
Большая идея
Есть несколько способов проверить свои ответы при использовании традиционного алгоритма умножения.
Урок Автор
Кэти Скиннер
Scottsdale, AZ
Уровень
Пятый класс
субъекты
Math
Число и операции
. число до четырех цифр на однозначное целое число и умножать два двузначных числа, используя стратегии, основанные на разрядности и свойствах операций. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
5.NBT.B.5
Свободно умножайте многозначные целые числа по стандартному алгоритму.
MP8
Ищите и выражайте регулярность в повторяющихся рассуждениях.
Включение – вовлечение учащихся в процесс обучения
2 минуты
Вопрос на включение:
Где вы раньше использовали большие числа при умножении, а если нет, то где, по вашему мнению, они используются в «реальном мире» .
Использование вопроса включения в начале каждого урока дает учащемуся «крючок», на который можно повесить новую информацию, и выявляет предыдущие знания.
Я не позволяю учащимся разговаривать за своими столами, потому что восприятие многозначного умножения в моем многовозрастном (4-м и 5-м) классе значительно отличается. Я хочу, чтобы мои пятиклассники поделились, где они использовали или видели многозначное умножение.
Первый ученик, которого я называю акциями, «Вы сказали нам, что ваш сын должен много умножать в средней школе. Мне придется делать умножение в средней школе». Я подтверждаю комментарий этого учащегося: «Да, вам нужно будет уметь выполнять большое умножение во время обучения в школе, но видел ли кто-нибудь, чтобы это применялось за пределами школы?» Я пытаюсь научить студентов думать о приложениях «реального мира».
Мне пришлось больше подумать, потому что я видел, что они не связывают это с реальными приложениями.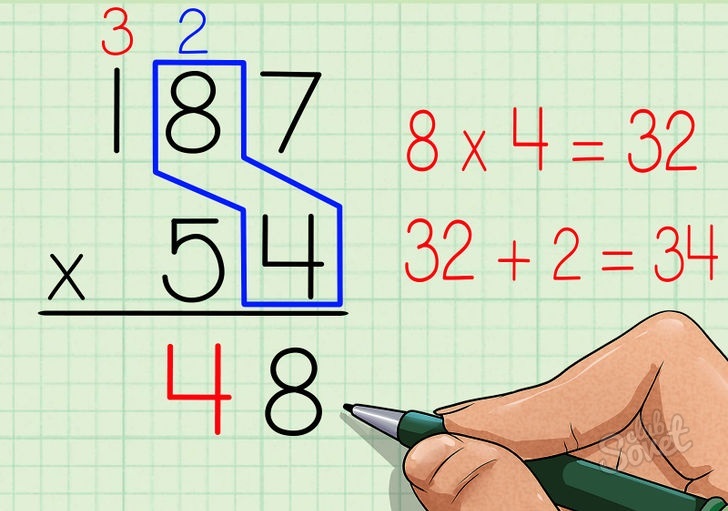 Через некоторое время один из студентов поднял руку, и предыдущий оратор бросил им коош, чтобы дать им понять, что они могут говорить. Он сказал: «Мой дядя кладет плитку и показывал мне, как найти площадь пола. Ему пришлось умножить 92 фута на 52 фута, чтобы узнать размер комнаты».
Через некоторое время один из студентов поднял руку, и предыдущий оратор бросил им коош, чтобы дать им понять, что они могут говорить. Он сказал: «Мой дядя кладет плитку и показывал мне, как найти площадь пола. Ему пришлось умножить 92 фута на 52 фута, чтобы узнать размер комнаты».
Затем другие студенты придумали конструкции и космические ссылки. Теперь, когда я заставил их подумать о том, где они могут использовать или увидеть многозначное умножение, я перехожу к обучению различным способам проверки их работы с помощью традиционного алгоритма.
Знакомство с несколькими способами умножения
15 минут
Советы по моделям умножения
Учащиеся 5-го класса должны уметь бегло умножать многозначные целые числа, используя традиционный алгоритм. Некоторым ученикам это трудно, особенно если они все еще считают на пальцах, чтобы овладеть базовыми навыками. Один из способов помочь учащимся, испытывающим затруднения, а также бросить вызов другим, состоит в том, чтобы учащиеся использовали другие стратегии умножения наряду с традиционным алгоритмом для решения задач. Это особенно подходит для учащихся 4-х классов, поскольку ожидается, что они начнут использовать «стандартный» алгоритм, но там, где все еще считается уместным использовать вычислительные алгоритмы, использующие позиционное значение и понимание операций. Например, четырехклассник может использовать площадную модель.
Это особенно подходит для учащихся 4-х классов, поскольку ожидается, что они начнут использовать «стандартный» алгоритм, но там, где все еще считается уместным использовать вычислительные алгоритмы, использующие позиционное значение и понимание операций. Например, четырехклассник может использовать площадную модель.
Один из моих студентов упомянул числа 92 на 52, поэтому я попросил студента сказать мне, что было бы разумным ответом. У меня были такие ответы, как 4500, и они объясняли, потому что если вы округлите каждое число и умножите 9 x 5, вы получите 45, а затем два нуля, поэтому вы прибавите их к 4500. Некоторые студенты использовали округление переднего конца, чтобы получить 100 x 50 для 5000.
После того, как мы составили список из 4 разумных ответов, я начал с того, что провел их по традиционному алгоритму, просматривая значения каждого столбца, когда они должны были переноситься. После завершения этого я спросил, есть ли какие-либо другие способы решения проблемы, чтобы мы могли проверить наши ответы. (Мы всегда должны проверять наши ответы!) Софи хотела использовать Решетку и подошла, чтобы решить проблему. Пока Софи пишет, студенты, сидящие в «аудитории», копируют ее работу в свои математические журналы для использования в качестве справочного материала.
(Мы всегда должны проверять наши ответы!) Софи хотела использовать Решетку и подошла, чтобы решить проблему. Пока Софи пишет, студенты, сидящие в «аудитории», копируют ее работу в свои математические журналы для использования в качестве справочного материала.
Другой студент подошел, чтобы попытаться выполнить стандартный алгоритм, и совершил распространенную ошибку, умножив 2 x 2, а затем 9 x 5, чтобы получить ответ 454. Он сел, не исправив свою ошибку. Позже, когда я с ним работал, он сказал, что понял, что его ответа нет в списке разумных ответов, но не знает, как это исправить. Позже в видео появился другой студент и правильно использовал традиционный алгоритм. Когда я просмотрел вместе со своим классом и сказал им, что Эй-Джей знал, что его ответ неразумен, они вернулись к своим математическим журналам и вычеркнули его работу. Многие уже ответили, что указывает на то, что это не был разумный ответ.
Ученик, которого вы видите, встает и идет перед доской, это Даичи, новый ученик из Японии.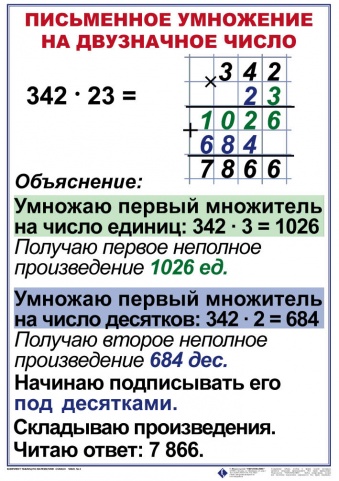 Он встал, чтобы взять свое устройство для перевода, и напечатал слова «разумный» и «оценка», поскольку я написал их на доске, и продолжал указывать на слова. Он также слышал, как студенты использовали эти слова, и я уверен, что ему было любопытно, что они означают. Дайчи появился в конце видео, чтобы показать, как он переносил числа под чертой — на картинке внизу доски есть еще один пример. Вы также можете увидеть, как другие ученики позаботились о Даичи, стерли цифры, дали ему маркер и затем указали на доску. Они все делают большую работу, чтобы он чувствовал себя вовлеченным. Он сделал ошибку по математике, но я уверен, что это было потому, что он нервничал перед классом. Когда я выключил камеру, он вернулся и изменил ответ.
Он встал, чтобы взять свое устройство для перевода, и напечатал слова «разумный» и «оценка», поскольку я написал их на доске, и продолжал указывать на слова. Он также слышал, как студенты использовали эти слова, и я уверен, что ему было любопытно, что они означают. Дайчи появился в конце видео, чтобы показать, как он переносил числа под чертой — на картинке внизу доски есть еще один пример. Вы также можете увидеть, как другие ученики позаботились о Даичи, стерли цифры, дали ему маркер и затем указали на доску. Они все делают большую работу, чтобы он чувствовал себя вовлеченным. Он сделал ошибку по математике, но я уверен, что это было потому, что он нервничал перед классом. Когда я выключил камеру, он вернулся и изменил ответ.
Чтобы удовлетворить потребности разных учащихся в моем классе (разновозрастной класс 4-го и 5-го классов), я разрешаю всем учащимся проверять свою работу с помощью калькулятора. Четвероклассники могли использовать любой формат умножения для решения задачи, но должны были решить 3 задачи по традиционному алгоритму. Пятиклассникам приходилось использовать традиционный алгоритм, но если они все еще не понимали его, они могли попробовать другой формат. Не каждый учащийся справился со всеми задачами, потому что я сосредоточился на беглости умножения многозначных целых чисел с использованием традиционного алгоритма, а не на скорости учащихся при выполнении задач. Предлагая учащимся связать разрядное значение и свою предыдущую работу с операциями, чтобы понять алгоритмы, которые они используют при умножении многозначных чисел, я выполняю математическое упражнение 8 – Ищите и выражайте регулярность в повторяющихся рассуждениях.
Пятиклассникам приходилось использовать традиционный алгоритм, но если они все еще не понимали его, они могли попробовать другой формат. Не каждый учащийся справился со всеми задачами, потому что я сосредоточился на беглости умножения многозначных целых чисел с использованием традиционного алгоритма, а не на скорости учащихся при выполнении задач. Предлагая учащимся связать разрядное значение и свою предыдущую работу с операциями, чтобы понять алгоритмы, которые они используют при умножении многозначных чисел, я выполняю математическое упражнение 8 – Ищите и выражайте регулярность в повторяющихся рассуждениях.
Я сидел на полу с группой студентов, которым нужна была помощь, чтобы решить каждую задачу в традиционной форме. Мои «эксперты» по умножению помогали другим. Эти учащиеся закончили всю страницу и завершили некоторые из них, используя другие методы, прежде чем они смогли продолжить помогать другим учащимся.
Другие способы умножения включают разложение чисел. Если задача 68 x 15, учащиеся
Практика нескольких способов умножения
25 минут
Позиционное значение Рассмотрено
Чтобы удовлетворить потребности разных учащихся в моем классе (разновозрастные 4-е и 5-е классы), у меня разные ожидания в зависимости от отдельного ученика, но обычно есть группа типичных 4-х и типичных 5-х классов. классные навыки.
классные навыки.
Чтобы соответствовать стандартам Common Core, четвероклассники могли использовать любой формат умножения для решения задачи, но должны были решить 3 задачи по традиционному алгоритму (4.NBT.5). Пятиклассникам приходилось использовать традиционный алгоритм, но если они все еще не понимали его, они могли попробовать использовать другую стратегию, такую как решетка, декомпозиция, стандарт и новый способ, который показал нам мой новый японский ученик (5.NBT.5).
Покажи мне: умножение
Пятиклассник, который любит использовать решетку, показывает классу, как это делается.
Не все учащиеся справились со всеми задачами, потому что я сосредоточился на беглости умножения многозначных целых чисел с использованием стандартного алгоритма, а не на скорости учащихся при выполнении задач.
Я сидел на полу с группой студентов, которые нуждались в помощи, решая каждую задачу в традиционной форме. Мои «эксперты» по умножению помогали другим. Эти учащиеся закончили всю страницу и завершили некоторые из них, используя другие методы, прежде чем они смогли продолжить помогать другим учащимся.
Я использую сайт The Math Worksheets Site для страниц практики навыков, который я использовал для этого урока.
Завершение — размышление ученика
2 минуты
Безумие умножения
Я всегда заставляю своих учеников размышлять над своим обучением, потому что это улучшает их усвоение материала. Сегодня мои ученики устно поразмышляли над содержанием и поведением. Я спросил у студентов попкорн: «Что вы сегодня узнали о многозначном умножении?» Ответы включали такие комментарии, как:
Я не понимаю всех шагов стандартного алгоритма, но могу использовать другой способ узнать ответы. Это поможет мне на тестах (районные бенчмарки через неделю).
Я использовал решетку в прошлом году, но вы сказали мне, что в 6-м классе мы не можем ее использовать, поэтому я усердно учился традиционным способом.
Я не понимаю этого, но я знаю, как сделать предположение в тесте с более чем одним ответом (множественный выбор), ища разумный ответ.
Следующие несколько дней мы продолжим практиковать многозначное умножение. Я также продолжу включать его в утренние математические пробуждения, предлагая учащимся решать по одной задаче в день.
Связанные уроки
TIMES MODULE M9 — Умножение целых чисел
Проект улучшения математического образования в школах (TIMES)
вернуться к указателю
Умножение целых чисел
Модуль 4-9: Число и алгебра 9.0003
Июнь 2011 г.
PDF-версия модуля
Предполагаемые знания
- Понимание разрядного значения применительно к целым числам (см. модуль «Счет и разрядное значение»).
- Понимание того, что сложение может быть смоделировано путем объединения наборов объектов, а также может быть смоделировано на числовой прямой.
- Понимание и свободное владение пропускным счетом.
- Понимание и свободное сложение двух однозначных чисел.
- Знакомство с использованием массивов для моделирования умножения.

- Использование символа умножения для обозначения «групп».
- Знание простых фактов умножения и деления.
Мотивация
Примеры использования умножения включают расчет стоимости шести предметов
стоимостью 25 центов каждый. Гораздо быстрее вычислить 6 × 25 умножением
, чем повторным сложением.
Умножение отвечает на такие вопросы, как:
1 Джуди купила 15 коробок конфет. В каждой коробке было 24 конфеты. Сколько шоколадок было у Джуди?
2 У Генри 16 катушек проволоки. Каждый рулон имеет длину 18 м. Какова общая длина провода, который есть у Генри?
Естественная геометрическая модель умножения в виде прямоугольной площади находит применение в измерениях. Таким образом, умножение обеспечивает раннюю связь между арифметикой и геометрией.
Свободное владение умножением снижает когнитивный стресс при изучении более поздних тем, таких как
г. как дивизия. Развитие твердого понимания арифметики необходимо для всей дальнейшей математики.
Содержание
Знакомство с умножением
Для целых чисел умножение эквивалентно многократному сложению.
Моделирование умножения с помощью массивов
Использование массивов для моделирования умножения очень важно. Например, 3 × 5 изображается как
Мы называем 15 произведением 3 и 5, а 3 и 5 множителями 15.
Глядя на строки массива, мы видим, что
3 × 5 = 5 + 5 + 5
Глядя на столбцы массива, мы также видим, что
5 × 3 = 3 + 3 + 3 + 3 + 3
Это иллюстрирует 3 × 5 = 5 × 3. Мы говорим, что умножение коммутативно.
Моделирование умножения с помощью пропуска счета
Счет с пропуском, например повторение 3, 6, 9, 12, 15,…, является одним из первых способов введения в повторяющееся сложение и, следовательно, в умножение. Это можно проиллюстрировать на числовой прямой, как показано ниже для 3 × 5 = 15.
3 × 5 = 15
На числовой прямой тот факт, что 3 + 3 + 3 + 3 + 3 = 5 + 5 + 5, не так очевиден; на приведенной выше диаграмме показано 5 + 5 + 5, тогда как 3 + 3 + 3 + 3 + 3 на числовой прямой выглядит совсем иначе.
Счет с пропусками важен, потому что он помогает детям выучить таблицу умножения.
Моделирование умножения на площадь
Замена объектов в массиве единицей или квадратом 1 × 1 вводит модель умножения площади. Это показано ниже для 3 × 5,9.0003
На данном этапе мы используем единичные квадраты вместо счетчиков или звездочек. Мы также можем использовать модель умножения площади для умножения дробей.
Изучение таблицы умножения
Свободное владение таблицей умножения необходимо для дальнейшего изучения математики и в повседневной жизни.
Если учащиеся могут складывать однозначное число с двузначным числом, они могут, по крайней мере, восстановить таблицу умножения, даже если они еще не научились бегло говорить. Поэтому очень важно, чтобы учащиеся могли свободно добавлять.
Мы настоятельно рекомендуем учащимся выучить факты умножения до 12 × 12. Это в первую очередь связано с тем, что таблица умножения на 12 необходима для расчета времени — в году 12 месяцев, в сутках 24 часа, а в сутках 60 минут. час. Знакомство с десятками пригодится в повседневной жизни, потому что упаковка в массивы 3 × 4 гораздо удобнее, чем в массивы 2 × 5. Кроме того, в таблице 12 × 12 есть много шаблонов, которые можно конструктивно использовать в предварительных алгебраических упражнениях.
час. Знакомство с десятками пригодится в повседневной жизни, потому что упаковка в массивы 3 × 4 гораздо удобнее, чем в массивы 2 × 5. Кроме того, в таблице 12 × 12 есть много шаблонов, которые можно конструктивно использовать в предварительных алгебраических упражнениях.
Простой подход к изучению таблиц состоит в том, чтобы повторять каждую строку либо наизусть, либо с пропуском счета. Однако учащиеся также должны уметь вспоминать отдельные факты, не прибегая ко всей таблице.
Глядя на таблицу умножения 12 × 12, создается впечатление, что нужно выучить 144 факта.
Однако есть несколько методов, которые можно использовать для уменьшения количества фактов, которые необходимо изучить.
- Коммутативность умножения немедленно уменьшает 144 до 78.
- Таблицы умножения на 1 и 10 очень просты, и их освоение сокращает количество фактов, которые нужно выучить, с
до 55.
- Таблицы умножения на 2 и 5 также легко выучить, а их овладение еще больше сокращает количество фактов, которые необходимо выучить, до 36.

- Таблицы умножения на 9 и 11 являются следующими по простоте пропуска подсчета, потому что 9 и 11 отличаются от 10 на 1. Это уменьшает количество фактов до 21.
- Квадраты полезны, и их можно выучить так же, как можно выучить таблицу умножения.
Это уменьшает количество терминов, которые необходимо выучить, до 15.
Какие бы техники ни использовались, целью должна быть беглость речи.
Свойства умножения
Коммутативность
Одним из преимуществ метода массивов и площадей является то, что свойства умножения более очевидны.
Как обсуждалось выше, переворачивание массива 3 × 5 на бок показывает, что 3 × 5 = 5 × 3, поскольку площадь не меняется.
| 3 × 5 = 5 × 3 | ||
Мы видели это раньше, рассматривая строки и столбцы отдельно, но мы также можем сделать это, повернув прямоугольник на бок, то есть вращением.
| 3 × 5 = 5 × 3 |
Свойство любого порядка
Другим важным свойством умножения является ассоциативность, которая гласит, что
a × (b × c) = (a × b) × c для всех чисел.
Ассоциативность умножения гарантирует однозначность выражения a × b × c. Обычно мы не учим ассоциативность умножения явно в 4-7 классах. Вместо этого мы учим свойству умножения любого порядка, которое является следствием свойств коммутативности и ассоциативности.
Свойство умножения любого порядка
Список чисел можно перемножать в любом порядке, чтобы получить произведение чисел.
Свойство умножения любого порядка аналогично свойству сложения любого порядка. И ассоциативность, и коммутативность — нетривиальные наблюдения; обратите внимание, что вычитание и деление не являются ни коммутативными, ни ассоциативными. Как только мы познакомимся с арифметическими операциями, мы склонны принимать как ассоциативность, так и коммутативность умножения как нечто само собой разумеющееся, точно так же, как и при сложении. Время от времени стоит задуматься о том, что коммутативность и ассоциативность в сочетании дают важные и мощные свойства любого порядка.
Время от времени стоит задуматься о том, что коммутативность и ассоциативность в сочетании дают важные и мощные свойства любого порядка.
Умножение трех целых чисел геометрически соответствует вычислению количества единичных кубов в (или объеме) прямоугольной призмы. Свойство умножения любого порядка означает, что мы можем вычислить этот объем, умножая длины сторон в любом порядке. Порядок расчета соответствует нарезке объема по-разному.
| 5 × 2 = 2 × 5 | (5 × 2) × 3 = (2 × 5) × 3 | |||
|
| |||
| 5 × 3 = 3 × 5 | (5 × 3) × 2 = (3 × 5) × 2 |
Распределение умножения над сложением и вычитанием.
Уравнение 3 × (2 + 4) = (3 × 2) + (3 × 4) является примером дистрибутивности
умножения над сложением. Для массивов это соответствует
г. по следующей схеме.
=
С площадями это соответствует диаграмме ниже.
| Площадь = 3 × 6 |
Умножение также является распределительным над вычитанием.
Например, 7 × (10 − 2) = 7 × 10 − 7 × 2. Это можно проиллюстрировать на модели площади.
Умственные стратегии
Свойство умножения любого порядка и распределительный закон умножения позволяют решать некоторые задачи на умножение без сложных вычислений.
Использование свойства произвольного порядка
Мы используем свойство произвольного порядка умножения, чтобы упростить вычисления,
изменяя порядок, в котором мы выполняем умножения. Например,
| 1 |
| ||
| |||
| 2 | 2 × 17 × 5 = 10 × 17 | ||
| 3 | 25 × 7 × 4 = 25 × 4 × 7 = 100 × 7. |
Иногда это переупорядочение происходит после того, как мы разложим один из множителей,
например, когда мы дважды удваиваем, чтобы умножить на четыре, как в
17 × 4 = (17 × 2) × 2 = 34 × 2 = 68.
Этот метод перемещения коэффициента от одного числа к другому для упрощения вычислений
имеет применение помимо многократного удвоения, как в
36 × 5 = 18 × (2 × 5) = 180.
Иногда его называют «пополам и вдвое».
щелкните для просмотра экрана
УПРАЖНЕНИЕ 1
Используйте свойство любого порядка для выполнения следующих умножений.
| а | 5 × 7 × 2 | б | 68 × 5 | в | 25 × 11 × 4 |
Использование распределительного свойства
Мы используем оба распределительных свойства для упрощения некоторых задач на умножение. Например,
Например,
7 × 101 = 7 × (100 + 1) = 700 + 7 = 707,
7 х 99 = 7 х (100 — 1) = 700 — 7 = 693,
7 × 102 = 7 × (100 + 2) = 700 + 14 = 714,
и
7 × 98 = 7 × (100 − 2) = 700 − 14 = 686.
Некоторые примеры такого рода можно использовать для разработки концепций, необходимых в формальном алгоритме. Такие наблюдения, как 14 × 60 = 14 × 6 × 10 и 14 × 600 = 14 × 6 × 100, имеют фундаментальное значение для понимания алгоритма умножения.
Вычисления, такие как
21 × 7 = 20 × 7 + 1 × 7 = 140 + 7 = 147
можно использовать сначала как мысленную стратегию, а затем использовать в качестве первых примеров в формальном алгоритме. Другие мыслительные стратегии, связанные с алгоритмом, включают такие наблюдения, как
.200 × 81 = 2 × 81 × 100 = 162 × 100 = 16 200
, где умножение на однозначные числа, кратные степеням десяти, на самом деле не сложнее, чем умножение на однозначное число и отслеживание разрядности.
щелкните для просмотра экрана
УПРАЖНЕНИЕ 2
Используйте распределительный закон для выполнения следующих умножений.
| и | 31 × 8 | б | 99 × 32 | в | 1001 × 34 | д | 102 × 8 |
щелкните для просмотра экрана
УПРАЖНЕНИЕ 3
Тождество (a − b)(a + b) = a2 − b2 также полезно для вычислений в уме.
Например: 49 × 51 = (50 − 1) × (50 + 1) = 2500 − 1 = 2499
Выполните каждое из следующих умножений, используя это тождество.
| и | 48 × 52 | б | 47 × 53 | в | 31 × 29 | д | 201 × 199 |
Письменные стратегии
Алгоритм работает наиболее эффективно, если он использует небольшое количество шагов, применимых во всех
ситуациях. Таким образом, алгоритмы не прибегают к методам, таким как использование почти двойников, которые эффективны в некоторых случаях, но бесполезны в большинстве случаев.
Таким образом, алгоритмы не прибегают к методам, таким как использование почти двойников, которые эффективны в некоторых случаях, но бесполезны в большинстве случаев.
Стандартный алгоритм не поможет вам умножить два однозначных числа. Крайне важно, чтобы учащиеся свободно владели умножением двух однозначных чисел, прежде чем приступать к любому формальному алгоритму.
Стандартные алгоритмы
Свойство распределения лежит в основе нашего алгоритма умножения, поскольку оно позволяет нам вычислять произведения по одному столбцу за раз, а затем складывать результаты вместе. Она должна быть усилена арифметически, геометрически и алгоритмически. Например, арифметически мы имеем 6 × 14 = 6 × 10 + 6 × 4, геометрически мы видим то же явление,
и алгоритмически реализуем это в следующем расчете.
Как только этот процесс и структура будут поняты, мы можем перейти к контрактному алгоритму.
Умножение на одну цифру
Сначала мы сокращаем расчет, отслеживая перенос цифр и добавляя сложение по ходу дела. Предыдущий расчет сокращается до
Предыдущий расчет сокращается до
в зависимости от того, где записаны цифры переноса.
Следует соблюдать осторожность даже на этой ранней стадии из-за сочетания умножения и сложения. Также обратите внимание, что точное расположение и размер переносимой цифры не имеют существенного значения для процесса и различаются в зависимости от культуры. Когда мы выполняем длинное умножение, в каждом столбце может возникнуть несколько цифр переноса, и их запись в макете может быть скорее помехой, чем помощью. Поэтому желательно развить достаточную беглость в умножении на одну цифру, чтобы учащийся мог выполнять вычисления, такие как
без необходимости явно записывать цифры переноса. Если учащемуся действительно необходимо записать цифры переноса, то мы рекомендуем поместить их над соответствующей колонкой и зачеркнуть, поскольку они включены в решение.
Умножение на однозначное число, кратное степени числа десять
Следующее наблюдение состоит в том, что умножение на однозначное число, кратное десяти, не сложнее, чем умножение на однозначное число, при условии, что мы отслеживаем разрядность. Итак, чтобы найти количество секунд в 14 минутах, мы вычисляем 9.0003
Итак, чтобы найти количество секунд в 14 минутах, мы вычисляем 9.0003
14 × 60 = 14 × 6 × 10 = 840
и реализовать его в такой схеме, как
Точно так же мы можем отслеживать более высокие степени числа десять, используя позиционное значение в наших интересах. Итак,
14 × 600 = 14 × 6 × 100 = 8400
становится
Для студентов, которые столкнулись с основным наблюдением в рамках своих упражнений по арифметике в уме, единственное новшество на этом этапе заключается в том, как организовать эти вычисления.
Умножение на двузначное число
Следующий когнитивный скачок происходит, когда мы используем дистрибутивность для умножения двух двузначных чисел. Это реализовано в виде двух продуктов упомянутых выше типов. Например,
74 × 63 = 74 × (60 + 3) = 74 × 60 + 74 × 3
используется в приведенном ниже двухэтапном расчете.
Это соответствует показанному ниже разложению площади.
На ранних стадиях стоит одновременно развивать арифметические, геометрические и алгоритмические подходы, показанные выше.
Распаковка каждой строки в длинном вычислении умножения с использованием явного распределения,
как в
Это 74 × 63 = (70 + 4)(60 + 3)
Это также соответствует разложению площади
3 Это расширенное длинное умножение неэффективно, но его можно использовать, чтобы подчеркнуть многократное использование дистрибутивности в процессе. Иллюстрация модели площади, используемая в этом случае, появляется позже как геометрическая интерпретация вычислений в алгебре.
Умножение многозначных чисел
Чем больше цифр в числах, которые мы умножаем, тем больше раз нам нужно применять распределительное свойство, и тем больше строк будет иметь наш расчет, как показано ниже.
Этот пример соответствует: 5974 × 3 + 5974 × 60 + 5974 × 200 + 5974 × 1000
Кроме того, умножение целых чисел никогда не становится более сложным.
Ссылки Вперед
Первое применение умножения, с которым учащиеся могут столкнуться, — это деление. При вычислении деления мы постоянно вычисляем кратные делителю, и отсутствие беглости с умножением является существенным препятствием в этом процессе. Материал этого модуля закладывает основу для умножения, а затем деления дробей и десятичных знаков.
Другие приложения умножения, которые встречаются раньше, включают проценты и потребительскую арифметику. Например, мы рассчитываем цену товара с учетом налога на товары и услуги, вычисляя 1,1-кратную его стоимость до налога на товары и услуги.
Знакомство с умножением и представлением чисел в виде произведений множителей прокладывает путь к одной из основных теорем математики.
Основная теорема арифметики: каждое целое число больше 1 может быть представлено как произведение простых чисел, и такое выражение уникально вплоть до порядка, в котором записаны множители.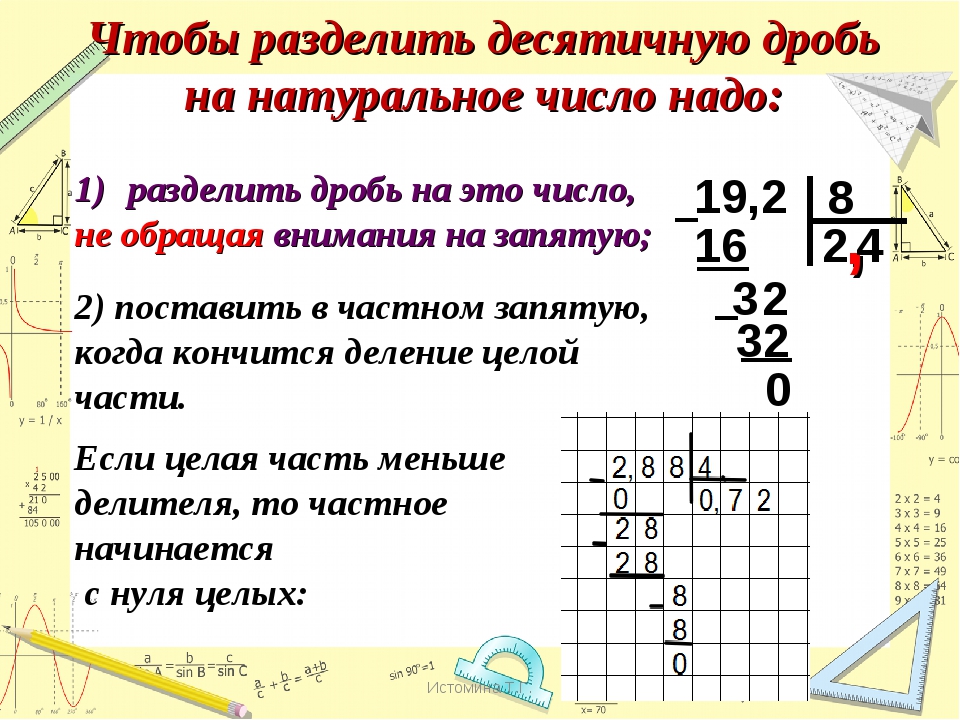 Например, 24 = 23 × 3 и 20 = 22 × 5,9.0003
Например, 24 = 23 × 3 и 20 = 22 × 5,9.0003
Фундаментальная теорема арифметики имеет далеко идущие последствия и приложения в информатике, программировании и криптографии с открытым ключом.
И последнее, но не менее важное: сильные знания арифметики подготавливают ученика к успеху в алгебре.
Использование таблицы умножения в качестве источника закономерностей
Способность определять закономерности и решать открытые задачи являются критически важными математическими навыками. Таблица умножения может использоваться как источник деятельности для обоих.
Занятие в классе
Нарисуйте сетку 10 × 10 и выделите на ней числа, кратные 9. Какой геометрический узор образуют в таблице числа, кратные 9, и почему он возникает? Какова арифметическая закономерность в цифрах чисел таблицы умножения на 9 и почему она возникает?
Занятие в классе
Нарисуйте сетку 12 × 12, на которой написаны числа от 1 до 144. Выберите запись, которая не находится на краю таблицы. Как числа непосредственно над ним и непосредственно под ним связаны с числом в выбранном вами поле? Что вы можете сказать о числах слева и справа от выбранного вами числа?
Как числа непосредственно над ним и непосредственно под ним связаны с числом в выбранном вами поле? Что вы можете сказать о числах слева и справа от выбранного вами числа?
История
Произведение двух чисел одинаково, независимо от того, как вы его вычисляете или как пишете ответ. Точно так же, как история чисел на самом деле связана с развитием числительных, история умножения — это в основном история процессов, которые люди использовали для выполнения вычислений. Разработка индийско-арабской нотации позиционных значений позволила реализовать эффективные алгоритмы арифметики и, вероятно, была главной причиной популярности и быстрого внедрения этой нотации.
Египетское дублирование
Одним из методов, который сильно отличается от стандартного алгоритма, является Египетское дублирование, датируемое до 1850 г. до н.э. Это сводит расчеты к последовательности удвоений вместе с окончательным добавлением.
Предположим, вы хотите умножить 63 на 22. Сначала напишите
, затем удвойте оба числа и запишите их ниже, чтобы получить
| 1 | 63 | |||
| 2 | 126 |
Продолжайте удваивать до тех пор, пока число в левом столбце не станет настолько большим, насколько это возможно, но не больше 22.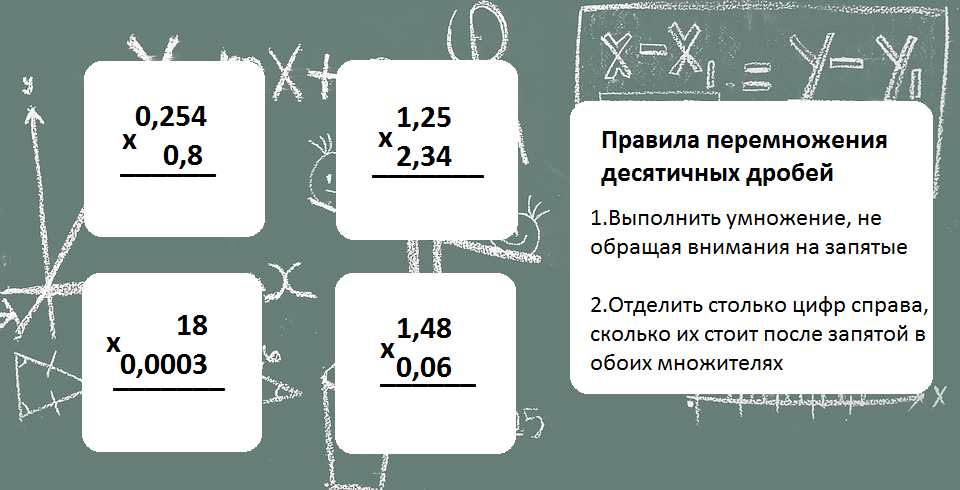 Итак, мы пишем
Итак, мы пишем
| . | 1 | 63 | ||
| 2 | 126 | |||
| 4 | 252 | |||
| 8 | 504 | |||
| 16 | 1008 |
и остановимся, потому что 32 больше, чем 22.
Теперь действуем в обратном направлении и начинаем с отметки 16; традиционно это делалось путем размещения строки слева от числа, как показано ниже.
Прибавление 8 к 16 дает число больше 22, поэтому мы не отмечаем строку выше.
Поскольку 16 + 4 ≤ 22, мы помечаем строку цифрой 4 в левом столбце.
Поскольку 16 + 4 + 2 = 22, мы помечаем строку цифрой 2 в левой колонке,
и поскольку 16 + 4 + 2 + 1 > 22 мы не помечаем верхнюю строку. Это оставляет нас с
Это оставляет нас с
| 1 | 63 | |||
| / | 2 | 126 | ||
| / | 4 | 252 | ||
| 8 | 504 | |||
| / | 16 | 1008 |
Добавление чисел в правом столбце отмеченных строк дает
1008 + 252 + 126 = 1386,
, что является произведением 22 × 63. Это работает, потому что
22 × 63 = (16 + 4 + 2) × 63 = 1008 + 252 + 126 = 1386.
Египетское дублирование основано на дистрибутивности и том факте, что каждое число может быть записано как сумма степеней 2.
щелкните для просмотра экрана
УПРАЖНЕНИЕ 4
Выполните следующее, используя египетское дублирование.
| и | 34 × 56 | б 57 × 34 |
Русский крестьянский метод
Как и египетское дублирование, русский крестьянский метод работает, потому что каждое число имеет уникальное выражение по основанию 2. Русский крестьянский метод сводит вычисления к последовательности удвоений и делений пополам вместе с окончательным сложением.
В качестве алгоритма Русский Крестьянский Метод работает следующим образом.
- Поместите два числа, которые вы хотите умножить, вверху двух столбцов.
- Создать еще одну строку из двух чисел, удвоив число в первом столбце
и уполовинить число во втором столбце, игнорируя любые остатки в процессе деления
пополам. - Повторяйте предыдущий шаг, пока число в столбце деления пополам не станет равным 1.
- Вычеркнуть все строки, в которых число в столбце деления пополам четное.
- Сложите все числа в столбце удвоения, которые не были зачеркнуты.

- Эта сумма равна произведению двух исходных чисел. Например, используя его для вычисления 63 × 22, мы пишем
| | | |
| 126 | 11 | |
| 252 | 5 | |
| | | |
| 1008 | 1 |
затем вычислить 126 + 252 + 1008 = 1386 и сделать вывод, что 63 × 22 = 1386.
Эта процедура работает всегда, но почему?
Предположим, мы хотим умножить 63 на 16. Начнем с того, что напишем 63 и 16 вверху двух столбцов
, а под каждым запишем числа, которые мы получим, удвоив единицу и 9.1845 г., разделив другой пополам.
| | | |
| | | |
| | | |
| | | |
| 1008 | 1 |
В этом случае произведение двух чисел в каждой строке равно произведению чисел непосредственно выше.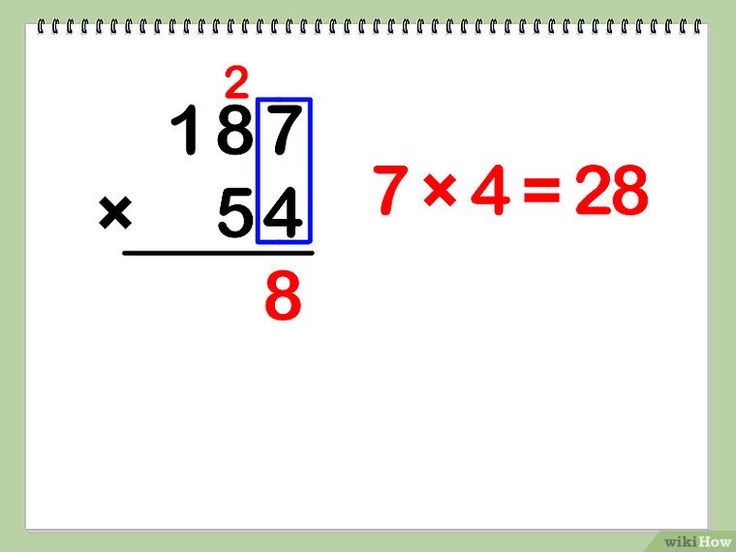 Например, 126 × 8 = 63 × 16. Следуя цепочке произведений, мы заключаем, что 63 × 16 = 1008 × 1 = 1008. Это работает особенно легко, потому что 16 — это степень числа 2.
Например, 126 × 8 = 63 × 16. Следуя цепочке произведений, мы заключаем, что 63 × 16 = 1008 × 1 = 1008. Это работает особенно легко, потому что 16 — это степень числа 2.
Предположим, вместо этого мы хотим умножить 63 на 14.
| | | |
| 126 | 7 | |
| 252 | 3 | |
| 504 | 1 |
Поскольку в первом делении нет остатков, 126 × 7 = 63 × 14, и первым шагом было просто переформулировать произведение другим способом. Мы можем смело вычеркнуть 63 × 14 и сделать вид, что его никогда не было. Однако на втором шаге мы проигнорировали остаток, и поэтому между двумя строками есть разница; в частности, 126 × 7 = 252 × 3 + 126 × 1. Обратите внимание, что разница между произведением в двух строках равна 126, числу в верхней строке столбца удвоения. Поскольку остаток от деления на 2 может быть только 0 или 1, на каждом шаге мы либо точно переформулируем задачу, либо выбиваем одну копию числа из столбца удвоения.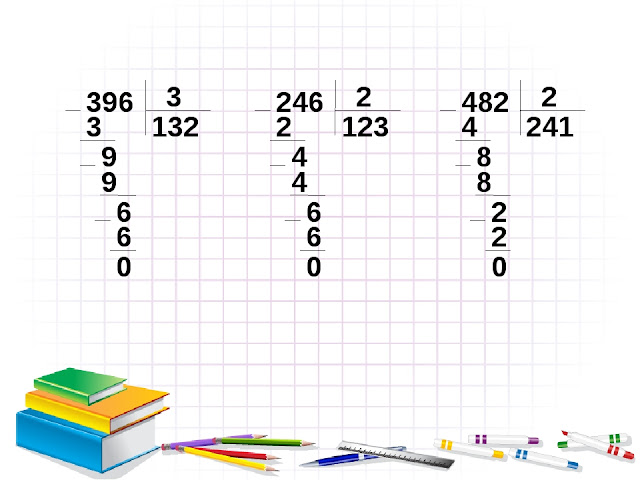 В этом расчете мы проигнорировали одну копию числа 126 и одну копию числа 252, прежде чем пришли к нашему выражению 504 × 1. Таким образом, наш исходный продукт 63 × 14 должен быть равен 504 + 252 + 126,9.0003
В этом расчете мы проигнорировали одну копию числа 126 и одну копию числа 252, прежде чем пришли к нашему выражению 504 × 1. Таким образом, наш исходный продукт 63 × 14 должен быть равен 504 + 252 + 126,9.0003
В общем случае может быть несколько строк, в которых у нас нет остатка, и несколько строк, в которых мы игнорируем остатки. Вычеркиваем те строки, для которых деление на 2 привело к точной переформулировке произведения в предыдущей строке; это точно соответствует строкам с четными числами в столбце деления пополам. Незачеркнутые числа в столбце удвоения соответствуют остаткам, а их сумма равна исходному произведению.
Итальянский или решетчатый метод
Другой метод, известный как итальянский метод или метод решетки, по существу является реализацией расширенной версии стандартного алгоритма, но в другой схеме. Метод очень старый, и он мог бы быть общепринятым, если бы его не было трудно распечатать. По-видимому, впервые он появился в Индии, но вскоре появился в работах китайцев и арабов. От арабов он попал в Италию, и его можно найти во многих итальянских рукописях 14 и 15 веков.
От арабов он попал в Италию, и его можно найти во многих итальянских рукописях 14 и 15 веков.
Здесь показано умножение 34 × 27.
34 × 27 = 918
В правом верхнем прямоугольнике вычислено 4 × 2. Цифра 8 помещается в нижний треугольник и 0 в верхний треугольник.
Затем вычисляется 3 × 2 и результат вводится, как показано.
В нижнем правом прямоугольнике вычисляется 4 × 7. Цифра 8 помещается в нижний треугольник, а цифра 2 — в верхний треугольник. Таким же образом записывается и результат 3×7.
Зеленая диагональ содержит единицы измерения.
Синяя диагональ содержит десятки.
Коричневая диагональ содержит сотни.
Цифры теперь суммируются по каждой диагонали, начиная справа, и каждый результат
записывается, как показано. Обратите внимание, что существует «перенос» от «диагонали десятков» к «диагонали сотен».0003
| и | 35 × 73 | б | 67 × 87 | в | 453 × 235 |
Ссылки
История математики: введение, 3-е издание, Виктор Дж.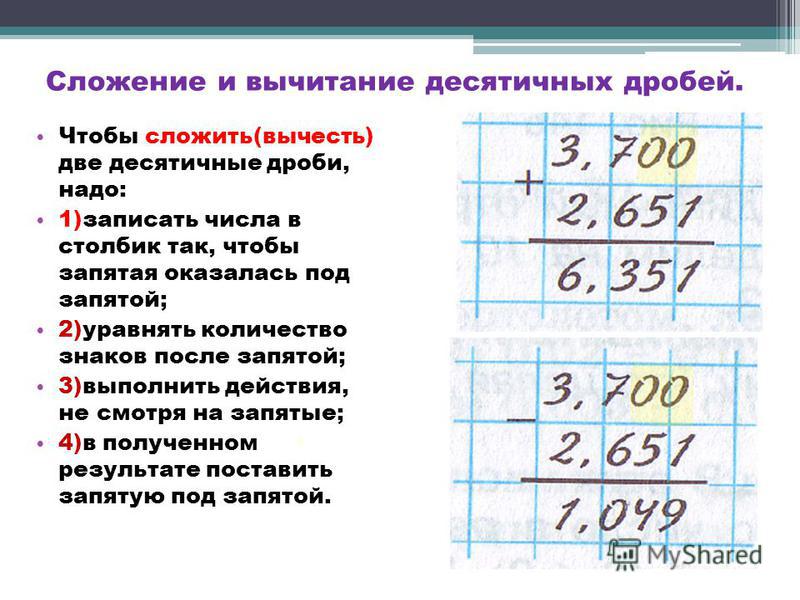 Кац, Аддисон-Уэсли, (2008)
Кац, Аддисон-Уэсли, (2008)
История математики, Д. Э. Смит, публикации Дувра, Нью-Йорк, (19)58)
https://en.wikipedia.org/wiki/Ancient_Egyptian_multiplication
Ответы на упражнения
Упражнение 1
| a | 70 | б | 340 | в | 1100 |
УПРАЖНЕНИЕ 2
| и | 248 | б | 3168 | в | 34 034 | д | 816 |
УПРАЖНЕНИЕ 3
| а | 2496 | б | 2491 | в | 899 | д | 39 999 |
УПРАЖНЕНИЕ 4
| и | 1904 | б | 1938 |
УПРАЖНЕНИЕ 5
| и | 2555 | б | 5829 | в | 106 455 |
Проект улучшения математического образования в школах (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Министерства образования, занятости и трудовых отношений правительства Австралии.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
2.1: Умножение целых чисел
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48836
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Умножение целых чисел
- понять процесс умножения
- уметь умножать целые числа
- уметь упростить умножение чисел, оканчивающихся на ноль
- уметь использовать калькулятор для умножения одного целого числа на другое
Умножение
Определение: Умножение
Умножение — это описание многократного сложения.
При сложении
\(5 + 5 + 5\)
число 5 повторяется 3 раза. Следовательно, мы говорим, что у нас есть три раза по пять, и описываем это, записав
\(3 \times 5\)
Таким образом,
\(3 \times 5 = 5 + 5 + 5\)
Определение: Множимое
При умножении повторяющееся слагаемое (прибавляемое число) называется множимым . В \(3\times 5\) 5 является множимым.
Определение: Множитель
Кроме того, при умножении число, обозначающее, сколько раз используется множимое, называется множителем . В \(3\times 5\) множитель равен 3.
Набор образцов A
Выразите каждое повторяющееся сложение как умножение. В каждом случае укажите множитель и множимое.
\(7 + 7 + 7 + 7 + 7 + 7\)
Решение
\(6 \х7\), Множитель равен 6. Множимое равно 7.
Набор образцов A
\(18 + 18 + 18\)
Раствор
\(3 \х18\). Множитель равен 3. Множимое равно 18.
Множимое равно 18.
Практический набор A
Выражайте каждое повторяющееся сложение как умножение. В каждом случае укажите множитель и множимое.
\(12 + 12 + 12 + 12\)
. Мультипликатор есть. Мультипликатор есть.
- Ответить
\(4 \умножить на 12\). Множитель равен 4. Множимое равно 12,9.0003
Тренировочный набор A
\(36 + 36 + 36 + 36 + 36 + 36 + 36 + 36\)
. Мультипликатор есть. Мультипликатор есть.
- Ответить
\(8 \х36\). Множитель равен 8. Множимое равно 36.
Тренировочный набор A
\(0 + 0 + 0 + 0 + 0\)
. Мультипликатор есть. Мультипликатор есть.
- Ответить
\(5 \х0\). Множитель равен 5. Множимое равно 0,9.0003
Тренировочный набор A
\(\underbrace{1847 + 1847 + \cdots + 1847}_{12 000 \text{раз}}\)
с. Мультипликатор есть. Множимое равно .me
Мультипликатор есть. Множимое равно .me
- Ответить
\(12 000 \умножить на 1847\). Множитель 12000. Мультипликатор равен 1847.
Определение: Факторы
При умножении умножаемые числа также называются множителями .
Определение: Продукты
Результат умножения называется произведением . В \(3 \times 5 = 15\) числа 3 и 5 называются не только множителем и множителем, но и множителями. Произведение равно 15.
Индикаторы умножения \(\times, \cdot, ()\)
Символ умножения (\(\times\)) — не единственный символ, используемый для обозначения умножения. Другие символы включают точку (\(\cdot\)) и пары скобок ( ). Выражения
\(3 \times 5, 3 \cdot 5, 3(5), (3)5, (3)(5)\)
представляют один и тот же продукт.
Процесс умножения с помощью одноразрядного множителя
Поскольку умножение представляет собой многократное сложение, мы не должны удивляться, обнаружив, что содержит . Перенос происходит, когда мы находим произведение 38 и 7:
Перенос происходит, когда мы находим произведение 38 и 7:
Сначала мы вычисляем \(7 \times 8 = 56\). Напишите 6 в колонке единиц. Несите 5. Затем возьмите \(7 \times 3 = 21\). Прибавьте к 21 5, которые были перенесены: \(21 + 5 = 26\). Произведение 266.
Набор образцов B
Найдите следующие продукты.
Решение
\(\begin{array} {lcl} {3 \times 4 = 12} &\ \ \ \ & {\text{Напишите 2, перенесите 1.}} \\ { 3 \times 6 = 18} &\ \ \ \ & {\text{Добавить к 18 полученную 1: 18 + 1 = 19.}} \end{массив}\)
Произведение равно 192.
Набор образцов B
Решение
\(\begin{array} {lcl} {5 \times 6 = 30} & \ \ \ \ & {\text{Напишите 0, перенесите 3.}} \\ {5 \times 2 = 10} & \ \ \ \ & {\ text{Добавить к 10 3, которые были перенесены: 10 + 3 = 13. Запишите 3, перенесите 1.}} \\ {5 \ умножить на 5 = 25} & \ \ \ \ & {\ text {Добавить к 25 1, которая была перенесена: 25 + 1 = 6.}} \ end {массив} \)
Произведение 2630.
Набор образцов B
Решение
\(\begin{array} {lcl} {9 \times 4 = 36} & \ \ \ \ & {\text{Запишите 6, перенесите 3. }} \\ {9 \times 0 = 0} & \ \ \ \ & {\text{Добавьте к 0 3, которые были перенесены: 0 + 3 = 13. Запишите 3.}} \\ {9 \times 8 = 72} & \ \ \ \ & {\ text {Запишите 2, перенесите 7.}} \\ {} & \ \ \ \ & {\ text {Поскольку больше не нужно выполнять умножения, запишите обе 1 и 6.}} \end{массив}\)
Произведение 16 236.
Тренировочный набор B
Найдите следующие продукты.
\(\begin{массив} {r} {37} \\ {\underline{\times \\ 5}} \end{массив}\)
- Ответить
185
Практический набор B
Найдите следующие продукты.
\(\begin{массив} {r} {78} \\ {\underline{\times \\ 8}} \end{массив}\)
- Ответить
624
Практический набор B
Найдите следующие продукты.
\(\begin{массив} {r} {537} \\ {\underline{\times \ \ \ \ 7}} \end{массив}\)
- Ответить
3 752
Практический набор B
Найдите следующие продукты.
\(\begin{array} {r} {40,019} \\ {\underline{\times \ \ \ \ \ \ \ \ \ 8}} \end{array}\)
- Ответить
320 152
Практический набор B
Найдите следующие продукты.
\(\begin{массив} {r} {301,599} \\ {\underline{\times \ \ \ \ \ \ \ \ \ \ \ 3}} \end{массив}\)
- Ответить
904 797
Процесс умножения с использованием многозначного множителя
В умножении, в котором множитель состоит из двух или более цифр, умножение должно происходить по частям . Процесс выглядит следующим образом:
- Первый неполный продукт Умножьте множимое на единицу множителя.
 Этот продукт называется первым частичным продуктом .
Этот продукт называется первым частичным продуктом . - Второе частичное произведение Умножьте множимое на разряд десятков множителя. Этот продукт называется вторым частичным продуктом . Поскольку в качестве множителя используется цифра десятков, второе частичное произведение записывается под первым частичным произведением, так что его крайняя правая цифра появляется в столбце десятков.
- При необходимости продолжайте поиск частичных произведений таким же образом. Запишите каждое число ниже предыдущего так, чтобы крайняя правая цифра находилась в столбце непосредственно под цифрой, которая использовалась в качестве множителя.
- Общий продукт Сложите частичные продукты, чтобы получить общий продукт .
Примечание
Может потребоваться иметь при себе каждый частичный продукт.
Набор образцов C
Умножьте 326 на 48.
Решение
Часть 1:
Часть 2:
Часть 3: Этот шаг не нужен, так как все цифры множителя уже использованы.
Часть 4: Добавьте частичные продукты, чтобы получить общий продукт.
Продукт 15 648.
Набор образцов C
Умножьте 5369 на 842.
Раствор
Часть 1:
Часть 2:
Часть 3:
2
Набор образцов C
Умножить 1508 на 206.
Решение
Часть 1:
Часть 2:
который получается сложением). Перейти к следующему частичному продукту.
Часть 3:
Артикул 310 648
Практический набор C
Умножить 73 на 14.
- Ответить
1 022
Тренировочный набор C
Умножить 86 на 52.
- Ответить
4 472
Тренировочный набор C
Умножить 419 на 85.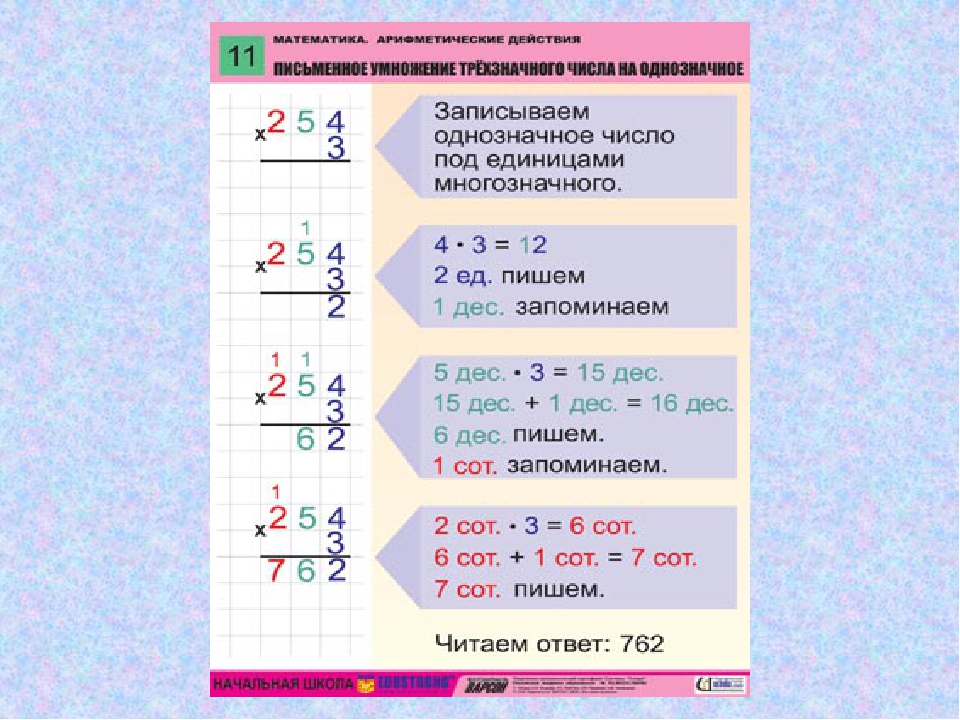
- Ответить
35 615
Тренировочный набор C
Умножьте 2376 на 613.
- Ответить
1 456 488
Тренировочный набор C
Умножить 8107 на 304.
- Ответить
2 464 528
Тренировочный набор C
Умножьте 66 260 на 1 008.
- Ответить
66 790 080
Тренировочный набор C
Умножить 209 на 501.
- Ответить
104 709
Тренировочный набор C
Умножить 24 на 10.
- Ответить
240
Тренировочный набор C
Умножьте 3809 на 1000.
- Ответить
3 809 000
Тренировочный набор C
Умножьте 813 на 10 000.
- Ответить
8 130 000
Умножение чисел, оканчивающихся на ноль
Часто при выполнении умножения один или оба множителя оканчиваются нулями. Такие умножения можно выполнить быстро, выровняв числа так, чтобы крайние правые цифры, отличные от нуля, находились в одном столбце.
Набор образцов D
Выполните умножение (49 000)(1 200).
\((49000)(1200)\) = \(\begin{массив} {r} {49000} \\ {\underline{\times \\ 1200}} \end{массив}\)
Начиная с 9 и 2 — самые правые ненулевые цифры, поместите их в тот же столбец.
Нарисуйте (возможно, мысленно) вертикальную линию, чтобы отделить нули от ненулевых.
Умножьте числа слева от вертикальной черты, как обычно, затем присоедините к правому концу этого произведения общее количество нулей.
Продукт 58 800 000
Практический набор D
Умножить 1800 на 90.
- Ответить
162 000
Тренировочный набор D
Умножьте 420 000 на 300.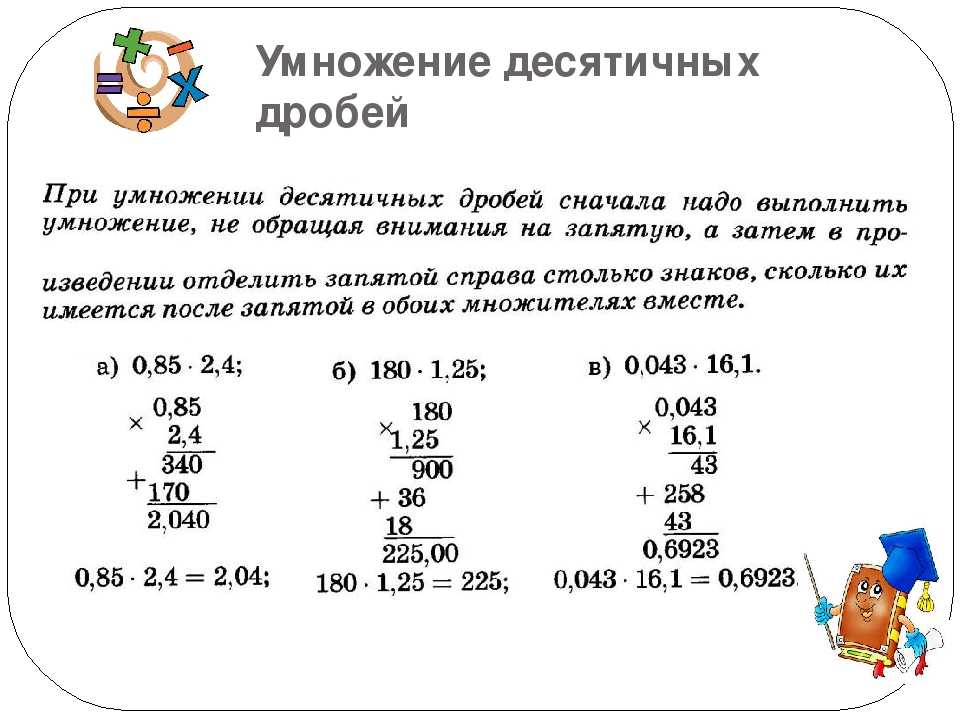
- Ответить
126 000 000
Тренировочный набор D
Умножить 20 500 000 на 140 000.
- Ответить
2 870 000 000 000
Калькуляторы
Большинство операций умножения выполняются с помощью калькулятора.
Набор образцов E
Умножьте 75 891 на 263.
Раствор
| Показания дисплея | ||
| Тип | 75891 | 75891 |
| Пресс | × | 75891 |
| Тип | 263 | 263 |
| Пресс | = | 19959333 |
Изделие 19,959 333.
Набор образцов E
Умножьте 4 510 000 000 000 на 1700.
Решение
| Показания дисплея | ||
| Тип | 451 | 451 |
| Пресс | × | 451 |
| Тип | 17 | 17 |
| Нажмите | = | 7667 |
Теперь на дисплее отображается 7667. Нам придется добавить нули самим. Всего 12 нулей. Прибавив 12 нулей к 7667, получим 7 667 000 000 000 000.
Продукт 7 667 000 000 000 000.
Набор образцов E
Умножьте 57 847 298 на 38 976.
Решение
Теперь на дисплее отображается 2,2546563 12. Что это за число? Это пример целого числа, записанного цифрой 9.0349 научное обозначение . Мы изучим эту концепцию, когда перейдем к десятичным числам.
Тренировочный набор E
Используйте калькулятор для выполнения каждого умножения.
\(52 \х27\)
- Ответить
1 404
Практический набор E
\(1 448 \умножить на 6 155\)
- Ответить
8 912 440
Практический набор E
\(8 940 000 \умножить на 205 000\)
- Ответить
1 832 700 000 000
Упражнения
В следующих задачах выполните умножение. Вы можете проверить каждый продукт с помощью калькулятора.
Вы можете проверить каждый продукт с помощью калькулятора.
Упражнение \(\PageIndex{1}\)
\(\begin{массив} {r} {8} \\ {\underline{\times 3}} \end{массив}\)
- Ответить
24
Упражнение \(\PageIndex{2}\)
\(\begin{массив} {r} {3} \\ {\underline{\times 5}} \end{массив}\)
Упражнение \(\PageIndex{3}\)
\(\begin{массив} {r} {8} \\ {\underline{\times 6}} \end{массив}\)
- Ответить
48
Упражнение \(\PageIndex{4}\)
\(\begin{массив} {r} {5} \\ {\underline{\times 7}} \end{массив}\)
Упражнение \(\PageIndex{5}\)
\(6 \умножить на 1\)
- Ответить
6
Упражнение \(\PageIndex{6}\)
\(4\х5\)
Упражнение \(\PageIndex{7}\)
\(75 \х3\)
- Ответить
225
Упражнение \(\PageIndex{8}\)
\(35 \х5\)
Упражнение \(\PageIndex{9}\)
\(\begin{массив} {r} {45} \\ {\underline{\times \ \ 6}} \end{массив}\)
- Ответить
270
Упражнение \(\PageIndex{10}\)
\(\begin{массив} {r} {31} \\ {\underline{\times \\ 7}} \end{массив}\)
Упражнение \(\PageIndex{11}\)
\(\begin{массив} {r} {97} \\ {\underline{\times \\ 6}} \end{массив}\)
- Ответить
582
Упражнение \(\PageIndex{12}\)
\(\begin{массив} {r} {75} \\ {\underline{\times 57}} \end{массив}\)
Упражнение \(\PageIndex{13}\)
\(\begin{массив} {r} {64} \\ {\underline{\times 15}} \end{массив}\)
- Ответить
960
Упражнение \(\PageIndex{14}\)
\(\begin{массив} {r} {73} \\ {\underline{\times 15}} \end{массив}\)
Упражнение \(\PageIndex{15}\)
\(\begin{массив} {r} {81} \\ {\underline{\times 95}} \end{массив}\)
- Ответить
7 695
Упражнение \(\PageIndex{16}\)
\(\begin{массив} {r} {31} \\ {\underline{\times 33}} \end{массив}\)
Упражнение \(\PageIndex{17}\)
\(57 \х64\)
- Ответить
3 648
Упражнение \(\PageIndex{18}\)
\(76 \х42\)
Упражнение \(\PageIndex{19}\)
\(894 \умножить на 52\)
- Ответить
46 488
Упражнение \(\PageIndex{20}\)
\(684 \х38\)
Упражнение \(\PageIndex{21}\)
\(\begin{массив} {r} {115} \\ {\underline{\times \\ 22}} \end{массив}\)
- Ответить
2 530
Упражнение \(\PageIndex{22}\)
\(\begin{массив} {r} {706} \\ {\underline{\times \\ 81}} \end{массив}\)
Упражнение \(\PageIndex{23}\)
\(\begin{массив} {r} {328} \\ {\underline{\times \\ 21}} \end{массив}\)
- Ответить
6 888
Упражнение \(\PageIndex{24}\)
\(\begin{массив} {r} {550} \\ {\underline{\times \\ 94}} \end{массив}\)
Упражнение \(\PageIndex{25}\)
\(930 \х26\)
- Ответить
24 180
Упражнение \(\PageIndex{26}\)
\(318 \х63\)
Упражнение \(\PageIndex{27}\)
\(\begin{массив} {r} {582} \\ {\underline{\times 127}} \end{массив}\)
- Ответить
73 914
Упражнение \(\PageIndex{28}\)
\(\begin{массив} {r} {247} \\ {\underline{\times 116}} \end{массив}\)
Упражнение \(\PageIndex{29}\)
\(\begin{массив} {r} {305} \\ {\underline{\times 225}} \end{массив}\)
- Ответить
68 625
Упражнение \(\PageIndex{30}\)
\(\begin{массив} {r} {782} \\ {\underline{\times 547}} \end{массив}\)
Упражнение \(\PageIndex{31}\)
\(\begin{массив} {r} {771} \\ {\underline{\times 663}} \end{массив}\)
- Ответить
511 173
Упражнение \(\PageIndex{32}\)
\(\begin{массив} {r} {638} \\ {\underline{\times 516}} \end{массив}\)
Упражнение \(\PageIndex{33}\)
\(1905 \х710\)
- Ответить
1 352 550
Упражнение \(\PageIndex{34}\)
\(5 757 \умножить на 5 010\)
Упражнение \(\PageIndex{35}\)
\(\begin{массив} {r} {3,106} \\ {\underline{\times 1,752}} \end{массив}\)
- Ответить
5 441 712
Упражнение \(\PageIndex{36}\)
\(\begin{массив} {r} {9300} \\ {\underline{\times 1130}} \end{массив}\)
Упражнение \(\PageIndex{37}\)
\(\begin{массив} {r} {7,057} \\ {\underline{\times 5,229}} \end{массив}\)
- Ответить
36 901 053
Упражнение \(\PageIndex{38}\)
\(\begin{массив} {r} {8,051} \\ {\underline{\times 5,580}} \end{массив}\)
Упражнение \(\PageIndex{39}\)
\(\begin{массив} {r} {5804} \\ {\underline{\times 4300}} \end{массив}\)
- Ответить
24 957 200
Упражнение \(\PageIndex{40}\)
\(\begin{массив} {r} {357} \\ {\underline{\times \\ 16}} \end{массив}\)
Упражнение \(\PageIndex{41}\)
\(\begin{массив} {r} {724} \\ {\underline{\times \ \ \ \ 0}} \end{массив}\)
- Ответить
0
Упражнение \(\PageIndex{42}\)
\(\begin{массив} {r} {2649} \\ {\underline{\times \ \ \ \\ 41}} \end{массив}\)
Упражнение \(\PageIndex{43}\)
\(\begin{массив} {r} {5,173} \\ {\underline{\times \ \ \ \ \ \ \ 8}} \end{массив}\)
- Ответить
41 384
Упражнение \(\PageIndex{44}\)
\(\begin{массив} {r} {1,999} \\ {\underline{\times \ \ \ \ \ \ \ 0}} \end{массив}\)
Упражнение \(\PageIndex{45}\)
\(\begin{массив} {r} {1666} \\ {\underline{\times \ \ \ \ \ \ \ 0}} \end{массив}\)
- Ответить
0
Упражнение \(\PageIndex{46}\)
\(\begin{массив} {r} {51 730} \\ {\underline{\times \ \ \ \ \ 142}} \end{массив}\)
Упражнение \(\PageIndex{47}\)
\(\begin{массив} {r} {387} \\ {\underline{\times 190}} \end{массив}\)
- Ответить
73 530
Упражнение \(\PageIndex{48}\)
\(\begin{массив} {r} {3400} \\ {\underline{\times \ \ \ \\ 70}} \end{массив}\)
Упражнение \(\PageIndex{49}\)
\(\begin{массив} {r} {460 000} \\ {\underline{\times \\ 14 000}} \end{массив}\)
- Ответить
6 440 000 000
Упражнение \(\PageIndex{50}\)
\(\begin{array} {r} {558,000,000} \\ {\underline{\times \ \ \ \ \ \ \ \ \ 81,000}} \end{array}\)
Упражнение \(\PageIndex{51}\)
\(\begin{массив} {r} {37 000} \\ {\underline{\times \ \ \ \ \ 120}} \end{массив}\)
- Ответить
4 440 000
Упражнение \(\PageIndex{52}\)
\(\begin{массив} {r} {498 000} \\ {\underline{\times \ \ \ \ \ \ \ \ \ \ \ 0}} \end{массив}\)
Упражнение \(\PageIndex{53}\)
\(\begin{массив} {r} {4 585 000} \\ {\underline{\times \ \ \ \ \ \ \ \ \ \ 140}} \end{массив}\)
- Ответить
641 900 000
Упражнение \(\PageIndex{54}\)
\(\ begin{array} {r} {30 700 000} \\ {\ underline{\ times \ \ \ \ \ \ \ \ \ \ \ \ 180}} \ end {array} \)
Упражнение \(\PageIndex{55}\)
\(\begin{массив} {r} {8000} \\ {\underline{\times \ \ \ \ \ 10}} \end{массив}\)
- Ответить
80 000
Упражнение \(\PageIndex{56}\)
Предположим, театр вмещает 426 человек. Если театр берет 4 доллара за билет и продает все места, сколько денег они получат?
Если театр берет 4 доллара за билет и продает все места, сколько денег они получат?
Упражнение \(\PageIndex{57}\)
На уроке английского языка студент должен прочитать 12 романов в течение семестра и подготовить отчет по каждому из них. Если в классе 32 ученика, сколько отчетов будет подготовлено?
- Ответить
384 отчета
Упражнение \(\PageIndex{58}\)
На уроке математики выпускной экзамен состоит из 65 задач. Если этот экзамен сдается 28 людям, сколько задач должен поставить инструктор?
Упражнение \(\PageIndex{59}\)
Преподаватель коммерческого права сдает экзамен из 45 задач двум своим ученикам. Если в каждом классе 37 человек, сколько задач инструктор должен будет оценить?
- Ответить
3330 задач
Упражнение \(\PageIndex{60}\)
Преподаватель алгебры сдает экзамен, состоящий из 43 задач, четырем ученикам. Если в классах 25, 28, 31 и 35 учеников, сколько задач учитель должен будет оценить?
Если в классах 25, 28, 31 и 35 учеников, сколько задач учитель должен будет оценить?
Упражнение \(\PageIndex{61}\)
В статистике термин «стандартное отклонение» относится к числу, которое рассчитывается на основе определенных данных. Если данные показывают, что одно стандартное отклонение составляет 38 единиц, сколько единиц составляют три стандартных отклонения?
- Ответить
114 шт.
Упражнение \(\PageIndex{62}\)
Безалкогольные напитки поставляются в коробках по 24 банки. Если супермаркет продает 857 коробок в течение одной недели, сколько банок было продано поштучно?
Упражнение \(\PageIndex{63}\)
В 1 минуте 60 секунд, а в 1 часе 60 минут. Сколько секунд в 1 часе?
- Ответить
3600 секунд
Упражнение \(\PageIndex{64}\)
В 1 минуте 60 секунд, в одном часе 60 минут, в одном дне 24 часа, а в одном году 365 дней. Сколько секунд в 1 году?
Сколько секунд в 1 году?
Упражнение \(\PageIndex{65}\)
Свет проходит 186 000 миль за одну секунду. Сколько миль проходит свет за один год? ( Подсказка: Можно ли использовать результат предыдущей задачи?)
- Ответить
5 865 696 000 000 миль в год
Упражнение \(\PageIndex{66}\)
Столовая начальной школы продает 328 обедов каждый день. Каждый обед стоит 1 доллар. Сколько денег приносит столовая за 2 недели?
Упражнение \(\PageIndex{67}\)
Компьютерная компания продает акции по 23 доллара за акцию. Если 87 человек купят по 55 акций каждый, сколько денег получится?
- Ответить
$110 055
Упражнения для повторения
Как в числе 421 998 могут быть десять тысяч?
Округлите 448 062 187 до ближайших сотен тысяч.
- Ответить
448 100 000
Найдите сумму.

 Закрепление теории по опорным схемам, составленным на предыдущем уроке
Закрепление теории по опорным схемам, составленным на предыдущем уроке


 Сколько стоит торт, если пирожное стоит 22 рубля?
Сколько стоит торт, если пирожное стоит 22 рубля? Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?
Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?
 Сколько стоит торт, если пирожное стоит 22 рубля?
Сколько стоит торт, если пирожное стоит 22 рубля? Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?
Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?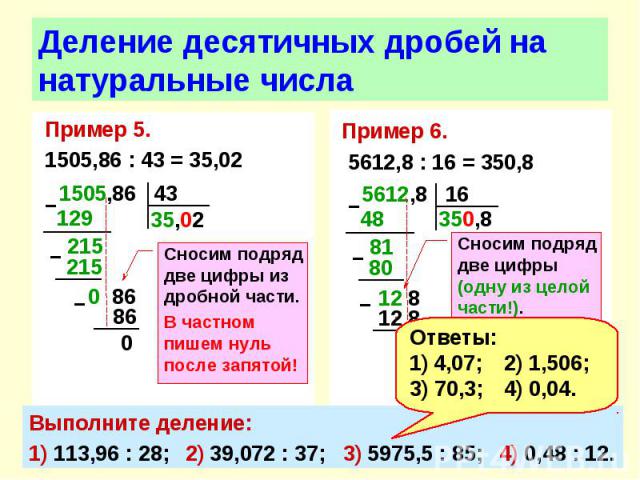
 09.16.
09.16.
 Выражение 7*8-4*12 означает:
Выражение 7*8-4*12 означает:
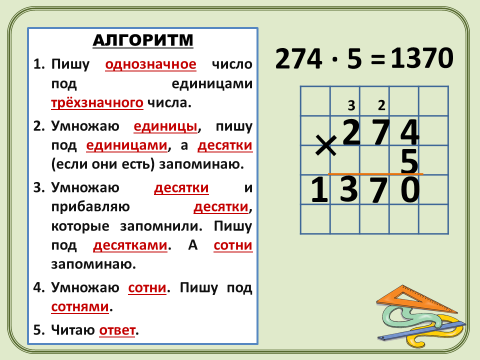 После выполнения задания поменяйтесь тетрадями и проверьте правильность выполнения у соседа по парте. При необходимости, помогите друг другу.
После выполнения задания поменяйтесь тетрадями и проверьте правильность выполнения у соседа по парте. При необходимости, помогите друг другу.









 (2 × 4 = 8)
(2 × 4 = 8) Теперь перенесите 6 десятков в столбец десятков.
Теперь перенесите 6 десятков в столбец десятков.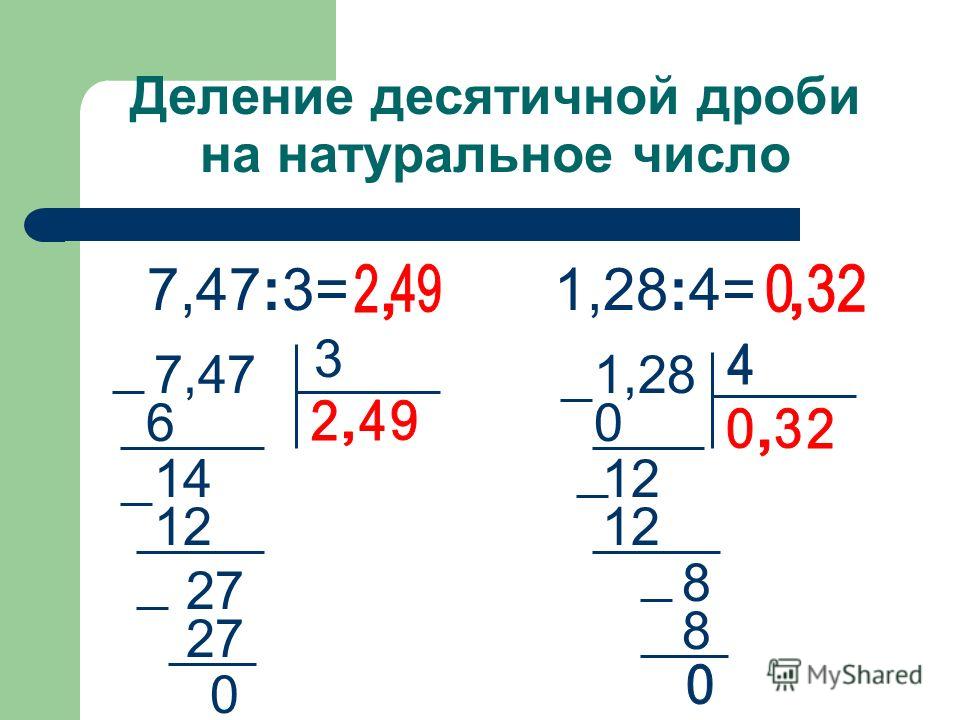 Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Итак, ответ будет 170 — 17 = 153.
Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Итак, ответ будет 170 — 17 = 153. Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.
Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов. Это нулевое свойство умножения. Например, 12 × 0 = 0,
Это нулевое свойство умножения. Например, 12 × 0 = 0, В этом случае 6 является множимым.
В этом случае 6 является множимым.



 Этот продукт называется первым частичным продуктом .
Этот продукт называется первым частичным продуктом .