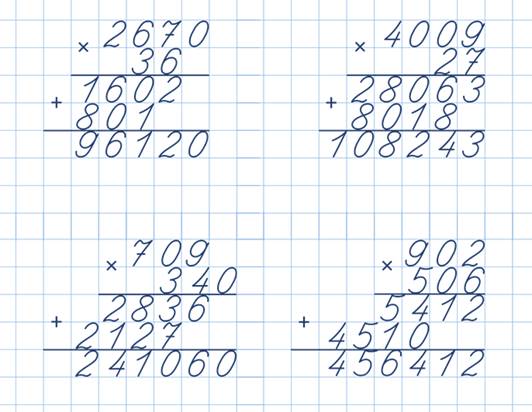Умножение чисел столбиком. 5 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Тема урока:
Умножение чисел столбиком
5 класс
С.М. Никольский и др.
Учитель Чернышова Анна
Владимировна
2. Цели урока:
Систематизировать, расширить иуглубить знания по данной теме.
Развивать
наблюдательность,
умение
анализировать,
вычислительные навыки.
Искать наиболее рациональные
пути решения задач.

3. Этапы урока:
1. Повторение.2. Изучение нового материала.
3. Решение упражнений и задач.
Самопроверка.
4. Математическая эстафета
5. Подведение итогов урока.
6. Домашнее задание.
Повторение:
a b=b a
(a b) с=a (b с)
a (b-с)=a b- a с
Переместительный закон
Сочетательный закон
Распределительный закон
Повторение:
a 0=0
При умножении любого числа на
нуль всегда будет нуль
a 1=а
При умножении любого числа на
единицу всегда получаем это
число
Рассмотрим выражение:
25 ∙ 589 ∙ 5 ∙ 125 ∙ 2 ∙ 4 ∙ 8 = ?
Чтобы найти значение этого выражения, не
обязательно перемножать все числа в столбик:
достаточно
воспользоваться
сочетательным
законом умножения.
Объединим попарно некоторые множители:
(25 ∙ 4) ∙ 589 ∙ (5 ∙ 2) ∙ (125 ∙ 8) = 100 ∙ 589 ∙
10 ∙ 10000 = 589 ∙ 10000000 = 589000000
Вычисление
произведения
однозначного и многозначного
чисел,
и
тем
более двух
многозначных чисел, требует
применения не только таблицы
умножения,
но
и
законов
сложения и умножения.

Вычислим произведение 723 ∙ 5 = ?
Можно представить число 723 в виде суммы
разрядных слагаемых, и каждое из этих
слагаемых умножить на 5, а затем сложить
полученные результаты.
723 ∙ 5 = (700 + 20 + 3) ∙ 5 = 700 ∙ 5 + 20 ∙ 5+
+ 3 ∙ 5 = 3500 + 100 + 15 = 3615
Можно записать вычисление значения
этого выражения столбиком:
При умножении трёх на пять получаем пятнадцать.
Пять записываем в разряд единиц, единицу прибавляем
в разряд десятков. При умножении двух на пять
получаем десять, плюс единица, которую мы запомнили,
получаем в разряде десятков единицу, единицу
добавляем к разряду сотен. При умножении семи на пять
получим тридцать пять, плюс один – тридцать шесть.
Ответ: 3615.
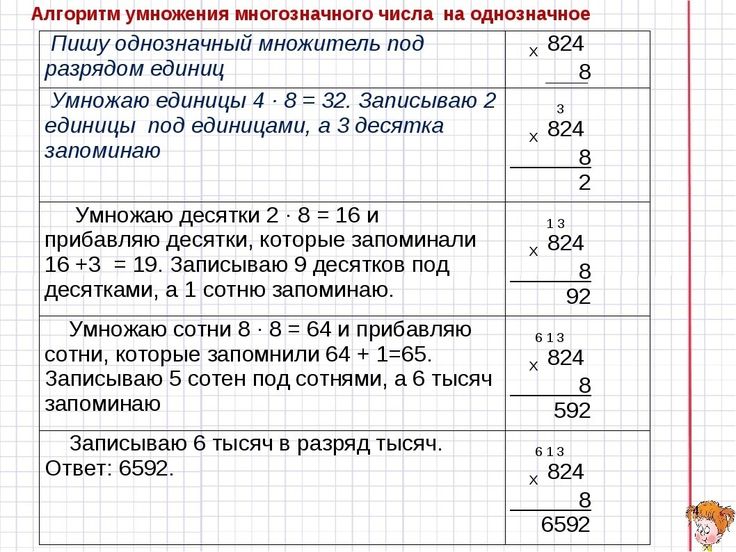
Рассмотрим ещё одно выражение: 329 ∙ 34 = ?
Запишем это произведение в столбик:
Сначала умножаем целиком верхнее число на
последнюю цифру нижнего числа, т.е. на 4. Результат
записываем под чертой под самой правой цифрой
справа налево.

Переходим к умножению числа 329 на 3.
Умножаем по тем же правилам, что и в
предыдущем вычислении.
Результат умножения на вторую цифру необходимо
записывать под второй цифрой результата первого
действия умножения.
Полученные числа под чертой складываем
по правилам сложения в столбик.
Упражнение:
Вычислите: 3256 ∙ 25 = ?
Решение: вычислим данное произведение в столбик:
Ответ: 81400.
Задача:
Пете ко Дню рождения надо было купить конфет. Он
купил конфеты трёх видов: «Батончики», «Мишка на севере»,
«Грильяж». «Батончиков» он купил 56 штук, «Мишек на
севере» – в 15 раз больше, чем «Батончиков», а «Грильяжа»
на 50 конфет больше, чем «Батончиков». Сколько всего
конфет купил Петя?
Варианты ответы: 1020, 1002, 1000, 992.
Решение:
1) 56 ∙ 15 = 840 (шт.) – «Мишка на севере».
2) 56 + 50 = 106 (шт.) – «Грильяж».
3) 56 + 840 + 106 = 1002 (шт.) – всего.
Ответ: 1002 штуки.
Математическая эстафета:
1 столбик
2 столбик
3 столбик
1) 12 10=
1) 15 10=
1) 17 10=
2) 24 2=
2) 31 3=
2) 71 9=
3) 42
х 12
3) 22
х 33
3) 53
х 31
4) 101
х 332
4) 101
х 648
4) 101
х 458
Домашнее задание:
Классная работа:
Проработать
презентацию, прочитать
параграф 1.
 10 с.34-35,
10 с.34-35,выполнить задание
письменно слайд 14.
Домашняя работа: с.36
№143 письменно
Спасибо за урок!
English Русский Правила
Умножение чисел столбиком
Технологическая карта урока.
Тема урока: Умножение натуральных чисел и его свойства.
Тип урока: урок систематизации и обобщения знаний и умений.
Оборудование: доска, задания для выполнения на уроке, интерактивная доска, проектор, карточки самооценивания, презентация.
Цели урока:
Обучающие: совершенствование навыка умножения натуральных чисел, применение рациональных приёмов вычислений. Продолжить работу над умножением натуральных чисел в столбик.
Развивающие: развивать умение анализировать,сравнивать, обобщать, делать выводы, развивать внимание, развивать устную речь.
Воспитательные: воспитывать умение высказывать свою точку зрения, слушать ответы других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству.

Методы:
По источникам знаний: словесные, наглядные;
По степени взаимодействия учитель-ученик: эвристическая беседа; интерактивный метод.
Относительно дидактических задач: подготовка к восприятию;
Относительно характера познавательной деятельности: активный метод, репродуктивный, частично- поисковый.
Планируемый результат.
УУД.
Личностные:умножают натуральные числа, используют свойства умножения, применяют рациональные приёмы для вычислений, формируют внимательность и аккуратность в вычислениях требовательное отношение к себе и к своей работе.
Познавательные: закрепляют навыки и умения применять алгоритмы при решении задач на умножение натуральных чисел и применение свойств умножения, систематизируют знания, обобщают и углубляют знания при решении задач по теме « Умножение натуральных чисел и его свойства», выбирают и формулируют познавательную цель, выражают смысл ситуации с помощью различных примеров.
Предметные: уметь в процессе реальной ситуации применять понятие умножение натуральных чисел и свойства умножения.
Регулятивные:
Самостоятельно формулируют познавательную цель и строят свои действия в соответствии с ней.
Планируют собственную деятельность, определяют средства для её осуществления.
Коммуникативные: регулируют собственную деятельность посредством речевых действий, умение слушать и вступать в диалог, воспитывать чувство взаимопомощи. Уважительное отношение к чужому умению, культуру учебного труда, требовательное отношение к себе и своей работе.
Технологическая карта урока математики в 5 классе
« Умножение натуральных чисел и его свойства».
Этап урока. | Задачи этапа. | Деятельность учителя. | Деятельность учеников. | Время. | Формируемые УУД | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.Организационный этап. | Создать благоприятный психологический настрой на работу. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Включаются в деловой ритм урока. | 1 | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности. Личностные: мотивация учения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Актуализация знаний Слайд№2-4. | Актуализация опорных знаний и способов действий. | 1. Организация устного счёта 60+9 =69 :3=23 -15=8 ∙12=96 :2=48 +12=60 2 Повторение теории 3. Закрепление теории по опорным схемам, составленным на предыдущем уроке | Участвуют в работе по повторению: в беседе с учителем отвечают на поставленные вопросы. | 5 | Познавательные: структурирование собственных знаний. Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. Регулятивные: контроль и оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся. Слайд №5-6 | Обеспечение мотивации учения детьми, принятие ими целей урока. | Мотивирует учащихся, вместе с ними определяет тему и цель урока, акцентирует внимание учащихся на значимость темы. 1) 21∙10= 6) 4∙1000= 2) 100∙65= 7) 63∙100= 3) 34∙3= 8) 18∙7= 4) 27∙5= 9) 81∙3= 5) 316∙10= 10) 6∙23= Вопросы: 1) Посмотрите внимательно на выражения, на какие группы их можно разделить? 2) Какие примеры помогают быстрее вычислять? 2∙5=10 25∙4=100 5∙20=100 125∙8=1 000 125∙16=125∙8∙2=2 000 3) Вычислите и запомните! | Определяют тему и цели урока. Отвечают на вопросы учителя. Предлагают рациональные способы вычислений, и записывают в тетрадь основные примеры.(слайд №3) | 4 | Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Слайд №7-8 | Показать разнообразие примеров на применение рациональных способов вычислений. | Организация и контроль за процессом решения примеров.
5) Какие свойства умножения можем применить при решении предложенных примеров?
Организация и контроль за процессом выполнения умножения в столбик вида: 467∙304 1) Посмотрите внимательно на выражения. Чем похожи примеры? 2) Что необходимо напомнить, друг другу, чтобы он избежал ошибок при вычислениях? 3) Выполните умножение в столбик 1) 467∙304=141968 2) 1208∙401=484408 3) 516∙309=159444 | Решают примеры (слайд№2). Проговаривают свойства умножения. На конкретных примерах учатся их применять. Выполняют задание на умножение натуральных чисел и применяют рациональные способы вычислений. Комментируют решения примеров. | 9 | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. Физкультминутка Слайд №9 | Смена деятельности. | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. «От улыбки хмурый день светлей» | Учащиеся сидят на месте и повторяют действия за учителем Учащиеся сменили вид деятельности и готовы продолжить работу | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6. Слайд №10 | Дать качественную оценку работы класса и отдельных учащихся. | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. с/р на листочках самооценки
| Учащиеся анализируют свою работу, выражают в слух свои затруднения и обсуждают правильность решения примеров и задач. | 4 | Личностные: формирование позитивной самооценки, учатся принимать причины успеха (неуспеха). Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений. Регулятивные:умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7..Рефлексия. Слайд №11 | Дать количественную оценку работы учащихся. | Подводят итоги работы. Организуют обсуждение: Слайд №8.
| Учащиеся подводят итоги своей работы: Я сегодня понял… Я сегодня научился… Мне понравилось…, Мне не понравилось. Я не понял… | 2 | Регулятивные: оценивание собственной деятельности на уроке. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. Информация о домашнем задании. Слайд №12 | Обеспечение понимания детьми содержания и способов выполнения домашнего задания. | Даёт комментарий к домашнему заданию. П. 1.10, № 142 (3 ст.), № 143 (1 и 2 ст.) | Учащиеся записывают в дневники задание | 3 |
Лист самооценки
Фамилия | Результат | |
1 | Устный счет | |
2 | Закончи предложение | |
3 | Найдите значение выражения | |
4 | Вычисли и запомни | |
5 | Вычисли удобным способом | |
6 | Умножение столбиком | |
с/р в-1 | ||
1 | Вычислите удобным способом 25·96·4= 306·8·125= | |
2 | Торт в 3 раза дороже, чем 5 пирожных. | |
3 | Выполните умножение 5075·68 |
Фамилия | Результат | |
1 | Устный счет | |
2 | Закончи предложение | |
3 | Найдите значение выражения | |
4 | Вычисли и запомни | |
5 | Вычисли удобным способом | |
6 | Умножение столбиком | |
с/р в-2 | ||
1 | Вычислите удобным способом 4·316·25= 207·125·8= | |
2 | Бочка вмещает воды в 9 раз больше, чем 4 ведра. | |
3 | Выполните умножение 4075·84 |
7.Рефлексия
Притча.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
— Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.
— Кто работал как первый человек?
— Кто работал добросовестно?
— Кто принимал участие в строительстве храма своих знаний?
Миссис Рейндель — Могучее умножение
Могучее умножение и доминантное деление
Если бы мне просто захотелось узнать, сколько полос или столбцов было, я мог бы сосчитать количество полос (14) и умножьте это число на 1 (потому что есть один набор столбцов), чтобы узнать, сколько существует полос или столбцов. 14×1= 14.
14×1= 14.
Если по какой-то причудливой причине я хочу знать, сколько разделов во всем заголовке, мне нужно взять количество столбцов (14), а затем подсчитать количество штук в одном разделе. (Я насчитал 26.) Затем я умножал столбцы на количество разделов в каждом столбце. 1 4 х 2 6 =
14 столбцов x 26 штук
Вышеприведенный заголовок является хорошей моделью для 14×26.
Итак, что такое 14×26?
Я могу решить эту проблему, используя модель области.
Я также могу решить эту проблему, разделив числа 14 и 26 на их позиционные значения.
2 6 = 20 + 6 и 1 4 = 10 + 4
Здесь происходит следующее:
2 0 x 10 + 20 x 4 и 6 x 10 + 6 x 4
20 x 10 = 200 + 20 x 4 = 80 и 6 x 10 = 60 + 6 x 4 = 24
200+80 = 280 и 60 + 24 = 84
сложите оба произведения вместе: 280 + 84 = 364
Итак, 26 x 14 = 364
В заголовке баннера выше 364 раздела.
В четвертом классе учащиеся могут использовать стандартный алгоритм для решения 26x 14
2 Вы видите, как работает разложение чисел на разряды
2 6 чтобы получить такой же ответ на 26×14 как стандартный алгоритм?
x 1 4
——————
1 0 4 Здесь я показал 2 разных метода.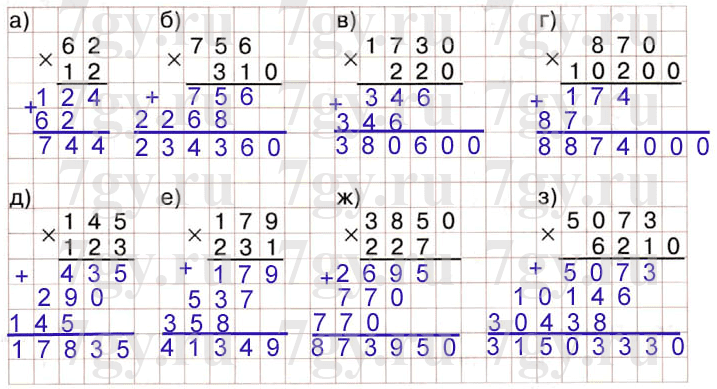
+ 2 6 0 для решения той же задачи 26×14
——————- Математика такая классная.
3 6 4 Есть несколько способов решить проблему!
Этот клип представляет собой разговор о числах умножения. Это отлично.
Трехзначное умножение 4 класс, 5 класс
В видеоролике ниже показаны 2 примера.
Нажмите на синюю ссылку ниже.
В этом примере показана модель области и стандартный алгоритм
, чтобы найти решение для:
3 5 2 x 4 8 1
(Это полный адрес, вы можете вырезать и вставить его в браузер.)
https://www.khanacademy.org/math/arithmetic/arith-review-multiply-divide/arith-review-place-value-area-models/v/multiplying-using-area-models-and-the-standard- алгоритм
Полезно помнить, как разбивать числа на их разрядные значения.
352= 300+50+2 481= 400+80+1
Теперь вы можете себе представить, где бы вы нарисовали линии, чтобы создать модель области? Объясните, как решить эту проблему?
400 80 1
300
50
2
Обратите внимание, что на этот раз я показал 352 как 300+50+2. В модели площади в ролике 352 записывается как 2+50+300.
Это свидетельствует о распределительном свойстве.
Какой ответ вы получили? Так же, как в видеоклипе?
Можете ли вы придумать другой способ решения 352×481?
многократное сложение или умножение ?
3+3+3=9 или, 3×3=9
Видеоклип внизу слева является хорошим введением в умножение.
Видеоклип ниже справа помогает показать, как связаны умножение и деление.
youtube.com/embed/dPksJHBZs4Q» allowfullscreen=»»/>Когда вы умножаете, подумайте: сколько групп из скольких вещей или сколько вещей в скольких группах. Когда мы умножаем, мы находим общее количество групп или вещей.
Берем 2 части и умножаем, чтобы найти целое.
Да, когда мы делим, мы берем целое и разделяем ~ или делим это целое на группы.
8 разделить на 2
Всего у меня 8 штук. * * * * * * * *
* * * * * * * *
Я разделяю их или делю 8 на 2 группы. * * * * l * * * *
В каждой группе по 4 элемента * * * * * * * *
Итак, 8 разделить на 2 равно 4
Ниже представлен забавный ролик, который помогает объяснить деление. Наслаждаться! (Ты будешь танцевать в такт?) 4 9 класс0005
класс 4,5
В Фейрпорте мы начинаем с метода деления, используя частичные частные, чтобы помочь нашим ученикам понять операцию с точки зрения разрядного значения. Посмотрите видеоклип ниже в качестве еще одной демонстрации.
Математика есть математика, это просто другой способ решения с упором на понимание разрядного значения.
класс (4)5
В приведенном выше примере показан другой способ деления. Это называется длинным делением.
5 класс
Ого! Это длинное деление с БОЛЬШИМИ числами.
Расслабьтесь, дети. Процесс такой же, как в примере выше.
Осталось совсем немного номеров! Дыши, ты понял!
Фотография выше была сделана в магазине домашних сладостей в Техасе.
Вы видите целых 5 лотков с конфетами.
Вам нужно знать, сколько конфет в одном полном лотке.
Можете ли вы оценить (т.е. не считая единиц), сколько конфет на этой картинке?
Будете ли вы использовать умножение, деление, сложение или вычитание, чтобы помочь вам?
Как знание числа в целом лотке поможет вам узнать, сколько их в 5 полных лотках?
Что делать с пропавшими конфетами? Они добавляются или вычитаются?
Если бы все подносы были полны, сколько было бы конфет?
Какой вкус должен быть внутри шоколада?
Умножение чисел с использованием разрядного значения (определение, типы и примеры)
Содержание
- Что такое разрядное значение?
- Использование значения места для умножения
- Использование значения места для умножения на 10, 100, или 1000
- Правила для умножения с 10, 100, или 1000
- Факты о умножении
- .

Что такое разрядное значение?
Значение разряда — это значение положения каждой цифры в числе.
Рассмотрим, например, число 242.
Разрядное значение цифры 2 на месте единиц равно 2 × 1 = 2 или 2 единицы.
Разрядное значение цифры 4 в разряде десятков равно 4 × 10 = 40 или 4 десятка.
Точно так же разрядное значение цифры 2 в сотых долях равно 2 × 100 = 200 или 2 сотых.
Использование разрядного значения при умножении
При умножении двух чисел учитывается разрядное значение каждой цифры в числах и осуществляется индивидуальное умножение.
Позже результаты отдельных умножений складываются, чтобы получить окончательный результат.
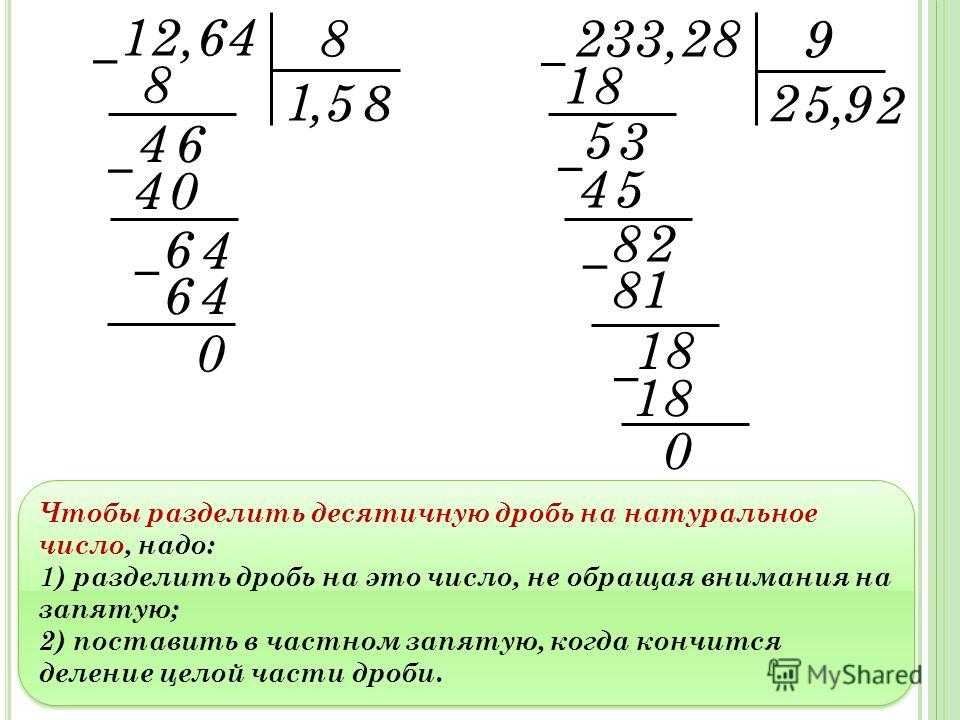
Давайте воспользуемся разрядным значением для вычисления 15 × 5. Мы нарисуем диаграмму разрядного значения для выполнения умножения.
\(\Стрелка вправо\)( 5 × 5) + (5 × 10)
= 25 + 50
= 75
Это можно представить в виде столбца следующим образом:
В приведенном выше умножении
(i) Цифра на единицах во втором числе умножается на цифру на единицах в первом числе.

(5 × 5) = 25 (Умножьте 5 и 5)(ii) Цифра, стоящая на месте единиц во втором числе, умножается на цифру на месте десятков в первом числе.
5 × 10 = 50 (Умножьте 5 на 10)
10 × 10(iii) Затем результаты обоих шагов складываются для получения окончательного результата.
25 + 50 = 75 (добавить)Аналогичные шаги будут предприняты для умножения чисел, имеющих цифры в разряде сотен или тысяч.
Использование разрядного числа для умножения на 10, 100 или 1000
Это простое применение умножения с разрядным значением, в котором мы упрощаем умножение, выражая числа, которые нужно умножить, через десятки, сотни или тысячи и позже выполните стандартное умножение.
Рассмотрим следующее умножение:
7 × 10 (здесь 10 можно записать как 1 десяток)
= 7 × 1 десяток
= 7 десятков
= 70
Рассмотрим другой пример:
9 × 2020 можно записать как 2 сотни)
9 × 2 сотни
= 18 сотен
= 1800
Правила умножения на 10, 100 или 1000
на 10, 100 или 1000.

- При умножении любого ненулевого числа на 10 просто добавьте ноль в конце этого числа.
Например:
5 × 10 = 50 - При умножении любого ненулевого числа на 100 просто добавьте два нуля в конце этого числа. Например:
5 × 100 = 500 - При умножении любого ненулевого числа числа на 1000, просто добавьте три нуля в конце этого числа.
Например:
2 × 1000 = 2000
Факты об умножении
- Если число умножается на 0, результатом будет 0.
10 × 0 = 0
0 × 0 = 0
112 × 0 = 0
- Если ненулевое число умножается на 10 100 или 1000 соответственно, произведением будет само число с 1, 2 или 3 нулями соответственно на конце.
- При умножении умножаемое число называется множимым, а число, на которое оно умножается, называется множителем.
Результат умножения называется произведением.
10 × 7 = 70
10 → множимое
7 → множитель
70 → произведение
- Если число умножается на 1, произведением будет само число.

Решенные примеры
Пример 1:
Найдите произведение для каждого из следующих умножений.
(i) 7 × 3 ________
(ii) 7 × 30 _________
(iii) 7 × 300 _________
(IV) 7 × 3000 __________
Решение:
(I) 7 × 3 = 21
(ii) 7 × 3 TENS
= 21 = 21592955
(ii) TENS
= 210
(III) 7 × 3 Сотни
= 21 Сотни
= 2100
(IV) 7 × 3 тысячи
= 21 тысячи
= 2100095 9000 2
= 21 тысячи
= 2100095 9000 2
05
5
5
5
05 = 21 тысячи
= 2100095
9000 21. Пример 2:
Найдите недостающий множитель.
(i) ______ × 100 = 600
(ii) 5 × ______ = 50
(iii) 9 × 20 = ______
Решение:
(i) Мы знаем, что
(
(i) Множимое) × (Множитель) = Произведение
Поскольку множимое умножается на 100, получается произведение 600, это означает, что множимое равно 6.

(ii) Мы знаем, что ) = Продукт
5 × _____= 50
Используя правило умножения числа на 10, мы видим, что множитель равен 10.
(iii) 9 × 20
= 180
Пример 3:
У продавца есть две разновидности блестящих ручек. 10 упаковок одного сорта по 5 ручек в каждой и 20 упаковок второго сорта по 7 ручек в каждой. Итак, сколько всего блестящих ручек у продавца?
Решение:
Первый сорт → 10 × 5 = 50 (умножение)
Второе сорт → 20 × 7 = 140 (умножение)
50 + 140
= 190 [Добавить]
. Всего у лавочника 190 блестящих ручек.
Пример 4:
У Лиама есть 2 коробки по 20 карамельных конфет в каждой. У него также есть 5 коробок по 30 шоколадных конфет в каждой.
Сколько всего конфет у Лиама?
Решение:
У Лиама есть 2 коробки по 20 карамельных конфет в каждой.

Общее количество карамельных конфет,
= 2 × 20
= 40 [Умножить]
Всего у Лиама 40 карамельных конфет.
У Лиама также есть 5 коробок по 30 кофейных конфет в каждой.
Общее количество шоколадных конфет,
= 5 × 30
= 150 [Умножить]
Всего у него 150 шоколадных конфет.
Итак, общее количество конфет у Лиама
= 40 + 150
= 190 [Добавить]
Следовательно, всего у Лиама 190 конфет.
Часто задаваемые вопросы
Какое свойство можно использовать для определения произведения числа на 0?
Согласно нулевому свойству умножения, если число умножить на ноль, произведение будет 0,
Что означает разрядное значение цифры в числе?
В математике каждая цифра в числе имеет определенное разрядное значение. Его можно определить как значение цифры в числе на основе ее позиции в числе.

- При умножении любого ненулевого числа на 10 просто добавьте ноль в конце этого числа.


 Применение знаний и умений в новой ситуации
Применение знаний и умений в новой ситуации работают в парах над поставленными задачами.
работают в парах над поставленными задачами. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
Контроль усвоения, обсуждение допущенных ошибок и их коррекция. Сколько стоит торт, если пирожное стоит 22 рубля?
Сколько стоит торт, если пирожное стоит 22 рубля? Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?
Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?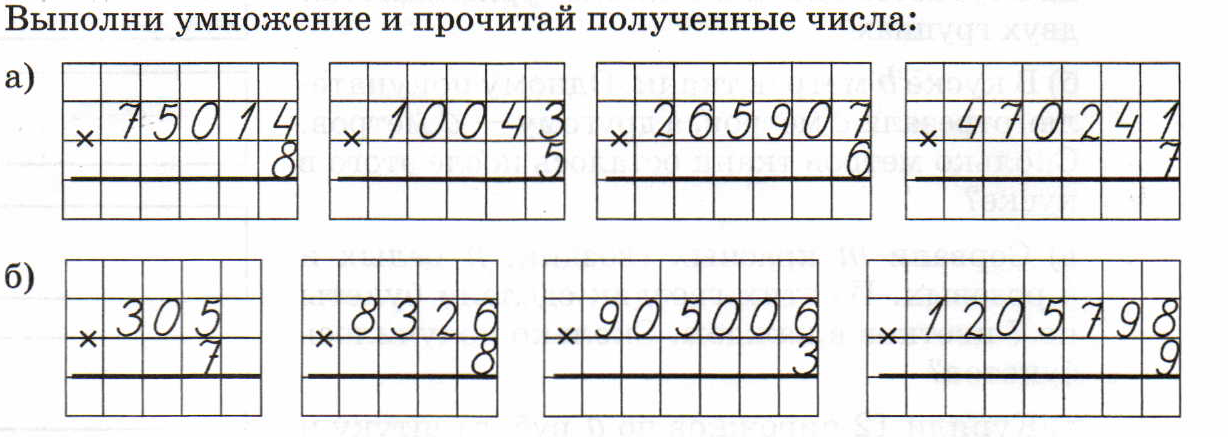
 Сколько стоит торт, если пирожное стоит 22 рубля?
Сколько стоит торт, если пирожное стоит 22 рубля? Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?
Сколько литров воды вмещает бочка, если в одно ведро входит 11 л воды?