тренажер по математике «Счет в пределах 20»

Сложение с переходом через 10

9+8

8+8

5+9

8+9

7+6

9+7

8+6

2+9

6+7

9+5

7+8

3+8

3+9

8+4

5+6

6+6

9+3

7+4

6+5

6+8

9+4

5+8

4+8

6+9

4+7

9+2

5+7

8+3

8+7

8+5

9+6

7+7

7+9

4+9

7+5

9+9

Вычитание с переходом через 10

18-9

13-7

13-4

16-7

14-7

15-9

13-8

15-8

11-8

12-5

11-9

11-4

15-6

12-4

13-5

13-9

14-6

11-6

11-7

12-9

12-6

11-5

12-8

12-3

11-3

15-7

14-9

13-6

11-2

14-8

16-9

13-7

17-8

14-5

16-8

17-9

Описание

Уважаемые коллеги, предлагаю вашему вниманию таблицы-карточки «Сложение с переходом через 10» и «Вычитание с переходом через 10».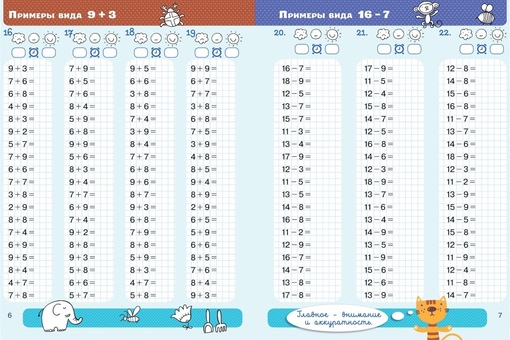

В них собраны все случаи сложения и вычитания в пределах 20.

Данные таблицы можно применять на уроках математики для отработки навыков устного счета в пределах 20. Такие таблицы можно применять как для индивидуальной работы, так и для работы со всем классом.

Работать можно по строкам и столбцам как слева – направо, так и справа — налево, как сверху – вниз, так и снизу – вверх, каждый раз получая новую цепочку математических выражений. Можно работать отдельно по каждой таблице, а можно объединить две.

Я распечатываю такую таблицу на каждого ученика и использую ее или на математической разминке в начале урока, или для дополнительных заданий тем ученикам, которые работают быстрее, или для индивидуальной работы с отстающими детьми.

Математические выражения можно списывать в тетрадь и находить их значения, можно просто называть только ответы, а можно устроить мини – соревнование в паре или группе, подобно лото, закрывая выражения их значениями.

Тренажер устного счета онлайн | Инструкция, нормы, разряды

 

ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ТРЕНАЖЕРА

Тренажер устного счета — легко и существенно повышает интеллектуальный потенциал человека.

Результатом приобретения навыков и здачи нормативной квалификации будет присвоение спортивного разряда (I разряд, II разряд, III разряд, кандидат в мастера спорта, мастер спорта и гроссмейстер).

1. Людей из группы выделяют как по умению красиво и правильно говорить, так и по умению быстро считать в уме, и относят их, как правило, к категории умных. Школьнику умение быстро считать в уме позволяет более успешно учиться, а инженеру и ученому сократить время получения результата их деятельности.
2. УС нужен не только школьникам, но и инженерам, учителям, медицинским работникам, ученым и руководителям разного уровня. Кто быстро считает, тому легче учиться и работать. УС – это не игрушка, хотя и развлекает. Он позволяет вернуться ученику на те “рельсы”, с которых он упал когда-то; повышает скорость и качество восприятия информации; дисциплинирует и производит точность во всем; приучает замечать детали и мелочи; приучает к экономии; создает образы предметов и явлений; позволяет предвидеть будущее и развивает интеллект человека.
3. «Евроремонт» в голове нужно начинать с простых арифметических действий, которые позволяют структурировать мозг.
4. Умение быстро считать в уме дает ученику уверенность в себе. Как правило, быстрее всех считают в уме те, кто хорошо учится в школе или в ВУЗе. Если отстающего ученика научить быстро считать в уме, то это обязательно благотворно повлияет на его успеваемость, и не только в естественных, но и во всех других предметах. Это доказано практикой.
5. Произвольное внимание и интерес во время устного счета меняет блуждающий взгляд отстающего ученика на фиксированный, а концентрация внимания достигает нескольких этажей глубины предмета или процесса, который изучается.
6. “Изучение математики дисциплинирует мышление, приучает к правильному словесному выражению мыслей, к точности, сжатости и ясности речи, воспитывает настойчивость, умение достигать намеченной цели, развивает работоспособность, способствует правильной самооценке владения предметом, который изучается”. (Кудрявцев Л.Д. – член-кор. РАН. 2006.).
7. Ученик, который научился быстро считать в уме, как правило, начинает и быстрее мыслить.
8. Тот, кто по своей природе хорошо считает, естественно обнаружит ум и в любой другой науке, а тот, кто считает медленно, учась этому искусству и овладевая им, сможет улучшить свой ум, сделать его острее (Платон).
9. Приобретенных навыков устного счета одним хватит на 5 — 10 лет, а другим на всю жизнь.
10. Нашим потомкам будет легче учиться и получать знания. Однако, культура устного счета всегда будет являться неотъемлемой частью общечеловеческой культуры.
11. Кто быстро считает в уме, тот, как правило, ясно мыслит, быстро воспринимает и глубже видит.
12. Освоение УС развивает образное, диаграммное и системное мышление, расширяет оперативную память, диапазон восприятия, приучает к мышлению на несколько ходов вперед, повышает качество мышления, оперируя количественными характеристиками объектов.
13. УС повышает ясность мышления, уверенность в себе, а также волевые качества (терпение, усидчивость, выносливость, трудолюбие). Приучает к глубокой и устойчивой концентрации внимания, домысливанию и договариванию начатых фраз (особенно у дошкольников и учеников начальных классов).

Счет в пределах 100 тренажер распечатать

Вариант 1.

Запиши число, в котором 2 дес. и 8 ед.

Запиши число, в котором 6 дес.

Запиши число, в котором 9 дес.

Запиши число, в котором 10 дес.

Уменьши каждое число на 20, ответ пиши под каждым числом

Расположи числа в порядке возрастания

27 4 72 6 56 34 2

Вариант 2.

__________________________________

47 5 82 3 68 54 8

Вариант 1.

1. Запиши число, в котором 2 дес. и 8 ед.

2. Запиши число, в котором 6 дес.

3. Запиши число, в котором 9 дес.

4. Запиши число, в котором 10 дес.

5. Уменьши каждое число на 20, ответ пиши под каждым числом

__________________________________

6. Расположи числа в порядке возрастания

27 4 72 6 56 34 2

_____________________________________

Вариант 2.

1. Запиши число, в котором 3 дес. и 7 ед.

2. Запиши число, в котором 6 дес.

3. Запиши число, в котором 9 дес.

4. Запиши число, в котором 10 дес.

5. Уменьши каждое число на 20, ответ пиши под каждым числом

__________________________________

6. Расположи числа в порядке возрастания

47 5 82 3 68 54 8

_____________________________________

В математике, конечно же, важно уметь думать и мыслить логически, но не менее важна в ней практика. Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами — сложение, вычитание, умножение, деление. А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям — тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.

Математика. Решаем примеры с переходом через десяток.

Тетрадь для отработки навыков сложения и вычитания с переходом через десяток. Не просто примеры, а интересные игры и задания.

Карточки-задания. Математика. Сложение и вычитание. 2 класс

Удобные карточки для учителя второклашек. 2 варианта на сложение и вычитание одного вида. Подойдут для организации самостоятельной работы по математике в зависимости от продвижения по программе.

Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е.Э.

Кочурова

В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку.

Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.

Математика тренажерная тетрадь для 2 класса

Тетрадь содержит не только примеры на сложение и вычитание, но и перевод единиц друг в друга, и сравнение результатов вычисления (больше-меньше).

3000 примеров по математике (счет в пределах 100 часть 1)

Тренажер со счетом на время. Время засекать на решение одной колонки примеров и записывать внизу в окошечке. Обратите внимание на колонки, которые ребенок решал более 5 минут, значит у него возникли сложности по этому виду примеров. Приведены примеры на сложение и вычитание в пределах десяти и с переходом через десяток, сложение и вычитание десятков, манипуляции в пределах сотни.

Счет от 0 до 100

В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100.

Считаем правильно. Рабочая тетрадь по математике. Г.В.Белых

Тетрадь также выполнена в виде тренажера, сплошные примеры и уравнения. Начинается со счета в пределах десяти, далее — в пределах сотни (сложение, вычитание, умножение и деление), заканчивается сравнением уравнений (примеры со знаками больше, меньше, равно).

Пособия пригодятся и учителям начальных классов в их работе, и родителям для занятий дома с детьми, в частности, в летние каникулы. Задания разных уровней сложности позволят осуществить дифференцированный подход к обучению.

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока:

• Совершенствовать вычислительные навыки и умение решать простые задачи.
• Закреплять устные приёмы сложения и вычитания.
• Развивать познавательный интерес, расширять знания об окружающем мире.
• Коррекция зрения по методу В.Ф.Базарного.
• Включить элемент опережающего обучения (раскрыть смысл действия умножения).
• Развивать внимание, логическое мышление, смекалку, умение рассуждать, мыслить, интерес к урокам математики.

Оборудование: мультимедийный проектор, компьютер, диск с презентацией, индивидуальные дифференцированные задания, электрифицированное раздаточное пособие с программой по математике для контроля знаний учащихся, ребусы.

Формы работы: коллективная, индивидуальная, дифференцированная.

Вид урока: нестандартный, урок-путешествие, урок-презентация.

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

1). (Слайд 1) Сообщение темы и цели урока

2) (Слайд 2) Эмоциональный настрой на урок

Долгожданный дан звонок —
Начинается урок.
Игры, шутки, всё для вас!
За работу, в добрый час!

II. ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1. Минутки чистописания

Ребята! Сегодня у нас необычный урок. Я приглашаю вас отправиться в морское путешествие в “Страну знаний”.

На протяжении всего путешествия мы будем закреплять навыки сложения и вычитания чисел в пределах 100. Путешествовать будем на корабле (Слайд 3)

Вы знаете, что все путешественники ведут дневники наблюдений.

Вашим дневником наблюдений будет ваша тетрадь, в которой вы будете вести все необходимые записи. Они должны быть чёткими и аккуратными.

Будьте все старательны,
А ёщё внимательны!

(Слайд 4) — На экране числа — это номера кают. Запишите их в тетради в порядке возрастания и вы узнаете название нашего корабля. Проверяем! Молодцы!

Итак, мы отправились в путешествие. Плыть мы будем долго, поэтому я предлагаю вам поиграть в “Домино”.

2. (Слайд 5) Игра “Домино”

Ребятам раздаются карточки, кроме одной. Её учитель ставит на магнитную доску. Учащиеся решают записанный на карточке пример. К доске должен выйти то ученик, у которого на левой части карточки записан ответ первого примера. Он ставит карточку рядом с первой. Записанный не ней пример решают все ученики, а к доске выходит тот, у которого на левой стороне карточки записан ответ второго примера, и ставит карточку справа от второй. Игра продолжается до тех пор, пока цепь всех карточек не будет выставлена на подставке по выше указанному правилу. Остальные ученики- контролёры.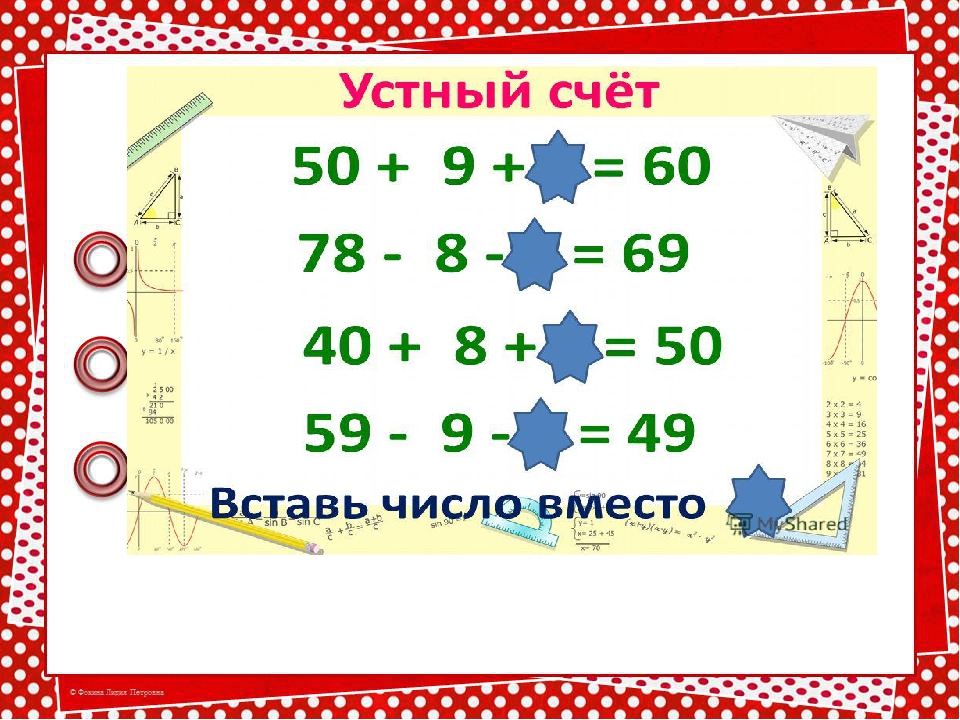 Они подтверждают или опровергают ответы учащихся, выходящих к доске.

3. (Слайд 6) Устный счёт “Математическая туманность

(работа с раздаточным материалом)

Нужна ваша помощь — а это ваши математические знания. Закончите, пожалуйста, решение примеров. (Ребята считают примеры и показывают ответы)

4. (Слайд 7) Математическая цепочка

Ребята, посмотрите, какие красивые птицы парят над морем! Какие у них большие крылья!

У какой птицы самый большой размах крыльев?

Найти ответ нам поможет математическая цепочка

Решить её надо верно. Ответ данной цепочки будет подсказкой

Познавательная минутка:

“Альбатросы-это морские птицы. Большую часть жизни они проводят над открытым морем или океаном, красиво скользя над волнами. Они достигают в длину до 1,5 метров. Альбатросам приходится перелетать очень большие расстояния, поэтому размах крыльев у них достигает до 4,5 метров. У этих птиц высоко развита способность к планируемому полёту. Эта птица может парить над океаном 6 суток, не сделав при этом ни одного взмаха крыльями. У них очень длинные крылья, поэтому альбатросы устраивают свои гнездования, чаще всего, на скалистых островках, круто поднимающихся из моря, или океана.”

5. (Слайд 8) Физминутка для глаз по методу профессора В.Ф.Базарного

Схема зрительно-двигательной траекторий (с помощью стрелок указаны основные траектории по которым должен двигаться взгляд учащегося в процессе выполнения физкультурных минуток: вверх — вниз, влево — вправо, по и против часовой стрелке, по восьмёрке. Каждая траектория изображается разным цветом. Это делает схему яркой и привлекает внимание).

5. (Слайд 9 ) “Страна Знаний”

Жители этой страны приготовили для вас задание не компьютере. Нужно отгадать математические кроссворды. Каждый из вас получит только по одному кроссворду, нужно его правильно решить и записать в тетрадь (учащиеся получают индивидуальное дифференцированное задание).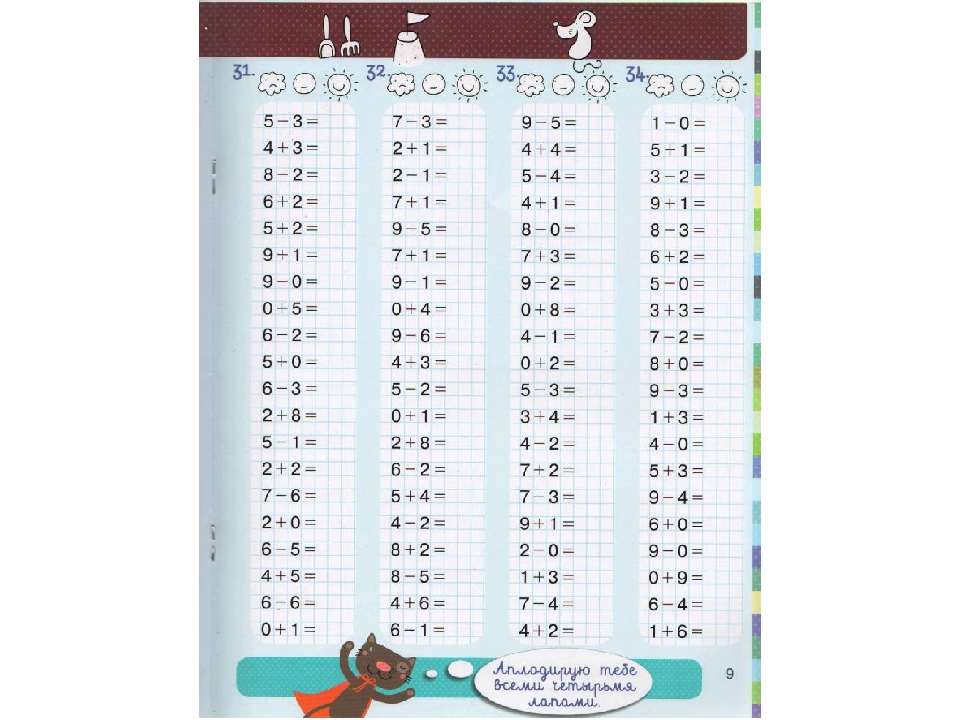

Проверяем! Молодцы! Справились с этим заданием.

А теперь нужно пройти математический лабиринт.

(Слайд 10) 1). Математический лабиринт (решение примеров у доски с комментированием)

(Слайд 11) — В это стране всё волшебное, даже солнышко с лучами. У каждого лучика своё задание

2). “Солнышко с лучами”

(Слайд 12) ПЕРВЫЙ ЛУЧ “Задача”

(электрифицированное раздаточное пособие для контроля знаний учащихся.Проверка:если лампочка загорается зелёным цветом — задача решена верно, а если красным — неверно.

(Слайд 13) ВТОРОЙ ЛУЧ “Посчитайка” (устный счёт)

Что такое умножение?
Этот умное сложение.
Ведь умней умножить раз,

Чем слагать весь целый час (коллективное чтение стихотворения)

(Слайд 14) ТРЕТИЙ ЛУЧ “Смекалка”

(математические ребус))

III. ИТОГ УРОКА

(Слайд 15) — Наше путешествие подходит к концу. Мы возвращаемся домой, в наш родной класс.

Не все тайны этой страны мы открыли. Многие лучики СОЛНЦА остались не открытыми. А это значит, что мы обязательно отправимся в морское путешествие на следующих уроках.

Если для вас путешествие было интересным и увлекательным, то прикрепите на это волшебное дерево красное яблоко, если не очень — зелёное.

IV. ДОМАШНЕЕ ЗАДАНИЕ: придумать математические кроссворды.

Используемая литература.

1. “Раз, два, три-отвечай” (математические развлечения для младших школьников) — Перкова О.И.. Москва: 1994г. Издательство Учебно-научного производственного центра “Энергомаш”

2. Т.Г.Жигалкина “Система игр на уроках математики в 1 и 2 классах”. М.: Новая школа, 1997г.

3. Т.И.Линго “Игры. Ребусы, загадки для мл. школьников.”- Ярославль: Академия развития, 1998г.

4. Р.Д. Триггер “Коррекционно-развивающее обучение”- Москва. :школьная пресса. 2004г.

5. Интернет-ресурсы.

Зрительный. ..

Читать полностью

Устному счету отведено несколько книг, включенных в общую серию «3000 примеров по математике». Каждая посвящена одной из важнейших программных тем, которые изучаются в 1-4 классах начальной школы. Количество примеров в книгах различно и увеличивается от класса к классу, от темы к теме. Всего для отработки навыков устного счета предлагается 3000 математических примеров.
В этом пособии представлен материал, направленный на формирование навыков устного счета по теме «Счет в пределах 100» для 2 класса.
Устный счет развивает сообразительность и внимание учащихся, воспитывает математическую находчивость и укрепляет память. Правильная постановка занятий устным счетом в начальной школе предполагает ежедневные и непродолжительные (от 5 до 10 минут) упражнения. Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счета всех форм:
Беглый слуховой счет. (Учитель устно называет пример и устно же, спустя несколько секунд, получает ответ. )
Зрительный счет. (Примеры записаны, а ответы называются либо устно, либо записываются учениками.)
Комбинированный счет. (Учитель диктует примеры, а ученик записывает ответы.) Устное решение задач.
Быстрота счета возникает в результате длительных тренировок. Но на первом месте должна стоять осознанность тех или иных приемов устных вычислений, а не механическое их применение. Устный счет должен предварять, дополнять или заключать ту часть урока, которой он подчинен.
Пособие можно использовать на уроках математики, а также для самостоятельной работы дома.

Скрыть

Устному счёту отведено несколько книг, включённых в общую серию «3000 примеров по математике». Каждая посвящена одной из важнейших программных тем, которые изучаются в 1–4 классах начальной школы. Количество примеров в книгах различно и увеличивается от класса к классу, от темы к теме. Всего для отработки навыков устного счёта предлагается 3000 математических примеров. В этом пособии представлен материал, направленный на формирование навыков устного счёта по теме «Счёт в пределах 100» для 2 класса. Устный счёт развивает сообразительность и внимание учащихся, воспитывает математическую находчивость и укрепляет память. Правильная постановка занятий устным счётом в начальной школе предполагает ежедневные и непродолжительные (от 5 до 10 минут) упражнения. Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счёта всех форм: Беглый слуховой счёт. (Учитель устно называет пример и устно же, спустя несколько секунд, получает ответ.) Зрительный счёт. (Примеры записаны, а ответы называются либо устно, либо записываются учениками.) Комбинированный счёт. (Учитель диктует примеры, а ученик записывает ответы.) Устное решение задач. Быстрота счёта возникает в результате длительных тренировок. Но на первом месте должна стоять осознанность тех или иных приёмов устных вычислений, а не механическое их применение. Устный счёт должен предварять, дополнять или заключать ту часть урока, которой он подчинен. Пособие можно использовать на уроках математики, а также для самостоятельной работы дома.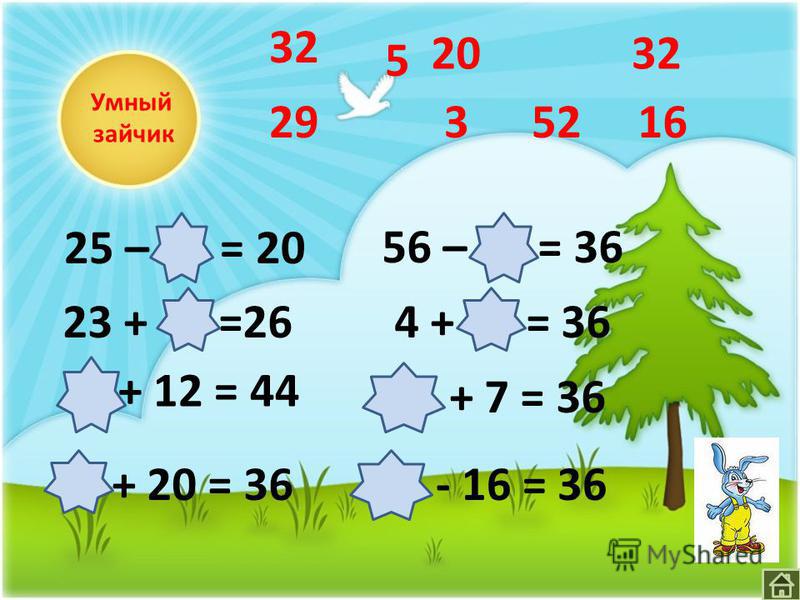

На нашем сайте вы можете скачать книгу «3000 примеров по математике. Устный счет. Счет в пределах 100. 2 класс» Узорова Ольга Васильевна, Нефедова Елена Алексеевна бесплатно и без регистрации в формате fb2, rtf, epub, pdf, txt, читать книгу онлайн или купить книгу в интернет-магазине.

Тренажер. Счет в пределах 20. 1 класс

Тренажер
Счет в пределах 20
1 класс
АБРОСЬКИНА И.В.
Учитель начальных классов
МБОУ СОШ № 4 г. Рассказово 2013 г
9
+ 3 =
16
–
8
=
8
+ 4 =
15
–
9
=
7
+ 4 =
18
–
9
=
5
+ 6 =
16
–
9
=
5
+ 8 =
14
–
7
=
8
+ 7 =
17
–
8
=
6
+ 6 =
13
–
4
=
7
+ 7 =
14
–
8
=
9
+ 2 =
15
–
8
=
3
+ 8 =
12
–
7
=
9
+ 5 =
15
–
7
=
5
+ 7 =
11
–
9
=
7
+ 6 =
12
–
6
=
8
+ 9 =
11
–
3
=
7 + 9
=
12
–
8
=

33. Источники

1 слайд
http://img-fotki.yandex.ru/get/5208/valenta-mog.74/0_63c6a_c6a13ab4_orig.jpg — фон
http://www.dvdtalk.ru/img/still/masha-i-medved-2/000001b.jpg — фон вариант 2
http://data.iplayer.fm/file/iv2jaho/3109762/75433428/Mishka__iz_m_f_Masha_i_medved_(iPlayer.fm).mp3?title=%D0%9C%D0%B8%D1%88%D0%BA%D0%B0++%D0%B8%D0%B7+%D0%BC%2F%D1%84+%22%D0%9C%D0%B0%D1%88%D0%B0+%D0%B8+%D0%BC%D0%B5%D0%B4%D0%B
2%D0%B5%D0%B4%D1%8C%22 – музыкальная композиция
2 слайд
http://legend.az/uploads/posts/2013-08/1376678390_77.jpg — фон
3 – 32 слайды
http://www.vmonitor.ru/pic/mults/20088/Masha_i_Medved_-1440×900.jpg — фон
http://multick.ru/uploads/posts/2012-02/1329156541_masha.png — фигурка Маши (пер. к след. слайду)
33 слайд
http://www.dvdtalk.ru/img/still/masha-i-medved-2/000001b.jpg — фон
Общее – файл использован для нарезки звуковых фрагментов в 2 – 32 слайды
http://data.iplayer.fm/file/iv2jaho/43434010/109026683/Luchshie_narezki_fraz_Mashi_iz_multfilma_Masha_i_medved_-_MASHA__Ochen_dobryj_den_(iPlayer.fm).mp3?title=%D0%9B%D1%83%D1%87%D1%88%D0%B8%D0%B5+%D0%BD%D0%B0%D1%80%D
0%B5%D0%B7%D0%BA%D0%B8+%D1%84%D1%80%D0%B0%D0%B7+%D0%9C%D0%B0%D1%88%D0%B8+%D0%B8%D0%B7+%D
0%BC%D1%83%D0%BB%D1%8C%D1%82%D1%84%D0%B8%D0%BB%D1%8C%D0%BC%D0%B0+%D0%9C%D0%B0%D1%88%D0%
B0+%D0%B8+%D0%BC%D0%B5%D0%B4%D0%B2%D0%B5%D0%B4%D1%8C+-+%D0%9C%D0%90%D0%A8%D0%90%29%22%D0%9E%D1%87%D0%B5%D0%BD%D1%8C+%D0%B4%D0%BE%D0%B1%D1%80%D1%8B%D0%B9+%D0%B4%D0%B5%D0%
BD%D1%8C%29%22

Как освоить устный счёт школьникам и взрослым

Кроме отличных оценок по математике, умение считать в уме даёт массу преимуществ на протяжении всей жизни. Упражняясь в вычислениях без калькулятора, вы:

• Держите мозг в тонусе. Для эффективной работы интеллект, как и мускулатура, нуждается в постоянных тренировках. Счёт в уме развивает память, логическое мышление и концентрацию, повышает способность к обучению, помогает быстрее ориентироваться в ситуации и принимать правильные решения.
• Заботитесь о своём психическом здоровье. Исследования показывают ^{, что при устном счёте задействованы участки мозга, ответственные за депрессию и тревожность. Чем активнее работают эти зоны, тем меньше риск неврозов и чёрной тоски.}
• Страхуетесь от проколов в бытовых ситуациях. Способность быстро посчитать сдачу, размер чаевых, количество калорий или проценты по кредиту защищает вас от незапланированных трат, лишнего веса и мошенников.

Освоить приёмы быстрого счёта можно в любом возрасте. Не беда, если сначала вы будете немного «тормозить». Ежедневно практикуйте основные арифметические операции по 10–15 минут и уже через пару месяцев достигнете заметных результатов.

Как научиться складывать в уме

Суммируем однозначные числа

Начните тренировку с элементарного уровня — сложения однозначных чисел с переходом через десяток. Эту технику осваивают в первом классе, но почему-то часто забывают с возрастом.

• Предположим, вам нужно сложить 7 и 8.
• Посчитайте, сколько семёрке не хватает до десяти: 10 − 7 = 3.
• Разложите восьмёрку на сумму трёх и второй части: 8 = 3 + 5.
• Добавьте вторую часть к десяти: 10 + 5 = 15.

Тот же приём «опоры на десятку» используйте при суммировании однозначных чисел с двузначными, трёхзначными и так далее. Оттачивайте простейшее сложение, пока не научитесь совершать одну операцию за пару секунд.

Суммируем многозначные числа

Основной принцип — разбить слагаемые числа на разряды (тысячи, сотни, десятки, единицы) и суммировать между собой одинаковые, начиная с самых крупных.

Допустим, вы прибавляете 1 574 к 689.

• 1 574 раскладывается на четыре разряда: 1 000, 500, 70 и 4. 689 — на три: 600, 80 и 9.
• Теперь суммируем: тысячи с тысячами (1 000 + 0 = 1 000), сотни с сотнями (500 + 600 = 1 100), десятки с десятками (70 + 80 = 150), единицы с единицами (4 + 9 = 13).
• Группируем числа так, как нам удобно, и складываем то, что получилось: (1 000 + 1 100) + (150 + 13) = 2 100 + 163 = 2 263.

Основная сложность — удержать в голове все промежуточные результаты. Упражняясь в таком счёте, вы заодно тренируете память.

Как научиться вычитать в уме

Вычитаем однозначные числа

Снова возвращаемся в первый класс и оттачиваем навык вычитания однозначного числа с переходом через десяток.

Предположим, вы хотите отнять 8 от 35.

• Представьте 35 в виде суммы 30 + 5.
• Из 5 вычесть 8 нельзя, поэтому раскладываем 8 на сумму 5 + 3.
• Вычтем 5 из 35 и получим 30. Затем отнимем от 30 оставшуюся тройку: 30 − 3 = 27.

Вычитаем многозначные числа

В отличие от сложения, при вычитании многозначных чисел на разряды нужно разбивать только то, которое вы отнимаете.

Например, вас просят отнять 347 от 932.

• Число 347 состоит из трёх разрядных частей: 300 + 40 + 7.
• Сначала вычитаем сотни: 932 − 300 = 632.
• Переходим к десяткам: 632 − 40. Для удобства 40 можно представить в виде суммы 30 + 10. Сперва вычтем 30 и получим 632 − 30 = 602. Теперь отнимем от 602 оставшиеся 10 и получим 592.
• Осталось разобраться с единицами, используя всё ту же «опору на десятку». Сперва вычитаем из 592 двойку: 592 − 2 = 590. А затем то, что осталось от семёрки: 7 − 2 = 5. Получаем: 590 − 5 = 585.

Как научиться умножать в уме

Лайфхакер уже писал о том, как быстро освоить таблицу умножения.

Добавим, что наибольшие трудности и у детей, и у взрослых вызывает умножение 7 на 8. Есть простое правило, которое поможет вам никогда не ошибаться в этом вопросе. Просто запомните: «пять, шесть, семь, восемь» — 56 = 7 × 8.

А теперь перейдём к более сложным случаям.

Умножаем однозначные числа на многозначные

По сути, здесь всё элементарно. Разбиваем многозначное число на разряды, перемножаем каждый на однозначное число и суммируем результаты.

Разберём на конкретном примере: 759 × 8.

• Разбиваем 759 на разрядные части: 700, 50 и 9.
• Умножаем каждый разряд по отдельности: 700 × 8 = 5 600, 50 × 8 = 400, 9 × 8 = 72.
• Складываем результаты, разбивая их на разряды: 5 600 + 400 + 72 = 5 000 + (600 + 400) + 72 = 5 000 + 1 000 + 72 = 6 000 + 72 = 6 072.

Умножаем двузначные числа

Тут уже рука сама тянется к калькулятору или хотя бы к бумаге и ручке, чтобы воспользоваться старым добрым умножением в столбик. Хотя ничего сверхсложного в этой операции нет. Просто нужно немного потренировать краткосрочную память.

Попробуем умножить 47 на 32, разбив процесс на несколько шагов.

• 47 × 32 — это то же, что и 47 × (30 + 2) или 47 × 30 + 47 × 2.
• Сначала умножим 47 на 30. Проще некуда: 47 × 3 = 40 × 3 + 7 × 3 = 120 + 21 = 141. Приписываем справа нолик и получаем: 1 410.
• Поехали дальше: 47 × 2 = 40 × 2 + 7 × 2 = 80 + 14 = 94.
• Осталось сложить результаты: 1 410 + 94 = 1 500 + 4 = 1 504.

Этот принцип можно применять и к числам с большим количеством разрядов, но удержать в уме столько операций не каждому под силу.

Упрощаем умножение

Кроме общих правил, есть несколько лайфхаков, облегчающих умножение на определённые однозначные числа.

Умножение на 4

Можно умножить многозначное число на 2, а потом снова на 2.

Пример: 146 × 4 = (146 × 2) × 2 = (200 + 80 + 12) × 2 = 292 × 2 = 400 + 180 + 4 = 584.

Умножение на 5

Умножьте исходное число на 10, а потом разделите на 2.

Пример: 489 × 5 = 4 890 / 2 = 2 445.

Умножение

на 9

Умножьте на 10, а затем отнимите от результата исходное число.

Пример: 573 × 9 = 5 730 − 573 = 5 730 − (500 + 70 + 3) = 5 230 − (30 + 40) − 3 = 5 200 − 40 − 3 = 5 160 − 3 = 5 157.

Умножение на 11

Приём сводится к следующему: впереди и сзади подставляем первую и последнюю цифры исходного числа. А между ними последовательно суммируем все цифры.

При умножении на двузначное число всё выглядит крайне просто.

Пример: 36 × 11 = 3(3+6)6 = 396.

Если сумма переходит через десяток, в центре остаётся разряд единиц, а к первой цифре добавляем один.

Пример: 37 × 11 = 3(3+7)7 = 3(10)7 = 407.

Чуть сложнее с умножением на более крупные числа.

Пример: 543 × 11 = 5(5+4)(4+3)3 = 5 973.

Как научиться делить в уме

Это операция, обратная умножению, поэтому и успех во многом зависит от знания всё той же школьной таблицы. Остальное — дело практики.

Делим на однозначное число

Для этого разбиваем исходное многозначное число на удобные части, которые точно будут делиться на наше однозначное.

Попробуем разделить 2 436 на 7.

• Выделим из 2 436 наибольшую часть, которая нацело разделится на 7. В нашем случае это 2 100. Получаем (2 100 + 336) / 7.
• Продолжаем в том же духе, только теперь с числом 336. Очевидно, что на 7 разделится 280. А в остатке будет 56.
• Теперь делим каждую часть на 7: (2 100 + 280 + 56) / 7 = 300 + 40 + 8 = 348.

Делим на двузначное число

Это уже высший пилотаж, но мы всё равно попытаемся.
Предположим, вам надо поделить 1 128 на 24.

• Прикидываем, сколько раз 24 может поместиться в 1 128. Очевидно, что 1 128 примерно в два раза меньше, чем 24 × 100 (2 400). Поэтому для «пристрелки» возьмём множитель 50: 24 × 50 = 1 200.
• До 1 200 нашему делимому 1 128 не хватает 72. Сколько раз 24 поместится в 72? Правильно, 3. А значит, 1 128 = 24 × 50 − 24 × 3 = 24 × (50 − 3) = 24 × 47. Стало быть, 1128 / 24 = 47.

Мы взяли не самый трудный пример, но пользуясь методом «пристрелки» и дроблением на удобные части, вы научитесь совершать и более сложные операции.

Что поможет освоить устный счёт

Для упражнений придётся ежедневно придумывать новые и новые примеры, только если вы сами этого хотите. В противном случае воспользуйтесь другими доступными способами.

Настольные игры

Играя в те, где необходимо постоянно вычислять в уме, вы не просто учитесь быстро считать. А совмещаете полезное с приятным времяпрепровождением в кругу семьи или друзей.

Карточные забавы вроде «Уно» и всевозможные варианты математического домино позволяют школьникам играючи освоить простое сложение, вычитание, умножение и деление. Более сложные экономические стратегии а-ля «Монополия» развивают финансовое чутьё и оттачивают сложные навыки счёта.

Что купить

• «Уно»;
• «7 на 9»;
• «7 на 9 multi»;
• «Трафик Джем»;
• «Хекмек»;
• «Математическое домино»;
• «Умножариум»;
• «Код фараона»;
• «Суперфермер»;
• «Монополия».

Мобильные приложения

С ними вы сможете довести устный счёт до автоматизма. Большинство из них предлагают решить примеры на сложение, вычитание, умножение и деление по программе младших классов. Но вы удивитесь, насколько это непросто. Особенно если задачи нужно щёлкать на время, без ручки и бумаги.

Математика: устный счёт, таблица умножения

Охватывает задания на устный счёт, которые соответствуют 1–6 классам школьной программы, включая и задачи на проценты. Позволяет тренировать скорость и качество счёта, а также настраивать сложность. Например, от простой таблицы умножения можно перейти к умножению и делению двузначных и трёхзначных чисел.

Математика в уме

Ещё один простой и понятный тренажёр устного счёта с подробной статистикой и настраиваемой сложностью.

1 001 задача для счёта в уме

В приложении используются примеры из пособия по математике «1 001 задача для умственного счёта», которое ещё в XIX веке составил учёный и педагог Сергей Рачинский.

Математические хитрости

Приложение позволяет легко и ненавязчиво освоить основные математические приёмы, которые облегчают и ускоряют устный счёт. Каждый приём можно отработать в тренировочном режиме. А потом поиграть на скорость вычислений с собой или соперником.

Quick Brain

Цель игры — правильно решить как можно больше математических примеров за определённый промежуток времени. Тренирует знание таблицы умножения, сложение и вычитание. А ещё содержит популярный математический пазл «2 048».

Веб-сервисы

Регулярно заниматься интеллектуальной зарядкой с числами можно и на математических онлайн-тренажёрах. Выбирайте необходимый вам тип действия и уровень сложности — и вперёд, к новым интеллектуальным вершинам. Вот лишь несколько вариантов.

• Математика.Club — тренажёр устного счёта.
• Школа Аристова — тренажёр устного счёта (охватывает двузначные и трёхзначные числа).
• «Развивайка» — тренировка устного счёта в пределах ста.
• 7gy.ru — тренажёр по математике (вычисления в пределах ста).
• Chisloboy — онлайн-игра на развитие скорости счёта.
• kid-mama — тренажёры по математике для 0–6 классов.

Читайте также 🧠🎓😤

«Детские презентации» — все материалы от Чечуевская Виктория

Автор Автор: Чечуевская Виктория
Домашняя страничка:
Всего презентаций в нашей базе: 28

Состав числа 10 — «Дом для гнома»

Цель презентации «Дом для гнома» в игровой, занимательной форме: закрепить знание учащимися первого класса состава чисел в пределах первого десятка, совершенствовать вычислительные навыки учащихся в пределах 10, развивать у детей …

Кот в сапогах — тренажер

Тренажер по математике «Кот в сапогах» предназначен для отработки навыков устного счёта в пределах первого десятка на уроках математики в 1 классе. Материал предназначен для фронтальной работы на уроке или …

Лунтик учится считать

Тренажер по математике «Лунтик учится считать» предназначен для отработки навыков устного счёта в пределах первого десятка на уроках математики в 1 классе. Материал предназначен для фронтальной работы на уроке или …

Игра-викторина по произведениям детских писателей

Презентация-викторина для первого класса. Цель презентации : • расширить и обобщить знания учащихся 1 класса о творчестве детских писателей; • расширить читательский кругозор младших школьников; • формировать у детей устойчивый …

А.С.Пушкин «Зимний вечер» (клип) Клип можно посмотреть без скачивания на нашем Ютуб канале — КВА-КВА TV Ролик создан в программе ФотоШОУPro с целью расширения и углубления знаний учащихся о творчестве А.С.Пушкина, подготовки детей к …

Ссылка на оригинал: https://youtu.be/IHEA4IY7loQ

Осень в стихах русских поэтов

Игра-викторина «Осень в стихах русских поэтов» для учащихся 4 классов создана с использованием технологического приёма «Анимированные пазлы» с целью систематизации знаний учащихся о творчестве русских поэтов-лириков и воспитания любви к …

Интерактивная викторина-тест по рассказам Н.Носова

Интерактивная викторина-тест по рассказам Н.Носова для учащихся 3-4 классов создана на основе шаблона Д.Иванова. Цель данного ресурса:в игровой форме обобщить и систематизировать знания учащихся о жизни и творчестве Н.Н. Носова, …

Тренажёр-игра «В гостях у ёжика» ( Математика 1 класс)

Тренажер-игра «В гостях у ёжика» предназначен для отработки навыков устного счёта в пределах второго десятка на уроках математики в 1 классе. Цели и задачи данного тренажёра: • отработка навыков устного …

Игра-тренажёр «Звёздная математика»

Игра-тренажёр «Звёздная математика» предназначен для отработки навыков устного счета в пределах первого десятка на уроках математики в 1 классе. Носит универсальный характер и может использоваться в работе по любому УМК. …

Игра-тренажёр «На стройке»

Игра-тренажёр «На стройке» предназначен для отработки навыков устного счета в пределах первого десятка на уроках математики в 1 классе. Носит универсальный характер и может использоваться в работе по любому УМК. …

«Том и Джерри» (устный счёт 1 класс)

Тренажер-игра «Том и Джерри» предназначен для проведения тренировочных упражнений в устных вычислениях, предусмотренных программой 1 класса и для отработки навыков устного счёта в пределах 10. Данный ресурс создан с использованием …

Пингвины (устный счёт 1 класс)

Тренажер-игра «Пингвины» предназначен для проведения тренировочных упражнений в устных вычислениях, предусмотренных программой 1 класса и для отработки навыков устного счёта в пределах 10. Данный ресурс создан с использованием технологического приёма …

Решение простых задач (1 класс)

Презентация выполнена с использованием технологического приема «Соты». В занимательной игровой форме данный ресурс поможет закрепить знания детей в решении простых задач на нахождение суммы и остатка, задач типа: «на меньше», …

Интерактивный тест «Знаешь ли ты русские фразеологизмы?»

Тест выполнен в программе Power Point 2007 с применением шаблона А.А.Баженова с целью: систематизировать и закрепить знания учащихся о фразеологизмах, отработать умение правильного употребления фразеологизмов в речи, формировать творческую активность …

Итоговый тест по русскому языку 2 класс

Итоговый тест по русскому языку 2 класс Итоговая проверка усвоения теоретического и практического материала по русскому языку во 2 классе. Перед использованием теста необходимо включить макросы. После прохождения теста изменения …

Итоговый интерактивный тест для 1 класса «Считаем вместе с фиксиками»

Итоговый интерактивный тест для 1 класса «Считаем вместе с фиксиками» выполнен на основе шаблона А. Баженова. Цель ресурса: проведение итоговой проверки качества усвоения практического и теоретического учебного материала за курс …

Тренажёр «Устный счёт в пределах 100»

Тренажер-игра для отработки навыков устного счёта в пределах 100 создан с использованием технологического приёма «Ромашка». Материал предназначен для фронтальной работы на уроке или во внеурочное время, а также для проведения …

Считаем с Божьей коровкой

Интерактивная раскраска-тренажёр по математике для 4 класса «Считаем с Божьей коровкой». Предназначен для отработки навыков устного счета во фронтальной и индивидуальной работе с учащимися.

Знаешь ли ты русские пословицы

Интерактивный тест «Знаешь ли ты русские пословицы» поможет ребятам проверить знание некоторых русских пословиц. Способствует развитию речи, образному мышлению, а также пробуждению интереса к данному жанру фольклора. Может использоваться как …

Животный мир Дальнего Востока России

Интерактивный плакат по окружающему миру «Животный мир Дальнего Востока России». 4 класс. УМК любой

Блог учителя Татьяны Немичевой: ТРЕНАЖЁР

          Ребята! Уважаемые родители, любящие дедушки и бабушки, гости и читатели блога!   Учение может быть интересным! Предлагаю Вам и вашему ребёнку ссылки на тесты, игры, программы.…

1.  1001 ВИКТОРИНА 
2. ТЕСТЫ (русский) 
3. БИБЛИОЗНАЙКА 
4. УРОКИ школьной программы 
5. ОБРАЗОВАТЕЛЬНЫЕ ТЕСТЫ 
6. ТАБЛИЦА СЛОЖЕНИЯ и УМНОЖЕНИЯ 
7. МУЗЕЙ русского слова
8. Интерактивная игра «В стране ребусов»
9. Интеллектуальный марафон (2 класс)
10. Интерактивная викторина «Космическая»
11. Викторина «Фразеологизмы. Доскажи словечко»;
12. Викторина «Знаешь ли ты фразеологизмы?»; 3-4 классы

ИНТЕРАКТИВНЫЕ ПЛАКАТЫ:

МАТЕРИАЛ К УРОКАМ:

ТАБЛИЦА СЛОЖЕНИЯ:

1. Состав числа 10, 9, 8 / отработка вычислительных навыков в пределах 10/.  
2. Интерактивная игра-тренажёр «Решаем с Леопольдом.  /Закрепление приёмов вычитания чисел с переходом через десяток в пределах 20/
3. Игра-тренажёр «Орехи для белочки. /закрепление знания табличных случаев — 1 класс/
4. Игра-тренажёр «Собери бананы», 1 класс /»Сложение и вычитание чисел в пределах 20/
5. Интерактивная игра-тренажёр «Помоги Русалке» / таблица сложения чисел в пределах 20/.  
6. Интерактивная игра-тренажёр «Игра в футбол», /закрепление сложения чисел в пределах 20/. 
7. Дидактическая игра «Найди домик» /сложение и вычитание в пределах 100, без перехода через разряд/.  
8. Интерактивный тренажер «Накорми собаку». Математика,  /таблица сложения в пределах 20/.
9. Тренажер по математике «Новогодний сюрприз», 1 класс
10. Презентация-тренажёр по математике «Состав чисел 2-10»; 1 класс
11. Интерактивный тест «Сложение и вычитание в пределах 100» /2 класс/
12. Итоговый тест (2 класс)
13. Интерактивный тренажёр «Сложение и вычитание в пределах 20»
14. Интерактивный тренажёр «Вычитание в пределах 100»
15. Интерактивный тренажёр «Сложение в пределах 100»
16. Дидактическая игра  «Ромашки для кошки»; 2 класс
17. Дидактическая игра «Давай поиграем»; 2 класс

ТАБЛИЦА УМНОЖЕНИЯ:

1. ТРЕНАЖЁР (ЯНДЕКС.Учебник)
2. ТРЕНАЖЁР
3. ТРЕНАЖЁР
4. Для устного счёта
5. Интерактивный тренажёр / отработка табличных случаев деления/
6. УЧИМСЯ СЧИТАТЬ (отличный тренажёр)
7. БИ2О2Т (учись считать играючи)
8. Тренажёр навыка умножения
9. Интерактивный тренажёр «Таблица умножения»
10. Презентация-тренажер «Таблица умножения»
11. Игра-тренажер «Нарядим елочку!»
12. Тренажёр «Таблица умножения»
13. Интерактивный тренажер «Играем в снежки»
14. Интерактивный тренажёр » В гости к Винни-Пуху. Табличное умножение и деление»; 3 класс
15. Пазл «Снежная Королева. Табличное деление«; 2-4 классы
16. Тренажер-игра «Незнайкина мозаика. Табличное умножение»; 2-4 классы

ЗАДАЧИ:

1. Игра — презентация «Колобок. Найди 10 отличий». / найти 10 отличий в картинках, нажав на них. В конце ребенку предлагается прослушать сказку./
2. Игра — сказка «Курочка Ряба»  /Ребёнку предлагается найти 6 слов, изображенных в картинках, нажав на них. В конце игры предлагается прослушать сказку/.

Помогите своему ребенку освоить хитрые числа для подростков | Scholastic

Подростковые числа могут быть очень сложными для понимания ранними математиками. Дошкольники обычно могут плавно сосчитать до десяти, а затем пропустить или запутать следующие числа.

Основная причина того, что числа с 11 по 19 так сложно освоить, заключается в том, что они не соответствуют общему правилу чтения чисел — языковая связь с подростковыми числами отличается от большинства других чисел. Например, 35 состоит из 3 десятков и 5 единиц и произносится как «тридцать пять».«Это произношение логично, так как ваш ребенок видит сначала число три, а затем число пять. Но рассмотрите число 17: оно состоит из 1 десятки и 7 единиц, но произносится как« семнадцать ». Ваш ребенок видит цифру 1, за которой следует цифра 7, поэтому по понятным причинам сбивает с толку тот факт, что первой говорится именно «семь».

Ваш ребенок начнет более глубоко понимать эти числа в детском саду и в первом классе, но вы можете развить у своего ребенка способность определять, читать и писать числа для подростков дома с помощью следующих пяти заданий:

1.Механический счет: Потренируйтесь считать вслух от 10 до 20 вместе с ребенком. По очереди произносите каждую цифру и поправляйте ее, если она делает какие-либо ошибки. Помогите ей правильно произнести каждое число. Чем больше она будет тренироваться, тем лучше научится говорить числа!

2. Карточки с числами для подростков: Запишите карточки с числами для подростков. Напишите по одному номеру на каждой карточке. Вы можете использовать эти карты по-разному:

• Перемешайте карточки и попросите ребенка расставить их по порядку от наименьшего к наибольшему.
• Используйте их как карточки, чтобы идентифицировать каждое подростковое число.
• Сыграйте в игру Teen War — как в обычную Math War, но только с числами для подростков

3. Подростки с тремя и четырьмя руками: Сыграйте в эту игру, чтобы показать ребенку, что числа для подростков состоят из 1 десятки и нескольких единиц. Поднимите все 10 пальцев. Затем попросите ребенка поднять несколько пальцев. Вместе все эти пальцы представляют собой подростковое число. Например, если ваш ребенок держит три пальца, а вы держите все пальцы, то число 13.

4. Поднос с песком для подростков: Используйте бумажную тарелку или поднос и немного песка, чтобы ваш ребенок писал разные числа для подростков, когда вы произносите их вслух. Вы также можете сделать это с кремом для бритья или взбитыми сливками! (Если вам тепло, попробуйте эти 10 способов попрактиковаться в математике на пляже.)

5. Пакет для подростков. Попросите ребенка связать 10 соломинок резинкой. Это составляет 1 десятку. Он может использовать Cheerios для их представления. Таким образом, один набор из 10 и семи Cheerios соответствует 17.В качестве дополнительной задачи ваш ребенок может написать уравнение, соответствующее числу подростка: 10 + 7 = 17.

Если ваш ребенок будет по-разному определять числа подростка, это поможет ему распознать и понять эти числа на более глубоком уровне. Продолжайте считать вместе с ребенком вслух и находите числа подростков в мире вокруг вас. Наслаждайтесь наблюдением, как ваш ребенок углубляет и укрепляет свое чувство числа. И помните: подростковые номера: между 10 и 20!

Почему важна индивидуальная переписка

Дети любят считать.Они считают все: от шагов, которые они делают, чтобы добраться из спальни до кухни, до количества друзей в школе каждый день. Подсчет помогает им понять мир и узнать, сколько чего-то. Со временем и с практикой дети развивают понимание «правил» или принципов счета.

Один из таких принципов известен как однозначное соответствие. Идея заключается в том, что числа соответствуют определенным количествам. Например, во время игры ребенок считает 1, 2, 3, 4, 5 точек на кубике и прыгает на 1, 2, 3, 4, 5 делений на доске, потому что 5 точек соответствуют 5 прыжкам.Число «пять» всегда соответствует точному количеству, независимо от того, что вы считаете.

Таким образом, отличительной чертой точного счета является то, что дошкольники начинают присваивать один номер и только один номер каждому объекту при подсчете. Мы видим это достижение, когда ребенок прикасается к каждому объекту или помечает его, произнося счетные слова. И это немалое достижение, так как требует точной синхронизации движений и речи.

В этом видео мы можем наблюдать за молодым математиком, который только начинает координировать свой устный счет с пометкой каждого блока по мере его подсчета.После нескольких попыток он показывает некоторую путаницу между тем, что он видит, и тем, что он говорит. Сроки еще не определены.

---

Чтобы полностью сфокусироваться на ребенке, щелкните здесь.

---

Но даже когда дети взаимно однозначно помечают каждый объект счетным словом, они могут еще не иметь полного представления о взаимно однозначном соответствии. Понимание соответствия между величиной и ее числовым названием (и цифрой) — это больше, чем просто пометка или отслеживание во время подсчета.

Дети часто сначала развивают чувство однозначного соответствия, играя с игрушками, которые требуют сопоставления одного объекта с одним пространством, например, складывание пластиковых яиц в коробку для яиц или подгонку фигур в головоломку. В конце концов, дети могут сами ставить предметы в соответствие друг с другом, например, накрывать стол с одной тарелкой и одной салфеткой на каждое сиденье. Но дети могут это делать, даже не понимая, что соответствующее количество тарелок, салфеток и сидений одинаково.

Важно обсуждать соответствия, которые возникают естественным образом и осмысленно в жизни маленьких детей. При надевании зимних перчаток каждый палец находит отверстие? На всех ли за столом хватит клея? Сколько гаражей нам нужно, чтобы припарковать все игрушечные грузовики?

У этого ученика совершенно другой вопрос. Ему нужно выяснить, как справедливо делиться куки-файлами между двумя друзьями.

---

Для демонстрации этого видео, используемого учителями, щелкните здесь.

---

Мы наблюдаем, как этот студент отсчитывает все печенье, раскладывая их по одному, туда и обратно, между двумя тарелками. Хотя он точно считает 10 файлов cookie, действие по раздаче файлов cookie — это не более чем сопоставление. Хотя он говорит, что эти две группы одинаковы, он не полностью понимает, что равным группам соответствует одно и то же число. Таким образом, он считает 5 печенек на одной тарелке, а затем ему нужно пересчитать печенье и на другой тарелке, вместо того, чтобы знать, что на ней также есть 5.

Углубляйте познания маленьких детей в числах посредством множества опытов и бесед о том, как индивидуальное сопоставление создает равные группы — если вы знаете число в одной из групп, то вы знаете число в другой. Это займет некоторое время. Понимание однозначного соответствия углубит у детей чувство числа и хорошо послужит им для счета и не только.

Просмотры сообщений: 20 494

Обучение счету пропусков {это больше, чем повторение!}

Наши главные советы по обучению счету пропусков — это гарантированные стратегии, позволяющие научить детей бегло считать на 2, 5 или 100 секунд.{Подсказка — это намного больше, чем пение!}

Вы когда-нибудь спрашивали ребенка, что такое счетчик пропусков? Могут ли они сказать вам ..? Они, вероятно, ответят скандированием 2,4,6,8…! Что здорово, за исключением того, что это просто … песнопение!

Прежде чем вы начнете обучать счету пропусков, мы предлагаем вам спросить своих детей: «Что такое счет пропусков?» а затем спросите: «ЗАЧЕМ нам это нужно?»

Мы регулярно задаем нашим учащимся эти вопросы о предварительных знаниях и любим использовать аналитическую доску модели Frayer для записи их понимания.Они действительно отличный инструмент, и у нас есть еще один для обучения чувству числа!

Мы создали 4 БЕСПЛАТНЫХ обучающих скипа счетчика Thinkboards и Skip Counting With Popsticks Mat специально для вас! Получите их в самом конце сообщения, но имейте в виду, что есть много других бесплатных подарков, разбросанных по всему посту!

* Этот пост содержит партнерские ссылки. APTR может получить небольшую комиссию за ссылку на вашу покупку без каких-либо дополнительных затрат для вас. Спасибо за использование наших ссылок для поддержки нашего сайта

Обучение счету пропусков

Обучение подсчету пропусков — это сложный процесс, в котором так много обучающих моментов.Мы провели исследование, чтобы выяснить, о чем идет речь и почему мы этому обучаем. Придерживайтесь этого списка пропуска учителей, и вы ничего не пропустите при планировании урока!

Вот все, что вам нужно знать об обучении счету пропусков:

Подсчет пропусков:

• Счет по числу, отличному от единицы, иногда его называют «счетом по…» 2, 5 или 100.
• Стратегия, помогающая детям более эффективно считать большие группы предметов
• Важная фундаментальная концепция, которая помогает детям развить беглость расчетов и чувство чисел
• Основа умножения и деления
• Предварительный курсор для перевода учащихся от подсчета по единицам к использованию числовых фактов.Например, вместо того, чтобы вычислять 12 + 4, считая 12, 13, 14, 15, 16, ученики могут сразу добавить 4 или, возможно, добавить 2 дважды

Пропуск игр со счетом

Вот некоторые из игр с подсчетом пропусков и ресурсы, которые помогут вам начать работу. Эти действия не сводятся только к воспеванию! Эти игры идеально подходят для математических центров и были созданы, чтобы помочь вашим детям научиться и понимать процесс подсчета пропусков, а также познакомить их с алгебраическими знаниями!

Подсказка: обязательно поговорите со своими детьми о том, как формируются числовые шаблоны, используя такой язык, как:

• увеличение / уменьшение
• больше / меньше
• больше / меньше
• вперед / назад
• заказать
• последовательность
• узор
• количество

Пазлы со счетной сеткой

Пазлы с числовой сеткой — это увлекательное занятие, которое поможет вашим ученикам запомнить схемы пропуска подсчета чисел.Эти сотни головоломок с сеткой побуждают учащихся замечать, как числа меняются или остаются неизменными в последовательности подсчета пропусков.

Пропустить счетный центр Игры

Обучить счету пропусков сложнее, чем повторять последовательность чисел. Дети должны знать, когда им следует пропустить счет, а также последовательность чисел.

Чтобы по-настоящему понять подсчет пропусков, им также нужны практические возможности для подсчета большого количества предметов! Им также нужно больше практики с обратным отсчетом пропусков, это кажется чрезвычайно трудным, особенно переходить от одного десятилетия к другому.

Вот несколько забавных печатных таблиц для подсчета по 2, 3, 4, 5, 10, которые можно использовать в своих математических центрах для глубокого понимания процесса.

Станьте VIP-участником и получите доступ ко всем ресурсам, которые мы когда-либо создавали, ПЛЮС 20 НОВЫХ ресурсов каждый месяц… за 3,08 доллара в месяц! Щелкните изображение ниже, чтобы узнать больше…

Трудности, с которыми сталкиваются дети при обучении пропуску счета

Некоторые из трудностей, с которыми дети сталкиваются при подсчете пропусков, включают:

• Пропустить обратный отсчет
• Начиная с ЛЮБОЙ отправной точки e.g не ноль или считать до десяти, начиная с 13
• Подсчет за десятилетие, например некоторые дети могут сказать 49, 50, 51 вместо 49, 59, 69
• Пересечение декад в трехзначных числах, например достижение 100, 110, 190 и т. д.

Пропустить подсчет действий

Ученикам необходимо пропускать счет каждый день, чтобы научиться бегло говорить. Но дело не только в устном воспевании. Обучение счету пропусков должно включать:

• Устный счет
• Подсчет физических объектов, чтобы узнать, сколько их есть — тоже отлично подходит для счета денег!
• Запись числовой строки для подсчета пропусков на сетке. Убедитесь, что вы не всегда используете сетку 10 на 10, поскольку дети видят только визуальный узор (раскрашивание), а не изменение значения разряда в кратных.
• В числовой строке и в Он подходит на каждом уровне, даже в более сложном контексте с использованием отрицательных чисел, дробей и десятичных знаков

Шаблоны подсчета пропусков

Используйте числовое наглядное пособие, такое как Брент Ворги, чтобы помочь учащимся изучить визуальные шаблоны в последовательностях счета пропусков. (Найдено в Mindset Maths Джо Боулерса).

Это настолько открытое задание, которое позволяет учащимся показать то, что они знают (и не знают), но в безопасной и позитивной обстановке.Учащиеся используют цветные карандаши, чтобы изобразить схемы подсчета пропусков, которые они могут увидеть на наглядном пособии

Как научить пропускать счет с помощью палочек для мороженого

Использование палочек для мороженого — еще один отличный способ попрактиковаться в пропуске подсчета числовых последовательностей. Это забавное дополнение к любой математической ротации или полезное занятие для начинающих. Для простой математической ротации дети просто посчитают палочки по 2 или сделают связки по 5 или 10, чтобы узнать, сколько их.

Изначально мы создали несколько версий этих поп-палочек для подсчета пропусков, используя отдельную цветовую палочку для каждой числовой последовательности.В нашей версии этого забавного упражнения со счетом пропусков мы:

• Записал числа цифрами и словами для дополнительной помощи, соединяющей числовые слова и цифры.
• Добавлены точки, чтобы показать, как числа относятся к количеству
• В комплекте 3 палочки для задач, которые дети использовали в качестве подсказок, в том числе
  • Счет вперед, назад
  • Продолжайте узор. Какой пропущенный номер?
  • Пропустить подсчет по?

Бесплатная игра с подсчетом пропусков для печати

Как только они убедились, мы попросили детей сделать свои собственные наборы палочек для мороженого с пропуском счета, используя натуральные палочки.Сохранение всего одного цвета сделало задачу немного более сложной!

Мы сделали распечатку вместе с упражнением, которое они использовали для демонстрации письменного представления числовой последовательности пропусков. Это также привело к подотчетности, когда они использовали поп-джойстики во время математических заданий. Чтобы получить БЕСПЛАТНУЮ копию коврика для подсчета очков, щелкните изображение ниже.

Плакаты со счетом без пропусков {БЕСПЛАТНАЯ печать}

Таблицы

и визуальные дисплеи в классе могут улучшить обучение и понимание учащимися.Они помогают вашим детям запоминать то, что они узнали, вспоминать и извлекать информацию для других занятий, а также могут расширить их мышление.

Посмотрите наши плакаты в классе с пропуском подсчета и щелкните изображение, чтобы получить БЕСПЛАТНЫЕ плакаты.

Бесплатный подсчет пропусков по 2 лабиринтам по математике

При обучении счету с пропуском важно включать упражнения, направленные на обучение детей порядку числовых рисунков, а не визуальному рисунку, который вы можете получить, раскрашивая в сетку.

Наш пакет лабиринтов с подсчетом пропусков по 2 числам включает 17 различных лабиринтов, которые можно пройти, только если вы понимаете числовую последовательность! Итак, вы знаете, что ваши дети не просто раскрашивают, они учатся!

Мы также собрали 3 БЕСПЛАТНЫХ счетных сетки, которые вы можете скачать. Щелкните изображение или розовый текст, чтобы получить БЕСПЛАТНЫЙ подсчет пропусков по 2 лабиринтам прямо сейчас!

Доска для размышлений с бесплатным подсчетом пропусков

Вот наши 4 шаблона для обучения счету пропусков.Щелкните изображение НИЖЕ, чтобы получить их!

Для их создания мы использовали комбинацию модели Frayer и Think Board, в том числе:

• Предварительно заполненная доска для размышлений, включая подсказки для; Определение — собственными словами учащихся, Процесс — место, где дети могут записать шаги, как пропустить счет, отличное место для тестирования партнерами, Факты / характеристики — место, где можно написать как можно больше о пропуске счета, Примеры и не примеры — показать примеры подсчета пропусков и что не является примером подсчета пропусков
• Доска 2 имеет те же заголовки «Определение», «Процесс», «Примеры — без примеров — Факты / характеристики», но без подсказок для учащихся в каждой ячейке.
• Третий шаблон бесплатного подсчета пропусков включает в себя места для детей, чтобы показать подсчет пропусков в числовой строке (вперед, назад от любой начальной точки), с материалами и процессом пропуска подсчета
• Последний бесплатный шаблон Thinkboard полностью пустой, так что вы можете создать свой собственный!

Щелкните это изображение, чтобы получить бесплатные рабочие листы.

Больше сообщений с пропуском подсчета…

БЕСПЛАТНЫЙ подсчет с пропуском по 2 лабиринтам

Обучение повторному добавлению

Бесплатные игры с подсчетом пропусков: печатные числа

Шаблоны Think Board

Индивидуальные переписки

Один из основных навыков математики в детском саду — это взаимно однозначное соответствие.В моей школе наша цель — дать ученикам возможность пересчитать до 32 предметов к концу детского сада. Этот тест включает в себя несколько ключевых компонентов, которые учащиеся должны освоить, чтобы успешно вести счет: индивидуальная переписка, сохранение организованности и соблюдение трюков, понимание того, что конечное число является общим числом, знание числовой последовательности и способность останавливаться. считая на определенное число. Как только вы узнаете, с чем ваши ученики борются, вы можете целенаправленно выбрать наиболее подходящие индивидуальные заочные вмешательства.

Все действия по счету, о которых я пишу, доступны в моем магазине Teachers Pay Teachers.

Оценка индивидуальной переписки — над чем они работают?

Дайте ребенку стопку предметов для пересчета. Наблюдайте за ними. Только наблюдая за их счетом, мы можем увидеть, что они понимают в отношении счета и над какими ключевыми идеями они все еще работают. Наблюдая за их индивидуальной перепиской, вы должны задать себе следующие вопросы

• Касаются ли они, касаются или указывают на каждый объект?
• Как они хранят объекты, чтобы они сосчитать их только один раз?
• Все цифры по порядку говорят?
• Не хватает каких-то цифр?
• Они помнят, сколько они насчитали?

Индивидуальная переписка

• индивидуальное соответствие
• индивидуальное соответствие
• индивидуальное соответствие

Если ваши дети борются с однозначным соответствием во время счета, есть несколько стратегий, которые вы можете использовать, чтобы помочь им.Студенты должны понимать, что один объект получает одно число. Вы хотите постоянно напоминать им, что нужно нажимать или перемещать каждый объект только один раз. Полезно иметь место для размещения каждого объекта, например, этих кругов, яблок, десяти рамок или чисел на числовой прямой. Используя эти листы, учащиеся могут переместить только один объект в одно место. У каждой точки также есть номер, чтобы отслеживать его при подсчете и укреплять понимание того, что каждому объекту присваивается только одно число.

При использовании этих листов я бы не давал каждый раз по 30 предметов.Начните с того, что дети могут делать сами. Затем, когда они станут уверены в своей индивидуальной переписке, увеличьте сумму. Например, если они могут дать каждому объекту только одно число до числа пять, а затем они начинают дважды нажимать объекты, дайте им 7 объектов для запуска. Через некоторое время вы можете увеличить его до 10 предметов.

Оставайтесь организованными, считая

Если ваши ученики понимают взаимно однозначное соответствие и каждый объект получает только одно число, но они случайно нажимают или перемещают объекты более одного раза, то они борются с неправильной организованностью во время счета.Важно четко обучить этих испытывающих трудности учащихся стратегиям оставаться организованными во время счета (существуют замечательные задания, основанные на запросах, которые побуждают учащихся открывать для себя, какие стратегии лучше всего подходят для счета, но учащиеся, испытывающие трудности, извлекают выгоду из явного обучения и многочисленных возможностей для практики. ).

Эти листы, которые действительно можно сделать с помощью простого куска ленты или линии на листе бумаги, идеально подходят для того, чтобы помочь учащимся отслеживать предметы, которые они считают.Обучайте и моделируйте для них, как они касаются предмета, сдвигают его на другую сторону листа, считают, а затем возвращаются на другую сторону, чтобы взять новый предмет. Я называю это «прикоснись и двигайся», чтобы я мог быстро напомнить студентам, пока они считают, что нужно оставаться организованными. Студентам, которые борются с этим, потребуется много, много возможностей практиковать это. Итак, имейте для практики множество предметов и сумм.

После того, как они подсчитали свои предметы, предложите им дважды проверить, снова посчитав (это вовлекает их во второй круг подсчета для еще большей практики).Я бы сделал это только один раз (туда и обратно), если бы я не изменил объекты, чтобы было интересно. Если ученики внезапно начнут глупеть или делать глупые ошибки, это может оказаться для них слишком много времени на практику, и вам следует попробовать еще раз в другой день. Бесполезно выталкивать их за пределы их концентрации внимания до такой степени, что они демонстрируют плохое поведение.

Счет до определенного числа

• индивидуальное соответствие
• индивидуальное соответствие
• индивидуальное соответствие

Некоторые студенты, особенно студенты, которые борются с импульсным контролем, испытывают трудности с индивидуальным соответствием и счетом до определенного количества.Например, если у меня 18 учеников и мне нужно 18 кубиков для их деятельности, мне нужно отсчитать только 18 кубиков и не более. Студенты могут с трудом остановиться на цифре 18 и продолжить счет. Обычно это происходит из-за того, что они настолько сосредоточены на счете, что забывают держать в уме окончательное число. Другая причина может заключаться в том, что они борются с импульсами и просто продолжают считать, прежде чем поймут, что переоценили.

Когда учащиеся борются с этим, они могут извлечь пользу из этих организационных листов.Таким образом, им нужно только сосредоточиться на запоминании числа, на котором нужно перестать считать. Каждый раз, когда вы тренируетесь, меняйте предметы и количество, но сохраняйте общую активность вмешательства неизменной. Вы даже можете написать разные числа на заметках или листках бумаги и раздать их студентам, с которыми вы работаете. Затем они могут вернуться к числу, на котором им следует остановиться, пока они считают, и когда они достигнут этого числа, будет легче не забыть остановиться.

Знание числовой последовательности при подсчете

Студенты часто испытывают трудности со знанием числовой последовательности при работе с однозначной корреспонденцией, особенно за пределами определенного числа.Детсадовцам, особенно в начале года, часто сложно запомнить последовательность чисел подростков. Есть несколько вещей, которые вы хотите, чтобы студенты поняли — определение чисел и знание их последовательности. Это понимание часто идет рука об руку.

Идентификационные номера следует начинать с оценки того, какие числа они могут идентифицировать. Затем вы можете использовать «Шпионские листы», «Прикрыть это» или «Прыжок по цифрам», когда вы набираете номер, и они должны найти его на своих листах.

Получи халяву!

Чтобы помочь студентам узнать числовую последовательность, вы хотите дать студентам несколько возможностей для устного счета вперед и назад. Вы можете добавить немного веселья, используя кости и движения, когда ученики должны делать прыжки или прыгать на разные числа.

• считая до 20
• считая до 20
• считая от 1 до 100

Вы также хотите дать учащимся множество возможностей для построения числовых линий. Есть забавные игры, такие как прятки, которые я упоминаю в моем продукте Teen Numbers, где ученики строят числовую линию, а затем они поворачиваются, и вы убираете одно число.Затем они должны выяснить, какого числа не хватает. Они также могли собрать головоломку с числами в порядке номеров. Другое упражнение называется «Ближайшие номера», где учащиеся должны ввести числа, стоящие до и после.

Также действительно эффективно комбинировать устный счет и построение числовой линии. Попросите учащихся использовать карточки с цифрами, чтобы построить числовую линию на земле. Затем наберите номер и попросите их прыгнуть к нему, громко считая каждый прыжок, а затем считайте в обратном порядке.Каждый раз, когда вы можете усилить счет вперед и назад, делайте это! Счет в обратном порядке — отличный способ помочь понять порядок чисел и понять, как получается число на единицу больше и меньше, что является основой сложения и вычитания!

Заключение

Индивидуальное соответствие — жизненно важный навык, необходимый детям для понимания счета, и он состоит из многих ключевых компонентов. Чтобы наилучшим образом поддержать ваших учащихся, испытывающих трудности со счетом, вам необходимо нацелить вмешательства на ключевые моменты, которые им не хватает.Я надеюсь, что эти занятия помогут вашим ученикам! Какие действия вы любите использовать со своими борющимися счетчиками?

Ищете дополнительную поддержку по математике? Ознакомьтесь с другими моими сообщениями в блоге по математике!

4 цели IEP для подсчета и количества элементов

Не знаю, как вы, но когда я начал учить писать цели IEP, было сложно. Потом я узнал, что мне нужно привести их в соответствие со стандартами. Что это вообще значило ?! Если бы мои ученики соответствовали стандартам своего класса, им не понадобились бы цели IEP.Именно тогда я начал много вникать в то, что все означает, и мне стало абсолютно НЕОБХОДИМО писать цели IEP. Я начал свое глубокое погружение с математических стандартов (математический ботаник здесь) и придумал 4 цели для подсчета и кардинальности, которые вы также можете использовать со своими учениками! Я планирую охватить некоторые общие основные стандарты и помочь вам написать ЗНАЧИМЫЕ цели IEP, СОГЛАСОВАННЫЕ со стандартами.

Итак, соответствие стандартам не означает, что ваши ученики будут овладевать стандартами на уровне своего класса.Для меня это означает, что студенты стремятся усвоить часть общих основных государственных стандартов.

В этом посте я собираюсь предоставить вам значимые цели IEP для стандартов детского сада по подсчету и количеству элементов. Я расскажу о цели, которую вы можете использовать, об общем базовом стандарте, которому он соответствует, и о нескольких упражнениях, которые помогут вам отслеживать прогресс по каждой цели. Готовы нырнуть со мной? Давай сделаем это!

---

1. Счет с корреспонденцией 1: 1

ЦЕЛЬ: К (дате), когда передано до (числа) объектов и получено указание «Подсчитать (объект)», (ученик) подсчитает объекты и сопоставит правильный номер с набором в X / X испытаниях в течение X недель, как измеряется учителем в виде карт.

Соответствует: CCSS.MATH.CONTENT.K.CC.B.4

По этому стандарту студенты практикуются и осваивают переписку 1: 1 в пределах 20. Часто мои студенты работают над овладением счетом 5-10 предметов. Они все еще работают над достижением стандарта, поэтому, когда я говорю, что ученик посчитает до 10 предметов и подберет правильное число, мы продвигаемся к конечной цели — 20 предметов.

Вот некоторые ресурсы, которые вы можете использовать для отслеживания прогресса в достижении этой цели в своем классе:

---

2.Сравнение чисел

ЦЕЛЬ: К (дате), когда ему даны две группы не более чем (количество) объектов, (ученик) определит группу с большим и меньшим количеством X / X испытаний в течение X недель, как измерено данными на диаграммах учителя.

Соответствует: CCSS.MATH.CONTENT.K.CC.C.6

Этот стандарт состоит из двух частей, в которых учащиеся сравнивают группы и числа. Поскольку мои ученики, как правило, более конкретные ученики, мне нравится писать эту цель на основе объектов. Таким образом, мои ученики могут либо подсчитать объекты, либо объединить их в пары, чтобы определить, в какой группе больше объектов.

Вот некоторые ресурсы, которые вы можете использовать для отслеживания прогресса в достижении этой цели в своем классе:

---

3. Механический счет

ЦЕЛЬ: К (дате), когда ему предложат «сосчитать до (число)», (ученик) будет правильно считать вслух последовательно в X / X испытаниях в течение X недель, как измерено данными, нанесенными на карту учителем.

Соответствует: CCSS.MATH.CONTENT.K.CC.A.1

Общий базовый стандарт требует, чтобы учащиеся до конца года вслух считали до 100. Для моих учеников, которые борются со счетом и количеством элементов, мы часто работаем над счетом до 10 или 20 в моем классе, и это нормально, потому что это шаг к стандартам детского сада.

Вот некоторые ресурсы, которые вы можете использовать для отслеживания прогресса в достижении этой цели в своем классе:

---

4. Написание чисел

ЦЕЛЬ: К (дате), когда ему будет присвоено число от (XX) и будет указано «(написать / проследить) (число)», ученик будет разборчиво писать номер в X / X испытаниях в течение X недель, как измерено данными на диаграммах учителя .

Соответствует: CCSS.MATH.CONTENT.K.CC.A.3

В то время как этот стандарт требует, чтобы наши студенты записывали числа для идентификации объектов, я разделил эту цель на более дискретный навык написания чисел.Мои ученики должны уметь записывать числа, чтобы полностью усвоить этот стандарт, поэтому для начала стоит разделить этот кусок, чтобы ученики работали над ним.

Вот некоторые ресурсы, которые вы можете использовать для отслеживания прогресса в достижении этой цели в своем классе:

---

Я надеюсь, что вы меньше нервничаете при написании целей IEP для ваших учеников о подсчете и множественности. Эти цели — еще не все, когда дело доходит до написания согласованных целей Common Core. Это отличная отправная точка, и настоящая магия целей IEP приходит, когда вы начинаете адаптировать эти цели IEP к ученику, с которым вы работаете в своем классе!

С какими стандартами Common Core вы хотите, чтобы цели соответствовали следующим? Напишите мне комментарий и дайте мне знать!

Math на кончиках ваших пальцев! Упрощенный подсчет с использованием числовых жестов

Авторы являются участниками проекта DREME Family Math .

Банкноты

[1] Визе, Х. (2003). Числа, язык и человеческий разум . Кембридж: Издательство Кембриджского университета.

[2] Домас Ф., Мёллер К., Хубер С., Уиллмс К. и Нюрк Х. С. (2010). Воплощенная численность: неявные ручные представления влияют на обработку символьных чисел в разных культурах. Познание , 116 (2), 251-266.

[3] Fuson, K. C. (1982). Дополнительно анализируется процедура расчетного решения. Сложение и вычитание: когнитивная перспектива, 67-81.

[4] Ifrah, G. (2000). Всеобщая история чисел: от предыстории до изобретения компьютера, перевод Дэвида Веллоса, Э. Ф. Хардинга, Софи Вуд и Яна Монка.

[5] Карбонно, К. Дж., Марли, С. С., и Селиг, Дж. П. (2013). Метаанализ эффективности обучения математике с конкретными манипуляциями. Журнал педагогической психологии , 105 (2), 380.

[6] Андрес, М., Ди Лука, С., и Пезенти, М. (2008). Подсчет пальцев: недостающий инструмент ?. Поведенческие и мозговые науки , 31 (6), 642-643.

[7] Гундерсон, Э.А., Спапен, Э., Гибсон, Д., Голдин-Мидоу, С., и Левин, С.С. (2015a). Жест как окно в знания детей о числах. Познание , 144, 14-28.

[8] Дехаэн, Станислас, Натали Цурио, Виктор Фрак, Лоуренс Рейно, Лоран Коэн, Жак Мелер и Бернар Мазойе. «Церебральная активация при умножении и сравнении чисел: исследование ПЭТ.» Neuropsychologia 34, № 11 (1996): 1097-1106.

[9] Заго, Л., Пезенти, М., Меллет, Э., Кривелло, Ф., Мазойер, Б., и Цурио-Мазойер, Н. (2001). Нейронные корреляты простого и сложного мысленного расчета. Нейроизображение , 13 (2), 314-327.

[10] Файоль М., Барруйе П. и Маринт К. (1998). Прогнозирование арифметических достижений от нервно-психологической деятельности: продольное исследование. Познание , 68 (2), B63-B70.

[11] Ноэль, Мари-Паскаль. «Пальчиковый гнозия: предсказатель числовых способностей у детей?». Детская нейропсихология 11,5 (2005): 413-430.

[12] Бертелетти, И., и Бут, Дж. Р. (2015). Восприятие пальцев в задачах однозначной арифметики. Границы психологии , 6 , 226.

[13] Грация-Бафаллуй, М., и Ноэль, М. П. (2008). Повышает ли тренировка пальцев детей младшего возраста численные показатели? кора , 44 (4), 368-375.

[14] Черч, Р. Б., и Голдин-Мидоу, С. (1986). Несоответствие жестов и речи как показатель переходного знания. Познание , 23 (1), 43-71.

[15] Освальд, М., Гибсон, Д., Баттс, Дж., Левин, С., и Голдин-Мидоу, С. (март 2019 г.) Спонтанное использование жестов кардинальных чисел. Документ, представленный на двухгодичном заседании Общества исследований в области развития детей в 2019 г., Балтимор, Массачусетс

Number Operations: Стратегическая инструкция подсчета номеров

ОПИСАНИЕ: Студента обучают четким стратегиям подсчета чисел для базового сложения и вычитания.Затем эти навыки практикуются с наставником (адаптировано из Fuchs et al., 2009).

МАТЕРИАЛЫ:

• Номер-строка (прилагается)
• Карточки с комбинациями цифр (математические факты) для базового сложения и вычитания
• Таблица результатов по инструкции по подсчету стратегических номеров (прилагается)

ПОДГОТОВКА: Репетитор обучает ученика использовать эти две стратегии счета для сложения и вычитания:

ДОПОЛНЕНИЕ: Студенту выдается копия соответствующей числовой строки (1-10 или 1-20 — см. Приложение).Когда ученик сталкивается с проблемой сложения с двумя слагаемыми, его учат начинать с большего из двух слагаемых и «подсчитывать» количество меньшего слагаемого, чтобы прийти к ответу на проблему.

ВЫЧИСЛЕНИЕ: Студенту дается копия соответствующей числовой строки (1-10 или 1-20 — см. Приложение). Студента учат обращаться к первому числу, фигурирующему в задаче на вычитание (уменьшаемому), как « число, с которого вы начинаете »и для обозначения числа, следующего за минусом (вычитание), как« минусовое число ».Учащемуся предлагается начать с минусового числа на числовой строке и сосчитать до начального числа, одновременно ведя текущий счет чисел, подсчитываемых на его или ее пальцах. Последний счет цифр, разделяющих минусовое число и начальное число, является ответом на проблему вычитания.

ЭТАПЫ ВМЕШАТЕЛЬСТВА: Для каждого занятия репетитор выполняет следующие шаги:

1. Создание карточек . Репетитор создает карточки сложения и / или вычитания задач, которые ученик должен выполнять.На каждой карточке отображаются цифры и знак операции, которые составляют проблему, но оставляют ответ пустым.
2. Пересмотрите стратегии подсчета голосов. В начале занятия репетитор просит ученика назвать два метода ответа на математический факт. Правильный ответ ученика — «Знай или считай». Затем репетитор просит ученика описать, как считать задачу на сложение и как подсчитать задачу на вычитание. Затем наставник дает студенту две задачи на сложение выборок и две задачи на вычитание и направляет ученика решить каждую, используя соответствующую стратегию подсчета.
3. Полная разминка карточек. Репетитор просматривает карточки сложения / вычитания с учеником в течение трех минут. Перед началом наставник напоминает ученику, что, когда ему показывают карточку, ученик должен попытаться вспомнить ответ по памяти, но если ученик не знает ответа, он или она должны использовать соответствующую стратегию подсчета. Затем репетитор просматривает карточки с учеником. Каждый раз, когда ученик делает ошибку, наставник советует ученику использовать правильную стратегию подсчета для решения.ПРИМЕЧАНИЕ. Если ученик циклически перебирает все карты в стопке до истечения трехминутного периода, наставник тасует карты и начинает заново.

   По истечении трех минут преподаватель подсчитывает количество просмотренных карточек и записывает количество карточек, которые ученик (а) идентифицировал по памяти, (б) решил с использованием стратегии подсчета и (в) был решен. не смог правильно ответить. Эти итоговые значения заносятся в Таблицу оценок инструкции по подсчету стратегических номеров .

4. Повторите просмотр карточек. Репетитор перемешивает карточки с математическими фактами, предлагает ученику побить свой предыдущий результат и снова просматривает карточки вместе с учеником в течение трех минут. Как и раньше, всякий раз, когда учащийся совершает ошибку, преподаватель дает ему указание использовать соответствующую стратегию подсчета. Кроме того, если ученик заполняет все карты в стопке за оставшееся время, наставник перемешивает стопку и продолжает показывать карты, пока не истечет время.
   По истечении трех минут репетитор снова подсчитывает количество просмотренных карточек и записывает количество карточек, которые ученик (а) идентифицировал по памяти, (б) решил, используя стратегию подсчета, и (в) не смог правильно ответить.Эти итоговые значения снова заносятся в Таблицу оценок инструкции по подсчету стратегических номеров .
5. Обеспечьте обратную связь по производительности. Репетитор дает студенту обратную связь о том, превысила ли (и насколько) успеваемость студента по второй пробной карточке с первой. Репетитор также хвалит ученика, если он побил предыдущий результат, или поощряет его, если ученик не побил предыдущий результат.

Ссылки

• Fuchs, L.С., Пауэлл, С. Р., Зитхалер, П. М., Чирино, П. Т., Флетчер, Дж. М., Фукс, Д., и Гамлет, К. Л. (2009). Влияние стратегического обучения счету, с осознанной практикой и без нее, на умение комбинировать числа среди учащихся с математическими трудностями. Обучение и индивидуальные различия 20 (2), 89-100.

.