A. Введение в моделирование арены [SS]

Моделирование является одним из самых мощных инструментов анализа, доступных тем, кто отвечает за проектирование и эксплуатацию сложных процессов или систем. В условиях растущей конкуренции моделирование стало очень мощным инструментом планирования, проектирования и управления системами. Он больше не рассматривается как крайняя мера, а сегодня рассматривается как незаменимая методология решения проблем для инженеров, проектировщиков и менеджеров [7].

В этой статье представлены некоторые важные функции программного обеспечения ARENA 3.0. Это поможет новичку понять основные понятия, необходимые для построения простой модели. Это, в свою очередь, могло бы стать трамплином для создания сложных моделей реального мира.

Простая имитационная модель

Рассмотрим простую имитационную модель. Предположим, у нас есть одноканальная система очередей (линий ожидания), такая как касса в аптеке. Время между приходом клиентов равномерно распределено от 1 до 10 минут. Это достигается с помощью вращающегося циферблата (например, тех, которые используются в некоторых настольных играх). Время, необходимое для обслуживания заявки, должно быть равномерно распределено от 1 до 6 минут. Одна матрица может использоваться для определения времени обслуживания. В системе есть две случайные величины, и если необходимо произвести большое количество показаний, необходим компьютер для генерации случайных величин и ведения бухгалтерского учета.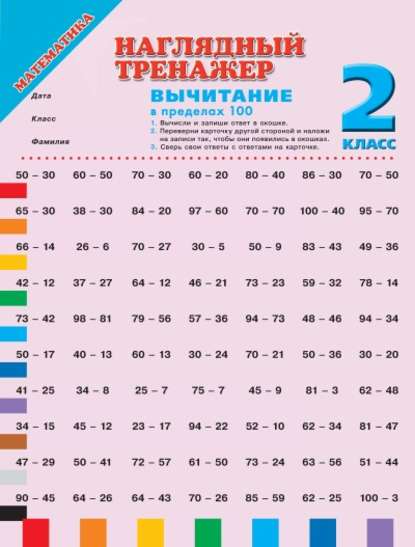 Чтобы адекватно моделировать системы реального мира, мы также должны иметь возможность генерировать реалистичные поведенческие характеристики. Например, время между прибытиями и сгенерированное время обслуживания должны допускать нечто иное, чем равномерное распределение, округленное до ближайшего целого числа [7].

Выбор распределения

Чтобы проверить совместимость набора наблюдаемых частот с некоторой теоретической частотой, мы должны сначала определить теоретическое распределение, которое мы хотим попробовать. Если мы имеем дело с дискретной переменной, мы фиксируем частоту появления каждого отдельного значения. Если переменная непрерывна, мы разбиваем диапазон значений на равный интервал или класс. Тогда относительная частота в каждом интервале представляет собой наблюдаемую частоту в каждом классе, деленную на общее количество точек данных [7].

После того, как мы получили относительное частотное распределение, выбор возможного вероятностного распределения, из которого оно может быть получено, становится делом суждения и опыта [7].

Основные концепции моделирования

В среде ARENA3.0 слово «сущность» является общим термином, используемым для обозначения любого лица, объекта или вещи, движение которых в системе вызывает изменение состояния системы. Каждый объект обладает некоторыми уникальными характеристиками, называемыми атрибутами . Например, на заводе задание может иметь атрибуты, определяющие номер детали, дату выполнения и приоритет задания. Термин переменных относится к набору изменяемых значений, характеризующих компоненты системы в целом. Пример переменной: TNOW. Он задает текущее значение моделируемого времени [8].

В структуре моделирования ARENA3.0 существует фундаментальное различие между Model и Experiment . Модель представляет собой функциональное описание компонентов системы и их взаимодействия. Эксперимент определяет экспериментальные условия, при которых модель используется для получения определенных выходных данных.

Процессы моделируются в SIMAN с помощью блок-схемы. Блок-схема представляет собой блок-схему, изображающую процесс, через который перемещаются объекты в системе. Блок-схема строится как последовательность блоков, формы и названия которых указывают на их общую функцию. Экспериментальный раздел программы состоит из элементов, которые задаются интерактивно в среде моделирования Arena [8].

Блоки
В следующем разделе кратко описаны различные блоки, используемые командой моделирования.

CREATE: Это один из нескольких механизмов, с помощью которых сущность (продукт) может войти в модель. Обычно он используется для моделирования процессов прибытия, в которых объекты последовательно входят в модель в соответствии с заданным шаблоном. Операндами блока Create являются

QUEUE: Предоставляет пространство ожидания для сущностей, чьи движения по модели были приостановлены на основе состояния системы. Пример — рабочая деталь Ожидание очереди обработки на занятой машине. Операнды блока очереди Идентификатор очереди , указывающий имя очереди, Емкость очереди и

SEIZE: Используется вместе с блоком очереди и используется для моделирования задержек состояния. Когда ресурс становится бездействующим, объект из предыдущего блока очереди входит в блок захвата и захватывает ресурс. Состояние ресурса теперь меняется с простоя на занято. Операнды блока захвата включают приоритет для выделения объектов, ожидающих одного и того же ресурса. Приоритет отдается тем сущностям, которые ждали дольше всех.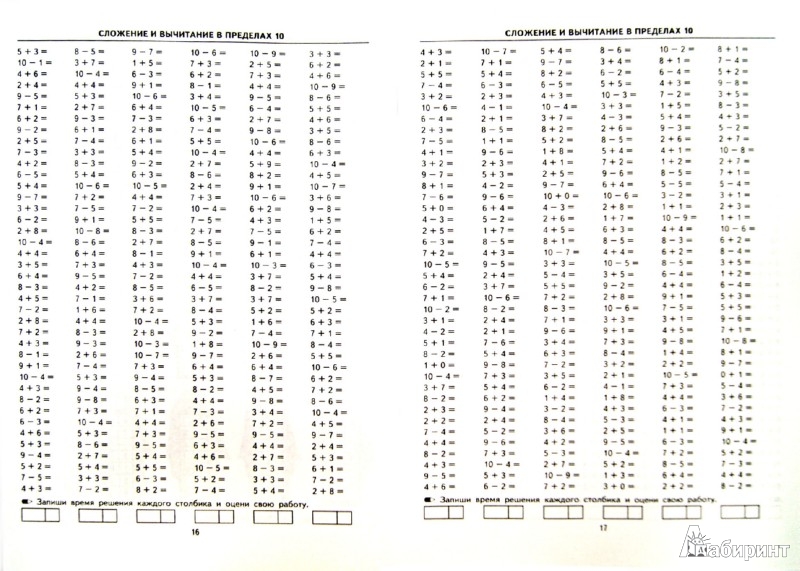 Идентификатор ресурса , указывающий ресурс, запрошенный ожидающим объектом, и количество единиц ресурса, запрошенного объектом [8].

ЗАДЕРЖКА: После того, как объекту были выделены необходимые ресурсы, он обычно выполняет трудоемкие действия, такие как настройка, обработка, проверка и т. д. В ARENA3.0 такие задержки можно моделировать с помощью блока DELAY. Операндами блока задержки являются

RELEASE: Когда действие, требующее ресурсов, завершено, объект, владеющий ресурсами, обычно освобождает их, чтобы они могли быть выделены объектам, либо ожидающим в настоящее время, либо еще не прибывшим в блоки QUEUE-SEIZE. Операнды блока захвата: Идентификатор ресурса , указывающий на только что освобожденный ресурс и Количество объектов для одновременного выпуска [8].

COUNT: Используется для подсчета количества событий, например, поступления деталей в систему, выхода из системы или отправки на доработку. Операнды блока Count включают идентификатор счетчика (имя счетчика) и приращение счетчика , для которого предполагается значение по умолчанию, равное единице [8].

DISPOSE: Обеспечивает механизм моделирования ухода сущностей из системы. Блок dispose имеет единственную точку входа, без операндов и без точек выхода. Все сущности, входящие в блок dispose, исключаются из модели [8].

ГРУППА : Обычно используется для группировки набора объектов, имеющих определенный набор характеристик. Репрезентативная сущность создается, перемещается по модели и ведет себя так, как если бы она была единой сущностью. Наиболее важным операндом группового блока является число для группы . Это обычно используется для моделирования производственного сценария, в котором набор деталей, соответствующих конкретному продукту, необходимо сгруппировать, прежде чем их можно будет собрать на машине [8].

SPLIT: Сущности, которые были сгруппированы, должны быть разделены или дегруппированы, прежде чем они будут удалены. Разделенный блок используется для того же. Уходящие сущности имеют исходные значения атрибутов, которые у них были при формировании множества сущностей [8].

ASSIGN: Всякий раз, когда атрибуты и переменные используются в модели, им необходимо присваивать значения во время выполнения модели. Это стало возможным благодаря блоку assign. Операнд блока: . Переменная или атрибут = значение 9.0008 . Каждый раз, когда объект проходит через блок ASSIGN, значение справа от знака равенства копируется в переменную или атрибут в левой части уравнения. Например, при прохождении сущностей через блок CREATE им может быть назначен тип задания 1,2,3 с определенной вероятностью принадлежности сущности к каждому типу [8].

ВЕТВЬ: Используется для направления объектов в разные разделы модели в зависимости от истинности или ложности условия. Операнды ответвительного блока следующие:

1. Максимальное количество ответвлений (обычно 1).
2. С (указывает вероятность и метку, на которую нужно направить сущность).
3. Else (указывает метку, на которую должен быть направлен объект, если условие else становится истинным).
4. Всегда (независимо от условия, при котором сущность должна быть отправлена ​​на конкретную метку).

Как описано ранее, эксперимент определяет экспериментальные условия, при которых модель используется для получения определенных выходных данных. Продолжительность симуляции, количество повторений симуляции, характеристики ресурсов и очередей и т. д. — все это зависит от экспериментальных условий. Используя специальные записи данных, называемые элементами, разрабатывается эксперимент. Обычно предпочтительнее войти в эксперимент перед входом в модель. Сначала определяя объекты, такие как ресурсы, в эксперименте, затем можно выбрать раскрывающийся список при графическом входе в модель [8].

Элементы
В следующем разделе кратко описаны различные элементы, используемые группой моделирования при разработке проекта.

PROJECT: Используется для описания проекта моделирования, используемого ARENA3.0 в маркировке сводного отчета SIMAN. Программа автоматически генерирует этот отчет в конце каждой репликации, если это определено условиями эксперимента. Операнды элемента включают Название проекта, Имя аналитика, Дата, Сводный отчет (да/нет). В первые два поля можно ввести максимум 24 символа [8].

QUEUES: Определяет информацию об очередях моделей. Операнды элемента очереди: , номер (определять не нужно), имя очереди, критерий ранжирования. Используются следующие критерии:

1. FIFO (First-in, First-out): Объекты ожидают в очереди в том порядке, в котором они прибыли.
2. LIFO (последний вошел, первый вышел): Объекты ранжируются в порядке, обратном их поступлению в очередь.
3. LVF (идентификатор атрибута): Очередь упорядочена по возрастанию значений указанного атрибута со связями, нарушенными правилом FIFO.
4. HVF (идентификатор атрибута): Очередь упорядочена по убыванию значений указанного атрибута со связями, нарушенными правилом FIFO [8].

РЕСУРСЫ: Определяет информацию о ресурсах моделей. Операнды включают Число (не требуется определять), Имя ресурса, Емкость, , которое определяет количество идентичных и взаимозаменяемых единиц, которые изначально существуют для ресурса. По умолчанию 1 [8].

СЧЕТЧИКИ: Этот элемент предоставляет описательную информацию о счетчиках, включенных в раздел модели. Операнды, включенные в элемент: Число (определять не нужно), Имя счетчика, Предел. Последний операнд указывает определенное значение, превышение которого приводит к завершению программы [8].

REPLICATE: Определяет Количество повторений , для которых должно выполняться моделирование, Время начала первой репликации и Длина репликации, , которая определяет продолжительность каждой репликации моделирования [8].

АТРИБУТЫ: и ПЕРЕМЕННЫЕ: Эти элементы предоставляют общую информацию о символических именах и свойствах атрибутов и переменных. Операнды элементов включают Номер (необязательно), Имя (индекс), Начальные значения. Второй операнд используется для указания массива с определенными значениями индекса. Каждый элемент в массиве имеет уникальное значение индекса, которое хранится в общем имени массива. Третья переменная используется для инициализации переменной до определенного значения [8].

СТАНЦИИ: Определяет информацию о станциях, используемых в модели. Операнды включают Номер (опционально), Имя станции [8].

SETS: Определяет группу похожих элементов, на которые можно ссылаться по общему имени и индексу набора. Элементы, составляющие множество, называются членами множества. Типичные наборы будут содержать группы ресурсов, очереди, станции, изображения, счетчики, подсчеты, выражения и т. д. Операнды элемента равны 9.0007 Номер (необязательно), Имя Набора и Членов набора. На последний операнд можно ссылаться по имени набора. Команда моделирования использовала функцию MemIdx (имя набора, имя члена) для создания модели производства. Эта функция возвращает порядковый номер определенного элемента в наборе. Имя элемента было первой станцией, на которой сущность вошла в модель [8].

SCHEDULES: Используется для изменения емкости ресурса с течением времени. Ресурс следует расписанию, зависящему от времени, как указано в элементе. Например, ресурс простаивает в течение первых 30 минут запуска моделирования. В этот период он имеет емкость 0. В течение следующих 30 минут работы ресурс может иметь емкость 1. Операнды элемента включают Идентификатор , который подается в блок ресурсов по расписанию, Емкость ресурса и Продолжительность емкости, , которая указывает мощность ресурса в течение определенного периода времени [8].

ПОСЛЕДОВАТЕЛЬНОСТИ: Определяет последовательность, в которой сущность посещает станции. Операнды включают Номер (необязательно), Имя последовательности, Идентификатор станции и Назначения (длительность задержки, назначение изображения или типа задания и т. д.) на каждой станции [8].

Инструменты проверки Arena3.0, используемые группой моделирования

1. КОНТРОЛЛЕР ЗАПУСКА: Позволяет пользователю пошагово выполнять выполнение модели, полностью управляя ею с помощью клавиатуры или мыши. Объект можно перемещать через один или несколько блоков, его значение можно проверить с помощью простых команд. Выполнение также может быть приостановлено в критических точках или когда указанные переменные достигают определенных значений. Контроллер выполнения также предоставляет доступ к исходным операторам моделей, которые могут быть перечислены во время выполнения [8].
2. АНИМАЦИЯ: Успешная проверка зависит от способности понять сложные взаимодействия между многими компонентами модели. Из всех методов, доступных для помощи в процессе проверки, анимация, без сомнения, является единственным и самым мощным доступным средством. Только анимация может представить динамически движущуюся картину множества взаимодействий, происходящих в симуляции. Анимация отображает одну и ту же информацию для всех компонентов модели одновременно [8].

Вернуться к оглавлению

  B. Модель производства компьютеров [LR]

Модель производства компьютеров отличается от модели автомобиля деталями, компоновкой и входными данными. Менее подробная, чем модель производства автомобилей, с точки зрения определения отдельных операций на этапе сборки, модель компьютерного производства имитирует пять основных этапов сборки и тестирования компьютеров. Этими процессами являются:

1. Сборка
2. Электрические испытания
3. Загрузка программного обеспечения
4. Окончательное тестирование и проверка
5. Упаковка

Каждая линия аналогична рабочей ячейке в том смысле, что материал непрерывно проходит через каждую стадию с минимальными запасами в процессе. На каждой ячейке производится полный продукт, в котором используется оборудование для каждой стадии производственного процесса.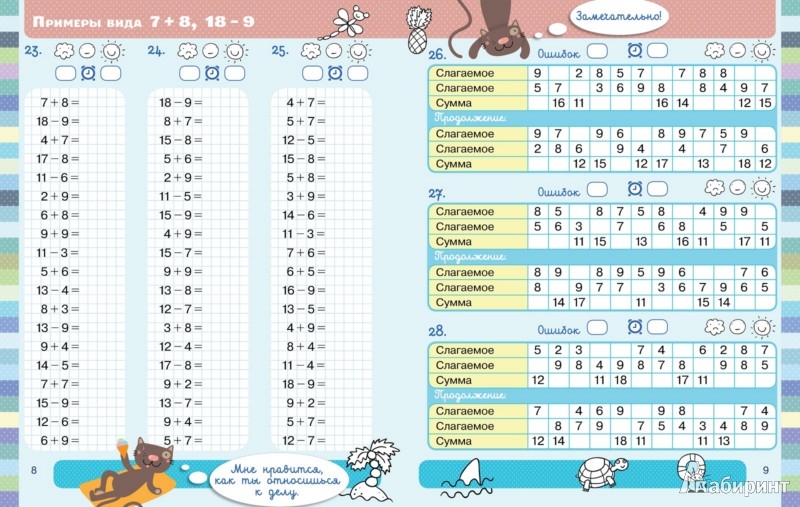

Как описано на веб-сайте производственной группы, типичный производственный завод состоит из четырех основных компонентов:

• Получение
• Производство Обработка
• Упаковка и
• Доставка

Получение
Заказы различных размеров поступают с интервалами и обрабатываются в порядке поступления. Для упрощения все запрошенные компьютеры в определенном порядке имеют одинаковую конфигурацию. Конфигурация состоит из типа процессора, количества плат и типа монитора. Модель определяет три типа процессоров, два типа плат и два типа мониторов. Эти атрибуты вероятностно назначаются каждому заказу с 12 возможными конфигурациями. Заказы отправляются на наименее загруженную линию, но ожидают исполнения до тех пор, пока стадия сборки не освободится. Модель предполагает, что все сырье для стадии сборки легкодоступно и его достаточно для выполнения каждого заказа. Логика обработки ордеров в Арене показана ниже.

Производство, обработка и упаковка
Как упоминалось ранее, схема производства состоит из двух повторяющихся параллельных линий. Заказы подаются на каждую линию, которая состоит из пяти этапов. Время обработки для каждого этапа: сборка — 12 минут, проверка электропроводки — 5 минут, загрузка программного обеспечения — 15 минут, окончательное испытание и проверка — 5 минут, упаковка — 5 минут. Коэффициент использования этапа сборки определяется характером поступающих заказов: размером каждого заказа и временем между заказами. Очереди и потенциальные узкие места могут возникать на этапах сборки и загрузки программного обеспечения, где время обработки велико. Эти проблемы можно решить, увеличив мощность ресурсов, например, добавив третий этап сборки или загрузив программное обеспечение для нескольких компьютеров одновременно. Упаковка включает в себя выбор соответствующего монитора для заказа и отправку пакетов в зону доставки.

Доставка
Хотя компьютерная модель специально не моделирует деятельность по доставке, модель достаточно гибкая, чтобы включить этот компонент позднее. Одним из соображений может быть объединение операций по упаковке и отгрузке в одной области.

Исходные данные для модели производства компьютеров не были получены из фактически существующих данных от какого-либо конкретного производителя компьютеров. Вместо этого были сделаны обоснованные предположения о размерах заказов и времени обработки. Хотя одним из принципов разработки любой имитационной модели является получение фактических данных, это требование было отменено, чтобы показать простую производственную модель, в которой используются параллельные производственные ячейки, а также то, как размеры, поступление и количество заказов влияют на коэффициент использования сборки.

Вернуться к содержанию

  C.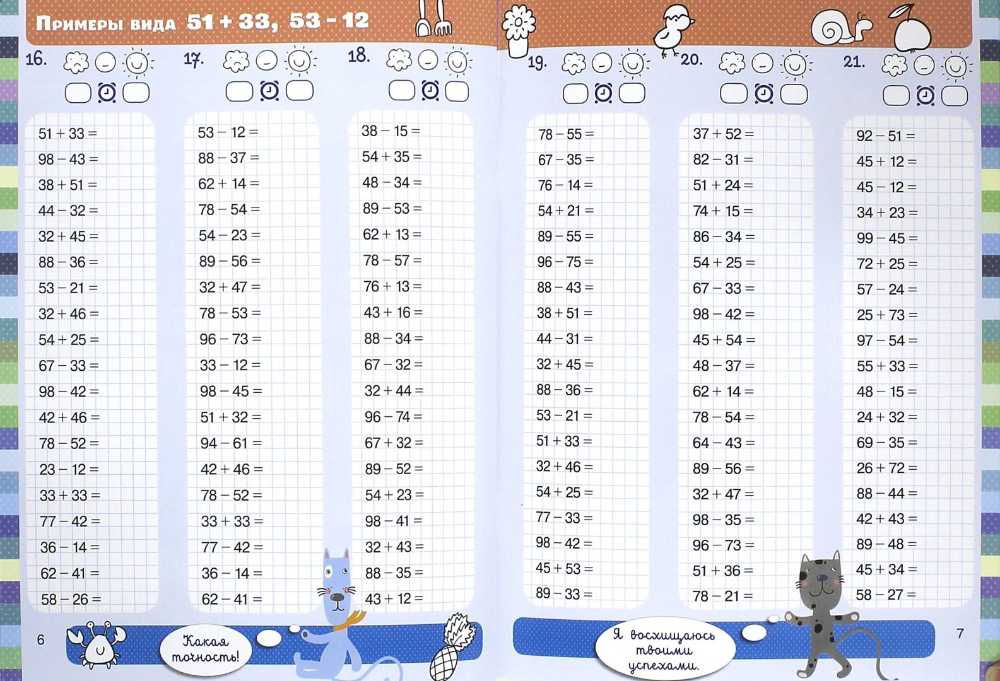 Модель производства автомобиля [AB]

Автомобиль, пожалуй, самое важное изобретение 20-го века, уступающее только электричеству. Он изменил жизнь человека невообразимым до его изобретения образом. «Мир путешествует на колесах» — модное слово 20-го века. Производство этих автомобилей — одновременно увлекательная и сложная задача. Команда моделирования смоделировала процесс производства универсалов, седанов и кабриолетов на автомобильном заводе Toyota.

Ниже приводится пошаговая процедура производства автомобилей в «Производственной системе Toyota»:

1. Производственный процесс начинается со сборки шасси. Шасси – это скелет автомобиля. Это деталь, на которой построен автомобиль.
2. Ось и шины устанавливаются на шасси в сборе.
3. На следующем этапе двигатель устанавливается на шасси. Двигатель – это силовая часть автомобиля. Мощность, вырабатываемая двигателем, используется для движения автомобиля. Двигатели преимущественно внутреннего сгорания.
4. Затем коробка передач устанавливается на шасси. Коробка передач — это компонент, который используется для изменения скорости, подаваемой на колеса.
5. Следующий этап включает установку радиатора в двигатель. Радиатор помогает охлаждать двигатель, передавая избыточное тепло окружающей среде за счет теплопроводности.
6. На следующем этапе сиденья устанавливаются на автомобиль.
7. Затем устанавливается аккумулятор и выполняются электрические соединения. Электрические соединения соединяют различные компоненты автомобиля с аккумуляторной батареей.
8. Затем кузов автомобиля устанавливается на шасси.
9. Ветровое стекло, двери и дворники устанавливаются на автомобиль вместе с капотом.
10. Выполнены последние штрихи по машине.
11. Затем автомобиль отправляется на осмотр и испытания, после чего его доставляют на стоянку и готовят к отправке.

Студенческая версия модели ограничивала количество используемых блоков. Задача состояла в том, чтобы использовать ограниченное количество доступных блоков, не упрощая процесс. Для этой цели использовались наборов вместе с атрибутами , такими как «Время работы» и «Время работы». Ниже приводится краткое описание атрибутов, переменных, наборов и счетчиков, используемых в модели.

Атрибуты

1. Рабочее время: Если задание, прибывающее на рабочую станцию, представляет собой Hardtop или Wagon, оно задерживается на время, указанное в атрибуте рабочего времени блока задержки.
2. Optime (время работы): Если задание, прибывающее на рабочую станцию, представляет собой седан, оно задерживается на время, указанное в атрибуте Op time блока задержки.
3. Setindex: Соответствует конкретной рабочей станции в наборе станций.
4. Timein (время выполнения): Обозначает время поступления задания в систему.
5. Тип работы (тип работы): Обозначает, что тип работы — хардтоп, универсал или седан.

1. Набор очередей: Обозначает все очереди на главной сборочной линии, которые последовательно посещаются заданием.
2. Набор станций: Соответствует всем станциям на главной сборочной линии, которые последовательно посещаются заданием.
3. Resourceset: Обозначает все ресурсы на главной сборочной линии, которые последовательно используются для задания.

1. Вагоны: Количество произведенных вагонов
2. Хардтопы: количество произведенных хардтопов
3. Седаны: Количество выпущенных седанов
4. Всего автомобилей: Общее количество произведенных автомобилей

1. Среднее
2. С
3. Станд.

Назад к содержанию

  D. Транспортная модель [AT]

Для любой организации, имеющей несколько производственных предприятий и огромный и обширный рынок, транспорт остается неотъемлемой частью ее общей системы. Транспортная модель, разработанная группой моделирования, служит ориентиром для изучения того, как автомобили, произведенные на конкретном предприятии, транспортируются в различные места.

Ниже приводится краткая процедура того, как происходит эта транспортировка:

1. Сначала все машины скапливаются на огромной стоянке, которая также служит погрузочной площадкой для грузовиков, перевозящих эти машины.
2. Когда указанное количество автомобилей будет доступно, они будут загружены на грузовики в соответствии с грузоподъемностью грузовиков.
3. Эти грузовики затем транспортируют автомобили в указанное место назначения, например, в док, где все эти грузовики затем передаются дистрибьютору.
4. В доке автомобили выгружаются из грузовиков, а затем загружаются на корабль.
5. После того, как корабль загружен до предела, его направляют к месту назначения, которым могут быть другие страны или внутри страны, но в разные штаты.

Атрибуты, переменные, последовательности и т. д., которые используются в модели, объясняются ниже:

Атрибуты: Time-In — единственный атрибут, используемый в модели, который определяет, в какое время автомобиль вошел в систему, как долго он находился в системе.
Расписания: Этот элемент описывает расписания для ресурсов, когда они доступны и когда их нет.
Счетчики: Подсчитывает общее количество автомобилей, перевезенных за указанное время.
Транспортеры: В этой модели используются два типа транспортеров: грузовики и корабли.

Назад к содержанию

История, как это работает и 4 ключевых шага

Что такое моделирование методом Монте-Карло?

Моделирование Монте-Карло используется для моделирования вероятности различных результатов в процессе, который трудно предсказать из-за вмешательства случайных величин. Это метод, используемый для понимания влияния риска и неопределенности.

Моделирование Монте-Карло используется для решения ряда проблем во многих областях, включая инвестиции, бизнес, физику и инженерию.

Его также называют моделированием множественной вероятности.

Ключевые выводы

• Моделирование методом Монте-Карло — это модель, используемая для прогнозирования вероятности различных исходов при наличии возможности случайных величин.
• Моделирование по методу Монте-Карло помогает объяснить влияние риска и неопределенности в моделях предсказания и прогнозирования.
• Моделирование Монте-Карло требует присвоения нескольких значений неопределенной переменной для получения нескольких результатов, а затем усреднения результатов для получения оценки.
• Моделирование по методу Монте-Карло предполагает совершенно эффективные рынки.

Моделирование Монте-Карло

Понимание моделирования Монте-Карло

При возникновении значительной неопределенности при составлении прогноза или оценки некоторые методы заменяют неопределенную переменную одним средним числом. Вместо этого моделирование Монте-Карло использует несколько значений, а затем усредняет результаты.

Моделирование по методу Монте-Карло имеет широкий спектр применений в областях, которые страдают от случайных переменных, особенно в бизнесе и инвестициях. Они используются для оценки вероятности перерасхода средств в крупных проектах и ​​вероятности того, что цена актива будет двигаться определенным образом.

Телекоммуникационные компании используют их для оценки производительности сети в различных сценариях, что помогает им оптимизировать свои сети. Финансовые аналитики используют их для оценки риска дефолта предприятия и для анализа производных инструментов, таких как опционы. Страховщики и бурильщики нефтяных скважин также используют их для измерения риска.

Моделирование Монте-Карло имеет множество применений за пределами бизнеса и финансов, например, в метеорологии, астрономии и физике элементарных частиц.

История моделирования методом Монте-Карло

Симуляция Монте-Карло была названа в честь игорного заведения в Монако, потому что случайность и случайные результаты играют центральную роль в этом методе моделирования, как и в таких играх, как рулетка, кости и игровые автоматы.

Этот метод был первоначально разработан Станиславом Уламом, математиком, который работал над Манхэттенским проектом, секретной попыткой создать первое атомное оружие. Он поделился своей идеей с Джоном фон Нейманом, коллегой по Манхэттенскому проекту, и они вместе усовершенствовали симуляцию Монте-Карло.

Как работает метод моделирования Монте-Карло?

Метод Монте-Карло признает проблему для любого метода моделирования: вероятность различных результатов не может быть точно определена из-за интерференции случайных переменных. Таким образом, моделирование методом Монте-Карло фокусируется на постоянно повторяющихся случайных выборках.

Моделирование методом Монте-Карло берет переменную, имеющую неопределенность, и присваивает ей случайное значение. Затем модель запускается и выдается результат. Этот процесс повторяется снова и снова, присваивая много разных значений рассматриваемой переменной. После завершения моделирования результаты усредняются, чтобы получить оценку.

Шаги моделирования Монте-Карло

Microsoft Excel или аналогичная программа может быть использована для создания моделирования Монте-Карло, которое оценивает вероятные движения цен на акции или другие активы.

В движении цены актива есть два компонента: дрейф, который представляет собой его постоянное направленное движение, и случайный ввод, который представляет собой волатильность рынка.

Анализируя исторические ценовые данные, вы можете определить дрейф, стандартное отклонение, дисперсию и среднее движение цены ценной бумаги. Это строительные блоки моделирования Монте-Карло.

4 этапа моделирования методом Монте-Карло

Шаг 1: Чтобы спроецировать одну возможную траекторию цены, используйте исторические данные о цене актива, чтобы сгенерировать серию периодических ежедневных доходностей с использованием натурального логарифма (обратите внимание, что это уравнение отличается от обычной формулы процентного изменения):

Периодический Ежедневный доход «=» л н ( Цена дня Цена предыдущего дня ) \begin{align} &\text{Периодический дневной доход} = ln \left ( \frac{ \text{Цена дня} }{ \text{Цена предыдущего дня} } \right ) \\ \end{align} ​Периодический дневной доход=ln(Цена предыдущего дняЦена дня​)​

Шаг 2: Затем используйте функции СРЗНАЧ, СТАНДОТКЛОН. П и ДИАПАЗОН для всего результирующего ряда, чтобы получить входные данные средней дневной доходности, стандартного отклонения и дисперсии соответственно. Дрейф равен:

Дрифт «=» Средний дневной доход − Дисперсия 2 где: Средний дневной доход «=» Произведено из Excel СРЕДНЯЯ функция из серии периодических ежедневных результатов Дисперсия «=» Произведено из Excel Функция VAR.P из серии периодических ежедневных доходностей \begin{align} &\text{Drift} = \text{Средний дневной доход} — \frac{ \text{Отклонение} }{ 2 } \\ &\textbf{где:} \\ &\text{Средний дневной доход } = \text{Составлено из Excel} \\ &\text{Функция СРЗНАЧ из серии периодических ежедневных доходностей} \\ &\text{Дисперсия} = \text{Составлено из Excel} \\ &\text{Функция VAR.P из серия периодических ежедневных возвратов} \\ \end{aligned} ​Drift=Средняя дневная доходность-2Variance​где:Средняя дневная доходность=Получено функцией Excel’sAVERAGE из серии периодических ежедневных доходностейVariance=Получено из функции ExcelVAR. P из серии периодических ежедневных доходностей​

В качестве альтернативы дрейф можно установить равным 0; этот выбор отражает определенную теоретическую ориентацию, но разница не будет огромной, по крайней мере, для более коротких таймфреймов.

Шаг 3: Затем получите случайный ввод:

Случайное значение «=» о × НОРМСТОБР(СЛЧИС()) где: о «=» Стандартное отклонение, полученное из Excel Функция STDEV.P из серии периодических ежедневных результатов НОРМСТОБР и СЛУЧАЙ «=» Функции Excel \begin{выровнено} &\text{Случайное значение} = \sigma \times \text{НОРМОСОБ(СЛЧИС())} \\ &\textbf{где:} \\ &\sigma = \text{Стандартное отклонение, полученное из Excel’s} \\ &\text{Функция СТАНДОТКЛОН.P из серии периодических ежедневных возвратов} \\ &\text{НОРМСТОБР и СЛЧ} = \text{функции Excel} \\ \end{выровнено} Случайное значение = σ × НОРМСТОБР (СЛУЧАЙ()), где: σ = стандартное отклонение, полученное из функции Excel STDEV.P из периодических ежедневных результатов серии НОРМСТОБР и СЛЧИС = функции Excel 9{ ( \text{Дрейф} + \text{Случайное значение} ) }\\ \end{выровнено} ​Цена следующего дня=Сегодняшняя цена×e(Дрейф+Случайное значение)​

Шаг 4: Чтобы возвести e в заданную степень x в Excel, используйте функцию EXP: EXP(x). Повторите этот расчет необходимое количество раз. (Каждое повторение соответствует одному дню.) Результатом является моделирование будущего движения цены актива.

Создавая произвольное количество симуляций, вы можете оценить вероятность того, что цена ценной бумаги будет следовать заданной траектории.

Объяснение результатов моделирования методом Монте-Карло

Частоты различных результатов, генерируемых этой симуляцией, образуют нормальное распределение, то есть кривую нормального распределения. Наиболее вероятная доходность находится в середине кривой, а это означает, что существует равная вероятность того, что фактическая доходность будет выше или ниже.

Вероятность того, что фактическая доходность будет в пределах одного стандартного отклонения от наиболее вероятной («ожидаемой») ставки, составляет 68%. Вероятность того, что она окажется в пределах двух стандартных отклонений, равна 9.5%, и что она будет находиться в пределах трех стандартных отклонений 99,7%.

Тем не менее, нет никакой гарантии, что произойдет наиболее ожидаемый результат или что фактические движения не превзойдут самые смелые прогнозы.

Важно отметить, что моделирование по методу Монте-Карло игнорирует все, что не встроено в движение цены, например, макротренды, лидерство компании, ажиотаж на рынке и циклические факторы).

Другими словами, он предполагает совершенно эффективный рынок.

Преимущества и недостатки моделирования методом Монте-Карло

Метод Монте-Карло помогает инвестору оценить вероятность прибыли или убытка от определенных инвестиций. Другие методы имеют ту же цель.

Моделирование Монте-Карло было создано, чтобы преодолеть кажущийся недостаток других методов оценки вероятного результата.

Никакое моделирование не может точно определить неизбежный исход. Метод Монте-Карло направлен на более надежную оценку вероятности того, что результат будет отличаться от прогноза.

Разница в том, что метод Монте-Карло проверяет ряд случайных величин, а затем усредняет их, а не начинает со среднего.

Как и любое финансовое моделирование, метод Монте-Карло использует исторические ценовые данные в качестве основы для прогнозирования будущих ценовых данных. Затем он нарушает шаблон, вводя случайные переменные, представленные числами. Наконец, он усредняет эти числа, чтобы получить оценку риска того, что модель будет нарушена в реальной жизни.

Как моделирование методом Монте-Карло используется в финансовых приложениях?

Моделирование Монте-Карло используется для оценки вероятности определенного дохода. Таким образом, он широко используется инвесторами и финансовыми аналитиками для оценки вероятного успеха инвестиций, которые они рассматривают. Некоторые распространенные варианты использования включают:

• Цены опционов на акции . Потенциальные движения цены базового актива отслеживаются с учетом всех возможных переменных. Результаты усредняются, а затем дисконтируются до текущей цены актива. Это предназначено для указания вероятной выплаты опционов.
• Оценка портфеля . Ряд альтернативных портфелей можно протестировать с помощью моделирования методом Монте-Карло, чтобы получить меру их сравнительного риска.
• Инвестиции с фиксированным доходом. Здесь случайной величиной является короткая ставка. Моделирование используется для расчета вероятного влияния изменений короткой ставки на инвестиции с фиксированной ставкой.

Какие профессии используют моделирование Монте-Карло?

Он может быть наиболее известен своими финансовыми приложениями, но моделирование Монте-Карло используется практически во всех профессиях, которые должны измерять риски и готовиться к их преодолению.

Например, телекоммуникационная компания может построить свою сеть таким образом, чтобы обеспечить постоянную поддержку всех своих пользователей. Для этого он должен рассмотреть все возможные варианты спроса на услугу. Он должен определить, выдержит ли система нагрузку в часы пик и пиковые сезоны.