когда и с чего начинать

 

Рада встрече, дорогие читатели!

Продолжаем постигать интерес по поводу ранних методик развития наших деток. О пользе раннего развития можно почитать здесь. Сегодня речь пойдет про обучение детей по методике Зайцева.

Содержание

1. Об авторе
2. Основные принципы методики
3. Волшебные кубики
4. Обучающие таблицы
5. Для какого возраста
6. Преимущества метода
7. Недостатки системы

Об авторе

Николай Александрович Зайцев (родился в 1939 г.) долгие годы работал воспитателем и учителем литературы, русского и английского языка. Имеет педагогическое образование. И работая долгие годы с детьми начинал практиковать раннее развитие. Это пришлось на начало 20 века.

Работал с разными детками: и в колонии для несовершеннолетних, и в детских домах, и в интернатах для умственно отсталых детишек, и  в обычных школах.

По мере накапливания своего педагогического опыта Зайцев делает для себя выбор, что ему интересно заниматься именно с детьми дошкольного возраста и речь заходит о зарождении новой школы раннего развития.

В 70-е годы прошлого столетия мало кто практиковал такого плана развитие, так как советское образование не принимало никаких новшеств подобного плана. Не было интернета, да и не в каждой деревеньке были библиотеки.

Информация застаивалась и не спешила разноситься. Прошло немало лет, пока к этой системе вновь вернулись и стали ее применять.

В 1989 г. было создано общество «Мазай», которое использовало программы развития Зайцева и он ведущий специалист. Здесь и берет начало активное распространение метода и начинается производство кубиков.

В 1992 г. автор немного модернизирует свою методику и значительно упрощает ее для доступности занятий в домашних условиях.

В наши дни система применяется довольно успешно и может быть многим знакома, используются в школах и детских садах.

Общество «Мазай» переименовано в ООО «Методики Зайцева» издает различные пособия и авторские разработки, такие как:

1. Кубики Зайцева. Для занятий в домашних условиях можно изготовить их самостоятельно (скачать шаблоны).
2. «240 картинок для обучения письму, чтению, рисованию». Отличный набор с карточками для занятий, который позволит вашему ребенку расширить словарный запас и знаний, научиться читать целыми словами и это просто увлекательная игра.
3. «Тысяча +» (скачать)  — обучение математике.
4. «Кто вокруг меня живет, что вокруг меня растет». Учебное пособие с карточками для детей, которые учатся читать.
5. «Песенки и потешки». Это реставрация русских народных и всеми любимых коротеньких стишков, которые были собраны из разных книг. К данной книге так же прилагается диск с песенками.
6. «Чистоговорки и скороговорки». Учимся правильно говорить.
7. Еще многочисленные игры и головоломки, мозаики и настольные игры.

 

 А так же является автором многих обучающих книг, например:

1. Зайцев Н. А., Струве Г. А. «Читай и пой» — веселые и неприхотливые песенки-потешки для занятий.
2. Зайцев Н.А. «Письмо. Чтение. Счет» (скачать книгу)
3. Так же рекомендую к прочтению еще вот такую книгу — Афанасова Е. Г. «Игротека письма и чтения Н.А.Зайцева», здесь популярно описаны методы игр и занятий. (скачать книгу)

Да, чуть не забыла, не лишним будет и то, что вы будете напевать склады на занятиях с ребенком, так ребенок легче воспринимает информацию и быстрее запоминает. А помогут вам в этом песенки-подпевки самого автора. (скачать)

При помощи методик Зайцева можно обучать детей чтению, письму, рисованию, математике и грамматике, географии, ботанике, зоологии, экологии, иностранным языкам и другим наукам. Под каждый предмет разработаны свои обучающие материалы и дидактические пособия.

Не смотря на успешную популярность, методика Зайцева так и не признана официально.

Основные принципы методики

Зайцев всерьез задумался о том, как преподносится учебный материал для детей. В то время это была голая структура: теория и закрепление материала — упражнение к уроку.

Ребенок быстро устает от таких занятий и большую часть информации не запоминает, либо запоминает, но не надолго.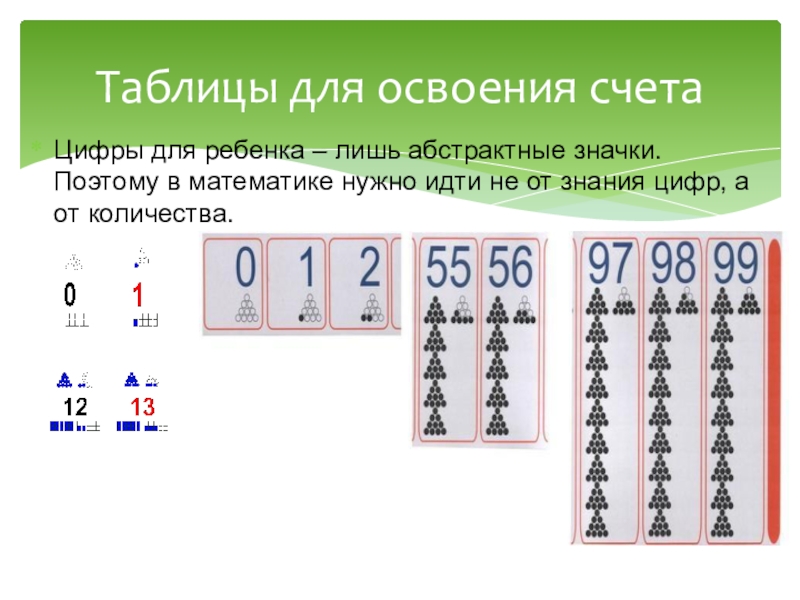

Зайцев решил внести изменения в эту педагогику и предложил совершенно новое понимание материала.

Особенность этого метода в том, что весь материал который необходимо изучить, сразу показывается ребенку и постоянно у него перед глазами систематизирован в виде специальных таблиц.

В основе методики лежат такие принципы, о которых все знают, но далеко не все их придерживаются. По методике Зайцева процесс обучения должен складываться из:

• Зрительное восприятие: ребенок осматривает кубик, здесь мы видим разные цвета.
• Осязание и тактильная память: от конкретного образа мы переходим к  действию. Даем ребенку посмотреть потрогать, покрутить, поиграть, может даже и бросить.
• Слух: озвучиваем слова — поем склады и каждый кубик по-разному звучит.
• Весь материал полностью систематизирован и представлен перед глазами в виде таблицы.

 Он убежден, что ребенок усваивает материал на 90 % лучше, когда учитель не проговаривает материал, а наглядно показывает его.

Если в русском языке дети сначала учат буквы, затем складывают слоги, затем полностью получают слово. Ни в одном языке мира не читают по буквам, это и усложняет и тормозит процесс обучения чтению.

 Многолетняя практика привела его к тому, что он изобретает специально разработанные кубики. Давайте поближе их рассмотрим.

Волшебные кубики

Зайцев дает нам новую модель обучения: склады. Он смоделировал свои кубики, на сторонах которых написаны склады. В комплектах которые вы можете встретить в продаже могут немного отличаться: по размеру, весу, материалу из которых изготовлены и наполнителям. Это 52 кубика (в которых 7 повторяются слоги для таких слов, например мама).

Склад в отличие от слога, это не только сочетание согласной и гласной, это может быть и отдельная буква, как в слове С-ЛО-Н или сочетание буквы и знака (мягкого или твердого) например ТЬ или НЬ.

Таким образом ребенку понятнее, так как он в недалеком прошлом таким образом учился выговаривать первые слова.

Например, МА-МА, МА-ШИ-НА. Так ребенок начинает говорить, так ему легче учиться читать.

Но в чем же их особенность?

• Они могут быть деревянные или железные. И не спроста. Железные обозначают звонкие склады, деревянные — глухие.
• Все буквы на них разных цветов, например, гласные — голубые, согласные — синие. Таким образом, мы можем отличать гласные от согласных.
• Знаки (твердый и мягкий) зеленым цветом.
• Большие и маленькие кубики, тоже имеют различия: на больших склады твердые, на маленьких — мягкие.
• Нет складов ЖЫ, ШЫ, ЖЯ, ЩЯ, что позволит ребенку не делать в словах грубые ошибки.
• Белый кубик со знаками препинания.

Так ребенок по складам знакомится со словами и начинает читать, лучше говорить. Затем можно переходить к обучающим таблицам.

Обучающие таблицы

Такие таблицы автор рекомендует вешать на стены или доску. Таким образом мы сразу наглядно видим весь материал. , помогает отследить, что прошли, что еще впереди.Является так называемым путеводителем. Зайцев разработал три вида таблиц:

1. Складовые, которые объединили в себе склады, составление из слов, так же разделение на звуки (звонкие, глухие).
2. Стосчетовые, которые объединили в себе числа от 0 до 99. При помощи такой таблицы можно производить математические действия в пределах ста.
3. Математические, более сложные операции с числами, свойства числе, действия, дроби и пр.

Для какого возраста

Система так же не привязана к конкретному возрасту. Вы можете начинать ее осваивать и в год, и в два, и в пять лет.

Для деток от 1 года: ребенок быстрее заговорит и одновременно освоит азы чтения. Но, на первых порах лучше с ним играть в простые игры: найди большой или маленький кубик, разложи по цветам или звукам.

От 3 лет и старше дети начинают читать уже через несколько уроков. Занятия можете моделировать сами и смотрите по своему ребенку, если ему интересно можете заниматься чаще, если не привлекает, отложите. Обычно детям нравится играться с кубиками, порой не по назначению.

Преимущества метода

1. Повторюсь, что занятия не привязаны к конкретному возрастному периоду можно и в год и в пять лет пользоваться данной методикой.
2. Дети быстро запоминают склады и начинают читать, как показала практика Зайцева.
3. Ваш ребенок никогда не сделает грубых ошибок в словах.
4. Методика доступна как для работы в коллективе, так и в домашнем индивидуальном использовании.
5. Можете обучаться в своем заданном темпе.
6. Довольно простой и наглядный материал.

1. В школе вам придется переучивать ребенка, так как ребенок, используя в составе слова склады не сможет правильно сделать фонетический состав слова. Так как склады не соответствуют слогам, ребенок будет путаться и ошибаться.
2. Методические пособия не из дешевых, могут позволить не каждые родители.
3. Для проведения занятий в домашних условиях самим родителям придется потратить достаточно времени, чтобы прочитать и самим освоить материал, а потом уже преподнести его для ребенка. Просто так сесть и позаниматься у вас не получиться! А если вы еще решите изготовить кубики своими руками, то придется потратить не один вечер на мастерство. И далеко не каждая мама располагает ресурсом времени (хотя для изготовления кубиков можно привлечь всех домочадцев).
4. Некоторые дети проглатывают окончания в словах.
5. Методика подходит только для правшей (спорно).

Ну, вот, дорогие родители, занимайтесь с вашими детками и будьте счастливы!

До новых встреч!

Пишите комменты и заходите в соц. сети!

С уважением, Юлия Полонская

Методика Николая Зайцева — семейный сайт nсuxolog.ru

«Грамота у всех народов — это умение читать, считать, писать.

Л. Н. Толстой

Практически всем известны кубики Зайцева, но мало кто знает, что они являются лишь частью, начальной ступенью методики Николая Александровича Зайцева, которая  включает в себя обучение чтению, математике, русскому и английскому языку. В отличие от методики М.

Монтессори, данная методика  является обучающей. Она позволяет дошкольнику освоить программу начальных классов, развить усидчивость, внимательность. Основной возраст, который задействует методика, от 2 до 7 лет.

Характерной чертой методики  Зайцева является отсутствие перегрузок, ослаблений зрения и осанки, столь характерных для большинства современных методик. Занятия проводятся в игровой и соревновательной форме. Зрение и осанка часто даже улучшаются.

Раннее обучение чтению и счету по методикам Н.Зайцева — надежнейшее средство диагностики. Дети ярко проявляются в деятельности, через несколько занятий любому педагогу без специальных тестов ясно, кто есть кто. Определяются как талантливые, чрезвычайно способные к обучению дети — «быстрые», так и «медленные», требующие особого внимания, а некоторые даже специального обследования. Чем раньше это выявится, тем больше будет шансов  выправить.

1. Обучение чтению.

Ребёнок постоянно чему-нибудь учится: ложкой кушать, а не руками; одеваться-раздеваться; зубы чистить, мыться; через скакалку прыгать, на коньках, велосипеде кататься; марки машин различать; рисовать, петь, танцевать… Как-то незаметно научился пользоваться телефоном, включать-переключать телевизор, видеомагнитофон, вот уже и к компьютеру приглядывается.

Среди прочих дел к четырём-пяти годам (без мучений и невероятных затрат времени, конечно) можно освоить чтение, сложение и вычитание в пределах ста хотя бы, письмо печатными буквами. Чтение дети осваивают даже легче и быстрее, чем продевание шнурков в дырочки и завязывание их бантиком.

2. Каллиграфия.

В «Пишу красиво» каждая буква расположена на отдельном листе и разложена на цветные элементы. Цвет определяет последовательность прописывания. Стрелочки указывают направление исполнения.

Освоив последовательность и направления прописывания элементов, начнём обводить чёрную «собранную» букве. Алгоритм не сложен, вполне понятен и доступен даже трёхлетнему ребёнку.

Сначала обводим пальчиками. Важно, чтобы рука запомнила вертикали, горизонтали, наклоны, овалы, полуовалы, очерёдность и направления прописывания элементов. Рука запомнит, если вам удастся организовать для неё всё большее количество повторений без ощущений монотонности, физической и психической утомляемости. Совершенно не важно, с какой буквы или цифры начинать, способ действий одинаков.

3. Грамматика русского языка.

Методики Зайцева — будь то обучение чтению, математике, английскому, русскому языку — предполагают постоянное присутствие на стенах комнаты, группы, класса комплекта таблиц, значительно облегчающих изучение каждой темы и предмета в целом. Объяснение нового материала, повторение, закрепление проводятся с опорой на таблицы. Сложнейшая подчас информация моментально добывается учащимися поворотом головы и передвижениями глаз, а не перелистыванием учебников и справочников.

Повесьте в классе большую географическую карту. Через месяц-другой ребята будут знать на ней все горы, моря, реки, чуть не каждый населенный пункт, представлять, где их искать на карте. Родной язык ближе математики с географией, языковые карты важней и интересней, в них даже ребенку хочется разобраться.

4. Математика.

По предлагаемой методике трех-четырехлетки знакомятся сразу с первой сотней, находят любое число на числовой ленте, к пяти годам решают задачи и примеры на сложение и вычитание в пределах не менее ста, знакомятся с умножением и делением, выучивают таблицу умножения, учатся прочитывать и записывать многозначные числа, знают названия геометрических фигур и, естественно, идут дальше.

Таблиц из комплектов «Тысячи+» и «Миллиона+» достаточно, чтобы дома, в группе или классе к семи-восьми годам пройти программу начальной школы без учебников.

5. Английский язык.

Манипулируя красочными кубиками и сверяясь по таблицам, учащиеся постигают грамматические азы иноязычной премудрости — составляют английские предложения… правильно!

Возможность совершения ошибок равна нулю, поскольку везде действует один четкий алгоритм — всё, не вписывающееся в рамки условий, отбрасывается. Настоящие пособия не имеют возрастных границ и вполне пригодны для изучения английского языка как в 7, так и в 97 лет.

Источник: metodikinz.ru

Эта статья может оказаться полезной для ваших друзей и знакомых. Расскажите о ней:

[PDF] Справочник по точным решениям обыкновенных дифференциальных уравнений, второе издание лянин2002Справочник ОЭ, title={Справочник по точным решениям обыкновенных дифференциальных уравнений, второе издание}, author={Андрей Д. Полянин и Валентин Зайцев}, год = {2002} }

• А. Полянин, В. Зайцев
• Опубликовано в 2002 г.
• Математика

View via Publisher

gbv.de

Разработка мезоскопического подхода к автономной линейной динамической системе с помощью квантовой формулировки

• Micó Ruiz, J. Carlos

• Физика

• 2016

В работе представлена ​​мезоскопическая подход к общим системам, моделируемым динамическими системами. Квантовая формулировка может быть получена их квантовой формулировкой из второго порядка…

ПОПАДАНИЕ СФЕР НА ГИПЕРБОЛИЧЕСКИЕ ПРОСТРАНСТВА 92$, начиная с точки $z=(\eta, \alpha)$ внутри гиперболического диска $U$ радиуса $\bar{\eta}$, получаем вероятность…

Новые точные решения оптимального потребления -инвестиционные задачи с экспоненциальной полезностью

• Р. Альярди

• Экономика

• 2020

недоступен. Мы предлагаем точные решения в нескольких особых случаях…

Плавное заполнение пропусков

• А. Иткин, А. Липтон

• Математика

  J. Comput. науч.

• 2018

Приблизительные локальные решения для одной проблемы и ограничений по общему уравнению Эмдена-Фаулера, е loro prolungamento regolare in condizioni asintotiche

• D. Iannone

• Информатика

• 2013

Il Presente Lavoro Tratta: Lo Studio di Soluzioni approssimate locali, per un’altra equazione della stessa classe, in condizioni asintotiche; все выводы и предложения finali.

Анизотропная космология в теории Саеса-Баллестера: классические и квантовые решения 04

Usamos la teoria de Saez- Ballester en el modelo anisotropico Bianchi I с баротропной жидкостью и постоянной космологией. Obtenemos las soluciones clasicas usando el enfoque де Гамильтон-Якоби. El…

Одно- и многоуединенные волновые решения одного класса нелинейных эволюционных уравнений

• Дэн-Шань Ван, Хунбо Ли

• Математика

• 2008

Квантовая дробная космология: теория K-сущности

• Дж. Сокорро, Дж. Росалес

• Физика

  Вселенная

• 2023

Используя конкретную форму скалярного поля квантовой сущности K, мы показываем, что в квантовом формализме дифференциальное уравнение дробного порядка в переменной скалярного поля для некоторых эпох в…

Моделирование поддержки населения принимающей стороны боевым противником

• М. Зупарич, С. Шеляг, М. Ангелова, Е Чжу, А. Каллониатис

• Психология

  J. Oper. Рез. соц.

• 2023

Аннотация Мы рассматриваем модель враждебной динамики, состоящую из трех популяций, помеченных Синим, Зеленым и Красным, которые развиваются в соответствии с системой нелинейных дифференциальных уравнений первого порядка. Красный…

Резонансы замкнутых мелководных бассейнов с тонкими плавающими упругими телами

Di erentialgleichungen: Losungsmethoden und Losungen

• E. Kamke

• Engineering

• 1977

Формованная пластиковая кегля для боулинга содержащий сердечник, проходящий по длине штифта по существу от его основания до его головки и состоящий из множество пластиковых сердечников различных размеров и…

Таблицы интегралов, рядов и произведений

• А. Белло

• Математика

• 1995

Дифференциальные уравнения с приложениями и историческими примечаниями

• Г. Ф. Симмонс

• Физика

• 1972

90 018 Пересмотр текста, которым восхищаются, отличающегося исключительной прозой и историческим/математическим контекстом, благодаря которому Симмонс ‘ книги классика. Хотя я не могу понять примеры…

Обыкновенные дифференциальные уравнения

• Дж. К. Беркилл, Г. Биркхофф, Г. Рота

• Математика

• 1964

Справочник по дифференциальным уравнениям

• А. Каньяда, П. Драбек, А. Фонда

• Математика 90 019

• 2004

Справочник по нелинейным уравнениям в частных производных

• A. Полянин, В. Зайцев

• Математика

• 2003

НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ И ЗАМЕЧАНИЯ ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ С ОДНОЙ ПРОСТРАНСТВЕННОЙ ПЕРЕМЕННОЙ Уравнения со степенными нелинейностями Уравнения с экспоненциальной нелинейностью Уравнения с гиперболическими нелинейностями… 92} + px + q = 0$$…

Согласованные асимптотические разложения

• П. Лагерстром

• Математика

• 1988

900 22 Проблема Штурма-Лиувилля

• К. Симпсон

• Математика

• 1991

В диссертации рассматривается задача Штурма-Лиувилля, типичный случай некоторого дифференциального уравнения с определенными граничными условиями. После краткого введения эта проблема исследуется с помощью…

ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ

• Г. Вайникко

• Математика

• 1981

Справочник обыкновенных дифференциальных уравнений ции: точные решения, методы и задачи

 @inproceedings{Polyanin2017HandbookOO,
  title={Справочник по обыкновенным дифференциальным уравнениям: точные решения, методы и задачи},
  author={Андрей Д. Полянин и Валентин Зайцев},
  год = {2017}
} 

• Полянин А.В., Зайцев В.В. 22 Определение значимых иммунологических временных масштабов для вакцин на основе мРНК-ЛНЧ у людей

  Компартмент A представлена ​​модель жидкой мРНК-вакцины, доставляемой наночастицами, и выявлена ​​возрастная зависимость, в частности, активация вакцины занимает больше времени и пик антител возникает раньше у пациентов в возрасте 55 лет и старше.

  О дискретных группах и разрешимых уравнениях нелинейных колебаний

  Рассматривается автономное обыкновенное дифференциальное уравнение Лиенара. Это уравнение и его обобщения возникают в теории нелинейных колебаний, динамических систем и т. д. В настоящее время для…

  Непрерывные динамические системы для взвешенной биполярной аргументации

  • Нико Потыка

  • Информатика

    КР

  90 011 2018

  Аксиоматические свойства модели дополняют существующие подходы и дают достаточные условия, при которых последовательные процедуры обновления могут быть легко преобразованы в четко определенные динамические системы с аналогичными гарантиями.

  О динамическом значении источников гравитационных волн, распределенных на разных высотах в атмосфере

  • А. Медведев, Г. Клаассен, Эрдал Йигит

  • Науки об окружающей среде, физика

    Журнал геофизических исследований: космическая физика

  • 2023

  Гравитационные волны (ГВ) генерируются на всех высотах в атмосфере, но источники над нижней стратосферой редко учитываются при параметризации, используемой в моделях общей циркуляции. Это…

  Численный расчет динамических моделей с нестепенными нелинейностями

  Рассмотрено решение актуальной задачи численного расчета динамических моделей с нелинейностями, описываемыми нестепенными элементарными функциями. Вычислительные трудности…

  Свежий взгляд на влияние гравитационных приливных сил на свободно падающую квантовую частицу

  Мы более внимательно и по-новому взглянем на влияние приливных сил на свободное падение квантовой гравитационное поле. Выведем соответствующий шредингеровский…

  Вклад вязкости в циркуляционные отложения при неустойчивости Рихтмайера–Мешкова

  • Хаочен Лю, Б. Ю, Хао Чен, Бинь Чжан, Хуэй Сюй, Хун Лю

  • Физика, наука об окружающей среде

    Journal of Fluid Mechanics 900 19

  • 2020

  Данное исследование посвящено процессу циркуляционного осаждения в неустойчивости Рихтмайера–Мешкова (РМИ).