Таблица умножения Пифагора
Изучение таблицы умножения начинается во втором классе, для ребёнка – это сложная задача, потому как все дети разные и не каждый может похвастаться феноменальной памятью. В этом случае на помощь придут родители и всем известная таблица Пифагора, с помощью которой можно значительно облегчить процесс усвоения новых знаний. Как правильно пользоваться таблицей Пифагора, и в чём её особенности, далее рассмотрим более подробно.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 15 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Подготовка к занятиям
Прежде всего родителям необходимо подготовиться к занятиям и постараться объяснить ребёнку как работает таблица. Можно взять готовую таблицу, которую часто печатают на обороте тетрадей, или распечатать несколько цветных таблиц, для лучшего восприятия.
Можно взять готовую таблицу, которую часто печатают на обороте тетрадей, или распечатать несколько цветных таблиц, для лучшего восприятия.
Главной особенностью таблицы Пифагора являются чёткие закономерности, которые выделены разными цветами. Когда ребёнок учит умножение столбиками, эти закономерности отследить намного сложнее, поэтому приходится методично заучивать информацию и постоянно её повторять.
Принцип работы таблицы
Таблица представляет собой простую комбинацию цифр, расположенных по горизонтали и вертикали. Необходимо объяснить ребёнку, что при умножении чисел сбоку и сверху, на пересечении строчек находится правильный ответ (результат умножения этих чисел). Также стоит повторить, что такое умножение и для чего используются вычисления.
Совет: Необходимо объяснить ребёнку, что с помощью умножения решать задачи проще. Это быстрый способ провести вычисления.
Ребёнку необходимо самому замечать закономерности, это поможет лучше понять принцип работы таблицы и быстрее её запомнить. Начинают изучение таблицы с простых примеров, постепенно продвигаясь дальше.
Начинают изучение таблицы с простых примеров, постепенно продвигаясь дальше.
Закономерности таблицы Пифагора
В таблице есть сразу несколько закономерностей, которые облегчают процесс её изучения:
- Умножая любое число на 1 число не меняется.
- В таблице умножения на 5, все результаты заканчиваются на 5 и 0. Если умножается чётное число – в конце будет 0, если же нечётное – 5.
- Умножая число на 10, в результате получаем то же число и добавляем к нему 0.
- Результаты умножения на 5 – это половина умножения на 10, например, 5 × 5 = 25, а 5 × 10 = 50.
- При умножении на 4, любое число два раза удваивается (Пример: умножим 5 × 4,
- При умножении числа на 9, если выписать ответы на листочке, можно также увидеть закономерность.
 Зная первую и вторую цифру предыдущего действия легко подсчитать следующий ответ. В ответе первая цифра будет на 1 меньше, а вторая – на 1 больше, например, 9, 18, 27.
Зная первую и вторую цифру предыдущего действия легко подсчитать следующий ответ. В ответе первая цифра будет на 1 меньше, а вторая – на 1 больше, например, 9, 18, 27.
Кроме основных закономерностей, ребёнку также стоит объяснить принцип коммутативности чисел. При перемене чисел местами их произведение не меняется, а это значит, что 5 × 4 = 20, также как 4 × 5 = 20.
Занятия необходимо проводить регулярно, повторяя пройденный материал. Лучше всего заниматься в игровой форме, когда у ребёнка есть желание, так новые знания будут усваиваться быстрее. Как только ребёнок поймёт закономерности, учить таблицу станет легче, так же как применять новые знания на практике.
УЗОРЫ ТАБЛИЦЫ ПИФАГОРА | Наука и жизнь
Таблица Пифагора. По горизонтали и по вертикали расположены числа натурального ряда; на пересечении столбцов и строк стоят их произведения. Диагональ таблицы образуют квадраты чисел. Таблицу можно продолжать вправо и вниз до бесконечности.
Цифры греческой ионийской нумерации.
Треугольная и квадратная таблицы умножения из «Арифметики», изданной в 1489 году в Германии.
Рис. 1. «Квадратные и треугольные числа».
Рис. 2. «Остатки по модулю 5» при k=5.
Рис. 3. «Трехцветные мозаики по остаткам» при k=13.
Рис. 4. «Разложенные мозаики» при k=29.
Рис. 5. «Трехцветные мозаики с дополнениями» при k=16.
Рис. 6. «Трехцветные мозаики — не плотные» при k=23.
Рис. 7. «Монохромный узор» при k=31.
Рис. 8. «Калейдоскоп узоров» при k=20.
Рис. 9. «Чередование сотен».
Рис. 10. «Чередование сотен точечное».
‹
›
Открыть в полном размере
Впервые таблица Пифагора примерно в том же виде, в каком ее печатают на обложках школьных тетрадей, но в ионийской нумерации, появилась в сочинении неопифагорейца Никомаха Геразского (I-II вв. н. э.) «Введение в арифметику». По словам Никомаха, эта таблица восходит «к самому Пифагору». Еще более древние таблицы умножения обнаружены на месопотамских глиняных табличках — их «возраст» около 5 тысяч лет.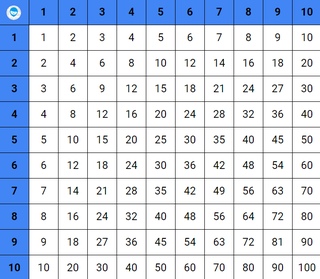
Таблицу Пифагора можно расширять вправо и вниз до бесконечности, соблюдая единственное условие: каждое число таблицы есть произведение номера строки и номера столбца, в которых оно стоит.
Расширенные таблицы умножения существуют давно. Так, например, в первой печатной математической книге на русском языке «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи» (Москва, 1682) имеется таблица умножения чисел от 1×1 до 100×100. (Ее название приводит И. Я. Депман в своей книге «История арифметики». — М.: Просвещение, 1965, с. 190.)
Таблица умножения скрывает в себе много замечательных математических закономерностей, поиск которых способен превратиться в увлекательное занятие, сулящее немало сюрпризов.
К изучению свойств расширенной таблицы Пифагора можно привлечь компьютер. Каждое число таблицы изобразим точкой (или клеткой) координатной плоскости монитора и в соответствии со свойствами чисел окрасим точки каким-либо цветом. Это реализуется с помощью шаблона программы, написанной на языке Turbo Basic version 1.1.
Это реализуется с помощью шаблона программы, написанной на языке Turbo Basic version 1.1.
screen 12
for n=1 to 120
for m=1 to 120
p=m*n
line (4*n,4*m)-(4*n+2,4*m+2),15,bf
if условие then line (4*n,4*m)-(4*n+2,4*m+2),1,bf
next m,n
При исполнении программы каждое число p расширенной таблицы Пифагора 120×120, находящееся на пересечении n-го столбца и m-й строки, будет изображаться белой клеткой, а числа, удовлетворяющие заданному в программе условию, — синими.
Так, на рис. 1 (программа 1) синим цветом выделены квадратные числа таблицы Пифагора: 1, 4, 9, 16, …, n2,… , зеленым — треугольные: 1, 3, 6, 10, …, 1/2n(n+1),… красным — числа одновременно и квадратные и треугольные: 1, 36, 1225, 41616 и т.д.
Чтобы получить представление о том, как в таблице Пифагора расположены числа, дающие одинаковые остатки при делении, например на 5, закрасим числа, дающие остатки 0, 1, 2, 3, 4, каждое своим цветом.
Аналогичное разбиение получается при делении чисел таблицы на любое другое натуральное число k, в чем легко убедиться, заменив в программе число 5 на него.
Благодаря свойству периодичности таблицы Пифагора по остаткам на экране возникают разнообразные мозаики. Очевидно, чем больше k, тем больше будет остатков r, тем больше потребуется цветов. Чтобы узоры не были слишком пестрыми, ограничимся, например, тремя цветами. Для этого остатки сгруппируем по модулю 3, то есть первым цветом закрасим числа таблицы с остатками 1, 4, 7, 10.., вторым — числа с остатками 2, 5, 8, 11.., а третьим — числа, кратные 3 (рис.3, программа 3).
Можно расчленить любую из этих мозаик на три одноцветные, дополняющие одна другую до полной мозаики. Каждая из них в отдельности тоже представляет интерес (рис.
Еще один вариант трехцветных мозаик приведен на рис. 5 (программа 5). Здесь для большей симметрии одинаковым цветом закрашены не только числа с одинаковым остатком r, но и числа с остатком, дополняющим r до k.
Интересные мозаики возникают и тогда, когда красят не все числа, а выборочно. Например, трехцветный узор на рис. 6 (программа 6).
Кружевной монохромный узор (рис.7, программа 7) возникает, если во всей таблице закрасить одинаковым цветом только числа, дающие остатки, сравнимые с одним и тем же натуральным числом.
А если в программу включить генератор случайных чисел для определения размеров квадратов k, лежащих в периоде номеров расширенной таблицы Пифагора и номеров цвета c, то с помощью компьютера таблица превратится в своеобразный калейдоскоп удивительных и неповторяющихся узоров (рис. 8, программа 8).
На рис. 9 (программа 9) показано, как в таблице Пифагора 32×32 чередуются числа нечетных и четных сотен. Здесь каждое число изображено клеткой синего или зеленого цвета. Причем числа первой, третьей, пятой и т. д. сотни закрашены синим, а числа второй, четвертой, шестой и т.д. — зеленым. Ясно, что если произведение n x m постоянно, то между числами существует обратная пропорциональность, поэтому чередующиеся синие и зеленые полосы имеют гиперболическую форму.
9 (программа 9) показано, как в таблице Пифагора 32×32 чередуются числа нечетных и четных сотен. Здесь каждое число изображено клеткой синего или зеленого цвета. Причем числа первой, третьей, пятой и т. д. сотни закрашены синим, а числа второй, четвертой, шестой и т.д. — зеленым. Ясно, что если произведение n x m постоянно, то между числами существует обратная пропорциональность, поэтому чередующиеся синие и зеленые полосы имеют гиперболическую форму.
С увеличением произведения n x m ширина полос уменьшается, а затем полосы и вовсе разрываются и распадаются на одноцветные островки, которые группируются с островками того же цвета, но из другой сотни, образуя симметричные формы (рис. 10, программа 10). Здесь каждое число таблицы 480×480 изображено точкой-пикселем. Загадочным образом таблица Пифагора не-ожиданно превращается в периодическую структуру. Интересно, чем это можно объяснить?
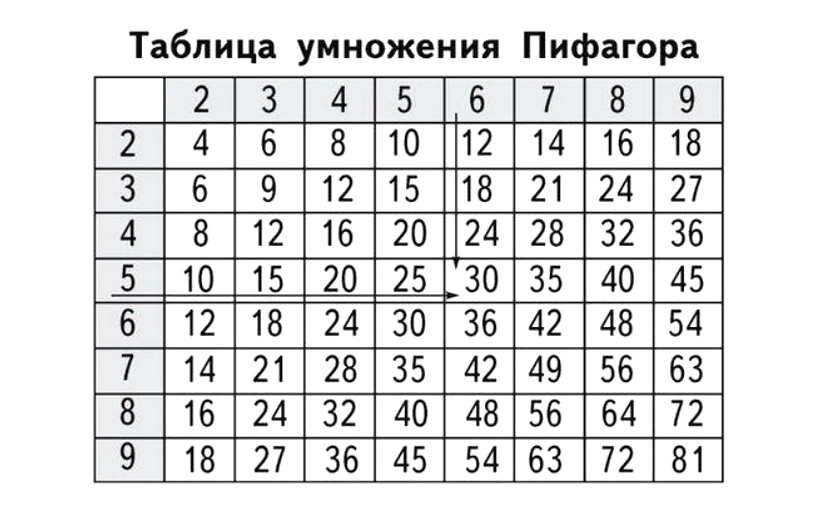
Если вы внимательно и терпеливо займетесь изучением свойств таблицы Пифагора, то, несомненно, отыщете новые, не менее красивые узоры на основе этой древней числовой схемы.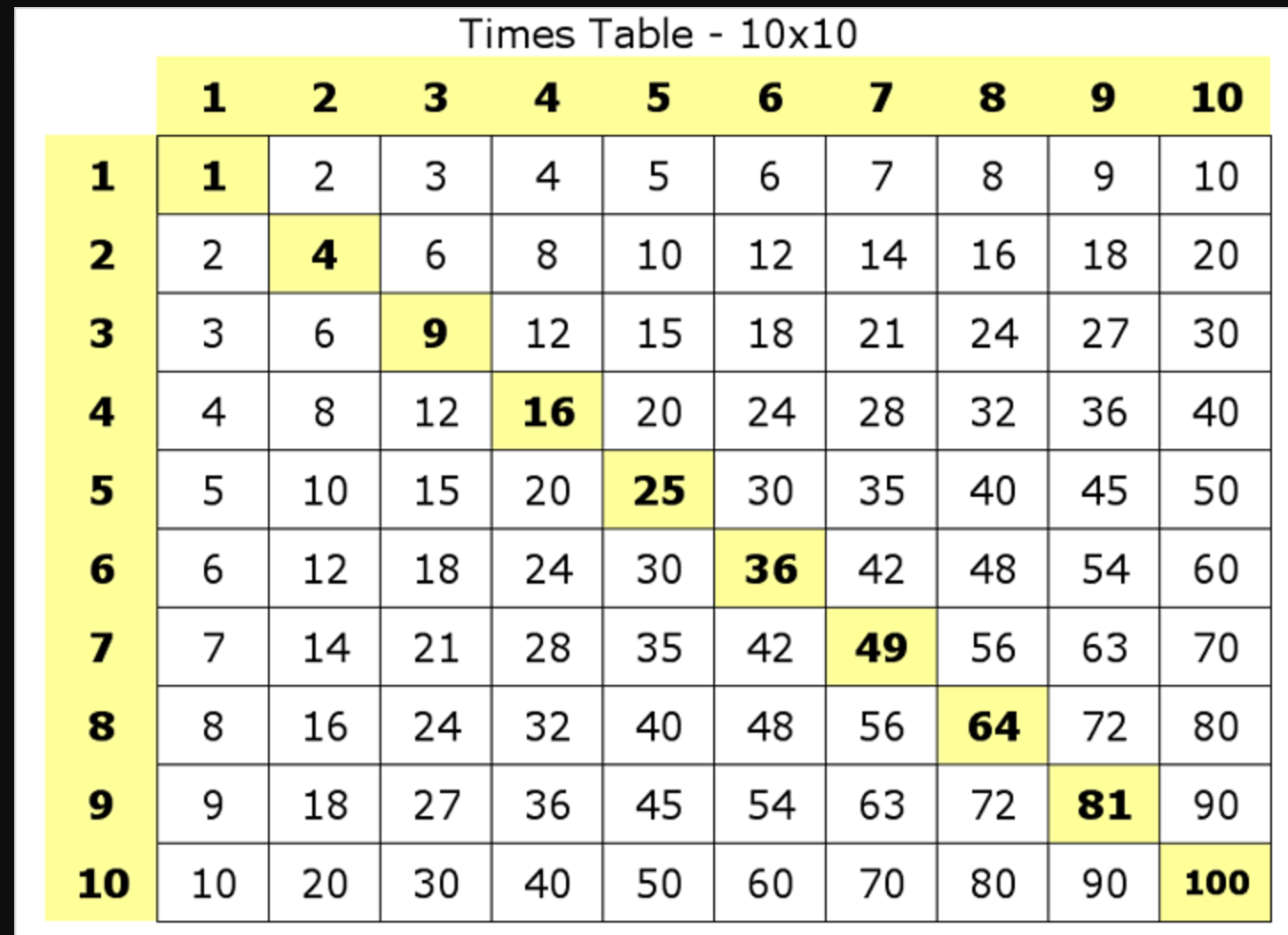 2
2
if p=q then line (4*n,4*m)-(4*n+2,4*m+2),9,bf
t=int(sqr(2*p))
if p=t*(t+1)/2 then line (4*n,4*m)-(4*n+2,4*m+2),2,bf
t=int(sqr(2*p))
if p=t*(t+1)/2 and p=q then line (4*n,4*m)-(4*n+2,4*m+2),4,bf
next m,n
2. «Остатки по модулю 5»
screen 12
for n=1 to 60
for m=1 to 60
p=m*n
c=p mod 5
line (8*n,8*m)-(8*n+6,8*m+6), c+9,bf
next m,n
3. «Трехцветные мозаики по остаткам»
screen 12
for k=1 to 50
cls
for n=1 to 120
for m=1 to 120
p=m*n
r=p mod k
c=r mod 3
line(4*n,4*m)-(4*n+2,4*m+2), 3*c+9,bf
next m,n,k
4. «Разложенные мозаики»
screen 12
for k=2 to 29 step 3
cls
for n=1 to 150
for m=1 to k
p=m*n
r=p mod k
c=r mod 3
line(4*n,4*m+165*c)-(4*n+ +2,4*m+165*c+2),3*c+9,bf
next m,n,k
5. «Трехцветные мозаики с дополнениями»
«Трехцветные мозаики с дополнениями»
screen 12
for k=1 to 50
for n=1 to 120
for m=1 to 120
p=m*n
r=p mod k
if r>k/2 then r=k-r
c= r mod 3
line(4*n,4*m)-(4*n+2,4*m+2), c,bf
next m,n,k
6. «Трехцветные мозаики — не плотные»
screen 12
for k=1 to 50
cls
for n=1 to 120
for m=1 to 120
p=m*n
r=p mod k
if r=1 or r=k-1 then line(4*n,4*m)-(4*n+2,4*m+2),9,bf
if r=k\2 or r=k-k\2 then line(4*n,4*m)-(4*n+2,4*m+2), 12,bf
if r=k\4 or r=k-k\4 then line(4*n,4*m)-(4*n+2,4*m+2), 15,bf
next m,n,k
7. «Монохромный узор»
screen 12
for k=1 to 50 step 3
cls
for n=1 to 120
for m=1 to 120
p=m*n
r=p mod k
if r mod 3=2 then line(4*n,4*m)-(4*n+2,4*m+2),14,bf
next m,n,k
8. «Калейдоскоп узоров»
«Калейдоскоп узоров»
screen 12
for i=1 to 50
c(1)=int(rnd(1)*6)
1 c(2)=int(rnd(1)*11)
if c(2)=c(1) then goto 1
2 c(0)=int(rnd(1)*16)
if c(0)=c(1) or c(0)=c(2) then 2
3 k=int(rnd(1)*43)+7
if k mod 3=0 then 3
for z=1 to 1000000
next z
cls
for n=1 to 120
for m=1 to 120
p=m*n
r=p mod k
if r>k/2 then r=k-r
c= r mod 3
line(4*n,4*m)-(4*n+2,4*m+2), c(c),bf
next m,n,i
9.»Чередование сотен»
screen 12
for n=1 to 60
for m=1 to 60
p=m*n
c=int(p\100) mod 2+1
line(8*n,8*m)-(8*n+6,8*m+6), c,bf
next m,n
10. «Чередование сотен точечное»
screen 12
for n=1 to 480
for m=1 to 480
p=n*m
p=int(p/100)
c=p mod 2+1
pset (n,m),c
next m,n
Монтессори-доска Пифагора и двуязычная таблица умножения
ByBetty 4 минуты чтения
Два любимых математических ресурса моей дочери — это доска Монтессори-Пифагора и наша двуязычная таблица умножения для печати! Эти инструменты помогают детям освоить умножение веселым и запоминающимся способом.
Этот пост может иметь партнерские ссылки. Если вы нажмете на партнерскую ссылку и совершите покупку, я получу небольшую комиссию, которая поддерживает этот образовательный веб-сайт без каких-либо дополнительных затрат для вас. Пожалуйста, смотрите политика раскрытия информации для получения подробной информации.
Таблицу умножения для печати и доску Пифагора можно использовать вместе с доской Монтессори для умножения и деления. Как правило, эти ресурсы умножения вводятся после удивительной таблицы сотен и доски сотен.
Поскольку мы воспитываем двуязычных детей, я создала таблицу умножения для печати на английском и китайском языках! Я также поделюсь различными способами, которыми моя дочь использовала таблицу умножения и доску Пифагора!
Рекомендуемые материалы для размножения
Перед загрузкой каких-либо материалов ознакомьтесь с Условиями и положениями. ©2023 АКАДЕМИЯ МЕЛА. Не делитесь никакими файлами без разрешения chalkacademy.com. Только эта ссылка на веб-сайт может быть передана.
©2023 АКАДЕМИЯ МЕЛА. Не делитесь никакими файлами без разрешения chalkacademy.com. Только эта ссылка на веб-сайт может быть передана.
- Таблица умножения для печати (английский, китайский, пустой)
- Ламинатор и пакеты для ламинирования
- Белая бумага для принтера
- Наклейки с точками Avery 0,75″ (убедитесь, что вы приобрели марку Avery, чтобы наклейки можно было легко отклеить)
- Опционально: наклейки для снятия царапин (розовые сердечки)
- Доска Монтессори Пифагора
- 快乐学算术 от 思嘉姐姐 – Математические песни на китайском языке
1. Как использовать печатную таблицу умножения
- Используйте ее в качестве контрольной для доски Пифагора. Это позволит ребенку проверить себя и дать им возможность работать самостоятельно.
- Заклейте номера наклейками с точками и напишите закрытые номера.
 Бонус: сделайте из наклеек забавный узор!
Бонус: сделайте из наклеек забавный узор! - Обложка номера с наклейками для снятия царапин; используйте монету, чтобы открыть скрытый номер!
- Практика написания пустой таблицы умножения
Хотя в математике мы в основном работаем с арабскими цифрами, моей дочери нравится смотреть на китайские цифры для справки, так как она обычно думает о числах на двух языках.
Вот пустая таблица умножения, которую моя дочь заполнила самостоятельно!
2. Как пользоваться доской Монтессори-Пифагора
Доска Монтессори-Пифагора — это наглядный, практический способ изучения таблицы умножения.
На доске 100 деревянных плиток с числами, которые ребенок может использовать для обнаружения закономерностей, пропуска счета и изучения коммутативного свойства.
Числа в верхней строке и крайнем левом столбце представляют 2 числа, которые умножаются (например, 3 x 6).
Хотя я купила доску Пифагора год назад, моя дочь увлеклась этой работой всего несколько месяцев назад. С тех пор она использует его 1-2 раза в неделю.
С тех пор она использует его 1-2 раза в неделю.
Когда моя дочь использует доску Пифагора, она думает, что играет.
Не осознавая, что учится, она постепенно запоминает таблицу умножения!
Ей нравится выбрасывать плитки, находить числа и расставлять их в правильном порядке.
Сама она обнаружила, что числа в каждом столбце повторяются по той же схеме, что и строки! Она также заметила закономерности нечетных и четных чисел.
Это красота обучения Монтессори!
3. Китайская математическая память с 快乐学算术 от 思嘉姐姐
Иногда мы слушаем 快乐学算术 от 思嘉姐姐 — математические песни на китайском языке для изучения математической лексики на китайском языке.
Трек 4 — 乘法小九九口诀, и детям, которые хорошо учатся на слух, может быть полезно послушать напевные китайские математические стишки для тренировки памяти.
Исследуйте этот : более 100 популярных китайских детских песенок и потешек
Ваш ребенок выучил таблицу умножения?
Я надеюсь, что вашему ребенку будет полезна доска Пифагора и двуязычная таблица умножения, которую можно распечатать. Если вы используете эти ресурсы для умножения дома, пожалуйста, оставьте комментарий ниже, чтобы поделиться своим опытом!
Если вы используете эти ресурсы для умножения дома, пожалуйста, оставьте комментарий ниже, чтобы поделиться своим опытом!
Дополнительные ресурсы по математике для детей
- Как я учу своих детей математике бесплатно без рабочих тетрадей и приложений
- 15 математических ресурсов для детей, изучающих китайский язык
- 数学帮帮忙 Книги по математике (двуязычные упрощенный китайский и английский)
- Все практические занятия по математике для дошкольников и младших школьников
Учебные задания по любой теме!
Чтобы подписаться на нашу образовательную рассылку, нажмите кнопку ниже.
Чем сегодня интересуется ваш ребенок? Нажмите ниже, чтобы узнать о занятиях и книгах, которые понравятся вашему ребенку.
461 акцииSTL-файл Таблица Пифагора・Модель для 3D-печати для загрузки・Культы
Руководство по чтению
3,50 €
Символы музыкальных нот
7,50 €
Лучшие файлы 3D-принтеров в категории Инструменты
Куб для калибровки тестов 20x20x20 мм
Бесплатно
бобин
Бесплатно
Подставка для батареи Bosch 12 В
1,29 €
Держатель инженерного молотка 100 г 027 I для шурупов или штифтовой доски
Бесплатно
капельный кран
бесплатно
Многоцветная рождественская свеча
Бесплатно
ПЭТ-машина — превращайте пластиковую бутылку в нить для 3D-печати
€11,02 -60%
€4,41
Чехол для зажигалки Chill Buddy
0,91 €
Бестселлеры категории Инструменты
ПЭТ-машина, сделай нить своими руками из пластиковых бутылок дома!
€50 -50%
€25
Контейнер для креатина — KETTLEBELL Держатель добавок
€1,20 -18%
€0,98
ENDER 3 S1, S1 PRO, ЭКСТРУДЕР SPRITE, 5015 КАНАЛЬНЫЙ ВЕНТИЛЯТОР, CR-BL TOUCH NO Y OFFSET, ДВОЙНОЙ 5015 КАНАЛЬНЫЙ ВЕНТИЛЯТОР
€3,22 -10%
€2,90
ARMY PAINTER 1.
 0 & 2.0 SPEED PAINT SPEEDPAINT COLOR SWATCH CAP — 17 МЛ И 18 МЛ — КРИСТАЛЛЫ
0 & 2.0 SPEED PAINT SPEEDPAINT COLOR SWATCH CAP — 17 МЛ И 18 МЛ — КРИСТАЛЛЫ5,83 €
Капельное орошение
1 €
Катушка для ниток Thread Buddy для пенопласта, квилтинга и аппликаций
5,51 €
Экструзионная линейка для Sovol SV06, SV06 Plus, SV07 (инструмент калибровки E-step)
€1 -25%
0,75 €
Минимус E3/Pro/V2
2,30 €
Generativ Design Y-Filamentsplitter Bambulab AMS-Extern RS-CONCEPTS
2,50 €
Ender 3, 3 V2, 3 pro, 3 max, двойной 40-мм осевой вентилятор, канал горячего конца / клык. CR-10, прямой привод Micro Swiss и совместимость с боуденом.
 Не требуется поддержка для печати
Не требуется поддержка для печати1,56 €
AR-15 Нижний MK8
6 €
Штабелируемые контейнеры для деталей Fast-Print
2,92 €
ВЕНТИЛЯТОР ВОЗДУХОВОДА V4 5015, 5020, ENDER 3 S1, S1 PRO, ЭКСТРУДЕР SPRITE, АКСЕЛЕРОМЕТР, СВЕТОДИОДНАЯ ПОЛОСА
2,87 €
canmaxfire
7 €
Мегапрочный бокс без винтов
5,50 €
Sonic Pad USB Free Fix
€0,78 -15%
€0,66
💖 Хотели бы вы поддержать культы?
Вам нравятся культы и вы хотите помочь нам продолжить приключение самостоятельно ? Обратите внимание, что мы небольшая команда из 3 человек , поэтому очень просто поддержать нас поддерживать деятельность и создавать будущие разработки .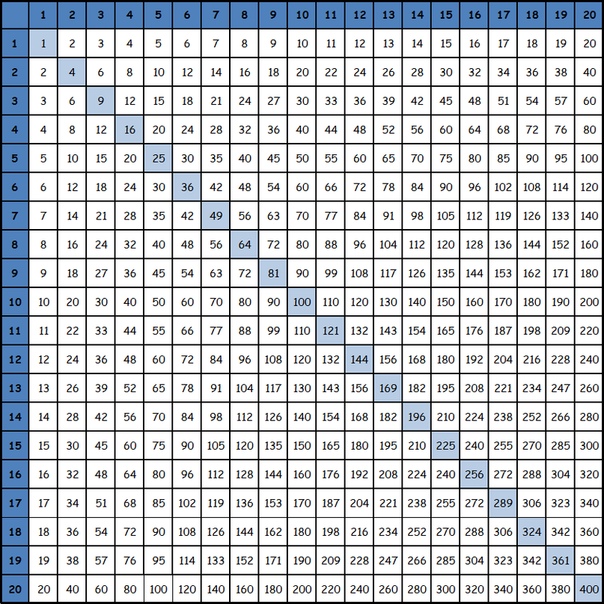
 Зная первую и вторую цифру предыдущего действия легко подсчитать следующий ответ. В ответе первая цифра будет на 1 меньше, а вторая – на 1 больше, например, 9, 18, 27.
Зная первую и вторую цифру предыдущего действия легко подсчитать следующий ответ. В ответе первая цифра будет на 1 меньше, а вторая – на 1 больше, например, 9, 18, 27.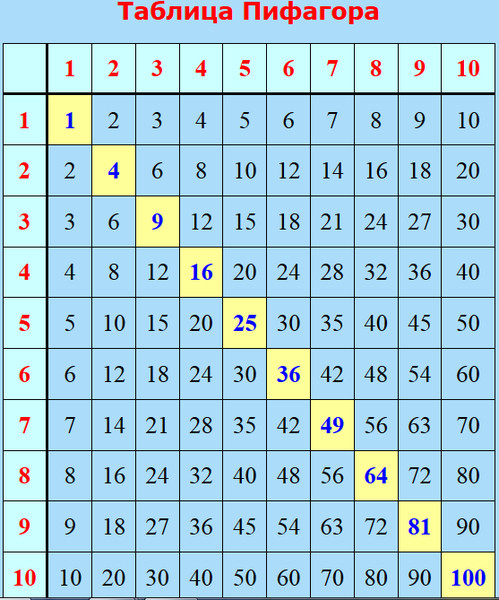 Бонус: сделайте из наклеек забавный узор!
Бонус: сделайте из наклеек забавный узор!