Педагогическая технология изучения чисел второго десятка. Автор к.п.н. Петкевич Н.В.

Согласно требованием программы к концу второго класса должны быть сформированы вычислительные навыки табличных случаев сложения и вычитания однозначных чисел.         

 Комплексное использование демонстрационных  и индивидуальных  наглядных  пособий обеспечит достижение положительного результата с наименьшими затратами сил и времени как учителя, так и ученика, что является необходимым условием здоровьесберегающих педтехнологий.

   Использование пособий в определенной последовательности обеспечивает этапы усвоения  информации по формированию понятия о сложении однозначных чисел с переходом через десяток и вычислительных навыков, путем  построения предметных (рисунки овощей), графических (кружочки) и знаковых (цифры) моделей.

   Благодаря  демонстрационным  пособиям с подвижными деталями учащиеся имеют возможность увидеть в динамике  формируемые понятия и действия сложение и вычитание, а при наличии у детей комплектов индивидуальных наглядных пособий «Математика от 1 до 20. Суперпапка» выполнить эти же действия самим.

    Большинство из представленных ранее пособий используется и для изучения чисел второго десятка. Это обеспечивает преемственность в предъявлении содержания учебного материала от простого к сложному и преемственность в последовательности выполнения учебных действий. Ориентиром в этой работе выступит последовательность использования наглядности. 

 I. Образование чисел от 11 до 20 

 1. Предъявление образа чисел. Работа с таблицами из демонстрационных наглядных пособий«Сказочный счет». 

 2. Образование чисел из одного десятка и нескольких единиц. Работа со второй частью демонстрационного и индивидуального наглядного пособия «Линейка «Счет от 1 до 20». 

 3. Построение предметной модели чисел при помощи «Абака». 

4. Построение графической, цветовой и знаковой модели чисел с использованием «Компьютера». 

 II. Сложение однозначных чисел с переходом через десяток 

 1. Построение предметной модели задачи при помощи «Абака».  

2. Построение ее графической, цветовой и знаковой модели с использованием «Компьютера» и ее преобразование, создание проблемной ситуации. 

 3. Построение знаковой модели при помощи «Линейки «Счет от 1 до 20». Запись на доске. 

 III. Состав чисел II десятка 

 1. Построение графической, цветовой и числовой модели состава чисел. Работа с демонстрационным и индивидуальным пособием «Компьютер». 

 2. Закрепление знаний. Самостоятельная работа в тетради. 

 3. Применение полученных знаний на новых информационных полях и в новых ситуациях. Работа с демонстрационными пособиями «Радужная горка» и «Числовая горка». 

 4. Взаимопроверка знаний. Работа «в паре» с индивидуальными пособиями «Радужная горка», «Числовая горка», «Столбик таблицы сложения однозначных чисел». 

 5. Проверка знаний учителем. Работа с «Цветовыми сигнальными карточками» и «Цветовой сигнальной лентой».  

ТЕХНОЛОГИЯ ИЗУЧЕНИЯ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА 

I. Образование числа 11

 1 . Предъявление образа числа 11. Работа с таблицами из «Сказочного счета».

                  а)                                    б)               Рис. 1

Иллюстрации к сказкам «Про Козленка, который умел считать до десяти» и «Красная шапочка». Образование числа 11. 

Рис. 1 а подсказывает название числа – одиннадцать (дцать – это сокращенное десять), а рис. 1 б, как его образовать. Дети находят число 11 на корпусе парусника и его модель в «Радужной горке» (нижний ряд 1 десяток и 1 белый с точкой шарик вверху). 

Аналогично происходит знакомство с числами 12, 13…19. 

2. Образование числа 11. 

Работа со второй частью «Линейки «Счет от 1 до 20». Сначала учитель, а затем учащиеся устанавливают окошко на своих линейках, как показано на рис. 2, и видят, что если к 10 прибавить 1, получается 11. 

Рис. 2. 

Линейка «Счет от 1 до 20» II ч. Модель числа 11. 

3. Построение предметной модели числа 11 при помощи «Абака» (рис. 3). 

По картинкам составляется задача: «В вазе лежало 10 яблок. В нее положили 1 грушу. Сколько фруктов стало в вазе?». Дети хором: 10 + 1 = 11(фр.). 

                                                                      Рис. 3. «Абак». Модель задачи. 

4. Построение графической, цветовой и знаковой модели числа 11 с использованием «Компьютера». 

Учащиеся, проговаривая, строят модель этой задачи при помощи «Компьютера» (рис. 4). 

Рис. 4. «Компьютер». Модель задачи. 

Таким образом, в процессе работы с наглядными пособиями ученики знакомятся с десятичным составом чисел от 11 до 19. 

II. Сложение однозначных чисел с 

переходом через десяток 

1. Построение предметной модели задачи при помощи «Абака». 

Чтобы не допустить «отлета математики от действительности» и обеспечить мотивацию путем распознавания в повседневной жизни проблем, требующих практического применения математических знаний, начнем работу с решения задачи. Например. Задача: «Хозяйка купила 7 помидоров и 5 огурцов. Сколько всего овощей купила хозяйка?» Условие задачи моделируется при помощи «Абака» (рис. 5). 

                                                    Рис. 5. «Абак». Предметная модель задачи. 

2. Построение ее графической, цветовой и знаковой модели с использованием «Компьютера» и ее преобразование, создание проблемной ситуации. 

Учитель предлагает учащимся построить модель условия задачи при помощи полосок из персонального «Компьютера» (рис. 6, а). «Сколько овощей купила хозяйка?» – спрашивает он. Учащиеся затрудняются дать ответ сразу. Кто-то пересчитывает все овощи, кто-то присчитывает к 7 кружочкам 5 по одному.

 

           а)                                     б)                                в)              

Рис. 6  (а, б, в,) «Компьютер». Построение и преобразование модели задачи. 

Учитель создает условие для выполнения вычислений более рациональным способом. Он хочет поставить полоску с 5 кружочками в верхний карман «Компьютера» Она не входит, поэтому она накладывается на него. Учитель спрашивает: «Что можно сделать с числом 5, чтобы разместить в «Компьютере»?

 И дети предлагают заменить его двумя полосками с 3 и 2 кружочками. Учитель ставит в верхний карман полоску с 3 кружочками, а в нижний – с 2 (рис. 6, в). 

– Сколько овощей купила хозяйка? (12) 

– Что мы сделали со II слагаемым? 

– Заменили числами 3 и 2. Учитель обобщает: «Мы заменили II слагаемое – 5 суммой удобных слагаемых 3 и 2, чтобы 7 дополнить до 10, и прибавили 2. 

Учащиеся моделируют эту же задачу на своих «Компьютерах» с проговариванием. 

3. Построение знаковой модели при помощи «Линейки «Счет от 1 до 20». 

Учитель на демонстрационном пособии «Линейка «Счет от 1 до 20» строит знаковую модель задачи (рис. 7). 

                                                            Рис. 7. «Линейка «Счет от 1 до 20». 

Знаковая модель задачи. Учащиеся строят эту же модель при помощи индивидуальных «Линеек «Счет от 1 до 20», сопровождая свои действия рассуждениями (хором): «Чтобы к 7 прибавить 5, надо к 7 прибавить 3, получится 10, (на линейке дана подсказка – удобное слагаемое 3), и к 10 прибавить 2, получится 12. Действия и рассуждения детей письменно оформляются на доске и в тетрадях в виде развернутой записи: 

7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 12 

Таким образом, при последовательном использовании комплекса наглядных пособий формируется понятие о сложении однозначных чисел с переходом через десяток. 

При формировании вычислительного навыка мы должны стремиться к свертыванию информации, т.е. избавиться от промежуточного результата 10, ибо он тормозит процесс вычислений. Поэтому фундаментом вычислительных навыков при сложении и вычитании однозначных чисел с переходом через десяток является знание состава чисел 11,12,…,18. 

Алгоритм изучение состава чисел рассмотрим на примере числа 11. 

III. Состав числа 11 

1. Построение графической, цветовой и числовой модели состава числа 11.

 Работа с демонстрационным и индивидуальным пособием «Компьютер». Для ограничения 10 кружков на доске нужно провести вертикальную линию, а на парту положить лист бумаги, ограничивающий десяток. В процессе совместной учебной деятельности строится модель числа 11. Учитель прикрепляет полоски при помощи магнитов и рядом записывает равенства, учащиеся размещают полоски на парте (рис. 8). 

                    Рис. 8. Развернутые модели состава числа 11. 

Построение данных моделей позволяет за счет цвета и графики ярко и четко предъявить информацию и обеспечить переход от конкретного – к абстрактному. 

2. Закрепление знаний. Самостоятельная работа в тетради. 

Учащиеся в тетрадях по клеточкам вычерчивают карандашом модели числа 11 (рис. 9). 

Рис. 9. Запись в тетради. 

Эта работа дает возможность акцентировать внимание на том, что I слагаемые уменьшаются на 1, а II — увеличиваются на 1, а сумма остается без изменения, и многократно повторить систематизированную информацию, что является необходимым условием запоминания таблицы сложения. 

Полностью таблица представлена как справочный материал на правом клапане «Суперпапки». 

Для закрепления состава числа 11 можно составить целую серию задач с использованием таблиц «Сказочный счет».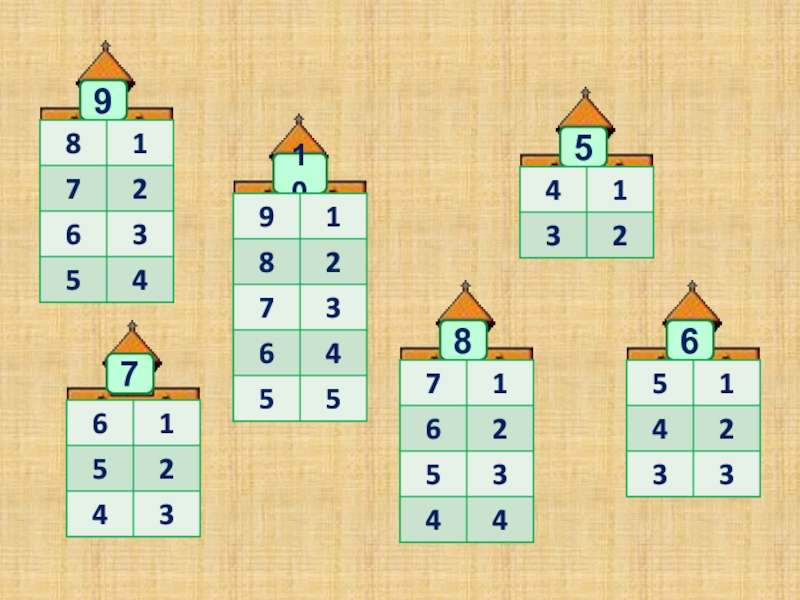 Например. «В гости к героям сказки «Волк и семеро козлят» пришли герои сказки «Сестрица Аленушка и братец Иванушка». Сколько стало героев сказок?» (9 + 2 = 11) и т. д. 

3. Применение полученных знаний на новых информационных полях и в новых ситуациях. Работа с демонстрационными пособиями «Радужная горка» и «Числовая горка». 

На иллюстрации к сказке «Про Козленка, который умел считать до десяти» из комплекта «Сказочный счет» изображен парусник, на парусе которого шариками представлены числа от 1 до 10, а на корпусе – числа от 11 до 20. 

Данную информацию можно использовать для закрепления знания состава числа. Работая в паре у доски, учащиеся устанавливают соответствие между а) парами шариков на парусе и числом 11 на корпусе парусника; б) парами шариков на парусе и парами чисел, составляющими число 11 в вертикальном столбике «Числовой горки». 

Обращается внимание на то, что из всех чисел, расположенных между 1 и 10, объединив их в пары, можно получить число 11. Эту зависимость дети видели при изучении состава чисел первого десятка.  

                                                                                        Рис. 10.  

На данном этапе было бы очень полезно составить задачи по моделям. Во-первых, мы замедлим темп урока, чтобы никто не отстал на самом важном этапе, а во-вторых, подключим воображение, фантазию, усилим ассоциативные связи.

 Например. 

1) В одной коробке лежало 9 простых карандашей, а в другой – 2 красных. Сколько карандашей в двух коробках? 

2) Для приготовления баклажанной икры повар взял 8 баклажанов и 3 помидора. Сколько всего овощей пошло на баклажанную икру? 

3) Для приготовления компота мама взяла 7 синих слив и 4 желтых. Сколько всего слив пошло на компот? 

4. Взаимопроверка знаний. Работа в парах. 

Учащиеся раскрывают «Суперпапку» и кладут ее на парту так, чтобы сверху были обе горки и клапан с таблицей сложения (рис. 11). 

Рис.11

1) Один ученик показывает кружочки: 9 серых и 2 красных кружочков, а другой – числа: 9 в сером квадрате и 2 в красном; 8 и 3 и т. д. Модели показываются сначала по порядку, а затем вперемешку. Проверяются по столбику выражений на клапане. Таким образом, они знакомятся с местом расположения данного столбика в системе знаний (рис. 10). Далее закрепление состава числа 11, обеспечивается переходом от абстрактного к конкретному, то есть от знаковой модели к предметной. 

2) Один ученик показывает — 9 + 2, а другой – 9 серых шариков и 2 красных и т.д. 

3) Один показывает на корпусе лодки число 11, а другой – на парусе 8 фиолетовых кружочков и 3 желтых и т.д. 

5. Проверка знаний учителем. Игра «Сигнальщики». 

На доске вывешивается «Цветовая сигнальная лента», в которой цвета радуги расположены по порядку, и рядом записываются соответствующие им числа, из которых можно составить число 11 – это 2, 3….9. 

Учитель, например, показывает число 8 или фиолетовый цвет на ленте, а учащиеся – оранжевую карточку (3). 

Итак, вся предыдущая работа была направлена на понимание и запоминание столбика таблицы сложения однозначных чисел с ответом 11, который является подсистемой в системе знаний.  

Работа над составом чисел 12, 13….18 проводится аналогично. 

Для проверки всей таблицы вывешивается «Цветовая сигнальная лента», в которой цвета радуги перемешаны, и рядом записываются по порядку числа 11, 12….18. 

Учитель, например, называет выражение 5 + 9 (или показывает зеленую и серую карточку из веера). 

Учащиеся видят, что число 14 написано рядом, например, с красным цветом и показывают красную карточку. (Цвет значения не имеет, он служит для обратной связи). 

Можно придумать много других игр и заданий. 

С огромным удовольствием дети работают с «Телефоном – справочником». Он же является самоучителем. 

При помощи «Квадрата с уголком», благодаря подвижной детали, можно построить всю таблицу сложения и вычитания. Многочисленные варианты работы с каждым пособием, входящим в комплект, описаны в методических рекомендациях. 

Эти учебно-наглядные пособия могут использоваться на всех этапах урока, в разных сочетаниях с другими средствами обучения, в том числе, и с учебником. Причем, детям предоставляется право выбирать наглядное пособие, при помощи которого можно выполнить то или иное задание из него. 

В начало статьи

Наглядные пособия

Главная

Состав чисел 10,11,12,13,14,15,16,17,18,19,20. Примеры и уравнения — Kid-mama — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7 — «Семья и Школа»

Содержание

Состав числа для дошкольников. Учимся раскладывать числа на части

К возрасту 5-6 лет ребёнок способен считать до 10 в прямом и обратном порядке, умеет пересчитывать и отсчитывать предметы, знает, как разложить числа на единицы, например, 4 равно 1, 1, 1 и 1. Это значит, что малыш уже готов осваивать состав числа до 10.

Аудио-версия статьи «СОСТАВ ЧИСЛА ДЛЯ ДОШКОЛЬНИКОВ» Тег audio не поддерживается вашим браузером. Скачать. СОСТАВ ЧИСЛА ДЛЯ ДОШКОЛЬНИКОВ

Содержание

Зачем учить состав числа

Как быстро научиться раскладывать числа на части 

• Действия с предметами
• Числовая линейка
• Наглядность
• Решение бытовых задач
• Знакомство с примерами

Игры и упражнения на закрепление состава чисел

• Сколько кругов?
• Прищепки
• Сколько в корзинке
• Числовые домики
• Упражнения на закрепление нескольких чисел
• Наглядный способ решения примеров

Советы для мам

В современной начальной школе детям приходится считать в уме. Лучше заранее научить дошкольников раскладывать числа на составные части. Знание состава числа позволит быстро справляться с примерами на сложение и вычитание. 

Зачем учить состав числа

После 5 лет можно знакомить дошкольников с составом чисел. Это нужно для заблаговременной подготовки к будущим урокам математики. Малыш уже способен понять, что каждое число, кроме единицы, состоит из двух меньших. 

К первому классу дети должны знать, что 10 можно разложить на 1 и 9, 5 и 5, 8 и 2, 7 и 3, 6 и 4, а 9 состоит из 5 и 4, 6 и 3 и так далее. Запомнив все парные сочетания в числах первого десятка, ребёнок с лёгкостью освоит сложение и вычитание. 

Научившись раскладывать числа на части, малыши легко справляются с примерами. Например, с такими: 2+3=5 или 4+1=5. Ребятишки знают, что состав числа 5 — это 2 и 3 или 4 и 1, поэтому считают быстро и без ошибок. 

Как быстро научиться раскладывать числа на части

Справиться с решением задачи вам поможет знание простых принципов. Чтобы малышу было понятней, всегда применяйте элемент игры и наглядность. Каждое занятие посвящайте одному числу. 

Обучение ребёнка разбейте на несколько этапов, переходя от простого к более сложному: 

Действия с предметами

В самом начале дошкольникам объясняют состав числа с помощью знакомых вещей. Можно раскладывать орешки, жёлуди, камешки и прочие однотипные предметы.

Числовая линейка

Для запоминания состава числа и решения примеров пригодится обычная линейка.

Допустим, нужно сложить 4 и 2. Малыш ставит пальчик или карандашик на первое из чисел — 4 и перемещает его на 2 деления вправо, до цифры 6.

Важно донести до ребёнка принцип: если нужно сложить два числа, двигаем палец вправо. Когда вычитаем, то перемещаем влево.

Аналогичные действия выполняют с числовыми лучами. 

Наглядность

Разместите в детской комнате красочные изображения числовых домиков и картинки с составом чисел. Обращайте на них внимание малыша, делайте пояснения. Благодаря зрительной памяти, информация усвоится быстрее.

Решение бытовых задач

Дети хорошо усваивают знания, необходимые в повседневной жизни. Накрывая на стол, положите 1 ложку. Спросите малыша, сколько нужно добавить ложек, если в доме 4 человека. 

Последует ответ ― 3. Значит, число 4 состоит из двух частей: 1 и 3. Принеси ложки и проверь. Как ещё их можно разложить? Правильно, 2 и 2. 

Знакомство с примерами

Когда дошкольник запомнит состав чисел, переходите к примерам. 

Используйте карточки с цифрами и знаками «плюс», «минус», «равно». Покажите малышу, как путём сложения и вычитания получить число 8 (2+6=8, 10—2=8) или другое. Постепенно у ребёнка сформируется представление о примерах.

Игры и упражнения на закрепление состава чисел

Регулярно занимаясь, дети быстро запоминают состав чисел до 10. Более сложная задача ― научиться раскладывать числа на части, понять, как это делается. В этом поможет подборка математических игр.  

Сколько кругов?

В качестве наглядного пособия предлагаем использовать набор двусторонних карточек с кружочками. Одна сторона у них синего цвета, другая красного. Показываем малышу карточку с пятью красными кругами. 

«Сосчитай количество кругов (5). 

Один повернём синей стороной, сколько осталось красных (4)?  

Запомни, число 5 состоит из двух частей — 4 и 1. Давай посмотрим, каким ещё может быть состав числа 5». Поочерёдно переворачиваем все круги, комментируя свои действия. 

Прищепки

Для игры, кроме карточек с цифрами до 10, пользуемся бельевыми прищепками. Их можно заменить канцелярскими скрепками. Число 1 приравниваем к одной прищепке, 2 ― к двум и так до десяти. 

Берём карточку с цифрой 4, прицепляем 4 прищепки с одной из сторон. Спрашиваем ребёнка: «Сколько всего прищепок? (4). Сейчас разделим число 4 на 2 части. Здесь оставляем три прищепки, на противоположной стороне прикрепим одну. Как ты думаешь, из каких частей состоит число 4? (3 и 1)».  

Покажите, как можно разделить иначе: 2 и 2. Упражняйтесь со всеми числами первого десятка. Чтобы сделать состав числа понятным для дошкольников, возьмите прищепки либо скрепки двух цветов. Игра развивает математическое мышление и моторику. 

Сколько в корзинке

Подготовьте комплекты карточек с числами от 1 до 10, их можно сделать самим. Ещё вам понадобятся 8 коробок, мисок или ведёрок. На каждой ёмкости нарисуйте число с трёх до десяти. 

Объясните ребёнку, что во все миски нужно положить по 2 цифры или карточки. Если сложить их вместе, должно получиться нарисованное число. Покажите пример: в миску с числом 6 можно положить цифры 5 и 1, 3 и 3, 2 и 4. Задача малыша ― применить одно из возможных сочетаний. 

Сначала играйте по очереди, чтобы кроха понял, как правильно действовать. Если ребёнок легко справляется, усложните задание: попросите использовать все комбинации. 

Числовые домики

Игра поможет дошкольникам запомнить состав чисел первого десятка. В качестве наглядного пособия используют 9 числовых домиков из нескольких этажей: от 2 до 10. Их можно скачать тут. 

Расскажите малышу, что у домиков есть хозяева — числа, нарисованные на крыше. На каждом этаже 2 квартиры (два окошка). Общее количество жильцов одного этажа должно совпадать с числом на крыше. Тогда хозяин разрешит поселиться. 

Покажите ребёнку, как заселить домик, где хозяйка цифра 4. Комментируйте ваши действия: «На первом этаже будут жить 0 и 4, вместе получим 4. На втором — пара 2 и 2, а на третьем (3 и 1)?» Спросите малыша, из каких чисел ещё состоит 4. 

Затем предложите крохе самому заселять домики, начав с первого этажа.

Учите рассуждать вслух, сколько жильцов должно быть в каждой квартире? На первых занятиях можно применять счётные палочки. Играя с домиками, дети быстро научатся раскладывать числа на части. 

Упражнения на закрепление нескольких чисел

Закрепить навыки счёта поможет подборка упражнений с картинками. Все задания можно скачать здесь.  

Помоги корабликам найти свою пристань. На борту кораблей написаны по 2 цифры, образующие состав числа одной из пристаней внизу рисунка. Применив сложение или вычитание, ребёнок сможет найти пристань для каждого кораблика. Например, к пристани с числом 5 идут корабли, на которых написано 4+1 и 3+2. Путь лучше начертить карандашом. 

Разложи на две части. Например, на картинке 10 яблок и 5 пар тарелок. Задача малыша – разложить яблоки так, чтобы в каждой паре их было 10. Повторяться нельзя. Другие задания:

Домики с пустыми квартирами. Ребёнку нужно вписать правильное число в каждую клеточку. 

Похожее задание выполняют в упражнении «Числовой ряд» . Если кроха пока не умеет рисовать цифры, попробуйте применить карточки. 

Скачать задания

Наглядный способ решения примеров

Использование счётных карточек и обычных предметов поможет научиться раскладывать числа на части. Наглядные действия облегчают выполнение заданий. Вот как можно решить пример с помощью любых орешков. 

Скажите малышу, что белочка нашла 6 орешков. Ей нужно спрятать одну часть в дупло, а другую в норку. Как их разложить? Покажите ребёнку все возможные комбинации: 3 и 3, 2 и 4, 5 и 1. Используйте карточки. 

Для изучения состава числа с дошкольниками подготовьте тетрадь в клетку и 2 карандаша разных цветов. Нарисуйте на странице шесть полосок размером 1 на 6 клеточек. Рядом напишите примеры. 

Закрашивая клеточки в полосках, малыши видят, как квадратики одного цвета убывают, а другого прибавляются. 

Советы для мам

Понять, что такое состав числа дошкольникам довольно сложно. Вам помогут игровые приёмы и маленькие хитрости: 

1. На прогулке, в магазине и дома используйте любую возможность для практического применения счёта. Решайте бытовые задачки. Старайтесь, чтобы малышу было интересно.

2. В начале освоения нового материала разрешите считать с помощью привычного «калькулятора» — пальчиков. Постепенно приучайте ребёнка к счёту в уме. При систематических занятиях вопрос: «4 это 1 и сколько?» и ему подобные не вызовет затруднений.

3. Поделитесь с малышом «большим секретом»: в состав каждого числа входит единица и предыдущее число.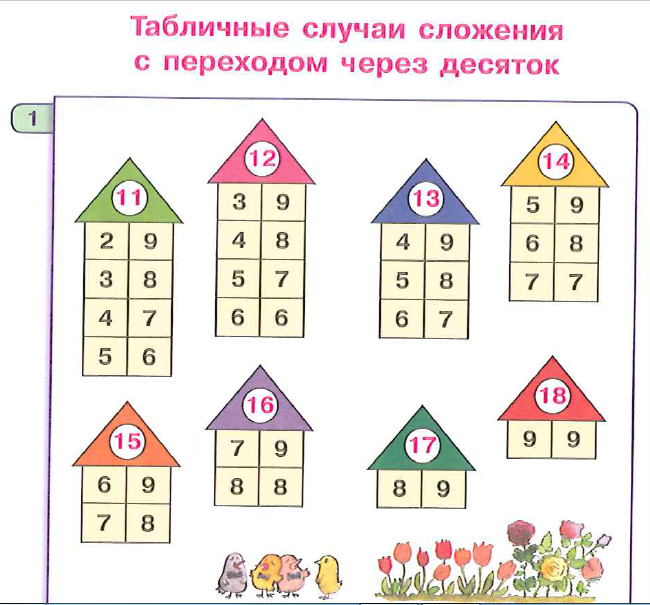 Например, 6 — это 1 и 5, 9 — 1 и 8. Так дети быстро научатся раскладывать числа на части и легче освоят вычитание. «Сколько будет, если от 9 отнять 1?» Ответ — 8.

4. Дошкольникам нравится меняться с мамой ролями, задавать аналогичные вопросы. Предоставьте возможность проявить инициативу, поощряйте самостоятельность будущих первоклашек. Устраивайте соревнования на скорость решения примеров.

В заключение повторим, что прочное запоминание состава чисел возможно лишь при условии регулярных упражнений. Чтобы ребёнок не утратил интерес к занятиям математикой, фантазируйте, меняйте игры и радуйтесь успехам малышей. 

Состав числа. Не может запомнить

1. Форум
2. Архив
3. Детская психология и развитие

Дочка в первом классе. Весь прошлый год делали примеры на состав числа. В школе тоже примеры — не запоминает, считает на пальцах, а в школе не разрешают на пальцах. Какой выход — заучивать, как таблицу умножения? Проблема только с этим, все остальные задания без проблем. Немного расстраиваюсь по этому поводу — сегодня поставили первые оценки, русский — 5, математика — между 3 и 4.

у сына такая же проблема. Все предметы — отлично, математика между 3 и 4. Уже во втором классе. Заучивать тоже не получается. Какой-то не понятный случай. В пределах 10 считает очень медленно, но вот двузначные числа складывает намного лучше. Я уже ему сама говорю — считай на пальцах — он не считает,стыдится и сидит тупит.
Какая-то незрелось каких-то отделов головного мозга видимо(((

Попробуйте в игровой форме его автоматизировать.
Есть очень много игр — и Pig 10, и Халли-Галли, и Крипто, и Pop for addition and substraction, и 7 eat 9.
Интересные игры описаны в книге для дошкольников у Жени Кац — с пальцами, но для показа пальцев нужны вычисления и ребенок все-таки запоминает.

может вам поможет, себе сохранила. Интересно.
http://www.pedlib.ru/Books/3/0318/3_0318-64.shtml#book_page_top

а здесь игры
http://www.familyeducation. ru/?module=forum&action=topic&id=48

Спасибо. Попробую.

а по числовой линейке считает? мои тоже в 1 классе, считают и на пальцах и по линейке. частенько задаю им примеры в устной форме. 6+4? 10! 10-4? аааа???? тупит! опять спрашиваю 6+4? 10! 10-4? ….6! а 10-6? ……? опять зависла….

По числовой линейке мы с ней целый год считали по тетрадям Ломоносовской школы. Все, что наглядно — она считает, как только в уме — полный провал.

Будем пытаться — главное теперь время найти, из школы приезжает в 4-6, по два часа тратим на домашнее задание. Вообще я думала, что ничего страшного в том, что дочка плохо знает состав числа, нет — в школе нагонит, оказывается нет, как-то быстренько они его пробежали за два с половиной месяца.

вот и у нас такая проблема уже второй год, а чтоб заниматься конкретно и в системе — ни как времени не можем изыскать. ((

Так их и надо именно наизусть..

спасибо! по первой ссылке упражнения не все понятны.. а на основе некоторых, так понимаю, созданы некоторые занятия для детей?

Да, заучивать. У нас была книга Узоровой — там куча однотипных примеров на состав числа, что помогает их проще заучить.

Я в шоке, никогда не учила сыновей такому. В жизни бы не подумала, что это сложно.

и я бы в жизни не подумала, если бы не мой младший сын((
Он сам удивляется, говорит что счет до 10 у него вызывает трудности, но вот сейчас занимаемся — прошу сложить 50 и 70 он с ходу отвечает 120. Но будет задумываться и тупить, если прошу сложить 5 и 7.

А про таблицу умножения есть спец-методики? А то у меня уже скоро нервный срыв будет от попыток научить ребенка. Учим, все запоминает, отвечает, а на следующий день девственно чистый мозг

Усачева пробовали? http://www.debotaniki.ru/2011/02/tablitsa-umnozheniya-v-stihah/

Спасибо, попробуем!

Жуть. У нас еще ни оценок, ни домашек. По теме — я б плакаты с составом числа нарисовала и кругом по дому развесила. Ну, и внимание ребенка на них обращать регулярно.

Кто-то более зрелый в этом плане и само собой легко идет, а кто-то не дозрел, тем сложно и надо помогать.

Со второй помнится мы учили.

Через неделю, а то и меньше, эти плакаты превращаются в обои, и ребенок на них не обращает внимания. Проверено.

Так за неделю есть шанс подтянуть. Потом, надо ж напоминать. Например, сели завтракать, спросили несколько примеров, если надо ребенок подсмотрел. Собираемся делать уроки — опять погоняли и т.д.

Именно зубрить надо. Нам в школе так и говорили. Я объясняла логически почему так, а не иначе. Приводила пример весов. На одной части прибавилось, на другой убавилось.

Вода камень точит. а вообще, советуют с 9 учить в обратном порядке. С младшим именно так и будем делать.

Да я уже пыталась во всяких порядках Он может наизусть пересказать любой мультик про смешариков, а их там штук двести, и не то, чтоб он их смотрел без перерыва, но ведь помнит.

Память есть, но почему-то на таблицу умножения он ее тратить не хочет.

Пример: говорю скажи вслух 10 раз 7Х8=56. Сказал. Потом спрашиваю, сколько будет 3Х3. Отвечает.

Задаю каверзный вопрос «А 7Х8 сколько?». «Не помню».

Заучивать.

Необходимо продолжить дома заниматься на наглядных примерах. Например, 6+4, сказать было 6 конфет дали еще 4 сколько стало, ребенок должен ответить, потом съела три, сколько осталось и т.п.брать реальные предметы не надо, просто их представлять в уме, сразу после этого все закрепить записанными действиями в математическом виде. Мы еще играли настоящими монетами, если отвечал сразу правильно забирал монеты себе. Заучить то можно, но лучше, если у заученного материала есть образное подкрепление, ребенок может в уме представлять что складывается (хоть на пальцах).

Состав числа действительно нужно заучить очень хорошо. Эти знания жизненно необходимы при решении примеров на сложение и вычитание.

Для того чтобы хорошо запомнить состав числа надо просто очень много раз повторить пары составляющие это число. Есть приложение для iPad и iPhone которое облегчает ребенку этот процесс превращая его в игру с привлекательными фишками и звуками. Приложение уже опробовано многими пользователями в течении нескольких лет. Это приложение несмотря на его простоту очень эффективно, о нем очень хорошо отзываются специалисты в Сингапуре, и его используют в своей практике многие образовательные учереждения по всему миру. Специально для посетителей eva.ru мы дарим 5 подарочных промокодов для этого приложения:
NR74EHTXJWR4
EX3R9R7KW6NL
LJETJTMH97KP
XHA4MNRMNF96
N4LAR3MRXXE7
Вы можете скачать его в App Store:
https://itunes.apple.com/ru/app/id575132700?mt=8

Для лучшего эффекта стимулируйте ребенка на прохождение игры и обязательно повторите прохождение через пару дней.

Открыть тему в окнах

Знаменитости в тренде

Хоть в суп, хоть в хлеб: четыре полезных блюда с тыквой

Российский сериал получил приз за лучший сценарий на фестивале в Испании

День святых и другие праздники: подборка фильмов о традициях в разных странах мира

Что такое составные числа? Определение, список, примеры, факты

В математике составные числа можно определить как числа, имеющие более двух делителей. Числа, которые не являются простыми, являются составными числами, потому что они делятся более чем на два числа.

Тест на делимость — это стандартный метод, используемый для нахождения составного числа. В этом тесте данное число делится на меньшее простое или составное число. Если оно полностью делится, число является составным числом.

Составные числа с нечетной цифрой на месте единицы являются нечетными составными числами. Проще говоря, все нечетные числа, не являющиеся простыми, являются нечетными составными числами. Например: 9, 15, 21 и т. д.

Составные числа с четной цифрой на месте единицы являются четными составными числами. Проще говоря, все четные числа, кроме 2, являются четными составными числами. Это потому, что никакое четное число (кроме 2) никогда не может быть простым числом.

Среди заданных чисел 179 не делится ни на одно число, кроме 1 и 179.; следовательно, это не составное число. 144 делится на 2, значит, это составное число.

1 Какое из следующих составных чисел является наименьшим? 9 11 14 2 Правильный ответ: 9 9 — наименьшее составное число. Оно имеет более двух делителей: 1, 3 и 9. 2 Какое из следующих чисел не является составным? 15 21 25 23 Правильный ответ: 23 23 не является составным числом. Он делится только на 1 и самого себя. 3 Какое из следующих чисел является составным? 11 13 17 20 Правильный ответ: 20 20 — составное число. Оно делится более чем на два множителя: 1, 2, 4, 5, 10 и 20. 4 Какое самое большое составное число из следующих? 47 33 35 39 Правильный ответ: 39 39 — наибольшее составное число среди всех вариантов, делителями которых являются 1, 3, 13 и 39. 47 — простое число.

Заключение
Составное число — это положительное целое число, которое делится на меньшие положительные целые числа, кроме 1 и самого себя. Составные числа можно определить с помощью метода делимости. Посетите SplashLearn, игровую обучающую платформу, чтобы найти больше интересных упражнений на составные числа.

Может ли число быть одновременно простым и составным?

Нет, число не может быть одновременно простым и составным. Простое число имеет ровно два делителя, 1 и само себя, а составное число имеет более двух делителей. Итак, все натуральные числа (кроме 1) либо простые, либо составные, но не то и другое вместе.

Является ли 0 составным числом?

Любое число, умноженное на ноль, дает произведение 0. Следовательно, 0 имеет бесконечное число множителей. Чтобы быть составным, число должно иметь более двух делителей, но не бесконечное их число. Следовательно, 0 не может считаться составным числом.

Какое самое маленькое составное число?

4 — наименьшее составное число.

Все ли четные числа составные?

Нет. Все четные числа, кроме 2, являются составными числами.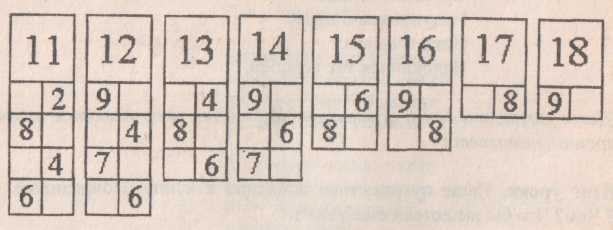 2 имеет только два делителя: 1 и 2.

Объяснение простых и составных чисел

В математике очень важно понимать разницу между простыми и составными числами. В то время как составные числа — это числа с более чем двумя делителями. Они просто противоположны простым числам. Простые числа — это те, которые имеют только два делителя, то есть 1 и само число. Простое число всегда натуральное число. Все натуральные числа, не являющиеся простыми, попадают в категорию составных чисел. Итак, составные числа делятся более чем на два числа. В этой статье мы узнаем следующее:

• Что такое простые и составные числа?
• Разница между простыми и составными числами
• Свойства простых и составных чисел
• Как определить простые и составные числа
• Факты о простых и составных числах
• Список составных чисел
• Таблица простых и составных чисел
0 9013 Что такое 9013 Простые числа?

Простое число — это положительное целое число. У него ровно два делителя: 1 и само число. Итак, если n — простое число, его делители будут равны 1 и самому n. Мы также можем определить простое число как число, которое является целым положительным числом и не является произведением любых двух других положительных целых чисел, кроме самого числа и 1.  9(82 589 933) — 1 — самое большое простое число за последнее время. Математики все еще находят больше.

Простые числа-близнецы
Простые числа, разность которых равна двум, являются простыми числами-близнецами. Например, 3 и 5, 5 и 7, 11 и 13 — это наборы простых чисел-близнецов. Другими словами, это два последовательных простых числа, между которыми находится только одно число. Взаимно простые числа
Взаимно простые числа — это два числа, у которых есть только 1 в качестве общего делителя. Например, 2 и 3, 4 и 5, 3 и 7, 4 и 9.являются взаимно простыми числами.

Свойства простых чисел

Ниже приведены некоторые свойства простых чисел:

• Каждое простое число больше 1 делится хотя бы на одно простое число.
• Каждое положительное целое число, четное и превышающее 2, можно представить в виде суммы двух простых чисел.
• 2 — единственное четное простое число.
• Все простые числа нечетные, кроме 2.
• Два простых числа взаимно просты друг с другом.
• Каждое составное число можно разложить на простые множители.

Список простых чисел

Ниже приведен список простых чисел от 1 до 100. Учащиеся могут понять концепцию простых чисел из этого списка и создать список, превышающий 100, для практики.

Список простых чисел

2, 3, 5, 7, 1, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Что такое составные числа?

В отличие от простого числа, составное число — это число, имеющее более двух делителей.

Мы можем определить составные числа как числа, которые могут быть получены путем умножения двух наименьших положительных целых чисел и содержат по крайней мере еще один делитель в дополнение к числу «1» и самому себе. Все четные числа больше 2 входят в число многих примеров составных чисел.

Итак, все ли четные числа составные?

Нет, 2 — четное простое число. На самом деле, это единственное четное число, которое является простым. Следовательно, мы не можем сказать, что все четные числа являются составными числами.

Типы составных чисел

Композитные числа составляют два типа:

• Нечетные составные номера
• Даже составные номера

нечетные составные числа

Все нечетные числа больше 1, которые не являются prime, нечетные композитные числа

. .

Примерами нечетных составных чисел являются 9, 15, 21 и другие.

Четные составные числа

Четные составные числа включают все четные целые числа, не являющиеся простыми числами.
Примерами четных составных чисел являются 4, 6, 8, 10 и другие.

Свойства составных чисел

Составные числа обладают следующими свойствами:

• Каждое составное число имеет более двух делителей
• Делители составных чисел без остатка
• Составные числа тоже являются своими факторами.
• 4 — наименьшее составное число
• Каждое составное число имеет как минимум два простых числа в качестве сомножителей.
• Составное число делится и на другие составные числа.

Список составных чисел

Ниже приведен список всех составных чисел от 1 до 100. Из этого списка учащиеся могут понять концепцию составных чисел и составить список, превышающий 100, для практики.

Список составных номеров

4. 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100

Как найти составные числа?

Вы должны найти множители числа, чтобы определить, является ли оно составным. Если множителей больше двух, то число составное. Мы можем выполнить тест на делимость, чтобы определить, является ли число простым или составным.

В тесте на делимость мы делим число на общие множители, такие как 2, 3, 5, 7, 11 и 13. Если эти множители не могут полностью разделить число, то это число является простым числом. Например, 22 делится на 2, что означает, что оно имеет делитель 2, отличный от 1 и 22. Следовательно, 22 — составное число.

Как найти простые числа?

Существует два метода, помогающих определить, являются ли данные числа простыми или составными.

Метод 1:

Любое простое число, кроме 2 и 3, можно записать в виде 6n + 1 или 6n – 1, где n — натуральное число.

Например:

6(1) – 1 = 5

6(1) + 1 = 7

Метод 2:

Для определения числа больше 40 как простого числа мы можем использовать по следующей формуле:

n2 + n + 41, где n= 0, 1, 2, ….и выше.

Например:

(0)2 + 0 + 41 = 41

(1)2 + 1 + 41 = 43

(2)2 + 2 + 41 = 47

Разница между простыми и составными числами

Существует множество различий между простыми и составными числами. В следующих таблицах перечислены некоторые ключевые различия между ними.

Простые числа	Составные числа
У них есть 2 множителя. Единица и само число.	У них более двух факторов.
Можно записать в виде произведения двух чисел.	Они могут быть записаны как произведение двух или более чисел
Пример: Делители 7 равны 1 и 7.	Пример: Делители 6 равны 1, 2, 3 и 6

Таблица простых и составных чисел

Ранее математики использовали числовые таблицы для записи всех простых чисел или простых факторизаций. Решето Эратосфена представляло собой список простых чисел. Этот метод обеспечивает карту-карту Эратосфена.
На следующей диаграмме простые числа до 100 показаны в цветных прямоугольниках. Все числа, кроме цветных прямоугольников, являются составными числами.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	. Разное

Столы с 11 по 20

АКЦИЯ НА 30 ДНЕЙ | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*

*T&C Apply

LearnPracticeDownload

Таблицы с 11 по 20 представляют собой список чисел, кратных от 11 до 20. Таблицы умножения с 11 по 20 помогут вам легко выучить и попрактиковаться в умножении. Это может быть чрезвычайно полезно при решении математических задач и расчетов. Таблица с 11 по 20 необходима учащимся для быстрого выполнения математических расчетов.

1.	Столы с 11 по 20
2.	Таблицы с 11 по 20 Скачать PDF
3.	Часто задаваемые вопросы по таблицам с 11 по 20

Таблицы с 11 по 20

Математические таблицы с 11 по 20 важны для основных расчетов, используемых при умножении и делении. Давайте выучим таблицы с 11 по 20 для всех чисел и вместе улучшим наши арифметические навыки.

Таблицы умножения от 11 до 20 PDF

Учащимся рекомендуется тщательно выучить эти таблицы с 1 по 10 для более быстрого выполнения математических расчетов. Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.

 

☛ Таблицы с 11 по 20 Скачать PDF

Таблицы с 11 по 20 Примеры

1. Пример 1: Клиент покупает 4 апельсина каждый день. Сколько апельсинов покупатель купит через 18 дней?

   Решение:

   Клиент покупает 4 апельсина в день. Следовательно, используя таблицы с 11 по 20, общее количество апельсинов, купленных покупателем за 18 дней, равно 4 × 18 = 72 апельсина.

2. Пример 2: Уолтер зарабатывает 20 долларов в час. Сколько денег он заработает, если будет работать 13 часов?

   Решение:

   Уолтер зарабатывает 20 долларов в час. Следовательно, используя таблицы с 11 по 20, общее количество денег, заработанных Уолтером за 11 часов, составляет 20 × 11 = 220 долларов.

3. Пример 3: Джонатан делает 10 кексов в день. Сколько кексов он испек за 13 дней?

   Решение:

   Джонатан печет 10 кексов в день. Следовательно, используя таблицы с 11 по 20, общее количество кексов, приготовленных через 13 дней, равно 10 × 13 = 130 кексов.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Записаться на бесплатный пробный урок

Часто задаваемые вопросы по таблицам с 11 по 20

Найдите значение 19, умноженное на 6, используя таблицы с 11 по 20.

Значение 19, умноженное на 6, из таблиц с 11 по 20 равно 19 × 6 = 114

Оцените, сколько раз нужно умножить 19, чтобы получить 76.

Используя таблицы с 11 по 20, мы имеем 19 × 4 = 76. Следовательно, 19 нужно умножить на 4, чтобы получить 76.

Сколько будет 15 умножить на 7 минус 4 плюс 5?

Из таблиц с 11 по 20 15 умножить на 7 равно 105. Следовательно, 15 × 7 — 4 + 5 = 105 — 4 + 5 = 106

Используя таблицы с 11 по 20, найдите значение 6 плюс 13 умножить на 3 минус 13 умножить на 8.

Из таблицы 13, 13 умножить на 3 = 39 и 13 умножить на 8 = 104. Следовательно, 6 + 13 × 3 — 13 × 8 = -59.

☛ Статьи по теме:

Скачать БЕСПЛАТНО учебные материалы

Рабочие листы таблицы умножения

Рабочие листы по математике и
наглядный учебный план

Таблицы от 1 до 20 — Таблицы умножения от 1 до 20

Таблицы с 1 по 20 являются список таблиц умножения. Таблица состоит из кратных целых чисел от 1 до 20. Математические таблицы от 1 до 20 помогут учащимся быстро решать задачи на умножение. Поскольку таблица 1 возвращает одно и то же значение (поскольку все числа умножаются на 1), мы можем пропустить ее и запомнить таблицы с 2 по 20 . Студенты могут сначала выучить математические таблицы от 1 до 10, а затем перейти к таблицам умножения больших чисел. Мы предоставили здесь советы и рекомендации по запоминанию таблиц для облегчения учащихся.

Запоминание таблиц умножения от 1 до 20 служит строительным блоком для связанных математических понятий, таких как деление, дроби, длинное умножение и алгебра, преподаваемые в начальной школе. Загружаемые PDF-файлы каждой таблицы приведены в конце статьи, чтобы помочь учащимся легко учиться и улучшать свои навыки решения проблем.

Содержание: Математические таблицы с 1 по 20 Таблицы с 1 по 5 Таблицы с 6 по 10 Таблицы с 11 по 15 Таблицы с 16 по 20 Таблицы с 2 по 20 (PDF) Таблица умножения Таблица Советы по запоминанию таблицы умножения Зачем учить таблицу умножения Примеры Часто задаваемые вопросы

Математические таблицы с 1 по 20

Математические таблицы от 1 до 20 являются основой арифметических вычислений, наиболее широко используемых при умножении и делении. Таблица 1 даст исходное число. Умножение любого числа на 1 дает исходное число. Например, 1× ‌5 = 5, 1× ‌9 = 9 и так далее.

Учащимся предлагается выучить таблицы с 1 по 10, так как это помогает решать основные задачи. Таблицы с 2 по 20 помогут им решить сложные вычисления. Таким образом, изучение таблицы умножения от 1 до 20 поможет учащимся:

• Для быстрого решения проблем
• Во избежание ошибок в расчетах

Примечание:

• Любое число, умноженное само на себя, дает квадрат числа.
• Сложение любых чисел «n» раз аналогично умножению числа на «n». Например, сложение числа 5 5 раз дает 25. (т. е.) 5+5+5+5+5 = 25. Что также равно 5, умноженному на 5, равно 25.

Ниже приведен полный список от 1 до 20 таблиц до 10 раз.

Таблицы с 1 по 5 Таблица 1 Таблица из 2 Таблица из 3 Таблица из 4 Стол из 5 1 ×‌ 1 = 1 2 ×‌ 1 = 2 3 × ‌1 = 3 4 × ‌1 = 4 5 × ‌1 = 5 1 ×‌ 2 = 2 2 ×‌ 2 = 4 3 × ‌2 = 6 4 × ‌2 = 8 5 × ‌2 = 10 1 × ‌3 = 3 2 × ‌3 = 6 3 × ‌3 = 9 4 × ‌3 = 12 5 × ‌3 = 15 1 × ‌4 = 4 2 × ‌4 = 8 3 × ‌4 = 12 4 × ‌4 = 16 5 × ‌4 = 20 1 × ‌5 = 5 2 × ‌5 = 10 3 × ‌5 = 15 4 × ‌5 = 20 5 × ‌5 = 25 1 × ‌6 = 6 2 × ‌6 = 12 3 × ‌6 = 18 4 × ‌6 = 24 5 × ‌6 = 30 1 × ‌7 = 7 2 × ‌7 = 14 3 × ‌7 = 21 4 × ‌7 = 28 5 × ‌7 = 35 1 × ‌8 = 8 2 × ‌8 = 16 3 × ‌8 = 24 4 × ‌8 = 32 5 × 8 = 40 1 × ‌9 = 9 2 × ‌9 = 18 3 × ‌9 = 27 4 × ‌9 = 36 5 × 9 = 45 1 × ‌10 = 10 2 × ‌10 = 20 3 × ‌10 = 30 4 × ‌10 = 40 5 × 10 = 50 Таблица с 6 по 10 Стол из 6 Стол из 7 Таблица из 8 Таблица из 9 Таблица из 10 6 × 1 = 6 7 × 1 = 7 8 × 1 = 8 9 × 1 = 9 10 × 1 = 10 6 × 2 = 12 7 × 2 = 14 8 × 2 = 16 9 × 2 = 18 10 × 2 = 20 6 × 3 = 18 7 × 3 = 21 8 × 3 = 24 9 × 3 = 27 10 × 3 = 30 6 × 4 = 24 7 × 4 = 28 8 × 4 = 32 9 × 4 = 36 10 × 4 = 40 6 × 5 = 30 7 × 5 = 35 8 × 5 = 40 9 × 5 = 45 10 × 5 = 50 6 × 6 = 36 7 × 6 = 42 8 × 6 = 48 9 × 6 = 54 10 × 6 = 60 6 × 7 = 42 7 × 7 = 49 8 × 7 = 56 9 × 7 = 63 10 × 7 = 70 6 × 8 = 48 7 × 8 = 56 8 × 8 = 64 9 × 8 = 72 10 × 8 = 80 6 × 9 = 54 7 × 9 = 63 8 × 9 = 72 9 × 9 = 81 10 × 9 = 90 6 × 10 = 60 7 × 10 = 70 8 × 10 = 80 9 × 10 = 90 10 × 10 = 100 Таблицы с 11 по 15 Таблица из 11 Таблица из 12 Таблица из 13 Таблица из 14 Таблица из 15 11 ×‌‌ 1 = 11 12 ×‌ 1 = 12 13 ×‌ 1 = 13 14 ×‌ 1 = 14 15 ×‌ 1 = 15 11 ×‌‌ 2 = 22 12 ×‌ 2 = 24 13 ×‌ 2 = 26 14 ×‌ 2 = 28 15 ×‌ 2 = 30 11 ×‌‌ 3 = 33 12 ×‌ 3 = 36 13 ×‌ 3 = 39 14 ×‌ 3 = 42 15 ×‌ 3 = 45 11 ×‌ 4 = 44 12 ×‌ 4 = 48 13 ×‌ 4 = 52 14 ×‌ 4 = 56 15 ×‌ 4 = 60 11 ×‌ 5 = 55 12 ×‌ 5 = 60 13 ×‌ 5 = 65 14 ×‌ 5 = 70 15 ×‌ 5 = 75 11 ×‌ 6 = 66 12 ×‌ 6 = 72 13 ×‌ 6 = 78 14 ×‌ 6 = 84 15 ×‌ 6 = 90 11 ×‌ 7 = 77 12 ×‌ 7 = 84 13 ×‌ 7 = 91 14 ×‌ 7 = 98 15 ×‌ 7 = 105 11 ×‌ 8 = 88 12 ×‌ 8 = 96 13 ×‌ 8 = 104 14 ×‌ 8 = 112 15 ×‌ 8 = 120 11 ×‌ 9 = 99 12 ×‌ 9 = 108 13 ×‌ 9 = 117 14 ×‌ 9 = 126 15 ×‌ 9 = 135 11 ×‌ 10 = 110 12 ×‌ 10 = 120 13 ×‌ 10 = 130 14 ×‌ 10 = 140 15 ×‌ 10 = 150 Таблицы с 16 по 20 Таблица из 16 Таблица из 17 Таблица из 18 Таблица из 19 Таблица из 20 16 ×‌ 1 = 16 17 ×‌ 1 = 17 18 ×‌ 1 = 18 19 ×‌ 1 = 19 20 ×‌ 1 = 20 16 ×‌ 2 = 32 17 ×‌ 2 = 34 18 ×‌ 2 = 36 19 ×‌ 2 = 38 20 ×‌ 2 = 40 16 ×‌ 3 = 48 17 ×‌ 3 = 51 18 ×‌ 3 = 54 19 ×‌ 3 = 57 20 ×‌ 3 = 60 16 ×‌ 4 = 64 17 ×‌ 4 = 68 18 ×‌ 4 = 72 19 ×‌ 4 = 76 20 ×‌ 4 = 80 16 ×‌ 5 = 80 17 ×‌ 5 = 85 18 ×‌ 5 = 90 19 ×‌ 5 = 95 20 ×‌ 5 = 100 16 ×‌ 6 = 96 17 ×‌ 6 = 102 18 ×‌ 6 = 108 19 ×‌ 6 = 114 20 ×‌ 6 = 120 16 ×‌ 7 = 112 17 ×‌ 7 = 119 18 ×‌ 7 = 126 19 ×‌ 7 = 133 20 ×‌ 7 = 140 16 ×‌ 8 = 128 17 ×‌ 8 = 136 18 ×‌ 8 = 144 19 ×‌ 8 = 152 20 ×‌ 8 = 160 16 ×‌ 9 = 144 17 ×‌ 9 = 153 18 ×‌ 9 = 162 19 ×‌ 9 = 171 20 ×‌ 9 = 180 16 ×‌ 10 = 160 17 ×‌ 10 = 170 18 ×‌ 10 = 180 19 ×‌ 10 = 190 20 ×‌ 10 = 200

Изучайте математические таблицы от 1 до 100 здесь, в BYJU’S.

Калькуляторы очень помогают при сложных вычислениях. Однако использование калькулятора для простых математических расчетов не является правильным способом. Это снизит навыки решения проблем у студентов, и они не будут достаточно уверенными, чтобы решать такие задачи в будущем. Поэтому всегда рекомендуется запоминать базовые таблицы умножения от 1 до 10. Для решения сложных задач учащимся предлагается выучить таблицы от 2 до 20.

Нет ничего лучше, чем полагаться на свою память. Запоминание таблицы умножения не только дает чувство уверенности в себе, но и позволяет держать информацию под рукой, чтобы быстро использовать ее в случае необходимости. Он укрепляет память учащихся, стимулирует у них способ наблюдения и удержания вещей. Учащиеся, освоившие таблицу умножения от 1 до 20, обнаруживают, что их скорость вычислений увеличилась, что положительно сказывается на их уверенности в математике.

Таблица умножения от 1 до 20

Математические таблицы также считаются таблицами умножения, потому что каждая таблица получается, когда мы умножаем определенное число на все числа для счета, т. е. 1, 2, 3, 4, 5, 6 и т. д.

Допустим, если нам нужно создать таблицу числа 4, то 4 умножается на все натуральные числа таким образом:

• 4 х 1 = 4
• 4 х 2 = 8
• 4 х 3 = 12
• 4 х 4 = 16
• 4 х 5 = 20

И так далее.

Примечание. Из приведенных выше таблиц с 1 по 20 мы можем увидеть и понять закономерности кратных чисел.

Список математических таблиц от 2 до 20 (с загружаемыми PDF-файлами)

Вот мы и составили таблицу умножения. Учащиеся могут подготовить математические таблицы со 2 по 20 по приведенным ниже ссылкам.

Таблицы умножения Таблица

Вот таблица таблицы умножения от 1 до 10.

× (Раз)	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Таким же образом мы можем создать диаграмму из таблиц с 11 по 20.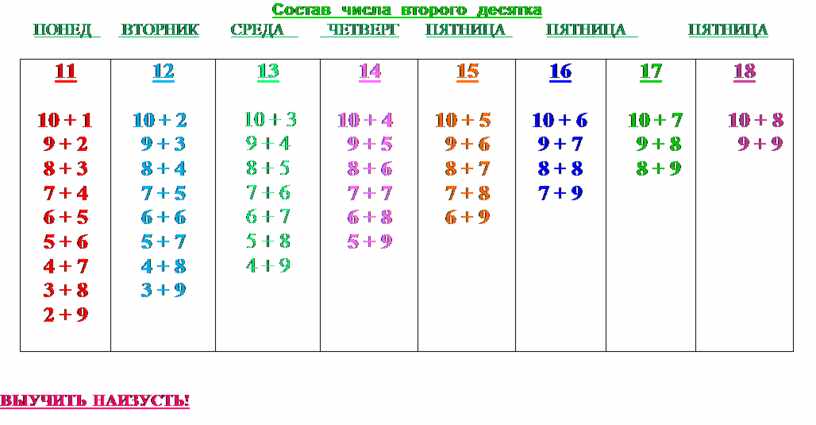

Советы по запоминанию таблиц умножения от 1 до 20

Давайте рассмотрим несколько советов по запоминанию этих математических таблиц.

1. В случае таблицы из 2 число увеличивается в 2 раза или число удваивается при умножении на 2. Например, 2 умножить на 6 означает, что здесь 6 удваивается; следовательно, результат равен 12. Следовательно, 2,4,6,8,10,12,14,16,18,20.
2. Таблица 5 имеет шаблон. Число заканчивается либо на 0, либо на 5. Следовательно, 5,10,15,20,25,…
3. Аналогично, таблица из 9также имеет узор. Если мы видим таблицу умножения на 9, разряд десятков чисел идет в порядке возрастания от 0 до 9, а разряд единиц чисел идет в порядке убывания от 9 до 0. Следовательно, 01,18, 27, 36, 45, 54, 63, 72, 81, 90.
4. Заучить таблицу умножения на 10 очень просто. Мы должны поставить ноль рядом с числом, умноженным на 10. Например, 10 умножить на 8 равно 80.

Зачем учить таблицу умножения?

Таблицы от 1 до 20 являются основой или основами изучения математики. Следовательно, каждому ученику необходимо выучить таблицы для легкого и быстрого расчета.

Таблицы с 1 по 10 являются основными, что помогает при выполнении простых арифметических операций. Когда учащиеся создают прочную основу по необходимым таблицам от 1 до 10, они способны выучить и пересчитать таблицу умножения от 11 до 20, что помогает решать сложные задачи. Для облегчения запоминания таблиц в младших классах предписано проводить скорострельные раунды, соревнования по чтению таблиц, контрольные работы и т. д. Запоминание таблиц помогает в быстрых вычислениях и экономит много времени. Необходимо выучить наизусть таблицы от 2 до 10 для фундаментальных оценок.

Мозг ребенка постоянно развивается. Таким образом, он постепенно открывается для восприятий. Изучая таблицы, они повторяют множество примеров, таких как 4×3=12 и 3×4=12. Постоянно наблюдая эти закономерности, они делают вывод, что любое число, умноженное на другое число, приводит к аналогичному результату, когда числа умножаются в другую сторону. Это улучшает способность восприятия ребенка.

Как освоить таблицу умножения от 1 до 20?

1] Способ применения таблицы умножения.

На данном этапе ученики хорошо разбираются в таблице умножения, и пришло время ее изучить. Репетитор должен сделать эту процедуру как можно более легкой для их участия.

2] Стимулировать учащихся к усвоению письменно или устно

Распознайте активный тон и предложите ученикам установить голос. Это может быть как стихотворение, так и песня. Можно также использовать визуальные представления. Таблицы — лучший способ заставить учащихся выучить таблицу умножения. Определите силу каждого ребенка и убедитесь, что каждый из них находится на одной волне. Если кто-то из учеников останется позади, у них могут возникнуть трудности в будущем.

3] Регулярно опрашивайте каждого ребенка

Проверьте ребенка, как только убедитесь, что он запомнил таблицу умножения. Это необходимо делать, когда их внимание сосредоточено на объекте, отличном от вопросов, связанных со школой. Это можно сделать так, чтобы получать удовольствие, не опасаясь неудачи. Неправильный ответ должен быть исправлен соответствующим объяснением в спокойной форме.

4] Помогите ребенку, когда он застрял

Обычно ученики ошибаются при умножении больших чисел. Некоторые из них запоминают неправильные ответы и изо всех сил пытаются перезагрузить свой разум правильным ответом. Если такая же проблема обнаружена у учащегося, то можно поэкспериментировать с практическим подходом, повесив записку на холодильник или создав шпаргалку вместе с проблемой.

Связанные статьи

• Столы с 15 по 20
• Столы от 12 до 15
• Таблицы с 1 по 10
• Столы с 12 по 20
• Столы с 21 по 30
• Таблицы с 11 по 30

Решенные примеры в таблицах с 1 по 20

Q.1: Чему равно пятое число, кратное 6?

Решение: Пятое кратное 6 = 5 x 6 = 30

Q.2: Если бы Сэм принес книгу за рупий. 10, то какова стоимость 12 таких книг?

Решение: Стоимость одной книги = рупий. 10

Стоимость 12 книг = 10 рупий x 12 = 120 рупий.

Q.3: Чему равно произведение 13 и 5? (Воспользуйтесь таблицами с 1 по 20, приведенными выше)

Решение: Произведение 13 и 5 = 13 x 5 = 65

Практический рабочий лист по таблицам с 1 по 20

Решите эти простые задачи на умножение, используя таблицы от 1 до 20. 2 х 3 = _____ 3 х 9 = _____ 5 х 10 = _____ 8 х 7 = _____ 11 х 4 = _____ 13 х 5 = _____ 15 х 8 = _____

Часто задаваемые вопросы по таблицам с 1 по 20

Q1

Как проще всего запомнить таблицу умножения?

Сложение — самый простой способ запомнить таблицу умножения. Как мы знаем, количество раз одно число умножается на другое число, а это значит, что оно было сложено само с собой снова и снова одно и то же количество раз, неоднократно. Например, 8 умножить на 4 означает, что 8 прибавляется четыре раза. Следовательно, 8+8+8+8 = 32,

Q2

Как запомнить таблицу Математика?

Чтобы запомнить таблицу по математике, мы должны учить таблицу снова и снова, либо устно произнося ее, либо записывая на бумаге, неоднократно. Кроме того, попробуйте решить вопросы, основанные на умножении чисел, чтобы учиться быстрее.

Q3

Что такое математическая таблица умножения?

В математике таблица умножения дает последовательное произведение двух чисел. Он показывает, когда число многократно добавляется к самому себе, каждый раз генерируется другое число. Обычно мы учим таблицы от 2 до 30 и запоминаем их, чтобы быстро решать математические задачи.

Q4

Как запомнить математические таблицы?

Создайте диаграмму математических таблиц от 2 до 20 и читайте ее каждый день, чтобы запомнить ее.

Q5

Как запомнить таблицу 9?

Самый простой способ запомнить таблицу 9 — сначала записать числа от 1 до 9, а затем записать их в обратном порядке.