Додавання і віднімання чисел у межах 20 1 клас
Скачать додавання і віднімання чисел у межах 20 1 клас djvu
Розробка уроку математики в 1 класі на заявлену тему з медіапрезентацією (додається), мета якого — учити учнів називати та записувати числа в межах 20; визначати місце числа; ознайомити з прийомом додавання й віднімання 1; удосконалювати обчислювальні навички, формувати вміння розв’язувати задачі опрацьованих видів. Розробки уроків за модельною навчальною програмою з математики — НУШ-2 Авторський колектив під керівництвом Романа Шияна — Математика 2 клас — розробки уроків НУШ — Урок Досліджуємо таблиці віднімання чисел у межах 20 — Розділ ІІ.
Презентація на тему: Прийоми усного додавання і віднімання у межах Додавання і віднімання чисел частинами. Завантажити презентацію. Отримати код.
Play. 1 / Скачати. Прийоми усного додавання і віднімання у межах Додавання і віднімання чисел частинами. Завантажити презентацію. Презентація по слайдам: Слайд 1. Тема уроку Прийоми усного додавання і віднімання у межах Додавання і віднімання чисел частинами. Слайд 2. Жив-був Дід-Цифроїд, Їв він цифри на обід. Скільки діток в цьому класі?
Слайд Слайд С. 10 №31 Геометричний матеріал. Слайд Додавання і віднімання двоцифрових чисел без переходу через десяток 1 Клас Урок математики. mb K. Урок 51 Математика 1 клас Складання та роз язування задач за малюнками. Математика 1клас Додавання та віднімання чисел виду 35 40 та 45 MB K. Урок 37 Математика 1 клас ДІЯ ДОДАВАННЯ НАЗВИ КОМПОНЕНТІВ І РЕЗУЛЬТАТУ ДІЇ ДОДАВАННЯ. MB K. Математика Урок 88 Знаходження невідомого доданка Рівняння. Додавання і віднімання в межах MB 1K.
Дія віднімання Властивості дії віднімання. Додавання і віднімання в межах Одеська СШ görünümler 1 B4 aylar önce. 1 клас. Математика. Додавання та віднімання іменованих чисел (ТижЧТ) Приєднуйтесь до нас також у: Facebook: Математика.1клас: Віднімання виду
Конспект уроку з використанням інтерактивних вправ.
Урок закріплення знань з елементами казки. ВКонтакте – универсальное средство для общения и поиска друзей и одноклассников, которым ежедневно пользуются десятки миллионов человек. Мы хотим, чтобы друзья, однокурсники, одноклассники, соседи и коллеги всегда оставались в контакте.
PDF, rtf, PDF, PDFПохожее:
Таблиця додавання чисел до 20. Табличне додавання і віднімання натуральних чисел
На даному уроці ви навчитеся складати і віднімати однозначні числа з переходом через розряд. Вирішуючи цікаві завдання, ви вивчите алгоритм додавання і віднімання чисел з переходом через десяток і познайомитеся з таблицею додавання однозначних чисел до 20. У вас буде можливість попрактикувати вивчений раніше матеріал на цікаві приклади.
Тема:Знайомство з основними поняттями в математиці
Урок: Додавання і віднімання однозначних чисел з переходом через розряд. Таблиця додавання до 20
За допомогою графічної моделі можна пояснити складання однозначних чисел з переходом через десяток.
Яким способом можна скласти 9 і 7? (Рис. 1)
Рис. 1
На графічній моделі видно, що перший доданок 9 треба доповнити до 10. Для цього розіб’ємо другий доданок на дві частини, одна з яких дорівнює числу 1, так як
9 + 1 \u003d 10, значить 7 \u003d 1 + 6. (рис. 2)
Рис. 2
Виконаємо додавання по частинах:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Відповідь: 9 + 7 \u003d 16.
Можна скласти ці числа по-іншому. (Рис. 3)
Рис. 3
Другий доданок 7 можна доповнити до 10. Для цього перший доданок розіб’ємо на дві частини, одна з яких дорівнює числу 3. Отже, 9 \u003d 3 + 6.
Рис. 4
Виконаємо додавання по частинах:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Перший доданок — 9, йому бракує до 10 однієї одиниці, тому другий доданок розбиваємо на частини. 5 — це 1 і 4. Додаємо до 9 спочатку одну одиницю, а потім ще чотири одиниці.
9 + 5 = 9 + (1 + 4) = 14
Перший доданок — 6, йому бракує до 10 чотирьох одиниць, тому другий доданок розбиваємо на частини: 4 і 2. Додаємо до 6 спочатку 4 і отримуємо десять одиниць, а потім залишилися дві одиниці.
6 + 6 = 6 + (4 + 2) = 12
Перший доданок — 4, йому бракує до 10 шести, тому другий доданок 8 розбиваємо на частини: 6 і 2. Додаємо до 4 спочатку шість одиниць і отримуємо десять одиниць, а потім залишилися дві одиниці.
4 + 8 = 4 + (6 + 2) = 12
У зменшуваному 15 — п’ять одиниць, тому від’ємник 7 розбиваємо на частини: 5 і 2. Віднімаємо з 15 спочатку п’ять одиниць, вийде 10. Потім з десяти віднімаємо залишилися дві одиниці.
15 — 7 = 15 — (5 + 2) = 8
У зменшуваному 16 — шість одиниць, тому від’ємник 9 розбиваємо на частини: 6 і 3. Віднімаємо спочатку з 16 шість одиниць, вийде 10. А потім з 10 віднімаємо залишилися три одиниці.
16 — 9 = 16 — (6 + 3) = 7
У зменшуваному 12 — дві одиниці, тому від’ємник 4 розбиваємо на частини: 2 і 2. З 12 віднімаємо 2, вийде 10. І від 10 віднімаємо 2.
12 — 4 = 12 — (2 + 2) = 8
Відповідь: 12 — 4 \u003d 8.
Використовувати прийом додавання і віднімання по частинах з переходом через десяток не завжди зручно, тому необхідно вивчити таблицю складання однозначних чисел до 20
напам’ять.На малюнку зображена таблиця, за допомогою якої вам буде легше вивчити випадки складання однозначних чисел до 20. (рис. 7)
Рис. 7
У кожному стовпчику перший доданок — однакове, а друге — збільшується на один, значить сума теж буде збільшуватися на один. Знайдемо значення цих сум.
Знайдемо значення цих сум.
9 + 2 \u003d 11, отже: 9 + 3 \u003d 12, розмірковуючи так, заповнюємо всю таблицю. (Рис. 8)
Рис. 8
У кожному рядку записані суми з однаковими відповідями. Виберіть спосіб, як вам легше буде запам’ятати відповіді: по стовпчиках або по рядках. Якщо ви добре вивчіть таблицю складання однозначних чисел до 20, то вам буде неважко виконувати і віднімання однозначних чисел в межах 20.
Список літератури
- Александрова Л.А., Мордкович А.Г. Математика 1 клас. — М: Мнемозина, 2012.
- Башмаков М.І., Нефедова М.Г. Математика. 1 клас. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 клас. — М7: Русское слово, 2012.
- Соціальна мережа працівників освіти ().
- 5klass.net ().
- Самоучка ().
Домашнє завдання
1. Згадайте як правильно складати і віднімати однозначні числа з переходом через розряд.
2. Допоможіть жабі вирішити приклади.
3. Вирішіть приклади і розфарбуйте малюнок.
Таблиці додавання і віднімання використовуються для навчання дітей рахунку або для перевірки їх навичок у складанні і відніманні. Для двох цих завдань використовуються різні таблиці. Обидва варіанти таблиць можна завантажити роздрукувати на цій сторінку
Таблиця додавання до 20 роздрукувати і скачати
Таблиця додавання використовується для навчання дітей. Вертикальний крайній лівий стовпець і горизонтальна верхня рядок є складові. Для того що б скласти два числа, потрібно знайти їх у вертикальному стовпці і в горизонтальному рядку. Перетин утворює суму цих двох доданків. Наприклад, як показано на малюнку нижче, 6 + 5 \u003d 11.
Ви можете роздрукувати таблицю додавання до 20 в форматі Word або PDF. Якщо вам потрібна таблиця додавання до 10, її можна легко зробити, видаливши непотрібні осередки в форматі Word. Якщо вам потрібна таблиця додавання більше, ніж до 20, то ви можете завантажити таблицю додавання в форматі Excel і додати потрібні стовпці і рядки копіюванням.
Таблиця віднімання до 20 роздрукувати і скачати
Як таблиці віднімання використовується та ж таблиця додавання, яку можна роздрукувати вище. Припустимо нам потрібно вирішити приклад 14 — 8 \u003d 6. Використовуючи, таблицю віднімання, знаходимо в поле таблиці діагональ з зменшуваним 14. На малюнку нижче ця діагональ виділена світло-зеленим кольором. Вибираємо на цій діагоналі число 14, яке знаходиться навпроти від’ємника 8. Вийшло в верхньому ряду число 6 і є відповідь.
Як ви можете побачити, для додавання і віднімання використовується одна і та ж таблиця додавання і віднімання, роздрукувати або завантажити яку ви можете за посиланнями вище в різних форматах.
Таблиця віднімання без відповідей роздрукувати і скачати
На даному уроці ви навчитеся складати і віднімати однозначні числа з переходом через розряд. Вирішуючи цікаві завдання, ви вивчите алгоритм додавання і віднімання чисел з переходом через десяток і познайомитеся з таблицею додавання однозначних чисел до 20. У вас буде можливість попрактикувати вивчений раніше матеріал на цікаві приклади.
Тема:Знайомство з основними поняттями в математиці
Урок: Додавання і віднімання однозначних чисел з переходом через розряд. Таблиця додавання до 20
За допомогою графічної моделі можна пояснити складання однозначних чисел з переходом через десяток.
Яким способом можна скласти 9 і 7? (Рис. 1)
Рис. 1
На графічній моделі видно, що перший доданок 9 треба доповнити до 10. Для цього розіб’ємо другий доданок на дві частини, одна з яких дорівнює числу 1, так як
9 + 1 \u003d 10, значить 7 \u003d 1 + 6. (рис. 2)
Рис. 2
Виконаємо додавання по частинах:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Відповідь: 9 + 7 \u003d 16.
Можна скласти ці числа по-іншому. (Рис. 3)
Рис. 3
Другий доданок 7 можна доповнити до 10. Для цього перший доданок розіб’ємо на дві частини, одна з яких дорівнює числу 3. Отже, 9 \u003d 3 + 6.
Для цього перший доданок розіб’ємо на дві частини, одна з яких дорівнює числу 3. Отже, 9 \u003d 3 + 6.
Рис. 4
Виконаємо додавання по частинах:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Перший доданок — 9, йому бракує до 10 однієї одиниці, тому другий доданок розбиваємо на частини. 5 — це 1 і 4. Додаємо до 9 спочатку одну одиницю, а потім ще чотири одиниці.
9 + 5 = 9 + (1 + 4) = 14
Перший доданок — 6, йому бракує до 10 чотирьох одиниць, тому другий доданок розбиваємо на частини: 4 і 2. Додаємо до 6 спочатку 4 і отримуємо десять одиниць, а потім залишилися дві одиниці.
6 + 6 = 6 + (4 + 2) = 12
Перший доданок — 4, йому бракує до 10 шести, тому другий доданок 8 розбиваємо на частини: 6 і 2. Додаємо до 4 спочатку шість одиниць і отримуємо десять одиниць, а потім залишилися дві одиниці.
4 + 8 = 4 + (6 + 2) = 12
У зменшуваному 15 — п’ять одиниць, тому від’ємник 7 розбиваємо на частини: 5 і 2. Віднімаємо з 15 спочатку п’ять одиниць, вийде 10. Потім з десяти віднімаємо залишилися дві одиниці.
15 — 7 = 15 — (5 + 2) = 8
У зменшуваному 16 — шість одиниць, тому від’ємник 9 розбиваємо на частини: 6 і 3. Віднімаємо спочатку з 16 шість одиниць, вийде 10. А потім з 10 віднімаємо залишилися три одиниці.
16 — 9 = 16 — (6 + 3) = 7
У зменшуваному 12 — дві одиниці, тому від’ємник 4 розбиваємо на частини: 2 і 2. З 12 віднімаємо 2, вийде 10. І від 10 віднімаємо 2.
12 — 4 = 12 — (2 + 2) = 8
Відповідь: 12 — 4 \u003d 8.
Використовувати прийом додавання і віднімання по частинах з переходом через десяток не завжди зручно, тому необхідно вивчити таблицю складання однозначних чисел до 20 напам’ять.
На малюнку зображена таблиця, за допомогою якої вам буде легше вивчити випадки складання однозначних чисел до 20. (рис. 7)
Рис. 7
У кожному стовпчику перший доданок — однакове, а друге — збільшується на один, значить сума теж буде збільшуватися на один. Знайдемо значення цих сум.
Знайдемо значення цих сум.
9 + 2 \u003d 11, отже: 9 + 3 \u003d 12, розмірковуючи так, заповнюємо всю таблицю. (Рис. 8)
Рис. 8
У кожному рядку записані суми з однаковими відповідями. Виберіть спосіб, як вам легше буде запам’ятати відповіді: по стовпчиках або по рядках. Якщо ви добре вивчіть таблицю складання однозначних чисел до 20, то вам буде неважко виконувати і віднімання однозначних чисел в межах 20.
Список літератури
- Александрова Л.А., Мордкович А.Г. Математика 1 клас. — М: Мнемозина, 2012.
- Башмаков М.І., Нефедова М.Г. Математика. 1 клас. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 клас. — М7: Русское слово, 2012.
- Соціальна мережа працівників освіти ().
- 5klass.net ().
- Самоучка ().
Домашнє завдання
1. Згадайте як правильно складати і віднімати однозначні числа з переходом через розряд.
2. Допоможіть жабі вирішити приклади.
3. Вирішіть приклади і розфарбуйте малюнок.
Додавання і віднімання в межах 20 презентація
Скачать додавання і віднімання в межах 20 презентація djvu
Табличне додавання і віднімання чисел в межах 20 ноя просмотра. Комментарии0. 0. filter812.ru Знайомимося з діями додавання і віднімання, вимірюванням довжини відрізків, поняттям і терміном «задача», вчимося знаходити невідомий доданок, від’ємник і зменшуване, складати рівності на віднімання з рівності на додавання. І все це в цікавій ігровій формі. З нашими іграми діти вивчають математику із задоволенням!•••.
Таблиці додавання і віднімання в межах Задачі на знаходження суми та остачі. Мета: вчити віднімати вирази виду 40 — 8; удосконалювати обчислювальні навички, розвивати вміння розв’язувати задачі за виразом, вчити змінювати запитання в задачі; виховувати любов до математики. № — Віднімання виду Знаходження значень виразів зі змінною. Методичний підхід до опрацювання додавання і віднімання в межах 20 з переходом через десяток, розроблений українською вченою Л. П.
П.
Кочиною заслуговує на увагу. Але, слід зазначити, що він спрямований на формування в учнів вузьких емпіричних узагальнень – способу додавання до кожного з чисел 9 6 та способу віднімання від певного числа 11 Прийом додавання та віднімання по частинах не є новим для учнів. Ще в межах 10 ми додавали та віднімали числа першого п’ятка по частинах, але в цій ситуації не мало значення, на які доданки розкладати друге число (доданок або від’ємник), тому обчислення здійснювалися кількома способами.
Вправи на засвоєння таблиць додавання і віднімання в межах Вимірювання і побудова відрізків. Урок математики в 1 класі Автор.». Скачать бесплатно презентацию на тему «Тема. Лічба в межах Вправи на засвоєння таблиць додавання і віднімання в межах Вимірювання і побудова відрізків. Урок математики в 1 класі Автор.» в filter812.ru (PowerPoint). Похожие презентации.
Урок – подорож із математики в 1 класі Складання прикладів на віднімання з прикладів на додаванняСкладання прикладів на віднімання з прикладів на додавання. Колобок Закріплення таблиць додавання та віднімання в межах Презентація допомагає узагальнити та систематизувати знання учнів з додавання та віднімання в межах 20 з переходом через десяток, допоможе навчити додавати приклади даного виду, розвивати чисельні навички, логіку, увагу, уміння користуватися математичними термінами.
Математика | Просмотров: | Загрузок: 88 | Добавил: OlgaVasboxlbox77 | Дата: | Комментарии (0). 2 клас. Математичний диктант. Числа Вирази з дужками на дві дії. Тренажер.
Я бачу, що на урок ви прийшли з хорошим настроєм. Покажіть виразом обличчя свій настрій. Посміхніться до мене, поділіться хорошим настроєм з товаришем. Я хотіла б аби такий настрій у вас в усіх був до кінця уроку. Лічба в межах Позначення чисел другого десятка цифрами. Повторення таблиць додавання і віднімання. Розв’язування задач.
Урок № Лічба в межах Утворення й назва чисел другого десятка. Розв’язування задач. Презентація допомагає узагальнити та систематизувати знання учнів з додавання та віднімання в межах 20 з переходом через десяток, допоможе навчити додавати приклади даного виду, розвивати чисельні навички, логіку, увагу, уміння користуватися математичними термінами.
Математика | Просмотров: | Загрузок: 88 | Добавил: OlgaVasboxlbox77 | Дата: | Комментарии (0). 2 клас. Математичний диктант.
Числа Вирази з дужками на дві дії. Тренажер.
fb2, PDF, rtf, fb2Похожее:
Таблиця додавання і віднімання в межах 10 презентація
Скачать таблиця додавання і віднімання в межах 10 презентація doc
Таблиці додавання і віднімання числа 1. Додавання і віднімання по 1 виду 4 1 1; 9 — 1 — 1 Навчальний урок з матем Урок 48 Математика 1 клас. Таблиці додавання і віднімання числа 2. Частина 1. 3 yıl önce. Навчальний урок з математики для 1 класу. Таблиці додавання і віднімання числа 2. Частина 1 Додавання і відні Таблиці додавання та віднімання числа 4.
Розв’язування простих задач різних видів. 3 yıl önce. 2клас #математика #теорія #НоваШкола Повністю урок дивись на нашому сайті Таблиці додавання та віднімання чисел 4, 5, 6, 7, 8, 9. Табличне додавання і віднімання чисел в межах 4 yıl önce. dom-v-teple.ru Знайомимося з діями додавання і віднімання, вимірюванням довжини відрізків. Навчальна компютерна презентація для уроку математики у 1 класі за підручником авторського колективу М.Ф.
Рівкінд, Л.В. Оляницької. Презентація містить достатню. Математика 1 клас «Додавання і віднімання. Порівняння кількості предметів. Знаки «+» і «-». Написання знаків «+» і «-»». Навчальна комп’ютерна презентація для уроку математики у 1 класі за підручником авторського колективу М. Ф.
Ф.
Рівкінд, Л.В. Оляницької. Презентація містить достатню кількість яскравих ілюстрацій, анімаційні ефекти. Урок № Тема уроку: Додавання і віднімання.
Порівняння кількості предметів. Знаки «+» і «-». Написання знаків «+» і «-». Просмотр содержимого документа «Презентація Порівняння чисел у межах Монета номіналом «10 к.».
Розпізнавання геометричних фігур.» Створено С.. Урок 41 Математика 1 клас. Зв’язок дії додавання і віднімання. Віртуальна Школа. Baxış 42K3 il əvvəl. Таблиці додавання і віднімання числа 1.
Частина 1. Віртуальна Школа. Baxış 10K3 il əvvəl. Тема: Формування обчислювальної навички додавання та віднімання в межах 10 Навчально-методичний комплект «Математика». 1 клас. Частина 1,.. Математика 1 клас/5ч. Додавання і віднімання від 0 до 5.
ТМ Розумники. Baxış 10K4 il əvvəl. Методичний підхід до опрацювання додавання і віднімання в межах 20 з переходом через десяток, розроблений українською вченою Л.П. Кочиною заслуговує на увагу. Але, слід зазначити, що він спрямований на формування в учнів вузьких емпіричних узагальнень – способу додавання до кожного з чисел 9 6 та способу віднімання від певного числа 11 Прийом додавання та віднімання по частинах не є новим для учнів. Ще в межах 10 ми додавали та віднімали числа першого п’ятка по частинах, але в цій ситуації не мало значення, на які доданки розкладати друге число (доданок або від’ємник), тому обчислення здійснювалися кількома способами.
Різновиди завдань на виділення властивостей і ознак предметів •розгляд демонстраційного зразка друкованої і писаної цифри на таблиці, у підручниках, зошиті з друкованою основою; •аналіз демонстраційного зразка цифри 5 на таблиці: •зіставлення писаної і друкованої цифри; Ознайомлення дітей з написанням цифри доцільно проводити в такій послідовності сприяє закріпленню умінь учнів лічити в межах в прямому і зворотньому порядку, визначати місце кожного числа в натуральному ряду, називати попереднє і наступне число.
Під час вивчення нумерації чисел необхідно вимагати у дітей застосування трьох відомих їм способів їх утворення.
Розробка уроку у формі подорожі на заявлену навчальну тему в 1 класі з медіапрезентацією (додається), мета якого — закріпити уміння додавати й віднімати в межах 10; удосконалювати навички усних обчислень, розвивати математичні. Закріпити уміння додавати і віднімати в межах Удосконалювати навички усних обчислень, розвивати математичні здібності учнів, пам’ять, мислення спостережливість, кмітливість.
Повторити геометричний матеріал. Виховувати охайність, культуру запису, інтерес до математики, любов до природи. Презентація з математики з теми » Додавання і віднімання в межах 20″. Скачать материал. библиотека материалов. Добавить в избранное.
1 / Описание презентации по отдельным слайдам: 1 слайд. Описание слайда: Додавання і віднімання 1 в межах Порівняння іменованих чисел. Розв’язування задач. Математичний диктант Наступне до числа: 17, 19, 10, Передує числу: 16, 17, 12, 20, 6. Запиши числа від 10 до Запиши числа від 20 до
EPUB, djvu, EPUB, docПохожее:
Урок №28 для 2 класу з математики за С.О. Скворцовою
№028 — Досліджуємо таблиці додавання чисел у межах 20.
Перед завантаженням матеріалу познайомтесь з правилами використання — >>Читати тут
Для отримання даного матеріалу натисніть клавішу «Завантажити матеріал» котра знаходиться внизу сторінки.
«____»___________20___ року
Конспект уроку математики з використанням навчального посібника «С.О. Скворцова та О.В. Онопрієнко»
Урок №28.
Мета: формувати обчислювальні навички, уміння розв’язувати задачі; актуалізувати знання прийомів додавання й віднімання чисел частинами, залежності суми від зміни одного з доданків, залежності різниці від зміни зменшуваного; дослідити залежність доданка від зміни іншого доданка при сталій сумі; проаналізувати складені таблиці додавання; закріпити знання грошових одиниць; формувати вміння розв’язувати задачі.
.Обладнання: мультимедійний комплект.
Хід уроку
- ОК (організація класу)
Створення позитивного психологічного клімату класу.
Ви вже навчилися додавати числа частинами, тому сьогодні на уроці ми будемо складати таблиці додавання чисел у межах 20. Ці таблиці ми будемо досліджувати, щоб зробити відкриття про залежність між сумою і доданками. Отже, сьогодні на вас чекає роль дослідників, винахідників. Ви, як справжні вчені, будете формулювати свої припущення — гіпотези — та підтверджувати або спростовувати їх!
- МНД (мотивація навчальної діяльності)
- АОЗ (актуалізація опорних знань)
- ВНМ (вивчення нового матеріалу)
Демонстрація навчальної презентації.
Слайд 2-5. Усне опитування.
Слайд 6-8. Хвилинка каліграфії.
Слайд 9. Рухлива вправа.
Слайд 10-11. Завдання 1. Вибери варіант і виконай обчислення за схемами.
Слайд 12. Завдання 2. Досліди, який компонент дії змінюється. На скільки? Як це впливає на результат? Закінчи обчислення.
Слайд 13. Завдання 3. Досліди, чому в рівностях однакові результати. Впиши пропущені доданки.
Слайд 14-16. Завдання 4. Розгадай «секрет» таблиць додавання.
Слайд 17. Перевір себе за правилом.
Слайд 18. Фізкультхвилинка.
Слайд 19. Завдання 5. Прочитай задачу. Дай відповіді на запитання.
Слайд 20-21. Завдання 6. Добери до задачі опорну схему та схематичний рисунок. Доповни їх. Розв’яжи задачу.
Слайд 22. Рухлива вправа.
Слайд 23-24. Завдання 2. Знайди значення виразів із коментарем.
Слайд 25. Завдання 4. Виконай дії за стрілочками. За потреби користуйся таблицями додавання.
Завдання 4. Виконай дії за стрілочками. За потреби користуйся таблицями додавання.
Слайд 26. Домашні тренувальні вправи.
- ЗВ (закріплення вивченого)
- Підсумок
- Рефлексія
Додавання та віднімання в межах 20 1 клас
Скачать додавання та віднімання в межах 20 1 клас rtf
Теоретичні уроки, тести та завдання за предметом Математика, 1 клас. Завдання створені професійними педагогами. МiйКлас — онлайн школа нового покоління. 1 клас. Математика. Додавання та віднімання іменованих чисел (ТижЧТ) Приєднуйтесь до нас також у: Facebook: Урок 77 Математика 1 клас. Лічба в межах Частина 1. Віртуальна Школа. Математика. 1 клас Порівнюємо числа в межах Кисіль Марина Вікторівна, учитель початкових класів Криворізької Віднімання чисел у межах Математичний диктант в межах 1клас математика.
Сіра T.А. Aufrufe 8 triocenter.ru 4 Monate. математичнийдиктант #вмежах20 #математика1клас. Таблиці додавання та віднімання чисел 4, 5, 6, 7, 8, 9. Нова Школа 1 клас. Aufrufe 22 triocenter.ru 3 years. Додавання і віднімання двоцифрових чисел без переходу через десяток [1 клас] урок математики. Мел. Baxış 45K6 ay əvvəl. Вчимо цифри, числа та розв`язуємо приклади з Їжачком Жекою.
Умачка Відео. Baxış K2 il əvvəl. НУШ Відеоурок математики для учнів 1 класу, в якому повторюємо як визначати кількість десятків та одиниць в Математика: Додавання чисел виду 8+5. Ірина Бикова.
Baxış ay əvvəl. Математика 1 клас/7ч. Тема. Додавання і віднімання в межах Мета: працювати над закріпленням і навичками додавати і віднімати в межах 20, порівнювати числа; формувати вміння розвязувати задачі; виховувати інтерес до уроку математики. Я відправила одну ще роботу на сайт та один запит на сертифікат.
А оплатила 2 сертифікати в Якщо можна швидше, тому що це для іншої людини. Доброго вечора. Поясніть, будь ласка, згідно методики оцінювання контрольних робіт з математики в початкових класах. (4 клас) Якою помилкою вважається помилка допущена в записі множення в стовпчик типу *5= Учень записав 5 під нулем(вчитель виправила, що треба було записати під 4), хоча результат правильний.
(4 клас) Якою помилкою вважається помилка допущена в записі множення в стовпчик типу *5= Учень записав 5 під нулем(вчитель виправила, що треба було записати під 4), хоча результат правильний.
Оцінка 9. за контрольну роботу.(Хоча ця помилка була в додатковому завданні) І чи вважається це за помилку?.
Вивчаємо математику у 1 класі, виконуючи завдання онлайн тренажерів. ГДЗ 2 клас нова програма. математика. українська мова. 2 клас → математика → Бевз Васильєва. Список кроків: Крок 1. вправа 1 вправа 2 вправа 3 вправа 4 вправа 5 вправа 6 вправа 7.
Крок 2. Тема. Додавання і віднімання в межах Мета: працювати над закріпленням і навичками додавати і віднімати в межах 20, порівнювати числа; формувати вміння розвязувати задачі; виховувати інтерес до уроку математики.
djvu, rtf, fb2, docПохожее:
Подорож до міста «Додавання та віднімання в межах 20» — Підручник Математика 2 клас В. Г. Бевз, Д. В. Васильєва 2019
Крок 1. Склад числа 10. Переставний закон додавання стор. 22 — 22
Крок 2.
 Додавання частинами. Додавання до числа 9
стор. 23 — 23
Додавання частинами. Додавання до числа 9
стор. 23 — 23Крок 3. Додавання одноцифрових чисел до числа 8 стор. 24 — 24
Крок 4. Додавання чисел до числа 7 стор. 25 — 25
Крок 5. Набуваємо досвіду стор. 26 — 26
Крок 6.
 Додавання чисел до числа 6
стор. 27 — 27
Додавання чисел до числа 6
стор. 27 — 27Крок 7. Додавання у межах 20 стор. 28 — 28
Крок 8. Віднімання одноцифрових чисел від числа 11 стор. 29 — 30
Крок 9. Віднімання чисел від чисел 12 і 13 стор. 30 — 31
Крок 10.
 Віднімання чисел від чисел 14 і 15
стор. 31 — 32
Віднімання чисел від чисел 14 і 15
стор. 31 — 32Крок 11. Віднімання чисел від чисел 16 і 17 стор. 32 — 33
Крок 12. Віднімання чисел від чисел 18 і 19 стор. 34 — 34
Крок 13. Віднімання чисел у межах 20 стор. 35 — 35
Крок 14.
 Таблиця додавання та віднімання у межах 20
стор. 36 — 36
Таблиця додавання та віднімання у межах 20
стор. 36 — 36Крок 15. Набуваємо досвіду стор. 37 — 37
Повторення. Розвивальні завдання стор. 38 — 38
2.2: Количественные данные — Статистика LibreTexts
График количественных данных похож на гистограмму, за исключением некоторых существенных отличий. Во-первых, на гистограмме категории можно расположить в любом порядке по горизонтальной оси. Для этих значений данных нет установленного порядка. Вы не можете сказать, как данные распределяются в зависимости от формы, поскольку форма может измениться, просто разместив категории в разном порядке. В случае количественных данных данные располагаются в определенном порядке, поскольку вы имеете дело с числами.Имея количественные данные, вы можете говорить о распределении, поскольку форма меняется лишь немного в зависимости от того, сколько категорий вы настроили. Это называется распределением частот .
В случае количественных данных данные располагаются в определенном порядке, поскольку вы имеете дело с числами.Имея количественные данные, вы можете говорить о распределении, поскольку форма меняется лишь немного в зависимости от того, сколько категорий вы настроили. Это называется распределением частот .
Это приводит ко второму отличию от гистограмм. На гистограмме категории, которые вы указали в таблице частот, были определены вами. В количественных данных категории представляют собой числовые категории, а числа определяются тем, сколько категорий (или так называемых классов) вы выбираете.Если у двух людей одинаковое количество категорий, то у них будет одинаковое частотное распределение. А в качественных данных может быть много разных категорий в зависимости от точки зрения автора.
Третье отличие состоит в том, что категории соприкасаются с количественными данными, и на графике не будет пробелов. Причина, по которой гистограммы имеют пробелы, заключается в том, чтобы показать, что категории не продолжаются, как это происходит в количественных данных. Поскольку график количественных данных отличается от качественных данных, ему присвоено новое название.Имя графика — гистограмма . Чтобы создать гистограмму, вы должны сначала создать частотное распределение. Идея частотного распределения состоит в том, чтобы взять интервал, охватываемый данными, и разделить его на равные подинтервалы, называемые классами.
Краткое описание шагов, связанных с распределением частот
- Найдите диапазон = наибольшее значение — наименьшее значение
- Выберите количество классов для использования. Обычно количество классов от пяти до двадцати.Пять классов используются, если имеется небольшое количество точек данных, и двадцать классов, если имеется большое количество точек данных (более 1000 точек данных). (Примечание: с этого момента категории будут называться классами.)
- Ширина класса = \ (\ dfrac {\ text {range}} {\ # \ text {classes}} \) Всегда округлять до следующего целого числа (даже если ответ уже является целым числом, переходите к следующему целому числу).
 Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него.Если вы округлите в большую сторону, то самое большое значение данных попадет в последний класс, и проблем не возникнет.
Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него.Если вы округлите в большую сторону, то самое большое значение данных попадет в последний класс, и проблем не возникнет. - Создайте классы. У каждого класса есть ограничения, которые определяют, какие значения попадают в каждый класс. Чтобы найти пределы класса, установите наименьшее значение в качестве нижнего предела класса для первого класса. Затем добавьте ширину класса к нижнему пределу класса, чтобы получить следующий нижний предел класса. Повторяйте, пока не получите все классы. Верхний предел класса для класса на единицу меньше нижнего предела для следующего класса.
- Чтобы классы действительно соприкасались, один класс должен начинаться там, где заканчивается предыдущий. Это известно как граница класса. Чтобы найти границы класса, вычтите 0,5 из нижнего предела класса и прибавьте 0,5 к верхнему пределу класса.
- Иногда бывает полезно найти середину класса. Процесс:
Средняя точка \ (= \ dfrac {\ text {нижний предел + верхний предел}} {2} \) - Чтобы определить количество точек данных, попадающих в каждый класс, просмотрите каждое значение данных и посмотрите, между границами какого класса оно находится.Использование меток может быть полезно при подсчете значений данных. Частота для класса — это количество значений данных, попадающих в класс.
Примечание
Приведенное выше описание предназначено для значений данных, которые являются целыми числами. Если значение данных имеет десятичные разряды, тогда ширина вашего класса должна быть округлена до ближайшего значения с тем же количеством десятичных знаков, что и исходные данные. Кроме того, в границах вашего класса должно быть на один десятичный знак больше, чем в исходных данных.Например, если ваши данные имеют один десятичный знак, тогда ширина класса будет иметь один десятичный знак, а границы класса формируются путем добавления и вычитания 0,05 из каждого предела класса.
Пример \ (\ PageIndex {1} \) создание таблицы частот
Пример \ (\ PageIndex {1} \) содержит сумму арендной платы, выплачиваемую каждый месяц за 24 студента курса статистики. Составьте относительное частотное распределение, используя 7 классов.
| 1500 | 1350 | 350 | 1200 | 850 | 900 |
| 1500 | 1150 | 1500 | 900 | 1400 | 1100 |
| 1250 | 600 | 610 | 960 | 890 | 1325 |
| 900 | 800 | 2550 | 495 | 1200 | 690 |
Решение
- Найдите диапазон:
наибольшее значение — наименьшее значение \ (= 2550-350 = 2200 \) - Выберите количество классов:
Указания по использованию 7 классов. - Найдите ширину класса:
width \ (= \ dfrac {\ text {range}} {7} = \ dfrac {2200} {7} \ приблизительно 314,286 \)
Округлите до 315
\ (\ color {text} {Всегда округлять до следующего целого числа, даже если ширина уже является целым числом.} \) - Найдите пределы класса:
Начните с наименьшего значения. Это нижний предел класса для первого класса. Добавьте ширину, чтобы получить нижнюю границу следующего класса. Продолжайте добавлять ширину, чтобы получить все нижние пределы.
\ (350 + 315 = 665 665 + 315 = 980 980 + 315 = 1295 \ rightleftharpoons \),
Верхний предел на единицу меньше следующего нижнего предела: поэтому для первого класса верхний предел класса будет \ (665-1 = 664 \).
Когда у вас есть все 7 классов, убедитесь, что последнее число, в данном случае 2550, по крайней мере равно наибольшему значению в данных. Если нет, значит, вы где-то ошиблись. - Найдите границы класса:
Вычтите 0,5 из нижнего предела класса, чтобы получить границы класса. Добавьте 0,5 к верхнему пределу класса для последней границы класса.
\ (350-0,5 = 349,5, \ quad 665-0,5 = 664,5, \ quad 980-0,5 = 979,5, \ quad 1295-0,5 = 1294,5 \ rightleftharpoons \)
Каждое значение в данных должно попадать ровно в один из классов .Никакие значения данных не должны попадать прямо на границу двух классов. - Найдите средние точки класса:
средняя точка \ (= \ dfrac {\ text {нижний предел} + \ text {верхний предел}} {2} \)
\ (\ dfrac {350 + 664} {2} = 507, \ dfrac {665 + 979} {2} = 822, \ rightleftharpoons \) - Подсчитайте и найдите частоту данных:
Просмотрите данные и поставьте отметку в соответствующем классе для каждой части данных, посмотрев, между границами классов, между которыми находится значение данных. Введите частоту, заменив каждый счет на число.
| Пределы классов | Границы классов | Средняя точка класса | Tally | Частота |
|---|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | |||| | 4 |
| 665-979 | 664,5-979,5 | 822 | \ (\ cancel {||||} \) ||| | 8 |
| 980-1294 | 979. 5-1294,5 5-1294,5 | 1137 | \ (\ cancel {||||} \) | 5 |
| 1295-1609 | 1294,5–1609,5 | 1452 | \ (\ cancel {||||} \) | | 6 |
| 1610-1924 | 1609,5-1924,5 | 1767 | 0 | |
| 1925-2239 | 1924 г.5-2239,5 | 2082 | 0 | |
| 2240-2554 | 2239,5-2554,5 | 2397 | | | 1 |
Убедитесь, что сумма частот совпадает с количеством точек данных.
Команда R для частотного распределения:
Для создания частотного распределения:
сводка (переменная) — так можно узнать минимум и максимум.
перерывов = seq (min, число выше max, by = ширина класса)
брейков — так что вы можете видеть брейки, которые сделал R.
variable.cut = cut (variable, breaks, right = FALSE) — это разделит данные на классы.
variable.freq = table (variable.cut) — будет создана частотная таблица.
variable.freq — отобразит таблицу частот.
Для данных в примере \ (\ PageIndex {1} \) команда R будет иметь следующий вид:
аренда <-c (1500, 1350, 350, 1200, 850, 900, 1500, 1150, 1500, 900, 1400, 1100, 1250, 600, 610, 960, 890, 1325, 900, 800, 2550, 495, 1200, 690) резюме (аренда)
Выход:
\ (\ begin {array} {cccccc} {\ text {Min}} & {1 \ text {st Qu.}} & {\ text {Median}} & {\ text {Mean}} & {3 \ text {rd Qu.}} & {\ text {Max}} \\ {350} & {837.5} & {1030. 0} & {1082.0} & {1331.0} & {2550 .0} \ end {array} \)
разрывов = seq (350, 3000, by = 315)
разрывов
Выход:
[1] 350 665 980 1295 1610 1925 2240 2555 2870
Это ваши нижние пределы частотного распределения. Теперь вы можете написать свою собственную таблицу.
rent.cut = cut (rent, breaks, right = FALSE)
rent.freq = table (rent.разрез)
Выход:
рент.рез
\ (\ begin {array} {cccccccc} {[350,665)} & {[665,980)} & {[980,1.3 e + 03)} & {[1.3e + 03, 1.61e + 03)} & {[ 1.61e + 03, 1.92e + 03)} & {[1.92e + 03, 2.24e + 03)} и {[2.24e + 03, 2.56e + 03)} и {[2.56e + 03, 2.87e + 03)} \\ {4} & {8} & {5} & {6} & {0} & {0} & {1} & {0} \ end {array} \)
Трудно определить основную форму распределения, глядя на распределение частот. Проще было бы посмотреть на график.График частотного распределения для количественных данных называется частотной гистограммой или просто гистограммой для краткости.
Определение \ (\ PageIndex {1} \): гистограмма
Гистограмма — это график частот по вертикальной оси и границ классов по горизонтальной оси. Прямоугольники, где высота — частота, а ширина — ширина класса, рисуются для каждого класса.
Пример \ (\ PageIndex {2} \: построение гистограммы
Нарисуйте гистограмму распределения из примера \ (\ PageIndex {1} \).
Решение
Границы классов отложены по горизонтальной оси, а частоты отложены по вертикальной оси. Вы можете нанести средние точки классов вместо границ классов. График 2.2.1 был создан с использованием средних точек, потому что это было легче сделать с помощью программного обеспечения, создавшего график. На R команда
Вы можете нанести средние точки классов вместо границ классов. График 2.2.1 был создан с использованием средних точек, потому что это было легче сделать с помощью программного обеспечения, создавшего график. На R команда
hist (variable, col = «введите нужный цвет», breaks, main = «введите нужный заголовок», xlab = «введите метку для горизонтальной оси»,
ylim = c (0, число выше максимальной частоты) — строит гистограмму с указанным цветом и с использованием разрывов, которые вы сделали для распределения частот.
В этом примере команда в R будет (при условии, что вы создали частотное распределение в R, как описано ранее):
hist (rent, col = «blue», breaks, right = FALSE, main = «Ежемесячная арендная плата, выплачиваемая студентами», ylim = c (0,8) xlab = «Ежемесячная арендная плата ($)»)
Рисунок \ (\ PageIndex {1} \): Гистограмма для ежемесячной арендной платыЕсли перед гистограммой не было создано частотного распределения, то команда будет выглядеть так:
hist (переменная, col = «введите нужный цвет», количество классов, main = «введите нужный заголовок», xlab = «введите метку для горизонтальной оси») — создает гистограмму с указанным цветом. и количество классов (хотя количество классов является приблизительным, и R создаст количество классов, близких к этому значению).
В этом примере команда R без созданного первой частотного распределения будет:
hist (rent, col = «blue», 7, main = «Ежемесячная арендная плата, выплачиваемая студентами», xlab = «Ежемесячная арендная плата ($)»)
Обратите внимание, что на графике обозначены оси, деления отмечены на каждой оси и есть заголовок.
Просматривая график, вы можете увидеть, что большинство студентов платят около 750 долларов в месяц за аренду, при этом около 1500 долларов — другая общая сумма. Как видно из графика, большинство студентов платят от 600 до 1600 долларов в месяц за аренду.Конечно, эти значения — всего лишь оценки из графика. Существует большой разрыв между классом в 1500 долларов и максимальным значением данных. Похоже, это говорит о том, что один студент платит намного больше, чем все остальные. Это значение можно считать выбросом. Выброс — это значение данных, которое далеко от остальных значений. Это может быть необычное значение или ошибка. Это значение данных, которое следует исследовать. В данном случае студент живет в очень дорогой части города, поэтому стоимость не является ошибкой, а просто очень необычной.Есть и другие аспекты, которые можно обсудить, но сначала необходимо ввести некоторые другие концепции.
Существует большой разрыв между классом в 1500 долларов и максимальным значением данных. Похоже, это говорит о том, что один студент платит намного больше, чем все остальные. Это значение можно считать выбросом. Выброс — это значение данных, которое далеко от остальных значений. Это может быть необычное значение или ошибка. Это значение данных, которое следует исследовать. В данном случае студент живет в очень дорогой части города, поэтому стоимость не является ошибкой, а просто очень необычной.Есть и другие аспекты, которые можно обсудить, но сначала необходимо ввести некоторые другие концепции.
Частоты полезны, но понимание относительного размера каждого класса в целом также полезно. Чтобы найти это, вы можете разделить частоту на общую, чтобы получить относительную частоту. Если у вас есть относительные частоты для всех классов, то у вас есть относительное распределение частот.
Определение \ (\ PageIndex {2} \)
Относительное распределение частот
Вариация частотного распределения — это относительное частотное распределение.Вместо того, чтобы указывать частоты для каждого класса, вычисляются относительные частоты.
Относительная частота \ (= \ dfrac {\ text {frequency}} {\ # \ text {точек данных}} \)
Это дает вам процент данных, которые попадают в каждый класс.
Пример \ (\ PageIndex {3} \) создания таблицы относительной частоты
Найдите относительную частоту для данных об уровне.
Решение
Из примера \ (\ PageIndex {1} \) частотное распределение воспроизводится в примере \ (\ PageIndex {2} \).
| Пределы классов | Границы классов | Средняя точка класса | Частота |
|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | 4 |
| 665-979 | 664,5-979,5 | 822 | 8 |
| 980-1294 | 979. 5-1294,5 5-1294,5 | 1127 | 5 |
| 1295-1609 | 1294,5–1609,5 | 1452 | 6 |
| 1610-1924 | 1609,5-1924,5 | 1767 | 0 |
| 1925-2239 | 1924,5-2239,5 | 2082 | 0 |
| 2240-2554 | 2239.5-2554,5 | 2397 | 1 |
Разделите каждую частоту на количество точек данных.
\ (\ dfrac {4} {24} = 0,17, \ dfrac {8} {24} = 0,33, \ dfrac {5} {24} = 0,21, \ rightleftharpoons \)
| Пределы классов | Границы классов | Средняя точка класса | Частота | Относительная частота |
|---|---|---|---|---|
| 350-664 | 349.5-664,5 | 507 | 4 | 0,17 |
| 665-979 | 664,5-979,5 | 822 | 8 | 0,33 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 | 0,21 |
| 1295-1609 | 1294. 5-1609,5 5-1609,5 | 1452 | 6 | 0,25 |
| 1610-1924 | 1609,5-1924,5 | 1767 | 0 | 0 |
| 1925-2239 | 1924,5-2239,5 | 2082 | 0 | 0 |
| 2240-2554 | 2239.5-2554,5 | 2397 | 1 | 0,04 |
| Итого | 24 | 1 |
Сумма относительных частот должна составлять 1 или 100%. (Это может немного отличаться из-за ошибок округления.)
График относительной частоты известен как гистограмма относительной частоты.Он выглядит идентично гистограмме частот, но по вертикальной оси отложена относительная частота, а не просто частоты.
Пример \ (\ PageIndex {4} \) построения гистограммы относительной частоты
Постройте гистограмму относительной частоты для распределения оценок из примера \ (\ PageIndex {1} \).
Решение
Границы классов отложены по горизонтальной оси, а относительные частоты отложены по вертикальной оси. (Это непросто сделать в R, поэтому используйте другую технологию для построения гистограммы относительной частоты.)
(Это непросто сделать в R, поэтому используйте другую технологию для построения гистограммы относительной частоты.)
Обратите внимание, что форма такая же, как и распределение частоты.
Еще одна полезная информация — сколько точек данных попадает ниже определенной границы класса. Например, учитель может захотеть узнать, сколько студентов набрало меньше 80%, врач может захотеть узнать, у скольких взрослых холестерин ниже 160, или менеджер может захотеть узнать, сколько магазинов имеет брутто менее 2000 долларов в день. Это известно как совокупная частота .Если вы хотите знать, какой процент данных попадает ниже определенной границы класса, тогда это будет совокупная относительная частота . Для совокупных частот вы определяете, сколько значений данных упало ниже верхнего предела класса.
Чтобы создать совокупное частотное распределение , подсчитайте количество точек данных, которые находятся ниже границы высшего класса, начиная с первого класса и заканчивая высшим классом. У последней границы высшего класса должны быть все точки данных под ней.Также включите количество точек данных ниже самой нижней границы класса, которая равна нулю.
Пример \ (\ PageIndex {5} \) создания совокупного частотного распределения
Создайте совокупное частотное распределение для данных в примере \ (\ PageIndex {1} \).
Решение
Частотное распределение данных показано в примере \ (\ PageIndex {2} \).
| Пределы классов | Границы классов | Средняя точка класса | Частота |
|---|---|---|---|
| 350-664 | 349.5-664,5 | 507 | 4 |
| 665-979 | 664,5-979,5 | 822 | 8 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 |
| 1295-1609 | 1294,5–1609,5 | 1452 | 6 |
| 1610-1924 | 1609. 5-1924,5 5-1924,5 | 1767 | 0 |
| 1925-2239 | 1924,5-2239,5 | 2082 | 0 |
| 2240-2554 | 2239,5-2554,5 | 2397 | 1 |
Теперь спросите себя, сколько точек данных попадает ниже каждой границы класса.Ниже 349,5 имеется 0 точек данных. Ниже 664,5 имеется 4 точки данных, ниже 979,5 имеется 4 + 8 = 12 точек данных, ниже 1294,5 имеется 4 + 8 + 5 = 17 точек данных, и продолжайте этот процесс, пока не достигнете границы верхнего класса. Это кратко описано в примере \ (\ PageIndex {4} \).
Чтобы получить кумулятивные частоты в R, вам необходимо выполнить команды для распределения частот. Как только вы это сделаете, используйте variable.cumfreq = cumsum (variable.freq) — создаст совокупные частоты для переменной
cumfreq0 = c (0, variable.cumfreq) — создает сводную таблицу частот для переменной.
cumfreq0 — отображает таблицу накопленной частоты.
В этом примере команда будет выглядеть так:
rent.cumfreq = cumsum (rent.freq)
cumfreq0 = c (0, rent.cumfreq)
cumfreq0
Выход:
\ (\ begin {array} {ccccccccc} {} & {[350,665)} & {[665,980)} & {[980,1.3e + 03)} & {[1.3e + 03, 1.61e + 03)} & {[1.61e + 03, 1.92e + 03)} & {[1.92e + 03,2.24e + 03)} & {[2.24e + 03, 2.56e + 03)} & {[2.56e + 03, 2.87e + 03)} \\ {0} & {4} & {12} & {17} & {23} & {23} & {23} & {24} & {24} \ end { массив} \)
Теперь введите это в таблицу. См. Пример \ (\ PageIndex {4} \).
| Пределы классов | Границы классов | Средняя точка класса | Частота | Накопленная частота |
|---|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | 4 | 4 |
| 665-979 | 664.5-979,5 | 822 | 8 | 12 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 | 17 |
| 1295-1609 | 1294,5–1609,5 | 1452 | 6 | 23 |
| 1610-1924 | 1609.5-1924,5 | 1767 | 0 | 23 |
| 1925-2239 | 1924,5-2239,5 | 2082 | 0 | 23 |
| 2240-2554 | 2239,5-2554,5 | 2397 | 1 | 24 |
Опять же, трудно смотреть на данные так, как они есть. График был бы полезен. График совокупной частоты называется ogive (o-jive). Чтобы создать ожив, сначала создайте шкалу по горизонтальной и вертикальной осям, которая будет соответствовать данным. Затем нанесите на график точки границы класса высшего класса в зависимости от совокупной частоты. Убедитесь, что вы включили точку с самой низкой границей класса и нулевой совокупной частотой. Тогда просто соедините точки.
График был бы полезен. График совокупной частоты называется ogive (o-jive). Чтобы создать ожив, сначала создайте шкалу по горизонтальной и вертикальной осям, которая будет соответствовать данным. Затем нанесите на график точки границы класса высшего класса в зависимости от совокупной частоты. Убедитесь, что вы включили точку с самой низкой границей класса и нулевой совокупной частотой. Тогда просто соедините точки.
Пример \ (\ PageIndex {6} \) отрисовка ожив
Нарисуйте ожив для данных в примере \ (\ PageIndex {1} \).
Решение
В R это будут следующие команды:
plot (breaks, cumfreq0, main = «title you want to use», xlab = «label you want to use», ylab = «label you want to use», ylim = c ( 0, число выше максимальной совокупной частоты) — строит линии оживляющего изображения
(разрывы, cumfreq0) — соединяет точки на огиве
В этом примере команды будут выглядеть так:
Plot (breaks, cumfreq0, main = «Совокупная частота ежемесячной аренды», xlab = «Ежемесячная арендная плата ($)», ylab = «Совокупная частота», ylim = c (0, 25))
строк (разрывы, cumfreq0)
Полезность огива состоит в том, чтобы позволить читателю узнать, сколько студентов платят меньше определенной суммы, а также какую сумму ежемесячной арендной платы платит определенное количество студентов.В качестве примера предположим, что вы хотите знать, сколько студентов платят менее 1500 долларов в месяц в аренду, затем вы можете увеличивать с 1500 долларов до тех пор, пока не попадете на график, а затем перейдете к осям совокупной частоты, чтобы увидеть, какое значение соответствует это значение. Оказывается, около 20 студентов платят менее 1500 долларов. (См. График 2.2.4 .)
Рисунок \ (\ PageIndex {4} \): Ogive для ежемесячной арендной платы в примере Кроме того, если вы хотите узнать сумму, которую 15 студентов платят меньше, тогда вы начинаете с 15 по вертикальной оси, а затем переходите к графику и вниз до горизонтальной оси, где линия пересекает график. Вы видите, что 15 студентов платят меньше 1200 долларов в месяц. (См. График 2.2.5 .)
Вы видите, что 15 студентов платят меньше 1200 долларов в месяц. (См. График 2.2.5 .)
Если вы построите график совокупной относительной частоты, то вы сможете узнать, какой процент ниже определенного числа, а не просто количество людей ниже определенного значения.
Формы раздачи:
Когда вы смотрите на распределение, обратите внимание на базовую форму. На гистограммах можно увидеть несколько основных форм.Однако имейте в виду, что некоторые дистрибутивы не имеют формы. Обычные формы — симметричные, скошенные и однородные. Другой интерес — сколько пиков может иметь график. Это называется модальным.
Симметричный означает, что вы можете сложить график пополам посередине, и две стороны выровняются. Вы можете думать о двух сторонах как о зеркальном отображении друг друга. Перекос означает, что один «хвост» графика длиннее другого. График смещен в сторону более длинного хвоста (в обратном направлении от ожидаемого).На однородном графике все столбцы имеют одинаковую высоту.
Модальный относится к количеству пиков. Унимодальный режим имеет один пик, а бимодальный — два. Обычно, если график имеет более двух пиков, модальная информация больше не представляет интереса.
Другими важными особенностями, которые следует учитывать, являются промежутки между столбиками, повторяющийся узор, степень разброса данных и расположение центра графика.
Примеры графиков
:Этот график примерно симметричный и одномодальный:
РисунокЭтот график симметричный и бимодальный:
РисунокЭтот график смещен вправо:
РисунокЭтот график смещен влево и имеет пробел:
РисунокЭтот график является однородным, поскольку все столбцы имеют одинаковую высоту:
ФигураПример \ (\ PageIndex {7} \) создания частотного распределения, гистограммы и огива
Следующие данные представляют собой процентное изменение уровня оплаты за обучение в государственных четырехлетних колледжах (с поправкой на инфляцию) с 2008 по 2013 год (Weissmann, 2013). Создайте частотное распределение, гистограмму и изображение для данных.
Создайте частотное распределение, гистограмму и изображение для данных.
| 19,5% | 40,8% | 57,0% | 15,1% | 17,4% | 5,2% | 13,0% |
| 15,6% | 51,5% | 15,6% | 14,5% | 22,4% | 19.5% | 31,3% |
| 21,7% | 27,0% | 13,1% | 26,8% | 24,3% | 38,0% | 21,1% |
| 9,3% | 46,7% | 14,5% | 78,4% | 67,3% | 21,1% | 22,4% |
| 5.3% | 17,3% | 17,5% | 36,6% | 72,0% | 63,2% | 15,1% |
| 2,2% | 17,5% | 36,7% | 2,8% | 16,2% | 20,5% | 17,8% |
| 30,1% | 63,6% | 17.8% | 23,2% | 25,3% | 21,4% | 28,5% |
| 9,4% | ||||||
Решение
- Найдите диапазон:
наибольшее значение — наименьшее значение = \ (78,4 \)% \ (- 2,2 \)% \ (= 76,2 \)% - Выберите количество классов:
Поскольку имеется 50 точек данных, следует использовать от 6 до 8 классов. Возьмем 8.
Возьмем 8. - Найдите ширину класса:
width \ (= \ dfrac {\ text {range}} {8} = \ dfrac {76.2 \%} {8} \ приблизительно 9,525 \% \)
Поскольку данные имеют один десятичный разряд, тогда ширина класса должна округляться до одного десятичного знака. Убедитесь, что вы округлились.
ширина \ (= 9,6 \)% - Найдите пределы класса:
\ (2,2 \% + 9,6 \% = 11,8 \%, 11,8 \% + 9,6 \% = 21,4 \%, 21,4 \% + 9,6 \% = 31,0 \%, \ leftrightharpoons \) - Найдите границы класса:
Поскольку данные имеют один десятичный знак, границы классов должны иметь два десятичных знака, поэтому вычтите 0.05 от нижнего предела класса, чтобы получить границы класса. Добавьте 0,05 к верхнему пределу класса для границы последнего класса.
\ (2.2-0.05 = 2.15 \%, 11.8-0.05 = 11.75 \%, 21.4-0.05 = 21.35 \% \ leftrightharpoons \)
Каждое значение в данных должно попадать ровно в один из классов. Никакие значения данных не должны попадать прямо на границу двух классов. - Найдите средние точки класса:
midpoint \ (= \ dfrac {\ text {lower limt} + \ text {upper limit}} {2} \)
\ (\ dfrac {2.2 + 11.7} {2} = 6.95 \% , \ dfrac {11.8 + 21.3} {2} = 16.55 \%, \ leftrightharpoons \) - Подсчитайте и найдите частоту данных:
| Пределы классов | Границы классов | Средняя точка класса | Tally | Частота | Относительная частота | Накопленная частота |
|---|---|---|---|---|---|---|
| 2,2-11,7 | 2,15-11,75 | 6.95 | \ (\ cancel {||||} | \) | 6 | 0,12 | 6 |
| 11,8–21,3 | 11,75-21,35 | 16,55 | \ (\ cancel {||||} \ cancel {||||} \ cancel {||||} \ cancel {||||} \) | 20 | 0,40 | 26 |
| 21,4-30,9 | 21. 35-30.95 35-30.95 | 26,15 | \ (\ cancel {||||} \ cancel {||||} | \) | 11 | 0,22 | 37 |
| 31,0-45,0 | 30,95-40,55 | 35,75 | \ (|||| \) | 4 | 0,08 | 41 |
| 40,6-50,1 | 40.55-50,15 | 45,35 | \ (|| \) | 2 | 0,04 | 43 |
| 50,2-59,7 | 50,15-59,75 | 54,95 | \ (|| \) | 2 | 0,04 | 45 |
| 59,8-69,3 | 59,75-69,35 | 64.55 | \ (||| \) | 3 | 0,06 | 48 |
| 69,4-78,9 | 69,35-78,95 | 74,15 | \ (|| \) | 2 | 0,04 | 50 |
Убедитесь, что сумма частот совпадает с количеством точек данных.
Этот график наклонен вправо, без пропусков. Это говорит о том, что большинство процентов увеличения платы за обучение составили около 16,55%, при этом в очень немногих штатах процентное увеличение превышает 45,35%.
Рисунок \ (\ PageIndex {12} \) : Ogive для уровней обучения в государственных четырехлетних колледжахГлядя на Ogive, вы можете увидеть, что в 30 штатах процентное изменение уровня обучения составило около 25% или меньше.
Бывают случаи, когда пределы классов в частотном распределении предопределены.Пример \ (\ PageIndex {8} \) демонстрирует эту ситуацию.
Пример \ (\ PageIndex {8} \) создания частотного распределения и гистограммы
Ниже приведены процентные оценки 25 студентов, обучающихся по курсу статистики. Составьте частотное распределение и гистограмму.
| 62 | 87 | 81 | 69 | 87 | 62 | 45 | 95 | 76 | 76 |
| 62 | 71 | 65 | 67 | 72 | 80 | 40 | 77 | 87 | 58 |
| 84 | 73 | 93 | 64 | 89 |
Решение
Поскольку эти данные представляют собой процентные оценки, имеет смысл делать классы кратными 10, поскольку оценки обычно составляют от 90 до 100%, от 80 до 90% и т. Д.Легче не использовать границы классов, а вместо этого использовать пределы класса и думать о том, что верхний предел класса соответствует нижнему пределу следующих классов, но не включает его. Например, класс 80–90 означает оценку от 80% до 90%, но не включая его. Учащийся с 89,9% будет в классе 80-90.
Д.Легче не использовать границы классов, а вместо этого использовать пределы класса и думать о том, что верхний предел класса соответствует нижнему пределу следующих классов, но не включает его. Например, класс 80–90 означает оценку от 80% до 90%, но не включая его. Учащийся с 89,9% будет в классе 80-90.
| Предел класса | Средняя точка класса | Tally | Частота |
|---|---|---|---|
| 40-50 | 45 | \ (|| \) | 2 |
| 50-60 | 55 | \ (| \) | 1 |
| 60-70 | 65 | \ (\ cancel {||||} || \) | 7 |
| 70-80 | 75 | \ (\ cancel {||||} | \) | 6 |
| 80-90 | 85 | \ (\ cancel {||||} || \) | 7 |
| 90-100 | 95 | \ (|| \) | 2 |
Похоже, что у большинства учащихся было от 60 до 90%. Этот график выглядит несколько симметричным, а также бимодальным. Такое же количество студентов зарабатывает от 60 до 70% и от 80 до 90%.
Этот график выглядит несколько симметричным, а также бимодальным. Такое же количество студентов зарабатывает от 60 до 70% и от 80 до 90%.
Существуют и другие типы графиков для количественных данных. Они будут исследованы в следующем разделе.
Домашнее задание
Упражнение \ (\ PageIndex {1} \)
- Средние доходы мужчин в каждом штате США, включая округ Колумбия и Пуэрто-Рико, приведены в примере \ (\ PageIndex {9} \) («Средний доход», 2013 г.).Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 7 классов.
42 951 долл. США 52 379 долл. США 42 544 долл. США 37 488 долл. США $ 49 281 $ 50 987 60 705 долл. США $ 50 411 $ 66 760 40 951 долл. США $ 43 902 45 494 долл. США 41 528 долл. США $ 50 746 $ 45 183 43 624 долл. США 43 993 долл. США $ 41 612 46313 долл. США 43 944 долл. США $ 56 708 60 264 долл. США $ 50 053 $ 50 580 40 202 долл. США 43 146 долл. США $ 41 635 42 182 долл. США 41 803 долл. США $ 53 033 60 568 долл. США $ 41 037 $ 50 388 $ 41 950 $ 44 660 $ 46 176 41420 долл.  США
США45 976 долл. США $ 47 956 $ 22 529 $ 48 842 41464 долл. США 40 285 долл. США 41 309 долл. США 43 160 долл. США $ 47 573 $ 44 057 52 805 долларов США 53 046 долл. США 42 125 долл. США $ 46 214 $ 51 630 Таблица \ (\ PageIndex {9} \): данные о среднем доходе для мужчин - Средние доходы женщин в каждом штате США, включая округ Колумбия и Пуэрто-Рико, приведены в примере \ (\ PageIndex {10} \) («Средний доход», 2013 г.).Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 7 классов.
31 862 долл. США 40 550 долларов США $ 36 048 $ 30 752 $ 41 817 $ 40 236 47 476 долл. США 40 500 долл. США $ 60,332 $ 33 823 $ 35 438 $ 37 242 31 238 долл. США 39 150 долл. США $ 34 023 $ 33 745 33 269 долл. США $ 32 684 31 844 долл. США 34 599 долл. США $ 48 748 $ 46 185 $ 36 931 40 416 долл.  США
США29 548 долл. США $ 33 865 31 067 долл. США 33 424 долл. США $ 35 484 $ 41 021 47 155 долл. США 32 316 долл. США 42 113 долл. США 33 459 долл. США 32 462 долл. США $ 35 746 31 274 долл. США $ 36 027 37 089 долл. США $ 22 117 $ 41 412 31 330 долл. США 31 329 долл. США 33 184 долл. США $ 35 301 $ 32 843 $ 38 177 40 969 долл. США 40 993 долл. США 29 688 долл. США $ 35 890 $ 34 381 Таблица \ (\ PageIndex {10} \): данные о среднем доходе женщин - Плотность людей на квадратный километр для африканских стран приведена в примере \ (\ PageIndex {11} \) («Плотность людей», 2013 г.).Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 8 классов.
15 16 81 3 62 367 42 123 8 9 337 12 29 70 39 83 26 51 79 6 157 105 42 45 72 72 37 4 36 134 12 3 630 563 72 29 3 13 176 341 415 187 65 194 75 16 41 18 69 49 103 65 143 2 18 31 Таблица \ (\ PageIndex {11} \): данные о плотности населения на квадратный километр - Закон о доступном медицинском обслуживании создал рынок, на котором люди могут приобрести планы медицинского обслуживания.
 В 2014 году взносы для 27-летнего человека по медицинскому страхованию бронзового уровня приведены в примере \ (\ PageIndex {12} \) («Рынок медицинского страхования», 2013 г.). Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 5 классов.
В 2014 году взносы для 27-летнего человека по медицинскому страхованию бронзового уровня приведены в примере \ (\ PageIndex {12} \) («Рынок медицинского страхования», 2013 г.). Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 5 классов.$ 114 $ 119 $ 121 $ 125 $ 132 $ 139 $ 139 $ 141 $ 143 $ 145 $ 151 $ 153 $ 156 $ 159 $ 162 $ 163 $ 165 $ 166 170 долл. США $ 170 $ 176 $ 177 $ 181 $ 185 185 долл. США $ 186 $ 186 $ 189 $ 190 $ 192 $ 196 $ 203 $ 204 $ 219 $ 254 $ 286 Таблица \ (\ PageIndex {12} \): данные о страховых взносах - Создайте гистограмму и гистограмму относительной частоты для данных в примере \ (\ PageIndex {9} \).Опишите форму и любые выводы, которые вы можете увидеть на графике.
- Создайте гистограмму и гистограмму относительной частоты для данных в примере \ (\ PageIndex {10} \).
 Опишите форму и любые выводы, которые вы можете увидеть на графике.
Опишите форму и любые выводы, которые вы можете увидеть на графике. - Создайте гистограмму и гистограмму относительной частоты для данных в примере \ (\ PageIndex {11} \). Опишите форму и любые выводы, которые вы можете сделать с помощью графика.
- Создайте гистограмму и гистограмму относительной частоты для данных в примере \ (\ PageIndex {12} \).Опишите форму и любые выводы, которые вы можете увидеть на графике.
- Создайте оживление для данных в примере \ (\ PageIndex {9} \). Опишите любые выводы, которые вы можете сделать с помощью графика.
- Создайте оживление для данных в примере \ (\ PageIndex {10} \). Опишите любые выводы, которые вы можете сделать с помощью графика.
- Создайте оживление для данных в примере \ (\ PageIndex {11} \). Опишите любые выводы, которые вы можете сделать с помощью графика.
- Создайте оживление для данных в примере \ (\ PageIndex {12} \). Опишите любые выводы, которые вы можете сделать с помощью графика.
- Студенты класса статистики сдали свой первый тест. Ниже приведены набранные ими баллы. Создайте частотное распределение и гистограмму для данных, используя ограничения классов, которые имеют смысл для данных об оценках. Опишите форму раздачи.
80 79 89 74 73 67 79 93 70 70 76 88 83 73 81 79 80 85 79 80 79 58 93 94 74 Таблица \ (\ PageIndex {13} \): данные теста 1 оценки - Студенты класса статистики сдали свой первый тест.
 Ниже приведены набранные ими баллы. Создайте частотное распределение и гистограмму для данных, используя ограничения классов, которые имеют смысл для данных об оценках. Опишите форму раздачи. Сравните с графиком в вопросе 13.
Ниже приведены набранные ими баллы. Создайте частотное распределение и гистограмму для данных, используя ограничения классов, которые имеют смысл для данных об оценках. Опишите форму раздачи. Сравните с графиком в вопросе 13.Таблица \ (\ PageIndex {14} \): данные теста 1, оценки 67 67 76 47 85 70 87 76 80 72 84 98 84 64 65 82 81 81 88 74 87 83
- Ответ
Посмотреть решения
Статистические данные и группировка данных
Данные можно определить как группы информации, которые представляют качественные или количественные атрибуты переменной или набора переменных, которые совпадают с говоря, что данные могут быть любым набором информации, описывающей данную сущность.Данные в статистике можно разделить на сгруппированные данные и несгруппированные данные.
Любые данные, которые вы собираете в первую очередь, не сгруппированы. Негруппированные данные — это данные в сырой. Примером разгруппированных данных является любой список чисел, который вы можете придумать.
Сгруппированные данные
Сгруппированные данные — это данные, организованные в группы, известные как классы. Сгруппированы
данные были «засекречены» и, таким образом, был проведен некоторый анализ данных,
это означает, что данные больше не являются сырыми.
Сгруппированы
данные были «засекречены» и, таким образом, был проведен некоторый анализ данных,
это означает, что данные больше не являются сырыми.
Класс данных — это группа данных, которая связана некоторым свойством, определяемым пользователем. Для Например, если вы собирали возраст людей, которых встречали, когда проходили на улице, вы можете сгруппировать их по классам как подростков, двадцатилетних, тридцатые, сороковые годы и так далее.Каждая из этих групп называется классом.
Каждый из этих классов имеет определенную ширину и называется классом . Интервал или Размер класса . Этот интервал между занятиями очень важен, когда речь идет о рисовании гистограмм и частотных диаграмм. Все классы могут иметь один и тот же размер класса или они могут иметь разные размеры классов в зависимости от того, как вы сгруппируйте свои данные.Интервал занятий всегда целое число.
Ниже приведен пример сгруппированных данных, в которых классы имеют одинаковый интервал классов.
| Возраст (лет) | Частота |
|---|---|
| 0–9 | 12 |
| 10-19 | 30 |
| 20 — 29 | 18 |
| 30 — 39 | 12 |
| 40–49 | 9 |
| 50–59 | 6 |
| 60 — 69 | 0 |
Решение:
Ниже приведен пример сгруппированных данных, где классы имеют разный интервал классов.
| Возраст (лет) | Частота | Интервал занятий |
|---|---|---|
| 0–9 | 15 | 10 |
| 10-19 | 18 | 10 |
| 20 — 29 | 17 | 10 |
| 30–49 | 35 год | 20 |
| 50–79 | 20 | 30 |
Расчет интервала между занятиями
Учитывая набор необработанных или разгруппированных данных, как бы вы сгруппировали эти данные в подходящие классы, с которыми легко работать и в то же время значимые?
Первый шаг — определить, сколько классов вы хотите иметь. Затем вы вычитаете
наименьшее значение в наборе данных из наибольшего значения в наборе данных, а затем
вы делите на количество классов, которые хотите иметь:
Затем вы вычитаете
наименьшее значение в наборе данных из наибольшего значения в наборе данных, а затем
вы делите на количество классов, которые хотите иметь:
Пример 1:
Сгруппируйте следующие необработанные данные в десять классов.
Решение:
Первый шаг — определить наибольшее и наименьшее число
.Интервал класса всегда должен быть целым числом, но в этом случае у нас есть десятичная дробь. номер.Решение этой проблемы — округлить до ближайшего целого числа.
В этом примере 2,8 округляется до 3. Итак, теперь ширина нашего класса будет 3; имея в виду что мы сгруппировали вышеуказанные данные в группы по 3, как в таблице ниже.
| Число | Частота |
|---|---|
| 1–3 | 7 |
| 4–6 | 6 |
| 7–9 | 4 |
| 10–12 | 2 |
| 13–15 | 2 |
| 16–18 | 8 |
| 19 — 21 | 1 |
| 22–24 | 2 |
| 25–27 | 3 |
| 28 — 30 | 2 |
Пределы классов и границы классов
Пределы класса относятся к фактическим значениям, которые вы видите в таблице. Взять пример
в приведенной выше таблице 1 и 3 будут пределами класса первого
класс. Пределы класса делятся на две категории: нижний предел класса и верхний предел.
ограничение класса. В таблице выше для первого класса 1 — это нижний класс.
предел, а 3 — верхний предел класса.
Взять пример
в приведенной выше таблице 1 и 3 будут пределами класса первого
класс. Пределы класса делятся на две категории: нижний предел класса и верхний предел.
ограничение класса. В таблице выше для первого класса 1 — это нижний класс.
предел, а 3 — верхний предел класса.
С другой стороны, границы классов не всегда соблюдаются в частотной таблице.Границы класса дают истинный интервал класса, и, как и ограничения класса, также разделены на нижние и верхние границы классов.
Связь между границами классов и интервалом между классами задается как следует:
Границы класса связаны с пределами класса заданными отношениями:
В результате вышеизложенного нижняя граница класса одного класса равна верхний класс граница предыдущего класса.
Пределы классов и границы классов играют разные роли, когда дело доходит до представления статистические данные схематически, как мы увидим через мгновение.
Ширина класса: простое определение — статистика Как к
Таблица распределения частот, показывающая ширину класса 7 для оценок IQ (например, 125-118 = 7)
Ширина класса относится к разнице между верхней и нижней границами любого класса (категории).В зависимости от автора это слово также иногда используется более конкретно для обозначения:
- Разница между верхними пределами двух последовательных (соседних) классов, или
- Разница между нижними границами двух последовательных классов.
Обратите внимание, что они отличаются от разницы между верхним и нижним пределами класса.
Расчет ширины класса в таблице распределения частот
Посмотрите видео или прочтите ниже:
В таблице частотного распределения классы должны иметь одинаковую ширину.Это позволяет относительно легко вычислить ширину класса, поскольку вы имеете дело только с одной шириной (в отличие от различных). Чтобы найти ширину:
- Вычислить диапазон всего набора данных путем вычитания самой низкой точки из самой высокой,
- Разделите на количество классов.
- Округлите это число в большую сторону (обычно до ближайшего целого числа).
Пример расчета ширины класса
Предположим, вы анализируете данные заключительного экзамена, сданного в конце курса статистики.Количество классов, на которые вы их разделяете, несколько произвольно, но следует помнить о нескольких вещах:
- Создайте достаточно категорий, чтобы у вас было более одного элемента в каждой категории.
- Выберите число, которым легко манипулировать; обычно от пяти до двадцати — хорошая идея. Например, если вы анализируете относительно небольшой класс из 25 студентов, вы можете решить создать частотную таблицу с пятью классами.
Пример: Найдите подходящий класс со следующим набором баллов учащихся:
52, 82, 86, 83, 56, 98, 71, 91, 75, 88, 69, 78, 64, 74, 81, 83, 77, 90, 85, 64, 79, 71, 64 и 83.
- Найдите диапазон, вычтя самый низкий балл из самого высокого: разница между максимальным и самым низким баллом: 98 — 52 = 46.
- Разделим на количество классов: 46/5, = 9,2.
- Округлите это число: 9,2≅ 10.
Список литературы
Глитон, Джеймс У. Раздаточный материал лекции: Организация и обобщение данных. Получено с http://www.unf.edu/~jgleaton/LectureTransCh3.doc от 27 августа 2018 г.
Gonick, L. (1993). Мультяшный справочник по статистике.HarperPerennial.
Джонс, Джеймс. Статистика: частотные распределения и графики. Получено с https://people.richland.edu/james/lecture/m170/ch02-def.html от 27 августа 2018 г.
Levine, D. (2014). Даже вы можете изучить статистику и аналитику: простое для понимания руководство по статистике и аналитике, 3-е издание. Пресс Pearson FT
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Пределы класса
Пределы классаПределы классов, границы классов, знаки классов.
- Пределы класса. По два на каждый класс.
Нижний предел класса — это наименьшее значение данных, которое может входить в класс.
Верхний предел класса — это наибольшее значение данных, которое может входить в класс.
Пределы класса имеют ту же точность, что и значения данных; такое же количество десятичные разряды как значения данных. - Границы классов. Это промежуточные точки, разделяющие
классы.
Граница нижнего класса данного класса получается усреднением верхнего предел предыдущего класса и нижний предел данного класса.
Граница высшего класса данного класса получается усреднением верхнего предел класса и нижний предел следующего класса. - Знаки класса. Это середина классов.
Они получены путем усреднения пределов.
Пример A. ДАННЫЕ: 210, 222, 233 и т. Д.
| Класс | Частота | Пределы класса | Границы классов | Знак класса | Размер класса |
| 180–199 | 2 | 180, 199 | 179.5, 199,5 | 189,5 | 20 |
| 200 — 219 | 5 | 200, 219 | 199,5, 219,5 | 209,5 | 20 |
| 220 — 239 | 12 | 220, 239 | 219,5, 239,5 | 229,5 | 20 |
| 240–259 | 6 | 240–259 | 239.5, 259,5 | 249,5 | 20 |
| 25 |
Пример B. ДАННЫЕ: 10.6, 11.7, 12.8 и т. Д.
| Класс | Частота | Пределы класса | Границы классов | Знак класса | Размер класса |
| 9.6 — 14,5 | 10 | 9,6, 14,5 | 9,55, 14,55 | 12,05 | 5 |
| 14,6 — 24,5 | 20 | 14,6, 24,5 | 14,55, 24,55 | 19,55 | 10 |
| 24,6 — 44,5 | 30 | 24,6, 44,5 | 24,55, 44,55 | 29.55 | 20 |
| 44,6 — 54,5 | 25 | 44,6, 54,5 | 44,55, 54,55 | 49,55 | 10 |
| 85 |
Открытые классы — это классы, не имеющие верхнего предела или нижний предел.
Частотное распределение дискретных и непрерывных переменных — MathsTips.com
Дискретные и непрерывные переменные были определены в статье «Введение в частотные распределения». Мы продолжим обсуждение частотных распределений в этой статье, перейдя к Частотным распределениям дискретных и непрерывных переменных.
Частотное распределение дискретной переменнойПоскольку дискретная переменная может принимать некоторые или дискретные значения в пределах своего диапазона изменения, будет естественным взять отдельный класс для каждого отдельного значения дискретной переменной, как показано в следующем примере, касающемся ежедневного количества автомобильных аварий во время 30 дней месяца.
3 4 4 5 5 3
4 3 5 7 6 4
4 3 4 5 5 5
5 5 3 5 6 4
5 4 4 6 5 6
Таблица № 2: Показывает распределение частоты ежедневного количества ДТП в течение месяца.
| Количество ДТП | Частота |
| 3 | 5 |
| 4 | 9 |
| 5 | 11 |
| 6 | 4 |
| 7 | 1 |
| Всего | 30 |
Для непрерывной переменной, если мы возьмем класс для каждого отдельного значения переменной, количество классов станет чрезмерно большим, что приведет к поражению цели табулирования.Фактически, поскольку непрерывная переменная может принимать бесконечное количество значений в пределах своего диапазона изменения, классификация или подразделение таких данных обязательно является искусственным. Вот некоторые рекомендации, которым следует следовать при разделении непрерывных данных на классы:
- Классы должны быть взаимоисключающими, т. Е. Не перекрываться. Никакие два класса не должны содержать одинаковый интервал значений переменной.
- Классы должны быть исчерпывающими, т. Е. Должны охватывать весь диапазон данных.
- Количество классов и ширина каждого класса не должны быть ни слишком маленькими, ни слишком большими. Другими словами, должно быть относительно меньше классов, если разница между наименьшим значением переменной и ее наибольшим значением мала, и относительно больше классов, если такая же разница велика. Эта разница между наименьшим значением переменной и наибольшим значением переменной называется диапазоном переменной или набором данных.
- Желательно, чтобы классы были одинаковой ширины.
Рассмотрим следующий пример относительно дневных максимальных температур в городе за 50 дней.
28 28 31 29 35 33 28 31 34 29
25 27 29 33 30 31 32 26 26 21
21 20 22 24 28 30 34 33 35 29
23 21 20 19 19 18 19 17 20 19
18 18 19 27 17 18 20 21 18 19
Минимальное значение = 17
Максимальное значение = 35
Диапазон = 35-17 = 18
Количество классов = 5 (скажем)
ширина каждого класса = 4
Таблица No.3: Показывает частотное распределение температуры в городе за 50 дней.
| Интервалы классов (температуры) | Частота |
| 17-20 | 17 |
| 21-24 | 7 |
| 25–28 | 10 |
| 29-32 | 9 |
| 33-36 | 7 |
| Всего | 50 |
Интервал класса: Весь диапазон значений переменных классифицируется в некоторых группах в виде интервалов.Каждый интервал называется интервалом класса.
Частота класса: Количество наблюдений в классе называется частотой класса или частоты класса.
Относительная частота: Относительная частота определяется как доля наблюдений, соответствующих определенному значению переменной или классу значений переменной. Относительная частота конкретного значения переменной или класса значений переменной получается делением частоты, соответствующей этому конкретному значению или этому конкретному классу, на общее количество наблюдений в наборе данных, т.е.е., общая частота.
Относительная частота любого значения или любого класса находится между 0 и 1. Мы вычисляем относительную частоту, если хотим получить представление об относительной важности конкретного значения или класса по отношению к общей частоте.
Частота в процентах: Иногда относительная частота выражается в процентах, то есть, что известно как процентная частота. Выраженная в процентах, процентная частота всех значений или всех классов должна составлять в сумме 100.
Пределы классов и границы классов:
Пределы класса — это две конечные точки интервала классов, которые используются для построения частотного распределения. Наименьшее значение переменной, которое может быть включено в интервал классов, называется нижним пределом класса этого интервала классов. Наибольшее значение переменной, которое может быть включено в интервал класса, называется верхним пределом класса этого интервала класса. Это не настоящие пределы или конечные точки интервала класса.Следовательно, пределы класса называются очевидными пределами класса.
Возьмем, например, Таблицу № 3. Интервалы классов 17-20, 21-24, 25-28, 29-32 и 33-36. Здесь, скажем, для класса 17-20 нижний предел класса равен 17, а верхний предел класса равен 20. Однако, если бы наблюдалось значение 20,5, он не был бы включен в этот класс. Наблюдение 20,5 будет включено в класс 21-24. Опять же, если бы было наблюдение 16,5, его бы включили в класс 17-20. Следовательно, фактически двумя фактическими конечными точками класса 17-20 являются 16.5 и 20.5. Это действительные или истинные пределы класса.
Две реальные конечные точки интервала класса называются границами класса. Их также называют реальными пределами класса. Основное правило состоит в том, что пределы классов должны иметь тот же десятичный разряд, что и набор данных, но границы классов должны иметь на один десятичный разряд больше. Например, предположим, что у нас есть следующий набор данных о весе группы студентов (в кг): 50,5, 50,8, 63,6, 48,4, 58,6 и 60,2. Здесь пределы класса должны иметь один десятичный знак, а границы классов — два десятичных знака.Мы получаем границы классов из пределов классов, разделив разницу между верхней границей класса и нижней границей следующего более высокого класса на две равные части. Скажем, мы рассматриваем классы 17-20 и 21-24. 21-20 = 1. И снова у нас есть. Мы добавляем 0,5 к верхнему пределу класса каждого класса и вычитаем 0,5 из нижнего предела класса каждого класса. Итак, границы классов 16,5-20,5, 20,5-24,5 и так далее. Для класса 16,5–20,5 16,5 — это нижняя граница класса, а 20,5 — верхняя граница.Следует отметить, что граница высшего класса нижнего класса совпадает с границей высшего класса следующего более высокого класса. Это вызовет путаницу. Где мы должны включить наблюдение, которое читается как 20,5? Ответ: 20,5 следует отнести к классу 20,5–24,5. Это потому, что правило состоит в том, что частота, соответствующая классу, обозначает количество наблюдений Границы нижнего класса, но границы верхнего класса. Это называется методом левого включения . Включая нижнюю границу класса, но не верхнюю границу класса, мы устраняем путаницу относительно того, где разместить наблюдение, которое случайно попадает в точку границы класса.
Открытые классы: Может случиться так, что некоторые значения в наборе данных будут чрезвычайно малы по сравнению с другими значениями набора данных, и аналогично некоторые значения будут чрезвычайно большими по сравнению. Тогда мы не используем нижний предел первого класса и верхний предел последнего класса.Такие классы называются открытыми классами.
Ширина класса: Длина класса называется шириной класса. Он также известен как размер класса.
,
U.C.B. является границей высшего класса
L.C.B. граница нижнего класса
Оценка класса: Средняя точка интервала класса называется оценкой класса. Это репрезентативная ценность всего класса.
Плотность частоты: Это частота на единицу ширины класса.Выдается:
Плотности частот необходимы для сравнения двух классов неравной ширины. Для классов равной ширины плотности частот пропорциональны частотам классов.
Относительная плотность частоты: Относительная плотность частоты класса — это относительная частота, деленная на ширину класса. Выдается:
Упражнение
1. Постройте частотное распределение переменной «длина слова» из следующего:
«Гребите на лодке плавно вниз по течению,
Весело, весело, весело, жизнь — всего лишь мечта.”
Рассчитайте относительные частоты и частоты в процентах.
2. Следующие данные основаны на ответах 50 сотрудников определенного офиса о расстояниях (в км) между их местом жительства и местом работы:
1,5 2,2 6,2 7,1 12,3 13,6 2,4 6,5 9,1 5,0
18,2 7,1 3,0 15,2 15,2 4,0 17,2 1,6 14,2 5,1
4,0 16,5 4,3 5,7 8,9 6,0 5,1 18,9 5,6 2,3
9,1 11,5 12,5 1,7 9,5 2,0 10,3 11,8 4,4 10,5
9,3 18,0 8,2 8.9 4,3 14,1 7,4 3,7 2,8 6,7
Постройте частотное распределение на основе этих данных.
Статистика: графики распределения частот
Статистика: графики распределения частотСтатистика: распределение частот и графики
Определения
- Необработанные данные
- Данные собраны в исходном виде.
- Частота
- Сколько раз встречается определенное значение или класс значений.
- Распределение частот
- Организация исходных данных в виде таблиц с классами и частотами.
- Категориальное распределение частот
- Частотное распределение, в котором данные являются только номинальными или порядковыми.
- Разгруппированное распределение частот
- Частотное распределение числовых данных. Необработанные данные не группируются.
- Групповое распределение частот
- Частотное распределение, при котором несколько номеров сгруппированы в один класс.
- Пределы классов
- Отделите один класс в сгруппированном распределении частот от другого.Пределы могли фактически появляются в данных и имеют пробелы между верхним пределом одного класса и нижняя граница следующего.
- Границы классов
- Отделите один класс в сгруппированном распределении частот от другого. Границы имеют на один десятичный знак больше, чем необработанные данные, и поэтому не отображаются в данных. Между верхней границей одного класса и нижней границей класса нет разрыва. следующий урок. Граница нижнего класса находится путем вычитания 0.5 единиц снизу предел класса и граница высшего класса находится путем добавления 0,5 единиц к высшему классу предел.
- Ширина класса
- Разница между верхней и нижней границами любого класса. Ширина класса также разница между нижними пределами двух последовательных классов или верхним пределы двух последовательных классов. Это не разница между верхним и нижним пределы того же класса.
- класс (середина)
- Число в середине класса.Он находится путем сложения верхнего и нижнего пределов и деление на два. Его также можно найти, добавив верхнюю и нижнюю границы и деление на два.
- кумулятивная частота
- Число значений меньше верхней границы класса для текущего класса. Это текущий итог частот.
- Относительная частота
- Частота, деленная на общую частоту. Это дает процент значений, попадающих в этот класс.
- кумулятивная относительная частота (относительная кумулятивная частота)
- Промежуточный итог относительных частот или кумулятивной частоты, деленный на общая частота.Дает процент значений ниже, чем у высшего класса граница.
- Гистограмма
- График, на котором данные отображаются с использованием вертикальных полос разной высоты для представления частоты. Горизонтальная ось может быть либо границами классов, либо отметками классов, либо ограничения класса.
- Полигон частот
- Линейный график. Частота расположена по вертикальной оси, а средние точки класса — размещены по горизонтальной оси. Эти точки соединены линиями.
- Огив
- Полигон накопленной частоты или относительной накопленной частоты. Вертикальная ось — кумулятивная частота или относительная кумулятивная частота. В горизонтальная ось — границы классов. График всегда начинается с нуля в самом низком граница класса и будет иметь общую частоту (для кумулятивной частоты) или 1,00 (для относительной совокупной частоты).
- Диаграмма Парето
- Столбиковая диаграмма для качественных данных с полосами, расположенными в соответствии с частотой.
- Круговая диаграмма
- Графическое изображение данных в виде кусочков пирога. Частота определяет размер ломтик. Число градусов в любом срезе — это относительная частота, умноженная на 360 градусов.
- Пиктограмма
- График, в котором для представления данных используются изображения.
- Участок стебля и листа
- График данных, в котором часть значения данных используется в качестве основы, а остальная часть значения данных (лист) для формирования групп или классов. Это очень полезно для быстрой сортировки данных.
Содержание Статистика
: сгруппированные распределения частот
Статистика: сгруппированные распределения частотСтатистика: сгруппированные распределения частот
Указания по занятиям
- Должно быть от 5 до 20 классов.
- Ширина класса должна быть нечетным числом. Это гарантирует, что средние точки класса будут целые числа вместо десятичных.
- Классы должны быть взаимоисключающими.Это означает, что никакое значение данных не может быть разделено на две части. разные классы
- Уроки должны быть всеобъемлющими или исчерпывающими. Это означает, что все значения данных должны быть включены.
- Уроки должны быть непрерывными. В частотном распределении нет пропусков. Классы, которые не должны быть включены в них значения (если только это не первый или последний класс, которые были отброшены).
- Классы должны быть равны по ширине. Исключение составляет первый или последний класс. Это возможно иметь «внизу»… «или» … и выше «класс. Часто используется с возрастом.
Создание сгруппированного распределения частот
- Найдите наибольшее и наименьшее значения
- Вычислить диапазон = максимум — минимум
- Выберите желаемое количество классов. Обычно это от 5 до 20.
- Найдите ширину класса, разделив диапазон на количество классов и округлив в большую сторону. Есть Здесь нужно остерегаться двух вещей. Вы должны округлить до , а не выкл.Обычно 3,2 округляется до равняется 3, но при округлении в большую сторону получается 4. Если диапазон, разделенный на количество классов, дает целочисленное значение (без остатка), то вы можете либо добавить единицу к количеству классов, либо добавить единицу в ширину класса. Иногда вы заперты в определенном количестве классов из-за инструкции. В тексте Блюмана не упоминается случай, когда нет остатка.
- Выберите подходящую начальную точку, меньшую или равную минимальному значению. Вы сможете cover: значения «ширина класса, умноженная на количество классов».Вам нужно прикрыть еще один значение, чем диапазон. Следуйте этому правилу, и все будет в порядке: Начальная точка плюс число классов, умноженное на ширину класса, должно быть больше максимального значения .
 Додавання частинами. Додавання до числа 9
стор. 23 — 23
Додавання частинами. Додавання до числа 9
стор. 23 — 23 Додавання чисел до числа 6
стор. 27 — 27
Додавання чисел до числа 6
стор. 27 — 27 Віднімання чисел від чисел 14 і 15
стор. 31 — 32
Віднімання чисел від чисел 14 і 15
стор. 31 — 32 Таблиця додавання та віднімання у межах 20
стор. 36 — 36
Таблиця додавання та віднімання у межах 20
стор. 36 — 36 Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него.Если вы округлите в большую сторону, то самое большое значение данных попадет в последний класс, и проблем не возникнет.
Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него.Если вы округлите в большую сторону, то самое большое значение данных попадет в последний класс, и проблем не возникнет.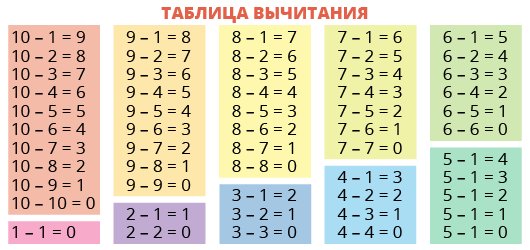
 Возьмем 8.
Возьмем 8. США
США США
США В 2014 году взносы для 27-летнего человека по медицинскому страхованию бронзового уровня приведены в примере \ (\ PageIndex {12} \) («Рынок медицинского страхования», 2013 г.). Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 5 классов.
В 2014 году взносы для 27-летнего человека по медицинскому страхованию бронзового уровня приведены в примере \ (\ PageIndex {12} \) («Рынок медицинского страхования», 2013 г.). Создайте частотное распределение, относительное частотное распределение и совокупное частотное распределение, используя 5 классов. Опишите форму и любые выводы, которые вы можете увидеть на графике.
Опишите форму и любые выводы, которые вы можете увидеть на графике.