Таблица на сложение 20 распечатать. Математический уголок на даче
Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу
Таблица сложения до 20 распечатать и скачать
Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.
Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.
Таблица вычитания до 20 распечатать и скачать
В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.
Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах.
Таблица вычитания без ответов распечатать и скачать
Самые первые примеры, с которыми знакомится ребенок еще до школы — это сложение и вычитание. Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их.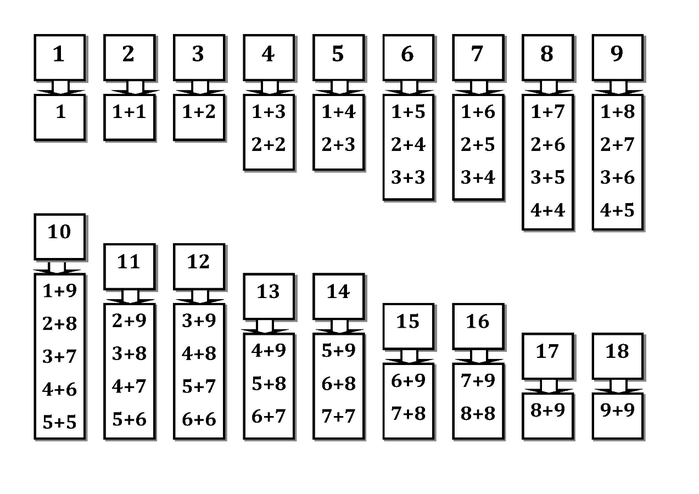
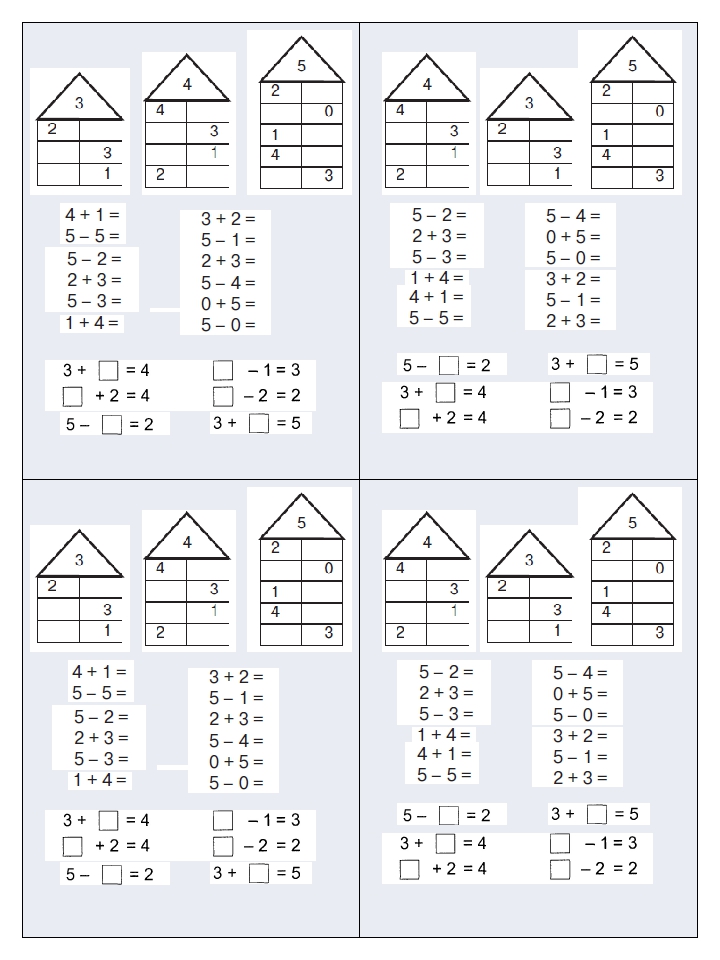
Если ваш ребенок первоклашка или только идет в первый класс — начните с повторения состава числа по домикам. А теперь можно браться и за примеры. Фактически сложение и вычитание в пределах десяти — это и есть первое практическое применение ребенком знания состава числа.
Кликайте по картинкам и открывайте тренажер в максимальном увеличении, далее можно скачать изображение себе на компьютер и распечатать в хорошем качестве.
Есть возможность разрезать А4 пополам и получить 2 листа с заданиями, если хотите уменьшить нагрузку на ребенка, или давать решать по столбику в день, если решили позаниматься летом.
Решаем столбик, отмечаем успехи: тучка — не очень хорошо решили, смайлик — хорошо, солнышко — замечательно!
Сложение и вычитание в пределах 10
А теперь вразброс!
И с пропусками (окошками):
Примеры на сложение и вычитание в пределах 20
К моменту, когда ребенок приступит к изучению этой темы математики, он должен очень хорошо, на зубок знать состав чисел первого десятка. Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток .
Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток .
Примеры для печати без перехода через десяток вперемешку:
Сложение и вычитание в пределах 20 с переходом через десяток основаны на приемах добавления до 10 или убавления до 10 соответственно, то есть на теме «состав числа 10», поэтому ответственно подойдите к изучению с ребенком этой темы.
Примеры с переходом через десяток (половина листа сложение, половина вычитание, лист также можно распечатать в формате А4 и разрезать пополам на 2 задания):
Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать и распечатать.
Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать и распечатать.
Таблица сложения до 20 распечатать и скачать
Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.
Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word.
Таблица вычитания до 20 распечатать и скачать
В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.
Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.
Таблица вычитания без ответов распечатать и скачать
Про наш я уже писала. Но из него мы похоже уже вырастаем. Во всяком случае, Дима свободно может считать от 1 до 100 и обратно. Понимаю, что вместе с ним растет и его потребности в математических знаниях. Вот и решила углубиться в изучении математики по системе Зайцева.
Таблица ста мне уже давно знакома, такая была даже у моих старших детей. Но у Зайцева есть еще столько интересных наработок. Одно только НО для большинства из них нужно очень много места. А его у нас в квартирах катастрофически не хватает.
На даче мы, наконец, сделали себе комнату. И, о чудо, у нас есть большая и пока не занятая стена! Я тут же решила, что на неё повешу. Предлагаю вашему вниманию наш математический уголок на даче:
Таблица сложения и вычитания в пределах 20.
Числовая лента от 0 до 100.
Правда, по методике она должна висеть в одну линию, но такой длинной стены у нас уж точно нет! Мои таблицы немного отличаются от Зайцевских, но суть их прежняя. В числовой ленте мне захотелось немного поиграть цветами. А делать цветной фон за цифрами – для меня, например, очень не экономично при печати. По-моему, достаточно, что сами цифры цветные. А к таблице сложения и вычитания в пределах 20 добавила и количества основных чисел – так мне кажется нагляднее.
Задания по таблицам можно прочитать на сайте Зайцева , где вы можете и заказать оригинальные пособия. Я же предлагаю то, что изготовила для своего сына. Документы будут в формате PDF, которые нужно распечатать на плотной бумаге.
Таблица сложения и вычитания в пределах до 20 на 5 листах, в которых нужно обрезать поля и склеить листы между собой. Я использовала обычный скотч и склеивала им с обратной стороны.
Числовая лента на 22 листах. Первых два десятка поместились на одном листе.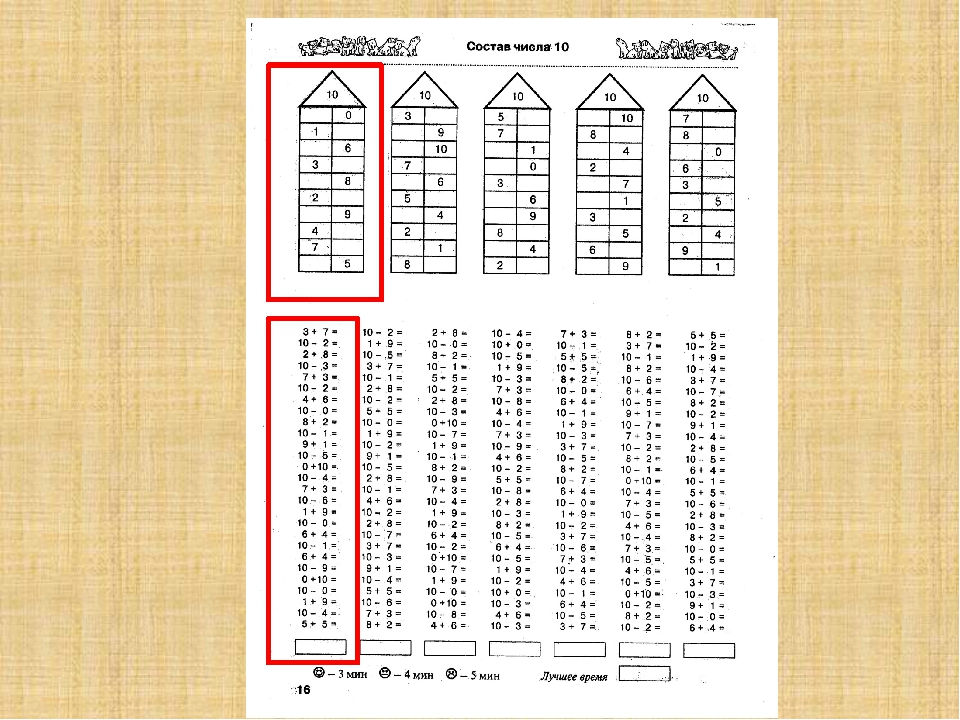 Их нужно только разрезать вдоль и склеить между 4 и 5, 14 и 15. От 20 до 59 тоже все понятно. А вот следующие десятки не влезали на один лист по ширине, поэтому вам придется немного потрудиться и сообразить при склеивании. Надеюсь, что вы справитесь.
Их нужно только разрезать вдоль и склеить между 4 и 5, 14 и 15. От 20 до 59 тоже все понятно. А вот следующие десятки не влезали на один лист по ширине, поэтому вам придется немного потрудиться и сообразить при склеивании. Надеюсь, что вы справитесь.
Диму очень впечатлили новые таблицы! Он сразу обратил внимание, что на одной таблице цифры черные и оранжевые, а на другой – зеленые. Ему очень понравилось путешествовать по числовой ленте в поисках чисел, которые я называю.
ИЗУЧАЕМ СОСТАВ ЧИСЛА — РАСПЕЧАТАЙ и ИГРАЙ :: Игры, в которые играют дети и Я
Здравствуйте-здравствуйте!
Сегодня покажу новые математические раскраски на изучение состава числа и поделюсь парой страничек, может, и вам пригодится.
Еще покажу несколько фото-моментов с урока — это для тех, кому интересно заглянуть ко мне на урок.
В начале занятия стараюсь делать массажную разминку для пальчиков. Одна из моих любимых разминок — с карандашами. В проекте ИГРАнаУРА — 2 будет игровой месяц с массажными играми, постараюсь к тому времени зафотографировать карандашную разминку.
Доминошки!
У меня много разных заданий с домино, но начали с простого — «переводили» точки в числа. Посчитай сколько точек — запиши число. Еще отрабатывали порядок действий — поработал с доминошкой — переверни, чтобы не сбиться.
Я обязательно уделяю время организационным вопросам: заостряю внимание детей на то как, где, зачем и почему именно так лучше делать.
Каждый получает свой набор доминошек, а значит надеяться не на кого — нужно включать голову и выполнять задания самостоятельно.
А это наши папочки для листочков с заданиями.
А это задание «найди и раскрась» на внимание. После того как дети познакомились с таким видом заданий — можно давать их уже и для самостоятельной работы.
Вот, например, после или перед занятием я проверяю домашние задания, а чтобы дети были при деле — даю им такие раскраски.
Дети: а что же здесь получится?
Я: это вы мне расскажете, если правильно выполните задание))
У некоторых ребят уже появилась даже своя методика раскрашивания!
Молодцы! Мыслят!
Ну и СОСТАВ ЧИСЛА.
За два занятия выяснила, что состав числа дети не знают((( примеры решают со скрипом… для некоторых даже 1+1 — «надо подумать»… кто-то забыл, а кто-то и не знал…
Состав числа это важно!
Сейчас меня закидают тапками методисты))) но общепринятые «домики» меня не устраивают — не работают они… дети не запоминают, что из чего состоит…
Только частые повторения могут дать результат, но просто зубрить — не наш метод)))
Так родились раскраски на изучение-закрепление состава числа.
Начали с саааамого простого.
Как я работаю с таким заданием:
Рассматриваем задание. Выбираем цвет. Договариваемся, что будем решать примеры так: шагаем по строчкам, пример за примером — «читаем» пример, решаем, смотрим в таблицу с ответами, каким цветом нужно раскрашивать клеточку с получившимся результатом, и только потом раскрашиваем.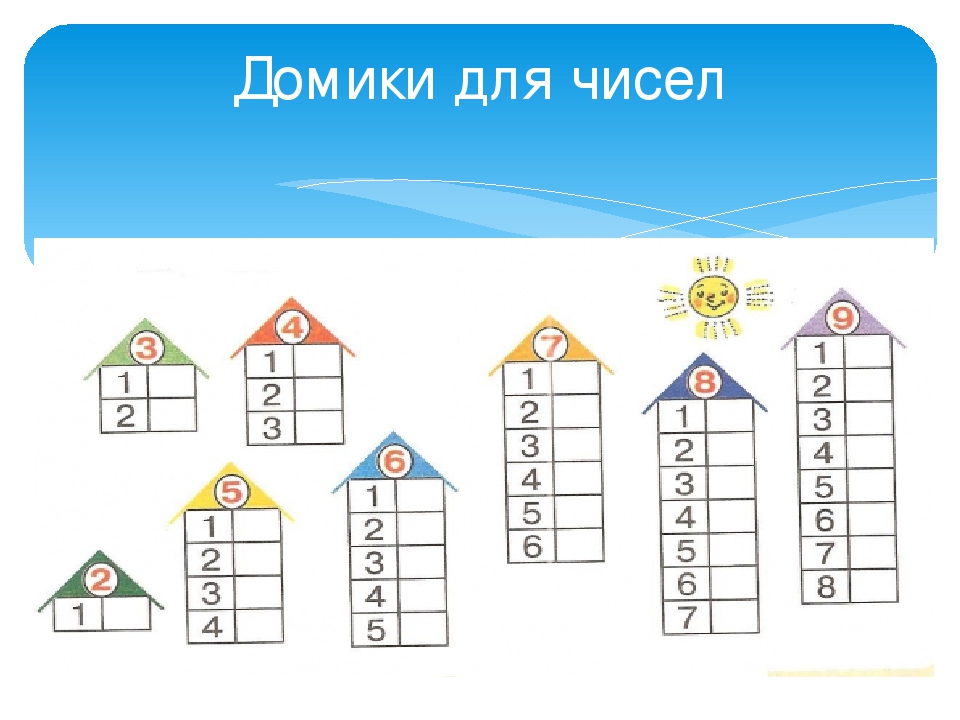
Две строки проговариваем и решаем вместе, а дальше уже каждый работает самостоятельно.
Если всё решили правильно, то получится узнаваемая картинка.
Ребёнок: ай… я ошибся… ааа что теперь делать…
Я: не расстраиваться, мы же с вами учимся! Хорошо, что ты увидел ошибку. Почему ошибка закралась в твой листочек?
Ребенок: я торопился…
Сделал вывод сам — в следующий раз вероятнее всего вспомнит свой опыт и, прежде чем раскрасить, проверит.
Я стараюсь подталкивать детей искать причины их ошибок.Моё пособие
СОСТАВ ЧИСЛА: от 1 ДО 10
Статья авторская
и предназначена только для частного ознакомления.
Копирование и публикация в других источниках
без моего письменного согласия
ЗАПРЕЩЕНЫ.
Автор: Наталья Чистоклетова
Новости моего блога
можно получать на вашу любимую почту,
а подписаться можно
ИГРАЙТЕ С РАДОСТЬЮ
НАТАЛЬЯ ЧИСТОКЛЕТОВА
Таблица на минус от 1 до 10.
 Как научить ребенка считать? Советуют педагоги
Как научить ребенка считать? Советуют педагогиПодготовка к игре — настройки
- Любые параметры и настройки могут быть изменены когда угодно, даже во время игры.
- Изначально игра настроена так:
- Тип вычисленией — Сложение до 10
- Премия 1 — шоколадка, премия 2 — печенье
- В игровой сессии 10 вычислений (арифметических примеров)
- Процент примеров, которые надо решить правильно для получения Премии 1 — 90%
- Процент примеров, которые надо решить правильно для получения Премии 2 — 70%
- Вы можете выбрать любой другой тип вычислений — в зависимости от того, что ребенок знает и что проходит в школе в данный момент. Типы вычислений в игре:
- Сложение, вычитание, сложение и вычитание (вперемешку):
- До 10
- До 20 (с переходом через десятку)
- До 20 (с переходом через десятку и без)
- До 30
- До 100
- Умножение, деление или любые комбинации -на 1, -на 2, -на 3.
 ……и т. д. до 10
……и т. д. до 10 - Сравнение чисел
- Сложение, вычитание, сложение и вычитание (вперемешку):
- Установите, сколько примеров будет в игровой сессии. Лучше начать с небольшого количества попыток — 5 или 10, чтобы не отбить у ребенка желание продолжать игру. Когда ребенок повысит надои:) улучшит показатели, можно переходить к серьезной игре с 100-200 примерами.
- Внесите процент правильно решенных примеров, за который выдаются 1 и 2 премии. Для начала лучше понизить процент. Например выбрать 70 и 50 процентов для 1 и 2 премий, соответственно. Позже ставки можно увеличить до 90 — 70. Или даже до 98% — 95% для совсем уж жутко умных детей:). Вносите только цифры, без знака %!
- Запишите премии, которые ребенок получит за 1 и 2 место.
- Настройки будут сохранены с помощью cookie (небольшого скрипта) и восстановлены, когда вы следующий раз откроете в браузере страницу с игрой.
Теперь можно начинать игру!
- Чтобы начать игру, нажмите кнопку СТАРТ
- Когда на экране появится пример, ребенок должен внести ответ после знака «=»
- Если играем в «сравнения», нужно внести соответствующий знак: .
 Для этого удобнее всего пользоваться кнопками, которые появятся рядом с кнопкой ДАЛЬШЕ
Для этого удобнее всего пользоваться кнопками, которые появятся рядом с кнопкой ДАЛЬШЕ - После того, как внесен результат, нужно нажать на кнопку ОК (или ENTER на клавиатуре), чтобы проверить правильно ли был решен пример.
- Если пример был решен правильно, на экране появится «Правильно». Если нет, «Неправильно» и верный ответ. В то же время, игра посчитает процент правильно решенных примеров
- Чтобы перейти к следующему примеру, нужно нажать кнопку ДАЛЬШЕ
- Когда сессия закончится, на экране появится премия, которую выиграл ребенок (или «ничего не выиграл») и процент правильно решенных за сессию примеров
- Чтобы начать новую сессию, нажмите кнопку НАЧАТЬ СНАЧАЛА.
Большие надежды:)
Чего можно ожидать от этой игры? Большой помощи в прохождении школьной программы! Как правило за 5-7 дней, в которые ребенок играет по 30-40 минут, он твердо усваивает очередной тип вычислений (например, сложение до 20 с переходом через десятку). И практически перестает делать ошибки в классе.
И практически перестает делать ошибки в классе.
Учим таблицу сложения и вычитания в пределах 10
Одной из важных задач курса математики за 1 класс является прочное усвоение детьми таблицы сложения и вычитания в пределах десяти. При изучении состава чисел важным моментом является опора на наглядность и игровую деятельность. Работа над изучением таблицы сложения и вычитания должна проводиться систематически, формы работы должны быть разнообразны. Только при таких условиях можно избежать скуки и монотонности, гарантировано прочное запоминание детьми состава чисел.
Конечно, это бумажные тренажёры по составу чисел.
Но больше всего детям нравятся интерактивные или онлайн игры! Игра является одним из важных средств в усвоении знаний, развитии и воспитании детей. Она может быть применена в рамках разных методов обучения. Очень важный момент в игре – преодоление препятствий, достижение целей, самостоятельный поиск. Все эти элементы игры развивают умственные способности школьника.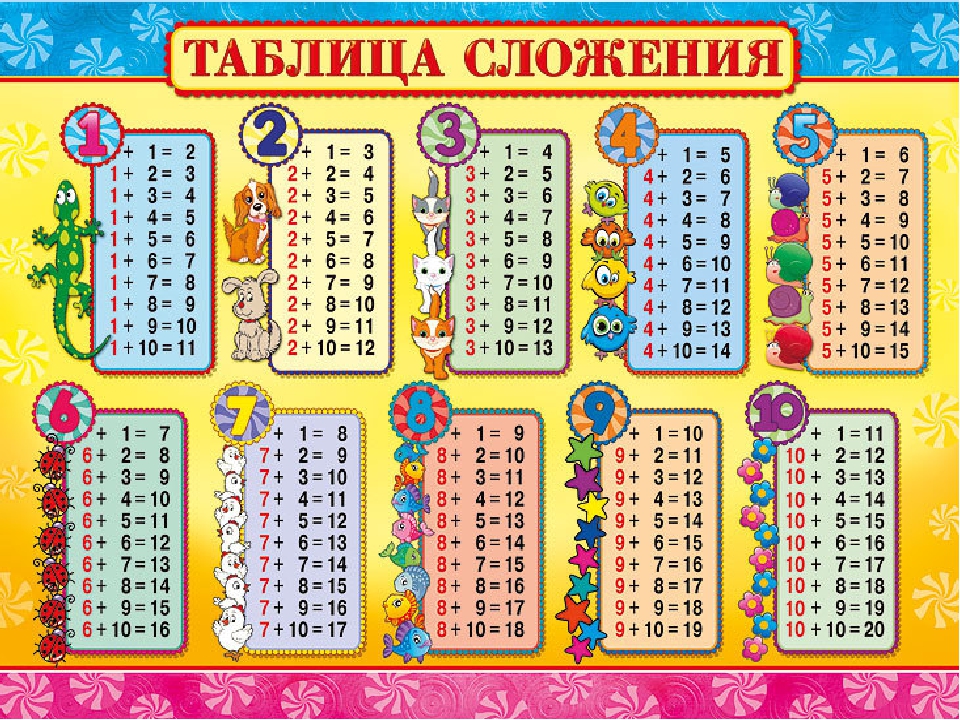 Именно с помощью различных компьютерных игр и тренажёров, заданий для интерактивного стола современный учитель может разнообразить виды работы, направленные на усвоение детьми таблицы сложения и вычитания. Они помогут ученикам не только довести до автоматизма навык устного счёта, но и дадут возможность закрепить правила работы в группе.
Именно с помощью различных компьютерных игр и тренажёров, заданий для интерактивного стола современный учитель может разнообразить виды работы, направленные на усвоение детьми таблицы сложения и вычитания. Они помогут ученикам не только довести до автоматизма навык устного счёта, но и дадут возможность закрепить правила работы в группе.
Состав числа 5
Состав числа 6
Состав числа 7
Состав числа 8
Состав числа 9
Состав числа 10
Далее представлены онлайн игр, направленные на закрепление и автоматизацию состава числа — это математические тренажеры, которые включают примеры и уравнения, помогут довести знание состава числа до автоматизма.
Однако, не забывайте и о других способах заучивания состава числа, так как долгое время находиться перед экраном компьютера ребенку вредно.
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.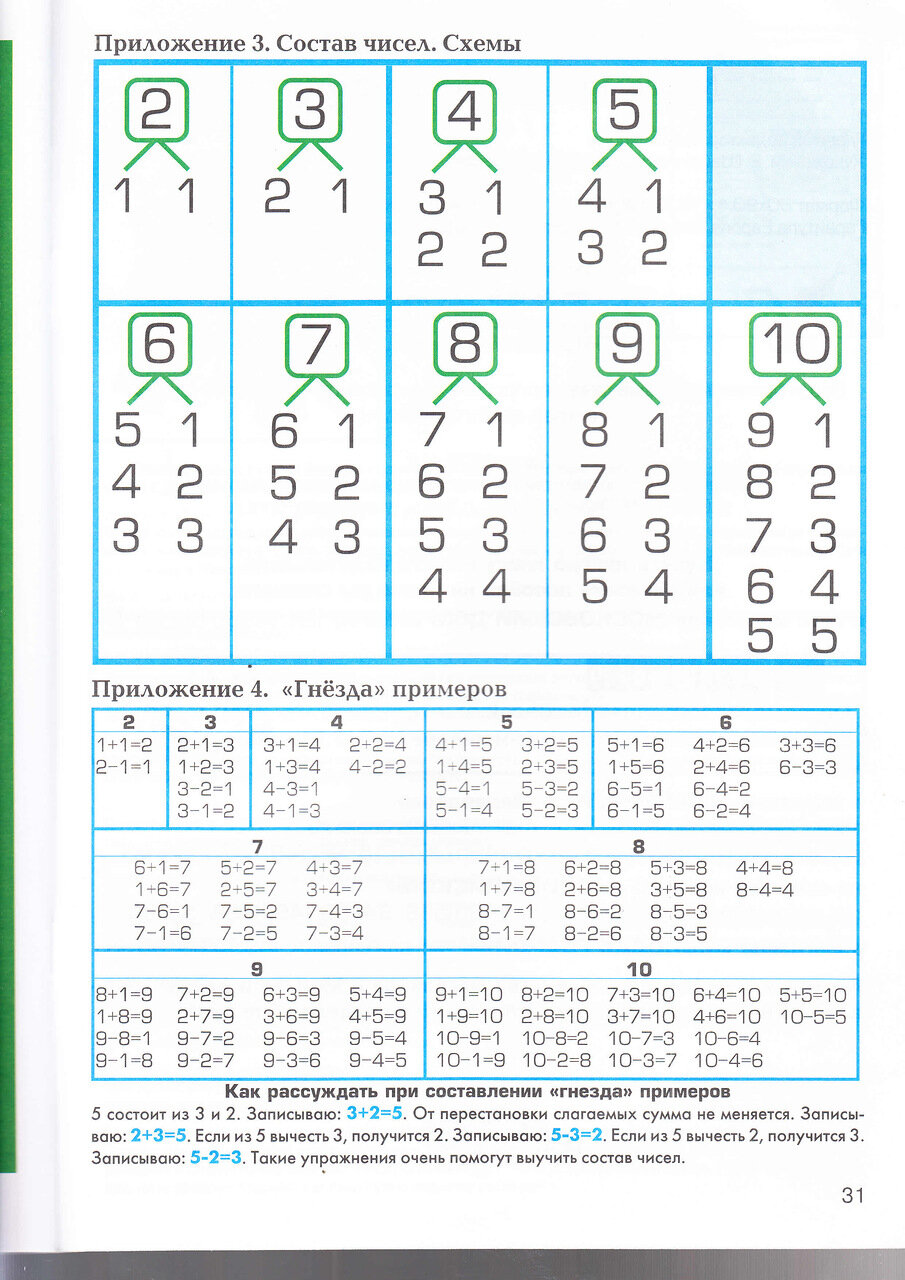
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу.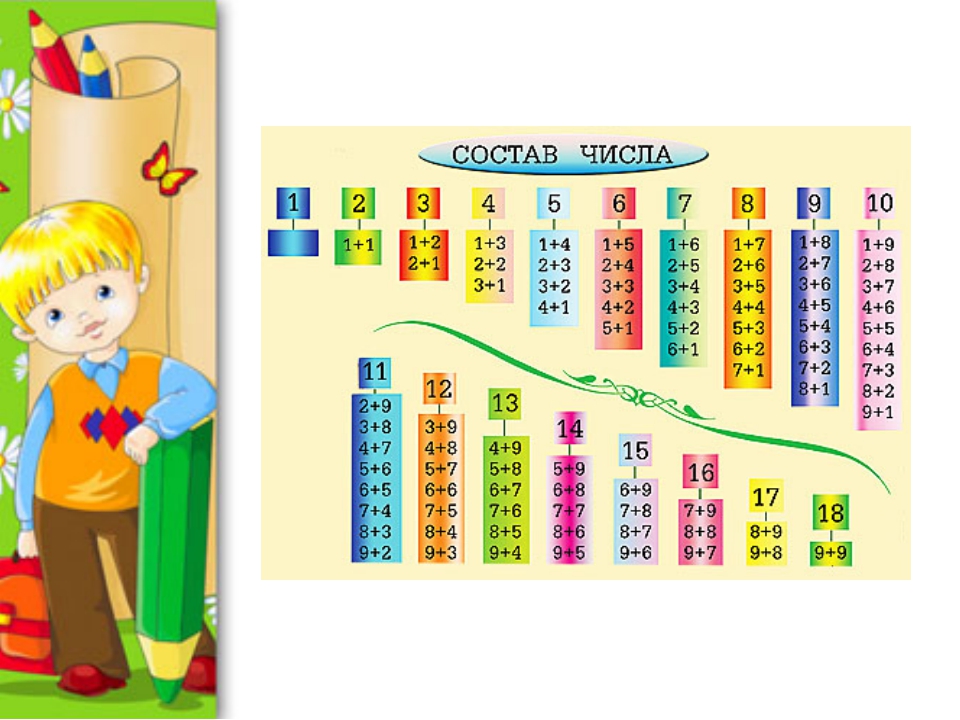 (рис. 8)
(рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().
- 5klass.net ().
- Самоучка ().
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Самые первые примеры, с которыми знакомится ребенок еще до школы — это сложение и вычитание. Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.
Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.
Если ваш ребенок первоклашка или только идет в первый класс — начните с повторения состава числа по домикам. А теперь можно браться и за примеры. Фактически сложение и вычитание в пределах десяти — это и есть первое практическое применение ребенком знания состава числа.
Кликайте по картинкам и открывайте тренажер в максимальном увеличении, далее можно скачать изображение себе на компьютер и распечатать в хорошем качестве.
Есть возможность разрезать А4 пополам и получить 2 листа с заданиями, если хотите уменьшить нагрузку на ребенка, или давать решать по столбику в день, если решили позаниматься летом.
Решаем столбик, отмечаем успехи: тучка — не очень хорошо решили, смайлик — хорошо, солнышко — замечательно!
Сложение и вычитание в пределах 10
А теперь вразброс!
И с пропусками (окошками):
Примеры на сложение и вычитание в пределах 20
К моменту, когда ребенок приступит к изучению этой темы математики, он должен очень хорошо, на зубок знать состав чисел первого десятка. Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток .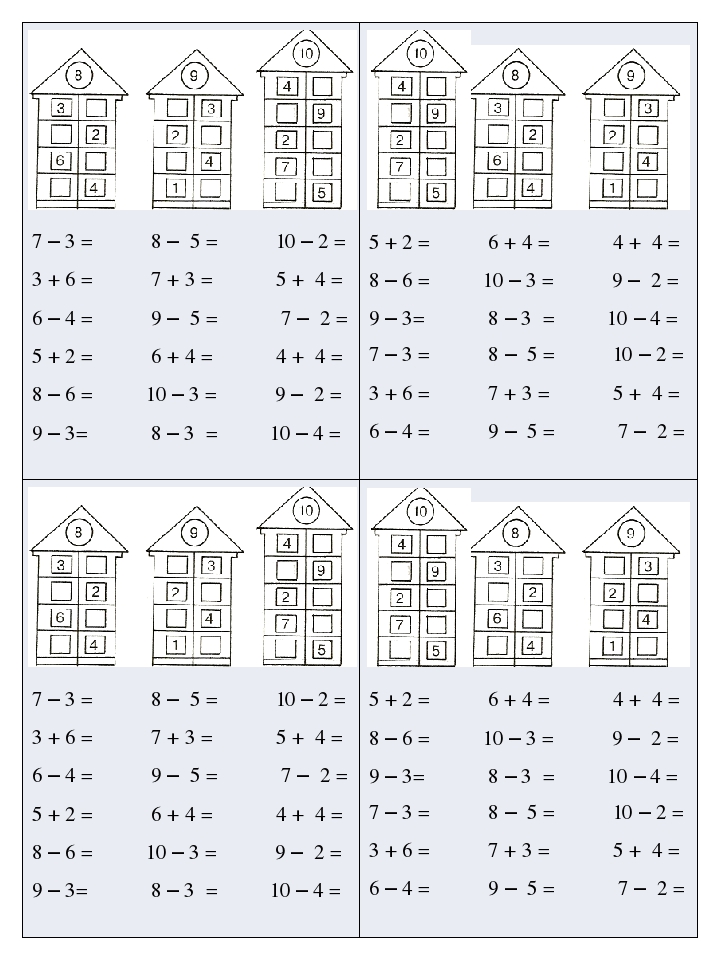
Примеры для печати без перехода через десяток вперемешку:
Сложение и вычитание в пределах 20 с переходом через десяток основаны на приемах добавления до 10 или убавления до 10 соответственно, то есть на теме «состав числа 10», поэтому ответственно подойдите к изучению с ребенком этой темы.
Примеры с переходом через десяток (половина листа сложение, половина вычитание, лист также можно распечатать в формате А4 и разрезать пополам на 2 задания):
Первый этап. Не используем запись числа
Первостепенная задача — научить считать до 10, н е используя соответствующие цифры. На первый план выходят действия с предметами. Например, была одна ложка, положили еще одну — стало две ложки. Потом можно увеличивать количество ложек, говоря название числа.
Помогут в решении этой задачи практические задания. Например, чаще спрашивать у ребенка о количестве чего-нибудь: сколько тарелок, сколько тапочек, сколько птиц на той ветке. Считать можно что угодно, даже ступеньки лестницы.
Считать можно что угодно, даже ступеньки лестницы.
Второй этап. Знакомство с самими цифрами.
В первом классе сначала изучается цифра 1, 2, 0, а потом уже 3, 4, 5, 6, 7, 8, 9. Обусловлено положение нуля тем, что ученику на первых порах сложно понять, почему пустота обозначается цифрой. И тогда, когда уже практикуются действия с цифрами, становится понятно, зачем нужен нуль. Например, было пять яблок на столе, пять съели. Осталось — ничего, то есть ноль.
Еще вариант: Показываются эти рисунки, и спрашивает учитель у детей: «Что изменилось?». Они отметят: «Ничего».
На втором образце показано, что если в одном квадрате три точки убрать совсем, то будет пустой квадрат и точек вообще не останется.
Главное правило, которые должны понять дети при счете до десяти: каждая цифра меньше последующей на один и больше прошлой цифры на один.
Приемы обучения счету до десяти:
- Игра в паровозик . Распространенная тренировка заучивания цифр, проводимая в первом классе.
 Выходит перед классом один ученик, он говорит, что он — вагон первый. После этого выходит еще один, и говорит: один и еще один будет два. И так продолжается до десяти. Потом операция делается в обратном порядке. Вагоны «распадаются» по одному. Цель этого упражнения — запоминание порядка чисел в прямом и обратном порядке.
Выходит перед классом один ученик, он говорит, что он — вагон первый. После этого выходит еще один, и говорит: один и еще один будет два. И так продолжается до десяти. Потом операция делается в обратном порядке. Вагоны «распадаются» по одному. Цель этого упражнения — запоминание порядка чисел в прямом и обратном порядке. - Показ на линейке . Это устаревший метод, основанный на механическом запоминании и наглядном доказательстве порядка чисел.
- Счет на пальцах . Традиционный и самый легкий для детей. Можно использовать на первой поре, пока ребенок не будет порядок цифр. Потом надо отучать от пальцев, рассказывая «секреты» превращений цифр.
- Использование смешных стихов и мультиков о числах . Интересно будет посмотреть мультик «Как козленок учился считать» или проговаривать считалки.
Стихотворения-запоминалки для изучения счета
Ягодный счет
По опушке шла лисичка:
— Раз, в корзинке земляничка,
Два — как небо голубика,
Три — румяная брусника,
А четыре — вот морошка,
Пять — смородины немножко,
Шесть — как бусинка калина,
Семь — как солнышко рябина,
Восемь — в лапке ежевика,
Девять — синяя черника,
Десять — сочная малина.
Вот и полная корзина!
Раз — рука, два — рука —
Лепим мы снеговика!
Три — четыре, три — четыре,
Нарисуем рот пошире!
Пять — найдем морковь для носа,
Угольки найдем для глаз.
Шесть — наденем шляпу косо.
Пусть смеется он у нас.
Семь и восемь, семь и восемь,
Мы сплясать его попросим.
Девять — десять — снеговик
Через голову — кувырк!
Ну и цирк!
Пошли пальчики гулять,
А вторые догонять,
Третьи пальчики бегом,
А четвертые пешком,
Пятый пальчик поскакал,
И в конце пути упал.
- Игра «Назови соседей числа» . Например, нужно назвать соседей числа 4.
- Упражнение «Цифры заблудились» . Нужно разложить по порядку беспорядочно разложенные картинки с цифрами. Есть другая интерпретация этого упражнения: Баба-Яга перепутала все цифры. Помоги расставить их правильно.
- Под забором было видно 10 лапок цыплят. Вопрос: сколько всего цыплят? — Счет двойками: 2, 4, 6, 8, 10 — пять цыплят.

- Сколько сапог надо подарить троим гусятам? Аналогично предыдущей задачке.
- Считать пятерками удобнее всего, наблюдая за часами.
Как выучить таблицу сложения и вычитания в пределах десяти?
После того как ребенок знает порядок числительных, полезно применять задания на состав числа. Можно, конечно, зазубрить состав числа 5, например, но лучше использовать игровые действия с предметами с параллельной установкой на запоминание.
Например:
В одной тарелке было 4 апельсина, а в другой — 2. Сколько всего апельсинов? (Задача на нахождение суммы)
Всего 6 яблок, а друзей — трое. Разделите каждому поровну, одинаково.
Сочетать с простыми задачами можно и маленькие схемы, которые легко применять на уроке и дома.
На переместительный закон сложения не сложно привести такой пример: одна тарелка с двумя яблоками лежит на столе, а другая тарелка с четырьмя яблоками — лежит рядышком, если поменять их местами, то все равно общее количество яблок останется неизменным.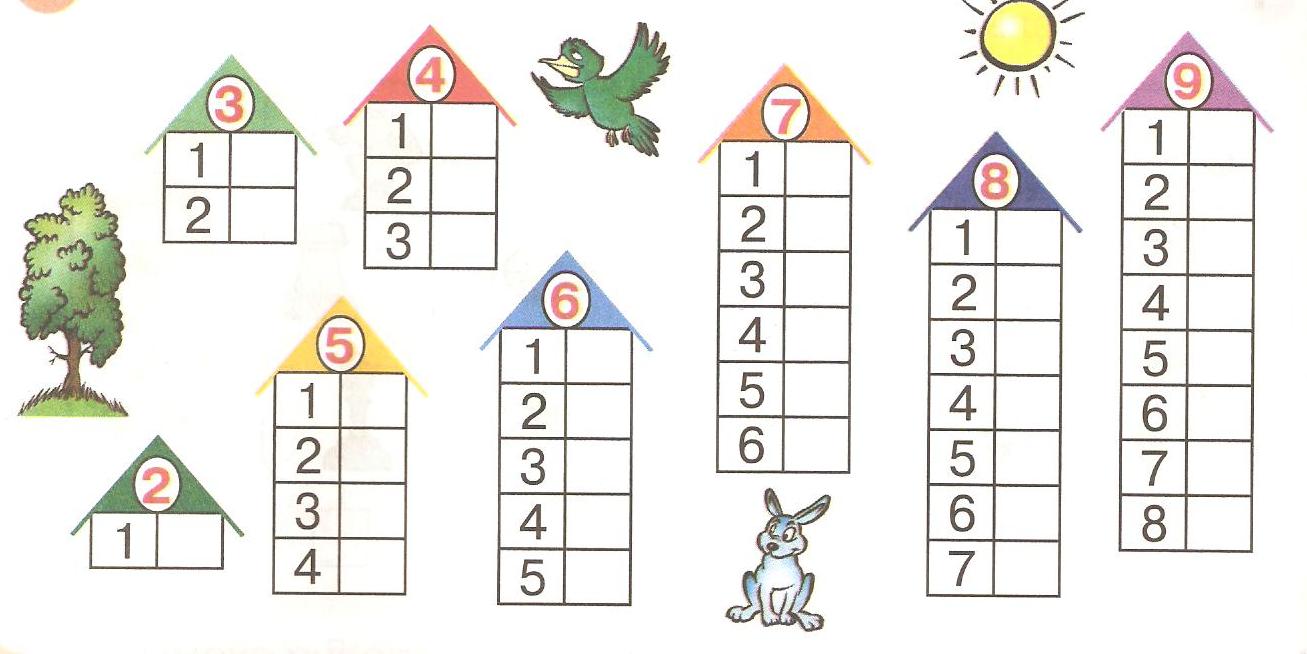
Как научить ребенка складывать и вычитать с переходом через десяток?
В приведенном ниже примере, чтобы сложить числа 8 и 5, второе слагаемое раскладывается так, чтобы дополнить первое слагаемое до десяти, а потом остаток прибавляется к десяти.
Что касается вычитания, то тут раскладывается уменьшаемое по разрядному составу. На примере 15 минус 8 мы видим, что число 15 раскладывается до своих разрядных единиц. В итоге всегда получается 10 и разрядные единички — 5. Теперь: вычитаемое надо разложить на слагаемые. Первым слагаемым будут разрядные единицы от 15-ти, а второе слагаемое подбирается (дети знают состав числа 8). Теперь остается от 10-ти отнять второе слагаемое от восьмерки. И ответ готов. Немного потренировавшись, можно будет легко решать подобные примеры в уме.
Таблица Разрядов и Классов чисел в Математике
Числа и цифры
Числа — это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины.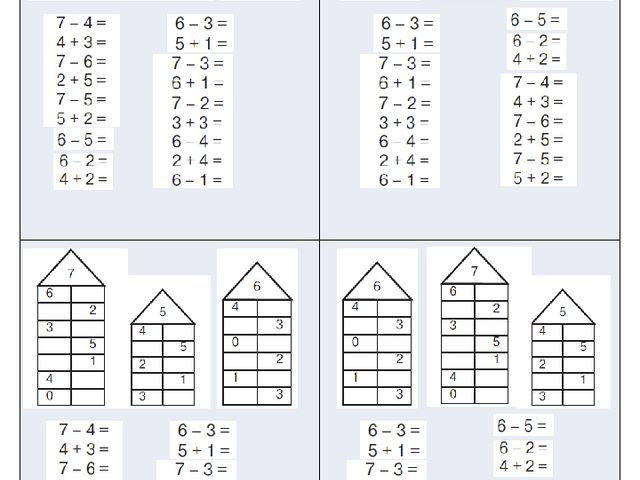
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
- Единица (1) — самое маленькое число, а самого большого числа не существует.
- Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трёхзначными, четырехзначными или многозначными. Наименьшее трёхзначное — 100, наибольшее — 999.
Наименьшее трёхзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
В онлайн-школе Skysmart веселый енот Макс и его друзя помогают ученикам подружиться с загадочной математической вселенной. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать.
Приходите на бесплатный вводный урок математики в Skysmart: познакомимся и поиграем в математику!
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Таблица классов:
Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
- 148 миллиардов 911 миллион 723 тысячи 296.
Когда читаем класс единиц, добавлять слово «единиц» в конце не нужно.
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
- 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.
При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще, чтобы визуально разделить разные классы чисел.
Разрядные единицы принято обозначать так:
- Единицы — единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
- Десятки — единицами второго разряда и записывают в числе на втором месте справа.

- Сотни — единицами третьего разряда и записывают на третьем месте справа.
- Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
- Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
- 55 единиц второго класса и 100 единиц первого класса;
- 110 единиц второго класса и 5 единиц первого класса;
- 7 единиц второго класса и 13 единиц первого класса.

Ответ:
- 55 100;
- 110 005;
- 7 013.
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
- 10 единиц = 1 десяток;
- 10 десятков = 1 сотня;
- 10 сотен = 1 тысяча;
- 10 тысяч = 1 десяток тысяч;
- 10 десятков тысяч = 1 сотня тысяч;
- 10 сотен тысяч = 1 миллион.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
Как рассуждаем:
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т.д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
- 11 627 — одиннадцать тысяч шестьсот двадцать семь.
- 31 502 — тридцать одна тысяча пятьсот два.
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Еще больше лайфхаков по математике — в онлайн-школе Skysmart. Чтобы увлечь ребенка предметом, мы придумали интерактивные задания с красочными героями, захватывающие математические комиксы и примеры, которые правда пригодятся в жизни.
Запишите ребенка на бесплатный вводный урок математики и начните заниматься в удовольствие уже завтра!
математика 1 класс примеры до 20 распечатать
Image Wallpaper and More collection of математика 1 класс примеры до 20 распечатать contain 30+ more images free download Распечатать примеры на скорость для 1 класса | Распечатать примеры .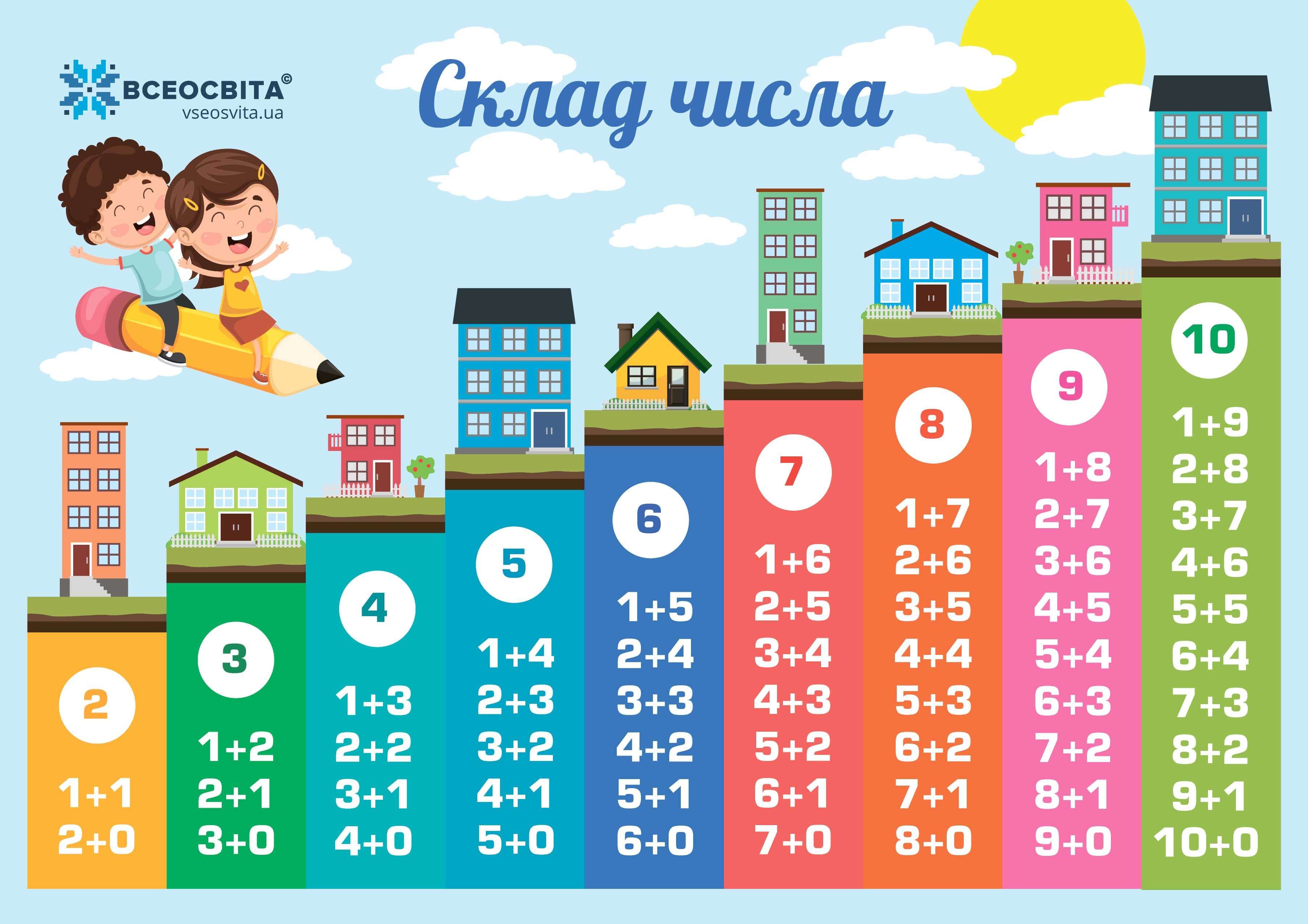 ..
..
Математические раскраски 1 класс Раскраски распечатать бесплатно.
Примеры — Счет в пределах 10 для детей от 5-6 лет
Математические раскраски 1 класс Раскраски распечатать бесплатно.
Тренажер таблицы сложения в пределах 20 — ПринтМания
13 cards in the collection «математика 1 кл» of the user Ольга …
Математика. Найди ошибку. Самостоятельные работы. 1 класс …
Примеры по математике — 1 класс — Распечатать в картинках
Математика: Решаем примеры в пределах 20 с переходом через десяток
Collection «1» of the user ✔️ in Yandex.Collections
математические примеры для 1 класса,распечатать (с изображениями …
Математика: Решаем примеры в пределах 20 с переходом через десяток
Математика. Реши задачу. Самостоятельные работы. 1 класс — Скачать …
примеры на сложение и вычитание в пределах 20 | 1 класс математика …
Решать примеры 1 класс тесты | Escola, Educação
Математические примеры для 1го класса | Математические примеры для . ..
..
примеры с пропущенными знаками для 1 класса распечатать …
Таблица сложения и вычитания распечатать 2 класс – Таблица …
Математика» 1 класс Составление и решение примеров на сложение.
Скачать бесплатно карточки по математике: сложение, вычитание …
Примеры в пределах 20 в несколько действий. Примеры по математике …
Карточки — Состав чисел от 11 до 20 [DOC] — Все для студента
Математика 1 класс. Самостоятельные работы » Я ученик. Сайт для …
примеры на сложение и вычитание в пределах 20 | 1 класс математика …
i.pinimg.com/originals/b5/9c/9a/b59c9a4a950f8e1…
Таблица сложения и вычитания распечатать 2 класс – Таблица …
примеры до 20 для 1 класса бесплатно распечатать (с изображениями …
Математика: Решаем примеры в пределах 20 с переходом через десяток
примеры на сравнение чисел для 1 класса распечатать | Математика …
Состав числа до 10 — Математика для детей Мама7я
Сравнение чисел до 20 (1 класс)
30000 примеров по математике, Счёт до 20, Цепочки примеров, 1 . ..
..
Узорова нефедова счет в пределах 20 скачать бесплатно …
Состав числа до 20 — Распечатать числовую таблицу
Задачи на сложение и вычитание чисел от 1 до 20. Примеры, решение …
Математические раскраски с примерами. Распечатать картинки для детей.
Примеры на сложение и вычитание в пределах 20
Таблица сложения и вычитания распечатать 2 класс – Таблица …
реши примеры вставив пропущенные цифры для 1 класса (с …
Состав числа до 20 — Распечатать числовую таблицу
Математические раскраски с примерами. Распечатать картинки для детей.
математика 1 класс примеры до 20 распечатать Images Collection Математические раскраски для 1 класса в пределах 10 Состав чисел до 20 — Таблица — Распечатать и заполнить Скачать бесплатно карточки по математике: сложение, вычитание …
Состав числа от 1 до 10 таблица домики
Состав числа до 10 домики — развивающие карточки для детейСогласно школьной программе, первоклашки должны уметь автоматически решать примеры на сложение и вычитание в пределах чисел первого и второго десятков.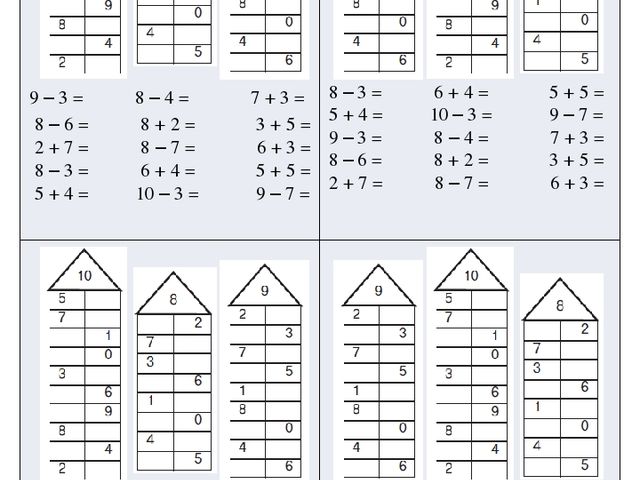
Для того, чтобы успешно справиться с поставленными задачами, детки должны знать из чего эти числа состоят. Вся проблема заключается в том, что информация эта — абстрактная и запомнить непоседливому малышу не так просто.
Поэтому преподносить ее нужно в форме увлекательной, наглядной и понятной. Лучше всего для нее подходят так называемые числовые домики — картинки и карточки, созданные специально для освоения дошколятами азов счета.
Мы тоже решили создать на нашем сайте тему «Состав числа до 10 домики» и предложить вам распечатать картинки и карточки в готовом виде.
Пример карточки:
В конце нашей статьи приведены такие карточки — разного формата и разных авторов.
Также подобные карточки для детей вы можете нарисовать сами. Это совсем не сложно и не требует каких-то особых знаний и талантов. Просто рисуем от руки прямоугольники — многоэтажки на листах бумаги.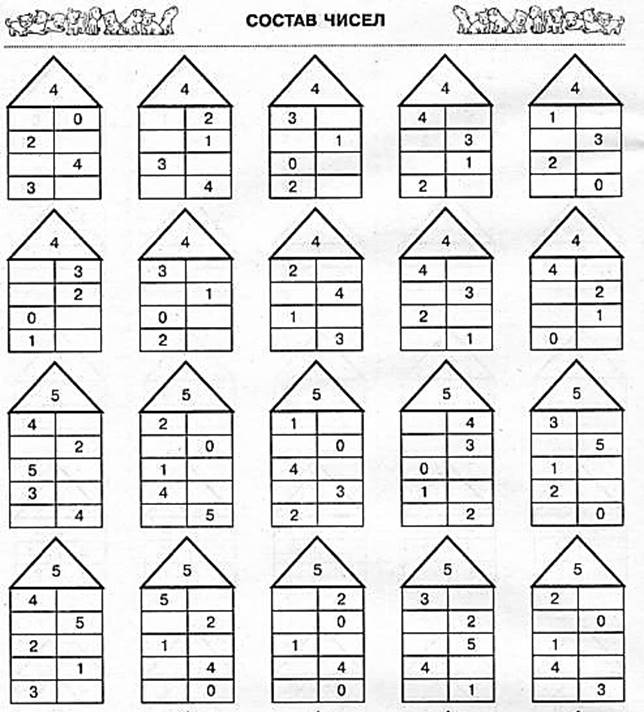
Рисуем карточки и объясняем ребенку правила
Как нарисовать числовой домик самому? Да очень просто:
- Сначала от руки на чистом листе бумаги изображаем каркас «пятиэтажки», затем делим его на этажи и дорисовываем крышу.
- На каждом этаже нужно изобразить по две квартиры (или два окошка). На крыше вместе с ребенком пишем цифру и объясняем малышу, что эта цифра — хозяин домика, который разрешает в нем жить только такому количеству жильцов, которое равно ему самому.
- Для «заселения» на первых порах можно использовать счетные палочки — чтобы ребенок не сбился со счета и не запутался.
Помогаем ребенку освоить состав числа до 10 в игре
Помните о том, что маленькие детки очень охотно и быстро учатся на примерах. Поэтому первую карточку вы должны будете заполнить сами. Не забывайте рассуждать вслух о том какая у вас цифра-хозяин и сколько жильцов вам нужно заселить в каждую квартиру, чтобы не нарушать его «правила».
Следующий домик ребенок должен «заселить» сам при вашей помощи. Помогите ему рассуждать и высчитывать сколько жильцов должно быть заселено в каждую квартиру и на каждый этаж.
Помогите ему рассуждать и высчитывать сколько жильцов должно быть заселено в каждую квартиру и на каждый этаж.
Закрепляем пройденное
Как помочь ребенку быстрее и легче запомнить состав числа до 10 и научиться считать? Ниже мы приводим еще несколько полезных советов и правил работы с карточками.
- Количество жильцов следует менять от этажа к этажу. При этом ребенок активно осваивает новые комбинации чисел. Например, в домике с цифрой-хозяином «6» они будут 1 и 5, 2 и 4, 3 и 3.
- Когда ваш малыш будет хорошо ориентироваться в комбинациях, можно переходить от счетных палочек к написанию цифр. Эта задача более трудная, поэтому прибегайте к постоянному повторению и помогайте своему чаду освоиться с новой деятельностью.
- Старайтесь постоянно освежать в памяти ребенка игру с карточками. Также старайтесь постепенно усложнять задание, переворачивая одну из карточек чистой стороной вверх и прося ребенка нарисовать этот домик и вспомнить состав числа, которое на нем изображено.

- Не забывайте о том, что без регулярного повторения и соответствующей заинтересованности в процессе вашему ребенку будет сложно запомнить пройденный материал.
Ну а для того, чтобы красивые и интересные карточки у вашего малыша всегда были перед глазами, используйте иллюстрации в нашей статье. Все эти красивые и разноцветные картинки можно распечатать и развесить в комнате ребенка, чтобы он постоянно их видел.
Состав числа до 10 домики — распечатать картинки и карточки
Реклама:
№ 1-10 План урока
Примечания:
Песня на этом уроке «Песня чисел» отлично подходит для обучения чисел и счета, но ее также можно использовать в качестве разминки или в любой момент урока. Наши ученики просто обожают эту песню и просят делать ее каждый класс.
Процедура урока:
Разогрев и техническое обслуживание:
Смотрите нашу страницу «Разминка и разминка».
Новое обучение и практика:
1.Воспроизведение «Песни чисел»
Воспроизведение песни. Прежде чем приступить к обучению любому из чисел, вы можете начать с этой песни. Заставьте всех встать и идти вперед и делать действия. Убедитесь, что вы делаете действия с детьми, чтобы они могли следовать за вами и копировать то, что вы делаете.
Прежде чем приступить к обучению любому из чисел, вы можете начать с этой песни. Заставьте всех встать и идти вперед и делать действия. Убедитесь, что вы делаете действия с детьми, чтобы они могли следовать за вами и копировать то, что вы делаете.
Текст песни «The Numbers Song»
1 — 2 — 3 — 4 — 5 Прыгай!
6 — 7 — 8 — 9 — 10 Прыгай!
Повернись и хлопни в ладоши
И прыгай!
1 — 2 — 3 — 4 — 5 Удар ногой!
6 — 7 — 8 — 9 — 10 Удар ногой!
Повернись и хлопни в ладоши
И пни!
1 — 2 — 3 — 4 — 5 покачиваться!
6 — 7 — 8 — 9 — 10 покачиваться!
Повернись и хлопни в ладоши
И покачивайся!
1 — 2 — 3 — 4 — 5 Прыгай!
6 — 7 — 8 — 9 — 10 Удар ногой!
Повернись и хлопни в ладоши
И прыгай!
Kick!
покачиваться!
и прыгай!
(скачать MP3 здесь)
Жесты для «Песни чисел»
В первый раз, когда вы играете песню, делайте жесты и поощряйте всех делать их вместе с вами.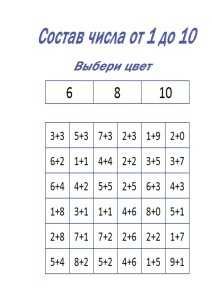
- Поскольку музыка в марширующем стиле, начните с того, что все с энтузиазмом идут на месте к ритму.
- Во время похода отсчитайте цифры на пальцах, пока они поются.
- Делайте каждое слово действия (например, прыгайте, поворачивайтесь, хлопайте в ладоши и т. Д.) В том месте, где они поются в песне.
У нас также есть видео, которое вы можете транслировать в классе, чтобы петь вместе (требуется подключение к Интернету):
2.Преподавайте числа вокаб 1-10
В зависимости от возраста вашего класса вы можете обучать числам в серии уроков. Для детей младше 3-х лет с двумя или тремя цифрами все в порядке, ученики старшего возраста могут больше изучать каждый урок.
Сядьте с учениками так, чтобы они смотрели на вас. Используйте некоторые знакомые предметы для обучения числам (например, в нашем случае мы используем пластиковые фрукты, когда преподаем урок фруктов перед числами). Сначала извлеките каждый из фруктов и поставьте каждый на пол / стол перед собой в ряд. Затем дотроньтесь до каждого плода и медленно сосчитайте (Учитель: «1 … 2 … 3»). Сделайте это два или три раза. Затем пусть весь класс повторяется, когда вы считаете / трогаете каждый фрукт.
Затем дотроньтесь до каждого плода и медленно сосчитайте (Учитель: «1 … 2 … 3»). Сделайте это два или три раза. Затем пусть весь класс повторяется, когда вы считаете / трогаете каждый фрукт.
Наконец, смоделируйте это с парой учеников — попросите одного или двух детей потрогать и посчитать фрукты, как остальные часы класса (много ободрить и поздравить их, когда закончите).
3. Студенты практикуют числа 1-10
Разложите студентов парами и дайте каждой паре несколько предметов (например,грамм. 3 пластиковых фрукта, 3 машины, 3 карандаша и т. Д.). Попросите учеников учиться считать и касаться предметов.
4. Игра «Положи в коробку»
Теперь возьмите большую коробку с предметами и убедитесь, что у вас достаточно предметов каждой категории для чисел, которым вы учите (например, 3 пластиковых фрукта, 3 машины, 3 карандаша и т. Д.). ). Бросай предметы по всему классу. Затем выберите ученика и скажите «Маркус, положи три (карандаши) в коробку». Когда ученик поднимает каждый предмет, убедитесь, что все считают (1… 2… 3). Затем попросите ученика подсчитать объекты, как он / она положит их в коробку. Сделай это со всеми. Наконец, для некоторого безумного веселья выбросьте все объекты и позвольте каждому карабкаться, чтобы найти, посчитать и снова положить все свои объекты обратно в коробку (все одновременно!).
Когда ученик поднимает каждый предмет, убедитесь, что все считают (1… 2… 3). Затем попросите ученика подсчитать объекты, как он / она положит их в коробку. Сделай это со всеми. Наконец, для некоторого безумного веселья выбросьте все объекты и позвольте каждому карабкаться, чтобы найти, посчитать и снова положить все свои объекты обратно в коробку (все одновременно!).
5. Слушать «Прикосновение к классу»
Попросите всех встать, а затем учитель выкрикивает предметы в классе, чтобы дети побежали к нему и дотронулись до него (напримерграмм. Т: «Все трогают три стола!», «Все трогают три книги!»). Возможные предметы в классе: столы, стулья, подушки, карандаши, цветные карандаши, книги, окна, обувь и т. Д. Хорошая идея — подготовить несколько фотографий предметов (например, 3 яблока, 3 супергероя, 3 лица монстра и т. Д.) и наклеить их на стены перед уроком. Затем студенты могут бегать и трогать их.
6. Спойте «Песню чисел» снова
Спойте песню еще раз (со всеми действиями), чтобы завершить часть действия этой темы урока. Вы также можете разместить на доске плакат с песней, чтобы ученики могли следить за тем, как они поют.
Вы также можете разместить на доске плакат с песней, чтобы ученики могли следить за тем, как они поют.
7. Прочитайте читателя в классе «Числа 1-10»
Перед началом занятия загрузите и распечатайте читателя «Числа 1-10». Это действительно забавная рифмованная история, которая понравится вашим ученикам. Просматривая каждую страницу, указывайте на картинки и выявляйте различных животных и то, что они делают, а также подсчитывайте, сколько их:
Учитель: (указывая на изображение змей на стр. 16) Какие это животные?
учеников: змей!
Учитель: Да, верно! Сколько здесь змей? Давайте посчитаем вместе.
ученики: (все вместе, как учитель указывает на каждую змею): 1,2,3,4,5,6,7,8.
Учитель: Хорошо! А какого цвета змеи?
учеников: зеленый, желтый, красный … и т. Д.
Учитель: Это верно! (Чтение) «8 длинных змей … (переходит на следующую страницу) … что это?
Ученики: Торты!
Учитель: Да! Торты на день рождения!» 8 длинных змей выпекают торты на день рождения! «
Вовлеките студентов в эту историю, задав им множество вопросов, например, какого цвета животные и какие забавные вещи они делают.
После прочтения рассказа раздайте каждому ученику рабочий лист читателя и прочитайте рассказ еще раз (не останавливаясь на вопросах и т. Д.), Пока ученики отслеживают цифры. Пусть все скажут, что цифры их отслеживают.
—
Кроме того, вы можете посмотреть нашу видео версию ридера (требуется подключение к Интернету):
8. Выполните рабочий лист «Трассировка 1-10».
Закончите с небольшим временем, выполняя рабочий лист чисел.Используйте лист «Трассировка 1-10» или любой другой лист номеров с нашего сайта (их много!). Пока студенты отслеживают цифры, ходите вокруг, следите и предлагайте много поддержки. Задайте всем вопросы (например, какое это число? «) И попросите каждого учащегося произнести число во время его отслеживания.
Заключение:
1. Назначьте домашнее задание: лист «Trace 1-10 Match-Up» или любой другой лист с номерами с нашего веб-сайта.
2. Завершите урок некоторыми идеями на нашей странице «Разминка и завершение».
График умножения 1-100 и 1-12 на Timestables.com
На этой странице есть таблица умножения 1-100 и 1-12. Эта веб-страница предназначена для детей младшего школьного возраста. Вы можете заниматься самостоятельно или со своими родителями. Изучите таблицы и произнесите их вслух, чтобы вы могли лучше их запомнить. Что также может быть интересно, таблица таблиц. Это удобный способ быстрого просмотра всех таблиц. Изучение таблиц времени — это базовый навык по математике и часть вашего математического образования, с которым вы будете регулярно сталкиваться при выполнении расчетов в старших классах.Это означает, что овладение этими суммами умножения важно не только сейчас, но и в будущем. Вы можете увидеть таблицу таблиц и все таблицы в последовательности с ответами под таблицей умножения с 1 по 12:| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 7 | 9 | 79 | 7 | 910 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 900 53 2224 | ||||
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | |||
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | |||
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |||
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | |||
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | |||
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | |||
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | |||
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | |||
| 11 | 0 | 11 | 22 | 33 90 054 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | |||
| 12 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
Какую таблицу умножения вы хотите выучить?
,Калькулятор округления чиселИспользование калькулятора
Калькулятор округления для округления чисел вверх или вниз до любого десятичного знака. Выберите те, которые округляют число до ближайшего доллара. Выберите сотые, чтобы округлить сумму до ближайшего цента.
Выберите те, которые округляют число до ближайшего доллара. Выберите сотые, чтобы округлить сумму до ближайшего цента.
Округление чисел
Скажи, что ты хотел округлить число 838.274. В зависимости от того, какую ценность места вы округлите, конечный результат будет отличаться.Округление 838.274:
- Округление до ближайшей сотни 800
- Округление до ближайшей десятки — 840
- Округление до ближайшего 838
- Округление до десятых — 838,3
- Округление до сотых — 838,27
Основные правила округления
Когда вы «округляетесь до ближайшего _____» независимо от того, что идет в пустом, шаги почти всегда одинаковы:
- Укажите, к какому ценному значению вы подходите.Чем меньше значение места, тем точнее будет конечный результат.
- Посмотрите на следующее наименьшее значение места, цифру справа от значения места, до которого вы округляете. Например, если вы хотите округлить до ближайшей десятки, вы посмотрите на те места.

- Если цифра в следующем наименьшем значении места меньше пяти (0, 1, 2, 3 или 4), вы оставляете цифру, которую хотите округлить, как есть. Любые цифры после этого числа (включая следующее наименьшее значение, которое вы только что посмотрели) становятся нулями или выпадающими, если они расположены после десятичной точки.Это называется округлением вниз.
- Если следующее наименьшее значение места больше или равно пяти (5, 6, 7, 8 или 9), вы увеличиваете значение округляемой цифры на единицу (+1). Как и прежде, все оставшиеся цифры до десятичной точки становятся нулями, а любые после десятичной точки удаляются. Это называется округлением.
Тур до ближайшей сотни: 3250
- Определите сотню цифр: 2 в 3250
- Определите следующую наименьшую стоимость места: 5 в 3250
- Эта цифра больше или равна пяти? Да, так что округлите.
- Увеличьте число сотен на единицу, чтобы 2 стало 3. Каждая цифра после становится нулем.
3250 округляется до ближайшей сотни 3300
Тур до ближайшей десятки: 323,5
- Определите десятки: цифра 2 в 323,5
- Определите следующую наименьшую стоимость места: 3 в 323,5
- Эта цифра больше или равна пяти? Нет, так что кругом вниз.

- Цифра десятков остается неизменной на 2. Каждая цифра после становится нулем. Цифры после десятичной точки сбрасываются.
323,5 округляется до ближайшей десятки 320
Тур до ближайшей десятки: 499
- Определите десятки: первые 9 в 499
- Определите следующее наименьшее значение места: второе 9 в 499
- Эта цифра больше или равна пяти? Да, так что округлите.
- Число десятков увеличивается на единицу. Поскольку 9 + 1 = 10, вам нужно нести 1 и добавить его к цифре в сотнях мест. Каждая цифра после становится нулем.
499 округляется до ближайшей десятки 500
Округление до ближайшего десятого: 0,74
- Укажите десятую цифру: 7 в 0,74
- Определите следующее наименьшее значение места: 4 в 0,74
- Эта цифра больше или равна пяти? Нет, так что кругом вниз.
- Десятки остаются неизменными на 7. Поскольку остальные цифры идут после десятичной точки, вы просто отбрасываете их.

0,74 с округлением до ближайшей десятой 0,7
Округление до ближайшей сотой: 3.141
- Укажите сотые цифры: 4 в 3,141
- Определите следующее наименьшее значение места: второе 1 в 3,141
- Эта цифра больше или равна пяти? Нет, так что кругом вниз.
- Цифра сотых остается прежней на 4. Перетащите цифры вправо от 4.
3,141 округляется до ближайшей сотой 3,14
Похожие калькуляторы
Чтобы узнать, как округлить число до ближайшего кратного, смотрите наш Круглый до ближайшего несколько калькулятор. Округлить до кратных целых чисел или десятичных дробей, таких как десятые, сотые, тысячные и т. Д.
Дальнейшее чтение
о.ком на Как округлить числа
MathPlayground: Как вы вокруг?
Math.com имеет несколько уроков по оценке и округлению.
,Красочные таблицы состава чисел до 10. Пособие «Числовые домики. Состав числа
Часто оказывается, что самое сложное в этой непростой теме- найти в множестве методик и вариантов один, подходящий конкретному ребёнку.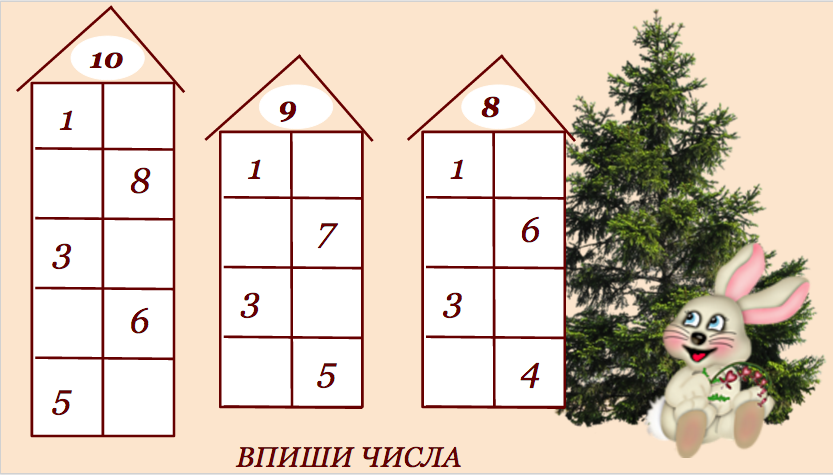 А ребёнок ещё только развивается, поэтому важно использовать в учебном процессе как можно больше каналов чувственного восприятия ребенка – и слух, и зрение, и осязание, а также подключать движение и речь.
Что-то упущено, не задействовано и тогда вдруг оказывается, что трудности возникают и у учеников второго класса, когда выясняется, что методы предыдущей работы не сработали. У ребёнка возникают, например, сложности с освоением сложения и вычитания двузначных чисел.
А ребёнок ещё только развивается, поэтому важно использовать в учебном процессе как можно больше каналов чувственного восприятия ребенка – и слух, и зрение, и осязание, а также подключать движение и речь.
Что-то упущено, не задействовано и тогда вдруг оказывается, что трудности возникают и у учеников второго класса, когда выясняется, что методы предыдущей работы не сработали. У ребёнка возникают, например, сложности с освоением сложения и вычитания двузначных чисел.
Для родителей, которые только готовят детей к школе или уже помогают делать уроки и для репетиторов, готовых «подтягивать хвосты», этот мой большой пост.
Книга Ананьев Б. Г., Антропова М. В. и др.
«Первоначальное обучение и воспитание детей о методе изучения чисел и методе изучения действий в работе над первым десятком — во многом объясняет сложность темы.
Самые распространённые приёмы изучения темы:
Абак и Супер папка с алгоритмом работы
Состав числа с шаблонами нумикон:
Объяснение с палочками Кюизенера
Монтессори разработала для этой цели специальный материал — красно-синие штанги
Кроме массы готовой продукции вроде магнитных досок и развивающих игр,всегда можно что-то быстро сделать вместе с ребёнком, например поиграть с рамочкой- десяткой . Посмотреть, в какие игры играю я, можно посмотреть блога.
Посмотреть, в какие игры играю я, можно посмотреть блога.
Помогает выучить наизусть состав чисел
обучающий клип-считалочка
Мнемотаблица- о методике можно почитать
Всё хорошо вовремя и должное внимание нужно уделить составу чисел ещё на дошкольной подготовке . Будет полезна серия рабочих тетрадей «Прописи математические». Каждому числу посвящена пропись. Кое- что можно распечатать из сокровищниц педагогов в liveInternet:
состав числа 10
состав числа 6
Отличная яркая рабочая тетрадь» Состав числа. Комбинаторика. Подготовка к школе. Для детей 5-7 лет»:
Моя любимая тетрадь для дошкольников :
рабочая тетрадь:
О методике ознакомления детей с составом числа — здесь можно почитать, что обычно делают педагоги в детском саду.
| бусинки |
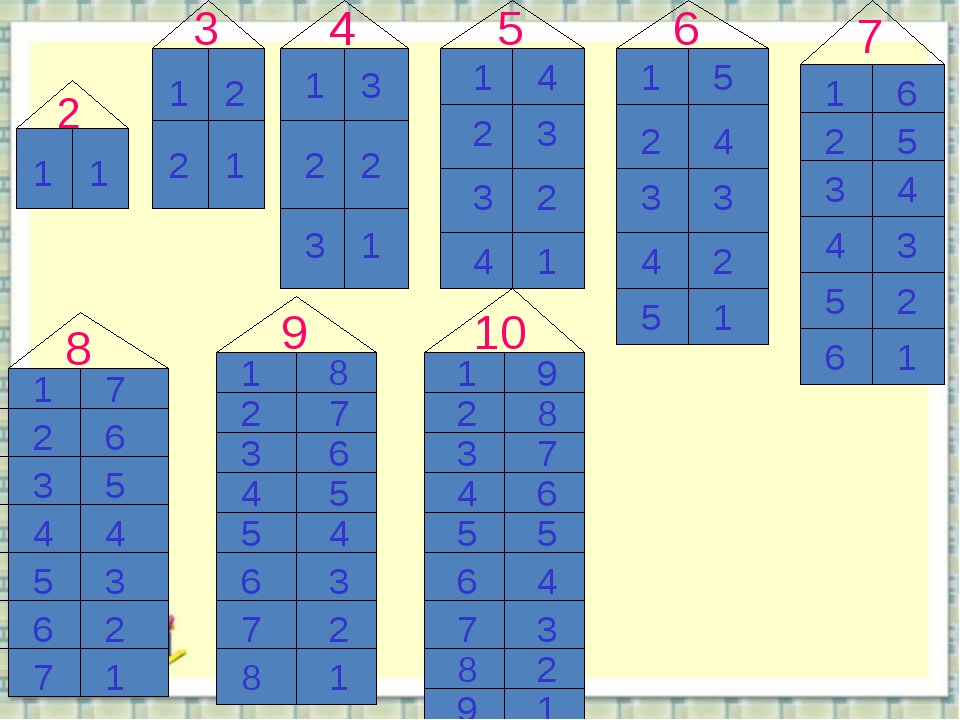
Числовые домики- самый популярный метод
Наглядное видео об устройстве домиков чисел
Обычное объяснение учителя на подготовке к школе:
1.
 Нарисуйте на листах бумаги домики в несколько этажей, на каждом этаже которого по две квартиры (окошка). На крыше домика вместе с ребенком напишите число и поясните, что это число на крыше — хозяин дома, который разрешает поселить на одном этаже только то количество жильцов, которое соответствует числу-хозяину. Для начала используйте для «расселения» счетные палочки или спички — это более наглядно, чем просто написанные цифры.
Нарисуйте на листах бумаги домики в несколько этажей, на каждом этаже которого по две квартиры (окошка). На крыше домика вместе с ребенком напишите число и поясните, что это число на крыше — хозяин дома, который разрешает поселить на одном этаже только то количество жильцов, которое соответствует числу-хозяину. Для начала используйте для «расселения» счетные палочки или спички — это более наглядно, чем просто написанные цифры.2. Заполните сами этажи первого домика, а затем поставьте эту задачу перед ребенком — он должен сам постараться расселить жильцов. Пусть одновременно ребенок проговаривает нужное количество, рассуждая примерно так: «Хозяин дома — число 6, если в одной квартире на этаже живет 2 жильца, то в другой должно жить 4».
3. Меняйте количество жильцов от этажа к этажу и повторяйте с ребенком новые комбинации чисел. В домике с хозяином 6 будут комбинации 1 и 5, 2 и 4, 3 и 3.
4. Перейдите от счетных палочек или спичек к написанным числам. Это труднее для детей, поэтому терпеливо повторяйте упражнение.
5. Постепенно усложняйте задание. Закрывайте один столбик окон и проговаривайте с ребенком соседей чисел. Так, если в домике с хозяином 8 на этаже живет 3, то его сосед 5. Постепенно ребенок сам сможет называть нужные числа.
6. Развесьте числовые домики в квартире так, чтобы ребенок видел их как можно чаще.
7. Время от времени переворачивайте один из домиков и просите ребенка нарисовать домик, вспомнив состав числа, на листочке по памяти.
Варианты числовых домиков для игр и демонстрации:
плакат с теремами
небольшой плакат сзаписью в виде 2+5
большие карточки с разными домиками
| скачать цветные числовые домики |
Интерактивная презентация «Заселяем домики» — по клику появляются числа-соседи
красочные постеры с домиками и счётным материалом.

| скачать домики |
Разные таблицы для изучения состава числа:
небольшая таблица
Онлайн тренажёры помогут быстро вспомнить тему школьникам:
тренажёр с лампочками
и числовые домики
Тренажёр:примеры и уравнения
Упражнения:
лото с картинками
Согласно школьной программе, первоклашки должны уметь автоматически решать примеры на сложение и вычитание в пределах чисел первого и второго десятков.
Для того, чтобы успешно справиться с поставленными задачами, детки должны знать из чего эти числа состоят . Вся проблема заключается в том, что информация эта — абстрактная и запомнить непоседливому малышу не так просто.
Поэтому преподносить ее нужно в форме увлекательной, наглядной и понятной . Лучше всего для нее подходят так называемые числовые домики — картинки и карточки, созданные специально для освоения дошколятами азов счета.
Мы тоже решили создать на нашем сайте тему «Состав числа до 10 домики» и предложить вамраспечатать картинки и карточки в готовом виде.
Пример карточки:
В конце нашей статьи приведены такие карточки — разного формата и разных авторов.
Также подобные карточки для детей вы можете нарисовать сами . Это совсем не сложно и не требует каких-то особых знаний и талантов. Просто рисуем от руки прямоугольники — многоэтажки на листах бумаги.
Рисуем карточки и объясняем ребенку правила
Как нарисовать числовой домик самому? Да очень просто:
- Сначала от руки на чистом листе бумаги изображаем каркас «пятиэтажки», затем делим его на этажи и дорисовываем крышу.
- На каждом этаже нужно изобразить по две квартиры (или два окошка).
 На крыше вместе с ребенком пишем цифру и объясняем малышу, что эта цифра — хозяин домика, который разрешает в нем жить только такому количеству жильцов, которое равно ему самому.
На крыше вместе с ребенком пишем цифру и объясняем малышу, что эта цифра — хозяин домика, который разрешает в нем жить только такому количеству жильцов, которое равно ему самому. - Для «заселения» на первых порах можно использовать счетные палочки — чтобы ребенок не сбился со счета и не запутался.
Помогаем ребенку освоить состав числа до 10 в игре
Помните о том, что маленькие детки очень охотно и быстро учатся на примерах. Поэтому первую карточку вы должны будете заполнить сами . Не забывайте рассуждать вслух о том какая у вас цифра-хозяин и сколько жильцов вам нужно заселить в каждую квартиру, чтобы не нарушать его «правила».
Следующий домик ребенок должен «заселить» сам при вашей помощи. Помогите ему рассуждать и высчитывать сколько жильцов должно быть заселено в каждую квартиру и на каждый этаж.
Закрепляем пройденное
Как помочь ребенку быстрее и легче запомнить состав числа до 10 и научиться считать? Ниже мы приводим еще несколько полезных советов и правил работы с карточками.
- Количество жильцов следует менять от этажа к этажу. При этом ребенок активно осваивает новые комбинации чисел. Например, в домике с цифрой-хозяином «6» они будут 1 и 5, 2 и 4, 3 и 3.
- Когда ваш малыш будет хорошо ориентироваться в комбинациях, можно переходить от счетных палочек к написанию цифр. Эта задача более трудная, поэтому прибегайте к постоянному повторению и помогайте своему чаду освоиться с новой деятельностью.
- Старайтесь постоянно освежать в памяти ребенка игру с карточками. Также старайтесь постепенно усложнять задание, переворачивая одну из карточек чистой стороной вверх и прося ребенка нарисовать этот домик и вспомнить состав числа, которое на нем изображено.
- Не забывайте о том, что без регулярного повторения и соответствующей заинтересованности в процессе вашему ребенку будет сложно запомнить пройденный материал.
Ну а для того, чтобы красивые и интересные карточки у вашего малыша всегда были перед глазами, используйте иллюстрации в нашей статье. Все эти красивые и разноцветные картинки можно распечатать и развесить в комнате ребенка, чтобы он постоянно их видел.
Все эти красивые и разноцветные картинки можно распечатать и развесить в комнате ребенка, чтобы он постоянно их видел.
Состав числа до 10 домики — распечатать картинки и карточки
Елизавета Савельева
Игра-пособие для детей старшего дошкольного возраста. Числовые домики , в которые нужно «заселить» нужную цифру. Игру можно использовать при закреплении темы “Состав чисел до 10 .
Вот таки числовые домики изготовлены мною для детей старшей группы, которые используются как на занятиях по ФЭМП, так и вне занятий — как настольная игра.
Я использовала вот такой простой набор : белый картон, набор цветного скотча, вспененный скотч, пробки от сока (вместе с резьбой, цветные маркеры,канцелярский нож, ножницы.
Освобождаем пробки от от ненужных деталей, чтобы облегчить приклеивание механизма к картону.
Пробки готовы к приклеиванию на поверхность картона.
При помощи цветного скотча создаем наши домики , приклеивая скотч на за раннее расчерченный картон. Под крышей нашего домика находиться число , которое и будет разложено на составляющие . Чем больше число , тем больше ячеек или этажей в домике .
Под крышей нашего домика находиться число , которое и будет разложено на составляющие . Чем больше число , тем больше ячеек или этажей в домике .
Цветными маркерами пишу цифры. Но их можно и распечатать и приклеить на любимый всеми скотч).
Дети с удовольствием пользуются данной игрой-пособием . Числовые домики помогают ребёнку запомнить в игровой форме, как можно составить числа от 2 до 10 .
Публикации по теме:
Конспект занятия «Путешествие в мир цифр. Цифра 10 и состав числа 10» Тема: «ПУТЕШЕСТВИЕ В МИР ЦИФР. ЗНАКОМСТВО С ЦИФРОЙ 10 И СОСТАВОМ ЧИСЛА 10». Возрастная группа: 5-6 лет. Форма совместной деятельности:.
Конспект занятия по математике «Состав числа из двух меньших» (старшая группа) Цель: Учить детей с помощью модели составлять число из двух меньших. Материал: Цифры, полоски бумаги, кружки. Методические приемы: Раздать.
Конспект интегрированного занятия по математике и конструированию «Состав числа 7» Конспект интегрированного занятия по математике и конструированию Тема: «Состав числа 7» Цель: Познакомить детей с образованием числа 7.
Конспект НОД по ФЭМП в подготовительной группе «Количественный состав числа 7» Задачи: учить составлять число 7 из двух меньших чисел и раскладывать его на два меньших числа. закреплять умение определять предыдущее,.
Конспект занятия «Цифра и состав числа 8» в старшей группе. Задачи: 1. Закрепить знание геометрических фигур. 2. Закрепить знание дней недели, их последовательности. 3. Развивать умение ориентироваться.
Конструкт по математике тема «Состав числа 4 из единиц» ТЕХНОЛОГИЧЕСКАЯ КАРТА ОРГАНИЗАЦИИ СОВМЕСТНОЙ ДЕЯТЕЛЬНОСТИ С ДЕТЬМИ Составитель: Воронина С. Н., воспитатель МАДОУ ЦРР – детский сад ГО Красноуфимск.
«Состав числа 5». НОД по образовательной области «Познавательное развитие» Тема «Состав числа 5» (подготовительная группа) Программное содержание: знакомить детей с составом числа 5, учить раскладывать число 5.
Понимание состава числа – залог правильного и четкого письменного и устного счета. Официально при зачислении в школу ребенок не обязан разбираться в математике, однако большинство малышей идут в 1 класс, владея элементарными арифметическими навыками. Помогая дошкольнику выучить счет до 10 и состав этого числа, вы серьезно облегчаете начало его учебы. Существует несколько эффективных методик, позволяющих проводить обучение в виде игры или в других бытовых ситуациях. Выясним, как заинтересовать ребенка и объяснить ему состав числа.
Помогая дошкольнику выучить счет до 10 и состав этого числа, вы серьезно облегчаете начало его учебы. Существует несколько эффективных методик, позволяющих проводить обучение в виде игры или в других бытовых ситуациях. Выясним, как заинтересовать ребенка и объяснить ему состав числа.
Когда начинать объяснять дошкольнику, что такое состав числа?
В возрасте 5-6 лет дети уже хорошо знают цифры, знакомятся с простыми арифметическими действиями. Именно в этом периоде стоит уделить немного времени на упражнения и объяснить ребенку состав чисел до 10. Однако важно, чтобы малыш уже освоил:
- прямой устный счет до 10;
- обратный счет от числа 10 до 1;
- пересчет и отсчет предметов;
- состав числа по единицам (например, 2 состоит из 1 и 1, 3 – из 1 и 1 и 1).
Все эти навыки свидетельствуют о том, что ребенку уже можно объяснить состав любого числа в пределах 10.
Что пригодится для домашних занятий?
Занятия станут эффективней, если заранее подготовиться и собрать необходимый учебный материал:
- палочки для счета;
- игровые кубики;
- карточки с изображениями цифр;
- разноцветные камешки или пуговицы;
- счеты;
- домики для чисел.

Вы можете приобрести готовые развивающие наборы в магазинах канцелярии или игрушек, либо смастерить все необходимые предметы вместе с ребенком. Второй вариант предпочтительнее.
Эффективные методики
Объяснять состав числа 10 нужно постепенно, разделив обучение на несколько логичных блоков. На первых занятиях следует уделить внимание цифрам 2 и 3, их взаимоотношениям и возможным комбинациям. Далее можно переходить к занятиям с наглядными карточками и уже после подключать числовые домики.
Занятие 1: осваиваем цифры 3, 2, 1
Возьмите любимые игрушки и вещи малыша (кубики, куклы, машинки). Начните упражнение с разбора числа 2 и покажите ребенку, какими способами его можно получить:
- Положите на стол перед малышом один предмет и попросите ребенка сделать так, чтобы их стало два. Обычно ему не сложно догадаться, как справиться с заданием. Если потребуется, дайте подсказку.
- Объясните малышу, что 2 является числом, состоящим всегда из пары единиц.

- Попросите ребенка выложить на стол по 2 понравившихся предмета.
- Когда двойка будет закреплена, переходите к изучению тройки. Расскажите ребенку, что если к 2 добавить 1 – получится 3. Положите перед ним две монетки и рядом еще одну. Малыш должен усвоить, что нет никакой разницы между 3 монетами вместе, 2 с 1 или 1 с 2.
Постепенно усложняйте задание. Четверку получить в игровой форме так же просто, как и тройку. Здесь могут помочь шахматы или шашки. Предложите ребенку выбрать 2 фигуры одного цвета (белый), а затем повторить задание. Спросите: сколько шахмат останется, если 1 светлую заменить на 1 темную? А что будет, если объединить 2 черные и 2 белые фигуры? В конце он должен понять, что получить число 4 можно при каждом возможном варианте перестановки.
Переходить к следующему блоку заданий стоит тогда, когда малыш поймет, что все эти действия приведут к результату известному заранее:
- 2 — это 1 + 1, 2 + 0;
- 3 — это 2 + 1, 1 + 2, 3 + 0;
- 4 — это 1 + 3, 2 + 2, 3 + 1, 4 + 0.

По такому же принципу объясните оставшиеся числа до 10.
Задание 2: числовые карточки
На этом этапе ребенок уже должен уяснить, что складывая разные цифры, можно получить любой результат. Но когда следует узнать состав определенного числа, нужно идти от обратного – от заранее выясненного ответа. Вам необходимо вместе с ним разобрать все пары слагаемых, приводящих к единому результату. Для этого отлично подойдут числовые карточки. Вариантов обучения несколько:
- Нарисуйте на карточках, например, 5 бабочек и предложите ребенку собрать нужное количество из предложенных заготовок.
- Предложите ему несколько раз самостоятельно собрать комбинации, при которых их сумма в итоге будет равняться 5.
- Попросите ребенка объяснить вам, как получить какое-либо число. Допускайте ошибки, малышам придется задействовать все свои способности чтобы их вычислить.
Приступать к последнему блоку заданий следует тогда, когда чадо сможет подбирать все варианты состава указанного числа.
Задание 3: числовые домики
Арифметические домики отлично помогают окончательно понять и закрепить в знаниях ребенка понятие о составе любого числа, а также развить навык устного счета.
Дом для чисел представляет собой здание, имеющее крышу и несколько этажей с квартирами в два ряда. Высота сооружения зависит от числа, к которому нужно подобрать все возможные комбинации цифр. Чтобы объяснить ребенку состав числа 2, достаточно нарисовать дом с двумя этажами (0+2, 1+1) и так далее.
Заготовки домиков можно найти в учебниках по математике или же изготовить самостоятельно из картона.
Как построить ход занятия:
- Положите на стол пустой дом, разместив в его крыше карточку с числом от 2 до 10 (пусть будет 6).
- Объясните ребенку, что на каждом уровне в квартирах находится столько людей, сколько написано на крыше.
- Поставьте условие: на первом этаже в 1 квартире живет всего один человек. Малышу нужно подумать и определить, сколько жильцов живет в квартире номер 2 (правильный ответ – 5).
- Теперь, когда алгоритм решения задачи ясен, попросите ребенка заселить все оставшиеся квартиры, меняя начальное количество жильцов на каждом новом этаже. В итоге на 2-м этаже будет 2 и 4 жильца, на 3-м – 3 и 3, на 4-м – 0 и 6. Таким образом, малыш сможет освоить все существующие комбинации цифр.
Небольшой лайфхак: расскажите, что любое число всегда состоит из 1 и предыдущей цифры по порядку. Так, если требуется выяснить состав числа 7, сразу готов первый ответ: 7 – это 1 и 6.
Когда все пары цифр и состав 10 будут освоены, можно усложнять задания.
Изучение второго десятка
Если вам удалось объяснить ребенку, что такое математический состав числа, то следует перейти к одному из самых сложных моментов – работе с десятками. Малыш обязательно спросит, почему 6+5=11, из-за чего оно так называется и записывается. В первую очередь расскажите, что для удобства большие числа считают десятками. Например, 6 и 4 – это один десяток. Поскольку в задаче требовалось прибавить 5, а 4 мы уже добавили, то не хватает всего единички. Поэтому выходит:
- 6+5 – это 6+4 и еще 1;
- 6+4=10;
- последнюю единицу записываем вместо 0, получается 11.
Сначала ребенку ничего не будет понятно, но спустя время он усвоит основный принцип работы с десятками. Облегчить задачку можно с помощью наглядного упражнения:
- попросите отсчитать 10 конфет и сложить в одну миску;
- теперь нужно отложить еще 7 лакомств в другую емкость;
- под каждой миской следует разместить карточку с изображением числа, соответствующему количеству конфет;
- попросите малыша сложить все вместе и сказать, сколько конфет получилось;
- для большего понимания объясните, что 10 в двузначном счете обозначают 1;
- правильный вариант: ребенок пишет единицу и 7 рядом, что означает 17.
Подобные примеры можно проводить и с большим количеством предметов. Например, дошкольник должен знать, что 32 – это 3 десятка плюс еще 2 единицы.
Как помочь ребенку?
Числа от 2 до 10 в повседневной жизни встречаются очень часто, а обучение счету – во многом креативный процесс. Помочь с освоением цифр просто даже без покупки специальных приспособлений:
- Малышу нравится спорт? Подсчитывайте с ним количество забитых мячей в ворота.
- Ребенок любит природу? Разглядывайте деревья на лужайке, сравнивайте, с какой стороны их больше, а с какой меньше.
- Чадо постоянно что-то рисует? Предложите ему изобразить определенное количество предметов на листе. Увлекается лепкой? Попросите смастерить фигурку с 3 лапами, 2 хвостами и 1 ухом.
- Хитрите. В течение дня спрашивайте у малыша «если я возьму у тебя одно печенье, то сколько у тебя останется?» и подобное.
В комфортной игровой атмосфере ребенок быстро разберется с составом всех чисел и будет считать 1 2 3 4 5 и до десятка правильно.
Если вашему малышу плохо дается устный счет, то можно предположить проблемы с мышлением, вниманием или недостатком концентрации. Направить энергию в нужное русло позволят игры от BrainApps. Сервис предлагает свыше 100 тренажеров, позволяющих развивать и совершенствовать интеллектуальные способности. Зарегистрировавшись на сайте, выберите необходимую категорию игр:
- Для улучшения памяти. Тренажеры типа «Числовой охват», «Запоминай и прокликай» и «Найди пару» разовьют объем памяти, улучшат ее точность и усовершенствуют объем внимания.
- Для развития мышления. Игры «Фруктовая математика», «Сравнение цифр по памяти» и «Перемещения» улучшат зрительную и пространственную память, разовьют логику и научат ребенка быстро находить ответы на поставленные вопросы.
- Для совершенствования внимания. Тренажеры «Найди фигуру», «Космос» и «Концентрация» помогут малышу лучше концентрироваться и направлять внимание в нужное русло.
Совместные игры с дошкольником онлайн – не только увлекательное, но и полезное хобби. Чадо сможет развиваться, достигать поставленных целей и соревноваться с вами или сверстниками. Все, что нужно – подключение к сети и свободное время.
Понимая важность объяснения состава чисел, старайтесь придерживаться предложенных рекомендаций, которые помогут дошколенку спокойно освоить и запомнить новую информацию:
- У всех бывают кризисы, но нужно помнить, что это временное явление.
- Давайте больше свободы. Часто требования родителей не соответствуют возможностям малыша. Подумайте, все ли ваши запреты обоснованы.
- Учитывайте детское мнение. Нужно четко понимать, что у дошкольника есть собственное мнение и суждения. Постарайтесь их принять.
- Заставлять малоэффективно. Назидание и приказной тон во время занятий не дадут положительного эффекта. Если малышу не хочется учить числа и примеры с цифрами 1 2 3 кажутся ему страшными, узнайте, в чем причина. Объясните, зачем и почему нужно учиться.
- Терпение и оптимизм – ваши лучшие спутники. Хорошее настроение, атмосфера любви, поддержки и взаимопонимания направляют стремления в нужное русло.
- Демонстрируйте свое доброжелательное отношение.
- Совместно находите и анализируйте ошибки.
- Обсуждайте варианты и способы устранения ошибок вместе.
- Поддерживайте и выражайте уверенность в том, что у него обязательно все получится.
Не забывайте закреплять результаты и включать в программу обучения развивающие мультфильмы и другие видео. 2 * 11 * 13 * 17 * 19 * 23 * 29 * 31 * 37
Простые числа — факты, примеры и таблица всего до 1000
Простое число можно разделить без остатка только на себя и на 1.Например, 17 можно разделить только на 17 и на 1.
Некоторые факты:
- Единственное четное простое число — 2. Все остальные четные числа можно разделить на 2.
- Если сумма цифр числа кратно 3, это число может быть разделено на 3.
- Ни одно простое число больше 5 не оканчивается на 5. Любое число больше 5, которое заканчивается на 5, можно разделить на 5.
- Ноль и 1 не являются считались простыми числами.
- Число, за исключением 0 и 1, может быть простым или составным числом.Составное число определяется как любое число больше 1, которое не является простым.
Чтобы проверить, является ли число простым, сначала попробуйте разделить его на 2 и посмотрите, получится ли у вас целое число. Если да, то это не может быть простое число. Если вы не получаете целое число, попробуйте разделить его на простые числа: 3, 5, 7, 11 (9 делится на 3) и так далее, всегда делите на простое число (см. Таблицу ниже).
Вот таблица всех простых чисел до 1000:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | ||
| 71 | 73 | 79 | 89 | 89 | 83 9000 | 103 | 107 | 109 | |||||||||||
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | |||||||||||
| 191 | 193 | 197 | 199 | 211 | 223 | 227 | 900 07|||||||||||||
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | ||||||||||
| 8358 | |||||||||||||||||||
| 8358 | |||||||||||||||||||
| 8358 313 | 317 | 331 | 337 | 347 | |||||||||||||||
| 349 | 353 | 359 | 367 | 373 | 379 | 8 383 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | ||||
| 463 | 8 467359 | ||||||||||||||||||
| 463 | 8 467359 | ||||||||||||||||||
| 463 | 8 467359 | 509 | 521 | 523 | |||||||||||||||
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | ||||||||||
| 601 | 607 | 8 | 607 | 8 | 643647 | 653 | |||||||||||||
| 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 835739 | 7357397 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | |||
| 809 | 811 | 821 | 835835835835 | 859 | |||||||||||||||
| 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | ||||||||||
| 941 | 947 | 953 | 967 | 8358 | 967 | 8 967 | 8 |
Примечание: второе издание этой книги доступно под названием Коды взлома с помощью Python
В этой главе рассматриваются темы:
· Простые и составные числа
· Сито Эратосфена
· Тест на первичность Рабина-Миллера
«Математики до сих пор тщетно пытались чтобы обнаружить некоторый порядок в последовательности простых чисел, и у нас есть причина верю, что это тайна, в которую человеческий разум никогда не проникнет.”
Леонард Эйлер, 18 -е математик века
Все шифры, описанные в этой книге, были на протяжении сотен лет, и все они (за исключением единовременного pad) легко ломаются компьютерами. Эти шифры очень хорошо работали, когда хакеры приходилось полагаться на карандаш и бумагу, чтобы взломать их, но теперь компьютеры могут манипулировать данные в триллионы раз быстрее, чем человек с карандашом.
Шифр RSA имеет несколько улучшений по сравнению с этим старым шифров, и это будет подробно описано в следующей главе.Однако шифр RSA потребует от нас сначала узнать о простых числах.
Простое число — это целое число (то есть целое число), которое больше 1 и имеет только два множителя: 1 и сам. Помните, что множители числа — это числа, которые можно умножить, чтобы получить исходный номер. Цифры 3 и 7 являются множителями 21. Число 12 имеет факторы 2 и 6, но также 3 и 4.
Каждое число делится на 1 и само себя. Цифры 1 и 21 — это делитель 21.Числа 1 и 12 являются множителями 12. Это потому, что 1 раз любое число всегда будет одним и тем же числом. Но если нет других факторов для этого числа это число простое.
Вот список простых чисел (обратите внимание, что 1 не считается простым числом):
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281… и так далее, FOREVER .
Существует бесконечное количество простых чисел. Это означает не существует «наибольшего» простого числа. Они просто становятся все больше и больше, просто как обычные числа. (См. http://invpy.com/infiniteprimes для доказательства этого.) В шифре RSA используются очень большие простые числа в ключи, которые он использует. Из-за этого будет слишком много ключей к брутфорсу. через.
Гугол — это число, у которого есть единица с сто нулей за ним:
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
(Немного истории: название поисковой компании Google возник из-за неправильного написания «гугол», но они решили, что им это нравится. орфография лучше и сохранила.)
A миллиардов миллиардов миллиардов гуголов имеет на двадцать семь нулей больше, чем гугол:
1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Но это крошечные числа. Типичное простое число, используемое в наша программа RSA будет содержать сотни цифр:
112,829,754,900,439,506,175,719,191,782,841,802,172,556,768,253,593,054,977,186,2355,84,979,780,304,652,423,405,148,425,447,063,090,165,759,070,742,102,132,335,103,295,947,000,718,386,333,756,395,799,633,478,227,612,244,071,875,721,006,813,307,628,061,280,861,610,153,485,352,017,238,548,269,452,852,733,818,231,045,171,038,838,387,845,888,589,411,762,622,041,204,120,706,150,518,465,720,862,068,595,814,264,819
Вышеупомянутое число настолько велико, я думаю, вы не даже прочитайте его, чтобы заметить опечатку в нем.
Целые числа, не являющиеся простыми числами, называются составными. числа, потому что они состоят как минимум из двух факторов, кроме 1 и сам номер. Их называют составными числами, потому что эти числа составлены простых чисел, умноженных вместе, например, составное число 1386 состоит из простых чисел 2 × 3 × 3 × 7 × 11.
Вот четыре факта о простых числах:
1. Prime числа — это целые числа больше 1, которые имеют только 1 и сами являются множителями.
2. Два — единственное четное простое число. (Хотя, думаю, это делает двоих очень нечетное простое число.)
3. Существует бесконечное количество простых чисел. Нет «самого большого простое число».
4. Умножение два простых числа дадут число, которое имеет только две пары множителей: 1 и само (как и все числа) и два простых числа, которые были перемножены. Например, 3 и 7 — простые числа. 3 умножить на 7 будет 21.Единственные факторы для 21 — это 1, 21, 3 и 7.
Сначала мы создадим модуль, который имеет функции, связанные с простые числа:
· isPrime () вернет либо True, либо Ложь, если переданное ему число простое или нет. Он будет использовать «делит тестовый »алгоритм.
· primeSieve () будет использовать «Сито Эратосфен »(объясненный позже) для генерации чисел.
Как и cryptomath.py, программа primeSieve.py предназначена только для импорта как модуль к другим нашим программам.При самостоятельном запуске он ничего не делает.
Откройте новое окно редактора файлов, щелкнув Файл ► Новое окно . Печатать следующий код в редактор файлов, а затем сохраните его как primeSieve.py.
Источник код для primeSieve.py
импорт математики
def isPrime (число):
если число <2:
return False
для i в диапазоне (2, int (math.sqrt (число)) + 1):
если число% i == 0:
return False
return True
def primeSieve (размер сита):
sieve = [True] * sieveSize
сито [0] = Ложь
sieve [1] = Ложь
для i в диапазоне (2, int (math.sqrt (sieveSize)) + 1):
указатель = я * 2
пока указатель решето [указатель] = Ложь указатель + = я простые числа = [] для я в диапазоне (размер сита): if sieve [i] == True: простые числа.добавить (я) вернуть простые числа primeSieve.py импорт математики Единственный модуль primeSieve.py
нуждается в математическом модуле. primeSieve.py def isPrime (число): если число <2: return False Запрограммируем isPrime ()
функция для возврата False, если число
Параметр — составное число и Истина, если параметр числовой является простым числом.Если число
меньше 2, мы знаем, что он не простой и может
просто верните False. primeSieve.py для i в диапазоне (2, int (math.sqrt (num)) + 1): если число% i == 0: return False return True У простого числа нет делителей, кроме 1 и самого себя. Итак, чтобы
узнать, является ли данное число простым или нет, нам просто нужно продолжать делить его на
целые числа и посмотрите, делит ли кто-нибудь из них равномерно число с остатком 0. Функция math.sqrt () будет
возвращает значение с плавающей запятой квадратного корня из переданного числа. Квадрат
корень числа можно умножить на себя, чтобы получить число. Например,
квадратный корень из 49 равен 7, потому что 7 × 7 равно 49. Например, чтобы узнать, является ли число 49 простым, разделите его на
целые числа начиная с 2: 49 ÷ 2 = 24 остатка
1 49 ÷ 3 = 16 остаток
1 49 ÷ 4 = остаток 12
1 49 ÷ 5 = 9 остаток
4 49 ÷ 6 = 8 остаток
1 49 ÷ 7 = 7 остаток
0 На самом деле вам нужно всего лишь число разделить на простое.
числа.Например, нет причин проверять, делит ли 6 число 49, потому что если оно
Если бы, тогда 2 разделило бы 49, так как 2 является множителем 6. Любое число , которое 6
делится равномерно, можно также равномерно делить на 2: Рисунок 23-1. 2 делит 6, а 6 делит X, поэтому 2
делит X. Поскольку существует целое число (не 1 или 49), которое равномерно
делит 49 (то есть имеет остаток от 0), мы знаем, что 49 не является простым
номер. Другой пример: 13: 13 ÷ 2 = 6 остаток
1 13 ÷ 3 = 4 остатка
1 13 ÷ 4 = 3 остатка
1 Ни одно целое число не делит 13 с остатком 0 (кроме
для 1 и 13, что не в счет).На самом деле, нам даже не нужно делить все на числа.
до 13. Нам нужно только проверить целые числа до (включительно) квадратного корня.
числа, которое мы проверяем на простоту. Квадратный корень из числа — это число
которое умножается само на себя, чтобы получить первое число. Квадратный корень из 25 равен
5, потому что 5 × 5 = 25. Квадратный корень из
13 примерно равно 3,6055512754639, потому что 3,6055512754639 × 3,6055512754639 = 13. Это означает, что когда мы тестировали 13
для простоты нам нужно было разделить только 2 и 3, потому что 4 больше, чем
корень квадратный из 13. Строка 18 проверяет, равен ли остаток от деления 0, используя
оператор% mod. Если цикл for в строке 17 никогда не возвращает значение False,
функция вернет True в строке 20. Сито Эратосфена (произносится как «эра, тау, ту,
колени ») — алгоритм вычисления простых чисел. Представьте себе кучу ящиков
для каждого целого числа все помечены как «простые»: Таблица 23-1. Пустое сито Эратосфена, с каждым
число помечено как «простое». Prime 1 Prime 2 Prime 3 Prime 4 Prime 5 Prime 6 Prime 7 Prime 8 Prime 9 Prime 10 Prime 11 Prime 12 Prime 13 Prime 14 Prime 15 Prime 16 Prime 17 Prime 18 Prime 19 Prime 20 Prime 21 Prime 22 Prime 23 Prime 24 Prime 25 Prime 26 Prime 27 Prime 28 Prime 29 Prime 30 Prime 31 Prime 32 Prime 33 Prime 34 Prime 35 Prime 36 Prime 37 Prime 38 Prime 39 Prime 40 Prime 41 Prime 42 Prime 43 Prime 44 Prime 45 Prime 46 Prime 47 Prime 48 Prime 49 Prime 50 Пометить 1 как «Не простое» (так как один
никогда не бывает простым).Затем отметьте все числа, кратные двум (кроме самого двух), как
«Не прайм». Это означает, что мы отметим целые числа 4 (2 × 2), 6 (2 × 3), 8 (2 ×
4), 10, 12 и т. Д. До 50 (наибольшее число, которое у нас есть) помечены как
«Не прайм»: Таблица 23-2. Сито с единицей и кратностью 2
(кроме самого 2) помечены как «не простые». Не Prime 1 Prime 2 Prime 3 Не Prime 4 Prime 5 Не Prime 6 Prime 7 Не Prime 8 Prime 9 Не Prime 10 Prime 11 Не Prime 12 Prime 13 Не Prime 14 Prime 15 Не Prime 16 Prime 17 Не Prime 18 Prime 19 Не Prime 20 Prime 21 Не Prime 22 Prime 23 Не Prime 24 Prime 25 Не Prime 26 Prime 27 Не Prime 28 Prime 29 Не Prime 30 Prime 31 Не Prime 32 Prime 33 Не Prime 34 Prime 35 Не Prime 36 Prime 37 Не Prime 38 Prime 39 Не Prime 40 Prime 41 Не Prime 42 Prime 43 Не Prime 44 Prime 45 Не Prime 46 Prime 47 Не Prime 48 Prime 49 Не Prime 50 Затем повторите это со всеми числами, кратными трем, кроме
три самих себя: 6, 9, 12, 15, 18, 21 и т. д. помечены как «Not Prime».потом
сделайте это для всех чисел, кратных четырем (кроме самого четырех), и для всех
кратные пяти (кроме самой пяти), вплоть до восьми. Мы останавливаемся на 8
потому что оно больше 7,071, квадратного корня из 50). Мы можем это сделать, потому что
все числа, кратные 9, 10, 11 и т. д., уже будут отмечены. Готовое сито выглядит так: Таблица 23-3. Готовое сито Эратосфена. Не Prime 1 Prime 2 Prime 3 Не Prime 4 Prime 5 Не Prime 6 Prime 7 Не Prime 8 Не Prime 9 Не Prime 10 Prime 11 Не Prime 12 Prime 13 Не Prime 14 Не Prime 15 Не Prime 16 Prime 17 Не Prime 18 Prime 19 Не Prime 20 Не Prime 21 Не Prime 22 Prime 23 Не Prime 24 Не Prime 25 Не Prime 26 Не Prime 27 Не Prime 28 Prime 29 Не Prime 30 Prime 31 Не Prime 32 Не Prime 33 Не Prime 34 Не Prime 35 Не Prime 36 Prime 37 Не Prime 38 Не Prime 39 Не Prime 40 Prime 41 Не Prime 42 Prime 43 Не Prime 44 Не Prime 45 Не Prime 46 Prime 47 Не Prime 48 Не Prime 49 Не Prime 50 Используя сито Эрастофена, мы вычислили, что
простые числа до 50: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43 и 47.Этот алгоритм сита хорош, когда мы хотим быстро узнать все
простые числа в
определенный диапазон номеров. Это намного быстрее, чем при использовании предыдущего
Алгоритм «деления теста», чтобы проверить, является ли 2 простым числом, затем проверить, является ли 3 простым числом, затем
проверить, простое ли число 4, и так далее. def primeSieve (размер сита): sieve = [True] * sieveSize сито [0] = Ложь sieve [1] = Ложь Функция primeSieve () возвращает
список всех простых чисел от 1 до sieveSize.Сначала в строке 27 создается список логических значений True, который является длиной sieveSize.
Индексы 0 и 1 равны
помечено как False, потому что 0
и 1 не простые числа. для i в диапазоне (2, int (math.sqrt (sieveSize)) + 1): указатель = я * 2 пока указатель решето [указатель] = Ложь указатель + = я Цикл for в строке 32 идет
через каждое целое число от 2 до квадратного корня из
sieveSize.Указатель переменной
начнется с первого числа, кратного i после i (это будет i * 2). потом
цикл while установит указатель
index в списке сита на False,
и строка 36 изменит указатель, чтобы указать на следующий
кратно i. простые числа = [] для я в диапазоне (размер сита): if sieve [i] == True: primes.append (i) После цикла for в строке 32
После завершения, сито-список будет содержать True для каждого индекса, который является простым числом.Мы можем создать
новый список (который начинается с пустого списка с простыми числами) и перебирает весь список sieve, а также добавляет и нумерует, если sieve [i] имеет значение True (что означает, что i является простым). Список простых чисел возвращается в строке 44. Функция isPrime () в primeSieve.py проверяет, можно ли разделить число поровну
диапазоном чисел от 2 до квадратного корня из числа. Но как насчет
число вроде 1,070,595,206,942,983? Если вы передадите это целое число в isPrime (), потребуется несколько секунд, чтобы определить, является ли оно
премьер или нет.И если число состоит из сотен цифр (например, простое
числа в программе шифрования RSA в следующей главе), она возьмет на себя
триллион лет, чтобы выяснить, что это один число простое или нет. Функция isPrime () в primeSieve.py слишком медленная для больших чисел, которые мы будем
использовать в шифре RSA. К счастью, есть алгоритм, называемый
Тест на простоту Рабина-Миллера, чем можно вычислить, являются ли такие большие числа простыми
или нет. Мы создадим новую функцию isPrime () в rabinMiller.py, который использует этот лучший алгоритм. В коде этого алгоритма используется продвинутая математика, и
как работает алгоритм, выходит за рамки этой книги. Как и функция gcd () в cryptomath.py,
эта книга просто представит код алгоритма, который вы можете использовать без
объяснение. Откройте новое окно редактора файлов и введите следующее
код. Сохраните этот файл как rabinMiller.py. Этот
Программа будет модулем, который предназначен для импорта другими программами. Вместо того, чтобы вводить список чисел в строке 43, просто
временно добавьте строки import pyperclip и pyperclip.copy (primeSieve (1000)) в файл primeSieve.py и запустите его. Это скопирует список
в буфер обмена, а затем вы можете вставить его в файл rabinMiller.py. Откройте новое окно редактора файлов, щелкнув Файл ► Новое окно . Печатать
следующий код в редактор файлов, а затем сохраните его как rabinMiller.ру. Источник
код для rabinMiller.py 1. 2. 3. 4.
случайный импорт 5. 6. 7.
def rabinMiller (число): 8. 9. 10.
s = число — 1 11.
t = 0 12.
а s% 2 == 0: 13. 14. 15.
s = s // 2 16.
т + = 1 17. 18.
для испытаний в диапазоне (5): 19.
a = random.randrange (2, число — 1) 20.
v = pow (a, s, num) 21.
если v! = 1: 22.
я = 0 23.
в то время как v! = (число — 1): 24.
если i == t — 1: 25.
return False 26.
еще: 27.
я = я + 1 28.
v = (v ** 2)% число 29.
return True 30. 31. 32.
def isPrime (число): 33. 34. 35. 36.
если (число <2): 37.
return False 38. 39. 40. 41. 42. 43. lowPrimes
= [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157,
163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241,
251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347,
349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439,
443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547,
557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643,
647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751,
757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859,
863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977,
983, 991, 997] 44. 45.
если число в lowPrimes: 46.
return True 47. 48. 49.
для Prime в LowPrimes: 50.
если (число% простое == 0): 51.
return False 52. 53. 54.
return rabinMiller (число) 55. 56. 57.
def generateLargePrime (размер ключа = 1024): 58. 59.
в то время как True: 60.
число = random.randrange (2 ** (размер ключа-1), 2 ** (размер ключа)) 61.
если isPrime (число): 62.
return num Если вы запустите интерактивную оболочку, вы можете импортировать модуль rabinMiller.py и вызывать в нем функции. Пытаться
введите в интерактивную оболочку следующее: >>>
импортный rabinMiller >>>
rabinMiller.generateLargePrime () 12288116834221104103052368351544323 020370036732110521534936076816199 >>>
rabinMiller.isPrime (45943208739848451) Ложь >>>
rabinMiller.isPrime (13) Истинно >>> rabinMiller.py 1. 2. 3. 4.
случайный импорт Алгоритм Рабина-Миллера использует случайные числа, поэтому мы импортируем
модуль random в строке 4. rabinMiller.py 7.
def rabinMiller (число): 8. 9. 10.
s = число — 1 11.
t = 0 12.
а s% 2 == 0: 13. 14. 15.
s = s // 2 16.
т + = 1 17. 18.
для испытаний в диапазоне (5): 19.
a = random.randrange (2, число — 1) 20.
v = pow (a, s, num) 21.
если v! = 1: 22.
я = 0 23.
в то время как v! = (число — 1): 24.
если i == t — 1: 25.
return False 26.
еще: 27.
я = я + 1 28.
v = (v ** 2)% число 29.
return True Математика алгоритма простоты Рабина-Миллера
выходит за рамки этой книги, поэтому код в этой функции не будет
объяснил. Алгоритм Рабина-Миллера также не является верным тестом для
первобытность; однако вы можете быть абсолютно уверены в его точности.(Хотя
этого недостаточно для коммерческого программного обеспечения для шифрования, это достаточно хорошо
для целей программ в этой книге.) Основное преимущество
Алгоритм Рабина-Миллера заключается в том, что это относительно простой тест на простоту и
на обычном компьютере запускается всего за несколько секунд. Если rabinMiller () возвращает True, то аргумент num равен
очень вероятно, что будет основным. Если rabinMiller ()
возвращает False, затем num
определенно составной. rabinMiller.py 32.
def isPrime (число): 33. 34. 35. 36.
если (число <2): 37.
return False Все числа меньше двух (например, единица, ноль и
отрицательные числа) не являются простыми, поэтому мы можем сразу вернуть False. rabinMiller.py 39. 40. 41. 42. 43. lowPrimes
= [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157,
163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241,
251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347,
349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439,
443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547,
557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643,
647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751,
757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859,
863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977,
983, 991, 997] 44. 45.
если число в lowPrimes: 46.
return True числа в списке lowPrimes
простые числа. (Да.) Мы можем немедленно вернуть True, если
число находится в нижнем прайм-листе
список. rabinMiller.py 48. 49.
для Prime в LowPrimes: 50.
если (число% простое == 0): 51.
return False Строка 49 проходит по каждому из простых чисел в списке lowPrimes.Целое число в num
модифицируется оператором% mod каждым простым числом
число в строке 50, и если оно равно 0, то
мы знаем, что простое делит число
и поэтому num не является простым. В этом случае строка 51
возвращает False. Проверка делимости числа на
все простые числа меньше 1000 не скажут нам, является ли число простым, но это может
скажите нам, составное ли число. Около 30% составных случайных чисел, созданных функцией generateLargePrime (), будут
определяется как составной путем деления на младшие простые числа.Деление на низкое
простые числа намного быстрее, чем выполнение полного алгоритма Рабина-Миллера на
число, поэтому этот ярлык может ускорить выполнение нашей программы. rabinMiller.py 53. 54.
return rabinMiller (число) Это все быстрые тесты, чтобы определить, является ли число
премьер или нет. Но если num не соответствует ни одному из этих
tests, затем передается rabinMiller ()
функция, чтобы проверить, простое оно или нет.Возвращаемое значение rabinMiller () будет возвращено isPrime (). Комментарий в строке 53 означает вызов rabinMiller () функция до
определить, является ли число простым. Пожалуйста, не звоните доктору Рабину или доктору Миллеру.
лично спросить их, простое ли у вас число. rabinMiller.py 57.
def generateLargePrime (размер ключа = 1024): 58. 59.
в то время как True: 60.
число = случайное.randrange (2 ** (размер ключа-1), 2 ** (размер ключа)) 61.
если isPrime (число): 62.
return num Функция generateLargePrime ()
вернет простое целое число. Это достигается за счет создания большого
случайное число, сохраняя его в num, а затем передавая num в isPrime (). Затем функция isPrime () проверит, является ли число составным, а затем передаст число
в rabinMiller () для более тщательного (и
вычислительно дорогостоящий) тест на простоту. Если число простое, то
строка 62 возвращает число. В противном случае бесконечный цикл
возвращается к строке 60, чтобы попробовать новое случайное число. Этот цикл продолжает попытки
и снова, пока не найдет число, которое isPrime ()
функция говорит, что это простое число. Простые числа обладают удивительными математическими свойствами. В виде
вы узнаете из следующей главы, они также являются основой используемых шифров
в актуальном профессиональном программном обеспечении для шифрования. Определение простого числа:
достаточно просто: число, которое имеет только один и сам в качестве факторов.Но
определение того, какие числа простые, а какие составные (т. е. не
prime) требует некоторого умного кода. Изменение числа со всеми числами от двух до
квадратный корень из числа — вот как наш isPrime ()
функция определяет, является ли это число простым или нет. Простое число никогда не будет
имеют остаток 0, когда он модифицируется любым числом (помимо его факторов, 1
и сам.) Но компьютеру может потребоваться некоторое время, чтобы вычислить, когда
проверка больших чисел на простоту. Сито Эрастотена можно использовать, чтобы быстро определить,
диапазон чисел является простым или нет, но для этого требуется много памяти. В шифре RSA используются очень большие простые числа.
длиной в сотни цифр. Сито Эрастотена и основная функция isPrime (), которая есть в primeSieve.py
недостаточно умны, чтобы обрабатывать такие большие числа. Алгоритм Рабина-Миллера использует некоторую математику, которая
простой код (но математические рассуждения слишком сложны для этого
книга), но это позволяет нам определить, является ли число, состоящее из сотен цифр
длинное — первое. В следующей главе мы будем использовать код простого числа, который мы
разработан для модуля rabinMiller.py в нашем RSA
Шифровальная программа. Наконец-то у нас будет более простой в использовании шифр, чем одноразовый.
pad cipher, но его нельзя взломать простыми хакерскими методами в этом
книга! Для справки, между различными заявленными решениями существует довольно значительная разница в скорости. Вот сравнительный код.Решение, на которое указал Леннарт, называется «историческим», решение, предложенное Муравьем, — «наивным», а решение RC — «регулярным выражением». Результат на моей машине для n = 100: Как видите, есть довольно большое несоответствие. Здесь снова 1000 (основные выходы удалены): Математика - не самый простой предмет для изучения и усвоения. На самом деле, у многих людей больше проблем с математикой, чем с любым другим предметом в школе.Математика состоит из правил, которые сложно понять, даже если вы хорошо разбираетесь в числах. Если вам нужна дополнительная помощь в понимании некоторых математических понятий, не стесняйтесь этого, потому что многие другие дети тоже испытывают трудности с математикой. Целые числа - это натуральные числа и их отрицательные числа. Помните, что натуральные числа - это традиционная система счисления, с которой вы знакомы, числа от {0, 1, 2, 3…}. Положительные целые числа идут от {1, 2, 3…}, а отрицательные целые числа идут от {-1, -2, -3…} и так далее.Эти два набора чисел известны как противоположности: 1 противоположен -1, 2 противоположен -2 и так далее. Когда вы работаете с числами, вы почти всегда работаете с целыми числами. Между тем, простые числа - это натуральные числа, которые можно разделить только на единицу или на себя. Первые несколько - это 2, 3, 5, 7, 11, 13 и 17. Исходя из этого списка, легко сделать предположение, что простые числа являются нечетными числами, но на самом деле это не так. Все простые числа являются нечетными, но не все нечетные числа являются простыми числами.Например, 9 можно разделить на 3, 25 можно разделить на пять, а 45 можно разделить как на 9, так и на 5. С другой стороны, число 1 не является простым числом. Составные числа - это в основном положительные целые числа, которые можно разделить на любое положительное число, кроме самих себя. Другими словами, составные числа противоположны простым числам. Примеры включают 4, 6, 8, 9, 10, 12 и 14. Все четные числа являются составными числами. В математике факториал - это, по сути, произведение всех положительных целых чисел, которые меньше или равны n , когда n записывается следующим образом: n ! . Пример: 6! = 1x2x3x4x5x6 = 720. Другими словами, факториал 6 будет равен 720, потому что вы умножаете каждое число до 6, чтобы получить ответ. Пи очень сложен. Пи используется для измерения окружностей и в большинстве случаев записывается просто как 3,14, но на самом деле число продолжается бесконечно. Это помогает математикам определить отношение длины окружности к ее диаметру. Первые несколько чисел Пи - 3,1415 Числа - не самая простая вещь для понимания, но как только вы их усвоите, это действительно может быть весело. Когда дело касается математики, очень важно просить о помощи. Если вы научитесь точно решать математические задачи, это значительно упростит жизнь и поможет вам преуспеть в школе. Для получения дополнительной информации посетите следующие сайты: Популярные товары Пример проверки, является ли целое число (введенное пользователем) простым числом или нет, с использованием управляющих операторов. Чтобы понять этот пример, вы должны знать следующие темы программирования R: Положительное целое число больше 1, не имеющее других делителей, кроме 1, а само число называется простым числом. Числа 2, 3, 5, 7, 11, 13 и т. Д. Являются простыми числами, поскольку не имеют других делителей. Но, 6 не является простым (оно составное), поскольку Выход 1 Выход 2 Здесь мы берем целое число от пользователя и проверяем, простое оно или нет.Числа, меньшие или равные 1, не являются простыми числами. Следовательно, мы продолжаем действовать только в том случае, если num больше 1. Мы проверяем, делится ли num точно на любое число от 2 до num - 1. Если мы найдем множитель в этом диапазоне, число не простое. В противном случае число простое. Мы можем уменьшить диапазон чисел, в котором ищем факторы. В приведенной выше программе наш диапазон поиска составляет от 2 до число - 1. Мы могли бы использовать диапазон, [2, число /2] или [2, число ** 0,5]. Более поздний диапазон основан на том факте, что составное число должно иметь множитель меньше квадратного корня из этого числа. В противном случае число простое. Добро пожаловать на нашу страницу со списком первых 5 простых чисел. На этой странице мы расскажем вам, что такое первые пять простых чисел и почему они простые. Вы также можете использовать наш калькулятор простых чисел, чтобы показать все простые числа в заданном диапазоне. Первые 5 простых чисел: Определение Другими словами, единственные множители простого числа - это 1 и само число. Однако 1 не считается простым числом. Чтобы найти первые пять простых чисел, мы начинаем с 2 (помните, что 1 не считается простым числом). Единственные делители 2 - это 1 и 2. Итак, 2 - простое число (на самом деле два - единственное четное простое число!) Затем мы проверяем 3. У тройки всего два множителя: 1 и 3. Итак, 3 - простое число. Затем мы проверяем 4. Четыре имеет три множителя: 1, 2 и 4. Итак, 4 не является простым числом (число, которое не является простым, называется составным) Далее мы тестируем 5.Пять имеет всего два множителя: 1 и 5. Значит, 5 простое. Затем мы проверяем 6. Шесть имеет четыре фактора: 1, 2, 3 и 6. Итак, 6 является составным. Теперь 7. Семь имеет только два множителя: 1 и 7. Итак, 7 простое. Далее идет 8. У восьмерки четыре фактора: 1, 2, 4 и 8. Итак, 8 составное. Теперь 9. Девять имеет три фактора: 1, 3 и 9. Итак, 9 составное. Следующее тестирование 10. Десять имеет четыре фактора: 1, 2, 5 и 10. Итак, 10 составное. Сейчас тестируем 11.Одиннадцать имеет только два множителя: 1 и 11. Итак, 11 простое число. Теперь у нас есть первые 5 простых чисел: 2, 3, 5, 7 и 11! Этот калькулятор использует решето Эратосфена для вычисления простых чисел от и до любых заданных чисел меньше миллиона. Попробуйте и убедитесь! Введите любое значение в наш калькулятор поиска простых чисел, и он найдет все простые числа до вашего значения включительно. Затем вы можете взять эту информацию, скопировать и вставить ее в другое место, если хотите! Взгляните на еще несколько наших рабочих листов, похожих на эти. Наша страница диаграмм простых чисел похожа на списки простых чисел на этой странице, но содержит диаграммы.
давая все простые числа до определенного значения. У нас есть диаграммы, показывающие все простые числа до ... Существует также калькулятор простых чисел, который вычислит все простые числа в пределах выбранных значений до миллиона. Наша страница со списком простых чисел похожа на диаграммы простых чисел на этой странице, но содержит диаграммы.
давая первый ... набор простых чисел. У нас есть графики, показывающие ... Существует также тестер простых чисел, который скажет вам, является ли данное число
простим и расскажем все множители этого числа. Сито Эрастосфена - это метод поиска простых чисел от 2 до любого заданного числа. Эратосфен был греческим математиком (а также поэтом, астрономом и музыкантом), который жил примерно с 276 г. до н.э. по 194 г. до н.э. Если вы хотите узнать больше о его решете для поиска простых чисел и распечатать некоторые рабочие листы «Сито Эратосфена», воспользуйтесь ссылкой ниже. Взгляните на нашу страницу простых чисел, которая четко описывает, что такое простые числа, а чем они не являются. Простое Сито ()
Функция
842 7015553694882717483780547440094637513125114712 94573241337844666680 076859566835016382556518967124821239703634581598364114600067163501963721834845554443584001849620509600312468757953899553441648428119 88338
исторический
Время в секундах: 0,14831 Чтобы найти первые N простых чисел в Python
из sys import argv
от времени импорта времени
def prime (i, простые числа):
для простых чисел:
если нет (i == prime или i% prime):
вернуть ложь
primes.add (i)
вернуть я
def исторический (n):
простые числа = набор ([2])
я, р = 2, 0
в то время как True:
если простое число (i, простые числа):
р + = 1
если p == n:
вернуть простые числа
я + = 1
def наивный (n):
из счетчика импорта itertools, islice
простые числа = (n для n в count (2), если все (n% d для d в диапазоне (2, n)))
вернуть islice (простые числа, 0, n)
def isPrime (n):
импорт ре
# см. http: // tinyurl.(11 +?) \ 1 + $ ',' 1 '* n) == Нет
def regexp (n):
import sys
N = int (sys.argv [1]) # количество требуемых простых чисел (из командной строки)
M = 100 # верхняя граница области поиска
l = list () # список результатов
в то время как len (l)
наивный
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 , 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229 , 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379 , 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541 ]
Время в секундах: 0.0219371318817
исторический
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 , 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229 , 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379 , 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541 ]
Время в секундах: 0.00515413284302
регулярное выражение
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 , 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229 , 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379 , 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541 ]
Время в секундах: 0.0733318328857
наивный
Время в секундах: 1.466
регулярное выражение
Время в секундах: 29.2350409031
Математика и числа для детей
Математика и числа для детей
R Программа для проверки простого числа
2 x 3 = 6 . Пример: Проверить простое число
# Программа для проверки, простое ли введенное число
# принять ввод от пользователя
число = как.целое число (readline (prompt = "Введите число:"))
flag = 0
# простые числа больше 1
if (num> 1) {
# проверьте факторы
flag = 1
for (i in 2: (num-1)) {
if ((число %% i) == 0) {
flag = 0
перерыв
}
}
}
если (число == 2) флаг = 1
if (flag == 1) {
print (paste (num, «простое число»))
} еще {
print (paste (num, «не простое число»))
}
Введите число: 25
[1] «25 - не простое число»
Введите число: 19
[1] «19 - простое число»
Первые 5 простых чисел
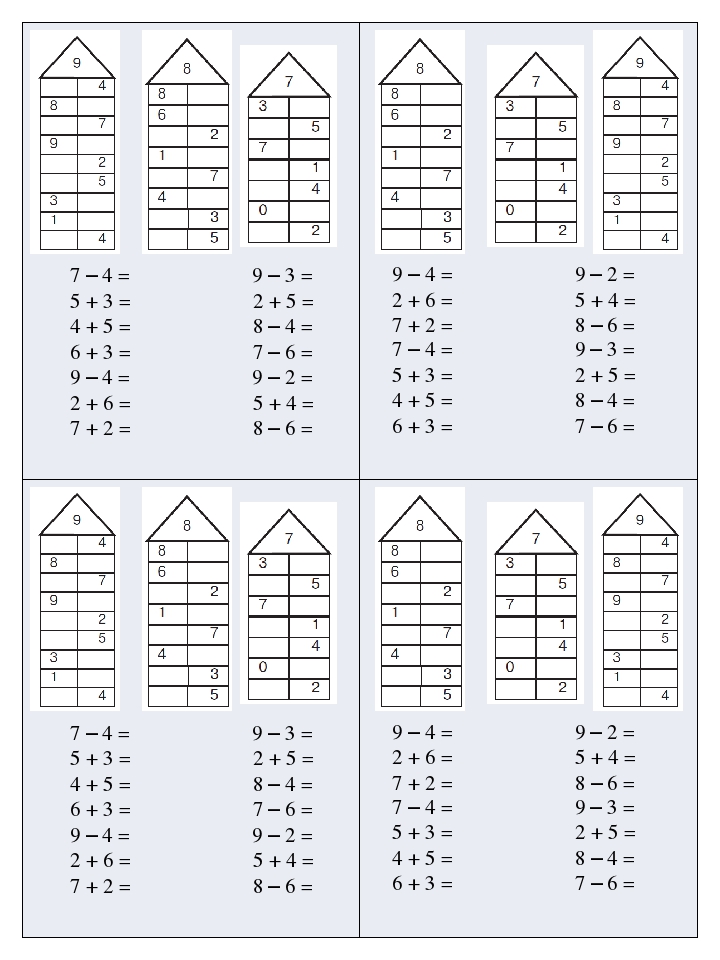 ……и т. д. до 10
……и т. д. до 10 Для этого удобнее всего пользоваться кнопками, которые появятся рядом с кнопкой ДАЛЬШЕ
Для этого удобнее всего пользоваться кнопками, которые появятся рядом с кнопкой ДАЛЬШЕ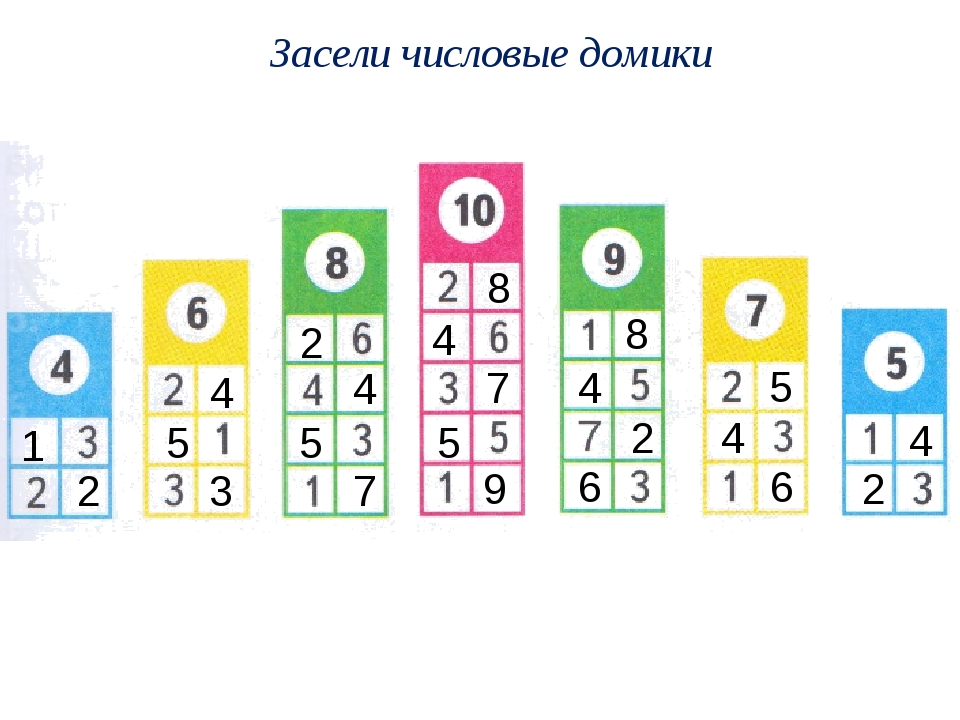 Выходит перед классом один ученик, он говорит, что он — вагон первый. После этого выходит еще один, и говорит: один и еще один будет два. И так продолжается до десяти. Потом операция делается в обратном порядке. Вагоны «распадаются» по одному. Цель этого упражнения — запоминание порядка чисел в прямом и обратном порядке.
Выходит перед классом один ученик, он говорит, что он — вагон первый. После этого выходит еще один, и говорит: один и еще один будет два. И так продолжается до десяти. Потом операция делается в обратном порядке. Вагоны «распадаются» по одному. Цель этого упражнения — запоминание порядка чисел в прямом и обратном порядке.
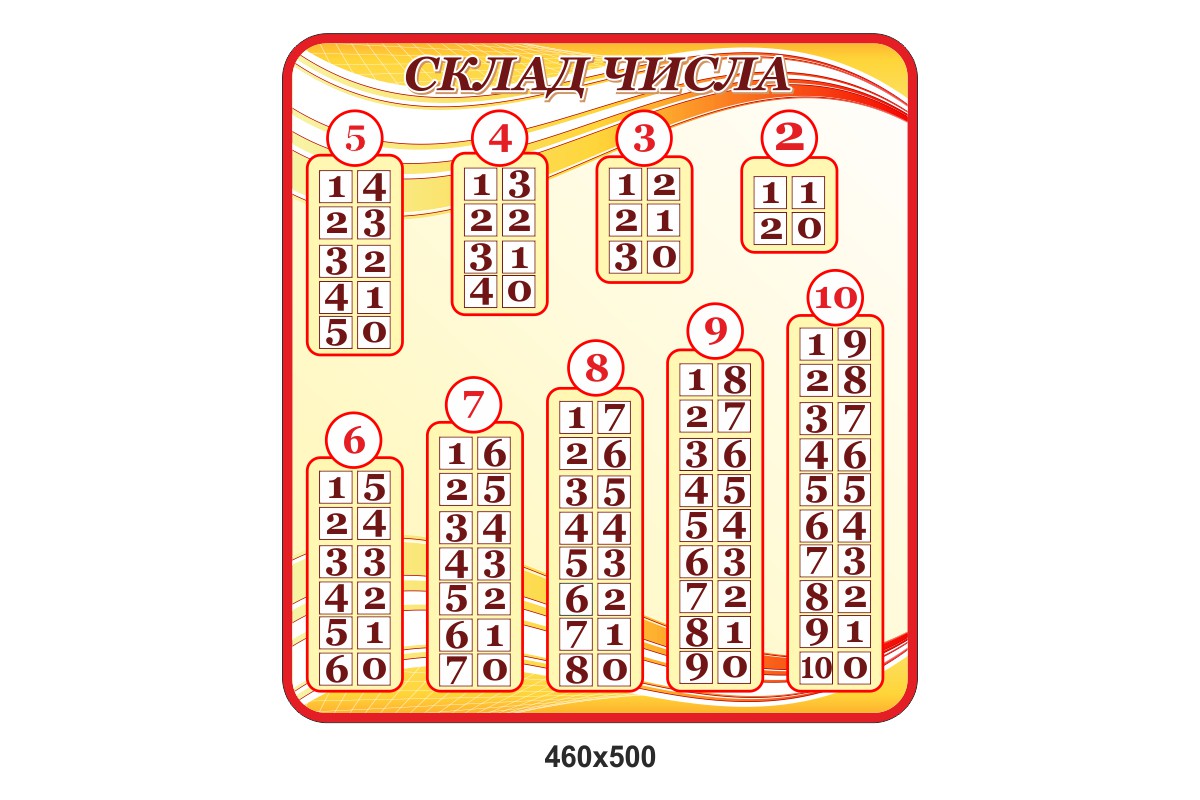
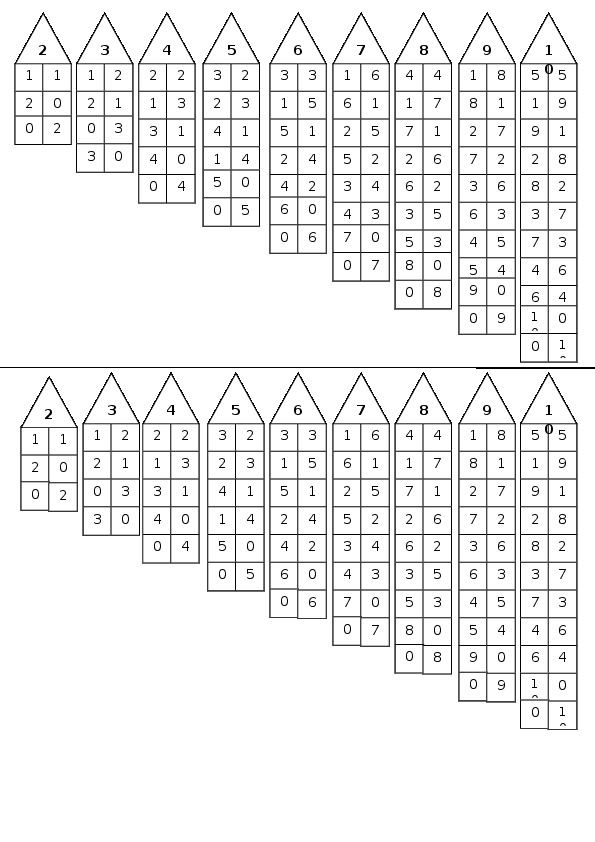



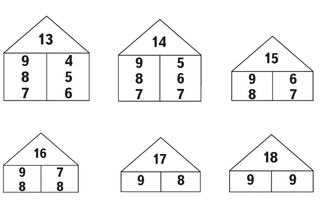

 На крыше вместе с ребенком пишем цифру и объясняем малышу, что эта цифра — хозяин домика, который разрешает в нем жить только такому количеству жильцов, которое равно ему самому.
На крыше вместе с ребенком пишем цифру и объясняем малышу, что эта цифра — хозяин домика, который разрешает в нем жить только такому количеству жильцов, которое равно ему самому.