Карточки для проверки знания таблицы умножения. | Картотека по математике (3 класс) на тему:
Опубликовано 19.08.2017 — 14:27 — Корнева Наталья Александровна
Материал поможет учитель провести проверочную работу по теме «Табличное умножение и деление»
Скачать:
Предварительный просмотр:
6 х 6 = | 24 : 4 = | 3 х 4 = | 28:7= | 8х9= | 36 : 4 = | 5 х 7 = | 42 : 6 = |
7 х 8 = | 72 : 9 = | 8 х 5 = | 36:6= | 5х4= | 49 : 7 = | 8 х 8 = | 45 : 5 = |
8 х 6 = | 15 : 3 = | 5 х 7 = | 56:7= | 3х3= | 30 : 6 = | 9 х 7 = | 12 : 6 = |
3 х 3 = | 14 : 7 = | 9 х 2 = | 48:6= | 8х8= | 64 : 8 = | 5 х 7 = | 18 : 6 = |
2 х 8 = | 15 : 5 = | 8 х 9 = | 24:8= | 6х6= | 18 : 9 = | 8 х 9 = | 35 : 5 = |
4 х 7 = | 63 : 9 = | 5 х 4 = | 21:3= | 9х9= | 16 : 4 = | 8 х 4 = | 54 : 6 = |
2 х 3 = | 27 : 9 = | 6 х 9 = | 14:7= | 5х6= | 35 : 7 = | 4 х 9 = | 72 : 8 = |
4 х 2 = | 32 : 4 = | 3 х 4 = | 81:9= | 7х3= | 18 : 2 = | 6х 6 = | 56 : 7 = |
2 х 2 = | 18 : 2 = | 3 х 9 = | 45:5= | 3х3= | 30 : 6 = | 9х 7 = | 36 : 6 = |
5 х 5 = | 42 : 7 = | 2 х 6 = | 21:3= | 8х2= | 63 : 7 = | 9х 5 = | 12 : 2 = |
6 х 6 = | 24 : 4 = | 3 х 4 = | 28:7= | 8х9= | 36 : 4 = | 5 х 7 = | 42 : 6 = |
7 х 8 = | 72 : 9 = | 8 х 5 = | 5х4= | 49 : 7 = | 8 х 8 = | 45 : 5 = | |
8 х 6 = | 15 : 3 = | 5 х 7 = | 56:7= | 3х3= | 30 : 6 = | 9 х 7 = | 12 : 6 = |
3 х 3 = | 14 : 7 = | 9 х 2 = | 48:6= | 8х8= | 64 : 8 = | 5 х 7 = | 18 : 6 = |
| 2 х 8 = | 15 : 5 = | 8 х 9 = | 24:8= | 6х6= | 18 : 9 = | 8 х 9 = | 35 : 5 = |
4 х 7 = | 63 : 9 = | 5 х 4 = | 21:3= | 9х9= | 16 : 4 = | 8 х 4 = | 54 : 6 = |
2 х 3 = | 27 : 9 = | 6 х 9 = | 14:7= | 5х6= | 35 : 7 = | 4 х 9 = | 72 : 8 = |
4 х 2 = | 32 : 4 = | 3 х 4 = | 81:9= | 7х3= | 18 : 2 = | 6х 6 = | 56 : 7 = |
2 х 2 = | 18 : 2 = | 3 х 9 = | 45:5= | 3х3= | 30 : 6 = | 9х 7 = | 36 : 6 = |
5 х 5 = | 42 : 7 = | 2 х 6 = | 21:3= | 8х2= | 63 : 7 = | 9х 5 = | 12 : 2 = |
6 х 6 = | 24 : 4 = | 3 х 4 = | 28:7= | 8х9= | 36 : 4 = | 5 х 7 = | 42 : 6 = |
7 х 8 = | 72 : 9 = | 8 х 5 = | 36:6= | 5х4= | 49 : 7 = | 8 х 8 = | 45 : 5 = |
8 х 6 = | 15 : 3 = | 5 х 7 = | 56:7= | 3х3= | 30 : 6 = | 9 х 7 = | 12 : 6 = |
3 х 3 = | 14 : 7 = | 9 х 2 = | 48:6= | 8х8= | 64 : 8 = | 5 х 7 = | 18 : 6 = |
2 х 8 = | 15 : 5 = | 8 х 9 = | 24:8= | 6х6= | 18 : 9 = | 8 х 9 = | 35 : 5 = |
4 х 7 = | 63 : 9 = | 5 х 4 = | 21:3= | 9х9= | 16 : 4 = | 8 х 4 = | 54 : 6 = |
2 х 3 = | 27 : 9 = | 6 х 9 = | 14:7= | 5х6= | 35 : 7 = | 4 х 9 = | 72 : 8 = |
4 х 2 = | 32 : 4 = | 3 х 4 = | 81:9= | 7х3= | 18 : 2 = | 6х 6 = | 56 : 7 = |
2 х 2 = | 18 : 2 = | 3 х 9 = | 45:5= | 3х3= | 30 : 6 = | 9х 7 = | 36 : 6 = |
5 х 5 = | 42 : 7 = | 2 х 6 = | 21:3= | 8х2= | 63 : 7 = | 9х 5 = | 12 : 2 = |
Поделиться:
Как быстро выучить таблицу умножения ребенку
Таблицы умножения в младшей школе родители боятся даже больше детей! Еще бы, ведь именно их учитель вызовет в школу, если что-то пойдет не так. Им будет укоризненно рассказывать о том, что с детьми нужно заниматься, а не пускать дело на самотек!
Им будет укоризненно рассказывать о том, что с детьми нужно заниматься, а не пускать дело на самотек!
Если вы мама или папа младшего школьника и уже в предвкушении домашних концертов под названием «таблица умножения», не отчаивайтесь! Вам не придется краснеть в школе. Ваш ребенок выучит таблицу легко, с удовольствием и быстрее всех в классе. Как? Есть способы, читайте и запоминайте!
Содержание:
- Миссия выполнима
- С чего начать учить таблицу умножения
- Правила умножения — новый этап изучения
- Таблица умножения Пифагора — в помощь взрослым и детям
- Порционная подача
- Не уставайте повторять
- Наглядная памятка
- Найдите применение математике
- Усложняйте поэтапно
- Без стресса
- Без сравнений
- Выбирайте свой путь
Миссия выполнима
Для начала, познакомьте ребенка с таблицей умножения. Весело, с улыбкой заинтересуйте его предстоящим процессом, лучше при помощи игр. Покажите, что таблица есть на каждой тетрадке и никто ее не собирается прятать. Обратите внимание малыша на 2 варианта: в классический столбик и в виде таблицы Пифагора.
Покажите, что таблица есть на каждой тетрадке и никто ее не собирается прятать. Обратите внимание малыша на 2 варианта: в классический столбик и в виде таблицы Пифагора.
Объясните, что зубрежка не понадобится. Чтобы правильные числа отскакивали от зубов, нужно просто понять принцип, а для этого достаточно уяснить правила умножения, научиться видеть закономерности и пользоваться таблицей Пифагора. Но обо всем по порядку.
Скачать и распечатать таблицу умножения ( 2,35 МБ)
С чего начать учить таблицу умножения
Выучить таблицу умножения можно только понимая принципы умножения, которые нужно подавать тоже, как игру. С этого и начните.
Если ребёнок чего-то не понял в школе, либо не связывает таблицу с темой умножения чисел, покажите ему, что все эти столбцы не более, чем решенные подряд простые примеры. Напомните, что умножение — это сумма одинаковых слагаемых.
Разложите примеры на слагаемые. Например, 4 х 2 = 4 + 4, где 4 слагаемое, а 2 — их количество.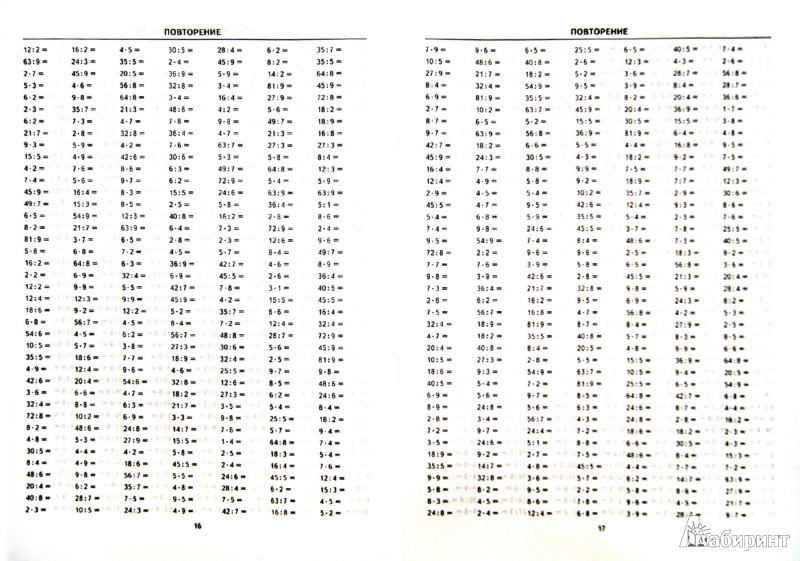 Если ребенок хорошо считает в уме, ему будет не сложно начать складывать простые числа. Это уже станет первым успехом, мотивацией продолжать дальше.
Если ребенок хорошо считает в уме, ему будет не сложно начать складывать простые числа. Это уже станет первым успехом, мотивацией продолжать дальше.
Детям со сложностями счета предложите пользоваться счетными палочками, чертить клеточки или даже загибать пальцы. Интегрируйте эти простые элементы в математические игры.
Еще одно правило умножения осчастливит ребенка. Расскажите ему о переместительном свойстве. Покажите, что перестановка множителей не влияет на результат. Задайте простой пример: 2 х 3, а потом поверните его и предложите умножить: 3 х 2. Начинающий ученик останется в восторге от того, что ему удалось правильно ответить на целых два примера. А это значит, что учить придется не всю таблицу, а лишь половину!
Правила умножения — новый этап изучения
На волне энтузиазма и в обнимку с первыми достижениями ребенка, переходите к следующему этапу «игры» — изучению правил умножения. Вот основные из них:
Вот основные из них:
- Если любое число умножать на 1, оно останется неизменным (задача упростилась еще на 9 примеров!).
- Число, умноженное на 2 — это оно же, но в «двойном экземпляре». То есть, когда перемножаются 4 х 2, означает, что к 4 прибавили 4. И результат при этом всегда получается четным, даже если на 2 умножали нечетное число.
- При умножении на 10 к первому множителю просто добавляется 0 (его можно без сомнений дописать в конце числа), в ответе выходят сплошные десятки.
- Умножая на 5, в ответе всегда получаешь число на 5 или 0. В случае, с умножением на четные числа — это будет ответ с нулем, а с нечетные — с пятеркой. Например, 5 x 5 = 25, а 5 х 8 =40.
- Еще одно правило, касающееся умножения на 5: при умножении на 5 результат всегда вдвое меньше результата умножения на 10. Например: 5 х 9 = 45, а 10 х 9= 90. Сорок пять в два раза меньше, чем девяносто.
- При умножении на 4 число нужно два раза удвоить. К примеру, стоит задача перемножить шесть на четыре.
 Например, 3 + 3 = 6, 6 + 6 = 12.
Например, 3 + 3 = 6, 6 + 6 = 12. - Умножая на 9, нужно записать числа в ряд: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Покажите ребенку закономерность, где каждый раз первое число увеличивается, а второе уменьшается на единицы. То есть, запомнить нужно только два первых числа цифрового ряда — 09 и 90 (здесь работает правило умножения на 10).
- Есть еще один необычный способ, который поможет быстро запомнить правила умножения на 9. Он помогает визуализировать происходящее и навсегда забыть о запинках в вопросах умножения на 9. Все очень просто! Мы умножаем: 5 x 9. А теперь ставим перед собой все пальцы. Пронумеруйте пальцы. Отсчитываем 5 пальчиков. Подсчитывает начинаем пальцы слева. Пятый загните. Слева у нас осталось 4 пальчика, а справа — 5. Остается их только сложить рядом. Таким образом, результат умножения 45.
Простые игры-подсказки повеселят и помогут научить детей умножению. Главное показывать на примерах, предлагать ему пробовать, приводить собственные примеры. Делайте это до тех пор, пока закономерности и правила не закрепятся в голове школьника.
Делайте это до тех пор, пока закономерности и правила не закрепятся в голове школьника.
Если все пройдет хорошо, дети получат огромное удовольствие, почувствуют себя настоящими фокусниками, запросто жонглирующими числами без ошибок и пауз.
Таблица умножения Пифагора — в помощь взрослым и детям
Вообще-то, таблица Пифагора — та же таблица умножения, но приведенная к более удобному виду. Почему-то детей учат зубрить столбики чисел, когда можно просто понять принцип умножения на примере таблицы Пифагора, научиться выдавать логические правильные ответы.
Дети будут в восторге от того, как это просто. Покажите, что в колонке слева и в верхней строке числа множители. В самой таблице — ответы (произведение).
Чтобы найти правильный ответ, нужно в уме (для начала можно пользоваться линейкой или карандашом) провести две линии (вертикальную и горизонтальную) до точки пересечения множителей в левой колонке и в верхней строке. Тут опять сработает правило о перестановке множителей. Не важно, какая линия будет первой. Ответ не поменяется.
Не важно, какая линия будет первой. Ответ не поменяется.
Скачать и распечатать таблица умножения Пифагора ( 510,8 KB)
Таблица Пифагора в образах ( 563,4 KB)
Чтобы доказать ребенку простоту таблицы, покажите ему как это работает на примере клеточек. Например, 3 х 2 = 6. 3 клеточки нарисуйте вертикально и 2 горизонтально. Обозначьте контуры полученного прямоугольника и пронумеруйте клеточки внутри его границ. Ребенок с удивлением обнаружит, что он состоит из того же числа клеточек, что и ответ примера.
Рисуйте как можно больше вариаций прямоугольников. Пусть это будут не только вертикальные, но и горизонтальные, маленькие и большие. Вместе считайте клеточки внутри них.
Задавайте друг другу математические задания по прямоугольникам и наоборот, соревнуйтесь, кто быстрее изобразит задачу в виде прямоугольника и выдаст правильный ответ. Визуализация примеров поможет ребенку быстрее считать и запоминать ответы.
Скачать пособие Различные способы изучения таблицы умножения.
Как ускорить изучение таблицы умножения и мотивировать ребенка продолжать с энтузиазмом? Есть несколько простых советов.
Порционная подача
Не пытайтесь быть впереди планеты всей, забудьте о родительских амбициях и огромном чувстве ответственности! Дайте детям возможность усваивать таблицу умножения постепенно, небольшими и приятными порциями в виде игр. Выделите на каждый столбик минимум по 3 дня, а лучше неделю. Учите играючи, закрепляйте материал, проверяя ответы в повседневной жизни.
Не уставайте повторять
Дети быстро запоминают и также быстро забывают, если материал с ними не повторять. Вот почему, если вы не хотите чтобы труды прошли даром, возвращаться к изученному нужно постоянно. Но без давления, на позитиве, примеряя к повседневным делам и событиям. Не делая упор на зазубривание! Только добровольное желание малыша. Сначала школьник будет медлить с ответами, но постепенно почувствует себя более уверенно, начнет отвечать быстрее и без ошибок.
Наглядная памятка
Отлично, если вы нарисуете обучающие плакаты или карточки вместе и закрепите их на видных местах в доме. Если нет, купите готовые. Пусть по одному плакату будет в каждой зоне: игровой, рабочей, для отдыха и пр. Картинки должны быть интересными и яркими. Не обязательно, чтобы это была таблица. Подойдут примеры, образцы сложения и умножения.
Найдите применение математике
Детям сложно что-то делать без понимания для чего это нужно. Чтобы закрепить интерес к таблице умножения, покажите как интересно она работает в реальной жизни.
Все просто, обращайте внимание ребенка на мелочи, окружающие его каждый день! Например, предложите накрыть стол к ужину. 4 члена семьи, каждому по 2 прибора. Пусть посчитает, сколько всего приборов нужно. Увидите, ребенок придет в восторг от того, что учил таблицу множителей не зря!
Усложняйте поэтапно
Не обязательно учить таблицу умножения в том порядке, в котором вы сами учили ее в детстве. Детям легче даются плавные переходы от простого к сложному. Например, для начала можно выучить все примеры, где числа умножаются на 1, на 2, на 5 и на 10, только потом переходить к остальным, например, умножению на восемь или на семь.
Детям легче даются плавные переходы от простого к сложному. Например, для начала можно выучить все примеры, где числа умножаются на 1, на 2, на 5 и на 10, только потом переходить к остальным, например, умножению на восемь или на семь.
Без стресса
Не позволяйте себе заводиться по мелочам, не расстраивайте маленького ученика криками и наказаниями. Такими методами вы можете добиться результата быстрее, но рискуете навсегда лишить школьника желания и интереса к учебе, не говоря уже о доверии к самым близким людям. Пусть первое серьезное достижение в области математики оставит в его памяти приятные воспоминания.
Без сравнений
Никогда не сравнивайте успехи и самого ребенка с другими. Он ваш, самый яркий и особенный. Он учится в меру своих способностей и не нуждается в критике.
Помните о мотивации. Не нужно ругать ребенка – поощряйте его, хвалите, играйте с младшим школьником, результат обязательно будет. Любые сравнения — огромный шаг назад, а иногда и падение в пропасть неуверенности и комплексов.
Выбирайте свой путь
Никто не знает ребенка лучше родителей. Подумайте, в каком виде малыш усваивает информацию быстрее и лучше? На слух? Отлично, проговаривайте таблицу умножения вместе, применяйте примеры на практике и получайте удовольствие от процесса!
Визуально? Плакаты и карточки с примерами, о которых мы уже писали, точно ускорят и упростят задачу по запоминанию таблицы.
А может, у школьника ассоциативная память? Отлично, вместе придумайте ассоциации для каждого действия, чисел, перемножать будет еще веселее и интереснее. Учите стишки-запоминалки.
Очень важно, чтобы родители и дети в таких непростых вопросах, как изучение таблицы умножения стали командой. Искренний интерес мам и пап питает мотивацию детей.
Ищите удобные способы запоминания, пробуйте видео, мультики, аудиозарисовки. Не отказывайтесь от подручных материалов, включая:
- счетные палочки;
- спички;
- кубики.
- колоду детских игральных карт.

Не бойтесь начинать считать с пальцев ребенка. Пробуйте все, что поможет правильно умножить и получить верный ответ.
Каждый метод хорош, если он не вредит, интересен ребенку и дает результат, пусть даже не так быстро, как хотелось бы родителям. Запаситесь терпением, настройтесь на позитив. Только так вы покорите первый общий Эверест под названием «Таблица умножения» вместе!
Купить пособие Ментальная арифметика «Таблица умножения» Abakus.
Рейтинг: 4.5/5 — 8 голосов
Тренажёр изучения таблицы умножения и деления онлайн
Тренажёр изучения таблицы умножения и деления онлайн2 * 3 значит 2 + 2 + 2
1 2 3 4 5 6 7 8 9 0 — C
Ответить
Для продолжения оформите Подписку
4 x 1 =
9 x 6 =
3 x 9 =
8 x 2 =
10 x 4 =
5 x 7 =
3 x 6 =
4 x 1 =
5 x 5 =
10 x 0 =
| 4 x 1 = | 9 x 6 = | 3 x 9 = | |||
| 8 x 2 = | 10 x 4 = | 5 x 7 = | |||
| 3 x 6 = | 4 x 1 = | 5 x 5 = | |||
| 10 x 0 = |
| 4 x 1 = | 9 x 6 = | 3 x 9 = | |||
| 8 x 2 = | 10 x 4 = | 5 x 7 = | |||
| 3 x 6 = | 4 x 1 = | 5 x 5 = | |||
| 10 x 0 = |
Попробуйте заниматься на более сложных тренажёрах
2 класс 3 класс 4 класс
Учим таблицу умножения для начальной школы на тренажере!
Таблицу умножения дети начинают изучать в первом классе,
однако многие сталкиваются с ней еще до школы. ..
Учить таблицу умножения было не простой задачей как для старшего поколения,
так и для современных детей.
Однако на сегодняшний день есть много различных игр и онлайн тренажеров для
того чтобы учить раз и навсегда таблицу умножения
..
Учить таблицу умножения было не простой задачей как для старшего поколения,
так и для современных детей.
Однако на сегодняшний день есть много различных игр и онлайн тренажеров для
того чтобы учить раз и навсегда таблицу умножения
Самая большая ошибка – это пробовать учить все разом.
Гораздо легче будет если примеры разделить на мини-блоки.
Например, начать на тренажере учить таблицу умножения от
одного
до пяти.
Для маленьких детей – это 3-4 карточки, более взрослым можно брать по 5-6 штук. Но, проверять знания лучше все таки занимаясь на тренажер «таблица умножения» выбирая задания в разброс.
Но, проверять знания лучше все таки занимаясь на тренажер «таблица умножения» выбирая задания в разброс.
На самом деле задача в два раза проще, чем кажется… Не надо запоминать, сколько будет 4 × 5 или 5 × 4. Достаточно выучить, что цифры 4 и 5 в любом порядке при умножении друг на друга дают 20.
Есть и другие закономерности в таблице умножения, которые облегчат изучение. Будет еще лучше если ребёнок найдет их сам, тогда он запоминает их навсегда.
Вот некоторые закономерности, которые упростят изучение таблицы умножения:
- При умножении на 1 любая цифра остаётся той же
- Чтобы умножить на два, надо просто прибавить столько же
- При умножении на 5 результат заканчивается на 5 или на 0
- Чтобы умножить на 5 любое чётное число, надо взять его половинку и приписать к ней 0 Например, 8 × 5: берём половинку от 8 — это цифра 4 — и приставляем к ней ноль: получается 40
- При умножении на 9 сумма цифр в результате обязательно будет равна 9.
Например, 2 × 9 = 18 (1 + 8 = 9). 3 × 9 = 27 (2 + 7 = 9)
- При умножении на 10, надо пририсовать к числу справа ноль
Как выучить таблицу умножения навсегда и быстро?
Для того чтобы ребенок запомнил таблицу умножения, важно не только выучить примеры, но и уделить время активному повторению, например, каждый день понемногу решать таблицу умножения онлайн. Это очень удобно, ведь ребенок может заниматься в любом месте: в машине, в магазине, в очереди.. На нашем тренажере таблица умножения с вводом ответа и подсказками
Начинать лучше с простых заданий. Например, отточить навыки умножение по таблице на тренажере на три и четыре, а затем переходить к заданиям сложнее
Каждодневные занятия на тренажере помогут выучить таблицу умножения быстро и легко, раз и навсегда!
Познакомься с другими тренажерами курса
Уравнения с одним неизвестным
Чтобы решать уравнения любой сложности важно хорошо закрепить эту тему в начале изучения
Скорей заниматься
Римские цифры
Множество примеров различной сложности помогут ребенку быстро запомнить римские цифры
Скорей заниматься
Меры измерения
Мер величин много и в них легко запутаться. Изучайте меры длины, времени и массы на тренажере
Изучайте меры длины, времени и массы на тренажере
Скорей заниматься
Визуализация данных в Python с помощью plt.scatter() — Real Python
Смотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Использование plt.scatter() для визуализации данных в Python
Важной частью работы с данными является возможность визуализировать их. В Python есть несколько сторонних модулей, которые вы можете использовать для визуализации данных. Одним из самых популярных модулей является Matplotlib и его подмодуль pyplot , часто упоминаемый с использованием псевдонима plt . Matplotlib предоставляет очень универсальный инструмент под названием plt.scatter() , который позволяет создавать как базовые, так и более сложные точечные диаграммы.
Ниже вы ознакомитесь с несколькими примерами, которые покажут вам, как эффективно использовать эту функцию.
В этом уроке вы узнаете, как:
- Создать точечную диаграмму с использованием
plt.scatter() - Использовать обязательные и необязательные входные параметры
- Настройка точечных диаграмм для базовых и более сложных графиков
- Представление более чем двух измерений на точечной диаграмме
Чтобы получить максимальную отдачу от этого руководства, вы должны быть знакомы с основами программирования Python и основами NumPy и его объекта ndarray . Вам не нужно быть знакомым с Matplotlib, чтобы следовать этому руководству, но если вы хотите узнать больше о модуле, ознакомьтесь с Python Plotting With Matplotlib (руководство).
Бесплатный бонус: Нажмите здесь, чтобы получить доступ к бесплатному руководству по ресурсам NumPy, в котором вы найдете лучшие учебные пособия, видео и книги для улучшения ваших навыков работы с NumPy.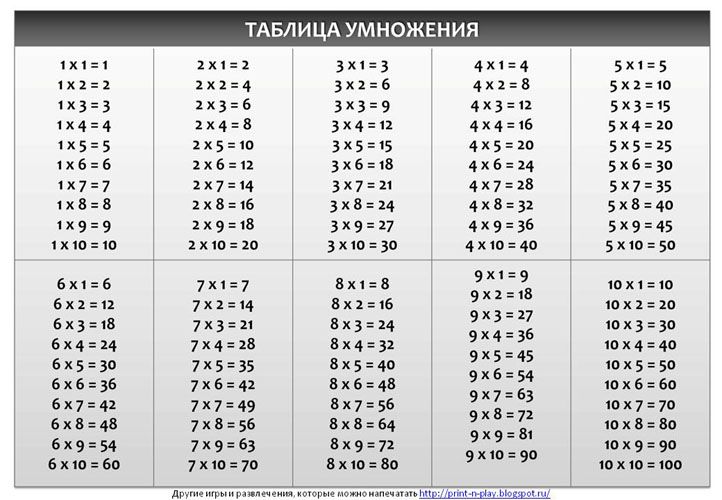
Создание точечных диаграмм
Точечная диаграмма — это визуальное представление того, как две переменные связаны друг с другом. Вы можете использовать точечные диаграммы, чтобы исследовать взаимосвязь между двумя переменными, например, ища любую корреляцию между ними.
В этом разделе руководства вы познакомитесь с созданием базовых диаграмм рассеивания с помощью Matplotlib. В последующих разделах вы узнаете, как дополнительно настраивать графики для представления более сложных данных с использованием более двух измерений.
Удалить рекламу
Начало работы с
plt.scatter() Прежде чем вы сможете начать работать с plt.scatter() , вам необходимо установить Matplotlib. Вы можете сделать это с помощью стандартного диспетчера пакетов Python, pip , выполнив в консоли следующую команду:
$ python -m pip установить matplotlib
Теперь, когда вы установили Matplotlib, рассмотрите следующий вариант использования.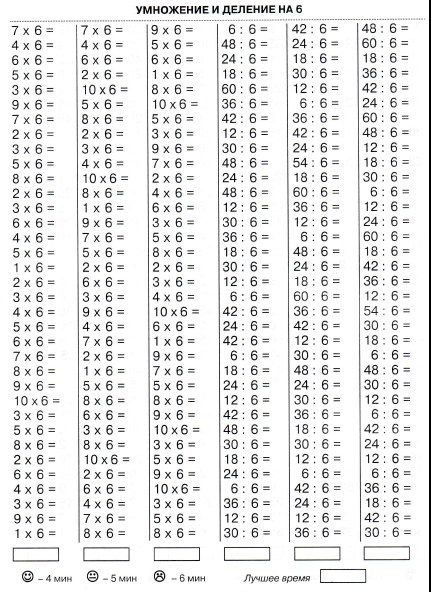 Кафе продает шесть различных видов апельсиновых напитков в бутылках. Владелец хочет понять взаимосвязь между ценой напитков и количеством каждого из них, которое он продает, поэтому он отслеживает, сколько каждого напитка он продает каждый день. Вы можете визуализировать эту связь следующим образом:
Кафе продает шесть различных видов апельсиновых напитков в бутылках. Владелец хочет понять взаимосвязь между ценой напитков и количеством каждого из них, которое он продает, поэтому он отслеживает, сколько каждого напитка он продает каждый день. Вы можете визуализировать эту связь следующим образом:
импортировать matplotlib.pyplot как plt цена = [2,50, 1,23, 4,02, 3,25, 5,00, 4,40] продаж_за_день = [34, 62, 49, 22, 13, 19] plt.scatter (цена, продажи_за_день) plt.show()
В этом сценарии Python вы импортируете подмодуль pyplot из Matplotlib, используя псевдоним plt . Этот псевдоним обычно используется по соглашению для сокращения имен модулей и подмодулей. Затем вы создаете списки с ценой и средними продажами в день для каждого из шести проданных апельсиновых напитков.
Наконец, вы создаете точечную диаграмму, используя plt.scatter() с двумя переменными, которые вы хотите сравнить, в качестве входных аргументов.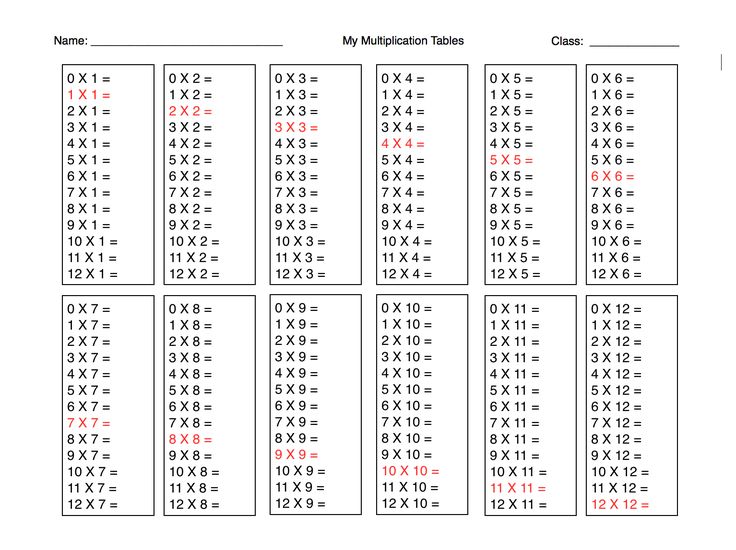 Поскольку вы используете сценарий Python, вам также необходимо явно отобразить фигуру с помощью
Поскольку вы используете сценарий Python, вам также необходимо явно отобразить фигуру с помощью plt.show() .
Когда вы используете интерактивную среду, такую как консоль или Jupyter Notebook, вам не нужно вызывать plt.show() . В этом уроке все примеры будут в виде скриптов и будут включать вызов plt.show() .
Вот результат этого кода:
Этот график показывает, что, как правило, чем дороже напиток, тем меньше товаров продается. Однако напиток, который стоит 4,02 доллара, является исключением, что может свидетельствовать о том, что это особенно популярный продукт. При таком использовании точечных диаграмм тщательная проверка может помочь вам изучить взаимосвязь между переменными. Затем вы можете провести дальнейший анализ, используя линейную регрессию или другие методы.
Сравнение
plt.scatter() и plt.plot() Вы также можете создать диаграмму рассеяния, показанную выше, с помощью другой функции в matplotlib. . Matplotlib  pyplot
pyplot plt.plot() — это функция построения графиков общего назначения, которая позволит вам создавать различные линейные или маркерные графики.
Вы можете получить тот же точечный график, что и полученный в разделе выше, с помощью следующего вызова plt.plot() , используя те же данные:
plt.plot(цена, продажи_за_день, "o") plt.show()
В этом случае вы должны были включить маркер "o" в качестве третьего аргумента, иначе plt.plot() построит линейный график. График, который вы создали с помощью этого кода, идентичен графику, который вы создали ранее с помощью plt.scatter() .
В некоторых случаях для базовой диаграммы рассеяния, которую вы строите в этом примере, может быть предпочтительнее использовать plt.plot() . Вы можете сравнить эффективность двух функций, используя модуль timeit :
время импорта импортировать matplotlib.pyplot как plt цена = [2,50, 1,23, 4,02, 3,25, 5,00, 4,40] продаж_за_день = [34, 62, 49, 22, 13, 19] Распечатать( "plt.scatter()", время.время( "plt.scatter(цена, продажи_за_день)", число=1000, глобальные = глобальные(), ), ) Распечатать( "plt.plot()", время.время( "plt.plot(цена, продажи_за_день, 'o')", число=1000, глобальные = глобальные(), ), )
Производительность будет разной на разных компьютерах, но когда вы запустите этот код, вы обнаружите, что plt.plot() значительно эффективнее, чем plt.scatter() . При выполнении приведенного выше примера в моей системе plt.plot() работало более чем в семь раз быстрее.
Если вы можете создавать точечные диаграммы с помощью plt.plot() , и это намного быстрее, зачем вам вообще использовать plt.scatter() ? Вы найдете ответ в оставшейся части этого руководства. Большинство настроек и расширенных возможностей, о которых вы узнаете в этом руководстве, возможны только при использовании plt. . Вот эмпирическое правило, которое вы можете использовать: scatter()
scatter()
- Если вам нужна базовая точечная диаграмма, используйте
plt.plot(), особенно если вы хотите отдать приоритет производительности. - Если вы хотите настроить точечную диаграмму, используя более продвинутые функции построения графиков, используйте
plt.scatter().
В следующем разделе вы начнете изучать более сложные способы использования plt.scatter() .
Удалить рекламу
Настройка маркеров на точечных диаграммах
Вы можете визуализировать более двух переменных на двумерной диаграмме рассеяния, настроив маркеры. Существует четыре основных функции маркеров, используемых в точечной диаграмме, которые можно настроить с помощью plt.scatter() :
- Размер
- Цвет
- Форма
- Прозрачность
В этом разделе руководства вы узнаете, как изменить все эти свойства.
Изменение размера
Вернемся к владельцу кафе, которого вы встретили ранее в этом уроке. Различные апельсиновые напитки, которые он продает, поступают от разных поставщиков и имеют разную норму прибыли. Вы можете отобразить эту дополнительную информацию на точечной диаграмме, отрегулировав размер маркера. Маржа прибыли указана в процентах в этом примере:
импортировать matplotlib.pyplot как plt импортировать numpy как np цена = np.asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40]) sales_per_day = np.asarray([34, 62, 49, 22, 13, 19]) profit_margin = np.asarray([20, 35, 40, 20, 27,5, 15]) plt.scatter(x=цена, y=продажи_за_день, s=прибыль_маржа * 10) plt.show()
Вы можете заметить несколько изменений по сравнению с первым примером. Вместо списков теперь вы используете массивы NumPy. Для данных можно использовать любую структуру данных, подобную массиву, и массивы NumPy обычно используются в приложениях такого типа, поскольку они позволяют поэлементных операций , которые выполняются эффективно. Модуль NumPy зависит от Matplotlib, поэтому вам не нужно устанавливать его вручную.
Модуль NumPy зависит от Matplotlib, поэтому вам не нужно устанавливать его вручную.
Вы также использовали именованных параметра в качестве входных аргументов в вызове функции. Параметры x и y являются обязательными, но все остальные параметры являются необязательными.
Параметр s обозначает размер маркера. В этом примере вы используете размер прибыли в качестве переменной для определения размера маркера и умножаете его на 9.0015 10 для более четкого отображения разницы в размерах.
Вы можете увидеть точечную диаграмму, созданную этим кодом ниже:
Размер маркера указывает размер прибыли для каждого продукта. Два апельсиновых напитка, которые продаются больше всего, также приносят наибольшую прибыль. Хорошая новость для владельца кафе!
Изменение цвета
Многие посетители кафе любят внимательно читать этикетки, особенно чтобы узнать содержание сахара в напитках, которые они покупают. Владелец кафе хочет подчеркнуть свой выбор здоровых продуктов в своей следующей маркетинговой кампании, поэтому он классифицирует напитки на основе содержания в них сахара и использует систему светофора, чтобы указать низкое, среднее или высокое содержание сахара в напитках.
Владелец кафе хочет подчеркнуть свой выбор здоровых продуктов в своей следующей маркетинговой кампании, поэтому он классифицирует напитки на основе содержания в них сахара и использует систему светофора, чтобы указать низкое, среднее или высокое содержание сахара в напитках.
Вы можете раскрасить маркеры на точечной диаграмме, чтобы показать содержание сахара в каждом напитке:
# ...
низкий = (0, 1, 0)
средний = (1, 1, 0)
высокий = (1, 0, 0)
сахар_содержание = [низкий, высокий, средний, средний, высокий, низкий]
plt.scatter(
х=цена,
у=продажи_за_день,
с=прибыль_маржа * 10,
c=sugar_content,
)
plt.show()
Вы определяете переменные low , medium и high как кортежи, каждый из которых содержит три значения, представляющие компоненты красного, зеленого и синего цветов в указанном порядке. Это значения цвета RGB. Кортежи для низкий , средний и высокий представляют зеленый, желтый и красный соответственно.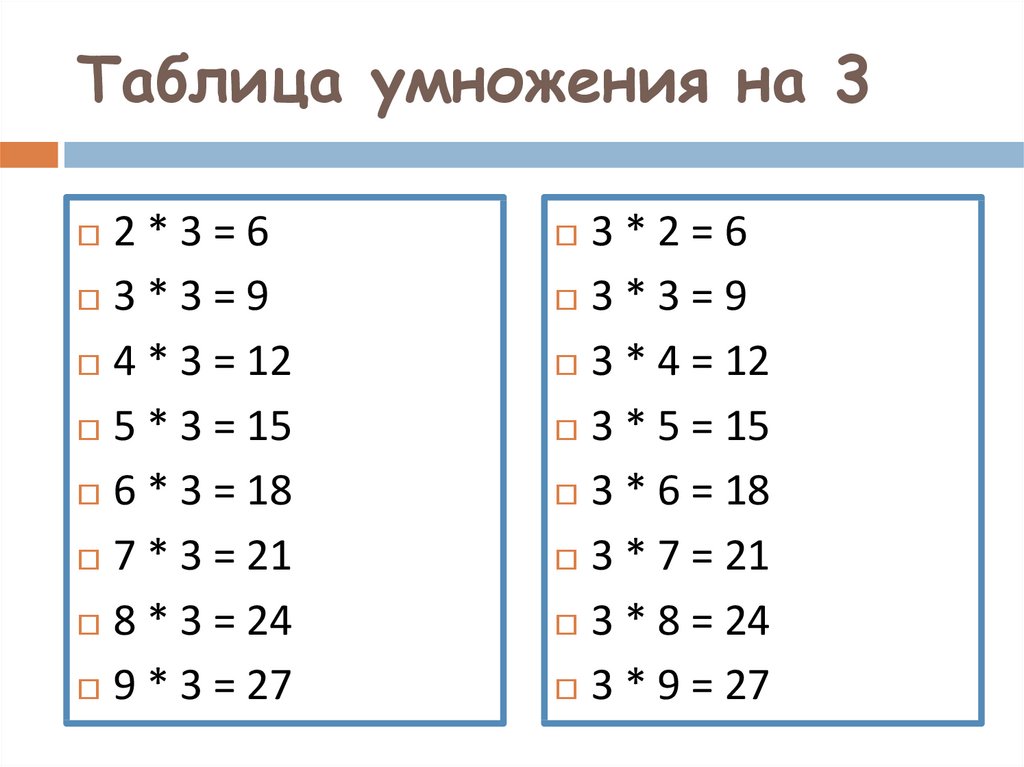
Затем вы определили переменную «сахар_содержание» для классификации каждого напитка. Вы используете необязательный параметр c в вызове функции, чтобы определить цвет каждого маркера. Вот точечная диаграмма, созданная этим кодом:
Владелец кафе уже решил убрать из меню самый дорогой напиток, так как он плохо продается и имеет высокое содержание сахара. Должен ли он также прекратить закупать самые дешевые напитки, чтобы повысить репутацию бизнеса в отношении здоровья, даже несмотря на то, что они хорошо продаются и приносят хорошую прибыль?
Удалить рекламу
Изменение формы
Владелец кафе нашел это упражнение очень полезным и хочет исследовать другой продукт. В дополнение к апельсиновым напиткам вы теперь также нанесете аналогичные данные для ассортимента зерновых батончиков, доступных в кафе:
.импортировать matplotlib.pyplot как plt импортировать numpy как np низкий = (0, 1, 0) средний = (1, 1, 0) высокий = (1, 0, 0) price_orange = np.asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40]) sales_per_day_orange = np.asarray([34, 62, 49, 22, 13, 19]) profit_margin_orange = np.asarray([20, 35, 40, 20, 27,5, 15]) Sugar_content_orange = [низкий, высокий, средний, средний, высокий, низкий] price_cereal = np.asarray([1,50, 2,50, 1,15, 1,95]) sales_per_day_cereal = np.asarray([67, 34, 36, 12]) profit_margin_cereal = np.asarray([20, 42,5, 33,3, 18]) сахара_content_cereal = [низкий, высокий, средний, низкий] plt.scatter( х=цена_оранжевый, y=продажи_за_день_оранжевый, s=profit_margin_orange * 10, c=sugar_content_orange, ) plt.scatter( х = цена_зерновых, y=продажи_за_день_зерновых, s=прибыль_прибыль_зерновые * 10, c=сахар_содержание_хлопья, ) plt.show()
В этом коде вы реорганизуете имена переменных, чтобы учесть, что теперь у вас есть данные для двух разных продуктов. Затем вы строите оба графика рассеяния на одном рисунке. Это дает следующий вывод:
К сожалению, вы больше не можете понять, какие точки данных относятся к апельсиновым напиткам, а какие к зерновым батончикам. Вы можете изменить форму маркера для одной из точечных диаграмм:
Вы можете изменить форму маркера для одной из точечных диаграмм:
импортировать matplotlib.pyplot как plt
импортировать numpy как np
низкий = (0, 1, 0)
средний = (1, 1, 0)
высокий = (1, 0, 0)
price_orange = np.asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40])
sales_per_day_orange = np.asarray([34, 62, 49, 22, 13, 19])
profit_margin_orange = np.asarray([20, 35, 40, 20, 27,5, 15])
Sugar_content_orange = [низкий, высокий, средний, средний, высокий, низкий]
price_cereal = np.asarray([1,50, 2,50, 1,15, 1,95])
sales_per_day_cereal = np.asarray([67, 34, 36, 12])
profit_margin_cereal = np.asarray([20, 42,5, 33,3, 18])
сахара_content_cereal = [низкий, высокий, средний, низкий]
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
)
plt.show()
Вы сохраняете форму маркера по умолчанию для данных апельсинового напитка.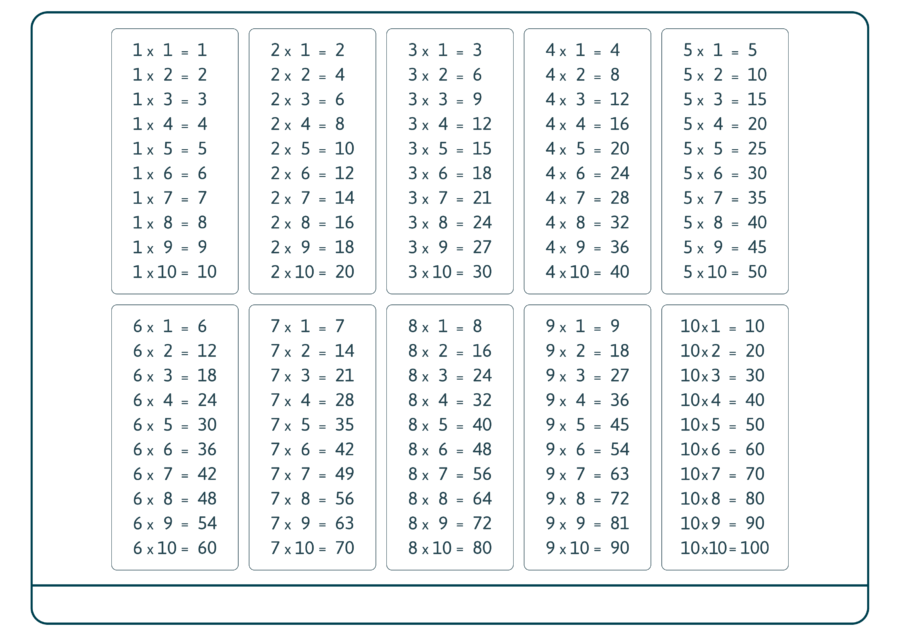 Маркером по умолчанию является
Маркером по умолчанию является "o" , что представляет собой точку. Для данных зернового батончика вы устанавливаете форму маркера на "d" , что представляет собой ромбовидный маркер. Вы можете найти список всех маркеров, которые вы можете использовать на странице документации по маркерам. Вот два графика рассеяния, наложенные на одну и ту же цифру:
Теперь вы можете отличить точки данных для апельсиновых напитков от точек данных для злаковых батончиков. Но есть одна проблема с последним созданным вами графиком, которую вы исследуете в следующем разделе.
Изменение прозрачности
Исчезла одна из точек данных апельсиновых напитков. Оранжевых напитков должно быть шесть, но на рисунке видно только пять круглых маркеров. Одна из точек данных зернового батончика скрывает точку данных апельсинового напитка.
Вы можете решить эту проблему визуализации, сделав точки данных частично прозрачными, используя альфа-значение:
# ... plt.scatter( х=цена_оранжевый, y=продажи_за_день_оранжевый, s=profit_margin_orange * 10, c=sugar_content_orange, альфа=0,5, ) plt.scatter( х = цена_зерновых, y=продажи_за_день_зерновых, s=прибыль_прибыль_зерновые * 10, c=сахар_содержание_хлопья, маркер = "д", альфа=0,5, ) plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики") plt.legend(["Апельсиновые напитки", "Злаковые батончики"]) plt.xlabel("Цена (денежная единица)") plt.ylabel("Средние продажи за неделю") пл.текст( 3.2, 55, "Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара", ) plt.show()
Вы установили значение alpha обоих наборов маркеров на 0,5 , что означает, что они полупрозрачны. Теперь вы можете увидеть все точки данных на этом графике, включая совпадающие:
Вы также добавили заголовок и другие метки к графику, чтобы дополнить рисунок дополнительной информацией о том, что отображается.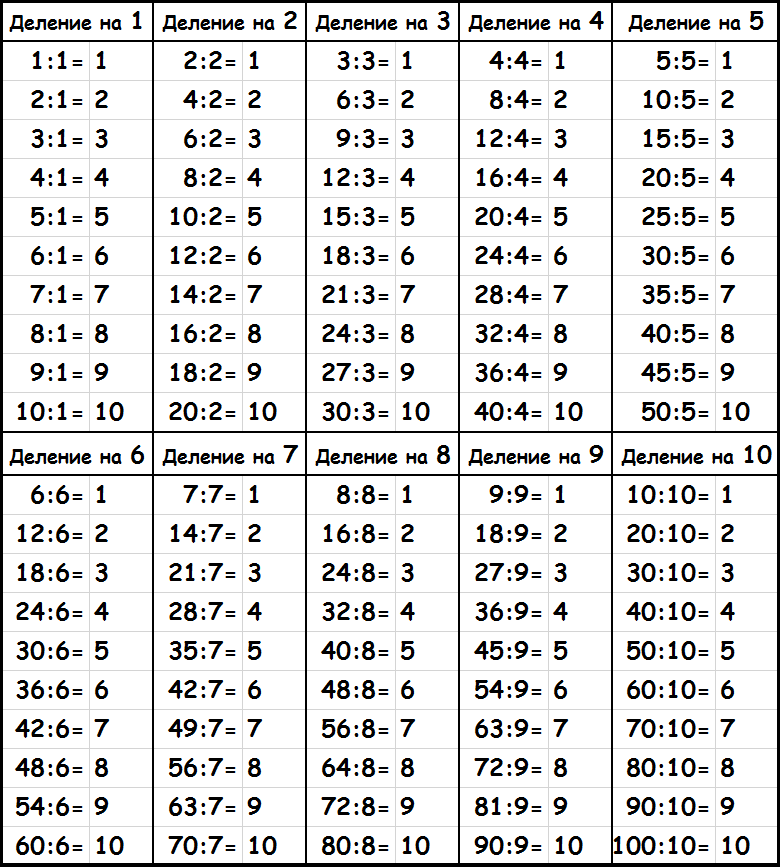
Настройка цветовой карты и стиля
На созданных вами диаграммах рассеяния вы использовали три цвета для обозначения низкого, среднего или высокого содержания сахара в напитках и зерновых батончиках. Теперь вы измените это, чтобы цвет напрямую отображал фактическое содержание сахара в продуктах.
Сначала вам нужно реорганизовать переменные Sugar_content_orange и Sugar_content_cereal , чтобы они представляли значение содержания сахара, а не только значения цвета RGB:
Sugar_content_orange = [15, 35, 22, 27, 38, 14] сахар_содержание_зерна = [21, 49, 29, 24]
Теперь это списки, содержащие процент рекомендуемого ежедневного количества сахара в каждом продукте. Остальной код остается прежним, но теперь вы можете выбрать цветовую карту для использования. Это сопоставляет значения цветам:
# ...
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
смап = "струя",
альфа=0,5,
)
plt. scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
смап = "струя",
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
2,7,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.colorbar()
plt.show()
scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
смап = "струя",
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
2,7,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.colorbar()
plt.show()
Цвет маркеров теперь основан на непрерывной шкале, и вы также отобразили цветовую полосу , которая действует как легенда для цвета маркеров. Вот результирующая диаграмма рассеяния:
Все графики, которые вы построили до сих пор, были отображены в собственном стиле Matplotlib. Вы можете изменить этот стиль, используя один из нескольких вариантов. Вы можете отобразить доступные стили с помощью следующей команды:
>>>
>>> пл.стиль.доступно [ "Соляризация_Свет2", "_classic_test_patch", "бмх", "классический", "темный_фон", "быстро", "пять тридцать восемь", "ггплот", "оттенки серого", "морской", "морской яркий", "морской дальтоник", "морской темный", "морская-темная-палитра", "мореборн-темная сетка", "морская глубина", "морской приглушенный", "морской блокнот", "морская бумага", "морская пастель", "морской постер", "морской разговор", "морские клещи", "бело-морской", "сиборн-белая сетка", "таблица-дальтоник10", ]
Теперь вы можете изменить стиль графика при использовании Matplotlib, используя следующий вызов функции перед вызовом plt.scatter() :
импортировать matplotlib.pyplot как plt импортировать numpy как np plt.style.use («морской рожденный») # ...
Это меняет стиль на стиль Seaborn, еще одного стороннего пакета визуализации. Вы можете увидеть другой стиль, построив окончательный график рассеяния, показанный выше, с использованием стиля Seaborn:
Вы можете узнать больше о настройке графиков в Matplotlib, а также есть дополнительные руководства на страницах документации Matplotlib.
Использование plt.scatter() для создания точечных диаграмм позволяет отображать более двух переменных. Вот переменные, представленные в этом примере:
| Переменная | Представлен |
|---|---|
| Цена | Ось X |
| Среднее количество проданных | Ось Y |
| Маржа прибыли | Размер маркера |
| Тип продукта | Форма маркера |
| Содержание сахара | Цвет маркера |
Возможность представления более двух переменных делает plt.scatter() очень мощным и универсальным инструментом.
Удалить рекламу
Изучение
plt.scatter () Далее plt.scatter() предлагает еще большую гибкость в настройке точечных диаграмм. В этом разделе вы узнаете, как маскировать данные с помощью массивов NumPy и точечных диаграмм на примере. В этом примере вы сгенерируете случайные точки данных, а затем разделите их на две отдельные области на одном графике рассеяния.
В этом примере вы сгенерируете случайные точки данных, а затем разделите их на две отдельные области на одном графике рассеяния.
Жительница пригородной зоны, увлекающаяся сбором данных, сопоставила время прибытия автобусов на своей местной автобусной остановке за шестимесячный период. Время прибытия по расписанию составляет 15 минут 45 минут первого часа, но она заметила, что истинное время прибытия следует нормальному распределению вокруг этого времени:
Этот график показывает относительную вероятность прибытия автобуса каждую минуту в течение часа. Это распределение вероятностей может быть представлено с помощью NumPy и np.linspace() :
импортировать matplotlib.pyplot как plt импортировать numpy как np среднее = 15, 45 сд = 5, 7 x = np.linspace(0, 59, 60) # Представляет каждую минуту в течение часа first_distribution = np.exp(-0,5 * ((x - среднее [0]) / sd[0]) ** 2) second_distribution = 0,9 * np.exp (-0,5 * ((x - среднее [1]) / sd [1]) ** 2) y = первое_распределение + второе_распределение у = у / макс (у) plt.plot(x, y) plt.ylabel("Относительная вероятность прибытия автобуса") plt.xlabel("Минуты после часа") plt.show()
Вы создали два нормальных распределения с центром в 15 и 45 минут после часа и просуммировали их. Вы устанавливаете наиболее вероятное время прибытия в значение 1 путем деления на максимальное значение.
Теперь вы можете смоделировать время прибытия автобуса, используя это распределение. Для этого можно создавать случайные времена и случайные относительные вероятности с помощью встроенного модуля random . В приведенном ниже коде вы также будете использовать списки:
случайный импорт
импортировать matplotlib.pyplot как plt
импортировать numpy как np
n_автобусов = 40
bus_times = np.asarray([random.randint(0, 59) для _ в диапазоне (n_buses)])
bus_likelihood = np.asarray([random.random() for _ in range(n_buses)])
plt.scatter(x=автобус_время, y=автобус_вероятность)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt. ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
Вы смоделировали 40 прибывающих автобусов, которые можно визуализировать с помощью следующей диаграммы рассеяния:
Ваш график будет выглядеть по-другому, поскольку данные, которые вы генерируете, случайны. Однако не все из этих моментов, вероятно, будут близки к реальности, которую пассажирка наблюдала на основе собранных и проанализированных ею данных. Вы можете построить распределение, которое она получила из данных смоделированных прибытий автобусов:
случайный импорт импортировать matplotlib.pyplot как plt импортировать numpy как np среднее = 15, 45 сд = 5, 7 х = np.linspace (0, 59, 60) first_distribution = np.exp(-0,5 * ((x - среднее [0]) / sd[0]) ** 2) second_distribution = 0,9 * np.exp (-0,5 * ((x - среднее [1]) / sd [1]) ** 2) y = первое_распределение + второе_распределение у = у / макс (у) n_автобусов = 40 bus_times = np.asarray([random.randint(0, 59) for _ in range(n_buses)]) bus_likelihood = np.asarray([random.random() for _ in range(n_buses)]) plt.scatter(x=автобус_время, y=автобус_вероятность) plt.plot(x, y) plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность") plt.ylabel("Относительная вероятность прибытия автобуса") plt.xlabel("Минуты после часа") plt.show()
Это дает следующий вывод:
Чтобы моделирование было реалистичным, необходимо убедиться, что случайные прибытия автобусов соответствуют данным и распределению, полученному из этих данных. Вы можете отфильтровать случайно сгенерированные точки, оставив только те, которые попадают в распределение вероятностей. Вы можете добиться этого, создав маску для точечной диаграммы:
# ...
in_region = автобус_вероятность < y[автобус_время]
out_region = автобус_вероятность >= y[автобус_время]
plt.scatter(
x=автобусное_время[в_регионе],
y=автобус_вероятность[в_регионе],
цвет = "зеленый",
)
plt. scatter(
x=bus_time[out_region],
y=автобус_вероятность[out_region],
цвет = "красный",
маркер = "х",
)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
scatter(
x=bus_time[out_region],
y=автобус_вероятность[out_region],
цвет = "красный",
маркер = "х",
)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
Переменные in_region и out_region представляют собой массивы NumPy, содержащие логические значения в зависимости от того, находятся ли случайно сгенерированные вероятности выше или ниже распределения y . Затем вы строите два отдельных графика рассеяния, один с точками, попадающими в распределение, а другой — с точками, не входящими в распределение. Точки данных, находящиеся выше распределения, не являются репрезентативными для реальных данных:
Вы сегментировали точки данных из исходной диаграммы рассеяния на основе того, попадают ли они в распределение, и использовали другой цвет и маркер для идентификации двух наборов данных.
Удалить рекламу
Просмотр основных входных параметров
Вы узнали об основных входных параметрах для создания точечных диаграмм в разделах выше. Вот краткое изложение ключевых моментов, которые следует помнить об основных входных параметрах:
| Параметр | Описание |
|---|---|
х и у | Эти параметры представляют две основные переменные и могут быть любыми типами данных, подобными массивам, например списками или массивами NumPy. Это обязательные параметры. |
с | Этот параметр определяет размер маркера. Это может быть число с плавающей запятой, если все маркеры имеют одинаковый размер, или структура данных, подобная массиву, если маркеры имеют разные размеры. |
с | Этот параметр представляет цвет маркеров. Обычно это либо массив цветов, таких как значения RGB, либо последовательность значений, которые будут отображены на карту цветов с помощью параметра cmap . |
маркер | Этот параметр используется для настройки формы маркера. |
смап | Если для параметра c используется последовательность значений, то этот параметр можно использовать для выбора сопоставления между значениями и цветами, обычно с использованием одной из стандартных карт цветов или пользовательской карты цветов. |
альфа | Этот параметр представляет собой число с плавающей запятой, которое может принимать любое значение от 9 до0015 0 и 1 и представляет прозрачность маркеров, где 1 представляет непрозрачный маркер. |
Это не единственные входные параметры, доступные с plt.scatter() . Вы можете получить доступ к полному списку входных параметров из документации.
Заключение
Теперь, когда вы знаете, как создавать и настраивать точечные диаграммы с помощью plt. , вы готовы приступить к практике с собственными наборами данных и примерами. Эта универсальная функция дает вам возможность исследовать ваши данные и представлять результаты в ясной форме. scatter()
scatter()
В этом уроке вы узнали, как:
- Создайте точечную диаграмму , используя
plt.scatter() - Использовать обязательные и необязательные входные параметры
- Настройка точечных диаграмм для базовых и более сложных графиков
- Представление более чем двух измерений с
plt.scatter()
Вы можете получить максимальную отдачу от визуализации, используя plt.scatter() , узнав больше обо всех функциях Matplotlib и работая с данными с помощью NumPy.
Смотреть сейчас Это руководство содержит связанный с ним видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Использование plt. scatter() для визуализации данных в Python
scatter() для визуализации данных в Python
Построение точечной диаграммы — Tableau
Применяется к: Tableau Desktop
Используйте точечные диаграммы для визуализации отношений между числовыми переменными.
В Tableau вы создаете точечную диаграмму поместив хотя бы одну меру на полку Columns и хотя бы одна мера на полке строк. Если эти полки содержат как измерения, так и меры, Tableau размещает меры как самые внутренние поля, что означает, что меры всегда находятся справа от любых измерений, которые вы также разместили на этих полках. Слово «внутренний» в данном случае относится к структуре таблицы.
| Создает простую точечную диаграмму | Создает матрицу точечных диаграмм |
Точечная диаграмма может использовать несколько типов меток.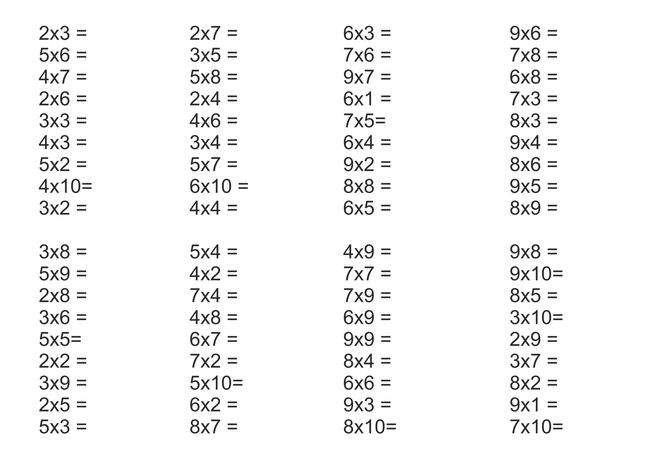 По умолчанию Табло
использует тип метки формы. В зависимости от ваших данных вы можете
хотите использовать другой тип метки, например, круг или квадрат. Дополнительные сведения см. в разделе Изменение типа метки в представлении.
По умолчанию Табло
использует тип метки формы. В зависимости от ваших данных вы можете
хотите использовать другой тип метки, например, круг или квадрат. Дополнительные сведения см. в разделе Изменение типа метки в представлении.
Чтобы использовать точечные диаграммы и линии тренда для сравнения продаж с прибылью, выполните следующие действия:
- Откройте источник данных Sample — Superstore.
Перетащите показатель Прибыль в Столбцы.
Tableau объединяет измеряют как сумму и создают горизонтальную ось.
Перетащите меру Sales в строки.
Tableau объединяет измеряют как сумму и создают вертикальную ось.
Показатели могут состоять из непрерывных числовых данных. Когда вы сопоставляете одно число с другим, вы сравниваете два числа; полученная диаграмма аналогична декартовой диаграмме с координатами x и y.

Теперь у вас есть точечная диаграмма с одной меткой:
Перетащите измерение «Категория» в «Цвет» на карточке «Метки».
Это разделяет данные на три метки — по одной для каждого элемента измерения — и кодирует метки с помощью цвета.
Перетащите измерение «Регион» в «Детали» на карточке «Метки».
Теперь в представлении стало намного больше меток. Количество меток равно количеству отдельных регионов в источнике данных, умноженному на количество отделов. (Если вам интересно, используйте кнопку «Отменить» на панели инструментов, чтобы посмотреть, что произошло бы, если бы вы отбросили параметр «Регион» на Форма вместо Детали.
 )
)Чтобы добавить линии тренда, на панели Аналитика перетащите модель Линии тренда в представление, а затем поместите ее на тип модели.
Линия тренда может обеспечить статистическое определение взаимосвязи между двумя числовыми значениями. Чтобы добавить линии тренда в представление, обе оси должны содержать поле, которое можно интерпретировать как число — по определению, это всегда имеет место с точечной диаграммой.
Tableau добавляет три линейные линии тренда — по одной для каждого цвета, который вы используете для различения трех категорий.
Наведите курсор на линии тренда, чтобы увидеть статистическую информацию о модели, которая использовалась для создания линии:
Дополнительные сведения см.
 в разделе Оценка значимости линии тренда. Вы также можете настроить линию тренда, чтобы использовать другой тип модели или включить доверительные интервалы. Дополнительные сведения см. в разделе Добавление линий тренда в визуализацию.
в разделе Оценка значимости линии тренда. Вы также можете настроить линию тренда, чтобы использовать другой тип модели или включить доверительные интервалы. Дополнительные сведения см. в разделе Добавление линий тренда в визуализацию.Проверь свою работу! См. шаги 1–7 ниже:
См. также
Пример: точечные диаграммы, агрегирование и гранулярность
Что такое точечная диаграмма и когда ее использовать
Когда вы изучали алгебру в старшей школе, вы, возможно, не осознавали, что однажды вам понадобится построить точечную диаграмму, чтобы продемонстрировать результаты в реальном мире.
В школе примеры, которые нам приходилось чертить, всегда казались глупыми. Количество часов, потраченных на подготовку к тесту, по сравнению с полученной оценкой за тест. Соотношение роста и веса группы людей. Или корреляция между продажами горячего кофе и наружной температурой.
Соотношение роста и веса группы людей. Или корреляция между продажами горячего кофе и наружной температурой.
Но как работающему взрослому (или, может быть, просто любознательному), вам много раз может понадобиться использовать школьную математику.
И создание точечной диаграммы определенно относится к таким случаям. Существует так много реальных приложений, которые предлагает точечная диаграмма, которые могут помочь вам или вашей аудитории визуализировать данные и их значение.
Давайте на секунду вернемся к школьной математике, потому что вы вполне могли оставить все знания о том, что такое точечная диаграмма, на своем нарисованном на столе столе.
Что такое точечная диаграмма?
Точечная диаграмма — это тип визуализации данных, показывающий взаимосвязь между различными переменными. Эти данные отображаются путем размещения различных точек данных между осями x и y.
По сути, каждая из этих точек данных выглядит «разбросанной» по графику, что и дало название этому типу визуализации данных.
Диаграммы рассеяния также могут называться диаграммами рассеивания или x-y-графиками, и смысл использования одного из них состоит в том, чтобы определить, существуют ли закономерности или корреляции между двумя переменными.
Взгляните на этот пример точечной диаграммы, взятой из одного из шаблонов Visme.
Настройте этот шаблон точечной диаграммы и сделайте его своим собственным! Редактировать и загрузить
Две переменные — это площадь дома в квадратных футах и его цена. Мы взяли примерный набор данных о нескольких домах, чтобы посмотреть, сможем ли мы определить взаимосвязь между этими двумя переменными.
Поскольку ось абсцисс идет от наименьшего размера к наибольшему, мы можем видеть небольшую положительную корреляцию, показывающую, что по мере увеличения квадратных метров увеличивается и цена.
Конечно, этому могут способствовать и другие факторы, такие как местоположение или недавний ремонт, но из этой диаграммы рассеяния мы видим, что существует корреляция между площадью в квадратных футах и стоимостью дома.
Паттерны или корреляции, обнаруженные на точечной диаграмме, будут иметь несколько различных характеристик.
- Линейная или нелинейная: линейная корреляция образует прямую линию в своих точках данных, в то время как нелинейная корреляция может иметь кривую или другую форму в точках данных.
- Сильная или слабая: при сильной корреляции точки данных находятся близко друг к другу, а при слабой корреляции точки данных находятся далеко друг от друга.
- Положительный или отрицательный: Положительная корреляция будет указывать вверх (т. е. значения x и y увеличиваются), а отрицательная корреляция будет направлена вниз (т. е. значения x увеличиваются, а соответствующие значения y увеличиваются). уменьшается).
Однако, если вы не видите какой-либо из этих функций на вашем графике, это означает, что между вашими данными нет корреляции.
Когда использовать точечную диаграмму
Для каждого типа диаграммы или графика существуют свои собственные правила, определяющие, когда лучше визуализировать данные для демонстрации вашей информации.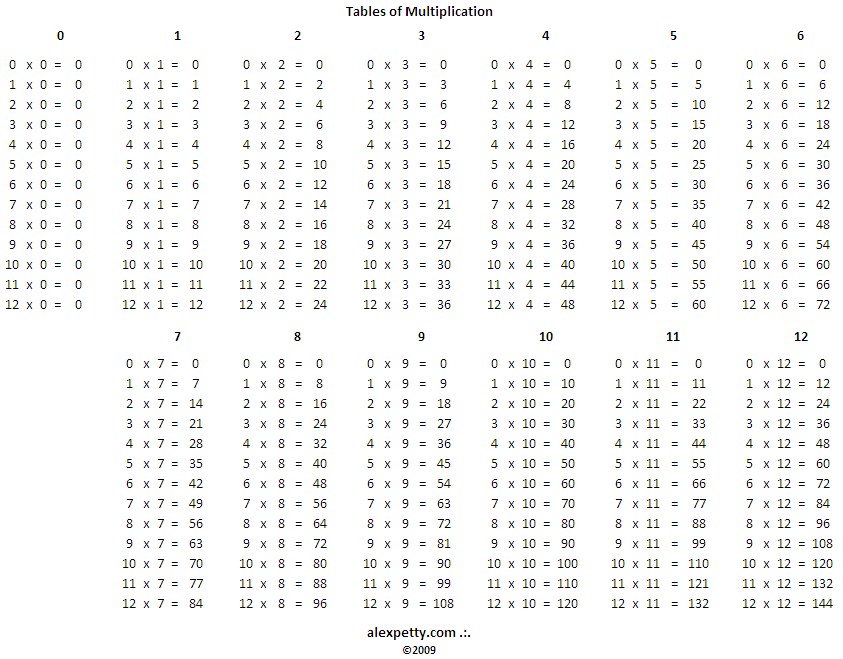
Давайте погрузимся в лучшее время, чтобы использовать точечную диаграмму для визуализации набора данных.
Используйте точечную диаграмму, чтобы определить, имеют ли две переменные взаимосвязь или корреляцию.
Вы пытаетесь понять, могут ли ваши две переменные что-то означать, когда они вместе? Построение диаграммы рассеяния с вашими точками данных может помочь вам определить, есть ли потенциальная связь между ними.
Допустим, вы управляете бизнесом по производству мороженого и хотите узнать, есть ли какая-то закономерность в том, почему ваши продажи в последнее время были низкими.
Вы можете создать точечный график для измерения различных факторов, включая температуру наружного воздуха.
Настройте этот шаблон точечной диаграммы и сделайте его своим собственным! Редактировать и загрузить
Вы всегда хотите построить свою точечную диаграмму с увеличением оси x и оси y по мере их выхода, чтобы вы могли определить корреляцию.
Как видно из приведенного выше примера, люди склонны покупать мороженое — холодный десерт — реже, когда на улице холодно.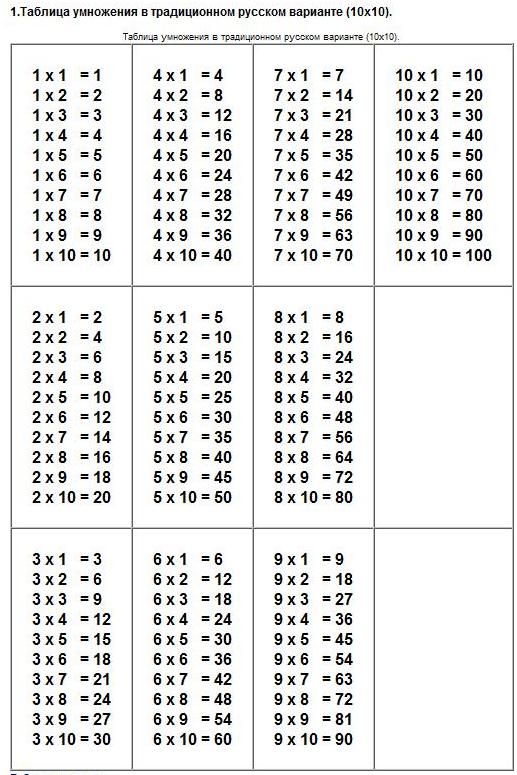
Используйте точечную диаграмму, если ваша независимая переменная имеет несколько значений для зависимой переменной.
Хорошо, давайте на минуту вернемся к уроку математики и рассмотрим, что означают независимые и зависимые переменные.
Во-первых, переменная — это то, что вы пытаетесь отслеживать или измерять. На каждом графике есть две переменные — независимая переменная, которая обычно отображается на оси X, и зависимая переменная, которая обычно изображается на оси Y.
Независимая переменная — это регулируемая переменная. Это то, что меняется естественным образом, или то, что меняет человек, манипулирующий экспериментом или графиком.
Зависимая переменная — это изучаемая или измеряемая переменная. В случае точечной диаграммы это переменная, которую мы ищем, чтобы определить, имеет ли она корреляцию с независимой переменной.
Если вы пытаетесь определить, есть ли корреляция между ростом и весом, рост будет размещен по оси x, а вес — по оси y, как в примере ниже.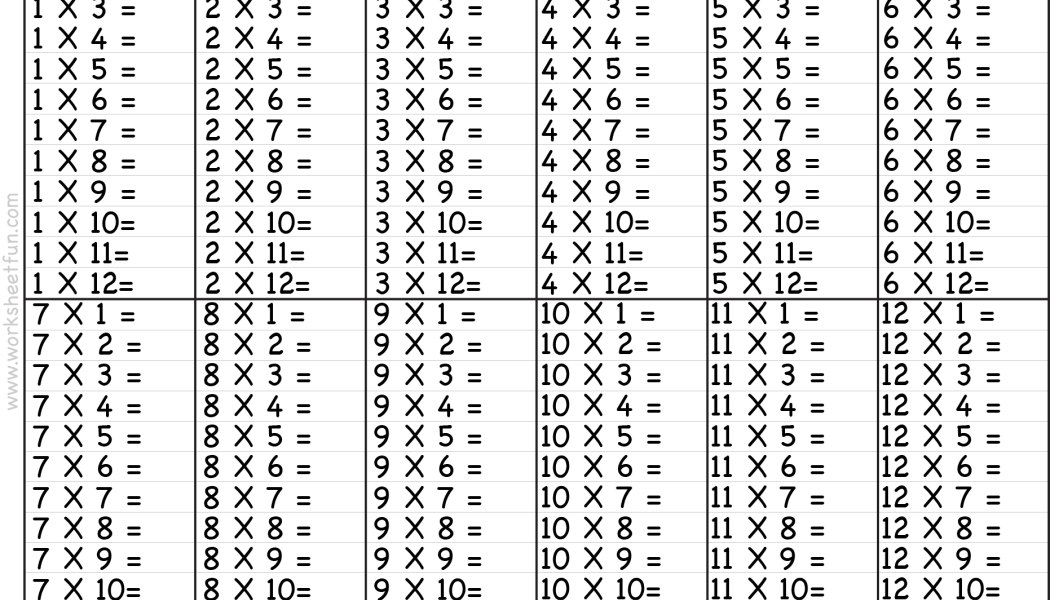
Настройте этот шаблон точечной диаграммы и сделайте его своим собственным! Редактировать и загрузить
Поскольку вес колеблется гораздо больше, чем рост, вполне вероятно, что у вас могут быть разные веса для одного и того же роста в ваших данных, что дает вам более одного значения зависимой переменной. для каждой независимой переменной.
Используйте точечную диаграмму, если у вас есть две переменные, которые хорошо сочетаются друг с другом.
Если у вас есть две переменные, которые хорошо сочетаются друг с другом, нанесение их на точечную диаграмму — отличный способ просмотреть их взаимосвязь и определить, является ли она положительной или отрицательной корреляцией.
Например, подумайте о массе тела при рождении в сравнении с гестационным возрастом (как долго ребенок находится в утробе матери). Было бы логично, если бы ребенок, способный дольше расти внутри своей матери, был бы крупнее и, следовательно, весил бы больше, верно?
Давайте посмотрим на эти данные на точечной диаграмме.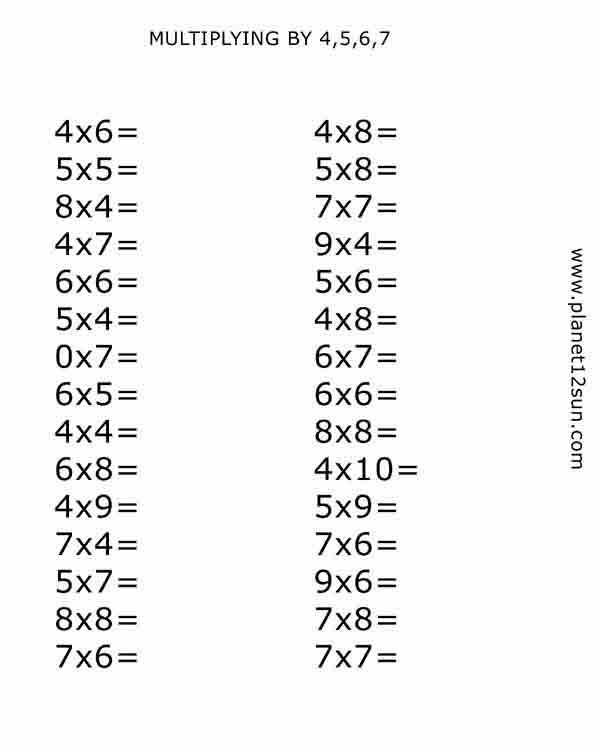
Настройте этот шаблон точечной диаграммы и сделайте его своим! Редактировать и загрузить
Как и следовало ожидать, чем дольше ребенок может «готовить», тем больше он весит при рождении.
Другими примерами переменных, которые, кажется, идут рука об руку, могут быть количество отработанных часов и заработанных денег, время обучения и качество при испытаниях или цена и размер бриллианта.
Когда не следует использовать точечную диаграмму
Точно так же, как в некоторых случаях имеет смысл использовать точечную диаграмму для визуализации ваших данных, есть несколько примеров, когда вы хотите держаться подальше от этого типа диаграммы .
Избегайте точечной диаграммы, когда ваши данные совершенно не связаны между собой.
Есть определенные переменные, которые делают очевидным отсутствие корреляции, поэтому точечная диаграмма была бы бесполезным способом визуализации вашей информации.
Например, если вы проводите случайный опрос в классе, полном учеников, то сведение воедино разного роста учеников и количества домашних животных на точечной диаграмме не имеет смысла.
Очевидно, что эти две переменные не имеют никакого отношения друг к другу, и, несмотря на то, что их все еще интересно отображать в виде графика, гистограмма (по одной для каждого значения данных) может быть здесь лучшим выбором.
Избегайте точечной диаграммы при наличии слишком большого набора данных.
Если на точечной диаграмме так много данных, что они загромождают весь график, это результат перерисовки.
Статистик Натан Яу довольно хорошо резюмирует это явление на графике ниже:
Источник изображения
В качестве другого примера взгляните на точечную диаграмму ниже. Он настолько плотный, что по сути становится одним большим пятном, и на такой диаграмме трудно что-либо прочитать.
Источник изображения
Однако есть несколько способов противодействовать перерисовке точечной диаграммы. Во-первых, рассмотрите возможность использования тепловой карты, которая показывает, где находятся наиболее насыщенные точками разделы ваших данных.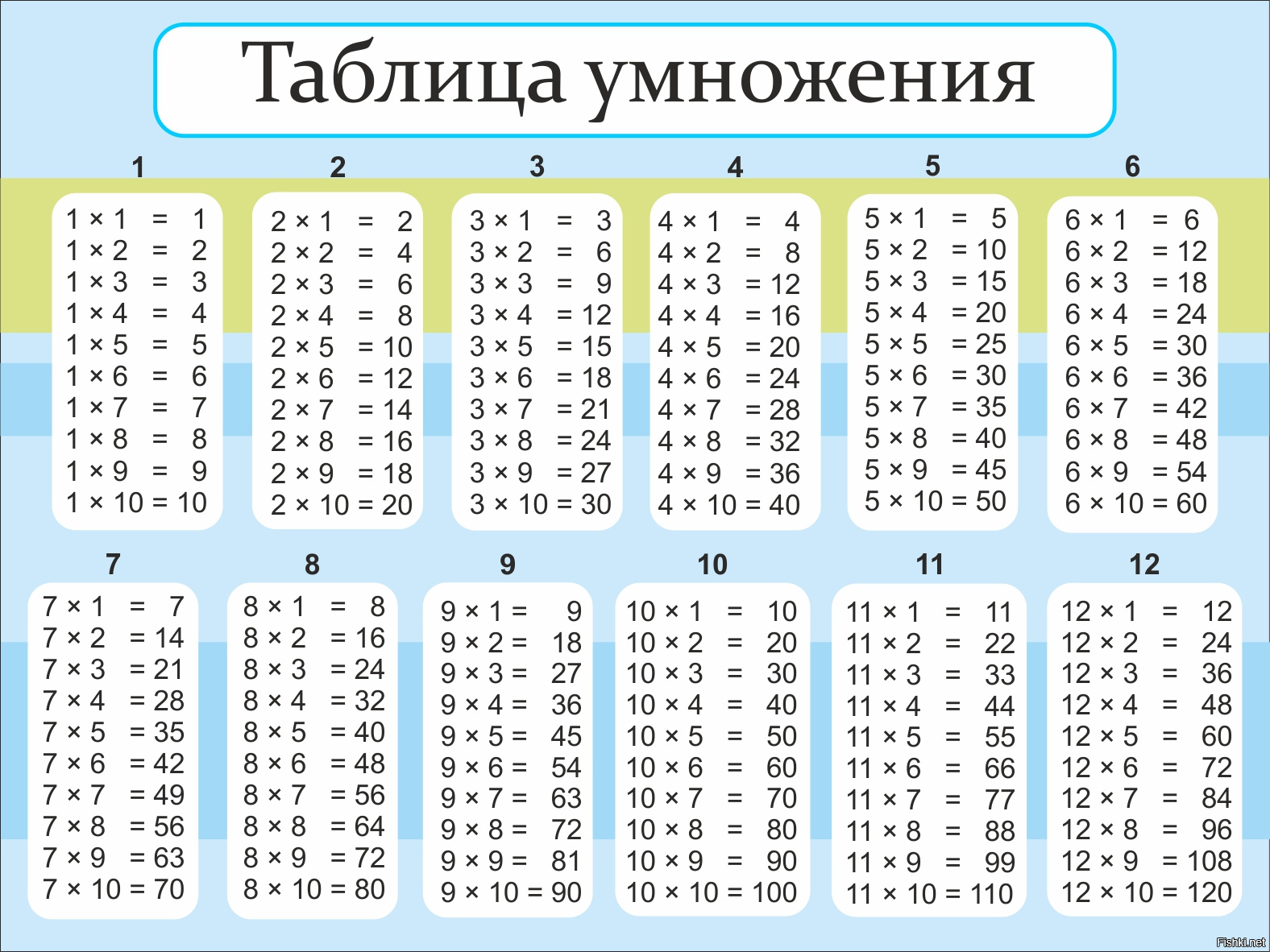
Вы также можете кодировать различные наборы данных цветом, использовать полупрозрачные точки данных для создания эффекта, похожего на тепловую карту, и многое другое.
Однако лучше всего избегать использования точечной диаграммы, когда у вас так много данных, что они превращаются в большие капли.
О чем следует помнить при работе с точечной диаграммой
Когда вы просматриваете свои данные, есть несколько моментов, о которых следует помнить, когда вы решите использовать точечный график для определения взаимосвязей или корреляции.
Корреляция не всегда является причинно-следственной связью.
Тот факт, что вы можете увидеть сильную положительную или отрицательную корреляцию в ваших данных, не обязательно означает, что ваша независимая переменная является причиной того, что ваша зависимая переменная измеряет то, что она есть.
Это корреляции, означающие, что ваша независимая переменная оказывает какое-то влияние на вашу зависимую переменную.
Вернемся к нашему примеру с продажей мороженого.
Хотя может показаться, что погода является непосредственной причиной снижения продаж, может быть множество других факторов, которые приводят к замедлению бизнеса.
Возможно, произошло стихийное бедствие, подобное урагану, которое привело к обязательной эвакуации и, следовательно, сокращению бизнеса. На улице мог открыться новый магазин мороженого, создав конкуренцию, которой раньше не было.
Иногда люди просто не хотят покупать мороженое. И хотя, конечно, более холодная погода может быть фактором, только потому, что вы видите корреляцию на графике рассеяния, не означает, что вы должны воспринимать ее как закон.
Вы можете иметь более одной зависимой переменной.
Ваш набор данных может включать более одной зависимой переменной, и вы все равно можете отслеживать это на точечной диаграмме.
Единственное, что вам нужно изменить, это цвет каждой зависимой переменной, чтобы вы могли сравнивать их друг с другом на точечной диаграмме.
Давайте вернемся к нашему примеру роста и веса.
На этом точечном графике мы добавили две разные зависимые переменные — мужскую и женскую — чтобы увидеть, есть ли разница между этими факторами. Мы раскрасили женские точки оранжевым цветом, а мужские — коричневым, чтобы можно было различать их.
Это еще один отличный способ избежать перерисовки. Обеспечение цветового кодирования ваших данных помогает выделить их, чтобы вы могли видеть больше своих точек.
Как создать точечную диаграмму с помощью Visme
Теперь, когда вы знаете все о том, что такое точечная диаграмма и когда вы ее используете, а когда нет, давайте начнем с нашего руководства о том, как вы можете на самом деле создать один.
Существует 16 различных типов диаграмм, которые вы можете создать прямо в Visme, и точечный график — только один из них! Подробнее о том, как начать работу, читайте ниже.
1. Начните с шаблона.
Прямо в Visme доступно несколько различных начальных шаблонов точечных диаграмм, к которым вы можете перейти и начать добавлять свои данные.
Просмотрите наш выбор и выберите тот, который вы хотите использовать. Это приведет вас к панели инструментов Visme с этим шаблоном прямо внутри, чтобы вы могли немедленно начать настраивать его в соответствии со своими потребностями.
2. Введите свои данные.
Нажмите на точечную диаграмму, и настройки графика появятся в левой части вашего редактора. Нажмите Chart Data для ввода ваших данных.
Информация по оси X будет отображаться в верхней строке, а соответствующие данные по оси Y — в нижней строке. Убедитесь, что все ваши числа на оси абсцисс расположены в порядке от наименьшего к наибольшему.
Если у вас более одной зависимой переменной, просто добавьте эту информацию в следующую строку для второй переменной, в четвертую строку для третьей и так далее.
Вы также можете перейти на вкладку Импорт данных , чтобы импортировать данные, которые вы уже собрали в файле Google Sheet или Excel.
3. Пометьте свои оси.

Перейдите в Настройки , третья вкладка в настройках графика. Нажмите, чтобы открыть вкладку Axis . Здесь вы можете настроить информацию по осям x и y и убедиться, что данные точечной диаграммы отображаются правильно.
Первое, что вам нужно сделать, это убедиться, что параметр Рассматривать метки как текст переключен на Выкл , иначе ваш точечный график будет больше похож на линейную диаграмму с точками.
Присвойте каждой оси метку, указывающую, что представляет собой переменная, и настройте шрифты в соответствии с остальной частью вашего дизайна, щелкнув значок шестеренки рядом с каждой осью. Или, как вы видите здесь, вы можете использовать отдельные текстовые области для маркировки вашего графика.
Ознакомьтесь с нашей статьей о сочетании шрифтов, чтобы определить, какие из них лучше всего использовать.
4. Цветовой код.
Вы можете полностью настроить каждую часть точечной диаграммы в редакторе Visme. Выберите цвет для каждой из точек вашей зависимой переменной, выберите цвет для ваших значений, ваших осей и заголовка вашей диаграммы.
Выберите цвет для каждой из точек вашей зависимой переменной, выберите цвет для ваших значений, ваших осей и заголовка вашей диаграммы.
Щелкните цветное поле рядом с каждой переменной или каждой меткой в настройках, чтобы получить доступ к палитре цветов. Выберите один из цветов, которые вы использовали в прошлых и предустановленных палитрах, или нажмите знак +, чтобы получить доступ к палитре цветов Visme.
Как только вы найдете цвета, подходящие для вашего контента или общего дизайна, вы можете перейти к следующему шагу.
5. Анимируйте точечный график.
И последнее, но не менее важное: оживите свою точечную диаграмму! Анимация поставляется с любым типом графика или диаграммы в редакторе Visme.
Это интересный способ создания интерактивного контента, если вы встраиваете точечную диаграмму на веб-страницу (как показано ниже) или делитесь ссылкой со своей аудиторией.
Вы можете выбрать один из пяти различных типов анимации для диаграммы: Линейная, Отскок, Эластичная, Упрощение и Упрощение.
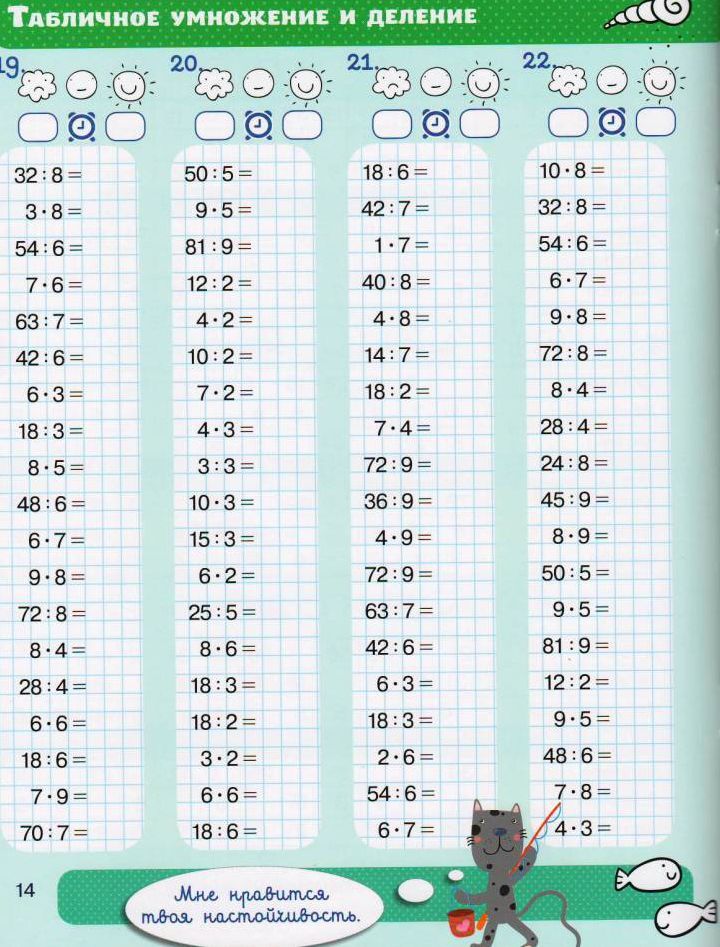 Например, 3 + 3 = 6, 6 + 6 = 12.
Например, 3 + 3 = 6, 6 + 6 = 12.

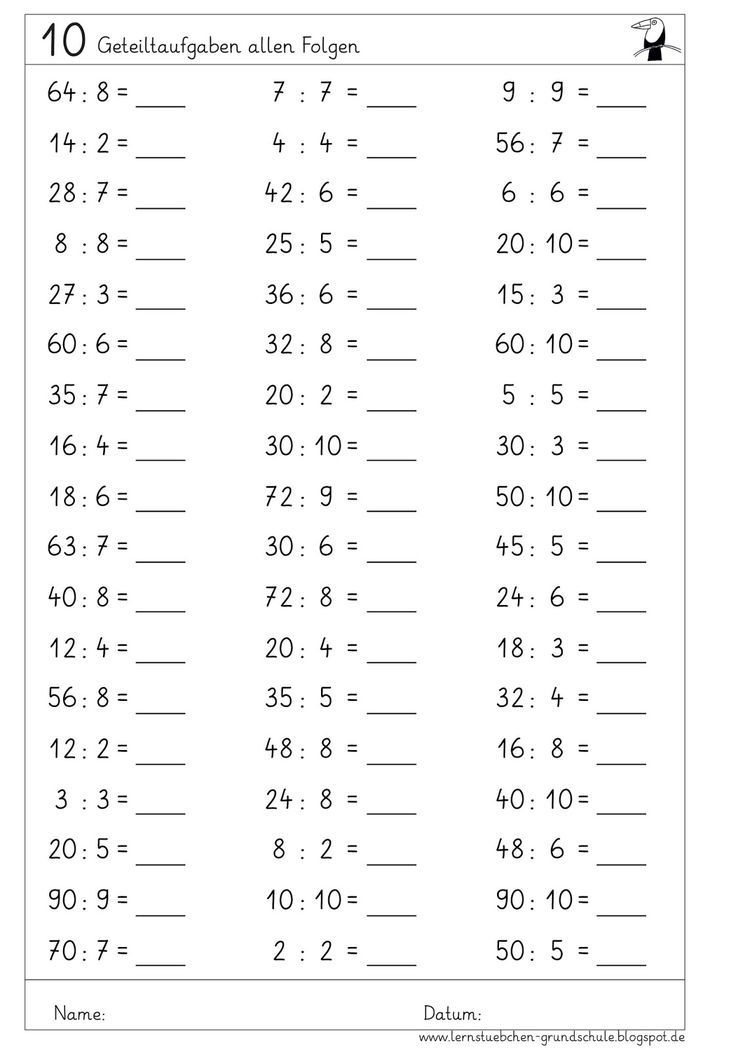 Например, 2 × 9 = 18 (1 + 8 = 9). 3 × 9 = 27 (2 + 7 = 9)
Например, 2 × 9 = 18 (1 + 8 = 9). 3 × 9 = 27 (2 + 7 = 9) pyplot как plt
цена = [2,50, 1,23, 4,02, 3,25, 5,00, 4,40]
продаж_за_день = [34, 62, 49, 22, 13, 19]
Распечатать(
"plt.scatter()",
время.время(
"plt.scatter(цена, продажи_за_день)",
число=1000,
глобальные = глобальные(),
),
)
Распечатать(
"plt.plot()",
время.время(
"plt.plot(цена, продажи_за_день, 'o')",
число=1000,
глобальные = глобальные(),
),
)
pyplot как plt
цена = [2,50, 1,23, 4,02, 3,25, 5,00, 4,40]
продаж_за_день = [34, 62, 49, 22, 13, 19]
Распечатать(
"plt.scatter()",
время.время(
"plt.scatter(цена, продажи_за_день)",
число=1000,
глобальные = глобальные(),
),
)
Распечатать(
"plt.plot()",
время.время(
"plt.plot(цена, продажи_за_день, 'o')",
число=1000,
глобальные = глобальные(),
),
)
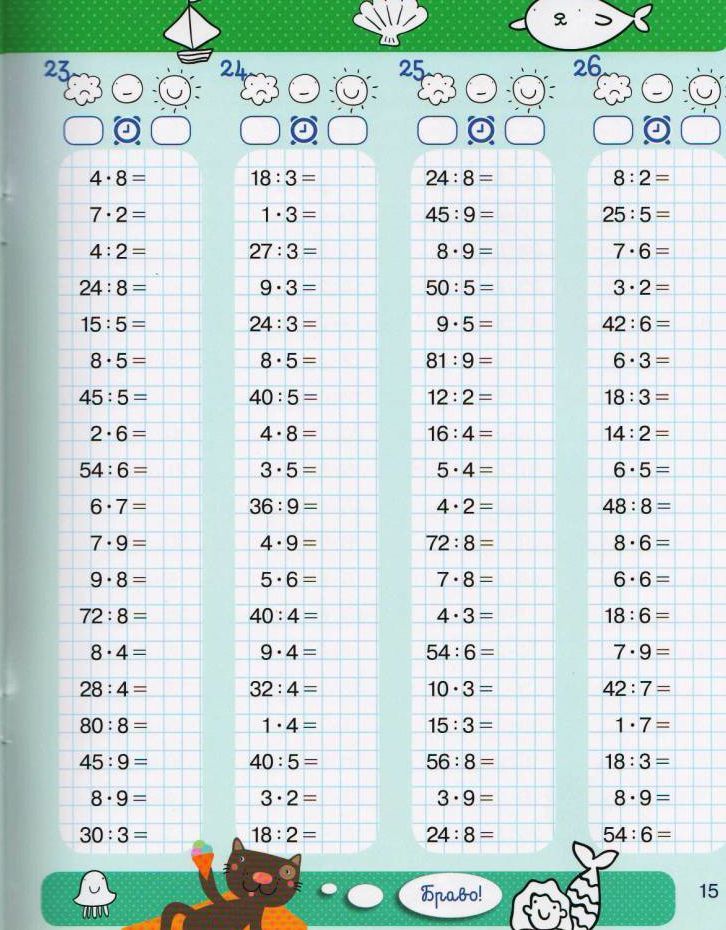 asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40])
sales_per_day_orange = np.asarray([34, 62, 49, 22, 13, 19])
profit_margin_orange = np.asarray([20, 35, 40, 20, 27,5, 15])
Sugar_content_orange = [низкий, высокий, средний, средний, высокий, низкий]
price_cereal = np.asarray([1,50, 2,50, 1,15, 1,95])
sales_per_day_cereal = np.asarray([67, 34, 36, 12])
profit_margin_cereal = np.asarray([20, 42,5, 33,3, 18])
сахара_content_cereal = [низкий, высокий, средний, низкий]
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
)
plt.show()
asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40])
sales_per_day_orange = np.asarray([34, 62, 49, 22, 13, 19])
profit_margin_orange = np.asarray([20, 35, 40, 20, 27,5, 15])
Sugar_content_orange = [низкий, высокий, средний, средний, высокий, низкий]
price_cereal = np.asarray([1,50, 2,50, 1,15, 1,95])
sales_per_day_cereal = np.asarray([67, 34, 36, 12])
profit_margin_cereal = np.asarray([20, 42,5, 33,3, 18])
сахара_content_cereal = [низкий, высокий, средний, низкий]
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
)
plt.show()
 ..
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
альфа=0,5,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
3.2,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.show()
..
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
альфа=0,5,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
3.2,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.show()
 scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
смап = "струя",
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
2,7,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.colorbar()
plt.show()
scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
смап = "струя",
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
2,7,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.colorbar()
plt.show()
 стиль.доступно
[
"Соляризация_Свет2",
"_classic_test_patch",
"бмх",
"классический",
"темный_фон",
"быстро",
"пять тридцать восемь",
"ггплот",
"оттенки серого",
"морской",
"морской яркий",
"морской дальтоник",
"морской темный",
"морская-темная-палитра",
"мореборн-темная сетка",
"морская глубина",
"морской приглушенный",
"морской блокнот",
"морская бумага",
"морская пастель",
"морской постер",
"морской разговор",
"морские клещи",
"бело-морской",
"сиборн-белая сетка",
"таблица-дальтоник10",
]
стиль.доступно
[
"Соляризация_Свет2",
"_classic_test_patch",
"бмх",
"классический",
"темный_фон",
"быстро",
"пять тридцать восемь",
"ггплот",
"оттенки серого",
"морской",
"морской яркий",
"морской дальтоник",
"морской темный",
"морская-темная-палитра",
"мореборн-темная сетка",
"морская глубина",
"морской приглушенный",
"морской блокнот",
"морская бумага",
"морская пастель",
"морской постер",
"морской разговор",
"морские клещи",
"бело-морской",
"сиборн-белая сетка",
"таблица-дальтоник10",
]
 plot(x, y)
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
plot(x, y)
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
 ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
 randint(0, 59) for _ in range(n_buses)])
bus_likelihood = np.asarray([random.random() for _ in range(n_buses)])
plt.scatter(x=автобус_время, y=автобус_вероятность)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
randint(0, 59) for _ in range(n_buses)])
bus_likelihood = np.asarray([random.random() for _ in range(n_buses)])
plt.scatter(x=автобус_время, y=автобус_вероятность)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
 scatter(
x=bus_time[out_region],
y=автобус_вероятность[out_region],
цвет = "красный",
маркер = "х",
)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
scatter(
x=bus_time[out_region],
y=автобус_вероятность[out_region],
цвет = "красный",
маркер = "х",
)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()

 )
) в разделе Оценка значимости линии тренда. Вы также можете настроить линию тренда, чтобы использовать другой тип модели или включить доверительные интервалы. Дополнительные сведения см. в разделе Добавление линий тренда в визуализацию.
в разделе Оценка значимости линии тренда. Вы также можете настроить линию тренда, чтобы использовать другой тип модели или включить доверительные интервалы. Дополнительные сведения см. в разделе Добавление линий тренда в визуализацию.