Решаем столбиком деление: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Содержание

Деление многочлена на многочлен с остатком примеры. Деление многочленов «столбиком» («уголком»). Решаем реальные примеры

Напомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде:

где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству:

Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов , отличных от нуля, степень произведения будет равна сумме степеней сомножителей.

Говорят, что один многочлен нацело (без остатка) делится на другой многочлен , если результатом деления является многочлен.

Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком , в результате которого и частное, и остаток будут многочленами.

Определение . Разделить многочлен a (x ) на многочлен b (x ) с остатком – это значит представить многочлен a (x ) в виде

где многочлен c (x ) – частное , а многочлен r (x ) – остаток , причем, степень остатка удовлетворяет неравенству:

является тождеством , т. е. равенством, справедливым при всех значениях переменной x .

При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.

Один из способов деления многочленов с остатком – это деление многочленов «уголком» , что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.

Пример . Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен

Делим первый член делимого 2x 4 на первый член делителя x 2 . Получаем первый член частного 2x 2 .

Умножаем первый член частного 2x 2 на делитель
x 2 — x + 1, а результат умножения

2x 4 — 2x 3 + 2x 2

пишем под делимым 2x 4 — x 3 + 5x 2 — 8x + 1 .

Вычитаем из делимого написанный под ним многочлен.

Получаем первый остаток

x 3 + 3x 2 — 8x .

Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член остатка x 3 на первый член делителя x 2 . Получаем второй член частного x .

Умножаем второй член частного x на делитель x 2 — x + 1 , а результат умножения

x 3 — x 2 + x

пишем под первым остатком x 3 + 3x 2 — 8x .

Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток

4x 2 — 9x + 1 .

Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. 2-4x+8$.

Сегодня мы узнаем, как выполняется деление многочленов друг на друга, причем выполнять деление мы будем уголком по аналогии с обычными числами. Это очень полезный прием, который, к сожалению, не изучают в большинстве школ. Поэтому внимательно прослушайте данный видеоурок. Ничего сложного в таком делении нет.

Для начала давайте разделим друг на друга два числа:

Как можно это сделать? В первую очередь, мы отсекаем столько разрядов, чтобы полученное числовое значение было больше чем то, на которое мы делим. Если мы отсечем один разряд, то получим пять. Очевидно, семнадцать в пять не вмещается, поэтому этого недостаточно. Берем два разряда — у нас выйдет 59 — оно уже больше, чем семнадцать, поэтому мы можем выполнить операцию. Итак, сколько раз семнадцать помещается в 59? Давайте возьмем три. Перемножаем и записываем результат под 59. Итого у нас получилось 51. Вычитаем и у нас вышло «восемь». Теперь сносим следующий разряд — пять. Делим 85 на семнадцать. Берем пять.

{2}}$. В итоге мы видим, что мы получили очень «красивый» ответ. Записываем его.

Вот и весь алгоритм. Ключевых моментов здесь два:

Всегда сравнивайте первую степень делимого и делителя — повторяем это на каждом шаге;
Если в исходном выражении пропущены какие-либо степени, при делении уголком их обязательно следует добавить, но с нулевыми коэффициентами, иначе ответ будет неправильным.

Больше никаких премудростей и хитростей в таком делении нет.

Материал сегодняшнего урока нигде и никогда не встречается в «чистом» виде. Его редко изучают в школах. Однако умение делить многочлены друг на друга очень поможет вам при решении уравнений высших степеней, а также всевозможных задач «повышенной трудности». Без данного приема вам придется раскладывать многочлены на множители, подбирать коэффициенты — и результат при этом отнюдь не гарантирован. Однако многочлены можно делить и уголком — так же, как и обычные числа! К сожалению, данный прием не изучают в школах.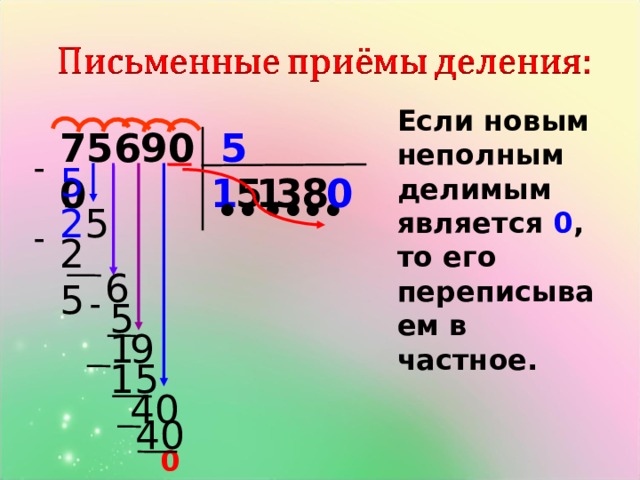 Многие учителя считают, что деление многочленов уголком — это что-то безумно сложное, из области высшей математики. Спешу вас заверить: это не так. Более того, делить многочлены даже проще, чем обычные числа! Посмотрите урок — и убедитесь в этом сами.:) В общем, обязательно возьмите этот прием на вооружение. Умение делить многочлены друг на друга очень пригодится вам при решении уравнений высших степеней и в других нестандартных задачах.

Я надеюсь, этот ролик поможет тем, кто работает с полиномами, особенно высших степеней. Это относится и к старшеклассникам, и к студентам университетов. А у меня на этом все. До встречи!

Естественно, никто при этом не заботится о том, чтобы школьники поняли, почему так можно делить. Чтобы восполнить вопиющий пробел в образовании таких ребят, привожу здесь метод деления полинома на полином столбиком, который на самом деле довольно прост и позволяет делить на полиномы произвольной степени.

Начнем с того, что для двух многочленов и ( не должен быть тождественно равным нулю) справедлива . Если же остаток нулевой, то говорят, что делится на без остатка.

А теперь давайте рассмотрим примеры: на них учиться делить полиномы проще.

Пример 1. Разделим на (обратите внимание, оба многочлена записаны по убыванию степеней ). Сначала запишу то, что должно получиться, а затем приведу объяснения, как это получить.

Получим остаток . Старший член этого остатка, который равен снова поделим на старший член делителя, который равен , получим , что и будет вторым членом частного. Делитель, умноженный на этот член, вычитаем из первого остатка. Получаем второй остаток, который равен нулю. На этом процесс деления заканчивается.

Легко проверить, что

Вообще говоря, деление заканчивается, как только степень полученного остатка будет меньше (строго меньше!) степени делителя. Давайте рассмотрим еще один пример.

Пример 2. Поделим на .

Деление закончено, поскольку степень последнего остатка меньше степени делителя (), иначе говоря, старший член остатка не делится нацело на старший член делителя.

Проверка. Действительно, нетрудно убедиться в том, что

Уравнение столбиком. Деление полиномов

В данной статье будут рассмотрены рациональные дроби, ее выделения целых частей. Дроби бывают правильными и неправильными. Когда в дроби числитель меньше знаменателя – это правильная дробь, а неправильная наоборот.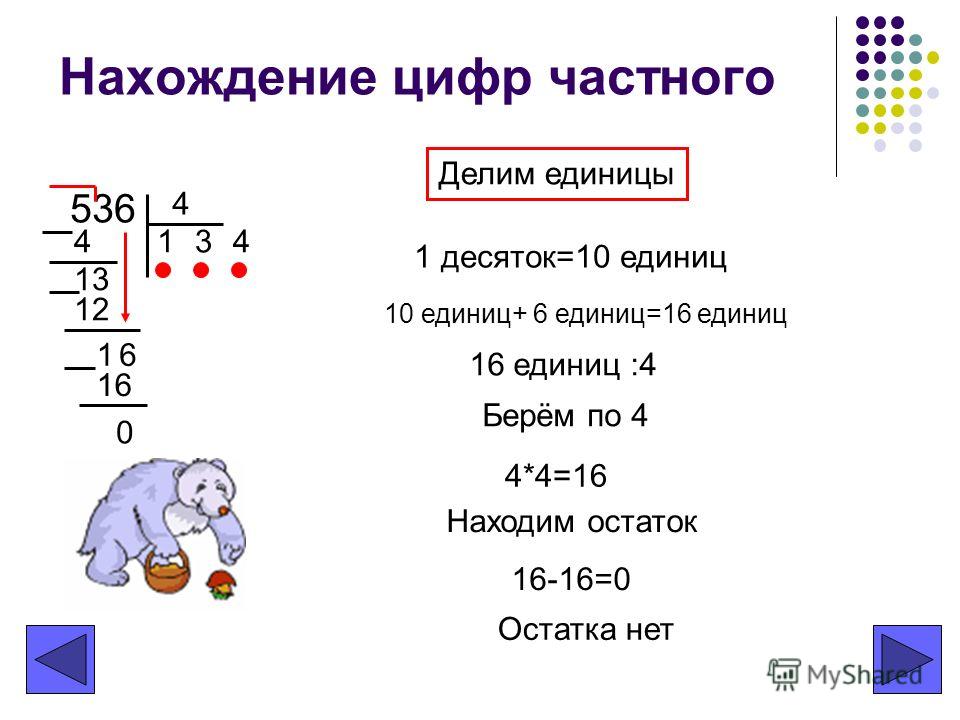

Рассмотрим примеры правильных дробей: 1 2 , 9 29 , 8 17 , неправильных: 16 3 , 21 20 , 301 24 .

Будем вычислять дроби, которые могут сократиться, то есть 12 16 — это 3 4 , 21 14 — это 3 2 .

При выделении целой части производится процесс деления числителя на знаменатель. Тогда такая дробь может быть представлена как сумма целой и дробной части, где дробная считается отношением остатка от деления и знаменателя.

Пример 1

Найти остаток при делении 27 на 4 .

Решение

Необходимо произвести деление столбиком, тогда получим, что

Значит, 27 4 = ц е л а я ч а с т ь + о с т а т о к з н а м е н а т е л ь = 6 + 3 4

Ответ: остаток 3 .

Пример 2

Произвести выделение целых частей 331 12 и 41 57 .

Решение

Производим деление знаменателя на числитель при помощи уголка:

Поэтому имеем, что 331 12 = 27 + 7 12 .

Вторая дробь является правильной, значит, целая часть равняется нулю.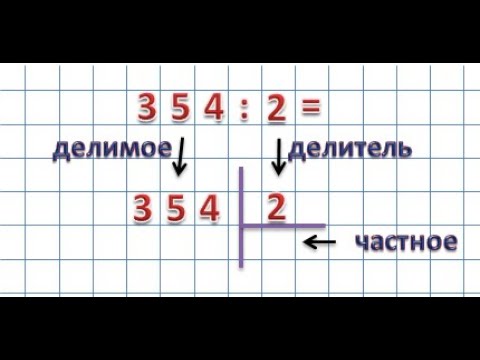

Ответ: целые части 27 и 0 .

Рассмотрим классификацию многочленов, иначе говоря, дробно-рациональную функцию. Ее считают правильной, когда степень числителя меньше степени знаменателя, иначе ее считают неправильной.

Определение 1

Деление многочлена на многочлен происходит по принципу деления углом, а представление функции как сумма целой и дробной частей.

Чтобы разделить многочлен на линейный двучлен, используется схема Горнера.

Пример 3

Произвести деление x 9 + 7 x 7 — 3 2 x 3 — 2 на одночлен 2 x 2 .

Решение

Воспользовавшись свойством деления, запишем, что

x 9 + 7 x 7 — 3 2 x 3 — 2 2 x 2 = x 9 2 x 2 + 7 x 7 2 x 2 — 3 2 x 3 2 x 2 + x 2 2 x 2 — 2 2 x 2 = = 1 2 x 7 + 7 2 x 5 — 3 4 x + 1 2 — 2 2 x — 2 .

Зачастую такого вида преобразования выполняются при взятии интегралов.

Пример 4

Произвести деление многочлена на многочлен: 2 x 3 + 3 на x 3 + x .

Решение

Знак деления можно записать в виде дроби вида 2 x 3 + 3 x 3 + x . Теперь необходимо выделить целую часть. Производим это при помощи деления столбиком. Получаем, что

Значит, получаем, что целая часть имеет значение — 2 x + 3 , тогда все выражение записывается как 2 x 3 + 3 x 3 + x = 2 + — 2 x + 3 x 3 + x

Пример 5

Разделить и найти остаток от деления 2 x 6 — x 5 + 12 x 3 — 72 x 2 + 3 на x 3 + 2 x 2 — 1 .

Решение

Зафиксируем дробь вида 2 x 6 — x 5 + 12 x 3 — 72 x 2 + 3 x 3 + 2 x 2 — 1 .

Степень числителя больше, чем у знаменателя, значит, что у нас имеется неправильная дробь. При помощи деления столбиком выдели целую часть. Получаем, что

Произведем деление еще раз и получим:

Отсюда имеем, что остаток равняется — 65 x 2 + 10 x — 3 , отсюда следует:

2 x 6 — x 5 + 12 x 3 — 72 x 2 + 3 x 3 + 2 x 2 — 1 = 2 x 3 — 5 x 2 + 10 x — 6 + — 65 x 2 + 10 x — 3 x 3 + 2 x 2 — 1

Существуют случаи, где необходимо дополнительно выполнять преобразование дроби для того, чтобы можно было выявить остаток при делении.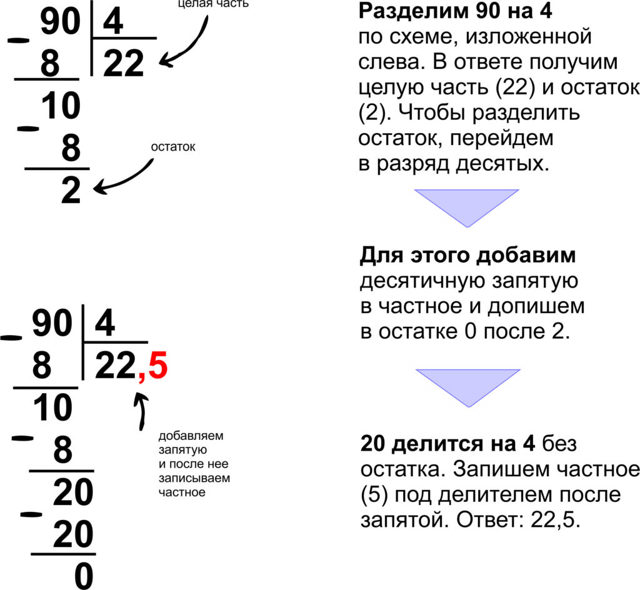 Это выглядит следующим образом:

3 x 5 + 2 x 4 — 12 x 2 — 4 x 3 — 3 = 3 x 2 x 3 — 3 — 3 x 2 x 3 — 3 + 3 x 5 + 2 x 4 — 12 x 2 — 4 x 3 — 3 = = 3 x 2 x 3 — 3 + 2 x 4 — 3 x 2 — 4 x 3 — 3 = 3 x 2 + 2 x 4 — 3 x 2 — 4 x 3 — 3 = = 3 x 2 + 2 x x 3 — 3 — 2 x x 3 — 3 + 2 x 4 — 3 x 2 — 4 x 3 — 3 = = 3 x 2 + 2 x (x 3 — 3) — 3 x 2 + 6 x — 4 x 3 — 3 = 3 x 2 + 2 x + — 3 x 2 + 6 x — 4 x 3 — 3

Значит, что остаток при делении 3 x 5 + 2 x 4 — 12 x 2 — 4 на x 3 — 3 дает значение — 3 x 2 + 6 x — 4 . Для быстрого нахождения результата применяют формулы сокращенного умножения.

Пример 6

Произвести деление 8 x 3 + 36 x 2 + 54 x + 27 на 2 x + 3 .

Решение

Запишем деление в виде дроби. Получим, что 8 x 3 + 36 x 2 + 54 x + 27 2 x + 3 . Заметим, что в числителе выражение можно сложить по формуле куба суммы. Имеем, что

8 x 3 + 36 x 2 + 54 x + 27 2 x + 3 = (2 x + 3) 3 2 x + 3 = (2 x + 3) 2 = 4 x 2 + 12 x + 9

Заданный многочлен делится без остатка.

Для решения используется более удобный метод решения, причем деление многочлена на многочлен считается максимально универсальным, поэтому часто используемым при выделении целой части. Итоговая запись должна содержать полученный многочлен от деления.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Приводится доказательство, что неправильную дробь, составленную из многочленов, можно представить в виде суммы многочлена и правильной дроби. Подробно разобраны примеры деления многочленов уголком и умножения столбиком.

Содержание

Теорема

Пусть P k (x) , Q n (x) — многочлены от переменной x степеней k и n , соответственно, причем k ≥ n . Тогда многочлен P k (x) можно представить единственным способом в следующем виде:
(1) P k (x) = S k-n (x) Q n (x) + U n-1 (x) ,
где S k-n (x) — многочлен степени k-n , U n-1 (x) — многочлен степени не выше n-1 , или нуль.

Доказательство

По определению многочлена:
;
;
;
,
где p i , q i — известные коэффициенты, s i , u i — неизвестные коэффициенты.

Введем обозначение:
.
Подставим в (1) :
;
(2) .
Первый член в правой части — это многочлен степени k . Сумма второго и третьего членов — это многочлен степени не выше k — 1 . Приравняем коэффициенты при x k :
p k = s k-n q n .
Отсюда s k-n = p k / q n .

Преобразуем уравнение (2) :
.
Введем обозначение: .
Поскольку s k-n = p k / q n , то коэффициент при x k равен нулю. Поэтому — это многочлен степени не выше k — 1 , . Тогда предыдущее уравнение можно переписать в виде:
(3) .

Это уравнение имеет тот же вид, что и уравнение (1) , только значение k стало на 1 меньше. Повторяя эту процедуру k-n раз, получаем уравнение:
,
из которого определяем коэффициенты многочлена U n-1 (x) .

Итак, мы определили все неизвестные коэффициенты s i , u l . Причем s k-n ≠ 0 . Лемма доказана.

Деление многочленов

Разделив обе части уравнения (1) на Q n (x) , получим:
(4) .
По аналогии с десятичными числами, S k-n (x) называется целой частью дроби или частным, U n-1 (x) — остатком от деления. Дробь многочленов, у которой степень многочлена в числителе меньше степени многочлена в знаменателе называется правильной дробью. Дробь многочленов, у которой степень многочлена в числителе больше или равна степени многочлена в знаменателе называется неправильной дробью.

Уравнение (4) показывает, что любую неправильную дробь многочленов можно упростить, представив ее в виде суммы целой части и правильной дроби.

По своей сути, целые десятичные числа являются многочленами, у которых переменная равна числу 10 . Например, возьмем число 265847. Его можно представить в виде:
.
То есть это многочлен пятой степени от 10 . Цифры 2, 6, 5, 8, 4, 7 являются коэффициентами разложения числа по степеням числа 10.

Поэтому к многочленам можно применить правило деления уголком (иногда его называют делением в столбик), применяемое к делению чисел. Единственное отличие заключается в том, что, при делении многочленов, не нужно переводить числа больше девяти в старшие разряды. Рассмотрим процесс деления многочленов уголком на конкретных примерах.

Пример деления многочленов уголком

Здесь в числителе стоит многочлен четвертой степени. В знаменателе — многочлен второй степени. Поскольку 4 ≥ 2 , то дробь неправильная. Выделим целую часть, разделив многочлены уголком (в столбик):

Приведем подробное описание процесса деления. Исходные многочлены записываем в левый и правый столбики. Под многочленом знаменателя, в правом столбике, проводим горизонтальную черту (уголок). Ниже этой черты, под уголком, будет целая часть дроби.

1.1 Находим первый член целой части (под уголком). Для этого разделим старший член числителя на старший член знаменателя: .

1.2 Умножаем 2 x 2 на x 2 — 3 x + 5 :
. Результат записываем в левый столбик:

1.3 Берем разность многочленов в левом столбике:

Итак, мы получили промежуточный результат:
.

Дробь в правой части неправильная, поскольку степень многочлена в числителе (3 ) больше или равна степени многочлена в знаменателе (2 ). Повторяем вычисления. Только теперь числитель дроби находится в последней строке левого столбика.
2.1 Разделим старший член числителя на старший член знаменателя: ;

2.2 Умножаем на знаменатель: ;

2.3 И вычитаем из последней строки левого столбика: ;

Промежуточный результат:
.

Снова повторяем вычисления, поскольку в правой части стоит неправильная дробь.
3.1 ;
3.2 ;
3.3 ;

Итак, мы получили:
.
Степень многочлена в числителе правой дроби меньше степени многочлена знаменателя, 1

;
2 x 2 — 4 x + 1 — это целая часть;
x — 8 — остаток от деления.

Пример 2

Выделить целую часть дроби и найти остаток от деления:
.

Выполняем те же действия, что и в предыдущем примере:

Здесь остаток от деления равен нулю:
.

Умножение многочленов столбиком

Также можно умножать многочлены столбиком, аналогично умножению целых чисел. Рассмотрим конкретные примеры.

Пример умножения многочленов столбиком

Найти произведение многочленов:
.

2.1
.

2.2
.

2.3
.
Результат записываем в столбик, выравнивая степени x .

3
;
;
;
.

Заметим, что можно было записывать только коэффициенты, а степени переменной x можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Пример 2

Найти произведение многочленов столбиком:
.

При умножении многочленов столбиком важно записывать одинаковые степени переменной x друг под другом. Если некоторые степени x пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы.

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль:
.
Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2 Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

2.3 Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

2.3 Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
.

Сегодня мы узнаем, как выполняется деление многочленов друг на друга, причем выполнять деление мы будем уголком по аналогии с обычными числами. Это очень полезный прием, который, к сожалению, не изучают в большинстве школ. Поэтому внимательно прослушайте данный видеоурок. {2}}$. В итоге мы видим, что мы получили очень «красивый» ответ. Записываем его.

Вот и весь алгоритм. Ключевых моментов здесь два:

Всегда сравнивайте первую степень делимого и делителя — повторяем это на каждом шаге;
Если в исходном выражении пропущены какие-либо степени, при делении уголком их обязательно следует добавить, но с нулевыми коэффициентами, иначе ответ будет неправильным.

Больше никаких премудростей и хитростей в таком делении нет.

Несколько лет назад с удивлением узнала, что сегодня в школах (даже во многих физ-мат школах), на кружках, да и в случаях “репетирования’’ не учат делить полиномы, или многочлены, в столбик. Самое забавное при этом, что схему Горнера школьники знают и используют для деления полиномов. Похоже, считается, что деление в столбик слишком сложно для неокрепшего разума, а вот выучить наизусть табличку, которая позволяет делить на многочлен первой степени, ему вполне по силам. Естественно, никто при этом не заботится о том, чтобы школьники поняли, почему так можно делить. Чтобы восполнить вопиющий пробел в образовании таких ребят, привожу здесь метод деления полинома на полином столбиком, который на самом деле довольно прост и позволяет делить на полиномы произвольной степени.

А теперь давайте рассмотрим примеры: на них учиться делить полиномы проще.

Сначала старший член делимого — это — поделим на старший член делителя, то есть на . Полученный результат, который равен , будет старшим членом частного. Теперь умножим делитель на этот многочлен (получим ) и вычтем полученный результат из делимого.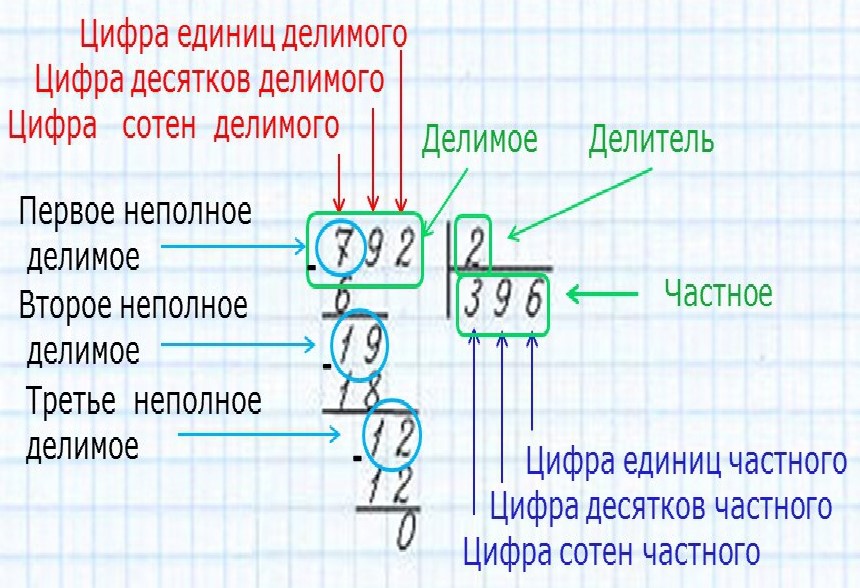 Получим остаток . Старший член этого остатка, который равен снова поделим на старший член делителя, который равен , получим , что и будет вторым членом частного. Делитель, умноженный на этот член, вычитаем из первого остатка. Получаем второй остаток, который равен нулю. На этом процесс деления заканчивается.

Легко проверить, что

Пример 2. Поделим на .

Проверка. Действительно, нетрудно убедиться в том, что

Пусть требуется

(2x 3 – 7x 2 + x + 1) ÷ (2x – 1).

Здесь дано произведение (2x 3 – 7x 2 + x + 1) и один множитель (2x – 1), – надо найти другой множитель. В данном примере сразу ясно (но вообще этого установить нельзя), что и другой, искомый, множитель, или частное, есть многочлен. Это ясно потому, что данное произведение имеет 4 члена, а данный множитель лишь 2. Однако, сказать заранее, сколько членов у искомого множителя – нельзя: может быть 2 члена, 3 члена и т. д. Вспоминая, что старший член произведения всегда получается от умножения старшего члена одного множителя на старший член другого (см. умножение многочлена на многочлен) и что членов, подобных этому, быть не может, мы уверены, что 2x 3 (старший член данного произведения) получится от умножения 2x (старший член данного множителя) на неизвестный старший член искомого множителя. Чтобы найти последний, придется, следовательно, разделить 2x 3 на 2x – получим x 2 . Это и есть старший член частного.

Вспомним затем, что при умножении многочлена на многочлен приходится каждый член одного многочлена умножать на каждый член другого. Поэтому данное произведение (2x 3 – 7x 2 + x + 1) представляет собою произведение делителя (2x – 1) на все члены частного. Но мы можем теперь найти произведение делителя на первый (старший) член частного, т. е. (2x – 1) ∙ x 2 ; получим 2x 3 – x 2 . Зная произведение делителя на все члены частного (оно = 2x 3 – 7x 2 + x + 1) и зная произведение делителя на 1-ый член частного (оно = 2x 3 – x 2), вычитанием мы можем найти произведение делителя на все остальные, кроме 1-го, члены частного. Получим

(2x 3 – 7x 2 + x + 1) – (2x 3 – x 2) = 2x 3 – 7x 2 + x + 1 – 2x 3 + x 2 = –6x 2 + x + 1.

Старший член (–6x 2) этого оставшегося произведения должен представлять собою произведение старшего члена делителя (2x) на старший член остального (кроме 1-го члена) частного. Отсюда найдем старший член остального частного. Надо –6x 2 ÷ 2x, получим –3x. Это и есть второй член искомого частного. Мы можем опять найти произведение делителя (2x – 1) на второй, только что найденный, член частного, т. е. на –3x.

Получим (2x – 1) ∙ (–3x) = –6x 2 + 3x. Из всего данного произведения мы уже вычли произведение делителя на 1-ый член частного и получили остаток –6x 2 + x + 1, представляющий собою произведение делителя на остальные, кроме 1-го, члены частного. Вычитая из него только что найденное произведение –6x 2 + 3x, получим остаток, представляющий собою произведение делителя на все остальные, кроме 1-го и 2-го, члены частного:

–6x 2 + x + 1 – (–6x 2 + 3x) = –6x 2 + x + 1 + 6x 2 – 3x = –2x + 1.

Разделив старший член этого оставшегося произведения (–2x) на старший член делителя (2x), получим старший член остального частного, или его третий член, (–2x) ÷ 2x = –1, – это и есть 3-й член частного.

Умножив на него делителя, получим

(2x – 1) ∙ (–1) = –2x + 1.

Вычтя это произведение делителя на 3-й член частного из всего оставшегося до сих пор произведения, т. е.

(–2x + 1) – (–2x + 1) = –2x + 1 + 2x – 1 = 0,

мы увидим, что в нашем примере произведение делится на остальные, кроме 1-го, 2-го и 3-го, члены частного = 0, откуда заключаем, что у частного больше членов нет, т. е.

(2x 3 – 7x 2 + x + 1) ÷ (2x – 1) = x 2 – 3x – 1.

Из предыдущего мы видим: 1) удобно располагать члены делимого и делителя по нисходящим степеням, 2) необходимо установить какой-либо порядок для выполнения вычислений. Таким удобным порядком можно считать тот, который употребляется в арифметике при делении многозначных чисел. Следуя ему, все предыдущие вычисления расположим так (сбоку даны еще краткие пояснения):

Те вычитания, какие здесь нужны, выполняются переменою знаков у членов вычитаемого, причем эти переменные знаки пишутся сверху.

Так, написано

Это значит: вычитаемое было 2x 3 – x 2 , а после перемены знаков получили –2x 3 + x 2 .

Благодаря принятому расположению вычислений, благодаря тому, что члены делимого и делителя расположены по нисходящим степеням и благодаря тому, что степени буквы x в обоих многочленах идут, понижаясь всякий раз на 1, оказалось, что подобные члены приходятся написанными друг под другом (напр.: –7x 2 и +x 2), почему легко выполнить их приведение. Можно подметить, что не все члены делимого нужны во всякий момент вычисления. Напр., член +1 не нужен в тот момент, где был найден 2-й член частного, и эту часть вычислений можно упростить.

Еще примеры:

1. (2a 4 – 3ab 3 – b 4 – 3a 2 b 2) ÷ (b 2 + a 2 + ab).

Расположим по нисходящим степеням буквы a и делимое и делитель:

(Заметим, что здесь, благодаря отсутствию в делимом члена с a 3 , в первом вычитании оказалось, что подписаны друг под другом не подобные члены –a 2 b 2 и –2a 3 b. Конечно, они не могут быть приведены в один член и написаны под чертою оба по старшинству).

В обоих примерах надо внимательнее относиться к подобным членам: 1) друг под другом часто оказываются написанными не подобные члены и 2) иногда (как, напр., в последнем примере, члены –4a n и –a n при первом вычитании) подобные члены выходят написанными не друг под другом.

Возможно выполнять деление многочленов в ином порядке, а именно: всякий раз разыскивать младший член или всего или остающегося частного. Удобно в этом случае располагать данные многочлены по восходящим степеням какой-либо буквы. Напр.:

Деление с остатком на 10, 100, 1000

Автор: edu1

Методическая копилка — Начальная школа

Тема: Деление с остатком на 10, 100, 1000.

Цели: ознакомление с делением на 10, 100 и 1000 с остатком.

Развивать творческое мышление, познавательную активность учащихся, стремление к достижению успеха в учебной деятельности ,совершенствовать вычислительные навыки, умение решать задачи;

Задачи:

Воспитывающая: воспитывать любовь к уроку математики, доброту.

Образовательная: учить выполнять деление с остатком на 10, 100, 1000;, умение решать задачи.

Развивающая: совершенствовать вычислительные навыки, развивать творческое мышление.

Планируемые результаты:

Личностные УУД: способствовать развитию интереса к математике, вычислительных навыков, формирование уважительного отношения к иному мнению, иной точки зрения.

Метапредметные результаты обучения:

Познавательные УУД: формирование умения самостоятельно формулировать проблему, ставить познавательные цели, самостоятельно создавать алгоритм для решения проблем творческого и поискового характера.

Регулятивные: формировать у обучающихся способность организовать свою учебную деятельность: целеполагание, планирование, контроль, коррекция и оценка своей деятельности, саморегуляция как способность к мобилизации сил и энергии, к волевому усилию и преодолению препятствий.

Коммуникативные: работать в парах, выполнять задания творческого и поискового характера, вступать в диалог с учителем, уметь высказываться.

Предметные результаты обучения:

Познавательные: научатся выполнять деление с остатком на 10, 100, 1000 и делать проверку; решать задачи изученных видов; выполнять преобразование единиц измерения, используя соотношения между ними; ориентироваться в материале учебника и находить по заданию учителя нужную информацию.

Оборудование: учебник 4 класс часть 2 М. И. Моро, мультимедийный проектор, презентация к уроку, карточки с заданиями, подарки-солнышки, рисунок яблони со съёмными яблоками, цветами и листьями, мяч.

Ход урока

I.Мотивация к уроку.

— Доброе утро, ребята! Меня зовут Людмила Михайловна. Сегодня я буду вести у вас урок.

Ребята моего класса из Пузачинской школы передали вам в подарок вот такое солнышко добра, чтобы вам на уроке было тепло и уютно. Положите его на ладошку. Оно согревает вас: ваши руки, тело и душу. Придаёт бодрость, заряжает энергией, будит воображение.

— Какое у вас настроение? Покажите жестами!!!

Вот с таким настроением мы и начнём урок.

II. Актуализация знаний

Устный счёт

1)Работаем в парах: в учебнике на с. 27 решим примеры, которые записаны на полях:

630: 70 *30- 89 + 29 : 3 + 30 = 100

2) №91

-Сколько раз по 100м содержится в 2 км? (20)

-Сколько раз по 15 с содержится в 1 мин? (4)

3) В бидоне было 36 л молока. Доярка наполнила 10 трёхлитровых банок. Сколько л молока осталось в бидоне? (36-3*10=6 (л))

4) В спортивную школу привезли 126 мячей. Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))

5)Презентация:

-Решите примеры:

800 : 2= 400

4 • 20=80

6 • 7=42

60 : 3= 20

30 • 2=60

-Вставьте числа в окошки: 3*8=(?)+27=(?)-39=(?):2=(?)*8=(?)-40=(?)*8

-Вычисли:

50:10 500:10 5000:10

600:100 6000:100 60000:100

7000:1000 70000:1000 700000:1000

III.Создание проблемной ситуации. Постановка проблемы.

-Посмотрите на примеры, записанные на доске:

68:10 400:100 3456:1000

340:10 827:100 7000:1000

На какие две группы их можно разделить? (Примеры на деление без остатка и примеры на деление с остатком)

-Запишите примеры в два столбика:

400:100 68:10

340:10 827:100

7000:1000 3456:1000

Примеры какого столбика мы умеем решать?

Найдите значения выражения первого столбика: (4, 34, 7)

Посмотрите на второй столбик.

Как вы думаете, какую проблему нам нужно решить на уроке, чему научиться? (Деление с остатком на 10,100,1000).

— Прочитайте тему урока в учебнике на стр. 27)

-Поставьте задачи, чему мы будем учиться с вами на уроке?

V. Построение проекта выхода из затруднения. Реализация построенного проекта.

1) Вспомните, как мы делим на 10, 100 и 1000.

(Чтобы число разделить на 10, достаточно убрать один нуль. Чтобы число разделить на 100, надо убрать два нуля и на 1000 надо убрать три нуля).

— Откройте тетради, запишите сегодняшнее число.

— Найдем значение выражений второго столбика. Никто не спешит, следите за мной.

— А сейчас рассмотрим второй столбик.

-Кто может предложить способ деления 68:10?

-Можем ли 68:10 без остатка?

— Какое число можем разделить на 10 без остатка? (60:10=6)

Правильно, возьмем наибольшее число до 68, которое делится на 10, — это 60. Разделим 60 на 10, что получим? (получим 6). .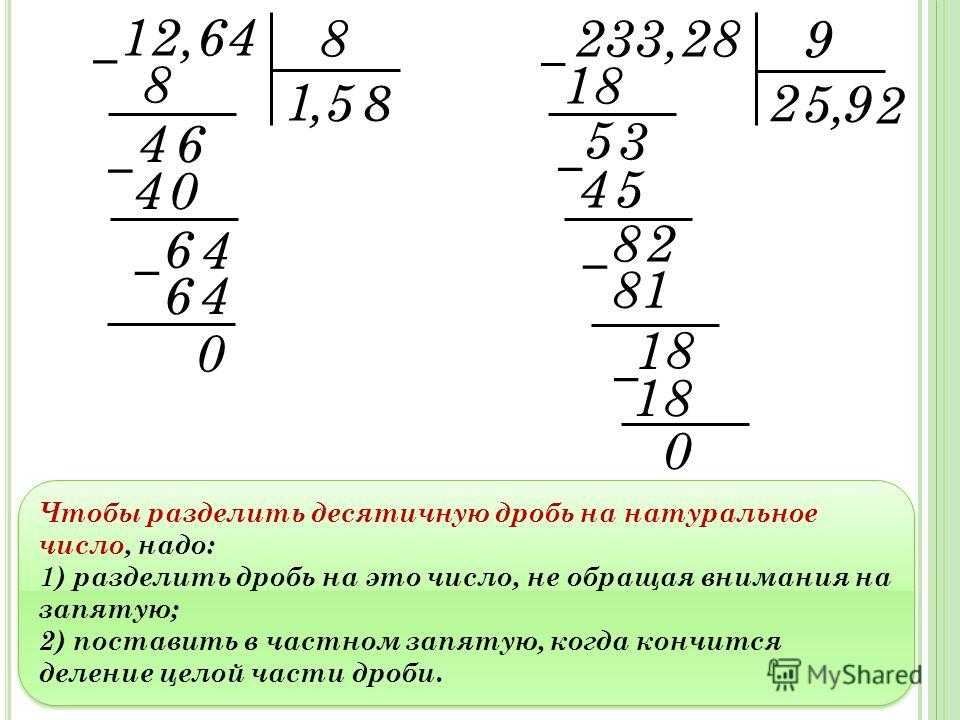

— Сколько останется в остатке?(68 – 60 = 8). Записываем это так 6 (ост. 8).

— Составим алгоритм деления с остатком на 10,100,1000:

1.Найдём наибольшее число, которое делится на 10,100,1000.

2.Разделим это число.

3. Найдём остаток (от делимого отнимем наибольшее число).

Мы вывели алгоритм деления с остатком на 10,100,1000. Давайте сверимся с научным источником – учебником с.27

VI.Первичное закрепление с проговариванием.

-Решите второй пример с объяснением.(827:100=8) остаток 27.

— Выйдите к доске и решите 3 пример с объяснением. (3456 : 1000 = 3) ост 456

— Далее мы выполним задание 96. Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96)

69 : 10 = 6 (ост 9) 238 : 10 = 23 (ост 8) 691 : 100 = 6 (ост 91)

78 : 10 = 7 (ост 8) 238 : 100 = 2 (ост 38) 691 : 10 = 69 (ост 1)

7825 : 100 = 78 (ост 25) 7825 : 1000 = 7 (ост 825)

— Какой вывод по этому заданию вы можете сделать? ( При делении на 10, в остатке будет одна цифра, а в частном будет число, записанное остальными цифрами делимого; при делении на 100 в остатке будет число, записанное двумя последними цифрами делимого, а в частном число, записанное остальными цифрами делимого. )

Для того чтобы этот вывод был усвоен сознательно, важно объяснить, почему это так: на 10 можно разделить все содержащиеся в числе десятки, а единицы остаются; аналогично для 100 и 1000.

— Есть еще 1 способ деления: нужно закрыть в числе столько цифр, сколько нулей в делителе. Получим целое число, а то, что закрыли – остаток

VII. Физкультминутка (под музыку повторяем движения животных)

VIII. Самостоятельная работа в группах с самопроверкой по эталону.

-Работа по карточкам:

327:10 1684:100

358:10 1605:1000

615:100 1730:100

IX. Повторение материала.

Решение задачи изученного вида:

№89 стр.27

-Прочитайте задачу.

-Можем ли мы сразу ответить на вопрос задачи? (Нет, нам неизвестна скорость машины.)

-Как можно найти скорость? (Расстояние разделим на время.)

-Что вы заметили? (6 нельзя разделить на 5. )

— А кто догадался, что нужно сделать? (6км перевести в метры: 6км=6000м.)

-Как изменятся теперь единицы скорости? (Скорость будет измеряться в метрах в минуту.)

-Как мы узнаем расстояние, пройденное за 40 мин?

-Что нужно сделать, прежде чем узнать, сколько пройдёт машина с такой же скоростью за 1 ч? (Надо 1ч перевести в минуты.)

-Запишите решение задачи выражениями.

6000:5=1200(м/мин)

1200*40=48000(м)

1200*60=72000(м)

Ответ: 48000м,72000м

№92 стр.27

-Прочитайте задание.

-Составьте первое уравнение.(х-20=40*6)

-Как его можно упростить? (Можно найти произведение чисел: 40*6=240)

-Что неизвестно в уравнении? (Уменьшаемое)

-Вспомните, как найти уменьшаемое. (К разности прибавить вычитаемое.)

-Запишите решение.

х-20=240

х=240+20

х=260

260-20=240

-Второе уравнение решается самостоятельно в парах.

15+х=800:20

15+х=40

х=40-15

х=25

15+25=40

XII. Рефлексия

Игра в мяч:

Бросаю мяч и называю выражение, дети ловят и называют ответ:

152:10, 375:100, 54:10,786:100, 2546:1000, 3452:100, 79:10, 897:100, 2457:1000,385:10, 893:10, 715:100, 2413:1000, 81:10, 95:10

— Урок у нас заканчивается. За это время выросло удивительное дерево, благодаря которому каждый из вас оценить себя.

-Если урок для вас прошел плодотворно, и вы справлялись с заданиями без ошибок — сорвите с дерева плоды – яблоки.

-Если вы допускаете ещё незначительные ошибки – сорвите цветы.

-Если на уроке вы не усвоили новый материал, вам ещё многое непонятно – зеленые листочки.

XIII. Подведение итогов урока

-Как разделить число на 10, 100, 1000?

-Как выполнить деление с остатком?

-Как можно проверить вычисления?

-Что является продуктом нашей работы?

— Повторение алгоритма деления с остатком на 10, 100, 1000.

Домашнее задание: переверните другой стороной ваши яблоки, листочки, цветы. Для вас индивидуальные домашние задания:

На яблоках-№94 с.27;

На цветах – 15928:100 15862:10 34518:100 135628:10 36704:10 52080:100;

На листочках — №93 с.27

-Объяснение заданий.

-Оценки за урок.

Технологическая карта

Этапы урока

Обучающие и развивающие компоненты задания

Деятельность учителя

Деятельность учащихся

Формы организации взаимодействия на уроке

Формируемые умения (универсальные учебные действия)

Мотивация к уроку.

Актуализация знаний.

Создание проблемной ситуации. Постановка проблемы.

Построение проекта выхода из затруднения. Реализация построенного проекта.

Первичное закрепление с проговариванием.

Физкультминутка

Самостоятельная работа в группах с самопроверкой по эталону.

Повторение материала.

Рефлексия

Подведение итогов урока

Домашнее задание

Эмоциональная, психологическая и мотивационная подготовка учащихся к усвоению изучаемого материала.

Устный счёт

1)Работаем в парах: в учебнике на с. 27 решим примеры на полях:

630: 70 *30- 89 + 29 : 3 + 30 = 100

2) №91

-Сколько раз по 100м содержится в 2 км? (20)

-Сколько раз по 15 с содержится в 1 мин? (4)

5)Презентация:

-Решите примеры:

800 : 2= 400

4 • 20=80

6 • 7=42

60 : 3= 20

30 • 2=60

-Вставьте числа в окошки: 3*8=(?)+27=(?)-39=(?):2=(?)*8=(?)-40=(?)*8

-Вычисли:

50:10 500:10 5000:10

600:100 6000:100 60000:100

7000:1000 70000:1000 700000:1000

68:10 400:100 3456:1000

340:10 827:100 7000:1000

Вспомните, как мы делим на 10, 100 и 1000.

— Откройте тетради, запишите сегодняшнее число.

— Найдем значение выражений второго столбика. Никто не спешит, следите за мной.

— А сейчас рассмотрим второй столбик.

-Кто может предложить способ деления 68:10?

-Можем ли 68:10 без остатка?

— Какое число можем разделить на 10 без остатка? (60:10=6)

— Сколько останется в остатке?(68 – 60 = 8). Записываем это так 6 (ост. 8).

— Составим алгоритм деления с остатком на 10,100,1000:

1.Найдём наибольшее число, которое делится на 10,100,1000.

2.Разделим это число.

3. Найдём остаток (от делимого отнимем наибольшее число).

Мы вывели алгоритм деления с остатком на 10,100,1000. Давайте сверимся с научным источником – учебником с.27

Решите второй пример с объяснением.(827:100=8) остаток 27.

— Выйдите к доске и решите 3 пример с объяснением. (3456 : 1000 = 3) ост 456

69 : 10 = 6 (ост 9) 238 : 10 = 23 (ост 8) 691 : 100 = 6 (ост 91)

78 : 10 = 7 (ост 8) 238 : 100 = 2 (ост 38) 691 : 10 = 69 (ост 1)

7825 : 100 = 78 (ост 25) 7825 : 1000 = 7 (ост 825)

под музыку повторяем движения животных

Работа по карточкам:

327:10 1684:100

358:10 1605:1000

615:100 1730:100

Решение задачи изученного вида:

№89 стр.27

№92 стр.27-составление и решение уравнения.

Игра в мяч.

Яблоня успеха.

Как разделить число на 10, 100, 1000?

-Как выполнить деление с остатком?

-Как можно проверить вычисления?

Индивидуальное домашнее задание для каждого ученика на сорванных яблоках: -№94 с. 27;

На цветах – 15928:100 15862:10 34518:100 135628:10 36704:10 52080:100;

На листочках — №93 с.27

— Доброе утро, ребята!

— Какое у вас настроение? Покажите жестами!!!

энергией, будит воображение. Вот с таким настроением мы и начнём урок

Совершенствует вычислительные навыки обучающихся, умение решать задачи

Демонстрирует разные виды заданий.

На какие две группы их можно разделить? (Примеры на деление без остатка и примеры на деление с остатком)

-Запишите примеры в два столбика:

400:100 68:10

340:10 827:100

7000:1000 3456:1000

Примеры какого столбика мы умеем решать?

Найдите значения выражения первого столбика: (4, 34, 7)

Как вы думаете, какую проблему нам нужно решить на уроке, чему научиться? (Деление с остатком на 10,100,1000).

— Прочитайте тему урока в учебнике на стр. 27)

Повторяют правило деления на 10, 100, 1000.

Решают с проговариванием

Выполняют упражнения

Работают в парах

Читают задачу, анализируют под руководством учителя, решают, самостоятельно записывают решение.

Анализируют содержание и составляют задачу.

Бросает мяч и называет выражение, которое надо решить.

Проверяет уровень усвоения материала.

Оценивает уровень обученности

Подводит итог урока.

Объясняет выполнение домашнего задания

Слушают учителя, повторяют за ним движения. Демонстрируют готовность к уроку.

Работают в парах

Повторяют единицы длины, времени.

Решают устно задачи.

Повторяют умножение и деление на 10,100,1000

Замечают проблему.

Такие выражения ещё решать не умеют.

Определяют тему и цели урока.

Контролирует правильность ответов.

Направляет на исследование выражения.

Контролирует правильность решения и объяснения.

Вместе с детьми выполняет упражнения.

Контролирует деятельность обучающихся в парах.

Проверка по эталону в призентации.

Задаёт вопросы для анализа: Можем ли мы сразу ответить на вопрос задачи? (Нет, нам неизвестна скорость машины.)

-Как можно найти скорость? (Расстояние разделим на время.)

-Что вы заметили? (6 нельзя разделить на 5.)

— А кто догадался, что нужно сделать? (6км перевести в метры: 6км=6000м.)

-Как изменятся теперь единицы скорости? (Скорость будет измеряться в метрах в минуту.)

-Как мы узнаем расстояние, пройденное за 40 мин?

-Запишите решение задачи выражениями.

6000:5=1200(м/мин)

1200*40=48000(м)

1200*60=72000(м)

Ответ: 48000м,72000м

Прочитайте задание.

-Составьте первое уравнение. (х-20=40*6)

-Как его можно упростить? (Можно найти произведение чисел: 40*6=240)

-Что неизвестно в уравнении? (Уменьшаемое)

-Вспомните, как найти уменьшаемое. (К разности прибавить вычитаемое.)

-Запишите решение.

х-20=240

х=240+20

х=260

260-20=240

-Второе уравнение решается самостоятельно в парах.

15+х=800:20

15+х=40

х=40-15

х=25

15+25=40

Ловят мяч и называют ответ выражения

Выбирают яблоко, если усвоили новый материал на отлично, не возникало затруднений на уроке;

Цветы, если возникают

затруднения при решении;

листья, если материал плохо усвоен.

Обобщают новые знания.

Слушают пояснения и задают вопросы.

Фронтальная, индивидуальная.

Фронтальная, индивидуальная

Фронтальная, индивидуаль-ная

Фронтальная, индивидуаль-ная.

Фронтальная.

Фронтальная, индивидуаль-ная

. Фронтальная.

Фронтальная, индивидуаль-ная

К.-планирует учебное сотрудничество с учителем и сверстниками.

Л.— имеют желание учиться, проявляют интерес к изучаемому предмету, понимают его важность.

П. – осмысленно читают тексты математического содержания в соответствии с поставленными целями и задачами; проводят несложные обобщения и используют математические знания в расширенной области применения; используют математические термины, символы и знаки.

Р.— понимают, принимают и сохраняют различные учебные задачи; осуществляют поиск средств для достижения учебной задачи.

К. – умеют слушать друг друга, строить понятные для партнёра по коммуникации речевые высказывания; могут работать в коллективе, уважают мнения других участников образовательного процесса.

Л. – способны адекватно рассуждать о причинах своего успеха или неуспеха, связывая успехи с усилиями, трудолюбием; проявляют познавательный интерес к изучению предмета.

Р. – принимают и сохраняют учебную задачу.

К. – проявляют готовность слушать.

П. — учатся выполнять деление с остатком на 10, 100, 1000 ;

Р. — контроль, коррекция и оценка своей деятельности.

Л. — способствовать развитию интереса к математике.

Л. – имеют установку на здоровый образ жизни.

К. – умение работать в парах, сотрудничать, выслушивать мнение собеседника, уметь высказываться.

П. – проводят анализ, синтез, сравнение, обобщение, аналогию;осознанно и произвольно строят речевые высказывания; осуществляют построение логической цепи рассуждений, доказательство.

Р. – осуществляют волевую саморегуляцию в ситуации затруднения.

К. – понимают различные позиции в подходе к решению задачи, задают вопросы для уточнения. Чётко и аргументированно высказывают свои оценки и предложения.

Л. – осуществление смыслообразова-ния; проявляют познавательный интерес к предмету.

Р.- контроль и оценка собственной деятельности.

П. – ориентируются в своей системе знаний – отличают новое от уже известного.

Л. – проявляют интерес к предмету.

П. –ориентируются в своей системе знаний – отличают новое от уже известного.

Р. – оценивают собственную деятельность на уроке.

Л. – проявляют интерес к предмету.

Р.- принимают и сохраняют учебную задачу, осуществляют поиск средств для её выполнения.

Решено: Разделить один столбец на другой

core.noscript.текст

6 ОТВЕТОВ 6

Этикетки

ААХ 1
Добро пожаловать 2
Академия 21
АДАПТ 87
Добавить столбец 1
Добавить новый столбец 1
Настройки администратора 1
Администрация 34
Adobe 163
Расширенная аналитика 1
Появление кода 5
Псевдоним Менеджер 96
Альтерикс 1
Альтерикс 2020.1 4
Академия Альтерикс 3
Альтерикс Аналитика 1
Центр аналитики Alteryx 2
Введение в сообщество Alteryx — студент MSA в CSUF 1
Альтерикс Коннект 1
Альтерикс Дизайнер 79
Альтерикс Двигатель 1
Галерея Альтерикс 1
Концентратор Alteryx 1
альтерикс с открытым исходным кодом 1
Alteryx Post ответ 1
Альтерикс Практика 129
Alteryx SDK API 1
Команда Альтерикс 1
Инструменты Alteryx 1
АльтериксФорГуд 1
Амазонка с3 183
Двигатель AMP 96
АНАЛИТИКА ИННОВАЦИЙ 1
Поддержка аналитических приложений 1
Аналитические приложения 18
Аналитические приложения ACT 1
Аналитика 2
Анализатор 19
Объявление 4
API 1205
Приложение 2
Добавить поля 1
Приложения 1386
Процесс архивирования 1
АРИМА 1
Присвоение метаданных CSV 1
Аутентификация 4
Автоматическое обновление 1
Банковское дело 1
Кодировка Base64 1
Базовая отчетность по таблицам 1
Пакетный макрос 1290
Новичок 1
Анализ поведения 237
Передовой опыт 2557
BI + аналитика + наука о данных 1
Книжный червь 2
Ошибка 631
Ошибки и проблемы 1
Расчет рабочих дней 1
Калгари 90
КАСС 70
Кошка Человек 1
Категория Приложения 1
Категория Соединители 1
Категория Документация 1
Категория Вход Выход 2
Категория Прогноз 1
Категория Пространственная 1
Категория Временной ряд 3
Категория Трансформация 1
Сертификация 4
Связанное приложение 252
Вызов 17
Диаграмма 1
Клиенты 5
Кластеризация 1
Общие случаи использования 3446
Связь 1
Сообщество 263
Объединить 1
Условный столбец 1
Условный оператор 1
СОЕДИНИТЕ И РЕШИТЕ 1
Соединители 1292
Содержит 1
Содержание 1
Управление контентом 8
Конкурс 6
Начало разговора 22
копия 1
COVID-19 4
Создайте новую электронную таблицу, используя существующий набор данных . 1
Управление учетными данными 3
Любопытный*Маленький 1
Функция пользовательской формулы 1
Пользовательские инструменты 1400
Создание приборной панели 1
Анализ данных 1
Анализ данных 2
Аналитика данных 1
Вызов данных 103
Очистка данных 5
Соединение данных 1
Исследование данных 2684
Загрузка данных 1
Наука о данных 31
Подключение к базе данных 2356
Подключения к базе данных 6
Наборы данных 4079
Дата 2
Дата и время 3
формат даты 1
Выбор даты 2
Дата Время 2708
Формат даты 1
даты 1
дата и время разбор 2
Дефект 10
Демографический анализ 197
Конструктор 1
Дизайнерское облако 122
Интеграция дизайнера 109
Разработчик 3154
Инструменты разработчика 2661
Обсуждение 2
Документация 471
Человек-собака 3
Скачать 1087
Дублирует строки 1
Дублирование строк 1
Динамический 1
Динамический ввод 1
Динамическое имя 1
Динамическая обработка 2645
динамическая замена 1
динамически создавать таблицы для входных файлов 1
Электронная почта 717
Уведомление по электронной почте 1
Инструмент электронной почты 2
Вставить 1
встроенный 1
Двигатель 88
Улучшение 4
Улучшения 2
Сообщение об ошибке 2260
Сообщения об ошибках 6
ЭТС 1
События 205
Эксель 1
Excel динамически объединять 1
Макрос Excel 1
Пользователи Excel 1
Исследователь 5
Выражение 1608
извлечь данные 1
Запрос функции 4
Фильтр 1
фильтр присоединиться 1
Финансовые услуги 1
гурман 4
Формула 2
формула или фильтр 1
Инструмент Формула 4
Формулы 2
Веселье 5
Нечеткое совпадение 710
Нечеткое соответствие 1
Галерея 573
Общий 176
Общее предложение 4
Генерация строковых и многострочных формул 1
Создать строки 1
Начало работы 1
Google Аналитика 182
группировка 1
Рекомендации 16
Всем привет ! 2
Справка 3654
Как раскрасить поля в строке на основе значения в другом столбце 1
Как сделать 1
Хаб 20. 4 2
Я новичок в Альтерикс. 1
идентификатор 1
В базе данных 1122
В базе данных 1
Введите 3999
Входные данные 2
Вход Выход 3
Вставка новых строк 1
Установить 4
Установка 408
Интерфейс 3
Инструменты интерфейса 1672
Введение 7
Итеративный макрос 982
Соединитель Jira 1
Присоединяйтесь к 1774
база знаний 1
Лицензии 1
Лицензирование 246
Список бегунов 1
Погрузчики 20
Загрузчики SDK 3
Оптимизатор местоположения 79
Поиск 1
Машинное обучение 171
Макрос 2
Макросы 2768
Картирование 1
Маркето 25
соответствие 1
Слияние 1
МонгоДБ 83
Создание нескольких переменных 1
MultiRowFormula 1
Нужна помощь 1
нужна помощь: как найти определенную строку во всех столбцах excel и вернуть этот clmn 1
Нужна помощь по Formula Tool 1
сеть 1
Эквивалент функции NetworkDays 1
Новый инструмент 1
Новости 1
Не твое дело 1
Не по теме 15
Управление финансов 1
Нефть и газ 1
Оптимизация 700
Любитель активного отдыха 1
Выход 4634
Выходные данные 1
пакет 1
Разобрать 2023
Сопоставление с образцом 1
Люди Человек 5
процентили 1
PowerBI 195
практические упражнения 1
Предиктивный 2
Прогнозный анализ 1263
Прогнозная аналитика 1
Препарат 5012
Предписывающая аналитика 235
Опубликовать 280
Питон 652
Qlik 57
квартили 1
Вопрос 15
Вопросы 2
Квадратные значения R 1
Инструмент R 681
RE GEX конвертировать 1
обновить проблему 1
Регулярное выражение 1,910
Удалить столбец 1
Отчет 2056
Ресурс 16
RestAPI 1
Управление ролями 3
Выполнить команду 564
Запуск рабочих процессов 12
Время выполнения 1
Продажи 301
Расписание 1
Расписание рабочих процессов 3
Планировщик 448
Ученый 3
Поиск 3
Поиск отзывов 16
Сервер 464
Настройки 914
Установка и конфигурация 93
SFTP 1
Sharepoint 440
Делюсь 2
Смартлист 1
Снежинка 1
Пространственный 1
Пространственный анализ 786
Студент 9
Проблема со стилем 1
Итого 1
Системное администрирование 2
Таблица 549
Столы 1
Технология 1
Интеллектуальный анализ текста 299
Миниатюра 1
Четверг Мысль 11
Временной ряд 443
Прогнозирование временных рядов 1
Советы и рекомендации 3806
Улучшение инструмента 9
Инструменты 1
Интересующая тема 44
Трансформация 2958
Транспонировать 1
Твиттер 50
Удасити 139
Уникальный 2
Не уверен на подходе 1
Обновления 3
Обновления 1
URL-адрес 1
Варианты использования 1
Дизайн взаимодействия с пользователем 2
Пользовательский интерфейс 47
Управление пользователями 5
Видео 2
ВидеоID 1
ВПР 1
Еженедельное испытание 1
Распределение Вейбулла Weibull. Dist 1
Количество слов 1
Рабочий процесс 7521
Рабочие процессы 1
Годфрак 1
Ютуб 1
YTD и QTD 1

« Предыдущий
Следующий »

Двухкратное деление мощности + 9 примеров

В этом учебном пособии по Power Bi мы обсудим различные примеры двухмерного деления мощности . А также мы обсудим следующие пункты:

Двойная мера мощности разделить один столбец на другой
Двойная мера мощности разделить два столбца
Двойная мера мощности разделить с фильтром
Двойная мера мощности разделить на ноль
Мера двойная мощность разделить на ноль по сумме
Показатель мощности bi разделить на строку за строкой
Показатель мощности bi разделить на два столбца из другой таблицы
Показатель мощности bi разделить столбец на число
Вычислить строку в столбце, деленную на сумму этого столбца

Таблица Содержание

Степень bi мера деления

В Power bi, чтобы разделить числитель на знаменатель, мы можем использовать функцию DIvide и оператор /

Если вы используете функцию деления, то вы должны передать числитель и знаменатель.

Синтаксис для функции деления:

 Разделить(<числитель>,<знаменатель>, <альтернативный результат>

Чтение функций связи Power Bi

Мера Power bi разделить один столбец на другой

Здесь мы увидим, как делить

Мы воспользуемся приведенной ниже таблицей, чтобы найти рейтинг кликов (CTR) по формуле Клики/Показы.

Разделим один столбец на другой.0003 Сначала мы рассчитаем сумму кликов и сумму показов, а затем рассчитаем сумму кликов/сумму показов, используя меру Power BI.

Загрузите данные, используя get data в power bi dektop.
Нажмите на новую меру на ленте, чтобы рассчитать сумму кликов.
Затем запишите следующую меру:

 Всего кликов = СУММА('Таблица'[Клик])

Далее мы найдем сумму показов, так что нажмите на новая мера .
Затем напишите следующую меру:

 Общее количество показов = СУММА('Таблица'[Показ])

Теперь мы рассчитаем рейтинг кликов (CTR), нажмите на новую меру.
Затем запишите приведенный ниже показатель:

 CTR = DIVIDE([Общее количество кликов],[Общее количество показов])

Теперь щелкните показатель, чтобы изменить десятичный формат на процентный.
Затем откроется лента инструмента измерения , в 9Раздел формата 0978 измените формат на процентов .

двойная мера мощности разделить один столбец на другой

Теперь, чтобы проверить меру, выберите визуализацию карты на панели визуализации.
В полях перетащите показатель CTR с панели полей.

двойная мера мощности разделить один столбец на другой

Прочитать инструкцию переключателя двойного измерения мощности с примерами.

Мы будем использовать примерную таблицу ниже, чтобы найти процент незавершенных задач.

power bi мера разделить два столбца

Сначала мы рассчитаем общее количество задач и общее количество выполненных задач, а затем обнаружим, что задача не выполнена. И, наконец, мы найдем процент невыполненных задач, разделив невыполненные задачи на общее количество задач.

Загрузите данные с помощью команды get data.
Нажмите на новую меру на ленте, чтобы вычислить сумму задачи.
Затем запишите следующую меру:

 Всего задач = СУММ(Таблица задач[Задачи])

Теперь мы рассчитаем сумму выполненных задач, щелкните новую меру на ленте.
Затем запишите следующую меру:

 TotalTaskCompleted = SUM(TaskTable[Completed])

Теперь мы обнаружим, что задача не выполнена, поэтому щелкните новую меру на ленте.
Затем запишите следующую меру:

 Не выполнено = [Всего задач] -[ВсегоЗаданийВыполнено]

Наконец-то мы найдем процент невыполненных задач, поэтому нажмите на новую меру на ленте.
Затем запишите новую меру:

 Процент невыполненных работ = РАЗДЕЛИТЬ([Не выполнено],[Всего задач],0)

Теперь, чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
В поле значения перетащите столбец имени задачи, Задачи, показатель выполненной задачи, показатель незавершенной задачи и процент невыполненной задачи.

двойная мера мощности разделить два столбца

Функция чтения счетчика в измерении Power BI

мера двойной мощности разделить с фильтром

Здесь мы увидим, как разделить два столбца и отфильтровать контекст, используя функцию деления и функцию фильтра в измерении.

Мы будем использовать приведенную ниже примерную таблицу для расчета процента совпадений без типа хранилища SIS.

power bi мера деления с фильтром

Сначала мы рассчитаем общий трафик и общую транзакцию продаж. Затем мы найдем процент попаданий, используя функцию деления, и, наконец, мы найдем процент попаданий, отфильтровав тип магазина.

Загрузите данные, используя get data в Power Bi Desktop.
Теперь мы создадим показатель, который будет рассчитывать общий трафик, поэтому щелкните новый показатель на ленте.
Затем запишите следующую меру:

 TotalTraffic = Sum(Sales[Traffic])

Мы найдем общую транзакцию, поэтому щелкните новую меру на ленте.
Затем запишите следующую меру:

 Общий трафик = Сумма (Продажи [Трафик])

Мы найдем частоту попаданий, поэтому для этого нажмите на новую меру.
Затем напишите приведенную ниже меру мощности bi:

 Показатель попаданий = РАЗДЕЛИТЬ ([Общее количество транзакций продаж], [Общий трафик], 0)

Из показателя обращений мы отфильтруем тип магазина SIS, затем мы покажем процент попаданий, поэтому для этого нажмите на новую меру .
Затем напишите следующую меру:

 HitRateFilter =
    ВЫЧИСЛИТЬ([Показатель попаданий],
        ФИЛЬТР(Продажи, Продажи[Тип магазина] <> "SIS")
    )

Щелкните меру фильтра Hit rate на панели полей, инструменты измерения откроются на ленте.
В разделе форматирования измените формат с общего на в процентах .

Теперь, чтобы проверить меру, щелкните визуализацию таблицы на панели визуализации в Power Bi.
В поле значений перетащите краткий столбец месяца, столбец типа магазина, столбец трафика, показатель количества попаданий и показатель фильтра числа попаданий

деление двойного показателя мощности с фильтром

Читать Как создать показатель на основе слайсера в Power BI

Разделение двойного показателя мощности на ноль

Здесь мы увидим, как обрабатывать ошибку деления на ноль с помощью функции деления в показателе .

Мы будем использовать приведенный ниже образец таблицы, где col1 будет числителем, а col2 — знаменателем. И в этих столбцах часть значения либо нулевая, либо нулевая.

деление по степени деления на ноль

Используя стандартное деление, мы увидим, какую ошибку мы получим, а затем воспользуемся функцией деления, чтобы решить эту ошибку.

Загрузите данные с помощью команды get data.
Нажмите на новую меру на ленте.
Затем напишите следующую меру:

 StandardDivision = СУММ(Таблица2[Столбец1])/СУММ(Таблица2[Столбец2])

Щелкните меру в области поля, затем в инструментах измерения измените формат меры в процент.

Теперь на снимке экрана ниже вы можете видеть, что когда числитель равен нулю, он показывает 0%.

Но когда знаменатель равен нулю или пуст, он показывает бесконечность, а когда числитель пуст, результат отображается как пустой.

мощность bi мера деление на ноль

Теперь мы воспользуемся функцией деления для решения этой ошибки, вместо бесконечности она покажет 0%.
Нажмите на новую меру на ленте.
Затем запишите приведенную ниже меру:

 Мера = ДЕЛИТЬ (СУММ (Таблица 2 [Столбец 1]), СУММ (Таблица 2 [Столбец 2]), 0)

На приведенном ниже снимке экрана вы можете видеть, что вместо бесконечности мы получаем 0 в качестве вывода, но в последней строке мы все еще получаем пустое значение, где числитель пуст.

деление меры мощности на ноль

Мы можем решить эту проблему, изменив указанную выше меру с помощью функций switch() и IsBlank().

Нажмите на эту меру, чтобы открыть ее.
Затем перепишите указанную выше меру:

 Мера = ПЕРЕКЛЮЧЕНИЕ(ИСТИНА(),ПУСТО(ДЕЛИТЬ(СУММ(Таблица2[Столбец1]), СУММ(Таблица2[Столбец2]),0)),0,ДЕЛИТЬ(СУММ(Таблица2 [Столбец1]), СУММ(Таблица2[Столбец2]),0))

Теперь на снимке экрана ниже видно, что ошибки нет и результат равен нулю.

двойная мера мощности разделить на ноль

Чтение показателя Power BI SUM

Разделение показателя Power bi на общую сумму

Здесь мы увидим, как рассчитать общий процент в процентах с помощью функции Division() в мере.

Мы будем использовать данные финансовой выборки для расчета общего процента продаж на основе продукта. Вы можете скачать образцы данных отсюда.

загрузить данные с помощью get data.
Нажмите на новую меру на ленте, чтобы рассчитать общий процент продаж.
Затем запишите следующую меру:

 % от общей суммы =
РАЗДЕЛЯТЬ (
    СУММА (финансы[Продажи]),
    ВЫЧИСЛИТЬ (СУММ('финансовые показатели'[Продажи]), ВСЕ('финансовые показатели'[Продукт]))
)

Теперь, чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
В поле значений перетащите столбец продукта, столбец продаж и показатель % от общего итога из области поля.

двойное измерение мощности разделить на общую сумму

Чтение двойного измерения мощности по категории

Мера двойного деления деление по строке за строкой

Здесь мы увидим, как разделить строку за строкой, а затем суммируем все строки деления с помощью меры.

Мы будем использовать приведенный ниже образец таблицы, чтобы разделить строку за строкой, а затем просуммируем все деления, используя функцию sumx.

мощность би мера разделить по строке за строкой

Например, сначала мы разделим по строкам общее количество задач и общее количество выполненных задач: 10/5 = 2,0; 11/3 = 3,67, 14/6 = 2,33, 25/25 = 1, 12/9 = 1,33, 18/9 = 2,0, 20/15 = 1,33

Затем просуммируем все деления:

2,0+3,63+2,33+1,0+1,33+2,0+1,33= 13,67

Загрузите данные с помощью команды получения данных
Щелкните Новая мера на ленте.
Затем запишите приведенную ниже меру

 Мера 2 = СУММ(TaskTable, [Всего задач]/[TotalTaskCompleted])

Теперь, чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
Затем в поле значения перетащите столбец имени задачи, столбец завершено, столбец задач и показатель Measure2 из области полей.

двойная мера мощности разделить на строку за строкой

Чтение двойная мера мощности вычесть

двойная мера мощности разделить два столбца из другой таблицы

Здесь мы увидим, как использовать двойную меру мощности разделить два столбца из другой таблицы.

Здесь у нас есть две таблицы, каждая из которых имеет один общий столбец, т.е. общий цвет.

Таблица 1

двойная мера мощности разделить два столбца из другой таблицы

Таблица 2

мера двойной мощности разделить два столбца из другой таблицы

Сначала просуммируем размер в таблице 1 по цветам, затем разделим на количество сотрудников. Например, сумма размера синего цвета равна 246, а затем делится на 6, что равно 246/6=41

. Загрузите данные, используя get data.
Нажмите на новую меру на ленте.
Затем запишите следующую меру:

 Результат =
var sumbycolor = ВЫЧИСЛИТЬ(СУММ('Таблица 3'[Размер]),ALLEXCEPT('Таблица 3','Таблица 3'[Цвет]))
var staffno = ВЫЧИСЛИТЬ(СУММ('Таблица 4'[Персонал]),ФИЛЬТР('Таблица 3','Таблица 3'[Цвет]=СВЯЗАННЫЕ('Таблица 4'[Цвет])))
Возврат DIVIDE(sumbycolor,staffno)

Теперь, чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
В поле значения перетащите столбец цвета, столбец нотоносца, столбец размера и показатель результата из области поля.

двойная мера мощности разделить два столбца из другой таблицы

Чтение меры Power BI IF с примерами

мера мощности двойного деления разделить столбец на число

Здесь мы увидим, как разделить столбец на число с помощью меры в степени двоичной.

Мы воспользуемся таблицей ниже, чтобы суммировать баллы по группам, а затем разделим каждый балл на сумму каждой группы.

мощность двойная мера разделить столбец на число

Загрузить данные с помощью get data.
Щелкните Новая мера на ленте.
Затем запишите следующую меру:

 Мера 3 =
РАЗДЕЛЯТЬ (
    СУММ («Таблица 5» [Оценка]),
    ВЫЧИСЛИТЬ ( СУММА («Таблица 5» [Оценка]), ALLSELECTED («Таблица 5» [Категория]))
)

Чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
Затем в поле значения перетащите столбец группы, столбец категории, столбец оценки и показатель 3 из области поля.

мощность bi мера разделить столбец на число

Вычислить строку в столбце, деленную на сумму этого столбца

Здесь мы увидим, как разделить значение строки столбца на сумму этого столбца .

Мы будем использовать приведенный ниже пример для вычисления строки в столбце, разделенной на сумму этого столбца.

вычислить строку в столбце, деленную на сумму этого столбца

Загрузить данные, используя get data.
Затем нажмите Новая мера на ленте.
Затем запишите следующую меру:

 Мера = Var denom= ВЫЧИСЛИТЬ (Сумма («Таблица» [Значения]), ВСЕ («Таблица»)))
Return SUM('Table'[Values])/denom

Чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
Затем перетащите столбец 1, столбец значений и показатель из области полей.

вычислить строку в столбце, деленную на сумму этого столбца

Вам также могут понравиться следующие учебные пособия по Power Bi:

Microsoft Power BI KPI Visual
Microsoft Power BI Stacked Column Chart
Как использовать Microsoft Power BI Точечная диаграмма
Комбинированная диаграмма Microsoft Power BI
Отчет Microsoft Power bi и панель мониторинга
Power BI Измерение умножения с примерами

В этом руководстве по Power bi мы обсудили различные типы примеров в Power Bi делит меру на . Эти примеры перечислены ниже:

Двойная мера мощности разделить один столбец на другой
Двойная мера мощности разделить два столбца
Двойная мера мощности разделить с фильтром
Двойная мера мощности разделить на ноль
Двойная мера мощности разделить на общий итог
Двойная мера мощности разделить по строкам
Двойная мера мощности разделить два столбца из разных таблиц
Двойная мера мощности разделить столбец на число

Бхавана Ратор

Бхавана Ратор — Microsoft MVP (3 раза в Office Apps & Services) и страстный консультант по SharePoint, имеющий около 10 лет опыта работы в сфере ИТ в отрасли, а также в технологиях .Net. Ей нравится делиться своими техническими знаниями в EnjoySharePoint.com и SPGuides.com

Data Frame, разделяя значения столбца на соответствующее значение строки — tidyverse

Rh22 19 ноября, 2020, 21:16 #1

Уважаемые,

У меня есть фрейм данных с одним столбцом даты и 8 столбцами с ценами на акции. Я пытаюсь разделить все значения столбца на соответствующее значение конкретной строки (т.е. на цену на определенную дату), чтобы нормализовать данные. К сожалению, я пока не придумал, как это сделать (лучшим решением будет решение, где можно выбрать конкретную дату строки, например 2020-03-02, чтобы быстро изменить базовые значения для нормализации данных, если нужный).

Спасибо!

Питерянвк 19 ноября 2020 г., 21:32 # 2

Привет,

Не совсем понятно, что вам нравится делать, поэтому, возможно, если мое предложение ниже не то, что вы ищете, создайте репрекс, следуя приведенному ниже руководству. Репрекс состоит из минимального кода и данных, необходимых для воссоздания проблемы/вопроса, который у вас есть. Инструкции по его созданию и распространению можно найти здесь:

Минимальный воспроизводимый пример состоит из следующих элементов: Минимальный набор данных, необходимый для воспроизведения проблемы Минимальный исполняемый код, необходимый для воспроизведения проблемы, который можно запустить по заданному набору данных, включая необходимую информацию об используемых пакетах. Давайте быстро рассмотрим каждый из них на примерах: Минимальный набор данных (пример данных) Вам необходимо предоставить фрейм данных, который достаточно мал, чтобы его можно было (разумно) вставить в сообщение, но достаточно велик, чтобы воспроизвести вашу проблему. Предположим, например, что вы работаете с фреймом данных радужной оболочки. голова (ирис) #> Чашелистик.Длина Чашелистик.Ширина Лепесток.Длина Лепесток.Ширина Виды #> 1 5,1 3,5 1,4 0,2…

Вы можете использовать group_by() из dplyr для выполнения действий над определенными строками, как эта библиотека

 (dplyr)
# Генерируем случайные данные
сет.сид(10)
мои данные = данные.кадр(
  date = as.Date(sample(c("2020-11-19", "2020-11-18"), 10, заменить = T)),
  знач1 = 1:10, знач2 = runif(10))
мои данные
#> дата значение1 значение2
#> 1 2020-11-19 1 0,65165567
#> 2 2020-11-19 2 0,56773775
#> 3 2020-11-18 3 0.11350898
#> 4 2020-11-18 4 0,59592531
#> 5 2020-11-18 5 0,35804998
#> 6 2020-11-19 6 0,42880942
#> 7 2020-11-18 7 0. 051
#> 8 2020-11-18 8 0,26417767
#> 9 2020-11-19 9 0,39879073
#> 10 2020-11-19 10 0,83613414
#Применить функции по группам (в данном случае по дате)
мои данные %>% group_by(дата) %>%
  мутировать (значение1 = масштаб (значение1) [ 1],
         знач2 = (знач.2 - мин.(знач.2)) / (макс.(знач.2) - мин.(знач.2)))
#> # Таблица: 10 x 3
#> # Группы: дата [2]
#> дата значение1 значение2
#> <дата>  
#> 1 2020-11-19-1,14 0,578
#> 2 2020-11-19 -0,892 0,386
#> 3 18.11.2020 -1,16 0,113
#> 4 18.11.2020 -0,675 1
#> 5 2020-11-18 -0,193 0,563
#> 6 2020-11-19 0,0991 0,0686
#> 7 18.11.2020 0,772 0
#> 8 18.11.2020 1,25 0,390
#> 9 2020-11-19 0,842 0
#> 10 19.11.2020 1.09 1

^{Создано 19 ноября 2020 г. пакетом reprex (v0.3.0)}

Надеюсь, это поможет,
PJ

Rh22 21 марта 2021 г., 1:18 #3

Привет @pieterjanvc

Возможно, я недостаточно ясно выразился. Давайте посмотрим на следующий пример фрейма данных, который похож на оригинал:

 data.frame(
      ЗапасА = с(15, 20, 26, 10, 5),
      СтокВ = с(27, 16, 15, 10, 23),
                            дата = as.factor(c("2020-03-01",
                                               "2020-03-02", "2020-03-03",
                                               "2020-03-04", "2020-03-04"))
                    )

Я пытаюсь разделить все значения столбцов StockA и StockB на значения в определенной строке. Например, я хочу, чтобы все значения в столбцах StockA и StockB были разделены на значения в строке 2020-03-02 (т.е. 20 и 16 соответственно). Поэтому значения в этой строке нормализуются до 1, а остальные значения корректируются соответствующим образом. Но кода для этого я не нашел, так как не хочу выделять соответствующие строки для кода по [х,] а явным указанием даты строки. Кроме того, исходный фрейм данных намного больше, поэтому его невозможно сделать вручную, просто разделив каждый столбец на значение строки.

Надеюсь, теперь стало понятнее. Заранее спасибо.

andresrcs 3 декабря 2020 г., 5:50 #4

Ты это имеешь в виду?

 библиотека (dplyr)
sample_df <- data.frame(
    ЗапасА = с(15, 20, 26, 10, 5),
    СтокВ = с(27, 16, 15, 10, 23),
    date = as.Date(c("2020-03-01",
                       "2020-03-02", "2020-03-03",
                       "2020-03-04", "2020-03-04"))
)
sample_df %>%
    мутировать (через (. cols = начинает_с («запас»),
                  .fns = ~ . /sample_df%>%
                      фильтр (дата == '2020-03-02') %>%
                      тянуть (cur_column ())
                  )
           )
#> StockA StockB дата
#> 1 0,75 1,6875 01.03.2020
#> 2 1.00 1.0000 2020-03-02
#> 3 1,30 0,9375 2020-03-03
#> 4 0,50 0,6250 04.03.2020
#> 5 0,25 1,4375 04.03.2020

^{Создано 20 ноября 2020 г. пакетом reprex (v0.3.0.9001)}

Rh22 20 ноября 2020 г., 9:07 #5

Привет @andresrcs

Да, это именно то, что я ищу, спасибо. Осталась только одна маленькая проблема:
Можно ли умножить все значения на 100, то есть чтобы нормированные значения были равны 100 вместо 1, а все остальные значения подстраивались соответствующим образом?

Я очень извиняюсь за свой вопрос, но я все еще новичок в RStudio.

andresrcs 24 ноября 2020 г., 21:43 #6

Вам просто нужно умножить

 sample_df %>%
    мутировать (через (. cols = начинает_с («запас»),
                  .fns = ~ . /sample_df%>%
                      фильтр (дата == '2020-03-02') %>%
                      тянуть(cur_column()) * 100)
    )

Если на ваш вопрос был дан ответ (даже вами!), не могли бы вы выбрать решение? Это помогает другим людям увидеть, какие вопросы все еще нуждаются в помощи, или найти решения, если у них есть похожие проблемы.

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Решаем столбиком деление: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Деление многочлена на многочлен с остатком примеры. Деление многочленов «столбиком» («уголком»). Решаем реальные примеры

Уравнение столбиком. Деление полиномов

Теорема

Доказательство

Деление многочленов

Пример деления многочленов уголком

Пример 2

Умножение многочленов столбиком

Пример умножения многочленов столбиком

Пример 2

Деление с остатком на 10, 100, 1000

Решено: Разделить один столбец на другой

Двухкратное деление мощности + 9 примеров

Степень bi мера деления

Мера Power bi разделить один столбец на другой

мера двойной мощности разделить с фильтром

Разделение двойного показателя мощности на ноль

Разделение показателя Power bi на общую сумму

Мера двойного деления деление по строке за строкой

двойная мера мощности разделить два столбца из другой таблицы

мера мощности двойного деления разделить столбец на число

Вычислить строку в столбце, деленную на сумму этого столбца

Data Frame, разделяя значения столбца на соответствующее значение строки — tidyverse

Добавить комментарий Отменить ответ