Таблицы «Состав числа». | Тренажёр (1 класс) на тему:
По теме: методические разработки, презентации и конспекты
Занятие по математике «Число 7. Цифра 7. Дополнение числа до любого заданного числа «Занятие по математике в «Школе успеха» с будущими первоклассниками. В разделе «Презентации» мной представлена презентация к этому занятию….
Открытый урок по русскому языку 2 класс по теме: «Изменение имён прилагательных по числам. Зависимость формы числа имени прилагательного от формы числа имени существительного»Тема: Изменение имён прилагательных по числам. Зависимость формы числа имени прилагательного от формы числа имени существительного.Педагогические цели: способствовать ознакомлению с единственным и мно…
Конспект урока математики «Умножение величины на число и числа на величину. Деление величины на число», 4 класс, ПНШКонспект урока по математике…
Конспект урока по математике «Деление на число 1.
Деление числа на само себя. Деление числа 0 на натуральное число» 3 классКонспект урока по математике «Деление на число 1.Деление числа на само себя. Деление числа 0 на натуральное число» 3 класс ПНШ…
Технологическая карта урока математики по теме: «Число 9. Получение числа 9 прибавлением 1 к предыдущему числу».Цель урока: познакомить с приёмом получения числа 9 путём прибавления 1 к предыдущему числу.Задачи урока:Образовательная: в ходе практической работы и наблюдений познакомить с образованием числа…
Урок математики в 3а классе на тему «Деление на число 1. Деление числа на само себя. Деление числа 0 на натуральное число.»Урок математики в 3а классе проведен по ОС «ГАРМОНИЯ». ЭТО УРОК ОТКРЫТИЯ НОВЫХ ЗНАНИЙ. ОСНОВНЫЕ ЦЕЛИ УРОКА :1. Учить делить число на число 1. Делить число на само себя. Делить число 0 на нат…
Карточки для деления многозначных чисел на однозначное число (двузначное число и трехзначное число)Карточки для автоматического подбора примеров на деление многозначных чисел на однозначное число (двузначное число и трехзначное число).
Для того, чтобы примеры поменялись необходимо в любой ячейке (же…
Орг. момент | Деятельность учителя | Деятельность учащихся | ||||||||||||||||||||||||
| — Начнём урок с повторения. Сейчас мы с вами поиграем в игру “Хлопки”. Поставьте руки на стол и хлопните в ладоши один раз. Это будет однозначное число, а два раза – когда называется двузначное число. |
| ||||||||||||||||||||||||
| — Итак, когда вы хлопаете один раз, а когда два? | Дети отвечают: 1 раз – однозначное число, 2 раза – двузначное число. | ||||||||||||||||||||||||
| — Чем отличаются двузначные числа от однозначных? — Начнём игру. Числа: 2, 17, 18, 7, 11, 1, 20, 5, 19, 4, … Молодцы, все справились. — Посмотрите, на доске записаны выражения: 9 + 8 8 + 4 7 + 6 6 + 5 |
| ||||||||||||||||||||||||
| — Прочитайте выражение, найдите его значение. Аналогично решаются остальные выражения. | (9 + 1 + 7 = 17). | ||||||||||||||||||||||||
| — Какие ответы у нас получились? — Назовите эти числа в порядке возрастания. | (17, 13, 12, 11 – записываются на доске) | ||||||||||||||||||||||||
| — Чем они похожи? | (Все двузначные) | ||||||||||||||||||||||||
| — Догадайтесь, по какому признаку число 17 может быть лишним среди остальных чисел? | (Оно больше остальных не на один) | ||||||||||||||||||||||||
| — Каким числом можно заменить 17, чтобы не нарушить построения? | (14 или 10) | ||||||||||||||||||||||||
Игра | — Следующее задание — игра “Рассели жильцов”. Ребята, жильцами математического дома являются цифры и математические знаки. Какие математические знаки вы знаете? Нам нужно вставить в окошки недостающие знак или цифру.
| Дети выполняют задания, выходя к доске по одному. | ||||||||||||||||||||||||
| — Следующее задание будет такое. У меня в руках две карточки с числами. На них написаны два числа, если их сложить, то получится число 11. | 9 и 2, 8 и 3, 7 и 4 и т.д. | ||||||||||||||||||||||||
Постановка цели | — Сегодня на уроке мы познакомимся с составом числа 12. |
| ||||||||||||||||||||||||
Объяснение нового материала | Оформление тетрадей, страница учебника 123, № 128. | Работа в тетради, с учебником. | ||||||||||||||||||||||||
| — Посмотрите внимательно на иллюстрацию и скажите, чем они все похожи? — Чем отличаются? На сколько кругов? | (Увеличиваются круги вне треугольника и в треугольнике) | ||||||||||||||||||||||||
| — А теперь посмотрим на ряд выражений. Догадайтесь, какому рисунку соответствует каждое выражение? | Дети сопоставляют рисунки и выражения. | ||||||||||||||||||||||||
| — Найдите первое выражение. Прочтите его (10+2). Какой рисунок соответствует выражению? Почему? | 10+2 (Первый) | ||||||||||||||||||||||||
| — Чему равно значение выражения? На каком именно числовом луче отмечено это выражение? Объясните, что показано стрелкой. | (12) | ||||||||||||||||||||||||
| — Рассмотри второе выражение (8+4). Какой рисунок ему соответствует? Докажите? Чему равно выражение? Найдите луч, на котором отмечено этот выражение. | (8+4) (12) | ||||||||||||||||||||||||
| Аналогично решаются остальные выражения 6+6, 7+5, 9+3. Выражения записываются на доске, а учащиеся записывают их в тетрадь. |
| ||||||||||||||||||||||||
| — Чем похожи равенства? | (Одинаковый ответ) | ||||||||||||||||||||||||
| — Что мы можем сказать обо всех равенствах? | (Они образуют числа 12) | ||||||||||||||||||||||||
| — Все ли варианты состава числа 12 мы написали? (не все) |
| ||||||||||||||||||||||||
| — Каких не хватает? (5+7, 4+8, 3+9, 2+10, 1+11) Давайте их тоже запишем в тетрадь. | (5+7, 4+8, 3+9, 2+10, 1+11) | ||||||||||||||||||||||||
| — Вывод: Итак, ребята, 12 – это сумма чисел … | Дети заканчивают предложение. | ||||||||||||||||||||||||
Физминутка | — Вы хорошо поработали, а теперь давайте отдохнём. Слушайте меня внимательно и повторяйте за мной. Буратино потянулся, Руки в стороны развёл, Видно, ключик не нашёл. Чтобы ключик нам достать, Надо на носочки встать. (повторяется 2 раза) — Продолжаем работу. |
| ||||||||||||||||||||||||
| — Следующее задание – сравни числа: 10 и 13, 9 и 12 Вставьте в квадратики числа, чтобы получились верные неравенства: 1 > 9 2 > 1 1 < 13 1 = 1 — Молодцы, вы хорошо справились. |
| ||||||||||||||||||||||||
Игра | — А сейчас я прочитаю загадку. Для того, чтобы её разгадать, необходимо выполнить определённое математическое действие. Итак, загадка-игра: Сам пустой, голос густой. | Дети собирают карточки в группах. (Получится слово “барабан”) | ||||||||||||||||||||||||
Подведение итогов урока | — Какая сегодня была тема урока? Соревнование: Кто назовёт больше вариантов состава числа 12? — Урок окончен. |
|
Угадайте, какие числа записаны на карточках? Объясните. — Теперь проверим, я открываю карточки.
Урок 4. Изучение чисел
Любое обучение счету и числам всегда должно начинаться с усвоения элементарных количественных понятий, таких как «много», «мало», «больше», «меньше», «поровну» и т.п. И дети легко уясняют их еще в ясельном возрасте. Ваша основная родительская задача – просто помочь им в этом. Формировать же навыки количественного сравнения можно в процессе каждодневной жизни. Так, вместе с малышом можно сравнивать количество конфет или бутербродов, квартир на площадках и ступенек на лесенках, косичек и бантиков у девчушек и т.
д. Однако приниматься сразу за большие группы предметов не нужно, ведь все должно начинаться с малого.
После освоения количественных понятий наступает пора знакомства малыша с миром чисел. Как вам уже известно, происходить это должно в интересной и увлекательной для ребенка форме, для чего и следует применять методы, рассмотренные нами в первых уроках.
Рассказывать крохе о числах нужно, не спеша и не стремясь «загрузить» в дитя как можно больше информации. Для начала осваивайте числа первого десятка, чтобы они хорошенько запомнились и усвоились, а также, чтобы была уяснена их очередность. Делать все это нужно ненавязчиво, занимаясь обычными домашними делами. Считайте, сколько людей находится дома, сколько чашек на столе, сколько окон в квартире, сколько пуговиц на куртке и т.д.
Когда знакомство с миром чисел будет завершено, можно приступать к разбору состава числа и решению простых задач.
Содержание:
Как познакомить ребенка с составом числа
Как известно, все числа, помимо единицы, можно раскладывать на другие числа.
Например, двойку можно разложить на две единицы, тройку – не единицу и двойку и т.д. Под этим и следует понимать состав числа, и объяснять его нужно в тот момент, когда ребенок освоил счет по порядку.
Дело в том, что разбирая числа на составляющие, малыш будет сразу же осваивать навык решения простых примеров. К примеру, уяснив для себя, что число «3» – это не только « 1», 1» и «1», но также «2» и «1», он автоматически поймет, что если сложить двойку и единицу, получится три.
ВАЖНОЕ ДОПОЛНЕНИЕ: Когда учите складывать своего малютку, следите, чтобы он не складывал разнородные объекты, т.к. в будущем у него могут возникнуть проблемы с решением математических задач. Объясняйте, что нельзя прибавлять фломастеры к кубикам, и что математические действия выполняются только с объектами, относящимися к одной категории.
Помимо прочего, научить ребенка составу числа можно и при помощи специальных методов. Об одном из них мы расскажем ниже.
Для реализации метода вам нужно подготовить:
- Карточки на состав числа*
- Большое количество кубиков, шариков или других одинаковых объектов
- Шашки разного цвета (могут подойти и одинаковые разноцветные пуговицы)
*Пример карточки на состав числа
Как только дидактический материал будет готов, можно начинать занятия.
Алгоритм таков:
- Для первого занятия подготовьте подобранные ранее объекты счета. Размер и внешний вид не имеют никакого значения. Главное, чтобы объекты относились к одной категории. Начинать занятие нужно с числа «2». Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами.
- Возьмите другие объекты и повторите задание с ними. Юный счетовод должен уяснить, что число «2» всегда будет состоять из двух единиц, независимо от того, какими он манипулирует объектами.
- Когда станет понятно, что число «2» освоено, незамедлительно начинайте работать с числом «3». Состав этого числа может быть представлен уже тремя вариантами: «1 + 1 +1», «1 + 2» и «2 + 1». Раскладывайте перед крохой объекты в самых разных вариациях, но с одной особенностью: если рассматриваете вариант сложения трех единиц, путь каждый предмет лежит на одинаковом расстоянии друг от друга; если рассматриваете вариант сложения единицы и двойки, то два предмета должны лежать рядом, а один – на расстоянии от них.
Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам. - Занятия с шашками выполняются параллельно занятиям с игрушками, либо отдельно от них. Задача проста: попросите ребенка положить перед собой (или на доску для шашек) четыре одинаковых шашки. Потом спросите, сколько будет шашек, если сложить две черных и две белых? Смысл в том, чтобы показать, что одно и то же число может быть представлено несколькими вариантами (в данном случае – независимо от цвета).
- Перед работой с карточками на состав числа их нужно приобрести или изготовить самостоятельно. Такие карточки бывают разных модификаций, и будет хорошо, если у вас тоже будет два варианта. Первый комплект состоит из разрезанных на две половинки карточек. На одной половинке изображается один объект, а на другой – 1, 2, 3 – 9 аналогичных объектов (кстати, половинки могут соединяться знаком «+», но полезно иметь и отдельный знак «+», а также отдельный знак «-»). Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.
- Продемонстрируйте малышу карточку, например, с пятью объектами. Попросите подобрать остальные изображения так, чтобы они составляли число пять. Здесь еще удобно меняться ролями, т.е. время от времени просите ребенка давать задания и вам, а вы не ленитесь их выполнять, причем иногда стоит специально ошибаться, чтобы малыш контролировал ваши действия и указывал на то, что вы делаете неправильно.
- Точно такое же задание можно выполнять с использованием карточек с цифрами. К примеру, вы можете показать ребенку карточку с цифрой «7», а он пусть сложит остальные карточки так, чтобы в разных вариантах получить это же число. Впоследствии переходите к более сложным числам (более десяти), объясняя малышу, что чем больше число, тем больше есть вариантов его составления.
Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам.
Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.
Проводить занятия нужно систематически, но не стоит сильно усердствовать. Дважды в день по 20-25 минут будет более чем достаточно. Уже через 1,5-2 месяца таких занятий ваше чадо в достаточной мере освоит состав числа и научится выполнять основные математические операции. Но чтобы повысить шансы на успех, в дополнение к предложенному методу вы можете использовать и составленные нами рекомендации.
Дополнительные рекомендации и советы
Знакомя ребенка с составом числа (и обучая счету вообще), старайтесь обращать как можно больше внимания на поведение своего чада. Наиболее частыми явлениями во время занятий являются отвлекаемость и невнимательность. Практически всегда это свидетельствует о том, что малыш потерял интерес к процессу и новая информация им уже не воспринимается.
Чтобы исправить положение дел, совсем необязательно прекращать домашний урок. Иногда бывает полезно просто повторить то, что уже было изучено. Вспомнив знакомый материал, выполнив несколько заданий и убедившись, что у него все получается, ребенок снова заинтересуется и будет готов к усвоению новых знаний.
Не гонитесь за результатом – обучайте свое чадо в умеренном темпе и давайте информацию постепенно. Вопреки ошибочному мнению, это вовсе не тормозит развитие маленького ученика, ведь небольшой объем знаний закрепляется прочнее, а это значит, что и переход к новым темам не за горами.
Арифметические задачи становятся для дошколят гораздо интереснее, если использовать в них игрушки, игры, монетки, разноцветные счетные палочки. Сначала считайте их сами, произнося цифры вслух, а затем просите ребенка повторить за вами.
Будет просто супер, если вы сделаете упражнения как можно более зрелищными. Можно выстраивать дорожки из монеток, делать городки и пирамидки из кубиков, разнообразными способами раскладывать карточки и картинки. Добавляя и убирая объекты, вы будете учить свое дитя прямому и обратному счету, сложению и вычитанию, соотнесению чисел и количества. Приобретя такие навыки еще в дошкольном возрасте, а также разобравшись с составом числа, ребенок будет намного легче справляться со школьными заданиями по математике и быстро выучит таблицу умножения (о том, как сделать это еще до школы, мы с вами тоже поговорим в одном из уроков).
Регулярные занятия прекрасно развивают логическое, пространственное, предметное и абстрактно-образное мышление, благодаря чему уже в 3-4 года маленький ученик сможет показывать хорошие результаты.
Тема освоения состава числа и простейших чисел, как вы заметили, совсем небольшая и несложная. Несколько труднее научить ребенка считать до 20 и до 100. В шестом уроке мы познакомим вас с эффективными принципами обучения детей счету и предложим несколько действенных методик, позволяющих научить детей считать до 10, до 20 и до 100, а также производить вычисления столбиком.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
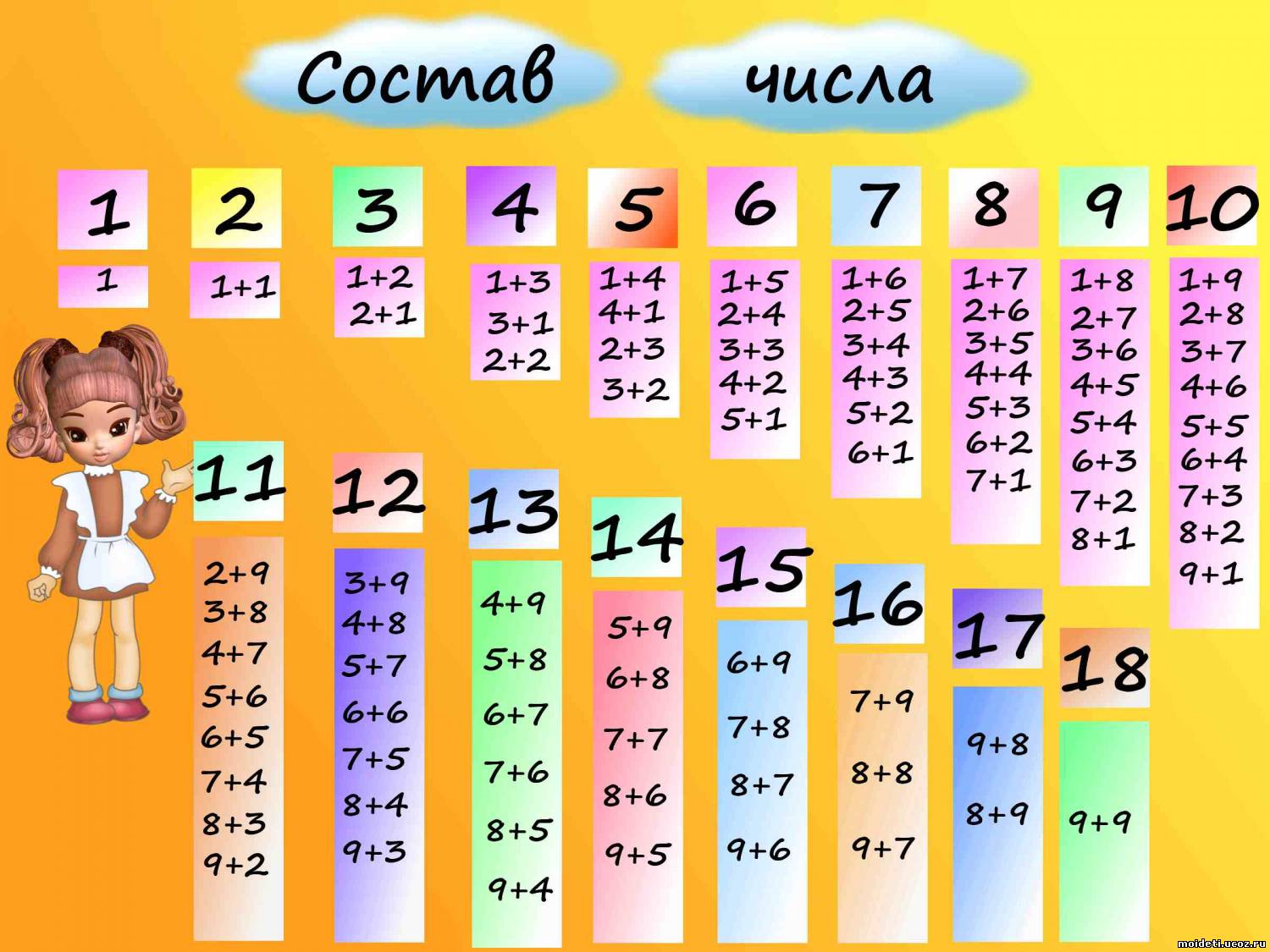
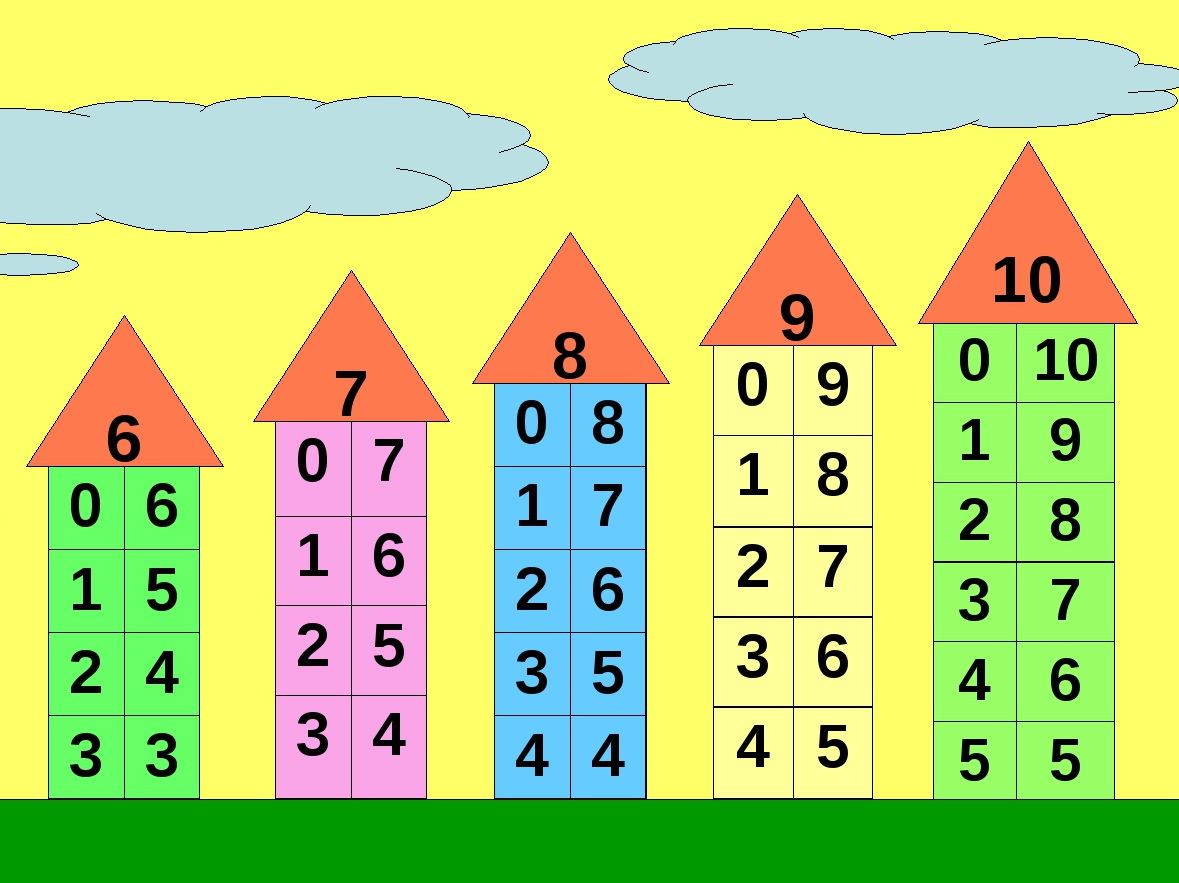
Таблица состава чисел до 10
Состав чисел от 1 до 10 начинаем изучать еще в курсе предшкольной подготовки. Без знания понятия число невозможно дальнейшее обучение математике. Таблица состава чисел до 10 помогает детям быстро и успешно запомнить компоненты чисел.
На таблице помещен ряд чисел от 1 до 10 с конкретным образом каждого числа. Используя эту таблицу, детям можно наглядно объяснить, что такое число. Глядя на таблицу, дети легко запоминают состав чисел.
Сначала нужно проработать первую пятерку чисел. Числа 1, 2, 3, 4, 5 изображены кружками красного цвета. Задаем вопрос: сколько надо добавить к трем, чтобы получилось пять? 3+?=5 Ребенок смотрит на вертикальную полоску с тремя красными кружками и видит, что до пяти нужно добавить два белых кружка. Таким образом ему легко запомнить состав чисел от 2 до 5.
Дальше переходим к верхней части таблицы и узнаем, какие числа больше пяти. Верхние кружки уже другого цвета.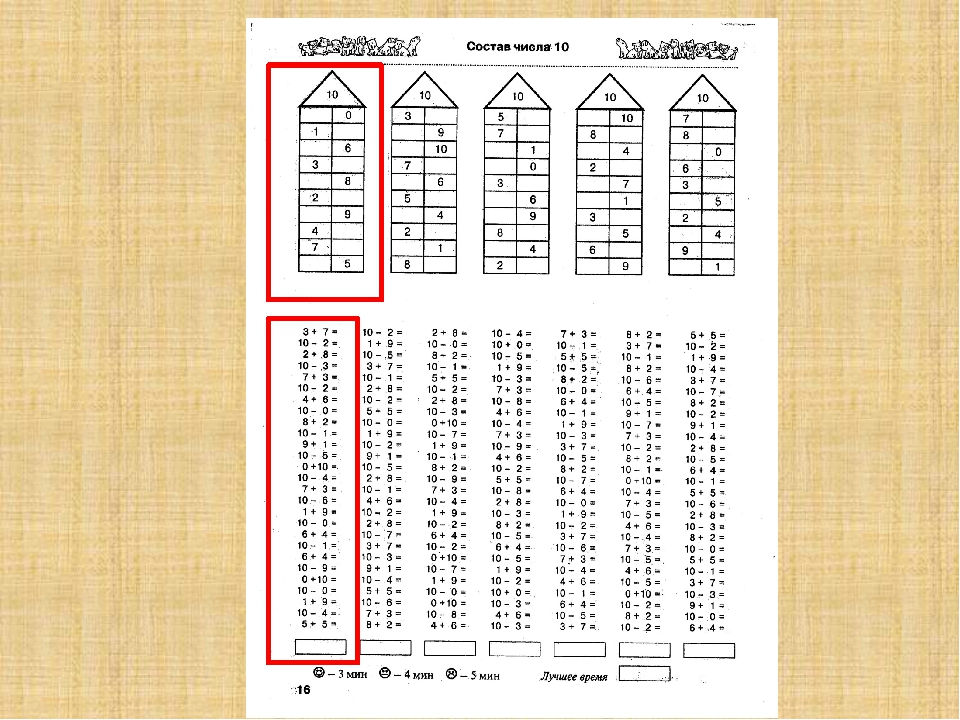
Работая с опорой на эту таблицу, дети запоминают, что 6=5+1, 7=5+2, 8=5+3 и так далее. По этой таблице даются все сведения о цифрах, числах и натуральном ряде чисел.
Первое время дети при ответах всегда опираются на эту таблицу. Бояться этого не следует. Постепенно по мере запоминания состава чисел, ребенок будет заглядывать в нее все реже и реже. Но некоторым детям необходим конкретный образ числа и натуральной последовательности чисел. Им можно пользоваться этой таблицей так долго, как это будет необходимо.
Самое главное, чтобы ребенок выполнял задания самостоятельно. Правильно выполненное без посторонней помощи задание всегда приносит ему чувство удовлетворения и радости, которое мы должны всемерно поддерживать.
Для закрепления состава чисел можно использовать веселую таблицу, в которой компоненты представлены ежиками, котиками, собачками и другими зверьками. Это забавно, но не менее полезно, чем простая таблица.
Кроме этой таблицы, есть много игровых упражнений, которые помогут вашему ребенку запомнить состав чисел до 10 и освоить эту важнейшую математическую тему.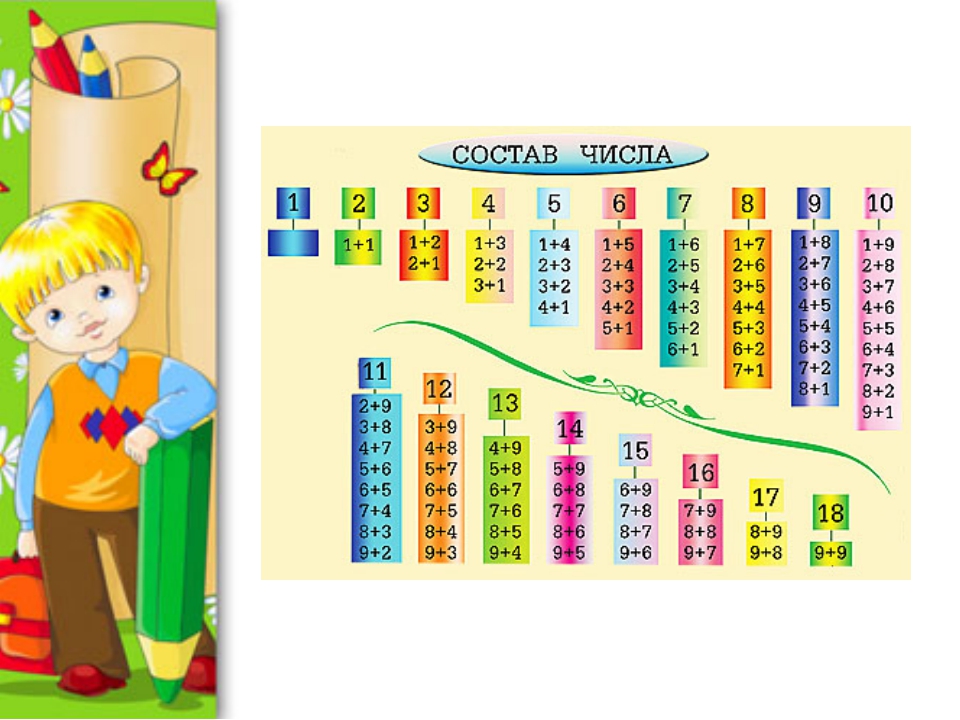
Оценить составные функции | Колледж алгебры
После того, как мы составим новую функцию из двух существующих функций, нам нужно иметь возможность оценивать ее для любого ввода в ее домене. Мы сделаем это с помощью конкретных числовых входных данных для функций, выраженных в виде таблиц, графиков и формул, и с переменными в качестве входных данных для функций, выраженных в виде формул. В каждом случае мы оцениваем внутреннюю функцию, используя начальный ввод, а затем используем вывод внутренней функции как ввод для внешней функции.
Оценка составных функций с помощью таблиц
При работе с функциями, заданными в виде таблиц, мы считываем входные и выходные значения из записей таблицы и всегда работаем изнутри наружу. Сначала мы оцениваем внутреннюю функцию, а затем используем вывод внутренней функции как вход для внешней функции.
Пример 5: Использование таблицы для вычисления составной функции
Используя приведенную ниже таблицу, оцените [латекс] f \ left (g \ left (3 \ right) \ right) [/ latex] и [latex] g \ left (f \ left (3 \ right) \ right) [/ латекс].
| [латекс] x [/ латекс] | [латекс] f \ влево (x \ вправо) [/ латекс] | [латекс] г \ левый (х \ правый) [/ латекс] |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
Решение
Чтобы оценить [латекс] f \ left (g \ left (3 \ right) \ right) [/ latex], мы начинаем изнутри с входным значением 3.
Затем мы оцениваем внутреннее выражение [latex] g \ left (3 \ right) [/ latex], используя таблицу, которая определяет функцию [latex] g: [/ latex] [latex] g \ left (3 \ right) = 2 [/латекс]. Затем мы можем использовать этот результат в качестве входных данных для функции [latex] f [/ latex], поэтому [latex] g \ left (3 \ right) [/ latex] заменяется на 2, и мы получаем [latex] f \ left (2 \ справа) [/ латекс]. Затем, используя таблицу, определяющую функцию [latex] f [/ latex], мы находим, что [latex] f \ left (2 \ right) = 8 [/ latex].
[латекс] \ begin {case} g \ left (3 \ right) = 2 \ hfill \\ f \ left (g \ left (3 \ right) \ right) = f \ left (2 \ right) = 8 \ hfill \ end {case} [/ latex]
Чтобы оценить [латекс] g \ left (f \ left (3 \ right) \ right) [/ latex], мы сначала вычисляем внутреннее выражение [latex] f \ left (3 \ right) [/ latex], используя первое таблица: [латекс] f \ left (3 \ right) = 3 [/ latex].Затем, используя таблицу для [latex] g \ text {, \ hspace {0.
17em}} [/ latex], мы можем оценить
[латекс] g \ left (f \ left (3 \ right) \ right) = g \ left (3 \ right) = 2 [/ латекс]
В таблице ниже представлены составные функции [latex] f \ circ g [/ latex] и [latex] g \ circ f [/ latex] в виде таблиц.
| [латекс] x [/ латекс] | [латекс] г \ левый (х \ правый) [/ латекс] | [латекс] f \ left (g \ left (x \ right) \ right) [/ латекс] | [латекс] f \ влево (x \ вправо) [/ латекс] | [латекс] g \ left (f \ left (x \ right) \ right) [/ латекс] |
| 3 | 2 | 8 | 3 | 2 |
Попробовать 3
Используя приведенную ниже таблицу, оцените [латекс] f \ left (g \ left (1 \ right) \ right) [/ latex] и [latex] g \ left (f \ left (4 \ right) \ right) [/ латекс].
| [латекс] x [/ латекс] | [латекс] f \ влево (x \ вправо) [/ латекс] | [латекс] г \ левый (х \ правый) [/ латекс] |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
Решение
Оценка составных функций с помощью графиков
Когда нам даются отдельные функции в виде графиков, процедура оценки составных функций аналогична процессу, который мы используем для оценки таблиц.
Мы считываем входные и выходные значения, но на этот раз с осей [latex] x \ text {-} [/ latex] и [latex] y \ text {-} [/ latex] графиков.
Практическое руководство. Имея составную функцию и графики отдельных функций, оцените ее, используя информацию, представленную на графиках.
- Найдите входные данные внутренней функции на оси [latex] x \ text {-} [/ latex] ее графика.
- Считайте вывод внутренней функции с оси [latex] y \ text {-} [/ latex] ее графика.
- Найдите выход внутренней функции на оси [latex] x \ text {-} [/ latex] графика внешней функции.
- Считайте вывод внешней функции по оси [latex] y \ text {-} [/ latex] на ее графике. Это результат составной функции.
Пример 6: Использование графика для вычисления составной функции
Используя графики на рисунке 3, оцените [латекс] f \ left (g \ left (1 \ right) \ right) [/ latex].
Рисунок 3
Решение
Рисунок 4
Чтобы оценить [латекс] f \ left (g \ left (1 \ right) \ right) [/ latex], мы начинаем с внутренней оценки.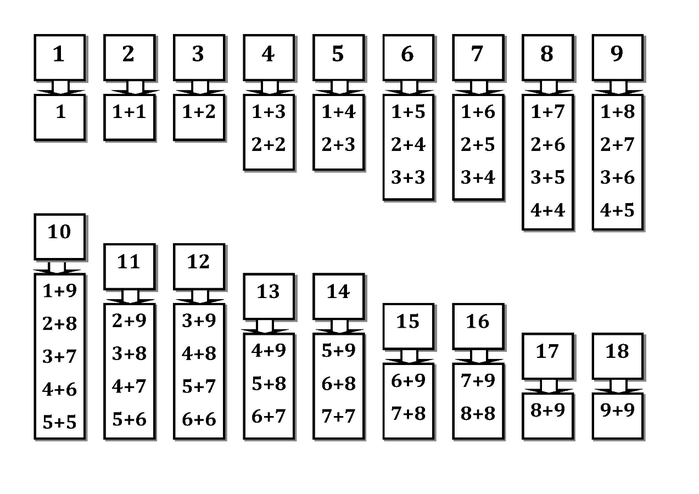
Мы оцениваем [латекс] g \ left (1 \ right) [/ latex], используя график [latex] g \ left (x \ right) [/ latex], находя вход 1 на [латексе] x \ ось текста {-} [/ latex] и нахождение выходного значения графика на этом входе. Здесь [латекс] g \ left (1 \ right) = 3 [/ latex]. Мы используем это значение в качестве входных данных для функции [latex] f [/ latex].
[латекс] f \ left (g \ left (1 \ right) \ right) = f \ left (3 \ right) [/ латекс]
Затем мы можем оценить составную функцию, посмотрев на график [latex] f \ left (x \ right) [/ latex], найдя вход 3 на [latex] x \ text {-} [/ latex] ось и считывание выходного значения графика на этом входе.Здесь [латекс] f \ left (3 \ right) = 6 [/ latex], поэтому [latex] f \ left (g \ left (1 \ right) \ right) = 6 [/ latex].
Попробовать 4
Используя рисунок 6, оцените [латекс] g \ left (f \ left (2 \ right) \ right) [/ latex].
Рисунок 6
Решение
Вычисление составных функций с помощью формул
При оценке составной функции, в которой мы либо создали, либо получили формулы, правило работы изнутри остается неизменным.
{2} -t [/ latex] и [latex] h \ left (x \ right) = 3x + 2 [/ latex], оцените
A) [латекс] h \ left (f \ left (2 \ right) \ right) [/ латекс]
B) [латекс] h \ left (f \ left (-2 \ right) \ right) [/ латекс]
Решение
Решение задач с алгебраическими структурами с помощью таблицы композиции
Задача-1:
Установите G = {1, ω, ω 2 } i.е., три корня из единицы и образуют конечную абелеву группу относительно умножения, также докажите это утверждение с помощью таблицы композиции.
Объяснение:
Дано, Set = G = {1, ω, ω 2 } , operation = ‘*’ т.е. умножение.
Чтобы доказать, что три корня из единицы образуют конечную абелеву группу, мы должны удовлетворять следующим пяти свойствам: свойство замыкания, ассоциативное свойство, свойство идентичности, обратное свойство и коммутативное свойство.
Примечание-: ω 3 = 1
1) Свойство замыкания —
∀ a, b ∈ G ⇒ a * b ∈ G a = 1, b = ω ∈ G ⇒ 1 * (ω) = ω = ω ∈ G
Следовательно, свойство замыкания выполняется.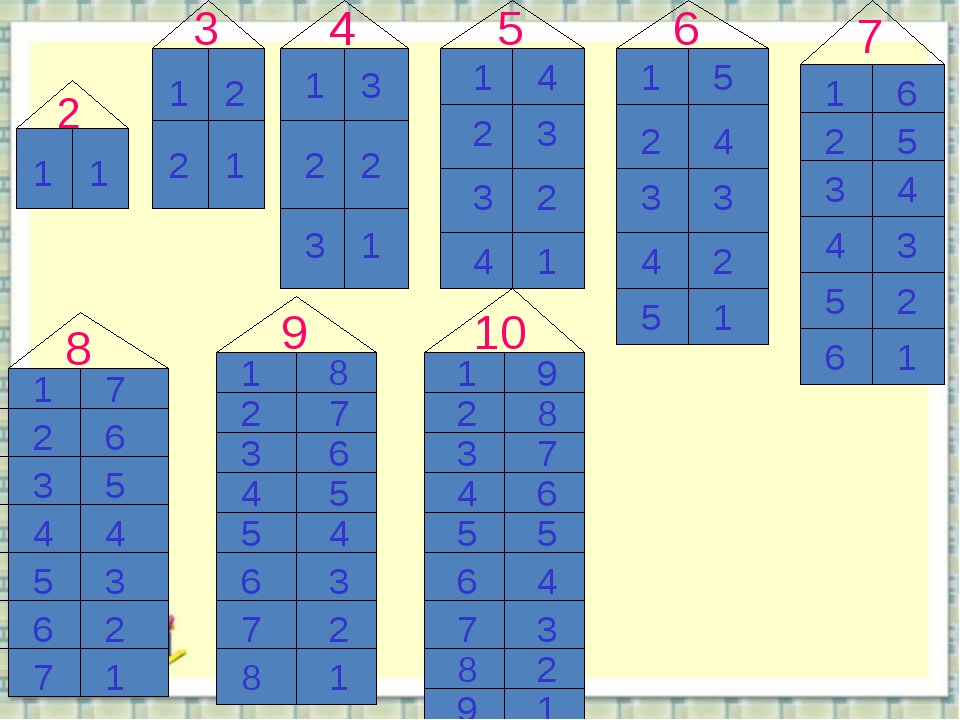
2) Ассоциативное свойство —
(a * b) * c = a * (b * c) ∀ a, b, c ∈ G
Пусть a = 1, b = ω и c = ω2
Так,
LHS = (a * b) * c
= (1 * ω) * ω 2 = ω 3 = 1
RHS = a * (b * c)
= 1 * (ω * ω 2 ) = ω 3 = 1
Следовательно, RHS = LHS Ассоциативное свойство также удовлетворяется
3) Свойство идентичности —
a * e = a ∀ a ∈ G e = identity = 1 (в случае умножения) 1 ∈ G Пусть a = 1 1 * 1 = 1 1 ∈ G Свойство идентичности тоже устраивает.
4) Обратное свойство —
Номер | Обратное |
|---|---|
1 | 1/1 = 1 | 9337
ω 2 | 1 / ω 2 = ω / ω 2 .ω = ω |
Здесь мы видим, что обратное значение 1 равно 1, обратное ω — ω2 и обратное ω2 — ω.
Эти инверсии принадлежат множеству G.
Итак, свойство Inverse также выполняется.
5) Коммутативное свойство —
a * b = b * a ∀ a, b ∈ G
Пусть a = 1, b = ω
LHS = а * б
= 1 * ω = ω
RHS = b * a
= ω * 1 = ω
LSH = RHS Коммутативное свойство также выполняется.
Мы видим, что все пять объектов недвижимости устраивают. Следовательно, три корня из единицы образуют конечную абелеву группу с операционным умножением.
Формирование таблицы композиции:
Шаг-1:
Запишите все элементы набора в строке и столбце и заданную операцию (*) в углу и умножьте элементы столбца на элемент строки один за другим и напишите его в строке, как показано на рисунке ниже.
Шаг 2:
После умножения каждого элемента столбца на элементы строки наша составная таблица будет выглядеть, как показано на рисунке ниже:
Шаг 3:
Мы знаем, что
ω 3 = 1 Итак, ω 4 = ω 3 .
ω = 1.ω = ω , поэтому наша таблица композиции становится
Шаг 4:
Нахождение инверсии элементов.
Нарисуйте горизонтальную и вертикальную линии от элементов идентичности в каждой строке, вертикальная линия представляет собой инверсию элементов строки, мы можем ясно видеть, что величина, обратная 1, равна 1, обратная величина ω — ω2, а обратная ω2 — ω.
Шаг-5:
Удовлетворяющие свойства абелевой группы из таблицы составов
- Мы видим, что в таблице составов все числа находятся в наборе G, следовательно, свойство замыкания выполняется.
- Мы видим, что все числа в таблице композиции принадлежат множеству G, следовательно, ассоциативное свойство выполняется.
- В таблице состава в каждой строке есть элемент идентичности 1, свойство идентичности выполнено.
- Мы видим, что обратное значение 1 равно 1, обратное ω — ω 2 и обратное ω 2 — ω. Все принадлежит множеству G, следовательно, также выполняется обратное свойство.
- Все числа в таблице составов принадлежат набору G, коммутативное свойство также выполняется.
Все принадлежит множеству G, следовательно, также выполняется обратное свойство.Следовательно, G = {1, ω, ω 2 } является абелевой группой относительно умножения.
Задача-2:
Задайте G = {1, -1, i, -i}, т.е. четыре корня из единицы, и сформируйте конечную абелеву группу относительно умножения.
Пояснение:
Четыре корня из единицы равны 1, -1, i, -i.Таким образом, наш набор будет иметь вид G = {1, -1, i, -i}
Operation = ‘*’ т.е. умножение.
Чтобы доказать, что четыре корня из единицы образуют конечную абелеву группу, мы должны удовлетворять следующим пяти свойствам: свойство замыкания, ассоциативное свойство, свойство идентичности, обратное свойство и коммутативное свойство.
1) Свойство замыкания —
∀ a, b ∈ G ⇒ a * b ∈ G a = i, b = -i ∈ G ⇒ я * (-i) = -i 2 = - (-1) = 1 ∈ G
Следовательно, свойство замыкания выполняется.
2) Ассоциативное свойство —
(a * b) * c = a * (b * c) ∀ a, b, c ∈ G
Пусть a = 1, b = -1 и c = i
Итак, LHS = (a * b) * c
= (1 * (-1)) * я = -i
RHS = a * (b * c)
= 1 * (-1 * я) = -i
Следовательно, RHS = LHS Ассоциативное свойство также удовлетворяется
3) Свойство идентичности —
a * e = a ∀ a ∈ G e = identity = 1 (в случае умножения) 1 ∈ G 1 * 1 = 1 1 ∈ G
Свойство идентичности также выполняется.
4) Обратное свойство —
a * (1 / a) = 1 ∀ a ∈ G, 1 / a ∈ G
Число | Обратное |
|---|---|
1 | 1/1 = 1 |
-1 | 1 / -1 = -1 |
i | 1 / i = i / ii = i / i 2 = -i |
-i | 1 / -i = i / -i.i = i / -i 2 = i |
Здесь мы видим, что обратное значение 1 равно 1, обратное -1 — 1, обратное значение i — -i и обратное значение -i — i.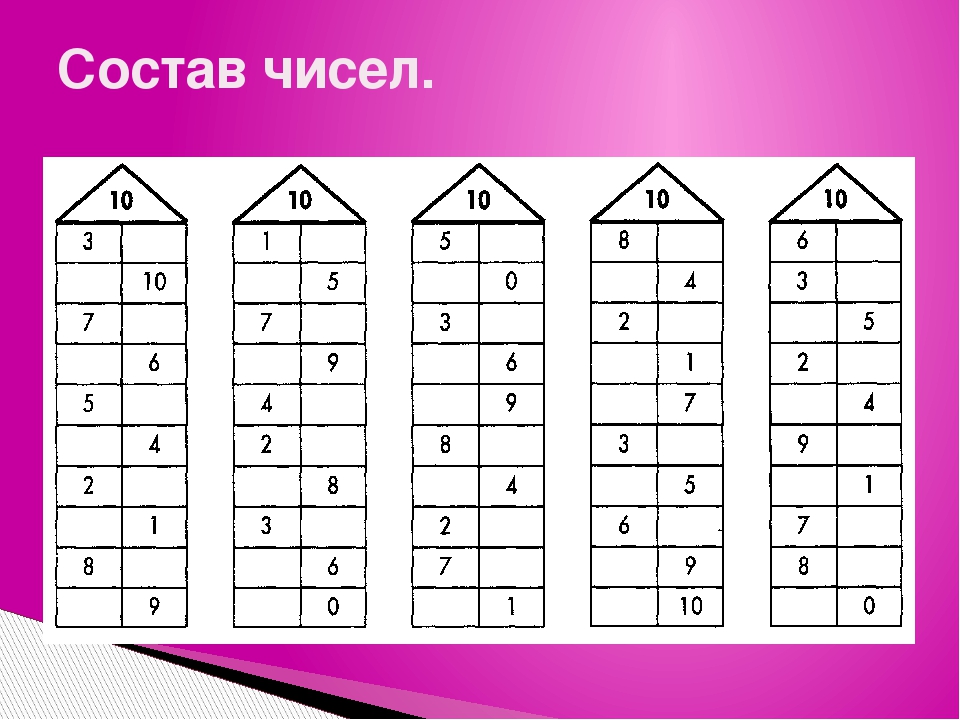
Эти инверсии принадлежат множеству G.
Итак, свойство Inverse также выполняется.
5) Коммутативное свойство —
a * b = b * a ∀ a, b ∈ G
Пусть a = 1, b = -1
LHS = а * б
= 1 * (-1) = -1
RHS = b * a
= 1 * (-1) = -1
LSH = RHS Коммутативное свойство также выполняется.
Мы видим, что все пять объектов недвижимости устраивают.Следовательно, четыре корня из единицы образуют конечную абелеву группу с операционным умножением.
СОСТАВ КОРМОВ | Таблицы состава кормов США и Канады: данные по питательности кормов США и Канады, третья редакция
К сожалению, эту книгу нельзя распечатать из OpenBook. Если вам нужно распечатать страницы из этой книги, мы рекомендуем загрузить ее в формате PDF.Посетите NAP.edu/10766, чтобы получить дополнительную информацию об этой книге, купить ее в печатном виде или загрузить в виде бесплатного PDF-файла.
«Предыдущая: ВВЕДЕНИЕ Предлагаемое цитирование: «СОСТАВ КОРМОВ».
Национальный исследовательский совет. 1982. США-Канадские таблицы состава кормов: данные по питательности кормов США и Канады, третья редакция . Вашингтон, округ Колумбия: The National Academies Press. DOI: 10.17226 / 1713.×
Ниже приведен неисправленный машинно-читаемый текст этой главы, предназначенный для предоставления нашим собственным поисковым системам и внешним машинам богатого, репрезентативного текста каждой книги с возможностью поиска по главам.Поскольку это НЕПРАВИЛЬНЫЙ материал, пожалуйста, рассматривайте следующий текст как полезный, но недостаточный прокси для авторитетных страниц книги.
СОСТАВ КОРМОВ 2 СОСТАВ КОРМОВ В таблицах 1–6 представлен состав основных кормов для США и Канады. Концентрации питательных веществ организованы как
следует:
Таблица 1 Энергетические значения, приблизительный анализ, состав стенок растительных клеток и клетчатка с кислотным детергентом
Таблица 2 Минеральный состав
Таблица 3 Витаминный состав
Таблица 4 Аминокислотные числа
Таблица 5 Содержание жиров и жирных кислот
Таблица 6 Состав минеральных добавок МЕЖДУНАРОДНАЯ НОМЕНКЛАТУРА КОРМОВ
Номенклатура кормов, в которой представлены аналитические данные, в первую очередь соответствует International Feed.
Словарь Харриса и др.(1980, 1981). Многие каналы в США имеют официальные названия и определения, обозначенные
Ассоциация американских чиновников по контролю за кормами (AAFCO, 1979). Однако часто эти имена являются обычными или торговыми.
имена и происхождение названия канала не соответствуют стандартизированной системе именования.
Международный словарь кормов разработан для того, чтобы дать каждому корму исчерпывающее название как можно более кратко.
Каждое имя канала было придумано с использованием дескрипторов, взятых из одного или нескольких из шести аспектов:
1.Происхождение, состоящее из научного названия (род, вид, разновидность) и общего названия (родовое название; порода или род; штамм или
химическая формула)
2. Часть, скармливаемая животным, пострадавшим от процесса (ов)
3. Процесс (ы) и обработка (я), которым подвергалась деталь.
4. Стадия зрелости или развития
5. Нарезка (применимо к кормовым растениям)
6. Оценка (официальные оценки с гарантиями)
В Таблице 7 указаны сроки созревания растений.
Полное международное имя канала состоит из всех дескрипторов, применимых к каналам.Определения для части и
дескрипторы процесса приведены Harris et al. (1981). МЕЖДУНАРОДНЫЕ КОРМОВЫЕ КЛАССЫ
Корма сгруппированы в восемь классов на основе их состава и их использования при составлении рационов (Таблица 8). Эти
классы по необходимости являются произвольными, и в пограничных случаях канал назначается классу в соответствии с его наиболее распространенным использованием в
типичная практика кормления. МЕЖДУНАРОДНЫЙ НОМЕР КОРМЫ (IFN)
Каждому международному названию корма присваивается пятизначный международный номер корма (IFN) для его идентификации.Этот
числовое представление является связующим звеном между международными названиями кормов и химическими и биологическими данными в США.
база данных. Цифры особенно полезны в качестве метки для вызова данных о питательных веществах для расчета рациона.
Номер класса корма
(Таблица 8) вводится перед IFN при составлении таблиц кормов.
Периодическая таблица элементов — Введение в химию — 1-е канадское издание
Дэвид В.Мяч
Глава 17 Приложение: Периодическая таблица элементов
В этой главе мы приводим некоторые данные о химических элементах. В периодической таблице, представленной в главе 3 «Атомы, молекулы и ионы», перечислены все известные химические элементы, упорядоченные по атомному номеру (то есть количеству протонов в ядре). Периодическая таблица Менделеева, возможно, лучший инструмент во всей науке; никакая другая отрасль науки не может резюмировать свои фундаментальные составляющие таким кратким и полезным образом.Многие физические и химические свойства элементов известны или понятны в зависимости от их положения в периодической таблице. Доступны периодические таблицы с различными химическими и физическими свойствами, указанными в поле каждого элемента.
Далее следует более сложная версия таблицы Менделеева, чем та, что была представлена в главе 3 «Атомы, молекулы и ионы». Интернет — отличное место для поиска периодических таблиц, содержащих дополнительную информацию.
Одним из пунктов большинства периодических таблиц является атомная масса каждого элемента.Для многих приложений для атомной массы необходимы только один или два десятичных знака. Однако в некоторых приложениях (особенно в ядерной химии; см. Главу 15 «Ядерная химия») требуется больше десятичных знаков. Атомные массы в Таблице 17.1 «Основы элементов Периодической таблицы» представляют количество десятичных знаков, признанных Международным союзом чистой и прикладной химии, всемирной организацией, которая разрабатывает стандарты по химии. Атомные массы некоторых элементов известны очень точно, с точностью до большого числа десятичных знаков.Атомные массы других элементов, особенно радиоактивных, точно не известны. Некоторые элементы, такие как литий, могут иметь различные атомные массы в зависимости от того, как изолированы их изотопы.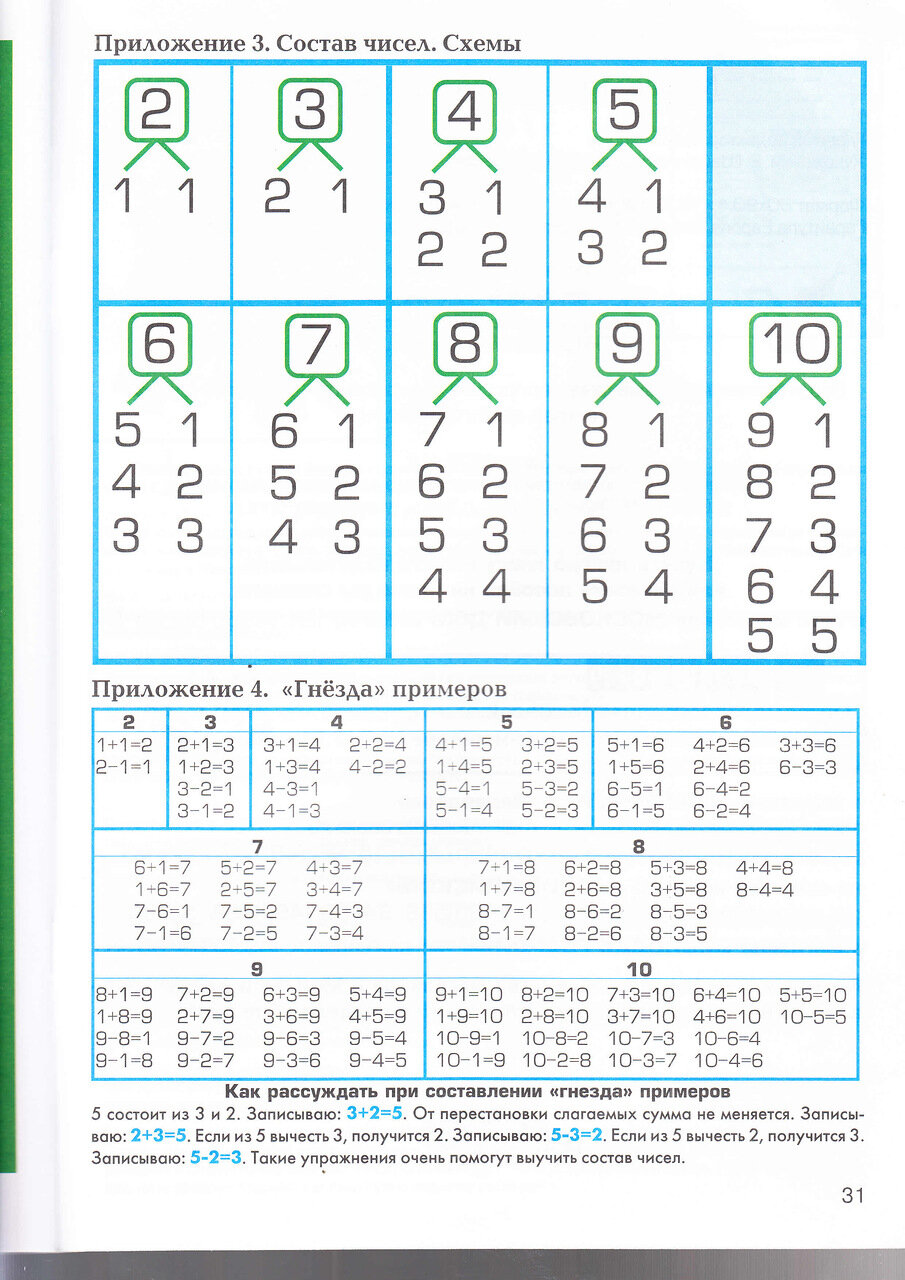
Интернет предлагает множество интерактивных ресурсов по периодической таблице. Например, см. Http://www.ptable.com.
Таблица 17.1 Основы элементов Периодической таблицы
| Имя | Атомный символ | Атомный номер | Атомная масса | Сноски | |
|---|---|---|---|---|---|
| актиний * | Ac | 89 | |||
| алюминий | Al | 13 | 26.9815386 (8) | ||
| америций * | Am | 95 | |||
| сурьма | Сб | 51 | 121,760 (1) | г | |
| аргон | Ar | 18 | 39,948 (1) | г, р | |
| мышьяк | как | 33 | 74. (2) | ||
| астатин * | в | 85 | |||
| барий | Ba | 56 | 137. 327 (7) | ||
| берклий * | Bk | 97 | |||
| бериллий | Be | 4 | 9.012182 (3) | ||
| висмут | Bi | 83 | 208.98040 (1) | ||
| бориум * | Bh | 107 | |||
| бор | B | 5 | 10.811 (7) | г, м, r | |
| бром | Br | 35 | 79,904 (1) | ||
| кадмий | КД | 48 | 112.411 (8) | г | |
| цезий (цезий) | CS | 55 | 132. | 19 (2) | |
| кальций | Ca | 20 | 40,078 (4) | г | |
| калифорний * | Cf | 98 | |||
| углерод | С | 6 | 12. 0107 (8) | г, р | |
| церий | Ce | 58 | 140,116 (1) | г | |
| хлор | класс | 17 | 35,453 (2) | г, м, r | |
| хром | Cr | 24 | 51,9961 (6) | ||
| кобальт | Co | 27 | 58.933195 (5) | ||
| коперниций * | Cn | 112 | |||
| медь | Cu | 29 | 63.546 (3) | г | |
| кюрий * | см | 96 | |||
| дармштадтиум * | DS | 110 | |||
| дубний * | Db | 105 | |||
| диспрозий | Dy | 66 | 162 500 (1) | г | |
| эйнштейний * | Es | 99 | |||
| эрбий | Er | 68 | 167. 259 (3) | г | |
| европий | Eu | 63 | 151,964 (1) | г | |
| фермий * | FM | 100 | |||
| фтор | F | 9 | 18.9984032 (5) | ||
| франций * | Fr | 87 | |||
| гадолиний | Gd | 64 | 157.25 (3) | г | |
| галлий | Ga | 31 | 69,723 (1) | ||
| германий | Ge | 32 | 72,64 (1) | ||
| золото | Au | 79 | 196.966569 (4) | ||
| гафний | Hf | 72 | 178,49 (2) | ||
| хассий * | HS | 108 | |||
| гелий | He | 2 | 4. 002602 (2) | г, р | |
| гольмий | Ho | 67 | 164,9 3032 (2) | ||
| водород | H | 1 | 1,00794 (7) | г, м, r | |
| индий | В | 49 | 114,818 (3) | ||
| йод | I | 53 | 126. (3) | ||
| иридий | Ir | 77 | 192.217 (3) | ||
| утюг | Fe | 26 | 55,845 (2) | ||
| криптон | Кр | 36 | 83,798 (2) | г, м | |
| лантан | Ла | 57 | 138. (7) | г | |
| лоуренсий * | Lr | 103 | |||
| свинец | Пб | 82 | 207.2 (1) | г, р | |
| литий | Li | 3 | [6,941 (2)] † | г, м, r | |
| лютеций | Лю | 71 | 174,967 (1) | г | |
| магний | мг | 12 | 24,3050 (6) | ||
| марганец | Мн | 25 | 54. 938045 (5) | ||
| мейтнерий * | Mt | 109 | |||
| менделевий * | Md | 101 | |||
| ртуть | Hg | 80 | 200.59 (2) | ||
| молибден | Пн | 42 | 95,94 (2) | г | |
| неодим | Nd | 60 | 144,242 (3) | г | |
| неон | Ne | 10 | 20,1797 (6) | г, м | |
| нептуний * | Np | 93 | |||
| никель | Ni | 28 | 58.6934 (2) | ||
| ниобий | Nb | 41 | 92. | (2)||
| азот | N | 7 | 14,0067 (2) | г, р | |
| нобелий * | № | 102 | |||
| осмий | Os | 76 | 190,23 (3) | г | |
| кислород | O | 8 | 15. 9994 (3) | г, р | |
| палладий | Pd | 46 | 106,42 (1) | г | |
| фосфор | -П, | 15 | 30,973762 (2) | ||
| платина | Pt | 78 | 195.084 (9) | ||
| плутоний * | Pu | 94 | |||
| полоний * | Po | 84 | |||
| калий | К | 19 | 39.0983 (1) | ||
| празеодим | Pr | 59 | 140. | (2) | |
| прометий * | PM | 61 | |||
| протактиний * | Па | 91 | 231.03588 (2) | ||
| радий * | Ra | 88 | |||
| радон * | Rn | 86 | |||
| рентген * | Rg | 111 | |||
| рений | Re | 75 | 186. 207 (1) | ||
| родий | Rh | 45 | 102, | ||
| рубидий | руб. | 37 | 85,4678 (3) | г | |
| рутений | Ру | 44 | 101,07 (2) | г | |
| резерфорд * | Rf | 104 | |||
| самарий | см | 62 | 150.36 (2) | г | |
| скандий | SC | 21 | 44.955912 (6) | ||
| сиборгий * | Sg | 106 | |||
| селен | SE | 34 | 78,96 (3) | г | |
| кремний | Si | 14 | 28,0855 (3) | г | |
| серебро | Ag | 47 | 107.8682 (2) | г | |
| натрий | Na | 11 | 22. 98976928 (2) | ||
| стронций | Sr | 38 | 87,62 (1) | г, р | |
| сера | S | 16 | 32,065 (5) | г, р | |
| тантал | Ta | 73 | 180.94788 (2) | ||
| технеций * | TC | 43 | |||
| теллур | Te | 52 | 127.60 (3) | г | |
| тербий | ТБ | 65 | 158, | (2) | |
| таллий | Tl | 81 | 204,3833 (2) | ||
| торий * | Чт | 90 | 232.03806 (2) | г | |
| тулий | ТМ | 69 | 168,9 3421 (2) | ||
| банка | Sn | 50 | 118.710 (7) | г | |
| титан | Ti | 22 | 47,867 (1) | ||
| вольфрам | Вт | 74 | 183,84 (1) | ||
| унунгексий * | Uuh | 116 | |||
| унунокций * | Uuo | 118 | |||
| унунпентиум * | Uup | 115 | |||
| унункадиум * | Uuq | 114 | |||
| унантриум * | Уут | 113 | |||
| уран * | U | 92 | 238. 02891 (3) | г, м | |
| ванадий | В | 23 | 50,9415 (1) | ||
| ксенон | Xe | 54 | 131,293 (6) | г, м | |
| иттербий | Yb | 70 | 173,04 (3) | г | |
| иттрий | Y | 39 | 88, (2) | ||
| цинк | Zn | 30 | 65.409 (4) | ||
| цирконий | Zr | 40 | 91,224 (2) | г | |
| * Элемент не содержит стабильных нуклидов. Однако три таких элемента (Th, Pa и U) имеют характерный земной изотопный состав, и для них атомная масса сведена в таблицу. | |||||
† Имеющиеся в продаже материалы Li имеют атомный вес в диапазоне от 6,939 до 6,996; если требуется более точное значение, оно должно быть определено для конкретного материала. | |||||
| г Известны геологические образцы, в которых изотопный состав элемента выходит за пределы нормального материала. Разница между атомной массой элемента в таких образцах и массой, приведенной в таблице, может превышать указанную погрешность. | |||||
| m Модифицированные изотопные композиции могут быть обнаружены в коммерчески доступном материале, поскольку он был подвергнут нераскрытому или непреднамеренному изотопному фракционированию. Возможны существенные отклонения атомной массы элемента от указанной в таблице. | |||||
| r Диапазон изотопного состава нормального земного материала не позволяет дать более точное значение A r (E); Табличные значения A r (E) и погрешность должны применяться к нормальному материалу. | |||||
Источник: по материалам Pure and Applied Chemistry 78, no. 11 (2005): 2051–66. © IUPAC (Международный союз теоретической и прикладной химии).
Просматривайте пользователей по общим свойствам — Amplitude
Эта статья поможет вам:
|
На диаграмме «Состав пользователей» показано распределение активных пользователей на основе одного свойства пользователя.Это сгруппированное представление дает представление о том, кто ваши пользователи и какими свойствами они обладают.
Прежде чем начать
Прежде всего, события не будут отображаться ни на каких диаграммах амплитуды до тех пор, пока инструменты не будут завершены, поэтому убедитесь, что вы это сделали. Вы обязательно захотите прочитать нашу статью о построении диаграмм в Amplitude, так как именно здесь вы узнаете основы пользовательского интерфейса Amplitude.
Вам также следует ознакомиться с нашим полезным списком определений Amplitude и убедиться, что вы понимаете разницу между свойствами пользователя и свойствами события.
Настройка анализа состава пользователей
Большинство диаграмм Amplitude полагаются на модуль событий для построения анализа. Диаграмма состава пользователей не является анализом, управляемым событиями, и поэтому в ней нет модуля событий, поэтому она работает немного иначе.
Вместо событий анализ состава пользователей опирается на пользовательских свойства . Выберите свойство пользователя, которое вас интересует, определите свои пользовательские сегменты, и диаграмма «Состав пользователей» отобразит разбивку значений этого свойства по указанным вами пользовательским сегментам.
В приведенном выше примере мы смотрим на сравнение пользователей вашего продукта в США и Германии с разбивкой по самому последнему значению количества сообществ, к которым они присоединились.
Чтобы построить собственный анализ состава пользователей, выполните следующие действия:
- В модуле композиции (где обычно находится модуль событий) выберите интересующее вас свойство пользователя.
- В модуле сегментации укажите сегмент пользователей, который вы хотите включить в этот анализ.Вы можете импортировать ранее сохраненный сегмент, щелкнув Сохраненные сегменты и выбрав нужный из списка. В противном случае Amplitude исходит из предположения, что ваш анализ будет нацелен на всех пользователей.
- Если вы не хотите импортировать ранее сохраненный пользовательский сегмент, вы можете начать создавать свой собственный, добавляя свойства. Для этого нажмите +, где , выберите свойство, которое вы хотите включить, и укажите значение свойства, которое вас интересует.
- Вы можете еще больше сузить фокус, указав Amplitude, что вы хотите включать только пользователей, которые уже выполнили определенные действия. Для этого нажмите + выполнить , затем выберите интересующее вас мероприятие.
- При желании добавьте еще один сегмент пользователя, нажав + Добавить сегмент и повторив шаги 3 и 4.
- Используйте средство выбора даты, чтобы установить период времени для анализа.
- В модуле метрик укажите для свойства пользователя значения , которые вам наиболее интересны:
Для этого нажмите + выполнить , затем выберите интересующее вас мероприятие.- Самое последнее значение будет учитывать только последних значения этого свойства пользователями. Это значение будет взято из последнего активного события пользователя. Например, пользователи, содержащиеся в корзине San Francisco ниже, — это те пользователи, которые в последний раз использовали это значение для свойства пользователя «[Amplitude] City» при выполнении последнего активного события:
Пользователи могут появляться только в одной ведро, когда выбрано самое последнее значение. - Все значения будет включать каждое значение , полученное вашими пользователями для рассматриваемого свойства в течение периода времени вашего анализа.Например, на приведенной выше диаграмме любые пользователи, которые запускали инструментальное событие Amplitude из Сан-Франциско и Нью-Йорка за последние 30 дней, будут включены в обоих сегментов .
- Значения перекрестных свойств покажут наборы свойств, которые пользователи имели в выбранном временном диапазоне. Эти корзины исключают друг друга; пользователи могут попасть только в одну корзину. Таблица ниже показывает, что большинство пользователей используют наш продукт только на одной платформе:
- Самое последнее значение будет учитывать только последних значения этого свойства пользователями. Это значение будет взято из последнего активного события пользователя. Например, пользователи, содержащиеся в корзине San Francisco ниже, — это те пользователи, которые в последний раз использовали это значение для свойства пользователя «[Amplitude] City» при выполнении последнего активного события:
Во всех случаях Amplitude будет выделять 13 лучших значений для вашего пользовательского свойства; любые другие значения будут сгруппированы в сегменте Другое .Значение в центре диаграммы — это значение суммы столбца в таблице данных разбивки; он включает только тех пользователей, которые входят в 100 самых популярных групп значений свойств пользователей по количеству пользователей.
Вы также можете просмотреть свои результаты в виде гистограммы:
И, конечно же, вы всегда можете проверить состав ваших групп пользователей с помощью микроскопа.
Таблица данных разбивки
Под диаграммой находится таблица данных о составе. В этой таблице перечислены 100 самых популярных значений свойств пользователей с наибольшим количеством пользователей.Сумма в столбце Поле внизу таблицы совпадает с суммой в центре диаграммы.
Вы также можете экспортировать таблицу как файл .CSV, нажав Экспорт CSV . Файл .CSV имеет ограничение в 10 000 строк; это означает, что с помощью CSV вы можете получить 10 000 самых популярных значений свойств пользователей по количеству пользователей.
Воздух — состав и молекулярный вес
Компоненты в сухом воздухе
Воздух представляет собой смесь нескольких газов, где двумя наиболее доминирующими компонентами в сухом воздухе являются 21 об.
% Кислорода и 78 об.% азот .Кислород имеет молярную массу 15,9994 г / моль, а азот имеет молярную массу 14,0067 г / моль. Поскольку оба эти элемента являются двухатомными в воздухе — O 2 и N 2 , молярная масса газообразного кислорода составляет 32 г / моль, а молярная масса газообразного азота составляет 28 г / моль.
Средняя молярная масса равна сумме мольных долей каждого газа, умноженной на молярную массу этого конкретного газа:
M смесь = (x 1 * M 1 +…… + x n * M n ) (1)
, где
x i = мольные доли каждого газа
M i = молярная масса каждого газа
молярная масса сухого воздуха 28,9647 г / моль. Состав и содержание каждого газа в воздухе показано на рисунках и в таблице ниже.
См.
Также Воздух Плотность при переменном давлении, Плотность и удельный вес при переменной температуре, Коэффициенты диффузии газов в воздухе, Динамическая (абсолютная) и кинематическая вязкость, Число Прандтля, Удельная теплоемкость при переменной температуре и Удельная теплоемкость при переменном давлении, теплопроводности, теплопроводности, свойствах в условиях газожидкостного равновесия и свойствах воздуха, для других свойств воздуха
Воздух обычно моделируется как однородный (без изменений или флуктуаций) газ со свойствами, усредненными из отдельные компоненты.
Для полного стола — поворот экрана!
| Компоненты в сухом воздухе | Объемное отношение = Молярное соотношение по сравнению с сухим воздухом | Молярная масса | Молярная масса в воздухе | Точка кипения | |||||||||||||||||||||||||||||
| Имя | Формула | [моль / моль воздух ] | [об. %] | [г / моль], [кг / кмоль] | 9017 9017 г / моль воздух ], [кг / кмоль воздух ] | [вес.%] | [K] | [° C] | [° F] | ||||||||||||||||||||||||
| Азот | N 2 | 0.78084 | 78,084 | 28,013 | 21,872266 | 75,511 | 77,4 | -195,8 | -320,4 | ||||||||||||||||||||||||
| Кислород | O 2 | 0.20946 | 0,20946 | 90,2 | -183,0 | -297,3 | |||||||||||||||||||||||||||
| Аргон | Ar | 0,00934 | 0,934 | 39,948 | 0.373025 | 1,29 | 87,3 | -185,8 | -302,5 | ||||||||||||||||||||||||
| Углекислый газ 1) | CO 2 | 0,000412 | 0,0412 | 44,010733 | -78,5 | -109,2 | |||||||||||||||||||||||||||
| Neon | Ne | 0,00001818 | 0,001818 | 20,180 | 0,000367 | 0. 0013 | 27,2 | -246,0 | -410,7 | ||||||||||||||||||||||||
| Гелий | He | 0,00000524 | 0,000524 | 4,003 | 0,000021 | 0,00007 | 4,2197 | 20,00007 | 4,2197 | CH 4 | 0,00000179 | 0,000179 | 16,042 | 0,000029 | 0,00010 | 111,7 | -161.5 | -258,7 | |||||||||||||||
| Криптон | Kr | 0,0000010 | 0,0001 | 83,798 | 0,000084 | 0,00029 | 119,8 | -153,4 | –244,0 | 9237 926 926 Водород 922 9220,0000005 | 0,00005 | 2,016 | 0,000001 | 0,000003 | 20,3 | -252,9 | -423,1 | ||||||||||||||||
| Ксенон | Xe | 0.00000009 | 0,000009 | 131,293 | 0,000012 | 0,00004 | 165,1 | -108,1 | -162,5 | ||||||||||||||||||||||||
| Средняя молярная масса воздуха | 28,964620 10 По данным NASA COпо уровню 2 в 1960 ок. 320 частей на миллион, 1970 ок. 328 частей на миллион, ок. 1980 г. 341 частей на миллион, прибл. 356 частей на миллион, 2000 прибл. 372 частей на миллион, прибл. 390 частей на миллион и прибл.412 ppmВернуться к началу
Другие компоненты в воздухе
Стандартные единицы давления, часто используемые в качестве альтернативы до «одной атмосферы»
таблица Менделеева | Определение, элементы, группы, сборы, тенденции и факты Изучите периодический закон химии, чтобы понять свойства элементов и их взаимосвязь. Объяснение таблицы Менделеева. Encyclopædia Britannica, Inc. Посмотреть все видео для этой статьиПериодическая таблица , полностью периодическая таблица элементов , в химии организованный массив всех химических элементов в порядке возрастания атомного номера, т. Е. общее количество протонов в атомном ядре. Когда химические элементы расположены таким образом, в их свойствах возникает повторяющийся образец, называемый «периодическим законом», в котором элементы в одном столбце (группе) имеют схожие свойства.Первоначальное открытие, сделанное Дмитрием И. Менделеевым в середине XIX века, имело неоценимое значение для развития химии. таблица МенделееваСовременная версия периодической таблицы элементов (для печати). Encyclopædia Britannica, Inc.Популярные вопросы Что такое периодическая таблица Менделеева?Что общего у групп периодической таблицы? Группы периодической таблицы отображаются в виде вертикальных столбцов, пронумерованных от 1 до 18. Откуда взялась периодическая таблица Менделеева?Расположение элементов в периодической таблице определяется их электронной конфигурацией. Из-за принципа исключения Паули не более двух электронов могут заполнить одну и ту же орбиталь. Первый ряд периодической таблицы состоит всего из двух элементов: водорода и гелия.Поскольку у атомов больше электронов, у них появляется больше орбит, доступных для заполнения, и поэтому строки содержат больше элементов, расположенных ниже в таблице. Почему периодическая таблица Менделеева разделяется? У периодической таблицы есть две строки внизу, которые обычно отделяются от основной части таблицы. Эти ряды содержат элементы ряда лантаноидов и актиноидов, обычно от 57 до 71 (от лантана до лютеция) и от 89 до 103 (от актиния до лоуренсия), соответственно. Фактически не было признано до второго десятилетия 20-го века, что порядок элементов в периодической системе соответствует порядку их атомных номеров, целые числа которых равны положительным электрическим зарядам атомных ядер, выраженным в электронных единицах. . В последующие годы был достигнут большой прогресс в объяснении периодического закона с точки зрения электронного строения атомов и молекул. Это разъяснение повысило ценность закона, который используется сегодня так же активно, как и в начале 20 века, когда он выражал единственную известную взаимосвязь между элементами. История периодического закона В первые годы XIX века произошло быстрое развитие аналитической химии — искусства различения различных химических веществ — и, как следствие, накопление обширных знаний о химических и физических свойствах как элементы, так и соединения. Столь быстрое расширение химических знаний вскоре потребовало классификации, поскольку на классификации химических знаний основана не только систематизированная химическая литература, но и лабораторные науки, благодаря которым химия передается как живая наука от одного поколения химиков к другому. Современная версия периодической таблицы элементов. Чтобы узнать название элемента, атомный номер, конфигурацию электронов, атомный вес и многое другое, выберите элемент из таблицы. Encyclopædia Britannica, Inc. J.W. Доберейнер в 1817 году показал, что объединяющий вес, означающий атомный вес, стронция находится посередине между весом кальция и бария, а несколько лет спустя он показал, что существуют другие такие «триады» (хлор, бром и йод [галогены] и литий, натрий и калий [щелочные металлы]). Ж.-Б.-А. Дюма, Л. Гмелин, Э. Ленссен, Макс фон Петтенкофер и Дж. П. Кук расширили предложения Доберейнера между 1827 и 1858 годами, показав, что аналогичные отношения простираются дальше, чем триады элементов: фтор добавляется к галогенам, а магний — к щелочноземельным элементам. Позднее были предприняты попытки показать, что атомные веса элементов могут быть выражены арифметической функцией, и в 1862 году А.-Э.-Б. де Шанкуртуа предложил классификацию элементов, основанную на новых значениях атомных весов, данных системой Станислао Канниццаро 1858 года. Де Шанкуртуа нанес атомные веса на поверхность цилиндра с окружностью 16 единиц, что соответствует приблизительному атомному весу кислород.Получившаяся спиральная кривая привела к тому, что тесно связанные элементы оказались в соответствующих точках выше или ниже друг друга на цилиндре, и, как следствие, он предположил, что «свойства элементов являются свойствами чисел», что является замечательным предсказанием в свете современных знаний. Классификация элементов В 1864 году J. | ||||||||||||||||||||||||||||||||
01 частей / миллион (ppm)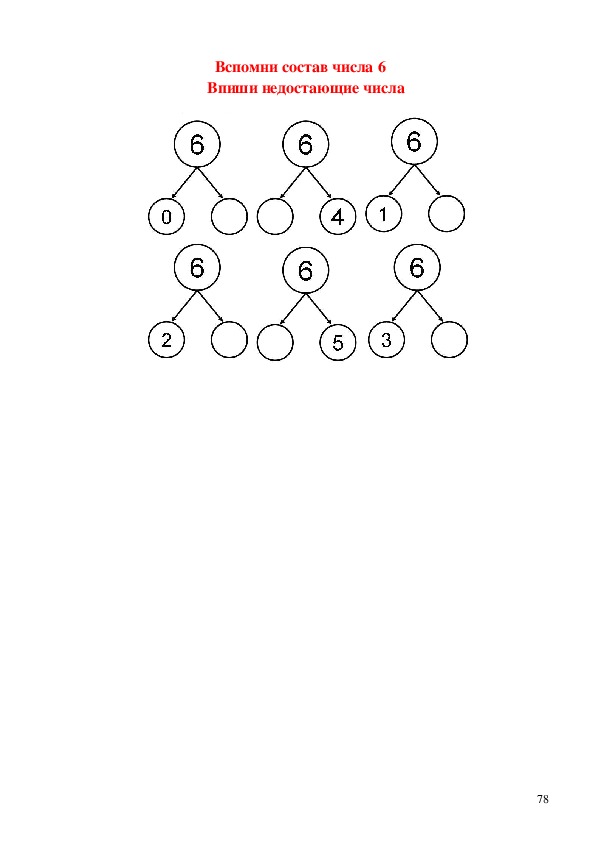 
Элементы в группе имеют очень похожие химические свойства, которые возникают из количества присутствующих валентных электронов, то есть количества электронов во внешней оболочке атома.
Для этого нет никаких научных причин.Это сделано только для того, чтобы стол стал более компактным.
Связи между соединениями обнаруживались легче, чем между элементами; так получилось, что классификация элементов на много лет отстала от классификации соединений. Фактически, между химиками не было достигнуто общего согласия относительно классификации элементов в течение почти полувека после того, как системы классификации соединений стали общепринятыми.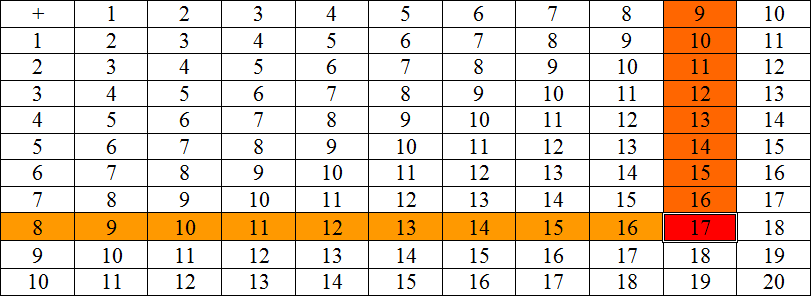
металлы, тогда как кислород, сера, селен и теллур были отнесены к одному семейству, а азот, фосфор, мышьяк, сурьма и висмут — к другому семейству элементов.